Dimension Reduction by Random Hyperplane Tessellations

Abstract

Given a subset K of the unit Euclidean sphere, we estimate the minimal number m=m(K) of hyperplanes that generate a uniform tessellation of K, in the sense that the fraction of the hyperplanes separating any pair x,y∈K is nearly proportional to the Euclidean distance between x and y. Random hyperplanes prove to be almost ideal for this problem; they achieve the almost optimal bound m=O(w(K)²) where w(K) is the Gaussian mean width of K. Using the map that sends x∈K to the sign vector with respect to the hyperplanes, we conclude that every bounded subset K of $\mathbb{R}^{n}$ embeds into the Hamming cube {−1,1}^m with a small distortion in the Gromov–Haussdorff metric. Since for many sets K one has m=m(K)≪n, this yields a new discrete mechanism of dimension reduction for sets in Euclidean spaces.

1 Introduction

Consider a bounded subset K of $\mathbb{R}^{n}$. We would like to find an arrangement of m affine hyperplanes in $\mathbb{R}^{n}$ that cut through K as evenly as possible; see Fig. 1 for an illustration. The intuitive notion of an “even cut” can be expressed more formally in the following way: The fraction of the hyperplanes separating any pair x,y∈K should be proportional (up to a small additive error) to the Euclidean distance between x and y. What is the smallest possible number m=m(K) of hyperplanes with this property? Besides having a natural theoretical appeal, this question is directly motivated by a certain problem of information theory, which we will describe later.

Fig. 1

A hyperplane tessellation of a set in the plane

In the beginning, it will be most convenient to work with subsets K of the unit Euclidean sphere S ⁿ⁻¹, but we will lift this restriction later. Let d(x,y) denote the normalized geodesic distance on S ⁿ⁻¹, so the distance between the opposite points on the sphere equals 1. A (linear) hyperplane in $\mathbb{R}^{n}$ can be expressed as a ^⊥ for some $a \in\mathbb{R}^{n}$. We say that points $x,y \in\mathbb{R}^{n}$ are separated by the hyperplane¹ if $\operatorname{sign}\langle a,x\rangle\ne\operatorname {sign}\langle a,y\rangle$.

Definition 1.1

(Uniform tessellation)

Consider a subset K⊆S ⁿ⁻¹ and an arrangement of m hyperplanes in $\mathbb{R}^{n}$. Let d _A (x,y) denote the fraction of the hyperplanes that separate points x and y in $\mathbb{R}^{n}$. Given δ>0, we say that the hyperplanes provide a δ-uniform tessellation of K if

$$ \bigl| d_A(x,y) - d(x,y) \bigr| \le\delta, \quad x,y \in K. $$

(1.1)

The main result of this paper is a bound on the minimal number m=m(K,δ) of hyperplanes that provide a uniform tessellation of a set K. It turns out that for a fixed accuracy δ, an almost optimal estimate on m depends only on one global parameter of K, namely the mean width. Recall that the Gaussian mean width of K is defined as

$$ w(K) = \mathbb{E}\sup_{x \in K} \bigl|\langle g,x \rangle\bigr|, $$

(1.2)

where $g \sim\mathcal{N}(0, I_{n})$ is a standard Gaussian random vector in $\mathbb{R}^{n}$.

Theorem 1.2

(Random uniform tessellations)

Consider a subset K⊆S ⁿ⁻¹ and let δ>0. Let

$$m \ge C \delta^{-6} w(K)^2 $$

and consider an arrangement of m independent random hyperplanes in $\mathbb{R}^{n}$ uniformly distributed according to the Haar measure. Then with probability at least 1−2exp(−cδ ² m), these hyperplanes provide a δ-uniform tessellation of K. Here and later, C,c denote positive absolute constants.

Remark 1.3

(Tessellations in stochastic geometry)

By the rotation invariance of the Haar measure, it easily follows that $\mathbb{E}d_{A}(x,y) = d(x,y)$ for each pair $x,y \in\mathbb{R}^{n}$. Theorem 1.2 states that with high probability, d _A (x,y) almost matches its expected value uniformly over all x,y∈K. This observation highlights the principal difference between the problems studied in this paper and the classical problems on random hyperplane tessellations studied in stochastic geometry. The classical problems concern the shape of a specific cell (usually the one containing the origin) or certain statistics of cells (e.g., “how many cells have volume greater than a fixed number”?); see [7]. In contrast to this, the concept of uniform tessellation we propose his paper concerns all cells simultaneously; see Sect. 1.5 for a vivid illustration.

1.1 Embeddings into the Hamming Cube

Theorem 1.2 has an equivalent formulation in the context of metric embeddings. It yields that every subset K⊆S ⁿ⁻¹ can be almost isometrically embedded into the Hamming cube {−1,1}^m with m=O(w(K)²).

To explain this statement, let us recall a few standard notions. An ε-isometry (or almost isometry) between metric spaces (X,d _X ) and (Y,d _Y ) is a map f:X→Y, which satisfies

$$\bigl| d_Y\bigl(f(x),f\bigl(x'\bigr)\bigr) - d_X\bigl(x,x'\bigr) \bigr| \le\varepsilon, \quad x,x' \in X, $$

and such that for every y∈Y one can find x∈X satisfying d _Y (y,f(x))≤ε. A map f:X→Y is an ε-isometric embedding of X into Y if the map f:X→f(X) is an ε-isometry between (X,d _X ) and the subspace (f(X),d _Y ). It is not hard to show that X can be 2ε-isometrically embedded into Y (by means of a suitable map f) if X has the Gromov–Haussdorff distance at most ε from some subset of Y. Conversely, if there is an ε-isometry between X and f(X) then the Gromov–Haussdorff distance between X and f(X) is bounded by ε.

Finally, recall that the Hamming cube is the set {−1,1}^m with the (normalized) Hamming distance the fraction of the coordinates where u and v are different.

An arrangement of m hyperplanes in $\mathbb{R}^{n}$ defines a sign map $f : \mathbb{R}^{n} \to\{-1,1\}^{m}$, which sends $x \in\mathbb{R}^{n}$ to the sign vector of the orientations of x with respect to the hyperplanes. The sign map is uniquely defined up to the isometries of the Hamming cube. Let $a_{1},\ldots, a_{m} \in\mathbb{R}^{n}$ be normals of the hyperplanes, and consider the m×n matrix A with rows a _i . The sign map can be expressed as

$$f(x) = \operatorname{sign}Ax, \quad f: \mathbb{R}^n \to\{-1,1 \}^m, $$

where $\operatorname{sign}Ax$ denotes the vector of signs of the coordinates 〈a _i ,x〉 of Ax. The fraction d _A (x,y) of the hyperplanes that separate points x and y thus equals

$$d_A(x,y) = d_H(\operatorname{sign}Ax, \operatorname{sign}Ay), \quad x,y \in\mathbb{R}^n. $$

Then looking back at the definition of uniform tessellations, we observe the following fact:

Fact 1.4

(Embeddings by uniform tessellations)

Consider a δ-uniform tessellation of a set K⊆S ⁿ⁻¹ by m hyperplanes. Then the set K (with the induced geodesic distance) can be δ-isometrically embedded into the Hamming cube {−1,1}^m. The sign map provides such an embedding.

This allows us to state Theorem 1.2 as follows.

Theorem 1.5

(Embeddings into the Hamming cube)

Consider a subset K⊆S ⁿ⁻¹ and let δ>0. Let

$$m \ge C \delta^{-6} w(K)^2. $$

Then K can be δ-isometrically embedded into the Hamming cube {−1,1}^m.

Moreover, let A be an m×n random matrix with independent $\mathcal{N}(0,1)$ entries. Then with probability at least 1−2exp(−cδ ² m), the sign map

$$ f(x) = \operatorname{sign}Ax, \quad f : K \to\{-1,1 \}^m $$

(1.3)

is an δ-isometric embedding.

1.2 Almost Isometry of K and the Tessellation Graph

The image of the sign map f in (1.3) has a special meaning. When the Hamming cube {−1,1}^m is viewed as a graph (in which two points u, v are connected if they differ in exactly one coordinate), the image of f defines a subgraph of {−1,1}^m, which is called the tessellation graph of K. The tessellation graph has a vertex for each cell and an edge for each pair of adjacent cells; see Fig. 2. Notice that the graph distance in the tessellation graph equals the number of hyperplanes that separate the two cells. Therefore, the definition of a uniform tessellation yields the following.

Fig. 2

The graph of a tessellation of a set in the plane. The dashed lines represent the edges

Fact 1.6

(Graphs of uniform tessellations)

Consider a δ-uniform tessellation of a set K⊆S ⁿ⁻¹. Then K is δ-isometric to the tessellation graph of K.

Hence, we can read the conclusion of Theorem 1.2 as follows: K is δ-isometric to the graph of its tessellation by m random hyperplanes, where m∼δ ⁻⁶ w(K)².

1.3 Computing Mean Width

Powerful methods to estimate the mean width w(K) have been developed in connection with stochastic processes. These methods include Sudakov’s and Dudley’s inequalities, which relate w(K) to the covering numbers of K in the Euclidean metric, and the sharp technique of majorizing measures (see [15, 22]).

Mean width has a simple (and known) geometric interpretation. By the rotational invariance of the Gaussian random vector g in (1.2), one can replace g with a random vector θ that is uniformly distributed on S ⁿ⁻¹, as follows:

$$w(K) = c_n \sqrt{n} \cdot\bar{w}(K), \quad\text{where } \bar{w}(K) = \mathbb{E}\sup_{x \in K} \bigl|\langle\theta,x\rangle\bigr|. $$

Here, c _n are numbers that depend only on n and such that c _n ≤1 and lim _n→∞ c _n =1. We may refer to $\bar{w}(K)$ as the spherical mean width of K. Let us assume for simplicity that K is symmetric with respect to the origin. Then 2sup _x∈K |〈θ,x〉| is the width of K in the direction θ, which is the distance between the two supporting hyperplanes of K whose normals are θ. The spherical mean width $\bar{w}(K)$ is then twice the average width of K over all directions.

1.4 Dimension Reduction

Our results are already non-trivial in the particular case K=S ⁿ⁻¹. Since $w(S^{n-1}) \le\sqrt{n}$, Theorems 1.2 and 1.5 hold with m∼n. But more importantly, many interesting sets K⊂S ⁿ⁻¹ satisfy $w(K) \ll\sqrt{n}$ and, therefore, make our results hold with m∼w(K)²≪n. In such cases, one can view the sign map $f(x) = \operatorname {sign}Ax$ in Theorem 1.5 as a dimension reduction mechanism that transforms an n-dimensional set K into a subset of {−1,1}^m.

A heuristic reason why dimension reduction is possible is that the quantity w(K)² measures the effective dimension of a set K⊆S ⁿ⁻¹. The effective dimension w(K)² of a set K⊆S ⁿ⁻¹ is always bounded by the algebraic dimension, but it may be much smaller and it is robust with respect to perturbations of K. In this regard, the notion of effective dimension is parallel to the notion of effective rank of a matrix from numerical linear algebra (see e.g. [20]). With these observations in mind, it is not surprising that the “true,” effective dimension of K would be revealed (and would be the only obstruction according to Theorem 1.5) when K is being squeezed into a space of smaller dimension.

Let us illustrate dimension reduction on the example of finite sets K⊂S ⁿ⁻¹. Since $w(K) \le C \sqrt{\log|K|}$ (see, e.g., [15, (3.13)]), Theorem 1.5 holds with m∼log|K|, and we can state it as follows.

Corollary 1.7

(Dimension reduction for finite sets)

Let K⊂S ⁿ⁻¹ be a finite set. Let δ>0 and m≥Cδ ⁻⁶log|K|. Then K can be δ-isometrically embedded into the Hamming cube {−1,1}^m.

This fact should be compared to the Johnson–Lindenstrauss lemma for finite subsets $K \subset\mathbb{R}^{n}$ ([12], see [17, Sect. 15.2]), which states that if m≥Cδ ⁻²log|K| then K can be Lipschitz embedded into $\mathbb{R}^{m}$ as follows:

$$\bigl| \bigl\| \bar{A}x - \bar{A}x'\bigr\| _2 - \bigl\| x-x' \bigr\| _2 \bigr| \le\delta\bigl\| x-x'\bigr\| _2, \quad x,x' \in K. $$

Here, $\bar{A} = m^{-1/2} A$ is the rescaled random Gaussian matrix A from Theorem 1.5. Note that while the Johnson–Lindenstrauss lemma involves a Lipschitz embedding from $\mathbb{R}^{n}$ to $\mathbb{R}^{m}$, it is generally impossible to provide a Lipschitz embedding from subsets of $\mathbb{R}^{n}$ to the Hamming cube (if there are points x,x′∈K that are very close to each other); this is why we consider δ-isometric embeddings.

Like the Johnson–Lindenstrauss lemma, Corollary 1.7 can be proved directly by combining concentration inequalities for d _A (x,y) with a union bound over |K|² pairs (x,y)∈K×K. In fact, this method of proof allows for the weaker requirement m≥Cδ ⁻²log|K|. However, as we discuss later, this argument cannot be generalized in a straightforward way to prove Theorem 1.5 for general sets K. The Hamming distance d _A (x,y) is highly discontinuous, which makes it difficult to extend estimates from points x,y in an ε-net of K to nearby points.

1.5 Cells of Uniform Tessellations

We mentioned two nice features of uniform tessellations in Facts 1.4 and 1.6. Let us observe one more property: all cells of a uniform tessellation have small diameter. Indeed, d _A (x,y)=0 iff points x,y are in the same cell, so by (1.1) we have the following.

Fact 1.8

(Cells are small)

Every cell of a δ-uniform tessellation has diameter at most δ.

With this, Theorem 1.2 immediately implies the following.

Corollary 1.9

(Cells of random uniform tessellations)

Consider a tessellation of a subset K⊆S ⁿ⁻¹ by m≥Cδ ⁻⁶ w(K)² random hyperplanes. Then, with probability at least 1−exp(−cδ ² m), all cells of the tessellation have diameter at most δ.

This result has also a direct proof, which moreover gives a slightly better bound m∼δ ⁻⁴ w(K)². We present this “curvature argument” in Sect. 3.

1.6 Uniform Tessellations in $\mathbb{R}^{n}$

So far, we only worked with subsets K⊆S ⁿ⁻¹. It is not difficult to extend our results to bounded sets $K \subset \mathbb{R}^{n}$. This can be done by embedding such a set K into S ⁿ (the sphere in one more dimension) with small bi-Lipschitz distortion. This elementary argument is presented in Sect. 6, and it yields the following version of Theorem 1.2.

Theorem 1.10

(Random uniform tessellations in $\mathbb{R}^{n}$)

Consider a bounded subset $K \subset\mathbb{R}^{n}$ with $\operatorname {diam}(K) = 1$. Let

$$ m \ge C \delta^{-12} w(K-K)^2. $$

(1.4)

Then there exists an arrangement of m affine hyperplanes in $\mathbb {R}^{n}$ and a scaling factor λ>0 such that

$$\bigl| \lambda \cdot d_A(x,y) - \|x-y\|_2 \bigr| \le\delta, \quad x,y \in K. $$

Here, d _A (x,y) denotes the fraction of the affine hyperplanes that separate x and y.

Remark 1.11

(Mean width in $\mathbb{R}^{n}$)

While the quantity w(K−K) appearing in (1.4) is clearly bounded by 2w(K), it is worth noting that the quantity w(K−K) captures more accurately than w(K) the geometric nature of the “mean width” of K. Indeed, $w(K-K) = \mathbb{E}h(g)$ where h(g)=sup _x∈K 〈g,x〉−inf _x∈K 〈g,x〉 is the distance between the two parallel supporting hyperplanes of K orthogonal to the random direction g, scaled by ∥g∥₂.

1.7 Optimality

The main object of our study is m(K)=m(K,δ), the smallest number of hyperplanes that provide a δ-uniform tessellation of a set K⊆S ⁿ⁻¹. One has

$$ \log_2 N(K,\delta) \le m(K,\delta) \le C \delta^{-6} w(K)^2, $$

(1.5)

where N(K,δ) denotes the covering number of K, i.e. the smallest number of balls of radius δ that cover K. The upper bound in (1.5) is the conclusion of Theorem 1.2. The lower bound holds because a δ-uniform tessellation provides a decomposition of K into at most 2^m cells each of which lies in a ball of radius δ by Fact 1.8.

To compare the upper and lower bounds in (1.5), recall Sudakov’s inequality [15, Theorem 3.18] that yields

$$\log N(K,\delta) \le C \delta^{-2} w(K)^2. $$

While Sudakov’s inequality cannot be reversed in general, there are many situations where it is sharp. Moreover, according to Dudley’s inequality (see [15, Theorem 11.17] and [18, Lemma 2.33]), Sudakov’s inequality can always be reversed for some scale δ>0 and up to a logarithmic factor in n. (See also [16] for a discussion of sharpness of Sudakov’s inequality.) So, the two sides of (1.5) are often close to each other, but there is in general some gap. We conjecture that the optimal estimate is

$$c w(K)^2 \le\sup_{\delta>0} \delta^2 m(K, \delta) \le C w(K)^2, $$

so the mean width of K seems to be completely responsible for the uniform tessellations of K.

Note that the lower bound in (1.5) holds in greater generality. Namely, it is not possible to have m<log₂ N(K,δ) for any decomposition of K into 2^m pieces of diameter at most δ. However, from the upper bound, we see that with a slightly larger value m∼w(K)², an almost best decomposition of K is achieved by a random hyperplane tessellation.

In this paper, we have not tried to optimize the dependence of m(K,δ) on δ. This interesting problem is related to the open question on the optimal dependence on distortion in Dvoretzky’s theorem. We comment on this in Sect. 3.2.

1.8 Related Work: Embeddings of K into Normed Spaces

Embeddings of subsets K⊆S ⁿ⁻¹ into normed spaces were studied in geometric functional analysis [13, 21]. In particular, Klartag and Mendelson [13] were concerned with embeddings into $\ell_{2}^{m}$. They showed that for m≥Cδ ⁻² w(K)² there exists a linear map $A: \mathbb{R}^{n} \to\mathbb{R}^{m}$ such that

$$\bigl| m^{-1/2} \|Ax\|_2 - 1 \bigr| \le\delta, \quad x \in K. $$

One can choose A to be an m×n random matrix with Gaussian entries as in Theorem 1.5, or with sub-Gaussian entries. Schechtman [21] gave a simpler argument for a Gaussian matrix, which also works for embeddings into general normed spaces X. In the specific case of $X = \ell_{1}^{m}$, Schechtman’s result states that for m≥Cδ ⁻² w(K)² one has

$$\bigl| m^{-1} \|Ax\|_1 - 1 \bigr| \le\delta, \quad x \in K. $$

This result also follows from Lemma 2.1 below.

1.9 Related Work: One-Bit Compressed Sensing

Our present work was motivated by the development of one-bit compressed sensing in [6, 11, 19] where Theorem 1.5 is used in the following context. The vector x represents a signal; the matrix A represents a measurement map $\mathbb{R}^{n} \to\mathbb{R}^{m}$ that produces m≪n linear measurements of x; taking the sign of Ax represents quantization of the measurements (an extremely coarse, one-bit quantization). The problem of one-bit compressed sensing is to recover the signal x from the quantized measurements $f(x) = \operatorname{sign}Ax$.

The problem of one-bit compressed sensing was introduced by Boufounos and Baraniuk [6]. Jacques, Laska, Boufounos, and Baraniuk [11] realized a connection of this problem to uniform tessellations of the set of sparse signals $K = \{x \in S^{n-1}: |\operatorname {supp}(x)| \le s\}$, and to almost isometric embedding of K into the Hamming cube {−1,1}^m. For this set K, they proved Corollary 1.9 with m∼δ ⁻¹ slog(n/δ) and a version of Theorem 1.5 for m∼δ ⁻² slog(n/δ). The authors of the present paper analyzed in [19] a bigger set of “compressible” signals $K' = \{ x \in S^{n-1}: \|x\|_{1} \le\sqrt{s} \}$ and proved for K′ a version of Corollary 1.9 with m∼δ ⁻⁴ slog(n/s). Since the mean widths of both sets K and K′ are of the order $\sqrt {s \log(n/s)}$, Theorem 1.5 holds for these sets with m∼δ ⁻⁶ slog(n/s). In other words, apart from the dependence of δ (which is an interesting problem), the prior results follow as partial cases from Theorem 1.5.

It is important to note that Theorem 1.5 addresses only the theoretical aspect of one-bit compressed sensing problem, which guarantees that the quantized measurement map $f(x) = \operatorname{sign}Ax$ well preserves the geometry of signals. But one also faces an algorithmic challenge – how to efficiently recover x from f(x), and specifically in polynomial time. We will not touch on this algorithmic aspect here but rather refer the reader to [19] and to our forthcoming work, which is based on the results of this paper.

1.10 Related Work: Locality-Sensitive Hashing

Locality-sensitive hashing is a method of dimension reduction. One takes a set of high-dimensional vectors in $\mathbb {R}^{n}$ and the goal is to hash nearby vectors to the same bin with high probability. More generally, one may desire that the distance between bins be nearly proportional to the distance between the original items. There have been a number of papers, which suggest to create such mappings onto the Hamming cube [1, 4, 8, 10, 14], some of which use a random hyperplane tessellation as defined in this paper. The new challenge considered herein is to create a locality-sensitive hashing for an infinite set.

1.11 Overview of the Argument

Let us briefly describe our proof of the results stated above. Since the distance in the Hamming cube {−1,1}^m can be expressed as (2m)⁻¹∥x−y∥₁, the Hamming cube is isometrically embedded in $\ell_{1}^{m}$. Before trying to embed K⊆S ⁿ⁻¹ into the Hamming cube as claimed in Theorem 1.5, we shall make a simpler step and embed K almost isometrically into the bigger space $\ell_{1}^{m}$ with m∼δ ⁻² w(K)². A result of this type was given by Schechtman [21]. In Sect. 2, we prove a similar result by a simple and direct argument in probability in Banach spaces.

Our next and nontrivial step is to reembed the set from $\ell_{1}^{m}$ into its subset, the Hamming cube {−1,1}^m. In Sect. 3, we give a simple “curvature argument” that allows us to deduce Corollary 1.9 on the diameter of cells, and even with a better dependence on δ, namely m∼δ ⁻⁴ w(K)². However, a genuine limitation of the curvature argument makes it too weak to deduce Theorem 1.2 this way.

We instead attempt to prove Theorem 1.2 by an ε-net argument, which typically proceeds as follows: (a) show that d _A (x,y)≈d(x,y) holds for a fixed pair x,y∈K with high probability; (b) take the union bound over all pairs x,y in an finite ε-net N _ε of K; (c) extend the estimate from N _ε to K by approximation. Unfortunately, as we indicate in Sect. 4 the approximation step (c) must fail due to the discontinuity of the Hamming distance d _A (x,y).

A solution proposed in [5, 11] was to choose ε so small that none of the random hyperplanes pass near points x,y∈N _ε with high probability. This strategy was effective for the set $K = \{x \in S^{n-1}: |\operatorname{supp}(x)| \le s\}$ because the covering number of this specific set K has a mild (logarithmic) dependence on ε, namely logN(K,ε)≤slog(Cn/εs). However, adapting this strategy to general sets K would cause our estimate on m to increase by a factor of n.

The solution we propose in the present paper is to “soften” the Hamming distance; see Sect. 4 for the precise notion. The soft Hamming distance enjoys some continuity properties as described in Lemmas 4.3 and 5.5. In Sect. 5.5, we develop the ε-net argument for the soft Hamming distance. Interestingly, the approximation step (c) for the soft Hamming distance will be based on the embedding of K into $\ell_{1}^{m}$, which incidentally was our point of departure.

1.12 Notation

Throughout the paper, C, c, C ₁, etc. denote positive absolute constants whose values may change from line to line. For integer n, we denote [n]={1,…,n}. The ℓ _p norms of a vector $x \in\mathbb{R}^{n}$ for p∈{0,1,2,∞} are defined as²

$$\begin{aligned} &\|x\|_0 = \bigl|\operatorname{supp}(x)\bigr| = \bigl| \bigl\{ i \in[n]: x(i) \ne0 \bigr\} \bigr|, \\ &\|x\|_1 = \sum_{i=1}^n |x_i|,\qquad \|x\|_2 = \biggl( \sum _{i=1}^n x_i^2 \biggr)^{1/2}, \qquad \|x\|_\infty= \max_{i \in[n]} |x_i|. \end{aligned}$$

We shall work with normed spaces $\ell_{p}^{n} = (\mathbb{R}^{n}, \|\cdot\| _{p})$ for p∈{1,2,∞}. The unit Euclidean ball in $\mathbb{R}^{n}$ is denoted $B_{2}^{n} = \{ x \in \mathbb{R}^{n}: \|x\|_{2} \le1 \}$ and the unit Euclidean sphere is denoted $S^{n-1} = \{ x \in\mathbb {R}^{n}: \|x\|_{2} = 1 \}$.

As usual, $\mathcal{N}(0,1)$ stands for the univariate normal distribution with zero mean and unit variance, and $\mathcal{N}(0,I_{n})$ stands for the multivariate normal distribution in $\mathbb{R}^{n}$ with zero mean and whose covariance matrix is identity I _n .

2 Embedding into ℓ ₁

Lemma 2.1

(Concentration)

Consider a bounded subset $K \subset\mathbb{R}^{n}$ and independent random vectors $a_{1},\ldots,a_{m} \sim\mathcal{N}(0,I_{n})$ in $\mathbb{R}^{n}$. Let

$$Z = \sup_{x \in K} \biggl| \frac{1}{m} \sum _{i=1}^m \bigl|\langle a_i,x\rangle\bigr| - \sqrt{\frac{2}{\pi}} \|x\|_2 \biggr|. $$

• (a) One has

  $$ \mathbb{E}Z \le\frac{4 w(K)}{\sqrt{m}}. $$

  (2.1)

• (b) The following deviation inequality holds:

  $$ \Pr{Z > \frac{4 w(K)}{\sqrt{m}} + u} \le2 \exp \biggl(- \frac{m u^2}{2 d(K)^2} \biggr), \quad u>0, $$

  (2.2)

  where d(K)=max _x∈K ∥x∥₂.

Proof

(a) Note that $\mathbb{E}|\langle a_{i},x\rangle| = \sqrt{\frac {2}{\pi}} \|x\|_{2}$ for all i. Let ε ₁,…,ε _m be a sequence of iid Rademacher random variables. A standard symmetrization argument (see [15, Lemma 6.3]) followed by the contraction principle (see [15, Theorem 4.12]) yields that

$$\begin{aligned} \mathbb{E}Z \le&2\mathbb{E}\sup_{x \in K} \biggl| \frac{1}{m} \sum_{i=1}^m \varepsilon_i \bigl\vert \langle a_i,x\rangle\bigr\vert \biggr| \le4\mathbb{E}\sup _{x \in K} \biggl| \frac{1}{m} \sum_{i=1}^m \varepsilon_i \langle a_i,x\rangle \biggr| \\ =& 4\mathbb{E}\sup_{x \in K} \biggl| \biggl\langle \frac{1}{m} \sum_{i=1}^m \varepsilon_i a_i, x \biggr\rangle \biggr|. \end{aligned}$$

By the rotational invariance of the Gaussian distribution, $\frac{1}{m} \sum_{i=1}^{m} \varepsilon_{i} a_{i}$ is distributed identically with $g/\sqrt{m}$ where $g \sim\mathcal{N}(0,I_{n})$. Therefore,

$$\mathbb{E}Z \le\frac{4}{\sqrt{m}} \mathbb{E}\sup_{x \in K} \bigl|\langle g,x\rangle\bigr| = \frac{4 w(K)}{\sqrt{m}}. $$

This proves the upper bound in (2.1).

(b) We combine the result of (a) with the Gaussian concentration inequality. To this end, we must first show that the map A↦Z=Z(A) is Lipschitz where A=(a ₁,…,a _m ) is considered as a matrix in the space $\mathbb{R}^{nm}$ equipped with Frobenius norm ∥⋅∥ _F (which coincides with the Euclidean norm on $\mathbb{R}^{nm}$). It follows from two applications of the triangle inequality followed by two applications of the Cauchy–Schwarz inequality that for $A = (a_{1},\ldots,a_{m}), B = (b_{1},\ldots,b_{m}) \in\mathbb {R}^{nm}$ we have

$$\begin{aligned} \bigl\vert Z(A) - Z(B) \bigr\vert \leq&\sup_{x \in K} \frac{1}{m} \sum_{i=1}^m \bigl\vert \langle a_i - b_i, x \rangle\bigr\vert \leq \frac {d(K)}{m} \sum_{i=1}^m \Vert a_i - b_i\Vert _2 \\ \leq&\frac{d(K)}{\sqrt{m}} \Vert A - B\Vert _F. \end{aligned}$$

Thus, Z has Lipschitz constant bounded by $d(K)/\sqrt{m}$. We may now bound the deviation probability for Z using the Gaussian concentration inequality (see [15, Eq. (1.6)]) as follows:

$$\Pr{ \vert Z - \mathbb{E}Z \vert \geq u} \leq2 \exp\bigl(-mu^2/2d(K)^2 \bigr). $$

The deviation inequality (2.2) now follows from the bound on $\mathbb{E}Z$ from (a). □

Remark 2.2

(Random matrix formulation)

One can state Lemma 2.1 in terms of random matrices. Indeed, let A be an m×n random matrix with independent $\mathcal{N}(0,1)$ entries. Then its rows a _i satisfy the assumption of Lemma 2.1, and we can express Z as

$$ Z = \sup_{x \in K} \biggl| \frac{1}{m} \|Ax \|_1 - \sqrt{\frac{2}{\pi }} \|x\|_2 \biggr|. $$

(2.3)

Using this remark for the set K−K, we obtain a linear embedding of K into ℓ ₁:

Corollary 2.3

(Embedding into ℓ ₁)

Consider a subset $K \subset\ell_{2}^{n}$ and let δ>0. Let

$$m \ge C \delta^{-2} w(K)^2. $$

Then, with probability at least 1−2exp(−mδ ²/32), the linear map $f : K \to\ell_{1}^{m}$ defined as $f(x) = \frac{1}{m} \sqrt{\frac{\pi}{2}} Ax$ is a δ-isometry. Thus K can be linearly embedded into $\ell_{1}^{m}$ with Gromov-Haussdorff distortion at most δ.

Proof

Let A be the random matrix as in Remark 2.2. Using Lemma 2.1 for K−K and noting the form of Z in (2.3), we conclude that the following event holds with probability at least 1−2exp(−mδ ²/32):

$$\biggl| \frac{1}{m} \|Ax-Ay\|_1 - \sqrt{\frac{2}{\pi}} \|x-y \|_2 \biggr| \le\frac{8w(K-K)}{\sqrt{m}} \le\frac{16 w(K)}{\sqrt{m}} \le \delta, \quad x,y \in K. $$

 □

Remark 2.4

The above argument shows in fact that Corollary 2.3 holds for

$$m \ge C \delta^{-2} w(K-K)^2. $$

As we noticed in Remark 1.11, the quantity w(K−K) more accurately reflects the geometric meaning of the mean width than w(K).

Remark 2.5

(Low M^∗ estimate)

Note that for the subspace E=kerA we have from (2.3) that $Z \ge\sup_{x \in K \cap E} \sqrt{\frac{2}{\pi}} \|x\|_{2} = \sqrt {\frac{2}{\pi}} \, d(K \cap E)$. Then Lemma 2.1 implies that

$$ \mathbb{E}d(K \cap E) \le\frac{6 w(K)}{\sqrt{m}}. $$

(2.4)

By rotation invariance of Gaussian distribution, inequality (2.4) holds for a random subspace E in $\mathbb{R}^{n}$ of given codimension m≤n, uniformly distributed according to the Haar measure. This result recovers (up to the absolute constant 6 which can be improved) the so-called low M ^∗ estimate from geometric functional analysis; see [15, Sect. 15.1].

Remark 2.6

(Dimension reduction)

As we emphasized in the Introduction, for many sets $K \subset\mathbb {R}^{n}$ one has w(K)≪n. In such cases, Corollary 2.3 works for m≪n. The embedding of K into $\ell_{1}^{m}$ yields dimension reduction for K (from n to m≪n dimensions).

For example, if K is a finite set then $w(K) \le C \sqrt{\log|K|}$ (see, e.g., [15, (3.13)]), and so Corollary 2.3 applies with m∼log|K|. This gives the following variant of the Johnson–Lindenstrauss lemma: every finite subset of a Euclidean space can be linearly embedded in $\ell_{1}^{m}$ with m∼log|K| and with small distortion in the Gromov–Haussdorff metric. Stronger variants of Johnson–Lindenstrauss lemma are known for Lipschitz rather than Gromov–Haussdorff embeddings into $\ell_{2}^{m}$ and $\ell_{1}^{m}$ [2, 21]. However, for general sets K (in particular for any set with nonempty interior), a Lipschitz embedding into lower dimensions is clearly impossible; still a Gromov–Haussdorff embedding exists due to Corollary 2.3.

3 Proof of Corollary 1.9 by a Curvature Argument

In this section, we give a short argument that leads to a version of Corollary 1.9 with a slightly better dependence of m on δ.

Theorem 3.1

(Cells of random uniform tessellations)

Consider a subset K⊆S ⁿ⁻¹ and let δ>0. Let

$$m \ge C \delta^{-4} w(K)^2 $$

and consider an arrangement of m independent random hyperplanes in $\mathbb{R}^{n}$ that are uniformly distributed according to the Haar measure. Then, with probability at least 1−2exp(−cδ ⁴ m), all cells of the tessellation have diameter at most δ.

The argument is based on Lemma 2.1. If points x,y∈K belong to the same cell, then the midpoint $z = \frac{1}{2}(x+y)$ also belongs to the same cell (after normalization). Using Lemma 2.1, one can then show that $\|z\|_{2} \approx\frac{1}{2}(\|x\|_{2} + \|y\|_{2}) = 1$. Due to the curvature of the sphere, this forces the length of the interval ∥x−y∥₂ to be small, which means that the diameter of the cell is small. The formal argument is below.

Proof

We represent the random hyperplanes as {a _i }^⊥, where $a_{1},\ldots,a_{m} \sim\mathcal{N}(0,I_{n})$ are independent random vectors in $\mathbb{R}^{n}$. Let δ,m be as in the assumptions of the theorem. We shall apply Lemma 2.1 for the sets K and $\frac{1}{2}(K+K)$ and for u=ε/2, where we set ε=δ ²/16. Since the diameters of both these sets are bounded by 1, we obtain that with probability at least 1−2exp(−cδ ⁴ m) the following event holds:

$$ \biggl| \sqrt{\frac{\pi}{2}} \frac{1}{m} \sum _{i=1}^m \bigl|\langle a_i,v\rangle\bigr| - \|v \|_2 \biggr| < \varepsilon, \quad v \in K \cup\frac{1}{2}(K+K). $$

(3.1)

Assume that the event (3.1) holds. Consider a pair of points x,y∈K that belong to the same cell of the tessellation, which means that

$$\operatorname{sign}\langle a_i,x\rangle= \operatorname {sign} \langle a_i, y\rangle, \quad i \in[m]. $$

To complete the proof, it suffices to show that ∥x−y∥₂≤δ. This will give desired diameter δ in the Euclidean metric. Furthermore, since for small δ the Euclidean and the geodesic distances are equivalent, the conclusion will hold for the geodesic distance as well.

We shall use (3.1) for x,y∈K and for the midpoint $z := \frac{1}{2}(x+y) \in\frac {1}{2}(K+K)$. Clearly, $\operatorname{sign}\langle a_{i}, z\rangle= \operatorname {sign}\langle a_{i},x\rangle= \operatorname{sign}\langle a_{i}, y\rangle$, hence

$$\bigl|\langle a_i,z\rangle\bigr| = \bigl|\langle a_i, x\rangle\bigr| + \bigl|\langle a_i,y\rangle\bigr|, \quad i \in[m]. $$

Therefore, we obtain from (3.1) that

$$\begin{aligned} \|z\|_2 &\ge\sqrt{\frac{\pi}{2}} \frac{1}{m} \sum_{i=1}^m \bigl|\langle a_i,z\rangle\bigr| - \varepsilon \\ &= \frac{1}{2} \biggl[ \sqrt{ \frac{\pi}{2}} \frac{1}{m} \sum_{i=1}^m \bigl|\langle a_i,x\rangle\bigr| + \sqrt{\frac{\pi}{2}} \frac {1}{m} \sum_{i=1}^m \bigl|\langle a_i,y\rangle\bigr| \biggr] - \varepsilon \\ &\ge\frac{1}{2} \bigl(\|x\|_2-\varepsilon+ \|y\|_2- \varepsilon\bigr) - \varepsilon = 1-2\varepsilon. \end{aligned}$$

(3.2)

By the parallelogram law, we conclude that

$$\|x-y\|_2^2 = 4 - \|x+y\|_2^2 = 4\bigl(1-\|z\|_2^2\bigr) \le16\varepsilon= \delta^2. $$

This completes the proof. □

3.1 Limitations of the Curvature Argument

Unfortunately, the curvature argument does not lend itself to proving the more general result, Theorem 1.2 on uniform tessellations. To see why, suppose x,y∈K do not belong to the same cell but instead d _A (x,y)=d for some small d∈(0,1). Consider the set of mismatched signs

$$T := \bigl\{ i \in[m]: \operatorname{sign}\langle a_i,x\rangle \ne \operatorname{sign}\langle a_i, y\rangle \bigr\} ; \qquad \frac {|T|}{m} = d. $$

These signs create an additional error term on the right-hand side of (3.2), which is

$$ \sqrt{\frac{\pi}{2}} \frac{1}{m} \sum _{i \in T} \bigl|\langle a_i,v_i\rangle\bigr| \quad \text{where } v_i \in\{x,y\}. $$

(3.3)

By analogy with Lemma 2.1, we can expect that this term should be approximately equal |T|/m=d. If this is true, then (3.2) becomes in our situation ∥z∥₂≥1−2ε−d, which leads as before to $\|x-y\|_{2}^{2} \lesssim\varepsilon+ d$. Ignoring ε, we see that the best estimate the curvature argument can give is $d(x,y) \lesssim\sqrt{d_{A}(x,y)}$ rather than d(x,y)≲d _A (x,y) that is required in Theorem 1.2.

The weak point of this argument is that it takes into account the size of T but ignores the nature of T. For every i∈T, the hyperplane {a _i }^⊥ passes through the arc connecting x and y. If the length of the arc d(x,y) is small, this creates a strong constraint on a _i . Conditioning the distribution of a _i on the constraint that i∈T creates a bias toward smaller values of |〈a _i ,x〉| and |〈a _i ,y〉|. As a result, the conditional expected value of the error term (3.3) should be smaller than d. Computing this conditional expectation is not a problem for a given pair x,y, but it seems to be difficult to carry out a uniform argument over x,y∈K where the (conditional) distribution of a _i depends on x,y.

We instead propose a different and somewhat more conceptual way to deduce Theorem 1.2 from Lemma 2.1. This argument will be developed in the rest of this paper.

3.2 Dvoretzky Theorem and Dependence on δ

The unusual dependence δ ⁻⁴ in Theorem 3.1 is related to the open problem of the optimal dependence on distortion in the Dvoretzky theorem.

Indeed, consider the special case of the tessellation problem where K=S ⁿ⁻¹ and $w(K) \sim\sqrt{n}$. Then Lemma 2.1 in its geometric formulation (see Eq. (2.3) and Corollary 2.3) states that $\ell_{2}^{n}$ embeds into $\ell_{1}^{m}$ whenever m≥Cε ⁻² n, meaning that

$$(1-\varepsilon) \|x\|_2 \le\|\varPhi x\|_1 \le(1+ \varepsilon) \|x\| _2, \quad x \in\mathbb{R}^n, $$

where $\varPhi= \sqrt{\frac{\pi}{2}} \frac{1}{m} A$. Equivalently, there exists an n-dimensional subspace of $\ell_{1}^{m}$ that is (1+ε)-Euclidean, where n∼ε ² m. This result recovers the well-known Dvoretzky theorem in V. Milman’s formulation (see [9, Theorem 4.2.1]) for the space $\ell_{1}^{m}$, and with the best known dependence on ε. However, it is not known whether ε ² is the optimal dependence for $\ell_{1}^{m}$; see [21] for a discussion of the general problem of dependence on ε in the Dvoretzky theorem.

These observations suggest that we can reverse our logic. Suppose one can prove the Dvoretzky theorem for $\ell_{1}^{m}$ with a better dependence on ε, thereby constructing a (1+ε)-Euclidean subspace of dimension n∼f(ε)m with f(ε)≫ε ². Then such construction can replace Lemma 2.1 in the curvature argument. This will lead to Theorem 3.1 for K=S ⁿ⁻¹ with an improved dependence on δ, namely with m∼f(δ ²)n. Concerning lower bounds, the best possible dependence of m on δ should be δ ⁻¹, which follows by considering the case n=2. This dependence will be achieved if the Dvoretzky theorem for $\ell _{1}^{m}$ is valid with n∼ε ^1/2 m. This is unknown.

4 Toward Theorem 1.2: a Soft Hamming Distance

Our proof of Theorem 1.2 will be based on a covering argument. A standard covering argument of geometric functional analysis would proceed in our situation as follows:

• (a) Show that d _A (x,y)≈d(x,y) with high probability for a fixed pair x,y. This can be done using standard concentration inequalities.

• (b) Prove that d _A (x,y)≈d(x,y) uniformly for all x,y in a finite ε-net N _ε of K. Sudakov’s inequality can be used to estimate the cardinality of N _ε via the mean width w(K). The conclusion will follow from step 1 by the union bound over (x,y)∈N _ε ×N _ε .

• (c) Extend the estimate d _A (x,y)≈d(x,y) from x,y∈N _ε to x,y∈K by approximation.

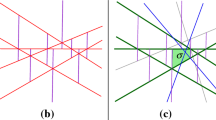
While the first two steps are relatively standard, step (c) poses a challenge in our situation. The Hamming distance d _A (x,y) is a discontinuous function of x,y, so it is not clear whether the estimate d _A (x,y)≈d(x,y) can be extended from a pair points x,y∈N _ε to a pair of nearby points. In fact, for some tessellations this task is impossible. Figure 3 shows that there exist very nonuniform tessellations that are nevertheless very uniform for an ε-net, namely one has d _A (x,y)=d(x,y) for all x,y∈N _ε . The set K in that example is a subset of the plane $\mathbb{R}^{2}$, and one can clearly embed such a set with into the sphere S ² as well.

Fig. 3

This hyperplane tessellation of the set $K =[-\frac{1}{2}, \frac{1}{2}] \times[-\frac{\varepsilon}{2},\frac {\varepsilon}{2}]$ is very non-uniform, as all cells have diameter at least 1. The tessellation is nevertheless very uniform for the ε-net $N_{\varepsilon}= \varepsilon\mathbb{Z}\cap K$, as d _A (x,y)=∥x−y∥₂ for all x,y∈N _ε

To overcome the discontinuity problem, we propose to work with a soft version of the Hamming distance. Recall that m hyperplanes are determined by their normals $a_{1},\ldots ,a_{m} \in\mathbb{R}^{n}$, which we organize in an m×n matrix A with rows a _i . Then the usual (“hard”) Hamming distance d _A (x,y) on $\mathbb {R}^{n}$ with respect to A with can be expressed as

$$ d_A(x,y) = \frac{1}{m} \sum _{i=1}^m {\bf1}_{\mathcal{E}_i}, \quad \text{where } \mathcal{E}_i = \bigl\{ \operatorname{sign}\langle a_i, x\rangle\ne\operatorname{sign}\langle a_i, y\rangle\bigr\} . $$

(4.1)

Definition 4.1

(Soft Hamming distance)

Consider an m×n matrix A with rows a ₁,…,a _m , and let $t \in\mathbb{R}$. The soft Hamming distance $d_{A}^{t}(x,y)$ on $\mathbb{R}^{n}$ is defined as

$$\begin{aligned} &d_A^t(x,y) = \frac{1}{m} \sum _{i=1}^m {\bf1}_{\mathcal{F}_i}, \quad\text{where} \\ &\mathcal{F}_i = \bigl\{ \langle a_i, x\rangle> t, \langle a_i, y\rangle< -t \bigr\} \cup\bigl\{ -\langle a_i, x\rangle> t, -\langle a_i, y\rangle< -t \bigr\} . \end{aligned}$$

(4.2)

Both positive and negative t may be considered. For positive t, the soft Hamming distance counts the hyperplanes that separate x,y well enough; for negative t, it counts the hyperplanes that separate or nearly separate x,y.

Remark 4.2

(Comparison of soft and hard Hamming distances)

Clearly, $d_{A}^{t}(x,y)$ is a nonincreasing function of t. Moreover,

$$\begin{aligned} d_A^t(x,y) =& d_A(x,y) \quad\text{for } t = 0; \\ d_A^t(x,y) \le& d_A(x,y) \quad\text{for } t \ge0; \\ d_A^t(x,y) \ge& d_A(x,y) \quad\text{for } t \le0. \end{aligned}$$

The soft Hamming distance for a fixed t is as discontinuous as the usual (hard) Hamming distance. However, some version of continuity emerges when we allow t to vary slightly.

Lemma 4.3

(Continuity)

Let $x,y,x',y' \in\mathbb{R}^{n}$, and assume that ∥Ax′∥_∞≤ε, ∥Ay′∥_∞≤ε for some ε>0. Then for every $t \in\mathbb{R}$ one has

$$d_A^{t+\varepsilon}(x,y) \le d_A^t \bigl(x+x',y+y'\bigr) \le d_A^{t-\varepsilon}(x,y). $$

Proof

Consider the events $\mathcal{F}_{i} = \mathcal{F}_{i} (x,y,t)$ from the definition of the soft Hamming distance (4.2). By the assumptions, we have |〈a _i ,x′〉|≤ε, |〈a _i ,y′〉|≤ε for all i∈[m]. This implies by the triangle inequality that

$$\mathcal{F}_i(x,y,t+\varepsilon) \subseteq\mathcal {F}_i\bigl(x+x',y+y',t\bigr) \subseteq \mathcal{F}_i(x,y,t-\varepsilon). $$

The conclusion of the lemma follows. □

We are ready to state a stronger version of Theorem 1.2 for the soft Hamming distance.

Theorem 4.4

(Random uniform tessellations: soft version)

Consider a subset K⊆S ⁿ⁻¹ and let δ>0. Let

$$m \ge C \delta^{-6} w(K)^2 $$

and pick $t \in\mathbb{R}$. Consider an m×n random (Gaussian) matrix A with independent rows $a_{1},\ldots,a_{m} \sim\mathcal{N}(0,I_{n})$. Then with probability at least 1−exp(−cδ ² m), one has

$$\bigl| d_A^t(x,y) - d(x,y) \bigr| \le\delta+ 2|t|, \quad x,y \in K. $$

Note that if we take t=0 in the above theorem, we recover Theorem 1.2. However, we find it easier to prove the result for general t, since in our argument we will work with different values of the t for the soft Hamming distance.

Theorem 4.4 is proven in the next section.

5 Proof of Theorem 4.4 on the Soft Hamming Distance

We will follow the covering argument outlined in the beginning of Sect. 4, but instead of d _A (x,y) we shall work with the soft Hamming distance $d_{A}^{t}(x,y)$.

5.1 Concentration of Distance for a Given Pair

At the first step, we will check that $d_{A}^{t}(x,y) \approx d(x,y)$ with high probability for a fixed pair x,y. Let us first verify that this estimate holds in expectation, i.e., that $\mathbb{E}d_{A}^{t}(x,y) \approx d(x,y)$. One can easily check that

$$ \mathbb{E}d_A(x,y) = d(x,y), $$

(5.1)

so we may just compare $\mathbb{E}d_{A}^{t}(x,y)$ to $\mathbb{E}d_{A}(x,y)$. Here is a slightly stronger result.

Lemma 5.1

(Comparing soft and hard Hamming distances in expectation)

Let A be a random Gaussian matrix be as in Theorem 4.4. Then, for every $t \in\mathbb{R}$ and every  $x, y \in \mathbb{R}^{n}$, one has

$$\bigl| \mathbb{E}d_A^t(x,y) - d(x,y) \bigr| \le \mathbb{E}\bigl|d_A^t (x,y) - d_A(x,y)\bigr| \le2|t|. $$

Proof

The first inequality follows from (5.1) and Jensen’s inequality. To prove the second inequality, we use the events $\mathcal{E}_{i}$ and $\mathcal{F}_{i}$ from Eqs. (4.1), (4.2) defining the hard and soft Hamming distances, respectively. It follows that

$$\begin{aligned} &\mathbb{E}\bigl|d_A^t (x,y) - d_A(x,y)\bigr| \\ &\quad{}= \mathbb{E} \biggl| \frac{1}{m} \sum_{i=1}^m ({\bf 1}_{\mathcal {E}_i} - {\bf1}_{\mathcal{F}_i}) \biggr| \\ &\quad{}\le\mathbb{E}|{\bf1}_{\mathcal{E}_1} - {\bf1}_{\mathcal{F}_1}| \quad \text{(by triangle inequality and identical distribution)} \\ &\quad{}= \mathbb{P}\{ \mathcal{E}_1 \bigtriangleup \mathcal{F}_1\} \\ &\quad{}\le\mathbb{P}\bigl\{ \bigl|\langle a_1,x\rangle\bigr| \le|t| \bigr\} + \mathbb {P}\bigl\{ \bigl|\langle a_1,y\rangle\bigr| \le|t| \bigr\} \\ &\quad{}\le2 \mathbb{P}\bigl\{ |g| \le|t| \bigr\} \quad\bigl(\text{where } g \sim \mathcal{N}(0,1)\bigr) \\ &\quad{}\le2|t| \quad\text{(by the density of the normal distribution).} \end{aligned}$$

 □

Now we upgrade Lemma 5.1 to an concentration inequality.

Lemma 5.2

(Concentration of distance)

Let A be a random Gaussian matrix as in Theorem 4.4. Then, for every $t \in\mathbb{R}$ and every $x,y \in\mathbb{R}^{n}$, the following deviation inequality holds:

$$\mathbb{P} \bigl\{ \bigl|d_A^t(x,y) - d(x,y)\bigr| > 2|t| + \delta \bigr\} \le2 \exp\bigl(-2 \delta^2 m\bigr), \quad\delta> 0. $$

Proof

By definition, $m \cdot d_{A}^{t}(x,y)$ has the binomial distribution Bin(m,p). The parameter $p = \mathbb{E}d_{A}^{t}(x,y)$ satisfies by Lemma 5.1 that

$$\bigl|p-d(x,y)\bigr| \le2|t|. $$

A standard Chernoff bound for binomial random variables states that

$$\mathbb{P} \bigl\{ \bigl|d_A^t(x,y) - p\bigr| > \delta \bigr\} \le2 \exp\bigl(-2 \delta^2 m\bigr), \quad\delta> 0, $$

see, e.g., [3, Corollary A.1.7]. The triangle inequality completes the proof. □

5.2 Concentration of Distance over an ε-Net

Let us fix a small ε>0 whose value will be determined later. Let N _ε be an ε-net of K in the Euclidean metric. By Sudakov’s inequality (see [15, Theorem 3.18]), we can arrange the cardinality of N _ε to satisfy

$$ \log|N_\varepsilon| \le C \varepsilon^{-2} w(K)^2. $$

(5.2)

We can decompose every vector x∈K into a center x ₀ and a tail x′ so that

$$ x = x_0 + x', \quad\text{where } x_0 \in N_\varepsilon, \ x' \in(K-K) \cap\varepsilon B_2^n. $$

(5.3)

We first control the centers by taking a union bound in Lemma 5.2 over the net N _ε .

Lemma 5.3

(Concentration of distance over a net)

Let A a random Gaussian matrix be as in Theorem 4.4. Let N _ε be a subset of S ⁿ⁻¹ whose cardinality satisfies (5.2). Let δ>0, and assume that

$$ m \ge C \varepsilon^{-2} \delta^{-2} w(K)^2. $$

(5.4)

Let $t \in\mathbb{R}$. Then the following holds with probability at least 1−2exp(−δ ² m):

$$\bigl|d_A^t(x_0,y_0) - d(x_0,y_0)\bigr| \le2|t| + \delta, \quad x_0,y_0 \in N_\varepsilon. $$

Proof

By Lemma 5.3 and a union bound over the set of pairs (x ₀,y ₀)∈N _ε ×N _ε , we obtain

$$\mathbb{P} \Bigl\{ \sup_{x,y \in N_\varepsilon} \bigl|d_A^t(x,y) - d(x,y)\bigr| > 2|t| + \delta \Bigr\} \le |N_\varepsilon|^2 \cdot2 \exp \bigl(-2 \delta^2 m\bigr) \le2 \exp\bigl(-\delta^2 m\bigr) $$

where the last inequality follows by (5.2) and (5.4). The proof is complete. □

5.3 Control of the Tails

Now we control the tails $x' \in(K-K) \cap\varepsilon B_{2}^{n}$ in decomposition (5.3).

Lemma 5.4

(Control of the tails)

Consider a subset K⊆S ⁿ⁻¹ and let ε>0. Let

$$m \ge C \varepsilon^{-2} w(K)^2. $$

Consider independent random vectors $a_{1},\ldots,a_{m} \sim\mathcal{N}(0,I_{n})$. Then with probability at least 1−2exp(−cm), one has

$$\frac{1}{m} \sum_{i=1}^m \bigl|\bigl\langle a_i,x'\bigr\rangle \bigr| \le\varepsilon \quad \textit{for all } x' \in(K-K) \cap\varepsilon B_2^n. $$

Proof

Let us apply Lemma 2.1 for the set $T = (K-K) \cap \varepsilon B_{2}^{n}$ instead of K, and for u=ε/8. Since d(K)=max _x′∈T ∥x′∥₂≤ε, we obtain that the following holds with probability at least 1−2exp(−cm):

$$\begin{aligned} \sup_{x' \in T} \frac{1}{m} \sum _{i=1}^m \bigl|\bigl\langle a_i,x' \bigr\rangle \bigr| &\le\sup_{x' \in T} \biggl| \frac{1}{m} \sum _{i=1}^m \bigl|\bigl\langle a_i,x' \bigr\rangle \bigr| - \sqrt{\frac{2}{\pi}} \|x'\|_2 \biggr| + \sqrt {\frac{2}{\pi}} \varepsilon \\ &\le\frac{4 w(T)}{\sqrt{m}} + \frac{\varepsilon}{8} + \sqrt {\frac{2}{\pi}} \varepsilon. \end{aligned}$$

(5.5)

Note that w(T)≤w(K−K)≤2w(K). So, using the assumption on m, we conclude that the quantity in (5.5) is bounded by ε, as claimed. □

5.4 Approximation

Now we establish a way to transfer the distance estimates from an ε-net N _ε to the full set K. This is possible by a continuity property of the soft Hamming distance, which we outlined in Lemma 4.3. This result requires the perturbation to be bounded in L _∞ norm. However, in our situation, the perturbations are going to be bounded only in L ₁ norm due to Lemma 5.4. So, we shall prove the following relaxed version of continuity.

Lemma 5.5

(Continuity with respect to L ₁ perturbations)

Let $x,y,x',y' \in\mathbb{R}^{n}$, and assume that ∥Ax′∥₁≤εm, ∥Ay′∥₁≤εm for some ε>0. Then for every $t \in\mathbb{R}$ and M≥1 one has

$$ d_A^{t+M\varepsilon}(x,y) - \frac{2}{M} \le d_A^t\bigl(x+x',y+y'\bigr) \le d_A^{t-M\varepsilon}(x,y) + \frac{2}{M}. $$

(5.6)

Proof

Consider the events $\mathcal{F}_{i} = \mathcal{F}_{i} (x,y,t)$ from the definition of the soft Hamming distance (4.2). By the assumptions, we have

$$\sum_{i=1}^m \bigl|\bigl\langle a_i, x'\bigr\rangle \bigr| \le\varepsilon m, \qquad \sum _{i=1}^m \bigl|\bigl\langle a_i, y'\bigr\rangle \bigr| \le\varepsilon m. $$

Therefore, the set

$$T := \bigl\{ i \in[m]: \bigl|\bigl\langle a_i, x'\bigr\rangle \bigr| \le M\varepsilon , \bigl|\bigl\langle a_i, y'\bigr\rangle \bigr| \le M\varepsilon \bigr\} \quad\text{satisfies} \quad\bigl|T^c\bigr| \le2m/M. $$

By the triangle inequality, we have

$$\mathcal{F}_i(x,y,t+M\varepsilon) \subseteq\mathcal {F}_i\bigl(x+x',y+y',t\bigr) \subseteq \mathcal{F}_i(x,y,t-M\varepsilon), \quad i \in T. $$

Therefore,

$$\begin{aligned} d_A^{t+M\varepsilon}(x,y) &= \frac{1}{m} \sum _{i=1}^m {\bf1}_{\mathcal {F}_i(x,y,t+M\varepsilon)} \le\frac{|T^c|}{m} + \frac{1}{m} \sum_{i \in T} {\bf1}_{\mathcal {F}_i(x,y,t+M\varepsilon)} \\ &\le\frac{2}{M} + \frac{1}{m} \sum_{i \in T} {\bf1}_{\mathcal {F}_i(x+x',y+y',t)} \le\frac{2}{M} + d_A^t \bigl(x+x',y+y'\bigr). \end{aligned}$$

This proves the first inequality in (5.6). The proof of the second inequality is similar. □

5.5 Proof of Theorem 4.4

Now we are ready to combine all the pieces and prove Theorem 4.4. To this end, consider the set K, numbers δ, m, t, and the random matrix A as in the theorem. Choose ε=δ ²/100 and M=10/δ.

Consider an ε-net N _ε of K as we described in the beginning of Sect. 5.2. Let us apply Lemma 5.3 that controls the distances on N _ε along with Lemma 5.4 that controls the tails. By the assumption on m in the theorem and by our choice of ε, both requirements on m in these lemmas hold. By a union bound, with probability at least 1−4exp(−cδ ² m) the following event holds: for every x ₀,y ₀∈N _ε and $x', y' \in(K-K) \cap \varepsilon B_{2}^{n}$, one has

$$\begin{aligned} \begin{aligned} &\bigl|d_A^{t-M\varepsilon}(x_0,y_0) - d(x_0,y_0)\bigr| \le2|t-M\varepsilon| + \delta/2, \\ &\bigl|d_A^{t+M\varepsilon}(x_0,y_0) - d(x_0,y_0)\bigr| \le2|t+M\varepsilon| + \delta/2, \end{aligned} \end{aligned}$$

(5.7)

$$\begin{aligned} &\bigl\| Ax'\bigr\| _1 \le\varepsilon m, \qquad\bigl\| Ay' \bigr\| _1 \le\varepsilon m. \end{aligned}$$

(5.8)

Let x,y∈K. As we described in (5.3), we can decompose the vectors as

$$ x = x_0 + x', \quad y = y_0 + y', \quad\text{where } x_0,y_0 \in N_\varepsilon, \ x',y' \in(K-K) \cap\varepsilon B_2^n. $$

(5.9)

The bounds in (5.8) guarantee that the continuity property (5.6) in Lemma 5.5 holds. This gives

$$\begin{aligned} &d_A^t(x,y) \le d_A^{t-M\varepsilon}(x_0,y_0) + \frac{2}{M} \\ &\phantom{d_A^t(x,y)}\le d(x_0,y_0) + 2|t| + 2M\varepsilon+ \frac{\delta}{2} + \frac {2}{M} \end{aligned}$$

by (5.7) and the triangle inequality. Furthermore, using (5.9) we have

$$\bigl|d(x_0,y_0) - d(x,y)\bigr| \le d(x_0,x) + d(y_0,y) \le\|x_0-x\|_2 + \| y_0-y\|_2 \le2 \varepsilon. $$

It follows that

$$d_A^t(x,y) \le d(x,y) + 2|t| + 2M\varepsilon+ \frac{\delta}{2} + \frac{2}{M} + 2\varepsilon. $$

Finally, by the choice of ε and M, we obtain

$$d_A^t(x,y) \le d(x,y) + 2|t| + \delta. $$

A similar argument shows that

$$d_A^t(x,y) \ge d(x,y) - 2|t| - \delta. $$

We conclude that

$$\bigl| d_A^t(x,y) - d(x,y) \bigr| \le\delta+ 2|t|. $$

This completes the proof of Theorem 4.4.

6 Proof of Theorem 1.10 on Tessellations in $\mathbb{R}^{n}$

In this section, we deduce Theorem 1.10 from Theorem 1.2 by an elementary lifting argument into $\mathbb{R}^{n+1}$. We shall use the following notation: Given a vector $x \in\mathbb {R}^{n}$ and a number $t \in\mathbb{R}$, the vector $x \oplus t \in\mathbb{R}^{n} \oplus\mathbb{R}= \mathbb {R}^{n+1}$ is the concatenation of $x \in\mathbb{R}^{n}$ and t. Furthermore, K⊕t denotes the set of all vectors x⊕t where x∈K.

Assume $K \subset\mathbb{R}^{n}$ has $\operatorname{diam}(K) = 1$. Translating K if necessary we may assume that 0∈K; then

$$ \frac{1}{2} \le\sup_{x \in K} \|x \|_2 \le1. $$

(6.1)

Also note that by assumption we have

$$ m \ge C \delta^{-12} w(K-K) \ge C \delta^{-12} w(K). $$

(6.2)

Fix a large number t≥2 whose value will be chosen later and consider the set

$$K' = Q(K \oplus t) \subseteq S^{n}, $$

where $Q: \mathbb{R}^{n+1} \to S^{n}$ denotes the spherical projection map Q(u)=u/∥u∥₂. We have

$$\begin{aligned} w\bigl(K'\bigr) &\le t^{-1} w(K \oplus t) \quad\text{(as $\|u\|_{2} \ge t$ for all $u \in K \oplus t$)} \\ &\le t^{-1} \bigl(w(K) + t \mathbb{E}|\gamma|\bigr) \quad \bigl(\text{where } \gamma\sim\mathcal{N}(0,1)\bigr) \\ &= t^{-1} w(K) + \sqrt{2/\pi} \le3w(K), \end{aligned}$$

where the last inequality holds because $w(K) \ge\sqrt{2/\pi} \sup_{x \in K} \|x\|_{2} \ge1/\sqrt{2\pi}$ by (6.1).

Then Theorem 1.2 implies that if $m \ge C \delta _{0}^{-6} w(K)^{2}$ for some δ ₀>0, then there exists an arrangement of m hyperplanes in $\mathbb {R}^{n+1}$ such that

$$ \bigl|d_A\bigl(x',y'\bigr) - d \bigl(x',y'\bigr)\bigr| \le\delta_0, \quad x',y' \in K'. $$

(6.3)

Consider arbitrary vectors x and y in K and the corresponding vectors x′=Q(x⊕t) and y′=Q(x⊕t) in K′. Let us relate the distances between x′ and y′ appearing in (6.3) to corresponding distances between x and y.

Let $a_{i} \oplus a \in\mathbb{R}^{n+1}$ denote normals of the hyperplanes. Clearly, x′ and y′ are separated by the ith hyperplane if and only if x⊕t and y⊕t are. This in turn happens if and only if x and y are separated by the affine hyperplane that consists of all $x \in\mathbb{R}^{n}$ satisfying 〈a _i ⊕a,x⊕t〉=〈a _i ,x〉+at=0. In other words, the hyperplane tessellation of K′ induces an affine hyperplane tessellation of K, and the fraction d _A (x′,y′) of the hyperplanes separating x′ and y′ equals the fraction of the affine hyperplanes separating x and y. With a slight abuse of notation, we express this observation as

$$ d_A\bigl(x',y'\bigr) = d_A(x,y). $$

(6.4)

Next, we analyze the normalized geodesic distance d(x′,y′), which satisfies

$$ \bigl| \pi\cdot d\bigl(x',y'\bigr) - \bigl\| x'-y'\bigr\| _2 \bigr| \le C_0 \bigl\| x'-y'\bigr\| _2^2. $$

(6.5)

Denoting t _x =∥x⊕t∥₂ and t _y =∥y⊕t∥₂ and using the triangle inequality, we obtain

$$\begin{aligned} \varepsilon :=& \bigl| \bigl\| x'-y'\bigr\| _2 - t^{-1} \|x-y\|_2 \bigr| \\ =& \bigl| \bigl\| t_x^{-1} (x \oplus t) - t_y^{-1} (y \oplus t) \bigr\| _2 - \bigl\| t^{-1} x - t^{-1} y \bigr\| _2 \bigr| \\ \le&\|x\| \bigl|t_x^{-1} - t^{-1}\bigr| + \|y\| \bigl|t_y^{-1} - t^{-1}\bigr| + t \bigl|t_x^{-1} - t_y^{-1}\bigr|. \end{aligned}$$

(6.6)

Note that (6.1) yields that $t \le t_{x}, t_{y} \le\sqrt {t^{2}+1}$. It follows that $|t_{x}^{-1} - t^{-1}| \le0.5 t^{-3}$ and the same bound holds for the other two similar terms in (6.6). Using this and (6.1), we conclude that ε≤t ⁻². Putting this into (6.5) and using the triangle inequality twice, we obtain

$$\begin{aligned} \bigl| \pi\cdot d\bigl(x',y'\bigr) - t^{-1} \|x-y \|_2 \bigr| \le& C_0 \bigl( t^{-1} \bigl\| x'-y'\bigr\| _2 + \varepsilon \bigr)^2 + \varepsilon \\ \le& C_0 \bigl( 2t^{-1} + t^{-2} \bigr)^2 + t^{-2} \le C_1 t^{-2}. \end{aligned}$$

Finally, we use this bound and (6.4) in (6.3), which gets us

$$ \bigl| \pi t \cdot d_A(x,y) - \|x-y\|_2 \bigr| \le \pi t \delta_0 + C_1 t^{-1}. $$

(6.7)

Now we can assign the values t:=2C ₁/δ and δ ₀=δ ²/(4πC ₁) so the right-hand side of (6.7) is bounded by δ, as required. Note that the condition $m \ge C \delta_{0}^{-6} w(K)^{2}$ that we used above in order to apply Theorem 1.2 is satisfied by (6.2). This completes the proof of Theorem 1.10.