Steiner Trees with Bounded RC-Delay

Abstract

We consider the Minimum Elmore Delay Steiner Tree Problem, which is a key problem in VLSI design: We are given a set of pins which have to be connected by a Steiner tree. One of the pins is the source. Challenging timing constraints impose tight bounds on the delay of propagating a signal from the source to the other pins. The commonly used measure is Elmore delay (Elmore in J Appl Phys 19:55–63, 1948). We consider two variants: minimizing the maximum Elmore delay or a weighted sum of Elmore delays. Both variants are strongly NP-hard even for very restricted special cases. Although it is a central problem in VLSI design (Kahng and Robins in On optimal interconnections for VLSI. Kluwer, Boston, 1995; Korte and Vygen in Building bridges—between mathematics and computer science. Springer, Berlin, pp 333–368, 2008), no approximation algorithms were known so far. In this work, we give the first constant-factor approximation algorithm. It works for both variants. The algorithm achieves an approximation ratio of 3.39 in the rectilinear plane and 4.11 in general metric spaces. We can show that our algorithm is best possible in a certain sense. We also demonstrate that our algorithm leads to improvements on real world VLSI instances compared to the currently used standard method of computing short Steiner trees.

1 Introduction

Due to its complexity, computing the physical layout of a modern computer chip is a task that is largely performed by automated software tools. In this physical design process many combinatorial optimization problems arise—see Held et al. [19] for an overview. In this work, we consider the Minimum Elmore Delay Steiner Tree Problem. It appears as one of the ten selected open problems in chip design in the list of Korte and Vygen [27] and occurs in routing: Here, pins located on the chip have to be connected by metal wires in order to allow propagation of computed information. This means that information is available at one pin (the source) and has to be sent to other pins (the sinks). Finding a connection transmitting the signal can then be formulated as a Steiner tree problem in a weighted graph or the rectlinear plane (wires never run diagonal) with pins as terminals.

Here, a signal can be regarded as a voltage change at the source pin, which triggers a voltage change at the sink pins. Tight timing constraints on the chip require the difference in time between these two events, called delay, to be as small as possible. Since the layout of the Steiner tree connecting the given set of pins has a large influence on signal delay, it is natural to formulate a mathematical optimization problem asking for a Steiner tree that minimizes source-sink delays. There are numerous ways to approximate signal delays ranging from very accurate but computationally expensive simulations to very simple but imprecise estimates (e.g. signal delay is a linear function in the distance between source and sink in the Steiner tree).

Fig. 1

Three Steiner trees for the same terminal set with probably very different source-sink delays. a Example of a shortest Steiner tree with presumably bad source-sink delays. The red sink t has a short distance to the source s, but the s–t path in the tree is very long. b A better Steiner tree with the same length. All paths are shortest paths here. Nevertheless, Elmore delay may not be optimal. c With regard to Elmore delay, this might be a better tree. The tree is a bit longer, but delay along the source-sink paths might be smaller due to less capacitance in some of the subtrees (Color figure online)

When it comes to getting a fast and reasonably accurate delay approximation, the model that is ubiquitously used in VLSI design is called the Elmore delay model [13]. In a Steiner tree, the Elmore delay between a root vertex s and a sink vertex t depends on the total length of the tree, the square of the length of the path from s to t in the tree, and on the capacitance of each subtree rooted at the vertices of this path, which is the sum of edge lengths plus the capacitances of all sink vertices in the subtree (see Fig. 1). This makes the Elmore delay formula an objective function which is comparatively complicated to state.

Although the Elmore delay model has been used for decades to evaluate signal delays of given Steiner trees, the problem of constructing a Steiner tree minimizing Elmore delay has only been approached heuristically without achieving any theoretical approximation bounds. Instead, the VLSI design community attacked this problem either by using heuristics without proven performance bounds or by simplifying the objective function to one which is better understood from a theoretical point of view, e.g. to the construction of short Steiner trees with bounded source-sink path lengths. We give a short summary of previous approaches:

Previous Work The rectilinear version of the Minimum Elmore Delay Steiner Tree Problem has received quite some attention in the past, but almost nothing is known from a theoretical point of view. Boese et al. show in [4] that for the variant minimizing the weighted sum of source-sink delays there is always an optimum solution using only Steiner points on the Hanan grid.¹ Therefore, they can solve the problem in exponential time. They also give an example in [3] showing that the existence of optimum solutions on the Hanan grid is generally not given for the variant minimizing maximum source-sink delay. Kadodi [22] and Peyer [28] show how to solve the problem of minimizing maximum source-sink delay for instances with at most three sinks optimally in constant time. For larger terminal sets, various heuristics have been implemented and evaluated in practice, but no performance bounds are proven [3–5, 35]. Moreover, there has been work by Cong et al. [10] on optimizing a simplification of the Elmore delay formula, which seems to be easier to optimize and yields an upper bound for the actual Elmore delay. Finally, Peyer et al. [29] give heuristics for improving the Elmore delay of a given rectilinear Steiner tree without increasing its length. A more extensive summary of results is given by the book of Kahng and Robins [23].

Related Work A related problem with more theoretically founded results is the construction of so called shallow-light Steiner trees, i.e. short Steiner trees with bounded source-sink path lengths. Here, one has to mention the Rectilinear Steiner Arborescence Problem, where the task is to construct a minimum length shortest-path tree in the rectilinear plane for a root vertex and a set of sinks. This problem is NP-hard as was shown by Shi and Su [34], but a 2-factor approximation can be achieved using the algorithm of Rao et al. [30] with the improvements of Córdova and Lee [11]. However, this result is only of minor interest for our purpose since it can produce very long trees. More precisely, Rao et al. [30] give an example that shows that the length of a shortest rectilinear shortest-path tree can be as long as $\varOmega (\log n)$ times the length of a shortest rectilinear Steiner tree, where n is the number of terminals. A more flexible approach is that of Khuller et al. [25], which also had a highly visible influence on the development of the algorithm we are going to present in this paper. They start with an initial short Steiner tree and a parameter $\varepsilon > 0$ and compute a tree where the distance from the source to every sink in the tree is at most $(1 + \varepsilon )$ times the distance in the metric space. To achieve this, they increase the length of the tree compared to the initial tree by a factor of at most $(1 + \frac{2}{\varepsilon })$. Their algorithm works for general metric spaces, and in case that the metric space is the rectilinear plane, Held and Rotter [20] improve this result for small values of $\varepsilon$ to produce a tree whose length only increases by a factor of $(2 + \lceil \log (\frac{2}{\varepsilon }) \rceil )$ if $0 < \varepsilon \le 2$.

As we can see, little is known about minimizing Elmore delay from a theoretical point of view, while on the other hand the simpler problem of constructing shallow-light Steiner trees is a lot better understood. However, simplifying the delay model to be a linear function in source-sink path lengths results in a significant loss of precision in practice and does not provide any non-trivial performance bounds in theory, as Proposition 2 will prove. For this reason it is crucial to have an algorithm that is capable of minimizing Elmore delay directly. In this work, we will present the first such algorithm with a provable performance guarantee.

The rest of the paper will be structured as follows: Sect. 2 will contain a short introduction to the Elmore delay model. In Sect. 3 we will formally define the Minimum Elmore Delay Steiner Tree Problem and show that short trees with short source-sink path lengths do not suffice for minimizing Elmore delay. In Sect. 4 we will then prove strong NP-hardness for a very restricted special case of our problem. Our main contribution will be in contained in Sect. 5: Here, we will present the first constant-factor approximation algorithm for constructing Steiner trees minimizing Elmore delay. In Sect. 6 we will prove that in a certain sense, this algorithm is best possible. Finally, Sect. 7 contains experimental results that show that our new algorithm leads to significant improvements on real world VLSI instances.

2 The Elmore Delay Model

The Elmore delay model is a rather simple method to approximate the signal delay through what is called an RC tree. It was originally introduced by Elmore [13] in 1948 and later on extended by Rubinstein, Penfield and Horowitz [32], who also give a simple formula that can be used for fast computation. Their model is a tree structured network consisting of a discrete number of resistors and capacitors, where each resistor has a fixed resistance and each capacitor has a fixed capacitance.

We number the k resistors and n capacitors for some $k,n \in {\mathbb {N}}$ consecutively with resistances $r_1, \ldots , r_k$ and capacitances $c_1, \ldots , c_n$ respectively, and let $C_j$ for $j \in \left\{ 1, \ldots , k \right\}$ denote the sum of capacitances of all capacitors in the subtree rooted at resistor j. They show that the Elmore delay at capacitor i is then given by $\sum _{j \in I} r_j \cdot C_j$, where $I \subseteq \left\{ 1, \ldots , k \right\}$ denotes the set of resistors on the path from the root to capacitor i. Figure 2 gives an illustration of this.

We omit their definition of an RC tree at this point but rather give a graph theoretical interpretation with emphasis on our application in VLSI design. In this regard, an RC tree can be modeled as a directed Steiner tree Y with a source s and a terminal set T, where s is the origin of the signal and the orientation of the edges corresponds to the direction in which the signal propagates. Here, the source s is regarded as a resistor with resistance $r(s) \ge 0$ and the sink vertices $t \in T$ are regarded as capacitors with capacitances $c(t) \ge 0, t \in T$. Each edge in the tree corresponds to a metal wire, which is simultaneously a resistor with resistance $R := r_{\text {wire}}\cdot l$ and capacitor with capacitance $C := c_{\text {wire}}\cdot l$, where l is the length of the wire and $r_{\text {wire}}, c_{\text {wire}}> 0$ are given constants. Steiner points do not have any resistance or capacitance.

Fig. 2

An RC tree with seven resistors and six capacitors: We have $C_6 = c_5 + c_6$ and $C_2 = c_2 + c_3 + c_4 + c_5 + c_6$. Resistor 2 imposes a delay of $r_2 \cdot C_2$. The capacitors accountable for the downstream capacitance of resistor 2 (green) are shown in red. Resistors closer to the root have a higher downstream capacitance and therefore impose higher delays per resistance unit (Color figure online)

Fig. 3

Left A wire with resistance R and capacitance C is modeled as two resistors with a capacitor in between. In terms of Elmore delay, it is equivalent to modelling it as two capacitors with a resistor in between (center). It is also the same as modelling it as k alternating resistors and capacitors with resistance R / k and C / k, respectively, and taking the limit for $k \rightarrow \infty$ (right shows $k=4$)

To match the previous model, a wire is divided into two resistors with resistance R / 2 and one capacitor with capacitance C in between, as shown in Fig. 3. It can be shown that in terms of Elmore delay, this is exactly the limit of dividing the wire into k alternating resistors and capacitors with resistance R / k and C / k, respectively, when k goes to infinity. Using this modelling of RC networks as Steiner trees we arrive at the following mathematical definition of Elmore delay:

Definition 1

Given a metric space (M, dist), an arborescence $Y=(V,E)$ rooted at $s \in V$ with resistance $r(s) \in {\mathbb {R}}_{\ge 0}$, a set of sinks $T \subseteq V$ with capacitances $c: T \rightarrow {\mathbb {R}}_{\ge 0}$ and vertex positions $p: V \rightarrow M$, we fix the following notation:

• For $v,w \in V$, we define $dist(v,w) := dist(p(v), p(w))$.

• Let $l(Y) := \sum _{(v,w) \in E} dist(v, w)$ denote the length of Y.

• For $v,w \in V$, let $P_Y(v,w)$ denote the v-w path in the underlying undirected graph of Y and $dist_Y(v,w) := \sum _{(x,y) \in P_Y(v,w)} dist(x,y)$ the distance of v and w in Y.

• For $v \in V$, let Y(v) denote the subtree rooted at v.

Then the Elmore delay to $t \in T$ is defined as

• $d_Y(t) := r(s) \cdot C_Y(s) + \sum _{(v,w) \in E(P_Y(s,t))} dist(v,w) \cdot \Big (\frac{dist(v,w)}{2} + C_Y(w)\Big )$,

where $C_Y(v) := l(Y(v)) + \sum _{t' \in V(Y(v))\cap T} c(t')$ is said to be the downstream capacitance of $v \in V$.

We partition the Elmore delay into the terms source delay and wire delay, where $sd(Y) := r(s) \cdot C_Y(s)$ is the source delay of Y and $wd_Y(t) := \sum _{(v,w) \in E(P_Y(s,t))} dist(v,w) \cdot \Big (\frac{dist(v,w)}{2} + C_Y(w)\Big )$ is the wire delay to t in Y.

We first want to remark that it is straightforward to check that Elmore delay is well-behaved with respect to Steiner points of degree 2 in the following sense: Given an edge (u, w) in the tree, inserting a Steiner point v of degree 2 will not decrease the Elmore delay to any sink, and it stays the same for all sinks if $dist(u,w) = dist(u,v) + dist(v,w)$.

In our definition of Elmore delay, the constants $r_{\text {wire}}$ and $c_{\text {wire}}$ do not appear as they can be normalized to be 1 for the sake of mathematical simplicity. A great advantage of the Elmore delay model is that it can be computed in linear time by first computing the downstream capacitances $C_Y(v), v \in V(Y)$, in reverse topological order, and then computing the delay to all vertices in topological order. This way it is fast to compute for a given tree while being reasonably accurate in most cases. It has been shown by Boese et al. [2] that even in cases where it is not very accurate, it is still a high fidelity estimate, which means that improving Elmore delay will almost certainly improve real delay simulated by tools that are too computationally expensive to be called more often than a very few times in the VLSI design flow. For these reasons, the Elmore delay model has been the delay model of choice in VLSI design for the last decades. For more on it, see also Gupta et al. [17], Peyer [28] or the book of Celik et al. [8].

3 The Problem Formulation

Looking at the definition of Elmore delay from Sect. 2, one can see that shortest Steiner trees produce minimum source delays, while Steiner trees connecting every sink directly to the source produce minimum wire delays. The main difficulty is to find a good tradeoff between both extremes. We now give the problem definition:

Problem: :

Minimum Elmore Delay Steiner Tree Problem (MDST).

Input: :

A metric space (M, dist), a source s with resistance $r(s) \in {\mathbb {R}}_{\ge 0}$, a set of sinks T with capacitances $c:T \rightarrow {\mathbb {R}}_{\ge 0}$ and positions $p: \left\{ s \right\} \cup T \rightarrow M$.

Task: :

Find a directed Steiner tree Y rooted at s and positions $p: V(Y) \backslash (\left\{ s \right\} \cup T) \rightarrow M$ minimizing

a):

$d(Y) := \max _{t \in T} d_Y(t)$ (MAX-MDST),

b):

$d(Y) := \sum _{t \in T} w (t) \cdot d_Y(t)$ for $w : T \rightarrow {\mathbb {R}}_{\ge 0}$ (SUM-MDST).

We first point out that in general metric spaces an optimum solution of the above problem does not have to exist. However, in the metric spaces that we are mainly interested in, namely metric graphs and the rectilinear plane, this is trivial for the former and easy to prove for the latter [33]. Secondly, we note that by setting r(s) sufficiently large, the MDST problem degenerates into the Shortest Steiner Tree Problem,² which is known to be NP-hard both in metric graphs and $({\mathbb {R}}^2, l_1)$ [14, 24]. Theorem 3 will even prove strong NP-hardness for a very restricted special case of the MDST problem.

Before starting the technical work, we want to remark a small subtlety in the problem formulation. To express a solution, we use a tree structure that we embed into the metric space by the mapping p, which is not required to be injective. There are applications in VLSI design where this model is more useful, e.g. the global routing step, where many vertices of the original routing graph are contracted to a single vertex, resulting in a grid graph that is much smaller than the actual routing graph. In this case it makes sense to allow multiple vertices (including terminals) of the tree to be mapped to the same spot in the metric space. This is not relevant when the goal is to construct a shortest Steiner tree, but it is when trying to minimize Elmore delay. For more on the VLSI routing problem see e.g. Gester et al. [16]. As already pointed out before, we now want to give an easy example that shows that constructing short Steiner trees with short source-sink paths does not suffice for achieving any non-trivial performance bound for minimizing Elmore delay:

Proposition 2

For any $k \in N$ and $\gamma < 1$ there is an instance of the MDST problem with $|T| = k$ and $(M, dist) = ({\mathbb {R}}, l_1)$ such that for every shortest Steiner tree Y we have $dist_Y(s,t) = dist(s,t)$ for all $t \in T$ and $d(Y) \ge \gamma k \cdot OPT$, where d(Y) can be measured in any of the two given objective functions and OPT denotes the optimum objective function value in that respective function.

Fig. 4

Illustration of the proof of Proposition 2: The shortest Steiner tree on the left is also a shortest-path tree, but the delay from the source to every sink is $\varOmega (k)$ times the delay that we get when connecting every sink directly to the source (right)

Proof

We first note that in $({\mathbb {R}}, l_1)$ every shortest Steiner tree is also a shortest-path tree. Let $p(s) = 0$, $p(t) = 1$ for all $t \in T$, $r(s) = 0$ and $c(t) = C$ for all $t \in T$. Now every shortest Steiner tree (without Steiner vertices of degree 2) connects some arbitrary sink $t \in T$ to s and links all sinks in T together with an arbitrary tree structure of edges of length 0. This yields a delay of $\frac{1}{2} + kC$ to every sink while connecting every sink directly to s yields a delay of $\frac{1}{2} + C$ to every sink, as shown in Fig. 4. By choosing C sufficiently large we get the result. $\square$

4 NP-Hardness

In this section we want to prove our hardness result:

Theorem 3

Both variants of the MDST problem are strongly NP-hard even for $|M|= 2$ or $(M, dist) = ({\mathbb {R}}^2, l_1)$ and all sinks have the same position.

Before giving the proof, we cite a theorem of Boese et al. [4] that is an extension of Hanan’s theorem [18] for the SUM-MDST problem:

Theorem 4

(Boese, Kahng, McCoy, Robins 1995) For any instance of the SUM-MDST problem with $(M, dist) = ({\mathbb {R}}^2, l_1)$ there exists an optimum solution using only Steiner points on the Hanan grid.

We will actually only prove Theorem 3 for SUM-MDST. Although Boese et al. also show in [3] that Theorem 4 does not hold for MAX-MDST, Theorem 3 can also be proven for MAX-MDST in a way very similar to what is presented here. This proof can be found in [33].

So if we only consider SUM-MDST, Theorem 4 tells us that $|M|=2$ is equivalent to $(M, dist) = ({\mathbb {R}}^2, l_1)$ and all sinks have the same position. Therefore we only need to consider the case $|M| = 2$ in our proof. This special case of the MDST problem can be regarded as a partitioning problem, and so it seems natural to apply a reduction from the 3-Partition Problem, which is known to be strongly NP-complete (see Garey and Johnson [15]):

Problem: :

3-Partition Problem.

Input: :

Numbers $a_1, \ldots , a_n \in {\mathbb {N}}$ with $n = 3m$ and $\sum _{j=1}^n a_i = mB$ for some $m,B \in {\mathbb {N}}$.

Task: :

Decide whether there exists a partitioning $\{ 1, ..., n \} = S_1 \dot{\cup } \,\cdots \dot{\cup } \,S_m$ such that $\sum _{j \in S_i} a_j = B$ for all $i = 1, \ldots , m$.

Usually, one restricts the problem further by requiring $\frac{B}{4} < a_j < \frac{B}{2}$ for all $j = 1, \ldots , n$. This special case remains strongly NP-hard [15], but we actually do not need this restriction. The idea of our proof will be the following:

Given a 3-Partition instance $a_1, \ldots , a_n$, $n=3m$, we create a SUM-MDST instance with $T = T' \cup T^*$, $T' = \left\{ t_1, \ldots , t_n \right\}$ and $T^* = \left\{ t^*_1, \ldots , t^*_m \right\}$, $w(t_j) = c(t_j) = a_j$, $j = 1, \ldots , n$, $w(t^*_i) = W$ and $c(t^*_i) = C$, $i = 1, \ldots , m$. As stated in the theorem, all sinks will have the same position and we will have $dist(s,t) = 1$ for all $t \in T$. We will choose r(s), W and C in such a way that

• It is never optimal to put two sinks of $T^*$ into the same set of the partition.

• It is never optimal to make a partition that consists of more than m sets.

If we have achieved this, every optimum solution Y of the SUM-MDST instance consists of exactly m sets and each set contains exactly one sink of $T^*$. It follows that the delay of any such solution is solely defined by the partitioning of $T' = T'_1 \dot{\cup } \,\cdots \dot{\cup } \,T'_m$ (where we allow that some $T'_i$ are the empty set). It can then be seen that $\sum _{i=1}^m d_Y(t^*_i)$ is independent of this partitioning of $T'$. Therefore, the total delay of the solution can be written as $K + \sum _{i=1}^m w(T'_i) \cdot c(T'_i) = K + \sum _{i=1}^m a(T'_i)^2$, where K is a suitable constant and for $T'_i = \left\{ t_{i_1}, \ldots , t_{i_k} \right\}$ we define $a(T'_i) := \sum _{j = 1}^k a_{i_j}$.

Since $\sum _{i=1}^m a(T'_i)$ is constant, we can apply the following Lemma in order to get that the delay is minimized by a partition $T' = T'_1 \dot{\cup } \,\cdots \dot{\cup } \,T'_m$ where all $a(T'_i)$ are equal:

Lemma 5

Given $S \in {\mathbb {R}}_{\ge 0}$ and $n \in {\mathbb {N}}$, consider the optimization problem $\min \left\{ \sum _{i=1}^n x_i^2 : \sum _{i=1}^n x_i = S, x \ge 0 \right\}$. Then the unique optimum solution is given by $x^*_i = \frac{S}{n}$, $i = 1, \ldots , n$. $\square$

Because such a partition exists if and only if $a_1, \ldots , a_n$ define a yes-instance of the 3-Partition Problem, we get the result. This was a coarse outline and now comes the formal proof:

Proof

Given a 3-Partition instance $a_1, \ldots , a_n \in {\mathbb {N}}$ with $n = 3m$ and $\sum _{j=1}^n a_j = mB$ for some $B \in {\mathbb {N}}$ that is polynomially bounded in the instance size, we construct an instance of the SUM-MDST problem according to the description above, i.e. with $A := \sum _{j=1}^n a_j$ we set

• $T = T' \dot{\cup } \,T^*$ with $T' = \left\{ t_1, \ldots , t_n \right\}$ and $T^* = \left\{ t_1^*, \ldots , t_m^* \right\}$,

• $p(t) = p(t')$ for all $t, t' \in T$, $dist(s,t) = 1$ for all $t \in T$,

• $w(t_j) = c(t_j) = a_j$ for $j = 1, \ldots , n$,

• $w(t_i^*) = W := 4Am^2$, $i = 1, \ldots , m$,

• $c(t_i^*) = C := 4Am^2$, $i = 1, \ldots , m$,

• $r(s) = 2A$,

For the rest of the proof we will identify solutions of the MDST instance with partitions of T in the sense that every tree defines a partition and every partition defines a set of trees with identical delays (edges of length 0 might be arranged arbitrarily). As outlined before, we first have to show that every optimum solution of the SUM-MDST instance consists of exactly m sets and that no two sinks from $T^*$ are in the same set of the partition. We will call a solution with these properties an m-set solution. So let Y be an arbitrary m-set solution and $Y_1$ be a solution where two sinks in $T^*$ are put into the same set of the partition. Then we have

$$\begin{aligned} \sum _{t \in T} w(t) \cdot d_Y(t)\le & {} w(T) \cdot \max _{t \in T} d_Y(t) \\\le & {} (mW + A) \bigg ( r(s) (m + A + mC) + \frac{1}{2} + A + C\bigg ) \\= & {} (mW \!+\! A) \bigg (r(s)(A \!+\! mC)\bigg ) \!+\! (mW + A) \bigg (r(s) m + \frac{1}{2} + A + C\bigg ) \\\le & {} (mW + A) \bigg (r(s)(A + mC)\bigg ) + (mW + A) \bigg (4Am + C\bigg ) \\= & {} (mW + A) \bigg (r(s)(A + mC)\bigg ) + \bigg (m + \frac{1}{4m^2}\bigg ) W \cdot \bigg (1 + \frac{1}{m}\bigg )C \\< & {} (mW + A) \bigg (r(s)(A + mC)\bigg ) + (m + 2)WC \\\le & {} \sum _{t \in T} d_{Y_1}(t), \\ \end{aligned}$$

where the last inequality follows from $(mW + A) \left( r(s)(A + mC)\right)$ being a lower bound for the weighted source delay in any solution and $(m+2)WC = (m-2)WC + 4WC$ being a lower bound for the weighted wire delay for the sinks in $T^*$ in $Y_1$, which is higher because two sinks of $T^*$ are in the same set of the partition (accounting for the 4WC term). Next, let Y again correspond to an m-set solution and $Y_2$ to a solution with more than m sets. With $S := (mW + A) r(s) (m + A +mC)$ we get:

$$\begin{aligned} \sum _{t \in T} w(t) \cdot d_Y(t)\le & {} (mW + A) \bigg ( r(s) (m + A + mC) + \frac{1}{2} + A + C\bigg ) \\= & {} S + (mW + A) \bigg (\frac{1}{2} + A + C\bigg ) \\= & {} S + mW \bigg ( \frac{1}{2} + C\bigg ) + mWA + AC + A \bigg (\frac{1}{2} + A\bigg ) \\< & {} S + mW \bigg ( \frac{1}{2} + C\bigg ) + 2mWA + 2A^2 \\= & {} S + mW \bigg ( \frac{1}{2} + C\bigg ) + r(s) \bigg (mW + A\bigg ) \\\le & {} (mW + A) \bigg (r(s) \Big (m+1 + A + mC\Big ) \bigg ) + mW\bigg (\frac{1}{2} + C\bigg ) \\\le & {} \sum _{t \in T} w(t) \cdot d_{Y_2}(t), \\ \end{aligned}$$

where this time the last inequality follows from $(mW + A) r(s) (m+1 + A + mC)$ being a lower bound for the weighted source delay if more than m sets are used, and $mW(\frac{1}{2} + C)$ being a lower bound for the weighted wire delay for the sinks in $T^*$ in any solution.

This means that any optimum solution has indeed m sets and each such set contains exactly one sink of $T^*$. Let $T = T_1 \dot{\cup } \,\cdots \dot{\cup } \,T_m$ define an m-set solution Y and set $T'_i := T_i \cap T'$, $i = 1, \ldots , m$. Then the delay of this solution can be written as

$$\begin{aligned} \sum _{t \in T} w(t) \cdot d_Y(t)&= mW \bigg (r(s) (m + A + mC) + \frac{1}{2} + \frac{A}{m} + C\bigg ) \\&\qquad + \sum _{i=1}^m \sum _{t \in T'_i} w(t) \bigg (r(s) (m + A + mC) + \frac{1}{2} + c(T'_i) + C\bigg ) \\&= K + \sum _{i=1}^m w(T'_i) \cdot c(T'_i) \\&= K + \sum _{i=1}^m a(T'_i)^2, \end{aligned}$$

where $K = w(T)\Big (r(s) (m + A + mC) + \frac{1}{2} + \frac{A}{m} + C\Big ) + w(T') \Big (\frac{1}{2} + C\Big )$ is a constant of the instance that is independent of the partition. Using Lemma 5, the term $K + \sum _{i=1}^m a(T'_i)^2$ is minimized if and only if $a(T'_i) = \frac{A}{m} = B$ for all $i = 1, \ldots , m$. It follows that an optimum solution of the SUM-MDST instance must define a feasible solution of the 3-Partition instance if there is one. As all occuring numbers are polynomially bounded in the size of the 3-Partition instance, we get the result. $\square$

5 The Algorithm

We have seen that the MDST problem is strongly NP-hard. Now we present the first constant-factor approximation algorithm. The algorithm will require an initial solution $Y_0$ and a parameter $\varepsilon > 0$ as additional input, where this initial solution $Y_0$ should be as short as possible. It is well known that the Shortest Steiner Tree Problem can be approximated efficiently (see e.g. the work of Korte and Vygen [26] for an overview on the topic). Now here comes the description of the algorithm.

Consider an instance of the MDST problem and let $Y_0$ and $\varepsilon > 0$ as described above. We may assume that $Y_0$ is a binary tree with root s such that the leaves of $Y_0$ are exactly the vertices in T.³ We also fix the terminology that reconnecting a subtree Y(v) for a tree Y and $v \in V(Y)$ to s by a shortest path means deleting the incoming edge of v from Y, choosing $x \in V(Y(v))$ with $dist(s,x) = \min _{w \in V(Y(v))} dist(s,w)$, connecting x to s and changing the orientation of the edges in E(Y(v)) such that they are directed away from s again.

Algorithm 6

Let Y be the tree that we are constructing, initially $Y = Y_0$. We traverse the vertices of $V(Y_0) \backslash \left\{ s \right\}$ in reverse topological order of $V(Y_0)$. Let $w \in V(Y_0) \backslash \left\{ s \right\}$ be a vertex that we are traversing and v its predecessor in Y. We check whether $C_Y(w) + dist(v,w) \ge \frac{\varepsilon }{2} \min \big \{dist(s,x) : x \in V(Y(w)) \cup \left\{ v \right\} \big \}$ and reconnect Y(w) to s by a shortest path (as described above) if the inequality is true. The algorithm stops when all vertices in $V(Y_0) \backslash \left\{ s \right\}$ have been traversed.

Fig. 5

Reconnection step of Algorithm 6: If $C_Y(w) + dist(v,w)$ is too large, the edge (v,w) is deleted from the tree. Connectivity is then reestablished by connecting s to a vertex of minimum distance in Y(w)

Figure 5 gives an illustration of the reconnection step of Algorithm 6. We note here that when $v = s$, a reconnect is always performed, even if it means deleting an edge and adding it again. This is a technicality that we will use to simplify the description of the following proofs. We start our analysis with an obvious bound for the running time of the algorithm.

Proposition 7

Algorithm 6 can be implemented in $O(\tau )$ time, where $\tau$ denotes the time it takes to compute dist(s, v) for all $v \in V(Y_0)$.⁴ $\square$

In order to analyze the performance guarantee of the algorithm, we first give simple lower bounds that we will use to establish the quality of our solution:

Definition 8

Given an MDST instance, let $smt(\left\{ s \right\} \cup T)$ denote the length of a shortest Steiner tree for $\left\{ s \right\} \cup T$. Then $lb_{sd}:= r(s) \cdot (smt(\left\{ s \right\} \cup T) + \sum _{t \in T} c(t))$ is a lower bound for the source delay and $lb_{wd}(t) := dist(s,t) \cdot \Big (\frac{dist(s,t)}{2} + c(t)\Big )$ is a lower bound for the wire delay to $t \in T$. The sum $lb(t) := lb_{sd}+ lb_{wd}(t)$ is a lower for the total delay to $t \in T$.

We want to point out here that both bounds can be achieved, but in general not simultaneously. A shortest Steiner tree will have a source delay equal to $lb_{sd}$, while a star with center s will have a wire delay of $lb_{wd}(t)$ to every sink. Note that $lb_{wd}$ is indeed a lower bound for the wire delay: Given a sink t, the path from s to t must have a length of at least dist(s, t). Given that Elmore delay cannot be reduced by inserting Steiner points of degree 2 and any Steiner point of degree larger than 2 on the path from s to t will in general only increase the delay to t by adding additional downstream capacitance to the edges, it is not possible to have a wire delay of less than $lb_{wd}(t)$ to t.

Basically, we will prove that for some functions $f,g: {\mathbb {R}}_{>0}\rightarrow {\mathbb {R}}_{>0}$ the source delay of the output is bounded by $f(\varepsilon ) \cdot r(s) C_{Y_0}(s)$ and the wire delay to each sink $t \in T$ by $g(\varepsilon ) \cdot lb_{wd}(t)$, where f will be decreasing while g will be increasing in $\varepsilon$. The next lemma gives the bound for the source delay. Before stating it, we add the following notation for a Steiner tree Y and a vertex $v \in V(Y)$:

• Let $\delta _Y(v) := \delta _Y^+(v) \cup \delta _Y^-(v)$, where $\delta _Y^+(v)$ ($\delta _Y^-(v)$) is the set of outgoing (incoming) edges of v.

• Let $\varGamma _Y(v) := \varGamma _Y^+(v) \cup \varGamma _Y^-(v)$ with $\varGamma _Y^+(v) := \left\{ w \in V: (v,w) \in E \right\}$ and $\varGamma _Y^-(v) := \left\{ w \in V: (w,v) \in E \right\}$ be the set of neighbours of v.

Lemma 9

Consider an instance of the MDST problem, an initial solution $Y_0$ and $\varepsilon > 0$. Then Algorithm 6 returns a solution Y with $C_Y(s) \le \left( 1 + \frac{2}{\varepsilon }\right) \cdot C_{Y_0}(s)$.

Proof

Let $\varGamma _Y^+(s) = \left\{ x_1, \ldots , x_k \right\}$ be the set of vertices that were reconnected to s during the algorithm. Let $e_i = (v_i, w_i) \in E(Y_0)$ be the edge that was deleted from the tree when $x_i$ was reconnected to s, $i = 1, \ldots , k$. We fix some $x \in \left\{ x_1, \ldots , x_k \right\}$. As in the description of the algorithm, let w be the vertex that was being traversed at the point of time when x was reconnected to s (possibly w = x), $Y'$ the tree directly before this reconnect and v the predecessor of w in $Y'$. Then by definition of the algorithm we know $C_{Y'}(w) + dist(v, w) \ge \frac{\varepsilon }{2} \min \left\{ dist(s,x), dist(s,v) \right\}$, because x was a vertex with minimum distance to s in $V(Y'(w))$. Since dist is a metric function, we know that $dist(s,x) - dist(v,w) \le dist(s,w) - dist(v,w) \le dist(s,v)$, so we have $dist(s,x) - dist(v,w) \le \min \left\{ dist(s,x), dist(s,v) \right\} \le \frac{2}{\varepsilon }\big (C_{Y'}(w) + dist(v, w)\big ) = \frac{2}{\varepsilon }\big (C_Y(x) + dist(v, w)\big )$, where (v, w) is the edge that was deleted in this step.

Noting that all $Y(x_i)$ are disjoint subtrees of $Y_0$ (apart from edge orientation), $e_i \ne e_j$ for all $i \ne j \in \{ 1, ..., k \}$ and $\left\{ e_1, \ldots , e_k \right\} \cap \bigcup _{j=1}^k E(Y(x_j)) = \emptyset$, we can bound the total length that was added to $Y_0$ by

$$\begin{aligned} \sum _{i=1}^k \Big ( dist(s,x_i) - dist(v_i, w_i) \Big ) \le \sum _{i=1}^k \frac{2}{\varepsilon } \Big ( C_Y(x_i)) + dist(v_i, w_i) \Big ) \le \frac{2}{\varepsilon } C_{Y_0}(s). \end{aligned}$$

Therefore, we get $C_Y(s) \le \left( 1 + \frac{2}{\varepsilon }\right) \cdot C_{Y_0}(s)$, proving the claim. $\square$

For the analysis of the wire delay, we first give an estimate that helps us to bound the wire delay of a sink by a more simplified formula. In order to do so, we extend the definition of wire delay by setting

• $wd_Y(x,z) := \sum _{(v,w) \in P_Y(x,z)} dist(v,w) \cdot \Big ( \frac{dist(v,w)}{2} + C_Y(w) \Big )$

for a solution Y of the MDST problem and $x,z \in V(Y)$ with $z \in V(Y(x))$. With this definition, we can formulate the next lemma:

Lemma 10

Let Y be a solution of an MDST instance, $x \in V(Y)$ and let y be a direct successor of x in Y, i.e. $(x, y) \in E(Y)$. Then we have

$$\begin{aligned} wd_Y(x,z) \le dist_Y(x,z) \cdot \bigg (\frac{dist(x,y) - dist_Y(y,z)}{2} + C_Y(y)\bigg ) \end{aligned}$$

for any $z \in V(Y(y))$.

Proof

Let P be the x-z path in Y and let $E(P) = \left\{ (v_1, w_1), \ldots , (v_k, w_k) \right\}$ be the edge set of P ordered from x to z (i.e. $v_1 = x$, $v_2 = y$ and $v_i = w_{i-1}$ for $i = 2, \ldots , k$). Using $C_Y(w_i) \le C_Y(y) - \sum _{j=2}^i dist(v_j, w_j)$ we get

$$\begin{aligned} wd_Y(x,z)&= \sum _{i=1}^k dist(v_i, w_i) \cdot \bigg ( \frac{dist(v_i, w_i)}{2} + C_Y(w_i) \bigg ) \le \sum _{i=1}^k dist(v_i, w_i)\\&\quad \cdot \bigg ( \frac{dist(v_i, w_i)}{2} + C_Y(y) -\sum _{j = 2}^k dist(v_j, w_j) +\sum _{j = i+1}^k dist(v_j, w_j) \bigg ) \\&= \sum _{i=1}^k dist(v_i, w_i) \cdot \bigg ( \frac{dist(v_i, w_i)}{2} + \sum _{j = i+1}^k dist(v_j, w_j) \bigg ) \\&\quad + \sum _{i=1}^k dist(v_i, w_i) \cdot \Big (C_Y(y) - \sum _{j = 2}^k dist(v_j, w_j)\Big ) \\&= \frac{1}{2}dist_Y(x,z)^2 + dist_Y(x,z) \cdot \Big (C_Y(y) - dist_Y(y,z)\Big ) \\&= dist_Y(x,z) \cdot \bigg ( \frac{dist_Y(x,z)}{2} + C_Y(y) - dist_Y(y,z) \bigg ) \\&= dist_Y(x,z) \cdot \bigg (\frac{dist(x,y) - dist_Y(y,z)}{2} + C_Y(y)\bigg ), \end{aligned}$$

where we used the general formula $(\sum _{i=1}^k a_i)^2 = \sum _{i=1}^k a_i (a_i + 2 \sum _{j=i+1}^k a_j)$ for any sequence $a_1, \ldots , a_k$ of real numbers. This proves the claim. $\square$

Now we are able to formulate and prove our main theorem:

Theorem 11

Given an instance of the MDST problem, an initial solution $Y_0$ and $\varepsilon > 0$, Algorithm 6 computes a solution Y such that

• $sd(Y) \le \left( 1 + \frac{2}{\varepsilon }\right) r(s) \cdot C_{Y_0}(s)$,

• $wd_Y(t) \le \max \left\{ (1 + \varepsilon )^2, \ 1 + \frac{1}{16} \varepsilon ^3 + \frac{3}{4} \varepsilon ^2 +2\varepsilon \right\} \cdot lb_{wd}(t)$ for all $t \in T$,

in $O(\tau )$ time, where $\tau$ denotes the time it takes to compute dist(s, v) for all $v \in V(Y_0)$.

Proof

The running time follows from Proposition 7 and the bound for the source delay from Lemma 9. Therefore, it only remains to show the claim for the wire delay. To this end, let $t \in T$ and let x be the unique vertex with $x \in V(P_Y(s,t))$ and $(s,x) \in E(Y)$. Let w be the vertex that was being traversed when x was reconnected to s and $Y'$ be the tree directly before this reconnect. When $w = t$, we have that t is connected directly to s in Y with $V(Y(t)) = \left\{ t \right\}$ due to the fact that t is a leaf in $Y_0$, so the claim is true.

Otherwise, w is a Steiner point and we let $\varGamma _{Y'}^+(w) = \left\{ u_1 \right\}$ or $\varGamma _{Y'}^+(w) = \left\{ u_1, u_2 \right\}$ depending on $|\varGamma _{Y'}^+(w)|$. Without loss of generality we may assume $x \in Y'(u_1) \cup \left\{ w \right\}$ and we set $C_1 := C_{Y'}(u_1) + dist(w, u_1)$ and $C_2 := C_{Y'}(u_2) + dist(w, u_2)$ if $|\varGamma _{Y'}(w)| = 2$ and $C_2 := 0$ otherwise. With $\alpha := 2wd_Y(t) / dist(s,t)^2$ it suffices to show $\alpha \le \max \{(1 + \varepsilon )^2, \ 1 + \frac{1}{16} \varepsilon ^3 + \frac{3}{4} \varepsilon ^2 +2\varepsilon \}$. In order to do so, we first note $C_Y(x) = C_{Y'}(w) = C_1 + C_2$ and prove $\alpha \le 1 + \frac{1}{16} \varepsilon ^3 + \frac{3}{4} \varepsilon ^2 +2\varepsilon$ in case $t \in V(Y'(u_1))$ and $\alpha \le (1 + \varepsilon )^2$ in case $t \in V(Y'(u_2))$. Since the latter case is the easier one, we will handle it first:

Case 1: $t \in V(Y'(u_2))$

Here, we can assume that $C_1 < \frac{\varepsilon }{2} dist(s,x)$ due to $x \in V(Y'(u_1)) \cup \left\{ w \right\}$ and $C_2 < \frac{\varepsilon }{2} dist(s,t)$ due to $t \in V(Y'(u_2))$—otherwise $Y'(u_1)$ or $Y'(u_2)$ would have been reconnected to s by the algorithm when $u_1$ and $u_2$ had been traversed. Therefore, $C_Y(x) = C_1 + C_2 < \frac{\varepsilon }{2} (dist(s,x) + dist(s,t))$ and we can use Lemma 10 to bound the wire delay of t by

$$\begin{aligned} wd_Y(t)&\le \Big (dist(s,x) + dist_Y(x,t)\Big ) \cdot \bigg ( \frac{dist(s,x) - dist_Y(x,t)}{2} + C_Y(x) \bigg ) \\&\le \Big (dist(s,x) + dist_Y(x,t)\Big ) \\&\qquad \cdot \bigg ( \frac{dist(s,x) - dist_Y(x,t)}{2} + \frac{\varepsilon }{2}\Big ( dist(s,x) + dist(s,t)\Big ) \bigg ) \\&=: h\Big (dist_Y(x,t), dist(s,t)\Big ), \end{aligned}$$

where dist(s, x) is regarded as a constant in the function h. Let the domain for h be ${\mathbb {R}}\times [dist(s,x), \infty )$, i.e. $dist_Y(x,t) \in {\mathbb {R}}$ and $dist(s,t) \in [dist(s,x), \infty )$ (this is clearly a superset of the set of feasible choices for $dist_Y(x,t)$ and dist(s, t) since x was a vertex with minimum distance to s in $V(Y'(w))$). Then the maximum value of $2 h(dist_Y(x,t), dist(s,t)) / dist(s,t)^2$ on this domain is an upper bound for $\alpha$, and since this function is monotonically decreasing in dist(s, t), its maximum value is attained for dist(s, t) minimum, i.e. $dist(s,t) = dist(s,x)$. Therefore, we can bound $\alpha$ by $2\beta / dist(s,x)^2$, where $\beta$ is the optimum objective function value of the optimization problem

$$\begin{aligned} \max \left\{ \Big (dist(s,x) + dist_Y(x,t)\Big ) \bigg ( \frac{dist(s,x) - dist_Y(x,t)}{2} + \varepsilon \cdot dist(s,x) \bigg ): dist_Y(x,t) \in {\mathbb {R}} \right\} \!. \end{aligned}$$

Solving this optimization problem by elementary analytical methods yields $\alpha \le (1 + \varepsilon )^2$, constituting the first term in the factor bounding the wire delay of $t \in T$.

Fig. 6

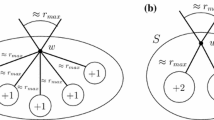
Left Situation of Case 2 in the proof of Theorem 11. Right The worst case is attained for $dist_Y(x,z) = dist_Y(z,t) = \frac{\varepsilon }{4} dist(s,x)$ and $dist_Y(z,w) = 0$. When x was reconnected to s, the green edge was added and the dashed red edge was deleted from the tree (Color figure online)

Case 2: $t \in V(Y'(u_1))$

Let z be the last common vertex on the s-t and s-w paths in Y, as shown in Fig. 6. Applying Lemma 10 twice, we can bound the wire delay to t by

$$\begin{aligned} wd_Y(t)&\le \Big (dist(s,x) + dist_Y(x,z)\Big ) \cdot \bigg (\frac{dist(s,x) - dist_Y(x,z)}{2} + C_1 + C_2\bigg ) \\&\qquad + dist_Y(z,t) \bigg (\frac{dist_Y(z,t)}{2} + C_1 - dist_Y(x,z)- dist_Y(z,w) - dist_Y(z,t)\bigg ) \\&=: f_1\Big (dist_Y(x,z), dist_Y(z,t), dist_Y(z,w)\Big ), \end{aligned}$$

i.e. $\alpha$ is at most the optimum value of the following maximization problem:

$$\begin{aligned} \max&\quad \frac{2 f_1\Big (dist_Y(x,z), dist_Y(z,t), dist_Y(z,w)\Big )}{dist(s,t)^2}\\ s.t.&\quad dist_Y(x,z) + dist_Y(z,t) + dist_Y(z,w) \le C_1, \\&\quad dist_Y(x,z), dist_Y(z,t), dist_Y(z,w) \ge 0. \end{aligned}$$

Now for the partial derivative $\frac{\partial f_1}{\partial \text {dist}_Y(z,t)}$ we have $\frac{\partial f_1}{\partial \text {dist}_Y(z,t)} (y) = C_1 - dist_Y(x,z) - dist_Y(z,w) - y$. This term is non-negative for $y \le C_1 - dist_Y(x,z) - dist_Y(z,w)$. Since we have $dist_Y(z,t) \le C_1 - dist_Y(x,z) - dist_Y(z,w)$ as a constraint, we can deduce that there must be a maximum of $f_1$ located on the hyperplane $dist_Y(x,z) + dist_Y(z,t) + dist_Y(z,w) = C_1$. Therefore, we can define

$$\begin{aligned}&f_2 \Big (dist_Y(x,z), dist_Y(z,t)\Big ) \\&\quad := \Big (dist(s,x) + dist_Y(x,z)\Big ) \bigg (\Big (dist(s,x) - dist_Y(x,z)\Big ) + 2(C_1 + C_2)\bigg )\\&\qquad + dist_Y(z,t)^2 \end{aligned}$$

and bound $\alpha$ by the optimum objective function value of the slightly simplified maximization problem

$$\begin{aligned} \max&\quad \frac{f_2\Big (dist_Y(x,z), dist_Y(z,t)\Big )}{dist(s,t)^2}\\ s.t.&\quad dist_Y(x,z) + dist_Y(z,t) \le C_1, \\&\quad dist_Y(x,z), dist_Y(z,t) \ge 0. \end{aligned}$$

In order to obtain an upper bound for $C_1$ and $C_2$, we use $C_1 \le \frac{\varepsilon }{2} dist(s,x)$ and $C_2 \le \frac{\varepsilon }{2}dist(s,w) \le \frac{\varepsilon }{2}(dist(s,t) + dist_Y(z,t) + dist_Y(z,w))$ (due to the triangle inequality) with the same argumentation as in Case 1 and get

$$\begin{aligned} 2(C_1 + C_2)&\le \varepsilon \bigg ( dist(s,x) + dist(s,t) + dist_Y(z,t) + dist_Y(z,w)\bigg ) \\&= \varepsilon \bigg (dist(s,x) + dist(s,t) - dist_Y(x,z) \\&\quad + dist_Y(x,z) + dist_Y(z,t) + dist_Y(z,w)\bigg ) \\&\le \varepsilon \bigg (\Big (\frac{\varepsilon }{2}+ 1\Big )dist(s,x) + dist(s,t) - dist_Y(x,z) \bigg ), \\ \end{aligned}$$

where we used $dist_Y(x,z) + dist_Y(z,t) + dist_Y(z,w) \le C_1 \le \frac{\varepsilon }{2} dist(s,x)$ to get the last inequality. This allows us to define a third function

$$\begin{aligned}&f_3\Big (dist_Y(x,z), dist_Y(z,t), dist(s,t)\Big ) \\&\quad := \Big (dist(s,x) + dist_Y(x,z)\Big ) \bigg (\Big (\frac{\varepsilon ^2}{2} + \varepsilon + 1\Big ) dist(s,x) +\varepsilon \cdot dist(s,t).\\&\quad \quad - (\varepsilon + 1) dist_Y(x,z)\bigg ) + dist_Y(z,t)^2 \end{aligned}$$

and a corresponding optimization problem

$$\begin{aligned} \max&\quad \frac{f_3\Big (dist_Y(x,z), dist_Y(z,t), dist(s,t)\Big )}{dist(s,t)^2}\\ s.t.&\quad dist_Y(x,z) + dist_Y(z,t) = \frac{\varepsilon }{2}dist(s,x), \\&\quad dist(s,t) \ge dist(s,x), \\&\quad dist_Y(x,z), dist_Y(z,t) \ge 0, \end{aligned}$$

whose optimum objective function value again bounds $\alpha$. Here, we could substitute $C_1$ by its upper bound $\frac{\varepsilon }{2}dist(s,x)$ and use equality in the first constraint due to the fact that the objective function is monotonically increasing in $dist_Y(z,t)$. To justify the constraint $dist(s,t) \ge dist(s,x)$ we recall that x was a vertex with minimum distance to s in $Y'(w)$. In order to obtain an optimization problem in only one variable that we are finally able to solve, we note that the objective function of the above program is monotonically decreasing in dist(s, t). Therefore, we can always assume that dist(s, t) is as small as possible, i.e. $dist(s,t) = dist(s,x)$. Moreover, we can substitute $dist_Y(z,t) = \frac{\varepsilon }{2}dist(s,x) - dist_Y(x,z)$. Finally, for

$$\begin{aligned}&f_4\Big (dist_Y(x,z)\Big ) \\&\quad := \Big (dist(s,x) + dist_Y(x,z)\Big ) \bigg (\Big (\frac{\varepsilon ^2}{2} + 2\varepsilon + 1 \Big )dist(s,x) - \Big (\varepsilon + 1\Big ) dist_Y(x,z)\bigg ) \\&\qquad + \Big (\frac{\varepsilon }{2}dist(s,x) - dist_Y(x,z)\Big )^2 \end{aligned}$$

we arrive at our last optimization problem

$$\begin{aligned} \max \left\{ \frac{f_4\Big (dist_Y(x,z)\Big )}{dist(s,x)^2}: dist_Y(x,z) \in \Big [0, \frac{\varepsilon }{2}dist(s,x)\Big ] \right\} . \end{aligned}$$

Again, this is an optimization problem that can be solved easily applying elementary analysis, and solving it yields a maximum for $dist_Y(x,z) = \frac{\varepsilon }{4} dist(s,x)$, resulting in $\alpha \le \frac{1}{16} \varepsilon ^3 + \frac{3}{4} \varepsilon ^2 +2\varepsilon + 1$, as desired. $\square$

We also get the following side result.

Corollary 12

Given an instance of the MDST problem, an initial solution $Y_0$ and $\varepsilon > 0$, Algorithm 6 computes a solution Y such that

• $C_Y(s) \le \left( 1 + \frac{2}{\varepsilon }\right) \cdot C_{Y_0}(s)$,

• $dist_Y(s,t) \le (1 + \varepsilon ) \cdot dist(s,t)$ for all $t \in T$,

in $O(\tau )$ time, where $\tau$ denotes the time it takes to compute dist(s, v) for all $v \in V(Y_0)$.

Proof

We only need to show the claim for the distances. We proceed as in the proof of Theorem 11: Let $t, x, w, u_1, u_2, C_1, C_2$ and $Y'$ be as in the proof. When $w = t$, we again get that t is connected directly to s, so the claim is true. Otherwise we again have two cases, namely $t \in Y'(u_1)$ and $t \in Y'(u_2)$:

Case 1: $t \in V(Y'(u_1))$

We again use $C_1 \le \frac{\varepsilon }{2} dist(s,x)$, because otherwise $Y'(u_1)$ would have been reconnected to s before. Then we get:

$$\begin{aligned} dist_Y(s,t) \le dist(s,x) + dist_Y(x,t) \le dist(s,x) + C_1 \le \left( 1 + \frac{\varepsilon }{2}\right) dist(s,x), \end{aligned}$$

and this is sufficient, because x was a vertex with minimum distance to s in $Y'(w)$, and so $dist(s,x) \le dist(s,t)$.

Case 2: $t \in V(Y'(u_2))$

Here we will use $C_1 \le \frac{\varepsilon }{2} dist(s,x)$ and $C_2 \le \frac{\varepsilon }{2} dist(s,t)$ as in the proof of Theorem 11, and we directly get:

$$\begin{aligned} dist_Y(s,t)&\le dist(s,x) + dist_Y(x,w) + dist_Y(w, t) \\&\le dist(s,x) + C_1 + C_2 \\&\le dist(s,x) + \frac{\varepsilon }{2} dist(s,x) + \frac{\varepsilon }{2} dist(s,t) \\&\le \left( 1 + \varepsilon \right) dist(s,t), \end{aligned}$$

proving the claim. $\square$

Corollary 12 shows that by setting $c(t) = 0$ for all $t \in T$, Algorithm 6 can also be used to construct shallow-light Steiner trees as introduced in Sect. 1, i.e. Steiner trees Y with $l(Y) \le \alpha \cdot smt(\left\{ s \right\} \cup T)$ and $dist_Y(s,t) \le \beta \cdot dist(s,t)$ for all $t \in T$ for some constants $\alpha , \beta \ge 1.$ Our algorithm then achieves the same tradeoff as the one of Khuller et al. [25], which is known to be optimal in general metric spaces. We will recapitulate this optimality result in Sect. 6 and use it to prove optimality of our algorithm.

The approximation bounds given by Algorithm 6 can also be restated as in the following corollary:

Corollary 13

Given an instance of the MDST problem, an initial solution $Y_0$ with $l(Y_0) \le \beta \cdot smt(\left\{ s \right\} \cup T)$ for some $\beta \ge 1$ and $\varepsilon > 0$, Algorithm 6 computes a tree Y such that $d_Y(t) \le \max \left\{ (1 + \frac{2}{\varepsilon })\beta , \ (1 + \varepsilon )^2, \ 1 + \frac{1}{16} \varepsilon ^3 + \frac{3}{4} \varepsilon ^2 +2\varepsilon \right\} \cdot lb(t)$ for all $t \in T$. $\square$

By Corollary 13, Algorithm 6 is a constant-factor approximation algorithm for the MDST problem for any choice of $\varepsilon$. To get the best approximation guarantee that is independent of the instance parameters, we choose $\varepsilon$ to be (a numerical approximation of) the solution of the equation $(1 + \frac{2}{\varepsilon })\beta = (1 + \varepsilon )^2$, since for $\beta \le 2$ the solution of this equation is small enough to never let the term $1 + \frac{1}{16} \varepsilon ^3 + \frac{3}{4} \varepsilon ^2 +2\varepsilon$ attain the maximum in the bound for the wire delay.⁵ This way we get $d_Y(t) \le \alpha \cdot lb(t)$ for all $t \in T$ for a constant $\alpha$ depending on $\beta$, and Table 1 shows the values of $\alpha$ in dependence of our given metric space and the running time that we are willing to spend for the construction of the initial short Steiner tree.

Table 1 Approximation bounds of Algorithm 6 for different metric spaces: “$O(n \log (n))$” means $O(|T| \log |T|)$ in $({\mathbb {R}}^2, l_1)$ and $O(|V| \log |V| + |E|)$ if (M, dist) is the metric closure of an edge-weighted graph $G=(V,E)$

For the row allowing all polynomial time algorithms we make use of the existence of a PTAS for the Shortest Steiner Tree Problem in $({\mathbb {R}}^2, l_1)$ (see Arora [1] or Rao and Smith [31]) and use the algorithm of Byrka et al. [7] with an approximation ratio of 1.39 for graphs. As algorithms for the second row we use the fact that a minimum terminal spanning tree yields a 2-approximation for the Shortest Steiner Tree Problem in all metric spaces and, as proven by Hwang [21], a $\frac{3}{2}$-approximation in $({\mathbb {R}}^2, l_1)$.⁶ Finally, we note that we can achieve an approximation ratio of 3.39 in all metric spaces in case that the input Steiner tree is a shortest Steiner tree (see e.g. Dreyfus and Wagner [12], Vygen [36], Chu and Wong [9] or Brazil and Zachariasen [6] for algorithms for computing shortest Steiner trees on not too large instances). A lower bound for the best possible maximum ratio between source-sink delay and our lower bound in general metric spaces can be found in Sect. 6. It turns out that our algorithm achieves this bound in case that the input Steiner tree is a shortest Steiner tree.

6 Optimality of the Algorithm

In this section we are going to prove that in a certain sense, the algorithm presented in Sect. 5 is best possible. In order to do so, we adapt a result from Khuller et al. [25] and apply it to our problem. They prove the following:

Theorem 14

(Khuller, Raghavachari, Young 1993) For any $\varepsilon _1 > 0$ and $\varepsilon _2 > \varepsilon _1$ there exists a finite metric space (M, dist) and a terminal set $\left\{ s \right\} \cup T$ with bijective positions $p: \left\{ s \right\} \cup T \rightarrow M$ such that for all Steiner trees Y for $\left\{ s \right\} \cup T$ the implication $dist_Y(s,t) \le (1 + \varepsilon _1) \cdot dist(s,t)$ for all $t \in T \Rightarrow l(Y) > (1 +\frac{2}{\varepsilon _2}) \cdot smt(\left\{ s \right\} \cup T)$ holds.

Proof

Let $\varepsilon _1 > 0$ and $\varepsilon _2 > \varepsilon _1$. For $k \in {\mathbb {N}}$ we consider the metric closure⁷ of the graph $G = (V,E)$ with $V = \left\{ s \right\} \cup T$, where $T = \left\{ c \right\} \cup \left\{ t_1, \ldots , t_k \right\} \cup \left\{ v_1, \ldots , v_q \right\}$ for some $k, q \in {\mathbb {N}}$. The edge set is constructed the following way: Connect s to c by a path of length $2 + \varepsilon _1$ and c to all vertices $t_i$, $i = 1, \ldots , k$, by a path of length $\varepsilon _1 + \delta$ for some $\delta > 0$. We subdivide these paths (including the one from s to c) by inserting vertices $v_1, \ldots , v_q$ of degree 2 so that all edges on these paths have length at most $\gamma$ for some $0 < \gamma < 2$ (q is chosen in such a way that this construction can be done). Finally, we connect s directly to all $t_i$, $i = 1, \ldots , k$, by an edge of length 2 (Fig. 7).

In this graph, we can construct a minimum spanning tree for the terminal set with total length $2 + \varepsilon _1 + k(\varepsilon _1 + \delta )$ by connecting s to c and c to $t_i$, $i = 1, \ldots , k$, and collecting all the terminals $v_i$, $i = 1, \ldots , q$, on the way. Therefore, $smt(\left\{ s \right\} \cup T) = 2 + \varepsilon _1 + k(\varepsilon _1 + \delta )$. On the other hand, let Y be a tree with $dist_Y(s,t) \le (1 + \varepsilon _1) \cdot dist(s,t)$ for all $t \in T$. Then Y must contain all edges $(s, t_i)$, $i = 1, \ldots , k$, and so $l(Y) = smt(\left\{ s \right\} \cup T) + k(2 - \gamma )$. For $\gamma = \delta = \frac{1}{k}$ we then have

$$\begin{aligned} \frac{l(Y)}{smt(\left\{ s \right\} \cup T)} = \frac{smt(\left\{ s \right\} \cup T) + k(2 - \gamma )}{smt(\left\{ s \right\} \cup T)} = 1 + \frac{2k - 1}{3 + \varepsilon _1 + k\varepsilon _1} \end{aligned}$$

Since $\lim _{k \rightarrow \infty } \frac{2k - 1}{3 + \varepsilon _1 + k\varepsilon _1} = \frac{2}{\varepsilon _1} > \frac{2}{\varepsilon _2}$, we may choose k large enough so that $l(Y) > (1 + \frac{2}{\varepsilon _2}) \cdot smt(\left\{ s \right\} \cup T)$, concluding the proof. $\square$

Fig. 7

The graph used to prove Theorem 14. The dashed black edge has length $2 + \varepsilon _1$, dashed blue edges have length $\varepsilon _1 + \delta$ for some small $\delta > 0$ and red edges have length 2. Dashed edges represent paths that are subdivided by edges of length at most $\gamma$ for some small $\gamma > 0$. All vertices except s (including the endpoints of edges of length $\le \gamma$) are terminals terminals (Color figure online)

This result can easily be extended to the MDST problem.

Corollary 15

For any $\varepsilon _1 > 0$ and $\varepsilon _2 > \varepsilon _1$ there exists an instance of the MDST problem with $|M| < \infty$ and $c(t) = 0$ for all $t \in T$ such that for all solutions Y the implication $wd_Y(t) \le (1 + \varepsilon _1)^2 \cdot lb_{wd}(t) \Rightarrow sd(Y) > (1 + \frac{2}{\varepsilon _2}) \cdot lb_{sd}$ holds.

Proof

If $c(t) = 0$ for all $t \in T$, we have $lb_{sd}= r(s) \cdot smt(\left\{ s \right\} \cup T)$ and the implication $dist_Y(s,t) > (1 + \varepsilon ) \cdot dist(s,t) \Rightarrow wd_Y(t) > (1 + \varepsilon )^2 \cdot lb_{wd}(t)$ for all solutions Y, $t \in T$ and $\varepsilon > 0$. Theorem 14 then yields the result. $\square$

Finally, we get a lower bound for the best possible maximum ratio between source-sink delay and our delay lower bounds:

Corollary 16

Let $\varepsilon ^* > 0$ be the positive solution of the equation $1+ \frac{2}{x} = (1+x)^2$. Then for all $0 < \varepsilon < \varepsilon ^*$ there exists an instance of the MDST problem with $|M| < \infty$ and $c(t) = 0$ for all $t \in T$ such that there is no tree Y with $d_Y(t) \le (1 + \varepsilon )^2 \cdot lb(t)$ for all $t \in T$.

Proof

Let $\varepsilon > 0$ with $\varepsilon < \varepsilon ^*$. We use the instance of Theorem 14 with $\varepsilon _1 = \varepsilon$ and $\varepsilon _2 = \varepsilon ^*$ and add a new sink $t^*$ with $p(t^*) = p(s)$. Let $\delta > 0$ be as in the proof of Theorem 14. We set $r(s) = \frac{\delta ^2}{2(1+\varepsilon )^2 \cdot smt(\left\{ s \right\} \cup T)}$ and assume there is a solution Y for this instance with $d_Y(t) \le (1+\varepsilon )^2 \cdot lb(t)$ for all $t \in T$. Consider a sink $t_i$, $i \in \{ 1, ..., k \}$, and assume Y does not connect $t_i$ to s by the direct edge $(s, t_i)$. Then we have

$$\begin{aligned} d_Y(t_i)&\ge \frac{(2 + 2\varepsilon + \delta )^2}{2} > \frac{(2 + 2\varepsilon )^2 + \delta ^2}{2} \\&= (1 + \varepsilon )^2 \bigg (2 + \frac{\delta ^2}{2(1 + \varepsilon )^2}\bigg ) = (1+\varepsilon )^2 lb(t_i), \end{aligned}$$

a contradiction. Therefore, Y must contain all edges $(s, t_i)$, $i = 1, \ldots , k$. But then we get

$$\begin{aligned} \frac{d_Y(t^*)}{lb(t^*)} = \frac{l(Y)}{smt(\left\{ s \right\} \cup T)} > \left( 1 + \frac{2}{\varepsilon ^*}\right) = (1 + \varepsilon ^*)^2 > (1 + \varepsilon )^2, \end{aligned}$$

a contradiction as well. $\square$

As already pointed out before, $(1 + \varepsilon ^*)^2$ with $\varepsilon ^*$ as in Corollary 16 above is exactly the approximation bound that we are able to achieve by application of Algorithm 6 in case that the initial tree $Y_0$ is a shortest Steiner tree (apart from the inaccuracy that stems from the fact that $\varepsilon ^*$ may not be a rational number). Moreover, Corollary 15 tells us that at least for small values of $\varepsilon$, i.e. $\varepsilon > 0$ s.t. $(1 + \varepsilon )^2 \ge 1 + \frac{1}{16} \varepsilon ^3 + \frac{3}{4} \varepsilon ^2 +2\varepsilon$, we will not be able to prove a result as Theorem 11 bounding source and wire delay by functions yielding smaller bounds. So in this sense, Algorithm 6 is best possible.

7 Experimental Results

We ran Algorithm 6 on instances of the rectilinear MDST problem extracted from state-of-the-art chips provided by IBM. In our experiments, we start with a short Steiner tree, apply our algorithm and compare source-sink delays of the initial Steiner tree to the ones of the result of our algorithm. Since computing short Steiner trees is today’s method of choice for VLSI routing, we can expose the benefits of our new algorithm this way. Here, the initial short Steiner tree is constructed optimally for $|T| \le 8$ using the approach of Chu and Wong [9], while it is computed by fast $\frac{3}{2}$-approximation algorithms for larger terminal sets.⁸ We then apply Algorithm 6 on this tree for every value of $\varepsilon \in [0.25, 25]$ that is a multiple of 0.25, and take the solution Y with the lowest delay, where we define the delay of a Steiner tree Y as $d(Y) := \max _{t \in T} d_Y(t) / lb(t)$ throughout this section. The running time is not listed in the table because it is very small on every testcase—we can solve the 719,690 instances on 45-2 in only 226 s even though we call Algorithm 6 100 times on every instance. The machine used for our experiments is an Intel Xeon CPU running at 3.46 GHz.

As one can see, the average number of terminals per instance is very small on every chip. This together with the fact that the source resistance value r(s) is fairly large on most instances explains why the shortest Steiner tree approach is already very close to the lower bound on average. Nevertheless, our algorithm still produces major improvements, reducing the average ratio between delay and lower bound further.

However, more important than the reduction in average delay is the reduction of the maximum ratio between delay and lower bound. Our algorithm can bound this ratio for every sink by a reasonable number, while we have connections with quite bad delays when using the shortest Steiner tree approach. This is a very desirable behaviour of our algorithm, as such outliers are likely to cause trouble in the design process.

Table 2 Experimental results of Algorithm 6: for a tree Y the delay of Y is defined as $d(Y) := \max _{t \in T} d_Y(t) / lb(t)$

On the other hand, one must keep an eye on the increase in wiring length, which may cause routability problems on the chip. Here, one needs a better approach than the one that we used for our experiments (i.e. always taking the tree with the best delay without considering wiring length at all), e.g. bounding the allowed capacitance for a particular tree depending on timing-criticality of the sinks, which is possible in our algorithm by picking the right values of $\varepsilon$. More precisely, it would be possible to fix a parameter $\alpha > 1$ and restrict the solution space of the problem to trees with a capacitance of at most $\alpha$ times the capacitance of a shortest Steiner tree. Given an approximation algorithm for the Shortest Steiner Tree Problem with approximation guarantee $\beta < \alpha$, we would still get a constant-factor approximation algorithm for this restricted version of the problem. It is also possible to bound the length of the resulting tree compared to the initial tree $Y_0$ by a factor of at most $\gamma > 1$, but using our bounds, one would need to choose a value of $\varepsilon$ that is at least $2(1 + \sum _{t \in T} c(t) / l(Y_0)) / (\gamma - 1)$. Since $\varepsilon$ now depends on $\sum _{t \in T} c(t) / l(Y_0)$, our analysis would not yield a constant-factor approximation algorithm.

However, in our experiments we just wanted to show the potential benefits of our algorithm when applied in VLSI design, and looking at the numbers in Table 2, Algorithm 6 proves to be a valuable improvement over the existing approach of exclusively using short Steiner trees to route the connections on a chip.