Improved Pseudo-polynomial Bound for the Value Problem and Optimal Strategy Synthesis in Mean Payoff Games

Abstract

In this work we offer an $O(|V|^2 |E|\, W)$ pseudo-polynomial time deterministic algorithm for solving the Value Problem and Optimal Strategy Synthesis in Mean Payoff Games. This improves by a factor $\log (|V|\, W)$ the best previously known pseudo-polynomial time upper bound due to Brim et al. The improvement hinges on a suitable characterization of values, and a description of optimal positional strategies, in terms of reweighted Energy Games and Small Energy-Progress Measures.

1 Introduction

A Mean Payoff Game (MPG) is a two-player infinite game $\varGamma := (V, E, w, \langle V_0, V_1 \rangle )$, which is played on a finite weighted directed graph, denoted $G^{\varGamma } := ( V, E, w )$, the vertices of which are partitioned into two classes, $V_0$ and $V_1$, according to the player to which they belong. It is assumed that $G^{\varGamma }$ has no sink vertex and that the weights of the arcs are integers, i.e., $w:E\rightarrow \{-W, \ldots , 0, \ldots , W\}$ for some $W\in \mathbf {N}$.

At the beginning of the game a pebble is placed on some vertex $v_s\in V$, and then the two players, named Player 0 and Player 1, move the pebble ad infinitum along the arcs. Assuming the pebble is currently on Player 0’s vertex v, then he chooses an arc $(v,v')\in E$ going out of v and moves the pebble to the destination vertex $v'$. Similarly, assuming the pebble is currently on Player 1’s vertex, then it is her turn to choose an outgoing arc. The infinite sequence $v_s,v,v'\ldots$ of all the encountered vertices is a play. In order to play well, Player 0 wants to maximize the limit inferior of the long-run average weight of the traversed arcs, i.e., to maximize $\liminf _{n\rightarrow \infty } \frac{1}{n}\sum _{i=0}^{n-1}w(v_i, v_{i+1})$, whereas Player 1 wants to minimize the $\limsup _{n\rightarrow \infty } \frac{1}{n}\sum _{i=0}^{n-1}w(v_i, v_{i+1})$. Ehrenfeucht and Mycielski [5] proved that each vertex v admits a value, denoted $\texttt {val}^{\varGamma }(v)$, which each player can secure by means of a memoryless (or positional) strategy, i.e., a strategy that depends only on the current vertex position and not on the previous choices.

Solving an MPG consists in computing the values of all vertices (Value Problem) and, for each player, a positional strategy that secures such values to that player (Optimal Strategy Synthesis). The corresponding decision problem lies in  [11] and it was later shown by Jurdziński [8] to be recognizable with unambiguous polynomial time non-deterministic Turing Machines, thus falling within the complexity class.

The problem of devising efficient algorithms for solving MPG s has been studied extensively in the literature. The first milestone was that of Gurvich, Karzanov and Khachiyan [7], in which they offered an exponential time algorithm for solving a slightly wider class of MPG s called Cyclic Games. Afterwards, Zwick and Paterson [11] devised the first deterministic procedure for computing values in MPG s, and optimal strategies securing them, within a pseudo-polynomial time and polynomial space. In particular, Zwick and Paterson established an $O(|V|^3 |E|\, W)$ upper bound for the time complexity of the Value Problem, as well as an upper bound of $O(|V|^4|E|\, W\,\log (|E|/|V|))$ for that of Optimal Strategy Synthesis [11].

Recently, several research efforts have been spent in studying quantitative extensions of infinite games for modeling quantitative aspects of reactive systems [2–4]. In this context quantities may represent, for example, the power usage of an embedded component, or the buffer size of a networking element. These studies have brought to light interesting connections with MPG s. Remarkably, they have recently led to the design of faster procedures for solving them. In particular, Brim et al.  [3] devised faster deterministic algorithms for solving the Value Problem and Optimal Strategy Synthesis in MPG s within $O(|V|^2 |E|\, W\log (|V|\,W))$ pseudo-polynomial time and polynomial space.

To the best of our knowledge, this is the tightest pseudo-polynomial upper bound on the time complexity of MPG s which is currently known.

Indeed, a wide spectrum of different approaches have been investigated in the literature. For instance, Andersson and Vorobyov [1] provided a fast sub-exponential time randomized algorithm for solving MPG s, whose time complexity can be bounded as $O(|V|^2 |E|\, \exp (2\, \sqrt{|V|\, \ln (|E| / \sqrt{|V|})}+O(\sqrt{|V|}+\ln |E|)))$. Furthermore, Lifshits and Pavlov [9] devised an $O(2^{|V|}\, |V|\, |E|\, \log W)$ singly-exponential time deterministic procedure by considering the potential theory of MPG s.

These results are summarized in Table 1.

Table 1 Complexity of the main Algorithms for solving MPG s

Contribution The main contribution of this work is that to provide an $O(|V|^2|E|\,W)$ pseudo-polynomial time and O(|V|) space deterministic algorithm for solving the Value Problem and Optimal Strategy Synthesis in MPG s. As already mentioned in the introduction, the best previously known procedure has a deterministic time complexity of $O(|V|^2 |E|\, W\log (|V|\,W))$, which is due to Brim et al.  [3]. In this way we improve the best previously known pseudo-polynomial time upper bound by a factor $\log (|V|\, W)$. This result is summarized in the following theorem.

Theorem 1

There exists a deterministic algorithm for solving the Value Problem and Optimal Strategy Synthesis of MPG s within $O(|V|^2 |E|\, W)$ time and O(|V|) space, on any input MPG $\varGamma =(V, E, w, \langle V_0, V_1 \rangle )$. Here, $W=\max _{e\in E}|w_e|$.

In order to prove Theorem 1, this work points out a novel and suitable characterization of values, and a description of optimal positional strategies, in terms of certain reweighting operations that we will introduce later on in Sect. 2.

In particular, we will show that the optimal value $\texttt {val}^{\varGamma }(v)$ of any vertex v is the unique rational number $\nu$ for which v “transits” from the winning region of Player 0 to that of Player 1, with respect to reweightings of the form $w-\nu$. This intuition will be clarified later on in Sect. 3, where Theorem 3 is formally proved.

Concerning strategies, we will show that an optimal positional strategy for each vertex $v\in V_0$ is given by any arc $(v,v')\in E$ which is compatible with certain Small Energy-Progress Measures (SEPMs) of the above mentioned reweighted arenas. This fact is formally proved in Theorem 4 of Sect. 3.

These novel observations are smooth, simple, and their proofs rely on elementary arguments. We believe that they contribute to clarifying the interesting relationship between values, optimal strategies and reweighting operations (with respect to some previous literature, see e.g. [3, 9]). Indeed, they will allow us to prove Theorem 1.

Organization This manuscript is organized as follows. In Sect. 2, we introduce some notation and provide the required background on infinite two-player games and related algorithmic results. In Sect. 3, a suitable relation between values, optimal strategies, and certain reweighting operations is investigated. In Sect. 4, an $O(|V|^2 |E|\, W)$ pseudo-polynomial time and O(|V|) space algorithm, for solving the Value Problem and Optimal Strategies Synthesis in MPG s, is designed and analyzed by relying on the results presented in Sect. 3. In this manner, Sect. 4 actually provides a proof of Theorem 1 which is our main result in this work.

2 Notation and Preliminaries

We denote by $\mathbf {N}$, $\mathbf {Z}$, $\mathbf {Q}$ the set of natural, integer, and rational numbers (respectively). It will be sufficient to consider integral intervals, e.g., $[a,b]:=\{z\in \mathbf {Z} \mid a\le z\le b\}$ and $[a,b):=\{z\in \mathbf {Z} \mid a \le z < b\}$ for any $a,b\in \mathbf {Z}$.

Weighted Graphs Our graphs are directed and weighted on the arcs. Thus, if $G=(V, E, w)$ is a graph, then every arc $e\in E$ is a triplet $e=(u,v,w_e)$, where $w_e = w(u,v)\in \mathbf {Z}$ is the weight of e. The maximum absolute weight is $W := \max _{e\in E} |w_e|$. Given a vertex $u\in V$, the set of its successors is $\texttt {post}(u) = \{ v \in V \mid (u,v) \in E \}$, whereas the set of its predecessors is $\texttt {pre}(u) = \{ v \in V \mid (v,u) \in E \}$. A path is a sequence of vertices $v_0v_1\ldots v_n\ldots$ such that $(v_i, v_{i+1}) \in E$ for every i. We denote by $V^*$ the set of all (possibly empty) finite paths. A simple path is a finite path $v_0v_1\ldots v_n$ having no repetitions, i.e., for any $i,j\in [0,n]$ it holds $v_i \ne v_j$ whenever $i\ne j$. The length of a simple path $\rho =v_0v_1\ldots v_n$ equals n and it is denoted by $|\rho |$. A cycle is a path $v_0v_1\ldots v_{n-1}v_n$ such that $v_0\ldots v_{n-1}$ is simple and $v_n = v_0$. The length of a cycle $C=v_0v_1\ldots v_n$ equals n and it is denoted by |C|. The average weight of a cycle $v_0\ldots v_n$ is $\frac{1}{n} \sum _{i=0}^{n-1} w(v_i,v_{i+1})$. A cycle $C=v_0v_1\ldots v_n$ is reachable from v in G if there exists a simple path $p=vu_1\ldots u_m$ in G such that $p\cap C\ne \emptyset$.

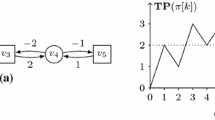
Arenas An arena is a tuple $\varGamma = ( V, E, w, \langle V_0, V_1\rangle )$ where $G^{\varGamma } := ( V, E, w )$ is a finite weighted directed graph and $( V_0, V_1)$ is a partition of V into the set $V_0$ of vertices owned by Player 0, and the set $V_1$ of vertices owned by Player 1. It is assumed that $G^{\varGamma }$ has no sink, i.e., $\texttt {post}(v)\ne \emptyset$ for every $v \in V$; still, we remark that $G^{\varGamma }$ is not required to be a bipartite graph on colour classes $V_0$ and $V_1$. Figure 1 depicts an example.

Fig. 1

An arena $\varGamma$

A game on $\varGamma$ is played for infinitely many rounds by two players moving a pebble along the arcs of $G^{\varGamma }$. At the beginning of the game we find the pebble on some vertex $v_s\in V$, which is called the starting position of the game. At each turn, assuming the pebble is currently on a vertex $v\in V_i$ (for $i=0, 1$), Player i chooses an arc $( v,v')\in E$ and then the next turn starts with the pebble on $v'$.

A play is any infinite path $v_0v_1\ldots v_n\ldots \in V^*$ in $\varGamma$. For any $i\in \{0,1\}$, a strategy of Player i is any function $\sigma _i:V^*\times V_i\rightarrow V$ such that for every finite path $p'v$ in $G^{\varGamma }$, where $p'\in V^*$ and $v\in V_i$, it holds that $(v, \sigma _i(p', v))\in E$. A strategy $\sigma _i$ of Player i is positional (or memoryless) if $\sigma _i(p, v_n) = \sigma _i(p', v'_m)$ for every finite paths $pv_n=v_0\ldots v_{n-1}v_n$ and $p'v'_m=v'_0\ldots v'_{m-1}v'_m$ in $G^{\varGamma }$ such that $v_n=v'_m\in V_i$. The set of all the positional strategies of Player i is denoted by $\varSigma ^M_i$. A play $v_0v_1\ldots v_n\ldots$ is consistent with a strategy $\sigma \in \varSigma _i$ if $v_{j+1} = \sigma (v_0v_1\ldots v_j)$ whenever $v_j\in V_i$.

Given a starting position $v_s\in V$, the outcome of strategies $\sigma _0 \in \varSigma _0$ and $\sigma _1 \in \varSigma _1$, denoted $\texttt {outcome}^{\varGamma }(v_s, \sigma _0, \sigma _1)$, is the unique play that starts at $v_s$ and is consistent with both $\sigma _0$ and $\sigma _1$.

Given a memoryless strategy $\sigma _i\in \varSigma ^M_i$ of Player i in $\varGamma$, then $G^{\varGamma }_{\sigma _i}=( V, E_{\sigma _i}, w)$ is the graph obtained from $G^{\varGamma }$ by removing all the arcs $( v,v')\in E$ such that $v\in V_i$ and $v'\ne \sigma _i(v)$; we say that $G^{\varGamma }_{\sigma _i}$ is obtained from $G^{\varGamma }$ by projection w.r.t. $\sigma _i$.

Concluding this subsection, the notion of reweighting is recalled. For any weight function $w,w':E\rightarrow \mathbf {Z}$, the reweighting of $\varGamma =(V, E, w, \langle V_0, V_1\rangle )$ w.r.t. $w'$ is the arena $\varGamma ^{w'}= (V, E, w', \langle V_0, V_1\rangle )$. Also, for $w:E\rightarrow \mathbf {Z}$ and any $\nu \in \mathbf {Z}$, we denote by $w+\nu$ the weight function $w'$ defined as $w'_e := w_e+\nu$ for every $e\in E$. Indeed, we shall consider reweighted games of the form $\varGamma ^{w-q}$, for some $q\in \mathbf {Q}$. Notice that the corresponding weight function $w':E\rightarrow \mathbf {Q}:e\mapsto w_e-q$ is rational, while we required the weights of the arcs to be always integers. To overcome this issue, it is sufficient to re-define $\varGamma ^{w-q}$ by scaling all the weights by a factor equal to the denominator of $q\in \mathbf {Q}$, namely, to re-define: $\varGamma ^{w-q}:=\varGamma ^{D\cdot w-N}$, where $N,D\in \mathbf {N}$ are such that $q=N/D$ and $\gcd (N,D)=1$. This re-scaling will not change the winning regions of the corresponding games, and it has the significant advantage of allowing for a discussion (and an algorithmics) which is strictly based on integer weights.

Mean Payoff Games A Mean Payoff Game (MPG) [3, 5, 11] is a game played on some arena $\varGamma$ for infinitely many rounds by two opponents, Player 0 gains a payoff defined as the long-run average weight of the play, whereas Player 1 loses that value. Formally, the Player 0’s payoff of a play $v_0v_1\ldots v_n\ldots$ in $\varGamma$ is defined as follows:

$$\begin{aligned} \texttt {MP}_0(v_0v_1\ldots v_n\ldots ):=\liminf _{n\rightarrow \infty } \frac{1}{n}\sum _{i=0}^{n-1}w(v_i, v_{i+1}). \end{aligned}$$

The value secured by a strategy $\sigma _0\in \varSigma _0$ in a vertex v is defined as:

$$\begin{aligned} \texttt {val}^{\sigma _0}(v):= \inf _{\sigma _1\in \varSigma _1}{} \texttt {MP}_0\big (\texttt {outcome}^{\varGamma }(v, \sigma _0, \sigma _1)\big ), \end{aligned}$$

Notice that payoffs and secured values can be defined symmetrically for the Player 1 (i.e., by interchanging the symbol 0 with 1 and inf with sup).

Ehrenfeucht and Mycielski [5] proved that each vertex $v\in V$ admits a unique value, denoted $\texttt {val}^{\varGamma }(v)$, which each player can secure by means of a memoryless (or positional) strategy. Moreover, uniform positional optimal strategies do exist for both players, in the sense that for each player there exist at least one positional strategy which can be used to secure all the optimal values, independently with respect to the starting position $v_s$. Thus, for every MPG $\varGamma$, there exists a strategy $\sigma _0\in \varSigma ^M_0$ such that $\texttt {val}^{\sigma _0}(v)\ge \texttt {val}^{\varGamma }(v)$ for every $v\in V$, and there exists a strategy $\sigma _1\in \varSigma ^M_1$ such that $\texttt {val}^{\sigma _1}(v)\le \texttt {val}^{\varGamma }(v)$ for every $v\in V$. Indeed, the (optimal) value of a vertex $v\in V$ in the MPG $\varGamma$ is given by:

$$\begin{aligned} \texttt {val}^{\varGamma }(v)= \sup _{\sigma _0\in \varSigma _0}\texttt {val}^{\sigma _0}(v) = \inf _{\sigma _1\in \varSigma _1}\texttt {val}^{\sigma _1}(v). \end{aligned}$$

Thus, a strategy $\sigma _0\in \varSigma _0$ is optimal if $\texttt {val}^{\sigma _0}(v)=\texttt {val}^{\varGamma }(v)$ for all $v\in V$. A strategy $\sigma _0\in \varSigma _0$ is said to be winning for Player 0 if $\texttt {val}^{\sigma _0}(v)\ge 0$, and $\sigma _1\in \varSigma _1$ is winning for Player 1 if $\texttt {val}^{\sigma _1}(v) < 0$. Correspondingly, a vertex $v\in V$ is a winning starting position for Player 0 if $\texttt {val}^{\varGamma }(v)\ge 0$, otherwise it is winning for Player 1. The set of all winning starting positions of Player i is denoted by $\mathcal{W}_i$ for $i\in \{0,1\}$. An example is shown in Fig. 2.

Fig. 2

An MPG on $\varGamma$, played from left to right, whose payoff equals $\frac{-1+1}{2}=0$

A finite variant of MPG s is well-known in the literature [3, 5, 11]. Here, the game stops as soon as a cyclic sequence of vertices is traversed (i.e., as soon as one of the two players moves the pebble into a previously visited vertex). It turns out that this finite variant is equivalent to the infinite one [5]. Specifically, the values of an MPG are in relationship with the average weights of its cycles, as stated in the next lemma.

Lemma 1

(Brim et al. [3]) Let $\varGamma = ( V, E, w, \langle V_0, V_1\rangle )$ be an MPG. For all $\nu \in \mathbf {Q}$, for all positional strategies $\sigma _0\in \varSigma ^M_0$ of Player 0, and for all vertices $v\in V$, the value $\texttt {val}^{\sigma _0}(v)$ is greater than $\nu$ if and only if all cycles C reachable from v in the projection graph $G^{\varGamma }_{\sigma _0}$ have an average weight w(C) / |C| greater than $\nu$.

The proof of Lemma 1 follows from the memoryless determinacy of MPG s. We remark that a proposition which is symmetric to Lemma 1 holds for Player 1 as well: for all $\nu \in \mathbf {Q}$, for all positional strategies $\sigma _1\in \varSigma ^M_1$ of Player 1, and for all vertices $v\in V$, the value $\texttt {val}^{\sigma _1}(v)$ is less than $\nu$ if and only if all cycles reachable from v in the projection graph $G^{\varGamma }_{\sigma _1}$ have an average weight less than $\nu$.

Also, it is well-known [3, 5] that each value $\texttt {val}^{\varGamma }(v)$ is contained within the following set of rational numbers:

$$\begin{aligned} S_{\varGamma }=\left\{ \frac{N}{D} \;|\;D\in [1, |V|],\, N\in [-D\, W, D\, W] \right\} {.} \end{aligned}$$

Notice that $|S_{\varGamma }|\le |V|^2 W$.

The present work tackles on the algorithmics of the following two classical problems:

• Value Problem. Compute for each vertex $v\in V$ the (rational) optimal value $\texttt {val}^{\varGamma }(v)$.

• Optimal Strategy Synthesis. Compute an optimal positional strategy $\sigma _0\in \varSigma ^M_0$.

Currently, the asymptotically fastest pseudo-polynomial time algorithm for solving both problems is a deterministic procedure whose time complexity has been bounded as $O(|V|^2|E|\, W\,\log (|V|\, W))$ [3]. This result has been achieved by devising a binary-search procedure that ultimately reduces the Value Problem and Optimal Strategy Synthesis to the resolution of yet another family of games known as the Energy Games. Even though we do not rely on binary-search in the present work, and thus we will introduce some truly novel ideas that diverge from the previous solutions, still, we will reduce to solving multiple instances of Energy Games. For this reason, the Energy Games are recalled in the next paragraph.

Energy Games and Small Energy-Progress Measures An Energy Game (EG) is a game that is played on an arena $\varGamma$ for infinitely many rounds by two opponents, where the goal of Player 0 is to construct an infinite play $v_0v_1\ldots v_n\ldots$ such that for some initial credit $c\in \mathbf {N}$ the following holds:

$$\begin{aligned} c + \sum _{i=0}^{j}w(v_i, v_{i+1})\ge 0,\quad \text {, for all } j \ge 0. \end{aligned}$$

(1)

Given a credit $c\in \mathbf {N}$, a play $v_0v_1\ldots v_n\ldots$ is winning for Player 0 if it satisfies (1), otherwise it is winning for Player 1. A vertex $v\in V$ is a winning starting position for Player 0 if there exists an initial credit $c\in \mathbf {N}$ and a strategy $\sigma _0\in \varSigma _0$ such that, for every strategy $\sigma _1\in \varSigma _1$, the play $\texttt {outcome}^{\varGamma }(v, \sigma _0, \sigma _1)$ is winning for Player 0. As in the case of MPG s, the EG s are memoryless determined [3], i.e., for every $v\in V$, either v is winning for Player 0 or v is winning for Player 1, and (uniform) memoryless strategies are sufficient to win the game. In fact, as shown in the next lemma, the decision problems of MPG s and EG s are intimately related.

Lemma 2

(Brim et al. [3]) Let $\varGamma =( V, E, w, \langle V_0, V_1 \rangle )$ be an arena. For all threshold $\nu \in \mathbf {Q}$, for all vertices $v\in V$, Player 0 has a strategy in the MPG $\varGamma$ that secures value at least $\nu$ from v if and only if, for some initial credit $c\in \mathbf {N}$, Player 0 has a winning strategy from v in the reweighted EG $\varGamma ^{w-\nu }$.

In this work we are especially interested in the Minimum Credit Problem (MCP) for EG s: for each winning starting position v, compute the minimum initial credit $c^*=c^*(v)$ such that there exists a winning strategy $\sigma _0\in \varSigma ^M_0$ for Player 0 starting from v. A fast pseudo-polynomial time deterministic procedure for solving MCP s comes from [3].

Theorem 2

(Brim et al. [3]) There exists a deterministic algorithm for solving the MCP within $O(|V|\,|E|\,W)$ pseudo-polynomial time, on any input EG $(V, E, w, \langle V_0, V_1\rangle )$.

The algorithm mentioned in Theorem 2 is the Value-Iteration algorithm analyzed by Brim et al. [3]. Its rationale relies on the notion of Small Energy-Progress Measures (SEPMs). These are bounded, non-negative and integer-valued functions that impose local conditions to ensure global properties on the arena, in particular, witnessing that Player 0 has a way to enforce conservativity (i.e., non-negativity of cycles) in the resulting game’s graph. Recovering standard notation, see e.g. [3], let us denote $\mathcal{C}_\varGamma =\{n\in \mathbf {N} \mid n\le |V|\, W\}\cup \{\top \}$ and let $\preceq$ be the total order on $\mathcal{C}_\varGamma$ defined as $x\preceq y$ if and only if either $y=\top$ or $x,y\in \mathbf {N}$ and $x\le y$.

In order to cast the minus operation to range over $\mathcal{C}_{\varGamma }$, let us consider an operator $\ominus :\mathcal{C}_\varGamma \times \mathbf {Z} \rightarrow \mathcal{C}_\varGamma$ defined as follows:

$$\begin{aligned} a\ominus b := \left\{ \begin{array}{l@{\quad }l} \max (0, a-b), &{} \text { if } a\ne \top \text { and } a-b\le |V|\,W ; \\ a\ominus b = \top , &{} \text { otherwise.} \\ \end{array}\right. \end{aligned}$$

Given an EG $\varGamma$ on vertex set $V = V_0 \cup V_1$, a function $f:V\rightarrow \mathcal{C}_\varGamma$ is a Small Energy-Progress Measure (SEPM) for $\varGamma$ if and only if the following two conditions are met:

• 1. if $v\in V_0$, then $f(v)\succeq f(v') \ominus w(v,v')$ for some $( v, v')\in E$;

• 2. if $v\in V_1$, then $f(v)\succeq f(v') \ominus w(v,v')$ for all $( v, v')\in E$.

The values of a SEPM, i.e., the elements of the image f(V), are called the energy levels of f. It is worth to denote by $V_f=\{v\in V\mid f(v)\ne \top \}$ the set of vertices having finite energy. Given a SEPM f and a vertex $v\in V_0$, an arc $(v, v')\in E$ is said to be compatible with f whenever $f(v)\succeq f(v')\ominus w(v,v')$; moreover, a positional strategy $\sigma ^f_0\in \varSigma ^M_0$ is said to be compatible with f whenever for all $v\in V_0$, if $\sigma ^f_0(v)=v'$ then $( v,v' )\in E$ is compatible with f. Notice that, as mentioned in [3], if f and g are SEPMs, then so is the minimum function defined as: $h(v)=\min \{f(v), g(v)\}$ for every $v\in V$. This fact allows one to consider the least SEPM, namely, the unique SEPM $f^*:V\rightarrow \mathcal{C}_\varGamma$ such that, for any other SEPM $g:V\rightarrow \mathcal{C}_\varGamma$, the following holds: $f^*(v)\preceq g(v)$ for every $v\in V$. Also concerning SEPMs, we shall rely on the following lemmata. The first one relates SEPMs to the winning region $\mathcal{W}_0$ of Player 0 in EG s.

Lemma 3

(Brim et al. [3]) Let $\varGamma =( V, E, w, \langle V_0, V_1\rangle )$ be an EG.

• 1. If f is any SEPM of the EG $\varGamma$ and $v\in V_{f}$, then v is a winning starting position for Player 0 in the EG $\varGamma$. Stated otherwise, $V_f\subseteq \mathcal{W}_0$;

• 2. If $f^*$ is the least SEPM of the EG $\varGamma$, and v is a winning starting position for Player 0 in the EG $\varGamma$, then $v\in V_{f^*}$. Thus, $V_{f^*}=\mathcal{W}_0$.

Also notice that the following bound holds on the energy levels of any SEPM (actually by definition of $\mathcal{C}_{\varGamma }$).

Lemma 4

Let $\varGamma =( V, E, w, \langle V_0, V_1 \rangle )$ be an EG. Let f be any SEPM of $\varGamma$. Then, for every $v\in V$ either $f(v)=\top$ or $0\le f(v)\le |V|\, W$.

Value-Iteration Algorithm The algorithm devised by Brim et al. for solving the MCP in EG s is known as Value-Iteration [3]. Given an EG $\varGamma$ as input, the Value-Iteration aims to compute the least SEPM $f^*$ of $\varGamma$. This simple procedure basically relies on a lifting operator $\delta$. Given $v\in V$, the lifting operator $\delta (\cdot , v): [V\rightarrow \mathcal{C}_{\varGamma }]\rightarrow [V\rightarrow \mathcal{C}_\varGamma ]$ is defined by $\delta (f,v)=g$, where:

$$\begin{aligned} g(u)=\left\{ \begin{array}{l@{\quad }l} f(u) &{} \text { if }\; u\ne v \\ \min \{f(v') \ominus w(v,v') \mid v'\in \texttt {post}(v) \} &{} \text { if }\; u=v\in V_0 \\ \max \{f(v') \ominus w(v,v') \mid v'\in \texttt {post}(v) \} &{} \text { if }\; u=v\in V_1 \\ \end{array} \right. \end{aligned}$$

We also need the following definition. Given a function $f:V\rightarrow \mathcal{C}_\varGamma$, we say that f is inconsistent in v whenever one of the following two holds:

• 1. $v\in V_0$ and for all $v'\in \texttt {post}(v)$ it holds $f(v) \prec f(v') \ominus w(v,v')$;

• 2. $v\in V_1$ and there exists $v'\in \texttt {post}(v)$ such that $f(v) \prec f(v') \ominus w(v,v')$.

To start with, the Value-Iteration algorithm initializes f to the constant zero function, i.e., $f(v)=0$ for every $v\in V$. Furthermore, the procedure maintains a list $\L$ of vertices in order to witness the inconsistencies of f. Initially, $v\in V_0\cap \L$ if and only if all arcs going out of v are negative, while $v\in V_1\cap \L$ if and only if v is the source of at least one negative arc. Notice that checking the above conditions takes time O(|E|).

As long as the list $\L$ is nonempty, the algorithm picks a vertex v from $\L$ and performs the following:

• 1. Apply the lifting operator $\delta (f,v)$ to f in order to resolve the inconsistency of f in v;

• 2. Insert into $\L$ all vertices $u\in \texttt {pre}(v){\setminus } \L$ witnessing a new inconsistency due to the increase of f(v).

  (The same vertex can’t occur twice in $\L$, i.e., there are no duplicate vertices in $\L$.)

The algorithm terminates when $\L$ is empty. This concludes the description of the Value-Iteration algorithm.

As shown in [3], the update of $\L$ following an application of the lifting operator $\delta (f,v)$ requires $O(|\texttt {pre}(v)|)$ time. Moreover, a single application of the lifting operator $\delta (\cdot , v)$ takes $O(|\text {post}(v)|)$ time at most. This implies that the algorithm can be implemented so that it will always halt within $O(|V|\,|E|\, W)$ time (the reader is referred to [3] in order to grasp all the details of the proof of correctness and complexity).

Remark The Value-Iteration procedure lends itself to the following basic generalization, which turns out to be of a pivotal importance in order to best suit our technical needs. Let $f^*$ be the least SEPM of the EG $\varGamma$. Recall that, as a first step, the Value-Iteration algorithm initializes f to be the constant zero function. Here, we remark that it is not necessary to do that really. Indeed, it is sufficient to initialize f to be any function $f_0$ which bounds $f^*$ from below, that is to say, to initialize f to any $f_0:V\rightarrow \mathcal{C}_\varGamma$ such that $f_0(v) \preceq f^*(v)$ for every $v\in V$. Soon after, $\L$ can be initialized in a natural way: just insert v into $\L$ if and only if $f_0$ is inconsistent at v. This initialization still requires O(|E|) time and it doesn’t affect the correctness of the procedure.

So, in the rest of this work we shall assume to have at our disposal a procedure named Value-Iteration(), which takes as input an EG $\varGamma =(V, E, w, \langle V_0, V_1\rangle )$ and an initial function $f_0$ that bounds from below the least SEPM $f^*$ of the EG $\varGamma$ (i.e., such that $f_0(v)\preceq f^*(v)$ for every $v\in V$). Then, Value-Iteration() outputs the least SEPM $f^*$ of the EG $\varGamma$ within $O(|V|\,|E|\,W)$ time and working with O(|V|) space.

3 Values and Optimal Positional Strategies from Reweightings

This section aims to show that values and optimal positional strategies of MPG s admit a suitable description in terms of reweighted arenas. This fact will be the crux for solving the Value Problem and Optimal Strategy Synthesis in $O(|V|^2 |E|\, W)$ time.

3.1 On Optimal Values

A simple representation of values in terms of Farey sequences is now observed, then, a characterization of values in terms of reweighted arenas is provided.

Optimal values and Farey sequences. Recall that each value $\texttt {val}^{\varGamma }(v)$ is contained within the following set of rational numbers:

$$\begin{aligned} S_{\varGamma }=\left\{ \frac{N}{D} \;|\;D\in [1, |V|],\, N\in [-DW, DW] \right\} . \end{aligned}$$

Let us introduce some notation in order to handle $S_{\varGamma }$ in a way that is suitable for our purposes. Firstly, we write every $\nu \in S_{\varGamma }$ as $\nu =i+F$, where $i=i_\nu =\lfloor \nu \rfloor$ is the integral and $F=F_\nu =\{\nu \}=\nu -i$ is the fractional part. Notice that $i\in [-W, W]$ and that F is a non-negative rational number having denominator at most |V|.

As a consequence, it is worthwhile to consider the Farey sequence $\mathcal{F}_n$ of order $n=|V|$. This is the increasing sequence of all irreducible fractions from the (rational) interval [0, 1] with denominators less than or equal to n. In the rest of this paper, $\mathcal{F}_n$ denotes the following sorted set:

$$\begin{aligned} \mathcal{F}_n=\left\{ \frac{N}{D} \;|\;0 \le N \le D\le n, \gcd (N,D)=1 \right\} . \end{aligned}$$

Farey sequences have numerous and interesting properties, in particular, many algorithms for generating the entire sequence $\mathcal{F}_n$ in time $O(n^2)$ are known in the literature [6], and these rely on Stern-Brocot trees and mediant properties. Notice that the above mentioned quadratic running time is optimal, as it is well-known that the sequence $\mathcal{F}_n$ has $s(n) = \frac{3\,n^2}{\pi ^2} + O(n\ln n) = \varTheta (n^2)$ terms.

Throughout the article, we shall assume that $F_0, \ldots , F_{s-1}$ is an increasing ordering of $\mathcal{F}_n$, so that $\mathcal{F}_n=\{F_j\}_{j=0}^{s-1}$ and $F_j < F_{j+1}$ for every j.

Also notice that $F_0=0$ and $F_{s-1}=1$.

For example, $\mathcal{F}_5=\{0, \frac{1}{5}, \frac{1}{4}, \frac{1}{3}, \frac{2}{5}, \frac{1}{2}, \frac{3}{5}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, 1 \}$.

At this point, $S_{\varGamma }$ can be represented as follows:

$$\begin{aligned} S_{\varGamma } = [-W, W) + \mathcal{F}_{|V|} = \left\{ i+F_j \;|\;i\in [-W, W),\, j\in [0, s-1]\right\} . \end{aligned}$$

The above representation of $S_{\varGamma }$ will be convenient in a while.

Optimal values and reweightings. Two introductory lemmata are shown below, then, a characterization of optimal values in terms of reweightings is provided.

Lemma 5

Let $\varGamma = ( V, E, w, \langle V_0, V_1 \rangle )$ be an MPG and let $q\in \mathbf {Q}$ be a rational number having denominator $D\in \mathbf {N}$. Then, $\texttt {val}^{\varGamma }(v) = \frac{1}{D}\texttt {val}^{\varGamma ^{w+q}}(v) - q$ holds for every $v\in V$.

Proof

Let us consider the play $\texttt {outcome}^{\varGamma ^{w+q}}(v, \sigma _0, \sigma _1)=v_0v_1\ldots v_n\ldots$ By the definition of $\texttt {val}^{\varGamma }(v)$, and by that of reweighting $\varGamma ^{w+q}$ ($= \varGamma ^{D\cdot w+N}$), the following holds:

$$\begin{aligned} \begin{array}{lll} \texttt {val}^{\varGamma ^{w+q}}(v) &{}=&{} \sup _{\sigma _0\in \varSigma _0}\inf _{\sigma _1\in \varSigma _1} \texttt {MP}_0(\texttt {outcome}^{\varGamma ^{w+q}}(v, \sigma _0, \sigma _1)) \\ &{} &{} \\ &{}=&{} \sup _{\sigma _0\in \varSigma _0}\inf _{\sigma _1\in \varSigma _1} \lim \inf _{n\rightarrow \infty }\frac{1}{n}\sum _{i=0}^{n-1}(D\cdot w(v_i, v_{i+1}) + N)\;\; \text {(if } q=N/D)\\ &{} &{} \\ &{}=&{} D\cdot \sup _{\sigma _0\in \varSigma _0}\inf _{\sigma _1\in \varSigma _1} \texttt {MP}_0(\texttt {outcome}^{\varGamma }(v, \sigma _0, \sigma _1)) + N\\ &{} &{} \\ &{}=&{} D\cdot \texttt {val}^{\varGamma }(v) + N. \end{array} \end{aligned}$$

Then, $\texttt {val}^{\varGamma }(v) = \frac{1}{D}\texttt {val}^{\varGamma ^{w+q}}(v) - \frac{N}{D} = \frac{1}{D}\texttt {val}^{\varGamma ^{w+q}}(v) - q$ holds for every $v\in V$.

$\square$

Lemma 6

Given an MPG $\varGamma = ( V, E, w, \langle V_0, V_1 \rangle )$, let us consider the reweightings:

$$\begin{aligned} \varGamma _{i,j}= \varGamma ^{w-i-F_j},\, \text { for any } i\in [-W, W]\text { and }j\in [0, s-1], \end{aligned}$$

where $s=|\mathcal{F}_{|V|}|$ and $F_j$ is the jth term of the Farey sequence $\mathcal{F}_{|V|}$.

Then, the following propositions hold:

• 1. For any $i\in [-W, W]$ and $j\in [0,s-1]$, we have:

  $$\begin{aligned} v\in \mathcal{W}_0(\varGamma _{i,j}) \text { if and only if } \texttt {val}^{\varGamma }(v)\ge i+ F_j; \end{aligned}$$

• 2. For any $i\in [-W, W]$ and $j\in [1,s-1]$, we have:

  $$\begin{aligned} v\in \mathcal{W}_1(\varGamma _{i,j}) \text { if and only if } \texttt {val}^{\varGamma }(v)\le i + F_{j-1}. \end{aligned}$$

Proof

• 1. Let us fix arbitrarily some $i\in [-W, W]$ and $j\in [0,s-1]$.

  Assume that $F_j = N_j/D_j$ for some $N_j,D_j\in \mathbf {N}$.

  Since

  $$\begin{aligned} \varGamma _{i,j}=( V, E, D_j(w - i) - N_j, \langle V_0, V_1 \rangle ), \end{aligned}$$

  then by Lemma 5 (applyed to $q=-i-F_j$) we have:

  $$\begin{aligned} \texttt {val}^{\varGamma }(v) = \frac{1}{D_j}\texttt {val}^{\varGamma _{i,j}}(v) + i + F_j. \end{aligned}$$

  Recall that $v\in \mathcal{W}_0(\varGamma _{i,j})$ if and only if $\texttt {val}^{\varGamma _{i,j}}(v)\ge 0$.

  Hence, we have $v\in \mathcal{W}_0(\varGamma _{i,j})$ if and only if the following inequality holds:

  $$\begin{aligned} \texttt {val}^{\varGamma }(v)&= \frac{1}{D_j}\texttt {val}^{\varGamma _{i,j}}(v) + i + F_j \\&\ge i + F_j. \end{aligned}$$

  This proves Item 1.

• 2. The argument is symmetric to that of Item 1, but with some further observations.

  Let us fix arbitrarily some $i\in [-W, W]$ and $j\in [1,s-1]$. Assume that $F_j = N_j/D_j$ for some $N_j,D_j\in \mathbf {N}$. Since $\varGamma _{i,j}=( V, E, D_j(w - i) - N_j, \langle V_0, V_1 \rangle )$, then by Lemma 5 we have $\texttt {val}^{\varGamma }(v) = \frac{1}{D_j}\texttt {val}^{\varGamma _{i,j}}(v) + i + F_j$. Recall that $v\in \mathcal{W}_1(\varGamma _{i,j})$ if and only if $\texttt {val}^{\varGamma _{i,j}}(v) < 0$.

  Hence, we have $v\in \mathcal{W}_1(\varGamma _{i,j})$ if and only if the following inequality holds:

  $$\begin{aligned} \texttt {val}^{\varGamma }(v)&= \frac{1}{D_j}\texttt {val}^{\varGamma _{i,j}}(v) + i + F_j \\&< i + F_j. \end{aligned}$$

  Now, recall from Sect. 2 that $\texttt {val}^{\varGamma }(v)\in S_{\varGamma }$, where

  $$\begin{aligned} S_{\varGamma }=\left\{ i+F_j \;|\;i\in [-W, W),\, j\in [0, s-1]\right\} {.} \end{aligned}$$

  By hypothesis we have:

  $$\begin{aligned} j \ge 1 \text { and } 0\le F_{j-1} < F_j, \end{aligned}$$

  thus, at this point, $v\in W_1(\varGamma _{i,j})$ if and only if $\texttt {val}^{\varGamma }(v) \le i + F_{j-1}$.

  This proves Item 2.

$\square$

We are now in the position to provide a simple characterization of values in terms of reweightings.

Theorem 3

Given an MPG $\varGamma = ( V, E, w, \langle V_0, V_1 \rangle )$, let us consider the reweightings:

$$\begin{aligned} \varGamma _{i,j}=\varGamma ^{w-i-F_j},\,\text { for any } i\in [-W, W] \text { and } j\in [1, s-1], \end{aligned}$$

where $s=|\mathcal{F}_{|V|}|$ and $F_j$ is the jth term of the Farey sequence $\mathcal{F}_{|V|}$.

Then, the following holds:

$$\begin{aligned} \texttt {val}^{\varGamma }(v) = i + F_{j-1} \text { if and only if } v\in \mathcal{W}_0(\varGamma _{i,j-1})\cap \mathcal{W}_1(\varGamma _{i, j}). \end{aligned}$$

Proof

Let us fix arbitrarily some $i\in [-W, W]$ and $j\in [1, s-1]$.

By Item 1 of Lemma 6, we have $v\in \mathcal{W}_0(\varGamma _{i,j-1})$ if and only if $\texttt {val}^{\varGamma }(v) \ge i + F_{j-1}$. Symmetrically, by Item 2 of Lemma 6, we have $v\in \mathcal{W}_1(\varGamma _{i, j})$ if and only if $\texttt {val}^{\varGamma }(v) \le i + F_{j-1}$. Whence, by composition, $v\in \mathcal{W}_0(\varGamma _{i,j-1})\cap \mathcal{W}_1(\varGamma _{i, j})$ if and only if $\texttt {val}^{\varGamma }(v) = i + F_{j-1}$. $\square$

3.2 On Optimal Positional Strategies

The present subsections aims to provide a suitable description of optimal positional strategies in terms of reweighted arenas. An introductory lemma is shown next.

Lemma 7

Let $\varGamma = ( V, E, w, \langle V_0, V_1 \rangle )$ be an MPG, the following hold:

• 1. If $v\in V_0$, let $v'\in \texttt {post}(v)$. Then $\texttt {val}^{\varGamma }(v')\le \texttt {val}^{\varGamma }(v)$ holds.

• 2. If $v\in V_1$, let $v'\in \texttt {post}(v)$. Then $\texttt {val}^{\varGamma }(v')\ge \texttt {val}^{\varGamma }(v)$ holds.

• 3. Given any $v\in V_0$, consider the reweighted EG $\varGamma _v= \varGamma ^{w-\texttt {val}^{\varGamma }(v)}$.

  Let $f_v:V\rightarrow \mathcal{C}_{\varGamma _v}$ be any SEPM of the EG $\varGamma _v$ such that $v\in V_{f_v}$ (i.e., $f_v(v)\ne \top$). Let $v'_{f_v}\in V$ be any vertex out of v such that $(v, v'_{f_v})\in E$ is compatible with $f_v$ in $\varGamma _v$.

  Then, $\texttt {val}^{\varGamma }(v'_{f_v})=\texttt {val}^{\varGamma }(v)$.

Proof

• 1. It is sufficient to construct a strategy $\sigma ^v_0\in \varSigma ^M_{0}$ securing to Player 0 a payoff at least $\texttt {val}^{\varGamma }(v')$ from v in the MPG $\varGamma$. Let $\sigma ^{v'}_0\in \varSigma ^M_{0}$ be a strategy securing payoff at least $\texttt {val}^{\varGamma }(v')$ from $v'$ in $\varGamma$. Then, let $\sigma ^v_0$ be defined as follows:

  $$\begin{aligned} \sigma ^v_0(u) = \left\{ \begin{array}{l@{\quad }l} \sigma ^{v'}_0(u), &{} \text { if }\; u\in V_0{\setminus }\{v\}; \\ \sigma ^{v'}_0(v), &{} \text { if }\; u=v \text { and } v\; is \text { reachable from } v' \text { in } G^{\varGamma }_{\sigma ^{v'}_0}; \\ v', &{} \text { if }\; u=v \text { and } v\; is\; not \text { reachable from } v' \text { in } G^{\varGamma }_{\sigma ^{v'}_0}. \end{array}\right. \end{aligned}$$

  We argue that $\sigma ^v_0$ secures payoff at least $\texttt {val}^{\varGamma }(v')$ from v in $\varGamma$. First notice that, by Lemma 1 (applied to $v'$), all cycles C that are reachable from $v'$ in $\varGamma$ satisfy:

  $$\begin{aligned} \frac{w(C)}{|C|}\ge \texttt {val}^{\varGamma }(v'). \end{aligned}$$

  The fact is that any cycle reachable from v in $G^{\varGamma }_{\sigma ^v_0}$ is also reachable from $v'$ in $G^{\varGamma }_{\sigma ^{v'}_0}$ (by definition of $\sigma ^v_0$), therefore, the same inequality holds for all cycles reachable from v. At this point, the thesis follows again by Lemma 1 (applied to v, in the inverse direction). This proves Item 1.

• 2. The proof of Item 2 is symmetric to that of Item 1.

• 3. Firstly, notice that $\texttt {val}^{\varGamma }(v'_{f_v})\le \texttt {val}^{\varGamma }(v)$ holds by Item 1. To conclude the proof it is sufficient to show $\texttt {val}^{\varGamma }(v'_{f_v})\ge \texttt {val}^{\varGamma }(v)$. Recall that $(v, v'_{f_v})\in E$ is compatible with $f_v$ in $\varGamma _v$ by hypothesis, that is:

  $$\begin{aligned} f_v(v)\succeq f_v(v'_{f_v}) \ominus \big (w(v, v'_{f_v})-\texttt {val}^{\varGamma }(v)\big ). \end{aligned}$$

  This, together with the fact that $v\in V_{f_v}$ (i.e., $f_v(v)\ne \top$) also holds by hypothesis, implies that $v'_{f_v}\in V_f$ (i.e., $f_v(v'_{f_v}) \ne \top$). Thus, by Item 1 of Lemma 3, $v'_{f_v}$ is a winning starting position of Player 0 in the EG $\varGamma _v$. Whence, by Lemma 2, it holds that $\texttt {val}^{\varGamma }(v'_{f_v})\ge \texttt {val}^{\varGamma }(v)$. This proves Item 3.

$\square$

We are now in position to provide a sufficient condition, for a positional strategy to be optimal, which is expressed in terms of reweighted EG s and their SEPMs.

Theorem 4

Let $\varGamma = ( V , E, w, \langle V_0, V_1 \rangle )$ be an MPG. For each $v\in V$, consider the reweighted EG $\varGamma _v = \varGamma ^{w-\texttt {val}^{\varGamma }(v)}$. Let $f_{v}:V\rightarrow \mathcal{C}_{\varGamma _v}$ be any SEPM of $\varGamma _v$ such that $v\in V_{f_v}$ (i.e., $f_v(v)\ne \top$). Moreover, assume: $f_{v_1}=f_{v_2}$ whenever $\texttt {val}^{\varGamma }(v_1)=\texttt {val}^{\varGamma }(v_2)$.

When $v\in V_0$, let $v'_{f}\in V$ be any vertex out of v such that $(v, v'_{f})\in E$ is compatible with $f_v$ in the EG $\varGamma _v$, and consider the positional strategy $\sigma ^*_0\in \varSigma ^M_{0}$ defined as follows:

$$\begin{aligned} \sigma ^*_0(v) = v'_{f_v} \text {, for every } v\in V_0. \end{aligned}$$

Then, $\sigma ^*_0$ is an optimal positional strategy for Player 0 in the MPG $\varGamma$.

Proof

Let us consider the projection graph $G_{\sigma ^*_0}^{\varGamma }=( V, E_{\sigma ^*_0}, w)$. Let $v\in V$ be any vertex. In order to prove that $\sigma ^*_0$ is optimal, it is sufficient (by Lemma 1) to show that every cycle C that is reachable from v in $G_{\sigma ^*_0}^{\varGamma }$ satisfies $\frac{w(C)}{|C|}\ge \texttt {val}^{\varGamma }(v)$.

• Preliminaries. Let $v \in V$ and let C be any cycle of length $|C|\ge 1$ that is reachable from v in $G^{\varGamma }_{\sigma ^*_0}$. Then, there exists a path $\rho$ of length $|\rho |\ge 1$ in $G^{\varGamma }_{\sigma ^*_0}$ and such that: if $|\rho |=1$, then $\rho =\rho _0\rho _1=vv$; otherwise, if $|\rho |>1$, then:

  $$\begin{aligned} \rho = \rho _0 \ldots \rho _{|\rho |} = v v_1 v_2 \ldots v_k u_1 u_2 \ldots u_{|C|} u_1, \end{aligned}$$

  where $vv_1\ldots v_k$ is a simple path, for some $k\ge 0$ and $u_1\ldots u_{|C|}u_1=C$ (Fig. 3).

  Fig. 3

  

  A cycle C that is reachable from v through $v_1\ldots v_k$ in $G^{\varGamma }_{\sigma ^*_0}$

• Fact 1. It holds $\texttt {val}^{\varGamma }(\rho _{i})\le \texttt {val}^{\varGamma }(\rho _{i+1})$ for every $i\in [0, |\rho |)$. Proof (of Fact 1) If $\rho _i\in V_0$ then $\texttt {val}^{\varGamma }(\rho _{i})=\texttt {val}^{\varGamma }(\rho _{i+1})$ by Item 3 of Lemma 7; otherwise, if $\rho _i\in V_1$, then $\texttt {val}^{\varGamma }(\rho _{i})\le \texttt {val}^{\varGamma }(\rho _{i+1})$ by Item 2 of Lemma 7. This proves Fact 1. In particular, notice that $\texttt {val}^{\varGamma }(v)\le \texttt {val}^{\varGamma }(u_1)$ when $|\rho |> 1$. $\square$

• Fact 2. Assume $C=u_1\ldots u_{|C|}u_1$, then $\texttt {val}^{\varGamma }(u_i)=\texttt {val}^{\varGamma }(u_1)$ for every $i\in [0, |C|]$. Proof (of Fact 2) By Fact 1, $\texttt {val}^{\varGamma }(u_{i-1})\le \texttt {val}^{\varGamma }(u_i)$ for every $i\in [2, |C|]$, as well as $\texttt {val}^{\varGamma }(u_{|C|})\le \texttt {val}^{\varGamma }(u_1)$. Then, the following chain of inequalities holds:

  $$\begin{aligned} \texttt {val}^{\varGamma }(u_1)\le \texttt {val}^{\varGamma }(u_2)\le \ldots \le \texttt {val}^{\varGamma }(u_{|C|})\le \texttt {val}^{\varGamma }(u_1). \end{aligned}$$

  Since the first and the last value of the chain are actually the same, i.e., $\texttt {val}^{\varGamma }(u_1)$, then, all these inequalities are indeed equalities. This proves Fact 2. $\square$

• Fact 3. The following holds for every $i\in [0, |\rho |)$:

  $$\begin{aligned} f_{\rho _i}(\rho _i), f_{\rho _i}(\rho _{i+1})\ne \top \text { and } f_{\rho _i}(\rho _i) \ge f_{\rho _i}(\rho _{i+1}) - w(\rho _i, \rho _{i+1}) + \texttt {val}^{\varGamma }(\rho _{i}). \end{aligned}$$

  Proof (of Fact 3) Firstly, we argue that any arc $(\rho _i, \rho _{i+1})\in E$ is compatible with $f_{\rho _i}$ in $\varGamma _{\rho _i}$. Indeed, if $\rho _i\in V_0$, then $(\rho _i, \rho _{i+1})$ is compatible with $f_{\rho _i}$ in $\varGamma _{\rho _i}$ because $\rho _{i+1}=\sigma ^*_0(\rho _i)$ by hypothesis; otherwise, if $\rho _i\in V_1$, then $( \rho _i, x)$ is compatible with $f_{\rho _i}$ in $\varGamma _{\rho _i}$ for every $x\in \texttt {post}(\rho _{i})$, in particular for $x=\rho _{i+1}$, by definition of SEPM. At this point, since $(\rho _i, \rho _{i+1})$ is compatible with $f_{\rho _i}$ in $\varGamma _{\rho _i}$, then:

  $$\begin{aligned} f_{\rho _i}(\rho _i) \succeq f_{\rho _i}(\rho _{i+1}) \ominus \big (w(\rho _i, \rho _{i+1}) - \texttt {val}^{\varGamma }(\rho _{i})\big ). \end{aligned}$$

  Now, recall that $\rho _i\in V_{f_{\rho _i}}$ (i.e., $f_{\rho _i}(\rho _i)\ne \top$) holds for every $\rho _i$ by hypothesis. Since $f_{\rho _i}(\rho _i)\ne \top$ and the above inequality holds, then we have $f_{\rho _i}(\rho _{i+1})\ne \top$. Thus, we can safely write:

  $$\begin{aligned} f_{\rho _i}(\rho _i) \ge f_{\rho _i}(\rho _{i+1}) - w(\rho _i, \rho _{i+1}) + \texttt {val}^{\varGamma }(\rho _{i}). \end{aligned}$$

  This proves Fact 3. $\square$

• Fact 4. Assume that the cycle $C=u_1\ldots u_{|C|}u_1$ is such that:

  $$\begin{aligned} \texttt {val}^{\varGamma }(u_i)=\texttt {val}^{\varGamma }(u_1)\ge \texttt {val}^{\varGamma }(v), \text { for every } i\in [1,|C|]. \end{aligned}$$

  Then, provided that $u_{|C|+1}= u_1$, the following holds for every $i\in [1, |C|]$:

  $$\begin{aligned} f_{u_1}(u_1), f_{u_{i+1}}(u_{i+1})\ne \top \text { and } f_{u_1}(u_1)\ge & {} f_{u_{i+1}}(u_{i+1}) - \sum _{j=1}^{i} w(u_j, u_{j+1})\\&+\, i\cdot \texttt {val}^{\varGamma }(v). \end{aligned}$$

  Proof (of Fact 4) Firstly, notice that $f_{u_1}(u_1), f_{u_{i+1}}(u_{i+1})\ne \top$ holds by hypothesis. The proof proceeds by induction on $i\in [1, |C|]$.

  • Base Case. Assume that $|C|=1$, so that $C=u_1u_1$. Then $f_{u_1}(u_1)\ge f_{u_1}(u_1) - w(u_1, u_1) + \texttt {val}^{\varGamma }(u_1)$ follows by Fact 3. Since $\texttt {val}^{\varGamma }(u_1)\ge \texttt {val}^{\varGamma }(v)$ by hypothesis, then the thesis follows.

  • Inductive Step. Assume by induction hypothesis that the following holds:

    $$\begin{aligned} f_{u_1}(u_1) \ge f_{u_{i}}(u_{i}) - \sum _{j=1}^{i-1} w(u_j, u_{j+1}) + (i-1)\cdot \texttt {val}^{\varGamma }(v). \end{aligned}$$

    By Fact 3, we have:

    $$\begin{aligned} f_{u_{i}}(u_{i})\ge f_{u_{i}}(u_{i+1}) - w(u_{i}, u_{i+1}) + \texttt {val}^{\varGamma }(u_{i}). \end{aligned}$$

    Since $\texttt {val}^{\varGamma }(u_{i+1})=\texttt {val}^{\varGamma }(u_{i})$ holds by hypothesis, then we have $f_{u_{i+1}} = f_{u_i}$. Recall that $\texttt {val}^{\varGamma }(u_i)\ge \texttt {val}^{\varGamma }(v)$ also holds by hypothesis.

    Thus, we obtain the following:

    $$\begin{aligned} f_{u_1}(u_1) \ge f_{u_{i+1}}(u_{i+1}) - \sum _{j=1}^{i} w(u_j, u_{j+1}) + i\cdot \texttt {val}^{\varGamma }(v). \end{aligned}$$

    This proves Fact 4.

• We are now in position to show that every cycle C that is reachable from v in $G^{\varGamma }_{\sigma ^*_0}$ satisfies $w(C)/|C|\ge \texttt {val}^{\varGamma }(v)$. By Fact 1 and Fact 2, we have $\texttt {val}^{\varGamma }(v)\le \texttt {val}^{\varGamma }(u_1)=\texttt {val}^{\varGamma }(u_i)$ for every $i\in [1, |C|]$. At this point, we apply Fact 4. Consider the specialization of Fact 4 when $i=|C|$ and also recall that $u_{|C|+1}=u_1$. Then, we have the following:

  $$\begin{aligned} f_{u_1}(u_1) \ge f_{u_1}(u_1) - \sum _{j=1}^{|C|} w(u_j, u_{j+1}) + |C|\cdot \texttt {val}^{\varGamma }(v). \end{aligned}$$

  As a consequence, the following lower bound holds on the average weight of C:

  $$\begin{aligned} \frac{w(C)}{|C|} = \frac{1}{|C|}\sum _{j=1}^{|C|} w(u_j, u_{j+1}) \ge \texttt {val}^{\varGamma }(v), \end{aligned}$$

  which concludes the proof.

$\square$

Remark 1

Notice that Theorem 4 holds, in particular, when f is the least SEPM $f^*$ of the reweighted EG $\varGamma _v$. This follows because $v\in V_{f^*}$ always holds for the least SEPM $f^*$ of the EG $\varGamma _v$, as shown next: by Lemma 2 and by definition of $\varGamma _v$, then v is a winning starting position for Player 0 in the EG $\varGamma _v$ (for some initial credit); now, since $f^*_v$ is the least SEPM of the EG $\varGamma _v$, then $v\in V_{f^*}$ follows by Item 2 of Lemma 3.

4 An $O(|V|^2 |E|\, W)$ Time Algorithm for Solving the Value Problem and Optimal Strategy Synthesis in MPG s

This section offers a deterministic algorithm for solving the Value Problem and Optimal Strategy Synthesis of MPG s within $O(|V|^2 |E|\, W)$ time and O(|V|) space, on any input MPG $\varGamma = ( V, E, w, \langle V_0, V_1\rangle )$.

Let us now recall some notation in order describe the algorithm in a suitable way.

Given an MPG $\varGamma = ( V, E, w, \langle V_0, V_1 \rangle )$, consider again the following reweightings:

$$\begin{aligned} \varGamma _{i,j}=\varGamma ^{w-i-F_j},\,\text { for any } i\in [-W, W] \text { and } j\in [0, s-1], \end{aligned}$$

where $s=|\mathcal{F}_{|V|}|$ and $F_j$ is the jth term of $\mathcal{F}_{|V|}$.

Assuming $F_j=N_j/D_j$ for some $N_j,D_j\in \mathbf {N}$, we focus on the following weights:

$$\begin{aligned} w_{i,j}=&w-i-F_j = w-i-\frac{N_j}{D_j}; \\ w'_{i,j}=&D_j\, w_{i,j} = D_j\, (w-i) - N_j. \end{aligned}$$

Recall that $\varGamma _{i,j}$ is defined as $\varGamma _{i,j}:=\varGamma ^{w'_{i,j}}$, which is an arena having integer weights. Also notice that, since $F_0 < \cdots < F_{s-1}$ is monotone increasing, then the corresponding weight functions $w_{i,j}$ can be ordered in a natural way, i.e., $w_{-W, 1} > w_{-W, 2} > \cdots > w_{W-1, s-1} >\cdots > w_{W, s-1}$. In the rest of this section, we denote by $f^*_{w'_{i,j}}:V\rightarrow \mathcal{C}_{\varGamma _{i,j}}$ the least SEPM of the reweighted EG $\varGamma _{i,j}$. Moreover, the function $f^*_{i,j}:V\rightarrow \mathbf {Q}$, defined as $f^*_{i,j}(v):=\frac{1}{D_j}f^*_{w'_{i,j}}(v)$ for every $v\in V$, is called the rational scaling of $f^*_{w'_{i,j}}$.

4.1 Description of the Algorithm

In this section we shall describe a procedure whose pseudo-code is given below in Algorithm 1. It takes as input an arena $\varGamma =(V, E, w, \langle V_0, V_1 \rangle )$, and it aims to return a tuple $( \mathcal{W}_0, \mathcal{W}_1, \nu , \sigma ^*_0 )$ such that: $\mathcal{W}_0$ and $\mathcal{W}_1$ are the winning regions of Player 0 and Player 1 in the MPG $\varGamma$ (respectively), $\nu :V\rightarrow S_\varGamma$ is a map sending each starting position $v\in V$ to its optimal value, i.e., $\nu (v)=\texttt {val}^{\varGamma }(v)$, and finally, $\sigma ^*_0:V_0\rightarrow V$ is an optimal positional strategy for Player 0 in the MPG $\varGamma$.

The intuition underlying Algorithm 1 is that of considering the following sequence of weights:

$$\begin{aligned}&w_{-W, 1} > w_{-W, 2} > \cdots > w_{-W, s-1} > w_{-W+1, 1} > w_{-W+1, 2} > \cdots > w_{W-1, s-1}\\&\qquad > \cdots > w_{W, s-1} \end{aligned}$$

where the key idea is that to rely on Theorem 3 at each one of these steps, testing whether a transition of winning regions has occurred.

Stated otherwise, the idea is to check, for each vertex $v\in V$, whether v is winning for Player 1 with respect to the current weight $w_{i,j}$, meanwhile recalling whether v was winning for Player 0 with respect to the immediately preceding element $w_{\texttt {prev}(i,j)}$ in the weight sequence above.

If such a transition occurs, say for some $\hat{v} \in \mathcal{W}_0(\varGamma _{\texttt {prev}(i,j)}) \cap \mathcal{W}_1(\varGamma _{i,j})$, then one can easily compute $\texttt {val}^{\varGamma }(\hat{v})$ by relying on Theorem 3; Also, at that point, it is easy to compute an optimal positional strategy, provided that $\hat{v}\in V_0$, by relying on Theorem 4 and Remark 1 in that case.

Each one of these phases, in which one looks at transitions of winning regions, is named Scan Phase. A graphical intuition of Algorithm 1 is given in Fig. 4.

An in-depth description of the algorithm and of its pseudo-code now follows.

Fig. 4

An illustration of Algorithm 1

• Initialization Phase To start with, the algorithm performs an initialization phase. At line 1, Algorithm 1 initializes the output variables $\mathcal{W}_0$ and $\mathcal{W}_1$ to be empty sets. Notice that, within the pseudo-code, the variables $\mathcal{W}_0$ and $\mathcal{W}_1$ represent the winning regions of Player 0 and Player 1, respectively; also, the variable $\nu$ represents the optimal values of the input MPG $\varGamma$, and $\sigma ^*_0$ represents an optimal positional strategy for Player 0 in the input MPG $\varGamma$. Secondly, at line 2, an array variable $f:V\rightarrow \mathcal{C}_{\varGamma }$ is initialized to $f(v)=0$ for every $v\in V$; throughout the computation, the variable f represents a SEPM. Next, at line 3, the greatest absolute weight W is assigned as $W=\max _{e\in E}|w_e|$, an auxiliary weight function $w'$ is initialized as $w'=w+W$, and a “denominator” variable is initialized as $D=1$. Concluding the initialization phase, at line 4 the size (i.e., the total number of terms) of $\mathcal{F}_{|V|}$ is computed and assigned to the variable s. This size can be computed very efficiently with the algorithm devised by Pawlewicz and Pătraşcu [10].

• Scan Phases After initialization, the procedure performs multiple Scan Phases. Each one of these is indexed by a pair of integers (i, j), where $i\in [-W, W]$ (at line 5) and $j\in [1, s-1]$ (at line 7). Thus, the index i goes from $-W$ to W, and for each i, the index j goes from 1 to $s-1$.

  At each step, we say that the algorithm goes through the (i, j)th scan phase. For each scan phase, we also need to consider the previous scan phase, so that the previous index $\texttt {prev}(i,j)$ shall be defined as follows: the predecessor of the first index is $\texttt {prev}(-W,1) := (-W, 0)$; if $j>1$, then $\texttt {prev}(i,j) := (i,j-1)$; finally, if $j=1$ and $i>-W$, then $\texttt {prev}(i,j) := (i-1, s-1)$.

  At the (i, j)th scan phase, the algorithm considers the rational number $z_{i,j}\in S_\varGamma$ defined as:

  $$\begin{aligned} z_{i,j} := i+F[j], \end{aligned}$$

  where $F[j]=N_j/D_j$ is the jth term of $\mathcal{F}_{|V|}$. For each j, F[j] can be computed very efficiently, on the fly, with the algorithm of Pawlewicz and Pătraşcu [10]. Notice that, since $F[0] < \cdots < F[s-1]$ is monotonically increasing, then the values $z_{i,j}$ are scanned in increasing order as well. At this point, the procedure aims to compute the rational scaling $f^*_{i,j}$ of the least SEPM $f^*_{w'_{i,j}}$, i.e.,

  $$\begin{aligned} f := f^*_{i,j} =\frac{1}{D_j} f^*_{w'_{i,j}}. \end{aligned}$$

  This computation is really at the heart of the algorithm and it goes from line 8 to line 15. To start with, at line 8 and line 9, the previous rational scaling $f^*_{\texttt {prev}(i,j)}$ and the previous weight function $w_{\texttt {prev}(i,j)}$ (i.e., those considered during the previous scan phase) are saved into the auxiliary variables $\texttt {prev\_}f$ and $\texttt {prev\_}w$.

  Remark. Since the values $z_{i,j}$ are scanned in increasing order of magnitude, then $\texttt {prev\_}f=f^*_{\texttt {prev}(i,j)}$ bounds from below $f^*_{i,j}$. That is, it holds for every $v\in V$ that:

  $$\begin{aligned} \texttt {prev\_}f(v)=f^*_{\texttt {prev}(i,j)}(v)\preceq f^*_{i,j}. \end{aligned}$$

  The underlying intuition, at this point, is that of computing the energy levels of $f=f^*_{i,j}$ firstly by initializing them to the energy levels of the previous scan phase, i.e., to $\texttt {prev\_}f=f^*_{\texttt {prev}(i,j)}$, and then to update them monotonically upwards by executing the Value-Iteration algorithm for EG s.

  Further details of this pivotal step now follow. Firstly, since the Value-Iteration has been designed to work with integer numerical weights only [3], then the weights $w_{i,j}=w-z_{i,j}$ have to be scaled from $\mathbf {Q}$ to $\mathbf {Z}$: this is performed in the standard way, from lines 12 to 15, by considering the numerator $N_j$ and the denominator $D_j$ of F[j], and then by setting:

  $$\begin{aligned} w'_{i,j}(e):=D_j\, \big (w(e)-i\big )-N_j \text {, for every } e\in E. \end{aligned}$$

  The initial energy levels are also scaled up from $\mathbf {Q}$ to $\mathbf {Z}$ by considering the values: $\lceil D_j\, \texttt {prev\_}f(v)\rceil$, for every $v\in V$ (line 15). At this point the least SEPM of $\varGamma ^{w'_{i,j}}$ is computed, at line 15, by invoking $\texttt {Value-Iteration}(\varGamma ^{w'_{i,j}}, \lceil D_j\, \texttt {prev\_}f\rceil )$, that is, by executing on input $\varGamma ^{w'_{i,j}}$ the Value-Iteration with initial energy levels given by: $\lceil D_j\,\texttt {prev\_}f(v)\rceil$ for every $v\in V$. Soon after that, the energy levels have to be scaled back from $\mathbf {Z}$ to $\mathbf {Q}$, so that, in summary, at line 15 they becomes:

  $$\begin{aligned} f=f^*_{i,j}=\frac{1}{D_j}\,\texttt {Value-Iteration}\left( \varGamma ^{w'_{i,j}}, \lceil D_j\, \texttt {prev\_}f\rceil \right) . \end{aligned}$$

  The correctness of lines 14–15 will be proved in Lemma 8.

  Here, let us provide a sketch of the argument:

  • 1. Since $F_0 < \cdots < F_{s-1}$ is monotone increasing, then the sequence $\{w'_{i,j}\}_{(i,j)}$ is monotone decreasing, i.e., for every i, j and $e\in E$, $w'_{\texttt {prev}(i,j)}(e) > w'_{i,j}(e)$. Whence, the sequence of rational scalings $\{f^*_{i,j}\}_{i,j}$ is monotone increasing, i.e., $f^*_{i, j}\preceq f^*_{\texttt {prev}(i, j)}$ holds at the (i, j)th step. The proof is in Lemma 8.

  • 2. At the (i, j)th iteration of line 8, it holds that $\texttt {prev\_}f=f^*_{\texttt {prev}(i, j)}$.

    This invariant property is also proved as part of Lemma 8.

  • 3. Since $\texttt {prev\_}f=f^*_{\texttt {prev}(i,j)}$, then $\texttt {prev\_}f\preceq f^*_{i,j}$.

    Thus, one can prove that $D_j\, \texttt {prev\_f}\preceq f^*_{w'_{i,j}}$.

  • 4. Since $w'_{i,j}(e)\in \mathbf {Z}$ for every $e\in E$, then $f^*_{w'_{i,j}}(v)\in \mathbf {Z}$ for every $v\in V$, so that $\lceil D_j\, \texttt {prev\_f}(v)\rceil \preceq f^*_{w'_{i,j}}(v)$ holds for every $v\in V$ as well.

  • 5. This implies that it is correct to execute the Value-Iteration, on input $\varGamma ^{w'_{i,j}}$, with initial energy levels given by: $\lceil D_j\,\texttt {prev\_}f(v)\rceil$ for every $v\in V$.

  Back to us, once $f=f^*_{i,j}$ has been determined, then for each $v\in V$ the condition:

  $$\begin{aligned} v \overset{?}{\in } \mathcal{W}_0(\varGamma _{\texttt {prev}(i,j)})\cap \mathcal{W}_1(\varGamma _{i,j}), \end{aligned}$$

  is checked at line 17: it is not difficult to show that, for this, it is sufficient to test whether both $\texttt {prev\_f}(v)\ne \top$ and $f(v)=\top$ hold on v (it follows by Lemma 8).

  If $v\in \mathcal{W}_0(\varGamma _{\texttt {prev}(i,j)})\cap \mathcal{W}_1(\varGamma _{i,j})$ holds, then the algorithm relies on Theorem 3 in order to assign the optimal value as follows: $\nu (v):=\texttt {val}^{\varGamma }(v)=z_{\texttt {prev}(i,j)}$ (line 18). If $\nu (v)\ge 0$, then v is added to the winning region $\mathcal{W}_0$ at line 20. Otherwise, $\nu (v)<0$ and v is added to $\mathcal{W}_1$ at line 22.

  To conclude, from lines 23 to 27, the algorithm proceeds as follows: if $v\in V_0$, then it computes an optimal positional strategy $\sigma ^*_0(v)$ for Player 0 in $\varGamma$: this is done by testing for each $u\in \texttt {post}(v)$ whether $(v,u)\in E$ is an arc compatible with $\texttt {prev\_}f$ in $\varGamma _{\texttt {prev}(i,j)}$; namely, whether the following holds for some $u\in \texttt {post}(v)$:

  $$\begin{aligned} \text {prev}\_ f(v) \overset{?}{\succeq } \text {prev}\_f(u) \ominus \text {prev}\_w(v, u). \end{aligned}$$

  If $(v,u)\in E$ is found to be compatible with $\texttt {prev\_}f$ at that point, then $\sigma ^*_0(v) := u$ gets assigned and the arc (v, u) becomes part of the optimal positional strategy returned to output. Indeed, the correctness of such an assignment relies on Theorem 4 and Remark 1.

  This concludes the description of the scan phases and also that of Algorithm 1.

4.2 Proof of Correctness

Now we formally prove the correctness of Algorithm 1. The following lemma shows some basic invariants that are maintained throughout the computation.

Lemma 8

Algorithm 1 keeps the following invariants throughout the computation:

• 1. For every $i\in [-W, W]$ and every $j\in [1, s-1]$, it holds that:

  $$\begin{aligned} f^*_{\texttt {prev}(i,j)}(v) \preceq f^*_{i,j}(v), \text { for every } v\in V; \end{aligned}$$

• 2. At the (i, j)th iteration of line 8, it holds that: $\texttt {prev\_}f=f^*_{\texttt {prev}(i, j)}$;

• 3. At the (i, j)th iteration of line 8, it holds that: $\lceil D_j \texttt {prev\_}f \rceil \preceq f^*_{{w'_{i,j}}}$;

• 4. At the (i, j)th iteration of line 15, it holds that:

  $$\begin{aligned} \frac{1}{D_j} \texttt {Value-Iteration}\left( \varGamma ^{w'_{i,j}}, \lceil D_j \texttt {prev\_}f \rceil \right) = f^*_{i,j}. \end{aligned}$$

Proof

• Proof (of Item 1). Recall that $w_{i,j}:=w-i-F_j$. Since $F_0< \cdots < F_{s-1}$ is monotone increasing, then: $w_{i,j}(e) < w_{\texttt {prev}(i,j)}(e)$ holds for every $e \in E$.

  In order to prove the thesis, consider the following function:

  $$\begin{aligned} g:V\rightarrow \mathbf {Q} \cup \{\top \} : v\mapsto \min \big ( f^*_{\texttt {prev}(i,j)}(v), f^*_{i,j}(v)\big ). \end{aligned}$$

  We show that $D_{\texttt {prev}(i,j)}\, g$ is a SEPM of $\varGamma ^{w'_{\texttt {prev}(i,j)}}$. There are four cases, according to whether $v\in V_0$ or $v\in V_1$, and $g(v)= f^*_{\texttt {prev}(i,j)}(v)$ or $g(v)= f^*_{i,j}(v)$.

  • Case: $v\in V_0$. Then, the following holds for some $u\in \texttt {post}(v)$:

    • Case: $g(v)= f^*_{\texttt {prev}(i,j)}(v)$:

      

    • Case: $g(v) = f^*_{i,j}(v)$:

      

      This means that (v, u) is an arc compatible with $D_{\texttt {prev}(i,j)}g$ in $\varGamma ^{w'_{\texttt {prev}(i,j)}}$.

  • Case: $v\in V_1$. The same argument shows that $(v,u)\in E$ is compatible with $D_{\texttt {prev}(i,j)}g$ in $\varGamma ^{w'_{\texttt {prev}(i,j)}}$, but it holds for all $u\in \texttt {post}(v)$ in this case.

  This proves that $D_{\texttt {prev}(i,j)}\, g$ is a SEPM of $\varGamma ^{w'_{\texttt {prev}(i,j)}}$. Since $f^*_{w'_{\texttt {prev}(i,j)}}$ is the least SEPM of $\varGamma ^{w'_{\texttt {prev}(i,j)}}$, then:

  $$\begin{aligned} f^*_{w'_{\texttt {prev}(i,j)}}(v)\preceq D_{\texttt {prev}(i,j)}\, g(v), \text { for every } v\in V. \end{aligned}$$

  Since $f^*_{w'_{\texttt {prev}(i,j)}}=D_{\texttt {prev}(i,j)}\,f^*_{\texttt {prev}(i,j)}$ and $g=\min ( f^*_{\texttt {prev}(i,j)}, f^*_{i,j})$, then:

  $$\begin{aligned} D_{\texttt {prev}(i,j)}\,f^*_{\texttt {prev}(i,j)} \preceq D_{\texttt {prev}(i,j)}\, \min ( f^*_{\texttt {prev}(i,j)}, f^*_{i,j}). \end{aligned}$$

  Whence $f^*_{\texttt {prev}(i,j)} = \min ( f^*_{\texttt {prev}(i,j)}, f^*_{i,j})$.

  This proves that $f^*_{\texttt {prev}(i,j)}(v) \preceq f^*_{i,j}(v)$ holds for every $v\in V$.

• Fact 1. Next, we prove that if Item 2 holds at the (i, j)th scan phase, then both Item 3 and Item 4 hold at the (i, j)th scan phase as well. Proof (of Fact 1) Assume that Item 2 holds. Let us prove Item 3 first. Since $f^*_{\texttt {prev}(i,j)} \preceq f^*_{i,j}$ holds by Item 1, and since $\texttt {prev\_}f=f^*_{\texttt {prev}(i,j)}$ holds by hypothesis, then $\texttt {prev\_}f(v)\preceq f^*_{i,j}(v)$ holds for every $v\in V$. Since $w'_{i,j}=D_j\, w_{i,j}$ and $f^*_{w'_{i,j}}=D_j\, f^*_{i,j}$, then $D_j\, \texttt {prev\_f}(v)\preceq f^*_{w'_{i,j}}(v)$ holds for every $v\in V$. Since $w'_{i,j}(e)\in \mathbf {Z}$ for every $e\in E$, then $f^*_{w'_{i,j}}(v)\in \mathbf {Z}$ for every $v\in V$, so that $\lceil D_j\, \texttt {prev\_f}(v)\rceil \preceq f^*_{w'_{i,j}}(v)$ holds for every $v\in V$ as well. This proves Item 3. We show Item 4 now. Since Item 3 holds, at line 15 it is correct to initialize the starting energy levels of Value-Iteration() to $\lceil D_j\, \texttt {prev\_}f(v) \rceil$ for every $v \in V$, in order to execute the Value-Iteration on input $\varGamma ^{w'_{i,j}}$. This implies the following:

  $$\begin{aligned} \texttt {Value-Iteration}(\varGamma ^{w'_{i,j}}, \lceil D_j\, \texttt {prev\_}f \rceil ) = f^*_{w'_{i,j}}. \end{aligned}$$

  We know that $\frac{1}{D_j}\, f^*_{w'_{i,j}}=f^*_{i,j}$. This proves that Item 4 holds and concludes the proof of Fact 1. $\square$

• Fact 2. We now prove that Item 2 holds at each iteration of line 8. Proof (of Fact 2) The proof proceeds by induction on (i, j). Base Case. Let us consider the first iteration of line 8; i.e., the iteration indexed by $i=-W$ and $j=1$. Recall that, at line 2 of Algorithm 1, the function f is initialized as $f(v)=0$ for every $v\in V$. Notice that f is really the least SEPM $f^*_{-W, 0}$ of $\varGamma _{-W, 0}=\varGamma ^{w+W}$, because every arc $e\in E$ has a non-negative weight in $\varGamma ^{w+W}$, i.e., $w_e+W\ge 0$ for every $e\in E$. Hence, at the first iteration of line 8, the following holds:

  $$\begin{aligned} \texttt {prev\_}f = \mathbf 0 = f^*_{-W, 0} = f^*_{\texttt {prev}(-W, 1)}. \end{aligned}$$

  Inductive Step. Let us assume that Item 2 holds for the $\texttt {prev}(i,j)$th iteration, and let us prove it for the (i, j)th one. Hereafter, let us denote $(i_p, j_p)=\texttt {prev}(i,j)$ for convenience. Since Item 2 holds for the $(i_p, j_p)$th iteration by induction hypothesis, then, by Fact 1, the following holds at the $(i_p, j_p)$th iteration of line 15:

  $$\begin{aligned} \frac{1}{D_{j_p}}\, \texttt {Value-Iteration}\left( \varGamma ^{w'_{i_p, j_p}}, \lceil D_{j_p}\, \texttt {prev\_}f \rceil \right) = f = f^*_{i_p, j_p}. \end{aligned}$$

  Thus, at the (i, j)th iteration of line 8:

  $$\begin{aligned} \texttt {prev\_}f = f = f^*_{i_p, j_p} = f^*_{\texttt {prev}(i,j)}. \end{aligned}$$

  This concludes the proof of Fact 2. $\square$

At this point, by Fact 1 and Fact 2, Lemma 8 follows. $\square$

We are now in the position to show that Algorithm 1 is correct.

Proposition 1

Assume that Algorithm 1 is invoked on input $\varGamma = ( V, E, w, \langle V_0, V_1\rangle )$ and, whence, that it returns $( \mathcal{W}_0, \mathcal{W}_1, \nu , \sigma _0 )$ as output.

Then, $\mathcal{W}_0$ and $\mathcal{W}_1$ are the winning sets of Player 0 and Player 1 in $\varGamma$ (respectively), $\nu :V\rightarrow S$ is such that $\nu (v)=\texttt {val}^{\varGamma }(v)$ for every $v\in V$, and $\sigma _0:V_0\rightarrow V$ is an optimal positional strategy for Player 0 in the MPG $\varGamma$.

Proof

At the (i, j)th iteration of line 17, the following holds by Lemma 8:

$$\begin{aligned} \texttt {prev\_}f = f^*_{\texttt {prev}(i,j)}\text { and } f=f^*_{i,j}. \end{aligned}$$

Our aim now is that to apply Theorem 3. For this, firstly observe that one can safely write $\texttt {prev\_}f = f^*_{i,j-1}$. In fact, since $F_0=0$ and $F_{s-1}=1$, then:

$$\begin{aligned} w_{\texttt {prev}(i, 1)} = w_{i-1,s-1} = w-i = w_{i,0},\;\; \text { for every }i\in [-W, W]. \end{aligned}$$

This implies that $w_{\texttt {prev}(i,j)}=w_{i,j-1}$ for every $i\in [-W, W]$ and $j\in [1, s-1]$.

Whence, $\texttt {prev\_f}=f^*_{\texttt {prev}(i,j)}=f^*_{i,j-1}$.

So, at the (i, j)th iteration of line 17, the following holds for every $v\in V$:

$$\begin{aligned}&\texttt {prev\_}f(v)\ne \top \text { and } f(v) \\&\quad = \top \; \textit{iff} \; f^*_{i,j-1}(v)\ne \top \text { and } f^*_{i,j}(v) = \top \;\; \text {[by Lemma 8]} \\&\qquad \qquad \; \textit{iff}\; v\in \mathcal{W}_0(\varGamma _{i,j-1}) \cap \mathcal{W}_1(\varGamma _{i,j}) \;\; \text {[by Item 1--2 of Lemma 3]} \\&\qquad \qquad \; \textit{iff}\; \texttt {val}^{\varGamma }(v)=i+F_{j-1} \;\; \text {[by Theorem 3]} \end{aligned}$$

This implies that, at the (i, j)th iteration of line 17, Algorithm 1 correctly assigns the value $\nu (v)=i+F[j-1]=i+F_{j-1}$ to the vertex v.

Since for every vertex $v\in V$ we have $\texttt {val}^{\varGamma }(v)\in S_\varGamma$ (recall that $S_\varGamma$ admits the following representation $S_\varGamma =\left\{ i+F_j \;|\;i\in [-W, W),\, j\in [0, s-1]\right\}$), then, as soon as Algorithm 1 halts, $\nu (v)=\texttt {val}^{\varGamma }(v)$ correctly holds for every $v\in V$. In turn, at line 20 and at line 22, the winning sets $\mathcal{W}_0$ and $\mathcal{W}_1$ are correctly assigned as well.

Now, let us assume that $\nu (v)=i+F_{j-1}$ holds at the (i, j)th iteration of line 18, for some $v\in V$. Then, the following holds on $\texttt {prev\_}w$ at line 9:

$$\begin{aligned} \texttt {prev\_}w = w_{\texttt {prev}(i,j)} = w_{i, j-1} = w-i-F_{j-1} = w-\nu (v) = w-\texttt {val}^{\varGamma }(v). \end{aligned}$$

Thus, at the (i, j)th iteration of line 25, for every $v\in V_0$ and $u\in \texttt {post}(v)$:

$$\begin{aligned}&\texttt {prev\_}f(v) \succeq \texttt {prev\_}f(u) \\&\quad \ominus \texttt {prev\_} w(v,u) \textit{iff} \; f^*_{\texttt {prev}(i,j)}(v) \succeq f^*_{\texttt {prev}(i,j)}(u) \ominus \big (w - \texttt {val}^{\varGamma }(v)\big ) \\&\qquad \qquad \qquad \textit{iff}\; (v, u) \text { is compatible with } f^*_{\texttt {prev}(i,j)}\text { in } \varGamma ^{w-\texttt {val}^{\varGamma }(v)} \end{aligned}$$

Recall that $f^*_{\texttt {prev}(i,j)}$ is the least SEPM of $\varGamma ^{w-\texttt {val}^{\varGamma }(v)}$, thus by Theorem 4 the following implication holds: if $(v, u) \text { is compatible with } f^*_{\texttt {prev}(i,j)}\text { in } \varGamma ^{w-\texttt {val}^{\varGamma }(v)}$, then $\sigma _0(v)=u$ is an optimal positional strategy for Player 0, at v, in the MPG $\varGamma$.

This implies that line 26 of Algorithm 1 is correct and concludes the proof. $\square$

4.3 Complexity Analysis

The present section aims to show that Algorithm 1 always halts in $O(|V|^2|E|\, W)$ time. This upper bound is established in the next proposition.

Proposition 2

Algorithm 1 always halts within $O(|V|^2|E|\, W)$ time and it works with O(|V|) space, on any input MPG $\varGamma = (V, E, w, \langle V_0, V_1\rangle )$. Here, $W=\max _{e\in E}|w_e|$.

Proof

(Time Complexity of the Init Phase) The initialization of $\mathcal{W}_0, \mathcal{W}_1, \nu , \sigma _0$ (at line 1) and that of f (at line 2) takes time O(|V|). The initialization of W at line 3 takes O(|E|) time. To conclude, the size $s=|\mathcal{F}_{|V|}|$ of the Farey sequence (i.e., its total number of terms) can be computed in $O(n^{2/3}\log ^{1/3}{n})$ time as shown by Pawlewicz and Pătraşcu in [10]. Whence, the Init phase of Algorithm 1 takes O(|E|) time overall.

(Time Complexity of the Scan Phases) To begin, notice that there are $O(|V|^2 W)$ scan phases overall. In fact, at line 5 the index i goes from $-W$ to W, while at line 7 the index j goes from 0 to $s-1$ where $s=|\mathcal{F}_{|V|}|=\varTheta (|V|^2)$. Observe that, at each iteration, it takes O(|E|) time to go from line 8 to line 14 and then from line 16 to line 27. In particular, at line 11, the jth term $F_j$ of the Farey sequence $\mathcal{F}_{|V|}$ can be computed in $O(n^{2/3}\log ^{4/3}{n})$ time as shown by Pawlewicz and Pătraşcu in [10].

Now, let us denote by $T^{15}_{i,j}$ the time taken by the (i, j)th iteration of line 15, that is the time it takes to execute the Value-Iteration algorithm on input $\varGamma ^{w'_{i,j}}$ with initial energy levels: $\lceil D_j\, f^*_{\texttt {prev}(i,j)}\rceil$. Then, the (i, j)th scan phase always completes within the following time bound: $O(|E|) + T^{15}_{i,j}$.

We now focus on $T^{15}_{i,j}$ and argue that the (aggregate) total cost $\sum _{i,j} T_{i,j}^{15}$ of executing the Value-Iteration algorithm for EG s at line 15 (throughout all scan phases) is only $O(|V|^2|E|\,W)$. Stated otherwise, we aim to show that the amortized cost of executing the (i, j)th scan phase is only O(|E|).

Recall that the Value-Iteration algorithm for EG s consists, as a first step, into an initialization (which takes O(|E|) time) and, then, in the continuous iteration of the following two operations: (1) the application of the lifting operator $\delta (f, v)$ (which takes $O(|\texttt {post}(v)|)$ time) in order to resolve the inconsistency of f in v, where f(v) represents the current energy level and $v\in V$ is any vertex at which f is inconsistent; and (2) the update of the list $\L$ (which takes $O(|\texttt {pre}(v)|)$ time), in order to keep track of all the vertices that witness an inconsistency. Recall that $\L$ contains no duplicates.

At this point, since at the (i, j)th iteration of line 15 the Value-Iteration is executed on input $\varGamma ^{w'_{i,j}}$, then a scaling factor on the maximum absolute weight W must be taken into account. Indeed, it holds that:

$$\begin{aligned} W'&:= \max \Big \{|w'_{i,j}(e)| \;\Big |\; e\in E,\; i\in [-W, W],\; j\in [0, s-1]\Big \} = O( |V|\,W ). \end{aligned}$$

Remark Actually, since $w'_{i,j}:=D_j(w-i)-N_j$ (where $N_j/D_j=F_j\in \mathcal{F}_{|V|}$), then the scaling factor $D_j$ changes from iteration to iteration. Still, $D_j\le |V|$ holds for every j.

At each application of the lifting operator $\delta (f,v)$ the energy level f(v) increases by at least one unit with respect to the scaled-up maximum absolute weight $W'$. Stated otherwise, at each application of $\delta (f,v)$, the energy level f(v) increases by at least 1 / |V| units with respect to the original weight W.

Throughout the whole computation, the rational scalings of the energy levels never decrease by Lemma 8: in fact, at the (i, j)th scan phase, Algorithm 1 executes the Value-Iteration with initial energy levels: $\lceil D_j\, f^*_{\texttt {prev}(i,j)}\rceil$. Whence, at line 15, the (i, j)th execution of the Value-Iteration starts from the (carefully scaled-up) energy levels of the $\texttt {prev}(i,j)$th execution; roughly speaking, no energy gets ever lost during this process. Then, by Lemma 4, each energy level f(v) can be lifted-up at most $|V|\,W' = O( |V|^2\, W )$ times.

The above observations imply that the (aggregate) total cost of executing the Value-Iteration at line 15 (throughout all scan phases) can be bounded as follows:

$$\begin{aligned} \sum _{\begin{array}{c} -W \le i \le W \\ 1\le j\le s-1 \end{array}} T^{15}_{i,j}&= \left( \sum _{\begin{array}{c} -W \le i \le W \\ 1\le j\le s-1 \end{array}} \underbrace{O(|E|)}_{{{\textit{init}\;\textit{cost}}}}\right) + \left( \sum _{v\in V}O\big (\underbrace{|\texttt {post(v)}|}_{{{\textit{lifting}\,\delta }}} + \underbrace{|\texttt {pre}(v)|}_{{{\textit{update}\;\L }}} \big ) \underbrace{O(|V|\, W')}_{\textit{Lemma}~4} \right) \\&= O\left( |V|^2 |E|\, W\right) + O\left( |V|^2 W\right) \, \sum _{v\in V} O\big (|\texttt {post(v)}| + |\texttt {pre}(v)| \big ) \\&= O\left( |V|^2 |E|\, W\right) \end{aligned}$$

Whence, Algorithm 1 always halts within the following time bound:

$$\begin{aligned} \textsc {Time}\Big (\texttt {solve\_MPG}\big (\varGamma \big )\Big ) =\sum _{\begin{array}{c} -W \le i \le W \\ 1\le j\le s-1 \end{array}} \left( O(E) + T^{15}_{i,j} \right)&= O(|V|^2 |E|\, W). \end{aligned}$$

This concludes the proof of the time complexity bound.

We now turn our attention to the space complexity.

(Space Complexity) First of all, although the Farey sequence $\mathcal{F}_{|V|}$ has $|\mathcal{F}_{|V|}|=\varTheta (|V|^2)$ many elements, still, Algorithm 1 works fine assuming that every next element of the sequence is generated on the fly at line 11. This computation can be computed in $O(|V|^{2/3}\log ^{4/3}{|V|})$ sub-linear time and space as shown by Pawlewicz and Pătraşcu [10]. Secondly, given i and j, it is not necessary to actually store all weights $w'_{i,j}(e):=D_j(w(e)-i)-N_j$ for every $e\in E$, as one can compute them on the fly provided that $N_j$, $D_j$, w and e are given. Finally, Algorithm 1 needs to store in memory the two SEPMs f and $\texttt {old\_}f$, but this requires only O(|V|) space. Finally, at line 15, the Value-Iteration algorithm employs only O(|V|) space. In fact the list $\L$, which it maintains in order to keep track of inconsistencies, doesn’t contain duplicate vertices and, therefore, its length is at most $|\L |\le |V|$. These facts imply altogether that Algorithm 1 works with O(|V|) space. $\square$

5 Conclusions

In this work we proved an $O(|V|^2 |E|\, W)$ pseudo-polynomial time upper bound for the Value Problem and Optimal Strategy Synthesis in Mean Payoff Games. The result was achieved by providing a suitable description of values and positional strategies in terms of reweighted Energy Games and Small Energy-Progress Measures.

On this way we ask whether further improvements are not too far away.