Abstract
We study an isoperimetric problem described by a functional that consists of the standard Gaussian perimeter and the norm of the barycenter. The second term is in competition with the perimeter, balancing the mass with respect to the origin, and because of that the solution is not always the half-space. We characterize all the minimizers of this functional, when the volume is close to one, by proving that the minimizer is either the half-space or the symmetric strip, depending on the strength of the barycenter term. As a corollary, we obtain that the symmetric strip is the solution of the Gaussian isoperimetric problem among symmetric sets when the volume is close to one. As another corollary we obtain the optimal constant in the quantitative Gaussian isoperimetric inequality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Gaussian isoperimetric inequality (proved by Borell [7] and Sudakov–Tsirelson [33]) states that among all sets with given Gaussian measure the half-space has the smallest Gaussian perimeter. Since the half-space is not symmetric with respect to the origin, a natural question is to restrict the problem among sets which are symmetric, i.e., either central symmetric (\(E = -E\)) or coordinate wise symmetric (n-symmetric). This problem turns out to be rather difficult as every known method that has been used to prove the Gaussian isoperimetric inequality, such as symmetrization [15] and the Ornstein-Uhlenbeck semigroup argument [1], seems to fail.
The Gaussian isoperimetric problem for symmetric sets or its generalization to Gaussian noise is stated as an open problem in [8, 19]. A natural candidate for the solution is the symmetric strip or its complement as this is the only reasonable one-dimensional candidate. In [4] Barthe proves that if one replaces the standard Gaussian perimeter by a certain anisotropic perimeter, the solution of the isoperimetric problem among n-symmetric sets is the symmetric strip or its complement. A somewhat similar result is by Latala and Oleszkiewicz [27, Theorem 3] who proved that the symmetric strip minimizes the Gaussian perimeter weighted with the width of the set among convex and symmetric sets with volume constraint. This result is related to the so-called S-conjecture, also proved in [27] (while the complex version was proved by Tkocz [34]). For the standard perimeter the problem is more difficult as a simple energy comparison shows (see [23]) that when the volume is exactly one half, the n-dimensional ball in \({\mathbb {R}}^n\) has smaller Gaussian perimeter than the symmetric strip. Similar difficulty appears also in the isoperimetric problem on the sphere for symmetric sets, where it is known that the union of two spherical caps does not always have the smallest surface area (see [4]). On the other hand, when the volume is close to one the symmetric strip has smaller perimeter than the n-dimensional ball. This suggests that the shape of the minimizer of the symmetric problem depends on the volume. Indeed, the conjecture states (see [23, Conjecture 1.3]) that the minimizer of the problem is always a cylinder \(B_r^k \times {\mathbb {R}}^{n-k}\), or its complement, for some k depending on the volume and on the dimension. Here \(B_r^k\) denotes the k-dimensional ball with radius r. In particular, when the volume is one half the conjecture states that the minimizer is the n-dimensional ball \(B_r^n\) and when the volume is close to one the minimizer is the symmetric strip \((-r,r) \times {\mathbb {R}}^{n-1}\). There is some numerical evidence to support this fact and the results by Heilman [22, 23] and La Manna [26] seem to indicate this. Note that if this conjecture is true, then the solution of the problem depends on the dimension of the ambient space.
To the best of the authors knowledge there are no other results directly related to this problem. In [14] Colding and Minicozzi introduce the Gaussian entropy, which is defined for sets as
where \(P_\gamma \) is the Gaussian perimeter defined below in (2). The Gaussian entropy is important since it is decreasing under the mean curvature flow and for this reason in [14] the authors studied sets which are stable for the Gaussian entropy. It was conjectured in [13] that the sphere minimizes the entropy among closed hypersurfaces (at least in low dimensions). This was proved by Bernstein and Wang [5] in low dimensions and more recently by Zhu [35] in every dimension. It is natural to guess that minimizing the Gaussian entropy is related to the Gaussian isoperimetric problem for symmetric sets when the volume is one half, as this gives the largest value for the symmetric problem as a function of volume. For instance, by the argument in [14] it follows that for every symmetric set E which is \(C^2\)-close to the n-dimensional ball \(B^n_R\) with volume \(\gamma (B^n_R) = 1/2\) it holds
for some \(\lambda \in (0,1)\). Therefore it sounds plausible that the ball minimizes both the Gaussian entropy among compact sets and the Gaussian perimeter among symmetric sets with volume one half. However, the latter does not follow directly from the result by Zhu, since e.g. the Gaussian entropy for sets in (1) is always larger than their Gaussian perimeter.
In this paper we partially prove the previously mentioned conjecture by showing that the symmetric strip is indeed the solution of the Gaussian isoperimetric problem for symmetric sets when the volume is close to one. Similarly, its complement is the solution when the volume is close to zero. We have an explicit estimate on how close to one the volume has to be. Most importantly this bound is independent of the dimension.
In order to describe the main result more precisely, we introduce our setting. Given a Borel set \(E\subset {\mathbb {R}}^n\), \(\gamma (E)\) denotes its Gaussian measure, defined as
If E is an open set with Lipschitz boundary, \(P_\gamma (E)\) denotes its Gaussian perimeter, defined as
where \({\mathcal {H}}^{n-1}\) is the \((n-1)\)-dimensional Hausdorff measure. We define the (non-renormalized) barycenter of a set E as
and define the function \(\phi :{\mathbb {R}}\rightarrow (0,1)\) as
Moreover, given \(\omega \in {\mathbb {S}}^{n-1}\) and \(s \in {\mathbb {R}}\), \(H_{\omega ,s}\) denotes the half-space of the form
while \(D_{\omega ,s}\) denotes the symmetric strip
where \(a(s)>0\) is chosen such that \(\gamma (H_{\omega ,s})=\gamma (D_{\omega ,s})\).
We approach the problem by studying the minimizers of the functional
under the volume constraint \(\gamma (E) = \phi (s)\). Note that the isoperimetric inequality implies that for \(\varrho =0\) the half-space is the only minimizer of (3), while it is easy to see that the quantity |b(E)| is maximized by the half-space. Therefore the two terms in (3) are in competition and we call the barycenter term repulsive, as it prefers to balance the volume around the origin. It is proven in [2, 16] that when \(\varrho \) is small, the half-space is still the only minimizer of (3). This result implies the quantitative Gaussian isoperimetric inequality (see also [3, 11, 30, 31]). It is clear that when we keep increasing the value \(\varrho \), there is a threshold, say \(\varrho _s\), such that for \(\varrho >\varrho _s\) the half-space \(H_{\omega ,s}\) is no longer the minimizer of (3). In this paper we are interested in characterizing the minimizers of (3) after this threshold. Our main result reads as follows.
MainTheorem
Let \(s \ge 10^3\). There is a threshold \(\varrho _s\) such that for \(\varrho \in [0,\varrho _s)\) the minimizer of (3) under the volume constraint \(\gamma (E) = \phi (s)\) is the half-space \(H_{\omega ,s}\), while for \(\varrho \in (\varrho _s, \infty )\) the minimizer is the symmetric strip \(D_{\omega ,s}\).
The result is sharp in the sense that the corresponding statement for s close to zero is false by the earlier discussion. On the other hand, the bound \(s \ge 10^3\) is most likely far from optimal.
As a corollary the above theorem provides the solution for the symmetric Gaussian problem, because symmetric sets have barycenter zero.
Corollary 1
Let \(s \ge 10^3\). For any symmetric set E with volume \(\gamma (E)=\phi (s)\) it holds
and the equality holds if and only if \(E=D_{\omega ,s}\) for some \(\omega \in {\mathbb {S}}^{n-1}\).
We remark that the bound \(s \ge 10^3\) is far from the conjectured value which is approximately \(s\ge 0,5\) (see [23]). We could slightly improve the bound on s, but as our proof is rather long, we prefer to avoid heavy computations and to state the theorem without trying to optimize this bound.
Another corollary of the theorem is the optimal constant in the quantitative Gaussian isoperimetric inequality (see [2, 16]) when the volume is close to one. Let us denote by \(\beta (E)\) the strong asymmetry
which measures the distance between a set E and the family of half-spaces.
Corollary 2
Let \(s \ge 10^3\). For every set E with volume \(\gamma (E)=\phi (s)\) it holds
The optimal constant is given by
It would be interesting to obtain a result analogous to Corollary 2 in the Euclidean setting, where the minimization problem which corresponds to (3) is introduced in [18], and on the sphere [6]. The motivation for this is that, by the result of the second author [24], the optimal constant for the quantitative Euclidean isoperimetric inequality implies an estimate on the range of volume where the ball is the minimizer of the Gamov’s liquid drop model [20]. This is a classical model used in nuclear physics and has gathered a lot of attention in mathematics in recent years [9, 10, 25]. We also refer to the survey paper [17] for the state-of-the-art in the quantitative isoperimetric and other functional inequalities.
The main idea of the proof is to study the functional (3) when the parameter \(\varrho \) is within a carefully chosen range \((\varrho _l,\varrho _r)\), depending on s, and to prove that within this range the only local minimizers, are the half-space \(H_{\omega ,s}\) and the symmetric strip \(D_{\omega ,s}\). We have to choose the lower bound \(\varrho _l\) large enough so that the symmetric strip is a local minimum of (3). On the other hand, we have to choose the upper bound \(\varrho _r\) small enough so that no other local minimum than \(H_{\omega ,s}\) and \(D_{\omega ,s}\) exist. Naturally also the threshold value \(\varrho _s\) has to be within the range \((\varrho _l,\varrho _r)\).
Our proof is based on reduction argument where we reduce the dimension of the problem from \({\mathbb {R}}^n\) to \({\mathbb {R}}\) when s is large enough. First, in Theorem 2 in Sect. 3 we develop further our ideas from [2] to reduce the problem from \({\mathbb {R}}^n\) to \({\mathbb {R}}^2\) by a rather short argument. In this step it is crucial that we are not constrained to keep the sets symmetric. In other words, minimizing (3) is more flexible than minimizing the Gaussian perimeter among symmetric sets, which makes it easier to reduce the dimension in the former problem than in the latter. The main challenge is thus to prove the theorem in \({\mathbb {R}}^2\) which we do in Theorem 3 in Sect. 4. We cannot apply the previous reduction argument anymore which makes the proof of Theorem 3 very involved. In some sense in this step we have to pay the price that we are minimizing the functional (3) which is much more difficult than solving the Gaussian symmetric problem in \({\mathbb {R}}^2\). Indeed, proving the main theorem in \({\mathbb {R}}^2\) is essentially the same as proving the quantitative isoperimetric problem with the sharp constant in \({\mathbb {R}}^2\) which, for instance, is not known in the Euclidean setting (see [12] for the best known result). We use an ad-hoc argument to reduce the problem from \({\mathbb {R}}^2\) to \({\mathbb {R}}\) essentially by deriving PDE type estimates from the Euler equation and from the stability condition. We give an independent overview of this argument at the beginning of the proof of Theorem 3 in Sect. 4. Finally, in Sect. 5 we solve the problem in \({\mathbb {R}}\) by a straightforward (but nontrivial) argument.
2 Notation and set-up
In this section we briefly introduce our notation and discuss about preliminary results. We remark that throughout the paper the parameters, associated with the volume, is assumed to be larger than\(10^3\)even if not explicitly mentioned. In particular, our estimates are understood to hold when\(s \ge 10^3\).
We denote the \((n-1)\)-dimensional Hausdorff measure with Gaussian weight by \({\mathcal {H}}^{n-1}_\gamma \), i.e., for every Borel set A we define
We minimize the functional (3) among sets with locally finite perimeter and have the existence of a minimizer for every \(\varrho \) by an argument similar to [2, Proposition 1]. If \(E \subset {\mathbb {R}}^n\) is a set of locally finite perimeter we denote its reduced boundary by \(\partial ^*E\) and define its Gaussian perimeter by
We denote the generalized exterior normal by \(\nu ^E\) which is defined on \(\partial ^* E\). As introduction to the theory of sets of finite perimeter and perimeter minimizers we refer to [29].
If the reduced boundary \(\partial ^* E\) is a smooth hypersurface we denote the second fundamental form by \(B_E\) and the mean curvature by \({\mathscr {H}}_E\), which for us is the sum of the principle curvatures. We adopt the notation from [21] and define the tangential gradient of a function f, defined in a neighborhood of \(\partial ^* E\), by \(\nabla _\tau f := \nabla f - \langle \nabla f , \nu ^E\rangle \nu ^E\). Similarly, we define the tangential divergence of a vector field by \(\mathrm {div}_\tau X := \mathrm {div}X - \langle DX \nu ^E, \nu ^E \rangle \) and the Laplace-Beltrami operator as \(\Delta _\tau f := \mathrm {div}_\tau (\nabla _\tau f)\). The divergence theorem on \(\partial ^* E\) implies that for every vector field \(X \in C_0^1(\partial ^* E ; {\mathbb {R}}^n)\) it holds
If \(\partial ^* E\) is a smooth hypersurface, we may extend any function \(f \in C_0^1(\partial ^* E)\) to a neighborhood of \(\partial ^* E\) by the distance function. For simplicity we will omit to indicate the dependence on the set E when this is clear, by simply writing \(\nu =\nu ^E\), \({\mathscr {H}}={\mathscr {H}}_E\) etc...
We denote the mean value of a function \(f : \partial ^* E \rightarrow {\mathbb {R}}\) by

and its average over a subset \(\Sigma \subset \partial ^* E\) by

We recall that for every number \(a \in {\mathbb {R}}\) it holds
Recall that \(H_{\omega ,s}\) denotes the half-space \(\{x\in {\mathbb {R}}^n \text { : } \langle x,\omega \rangle < s\}\) and \(D_{\omega ,s}\) denotes the symmetric strip \(\{x\in {\mathbb {R}}^n \text { : } | \langle x,\omega \rangle | <a(s)\}\), where a(s) is chosen such that \(\gamma (D_{\omega ,s}) = \gamma (H_{\omega ,s}) = \phi (s)\). For future purpose it is important to estimate the asymptotic behavior of the quantities a(s) and \(P(D_{\omega ,s})\). We claim that
and
These bounds are probably well known but we sketch the proof in the Appendix for the reader’s convenience. In particular, it follows from (5) and from our main theorem that the threshold value \(\varrho _s\) has the asymptotic behavior
This follows from the fact that \(\varrho _s\) is the unique value of \(\varrho \) for which the functional (3) satisfies \({\mathcal {F}} (H_{\omega ,s})= {\mathcal {F}} (D_{\omega ,s})\), i.e.,
by taking into account that \(|b(H_{\omega ,s})|=e^{-s^2/2}/\sqrt{2\pi }\).
In order to simplify the upcoming technicalities we replace the volume constraint in the original functional (3) with a volume penalization. We redefine \({\mathcal {F}}\) for any set of locally finite perimeter as
where we choose
As with the original functional the existence of a minimizer of (7) follows from [2, Proposition 1]. It turns out that the minimizers of (7) are the same as the minimizers of (3) under the volume constraint \(\gamma (E) = \phi (s)\), as proved in the last section. The advantage of having a volume penalization is that it helps us to bound the Lagrange multiplier in a simple way. The constants \(\sqrt{\pi /2}\) and \(\sqrt{2\pi }\) in front of the last two terms are chosen to simplify the formulas of the Euler equation and the second variation.
As we explained in the introduction, the idea is to restrict the parameter \(\varrho \) in (7) within a range, which contains the threshold value \(\varrho _s\) defined by (6) and such that the only local minimizers of (7) are the half-space and the symmetric strip. To this aim we assume from now on that \(\varrho \) is in the range
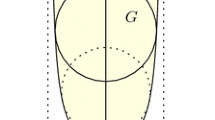
Note that by (5) the threshold value \(\varrho _s\) defined by (6) is within this interval. If we are able to show that when \(\varrho \) satisfies (9) the only local minimizers of (7) are \(H_{\omega ,s}\) and \(D_{\omega ,s}\), we obtain the main result. Indeed, when \(\varrho \in (\varrho _l,\varrho _s)\) it holds \({\mathcal {F}}(H_{\omega ,s})< {\mathcal {F}}(D_{\omega ,s})\) by (6) and the minimizer is \(H_{\omega ,s}\). It is then not difficult to see that for every value \(\varrho \) smaller than \(\varrho _l\), the minimizer is still \(H_{\omega ,s}\). Indeed, the half-space has the barycenter with the largest norm and it is favored by a smaller \(\varrho \). Similarly, when \(\varrho \in (\varrho _s,\varrho _r)\) in (9) it holds \({\mathcal {F}}(D_{\omega ,s})< {\mathcal {F}}(H_{\omega ,s})\) again by (6) and the minimizer is \(D_{\omega ,s}\). Hence, for every value \(\varrho \) larger than \(\varrho _r\), \(D_{\omega ,s}\) is still the minimizer of (7), since it has barycenter zero. In Fig. 1 we have sketched the situation.
We have also the following a priori perimeter bounds for minimizer E of (7) (see the Appendix for the proof),
For the reader’s convenience we summarize the results concerning the regularity of minimizers and the first and the second variation of (7) contained in [2, Section 4] in the following theorem.
Theorem 1
Let E be a minimizer of (7). Then the reduced boundary \(\partial ^*E\) is a relatively open, smooth hypersurface and satisfies the Euler equation
The Lagrange multiplier \(\lambda \) can be estimated by \(|\lambda | \le \Lambda \). The singular part of the boundary \(\partial E \setminus \partial ^*E\) is empty when \(n <8\), while for \(n \ge 8\) its Hausdorff dimension can be estimated by \(\dim _{{\mathcal {H}}}(\partial E \setminus \partial ^*E) \le n-8\). Moreover, the quadratic form associated with the second variation is non-negative
for every \(\varphi \in C_0^\infty (\partial ^* E)\) which satisfies \(\int _{\partial ^* E} \varphi \, d{\mathcal {H}}^{n-1}_\gamma = 0\).
The Euler equation (11) yields important geometric equations for the position vector x and for the Gauss map \(\nu \). For arbitrary \(\omega \in {\mathbb {S}}^{n-1}\) we write
If \(\{e^{(1)},\ldots ,e^{(n)}\}\) is a canonical basis of \({\mathbb {R}}^n\) we simply write
From (11) and from the fact \(\Delta _\tau x_\omega = - {\mathscr {H}}\nu _\omega \) [28, Proposition 1] we have
Moreover, from (11) and from the fact \(\Delta _\tau \nu _\omega = - |B_E|^2 \nu _\omega + \langle \nabla _\tau {\mathscr {H}}, \omega \rangle \) [21, Lemma 10.7] we get
By the divergence theorem on \(\partial ^* E\) we have that for any functions \(\varphi \in C_0^\infty (\partial ^* E)\) and \(\psi \in C^1(\partial ^* E)\) it holds
The previous equality implies the following integration by parts formula
We will use along the paper the above formula with \(\varphi = x_\omega \) or \(\varphi = \nu _\omega \). Also if they do not belong to \(C_0^\infty (\partial ^* E)\), we are allowed to do so by an approximation argument (see [2, 32]).
Remark 1
We associate the following second order operator L with the first four terms in the quadratic form (12),
where \(\varphi \in C_0^\infty (\partial ^* E)\). By integration by parts the inequality (12) can be written as
Note that when the vector \(\omega \) is orthogonal to the barycenter, i.e., \(\langle \omega , b \rangle = 0\), then by (14) the function \(\nu _\omega \) is an eigenfunction of L and satisfies
For every \(\omega \in {\mathbb {S}}^{n-1}\) it holds by the divergence theorem in \({\mathbb {R}}^n\) that
In particular, when \(\langle \omega , b \rangle = 0\) the function \(\varphi = \nu _\omega \) has zero average. Therefore by Remark 1 it is natural to use \(\nu _\omega \) with \(\langle \omega , b \rangle = 0\) as a test function in the second variation condition (12).
The equality \(\int _{\partial ^* E} \nu _\omega \, d{\mathcal {H}}^{n-1}_\gamma = -\sqrt{2\pi }\langle b, \omega \rangle \) for every \(\omega \in {\mathbb {S}}^{n-1}\) also implies
In particular, we have by (9), (10)
We conclude this preliminary section by providing further “regularity” estimates from (13) for the minimizers of (7). We call the estimates in the following lemma “Caccioppoli inequalities” since they follow from (13) by an argument which is similar to the classical proof of Caccioppoli inequality known in elliptic PDEs. This result is an improved version of [2, Proposition 1].
Lemma 1
(Caccioppoli inequalities) Let \(E \subset {\mathbb {R}}^n\) be a minimizer of (7). Then for any \(\omega \in {\mathbb {S}}^{n-1}\) it holds
and
Proof
Let us first prove (18). To simplify the notation we define
We multiply (13) by \(x_\omega \) and integrate by parts over \(\partial ^* E\) to get
We estimate the right-hand-side of (20) in the following way. We estimate the first term by Young’s inequality
where the last inequality follows from the bound on the Lagrange multiplier
given by Theorem 1 and by our choice of \(\Lambda \) in (8). Since \(|\nabla _\tau x_\omega |^2 = 1-\nu _\omega ^2 \le 1\), we may bound the second term simply by
Finally we bound the last term again by Young’s inequality and by \(\varrho |b| \le \frac{3}{2s^2}\) (given in (17))
By using these three estimates in (20) we obtain
If the barycenter is zero the claim follows immediately from (21). If \(b \ne 0\), we first use (21) with \(\omega = \frac{b}{|b|}\) and obtain
This implies
Therefore we have by (21)
which yields the claim.
The proof of the second inequality is similar. We multiply the equation (13) by \((x_\omega - {\bar{x}}_ \omega )\) and integrate by parts over \(\partial ^* E\) to get
By estimating the three terms on the right-hand-side precisely as before, we deduce
where the last inequality follows from (22). This implies (19). \(\square \)
3 Reduction to the two dimensional case
In this section we prove that it is enough to obtain the result in the two dimensional case. More precisely, we prove the following result.
Theorem 2
Let E be a minimizer of (7). Then, up to a rotation, \(E=F\times {\mathbb {R}}^{n-2}\) for some set \(F\subset {\mathbb {R}}^2\).
Proof
Let \(\{e^{(1)},\ldots ,e^{(n)}\}\) be an orthonormal basis of \({\mathbb {R}}^n\). We begin with a simple observation: if \(i \ne j\) then by the divergence theorem
In particular, the matrix \(A_{ij} = \int _{\partial E} x_i \nu _j \, d {\mathcal {H}}_\gamma ^{n-1}\) is symmetric. We may therefore assume that \(A_{ij}\) is diagonal by changing the basis of \({\mathbb {R}}^n\) if necessary. In particular, it holds
By reordering the elements of the basis we may also assume that
for \(j\in \{1,\dots ,n-1\}\).
Since we assume \(n\ge 3\), we may choose a direction \(\omega \in {\mathbb {S}}^{n-1}\) which is orthogonal both to the barycenter b and to \(e^{(1)}\). To be more precise, we choose \(\omega \) such that \(\langle \omega ,b\rangle =0\) and \(\omega \in \mathrm {span}\{e^{(2)},e^{(3)}\}\). Since \(\langle \omega ,b\rangle =0\), (16) yields \({\bar{\nu }}_\omega = 0\). In other words, the function \(\nu _\omega \) has zero average. We use \(\varphi =\nu _\omega \) as a test function in the second variation condition (12). According to Remark 1 we may write the inequality (12) as
where the operator L is defined in (15). Since \(\omega \) is orthogonal to b we deduce by Remark 1 that \(\nu _\omega \) is an eigenfunction of L and satisfies \(L[\nu _\omega ] = - \nu _\omega \). Therefore we get
The crucial step in the proof is to estimate the second term in (25), by showing that it is small enough. This is possible due to the fact that \(\omega \) is orthogonal to \(e^{(1)}\). Indeed, by using (23) and the fact that \(\omega \in \mathrm {span}\{e^{(2)},e^{(3)}\}\), and then Cauchy-Schwarz inequality, we get
We estimate the first term on the right-hand-side first by (24), then by the Caccioppoli estimate (18) and finally by (10)
Since we assume \(\varrho \le \frac{7\sqrt{2 \pi }}{5s^2} e^{\frac{s^2}{2}}\) (see (9)), the previous two inequalities yield
for some \(\mu < 1\). Then, by collecting (25) and (27) we obtain
This implies \(\nu _\omega = 0\). We have thus reduced the problem from n to \(n-1\). By repeating the previous argument we reduce the problem to the planar case. \(\square \)
Remark 2
We have to be careful in our choice of direction \(\omega \), and in general we may not simply choose any direction orthogonal to the barycenter b. Indeed, let \(\omega \in {\mathbb {S}}^{n-1}\) be a vector such that \(\langle b, \omega \rangle = 0\) and let \(v \in {\mathbb {S}}^{n-1}\) be such that
Then, by using Cauchy–Schwarz inequality, we may estimate the second term in (25) by
We can estimate the term \(\frac{\varrho }{\sqrt{2\pi }} \int _{\partial ^* E} x_\upsilon ^2 \, d{\mathcal {H}}^{n-1}_\gamma \) at our best via (9), (10) and (18), obtaining
Unlike (27), this estimate is not good enough. Note that we cannot shrink \(\varrho \), since we have the constrain given by (9).
Remark 3
In the next section we will reduce the problem to the one dimensional case. In doing that, we can assume that it holds

and then in particular
Indeed, when  , the Caccioppoli estimate (19) yields
, the Caccioppoli estimate (19) yields

With this estimate the further dimensional reduction can be done by simply using the argument in the proof of Theorem (2): given a vector \(\omega \in {\mathbb {S}}^{n-1}\) such that \(\langle b, \omega \rangle = 0\), we have
for some \(\mu < 1\). In other words, the crucial estimate (27) in the proof of Theorem 2 holds and we can conclude that \(\nu _\omega = 0\).
Remark 4
We may reduce the problem to the one dimensional case also if \(b=0\), since we may use \(\omega =e^{(2)}\) in the previous argument (\(\nu _\omega \) has zero average and \(\int _{\partial ^* E}x_2^2\) is small enough). However, this is a special case and a priori nothing guarantees that \(b=0\).
Remark 5
The result of this section holds when s is large enough and the reader may wonder what happens when the parameter s is close to zero. The conjecture in [23] states that the n-dimensional ball is the solution of the symmetric isoperimetric problem when \(s=0\) . Since \(\gamma (B_{\sqrt{n}}^n) \rightarrow 1/2\) as \(n\rightarrow \infty \) and
as \(n\rightarrow \infty \) we should choose the value of \(\varrho \) in the functional \({\mathcal {F}}\) such that \({\mathcal {F}} (H_{\omega ,0})> {\mathcal {F}} (B_{\sqrt{n}}^n)\), i.e.,
With this threshold we cannot apply our dimensional reduction argument for \(s=0\), which is in accordance with the conjecture. Indeed, when \(s=0\) the Caccioppoli estimate (18) becomes weaker, since the perimeter term in its right-hand side becomes dominant.
4 Reduction to the one dimensional case
In this section we will prove a further reduction of the problem, by showing that it is enough to obtain the result in the one dimensional case. This is technically more involved than Theorem 2 and requires more a priori information on the minimizers.
Theorem 3
Let E be a minimizer of (7). Then, up to a rotation, \(E=F\times {\mathbb {R}}^{n-1}\) for some set \(F\subset {\mathbb {R}}\).
Thanks to Theorem 2 we may assume from now on that \(n=2\). In particular, by Theorem 1 the boundary is regular and \(\partial E=\partial ^* E\). Moreover the Euler equation and (14) simply read as
where k is the curvature of \(\partial E\).
The idea is to proceed by using the second variation argument once more, but this time in a direction that it is not necessarily orthogonal to the barycenter. This argument does not reduce the problem to \({\mathbb {R}}\), but gives us the following information on the minimizers.
Lemma 2
Let \(E \subset {\mathbb {R}}^2\) be a minimizer of (7). Then

Moreover, there exists a direction \(v \in {\mathbb {S}}^1\) such that

Observe that the estimate (33) implies that \(\nu _v\) is close to a constant and thus \(\partial E\) is flat in shape. In particular, this estimate excludes the minimizers to be close to the disk.
Proof
We begin by showing that for any \(\omega \in {\mathbb {S}}^1\) it holds
To this aim we choose \(\varphi =\nu _\omega -{\bar{\nu }}_\omega \) as a test function in the second variation condition (12). We remark that because \(\omega \) might not be orthogonal to the barycenter b, neither \(\nu _\omega \) nor \(\nu _\omega -{\bar{\nu }}_\omega \) is an eigenfunction of the operator L associated with the second variation defined in Remark 1. We multiply the equation (31) by \(\nu _\omega \) and integrate by parts to obtain
and simply integrate (14) over \(\partial E\) to get
Hence, by also using \({\bar{\nu }} P_\gamma (E) = - \sqrt{2 \pi } \, b\) (see (16)), we may write
where in the last inequality we have used (9) and (10). The above inequality and the second variation condition (12) with \(\varphi =\nu _\omega -{\bar{\nu }}_\omega \) imply (34).
Let us consider an orthonormal basis \(\{e^{(1)}, e^{(2)}\}\) of \({\mathbb {R}}^2\) and assume \(\int _{\partial E}x_1^2 \,d {\mathcal {H}}_\gamma ^1\ge \int _{\partial E}x_2^2 \,d{\mathcal {H}}_\gamma ^1\). As in (26), we use the Caccioppoli estimate (18) and (10) to get
We choose a direction \(v \in {\mathbb {S}}^1\) which is orthogonal to the vector \(\int _{\partial E}x_1(\nu -{\bar{\nu }}) \,d {\mathcal {H}}_\gamma ^1\). Since  , we have
, we have

Then, by the above equality, by Cauchy–Schwarz inequality and by (37) we have
With the bound \(\varrho \le \frac{7\sqrt{2 \pi }}{5s^2} e^{\frac{s^2}{2}}\) (see 9), the previous inequality yields
Hence, the inequality (34) implies
From this inequality we have immediately (33), and also (32), if \({\bar{\nu }}_v\) is not zero. If instead \({\bar{\nu }}_v=0\), then also \(\nu _v = 0\) by (33). Thus \(\partial E\) is flat, \(k = 0\) and (32) holds again. \(\square \)
We will also need the following auxiliary result.
Lemma 3
Let \(E \subset {\mathbb {R}}^2\) be a minimizer of (7). Then, for every \(x \in \partial E\) it holds
Proof
We argue by contradiction by assuming that there exists \({\tilde{x}} \in \partial E \) such that \(|{\tilde{x}}| < s - 1\). For this \({\tilde{x}}\) we will show that
We remark that \({\mathcal {H}}^1\) is the standard Hausdorff measure, i.e., \({\mathcal {H}}^1(\partial E \cap B_{1/2}({\tilde{x}}))\) denotes the length of the curve. We divide the proof of (39) in two cases.
Assume first that there is a component of \(\partial E\), say \({\tilde{\Gamma }}\), which is contained in the disk \(B_{1/2}({\tilde{x}})\). By regularity, \({\tilde{\Gamma }}\) is a smooth Jordan curve which encloses a bounded set \({\tilde{E}}\), i.e., \({\tilde{\Gamma }} = \partial {\tilde{E}}\). Note that then it holds \({\tilde{E}} \subset B_{R}\) for \( R= s - 1/2\). We integrate the Euler equation (30) over \(\partial {\tilde{E}}\) with respect to the standard Hausdorff measure and obtain by the Gauss-Bonnet formula and by the divergence theorem that
where in the last inequality we have used \(\varrho |b| \le \frac{3}{2s^2}\) (given in (17)) and the fact that for all \(x \in {\tilde{E}}\) it holds \(|x| \le s - 1/2\). The isoperimetric inequality in \({\mathbb {R}}^2\) implies
Therefore since \(|\lambda | \le s + 1\) we obtain from (40) that
This implies \({\mathcal {H}}^1({\tilde{\Gamma }}) \ge \frac{1}{s}\) and the claim (39) follows.
Let us then assume that no component of \(\partial E\) is contained in \(B_{1/2}({\tilde{x}})\). In this case the boundary curve passes \({\tilde{x}}\) and exits the disk \(B({\tilde{x}},\frac{1}{2})\). In particular, it holds \({\mathcal {H}}^1(\partial E \cap B_{1/2}({\tilde{x}}))\ge 1/2\) which implies (39).
Since for all \(x \in \partial E \cap B_{1/2}({\tilde{x}})\) it holds \(|x| \le s -1/2\), the estimate (39) implies
This contradicts (10). \(\square \)
For the remaining part of this section we choose a basis \(\{e^{(1)},e^{(2)}\}\) for \({\mathbb {R}}^2\) such that \(e^{(1)} = v\), where v is the direction in Lemma 2 and \(e^{(2)}\) is an orthogonal direction to that. Let us define
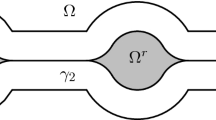
In the next lemma we use (33) to obtain that the Gaussian measure of \(\{x \in \partial E : |x_2| \le \tfrac{s}{3} \}\) is small. This implies, from the measure point of view, that \(\Sigma _+\) and \(\Sigma _-\) are almost disconnected. This enables us to variate \(\Sigma _+\) and \(\Sigma _-\) separately, which will be crucial in the proof of Theorem 3.
Lemma 4
Let \(E \subset {\mathbb {R}}^2\) be a minimizer of (7) and assume (28) holds. Then there is a number \(a_+ \in (0,s+1]\) such that
Moreover, it holds
Proof
Inequality (41). We first show that
where the number \((|\nu _2|)_{\Sigma _+}\) is the average of \(|\nu _2|\) on \(\Sigma _+\). By (29) and (33) we obtain
Since
we have (43).
To prove the inequality (41) we multiply the equation (13), with \(\omega = e_2\), by \((x_2+\lambda \nu _2)\) and integrate by parts
We estimate the first term on the right-hand-side by Young’s inequality and by \(|\lambda | \le s+1\)
and the second as
Hence, we have by \(\varrho |b|\le \frac{1}{s^2}\) (from (17) and (29)), (18) and (32) that
Therefore it holds (recall that \(x_2 \ge 0\) on \(\Sigma _+\))
Hence, by (43) and \(|\lambda | \le s+1\) we deduce
The claim then follows from \(|\lambda | \le s+1\).
Inequality (42). We have by (18), (19), (29), and (33) that

We also have from (38) that for every \(x \in \{ x \in \partial E : |x_2| \le \frac{s}{3} \}\) it holds
These three inequalities imply
This yields the inequality (42) when \(|{\bar{\nu }}_1| \ge \frac{1}{2}\). Let us then assume that it holds
We choose the Lipshitz continuous cut-off function \(\zeta : {\mathbb {R}}\rightarrow [0,1]\) such that
and
We multiply the equation (13), with \(\omega =e_1\), by \(x_1 \zeta ^2(x_2)\) and integrate by parts
We estimate the first term on the right-hand-side by Young’s inequality and by \(|\lambda | \le s+1\)
where we have written \(\zeta = \zeta (x_2)\) for short. We estimate the second term by using \(|\nabla _\tau \zeta (x_2)| = |\zeta '(x_2)| |\nabla x_2| \le \frac{12}{s}|\nu _1|\) as follows
for \({\tilde{C}} = 7200\). We estimate the third term simply by using \(\varrho |b| \le \frac{1}{s^2}\)
Hence, we deduce from (45) and from the three above inequalities that
Recall that \(\zeta = 0\) when \(|x_2| \ge \frac{5s}{12}\) and that by (38) we have \(|x|^2 \ge (s-1)^2\) on \(\partial E\). In particular, for every \(x \in \{ x \in \partial E : |x_2| \le \frac{5s}{12} \}\) it holds
and \(|x|^2 \le \frac{3}{2} x_1^2\). Therefore the two previous inequalities yield
with \({\tilde{c}} = \frac{49}{62}\).
We write the first term on the right-hand-side of (46) as
Therefore (46) implies
The first term on the right-hand-side of (47) can be estimate by (33) and the assumption \(|{\bar{\nu }}_1 | < \frac{1}{2}\) as
Then, noted that \(\zeta (x_2) =1 \) for \(|x_2| \le \tfrac{s}{3}\) and that  by (33), we have
by (33), we have
and (42) follows since we assume \(s \ge 10^3\). \(\square \)
We are now ready to prove the reduction to the one dimensional case.
Proof of Theorem 3
We recall that
As we mentioned in Remark 2, using \(\varphi =\nu _e\) with \(e \in {\mathbb {S}}^1\) orthogonal to the barycenter as a test function in the second variation inequality (12), does not provide any information on the minimizer since the term \(|\int _{\partial E} x\, \nu _e\, d {\mathcal {H}}_\gamma ^1|\) can be too large and thus (25) becomes trivial inequality. We overcome this problem by essentially variating only \(\Sigma _+\) while keeping \(\Sigma _-\) unchanged, and vice-versa (see Fig. 2). To be more precise, we restrict the class of test function to \(\varphi \in C^\infty (\partial E)\) with zero average and which satisfy \(\varphi (x) = 0\) for every \(x \in \partial E \cap \{ x_2 \le - \tfrac{s}{3} \}\) (or \(\varphi (x) = 0\) for every \(x \in \partial E \cap \{ x_2 \ge \tfrac{s}{3} \}\)). The point is that for these test function an estimate similar to (27) holds,
Indeed, we first write
where \(a_+\) is from (41). We estimate the first term in the last line by (44)
while for the second term we use (41) and (42) (we recall that Remark 3 allows us to assume (28))
Hence, we get (48) thanks to (10) and \(\varrho \le \frac{7\sqrt{2 \pi }}{5s^2} e^{\frac{s^2}{2}}\) from (9).
In order to explain the idea of the proof, we assume first that \(\Sigma _+\) and \(\Sigma _-\) are different components of \(\partial E\). This is of course a major simplification but it will hopefully help the reader to follow the actual proof below. In this case we may use the following test functions in the second variation condition,
for \(i=1,2\), where \((\nu _i)_{\Sigma _+}\) is the average of \(\nu _i\) on \(\Sigma _+\). We use \(\varphi _i\) as a test function in the second variation condition (12) and use (48) to obtain
By using the equalities (35) and (36), rewritten on \(\Sigma _+\), we get after straightforward calculations
for \(i=1,2\). By adding up the previous inequality for \(i = 1,2\) we get
This can be rewritten as
By Jensen’s inequality \(1-(\nu _1)_{\Sigma _+}^2-(\nu _2)_{\Sigma _+}^2\ge 0\), while \(|\varrho \langle b, \nu \rangle | \le \frac{3}{2s^2}\) which follows from (17). Therefore \(k= 0\) and \(\Sigma _+\) is a line. It is clear that a similar conclusion holds also for in \(\Sigma _-\).
When \(\Sigma _+\) and \(\Sigma _-\) are connected the argument is more involved, since we need a cut-off argument in order to “separate” \(\Sigma _+\) and \(\Sigma _-\). This is possible due to (42), which implies that the perimeter of the minimizer in the strip \(\{ |x_2| \le s/3 \}\) is small. Therefore the cut-off argument produces an error term, which by (42) is small enough so that we may apply the previous argument. However, the presence of the cut-off function makes the estimates more complicated and since the argument is technically involved we split the rest of the proof in two steps.
Step 1. Without loss of generality we may assume that \({\mathcal {H}}_\gamma ^{1}(\Sigma _+) \ge {\mathcal {H}}_\gamma ^{1}(\Sigma _-)\). Let us denote
In the first step we prove
We do this by proving the counterpart of (50), which now reads as
for \(i=1,2\). Let us show first how (51) follows from (52).
Indeed, by \(\varrho |b|\le \frac{3}{2s^2}\) we have

Therefore we have

Thus we obtain from (52)

Note that \(\sum _{i=1}^2 \int _{\Sigma _+} \langle b, e_i \rangle \nu _i \, d {\mathcal {H}}_\gamma ^{1} = \int _{\Sigma _+} \langle b, \nu \rangle \, d {\mathcal {H}}_\gamma ^{1}\). Therefore, by adding the above inequality with \(i =1,2\) we obtain
which implies (51) (since \(\frac{4}{3} \cdot 244 < 330\)).
We are left to prove (52). We will use the second variation condition (12) with test function
for \(i=1,2\). Here \(\zeta : {\mathbb {R}}\rightarrow [0,1]\) is a smooth cut-off function such that
and \(\alpha _i\) is chosen so that \(\varphi _i\) has zero average and c is a number such that \(c >3\). This choice is the counterpart of (49) in the case when \(\partial E\) is connected. In particular, the cut-off function \(\zeta \) guarantees that \(\varphi _i(x) = 0\), for \(x \in \partial E \cap \{ x_2 \le -\tfrac{s}{3} \}\). Therefore the estimate (48) holds and the second variation condition (12) yields
Let us simplify the above expression. Recall that the test function is \(\varphi = (\nu _i - \alpha _i) \zeta \), where \(\zeta = \zeta (x_2)\). By straightforward calculation
Therefore we have by the above equality and by multiplying the equation (31) with \(\varphi _i \zeta \) that
where the remainder term is
On the other hand, multiplying (31) with \(\zeta ^2\) and integrating by parts yields
where the remainder term is
Collecting (53), (54) and (56) yields
where the remainder terms \(R_1\) and \(R_2\) are given by (55) and (57) respectively.
Let us next estimate the remainder terms in (58). Since \(|\nabla _\tau \zeta (x)| \le c/s\), for \(-s/3< x_2 < 0\) and \(\nabla _\tau \zeta (x) = 0\) otherwise, it holds
We may therefore estimate \(R_2\) (given by (57)) by Young’s inequality as
Similarly we may estimate \(R_1\), given by (55), as
To estimate the first term in the right we recall that \(\int _{\partial E} \varphi _i \, d {\mathcal {H}}_\gamma ^1=0\) and therefore \(\int _{\partial E} \varphi _i \zeta \, d {\mathcal {H}}_\gamma ^1 = \int _{\partial E} \varphi _i (\zeta -1) \, d {\mathcal {H}}_\gamma ^1\). Since \(\varphi _i (\zeta -1) =0\) on \(\partial E \cap \{-\tfrac{s}{3}< x_2 < 0 \}\), we deduce by \(\varrho |b|\le \frac{3}{2s^2}\) that
Hence, we choose c close to 3 in the definition of \(\zeta \) and deduce from (58)
Recall that \(C_+ = \frac{1}{s^2} {\mathcal {H}}_\gamma ^1\big (\partial E \cap \{-\tfrac{s}{3}< x_2 < 0 \}\big )\).
By a similar argument we may also get rid of the cut-off function \(\zeta \) in (59). Indeed by \(\varrho |b|\le \frac{3}{2s^2}\) we have \(-\int _{\partial E} \varrho \langle b , \nu \rangle \zeta ^2 \, d {\mathcal {H}}_\gamma ^1 \ge -\int _{\Sigma _+} \varrho \langle b , \nu \rangle \, d {\mathcal {H}}_\gamma ^1 - \frac{3}{2} C_+\). Similarly we get \(-\alpha _i \int _{\partial E} \varrho \langle b , e_i \rangle \zeta ^2 \, d {\mathcal {H}}_\gamma ^1 \le -\alpha _i \int _{\Sigma _+} \varrho \langle b , e_i \rangle \, d {\mathcal {H}}_\gamma ^1 + \frac{3}{2} C_+\). Therefore we obtain from (59) that
We need yet to replace \(\alpha _i\) by \((\nu _i)_{\Sigma _+}\) in order to obtain (52). We do this by showing that \(\alpha _i\) is close to the average \((\nu _i)_{\Sigma _+}\). To be more precise we claim that
Indeed, since \(\zeta =1\) on \(\Sigma _+\) we may write
Since \(\zeta = 0 \) when \(x_2 \le -s/3\) we may estimate
The inequality (61) then follows from \(\int _{\partial E}(\alpha _i - \nu _i)\zeta \, d {\mathcal {H}}_\gamma ^1 = - \int _{\partial E} \varphi _i \, d {\mathcal {H}}_\gamma ^1 = 0\).
Recall that we assume \({\mathcal {H}}_\gamma ^1(\Sigma _+) \ge {\mathcal {H}}_\gamma ^1(\Sigma _-)\). In particular, this implies
We use (62) and (32) to conclude that
We estimate (60) using \(\varrho |b|\le \frac{3}{2s^2}\), (61) and (63), and get
Finally the inequality (52) follows from
Step 2. Recall that we assume \({\mathcal {H}}_\gamma ^1(\Sigma _+) \ge {\mathcal {H}}_\gamma ^1(\Sigma _-)\). Let us show that also \(\Sigma _-\) satisfies (62), i.e., \({\mathcal {H}}_\gamma ^1(\Sigma _-) \ge \frac{1}{8} P_\gamma (E)\). To this aim we deduce from (51) that
We use (28) and the inequality above to obtain
Hence, by (33), we have \({\mathcal {H}}_\gamma ^1(\Sigma _-) \ge \frac{1}{8}P_\gamma (E)\).
We may thus use precisely the same argument as in the first step to prove the estimate (51) also for \(\Sigma _-\), i.e.,
where
We have by (63)  . Therefore we obtain from (51)
. Therefore we obtain from (51)
Similarly (64) (and an estimate analogous to (63) with \(\Sigma _-\) in place of \(\Sigma _+\)) implies
By adding these together and using (42) we obtain

We proceed by recalling the equation (31) for \(\nu _1\), i.e.,
We integrate this over \(\partial E\) and use (65) to get

Note that by \({\bar{\nu }} P_\gamma (E) = - \sqrt{2 \pi } \, b\) (given in (16)) we have \(|{\bar{\nu }}|\, \langle b, e^{(1)}\rangle = - |b| {\bar{\nu }}_1\). Thus we deduce from the above inequality that

Using (29) and the inequality  (given by (33)) we estimate
(given by (33)) we estimate

Therefore we deduce from (66)
We use \( \varrho |b| \ge \frac{1}{s^2} |{\bar{\nu }}|\) (from (17)) to conclude
and thus \({\bar{\nu }}_1 = 0\) since \(s \ge 10^3\). But then (33) implies
(recall that we chose \(e_1 = v\)) and we have reduced the problem to the one dimensional case. \(\square \)
5 The one dimensional case
In this short section we finish the proof of the main theorem which states that the minimizer of (7) is either the half-space \(H_{\omega , s}\) or the symmetric strip \(D_{\omega , s}\). By the previous results it is enough to solve the problem in the one-dimensional case. Surprisingly even this result does not seem to be trivial, even if its proof is based on elementary one-dimensional analysis.
Theorem 4
The minimizer \(E \subset {\mathbb {R}}\) of (7) is either \((-\infty , s)\), \((-s,\infty )\) or \((-a(s), a(s))\).
Proof
As we explained in Sect. 2, we have to prove that, when \(\varrho \) is in the interval (9), the only local minimizers of (7) are \((-\infty , s)\), \((-s,\infty )\) and \((-a(s), a(s))\).
Let us first show that the minimizer E is an interval. Recall that since \(E \subset {\mathbb {R}}\) is a set of locally finite perimeter it has locally finite number of boundary points. Moreover, since there is no curvature in dimension one the Euler equation (11) reads as
By (38) we have that \((-s+1, s-1) \subset E\). It is therefore enough to prove that the boundary \(\partial E\) has at most one positive and one negative point. Assume by contradiction that \(\partial E\) has at least two positive points (the case of two negative points is similar).
If x is a positive point which is closest to the origin on \(\partial E\) then \(\nu (x) = 1\). On the other hand, if y is the next boundary point, then \(\nu (y) =-1\). Then the Euler equation yields
By \(\varrho |b| \le \frac{3}{2s^2}\) (given in (17)) we conclude that
which is a contradiction since \(x,y >0\).
The minimizer of (7) is thus an interval of the form
where \(s-1 \le x, y\le \infty \). Without loss of generality we may assume that \(x \le y\). In particular, we have
Using the bound on the perimeter (10) we conclude that \(x < s + 1/s\). To bound y from above we use the Euler equation (67)
Thus we conclude from \(\varrho |b| \le \frac{3}{2s^2}\) that
Let us next prove that the minimizer has the volume \(\gamma (E) = \phi (s)\). Indeed, it is not possible that \(\gamma (E) < \phi (s)\), because by enlarging E we can decrease its perimeter, barycenter and the volume penalization term in (7). Also \(\gamma (E) >\phi (s)\) is not possible. If this was the case we may perturb the set E by
Then \(\phi (s)\le \gamma (E_t) < \gamma (E)\) and
taking again into account that \(\varrho |b(E)| \le \frac{3}{2s^2}\). But since \(x < s + 1/s\) the above inequality yields \(\frac{d}{dt} {\mathcal {F}}(E_t) \bigl |_{t=0} <0\), which contradicts the minimality of E. Note that since \(E = (-x,y)\) has the volume \(\phi (s)\) and \(x \le y\), it holds \(s \le x \le a(s) \le y\).
Let us finally show that if a local minimizer is a bounded interval \(E = (-x, y)\) for \(s \le x \le y <\infty \), then necessarily \(x = y = a(s)\). We study the value of the functional (7) for intervals \(E_t = (-\alpha (t), t)\) with \(s\le \alpha (t) \le a(s) \le t\), which have the volume \(\gamma (E_t) = \phi (s)\). By the inequality (68) we need only to study the case when \(a(s) \le t < s + \tfrac{5}{s}\). This leads us to study the function \(f : [a(s), s + \tfrac{5}{s}) \rightarrow {\mathbb {R}}\),
The volume constraint reads as \(\int _{-\alpha (t)}^t e^{-\frac{u^2}{2}} \, du = \sqrt{2 \pi } \, \phi (s)\). By differentiating this we obtain
From (69) we conclude that for \(t \ge \alpha (t)\) it holds \(0> \alpha '(t) > -1\).
Our goal is to show that f has at most two critical points. Moreover, it holds \(\alpha (a(s)) = a(s)\) and therefore by symmetry \(f'(a(s)) = 0\). We will also show that this point \(t = a(s)\) is a strict local minimum. Therefore if the function f would have another local minimum say at \({\tilde{t}}\), there would be a third critical point in \((a(s),{\tilde{t}})\). This is a contradiction and we conclude the proof.
To this aim we differentiate f once and use (69) to get
Therefore at a critical point it holds
We are interested in the sign of \(f''(t)\) at critical points in the interval \([a(s), s + \tfrac{5}{s})\). To simplify the notation we denote the barycenter of \(E_t = (-\alpha (t), t)\) by
By differentiating f twice and by using (69) and (70) we obtain
at a critical point t. Let us write \(\varrho = \frac{\varrho _0 \sqrt{2 \pi }}{s^2} e^{\frac{s^2}{2}}\), where \(\tfrac{6}{5} \le \varrho _0 \le \tfrac{7}{5}\). In order to analyze the sign of \(f''(t)\) at critical points we define \(g : [a(s), s + \tfrac{5}{s}) \rightarrow {\mathbb {R}}\) as
As we mentioned, the end point \(t = \alpha (t) = a(s) >s\) is of course a critical point of f. Let us check that it is a local minimum. We have for the barycenter \(b_{a(s)}= 0\), \(\alpha '(a(s)) = -1\) by (69) and \( 2e^{-\frac{a(s)^2}{2}} > e^{-\frac{s^2}{2}} \) by (5). Therefore it holds
In particular, we deduce that \(t = a(s)\) is a strict local minimum of f.
Let us next show that g is strictly decreasing. We first obtain by differentiating (69) that
By recalling that \(|\alpha '(t)| \le 1\) and \(\alpha (t) \le a(s) \le s + \ln 2/s\) by (4), we get that \(|\alpha ''(t)| \le 2s\, |\alpha '(t)| + 6/s\) for \(t \in [a(s), s + \tfrac{5}{s})\). By \(\alpha (t) \ge s\) we have \(\varrho |b_t| \le \frac{\varrho _0}{s^2} e^{-\frac{\alpha ^2(t)}{2}} e^{\frac{s^2}{2}} \le \frac{2}{s^2}\). Moreover, by differentiating the barycenter (71) and using (69) we get \(\varrho \, |b_t'| \le 4/s\). We may then estimate the derivative of g as
Next we observe that (69) and \(\alpha (t) \le a(s) \le s + \ln 2/s\) imply
Therefore we deduce from the above two inequalities and from \(\varrho _0 \ge \frac{6}{5} > \frac{8}{7}\) that g is strictly decreasing on \([a(s), s + \tfrac{5}{s})\).
Recall that \(g(a(s))>0\). Since g is strictly decreasing, there is \(t_0 \in (a(s), s + \tfrac{5}{s})\) such that \(g(t)>0\) for \(t \in [a(s),t_0)\) and \(g(t)<0\) for \(t \in (t_0,s + \tfrac{5}{s})\). Therefore the function f has no other local minimum on \([a(s), s + \tfrac{5}{s})\) than the end point \(t = a(s)\). Indeed, if there were another local minimum on \((a(s), t_0]\) there would be at least one local maximum on \((a(s), t_0)\). This is impossible as the previous argument shows that \(f''(t) >0\) at every critical point on \((a(s), t_0)\). Moreover, from \(g(t)<0\) for \(t \in (t_0,s + \tfrac{5}{s})\) we conclude that there are no local minimum points on \((t_0,s + \tfrac{5}{s}]\). This completes the proof. \(\square \)
References
Bakry, D., Ledoux, M.: Lévy-Gromov isoperimetric inequality for an infinite dimensional diffusion generator. Invent. Math. 123, 259–281 (1995)
Barchiesi, M., Brancolini, A., Julin, V.: Sharp dimension free quantitative estimates for the Gaussian isoperimetric inequality. Ann. Probab. 45, 668–697 (2017)
Barchiesi, M., Julin, V.: Robustness of the Gaussian concentration inequality and the Brunn–Minkowski inequality. Calc. Var. Partial Differ. Equ. 56, Art. n.80 (2017)
Barthe, F.: An isoperimetric result for the Gaussian measure and unconditional sets. Bull. Lond. Math. Soc. 33, 408–416 (2001)
Bernstein, J., Wang, L.: A sharp lower bound for the entropy of closed hypersurfaces up to dimension six. Invent. Math. 206, 601–627 (2016)
Bögelein, V., Duzaar, F., Fusco, N.: A quantitative isoperimetric inequality on the sphere. Adv. Calc. Var. 10, 223–265 (2017)
Borell, C.: The Brunn–Minkowski inequality in Gauss space. Invent. Math. 30, 207–216 (1975)
Chakrabarti, A., Regev, O.: An optimal lower bound on the communication complexity of gap-Hamming-distance. In: STOC’11—Proceedings of the 43rd ACM Symposium on Theory of Computing, pp. 51–60. ACM, New York (2011)
Choksi, R., Muratov, C.B., Topaloglu, I.: An old problem resurfaces nonlocally: Gamow’s liquid drops inspire today’s research and applications. Not. Am. Math. Soc. 64, 1275–1283 (2017)
Choksi, R., Peletier, M.: Small volume fraction limit of the diblock copolymer problem: I. Sharp-interface functional. SIAM J. Math. Anal. 42, 1334–1370 (2012)
Cianchi, A., Fusco, N., Maggi, F., Pratelli, A.: On the isoperimetric deficit in Gauss space. Am. J. Math. 133, 131–186 (2011)
Cicalese, C., Leonardi, G.P.: Best constants for the isoperimetric inequality in quantitative form. J. Eur. Math. Soc. 15, 1101–1129 (2013)
Colding, T.H., Ilmanen, T., Minicozzi, W.P., William, P., White, B.: The round sphere minimizes entropy among closed self-shrinkers. J. Differ. Geom. 95, 53–69 (2013)
Colding, T.H., Minicozzi, W.P.: Generic mean curvature flow I: generic singularities. Ann. Math. 175, 755–833 (2012)
Ehrhard, A.: Symétrisation dans l’espace de Gauss. Math. Scand. 53, 281–301 (1983)
Eldan, R.: A two-sided estimate for the Gaussian noise stability deficit. Invent. Math. 201, 561–624 (2015)
Fusco, N.: The quantitative isoperimetric inequality and related topics. Bull. Math. Sci. 5, 517–607 (2015)
Fusco, N., Julin, V.: A strong form of the quantitative isoperimetric inequality. Calc. Var. Partial Differ. Equ. 50, 925–937 (2014)
Filmus, Y., Hatami, H., Heilman, S., Mossel, E., O’Donnell, R., Sachdeva, S., Wan, A., Wimmer, K.: Real Analysis in Computer Science: A collection of Open Problems. Available online (2014)
Gamow, G.: Mass defect curve and nuclear constitution. Proc. R. Soc. Lond. A 126, 632–644 (1930)
Giusti, E.: Minimal Surfaces and Functions of Bounded Variations. Birkhäuser, Boston (1994)
Heilman, S.: Low Correlation Noise Stability of Symmetric Sets. Preprint (2015)
Heilman, S.: Symmetric convex sets with minimal Gaussian surface area. Preprint (2017)
Julin, V.: Isoperimetric problem with a Coulombic repulsive term. Indiana Univ. Math. J. 63, 77–89 (2014)
Knüpfer, H., Muratov, C.B.: On an isoperimetric problem with a competing nonlocal term II: The general case. Commun. Pure Appl. Math. 67, 1974–1994 (2014)
La Manna, D.A.: Local minimality of the ball for the Gaussian perimeter. Adv. Calc. Var. 12, 193–210 (2019)
Latala, R., Oleszkiewicz, K.: Gaussian measures of dilatations of convex symmetric sets. Ann. Probab. 27, 1922–1938 (1999)
Lawson, H.B.: Lectures on Minimal Submanifolds, Vol. I. Mathematics Lecture Series, vol. 9, 2nd edn. Publish or Perish Inc, Wilmington (1980)
Maggi, F.: Sets of Finite Perimeter and Geometric Variational Problems: An Introduction to Geometric Measure Theory. Cambridge Studies in Advanced Mathematics, vol. 135. Cambridge University Press, Cambridge (2012)
Mossel, E., Neeman, J.: Robust dimension free isoperimetry in Gaussian space. Ann. Probab. 43, 971–991 (2015)
Mossel, E., Neeman, J.: Robust optimality of Gaussian noise stability. J. Eur. Math. Soc. 17, 433–482 (2015)
Rosales, C.: Isoperimetric and stable sets for log-concave perturbatios of Gaussian measures. Anal. Geom. Metr. Spaces 2, 328–358 (2014)
Sudakov, V.N., Tsirelson, B.S.: Extremal properties of half-spaces for spherically invariant measures. Zap. Naučn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 41, 14–24, 165 (1974)
Tkocz, T.: Gaussian measures of dilations of convex rotationally symmetric sets in \({\mathbb{C}}^N\). Electron. Commun. Probab. 16, 38–49 (2011)
Zhu, J.: On the entropy of closed hypersurfaces and singular self-shrinkers. J. Differ. Geom. (to appear)
Acknowledgements
The first author was supported by INdAM and by the project VATEXMATE. The second author was supported by the Academy of Finland Grant 314227.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
We first prove the inequalities (4) and (5). In fact, the proof gives us a slightly stronger estimate than (4). We recal that we are assuming \(s \ge 10^3\).
Lemma 5
The following estimates hold:
and
Proof
The right-hand inequality in (72) follows from the isoperimetric inequality \(P_\gamma (D_{\omega ,s}) > P_\gamma (H_{\omega ,s})\) which we may write as \(2 e^{-\frac{a(s)^2}{2}} > e^{-\frac{s^2}{2}}\). This implies
In order to show the right-hand inequality in (73) we first note that the function \(\psi : [0, \infty ) \rightarrow {\mathbb {R}}\),
is increasing. Indeed, its first derivative is
and by a second order analysis it is easy to show that the quantity \(\psi '(x) e^{-\frac{x^2}{2}}\) is positive. The volume condition \(\gamma (D_{\omega ,s}) = \phi (s)\) can be written as
Since \(\psi \) is increasing and \(a(s) > s\) we deduce by the upper bound for a(s) that
Hence we have the right-hand inequality in (73).
To prove the left-hand inequality in (72) we use the above estimate to obtain
In order to prove the inequality we need to show that
This is equivalent to
Use the fact that for \(0<y<1/9\) it holds \(\ln (1 + y) \ge 9y/10\) to estimate
The claim follows from the fact that \(\ln ^2 \left( 2-2/s^2\right) < 9(1 - \ln 2)/5\).
In order prove the left-hand inequality in (73) we first obtain, by integrating by parts twice, that
This implies
Then the volume condition \(\gamma (D_{\omega ,s}) = \phi (s)\) yields
and therefore we have by (72) that
\(\square \)
Finally we prove the perimeter bounds in (10).
Lemma 6
Let E be a minimizer of (7). Then it holds
Proof
The bound from above follows by the minimality and by (73):
The proof of the lower bound is slightly more difficult. Let \({\bar{s}}\) be such that \(\gamma (E) = \phi ({\bar{s}})\). The value \({\bar{s}}\) has to be non-negative, otherwise \({\mathcal {F}}(E)>{\mathcal {F}}({\mathbb {R}}^n\setminus E)\). If \({\bar{s}}\le s\), then the claim follows easily by the Gaussian isoperimetric inequality. If instead \({\bar{s}}> s\), then again by the isoperimetric inequality we have
Define function \(f:[s, \infty ) \rightarrow {\mathbb {R}}\), \(f(x) := e^{-\frac{x^2}{2}} + (s + 1) \int _s^{x} e^{-\frac{t^2}{2}} \, dt\). By differentiating we get
The function is thus increasing up to \(x = s + 1\) and then decreasing. Denote \({\hat{s}}=s+ \frac{1}{6s}\). Let us show that \(f(x) > {\mathcal {F}}(D_{\omega ,s})\) for every \(x \ge {\hat{s}}\).
Note that \(f'(x) \ge \frac{1}{2} e^{-\frac{s^2}{2}}\) for every \(x \in (s, {\hat{s}})\). Therefore since \(f(s) = e^{-\frac{s^2}{2}}\) we get
Moreover we have by (74) that
By the earlier analysis we deduce that for every \(x \ge {\hat{s}}\) it holds
Hence we conclude by (73) that \(f(x) > P_\gamma (D_{\omega ,s})= {\mathcal {F}}(D_{\omega ,s})\) for every \(x \ge {\hat{s}}\). This in turn implies that necessarily \({\bar{s}} < {\hat{s}}\). By the isoperimetric inequality we then have that
\(\square \)
Rights and permissions
About this article
Cite this article
Barchiesi, M., Julin, V. Symmetry of minimizers of a Gaussian isoperimetric problem. Probab. Theory Relat. Fields 177, 217–256 (2020). https://doi.org/10.1007/s00440-019-00947-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-019-00947-9