Nonlinear thermo-mechanical dynamic buckling and vibration of FG-GPLRC circular plates and shallow spherical shells resting on the nonlinear viscoelastic foundation

Abstract

This research aims to establish the semi-analytical approach for nonlinear dynamic buckling and vibration responses of functionally graded graphene platelet reinforced composite (FG-GPLRC) circular plates and spherical shells subjected to time-dependent radial pressure and thermal loads. The higher-order shear deformation theory with von Karman’s nonlinearities and the nonlinear viscoelastic foundation model is used to establish the expression of the fundamental equations of considered structures. The shells and plates are considered with clamped and immovable edge, and shallow curvature of the shells is applied. The Lagrange function is applied to establish the total energy of structures, and the potential function of viscous damping of the viscoelastic foundation is expressed using the Rayleigh dissipation function. The motion equation of the structures can be formulated using the Euler–Lagrange function. The dynamic responses are obtained using the numerical method, and the critical dynamic buckling loads are obtained using the dynamic buckling criterion of Budiansky–Roth. The large effects of material parameters, geometrical parameters, and nonlinear viscoelastic foundation on dynamic responses of considered structures are investigated and discussed in many numerical examples.

1 Introduction

Circular plates are typical structures in engineering with many applications. The more complex structures of circular plates are the shallow spherical shells with only a shallow curvature, the load-carrying capacity of the structures significantly improved, and their applications are popular, and the research on their mechanical behavior is an important problem in the world [1,2,3].

Functionally graded material (FGM) is an advanced type of multifunctional composite, with variations in component materials for the important purpose of controlling variation in electro-thermo-mechanical, or other technical properties. Reddy et al. [4] used the classical, first-order shear deformation theory (FSDT) and higher-order shear deformation theory (HSDT) to analyze the linear bending behavior of FGM circular plates with axisymmetric displacements. The variable-thickness circular FGM plates were analyzed using the FSDT and differential quadrature method with the plate–foundation interaction by Ghomshei [5]. Shariyat and Alipour [6] presented the semi-analytical formulations to analyze the dynamic stress of sandwich FGM circular plates with a consistent power series solution. Dynamic behavior and vibration of FGM circular plates were mentioned in the thermally postbuckled state [7], with generalized differential quadrature rule [8], and using the nonlinear Chebyshev-based collocation technique [9]. FGM square and circular plates were considered in bending and linear frequency problems using a strain-based finite element formulation [10]. By using the Donnell–Mushtari–Vlasov theory, the thermal and mechanical buckling behavior of FGM spherical shells was investigated [11] considering the simplified kinematic relations of Sanders. The FGM deep spherical shells with piezoelectric actuators were considered [12] in the thermal buckling problem using an analytical approach. An analytical solution for elastic waves in FGM spherical shells was proposed [13] using the separation of variables technique to displacements. An adjacent equilibrium is established to investigate the linear buckling problem of FGM annular spherical segments with parallel stiffeners using the Galerkin method [14]. Different boundary conditions were considered to investigate the bending and vibration of FGM annular plates on the nanoscale using FSDT and a nonlocal stress-driven model [15]. The superior load-carrying capacity of sandwich plates and shells was mentioned and validated in many studies [16,17,18,19]. First-order shear deformable multilayer FGM and sandwich porous FGM spherical shells were mentioned in the nonlinear vibration problem with shell–foundation interaction and thermal temperature [17, 18]. By using the Ritz energy method, the nonlinear thermo-mechanical buckling behavior of higher-order shear deformable FGM sandwich spherical shells was performed with the effects of porous core [19].

The functionally graded graphene platelet reinforced composite (FG-GPLRC) is known as the next type of FGM. Many studies showed that the load-carrying capacity of FG-GPLRC structures increases significantly with only a small amount of graphene platelet (GPL) added to the isotropic matrix. The thermal backbone curve, dynamic response, and dynamic instability of beams made from FG-GPLRC were investigated with beam–foundation interaction [20], with moving load [21], and with isotropic core [22]. Nonlinear large deflection, vibration, thermal dynamic response, bending, buckling, and postbuckling analyses of FG-GPLRC rectangular plates and doubly curved shell panels were studied using the generalized differential quadrature (GDQ) method [23, 24], using the variational differential quadrature and finite element methods [25], using the Navier technique [26, 27], using the Ritz method [28, 29], and using the Chebyshev polynomials [30]. Some other special structures such as rotating microplates [31], folded plates [32], and conical shells [33] made from FG-GPLRC were also investigated in vibration, dynamic response, bending, and buckling problems, respectively. Bending, buckling, and vibration responses of FG-GPLRC circular plates were mentioned using the 3D poroelasticity theory [34], the mesh-free approach [35], and the GDQ method [36]. FG-GPLRC annular plates were mentioned [37,38,39] in the problems of thermal buckling and vibration analysis using the FSDT and HSDT. Thermo-elastic, bending, and mechanical buckling responses of FG-GPLRC spherical shells using the Galerkin method [40], using the layerwise differential quadrature method [41], using the state space method [42], and using the finite element method [43]. By using the HSDT and Ritz energy method, the nonlinear thermal and mechanic buckling behavior of FG-GPLRC spherical shells was studied [44, 45] taking into account the effects of porous core [44] and the effects of nonlinearity of foundation [45]. Nonlinear thermal buckling responses of FG-GPLRC circular plates and spherical shells were investigated [46] using the FSDT and Galerkin method with the trigonometric forms of deflection and rotation.

Vibration and dynamic buckling behavior has many important meanings in engineering, typically in complex mechanical systems [47], in rotor systems [48, 49], in ship pipeline systems [50], and in piles with large slenderness ratios [51]. For FGM and FG-GPLRC circular plate and spherical shell structures, the vibration and dynamic buckling behavior was also mentioned [7,8,9, 17, 18, 36, 42, 43].

The advantages of HSDT compared with classical plate and shell theories and FSDT were shown and validated in many reports with the well-suitable thick composite plates and shells. However, the literature also showed a lack of research on the nonlinear dynamic thermo-mechanical behavior of circular plates and spherical shells.

According to the great knowledge of the authors, there is no study on the dynamic responses of higher-order shear deformable FG-GPLRC spherical shells and circular plates resting on the nonlinear viscoelastic foundation. In this study, the motion equation including the potential energy of damping of the foundation of the structures is expressed by using the Lagrange function, Euler–Lagrange equations, and Rayleigh dispassion function. The time-dependent radial pressure and time-dependent thermal load are applied to the structures, and the fundamental frequencies, vibration responses, phase planes, and thermal dynamic buckling are investigated. In the numerical examples, the significant effects of the geometrical, material, and elastic foundation parameters on the dynamic behavior of the FG-GPLRC spherical shells and circular plates are validated and evaluated.

2 Geometrical and material features of FG-GPLRC spherical shells and circular plates and fundamental formulas

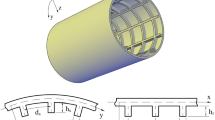
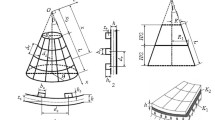
The shallow curvature of spherical shells is assumed in Fig. 1, and the quasi-polar coordinate system $\left( {r,\,\theta ,\,z} \right)$ is approximated from the spherical coordinate system $\left( {\varphi ,\,\theta ,\,z} \right)$ with $r = R_{0} \sin \varphi$, the circumferential and meridional directions $\theta$ and $\varphi$, the main radius $R_{0}$, base radius $R_{1}$, and centripetal axis $z$. The displacements of circular plates and spherical shells are assumed to be axisymmetric, and time-dependent radial pressure $q$ and thermal load $\Delta T$ are applied with the nonlinear viscoelastic interaction of the foundation.

Fig. 1

Configurations, material distributions, and coordinate system of considered structures

The shells and plates are considered with five distributions of GPLs: U, X, O, V, and Λ distributions, according to the linear functions through the shell and plate thicknesses $\left( { - \frac{h}{2} \le z \le \frac{h}{2}} \right)$, as

$$ W_{{{\text{GPL}}}} = \left\{ {\begin{array}{*{20}c} {W_{{{\text{GPL}}}}^{*} } & {\text{U distribution,}} \\ {4\frac{\left| z \right|}{h}W_{{{\text{GPL}}}}^{*} } & {\text{X distribution,}} \\ {2\left( {1 - \frac{2\left| z \right|}{h}} \right)W_{{{\text{GPL}}}}^{*} } & {\text{O distribution,}} \\ {\left( {1 - \frac{2z}{h}} \right)W_{{{\text{GPL}}}}^{*} } & {\text{V distribution,}} \\ {\left( {1 + \frac{2z}{h}} \right)W_{{{\text{GPL}}}}^{*} } & {\Lambda {\text{ distribution,}}} \\ \end{array} } \right. $$

(1)

where $W_{{{\text{GPL}}}}^{*}$ is the average GPL mass fraction.

The volume fraction of the GPLs can be defined as

$$ V_{{{\text{GPL}}}} = \frac{{\rho_{m} W_{{{\text{GPL}}}} }}{{\rho_{m} W_{{{\text{GPL}}}} + \rho_{{{\text{GPL}}}} \left( {1 - W_{{{\text{GPL}}}} } \right)}}, $$

(2)

where $V_{m} + V_{{{\text{GPL}}}} = 1$, the subscripts ${\text{GPL}}$ and $m$ denote the GPL and matrix, respectively, $\rho$ is the denote of density, and $V$ is the denote of volume fraction.

The elastic modulus of the shells and plates can be estimated based on the Halpin–Tsai model, as [38]

$$ \overline{E} = \frac{{3E_{m} \left( {1 + \Theta_{1} \Gamma_{1} V_{{{\text{GPL}}}} } \right)}}{{8\left( {1 - \Gamma_{1} V_{{{\text{GPL}}}} } \right)}} + \frac{{5E_{m} \left( {1 + \Theta_{2} \Gamma_{2} V_{{{\text{GPL}}}} } \right)}}{{8\left( {1 - \Gamma_{2} V_{{{\text{GPL}}}} } \right)}}, $$

(3)

where

$$ \Gamma_{1} = \frac{{E_{GPL} - E_{m} }}{{E_{GPL} + \Theta_{1} E_{m} }},\,\,\Gamma_{2} = \frac{{E_{GPL} - E_{m} }}{{E_{GPL} + \Theta_{2} E_{m} }},\,\,\Theta_{1} = \frac{{2a_{GPL} }}{{t_{GPL} }},\,\,\Theta_{2} = \frac{{2b_{GPL} }}{{t_{GPL} }}, $$

(4)

where $E$ is the elastic modulus, $a_{{{\text{GPL}}}}$ and $b_{{{\text{GPL}}}}$ are, respectively, the length and width, and $t_{{{\text{GPL}}}}$ is the thickness of the GPLs.

The Poisson ratio $\overline{\nu }$, thermal expansion coefficient $\overline{\alpha }$, and density $\overline{\rho }$ of FG-GPLRC shells and plates are determined according to the mixture rule as

$$ \begin{gathered} \overline{\nu } = \nu_{m} V_{m} + \nu_{{{\text{GPL}}}} V_{{{\text{GPL}}}} , \hfill \\ \overline{\alpha } = \alpha_{m} V_{m} + \alpha_{{{\text{GPL}}}} V_{{{\text{GPL}}}} , \hfill \\ \overline{\rho } = \rho_{m} V_{m} + \rho_{{{\text{GPL}}}} V_{{{\text{GPL}}}} . \hfill \\ \end{gathered} $$

(5)

By adding the thermal stresses caused by the uniformly distributed thermal load $\Delta T$(counted from the initial free thermal stress state to the final thermal stress state), Hookian law is applied to the FG-GPLRC shells and plates, as [19]

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{r} } \\ {\sigma_{\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } \\ \end{array} } \right]\left\{ {\left[ {\begin{array}{*{20}c} {\varepsilon_{r} } \\ {\varepsilon_{\theta } } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {\overline{\alpha }} \\ {\overline{\alpha }} \\ \end{array} } \right]\Delta T} \right\},\,\,\,\sigma_{rz} = \overline{Q}_{44} \varepsilon_{rz} , $$

(6)

where the reduced stiffnesses of shells and plates can be calculated by

$$ \overline{Q}_{11} = \overline{Q}_{22} = \frac{{\overline{E}}}{{1 - \overline{\nu }^{2} }},\,\,\,\,\,\overline{Q}_{12} = \frac{{\overline{E}\overline{\nu }}}{{1 - \overline{\nu }^{2} }},\,\,\,\,\,\overline{Q}_{44} = \frac{{\overline{E}}}{{2 + 2\overline{\nu }}}. $$

(7)

The axisymmetric displacements at a distance $z$ from the mid-surface of the spherical shells and circular plates can be derived using the theory of the HSDT, as [44]

$$ \left\{ {\begin{array}{*{20}c} {\overline{u}} \\ {\overline{v}} \\ {\overline{w}} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {u\left( r \right) + \phi \left( r \right)z - \left[ {\phi \left( r \right) + w\left( r \right)_{,r} } \right]\frac{{4z^{3} }}{{3h^{2} }}} \\ 0 \\ {w^{*} \left( r \right) + w\left( r \right)} \\ \end{array} } \right\}, $$

(8)

where $\overline{u} = \overline{u}\left( {r,z} \right),\,\,\overline{v} = \overline{v}\left( {r,z} \right),$ and $\overline{w} = \,\overline{w}\left( {r,z} \right)$; $\phi \left( r \right)$ is the rotation; and $w^{*} \left( r \right)$ is the imperfect deflection of structures.

The expressions of the strains at a distance $z$ from the mid-surface can be applied as [44]

$$ \left\{ \begin{gathered} \varepsilon_{r} \hfill \\ \varepsilon_{\theta } \hfill \\ \varepsilon_{rz} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} \overline{\varepsilon }_{r} \hfill \\ \overline{\varepsilon }_{\theta } \hfill \\ \overline{\varepsilon }_{rz} \hfill \\ \end{gathered} \right\} + z\left\{ {\begin{array}{*{20}c} {\phi_{,r} } \\ {\frac{\phi }{r}} \\ 0 \\ \end{array} } \right\} - z^{2} \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {\lambda \left( {\phi + w_{,r} } \right)} \\ \end{array} } \right\} - z^{3} \left\{ {\begin{array}{*{20}c} {\lambda \left( {\phi_{,r} + w_{,rr} } \right)} \\ {\lambda \left( {\frac{\phi }{r} + \frac{1}{r}w_{,r} } \right)} \\ 0 \\ \end{array} } \right\}, $$

(9)

where $\lambda = {4 \mathord{\left/ {\vphantom {4 {3h^{2} }}} \right. \kern-0pt} {3h^{2} }}$.

The mid-surface strains $\overline{\varepsilon }_{r} ,\,\overline{\varepsilon }_{\theta } ,\,\overline{\varepsilon }_{rz}$ combined with the nonlinearities of von Karman, presented as [19]

$$ \left\{ {\begin{array}{*{20}c} {\overline{\varepsilon }_{r} } \\ \begin{gathered} \overline{\varepsilon }_{\theta } \hfill \\ \overline{\varepsilon }_{rz} \hfill \\ \end{gathered} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {u_{,r} - \frac{w}{{R_{0} }} + w_{,r} w_{,r}^{*} + \frac{1}{2}w_{,r}^{2} } \\ \begin{gathered} - \frac{w}{{R_{0} }} + \frac{u}{r} \hfill \\ \phi + w_{,r} \hfill \\ \end{gathered} \\ \end{array} } \right\}. $$

(10)

The fundamental relations are generally written for the spherical shells, and the results for circular plates are obtained by applying the infinity for the main radius $\left( {R_{0} \to \infty } \right)$.

The extension forces, shear forces, moments, higher-order moments, and higher-order shear forces of the shells and plates with axisymmetrical deformation are determined by integrating Hooke’s law, as

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {N_{r} } \\ {N_{\theta } } \\ {M_{r} } \\ {M_{\theta } } \\ {P_{r} } \\ {P_{\theta } } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & {C_{11} } & {C_{12} } & {D_{11} } & {D_{12} } \\ {B_{12} } & {B_{22} } & {C_{12} } & {C_{22} } & {D_{12} } & {D_{22} } \\ {C_{11} } & {C_{12} } & {F_{11} } & {F_{12} } & {G_{11} } & {G_{12} } \\ {C_{12} } & {C_{22} } & {F_{12} } & {F_{22} } & {G_{12} } & {G_{22} } \\ {D_{11} } & {D_{12} } & {G_{11} } & {G_{12} } & {H_{11} } & {H_{12} } \\ {D_{12} } & {D_{22} } & {G_{12} } & {G_{22} } & {H_{12} } & {H_{22} } \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}c} {\overline{\varepsilon }_{r} } \\ {\overline{\varepsilon }_{\theta } } \\ {\phi_{,r} } \\ {\frac{\phi }{r}} \\ { - \lambda \left( {\phi_{,r} + w_{,rr} } \right)} \\ { - \lambda \left( {\frac{\phi }{r} + \frac{1}{r}w_{,r} } \right)} \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\overline{\Phi }_{1} } \\ {\overline{\Phi }_{1} } \\ {\overline{\Phi }_{2} } \\ {\overline{\Phi }_{2} } \\ {\overline{\Phi }_{3} } \\ {\overline{\Phi }_{3} } \\ \end{array} } \right\}\Delta T, \hfill \\ \left\{ {\begin{array}{*{20}c} {Q_{r} } \\ {R_{r} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {I_{44} } & {I_{45} } \\ {I_{45} } & {I_{55} } \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}c} {\overline{\varepsilon }_{rz} } \\ { - \lambda \left( {\phi + w_{,r} } \right)} \\ \end{array} } \right\}, \hfill \\ \end{gathered} $$

(11)

where

$$ \left( {B_{ij} ,C_{ij} ,F_{ij} ,D_{ij} ,G_{ij} ,H_{ij} } \right) = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\overline{Q}_{ij} \left( {1,z,z^{2} ,z^{3} ,z^{4} ,z^{6} } \right){\text{d}}z} ,\quad \left( {ij = 1,2} \right), $$

$$ \begin{gathered} \left( {I_{44} ,I_{45} ,I_{55} } \right) = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\overline{Q}_{44} \left( {1,z^{2} ,z^{4} } \right){\text{d}}z} , \hfill \\ \left( {\overline{\Phi }_{1} ,\overline{\Phi }_{2} ,\overline{\Phi }_{3} } \right) = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\left( {\overline{Q}_{11} + \overline{Q}_{12} } \right)\overline{\alpha }\left( {1,z,z^{3} } \right){\text{d}}z} . \hfill \\ \end{gathered} $$

Considering the foundation reaction of the nonlinear foundation model [36], and assuming that the in-plane and rotary kinetic energy components are small and neglected [1, 3, 8, 17, 18], the thermo-elastic strain energy of the structures and the work done by the external loads taking into account the nonlinear interaction of the foundation are expressed, respectively, by

$$ \overline{U}_{{\text{int}}} = \pi \int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\int\limits_{0}^{{R_{1} }} {\left[ {\sigma_{r} \left( {\varepsilon_{r} - \overline{\alpha }\Delta T} \right) + \sigma_{\theta } \left( {\varepsilon_{\theta } - \overline{\alpha }\Delta T} \right) + \sigma_{rz} \varepsilon_{rz} } \right]} \,r{\text{d}}r{\text{d}}z} , $$

(12)

$$ \overline{U}_{{{\text{ext}}}} = 2\pi \int\limits_{0}^{{R_{1} }} {qwr{\text{d}}r} - \pi \int\limits_{0}^{{R_{1} }} {\left\{ {\left[ {K_{1} w + \frac{1}{2}K_{3} w^{3} - K_{2} \left( {w_{,rr} + \frac{1}{r}w_{,r} } \right)} \right]w} \right\}r{\text{d}}r} , $$

(13)

$$ \overline{U}_{T} = \pi \int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\int\limits_{0}^{{R_{1} }} {\overline{\rho }\overline{w}_{,t}^{2} r{\text{d}}r{\text{d}}z} } , $$

(14)

where the linear Winkler stiffness is denoted by $K_{1}$ (N/m³), the linear Pasternak stiffness is denoted by $K_{2}$ (N/m), and the nonlinear stiffness is $K_{3}$ (N/m⁵). The nonlinear stiffness $K_{3}$ may be negative or positive, respectively, modeling the softening or hardening foundations.

From Eqs. (12), (13), and (14), the total potential energy is obtained as

$$ \overline{U} = \overline{U}_{T} - \overline{U}_{{\text{int}}} + \overline{U}_{{{\text{ext}}}} . $$

(15)

3 Solution forms and solving procedure

The clamped, immovable, and axisymmetric boundary conditions of the structures are considered as

$$ \begin{gathered} {\text{At}}\,\,r = 0:\,\,\,\,\,\,\,\,u = 0,\,\,\,\,\phi = 0,\,\,\,\,\,w_{,r} = 0,\,\,\,w = {\text{finite,}} \hfill \\ {\text{At}}\,\,r = R_{1} :\,\,\,\,w = 0,\,\,\,w_{,r} = 0,\,\,\,\phi = 0,\,\,\,\,\,u = 0\,. \hfill \\ \end{gathered} $$

(16)

The solutions that satisfied the considered boundary conditions can be assumed to be in the forms, as [45]

$$ \begin{gathered} u = U\frac{{r\left( {R_{1} - r} \right)}}{{R_{1}^{2} }},\,\,\,\,\,\,\phi = \Phi \frac{{r\left( {R_{1}^{2} - r^{2} } \right)}}{{R_{1}^{3} }},\, \hfill \\ w = W\frac{{\left( {R_{1}^{2} - r^{2} } \right)^{2} }}{{R_{1}^{4} }},\,\,\,w^{*} = \kappa h\frac{{\left( {R_{1}^{2} - r^{2} } \right)^{2} }}{{R_{1}^{4} }},\, \hfill \\ \end{gathered} $$

(17)

where $\kappa$ is the size of the geometrical imperfection, and the imperfection $w^{*}$ is chosen to be the same form of deflection of the structures.

To simulate the viscous damping effect of the foundation, the Rayleigh dissipation function is used and combined with the Euler–Lagrange equations, as

$$ \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\partial \overline{U}}}{{\partial \dot{W}}}} \right) - \frac{{\partial \overline{U}}}{\partial W} + \frac{{\partial d_{1} }}{{\partial \dot{W}}} = 0,\, \hfill \\ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\partial \overline{U}}}{{\partial \dot{U}}}} \right) - \frac{{\partial \overline{U}}}{\partial U} = 0\,, \hfill \\ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\partial \overline{U}}}{{\partial \dot{\Phi }}}} \right) - \frac{{\partial \overline{U}}}{\partial \Phi } = 0, \hfill \\ \end{gathered} $$

(18)

where the viscoelastic potential function of the foundation $d_{1} = \pi \int\limits_{0}^{{R_{1} }} {\tau \dot{w}^{2} r{\text{d}}r}$.

Substituting Eq. (17) into the total potential energy (15), and then into Eq. (18), the motion equations of the structures are obtained as

$$ b_{11} {\mkern 1mu} U + b_{12} {\mkern 1mu} \Phi + b_{13} {\mkern 1mu} W + b_{14} {\mkern 1mu} W\left( {W + 2\kappa h} \right) = 0, $$

(19)

$$ b_{12} U + {\mkern 1mu} b_{22} \Phi + b_{23} W + b_{24} W\left( {W + 2\kappa h} \right){\mkern 1mu} = 0, $$

(20)

$$ \begin{gathered} b_{31} {\mkern 1mu} U + b_{32} {\mkern 1mu} \Phi + b_{33} {\mkern 1mu} U\left( {W + \kappa h} \right) + b_{34} \Phi \left( {W + \kappa h} \right) + b_{35} {\mkern 1mu} W\left( {W + {{4\kappa h} \mathord{\left/ {\vphantom {{4\kappa h} 3}} \right. \kern-0pt} 3}} \right) \hfill \\ + b_{36} {\mkern 1mu} W\left( {W + \kappa h} \right)\left( {W + 2\kappa h} \right) + b_{37} {\mkern 1mu} W^{3} K_{3} + b_{38} W + b_{39} \Delta T{\mkern 1mu} \left( {W + \kappa h} \right) \hfill \\ + b_{310} {\mkern 1mu} \Delta T + b_{311} {\mkern 1mu} q - \frac{\pi }{5}R_{1}^{2} \left( {\tau \dot{W} + b_{312} \ddot{W}} \right) = 0, \hfill \\ \end{gathered} $$

(21)

where

$$ b_{11} = - \frac{\pi }{{6{\mkern 1mu} }}\left( {B_{22} + 2{\mkern 1mu} B_{11} } \right){\mkern 1mu} ,\,\,b_{12} = \frac{\pi }{60}\left[ {\lambda \left( {14{\mkern 1mu} D_{22} + 34{\mkern 1mu} D_{11} {\mkern 1mu} } \right) - 14{\mkern 1mu} C_{22} - 34{\mkern 1mu} C_{11} } \right], $$

$$ b_{13} = - \frac{{\lambda \pi {\mkern 1mu} }}{{15R_{1} }}\left( {34D_{11} + 14D_{22} } \right) + \frac{{\pi R_{1} }}{{R_{0} }}\left( {3B_{11} + 19B_{22} + 22B_{12} } \right),\,\,b_{14} = \frac{\pi }{{315{\mkern 1mu} R_{1} }}\left( {46{\mkern 1mu} B_{11} - 82{\mkern 1mu} B_{12} } \right),\, $$

$$ \begin{aligned} b_{22} & = \frac{\pi }{12}\left[ {\lambda \left( {24G_{11} + 6I_{45} R_{1}^{2} + 8G_{22} } \right)} \right. \\ & \left. {\quad - \lambda^{2} \left( {12H_{11} + 9R_{1}^{2} I_{55} + 4H_{22} } \right) + I_{44} R_{1}^{2} + 4F_{22} + 12F_{11}} \right], \\ \end{aligned} $$

$$ \begin{gathered} b_{23} = - \frac{{\pi \left[ {\left( { - 3{\mkern 1mu} I_{55} {\mkern 1mu} R_{1}^{2} - {{4H_{22} } \mathord{\left/ {\vphantom {{4H_{22} } 3}} \right. \kern-0pt} 3} - 4{\mkern 1mu} H_{11} {\mkern 1mu} } \right)\lambda^{2} - {\mkern 1mu} {{R_{1}^{2} I_{44} } \mathord{\left/ {\vphantom {{R_{1}^{2} I_{44} } 3}} \right. \kern-0pt} 3} + \left( {4{\mkern 1mu} G_{11} + 2{\mkern 1mu} I_{45} {\mkern 1mu} R_{1}^{2} + {{4G_{22} } \mathord{\left/ {\vphantom {{4G_{22} } 3}} \right. \kern-0pt} 3}{\mkern 1mu} } \right)\lambda } \right]}}{{R_{1} }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, - {\mkern 1mu} \frac{{\pi R_{1} \left[ {\left( {{{{{2D_{11} } \mathord{\left/ {\vphantom {{2D_{11} } 3}} \right. \kern-0pt} 3} + 8D_{12} } \mathord{\left/ {\vphantom {{{{2D_{11} } \mathord{\left/ {\vphantom {{2D_{11} } 3}} \right. \kern-0pt} 3} + 8D_{12} } 3}} \right. \kern-0pt} 3}{\mkern 1mu} + 2{\mkern 1mu} D_{22} {\mkern 1mu} } \right)\lambda - {{8C_{12} } \mathord{\left/ {\vphantom {{8C_{12} } 3}} \right. \kern-0pt} 3} - 2{\mkern 1mu} C_{22} - {{2C_{11} } \mathord{\left/ {\vphantom {{2C_{11} } 3}} \right. \kern-0pt} 3}{\mkern 1mu} {\mkern 1mu} } \right]{\mkern 1mu} }}{{8R_{0} }}, \hfill \\ \end{gathered} $$

$$ b_{24} = - {\mkern 1mu} \frac{{\pi {\mkern 1mu} \left[ {\left( {{{2D_{11} } \mathord{\left/ {\vphantom {{2D_{11} } 3}} \right. \kern-0pt} 3}{\mkern 1mu} - 2{\mkern 1mu} D_{12} } \right)\lambda + 2{\mkern 1mu} C_{12} - {{2C_{11} } \mathord{\left/ {\vphantom {{2C_{11} } 3}} \right. \kern-0pt} 3}} \right]}}{{5R_{1} }},\, $$

$$ b_{31} = \frac{{\pi R_{1} {\mkern 1mu} \left( {19{\mkern 1mu} B_{22} + 22{\mkern 1mu} B_{12} + 3{\mkern 1mu} B_{11} } \right)}}{{105{\mkern 1mu} R_{0} }} - {\mkern 1mu} \frac{{\pi {\mkern 1mu} \lambda \left( {14{\mkern 1mu} D_{22} + 34{\mkern 1mu} D_{11} } \right)}}{{15R_{1} }}, $$

$$ \begin{gathered} b_{32} = - \frac{{\pi \left[ {\left( { - 3{\mkern 1mu} R_{1}^{2} I_{55} - {{4H_{22} } \mathord{\left/ {\vphantom {{4H_{22} } 3}} \right. \kern-0pt} 3}{\mkern 1mu} - 4{\mkern 1mu} H_{11} } \right)\lambda^{2} - {\mkern 1mu} {{I_{44} {\mkern 1mu} R_{1}^{2} } \mathord{\left/ {\vphantom {{I_{44} {\mkern 1mu} R_{1}^{2} } 3}} \right. \kern-0pt} 3} + \left( {2{\mkern 1mu} I_{45} {\mkern 1mu} R_{1}^{2} + {{4G_{22} } \mathord{\left/ {\vphantom {{4G_{22} } 3}} \right. \kern-0pt} 3}{\mkern 1mu} + 4{\mkern 1mu} G_{11} } \right)\lambda } \right]}}{{R_{1} }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, - \frac{{\pi {\mkern 1mu} R_{1} \left[ {\lambda \left( {{{8D_{12} } \mathord{\left/ {\vphantom {{8D_{12} } 3}} \right. \kern-0pt} 3} + {{2D_{11} } \mathord{\left/ {\vphantom {{2D_{11} } 3}} \right. \kern-0pt} 3}{\mkern 1mu} + 2{\mkern 1mu} D_{22} {\mkern 1mu} } \right) - {{8C_{12} } \mathord{\left/ {\vphantom {{8C_{12} } 3}} \right. \kern-0pt} 3} - {{2C_{11} } \mathord{\left/ {\vphantom {{2C_{11} } 3}} \right. \kern-0pt} 3}{\mkern 1mu} {\mkern 1mu} - 2{\mkern 1mu} C_{22} } \right]}}{{8R_{0} }}, \hfill \\ \end{gathered} $$

$$ b_{33} = \frac{{2{\mkern 1mu} \pi {\mkern 1mu} \left( { - 82{\mkern 1mu} B_{12} + 46{\mkern 1mu} B_{11} } \right)}}{{315{\mkern 1mu} R_{1} }}, $$

$$ b_{34} = \frac{{2\pi {\mkern 1mu} \left[ {\left( { - 2{\mkern 1mu} D_{11} + 6{\mkern 1mu} D_{12} } \right)\lambda + 2{\mkern 1mu} C_{11} - 6{\mkern 1mu} C_{12} } \right]}}{{15R_{1} }}, $$

$$ b_{35} = \frac{{4\lambda {\mkern 1mu} \pi \left( {2{\mkern 1mu} D_{11} - 6{\mkern 1mu} D_{12} } \right)}}{{5R_{1}^{2} }} + {\mkern 1mu} \frac{{4\pi \left( {{\mkern 1mu} B_{11} + B_{12} } \right)}}{{5R_{0} }},\,\,b_{36} = - \pi \frac{{128{\mkern 1mu} B_{11} {\mkern 1mu} }}{{105{\mkern 1mu} R_{1}^{2} }},\,\,b_{37} = - {{{\mkern 1mu} \pi {\mkern 1mu} R_{1}^{2} } \mathord{\left/ {\vphantom {{{\mkern 1mu} \pi {\mkern 1mu} R_{1}^{2} } 9}} \right. \kern-0pt} 9}, $$

$$ \begin{gathered} b_{38} = {\mkern 1mu} \frac{{\pi {\mkern 1mu} \left[ { - {\mkern 1mu} {{{\mkern 1mu} R_{1}^{4} K_{1} } \mathord{\left/ {\vphantom {{{\mkern 1mu} R_{1}^{4} K_{1} } {20}}} \right. \kern-0pt} {20}} - 4{\mkern 1mu} \lambda^{2} \left( {H_{11} + {{H_{22} } \mathord{\left/ {\vphantom {{H_{22} } 3}} \right. \kern-0pt} 3}} \right) + R_{1}^{2} \left( {2{\mkern 1mu} I_{45} {\mkern 1mu} \lambda - {{K_{2} } \mathord{\left/ {\vphantom {{K_{2} } 3}} \right. \kern-0pt} 3} - 3{\mkern 1mu} \lambda^{2} I_{55} - {{I_{44} } \mathord{\left/ {\vphantom {{I_{44} } 3}} \right. \kern-0pt} 3}} \right)} \right]}}{{4R_{1}^{2} }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + {\mkern 1mu} \frac{{2\pi {\mkern 1mu} \lambda {\mkern 1mu} \left( {{\mkern 1mu} D_{11} + 3{\mkern 1mu} D_{22} + 4D_{12} } \right)}}{{3R_{0} }} - {\mkern 1mu} \frac{{R_{1}^{2} \pi {\mkern 1mu} \left( {B_{11} + B_{22} + 2{\mkern 1mu} B_{12} } \right)}}{{5R_{0}^{2} }}, \hfill \\ \end{gathered} $$

$$ b_{39} = \frac{4}{3}\pi \overline{\Phi }_{1} ,\,\,b_{310} = - \frac{{2R_{1}^{2} \pi \overline{\Phi }_{1} }}{{3R_{0} }},\,\,b_{311} = \frac{\pi }{3}R_{1}^{2} ,\,\,b_{312} = \int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\overline{\rho }} dz. $$

The amplitudes $U$ and $\Phi$ can be obtained by solving Eqs. (19) and (20); then, substituting them into Eq. (21) leads to

$$ \begin{gathered} \left( {{\mkern 1mu} c_{11} b_{31} + b_{38} + {\mkern 1mu} c_{21} b_{32} } \right)W + \left( {{\mkern 1mu} {\mkern 1mu} c_{21} b_{34} + c_{11} b_{33} } \right)W\left( {h\kappa + W} \right) \hfill \\ + \left( {{\mkern 1mu} {\mkern 1mu} c_{22} b_{32} + c_{12} b_{31} } \right)W\left( {2{\mkern 1mu} \kappa h + W} \right) + b_{35} {\mkern 1mu} W\left( {W + {{4\kappa h} \mathord{\left/ {\vphantom {{4\kappa h} 3}} \right. \kern-0pt} 3}} \right) \hfill \\ + \left( {{\mkern 1mu} c_{22} b_{34} + b_{36} + {\mkern 1mu} c_{12} b_{33} } \right)W\left( {2\kappa {\mkern 1mu} h + W} \right)\left( {\kappa h + W} \right) \hfill \\ + b_{37} {\mkern 1mu} K_{3} W^{3} + b_{39} \Delta T{\mkern 1mu} \left( {h\kappa + W} \right) + \Delta Tb_{310} + {\mkern 1mu} qb_{311} = \frac{{\pi R_{1}^{2} }}{5}\left( {b_{312} \ddot{W} + \tau \dot{W}} \right), \hfill \\ \end{gathered} $$

(22)

where

$$ \begin{gathered} c_{11} = \frac{{b_{12} {\mkern 1mu} b_{23} - b_{13} {\mkern 1mu} b_{22} }}{{b_{11} {\mkern 1mu} b_{22} - b_{12}^{2} }},\,\,\,\,\,\,\,\,c_{12} = \frac{{b_{12} {\mkern 1mu} b_{24} - b_{14} {\mkern 1mu} b_{22} }}{{b_{11} {\mkern 1mu} b_{22} - b_{12}^{2} }}, \hfill \\ c_{21} = \frac{{b_{12} {\mkern 1mu} b_{13} - b_{11} {\mkern 1mu} b_{23} }}{{b_{11} {\mkern 1mu} b_{22} - b_{12}^{2} }},\,\,\,\,\,\,\,\,\,c_{22} = \frac{{b_{12} {\mkern 1mu} b_{14} - b_{11} {\mkern 1mu} b_{24} }}{{b_{11} {\mkern 1mu} b_{22} - b_{12}^{2} }}. \hfill \\ \end{gathered} $$

For forced vibration behavior, the exited load is applied in the harmonic form over time $q = Q\sin \Omega t$ into Eq. (22), and then, the Runge–Kutta method is used to solve the obtained equation to obtain the time–deflection responses of the structures. For free vibration, by neglecting the nonlinearities, the viscous damping component, and the forced load, the linear and free equation of motion is obtained. The expression of the natural frequency can be obtained as

$$ \omega = \sqrt { - \frac{{5\left( {c_{11} b_{31} + c_{21} b_{32} + \Delta Tb_{39} + b_{38} } \right)}}{{b_{312} \pi R_{1}^{2} }}} . $$

(23)

For the dynamic buckling behavior, linearly time-dependent mechanical and thermal loads are applied. That is, $q = \zeta t$ and $\Delta T = \xi t$, where $\zeta$ (Pa/s) is the loading speed of mechanical load and $\xi$ (K/s) is the loading speed of thermal load. The Runge–Kutta method is used to determine the dynamic response curve of structures. The dynamic buckling load can be chosen at any point of buckling region according to the Budiansky–Roth criterion. In this paper, the inflection point of the buckling region of the dynamic responses of structures is chosen for the buckling point, obtained when

$$ \left. {\frac{{{\text{d}}^{2} W}}{{{\text{d}}\Delta T^{2} }}} \right|_{{\Delta T = \Delta T_{cr} }} = 0. $$

(24)

The static bifurcation buckling criterion can be obtained in the case of the perfect circular plates $\left( {\kappa = 0,\,\,R_{0} \to \infty } \right)$; from Eq. (22), the expression of the static buckling thermal loads is obtained when $W \to 0$, as

$$ \Delta T_{cr} = - \frac{{b_{31} c_{11} + b_{32} c_{21} + b_{38} }}{{b_{39} }}. $$

(25)

4 Numerical results and discussions

In this paper, the numerical results on the fundamental frequencies for the FG-GPLRC circular plates are used to validate the present approach. Two results on the fundamental frequency parameters of Chien and Phuc [35] based on the mesh-free method, and of Javani et al. [36] based on the generalized differential quadrature method, are compared with those of the present results, as presented in Table 1. Next, the validation of dimensionless fundamental frequencies for isotropic spherical shells is mentioned in Table 2, with the works of Varadan and Pandalai [1] using the energy method, Sathyamoorthy [2] and Phuong et al. [17] using the Galerkin method, and Haboussi et al. [43] using finite element method. As can be seen, the results of these comparisons affirm the validity of the present approach.

Table 1 Comparisons of dimensionless fundamental frequencies $\overline{\omega } = \omega R^{2} \sqrt {{{\rho_{m} h} \mathord{\left/ {\vphantom {{\rho_{m} h} {D_{m} }}} \right. \kern-0pt} {D_{m} }}}$ of FG-GPLRC circular plates ($R_{1}$ = 1 m, $D_{m} = {{E_{m} h^{3} } \mathord{\left/ {\vphantom {{E_{m} h^{3} } {12\left( {1 - \nu_{m}^{2} } \right)}}} \right. \kern-0pt} {12\left( {1 - \nu_{m}^{2} } \right)}}$, $E_{m}$ = 3.0GPa, $\nu_{m}$ = 0.34, $\rho_{m}$ = 1200 kg/m³, $W_{GPL}^{*}$ = 1%)

Table 2 Validation of dimensionless fundamental frequencies ${{\omega^{*} = \omega } \mathord{\left/ {\vphantom {{\omega^{*} = \omega } {\left[ {\frac{h}{{R_{1} }}\sqrt {{{E_{m} } \mathord{\left/ {\vphantom {{E_{m} } {\left( {\rho_{m} R_{1}^{2} } \right)}}} \right. \kern-0pt} {\left( {\rho_{m} R_{1}^{2} } \right)}}} } \right]}}} \right. \kern-0pt} {\left[ {\frac{h}{{R_{1} }}\sqrt {{{E_{m} } \mathord{\left/ {\vphantom {{E_{m} } {\left( {\rho_{m} R_{1}^{2} } \right)}}} \right. \kern-0pt} {\left( {\rho_{m} R_{1}^{2} } \right)}}} } \right]}}$ for isotropic spherical shells ($H_{0} = {{R_{1}^{2} } \mathord{\left/ {\vphantom {{R_{1}^{2} } {\left( {2R_{0} } \right)}}} \right. \kern-0pt} {\left( {2R_{0} } \right)}}$)

In this section, to illustrate the present semi-analytical approach, the copper matrix/GPLs spherical shells and circular plates are numerically investigated. By referring to the work of Wang et al. [38], the material parameters of GPLs and copper matrix can be determined.

Fundamental frequencies of circular plates and circular spherical shells with different GPL distributions and mass fractions are investigated in Table 3. As can be observed, with only the shallow curvature, the fundamental frequencies of spherical shells are significantly larger than those of corresponding circular plates. In both cases of plates and spherical shells, great fundamental frequencies can be observed with X structures. The large GPL mass fraction far from the mid-surface of the structures causes the increase of stiffnesses of the X structures than those of other structures with other distribution types. With a small amount of GPL added to the structures (no more than 1% in mass fraction), the fundamental frequencies increase markedly.

Table 3 Fundamental frequencies (rad/s) of FG-GPLRC circular plates and circular spherical shells with different GPL distributions and mass fractions ($h$ = 0.012 m, $R_{1} = 20h$, $R_{0} = {{R_{1} } \mathord{\left/ {\vphantom {{R_{1} } {0.2}}} \right. \kern-0pt} {0.2}}$, $\kappa$ = 0, $\Delta T$ = 100 K, $K_{1}$ = 10 MN/m³, $K_{2}$ = 0.1 MN/m)

The forced vibration responses of FG-GPLRC spherical shells and circular plates with different GPL distribution laws are investigated in Fig. 2a. It seems that the vibration periods of the plates with different GPL distribution laws do not differ significantly. However, the vibration amplitude of the X plate is significantly smaller than that of other plates with different distribution laws. Effects of GPL mass fraction on the vibration responses of FG-GPLRC circular plates can be observed in Fig. 2b. When the GPL mass fraction increases, the vibration amplitude of the plate largely decreases, and the vibration response form significantly changes after a long enough period. Effects of structure curvature of spherical shells on the vibration responses are investigated in Fig. 2c. In the comparison of the vibration amplitude of circular plate and spherical shells, it can be seen that the vibration amplitude of structures significantly decreases with only the shallow curvature. Additionally, the vibration amplitude of the spherical shell increases when the shell thickness decreases as shown in Fig. 2d.

Fig. 2

Effects of material and geometrical parameters on the dynamic responses of FG-GPLRC spherical shells and circular plates

The harmonic beat phenomenon of FG-GPLRC spherical shells can be observed in Fig. 3a. As can be seen, the harmonic beat phenomenon occurs if the forced frequency of harmonic loads approaches the fundamental frequency of FG-GPLRC spherical shells. In addition, the nonlinear vibration amplitude and the beat length rapidly increase when the forced frequency approaches the fundamental frequency of the shell. The large effects of imperfection on the nonlinear vibration responses of plates are investigated in Fig. 3b. The vibration amplitude of the imperfect plate is clearly larger than that of the perfect plate, and the response curve of a perfect plate is much smoother than that of an imperfect plate.

Fig. 3

Effects of load amplitude, imperfection, nonlinear foundation stiffness, and damping coefficient of foundation on the dynamic responses of FG-GPLRC spherical shells and circular plates

The effects of the nonlinear parameter of the foundation are investigated in Fig. 3c. As can be observed, taking the case of zero nonlinear foundation coefficient as the reference, the positive nonlinear foundation coefficient strongly reduces the vibration amplitude, whereas the negative nonlinear foundation coefficient increases the vibration amplitude significantly. The viscous damping coefficient of the foundation also greatly affects the vibration responses of the circular plate (see Fig. 3d). The results show that the vibration amplitude decreases sharply when the viscous damping coefficient increases after a large enough number of periods.

The phase planes of FG-GPLRC circular plates and spherical shells are studied in Fig. 4a–d, when the forced frequency is approximately the fundamental frequency. For both cases of FG-GPLRC plates and shells, as can be seen, when the amplitude of forced loads is small, the attraction area is clearly shown. However, when the amplitude of forced loads increases, the attraction area tends to split into two.

Fig. 4

Phase planes of circular plates and spherical shells

The static and dynamic critical thermal buckling loads of FG-GPLRC circular plates are presented in Table 4. In these investigations, the thermal loads increase rapidly and linearly with the thermal loading speed $\xi$, over time. The obtained results show that the static thermal buckling load is always smaller than the dynamic thermal buckling load, and the dynamic thermal buckling load increases when the thermal loading speed increases. The thermal buckling loads of the X circular plates are much larger than those of the circular plates with different distribution laws.

Table 4 Dynamic critical thermal buckling load $\Delta T_{cr}$(K) of FG-GPLRC circular plates ($W_{GPL}^{*}$ = 0.7%, $h$ = 0.012 m, $R_{1} = 20h$, $\kappa$ = 0, $q$ = 0 N/m², $\tau$ = 0.1 kN.s/m³, $K_{1}$ = 100 MN/m³, $K_{2}$ = 1.0 MN/m)

The dynamic mechanical responses of FG-GPLRC circular plates and spherical shells subjected to linearly time-dependent radial pressure are investigated in Fig. 5a, b, respectively. The results in Fig. 5a show that the buckling region does not appear for FG-GPLRC circular plates, and the response curve is lowered as the GPL mass fraction increases. Oppositely, the buckling region can be observed relatively clearly for FG-GPLRC spherical shells. It is shown more clearly with a negative nonlinear foundation stiffness, whereas it is not clearly shown with a positive nonlinear foundation stiffness.

Fig. 5

Dynamic mechanical and thermal responses of FG-GPLRC circular plates and spherical shells

Figure 5c–f presents the thermal responses of FG-GPLRC circular plates and spherical shells subjected to linearly time-dependent thermal loads. The dynamic thermal buckling region can be observed for FG-GPLRC plates (Fig. 5c, e, f), and oppositely for spherical shells (Fig. 5d). It seems that the slope of the buckling region does not vary significantly with different GPL distribution laws. Due to the curvature of the spherical shell, reverse deflection can be observed as the temperature increases as shown in Fig. 5c. The dynamic thermal response curves of FG-GPLRC circular plates with different thermal loading speeds are investigated in Fig. 5e. When the thermal loading speed increases, the maximal amplitude of buckling region increases and vibration amplitude of postbuckling state also increases. The dynamic thermal buckling load slightly changes when the nonlinear foundation stiffness changes; however, the trend of the dynamic curve changes significantly.

5 Conclusions

A new semi-analytical approach to investigate the nonlinear dynamic response behavior of FG-GPLRC circular plates and spherical shells subjected to time-dependent radial pressure and thermal loads is presented in this paper. The HSDT with a nonlinear viscoelastic foundation model is used to establish the expression of the fundamental equations. The Lagrange function is applied to establish the total energy of structures, and the potential function of viscous damping of the viscoelastic foundation is expressed using the Rayleigh dissipation function. The motion equation of the structures can be formulated using the Euler–Lagrange function. Budiansky–Roth criterion is applied to determine the dynamic thermal buckling loads of the structures. Some important remarks are achieved from the numerical investigations as:

• The vibration amplitude of the plate largely decreases, and the vibration response form significantly changes after a long enough period when the GPL mass fraction increases,

• Taking the case of zero nonlinear foundation coefficient as the reference, the positive nonlinear foundation coefficient strongly reduces the vibration amplitude, whereas the negative nonlinear foundation coefficient increases the vibration amplitude significantly.

• For both cases of FG-GPLRC plates and shells, as can be seen, when the amplitude of forced loads is small, the attraction area is clearly shown. However, when the amplitude of forced loads increases, the attraction area tends to split into two.

• The dynamic thermal buckling region can be observed for FG-GPLRC plates, and oppositely for spherical shells.