Analytical H₂ optimization for the design parameters of lever-type stiffness-based grounded damping dynamic vibration absorber with grounded stiffness

Abstract

A novel lever-type stiffness-based grounded damping dynamic vibration absorber with grounded stiffness is presented in this paper, and the analytical design parameters are derived in detail. At the first, the equations of motion are established and the analytical solution of the primary structure displacement is obtained. It is found that with the introduction of grounded stiffness, the coupled system could be unstable and the stability condition is established. Then, the optimum stiffness ratio, the optimum damping ratio and the optimum grounded stiffness ratio are expressed as the function of mass ratio and lever ratio by minimizing the mean squared displacement response of the primary structure previously established. From the results analysis, the system stability is verified, and it is found that with the change in the lever ratio when the mass ratio is selected, there are three cases for the optimum grounded stiffness ratio, i.e., negative, zero and positive. Thus, for the vibration reduction of primary structure, the proposed dynamic vibration absorber (DVA) with positive grounded stiffness has the best control performance among the three cases. Compared with some typical designed DVAs under harmonic and random excitation, the results show that with the proposed optimum DVA the resonance amplitude and the frequency band of vibration reduction can greatly reduce and broadened, respectively, and the random vibration mitigation can be greatly increased. According to the existing literature, the proposed lever-type stiffness mechanism is justified, which means that the proposed DVA is practical and can be used in many engineering applications.

1 Introduction

With the increasing demand for securing structures against external dynamic loads such as winds, earthquakes, and ground movements, methods of controlling vibration of mechanical equipment are attracting more and more attention. One of the proposed methods is based on the dynamic vibration absorber (DVA), which is one of the common mass–spring–damper devices for controlling vibrations. Such device attached to primary structure reduces its excessive vibrations by designing its parameters reasonably [1]. The damperless dynamic vibration absorber was first introduced more than 100 years ago by [2]. However, this first DVA has only shown its effectiveness in a narrow frequency range close to the natural frequency of the primary system. An improved version of DVA including damper in parallel with the spring called Voigt-type DVA was then proposed by Den Hartog and Ormondroyd, which could suppress the amplitude of the primary system in a wider frequency range [3]. Furthermore, for an optimal work of this device, the fixed point theory was proposed for the first time to find the tuning parameters of the Voigt-type DVA, which has become a classic conclusion in vibration engineering textbooks [4, 5]; in addition, the equal modal damping design has been proposed [6]. Subsequently, fixed point theory was used to design a wider variety of DVA layouts. A first variety of DVA was proposed in [7, 8], which constituted a three-element vibration absorber (TEVA) whose optimization plan was schematized. Comparison of control performance against Voigt-type DVA gave advantages to TEVA in vibration reduction effect. For even better control performance, DVA with grounded damper configuration called grounded DVA has been proposed by [9]. The las variety of DVA was completed in [10] by proposing a Maxwell viscoelastic model that replaces the grounded damper in [9], resulting in a grounded three-element DVA whose optimal parameters were found. However, it is found in the performance analysis of the DVAs mentioned above that they require a large mass ratio between the DVA mass and the controlled primary structure mass, which complicates the installation and creates a conflict with the architecture of the controlled structure. In addition, work in [11] has shown that a practical mass ratio must be less than 25%, which limits the performance of the above DVAs. Considering the above, improving the performance of DVAs could take into account the introduction of new mechanical elements. Therefore, adaptive passive, semi-active, smart dynamic vibration absorbers have been proposed by [12].

Research on studying the effect of vibration reduction through negative stiffness components has been intensively developed in recent years in a wide scope of application due to their advantages of large bearing capacity, small deformation, and good controllability [13,14,15,16]. The negative stiffness element has also been introduced in the whole aforementioned variety of DVAs [17,18,19,20]. Moreover, in recent work, the three-element DVA based on the standard linear solid rheological model with negative stiffness has been proposed for effective vibration reduction of vibrating primary system [21]. Based on the optimization results according to the fixed point theory [5], it was found that DVAs with reasonable grounded negative stiffness elements by [17,18,19,20] have better vibration reduction performance compared to original DVAs without negative stiffness element by [5, 7,8,9,10]. In fact, negative stiffness can reduce the resonance peak of the primary structure response and widens the vibration suppression bandwidth. However, there are major drawbacks associated with the use of negative stiffness device; it is complex to achieve in practice, exhibits considerable nonlinearity, make the system unstable and further amplifies the primary structure response at low-frequencies region. Meanwhile, improved negative stiffness devices are produced in [22,23,24,25].

The concept of lever mechanism was first introduced by [26, 27] who developed a mechanical device called dynamic anti-resonant vibration isolator (DAVI) to improve the control performance and stability of mechanical structures. Thus, anti-resonance in DAVI has been exploited in the aerospace industry for applications such as isolating the fuselage of a helicopter against vibrations caused by its rotors, as described in [28]. It should be noted that the DAVI acts as a vibration isolator while DVA acts as vibration absorber. However, DVAI allowed to introduce for the first time the concept of inerter device which was later better designed in [29] and used by [30] to design inerter-based absorbers. An example of the DAVI concept can be schematically found in [31]. Although the DAVI system is widely used in industrial and other applications [32,33,34], the lever mechanism has recently been introduced into DVAs to improve vibration reduction effect of primary structure. First, the introduction of grounded positive stiffness in the Ren's configuration, coupled with lever mechanism showed better control performance when the inertia of the lever-DVA reaches a certain value [35]. The benefice control performance of the proposed different versions of DVA based on the lever mechanism and grounded stiffness including the properties of the two end of inerter device was investigated in [36, 37]. Due to the introduction of lever mechanism into DVAs as in the preview works, there are some major drawbacks as the inter-layer installation and the location dependence, and the DVA and the controlled structure operate as two adjacent structures resulting in operational complexity and require large installation space. Moreover, according to the equations in [35,36,37], the effect of the lever mechanism is to amplify the mass of the DVA, which leads to improved vibration control. However, the current state of the art of DVA systems does not include the use of a lever-type stiffness mechanism in place of the grounded damping DVA main spring with grounded stiffness to improve overall capacity system vibration reduction, including providing closed-form analytical expressions for design parameters under random excitation.

The main objective of this work is to evaluate the effectiveness of a lever-type stiffness-based grounded damping dynamic vibration absorber with grounded stiffness connected to a single-degree-of-freedom primary structure, thus filling the aforementioned gap in the literature. The lever mechanism was introduced to form the lever-type stiffness, which does not modify the installation space of the DVA, only the stiffness characteristics. The closed-form equations for the optimal design parameters of the proposed DVA are derived using the H₂ optimization method [38,39,40,41,42] considering the primary system under random excitation. It is found that with the change in the lever ratio for a fixed mass ratio, there are three cases of values for the optimal grounding stiffness ratio, i.e., negative, zero and positive. For these three value cases, numerical simulation is performed to further ensure the accuracy of the closed-form analytical equations for the optimal design parameters. Analysis of the effect of the lever ratio shows that it modifies the response characteristics of the primary structure. Therefore, compared with other DVAs, the proposed DVA in all three cases significantly improves the control performance over a wider band. Furthermore, the positive optimal grounded stiffness will make the maximum displacement of the primary structure to a level lower than its static response without DVA. These results constitute an important interest for the fields of application in engineering.

The rest of paper is organized as follows. In the next section, mathematical model of the proposed DVA is presented and the corresponding displacement transfer function of the primary structure is derived, including the stability analysis of the coupled system. In Sect. 3, the H₂ optimization procedure is conduced and the closed-form analytical equations for the optimal design parameters are derived, including the results analysis. In Sect. 4, the performance comparison is performed with respect to others typical DVAs in frequency domain and time domain, respectively, and some conclusions are drawn in Sect. 5.

2 Mechanical model

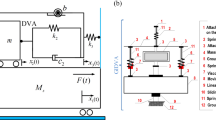
The novel lever-type stiffness-based grounded damping dynamic vibration absorber with grounded stiffness (hereinafter referred to as GL-grounded type DVA model) is proposed here to improve the displacement vibration reduction of a single-degree-of-freedom (SDOF) primary structure, as displayed in Fig. 1. For this purpose, the governing equations of the SDOF primary structure equipped with the proposed vibration absorber are first derived in this section; then, the dimensionless transfer function relevant to the primary structure displacement is established for the design optimization. Because the coupled system in Fig. 1 could be unstable with the introduction of negative stiffness, the stability bounds will be established from the transfer function.

Fig. 1

The schematic model of a SDOF primary structure controlled with the proposed GL-grounded type DVA model

2.1 Governing equations of a SDOF structure

A SDOF primary structure with mass m₁, stiffness k₁ is considered in Fig. 1. To reduce its displacement vibrations, the proposed vibration absorber is attached, as shown in Fig. 1. However, the proposed DVA is composed of a mass m₂ connected to the primary structure by the lever-type stiffness with spring k₂ and then to the ground by a parallel stiffness spring k₃ and dashpot c₂. According to the lever mechanism in Fig. 1, the distance between the attached points N and O is noted as ${{\ell}}_{a}$ while the distance between the attached points N and M is the length rod of the lever denoted as ${{\ell}}_{b}$. The lever rod can pivoted at point O. Thus, it can be seen that only the end of the spring k₂ fixed to the lever at point M can be stretched or compressed according to the relative displacement between the primary mass m₁ and secondary mass m₂, so that the stiffness characteristics of the spring k₂ are modified to improve the vibration reduction performance. According to the results in [26, 27, 43], it can be concluded that the proposed vibration absorber with lever mechanism can be easily achieved and used in the required engineering structures of the fields of vibration control.

Considering the SDOF primary structure under force excitation $f\left(t\right)$ as presented in Fig. 1, the displacements of the primary structure and the DVA are denoted by x₁ and x₂, respectively. Thus, when the small engineering displacements are considered, the terminal of the spring k₂ at M performs only the linear vertical displacement expressed as [37, 43]

$$x_{0} = Lx_{1} - (L - 1)x_{2} = L\left( {x_{1} - \beta x_{2} } \right)$$

(1)

where $L={{\ell}}_{b}/{{\ell}}_{a}$ is the lever ratio and $\beta =(L-1)/L$ denotes the introduced parameter for simplification. It can be seen from Eq. (1) that the corner displacement x₀ is related to the displacement x₁ and x₂, which means that the coupled system in Fig. 1 has two degrees of freedom denoted by x₁ and x₂. Neglecting the friction in the motion procedure and applying the energetic method based on the Lagrange formalism [44], the differential equations of motion for the coupled system in Fig. 1 can be established as follows:

$$\left\{ {\begin{array}{*{20}l} {m_{1} \ddot{x}_{1} + L^{2} k_{2} \left( {x_{1} - \beta x_{2} } \right) + k_{1} x_{1} = f(t)} \hfill \\ {m_{2} \ddot{x}_{2} + c_{2} \dot{x}_{2} + L^{2} \beta k_{2} \left( {\beta x_{2} - x_{1} } \right) + k_{3} x_{2} = 0} \hfill \\ \end{array} } \right.$$

(2)

2.2 The dimensionless transfer function

$$\mu = \frac{{m_{2} }}{{m_{1} }},{\mkern 1mu} \,\alpha = \frac{{k_{2} }}{{k_{1} }},{\mkern 1mu} \,\xi = \frac{c}{{2m_{1} \omega_{1} }},{\mkern 1mu} \,n = \frac{{k_{3} }}{{k_{1} }},{\mkern 1mu} \,\omega_{1} = \sqrt {\frac{{k_{1} }}{{m_{1} }}} ,{\mkern 1mu} \,q = \frac{\omega }{{\omega_{1} }}$$

(3)

The following parameters transformation are considered in order to normalize the differential equations of motion in Eq. (2), that is where the nomenclature of the above parameters is presented in Table 1. Furthermore, considering the resizing time as $t=\tau /{\omega }_{1}$ one can get $d/dt={\omega }_{1}(d/d\tau )$ and ${d}^{2}/{dt}^{2}={\omega }_{1}^{2}({d}^{2}/{d\tau }^{2})$, and the normalized equations of motion can be derived as

$$\left\{ {\begin{array}{*{20}l} {\ddot{x}_{1} + L^{2} \alpha \left( {x_{1} - \beta x_{2} } \right) + x_{1} = f\left( \tau \right)k_{1}^{ - 1} } \hfill \\ {\mu \ddot{x}_{2} + 2\xi \dot{x}_{2} + \beta L^{2} \alpha \left( {\beta x_{2} - x_{1} } \right) + nx_{2} = 0} \hfill \\ \end{array} } \right.$$

(4)

Table 1 Nomenclature

By applying the Laplace transform of Eq. (4), the normalized form of the differential equations of motion can be expressed in the frequency domain as follows:

$$\left\{ {\begin{array}{*{20}l} {s^{2} X_{1} + L^{2} \alpha \left( {X_{1} - \beta X_{2} } \right) + X_{1} = f\left( \tau \right)k_{1}^{ - 1} } \hfill \\ {\mu s^{2} X_{2} + 2\xi sX_{2} + \beta L^{2} \alpha \left( {\beta X_{2} - X_{1} } \right) + nX_{2} = 0} \hfill \\ \end{array} } \right.$$

(5)

where $s=jq$ is the dimensionless complex frequency and $j=\sqrt{-1}$ the imaginary unit number. X and F are the displacements and force amplitude, respectively. Denoting by $H\left(jq\right)=K{X}_{1}/F$, the dimensionless transfer function of the force excitation to the primary structure displacement, and solving Eq. (5) with respect to X₁, one can get

$$H\left( {jq} \right) = \frac{{k_{1} X_{1} }}{F} = \frac{{b_{2} \left( {jq} \right)^{2} + b_{1} \left( {jq} \right) + b_{0} }}{{a_{4} \left( {jq} \right)^{4} + a_{3} \left( {jq} \right)^{3} + a_{2} \left( {jq} \right)^{2} + a_{1} \left( {jq} \right) + a_{0} }}$$

(6)

$$\left\{ {\begin{array}{*{20}l} {a_{4} = \mu } \hfill & {} \hfill \\ {a_{3} = 2\xi } \hfill & {} \hfill \\ {a_{2} = \alpha \beta^{2} L^{2} + L^{2} \alpha \mu + \mu + n} \hfill & {b_{2} = \mu } \hfill \\ {a_{1} = 2L^{2} \alpha \xi + 2\xi } \hfill & {b_{1} = 2\xi } \hfill \\ {a_{0} = \alpha \beta^{2} L^{2} + L^{2} \alpha n + n} \hfill & {b_{0} = \alpha \beta^{2} L^{2} + n} \hfill \\ \end{array} } \right.$$

(7)

where the corresponding values of the coefficients in the numerator and denominator of the above transfer function can be listed as follows:

2.3 The stability analysis

The grounded spring k₃ is introduced into the vibration absorber in order to improve the control performance. However, if the stiffness value of the grounded spring k₃ becomes negative, the coupled system in Fig. 1 can become unstable for an inappropriate negative stiffness value. Therefore, considering negative stiffness value of the grounded spring k₃, the limits of the stability range within which the coupled system remains stable must be specified. According to the transfer function expressed in Eq. (6), the polynomial characteristic equation of the coupled system can be derived as

$$s^{4} + \left( {a_{3} /a_{4} } \right)s^{3} + \left( {a_{2} /a_{4} } \right)s^{2} + \left( {a_{1} /a_{4} } \right)s + \left( {a_{0} /a_{4} } \right) = 0$$

(8)

Thus, the coupled system is asymptotically stable according to the Routh–Hurwitz stability criterion [45,46,47], if and only if all the eigenvalues of Eq. (8) lie in the half of the complex plan and all the polynomial coefficients of the characteristic equation are positive. This stability criterion can be resumed according to the following necessary conditions

$$\left\{ \begin{gathered} \left( {a_{3} /a_{4} } \right) > 0,{\mkern 1mu} {\mkern 1mu} \left( {a_{2} /a_{4} } \right) > 0 \hfill \\ \left( {a_{1} /a_{4} } \right) > 0,{\mkern 1mu} {\mkern 1mu} \left( {a_{0} /a_{4} } \right) > 0 \hfill \\ \left( {a_{3} /a_{4} } \right)\left( {a_{2} /a_{4} } \right) > \left( {a_{1} /a_{4} } \right) \hfill \\ \left( {a_{3} /a_{4} } \right)\left( {a_{2} /a_{4} } \right)\left( {a_{1} /a_{4} } \right) > \left( {a_{1} /a_{4} } \right)^{2} + \left( {a_{3} /a_{4} } \right)^{2} \left( {a_{0} /a_{4} } \right) \hfill \\ \end{gathered} \right.$$

(9)

$$n > - \frac{{\alpha \beta^{2} L^{2} }}{{1 + L^{2} \alpha }} = \beta^{2} \left( { - 1 + \frac{1}{{1 + L^{2} \alpha }}} \right)$$

(10)

Using Eqs. (7) in (9), the stability constraint on the possible stiffness value of the grounded spring k₃ has been established as where the lower bound on grounded spring stiffness value is $n_{{{\text{lw}}}} = - \frac{{\alpha \beta^{2} L^{2} }}{{1 + L^{2} \alpha }}$ for given value of stiffness ratio $\alpha$ and lever ratio$L$. Furthermore, as $0<\frac{1}{1+{L}^{2}\alpha }<1$ and$\beta <1$, it can be concluded from Eq. (10) that the lower bound on the grounded stiffness ratio value n should be always greater than -1 for any positive stiffness ratio $\alpha$ and lever ratio$L$. Therefore, the absolute value of stiffness value of the grounded spring k₃ should be always inferior to that of the primary structure k₁. In the following section, the stiffness ratio $\alpha$ can be expressed as a function of mass ratio $\mu$ and lever ratio$L$, which means that the effective lower bound on grounded stiffness ratio n can be further derived as a function of mass ratio.

3 H ₂ optimization of the design of the proposed DVA

The H₂ optimization is used to derive the optimal design parameters of the vibration absorbers when the controlled primary structure is considered under random excitation. The objective is to minimize the mean squared displacement or the standard deviation (called H₂-norm) of the primary structure for overall frequencies [38,39,40,41,42]. First, in order to perform the H₂ optimization, the performance measure that is the mean squared displacement value of the primary structure should be established.

3.1 H₂ performance measure formulation

$$\sigma^{2} = \frac{{E[x_{1}^{2} ]}}{{2\pi S_{f} \omega_{1} /k_{1}^{2} }} = \frac{{\left\langle {x_{1}^{2} } \right\rangle }}{{2\pi S_{f} \omega_{1} /k_{1}^{2} }}$$

(11)

considers that the primary structure is under random white noise force excitation process $f(t)$ with uniform power spectral density (PSD), that is, $S_{f} (\omega ) = S_{f}$ at the whole excitation frequency range $\omega \in \Re^{ + }$. The input PSD is therefore $S_{{X_{1} @f}} = S_{f} \left| {H(j\omega )} \right|_{@f}^{2}$. Thus, the performance measure formulation is to be minimized, i.e., the dimensionless squared displacement variance $\sigma^{2}$ has been formulated as

$$\left\langle {x_{1}^{2} } \right\rangle = \int_{ - \infty }^{ + \infty } {S_{f} } \left| {H(j\omega )} \right|^{2} d\omega = \frac{{S_{f} \omega_{1} }}{{k_{1}^{2} }}\int_{ - \infty }^{ + \infty } {\left| {H(jq)} \right|^{2} } dq$$

(12)

where the denominator $2\pi S_{f} \omega_{1} /k_{1}^{2}$ is introduced to derive the dimensionless displacement variance of the primary structure. It should be noted that $E[{\mkern 1mu} {\mkern 1mu} ]$ and $\langle$$\rangle$ represent the ensemble and the time averages operator, respectively. By using the last symbol $\langle$$\rangle$, the derived expression of the mean square displacement response of the primary structure is formulated as.

Substituting Eq. (12) in Eq. (11), the dimensionless mean squared value of the primary structure displacement, which represent the performance measure formulation, can be expressed as

$$\sigma^{2} = \frac{1}{2\pi }\int_{ - \infty }^{ + \infty } {\left| {H(jq)} \right|^{2} } dq$$

(13)

To compute the integral (13), the following formula by Gradshteyn and Ryzhik [48] is used. Therefore, because the transfer function expression is formulated in the form of Eq. (6), the integration problem in Eq. (13) has been derived as

$$\int_{ - \infty }^{ + \infty } {\left| {H\left( {jq} \right)} \right|^{2} } dq = \pi \frac{{\left[ \begin{gathered} \left( {b_{0}^{2} /a_{0} } \right)\left( {a_{2} a_{3} - a_{1} a_{4} } \right) + a_{3} \left( {b_{1}^{2} - 2b_{0} b_{1} } \right) \hfill \\ + a_{1} \left( {b_{2}^{2} - 2b_{1} b_{3} } \right) + \left( {b_{3}^{2} /a_{4} } \right)\left( {a_{1} a_{2} - a_{0} a_{3} } \right) \hfill \\ \end{gathered} \right]}}{{a_{1} \left( {a_{2} a_{3} - a_{1} a_{4} } \right) - a_{0} a_{3}^{2} }}$$

(14)

Then, substituting Eqs. (7) in (14) and combining with Eq. (13), the resulting analytical expression of the mean squared response of the primary structure displacement, considered as the performance measure formulation in this paper, has been derived as

$$\sigma^{2} = F\left( {\mu ,\alpha ,n} \right)\xi + \frac{{G\left( {\mu ,\alpha ,n} \right)}}{\xi }$$

(15)

where

$$\left\{ \begin{gathered} F(\mu ,\alpha ,n) = \frac{1}{{L^{4} \beta^{2} \alpha^{2} }} \hfill \\ G(\mu ,\alpha ,n) = \frac{{\left[ \begin{gathered} L^{6} \alpha^{3} \beta^{6} + L^{4} \left( {\left( {3n - 2\mu } \right)\beta^{4} + \left( {\mu^{2} - 2\mu n} \right)\beta^{2} + \mu^{2} n} \right)\alpha^{2} \hfill \\ + L^{2} \left( {\mu - n} \right)\left( {\beta^{2} \mu - 3\beta^{2} n + 2\mu n} \right)\alpha + n\left( {\mu - n} \right)^{2} \hfill \\ \end{gathered} \right]}}{{4L^{4} \alpha^{2} \beta^{2} \left( {\left( {L^{2} \beta^{2} + L^{2} n} \right)\alpha + n} \right)}} \hfill \\ \end{gathered} \right.$$

(16)

3.2 Optimal parameters derivation

The H₂ performance measure formulation as the mean squared displacement response of the primary structure has been derived in Eq. (15) according to Eq. (16). However, from the mean squared value expression in Eq. (15), the extreme value theory $\partial \sigma^{2} /\partial \xi = 0$ can lead to the minimum displacement variance of the primary structure and its corresponding optimal damping ratio as follows

$$\sigma_{{{\text{opt}}}}^{2} = 2\sqrt {G(\mu ,\alpha ,n)F(\mu ,\alpha ,n)}$$

(17)

$$\xi_{{{\text{opt}}}} = \sqrt {\frac{G(\mu ,\alpha ,n)}{{F(\mu ,\alpha ,n)}}}$$

(18)

$$\alpha_{{{\text{min}},{\text{max}}}} = \frac{{\left( {6\beta^{2} - 3\mu \pm \sqrt {4\beta^{4} - 36\mu \beta^{2} + 9\mu^{2} } } \right)\mu }}{{4\beta^{4} L^{2} }}$$

(19)

According to Eq. (17), the mean squared value is related to the three design parameters $\left\{ {\mu ,{\mkern 1mu} \alpha ,{\mkern 1mu} n} \right\}$, which mean that the mean squared value can be further minimized. However, when considering that the mass ratio $\mu$ is given in advance, the resulting problem is to optimize the design parameters $\left\{ {\alpha ,{\mkern 1mu} n} \right\}$ by simultaneously solving the extreme conditions $\partial \sigma^{2} /\partial \alpha = \partial \sigma^{2} /\partial n = 0$. By performing this, it can be found that it is not possible to derive the optimal analytical expressions for the design parameters $\left\{ {\alpha ,{\mkern 1mu} n} \right\}$ that minimize the mean squared value in Eq. (17). In other words, there are no optimal solutions for the design of the lever-type stiffness-based grounded damping DVA with grounded stiffness (GL-grounded type DVA model) when we choose to optimize the parameters $\left\{ {\alpha ,{\mkern 1mu} n} \right\}$. In the particular case where n = 0, the extreme condition $\partial \sigma^{2} /\partial \alpha = 0$ leads to two positive and meaningful solutions for $\alpha$ as follows.

which are relevant to two sub-optimal designs of the lever-type stiffness-based grounded damping DVA model without grounded stiffness. As a result, the above local minimum and maximum of stiffness ratios are practical according to the following conditions on the mass ratio $\mu$ and lever ratio $L$ given by Eq. (20) as

$$L > L_{{{\text{lw}}}} = \frac{2}{{2 - \sqrt {\left( {12\sqrt 2 + 18} \right)\mu } }},{\mkern 1mu} {\mkern 1mu} \mu < \frac{4}{12\sqrt 2 + 18} \approx 0.114$$

(20)

The dimensionless mean squared displacement of the primary structure of lever-type stiffness-based grounded damping DVA is calculated from Eq. (15) with the grounded stiffness ratio n = 0, lever ratio $L=2$ and mass ratio $\mu = 0.1$, and the results are displayed in Fig. 2. No global minimum of the mean squared displacement exists and the local minimum and maximum points of the mean squared displacement of the primary structure related to the local minimum and maximum of stiffness ratios can be found in Fig. 2 for illustration.

Fig. 2

Mean squared displacement contours of the primary structure of lever-type stiffness-based grounded damping DVA

According to Eq. (20), it is found that the lower bound of the lever ratio for a practical H₂-optimized lever-type stiffness-based grounded damping DVA design is related to the mass ratio, which is convenient for $\mu < 0.114$. However, according to Fig. 3, the lower bound on the lever ratio for a practical H₂-optimized lever-type stiffness-based grounded damping DVA design quickly becomes large with increasing mass ratio in the range $\mu < 0.114$. Thus, according to the results in Eq. (19), and the conditions described by Eq. (20), there is no a global solution for the H₂-optimized lever-type stiffness-based grounded damping DVA design when we choose to optimize the parameters $\left\{ {\xi ,{\mkern 1mu} n} \right\}$. In addition, from Eq. (20) and Fig. 3, it can be concluded that a practical H₂-optimized lever-type stiffness-based grounded damping DVA design with a sub-optimal stiffness ratio $\alpha$ is useless for mass ratios $\mu > 0.114$ and requires a large lever ratio (for example, when $\mu = 0.1$, the lever ratio should be greater than 15.4), which is not practical in terms of mechanization and installation space. From the above, it is relevant to find a global solution for optimal design of the lever-type stiffness-based grounded damping DVA. Note also that we did not obtain solutions for the optimal design of the lever-type stiffness-based grounded damping DVA when it comes to optimized parameters $\left\{ {\alpha ,{\mkern 1mu} n} \right\}$ that minimize the mean squared value in Eq. (17). Thus, in the following, an approach to derive global solutions of the design of lever-type stiffness-based grounded damping DVA with grounded stiffness is discussed, which can be also applied for the design of the lever-type stiffness-based grounded damping DVA without grounded stiffness.

Fig. 3

The relationship between mass ratio and lower limit on lever ratio for practical sub-optimal H₂-optimized lever-type stiffness-based grounded damping DVA

To derive the global optimal design of the proposed vibration absorber in this paper with lever-type stiffness and grounded stiffness, we first assume that the stiffness ratio $\alpha$ is given in advance. As result, the objective becomes to find the optimal values of $\mu$ and n which further minimize the mean squared displacement value in Eq. (17). Thus, to verify the optimization process, the variation of the mean squared displacement value is investigated in three-dimensional surface plots as shown in Fig. 4, for stiffness ratio $\alpha = 0.05$ and lever ratio$L=2$. From Fig. 4, it can be found that the mean squared displacement of the primary structure with attached lever-type stiffness-based grounded damping DVA with grounded stiffness has a global minimum value, which demonstrates that the global solutions of the H₂ optimal lever-type stiffness-based grounded damping DVA with grounded stiffness design can be derived by optimizing the parameters $\left\{ {\mu ,{\mkern 1mu} n} \right\}$ for minimizing the mean squared value in Eq. (17). Therefore, the adopted optimization process in this paper is correct, which can be achieved by applied the extreme value theory from the mathematical principle. Thus, by differentiating Eq. (17) with respect to mass ratio $\mu$ and grounded stiffness ratio n, respectively, the result equal to zero can be presented as.

$$\left\{ \begin{gathered} \frac{{\partial \sigma^{2} }}{\partial \mu } = - \frac{{\left[ {L^{2} \alpha \beta^{2} - L^{2} \alpha \mu - \mu + n} \right]}}{{2L^{4} \alpha^{2} \beta^{2} \xi_{{{\text{opt}}}} }} = 0 \hfill \\ \frac{{\partial \sigma^{2} }}{\partial n} = \frac{{\left[ \begin{gathered} L^{8} \alpha^{4} \beta^{6} - 2L^{6} \alpha^{3} \beta^{6} + L^{4} \left( {2\beta^{4} \mu - n\left( {2\beta^{2} + n} \right)\left( {3\beta^{2} - 2\mu } \right)} \right)\alpha^{2} \hfill \\ + 2L^{2} n\left( {2\mu \beta^{2} - n\left( {3\beta^{2} - 2\mu + n} \right)} \right)\alpha + 2n^{2} \left( {\mu - n} \right) \hfill \\ \end{gathered} \right]}}{{ - 4\left( {L^{2} \alpha \beta^{2} + L^{2} \alpha n + n} \right)^{2} L^{4} \alpha^{2} \beta^{2} \xi_{{{\text{opt}}}} }} = 0 \hfill \\ \end{gathered} \right.$$

(21)

Fig. 4

Three-dimensional surface plots of mean squared displacement of the primary structure with attached lever-type stiffness-based grounded damping DVA with grounded stiffness varies with the mass ratio and the negative stiffness ratio at the stiffness ratio $\alpha = 0.05$ and lever ratio $L = 2$

By solving Eq. (18) as a set of two parametric equations simultaneously, the optimal mass ratio and the optimal grounded stiffness ratio can be derived and presented in the analytical mathematical form as the functions of stiffness $\alpha$ and lever ratio $L$, respectively, as

$$\mu_{{{\text{opt}}}} = \frac{{2L^{4} \alpha^{2} \beta^{2} }}{{\left( {L^{2} \alpha + 1} \right)^{2} }}$$

(22)

$$n_{{{\text{opt}}}} = \frac{{L^{2} \alpha \beta^{2} \left( {L^{2} \alpha - 1} \right)}}{{L^{2} \alpha + 1}}$$

(23)

Furthermore, the optimal grounded stiffness ratio can be expressed as a function of its lower limit as $n_{{{\text{opt}}}} = n_{{{\text{lw}}}} \left( {1 - L^{2} \alpha } \right)$. Therefore, as it is assumed that $\left| {1 - L^{2} \alpha } \right| < 1$ for given $\left\{ {\alpha ,{\mkern 1mu} L} \right\}$, it can be concluded that $n_{{{\text{opt}}}} > n_{{{\text{lw}}}}$. This result means that the H₂-optimized dynamic vibration absorber with optimal grounded stiffness ratio expressed in Eq. (23) remains stable for given any value of stiffness ratio and lever ratio so that $\left| {1 - L^{2} \alpha } \right| < 1$. In these conditions, by using Eqs. (22) and (23) into Eqs. (17) and (18), respectively, the resulting optimal minimum mean squared displacement value of the primary structure and the corresponding optimal damping ratio can be derived, respectively, as follows

$$\sigma_{{{\text{opt}}}}^{2} = \sqrt {\frac{4}{{\left( {L^{2} \alpha + 1} \right)^{3} }}}$$

(24)

$$\xi_{{{\text{opt}}}} = \sqrt {\frac{{\beta^{4} L^{8} \alpha^{4} }}{{\left( {L^{2} \alpha + 1} \right)^{3} }}}$$

(25)

In practice, the mass ratio $\mu$ cannot exceed the upper limit of the practical range required by the engineering applications. Suppose that $\mu_{{{\text{up}}}}$ is the upper limit of the mass ratio below which the lever-type stiffness-based grounded damping DVA with grounded stiffness model can work according to the practical engineering requirements. Therefore, the practical operating range of the stiffness ratio $\alpha$ can be derived with respect to the upper value $\mu_{{{\text{up}}}}$ by setting $\mu_{{{\text{opt}}}} \le \mu_{{{\text{up}}}}$. Accordingly, one can get

$$0 < \alpha \le \frac{{\sqrt {2\beta^{2} \mu_{up} } + \mu_{up} }}{{\left( {2\beta^{2} - \mu_{up} } \right)L^{2} }}$$

(26)

In the parameters optimization process of vibrations absorbers, including the H₂ optimization method of DVAs [8, 49], the mass $m_{2}$ of the DVA, that is, the mass ratio $\mu$, is generally known in advance. This means that the optimal design parameters of the vibration absorber are more practical when expressed as a function of mass ratio [3,4,5, 7,8,9, 38,39,40,41,42]. Therefore, in the following section, a reformulation process of the optimal parameters is applied.

3.3 Reformulation of optimal parameters versus mass ratio

$$\alpha_{{{\text{opt}}}} = \frac{{\sqrt {2\beta^{2} \mu } + \mu }}{{\left( {2\beta^{2} - \mu } \right)L^{2} }}$$

(27)

Suppose that the optimal mass ratio $\mu_{{{\text{opt}}}}$ in the practical engineering situation should be equal to $\mu$(that is $\mu_{{{\text{opt}}}} = \mu$) with $\mu \le \mu_{{{\text{up}}}}$. According to Eq. (22), it can be found that the given optimal mass ratio $\mu$ is related to only one positive value of the stiffness ratio $\alpha$. In these conditions, one can establish that the resulting stiffness ratio $\alpha$ from Eq. (22) expressed as a function of mass ratio $\mu$ and lever ratio $L$ corresponding to the optimal stiffness ratio $\alpha_{{{\text{opt}}}}$. Accordingly, by setting $\mu_{{{\text{opt}}}} = \mu$ in Eq. (22), one can get.

Then, by substituting the obtained optimal stiffness ratio $\alpha_{{{\text{opt}}}}$ in Eqs. (23)–(25), the global optimal analytical solutions to the design parameters of the proposed dynamic vibration absorber can be established as a function of mass ratio $\mu$ and lever ratio $L$ and summarized in Table 2. From Table 2, it can be seen that the design parameters values of the proposed DVA are always positive and practical for any lever ratio $L > 1$ and mass ratio $\mu < 0.25$, which covers the most engineering situation in practice. Moreover, the H₂-optimized lever-type stiffness-based grounded damping DVA with grounded stiffness has the global minimum mean squared displacement according to Fig. 4, which demonstrated the correctness of the optimization process. Indeed, according to the current results based on the optimized parameters $\left\{ {\xi_{{{\text{opt}}}} ,{\mkern 1mu} \alpha_{{{\text{opt}}}} } \right\}$, the H₂ optimal design of lever-type stiffness-based grounded damping DVA is no longer limited in the range of mass ratio $\mu < 0.114$ as previously shown in Eq. (20), but can be used for any mass ratio $\mu < 0.25$ and lever ratio $L > 1$. From the above results, the contribution of this paper is significant.

Table 2 The formulas of the H₂-optimized DVAs models in this paper

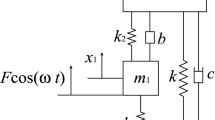
For other contributions in this paper, it should be noticed that the proposed dynamic vibration absorber model (hereinafter referred to as GL-grounded type model) can be degenerated into two typical DVAs. When $L = \beta = 1$, the optimal results for the grounded damping DVA with negative stiffness in Fig. 5a (hereinafter referred to as NS-grounded type model) can be derived. Furthermore, when $L = \beta = 1$, and $k_{3} = 0$, the optimal results for the grounded damping DVA in Fig. 5b (hereinafter referred to as Grounded type model) can be derived. Moreover, the optimal design parameters of the two DVAs in Fig. 5a and b based on the H₂ optimization are derived for the first time in this paper. The Voigt-type DVA (hereinafter referred to as Voigt-type model) is introduced here in Fig. 5c for comparison purpose. However, based on the optimization process in this paper, the optimal parameters of these DVAs are summarized in Table 2.

Fig. 5

Three dynamic vibration absorbers. a Grounded damping type DVA with negative stiffness. b Grounded damping type DVA and c Voigt-type DVA

3.4 Results analysis

The results analysis is carried out for the GL-grounded type DVA. Its optimal design parameters are summarized in Table 2, and the mean squared displacement of the primary structure with respect to the mass ratio $\mu$ can be found according to Eqs. (24) and (27). To study the effect of different lever ratios, the mass ratio varies from 0 to 0.2, which is suitable for the mass ratio range of practical engineering. Thus, as the mass ratio increases within the range of practical values for a select lever ratio, the optimal stiffness ratio $\alpha_{{{\text{opt}}}}$ and the optimal damping ratio $\xi_{{{\text{opt}}}}$ all increase while the grounded stiffness ratio $n_{{{\text{opt}}}}$ first decreases and then increases as shown in Fig. 6a, b and c, respectively. According to Fig. 6, the increase in the values of the optimal design parameters becomes more significant when the mass ratio takes larger values. Furthermore, for a given mass ratio, increasing the lever ratio will decrease both stiffness ratios and damping ratio as shown in Fig. 6a, b and c, respectively. As displayed in Fig. 6, the effect of the leverage ratio on the optimal design parameters is more significant as the mass ratio is higher. However, as shown in Fig. 6b, small mass ratios are more suitable to avoid high damping ratios.

Fig. 6

The relationships between optimal parameters and system parameters

To validate the results, the optimal grounded stiffness ratio $n_{{{\text{opt}}}}$ must verify the stability condition given by Eq. (10). To examine the latter case, the difference $n_{{{\text{opt}}}} - n_{lw}$ is calculated as follows

$$n_{{{\text{opt}}}} - n_{{{\text{lw}}}} = \frac{{\mu \beta \left( {2\beta + \sqrt {2\mu } } \right)}}{{2\left( {2\beta^{2} - \mu } \right)}}$$

(28)

From Eq. (28), it is established that the optimal grounded stiffness ratio $n_{{{\text{opt}}}}$ guarantees the stability of the coupled system in Fig. 1 under conditions that $n_{{{\text{opt}}}} > n_{{{\text{lw}}}}$; that is $2\beta^{2} - \mu > 0$, which leads to $L > 1/\left( {1 - \sqrt {\mu /2} } \right)$ for given mass ratio $\mu$. Furthermore, regarding the optimal grounded stiffness ratio expression $n_{{{\text{opt}}}}$ in Table 2 relevant to the GS-grounded damping DVA, an interesting phenomenon can be observed. Indeed, when the lever ratio is chosen, the increase in the mass ratio causes the optimal grounded stiffness ratio $n_{{{\text{opt}}}}$ to pass through negative values, a zero value and positive values, as shown in Fig. 6(c). That is to say, the optimal grounded stiffness ratio can be negative, zero or positive, which can mathematically be illustrated as follows

$$\left\{ {\begin{array}{*{20}l} {n_{{{\text{opt}}}} < 0,} \hfill & {{\text{if}}\quad L > 1/\left( {1 - \sqrt {2\mu } } \right)} \hfill \\ {n_{{{\text{opt}}}} = 0,} \hfill & {{\mkern 1mu} {\text{if}}\quad L = 1/\left( {1 - \sqrt {2\mu } } \right)} \hfill \\ {n_{{{\text{opt}}}} > 0,{\mkern 1mu} } \hfill & {{\text{if}}\quad 1/\left( {1 - \sqrt {\mu /2} } \right) < L < 1/\left( {1 - \sqrt {2\mu } } \right)} \hfill \\ \end{array} } \right.$$

(29)

where $L_{{{\text{lw}}}} = 1/\left( {1 - \sqrt {\mu /2} } \right)$ is the lower limit on the lever ratio derived from equations $\left\{ {\xi_{{{\text{opt}}}} ,{\mkern 1mu} \alpha_{{{\text{opt}}}} } \right\} > 0$. Furthermore, it should be noticed that the optimal grounded stiffness ratio $n_{{{\text{opt}}}}$ is expressed with only one formula but can present three different cases of value, that is, negative, zero and positive. For convenient, these three cases are referred to in order as case 1, case 2 and case 3 in the following section. Considering Eq. (29), the value of lever ratio L for given mass ratio $\mu$ will determine each case.

The effect of lever ratio on the mean squared displacement reduction performance of the primary structure is studied in Fig. 6d, with the mass ratio varying from 0 to 0.2 to cover the range of engineering practice. From this figure, it can be seen that the response value is even weaker as the lever ratio is smaller. However, the lever ratio must remain superior to unity $\left( {L > 1} \right)$ at a meaningful value.

When the H₂ design of GL-grounded damping DVA is used to reduce the frequency response of the primary system under harmonic excitation, the damping effect of the above three grounded stiffness ratio cases can be compared. Figure 7 illustrates this comparison for a mass ratio $\mu = 0.1$. The parameters selected are shown in Table 3 for each case. The numerical solution is established using the fourth-order Runge–Kutta method. Case (a) denotes the analytical solution, and case (b) illustrates the numerical solution. From Fig. 7, it can be seen that in the three cases, the analytical and numerical solution curves of the primary structure completely consistent, which demonstrated the correctness of the derived analytical solution. Furthermore, from Table 3 and Fig. 7, it can be seen that the DVA gives best control performance in case 3 and worst in case 1. This does not mean that positive stiffness can be chosen as grounded stiffness under any conditions. There are limitations on the lever ratio. For further explanation, the response value of the mean squared displacement of the primary structure in Fig. 6d decreases as the lever ratio becomes smaller, which is suitable for the effect of positive grounded stiffness ratio. However, according to the lever mechanism in Fig. 1, the lever ratio must remain greater than unity $\left( {L > 1} \right)$, which is theoretically confirmed by the lower limit $L_{{{\text{lw}}}} = 1 \, /\left( {1 - \sqrt {\mu /2} } \right) \,$ set on the lever ratio.

Fig. 7

The amplitude–frequency response curves in three different cases of $n_{{{\text{opt}}}}$

Table 3 The specific parameters of the GS-grounded damping LDVA in different case of $n_{{{\text{opt}}}}$

4 Performance comparison

To illustrate the vibration reduction performance of the DVA proposed in this paper in Fig. 1, Fig. 5 shows three compared DVAs. The two first DVAs in Fig. 5 are optimized for the first time in this paper, and the optimal parameters are presented in Table 2. The third DVA in Fig. 5 is the Voigt-type DVA with the parameters presented in the literature [49] and in this paper are given in Table 2.

4.1 The response of the primary structure to harmonic excitation

In order to compare the control performance under harmonic excitation, the optimal design parameters based on the H₂ optimization are considered for all the DVAs, and the value of the mass ratio is chosen as $\mu = 0.1$. From this value, the corresponding optimal parameter values of the compared DVAs in Fig. 5 can be calculated according to Table 2, and those of the presented DVA in this paper are displayed in Table 3 in the three different cases of lever ratio, that is, the three cases of grounded stiffness ratio. The normalized amplitude–frequency curves are compared in Fig. 8. Two performance criteria are investigated from this figure, which is the peak amplitude reduction and the frequency suppression bandwidth of vibration suppression, the definition of which is illustrated in Fig. 8. Accordingly, their values related to each DVA are summarized in Table 4. Based on this table, the proposed H₂-optimized GL-grounded type DVA has the superior performance in vibration control than other H₂-optimized DVAs displayed in Fig. 5, which is demonstrated by the broadest suppression bandwidth and the minimal peak amplitude of controlled primary structure. To quantify this control performance, the vibration reduction percentage $\gamma_{{{\text{PA}}}} (\% )$ of the response peak amplitude and the improvement suppression bandwidth percentage $\gamma_{{{\text{SB}}}} (\% )$ by the H₂-optimized GL-grounded type DVA with respect to other H₂-optimized DVAs in Fig. 5 can be described by the following relationships

$$\gamma_{{{\text{PA}}}} (\% ) = \left( {\frac{{\left( {{\text{PA}}} \right)_{{{\text{other}}{\kern 1pt} {\kern 1pt} {\text{type}}}} - \left( {{\text{PA}}} \right)_{{\text{GL - type}}} }}{{\left( {{\text{PA}}} \right)_{{{\text{other}}{\kern 1pt} {\kern 1pt} {\text{type}}}} }}} \right) \times 100$$

(30)

$$\gamma_{{{\text{SB}}}} (\% ) = \left( {\frac{{{\text{SB}}_{{\text{GL - type}}} - {\text{SB}}_{{{\text{other}}{\kern 1pt} {\kern 1pt} {\text{type}}}} }}{{{\text{SB}}_{{\text{GL - type}}} }}} \right) \times 100$$

(31)

Fig. 8

The amplitude–frequency response curves of the compared H₂-optimized DVAs-equipped primary structure

Table 4 Frequency bandwidths of vibration reduction and peak amplitude of the primary structure with attached four different DVAs for $\mu = 0.1$

Thus, when the H₂-optimized GL-grounded type DVA is compared with the H₂-optimized Voigt-type DVA, grounded type DVA and NS-grounded type DVA, respectively, according to Table 4 and Eqs. (30) and (31), one can get the following results. For peak amplitude reduction improvement, 74.86%, 69.93% and 28.93% in case 1; 77.23%, 72.77% and 35.64% in case 2; and 85.08%, 82.16% and 57.83% in case 3 have been obtained, respectively. For a broader suppression bandwidth improvement, 61.42%, 59.92% and 58.37% in case 1; 61.42%, 59.92% and 58.37% in case 2; and 61.42%, 59.92% and 58.37% in case 3 have been obtained, respectively. To understand these control performances, it can be seen that as the value of the lever ratio increases, the resonant frequencies of the primary structure increase. This effect leads into a great vibration suppression and a broader suppression bandwidth. It is also shown that the case 3 of the proposed DVA with positive grounded stiffness has the best control performance when compared the DVA with other typical DVAs in Fig. 5 under harmonic excitation.

Next, the time history response analysis for swept sine force excitation signal is conducted to validate the efficiency of the proposed DVA in three cases. Therefore, the considered swept sine force excitation signal is presented in Eq. (32) as [50]

$$f(\tau ) = \sin \left[ {\frac{{\Omega_{1} T}}{{\ln \left( {\Omega_{2} /\Omega_{1} } \right)}}\exp \left( {\frac{\tau }{T}\ln \left( {\frac{{\Omega_{2} }}{{\Omega_{1} }}} \right)} \right)} \right]$$

(32)

where $\Omega$ ₁ is the initial frequency, $\Omega$ ₂ is the final frequency and $T$ is the time duration of the swept sine force excitation. Because the resonant frequency of the primary structure is located between $\Omega \in [0.5, 1.5]$, $\Omega$ ₁ = 0.5 and $\Omega$ ₂ = 1.5 are selected for the swept sine excitation signal plotted in Fig. 9 considering $T=100$. Based on the fourth-order Runge–Kutta method under optimum parameters in Table 2 for $\mu =0.1$, the responses of the primary structures can be derived. Here, we take the primary mass as m₁ = 1 kg and stiffness of the primary system as k₁ = 100 N/m. For performed time histories, it is assumed that the structures are rest when $\tau$=0.

Fig. 9

The swept sine force excitation signal generation

Figure 10 shows the normalized displacement response of the primary structure with absorbers. Clearly, when the DVAs are used, the response of the primary system is mitigated, with a large reduction provided by the proposed GL-grounded type DVA with positive grounded stiffness, as predicted by the previous comparisons. More precisely, the maximum dynamic response of the primary structure controlled by Voigt-type DVA, grounded type DVA, NS-grounded type DVA and the GL-grounded type DVA in case 3 is evaluated 0.0478, 0.0463, 0.0185, 0.0078. The dynamic response of GL-grounded type DVA-controlled primary structure is compared to the other DVAs controlled primary structure. Accordingly, the dynamic response reduction capacity of GL-grounded type is 83.68%, 83.15%, and 57.84% superior to Voigt type, grounded type, NS-grounded type, respectively.

Fig. 10

Normalized displacement response of the primary system under swept sine force excitation

4.2 The response of the primary structure to random excitation

In many practical engineering situations, random response of primary structure to random force excitation should be reduced. Accordingly, the control performance of the proposed H₂-optimized GL-grounded type DVA is investigated in comparison with other typical DVAs in Fig. 5 under random force excitation of primary structure. For this purpose, in the following sections, two performance criteria are evaluated, namely the analytical mean squared displacement reduction and the time history displacement response reduction of the primary structure, respectively.

4.2.1 The analytical mean squared displacement reduction

The analytical minimal mean squared displacement responses of the considered DVAs in this paper are summarized in Tables 5, under a white noise power spectrum of force excitation. These mean squared values are compared in Fig. 11 for the practical mass ratio range of $0.01 \le \mu \le 0.2$. Only the case 3 of the proposed DVA with positive grounded stiffness and lever ratio $L = 1.5$ is considered for this comparison. Thus, from Fig. 11a, it can be seen that the proposed DVA has the smallest mean squared value with respect to the other DVAs. As result, Fig. 11b shows that when the proposed DVA is used in the case 3, 82.40–98.94% improvement can be obtained as compared with Voigt-type DVA, 81.79–98.70% improvement can be attained as compared with the grounded type DVA, and 21.94–97.94% improvement can also be achieved as compared with the NS-grounded type DVA. So, the proposed GL-grounded type DVA outperforms the considered DVAs in Fig. 5. However, the above results can be more understand considering the time domain evaluation.

Table 5 The analytical formulas of the minimal mean squared displacements

Fig. 11

a Optimal minimum mean squared displacement of the compared H₂-optimized DVAs-equipped primary structure. b Percentage improvement of GL-grounded type DVA with respect to other DVAs

4.2.2 The time history response reduction

The performance in the time history response reduction of the primary structure is evaluated. For this purpose, 50 s random white noise excitation is constructed as the input force excitation by 5000 normalized random numbers with zero mean value and unit variance. As a result, the time history of the random force excitation is shown in Fig. 12. To examine the random response of primary structure, consider the primary mass as m₁ = 1 kg and the primary stiffness as $k_{1} = 100N/m$[20, 21, 37]. Accordingly, the corresponding optimal parameter values $m_{2}$, $k_{i} \left( {i = 2,3} \right)$ and $c_{2}$ related to each DVA can be derived from the analytical results in Tables 2. For the numerical simulation, the fourth-order Runge–Kutta method is used, and the time history response of the primary structure without control is first presented in Fig. 13. However, for the controlled primary structure, the time history response result for each DVA is displayed in Figs. 14–19. The displacement variances and decrease ratios of the primary structure with different DVA are summarized in Table 6, including the case of uncontrolled one.

Fig. 12

The time history of the random force excitation

Fig. 13

The time history of uncontrolled primary structure

Fig. 14

The time history of the Voigt-type DVA-equipped primary structure

Table 6 The displacement variances and decrease ratios of the primary structures

From Figs. 13, 14, 15, 16, 17, 18 and 19 and Table 6, it is obvious that the proposed H₂-optimized GL-grounded type DVA in this paper shows superior random vibration reduction performance than other H₂ optimized DVAs in Fig. 5, even when the primary structure is under random force excitation. These results also verify that the proposed H₂-optimized DVA in different cases can greatly reduce the peak value of the statistical response of the primary structure displacement in the whole-frequency range, especially with the positive grounded stiffness. Thus, under random excitation, the lever-type stiffness-based grounded damping dynamic vibration absorber with grounded stiffness displays superior performance, indicating that the introduction of lever-type stiffness to the DVA model has a beneficial random vibration reduction effect. Therefore, the combined application of the lever-type stiffness and positive grounded stiffness has a significant vibration reduction effect and can provide ideas and beneficial choice for the design of vibration isolation system in seismic protection of buildings, as illustrated in Fig. 20. Figure 20 is the simplifying representation, where m_tot is the total mass of building under dynamic load (F), and k_b and c_b are the stiffness and inherent damping of the conventional base isolation, respectively.

Fig. 15

The time history of the grounded-type DVA-equipped primary structure

Fig. 16

The time history of the NS-grounded type DVA-equipped primary structure

Fig. 17

The time history of the GL-grounded type DVA-equipped primary structure in case 1

Fig. 18

The time history of the GL-grounded type DVA-equipped primary structure in case 2

Fig. 19

The time history of the GL-grounded type DVA-equipped primary structure in case 3

Fig. 20

The lever-type stiffness-based grounded damping dynamic vibration absorber with grounded stiffness as system isolation for seismic protection of buildings

5 Conclusion

A novel lever-type stiffness-based grounded damping DVA with grounded stiffness is investigated in this paper. The optimum stiffness ratio, the optimum damping ratio and the optimum grounded stiffness ratio are derived as the function of mass ratio $\mu$ and lever ratio $L$ by minimizing the mean squared displacement response of the primary structure previously established. From the results analysis, it is found that with the change in the lever ratio for fixed value of mass ratio, there are three different values for the optimum grounded stiffness ratio, i.e., negative, zero and positive. The optimum grounded is negative if $L > 1/\left( {1 - \sqrt {2\mu } } \right)$, zero if $L = 1/\left( {1 - \sqrt {2\mu } } \right)$, and positive if $1/\left( {1 - \sqrt {\mu /2} } \right) < L < 1{ /}\left( {1 - \sqrt {2\mu } } \right)$. Thus, the results shown that the smaller the value of the lever ratio $L$, the better the vibration reduction of primary structure for the proposed DVA with positive grounded stiffness. However, among the three cases of grounded stiffness, the negative stiffness has the worst control performance, but under certain practical conditions, it would be necessary to choose it. By comparing with respect to other designed DVAs in the same conditions as harmonic and random excitations, the results shown that with the DVA in this paper, the resonance amplitude and the frequency band of vibration reduction can greatly reduce and broadened, respectively, and the random vibration mitigation can be greatly increased. According to the existing literature, the proposed lever-type stiffness mechanism is justified, which means that the proposed DVA is practical and can be used in many engineering applications, as system isolation for seismic protection of buildings.