Peridynamics for failure prediction in variable angle tow composites

Abstract

This study presents a peridynamic (PD) approach to model progressive failure in fiber steered composites. The force density vectors in the PD equation of motion are derived explicitly for in-plane, transverse normal and transverse shear deformations in terms of the engineering material constants. The PD bonds enable the interaction of material points within each ply as well as their interaction with other material points in the adjacent plies. The PD equilibrium equation is solved by employing implicit techniques in an iterative form to account for damage progression based on the Hashin failure criteria for in-ply bonds and critical energy density release rate for inter-ply bonds. The capability of this approach is demonstrated by considering a lamina and two different variable tow angle laminates with a circular cutout under tension. It captures the correct deformation field as well as the damage initiation site and its progressive growth.

1 Introduction

Advanced composite materials have played a significant role in the development of cutting-edge lightweight space technologies for space exploration. As space exploration continues to evolve, the current and the future missions continually demand the advancement of composite materials and technologies to a yet more sophisticated horizon. Current research on space technologies focusing to advance pre-impregnated composite materials with continuous or short fibers also seeks for their high stiffness, low coefficient of thermal expansion, low moisture absorption ability, resistance to extreme temperature ranges, and out-gassing ability, in addition to their being extremely light weight. Conventional straight-fiber laminated composites offer a limited tailoring option by designing the stacking sequence with constant ply-angles along the thickness direction. With the introduction of new manufacturing technologies such as advanced fiber placement (AFP), engineers now have the capability to harness the full potential of nonconventional variable stiffness laminated composites using in-plane fiber steering.

Stiffness variation can be achieved by modifying the stacking sequences at each location by steering the fibers in each ply to produce continuous curvilinear fiber paths, which are also referred to as variable angle tow (VAT) composites. The design of nonconventional variable stiffness laminated composites has gained much more interest because of its challenge and promising performance. Its design practicality requires allowable database which requires extensive testing. However, it is not tractable to build databases that cover all different possible stacking sequences for VAT composites. In addition, fiber-steered composites might present different failure mechanisms than conventional composites. Therefore, accurate modeling and simulation tools are essential for virtual testing and reliable design of VAT composites. Virtual testing requires coupled modeling and simulations of fiber placement and structural response for progressive failure analysis.

Silling [1] and Silling et al. [2] introduced the peridynamic (PD) theory in order to address damage initiation and propagation in an isotropic material at multiple sites with arbitrary paths. In the PD theory, the internal forces are expressed through nonlocal interactions between the material points within a continuous body, and damage is part of the constitutive model. Damage is introduced through the removal of interactions (bonds) between the points based on a particular criteria, making the progressive failure analysis more practical. The PD equations of motion are classified as “Bond-Based (BB),” “Ordinary State-Based (OSB)” and “Non-Ordinary State-Based (NOSB)” PD. In the BB-PD formulation, the interaction of a pair of material points is independent of the influence of other points in their domain of interaction. However, the OSB- and NOSB-PD formulation is dependent on the influence of other points within their individual domains of interaction. In the past decade, PD has been widely adopted and applied to various engineering applications. An extensive literature survey on PD is given by Madenci and Oterkus [3].

This study presents a PD approach for modeling variable angle tow composites as an extension of the approach by Madenci et al. [4,5,6]. The derivation of the PD equation of motion accounts for the in-plane, transverse normal and transverse shear deformations. The force density vectors in the PD equation of motion are derived in terms of the engineering material constants. The capability of this approach for progressive failure is demonstrated through damage initiation and growth in two different VAT laminates with a hole under tension.

2 Approach

The laminate can be composed of $N$ plies with varying ply thickness, $h_{n}$. A material point ${\mathbf{x}}_{n}$ located on the nth ply has coordinates $(x_{n} ,y_{n} ,z_{n} )$ with respect to the reference coordinate system, $(x,y,z)$. The material point, ${\mathbf{x}}_{n}$, experiences displacement, ${\mathbf{u}}^{(n)} (t)$ at time $t$. The subscript or superscript $n$ denotes the ply number with $(n = 1,..,N)$. The fiber path parameterization in each ply of the laminate is achieved by [7]

$$ \theta_{n} (x_{n} ) = T_{0}^{n} + (T_{1}^{n} - T_{0}^{n} )\frac{{2\left| {x_{n} - L{/}2} \right|}}{L} $$

(1)

where $T_{0}^{n}$ and $T_{1}^{n}$ are the fiber orientation angles at the center and along the edges of the $n{\text{ - th}}$ ply, respectively. The origin of the coordinate system, $(x_{n} ,y_{n} ,z_{n} )$ is located at the lower left corner of the lamina with dimension of $L$ and $W$ in the $x{ - }$ and $y{ - }$ directions, respectively.

The equilibrium equations for the $n{\text{ - th}}$ ply are expressed as

$$ \rho_{n} \ddot{u}_{\alpha }^{(n)} = \sigma_{\alpha \beta ,\beta }^{(n)} + b_{\alpha }^{(n)} $$

(2)

in which $\rho_{n}$ is the mass density, and $u_{\alpha }^{(n)}$, $\sigma_{\alpha \beta }^{(n)}$ and $b_{\alpha }^{(n)}$ with $\alpha = x,y,z$ represent the displacement, stress and body force components, respectively. For an orthotropic lamina in a state of plane stress, the stress components can be related to the strain components as

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx}^{(n)} } \\ {\sigma_{yy}^{(n)} } \\ {\sigma_{zz}^{(n)} } \\ {\sigma_{yz}^{(n)} } \\ {\sigma_{xz}^{(n)} } \\ {\sigma_{xy}^{(n)} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11}^{(n)} } & {\overline{Q}_{12}^{(n)} } & {\overline{Q}_{13}^{(n)} } & 0 & 0 & {\overline{Q}_{16}^{(n)} } \\ {\overline{Q}_{12}^{(n)} } & {\overline{Q}_{22}^{(n)} } & {\overline{Q}_{23}^{(n)} } & 0 & 0 & {\overline{Q}_{26}^{(n)} } \\ {\overline{Q}_{13}^{(n)} } & {\overline{Q}_{23}^{(n)} } & {\overline{Q}_{33}^{(n)} } & 0 & 0 & {\overline{Q}_{36}^{(n)} } \\ 0 & 0 & 0 & {\overline{Q}_{44}^{(n)} } & {\overline{Q}_{45}^{(n)} } & 0 \\ 0 & 0 & 0 & {\overline{Q}_{45}^{(n)} } & {\overline{Q}_{55}^{(n)} } & 0 \\ {\overline{Q}_{16}^{(n)} } & {\overline{Q}_{26}^{(n)} } & {\overline{Q}_{36}^{(n)} } & 0 & 0 & {\overline{Q}_{66}^{(n)} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{(n)} } \\ {\varepsilon_{yy}^{(n)} } \\ {\varepsilon_{zz}^{(n)} } \\ {\gamma_{yz}^{(n)} } \\ {\gamma_{xz}^{(n)} } \\ {\gamma_{xy}^{(n)} } \\ \end{array} } \right\} $$

(3)

in which the parameters, $\overline{Q}_{ij}^{(n)}$, are expressed in terms of the fiber orientation angle, $\theta_{n} (x)$ from the x-axis, and the material constants $E_{11} ,E_{22} ,E_{33} ,v_{12} ,v_{13} ,v_{23} ,G_{12} ,G_{23}$ and $G_{13}$, [8]. Substituting for the stress components in the equilibrium equations along with the strain–displacement (kinematic) relations results in

$$ \rho_{n} {\boldsymbol{\ddot{u}}}^{(n)} = {\mathbf{L}}^{(n)} + {\tilde{\mathbf{L}}}^{(n)} + {\hat{\mathbf{L}}}^{(n)} + {\mathbf{b}}^{(n)} $$

(4)

where ${\mathbf{L}}^{(n)}$, ${\tilde{\mathbf{L}}}^{(n)}$ and ${\hat{\mathbf{L}}}^{(n)}$ represent the internal force vectors arising from in-plane, transverse shear and transverse normal deformations, respectively. They are defined as

$$ {\mathbf{L}}^{(n)} ({\mathbf{x}}) = {\mathbf{D}}^{(n)} ({\mathbf{x}}){\mathbf{u}}^{(n)} $$

(5a)

$$ {\tilde{\mathbf{L}}}^{(n)} ({\mathbf{x}}) = {\tilde{\mathbf{D}}}^{(n)} ({\mathbf{x}}){\mathbf{u}}^{(n)} $$

(5b)

and

$$ {\hat{\mathbf{L}}}^{(n)} ({\mathbf{x}}) = {\hat{\mathbf{D}}}^{(n)} ({\mathbf{x}}){\mathbf{u}}^{(n)} $$

(5c)

where the matrices ${\mathbf{D}}^{(n)}$, ${\tilde{\mathbf{D}}}^{(n)}$ and ${\hat{\mathbf{D}}}^{(n)}$ are expressed as

$$ {\mathbf{D}}^{(n)} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11}^{(n)} \partial_{xx} + 2\overline{Q}_{16}^{(n)} \partial_{xy} + \overline{Q}_{66}^{(n)} \partial_{yy} } & {\overline{Q}_{16}^{(n)} \partial_{xx} + \left( {\overline{Q}_{12}^{(n)} + \overline{Q}_{66}^{(n)} } \right)\partial_{xy} + \overline{Q}_{26}^{(n)} \partial_{yy} } & 0 \\ {\overline{Q}_{16}^{(n)} \partial_{xx} + \left( {\overline{Q}_{12}^{(n)} + \overline{Q}_{66}^{(n)} } \right)\partial_{xy} + \overline{Q}_{26}^{(n)} \partial_{yy} } & {\overline{Q}_{66}^{(n)} \partial_{xx} + 2\overline{Q}_{26}^{(n)} \partial_{xy} + \overline{Q}_{22}^{(n)} \partial_{yy} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right] $$

(6a)

$$ {\tilde{\mathbf{D}}}^{(n)} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{55}^{(n)} \partial_{zz} } & {\overline{Q}_{45}^{(n)} \partial_{zz} } & {\overline{Q}_{55}^{(n)} \partial_{xz} + \overline{Q}_{45}^{(n)} \partial_{yz} } \\ {\overline{Q}_{45}^{(n)} \partial_{zz} } & {\overline{Q}_{44}^{(n)} \partial_{zz} } & {\overline{Q}_{45}^{(n)} \partial_{xz} + \overline{Q}_{44}^{(n)} \partial_{yz} } \\ {\left( {\overline{Q}_{55}^{(n)} + \overline{Q}_{31}^{(n)} } \right)\partial_{xz} + \left( {\overline{Q}_{45}^{(n)} + \overline{Q}_{36}^{(n)} } \right)\partial_{yz} } & {\left( {Q_{45}^{(n)} + Q_{36}^{(n)} } \right)\partial_{xz} + \left( {Q_{44}^{(n)} + \overline{Q}_{32}^{(n)} } \right)\partial_{yz} } & 0 \\ \end{array} } \right] $$

(6b)

and

$$ {\hat{\mathbf{D}}}^{(n)} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & {\overline{Q}_{55}^{(n)} \partial_{xx} + 2\overline{Q}_{45}^{(n)} \partial_{xy} + \overline{Q}_{44}^{(n)} \partial_{yy} + \overline{Q}_{33}^{(n)} \partial_{zz} } \\ \end{array} } \right] $$

(6c)

where $\partial_{\alpha \beta }^{{}} = \frac{{\partial^{2} }}{\partial \alpha \partial \beta }$ with respect to $(\alpha ,\beta = x,y,z)$.

As suggested by Madenci and Oterkus [9], the equilibrium equation, Eq. (4) can be recast in PD form as

$$ \begin{gathered} \rho_{n} {\boldsymbol{\ddot{u}}}^{(n)} = \int\limits_{{H_{{{\mathbf{x}}_{n} }} }} {\left( {{\mathbf{t}}^{(n)} ({\mathbf{u}}^{(n)} {\mathbf{,u^{\prime}}}^{(n)} - {\mathbf{t^{\prime}}}^{(n)} ({\mathbf{u}}^{(n)} {\mathbf{,u^{\prime}}}^{(n)} )} \right)dV_{{{\mathbf{x}}^{\prime}}} } + \hfill \\ \int\limits_{{H_{{{\mathbf{x}}_{n} }} }} {\left( {{\tilde{\mathbf{t}}}^{(n)} ({\mathbf{u}}^{(n)} ,{\mathbf{u^{\prime}}}^{(m)} ) - {\tilde{\mathbf{t}}}^{\prime (m)} ({\mathbf{u}}^{(n)} ,{\mathbf{u^{\prime}}}^{(m)} )} \right)dV_{{{\mathbf{x}}^{\prime } }} } + \int\limits_{{H_{{{\mathbf{x}}_{n} }} }} {\left( {{\hat{\mathbf{t}}}^{(n)} ({\mathbf{u}}^{(n)} {\mathbf{,u^{\prime}}}^{(m)} ) - {\mathbf{\hat{t^{\prime}}}}^{(m)} ({\mathbf{u}}^{(n)} ,{\mathbf{u^{\prime}}}^{(m)} )} \right)dV_{{{\mathbf{x}}^{\prime } }} } + {\mathbf{b}}_{n} \hfill \\ \end{gathered} $$

(7)

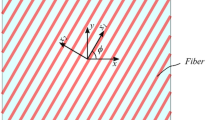
where ${\mathbf{u}}^{(n)}$ and ${\mathbf{u^{\prime}}}^{(n)}$ are the displacement vectors at points ${\mathbf{x}}_{n}$ and ${\mathbf{x^{\prime}}}_{n}$, respectively. The force density vectors $({\mathbf{t}}^{(n)} ,{\mathbf{t^{\prime}}}^{(n)} )$ develop due to in-plane deformation between material points, ${\mathbf{x}}_{n}$ and ${\mathbf{x^{\prime}}}_{n}$. The force density vectors $({\tilde{\mathbf{t}}}^{(n)} ,{\mathbf{\tilde{t^{\prime}}}}^{(m)} )$ and $({\hat{\mathbf{t}}}^{(n)} ,{\mathbf{\hat{t^{\prime}}}}^{(m)} )$ develop due to transverse shear deformation and transverse normal deformations, respectively, between material points, ${\mathbf{x}}_{n}$ and ${\mathbf{x^{\prime}}}_{m}$. The horizon of point ${\mathbf{x}}_{n}$ is specified as $H_{{{\mathbf{x}}_{n} }}$ representing its domain of interaction as shown in Fig. 1. The interactions of this point with the others through intra- and inter-layer bonds are also depicted in Fig. 1. The in-plane interactions occur only within each ply.

Fig. 1

Interaction of material point ${\mathbf{x}}_{n}$ with other points ${\mathbf{x^{\prime}}}_{n}$ and ${\mathbf{x^{\prime}}}_{m}$ located on the same ply and other plies, respectively

As derived by Madenci et al. [6], the force density vectors can be expressed as

$$ {\mathbf{t}}^{(n)} = {\mathbf{k}}_{n} \left( {{\mathbf{u}}^{(n)} - {\mathbf{u^{\prime}}}^{(n)} } \right) $$

(8a)

$$ {\tilde{\mathbf{t}}}^{(n)} = {\tilde{\mathbf{k}}}_{n} \left( {{\mathbf{u}}^{(n)} - {\mathbf{u^{\prime}}}^{(m)} } \right) $$

(8b)

and

$$ {\hat{\mathbf{t}}}^{(n)} = {\hat{\mathbf{k}}}_{n} \left( {{\mathbf{u}}^{(n)} - {\mathbf{u^{\prime}}}^{(m)} } \right) $$

(8c)

in which ${\mathbf{k}}_{n}$, ${\tilde{\mathbf{k}}}_{n}$ and ${\hat{\mathbf{k}}}_{n}$ are defined as

$$ {\mathbf{k}}_{n} = \left[ {\begin{array}{*{20}c} { - A_{n} ({\mathbf{x}}_{n} )} & { - B_{n} ({\mathbf{x}}_{n} )} & 0 \\ { - B_{n} ({\mathbf{x}}_{n} )} & { - C_{n} ({\mathbf{x}}_{n} )} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right] $$

(9a)

$$ {\tilde{\mathbf{k}}}_{n} = \left[ {\begin{array}{*{20}c} { - \tilde{A}_{n} ({\mathbf{x}}_{n} )} & { - \tilde{B}_{n} ({\mathbf{x}}_{n} )} & { - \frac{{\tilde{C}_{n} ({\mathbf{x}}_{n} ) + \tilde{F}_{n} ({\mathbf{x}}_{n} )}}{2}} \\ { - \tilde{B}_{n} ({\mathbf{x}}_{n} )} & { - \tilde{D}_{n} ({\mathbf{x}}_{n} )} & { - \frac{{\tilde{E}_{n} ({\mathbf{x}}_{n} ) + \tilde{G}_{n} ({\mathbf{x}}_{n} )}}{2}} \\ { - \frac{{\tilde{C}_{n} ({\mathbf{x}}_{n} ) + \tilde{F}_{n} ({\mathbf{x}}_{n} )}}{2}} & { - \frac{{\tilde{E}_{n} ({\mathbf{x}}_{n} ) + \tilde{G}_{n} ({\mathbf{x}}_{n} )}}{2}} & 0 \\ \end{array} } \right] $$

(9b)

and

$$ {\hat{\mathbf{k}}}_{n} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & { - \hat{A}_{n} ({\mathbf{x}}_{n} )} \\ \end{array} } \right] $$

(9c)

The coefficients appearing in these matrices can be expressed in terms of the PD functions, $g_{2}^{{p_{1} p_{2} p_{3} }} ({{\varvec{\upxi}}},w(|{{\varvec{\upxi}}}|))$ with $p_{1} ,p_{2} ,p_{3} = 0,1,2$ and ${{\varvec{\upxi}}} = {\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n}$ or ${{\varvec{\upxi}}} = {\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m}$ as

$$ A_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{n} ,)\left( {\overline{Q}_{11}^{(n)} g_{2}^{200} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n} ) + 2\overline{Q}_{16}^{(n)} g_{2}^{110} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n} ) + \overline{Q}_{66}^{(n)} g_{2}^{020} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n} )} \right) $$

(10a)

$$ B_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{n} )\left( {\overline{Q}_{16}^{(n)} g_{2}^{200} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n} ) + \left( {\overline{Q}_{12}^{(n)} + \overline{Q}_{66}^{(n)} } \right)g_{2}^{110} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n} ) + \overline{Q}_{26}^{(n)} g_{2}^{020} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n} )} \right) $$

(10b)

$$ C_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{n} )\left( {\overline{Q}_{66}^{(n)} g_{2}^{200} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n} ) + 2\overline{Q}_{26}^{(n)} g_{2}^{110} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n} ) + \overline{Q}_{22}^{(n)} g_{2}^{020} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{n} )} \right) $$

(10c)

and

$$ \tilde{A}_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{m} )\overline{Q}_{55}^{(n)} g_{2}^{002} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) $$

(11a)

$$ \tilde{B}_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{m} )\overline{Q}_{45}^{(n)} g_{2}^{002} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) $$

(11b)

$$ \tilde{C}_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{m} )\left( {\overline{Q}_{45}^{(n)} g_{2}^{011} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) + \overline{Q}_{55}^{(n)} g_{2}^{101} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} )} \right) $$

(11c)

$$ \tilde{D}_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{m} )\overline{Q}_{44}^{(n)} g_{2}^{002} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) $$

(11d)

$$ \tilde{E}_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{m} )\left( {\overline{Q}_{44}^{(n)} g_{2}^{011} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) + \overline{Q}_{45}^{(n)} g_{2}^{101} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} )} \right) $$

(11e)

$$ \tilde{F}_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{m} )\left( {\left( {\overline{Q}_{55}^{(n)} + \overline{Q}_{31}^{(n)} } \right)g_{2}^{101} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) + \left( {\overline{Q}_{45}^{(n)} + \overline{Q}_{36}^{(k)} } \right)g_{2}^{011} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} )} \right) $$

(11f)

$$ \tilde{G}_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{m} )\left( {\left( {\overline{Q}_{45}^{(n)} + \overline{Q}_{36}^{(k)} } \right)g_{2}^{101} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) + \left( {\overline{Q}_{44}^{(n)} + \overline{Q}_{32}^{(n)} } \right)g_{2}^{011} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} )} \right) $$

(11g)

and

$$ \hat{A}_{n} ({\mathbf{x}}_{n} ) = \mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{m} )\left( \begin{gathered} \overline{Q}_{55}^{(n)} g_{2}^{200} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) + 2\overline{Q}_{45}^{(n)} g_{2}^{110} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) \hfill \\ + \overline{Q}_{44}^{(n)} g_{2}^{020} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) + \overline{Q}_{33}^{(n)} g_{2}^{002} ({\mathbf{x}}_{n} - {\mathbf{x^{\prime}}}_{m} ) \hfill \\ \end{gathered} \right) $$

(11h)

The PD functions,$g_{2}^{{p_{1} p_{2} p_{3} }} ({{\varvec{\upxi}}},w(|{{\varvec{\upxi}}}|))$, introduced by Madenci et al. [10,11,12] enable the nonlocal form of differentiation as

$$ \frac{{\partial^{{p_{1} + p_{2} + p_{3} }} f({\mathbf{x}})}}{{\partial x_{1}^{{p_{1} }} \partial x_{2}^{{p_{2} }} \partial x_{3}^{{p_{3} }} }} = \int\limits_{{H_{{{\mathbf{x}}_{n} }} }} {f({\mathbf{x}} + {{\varvec{\upxi}}})g_{2}^{{p_{1} p_{2} p_{3} }} ({{\varvec{\upxi}}},w(|{{\varvec{\upxi}}}|))dV_{{{\mathbf{x}}^{\prime}}} } $$

(12)

in which $p_{i}$ ($i = 0,1,2$) denotes the order of differentiation with respect to variable $x_{i}$ with $i = 1,2,3$. The failure (status) parameter $\mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{n} )$ enables the inclusion of damage initiation and growth in the material response. If the failure criterion is satisfied, the status variable $\mu ({\mathbf{x}}_{n} ,{\mathbf{x^{\prime}}}_{n} )$ is set to zero. The parameter $w(|{{\varvec{\upxi}}}|) = \delta^{2} {/}|{{\varvec{\upxi}}}|^{2}$ is non-dimensional and specifies the degree of interaction among the material points. The coefficients appearing in the PD force density vectors do not require any calibration; thus, surface correction is not necessary.

3 Failure prediction

Peridynamics permits bond breakage when the failure criterion is satisfied; thus, the bond forces vanish. Breakage of the bonds between the material points is reflected in the PD equation of motion through the failure (status) parameter. The in-plane bonds are removed due to fiber breakage and matrix cracking, and the interlayer bonds due to delamination. In this study, failure prediction for fiber breakage and matrix cracking is based on Hashin-type stress criteria [13] in conjunction with the visibility criteria [14], and delamination failure is based on the energy release rate criterion as demonstrated by Hu and Madenci [15, 16].

3.1 In-plane damage prediction

In each ply, Hashin criteria [13] identifies matrix cracking and fiber failure by applying the following failure indices:

3.1.1 Tensile fiber failure

$$ \left( {e_{f(r)}^{t} } \right)^{2} = \left( {\frac{{\sigma_{11(r)} }}{{X_{t} }}} \right)^{2} + \left( {\frac{{\sigma_{12(r)} }}{S}} \right)^{2} = 1{\text{ for }}\left( {\sigma_{11(r)} } \right) \ge 0{\text{ and }}\left( {\frac{{\sigma_{11(r)} }}{{X_{t} }}} \right)^{2} > \left( {\frac{{\sigma_{12(r)} }}{S}} \right)^{2} $$

(13a)

3.1.2 Compressive fiber failure

$$ \left( {e_{f(r)}^{c} } \right)^{2} = \left( {\frac{{\sigma_{11(r)} }}{{X_{c} }}} \right)^{2} = 1{\text{ for }}\left( {\sigma_{11(r)} } \right) \le 0 $$

(13b)

3.1.3 Tensile matrix failure

$$ \left( {e_{m(r)}^{t} } \right)^{2} = \left( {\frac{{\sigma_{22(r)} }}{{Y_{t} }}} \right)^{2} + \left( {\frac{{\sigma_{12(r)} }}{{S_{{}} }}} \right)^{2} = 1{\text{ for }}\left( {\sigma_{22(r)} } \right) \ge 0 $$

(13c)

3.1.4 Compressive matrix failure

$$ \left( {e_{m(r)}^{c} } \right)^{2} = \left[ {\left( {\frac{{Y_{c} }}{2S}} \right)^{2} - 1} \right] \, \left( {\frac{{\sigma_{22(r)} }}{{Y_{c} }}} \right) + \left( {\frac{{\sigma_{22(r)} }}{2S}} \right)^{2} + \left( {\frac{{\sigma_{12(r)} }}{S}} \right)^{2} = 1{\text{ for }}\left( {\sigma_{22(r)} } \right) \le 0 $$

(13d)

where $\sigma_{ij}$ denotes the stress components with respect to the material coordinate system aligned with longitudinal (fiber) and transverse directions. The parameters $X$ and $Y$ represent the allowable strength in longitudinal and transverse directions. The subscripts $t$ and $c$ denote the tensile and compressive loading, respectively. The parameter $S$ denotes the allowable shear strength. The maximum value of the failure index identifies the failure mode.

$$ F_{(r)} = {\text{max}}\left\{ {e_{f(r)}^{t} ,e_{f(r)}^{c} ,e_{m(r)}^{t} ,e_{m(r)}^{c} } \right\}\;{\text{with}}\;r = 1,..,R $$

(14)

where $r = 1,..,R$ is the total number of PD points. Based on the stress field at each material point, the failure index with a value of $F_{(r)} \ge 1$ indicates damage in the material. However, it is necessary to identify the PD bond with max failure index. First, it is necessary to establish the material point, ${\mathbf{x}}_{(k)}$ with the max failure index as

$$ F_{(k)} = {\text{max}}\{ F_{(1)} ,F_{(2)} , \ldots ,F_{(R)} \} $$

(15)

Second, it is necessary to identify the material point, ${\mathbf{x}}_{(j)}$ with maximum failure index in the family of point, ${\mathbf{x}}_{(k)}$

$$ F_{(j)} = {\text{max}}\{ F_{(1)} ,F_{(2)} , \ldots ,F_{{(N_{(k)} )}} \} $$

(16)

If the failure index of this bond satisfies Hashin criteria, an incremental cut, ${\mathbf{c}}_{(k)(j)}^{{}}$, is introduced at the center of the bond between ${\mathbf{x}}_{(k)}^{{}}$ and ${\mathbf{x}}_{(j)}^{{}}$. It is defined as

$$ {\mathbf{c}}_{(k)(j)}^{{}} = ({\mathbf{x}}_{(k)}^{{}} + {\mathbf{x}}_{(j)}^{{}} ){/}2 $$

(17)

The extent and direction of the cut indicated by red dotted line in Fig. 2 is defined by

$$ \left[ {{\mathbf{c}}_{(k)(j)}^{{}} + \frac{\Delta }{2}{\mathbf{t}}_{(k)(j)}^{{}} ,{\mathbf{c}}_{(k)(j)}^{{}} - \frac{\Delta }{2}{\mathbf{t}}_{(k)(j)}^{{}} } \right] $$

(18)

in which $\Delta$ is the spacing between the points, and ${\mathbf{t}}_{(k)(j)}$ is a unit vector either in the direction or perpendicular to the fiber depending on the failure mode. The other points of the bonds connected to point ${\mathbf{x}}_{(k)}$ and ${\mathbf{x}}_{(j)}$ crossing the crack path are no longer visible to each other. Therefore, these bonds are broken according to the visibility criteria suggested by Belytschko et al. [14] and Madenci et al. [4]. As shown in Fig. 2, broken and unbroken bonds are distinguished by dashed blue and solid black lines, respectively.

Fig. 2

Description of visibility for damage progression

3.2 Delamination prediction

Based on the critical energy release rate, failure of interlayer bonds results in delamination. When the energy release rate reaches its critical value, the bond is broken. As defined by Silling and Askari [17], the stretch corresponding to bond ${{\varvec{\upxi}}}_{(k)(j)} = {\mathbf{x}}_{(j)} - {\mathbf{x}}_{(k)}$ is defined as

$$ s_{(k)(j)} = \frac{{\left\| {({\mathbf{x}}_{(j)} + {\mathbf{u}}_{(j)} ) - ({\mathbf{x}}_{(k)} + {\mathbf{u}}_{(k)} )} \right\| - \left\| {{\mathbf{x}}_{(j)} - {\mathbf{x}}_{(k)} } \right\|}}{{\left\| {{\mathbf{x}}_{(j)} - {\mathbf{x}}_{(k)} } \right\|}} $$

(19)

Therefore, the incremental stretch, $\Delta s_{(k)(j)}$, can be obtained as

$$ \Delta s_{(k)(j)} = \frac{{\left\| {({\mathbf{x}}_{(j)} + \Delta {\mathbf{u}}_{(j)} ) - ({\mathbf{x}}_{(k)} + \Delta {\mathbf{u}}_{(k)} )} \right\| - \left\| {{\mathbf{x}}_{(j)} - {\mathbf{x}}_{(k)} } \right\|}}{{\left\| {{\mathbf{x}}_{(j)} - {\mathbf{x}}_{(k)} } \right\|}} $$

(20)

where $\Delta {\mathbf{u}}_{(k)}$ and $\Delta {\mathbf{u}}_{(j)}$ represent incremental displacements at points ${\mathbf{x}}_{(k)}$ and ${\mathbf{x}}_{(j)}$, respectively.Under the assumption of small deformation, the elastic micropotential of the transverse shear and transverse normal bonds at ${\mathbf{x}}_{(k)}$ are determined, respectively, as

$$ \tilde{w}_{(k)(j)} = \sum\limits_{i = 1}^{{N^{inc} }} {{\tilde{\mathbf{t}}}^{i}_{(k)(j)} \cdot \frac{{{{\varvec{\upxi}}}_{(k)(j)} }}{{\left\| {{{\varvec{\upxi}}}_{(k)(j)} } \right\|}}\Delta s_{(k)(j)}^{i} } $$

(21a)

and

$$ \hat{w}_{(k)(j)} = \sum\limits_{i = 1}^{{N^{inc} }} {{\hat{\mathbf{t}}}^{i}_{(k)(j)} \cdot \frac{{{{\varvec{\upxi}}}_{(k)(j)} }}{{\left\| {{{\varvec{\upxi}}}_{(k)(j)} } \right\|}}\Delta s_{(k)(j)}^{i} } $$

(21b)

where $N^{{{\text{inc}}}}$ is the total number of increments, ${\tilde{\mathbf{t}}}^{i}_{(k)(j)}$ and ${\hat{\mathbf{t}}}^{i}_{(k)(j)}$ are force density vectors at the $i{\text{ - th}}$ increment for transverse shear and transverse normal bonds, respectively, defined in Eq. 8b and 8c. The strain energy stored at ${\mathbf{x}}_{(k)}$ due to the deformation of the bond between two material points ${\mathbf{x}}_{(k)}$ and ${\mathbf{x}}_{(j)}$ can be expressed as.

$$ \tilde{W}_{(k)}^{{}} = \frac{1}{2}\frac{{\tilde{w}_{(k)(j)} + \tilde{w}_{(j)(k)} }}{2}V_{(k)} V_{(j)} \;{\text{for}}\;{\text{transverse}}\;{\text{shear}}\;{\text{bond}} $$

(22a)

and.

$$ \hat{W}_{(k)} = \frac{1}{2}\frac{{\hat{w}_{(k)(j)} + \hat{w}_{(j)(k)} }}{2}V_{(k)} V_{(j)} \;{\text{for}}\;{\text{transverse}}\;{\text{normal}}\;{\text{bond}} $$

(22b)

where $V_{(k)}$ and $V_{(k)}$ are volumes of material points ${\mathbf{x}}_{(k)}$ and ${\mathbf{x}}_{(j)}$, respectively. The delamination area can be approximated as $A = K(\Delta x)^{2}$ where $\Delta x$ is the in-plane spacing between the material points and $K$ is the number of material points across the delamination area, $A$. Under the assumption that the state of deformation does not change significantly across the delamination area $A$, the energy release rate at each material point can be approximated as [15, 16]

$$ G_{(k)} = \frac{{\tilde{W}_{(k)}^{{}} + \hat{W}_{(k)}^{{}} }}{A} = \sum\limits_{j = 1}^{{K_{(k)}^{s} }} {(\frac{{\tilde{w}_{(k)(j)} + \tilde{w}_{(j)(k)} }}{2})\frac{{V_{(k)} V_{(j)} }}{{2(\Delta x)^{2} }}} + \sum\limits_{j = 1}^{{K_{(k)}^{n} }} {(\frac{{\hat{w}_{(k)(j)} + \hat{w}_{(j)(k)} }}{2})\frac{{V_{(k)} V_{(j)} }}{{2(\Delta x)^{2} }}} $$

(23)

and $K_{(k)}^{s}$ and $K_{(k)}^{n}$ denote the number of interlayer shear and normal bonds, respectively, associated with material point ${\mathbf{x}}_{(k)}$ which is located on either the lower or upper side of the lamina.

Based on the direction of displacement components, the energy release rate available at material point ${\mathbf{x}}_{(k)}$ can be decomposed into three different mode contributions of interlaminar strain energy release rate

$$ G_{(k)} = G_{I(k)} + G_{II(k)} + G_{III(k)} $$

(24a)

where

$$ G_{I(k)} = \sum\limits_{j = 1}^{{K_{(k)}^{s} }} {\tilde{G}_{I(k)(j)} } + \sum\limits_{j = 1}^{{K_{(k)}^{n} }} {\hat{G}_{I(k)(j)} } $$

(24b)

$$ G_{II(k)} = \sum\limits_{j = 1}^{{K_{(k)}^{s} }} {\tilde{G}_{II(k)(j)} } + \sum\limits_{j = 1}^{{K_{(k)}^{n} }} {\hat{G}_{II(k)(j)} } $$

(24c)

$$ G_{III(k)} = \sum\limits_{j = 1}^{{K_{(k)}^{s} }} {\tilde{G}_{III(k)(j)} } + \sum\limits_{j = 1}^{{K_{(k)}^{n} }} {\hat{G}_{III(k)(j)} } $$

(24d)

in which

$$ \tilde{G}_{I(k)(j)} = \sum\limits_{i = 1}^{{N^{inc} }} {(\frac{{\tilde{t}_{z(k)(j)}^{i} - \tilde{t}_{z(j)(k)}^{i} }}{2})\frac{{\xi_{z(k)(j)} }}{{\left\| {{{\varvec{\upxi}}}_{(k)(j)} } \right\|}}} \frac{{\Delta s_{(k)(j)}^{i} V_{(k)} V_{(j)} }}{{2(\Delta x)^{2} }} $$

(25a)

$$ \hat{G}_{I(k)(j)} = \sum\limits_{i = 1}^{{N^{inc} }} {(\frac{{\hat{t}_{z(k)(j)}^{i} - \hat{t}_{z(j)(k)}^{i} }}{2})\frac{{\xi_{z(k)(j)} }}{{\left\| {{{\varvec{\upxi}}}_{(k)(j)} } \right\|}}} \frac{{\Delta s_{(k)(j)}^{i} V_{(k)} V_{(j)} }}{{2(\Delta x)^{2} }} $$

(25b)

$$ \tilde{G}_{II(k)(j)} = \sum\limits_{i = 1}^{{N^{inc} }} {(\frac{{\tilde{t}_{x(k)(j)}^{i} - \tilde{t}_{x(j)(k)}^{i} }}{2})\frac{{\xi_{x(k)(j)} }}{{\left\| {{{\varvec{\upxi}}}_{(k)(j)} } \right\|}}} \frac{{\Delta s_{(k)(j)}^{i} V_{(k)} V_{(j)} }}{{2(\Delta x)^{2} }} $$

(25c)

$$ \hat{G}_{II(k)(j)} = \sum\limits_{i = 1}^{{N^{inc} }} {(\frac{{\hat{t}_{x(k)(j)}^{i} - \hat{t}_{x(j)(k)}^{i} }}{2})\frac{{\xi_{x(k)(j)} }}{{\left\| {{{\varvec{\upxi}}}_{(k)(j)} } \right\|}}} \frac{{\Delta s_{(k)(j)}^{i} V_{(k)} V_{(j)} }}{{2(\Delta x)^{2} }} $$

(25d)

$$ \tilde{G}_{III(k)(j)} = \sum\limits_{i = 1}^{{N^{inc} }} {(\frac{{\tilde{t}_{y(k)(j)}^{i} - \tilde{t}_{y(j)(k)}^{i} }}{2})\frac{{\xi_{y(k)(j)} }}{{\left\| {{{\varvec{\upxi}}}_{(k)(j)} } \right\|}}} \frac{{\Delta s_{(k)(j)}^{i} V_{(k)} V_{(j)} }}{{2(\Delta x)^{2} }} $$

(25e)

$$ \hat{G}_{III(k)(j)} = \sum\limits_{i = 1}^{{N^{inc} }} {(\frac{{\hat{t}_{y(k)(j)}^{i} - \hat{t}_{y(j)(k)}^{i} }}{2})\frac{{\xi_{y(k)(j)} }}{{\left\| {{{\varvec{\upxi}}}_{(k)(j)} } \right\|}}} \frac{{\Delta s_{(k)(j)}^{i} V_{(k)} V_{(j)} }}{{2(\Delta x)^{2} }} $$

(25f)

$\tilde{t}_{x(k)(j)}^{i}$, $\tilde{t}_{y(k)(j)}^{i}$ and $\tilde{t}_{z(k)(j)}^{i}$ are the components of force density vector of the interlayer shear bond, and $\hat{t}_{x(k)(j)}^{i}$, $\hat{t}_{y(k)(j)}^{i}$ and $\hat{t}_{z(k)(j)}^{i}$ are the components of force density vector of the interlayer normal bond at the $i{\text{ - th}}$ increment and $\xi_{x(k)(j)}$, $\xi_{y(k)(j)}$ and $\xi_{z(k)(j)}$ are components of relative position of the bond, ${{\varvec{\upxi}}}_{(k)(j)}$. Note that, Eq. (25) is derived with the fact that ${{\varvec{\upxi}}}_{(k)(j)} = - {{\varvec{\upxi}}}_{(j)(k)}$ and $\Delta s_{(k)(j)}^{i} = \Delta s_{(j)(k)}^{i}$.

As suggested by Benzeggagh and Kenane [18], the critical interlaminar fracture toughness $G_{c(k)}$ of a material point ${\mathbf{x}}_{(k)}$ is stated as

$$ G_{c(k)} = G_{Ic} + (G_{IIc} - G_{Ic} )\left( {\frac{{G_{II(k)} + G_{III(k)} }}{{G_{I(k)} + G_{II(k)} + G_{III(k)} }}} \right)^{\eta } $$

(26)

where $G_{Ic}$ and $G_{IIc}$ are the measured fracture toughness values for Mode I and II delamination initiations. The exponent $\eta$ is determined empirically based on curve fitting of the experimental data from different mixed-mode ratios. In this study, fracture toughness $G_{IIc}$ and $G_{IIc}$ are extracted from references [19, 20], and exponent $\eta$ is assumed to be 1.0 because of lack of data. The critical interlaminar fracture toughness $G_{c(k)}$ of a material point is distributed among the interlayer bonds of material point ${\mathbf{x}}_{(k)}$. The distribution is assumed to be uniform among the interlayer bonds as

$$ G_{c(k)(j)} = \tilde{G}_{c(k)(j)} = \hat{G}_{c(k)(j)} = \frac{{G_{c(k)} }}{{N_{(k)}^{s} + N_{(k)}^{n} }} $$

(27)

This equation establishes the fracture criterion for a single interlayer bond. Thus, failure occurs when.

$$ \frac{{\tilde{G}_{(k)(j)} }}{{G_{c(k)(j)} }} = \frac{{\tilde{G}_{I(k)(j)} + \tilde{G}_{II(k)(j)} + \tilde{G}_{III(k)(j)} }}{{G_{c(k)(j)} }} \ge 1\;{\text{for}}\;{\text{transverse}}\;{\text{shear}}\;{\text{bonds}} $$

(28a)

and.

$$ \frac{{\hat{G}_{(k)(j)} }}{{G_{c(k)(j)} }} = \frac{{\hat{G}_{I(k)(j)} + \hat{G}_{II(k)(j)} + \hat{G}_{III(k)(j)} }}{{G_{c(k)(j)} }} \ge 1\;{\text{for}}\;{\text{transverse}}\;{\text{shear}}\;{\text{bonds}} $$

(28b)

3.3 Failure parameter

The failure (status) parameter $\mu_{(k)(j)}$ is defined as

$$ \mu_{(k)(j)} = \left\{ {\begin{array}{*{20}l} {1{\text{ unbroken or visible bond }}} \hfill \\ {0{\text{ broken or invisible bond }}} \hfill \\ \end{array} } \right. $$

(29)

As suggested by Silling and Askari [17], the local damage $\varphi_{(k)}$ at point ${\mathbf{x}}_{(k)}$ can be measured as the ratio of the number of broken bonds to the total number of initially intact bonds as

$$ \varphi_{(k)} = 1 - \frac{{\sum\limits_{j = 1}^{{N_{(k)} }} {\mu_{(k)(j)} } }}{{N_{(k)} }} $$

(30)

The local damage $\varphi_{(k)}$ ranges from zero to one and is an indicator of possible crack formation within a body.

4 Numerical results

The capability of this approach is demonstrated by considering a VAT lamina with a circular cutout under tension. The geometry and loading conditions are shown in Fig. 3. Tensile loading is applied in the form of displacement increments of $\Delta u_{0} = 0.005{\text{ mm}}$ until failure. Its elastic properties are specified as $E_{11} = 173{\text{ GPa}}$, $E_{22} = 7.2{\text{ GPa}}$, $G_{12} = 3.76{\text{ GPa}}$, and $\nu_{12} = 0.29$. It has dimensions of $L = 50.{\text{ mm}}$ $W = 60.{\text{ mm}}$ with thickness of $h = 1.0{\text{ mm}}$. The cutout radius is $a = 10.{\text{ mm}}$.

Fig. 3

The geometry and boundary conditions of a VAT composite with a circular hole

The tow-steered fiber path in the lamina is defined as $< T_{0}^{1} { = 0}^{ \circ } {|}T_{1}^{1} { = 40}^{ \circ } >$. Their curvilinear fiber paths are shown in Fig. 4. The variation of horizontal and vertical displacement components from PD and FEM simulations is shown in Figs. 5 and 6, respectively. Also, the PD displacement results are compared with those of FEM along horizontal and vertical central lines in Figs. 7 and 8, respectively. These figures reveal that the PD predictions are in close agreement with the high-fidelity finite element predictions. Figure 9 shows crack initiation and it growth along the fiber path at failure. The progressive failure is natural, and it is achieved by removing the PD bonds. As expected, it follows the fiber path.

Fig. 4

Fiber paths in each layer corresponding to $< T_{0}^{{}} = 0^{ \circ } {|}T_{1}^{{}} = 40^{ \circ } >$

Fig. 5

Horizontal displacement predictions in a VAT laminate with a hole under displacement constraints of $u_{0} = 0.1\;{\text{mm}}$: a FEM and b PD

Fig. 6

Vertical displacement predictions in a VAT laminate with a hole under displacement constraints of $u_{0} = 0.1\;{\text{mm}}$: a FEM and b PD

Fig. 7

Comparison of FEM and PD displacement predictions along the horizontal central line: a horizontal displacement and b vertical displacement

Fig. 8

Comparison of FEM and PD displacement predictions along vertical central line: a horizontal displacement and b vertical displacement

Fig. 9

PD vertical displacement and crack path predictions at failure load of $u_{0} = 0.25\;{\text{m}}$

Further demonstration of this approach is achieved by considering two different VAT laminates with a circular cutout under tension as shown in Fig. 3. Its elastic properties are specified as $E_{11} = 164.3{\text{ GPa}}$, $E_{22} = 8.977{\text{ GPa}}$, $G_{12} = 5.02{\text{ GPa}}$, and $\nu_{12} = 0.32$. The laminates are made of four plies having the same fiber orientation with ply thickness of $h = 0.2{\text{ mm}}$. The fiber orientation of the plies in each laminate is specified as either $[ < T_{0}^{{}} = 0^{ \circ } {|}T_{1}^{{}} = 40^{ \circ } > ]_{4}$ or $[ < T_{0}^{{}} = 90^{ \circ } {|}T_{1}^{{}} = 60^{ \circ } > ]_{4}$. The cutout located at the center has a radius of $a = 5{\text{ mm}}$. The strength parameters in Hashin criteria are specified as $X_{t} = 2905\,{\text{GPa}}$, $X_{c} = 1680\,{\text{GPa}}$, $Y_{t} = 100\,{\text{GPa}}$, $Y_{c} = 247\,{\text{GPa}}$, $S = 80\,{\text{GPa}}$, and the critical energy release rate values are $G_{Ic} = 0.256\,{\text{N/mm}}$ and $G_{IIc} = 0.6499\,{\text{N/mm}}$. Each ply of the laminate is discretized with a grid spacing of $\Delta = 0.2{\text{ mm}}$. The computational domain has a total number of 300,000 PD points. The curvilinear fiber paths defined by $< T_{0}^{{}} = 0^{ \circ } {|}T_{1}^{{}} = 40^{ \circ } >$ and $< T_{0}^{{}} = 90^{ \circ } {|}T_{1}^{{}} = 60^{ \circ } >$ are shown in Fig. 10.

Fig. 10

Fiber paths in each layer corresponding to a $< T_{0}^{{}} = 0^{ \circ } {|}T_{1}^{{}} = 40^{ \circ } >$, b $< T_{0}^{{}} = 90^{ \circ } {|}T_{1}^{{}} = 60^{ \circ } >$

The horizontal and vertical displacement components in a laminate with layup of $< T_{0}^{{}} = 0^{ \circ } {|}T_{1}^{{}} = 40^{ \circ } >$ and $< T_{0}^{{}} = 90^{ \circ } {|}T_{1}^{{}} = 60^{ \circ } >$ are shown in Figs. 11 and 12, respectively. These figures represent the overall laminate deformations.

Fig. 11

PD displacement predictions in a VAT laminate of $< T_{0}^{{}} = 0^{ \circ } {|}T_{1}^{{}} = 40^{ \circ } >$ under a displacement constraint of $u_{0} = 0.01\;{\text{mm}}$: a horizontal and b vertical components

Fig. 12

PD displacement predictions in a VAT laminate of $< T_{0}^{{}} = 90^{ \circ } {|}T_{1}^{{}} = 60^{ \circ } >$ under a displacement constraint of $u_{0} = 0.01\;{\text{mm}}$: a horizontal and b vertical components

Figure 13 shows damage progression in the laminate with layup of $< T_{0}^{{}} = 0^{ \circ } {|}T_{1}^{{}} = 40^{ \circ } >$ at two stages. The damage reflects both in-plane cracking and delamination. At the first stage subjected to the displacement loading of $u_{0} = 0.16\,{\text{mm}}$, two small cracks propagate perpendicular to the loading direction following the fiber path. As the loading increases, the cracks propagate along the fiber path to the laminate sides where the fiber layup is $T_{1}^{{}} = 40^{ \circ }$.

Fig. 13

PD damage predictions in a VAT laminate of $< T_{0}^{{}} = 0^{ \circ } {|}T_{1}^{{}} = 40^{ \circ } >$ at two stages under a displacement constraint of: a $u_{0} = 0.16\;{\text{mm}}$ and b $u_{0} = 0.25\;{\text{mm}}$(final loading)

Figure 14. shows damage progression in the laminate with layup of $< T_{0}^{{}} = 90^{ \circ } {|}T_{1}^{{}} = 60^{ \circ } >$ also at two stages under $u_{0} = 0.02\,{\text{mm}}$ loading. Two parallel cracks initiate around the cutout, as shown in Fig. 14a. Note that in this layup, fiber orientation is close to $90^{ \circ }$ and cracks propagate parallel to the loading due to matrix failure. Unlike the layup with $< T_{0}^{{}} = 0^{ \circ } {|}T_{1}^{{}} = 40^{ \circ } >$, these cracks do not propagate further as the load increases. Instead, some other parallel cracks initiate and propagate to some extent. These individual cracks always follow the fiber path due to the matrix failure.

Fig. 14

PD damage predictions in a VAT laminate of $< T_{0}^{{}} = 90^{ \circ } {|}T_{1}^{{}} = 60^{ \circ } >$ at two stages under a displacement constraint of: a $u_{0} = 0.02\;{\text{mm}}$ and b $u_{0} = 0.08\;{\text{mm}}$  (final loading)

5 Conclusions

This study presents a peridynamics approach to model and predict progressive failure in VAT composite without any limitation to specific fiber orientation and material properties. Its capability is demonstrated by recovering the expected deformation field and damage propagation path. The progressive damage predictions capture the general characteristics of the experimentally observed damage patterns. The equilibrium equation is solved by employing implicit techniques for computational efficiency. This approach offers a reliable model for progressive failure and strength prediction of VAT composites with arbitrary layup under complex quasi-static loading.