1 Introduction

Vibration control of flexible structures subjected to time-varying loads is a problem relevant to vehicle/pedestrian–bridge interaction, maglev guideways, overhead cranes or catenary–pantograph interaction dynamics [1,2,3,4,5,6,7]. Recent years have seen a strong emphasis on increasing structural efficiency and reducing structures’ weight. Achievement of these design requirements presents a complex set of challenges for structural engineers as structures become more flexible, and this can lead to excessive vibration levels. The literature presents a wide range of solutions for vibration control of structures subjected to moving loads, and they range from passive solutions which have the advantage of simplicity and low cost to active control methods. It was shown that passive or semi-active solutions [8,9,10,11] could provide increased damping in the system and mitigate the steady-state vibration response. An active vibration solution, on the other hand, is usually designed to provide a stronger control action on a shorter time interval. Using active control, the maximum structure deflection or acceleration can be constrained within prescribed limits, and a more flexible control action for a structure subjected to fast-changing loads can be provided.

One of the main difficulties when modelling the interaction dynamics and particularly when designing a controller for a structure acted upon by moving loads resides in the fact that the action of the loads is time-varying. This imposes certain requirements for the controller that needs a very quick action to react to rapidly varying loads. Therefore, the action of the controller should address mostly the excitation rather than the structure’s parameters.

The research literature presents a wide range of theoretical algorithms for structures under moving loads modelled as Euler–Bernoulli beams proposed by different researchers [12,13,14,15,16,17,18]. Many of these studies presented solutions based on modal space models. For instance, Sloss et al. [12] proposed a displacement-proportional feedback control with the objective of confining the maximum midspan deflection within prescribed limits. The time-varying aspect of the problem was considered in Nikkhoo et al. [13] where an optimal control algorithm with variable state-feedback gain was used. The study analysed the numerical response of the structure under different moving masses. Liu et al. [14] studied the problem considering probabilistic uncertainties. The control problem was formulated as a tracking problem by Lin and Trethewey [15]. They proposed a strategy based on a combination of open-loop and closed-loop controls. The state-space equations of the system were formulated based on a finite element model, which had the advantage that the states were physically measurable variables as compared with a formulation based on a modal model. Other studies looked at problems of robust or optimal control [16, 17].

When the load moves at constant speed, the control problem can be formulated as a terminal time problem. Using this approach, Stancioiu and Ouyang [18] showed that for a particular placement of the actuators underneath the supporting structure, a control solution with time-varying gains would improve the displacement response of the structure as compared with a typical linear time-invariant solution with constant gains. Theoretical solutions for single-span structures based on hybrid methods or time-delay control for structures with nonlinearities were also studied [19, 20]. Bani-Hani and Alawneh [21] investigated two linear quadratic Gaussian controllers designed to regulate the post-tensioned tendon forces of a bridge subjected to a moving oscillator. Many of the open-loop control solutions can present stability and robustness problems. Wasilewski and Pisarski [22] proposed an adaptive control solution where the controller took into account the speed variations of the loads. Kong et al. [23] presented control solutions for an experimentally validated model of a maglev vehicle. The objective of the controller was the reduction of the air gap fluctuations and the vertical accelerations of the cabin. The supporting structure was modelled as a simply supported Euler–Bernoulli beam. They proposed a Kalman estimator for the states of the system, which combined modal response of the supporting structure, vehicle cabin displacements and velocities and current in the electromagnetic suspension.

Although there is an impressive body of works on theoretical aspects of control design, to the authors’ best knowledge, there are fewer examples of experimental studies of active control with application to bridge dynamics and the general moving load problem. Auperin et al. [24] proposed a solution based on integral force feedback implemented using a hydraulic actuator. The feasibility of a full-scale active vibration control system based on independent modal space control was studied by Shelley et al. [25]. The structural control system was implemented using a proof-mass hydraulic actuator, on a full-scale steel-truss highway bridge with a very good response reduction. They also pointed out some of the maintenance and safety requirements of such a solution. Casado et al. [26] presented an active absorber solution for a real four-span footbridge structure. Similar solutions for an existing flexible stress-ribbon footbridge were presented by Moutinho et al. [27], whereas Patten et al. [28] designed a semi-active hydraulic vibration absorber for a single-lane test bridge. The performance of the actuator was tested on two different set-ups: one with a single actuator located at midspan and the second with two actuators, the latter of which showed better improvement of the response.

Dniewicz et al. [29] proposed a semi-active solution and pointed out several drawbacks of using controllable dampers which usually have complex velocity–force relations, and the proposed solutions can have sensitivity to system parameters variation. Pisarski [30] proposed a semi-active control solution with rotational magnetorheological dampers. The rotational motion of the dampers was transformed to translational motion using a kinematic mechanism. These methods were tested on small-scale experimental models.

Both active and semi-active control solutions come with added complexity and potentially increased maintenance cost. There can also be connection problems that can result in loss of the signal from sensors, which will make the actuator or the semi-active device inactive [25]. The importance of an active system for vibration suppression, even at an increased cost, was emphasised by many authors. The interest in active control increases when dealing with light and flexible structures [26, 27, 31, 32]. In this case, the actuation solutions require less energy, and the forces required for control are smaller with important effects on the cost and maintenance. On the other hand, it can provide effective control for structures with significant parameters uncertainties [33]. A particularly important case where an active solution is attractive is when the control problem and the objective are formulated and aims at controlling the output response against the effect of the external disturbances, in this case the moving loads acting on the structure, which is one of the main objectives of this study.

Many of the active strategies proposed in the research literature and validated numerically assume that the designed control solution can be applied directly to the structure. In many of the investigations, the solution relies on a full knowledge of the states, which in the case of a modal space model for the supporting structure cannot be measured. For this reason, a practical solution based on this strategy would require an estimator, which can be difficult to implement due to the required fast acquisition and control times even when the dynamic system modelling of the structure is observable.

The dynamics of the actuation can also present challenges as it may reduce the stability limits of the system. Depending on the type of the actuation, some control strategies, mainly those based on bang-bang or on fast switching of the control action, cannot be easily achieved. There is always a trade-off between the numerical solution performance and its implementation. An equally challenging problem when dealing with a complex structure is the fact that an accurate model may present controllability and observability issues, which makes a state-design time-varying control-based strategy very difficult, if not impossible, to use.

The aim of this study is the design of an active controller for a light flexible structure under the action of time-varying loads that opposes directly the effect of the loads. It presents and implements an active control solution designed for a small-scale structure modelled as a four-span simply supported beam under the action of moving loads. The complexity of the structure including the actuators’ dynamics does not allow the direct use of a state-feedback control, and a simplified model is used for preliminary design and tuning of the controller.

Although the structural system itself is stable, in most cases the inclusion of the actuator’s dynamics changes the stability margins of the system; therefore, the control solution needs to include a compensator. The main assumption for the proposed control method is that the individual spans can be tested and tuned as single-input single-output systems, and it is justified by the fact that the influence of the actuator to adjacent spans is very small.

For the uncompensated system, the negative displacement feedback, as compared with positive displacement or negative velocity feedback, provides better results as the dynamics of the moving load—structure interaction requires an increased control effort when the structure is under the action of the moving loads. A solution based on positive displacement feedback or velocity feedback will improve the damping properties of the system and the free vibration transient response but will have little effect on the shape and maximum deflection of the structure when the beam is under the action of moving loads. On the other hand, the use of the velocity feedback becomes difficult when the signal-to-noise ratio is high.

The control solution obtained and experimentally tested provides a good improvement of the beam’s deflection at sensors locations, but the requirement of a control gain selected to match the magnitude of the load leaves the problem open to an adaptive control method. The chosen example also shows that the implementation of the method using displacement laser transducers and electrodynamic actuation has certain limitations.

2 Experimental set-up and structural control model identification

2.1 Experimental set-up

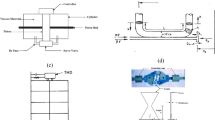
The supporting structure investigated is a continuous four-span simply supported thin plate of length \(L=\) 3640 mm with constant section 10.1 × 3 mm2 and constant span length \({L}_{S}\). The structure is similar to the structure described and modelled in previous studies [5, 6, 27]. Based on the results from these studies, the structure is modelled as a Euler–Bernoulli beam and the torsional modes are neglected. Each span is actuated by one Data Physics GW V4 modal shaker placed close to the midspan coordinate. The first two spans of the structure are represented in Fig. 1. The moving structures are two miniature carriages with rigid suspensions that enter the beam at different arrival times \({t}_{j}\) and at different speeds \({v}_{j}\).

Fig. 1
figure 1

Schematic of the experimental set-up. Two spans of the supporting structure with one carriage moving at constant speed \({v}_{j}\) in \(x\)—direction

Full size image

The carriages can be loaded with steel blocks (Fig. 2). The total mass of the moving structures with loads can be changed from 4.4 kg up to around 14 kg by changing or combining the blocks.

Fig. 2
figure 2

Experimental set-up

Full size image

The structure is equipped with Micro-Epsilon optoNCDT1401 laser displacement sensors located at 0.54, 1.23, 2.39 and 2.98 m along the beam (one for each span), and it is actuated by four Data Physics GW V4 Modal shakers (also one for each span).

2.2 Structural model identification

A similar experimental set-up with a plastic guide rail and moving balls modelled as moving masses was validated in Stancioiu et al. [5]. Yang et al. [6] presented a more detailed model of the supporting structure with brass guiding rails using finite elements. The model was cross-validated against modal test data and experimental moving load tests.

The first modelling assumption made in this case, based on previous results [5], is that the supporting structure can be modelled as a Euler–Bernoulli beam. For this experiment, two guiding rails were glued on top of the beam. This increased the rigidity of the beam as compared with the model presented in [5] where the guiding rails were made of plastic and had little effect on the transverse rigidity of the structure. In this respect, modal tests and finite element models were used to find an equivalent beam section that can model the structure with the two brass rails as an Euler–Bernoulli beam with the required level of accuracy.

Under this assumption, the equation of motion governing the dynamic deflection of the structure is:

$$EI\frac{{\partial^{4} w}}{{\partial x^{4} }}\left( {x,t} \right) + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }}\left( {x,t} \right) + \rho Ac\frac{\partial w}{{\partial t}}\left( {x,t} \right) = f_{{\text{L}}} \left( {x,t} \right) + f_{{\text{A}}} \left( {x,t} \right)$$
(1)

where \(EI\) and \(\rho A\) are the flexural rigidity and mass per unit length of the beam, \(\rho Ac\) represents a mass proportional damping, in a later stage \(c\) will be represented as \(2\pi \zeta \omega_{n}\) with \(\omega_{n}\) the nth natural frequency of the structure and \(\zeta\) a constant damping ratio, \(f_{{\text{L}}} \left( {x,t} \right)\) represents the dynamic loading of the structure and \(f_{{\text{A}}} \left( {x,t} \right)\) the action of the shakers which also includes the control effort.

The second assumption made is that the carriage’s action over the beam can be modelled as the action of a moving mass, ignoring the effects of mass moment of inertia of the carriage as the ratio between one beam span and the carriage wheelbase is 910/124.

Using this second assumption, the effect of the dynamic forces acting on the structure can be modelled as the effect of the action of \(n\) masses \({m}_{j}\) moving at independent speeds \({v}_{j}\), which enters the beam at times, \(t_{j}\):

$$f_{{\text{L}}} \left( {x,t} \right) = - \mathop \sum \limits_{j = 1}^{n} m_{j} \left( {\ddot{w}\left( {x_{j} \left( t \right),t} \right) + {\text{g}}} \right)G\left( {v_{j} ,L,t_{j} } \right)\delta \left( {x - x_{j} \left( t \right)} \right)$$
(2)

In this equation, \(G\left( {v_{j} ,L,t_{j} } \right)\) is a windowing function equal to 1 when the carriage of mass \(m_{j}\) moves along the beam and zero when it steps outside of the beam’s length; the dot denotes the total derivative with respect to time. The term \(\delta \left( {x - x_{0} } \right)\) is the Dirac delta function. When the carriages are not present on the structure, the dynamic loading is \(f_{L} \left( {x,t} \right) = 0\).

When the friction between the moving parts of the carriage is important, the speed is no longer constant along the beam and it is assumed to decay linearly in time: \({v}_{j}={v}_{j0}-{a}_{j}(t-{t}_{j})\), where \({v}_{j0}\) and \({a}_{j}\) are the initial velocity and the constant deceleration along the beam.

In this case, the moving coordinate is: \({x}_{j}\left(t\right)={v}_{j0}(t-{t}_{j})-{a}_{j}{\left(t-{t}_{j}\right)}^{2}/2\) and the dynamic force becomes:

$$\begin{aligned} {f}_{\mathrm{L}}\left(x,t\right)&=-\sum_{j=1}^{n}{m}_{j}\left(-{a}_{j}\frac{\partial w}{\partial x}\left({x}_{j}\left(t\right),t\right)+{\left({v}_{j0}-{a}_{j}\left(t-{t}_{j}\right)\right)}^{2}\frac{{\partial }^{2}w}{\partial {x}^{2}}\left({x}_{j}\left(t\right),t\right)\right.\\ &\quad \left. +2\left({v}_{j0}-{a}_{j}\left(t-{t}_{j}\right)\right)\frac{{\partial }^{2}w}{\partial x\partial t}\left({x}_{j}\left(t\right),t\right)+\frac{{\partial }^{2}w}{\partial {t}^{2}}\left({x}_{j}\left(t\right),t\right) +\mathrm{g}\right)\\ &\quad G\left({v}_{j0},{a}_{j},L,{t}_{j}\right)\delta \left(x-{v}_{j0}\left(t-{t}_{j}\right)+\frac{{a}_{j}}{2}{\left(t-{t}_{j}\right)}^{2}\right) \end{aligned}$$
(3)

The action of the modal shakers positioned on the structure at coordinates \({x}_{\mathrm{a}i}\) is modelled as:

$${f}_{\mathrm{A}}\left(x,t\right)= \sum_{i=1}^{{N}_{\mathrm{a}}}\left({k}_{i}w\left(x,t\right)+{c}_{i}\dot{w}\left(x,t\right)\right)\delta \left(x-{x}_{\mathrm{a}i}\right)-\sum_{i=1}^{{N}_{\mathrm{a}}}{f}_{\mathrm{c}i}\delta \left(x-{x}_{\mathrm{a}i}\right)$$
(4)

The first component models the shakers as spring-damper systems with spring and damping constants \({k}_{i}\) and \({c}_{i}\). The second component is the control effort \({f}_{\mathrm{c}i}\) at each span (\({N}_{\mathrm{a}}=4\)), and it is the response of the shaker to a voltage input.

In this case, the actuators (DataPhysics GW V4 Modal Shaker and PA30E Power Amplifier) under the voltage \({u}_{i}<10 V\) are modelled as first-order systems [34, 35] with the transfer function from the control voltage input (\({u}_{i}\)) to the actuation force (\({f}_{\mathrm{c}i}\)) given by:

$${f}_{\mathrm{c}i}=\frac{\beta }{\gamma +s}{u}_{i}$$
(5)

which corresponds to the state-space representation:

$$\begin{aligned} \dot{f}_{{{\text{c}}i}} & = - \gamma f_{{{\text{c}}i}} + \beta u_{i} \\ y & = f_{{{\text{c}}i}} \\ \end{aligned}$$
(6)

The response of the structure will be assessed by the time history of beam deflections at the laser sensor positions, \(w({x}_{\mathrm{s}i},t)\). A numerical approximation of the solution of beam deflection will be sought as:

$$w\left(x,t\right)= {{\varvec{\uppsi}}}^{\mathrm{T}}\left(x\right)\mathbf{q}(t)$$
(7)

where the vectors \(\mathbf{q}(t)\) and \({\varvec{\uppsi}}(x)\) are the modal coordinates and the normal modes of the beam structure [5] without the viscoelastic supports. The effect of the shakers modelled as elastic supports is included as forces acting at \({x}_{\mathrm{a}i}\) locations.

By using the orthogonality of the beam’s mode functions, a full set of equations can be written in modal coordinates as:

$$\begin{aligned} \left( {{\mathbf{M}} + {\Delta} {\mathbf M}\left( t \right)} \right){{\ddot{\mathbf{q}}}} & = - \left( {{\mathbf{K}} + {\mathbf{K}}_{{\text{a}}} + {\Delta} {\mathbf K}\left( t \right)} \right){\mathbf{q}} - \left( {{\mathbf{D}} + {\mathbf{D}}_{{\text{a}}} + {\Delta} {\mathbf D}\left( t \right)} \right){\dot{\mathbf{q}}} \\ & \quad + \left[ {{{\varvec{\uppsi}}}\left( {x_{{{\text{a}}1}} } \right) \ldots {{\varvec{\uppsi}}}\left( {x_{{{\text{a}}4}} } \right)} \right]{\mathbf{f}}_{{\text{c}}} - \mathop \sum \limits_{j = 1}^{n} m_{{\varvec{j}}} {\text{g}}\user2{ }{{\varvec{\uppsi}}}\left( {x_{j} \left( t \right)} \right) \\ {\dot{\mathbf{f}}}_{{\mathbf{c}}} & = - \gamma {\mathbf{I}}_{4} {\mathbf{f}}_{{\mathbf{c}}} + \beta {\mathbf{I}}_{4} {\mathbf{u}} \\ \end{aligned}$$
(8)

The number of actuators in this investigation is limited to four, one for each span, and \({\mathbf{f}}_{\mathbf{c}}\) and \(\mathbf{u}\) are the vectors of output forces \({f}_{\mathrm{c}i}\) and input voltages \({u}_{i}\) at each actuator. The addition of any compensator in the feedback path will change the last equations of system (8) including supplementary states describing the dynamics of the compensator.

The time-invariant part of the structural model (8) is defined by the modal matrices of the beam structure \(\mathbf{M}\), D, and K [34, 35] and \({\mathbf{K}}_{\mathrm{a}}\) and \({\mathbf{D}}_{\mathrm{a}}\). The matrices \({\mathbf{K}}_{\mathrm{a}}\) and \({\mathbf{D}}_{\mathrm{a}}\) model the action of the shakers and are explicitly given by:

$$\begin{aligned} {\mathbf{K}}_{{\text{a}}} & = \mathop \sum \limits_{i = 1}^{4} k_{i} {{\varvec{\uppsi}}}\left( {x_{{{\text{a}}i}} } \right){{\varvec{\uppsi}}}^{{\text{T}}} \left( {x_{{{\text{a}}i}} } \right) \\ {\mathbf{D}}_{{\text{a}}} & = \mathop \sum \limits_{i = 1}^{4} c_{i} {{\varvec{\uppsi}}}\left( {x_{{{\text{a}}i}} } \right){{\varvec{\uppsi}}}^{{\text{T}}} \left( {x_{{{\text{a}}i}} } \right) \\ \end{aligned}$$
(9)

The system matrices in Eq. (8) have also a time-varying part \(\Delta \mathbf{M}(t)\), \(\Delta \mathbf{D}(t)\) and \(\Delta \mathbf{K}\left(t\right)\), describing the action of the moving carriages. The time-dependent matrices \(\Delta \mathbf{M}(t)\), \(\Delta \mathbf{D}(t)\) and \(\Delta \mathbf{K}\left(t\right)\) for carriages moving at varying speeds \({v}_{j}={v}_{j0}-{a}_{j}(t-{t}_{j})\) are explicitly defined by:

$$\begin{aligned} {\Delta }{\mathbf{M}}\left( t \right) & = \mathop \sum \limits_{j = 1}^{n} m_{j} {{\varvec{\uppsi}}}\left( {v_{j} t} \right){{\varvec{\uppsi}}}^{{\text{T}}} \left( {v_{j} t} \right)G\left( {v_{j} ,L,t_{j} } \right) \\ {\Delta }{\mathbf{D}}\left( t \right) & = 2\mathop \sum \limits_{j = 1}^{n} m_{j} \left( {v_{j0} - a_{j} \left( {t - t_{j} } \right)} \right){{\varvec{\uppsi}}}\left( {v_{j} t} \right) \left( {{{\varvec{\uppsi}}}^{\prime}\left( {v_{j} t} \right)} \right)^{{\text{T}}} G\left( {v_{j} ,L,t_{j} } \right) \\ {\Delta }{\mathbf{K}}\left( t \right) & = \mathop \sum \limits_{j = 1}^{n} m_{j} {{\varvec{\uppsi}}}\left( {v_{j} t} \right)\left( {\left( {v_{j0} - a_{j} \left( {t - t_{j} } \right)} \right)^{2} {\mathbf{\psi^{\prime\prime}}}\left( {v_{j} t} \right) - a_{j} {\mathbf{\psi^{\prime}}}\left( {v_{j} t} \right)} \right)^{{\text{T}}} G\left( {v_{j} ,L,t_{j} } \right) \\ \end{aligned}$$
(10)

After the time instant when the carriages leave the beam, or before the next one moves on the beam \({f}_{L}\left(x,t\right)=0\), the structure vibrates freely. The dynamic equations in modal coordinates are time-invariant:

$$\begin{aligned} {M\ddot{\mathbf{q}}} & = - \left( {{\mathbf{K}} + {\mathbf{K}}_{{\text{a}}} } \right){\mathbf{q}} - \left( {{\mathbf{D}} + {\mathbf{D}}_{{\text{a}}} } \right){\dot{\mathbf{q}}} + \left[ {{{\varvec{\uppsi}}}\left( {x_{{{\text{a}}1}} } \right) \ldots {{\varvec{\uppsi}}}\left( {x_{{{\text{a}}4}} } \right)} \right]{\mathbf{f}}_{{\text{c}}} \\ {\dot{\mathbf{f}}}_{{\mathbf{c}}} & = - \gamma {\mathbf{I}}_{4} {\mathbf{f}}_{{\mathbf{c}}} + \beta {\mathbf{I}}_{4} {\mathbf{u}} \\ \end{aligned}$$
(11)

and have as initial conditions the final values of the solutions of Eq. (8). This way Eqs. (8) and (11) characterise the controlled system, with or without the action of the moving carriages, whereas the non-controlled system equations are:

$$\left( {{\mathbf{M}} + {\mathbf{\Delta M}}\left( t \right)} \right){\mathbf{\ddot{q}}} = - \left( {{\mathbf{K}} + {\mathbf{K}}_{{\text{a}}} + {\mathbf{\Delta K}}\left( t \right)} \right){\mathbf{q}} - \left( {{\mathbf{D}} + {\mathbf{D}}_{{\text{a}}} + {\mathbf{\Delta D}}\left( t \right)} \right){\dot{\mathbf{q}}} - \mathop \sum \limits_{j = 1}^{n} m_{{\varvec{j}}} {\text{g}}\user2{ }{{\varvec{\uppsi}}}\left( {v_{j} t} \right)$$
(12)

The output equations representing the numerically estimated deflection signals at the laser sensors’ positions \({x}_{\mathrm{s}i}\) are:

$$y\left({x}_{\mathrm{s}i},t\right)={{\varvec{\uppsi}}}^{\mathrm{T}}\left({x}_{\mathrm{s}i}\right)\mathbf{q}(t)$$
(13)

Equations (8) and (10) together with the outputs (13) show two stages of the same system. The first stage is when the beam is under the action of the moving loads. In this stage, the controller has a stronger action aimed mainly at reducing the effect of the loads. The second stage is when the supporting structure vibrates freely as a linear time-independent system and just an increase in the damping ratio of the system can be enough to improve the system’s response. Many researchers have considered separate actions for these two stages [18, 19].

3 Simplified disturbance control model for the problem of moving loads

The main control objective in this investigation focuses on the reduction of the supporting structure’s deflection at sensor’s locations along the structure. This is an objective similar to the one used by Sloss et al. [12]. In many applications of the moving load problem related to bridge vibration, the objective is formulated in midspan accelerations, but this objective will not be studied here.

The modal space system of a complex supporting structure like the one investigated here has a high number of states in relation to the number of inputs and outputs. This affects the controllability and the observability of the system and makes many of the state-space control methods difficult to apply directly. In particular, a feedback control solution for a system where the states are modal space variables (modal displacements and velocities) is even more difficult to design as there is no direct access to the states via measurements. The solution of an observer, available only when the observability of the system is not compromised, may not be an option due to the requirement of fast acquisition and control rates by the physical controller.

The practical control solution required for this investigation needs also to consider the noisy measured deflection responses as inputs to the controller. As opposed to many previously published theoretical studies, the design method used now requires greater attention to stability margins and the sensors’ noise.

A simplified model of the interaction can be obtained modelling the dynamic loading (2) as:

$${f}_{\mathrm{L}}\left(x,t\right)=-\sum_{j=1}^{n}{m}_{j}\mathrm{g} G\left({v}_{j},L,{t}_{j}\right)\delta \left(x-{x}_{j}\left(t\right)\right)$$
(14)

The main assumption in this case is that the carriages can be approximated as moving forces. This is a simplification of the model presented in the first section, but it is used only for the control design. For different moving speeds and masses tested, the moving force model shows a difference of maximum deflection of less than 4% when compared with experimental data. The final control solution is numerically tested against the full numerical model and against the experimental model considering variations in loads distribution.

In a first approach to design, the system considered consists of a supporting structure with only one span and one actuator located at a given coordinate \({x}_{\mathrm{a}}\). The structure is under the action of a force that moves at constant speed; therefore, the dynamic system associated with this problem is time-invariant. The model also considers the actuator as an active support with an active and passive state, similar to the real case presented in paragraph 2.

With the same notations, the system of equations that governs the dynamics of the problem is given by:

$$\begin{aligned} {\mathbf{M}}\ddot{\mathbf{q}} + \left( {{\mathbf{D}} + {\mathbf{D}}_{{\text{a}}}} \right){\dot{\mathbf{q}}} + \left( {{\mathbf{K}} + {\mathbf{K}}_{{\text{a}}} } \right){\mathbf{q}} & = - {{\varvec{\uppsi}}}\left( {vt} \right)m{\text{g}} + {{\varvec{\uppsi}}}\left( {x_{{\text{a}}} } \right)f_{{\text{c}}} \\ \dot{f}_{{\text{c}}} & = - \gamma f_{{\text{c}}} + \beta u \\ \end{aligned}$$
(15)

In this investigation, the model of the actuator is a first-order filter with a very low time constant \(\tau =1/\gamma \approx\) 0.03 s. As a consequence, this has little effect on a low-frequency signal, but as the frequency increases towards 47 Hz the magnitude of the signal decays with 20 dB/decade.

The control design method in this investigation has as objective the active reduction of the deflection at \({x}_{\mathrm{s}}\) under the action of the moving load \({{\varvec{\uppsi}}}^{\mathrm{T}}\left(vt\right)m\mathrm{g}\).

The action of the moving load is explicitly given by \({f}_{\mathrm{d}i}=m\mathrm{g sin}(i\omega t)\) for i = 1 to the mode number and \(\omega =v/L\). For simplicity, in this paragraph \(m\mathrm{g}\) = 1 N.

In Laplace space, the modified equation, using \({f}_{\mathrm{d}i}\) forces as disturbances, can be written as:

$$\left[{s}^{2}\mathbf{M}+s\left(\mathbf{D}+{\mathbf{D}}_{\mathbf{a}}\right)+\left(\mathbf{K}+{\mathbf{K}}_{\mathbf{a}}\right)\right]\mathbf{Q}\left(s\right)={\mathbf{B}}_{\mathbf{d}}{\mathbf{F}}_{\mathbf{d}}+{{\varvec{\uppsi}}}^{\mathrm{T}}\left({x}_{\mathrm{a}}\right)\frac{\beta }{s+\gamma }U(s)$$
(16)

where the matrix \({\mathbf{B}}_{\mathbf{d}}\) is the identity matrix of appropriate order. The output of the system consists of beam deflection at a given coordinate \({x}_{\mathrm{s}}\).

The deflection of the structure is caused by the action of the force \({\mathbf{F}}_{\mathbf{d}}\). For the open-loop system shown in Fig. 3, when the control action is zero, the response of the system is simply the deflection at the measured location under the action of the force. In an open-loop set-up when the control input is the negative of the disturbance, the maximum deflection will reduce. The reduction depends on the scaling of the control action. The design of the controller also needs to consider the saturation limits on the voltage input to the actuator.

Fig. 3
figure 3

Block diagram of the simplified system, only two modes considered in this representation

Full size image

In the numerical case considered here, a control function that follows only the first disturbance force \({f}_{\mathrm{d}1}\), proportional to the first mode \({\psi }_{1}\left(vt\right)\), is shown to improve the response of the open-loop system both in displacement and in velocity. It is also possible to use tuning methods to add a compensator to the system.

An open-loop control architecture can be a feasible solution, and it was shown in numerical examples [18] that for simple structures it can provide solutions when the problem is formulated as terminal time optimal control, but it has a couple of known disadvantages when it comes to practical implementation. First of all, it requires information about the kinematics of the motion of the load, in particular the exact entry time and the moving speed. If this information is not precise and accurate, it may negatively affect the performance, although the numerical example used in this investigation showed to accommodate small speed variations. One other disadvantage is that it assumes the shape of the control input is known, which for the case of a more complex structure may require complex offline calculations.

In almost all the practical cases, a feedback control action is preferred. Due to the fact that the deflection response of the system is similar to the shape of the control used as input for the open-loop control (Fig. 3), the system is completed by closing the lower forward path in a loop feeding back the measured deflection output to the controller. The deflection signal, measured with laser sensors, contains a certain amount of noise, which can be modelled as a band-limited white noise.

Although the uncompensated closed-loop structural dynamic system is always stable, the addition of the dynamics of the actuator changes the characteristics of the response and reduces the stability margins. The stability problem can be also negatively affected by the high level of noise.

A direct output feedback, with no compensation, will reduce the damping in the system and increase the amplitude of the small oscillations in the system, which becomes a problem for the multi-span structure. Depending on the value of the feedback gain, the system operates at small stability margins. In order to improve the response and increase the stability margins, the system is compensated by adding proportional and derivative compensation (Fig. 4). The system response can be simulated in Simulink, and the tuning of the compensators can be achieved interactively using Control System Designer App. For reduced-order models, a state-feedback numerical solution for a linear regulator with an objective quadratic in deflection and control effort can be obtained. The tuning tasks for the deflection feedback design can be formulated in time or frequency using the response of the linear regulator as the target.

Fig. 4
figure 4

Compensated displacement feedback response

Full size image

The response of the system modelled as a continuous system is improved and also shows a good reduction of the level of noise. For a real zero (\(-{K}_{\mathrm{P}}/{K}_{\mathrm{D}}\)) positioned closer to the origin than the actuator’s pole, the stability margins of the system are improved. The architecture based on dSpace and Simulink cannot realise directly the controller shown in Fig. 4. In this case, a pole is added further away on the real axis and the compensator structures becomes: \(({K}_{\mathrm{D}}s+{K}_{\mathrm{P}})/(1+0.001s)\). The closed-loop system shows a good reduction of deflection, comparable with the deflection obtained using state-feedback design and is able to deal with sensor noise (Fig. 5).

Fig. 5
figure 5

Deflection response of the non-controlled system (continuous blue line), closed-loop deflection feedback (dotted green line) and closed-loop state-feedback control (LQR) (dashed yellow line). (Color figure online)

Full size image

When the system is under the action of a set of loads with different speeds \({v}_{j}\) and different masses \({m}_{j}\), the amplitude and the frequency of the equivalent load need to be changed to \({f}_{\mathrm{d}i}={A}_{j}\mathrm{sin}(i{\omega }_{j}t)\), where \({A}_{j}={m}_{j}\mathrm{g}\)/\(m\mathrm{g}\) is given a set of values between 0.6 and 1.3, and \({\omega }_{j}={v}_{j}/L\) lies between 3 and 6 rad/s. The amplitude of the deflection response shows certain variation.

In order to strengthen the effect of the control when the mass is heavier, a nonlinear control action is considered.

The control action \(u\left(t\right)\) is proportional to \({w}^{3}({x}_{\mathrm{s}},t)\), and the set-up uses a similar compensation to the case of linear control action. The effect of the controller reduces the variation in the response for heavier loads but has a weaker action when the amplitude of the response is smaller (Fig. 6).

Fig. 6
figure 6

Responses under closed-loop control action: linear (continuous blue line), nonlinear (dotted green line) displacement feedback as shown in the legend. (Color figure online)

Full size image

Numerically the performance of the systems can be compared with the performance of a linear quadratic regulator (Fig. 7).

Fig. 7
figure 7

Comparison of linear quadratic control and deflection feedback control, blue continuous line—linear quadratic control, green dotted line—linear deflection feedback, orange dashed line—cubic deflection feedback. (Color figure online)

Full size image

From this simplified model, it can be seen that the effect of the actuator impacts on the stability margins of the closed-loop system; therefore, a direct deflection feedback cannot be used. The controller architecture needs tuning and additional compensation.

In the case of the multiple span beam structure, this method can apply under the assumption that the effect of a controller applied at one span has little effect on the adjacent spans. The case of a multi-span beam requires further attention as the position of the actuators and sensors, which influences the position of the zeros of the system, can affect the stability margins of the structural system even if the dynamics of the actuator is ignored.

The same principles can apply for this case but due to the complexity of the structure in order to keep the stability margins of the systems within reasonable values supplementary compensation is added on the forward path. The addition of a lead compensator in the forward path increases the stability margins. The response of the linear displacement feedback shows that in the case of a single-span structure an improvement on the deflection response (Fig. 8). The controller can tolerate sensor noise. For the simulation shown in Fig. 8, 5% noise was added to the feedback loop.

Fig. 8
figure 8

Compensated deflection feedback for a four-span beam, dotted green line—without control, continuous blue line—with control, a deflection at first span, b deflection at the second span. (Color figure online)

Full size image

The comparison between the nonlinear (cubic) feedback and the linear feedback is shown in Fig. 9. The structure is subjected to a set of moving loads with different entry times.

Fig. 9
figure 9

Comparison between linear (continuous green line) and nonlinear (dotted blue line) deflection feedback; a first spans, b second span of the structure. (Color figure online)

Full size image

The response of the structure follows the same pattern for the case of a single-span structure. The cubic deflection control works better at high amplitudes, but the linear feedback has a higher capacity to reduce low-level amplitude values.

A variability study run for a set of random loads with random constant speeds shows that the performance of the controller using linear deflection feedback is comparable with the performance of the linear quadratic controller (Fig. 10). For the nonlinear feedback controller, the variability of the deflection response is lower. The pattern shown in Fig. 10b repeats for the third and fourth spans of the structure.

Fig. 10
figure 10

Variability plot of the deflection response for system with no control action (no control), linear deflection feedback (LinF), cubic deflection feedback (nonLF) and equivalent linear quadratic regulator (LQR); a first span, b second span

Full size image

The values of the random constant speeds show no correlation to the maximum deflection response (Fig. 11a, b, c), but the values of the loads show a strong correlation with the response (Fig. 11d, e, f).

Fig. 11
figure 11

Correlation between the speed and maximum deflection (a, b, c) and moving load and maximum deflection (d, e, f) for system with no control action (a, d), linear deflection feedback (b, e) and cubic deflection feedback (c, f)

Full size image

The numerical values used for the simplified models reflect the structural parameters of the laboratory structure. Numerical simulation showed that a controller based on negative deflection feedback can improve the response of the system to the action of the moving loads, but due to poor stability margins it cannot be applied directly. It also showed that in the case of a structure with multiple spans, the control gains need to change at different spans, with a lower gain for the first span.

4 Numerical and experimental results

The system equations in state-space form are solved using MATLAB. The analog-to-digital conversion, processing and digital-to-analog conversion for the experimental data are implemented using a dSpace 1104 R&D controller board.

The measured signals \(w({x}_{\mathrm{s}i},t)\) collected by the laser sensors located at coordinates \({x}_{\mathrm{s}i}\) along the beam are low-pass-filtered and scaled to millimetres. Due to the simplified model of the actuator and the high signal-to-noise ratio, the controller shows a higher tendency to destabilise the system.

In order to strengthen the effect of the feedback and the spread of the controller gain values, at higher deflection, the cubic dependence of the displacement is also tested. For an objective function formulated in terms of maximum deflection value, a nonlinear control action is expected to improve the performance as it strengthens the control action for heavier moving loads as compared with a linear displacement feedback action.

4.1 Structural model validation

The validity of the numerical model of the structure under the action of the moving carriages when the actuators are switched off can be verified by comparing numerically calculated deflection values \(w\left({x}_{\mathrm{s}i},t\right)\) at sensor locations and experimentally measured values. Figure 12 shows a comparison between the numerical and the experimental data for the case when two carriages are travelling along the beam. The numerical values of the two masses used for the numerical model are: \({m}_{1}\) = 5.1 kg and \({m}_{2}\) = 5.1 kg. The carriages are launched with initial speeds estimated at \({v}_{10}\) = 1.28 m/s and \({v}_{20}\) = 1.29 m/s. The time delay is estimated at 2.88 s.

Fig. 12
figure 12

Time history of beam’s deflection at the four sensor locations for two masses moving along the beam, no control action, blue solid line—numeric, green dotted line—experimental data. (Color figure online)

Full size image

The predicted deflections follow closely the experimentally measured time histories, but the later have additional high-frequency oscillations, which cannot be captured by the model. It can be also seen that the deflection at the first sensor is about 20% higher than the deflection at the location of the other three sensors.

4.2 Structural active control model validation

The numerical model for the dynamics of the carriage–structure interaction when the linear displacement feedback controller’s action is used is compared in Fig. 13 with the experimentally obtained data.

Fig. 13
figure 13

Time history of the deflection at sensor location for two masses moving along the beam, linear feedback control, blue solid line—numeric, green dotted line—experimental data. (Color figure online)

Full size image

The numerical values used for the two masses are the same as for the example studied before. The initial moving speeds of the two carriages in this example are estimated at: \({v}_{10}\) = 1.22 m/s and \({v}_{20}\) = 1.12 m/s, and the time delay between the launches is 2.22 s. The only noticeable discrepancies between the simulated and experimentally measured data are a small overshoot of the former, which appears when a carriage moves from one span to another (Fig. 13). The recorded maximum values for deflection are about − 0.8 mm for the first span and − 0.6 mm for the rest of the beam.

4.3 Experimental assessment of the control action

A comparison between the experimentally measured deflections at sensor coordinates for the controlled and uncontrolled structure is shown in Fig. 14. The two carriages are launched at slightly different initial velocity values.

Fig. 14
figure 14

Time history of deflection response at sensor positions for experimentally determined data (a, b, c, d), minimum values of the measured deflections in mm (e), dotted green line—controlled system, continuous blue line—no control. (Color figure online)

Full size image

The uncontrolled structure has greater values in both the maximum deflection and the overshoot when the mass passes by one of the beam’s supports. These are both significantly reduced when the structure is controlled.

The maximum values of the deflection are shown in Fig. 14e, and it can be seen that the highest value of the deflection occurs at the first span. After the first span, the maximum deflection decreases, and it becomes almost constant. A higher value for the first span is also observed for the case when only one carriage travels along the beam.

On average, the reduction in absolute values of the maximum deflection obtained is 33% for the first span and then increases to over 37% (Fig. 14e).

The control effort estimated using the force measured at the actuator positions (\({f}_{\mathrm{a}i}\)) is shown in Fig. 15. The force measured for the case when the structure is not controlled (blue line) shows only the reaction of the beam. When the structure is under control action, the shaker produces an additional force filtered by its own dynamics proportional to the deflection and opposing it.

Fig. 15
figure 15

Time history of experimentally measured actuator forces (a, b, c, d), maximum force in N (e); dotted green line—controlled system; continuous blue line—no control. (Color figure online)

Full size image

The maximum values of this extra force are estimated and used to assess the control effort. Figure 15e shows that the maximum force occurs at the last span. This is also the case when the beam is under the action of only one carriage.

The relative differences between the deflection responses and forces at the four locations for the two states of the system (control and no control) are shown in Table 1.

Table 1 Relative difference for deflection at sensor’s positions and force at actuator position for two carriages launched along the beam
Full size table

All these results are similar to the case when only one mass of 5.1 kg travels along the beam. The relative differences between the case when the structure is not controlled and controlled are shown in Table 2.

Table 2 Relative difference between controlled and uncontrolled structural response for one carriage launched along the beam (5.1 kg)
Full size table
Table 3 Relative differences between deflection at sensor positions and between forces at actuators position for one carriage launched along the beam (9.5 kg)
Full size table

For these tests, it can be seen that in both cases there is an average deflection reduction of about 40% except for the first span where this falls to about 30%. The recorded force shows an increase of about 40% for all the spans except the third where the force increase to about 50% but with no significant effect on the deflection. The signal from the controller is amplified by a DataPhysics PA30E Power Amplifier before being sent to the modal shaker. Although the amplifier’s potentiometer is manually set in the same position for all the channels, it is possible that small amplification gain variations may occur.

To get a better insight into how the controller’s effect is affected by moving speed and mass variability, a carriage with different loads is launched at random initial speeds along the beam. For a launching speed varying between 1.11 and 1.46 m/s and a mass variation between 5.2 and 5.9 kg, the maximum deflection values and maximum force values are represented in Fig. 16.

Fig. 16
figure 16

Variability of deflection response at sensor’s position (a, b) and force at shakers’ position (c, d) at the four spans for one carriage launched along the beam with different loads and initial conditions. (Color figure online)

Full size image

The observed trends for the deflection response with higher values at the first span remain, but the controller’s action shows a more robust performance as the variability in the deflection response reduces (Fig. 16b). From the force variation boxplots (Fig. 16c, d), it can be seen that the controller contribution (assessed by the difference between the forces at shaker’s positions measured for the non-controlled and controlled systems) for the first span is only about 6–7 N, whereas for the rest of the spans this increases to about 10 N.

Increasing the mass of the moving structure changes slightly the patterns observed in Fig. 16. For a mass varying between 9.5 and 10.98 kg moving at speeds varying between 0.9 and 1.33 m/s, the variability observed in the response increases. The absolute value of the maximum deflection increases on average by about one mm. The same change of patterns is true for the relative differences between the responses of the controlled and uncontrolled structure (Table 3).

4.4 Nonlinear control action

In order to obtain a better robustness of the response, a cubic dependence on the deflection (22) is tested. For the theoretical model, cubic dependence of the deflection increases the control action for larger displacements but has a smaller influence on the small deflection range.

For the experimental tests run with masses over 9 kg, the nonlinear control action improves the maximum deflection response and the robustness of the deflection performance. Figure 17 shows the variability of the response for a mass variation between 9.5 and 11 kg for the three cases considered: no control, linear displacement control and nonlinear (cubic) displacement control.

Fig. 17
figure 17

Variability of deflection at sensor’s position (a, b, c) and force at shakers’ position (d, e, f) at the four spans for one carriage travelling along the beam with different loads and initial velocities. (Color figure online)

Full size image

For an increase in the moving load mass to 15.5 kg, the actuators reach saturation and the linear model does no longer give an accurate response.

5 Conclusions

This paper addresses the problem of active vibration control of a multi-span structure under the action of multiple moving carriages both from a numerical and from an experimental perspective. The background of this problem includes industrial applications as single-lane bridge–vehicle dynamic interaction and is concerned with the mitigation of excessive deflection levels under heavy traffic.

The assumptions that the supporting structure can be modelled as a Euler–Bernoulli beam and the carriages as moving masses prove accurate for this investigation. Two displacement feedback methods for vibration control of this four-span beam are studied. The objective of the control is to reduce the maximum deflection of the structure under the action of the loads. The first of the methods scales and applies the feedback output from the displacement sensors to the dynamic actuators. The second method uses a cubic displacement signal. The experimental application of both methods requires the addition of a compensator to the system. The design and tuning of the compensation were achieved using a simplified model.

These two methods are extensively investigated numerically and experimentally. It is shown by numerical simulation validated by experimental tests on a small-scale stand that both methods can effectively reduce the vibration response of the structure under moving masses and that the active control implementation based on laser deflection sensors and modal shakers provides an effective method for reducing the maximum deflections at given locations for low and medium masses acting on the structure. Moreover, the nonlinear (cubic) displacement feedback affords a better control action for high deflection.

Some of the practical aspects that need to be taken into account when the method is implemented experimentally are pointed out. The electromagnetic actuation supplies a reasonably fast and a large magnitude response force but is less efficient when the mass of the moving loads increases. The stability margin of the system does not allow the necessary increase in the control gain. This limits the effectiveness of the solution for high values of the moving mass, which would simulate the action of very heavy vehicles. On the other hand, the deflection signals measured by laser sensors show a poor signal-to-noise ratio.