A vehicle–track beam matching index in EMS maglev transportation system

Abstract

In order to study the stability and bifurcation of the EMS maglev transportation system, an index that can evaluate the matching degree between the EMS vehicle and track beam is proposed. The coupling system is simplified reasonably and the ordinary differential equations model of EMS basic levitation unit and track beam coupling system is established based on the interaction principle between vehicle and track beam. The bifurcation characteristics of the model equilibrium point with two key parameters of the track beam are calculated by theoretical analysis and numerical simulation. The Lyapunov coefficient of the bifurcation points is calculated to determine which Hopf bifurcation occurred. The Hopf bifurcation diagram of the coupling system with two key parameters of the track beam is drawn, respectively, and the stability of the model equilibrium point under different parameters and the size of its convergence range are determined. An index of matching degree between the parameters of EMS maglev vehicle and track beam is defined by the ratio between the size of the stability region and the static deflection of the track beam.

1 Introduction

With the development of the national economy, China’s urban traffic is increasingly congested, and the development of urban rail transit is an effective way to improve this situation [1]. Electromagnetic levitation system (EMS) maglev train, due to its low noise, non-contact operation, and strong climbing ability, has attracted much attention in recent years [2]. Shanghai high-speed maglev operation line, Changsha medium–low-speed maglev express line, Beijing medium–low-speed maglev line S1 and the Incheon Airport line in South Korea all use the EMS maglev transportation system.

However, it should be pointed out that there are still some problems that hinder its engineering application. For instance, the vehicle–track coupling dynamic effect significantly affects the running stability and construction cost of a maglev transportation system. The vehicle–track coupling vibration is particularly serious during stationary state or low-speed operation, which may lead to the instability of the levitation system [3]. The track beam of the EMS maglev usually adopts the elevated mode, and its flexibility is the main cause of the self-excited vibration of the vehicle–track system [4, 5], which has a significant influence on the levitation stability [6, 7].

Aiming at the dynamic coupling effect of a maglev vehicle and track beam, many experts have carried out studies from the perspectives of electromagnetics, multi-body system dynamics, and control system. Liang [8] systematically expounded the characteristics of magnet-track relationship and the influence of control system parameters on the vibration of the maglev vehicle. Zhao [9, 10] simplified the vehicle into a mass model of five rigid body and 10 degrees of freedom and equated the electromagnetic force with the linear spring-damping force to establish a vehicle–track beam coupled vibration model of high-speed maglev. Zou [11] used the double-loop PID algorithm to study the vibration phenomenon in the vehicle–track coupled maglev system, coming to the conclusion that the homoclinic bifurcation, Hopf bifurcation, secondary Hopf bifurcation, and chaos in the system are the root causes of the vibration of the maglev system. Wang [12, 13] studied the influence of the delay of the control system on the stability of the maglev system, analyzed the 1:3 subharmonic resonance response at the equilibrium point under the joint action of positional time delay and track disturbance, and pointed out that the time delay parameters can not only suppress the subharmonic response, but also control the generation of chaos. Zhang [14] calculated the periodic solution caused by Hopf bifurcation using the center manifold and normal form theory as well as the perturbation method of pseudo-oscillator analysis, respectively, and verified its validity by numerical simulation. Li [15] used Nyquist stability criterion, Routh table, and root locus map to obtain the stability conditions of the vehicle–track beam coupled system in static levitation state; Kim [16, 17] conducted a coupled numerical calculation based on a complete three-dimensional vehicle–track beam model and compared it with the experimental results to prove the validity of the model. Liu [18] established a dynamics model of a single levitation frame in low-speed maglev train with four independent closed-loop control, and simulated and analyzed the coupling effect of the levitation frame. Wang [19] designed a state observer to introduce the vibration state of the electromagnet, track beam, and car body into the control system and used the linear matrix inequality method to solve the state feedback gain matrix, which shows a better performance. Li [20] compiled the simulation analysis software VTBIM for the vehicle–track beam coupling vibration in medium–low-speed maglev and verified the validity of the model through the comparison between the simulation and test results.

The above-mentioned researches have achieved a lot of meaningful results and have a good effect on guiding the engineering practice of building an EMS maglev transportation system. However, the coupling vibration mechanism between the EMS maglev train and the track beam has not been fully explained. In order to avoid the coupling vibration, the measure taken in engineering application is to increase the stiffness of track beam as much as possible. This not only increased the engineering cost greatly, but also failed to eliminate the coupling vibration completely. Therefore, in order to provide intuitive and reliable guidance for engineering applications, it is urgent to put forward a quantitative index to evaluate the matching relationship of EMS maglev transportation system.

The instability caused by self-excited vibration also exists in the traditional railway system, and Hopf bifurcation theory is widely used to explain this phenomenon [21,22,23]. Literature [24,25,26] analyzed the critical speed of the wheelset or bogie when the hunting occurred by Hurwitz determinant or root locus method, respectively, and the central manifold theorem is adopted to reduce the dimension of the system under the critical speed, then the bifurcation form of the wheelset or bogie has been analyzed, and its periodic solution also has been calculated, so as to clarify the factors which may affect the hunting phenomenon. The coupling vibration of the EMS maglev train is similar to the hunting phenomenon of traditional railway vehicles. With the variation of the parameters of control system or track beam, the stability of the equilibrium point of the coupling system formed by the maglev train and the track beam will change, this is also the fundamental reason for the coupling vibration between the maglev train and the track beam. So it is necessary to explain this phenomenon with Hopf bifurcation theory.

In recent years, Hopf bifurcation and codimension-two bifurcation theory have been widely applied in the study of traditional railways, while there are not many applications on the maglev transportation system. Considering that the analysis of high-dimensional system is complex and difficult in the traditional Hopf bifurcation analysis, Kuznetsov [27] proposed a projection technology to simplify the process of Hopf bifurcation analysis of high-dimensional system. And the projection technology has also been applied in this paper.

Based on the researches above, this paper established the ordinary differential equations (ODEs) model of the basic levitation unit and the track beam of the EMS maglev transportation system, and the stability has been analyzed by bifurcation theory. A matching index that can fully reflect the comprehensive performance of vehicle and track beam system has been proposed.

2 Model of the system and differential equation of the motion

The EMS maglev transportation system is suitable for both high-speed as well as medium–low-speed design, and the track beam adopts a simply supported beam structure. Taking the medium–low-speed maglev as an example, the body of a maglev vehicle is generally supported by 3–5 levitation frames through air springs. Each levitation frame consists of two levitation modules distributed on both sides of the track, connected by anti-roll beams and suspenders. Each levitation module contains four electromagnet coils, with two of them connected in series as a group and forming a basic levitation unit together with a levitation controller and a sensor. Figure 1 shows a schematic diagram showing the relative positional relationship between the vehicle and the track beam. The 3D model of the medium–low-speed maglev bogie is shown in Fig. 2.

Fig. 1

Relative positional relationship between vehicle and track beam

Fig. 2

3D model of the medium–low-speed maglev bogie

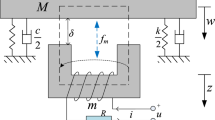
As each basic levitation unit can be approximated as an independent control upon decoupling of the levitation frame, the system can be simplified into a coupled dynamics model of a basic levitation unit and a flexible track beam, as shown in Fig. 3.

Fig. 3

Dynamics model of coupling of a basic levitation unit and track beam

In the figure, m is the mass of the levitation frame carried by a levitation unit, M is the mass of the vehicle body carried by a levitation unit, $w\textit{(t)}$ is the deflection of the track beam, $z_{1}(t)$ and $z_{2}(t)$ are the vertical displacement of the levitation frame and car body, respectively, $k_{s}$ and $c_{s}$ are the secondary levitation stiffness and damping of a levitation unit, F is the electromagnetic force of a coil, A is the area of the electromagnet plate corresponding to one coil, N is the number of the coil turns, and R is the coil resistance, with one levitation unit containing two coils. The electromagnet plate is opposite to the F-shaped track plate. The levitation control system controls the voltage $u\textit{(t)}$ across the coil to change the coil current $i\textit{(t)}$, thereby changing the electromagnetic attractive force $F\textit{(i, c)}$ to achieve the stability of levitation gap $c \textit{(t)}$. The electromagnetic force $F\textit{(i, c)}$ is a function of coil current and the levitation gap and is given by:

$$\begin{aligned} F(i,c)=\frac{\mu _0 N^{2}A}{4}\left( {\frac{i}{c}} \right) ^{2} \end{aligned}$$

(1)

where $\mu _0$ is the permeability in vacuum.

The coil current is driven by a control voltage that simultaneously drives two magnetic coils. According to Kirchhoff’s law, the relationship between coil current and control voltage can be written as:

$$\begin{aligned} \frac{u}{2}=iR+L_0 \dot{i}-k_L \dot{c}, \end{aligned}$$

(2)

where the coefficient $L_0 =\frac{\mu _0 N^{2}A}{2c}$, $k_L =\frac{\mu _0 N^{2}Ai}{2c^{2}}$.

The equation of mechanical system dynamics is given by

$$\begin{aligned} \left\{ {\begin{array}{l} {m {\ddot{z}}_{1} + c_{s}({\dot{z}_{1} - \dot{z}_{2} }) + k_{s} ( {z_{1} - z_{2} }) = - 2F +({m + M})g} \\ {M{\ddot{z}}_{2} - c_{s} ({\dot{z}_{1} - \dot{z}_{2} }) - k_{s}({z_{1} - z_{2} }) = 0} \\ \end{array}} \right. \end{aligned}$$

(3)

where g is the acceleration of gravity, and the zero points $z_1$ and $z_2$ are in the static equilibrium position.

Since the levitation system is unstable when there is no feedback, it is necessary to have feedback control on the current, so as to have feedback on the deviation of the levitation gap and the vibration speed. The levitation gap can be directly measured by the sensor, and the vibration speed needs to be obtained through state reconstruction of the signals received from the gap sensor and the acceleration sensor mounted on the electromagnet. The state observer can be obtained by the Luenberger observer theory [28]. To design the observer, the following system is established:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{Y}}=A_0 Y + B_0 \ddot{z}_1 \\ Z=C_0 Y\\ \end{array}}} \right. \end{aligned}$$

(4)

Where, $Y=\left[ {{\begin{array}{l} {c-c_0 } \\ {\dot{c}} \\ \end{array} }} \right]$, $A_0 =\left[ {{\begin{array}{ll} 0&{}\quad 1 \\ 0&{}\quad 0 \\ \end{array} }} \right]$, $B_0 =\left[ {{\begin{array}{ll} 0 \\ 1 \\ \end{array} }} \right]$, $C_0 =\left[ {{\begin{array}{ll} 1&{}\quad 0 \\ \end{array} }} \right]$.

It is easy to know that $\left[ {{\begin{array}{ll} {C_0 }&{} {A_0 } \\ \end{array} }} \right]$ can be observed, so the observer can be designed as follows:

$$\begin{aligned} \dot{Y}_0 =A_0 Y_0 +B_0 \ddot{z}_1 + L(Z-C_0 Y_0) \end{aligned}$$

(5)

where $Y_0 =\left[ {{\begin{array}{ll} {y_1 }&{} {y_2 } \\ \end{array} }} \right] ^{T}$; L is the observer coefficient vector. The system poles can be distributed in the left half-plane of the complex plane by selecting a reasonable value of L, so that $Y_0$ can converge to Y. The observer is shown in Eq. (6) after taking $L=\left[ {{\begin{array}{ll} {2\xi _0 \omega _0 }&{} {\omega _0 ^{2}} \\ \end{array} }} \right] ^{T}$ into Eq. (5).

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{y}_{1} = y_{2} + 2\xi _{0} \omega _{0} \left( {c - c_{0} - y_{1} } \right) } \\ {\dot{y}_{2} = \ddot{z}_{1} + \omega _{0} ^{2} \left( {c - c_{0} - y_{1} } \right) ~~~~~} \\ \end{array} } \right. \end{aligned}$$

(6)

where $c_0$ is the rated levitation gap, $\xi _0$ and $\omega _0$ are the observer coefficients, $y_2$ is the vibration velocity signal obtained by the observer, and $y_1$ is the filtered gap deviation signal obtained by the observer.

The coil current feedback is needed in the levitation control to speed up the system response due to the inductance of electromagnet coils. The feedback system is divided into two feedback loops, the inner loop and the outer loop. The outer loop obtains the target current through gap feedback information and transmits it to the inner loop. The inner loop adjusts the voltage according to the difference between the target current and the actual current of the coil, so as to accelerate the response of the system. The target levitation current of outer loop can be expressed as:

$$\begin{aligned} i_e =k_P y_1 +k_D y_2 +i_0 \end{aligned}$$

(7)

where $k_P$ and $k_D$ are state feedback coefficients, $i_0$ is the stable levitation current, and $i_0 =\frac{c_0 }{N}\sqrt{\frac{2\left( {m+M} \right) g}{\mu _0 A}}$.

$$\begin{aligned} \hbox {The voltage calculated by the inner loop can be expressed as: }u=k_e (i_e -i)+2Ri \end{aligned}$$

(8)

where $k_e$ is the current feedback coefficient.

The current equation of controller and electromagnet can be obtained by taking Eqs. (7) and (8) into Eq. (2).

$$\begin{aligned} \dot{i} = \frac{i}{c}\dot{c} + \frac{{k_{e} c}}{{\mu _{0} N^{2} A}}\left( {k_{P} y_{1} + k_{D} y_{2} - i + i_{0} } \right) \end{aligned}$$

(9)

According to the Euler–Bernoulli beam model, the track beam dynamics equation is given by

$$\begin{aligned} EI\frac{{\partial ^{4} W\left( {x,t} \right) }}{{\partial x^{4} }} + \bar{m}\frac{{\partial ^{2} W\left( {x,t} \right) }}{{\partial t^{2} }} + \bar{c}\frac{{\partial W\left( {x,t} \right) }}{{\partial t}} = P\left( {x,t} \right) , \end{aligned}$$

(10)

where $W\left( {x,t} \right)$ is the deflection of the beam at position x and time t, $P\left( {x,t} \right)$ is the load of the beam at position x and time t, EI is the bending stiffness of the beam, and $\bar{m}$ is the linear density of the beam and $\bar{c}$ is the damping coefficient of the beam.

The track beam of the medium–low-speed maglev transportation system mostly adopts a simply supported structure. According to the modal superposition theory, the deflection of the beam can be expressed as the product of the modal function and the modal coordinates:

$$\begin{aligned} W\left( {x,t} \right)= & {} \mathop \sum \nolimits _{n=1}^\infty q_n \left( t \right) \phi _n \left( x \right) \end{aligned}$$

(11)

$$\begin{aligned} M_{n} \ddot{q} _{n} + C_{n} \dot{q}_{n} + K_{n} q_{n}= & {} \mathop \smallint \limits _{0}^{L} \phi _{n} \left( x \right) P\left( {x,t} \right) {\mathrm{d}}x \end{aligned}$$

(12)

where $q_n \left( t \right)$ is the modal coordinate of order n ($n=1,2,3{\ldots }$) of the track beam, and $\phi _n \left( x \right)$ is the modal function of order n ($n=1,2,3{\ldots }$) of the track beam. The modal mass $M_n$, modal damping $C_n$, and modal stiffness $K_n$ are expressed as: $M_n =\frac{L}{2}\bar{m}$, $C_n =\frac{L}{2}\times 2\xi _n \bar{m}\omega _n$, $K_n =\frac{L}{2}\frac{n^{4}\pi ^{4}}{L^{4}}EI$. L is the length of the track beam, $\xi _n$ is the damping ratio of order n ($n=1,2,3{\ldots }$), $\omega _n$ is the circular frequency of order n ($n=1,2,3{\ldots }$), and $\omega _n =\frac{n^{2}\pi ^{2}}{L^{2}}\sqrt{\frac{EI}{\bar{m}}}$.

Since the electromagnets supporting the vehicle are approximately continuous, as shown in Fig. 1, the self-excited vibration is most likely to occur when the vehicle is levitated in the middle part of the track beam. Neglecting the correlation between the electromagnetic force and the longitudinal position of the electromagnet, it can be obtained that

$$\begin{aligned} \mathop \smallint \limits _0^L \phi _n \left( x \right) P\left( {x,t} \right) \mathrm{d}x= & {} \mathop \int \limits _{\frac{L-l}{2}}^{\frac{L+l}{2}} \phi _n \left( x \right) \mathrm{d}x\cdot \frac{1}{l}p\left( t \right) \end{aligned}$$

(13)

$$\begin{aligned} w_n \left( t \right)= & {} \mathop \int \limits _{\frac{L-l}{2}}^{\frac{L+l}{2}} \phi _n \left( x \right) \mathrm{d}x\cdot \frac{1}{l}q_n \left( t \right) , \end{aligned}$$

(14)

where l is the length of the vehicle, $p\left( t \right)$ is the total levitation force of the vehicle, $w_n \left( t \right)$ is the average deflection corresponding to the nth order, and the modal function is $\phi _n \left( x \right) =\hbox {sin}\left( {\frac{n\pi x}{L}} \right)$.

Since the high-order modal of the track beam has a large damping ratio but has little contribution to the deflection, it is suitable to consider only the first-order modal of the track beam. It is proved by engineering practices that almost all self-excited vibration problems are caused by the instability of the first-order modal of the bridge [15], so the effect of higher-order modals is ignored in the paper when there is no special explanation.

Substitute Eqs. (13) and (14) into Eq.(12), and make the equivalent deflection of the track beam $w=w_1$, the dynamics equation of the track beam corresponding to a basic levitation unit is:

$$\begin{aligned} \ddot{w} + \xi _{1} \omega _{1} \dot{w} + \omega _{1} ^{2} w = \sigma \left[ {2F - \left( {m + M} \right) g} \right] , \end{aligned}$$

(15)

where $\omega _1$ and $\xi _1$ are the first-order modal frequency and damping ratio of the track beam, $\sigma$ is the gain coefficient of the force of the vehicle acting on the track beam, and $\sigma =\frac{8kL}{\pi ^{2}l^{2}\bar{m}}\hbox {sin}^{2}\frac{\pi l}{2L}$. k is the number of basic levitation units included in the medium–low-speed maglev vehicles.

In conclusion, Eq. (3) represents the motion of the vehicle system, Eq. (15) represents the flexibility of the track beam, Eq. (10) represents the levitation control system and the change of the coil current, and Eq. (6) represents the state observer. Combined with all the equations mentioned above, the ordinary differential equations describing the motion of a medium–low-speed maglev system can be obtained. The state vector is set as $x = \left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} ,x_{7} ,x_{8} ,x_{9} } \right] ^{T} = \left[ {z_{1} ,\dot{z}_{1} ,z_{2} ,\dot{z}_{2} ,w,\dot{w},i - i_{0} ,y_{1} ,y_{2} - \dot{z}_{1} } \right] ^{T}$, and the levitation gap $c=x_1 -x_5 +c_0$. The ODEs model of the levitation unit and track beam is presented as follows.

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_{1} = x_{2} \\ \dot{x}_{2} = - \frac{{\mu _{0} N^{2} A}}{{2m}}\left( {\frac{{x_{7} + i_{0} }}{{x_{1} - x_{5} + c_{0} }}} \right) ^{2} + \frac{{M + m}}{m}g - \frac{{c_{s} }}{m}\left( {x_{2} - x_{4} } \right) - \frac{{k_{s} }}{m}\left( {x_{1} - x_{3} } \right) \\ \dot{x}_{3} = x_{4} \\ \dot{x}_{4} = \frac{{c_{s} }}{M}\left( {x_{2} - x_{4} } \right) + \frac{{k_{s} }}{M}\left( {x_{1} - x_{3} } \right) \\ \dot{x}_{5} = x_{6} \\ \dot{x}_{6} = - \omega _{1} ^{2} x_{5} - 2\xi _{1} \omega _{1} x_{6} + \sigma \left[ {\frac{{\mu _{0} N^{2} A}}{2}\left( {\frac{{x_{7} + i_{0} }}{{x_{1} - x_{5} + c_{0} }}} \right) ^{2} - \left( {m + M} \right) g} \right] \\ \dot{x}_{7} = \frac{{x_{7} + i_{0} }}{{x_{1} - x_{5} + c_{0} }}\left( {x_{2} - x_{6} } \right) + \frac{k_e (x_{1}-x_5 +c_0)}{\mu _0 N^2 A}[k_p x_8 + k_D (x_9 +x_2)-x_7] \\ \dot{x}_{8} = x_{9} + x_{2} + 2\xi _{0} \omega _{0} \left( {x_{1} - x_{5} - x_{8} } \right) \\ \dot{x}_{9} = \omega _{0} ^{2} \left( {x_{1} - x_{5} - x_{8} } \right) \end{array}}\right. \end{aligned}$$

(16)

3 Bifurcation analysis of ODEs model

In this paper, the influence of the parameters of track beam on levitation stability is discussed. There are three parameters in the ODEs model of the levitation unit and track beam which described in Eq. (16.), the first-order modal frequency $\omega _1$, the first-order modal damping ratio $\xi _1$ and the gain coefficient of the force $\sigma$. Considering that the variation range of the first-order modal damping ratio $\xi _1$ is very small in practical application, the first-order modal frequency $\omega _1$ and the gain coefficient of the force $\sigma$ of the track beam are selected as the bifurcation parameters, with $\alpha =\left[ {\omega _1 ,\sigma } \right] ^{T}$. The ODE model (16) can be written in a more compact form: $\dot{x}=J(\alpha )x+F_{\mathrm{non}}(x,\alpha )$, where J is the Jacobian matrix of the model, $F_{\mathrm {non}} \left( {x,\alpha } \right)$ is the nonlinear part of the model. Obviously, $x=0$ is a steady-state solution of the system. To calculate the degradation normal form, the center manifold reduction method is usually used to simplify the complex high-dimensional system into the corresponding planar system, and then transform it into an equivalent planar normal form through homeomorphic mapping. As these methods are very complex and difficult to program for the theoretical and numerical analysis of high-dimensional systems, the projection technique is used here, and the center manifold reduction and normalization are adopted simultaneously [27].

Assuming that when $\alpha =\alpha _c =\left[ {\omega _{1c} ,\sigma _c } \right]$, the Jacobian matrix of the ODEs model (16) has one and only one pair of pure imaginary eigenvalue $\lambda _{1,2} =\pm {i}\omega _c$ and $\omega _c >0$, and the remaining eigenvalues all have negative real parts. Expand the ODEs model (16) near $\hbox {x}=0$ and get $\dot{x}=J_c x+ F_{\mathrm{non}}(x,\alpha _c)$, where $J_c =J\left( {\alpha _c } \right)$ is the Jacobian matrix of the Hopf bifurcation point and $F_{\mathrm {non}} \left( {x,\alpha _c } \right) =O(||x||^{2})$ is sufficiently smooth near the equilibrium point. Expanding the nonlinear part with symmetric multi-linear vector functions, we obtain

$$\begin{aligned} F_{\mathrm {non}} \left( x \right) =\frac{1}{2}B\left( {x,x} \right) +\frac{1}{6}C\left( {x,x,x} \right) +O(||x||^{4}) \end{aligned}$$

(17)

where $B\left( {\xi ,\eta } \right)$ and $C\left( {\xi ,\eta ,\zeta } \right)$ are symmetric multi-linear vector functions of $\xi ,\eta ,\zeta \in {\mathbb {C}}^{9}$ and can be expressed as

$$\begin{aligned} B_i \left( {\xi ,\eta } \right)= & {} \mathop \sum \limits _{j,k=1}^9 \frac{\partial ^{2}F_{\mathrm {noni}} \left( {x,\alpha _c } \right) }{\partial x_j \partial x_k }|_{x=0} \xi _j \eta _k , i=1,\ldots ,9, \end{aligned}$$

(18)

$$\begin{aligned} C_i \left( {\xi ,\eta ,\zeta } \right)= & {} \mathop \sum \limits _{j,k,l=1}^9 \frac{\partial ^{3}F_{\mathrm {noni}} \left( {x,\alpha _c } \right) }{\partial x_j \partial x_k \partial x_l }|_{x=0} \xi _j \eta _k \zeta _l , i=1,\ldots ,9. \end{aligned}$$

(19)

Introducing two complex eigenvectors $p_c$ and $q_c$ corresponding to pure imaginary eigenvalues, we obtain

$$\begin{aligned} J_c q_c ={i}\omega _c q_c , J_c ^{T}p_c =-{i}\omega _c p_c, \end{aligned}$$

(20)

It is required to satisfy the normalization condition $\langle p_c ,q_c \rangle =1$, where $\langle p,q\rangle$ is the inner product function of $p,q\in {\mathbb {C}}^{9}$, which is defined as $\langle p,q\rangle =\mathop \sum \nolimits _{i=1}^9 \bar{p}_i q_i \in {\mathbb {C}}^1$.

$J_{c}$ corresponds to the eigenvalue subspace of $q_c$ and $\bar{q}_c$ as $T^{c}=span\left\{ {\hbox {Re}\left( {q_c } \right) ,\hbox {Im}\left( {q_c } \right) } \right\}$. If $T^{s}$ is the eigenvalue subspace corresponding to other eigenvalues of $J_{\mathrm{c}}$, then there is $T^{s}=\{y|y\in {\mathbb {R}}^{9},\langle p_c ,y\rangle =0\}$, and the state space $x\in {\mathbb {R}}^{9}$ can be decomposed into

$$\begin{aligned} x = zq_{c} + \bar{z}\bar{q}_{c} + y,~~zq_{c} + \bar{z}\bar{q}_{c} \in T^{c} ,{{~~}}y \in T^{s} \end{aligned}$$

(21)

and then

$$\begin{aligned} \left\{ {\begin{array}{l} {z=\langle p_c ,x\rangle } \\ {y=x-\langle p_c ,x \rangle q_c -\langle {\bar{p}}_c ,x \rangle \bar{q}_c} \\ \end{array} } \right. \end{aligned}$$

(22)

In the coordinates (z, y), the ODEs model is written as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z} = i\omega _{c} z + \langle p_{c} ,F_{{non}} ({zq_{c} + \bar{z}\bar{q}_{c} + y})\rangle \\ \dot{y} = J_{c} y + F_{{non}} ({zq_{c} + \bar{z}\bar{q}_{c} + y}) - \langle p_{c} ,F_{{non}}({zq_{c} + \bar{z}\bar{q}_{c} + y})\rangle q_c \\ - \langle \bar{p}_{c} ,F_{{non}}({zq_{c} + \bar{z}\bar{q}_{c} + y})\rangle \bar{q}_{c} \\ \end{array}\right. \end{aligned}$$

(23)

Substituting the equation (17) into (23), and using the center manifold reduction and Poincaré canonical theory, the first Lyapunov coefficient of the ODEs model at the Hopf bifurcation point can be obtained, and then the type of Hopf bifurcation of the system is determined accordingly. The first Lyapunov coefficient is [22]

$$\begin{aligned} l_{1} ( {\alpha _{c} })= & {} \frac{1}{{2\omega _{c} }}Re[\langle p_{c} ,C( {q_{c} ,q_{c} ,\bar{q}_{c} })\rangle - 2\langle p_{c} ,B( {q_{c} ,J_{c} ^{{ - 1}} B( {q_{c} ,\bar{q}_{c} })} )\rangle \nonumber \\&+\, \langle p_{c} ,B( {\bar{q}_{c} ,( {2i\omega _{c} I - J_{c} })^{{ - 1}} B( {q_{c} ,q_{c} })})\rangle ] \end{aligned}$$

(24)

If $l_{1}(\alpha _c ) < 0$, the system generates supercritical Hopf bifurcation at the bifurcation point, and the stable equilibrium point loses stability, with a stable limit cycle split. If $l_{1}(\alpha _c )> 0$, then the system generates subcritical Hopf bifurcation at the bifurcation point, and an unstable limit cycle merges with the stable equilibrium point to become an unstable equilibrium point. If $l_{1}(\alpha _c ) = 0$, the system has a codimension-two bifurcation, and the second Lyapunov coefficient $l_{2}(\alpha _c )$ of the system needs to be calculated to determine the type of bifurcation. If $l_{2}(\alpha _c ) \ne$ 0 and the crossing condition is satisfied, Bautin bifurcation will occur. However, in actual engineering, the condition of $l_{1}(\alpha _c ) = 0$ is too harsh to meet, and there is little engineering significance in considering the characteristics of codimension-two bifurcation, so the corresponding calculation process is no longer given.

Since the ODE model (16) is a nine-dimensional system, it is necessary to combine numerical analysis with the theoretical analysis. According to the parameters described in “Appendix”, the Hopf bifurcation point of the model can be obtained through the root locus method by monitoring the maximum value of the real part of the eigenvalue of the Jacobian matrix $J_{c}$. At the same time, the crossing condition can also be monitored. Combining the root locus method with equation (24), the variation law of the first Lyapunov coefficient with $\omega _1$ and $\sigma$ can be obtained, and the type of bifurcation can be determined at the same time.

Figure 4 shows the variation of the bifurcation point in the parameter space $span\left\{ {\omega _1 ,\sigma } \right\}$ and gives the type of bifurcation.

Fig. 4

Codimension-two bifurcation diagram of the ODEs model

The parameter space shown in Fig. 4 is divided into two parts, the region S and the region U, by the bifurcation curve. The eigenvalues of the Jacobian matrix $J( {\alpha ^{S}})$ of the ODEs model at the equilibrium point $x=0$ have a negative real part in the region S, while the ODEs model in the region U has at least one pair of conjugate complex eigenvalues with positive real parts at the Jacobian matrix $J( {\alpha ^{U}})$ at the equilibrium point $\hbox {x}=0$. The boundary between the region S and the region U is the curve composed of Hopf bifurcation points. The ODEs model has a pair of pure imaginary eigenvalues at the Jacobian matrix $J({\alpha ^{C}})$ at the equilibrium point $x=0$, and the remaining eigenvalues all have negative real parts. The boundary is divided into four parts. On the boundaries I and III, the first Lyapunov coefficient, $l_{1}(\alpha _c )> 0$, is the subcritical Hopf bifurcation point, and on the boundary II and IV, the first Lyapunov coefficient, $l_{1}(\alpha _c )< 0$, is the supercritical Hopf bifurcation point. The three junctions a, b, and c between the boundaries I, II, III, and IV are the codimension-two bifurcation points. (Each refers to the non-tangential change of the parameters, that is, when the direction of the parameter changes satisfies the crossing condition.)

4 The vehicle–track beam matching index

Figure 4 can be used to determine the topological variation of the solution near the equilibrium point of the system. However, in order to propose an index reflecting the matching between the vehicle and the track beam of the EMS maglev transportation system, so as to guide the engineering practice, it is not enough to just examine the local characteristics of the solution near the equilibrium point, The convergence range of the equilibrium point also needs to be analyzed. A matching index can be defined as the ratio of the index of the convergence range of the equilibrium point to the index of a typical disturbance. In this section, the characteristic indexes of the convergence ranges of a system equilibrium point and a typical disturbance will be defined, so that to define the matching index of a vehicle and a track beam of EMS maglev transportation system through their ratio.

In order to define the characteristic index of the convergence range of the equilibrium point of the coupling system, the periodic solutions near the equilibrium point need to be analyzed. The orthogonal collocation method and Newton–Raphson iterative method are adopted to track the evolution of the periodic solution and the steady-state solution, and the eigenvalues of the Jacobian matrix at the equilibrium point and the Floquet multipliers of the Poincaré map near the periodic solution are detected, as they represent the stability information of the equilibrium point and the limit cycle, respectively.

The range of the values of the EMS maglev traffic in real projects determines that the gain coefficient $\sigma$ of the force of the vehicle acting on the track beam is about $2\sim 6\times 10^{-4}$, and the first-order modal frequency of the track beam is about $6\sim 30\hbox {Hz}$, that is, the range of $\omega _1$ is $40\sim 190$ rad/s. Figure 5 shows the Hopf bifurcation diagram of the medium–low-speed maglev traffic system with the change of $\omega _1$ and $\sigma$, where the dashed line indicates unstable equilibrium point or limit cycle, the solid line indicates the stable equilibrium point or limit cycle, and the dot–dash line indicates the physical limit of the levitation gap. When the limit is reached, the collision will occur. The symbols * and o represent the Hopf bifurcation point and the amplitude at which the unstable limit is tangent to the physical limit, respectively. It is worth noting that due to the physical limits of the maglev transportation system, the completely smooth ODEs model (15) does not describe the global behavior of the system. Thus, the model (15) needs to be corrected as follows:

• (1) Since the coil current is not reversible, its minimum value is 0 A, that is, when $x_7 <-i_0$, $x_7$ in the model (15) takes the value $-i_0$;

• (2) Since the levitation gap range is $0\sim 18\hbox { mm}$, the calculation is stopped when $x_1 -x_5 <-c_0$ or $x_1 -x_5 >18\hbox { mm}-c_0$.

Fig. 5

Hopf bifurcation diagram of the system with the change of $\omega _1$ and $\sigma$: a$\sigma =4\times 10^{-4}$ and b$\omega _1 =100\hbox { rad}/s$

Figure 5 shows that the subcritical Hopf bifurcation occurs in the medium–low-speed maglev traffic system at Hopf bifurcation points $\hbox {A}_{1}$ and $\hbox {A}_{2}$. As the parameters change, an unstable limit cycle and a stable equilibrium point merge into an unstable equilibrium point, which is consistent with the results of the theoretical analysis. $\hbox {b}_{1}$ and $\hbox {b}_{2}$ are the gap amplitudes when the unstable limit cycle is tangent to the physical limit of the gap. Due to the asymmetrical nature of the electromagnetic force, the amplitudes corresponding to the $\hbox {b}_{1}$ and $\hbox {b}_{2}$ points are not equal. When $\omega _1 =100\hbox { rad}/s$, the tangent value $\sigma$ of the unstable limit cycle and the physical limit of the gap is about $0.7 \times 10^{-4}$, which is much smaller than the value $\sigma$ allowed by the system parameters that may appear in the real engineering projects, thus the value is not shown in Fig. 5b.

In order to better understand the global topological characteristics of the medium–low-speed maglev transportation system near the bifurcation point, three sets of parameter values: $\alpha _1 =\left[ {100\hbox { rad}/\hbox {s},4\times 10^{-4}} \right] ^{\mathrm {T}}$, $\alpha _2 =\left[ {105\hbox { rad}/\hbox {s},5\times 10^{-4}} \right] ^{\mathrm {T}}$ and $\alpha _3 =\left[ {85\hbox { rad}/\hbox {s},3.7\times 10^{-4}} \right] ^{\mathrm {T}}$ are selected for numerical integration. A non-stiff differential equation solver (the standard NDSolve function in MATHEMATICA) is used for the numerical integration. The system response is shown in Figs. 6, 7 and 8.

Fig. 6

System response when the parameter takes the value $\alpha _1$: a time history curve and b phase diagram

Figure 6 shows the system response when the parameter takes the value $\alpha _1 =[{100\hbox { rad}/\hbox {s},4\times 10^{-4}}]^{\mathrm {T}}$. Two different initial values are selected for numerical integration, where the initial value of the blue solid line is $x_0 =[0,0,0,0, {x}_{50} ,0,0,0,0]^{\mathrm{T}} =[0,0,0,0,-0.0015\hbox { m},0,0,0,0]^{\mathrm{T}}$ and the system vibration converges, while the initial value of the red dashed line is $x_0 =[0,0,0,0,x_{50} ,0,0,0,0]^{\mathrm{T}} =[0,0,0,0,-0.0022\hbox { m},0,0,0,0]^{\mathrm{T}}$ and the system vibration diverges and collides at approximately 1.62s. The black dotted line is the physical limit of the gap. It is worth noting that, since it is a nine-dimensional system, the phase diagram shown in Fig. 6b is only the projection of the system phase space on the two-dimensional plane formed by the two-state variables of the gap and the gap differential, resulting in the visual intersection of the curves. In a complete nine-dimensional phase space, there is no intersection of the curves.

Fig. 7

System response when the parameter takes the value $\alpha _2$: a time history curve and b phase diagram

Figure 7 shows the system response when the parameter takes the value $\alpha _2 =\left[ {105\hbox { rad}/\hbox {s},5\times 10^{-4}} \right] ^{\mathrm {T}}$. When the initial value $x_0 =[0,0,0,0,x_{50} ,0,0,0,0]^{\mathrm{T}} =[0,0,0,0,-0.0001\hbox { m},0,0,0,0]^{\mathrm{T}}$ is selected for numerical integration, the system vibration diverges and collides at about 1.16 s.

Fig. 8

System response when the parameter takes the value $\alpha _3$: a time history curve and b phase diagram

Figure 8 shows the system response when the parameter takes the value $\alpha _3 =\left[ {85\hbox { rad}/\hbox {s},3.7\times 10^{-4}} \right] ^{\mathrm {T}}$. Two different initial values are selected for numerical integration, where the initial value of the blue solid line is $x_0 =[0,0,0,0,x_{50} ,0,0,0,0]^{\mathrm{T}} =[0,0,0,0,-0.004\hbox { m},0,0,0,0]^{\mathrm{T}}$ and the system vibration converges, while the initial value of the red dashed line is $x_0 =[0,0,0,0,x_{50} ,0,0,0,0]^{\mathrm{T}} =[0,0,0,0,-0.0046\hbox { m},0,0,0,0]^{\mathrm{T}}$, and the system vibrations converges if the physical limits of the gap is not taken into consideration, but due to the existence of physical limits, collisions occur before convergence.

The three sets of parameter values represent three typical cases of the structure of the solution of the ODEs model of the levitation unit and track beam. When the parameter takes the value $\alpha _1$, due to the existence of the unstable limit cycle, the system vibration converges without disturbance when the initial value is within the convergence domain of the equilibrium point, whereas the system diverges without disturbance when the parameter is beyond the convergence domain. When the parameter takes the value $\alpha _2$, due to the instability of the equilibrium point, the system diverges without disturbance, as long as the initial value is not exactly at the equilibrium point. When the parameter takes the value $\alpha _3$, the system converges as long as the initial value does not make collision occur. Thus, the structure of the solution of the ODEs model of the levitation unit and track beam can be used to define the index h of the convergence range of an equilibrium point. If the system equilibrium point is unstable, then $h= 0$; if the equilibrium point is stable and there is an unstable limit cycle, then h is the difference between the maximum value of the levitation gap corresponding to the limit cycle and the rated levitation gap $c_0$; if the equilibrium point is stable, and there is no unstable limit cycle or the limit cycle is beyond the physical limit of the system, then h is the difference between the maximum gap allowed by the physical limit of the system and the rated levitation gap $c_0$.

In order to define the stability index of an EMS coupling system, it is necessary to define a typical characteristic index of the initial disturbance. Here, the equivalent static deflection w0 of the track beam in the corresponding simplified OEDs model of the coupling system between the basic levitation unit and the track beam is adopted when the vehicle is levitated in the middle section of the track beam, it can be obtained from Eq. (15):

$$\begin{aligned} w_0 =\frac{\sigma \left( {m+M} \right) g}{\omega _1 ^{2}} \end{aligned}$$

(25)

The matching index of EMS maglev vehicle and track beam can be defined as the ratio of the convergence range of the equilibrium point h to the characteristic index of a typical initial disturbance $w_0$, just as shown in Eq. (26).:

$$\begin{aligned} \chi =\frac{h}{w_0 } \end{aligned}$$

(26)

In general, if $\chi =0$, the medium–low-speed maglev system cannot achieve stabilized static levitation, indicating the poor matching between the vehicle and the track beam; if the value of $\chi$ is very small, the maglev system can achieve stabilized static levitation under minor disturbances, but loses stability with slightly larger disturbance, indicating poor matching between the vehicle and the track beam; if the value of $\chi$ is relatively large, the maglev system can achieve stabilized static levitation under small disturbances, and only loses stability under major disturbance, indicating good matching between the vehicle and the track beam; if the value of $\chi$ is very large, the maglev system can still have stabilized static levitation under large disturbance, and may collide when it is greatly disturbed, but it is able to return to stabilized state quickly, indicating the best matching between the vehicle and the track beam.

5 A numerical example of the matching index

In order to explain the calculation method of the matching index of EMS maglev vehicle and track beam, a coupled dynamics model of a complete maglev vehicle and track beam is established as a numerical example, a medium–low-speed maglev vehicle with three levitation frames statically levitated in the middle of the simply supported track beam, as shown in Fig. 1.

The form of the vehicle system is shown in Fig. 9. It consists of three levitation frames and a car body with four rigid bodies. Each rigid body has two degrees of freedom which are vertical motion and pitching motion, and the model has a total of eight degrees of freedom. $m_{\mathrm{b}}$, $j_{\mathrm{b}}$, $m_{\mathrm{s}}$, $j_{\mathrm{s}}$ are the mass and moment of inertia of the vehicle and the levitation frame, respectively. The levitation frame and the car body are connected by a secondary levitation composed of a linear spring and damping. $k_{2}$ and $c_{2}$ are the secondary levitation stiffness and damping of the system, respectively. The rigid body of the levitation frame is subjected to two levitation forces. s is half of the distance between the force centers of the levitation forces, $s_{0}$ is the center-to-center distance between two levitation frames, and $f_{1 }\sim f_{6}$ are the electromagnetic forces.

Fig. 9

The form of the vehicle system model

Vehicle system dynamics equations can be obtained by vibration mechanics and expressed as:

$$\begin{aligned} M_\mathrm{v} \ddot{x} _\mathrm{v} +C_\mathrm{v} \dot{x}_\mathrm{v} +K_\mathrm{v} x_\mathrm{v} =f_\mathrm{v}, \end{aligned}$$

(27)

where the state vector is $x_{\mathrm{v}} =\left[ {z_1 \left( t \right) ,\theta _1 \left( t \right) ,z_2 \left( t \right) ,\theta _2 \left( t \right) ,z_3 \left( t \right) ,\theta _3 \left( t \right) ,z_0 \left( t \right) ,\theta _0 \left( t \right) } \right] ^{\mathrm {T}}$, $z_{\mathrm{i}} \left( t \right) ,\theta _{\mathrm{i}} \left( t \right) ,i=0,1,2,3$ are the floating and sinking, nodding coordinates of the car body and the levitation frame, respectively, the mass matrix is $M_{\mathrm{v}} =diag\left( {m_{\mathrm{s}} ,j_{\mathrm{s}} ,m_{\mathrm{s}} ,j_{\mathrm{s}} ,m_{\mathrm{s}} ,j_{\mathrm{s}} ,m_{\mathrm{b}} ,j_{\mathrm{b}} } \right)$,

$$\begin{aligned}&\hbox {the damping matrix is }C_{\mathrm{v}} =\left[ {{\begin{array}{llllllll} {c_2 }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {-c_2 }&{}\quad {c_2 s_0 } \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {c_2 }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {-c_2 }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {c_2 }&{}\quad 0&{}\quad {-c_2 }&{}\quad {-c_2 s_0 } \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ {-c_2 }&{}\quad 0&{}\quad {-c_2 }&{}\quad 0&{}\quad {-c_2 }&{}\quad 0&{}\quad {3c_2 }&{}\quad 0 \\ {c_2 s_0 }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {-c_2 s_0 }&{}\quad 0&{}\quad 0&{}\quad {2c_2 s_0^2 } \\ \end{array} }} \right] , \\&\hbox {the stiffness matrix is }K_{\mathrm{v}} =\left[ {{\begin{array}{llllllll} {k_2 }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {-k_2 }&{}\quad {k_2 s_0 } \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {k_2 }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {-k_2 }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {k_2 }&{}\quad 0&{}\quad {-k_2 }&{}\quad {-k_2 s_0 } \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ {-k_2 }&{}\quad 0&{}\quad {-k_2 }&{}\quad 0&{}\quad {-k_2 }&{}\quad 0&{}\quad {3k_2 }&{}\quad 0 \\ {k_2 s_0 }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {-k_2 s_0 }&{}\quad 0&{}\quad 0&{}\quad {2k_2 s_0^2 } \\ \end{array} }} \right] \end{aligned}$$

and the force vector is $f_{\mathrm{v}} =[ {-f_1 -f_2 ,s( {f_1 -f_2 }),-f_3 -f_4 ,s( {f_3 -f_4 }),-f_5 -f_6 ,s( {f_5 -f_6 }),0,0}]^{\mathrm {T}}$.

The model of the electromagnetic levitation system is the same as that described in Chapter 2. It is worth noting that each electromagnetic levitation force in the model equals the electromagnetic force of the four electromagnetic coils minus the vehicle gravity supported by the coils.

$$\begin{aligned} f_j =4F({i_j ,c_j })-\left( {\frac{1}{2}m_s +\frac{1}{6}m_b } \right) \end{aligned}$$

(28)

where $i_j$ and $c_j$ are currents and gaps corresponding to the $\hbox {j}$th basic levitation unit.

The model of the track beam is shown in Fig. 10. $f_{1}\sim f_{6}$, s and $s_{0 }$ are the same as Fig. 9, and L is the length of the track beam.

Fig. 10

Forces acting on the track beam

The dynamics equation of the track beam, with the first, second, and third-order modals taken, can be given by

$$\begin{aligned} \ddot{q}_{n} + \xi _{n} \omega _{n} \dot{q}_{n} + \omega _{n} ^{2} q_{n}= & {} \frac{2}{{\bar{m}L}}\mathop \sum \limits _{{j = 1}}^{6} \left[ {f_{j} + \left( {\frac{1}{2}m_{s} + \frac{1}{6}m_{b} } \right) } \right] {\text {sin}}\left( {\frac{{n\pi x_{j} }}{L}} \right) ,n = 1,2,3,\nonumber \\ W_{j} \left( t \right)= & {} \mathop \sum \limits _{{n = 1}}^{3} q_{n} \left( t \right) \phi _{n} \left( {x_{j} } \right) , \end{aligned}$$

(29)

where $x_j$ is the position of $f_j$ on the track beam, and $W_j$ is the deflection of the track beam corresponding to the electromagnetic force $f_j$. Equation (29) shows that the equilibrium point of the track beam equation is not at the original point.

The simulation platform is MATHEMATICA, which is an algebraic system software, and a non-stiff differential equation solver (the standard NDSolve function) is used for the numerical integration.

If the turnout beam of a certain medium–low-speed maglev is 18 m simply supported steel structural beam, the linear density is $\bar{m}=1920\hbox { kg/m}$, and the bending stiffness $EI=2.26\times 10^{10}\hbox { N}\cdot \hbox {m}^{2}$, the first three modal frequency can be calculated at 16.63 Hz, 66.53 Hz, 149.7 Hz, that is, $\omega _1 =104.51\hbox { rad/s}$, $\omega _2 =418.04\hbox { rad/s}$, $\omega _3 =940.591\hbox { rad/s}$. The total length of the vehicle is l2.1 m, and the whole vehicle contains 12 basic levitation units, then the gain coefficient of the force of the vehicle acting on the track beam is $\sigma =\frac{8kL}{\pi ^{2}l^{2}\bar{m}}\hbox {sin}^{2}\frac{\pi l}{2L}=4.7\times 10^{-4}$. The equilibrium point of the basic levitation unit system is unstable, and the matching index $\chi =0$. As long as the initial value of the system is not exactly equal to the equilibrium point, the system is diverged. As shown in Fig. 11, the lines are the levitation gaps corresponding to the first, second and basic levitation units, respectively. The initial state is that the vehicle is pressed downward from the free position of the track beam, the track beam deflects under pressure, and the initial value of each state is 0.

Fig. 11

Gap response of the vehicle when statically levitated on the turnover beam

Fig. 12

Unstable limit cycle of the system after reducing the bending stiffness

If the bending stiffness of the track beam is reduced, and it is set that $EI=1.96\times 10^{10}\hbox { N}\cdot \hbox {m}^{2}$, the first, second and third-order modal frequencies of track beams can be calculated as 15.49 Hz, 61.96 Hz, 139.41 Hz, that is, $\omega _1 =97.33\hbox { rad/s}$, $\omega _2 =389.307\hbox { rad/s}$, $\omega _3 =875.941\hbox { rad/s}$. At this time, the static deflection of the track beam of the basic levitation unit system is $w_0 =\frac{\sigma \left( {m+M} \right) g}{\omega _1 ^{2}}=0.826\hbox { mm}$. The unstable limit cycle is shown in Fig. 12, where $h = 3.43\hbox { mm}$, and the matching index $\chi =\frac{h}{w_0 }=4.15$. When the initial value is small, the system converges. When the initial value is large, the system diverges and the system has good nonlinear stability. Figure 13 shows the response of the levitation gap corresponding to the first, second, and third basic levitation units with different initial disturbances, respectively. Vehicle (a) is pressed downward from the free position of the track beam, the track beam deflects under pressure, and the initial value of each state is 0, while vehicle (b) is pressed downward from the free position of the track beam, the track beam deflects under pressure, and the initial value of each state is 0 except for $q_1$, which has the initial value of 3 mm.

Fig. 13

Response of the levitation gap after reducing the bending stiffness: a$q_1 \left( 0 \right) =0$ and b$q_1 \left( 0 \right) =3\hbox { mm}$

It can be seen that greater bending stiffness of the track beam does not necessarily make the system perform better, because a greater bending stiffness leads to a higher main frequency of the track beam, which means worse performance near the bifurcation point. Sometimes a slight decrease in the stiffness of the track beam contributes to better system performance.

6 Conclusion

In this paper, the nonlinear dynamics characteristics of the EMS maglev system are studied in detail. The nonlinear coupled dynamics model consisting of the basic levitation unit and flexible track beam of the vehicle under static levitation conditions is established, and the degree of freedom of the system is reduced without losing the basic characteristics. Through analysis of the ODEs model of the levitation unit and track beam, the following conclusions are drawn:

• (1) Through the bifurcation analysis of the nonlinear coupled model, it is determined that under certain bifurcation parameters, Hopf bifurcation and codimension-two bifurcation occur in the medium–low-speed maglev system; by calculating the first Lyapunov coefficient of the bifurcation point, the type of bifurcation is determined and the codimension-two bifurcation diagram obtained, and it is concluded that the bifurcation of the system is subcritical Hopf bifurcation under the possible parameters of engineering practice.

• (2) In order to determine the stable range of equilibrium point and the existence and stability of periodic solutions of the system of the levitation unit and track beam, the Hopf bifurcation diagram of the system with the change of the track beam parameters is drawn under the possible parameters in engineering practice, and the size of the unstable limit loops of the system under different parameters is determined. The parameter domain is decomposed into three regions according to the difference of the global topological structure of the solutions, and the different characteristics of the three regional solutions are obtained through numerical integration.

• (3) A matching index of EMS maglev transportation system is defined. And the matching index can be defined as the ratio of the convergence range of the equilibrium point to the characteristic index of a typical initial disturbance. Finally, an example is given to illustrate the calculation method of the index.

Appendix: Description and value of parameters in EMS maglev system

Parameter	Description	Value
m	Mass of the levitation frame carried by a levitation unit	550 kg
M	Mass of the vehicle body carried by a levitation unit	1150 kg
g	Acceleration of gravity	$9.8\hbox { m/s}^{2}$
$k_{s}$	Secondary levitation stiffness of a levitation unit	12,000 N/m
$c_{s}$	Secondary levitation damping of a levitation unit	900 N s/m
${{\mu }} _{0}$	Permeability in vacuum	${4}{{\pi }} \times {10}^{-{ 7}}$ T m/A
N	Number of the coil turns of the electromagnet	360
A	Area of the electromagnet plate corresponding to one electromagnetic coil	$0.0184\hbox { m}^{2}$
$c_{0}$	Rated levitation gap	8 mm
$i_{0}$	Stable levitation current	26.68 A
${{\omega }} _{0}$	State observer coefficient 1	130
${{\xi }} _{0}$	State observer coefficient 2	2
$k_{P}$	Gap feedback coefficient	5000
$k_{D}$	Velocity feedback coefficient	150
$k_{e}$	Current feedback coefficient	25
${{\omega }} _{1}$	The first-order modal frequency of the track beam	–
${{\xi }} _{1}$	The first-order modal damping ratio of the track beam	0.5%
${{\sigma }}$	Gain coefficient of the force of the vehicle acting on the track beam	–
$m_{s}$	Mass of the levitation frame	2200 kg
$j_{s}$	Moment of inertia of the levitation frame	$1377\hbox { kg m}^{2}$
$m_{b}$	Mass of the vehicle	13,800 kg
$j_{b}$	Moment of inertia of the vehicle	$159{,}365\hbox { kg m}^{2}$
$k_{2}$	Secondary levitation stiffness	48,000 N/m
$c_{2}$	Secondary levitation damping	3600 N s/m