1 Introduction

The rotor-bearing systems are widely used in rotating equipment such as aero-engine, gas turbines, etc., the physical parameters of the rotor-bearing system directly affect the responses of the rotating machine [1]. In such rotating machinery, bolted joints are widely employed to connect adjacent disks to make multiple parts into an integrated one, and achieve high stiffness [2, 3]. In the previous studies on dynamic analysis of the rotor-bearing system, finite element simulation and mathematical modeling combined with experimental research are commonly used [4, 5]. For example, Zeng et al. [6] and Eryilmaz et al. [7] studied the effects of structural parameters on rotor dynamics by using the nonlinear finite element simulation method. However, due to the time-consuming problems, many scholars prefer to use a mathematical model [8, 9]. As for the rotor systems with bolted joints, Luo et al. [10] derived the mathematical model of the bolted disk-disk joint to study the effect of bolted joint parameters on critical speed. Sun et al. [11] established a dynamic model of the drum-disk-shaft system, where the assembly relationship at the mating surface is considered. Wang et al. [12] derived the dynamic model of a rod fastening rotor-bearing system based on the D’Alembert principle, in which the contact interface is modeled through a nonlinear stiffness spring. Liu et al. [13] established the finite element model of a rod-fastening rotor-bearing system to study the effect of pre-tightening force on motion stability. The modeling approaches applied in the above researches are based on physical characteristics, which are referred to as physical models.

The mathematical model is fundamental in engineering design, simulation, and analysis, which can be used to reveal information about the dynamic characteristics of the system. The mathematical model can be cataloged into two types [14]. One way, called the physical model, which can be very complex in the modeling process. An alternative approach that only depends on the data is referred to as system identification [15, 16]. System identification is an approach of identifying the dynamic systems from the input and output signals, which is developed from control theory and has become a useful tool applied to the modeling and analysis of a wide range of real nonlinear systems [17, 18]. There are extensively published papers on dynamic system modeling based on system identification techniques, including Nonlinear Auto-Regressive with exogenous (NARX methods), which is focused on in this article. The NARX models have been successfully used to represent nonlinear systems and dynamic behavior analysis [19,20,21]. There have been a lot of researches on the analysis and design in combination with the NARX model. Peng et al. [22] established the mathematical model of aluminum plate based on the NARX model, and then a fault diagnosis is carried out. AraújoT et al. [23] constructed the representation model of the Quanser Server Base Unit, the relationship between the voltage applied to the motor and position was successfully established. Besides, the NARX models based modeling method has also been applied in scenarios such as steel plate identification [24] and modeling of global magnetic disturbance in near-earth space [25]. These suggest that NARX model-based dynamic modeling is a topic worthy of further study.

In the above researches, however, the identified model cannot provide insight into the effect of physical parameters on system response [26]. Therefore, the focus was with more of an emphasis on parameter-dependent Common Model Structure (CMS) detection over recent years. The NARX model with parameters of interest for design provides an effective solution to this issue, where the physical parameters appear as coefficients explicitly. This model is also known as the dynamic parametrical model [27]. The critical tasks in the identification of the dynamic parametrical model include detecting the CMS, estimating the associated coefficients, and establishing the function of the coefficients of the model with respect to the physical parameter [14]. To obtain the CMS, Wei et al. [26] proposed the Extended Forward Orthogonal Regression (EFOR) algorithm, and the average approximate minimum description length criterion is introduced to determine the number of model terms used for representing the underlying system.

Although the NARX model-based dynamic parametrical model identification is an attractive approach, however, it has difficulties in aerospace applications [28]. This is because the input signal used for system identification has to be Gaussian white noise signal, which is a restriction for the sinusoidal excitation structures, such as the rotor-bearing system. Although the foregoing works provide insight into the modeling process and specific algorithm for the identification of nonlinear systems, few reports, according to the authors’ knowledge, has been found on the NARX model-based dynamic parametrical model identification for a rotor-bearing system. To solve the aforementioned problem, in our previous work [29], a new modeling method that applies a multi-harmonic signal generated through the speed-up process to conduct system identification is proposed. This method successfully established the NARX models to reflect the output characteristics of the rotor-bearing system in the simulation and experiment. However, the models themselves are multi-model forms to cover the complete operating regime. In addition, Westwick et al. [30] applied a time-domain random odd multi-sine signal to identify a NARX model. The signal was obtained by splicing multiple sets of sinusoidal signals together, with each signal separated by 100 zeros, the proposed modeling method was similar to that in [29]. Zhang et al. [31] proposed a method using a NARX neural network to identify a gyro-stabilized platform, in which a swept-frequency signal was used as the driving signal. The swept-frequency signal was similar to that described in [29], which was obtained by splicing multiple sets of time-domain harmonic signals into a single set of signals.

From the above studies, it can be seen that a Gaussian white noise signal is needed in the traditional modeling process of a dynamic parametrical model. However, rotating machinery is a typical sinusoidal loading structure, and Gaussian white noise cannot be generated in the normal operation of such structure. In order to solve this issue, this study proposes a frequency sweep system identification method for NARX model-based dynamic parametrical model identification of rotating machinery. Compared with existing system identification methods that depend on time-domain signals to establish the dynamic parametrical model of nonlinear systems, the method proposed in this study is based on frequency-domain data. The corresponding frequency domain version modeling framework is derived in the paper, and the candidate model term dictionary composed of frequency-domain data is also introduced. The PRESS-based EFOR algorithm [32] is applied to obtain the CMS of the rotor system in this paper. A numerical case study is conducted based on a rotor-bearing system with a bolted joint structure. Finally, an experimental study is also carried out. These study cases are illustrated to demonstrate that the method proposed in this paper can gain a new and feasible method into dynamic parametrical modeling of the rotor system. The proposed method can overcome the difficultly of establishing a dynamic model of complex rotating machinery using traditional physical modeling methods. Moreover, as the model structure can be written down explicitly, it is convenient for the analysis and design of dynamic systems through the established dynamic parametrical model. For example, structural damage detection [22], design of nonlinear systems [27], and analysis of the effects of characteristic parameters [33]. This suggests that NARX model-based dynamic parametrical model identification is a topic worthy of further study.

The rest of the paper is organized as: A brief description of the traditional NARX model with a physical parameter and the novel frequency domain version modeling framework are presented in Sect. 2. The identification process which includes detecting the CMS, evaluate the coefficients, and model validation method is presented in Sect. 3. The identification of a rotor-bearing system with a bolted joint structure is presented in Sect. 4, including constructing the finite element model of the underlying system and system identification. Section 5 demonstrates the application of the proposed method on the rotor test rig. Finally, the conclusions are summarized in Sect. 6.

2 Modeling framework of the dynamic parametrical model for the rotor system

The frequency sweep dynamical parametrical system identification methodology proposed for the rotor-bearing system modeling and analysis is an identification procedure aiming at establishing a mathematical model from the harmonic input and associated output data. This section describes the novel frequency domain version modeling framework for the proposed method starting from the review of the conventional NARX model with a physical parameter.

2.1 Conventional modeling framework of the NARX model with a physical parameter

It has been reported that the CMS with the design parameter can be represented by [27]

$$\begin{aligned} y(t) & = F(y(t - 1), \ldots y(t - n_{y} ),u(t - 1), \ldots u(t - n_{u} ),{{\varvec{\uptheta}}}({{\varvec{\upxi}}})) \\ \;\;\;\;\;\; & = \theta_{0} ({{\varvec{\upxi}}}) + \sum\limits_{{i_{1} = 1}}^{n} {\theta_{{i_{1} }} ({{\varvec{\upxi}}})} + \cdots + \sum\limits_{{i_{1} = 1}}^{n} { \cdots \sum\limits_{{i_{l} = i_{l - 1} }}^{n} {\theta_{{i_{1} \cdots i_{l} }} ({{\varvec{\upxi}}})\prod\limits_{k = 1}^{l} {x_{{i_{k} }} (t)} } } \\ \end{aligned}$$
(1)

where \(F( \cdot )\) is the unknown polynomial function which needs to be identified; t represents the time instant;\(n_{u}\) and \(n_{y}\) are the maximum time delay of the system output \(y( \cdot )\) and input \(u( \cdot )\), respectively; \({{\varvec{\uptheta}}}({{\varvec{\upxi}}})\) is the coefficient matrix of the model (1), where ξ represents a vector composed of the physical parameter values, ξ = [ξ1, ξ2,…, ξS], the subscript S represents the number of parameter values; \(n = n_{u} + n_{y}\); l is the highest order of nonlinearity, and

$$x_{m} (t) = \left\{ {\begin{array}{*{20}l} {u(t - m),1 \le m \le n_{u} } \hfill \\ {y(t - (m - n_{u} )),n_{u} + 1 \le m \le n_{u} + n_{y} } \hfill \\ \end{array} } \right.$$
(2)

Assume that the input and output variables of a single-input and single-output system under K different design parameter values have been obtained, the nonlinear dynamic parametrical model with K different cases of parameter properties can be written into the following matrix form as:

$$\it \it \it {\mathbf{y}}_{k} = {\mathbf{P}}_{k} {{\varvec{\uptheta}}}_{k} ,k = 1, \ldots ,K$$
(3)

where \({\mathbf{y}}_{k}\) represents the vector contains system output \(y_{k} (t)\) corresponding to K physical parameter values; \({\mathbf{P}}_{k} { = [}p_{k,1} (t),p_{k,2} (t), \ldots ,p_{k,M} (t){]}\) are time-domain version model term dictionary composed of delayed system input and output variables; pk,m (t) represents the regressor formed by combinations of model terms chosen from [uk (t − 1),…, uk (t − nu), yk (t − 1),…, yk (t − ny)]; \({{\varvec{\uptheta}}}_{k} { = }[\theta_{k,1} ,\theta_{k,2} , \ldots ,\theta_{k,M} ]^{{\text{T}}}\) represents the coefficient vector corresponding to the kth physical parameter value; θk,m represents the model coefficients; M is the total number of potential model terms, \(M = (n + l)!/n!/l!\).

Remark 1

It is worth mentioning that when K = 1, model (1) and (3) are traditional NARX models [14]. The framework described in this section can be used to predict the system output associated with the kth physical parameter value, and make the difference with single-input and multiple-output scenarios.

2.2 A novel frequency-domain version modeling framework with physical parameter

Due to the lack of the random signal as input which is required in the dynamic parametrical model identification, for the rotor-bearing systems, the traditional method cannot be used. Therefore, a frequency sweep methodology is proposed, starting from characterizing the harmonic input and associated output signals according to the data in the frequency spectrum corresponding to the key harmonics. And then the associated frequency domain version modeling framework with a physical parameter can be deduced based on the time domain version modeling framework. The deriving process is described as follows.

According to Eq. (1) and the linear properties of the Discrete-Time Fourier Transform (DTFT), a frequency-domain version NARX model with physical parameter under rotating speed Ω1 can be written as:

$$\begin{aligned} Y^{{(\Omega_{1} )}} (j\omega ) & = \sum\limits_{{i_{1} = 1}}^{n} {\theta_{{i_{1} }} ({{\varvec{\upxi}}}) \times } {\text{DTFT[}}x_{{i_{1} }} (t)] + \cdots + \sum\limits_{{i_{1} = 1}}^{n} { \cdots \sum\limits_{{i_{l} = i_{l - 1} }}^{n} {\theta_{{i_{1} \cdots i_{l} }} ({{\varvec{\upxi}}}) \times {\text{DTFT[}}\prod\limits_{k = 1}^{l} {x_{{i_{k} }} (t)]} } } \\ \;\;\;\;\;\;\;\;\;\;\;\;\; & = \sum\limits_{{i_{1} = 1}}^{{N_{1} }} {\theta_{{i_{1} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{1} }}^{{(\Omega_{1} )}} (j\omega )} + \sum\limits_{{i_{2} = 1}}^{{N_{2} }} {\theta_{{i_{2} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{2} }}^{{(\Omega_{1} )}} (j\omega )} + \cdots + \sum\limits_{{i_{l} = 1}}^{{N_{l} }} {\theta_{{i_{l} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{l} }}^{{(\Omega_{1} )}} (j\omega )} \\ \end{aligned}$$
(4)

where \({\text{DTFT[}} \cdot {]}\) represent the Discrete-Time Fourier Transform, i.e., \(Y^{{(\Omega_{1} )}} (j\omega ) = {\text{DTFT[}}y^{{(\Omega_{1} )}} (t)]\); Ω is rotation speed; jω represents the harmonics; and

$$N_{l} = \frac{{\prod\limits_{i = 0}^{l - 1} {(n + i)} }}{l!}$$
(5)

Then, the frequency sweep process can then be described by the following:

$$\begin{aligned} Y^{{(\Omega_{1} )}} (j\omega ) & = \sum\limits_{{i_{1} = 1}}^{{N_{1} }} {\theta_{{i_{1} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{1} }}^{{(\Omega_{1} )}} (j\omega )} + \sum\limits_{{i_{2} = 1}}^{{N_{2} }} {\theta_{{i_{2} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{2} }}^{{(\Omega_{1} )}} (j\omega )} + \cdots + \sum\limits_{{i_{l} = 1}}^{{N_{l} }} {\theta_{{i_{l} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{l} }}^{{(\Omega_{1} )}} (j\omega )} \\ Y^{{(\Omega_{2} )}} (j\omega ) & = \sum\limits_{{i_{1} = 1}}^{{N_{1} }} {\theta_{{i_{1} }}^{{(\Omega_{2} )}} ({{\varvec{\upxi}}})P_{{i_{1} }}^{{(\Omega_{2} )}} (j\omega )} + \sum\limits_{{i_{2} = 1}}^{{N_{2} }} {\theta_{{i_{2} }}^{{(\Omega_{2} )}} ({{\varvec{\upxi}}})P_{{i_{2} }}^{{(\Omega_{2} )}} (j\omega )} + \cdots + \sum\limits_{{i_{l} = 1}}^{{N_{l} }} {\theta_{{i_{l} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{l} }}^{{(\Omega_{2} )}} (j\omega )} \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \cdots \\ Y^{{(\Omega_{p} )}} (j\omega ) & = \sum\limits_{{i_{1} = 1}}^{{N_{1} }} {\theta_{{i_{1} }}^{{(\Omega_{p} )}} ({{\varvec{\upxi}}})P_{{i_{1} }}^{{(\Omega_{p} )}} (j\omega )} + \sum\limits_{{i_{2} = 1}}^{{N_{2} }} {\theta_{{i_{2} }}^{{(\Omega_{p} )}} ({{\varvec{\upxi}}})P_{{i_{2} }}^{{(\Omega_{p} )}} (j\omega )} + \cdots + \sum\limits_{{i_{l} = 1}}^{{N_{l} }} {\theta_{{i_{l} }}^{{(\Omega_{p} )}} ({{\varvec{\upxi}}})P_{{i_{l} }}^{{(\Omega_{p} )}} (j\omega )} \\ \end{aligned}$$
(6)

where \(j\omega\) is the harmonics corresponding to the rotating speed \(\Omega_{{\text{s}}} \;(s = 1,2, \ldots ,p)\); P(Ωp) il(jω) represents the lth-order model term corresponding to Ωp.

By characterizing system input and output signals by the frequency domain data corresponding to first-order harmonics associated with the frequency sweep process, a general form of the modeling framework can be written as:

$$\begin{aligned} Y^{{(\Omega_{1} )}} (j{1}\omega_{{1}} ) & = \sum\limits_{{i_{1} = 1}}^{{N_{1} }} {\theta_{{i_{1} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{1} }}^{{(\Omega_{1} )}} (j{1}\omega_{{1}} )} + \sum\limits_{{i_{2} = 1}}^{{N_{2} }} {\theta_{{i_{2} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{2} }}^{{(\Omega_{1} )}} (j{1}\omega_{{1}} )} + \cdots + \sum\limits_{{i_{l} = 1}}^{{N_{l} }} {\theta_{{i_{l} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{l} }}^{{(\Omega_{1} )}} (j{1}\omega_{{1}} )} \\ Y^{{(\Omega_{2} )}} (j{1}\omega_{{2}} ) & = \sum\limits_{{i_{1} = 1}}^{{N_{1} }} {\theta_{{i_{1} }}^{{(\Omega_{2} )}} ({{\varvec{\upxi}}})P_{{i_{1} }}^{{(\Omega_{2} )}} (j{1}\omega_{{2}} )} + \sum\limits_{{i_{2} = 1}}^{{N_{2} }} {\theta_{{i_{2} }}^{{(\Omega_{2} )}} ({{\varvec{\upxi}}})P_{{i_{2} }}^{{(\Omega_{2} )}} (j{1}\omega_{{2}} )} + \cdots + \sum\limits_{{i_{l} = 1}}^{{N_{l} }} {\theta_{{i_{l} }}^{{(\Omega_{1} )}} ({{\varvec{\upxi}}})P_{{i_{l} }}^{{(\Omega_{2} )}} (j{1}\omega_{{2}} )} \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \cdots \\ Y^{{(\Omega_{p} )}} (j{1}\omega_{p} ) & = \sum\limits_{{i_{1} = 1}}^{{N_{1} }} {\theta_{{i_{1} }}^{{(\Omega_{p} )}} ({{\varvec{\upxi}}})P_{{i_{1} }}^{{(\Omega_{p} )}} (j{1}\omega_{p} )} + \sum\limits_{{i_{2} = 1}}^{{N_{2} }} {\theta_{{i_{2} }}^{{(\Omega_{p} )}} ({{\varvec{\upxi}}})P_{{i_{2} }}^{{(\Omega_{p} )}} (j{1}\omega_{p} )} + \cdots + \sum\limits_{{i_{l} = 1}}^{{N_{l} }} {\theta_{{i_{l} }}^{{(\Omega_{p} )}} ({{\varvec{\upxi}}})P_{{i_{l} }}^{{(\Omega_{p} )}} (j{1}\omega_{p} )} \\ \end{aligned}$$
(7)

where \(j1\omega_{s} \;(s = 1,2, \ldots ,p)\) represent the first-order harmonics corresponding to rotating speed \(\Omega_{s}\).

The frequency-domain version modeling framework of Eq. (7) can then be expressed as a matrix form as:

$${\tilde{\mathbf{Y}}}_{k} ={\tilde{\mathbf{P}}}_{k} {{\varvec{\uptheta}}}_{k} ,k = 1, \ldots ,K$$
(8)

where \({\tilde{\mathbf{Y}}}_{k}\) represent system output vector in the frequency domain, \({\tilde{\mathbf{Y}}}_{k} = [Y_{k}^{{(\Omega_{1} )}} (j{1}\omega_{1} )\;,Y_{k}^{{(\Omega_{2} )}} (j{1}\omega_{2} )\; \cdots \;\;Y_{k}^{{(\Omega_{l} )}} (j{1}\omega_{l} )]^{{\text{T}}}\), and \({\tilde{\mathbf{P}}}_{k}\) is the frequency-domain version candidate model term dictionary associated with the kth parameter values, where

$$\begin{aligned} {\tilde{\mathbf{P}}}_{k} & = [\begin{array}{*{20}c} {{\tilde{\mathbf{P}}}_{{k,i_{1} = 1}} (j1\omega )} & \cdots & {{\tilde{\mathbf{P}}}_{{k,i_{1} = N_{1} }} (j1\omega )} & {{\tilde{\mathbf{P}}}_{{k,i_{2} = 1}} (j1\omega )} & \cdots & {{\tilde{\mathbf{P}}}_{{k,i_{2} = N_{2} }} (j1\omega )} & \cdots & {{\tilde{\mathbf{P}}}_{{k,i_{l} = N_{l} }} (j1\omega )} \\ \end{array} ] \\ \;\;\;\; & = \left[ {\begin{array}{*{20}c} {P_{{k,i_{1} = 1}}^{{(\Omega_{1} )}} (j{1}\omega_{1} )} & \cdots & {P_{{k,i_{1} = N_{1} }}^{{(\Omega_{1} )}} (j{1}\omega_{1} )} & {P_{{k,i_{2} = 1}}^{{(\Omega_{1} )}} (j{1}\omega_{1} )} & \cdots & {P_{{k,i_{2} = N_{2} }}^{{(\Omega_{1} )}} (j{1}\omega_{1} )} & \cdots & {P_{{k,i_{l} = N_{l} }}^{{(\Omega_{1} )}} (j{1}\omega_{1} )} \\ {P_{{k,i_{1} = 1}}^{{(\Omega_{2} )}} (j{1}\omega_{2} )} & \cdots & {P_{{k,i_{1} = N_{1} }}^{{(\Omega_{2} )}} (j{1}\omega_{2} )} & {P_{{k,i_{2} = 1}}^{{(\Omega_{2} )}} (j{1}\omega_{2} )} & \cdots & {P_{{k,i_{2} = N_{2} }}^{{(\Omega_{2} )}} (j{1}\omega_{2} )} & \cdots & {P_{{k,i_{l} = N_{l} }}^{{(\Omega_{2} )}} (j{1}\omega_{2} )} \\ { \vdots {\kern 1pt} } & {} & { \vdots {\kern 1pt} } & { \vdots {\kern 1pt} } & {} & { \vdots {\kern 1pt} } & \ddots & { \vdots {\kern 1pt} } \\ {P_{{k,i_{1} = 1}}^{{(\Omega_{p} )}} (j{1}\omega_{p} )} & \cdots & {P_{{k,i_{1} = N_{1} }}^{{(\Omega_{p} )}} (j{1}\omega_{p} )} & {P_{{k,i_{2} = 1}}^{{(\Omega_{p} )}} (j{1}\omega_{p} )} & \cdots & {P_{{k,i_{2} = N_{2} }}^{{(\Omega_{p} )}} (j{1}\omega_{p} )} & \cdots & {P_{{k,i_{l} = N_{l} }}^{{(\Omega_{p} )}} (j{1}\omega_{p} )} \\ \end{array} } \right] \\ \end{aligned}$$
(9)

Remark 2

Different from the conventional time-domain model term dictionary \({\mathbf{P}}_{k}\), data in the frequency domain version model term dictionary \({\tilde{\mathbf{P}}}_{k}\) are complex numbers, where the real and imaginary parts should be separated and glued together. This process can be represented by the following:

$${\hat{\mathbf{Y}}}_{k} = \left[ {\begin{array}{*{20}c} {{\text{Re}}\;{\tilde{\mathbf{Y}}}_{k} } \\ {{\text{Im}} \;{\tilde{\mathbf{Y}}}_{k} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\text{Re}}\;{\tilde{\mathbf{P}}}_{k} } \\ {{\text{Im}} \;{\tilde{\mathbf{P}}}_{k} } \\ \end{array} } \right]{{\varvec{\uptheta}}}_{k} = {\hat{\mathbf{P}}}_{k} {{\varvec{\uptheta}}}_{k}$$
(10)

where Re and Im are the real and imaginary parts, respectively, \({\hat{\mathbf{P}}}_{k}\) is the final candidate model term dictionary used for dynamic parametrical model identification, \({\hat{\mathbf{P}}}_{k} = [\;{\hat{\mathbf{p}}}_{k,1} ,{\hat{\mathbf{p}}}_{k,2} , \ldots ,{\hat{\mathbf{p}}}_{k,M} ]\).

3 Determination of the dynamic parametrical model

This section introduced the PRESS-based EFOR algorithm [32], which is proposed for the single-input multiple-output scenarios, to obtain the CMS of the rotor system. Moreover, the parameter estimation method and model validation criterion are also summarized. In the following, the identification process will be briefly outlined.

Step 1 Orthogonalization of the models

To minimize the predicting error, the regression matrix \({\hat{\mathbf{P}}}_{k}\) needs to be orthogonalized [34], and then model (10) can be rewritten as

$${\hat{\mathbf{Y}}}_{k} = {\hat{\mathbf{P}}}_{k} {{\varvec{\uptheta}}}_{k} { = }{\mathbf{W}}_{k} {\mathbf{G}}_{k}$$
(11)

where \({\mathbf{W}}_{k}\) is the orthogonal matrix formed by the orthogonal vectors \({\mathbf{w}}_{{{\mathbf{k,1}}}} ,{\mathbf{w}}_{{{\mathbf{k,2}}}} , \ldots {\mathbf{w}}_{{{\mathbf{k,M}}}}\); \({\mathbf{G}}_{k}\) is the matrix of coefficients corresponding to \({\mathbf{W}}_{k}\), \({\mathbf{G}}_{k} { = [}g_{k,1} ,g_{k,2} , \ldots ,g_{k,M} {]}^{{\text{T}}}\). \({\mathbf{w}}_{{{\mathbf{k,m}}}}\) and \(g_{k,m}\) can be calculated by Eqs. (12) and (13), respectively.

$${\mathbf{w}}_{{{\mathbf{k,m}}}} = {\hat{\mathbf{p}}}_{{{\mathbf{k,m}}}} - \sum\limits_{i = 1}^{m - 1} {\frac{{\left\langle {{\hat{\mathbf{p}}}_{k,m} ,{\mathbf{w}}_{{{\mathbf{k,i}}}} } \right\rangle }}{{\left\langle {{\mathbf{w}}_{{{\mathbf{k,i}}}} ,{\mathbf{w}}_{{{\mathbf{k,i}}}} } \right\rangle }}} {\mathbf{w}}_{{{\mathbf{k,i}}}} , \, m = 1,2, \ldots ,M$$
(12)
$$g_{k,m} = \frac{{\left\langle {{\hat{\mathbf{Y}}}_{k} ,{\mathbf{w}}_{k,m} } \right\rangle }}{{\left\langle {{\mathbf{w}}_{k,m} ,{\mathbf{w}}_{k,m} } \right\rangle }}, \, m = 1,2, \ldots ,M$$
(13)

where \(< \cdot , \cdot >\) represents the inner product.

Step 2 The common model structure detection

In the searching process, the model terms are selected based on the mean squared PRESS error [32], which can be calculated at the sth searching step by

$$J_{k,m}^{(s)} = \frac{1}{Z}\frac{{ < {{\varvec{\upvarepsilon}}}_{k,m}^{(s)} ,{{\varvec{\upvarepsilon}}}_{k,m}^{(s)} > }}{{ < {{\varvec{\upbeta}}}_{k,m}^{(s)} ,{{\varvec{\upbeta}}}_{k,m}^{(s)} > }}, \, m = 1,2, \ldots ,M$$
(14)

where

$$\beta_{k,m}^{(s)} (t) = \beta_{k,m}^{(s - 1)} (t) - \frac{{(w_{k,m}^{(s)} (t))^{2} }}{{ < {\mathbf{w}}_{k,m}^{(s)} ,{\mathbf{w}}_{k,m}^{(s)} > }},t = 1,2, \ldots ,Z$$
(15)
$$\varepsilon_{k,m}^{(s)} (t) = \varepsilon_{k,m}^{(s - 1)} (t) - w_{k,m}^{(s)} (t)\frac{{{\hat{\mathbf{Y}}}_{k}^{{\text{T}}} {\mathbf{w}}_{k,m}^{(s)} }}{{ < {\mathbf{w}}_{k,m}^{(s)} ,{\mathbf{w}}_{k,m}^{(s)} > }},t = 1,2, \ldots ,Z$$
(16)

With \(\varepsilon_{k,m}^{(0)} (t) = {\hat{\mathbf{Y}}}_{k}\), \(\beta_{k,m}^{(0)} (t) = 1\), and \({\overline{\mathbf{w}}}_{k,m}^{(1)} = {\hat{\mathbf{p}}}_{{{\mathbf{k,m}}}}\).

The selected vector can be chosen as \({\overline{\mathbf{p}}}_{k,1} = {\hat{\mathbf{p}}}_{{k,l_{s} }}^{(1)}\), where \(l_{s}\) can be calculated by

$$l_{s} = \arg \min \left\{ {\frac{1}{K}\sum\limits_{k = 1}^{K} {J_{k,m}^{(s)} } } \right\},\;\;k = 1,2, \ldots ,K$$
(17)

This step is repeated until the average Bayesian Information Criterion (BIC) [35] value at the sth step lager than the (s − 1) step, the average BIC value at each searching step can be calculated by

$$\begin{array}{*{20}c} {{\text{BIC}}} \\ \end{array} {(}s{) = }\frac{1}{K}\sum\limits_{k = 1}^{K} {\left[ {1 + \frac{s\ln Z}{{Z - s}}} \right]\frac{1}{Z}\sum\limits_{t = 1}^{Z} {(\varepsilon_{k}^{(s)} (t))^{2} } }$$
(18)

where Z represents the total number of sampling points of system output.

Step 3 Evaluation of the coefficients

The linearized representation of the detected model can be written as

$${\hat{\mathbf{Y}}}_{k} = \sum\limits_{{m_{0} = 1}}^{{M_{0} }} {\overline{\theta }_{{k,m_{0} }} {\overline{\mathbf{p}}}_{{k,m_{0} }} } ,\;\;m_{0} = 1,2, \ldots ,M_{0}$$
(19)

where \({\overline{\mathbf{p}}}_{{k,m_{0} }}\) is the selected model terms from \({\hat{\mathbf{P}}}_{k}\); \(M_{0}\) is the number of the selected model terms; The coefficients \(\overline{\theta }_{{k,m_{0} }}\) can be evaluated by the Inverse-Gram-Schmidt algorithm [36]:

$$\left\{ {\begin{array}{*{20}l} {\overline{\theta }_{{k,M_{0} }} = \overline{g}_{{k,M_{0} }} } \hfill \\ {\overline{\theta }_{{k,M_{0} - 1}} = \overline{g}_{{k,M_{0} - 1}} - a_{{M_{0} - 1,M_{0} }} \overline{\theta }_{{k,M_{0} }} } \hfill \\ {\overline{\theta }_{{k,M_{0} - 2}} = \overline{g}_{{k,M_{0} - 2}} - a_{{M_{0} - 2,M_{0} - 1}} \overline{\theta }_{{k,M_{0} - 1}} - a_{{M_{0} - 2,M_{0} }} \overline{\theta }_{{k,M_{0} }} } \hfill \\ {\quad \quad \quad \vdots } \hfill \\ {\overline{\theta }_{{k,m_{{0}} }} = \overline{g}_{{k,m_{{0}} }} - \sum\limits_{{i = m_{{0}} + 1}}^{{M_{0} }} {a_{{m_{{0}} ,i}} \overline{\theta }_{k,i} } } \hfill \\ \end{array} } \right.$$
(20)

where

$$a_{{m_{{0}} ,i}} = \frac{{\left\langle {{\overline{\mathbf{p}}}_{k,i} ,{\overline{\mathbf{w}}}_{{k,m_{{0}} }} } \right\rangle }}{{\left\langle {{\overline{\mathbf{w}}}_{{k,m_{{0}} }} ,{\overline{\mathbf{w}}}_{{k,m_{{0}} }} } \right\rangle }},\;\;1 \le m_{{0}} \le M_{0} - 1$$
(21)

Step 4 Determinate the function of the coefficients of the NARX model by design parameter values

The relationship between the physical parameter \({{\varvec{\upxi}}}\) (\({{\varvec{\upxi}}} = [\xi_{1} ,\xi_{2} , \ldots ,\xi_{S} ]\)) and the coefficients of the NARX model can be revealed by a polynomial function [14], which can be expressed as

$$\overline{\theta }_{{k,m_{0} }} \left( {{\varvec{\upxi}}} \right) = \sum\limits_{{j_{1} = 0}}^{J} { \cdots \sum\limits_{{j_{K} = 0}}^{J} {\beta_{{j_{1} , \ldots ,j_{S} }} \xi_{1}^{{j_{1} }} \cdots \xi_{K}^{{j_{K} }} } }$$
(22)

where J is the degree of the polynomial function; \(\beta_{{j_{1} , \ldots ,j_{S} }}\) is the corresponding coefficients, which can be estimated using the least square algorithm [37].

Step 5 Model validation

The objective of the identification is to find an approximation mathematical model that produces the minimum errors comparing with the real responses under different design parameter values. This paper focus on the Normalized Mean Square Error (NMSE) [38, 39] properties of the identified model, which can be expressed as

$${\text{NMSE}} = \frac{{\sum_{t = 1 \, }^{Z} [y_{p} (t) - y(t)]^{2} }}{{\sum_{t = 1}^{Z} [y_{p} (t)]^{2} }}$$
(23)

where \(y_{p} (t)\) is the prediction output at time instant t, \(y(t)\) is the actual output at time instant t, Z is the total number of sampling points.

The flow chart of the identification process is shown in Fig. 1.

Fig. 1
figure 1

The flowchart of the identification process

Full size image

Remark 3

Model (19) was obtained by the frequency domain data obtained by the frequency sweep process, as described from Eq. (6) to Eq. (10). But the identified model can be used to predict the time domain system output due to the linear properties of the DTFT.

4 Numerical case study

In aero-engines, a large number of bolted joints are applied to connect the disks [40], and the bolts are distributed in the circumference to fasten the adjacent disks as shown in Fig. 2a, where the three-dimensional model illustrates a simplified form of bolted-joint structure. As reported in the literature [41, 42], the bolted joint structure plays an important role in the rotor dynamic characteristics. The piecewise linear stiffness [43] affects system output significantly. Therefore, this section takes the turning point of piecewise linear stiffness as a physical parameter to demonstrate the feasibility of the proposed approach, starting from the modeling of the rotor system based on the finite element method.

Fig. 2
figure 2

Bolted joint structure in the aero-engine and the simplified model: a bolted joint structure in the aero-engine and the simplified bolted joint structure, b simplified rotor-bearing system with a bolted joint structure

Full size image

4.1 Modeling and analysis of the rotor-bearing system with a bolted joint

According to the simplified bolted-disk joint rotor-bearing system shown in Fig. 2, the finite element model shown in Fig. 3 is established. The shaft is discretized into 13 elements, the left shaft is divided into 5 elements, and the right shaft is divided into 8 elements. There are many reports about modeling of the rotor system based on the finite element modeling method (see [44,45,46,47,48]), the main task in this section is the modeling of the bolted joint structure.

Fig. 3
figure 3

Schematic diagram of the finite element model for the rotor system with a bolted joint: a neglecting the bolted joint, b finite element of the bolted joint

Full size image

In this model, the simplified jointed structure is treated as a novel two-node element with four degrees of freedom at each node (see Fig. 3b), where \(k_{\theta }\) and \(k_{S}\) are the angular stiffness and shear stiffness between two disks. And then the total displacement vector of the bolted joint can be determined as:

$${{\varvec{\updelta}}}_{J}^{e} = \left[ {u_{1} \, w_{1} \, \theta_{1} \, \varphi_{1} \, u_{2} \, w_{2} \, \theta_{2} \, \varphi_{2} } \right]^{{\text{T}}}$$
(24)

where u and w represent the lateral displacement, respectively; θ and φ are angular displacement about x and y axes, respectively; the subscript 1,2 denote the nodes associated with disk 1 and disk 2, respectively.

The kinetic energy and potential energy of the bolted joint can be written as

$$\begin{aligned} T & = \frac{1}{2}m_{1} \dot{u}_{1}^{2} + \frac{1}{2}m_{1} \dot{w}_{1}^{2} + \frac{1}{2}m_{2} \dot{u}_{2}^{2} + \frac{1}{2}m_{2} \dot{w}_{2}^{2} + \frac{1}{2}J_{d1} \Omega^{2} + \frac{1}{2}J_{d2} \Omega^{2} \\ \;\;\; & \quad + \frac{1}{2}J_{d1} \dot{\theta }_{1}^{2} + \frac{1}{2}J_{d1} \dot{\varphi }_{1}^{2} + \frac{1}{2}J_{d2} \dot{\theta }_{2}^{2} + \frac{1}{2}J_{d2} \dot{\varphi }_{2}^{2} + \Omega J_{p1} \dot{\theta }_{1} \dot{\varphi }_{1} + \Omega J_{p2} \dot{\theta }_{2} \dot{\varphi }_{2} \\ \end{aligned}$$
(25)
$$V = \frac{1}{2}k_{s} (u_{2} - u_{1} )^{2} + \frac{1}{2}k_{s} (w_{2} - w_{1} )^{2} + \frac{1}{2}k_{\theta } (\theta_{2} - \theta_{1} )^{2} + \frac{1}{2}k_{\theta } (\varphi_{2} - \varphi_{1} )^{2}$$
(26)

where m1 and m2 are the mass of disk 1 and disk 2, respectively; Jd1 and Jd2 are diametral moments of inertia of disk 1 and disk 2, respectively; Jp1 and Jp2 are polar moments of inertia of disk 1 and disk 2, respectively.

By applying the Lagrange’ approach [49], the governing equation of jointed structure is obtained as

$${\mathbf{M}}_{J}^{e} {\ddot{\mathbf{\delta }}}_{J}^{e} - \Omega {\mathbf{G}}_{J}^{e} {\dot{\mathbf{\delta }}}_{J}^{e} + {\mathbf{K}}_{J}^{e} {{\varvec{\updelta}}}_{J}^{e} = {\mathbf{Q}}_{J}^{e}$$
(27)

where \({\mathbf{M}}_{J}^{e}\), \({\mathbf{G}}_{J}^{e}\), and \({\mathbf{K}}_{J}^{e}\) are mass matrix, gyroscopic matrix, and stiffness matrix of the jointed element, respectively;\({\mathbf{Q}}_{J}^{e}\) is the external force matrix which mainly contains the unbalanced force of the disks; \(\Omega\) represents the rotational speed of the rotor system. The details of the matrices are given in “Appendix A”.

The general form of the finite element model of the shafts are established as

$${\mathbf{M}}_{L}^{b} {\ddot{\mathbf{\delta }}}_{L}^{b} + ({\mathbf{C}}_{L}^{b} - \Omega {\mathbf{G}}_{L}^{b} ){\dot{\mathbf{\delta }}}_{L}^{b} + {\mathbf{K}}_{L}^{b} {{\varvec{\updelta}}}_{L}^{b} = {\mathbf{Q}}_{L}^{s}$$
(28)
$${\mathbf{M}}_{R}^{b} {\ddot{\mathbf{\delta }}}_{R}^{b} + ({\mathbf{C}}_{R}^{b} - \Omega {\mathbf{G}}_{R}^{b} ){\dot{\mathbf{\delta }}}_{R}^{b} + {\mathbf{K}}_{R}^{b} {{\varvec{\updelta}}}_{R}^{b} = {\mathbf{Q}}_{R}^{s}$$
(29)

where \({\mathbf{M}}_{L}^{b}\), \({\mathbf{M}}_{R}^{b}\) are mass matrices of the left and right shafts; \({\mathbf{C}}_{L}^{b}\), \({\mathbf{C}}_{R}^{b}\) are damping matrices of the left and right shafts; \({\mathbf{K}}_{L}^{b}\), \({\mathbf{K}}_{R}^{b}\) are stiffness matrices of the left and right shafts; \({\mathbf{Q}}_{L}^{s}\), \({\mathbf{Q}}_{R}^{s}\) are external force matrices acting on both sides of the system; δb L and δb R are the displacement vectors of the left and right shafts, respectively.

Based on the governing equations of the bolted joint and shafts, the finite element model of the rotor system can be established as

$${ {\varvec{M}\ddot{\varvec\delta }}} + ({\varvec{C}} - \Omega {\varvec{G}}){\dot{\varvec{\delta }}} + {\varvec{K}}{\varvec{\delta}} = {\varvec{Q}}$$
(30)

where \({\mathbf{M}}\) is the mass matrix of the system; \({\mathbf{C}}\) is the damping matrix of the system; \({\mathbf{G}}\) is the gyroscopic matrix of the system; \({\mathbf{K}}\) is the stiffness matrix of the system; \({{\varvec{\updelta}}}\) is the displacement vector of the rotor system; \({\mathbf{Q}}\) represents the external force matrix of the overall rotor system. The schematic diagram of the assembly of matrices of the underlying system is shown in Fig. 4.

Fig. 4
figure 4

Schematic diagram of the assembly of matrices of the rotor-bearing system with a bolted joint structure

Full size image

It should be stressed that the shaft is modeled using Timoshenko beam elements, of which the mass, stiffness, and gyroscopic matrices are given in the literature [50]. Moreover, the damping matrices are formulated by using the Rayleigh damping matrix [51], and the external force vectors are mainly contained nonlinear forces from ball bearings. The materials and dimensional parameter values of the rotor are listed in Table 1. The supporting bearings are deep groove ball bearings, both of which are the same and the parameter values are shown in Table 2. The nonlinear force generated by the bearings can be calculated by [52, 53]

$$\left\{ {\begin{array}{*{20}l} {f_{x}^{b} = - k_{B} \sum\limits_{j = 1}^{{N_{b} }} {\left( {x\cos \theta_{j} + y\sin \theta_{j} - \gamma } \right)^{1.5} H\left( {x\cos \theta_{j} + y\sin \theta_{j} - \gamma } \right)\cos \theta_{j} } } \hfill \\ {f_{y}^{b} = - k_{B} \sum\limits_{j = 1}^{{N_{b} }} {\left( {x\cos \theta_{j} + y\sin \theta_{j} - \gamma } \right)^{1.5} H\left( {x\cos \theta_{j} + y\sin \theta_{j} - \gamma } \right)\sin \theta_{j} } } \hfill \\ \end{array} } \right.$$
(31)
Table 1 Dimensional parameter values of the rotor system
Full size table
Table 2 Dimensional parameter values of the ball bearing
Full size table

where \(k_{B}\) is the contact stiffness; \(\theta_{j}\) is the angle location of the jth rolling ball; \(N_{b}\) is the number of balls; \(\gamma\) is the radial clearance of the bearing; \(H( \cdot )\) is the Heaviside function.

The angular stiffness characteristics of the bolted joint structure are piecewise linear, and the transition takes place when the external force equal to preload [54, 55]. The relative rotation angle at the transition point (denotes by the symbol \(\Phi_{{0}}\)) in the range of \(\Phi_{0} = [8 \times 10^{ - 6} ,10 \times 10^{ - 6} ,1{2} \times 10^{ - 6} ]\;{\text{rad}}\) is chosen to be studied here, and then provide a basis for the dynamic parametrical model identification in Sect. 4.2. The relationship between the angular stiffness \(k_{\theta }\) and \(\Phi_{{0}}\) can be described by

$$k_{\theta } { = }\left\{ {\begin{array}{*{20}c} {k_{\theta 1} ,\left| \Phi \right| \ge \left| {\Phi_{0} } \right|} \\ {k_{\theta 2} ,\left| \Phi \right| < \left| {\Phi_{0} } \right|} \\ \end{array} } \right.$$
(32)

where \(k_{\theta 1}\) is the angular stiffness in the first stage; \(k_{\theta 2}\) is the angular stiffness in the second stage; \(\Phi\) represents the relative angular between disk1 and disk2, \(\Phi = \sqrt {(\theta_{1} - \theta_{2} )^{2} + (\varphi_{1} - \varphi_{2} )^{2} }\). The detailed description of kθ1, kθ2, and Φ can be found in the literature [54].

In this section, kθ1 and kθ2 are assumed to keep the same in all the cases (\(k_{\theta 1} = 23 \times 10^{8} \;{\text{Nm}}/{\text{rad}}\) and \(k_{{\theta {2}}} = 2.3 \times 10^{8} \;{\text{Nm}}/{\text{rad}}\)). The angular stiffness with different transition points is shown in Fig. 5. The Newmark-β method was used to solve the governing Eq. (30), while the critical speed of the rotor-bearing system can be calculated as \(\omega_{0} = 1140\;{\text{rev/min}}\), which is shown in Fig. 6. It can be seen that the critical speed of the rotor system described in this section is not affected by the transition point, but the associated amplitude is getting smaller as the transition point decreases. This is due to the degradation of the angular stiffness of the bolted joint. Furthermore, the output spectrum of the rotor system, in the horizontal direction, is demonstrated in Fig. 7, showing that the first harmonic is the main frequency component. Therefore, the identified model should reveal the system output signals, as well as the first harmonic of the underlying system.

Fig. 5
figure 5

Comparison of angular stiffness under different transition points

Full size image
Fig. 6
figure 6

Comparison of the critical speed of the rotor-bearing system under different transition points

Full size image
Fig. 7
figure 7

Spectrum of the rotor system with different transition points: a \(\Phi_{0} = 8 \times 10^{ - 6} \;{\text{rad}}\); b \(\Phi_{0} = 10 \times 10^{ - 6} \;{\text{rad}}\); c \(\Phi_{0} = 12 \times 10^{ - 6} \;{\text{rad}}\)

Full size image

4.2 Identification of the rotor system based on the proposed approach

The aim here is to apply the proposed method to the rotor system described in Sect. 4.1 and identified a CMS to represent the underlying system, and then validate it by using the model predicted output method [56]. The input signals \(u(t)\) are chosen as the unbalanced force of disk 1 with \(\Omega \in [360:60:2700]\;{\text{rev/min}}\), 120 data sets of displacement responses of disk 1, in the horizontal direction, corresponding to \(\Phi_{0} = [8 \times 10^{ - 6} ,10 \times 10^{ - 6} ,1{2} \times 10^{ - 6} ]\;{\text{rad}}\) are collected for model identification. Moreover, the data sets corresponding to Φ0 = 9 × 10−6 rad were used to test the proposed frequency sweep dynamic parametrical model identification approach. In these cases, 25,600 data are collected under every operating speed.

The identification results are given in Table 3, where a total of 7 terms are selected according to the detecting result at each searching step. Thus, a dynamic parametrical model for the rotor system is determined to be:

$$\begin{aligned} \hat{Y}_{k} (t) & = \overline{\theta }_{1} (\Phi_{0} )y\left( {t - 1} \right) + \overline{\theta }_{2} (\Phi_{0} )y\left( {t - 2} \right) + \overline{\theta }_{3} (\Phi_{0} )u\left( {t - 1} \right) + \begin{array}{*{20}l} {\overline{\theta }_{4} (\Phi_{0} )u\left( {t - 2} \right)u\left( {t - 3} \right)} \hfill \\ \end{array} \\ \;\;\;\;\;\;\; & \quad+ \overline{\theta }_{5} (\Phi_{0} )u\left( {t - 1} \right)u\left( {t - 2} \right) + \overline{\theta }_{6} (\Phi_{0} )u\left( {t - 3} \right) + \overline{\theta }_{7} (\Phi_{0} )\begin{array}{*{20}l} {u\left( {t - 1} \right)y\left( {t - 1} \right)} \hfill \\ \end{array} \\ \end{aligned}$$
(33)
Table 3 The CMS identified by using the traditional EFOR algorithm and the associated coefficients
Full size table

where the coefficients \(\overline{\theta }_{{m_{0} }} (\Phi_{0} ),(m_{0} = 1,2, \ldots ,7)\) has a functional relationship with the physical parameters, this study adopts the following three-order polynomial expression to describe the relationship between Φ0 and \(\overline{\theta }_{{m_{0} }} (\Phi_{0} )\).

$$\overline{\theta }_{{m_{0} }} (\Phi_{0} ){ = }\beta_{{m_{0} ,0}} + \beta_{{m_{0} ,1}} \Phi_{0} + \beta_{{m_{0} ,2}} \Phi_{0}^{2} + \beta_{{m_{0} ,3}} \Phi_{0}^{3}$$
(34)

The coefficient \(\beta_{{m_{0} ,i}}\) can be estimated by using the least square algorithm, which is shown in Table 4. The datasets, corresponding to \(\Phi_{0} = {9} \times 10^{ - 6} \;{\text{rad}}\) are used to test the identified dynamic parametrical model. The comparisons of the outputs (low rotation speed, critical speed, high rotation speed cases) of the identified model and the real system are presented in Figs. 8 and 9, where the output in the frequency domain is obtained by using the DTFT. Clearly, the proposed approach can provide an accurate model to represent the underlying system in both the time and frequency domain.

Table 4 Results for the parameters \(\beta_{{m_{0} ,i}}\) in Eq. (32)
Full size table
Fig. 8
figure 8

Comparison of system output in the time domain: a low speed (\(\Omega = 480\;{\text{rev/min}}\)); b critical speed (\(\Omega = 1140\;{\text{rev/min}}\)); c high speed (\(\Omega = 2100\;{\text{rev/min}}\))

Full size image
Fig. 9
figure 9

Comparison of system output in the frequency domain: a low speed (\(\Omega = 480\;{\text{rev/min}}\)); b critical speed (\(\Omega = 1140\;{\text{rev/min}}\)); c high speed (\(\Omega = 2100\;{\text{rev/min}}\))

Full size image

The NMSE model validation criterion is used for assessing the accuracy of the identified model, the NMSE values in the previous three validation cases are \(2.8146 \times 10^{ - 4}\), \({7}{\text{.4954}} \times {10}^{ - 6}\), and \({0}{\text{.0016}}\), proving that the proposed identification approach can provide a reliable model to reveal the underlying system.

It should be stressed that the model structure obtained by using the proposed identification approach is unique, to represent the rotor system under different rotation speeds and physical parameter value. This is a significant advantage of this work, compared with our previous work reported in [29].

5 Experimental illustration

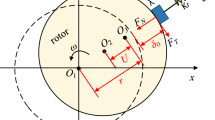
A bolted joint rotor-bearing test rig with an electric tightening wrench was taken for experimental validation in this section, where the bolts are distributed circumferentially to connect two disk-drum structures. The tightening torque can be controlled accurately by the electric tightening wrench through the controller. The eddy current displacement sensor is arranged at the vibration shaft near the drum to measure the horizontal responses for system identification. Moreover, the data are collected by the NI-9229 acquisition card. The experimental setup is shown in Fig. 10. The parameters of the rotor-bearing test rig are shown in Table 5.

Fig. 10
figure 10

Test rig of a rotor-bearing system with bolted joint structure and data collection setup

Full size image
Table 5 Dimensional parameter values of the rotor system test rig
Full size table

In this experimental case, the tightening torque \(f_{0}\) is chosen as a physical parameter. And then, a total of \(3 \times {11} \times 15500{ = 511500}\) data of system response corresponding to f0 = [4, 8, 12] Nm, under the rotation speed \(\Omega \in [1080:60:1200]\;{\text{rev/min}}\) are collected. Moreover, the data sets corresponding to \(f_{0} = 6\;{\text{Nm}}\) were used to test the identified dynamic parametrical model. Because of the difficulty of measuring the input signals, \(u(t) = 0.3 \times 10^{6} \Omega^{2} \cos (\Omega t)\) is used to calculate the input signals. The identification results by using the proposed approach are given in Table 6, where a total of 8 terms are selected. Thus, the dynamic parametrical model for the underlying system is identified as

$$\begin{aligned} \hat{Y}_{k} (t) & = \overline{\theta }_{1} (f_{0} )y\left( {t - 1} \right) + \overline{\theta }_{2} (f_{0} )y\left( {t - 2} \right) + \overline{\theta }_{3} (f_{0} )u\left( {t - 1} \right) + \begin{array}{*{20}l} {\overline{\theta }_{4} (f_{0} )u\left( {t - 2} \right)} \hfill \\ \end{array} \\ \;\;\;\;\;\;\; &\quad + \overline{\theta }_{5} (f_{0} )y\left( {t - 2} \right)^{2} + \overline{\theta }_{6} (f_{0} )u\left( {t - 3} \right) + \overline{\theta }_{7} (f_{0} )\begin{array}{*{20}l} {u\left( {t - 4} \right)} \hfill \\ \end{array} + \overline{\theta }_{8} (f_{0} )\begin{array}{*{20}l} {y\left( {t - 1} \right)y\left( {t - 2} \right)} \hfill \\ \end{array} \\ \end{aligned}$$
(35)
Table 6 The CMS identified by using the traditional EFOR algorithm and the associated coefficients
Full size table

The coefficients \(\overline{\theta }_{{m_{0} }} (f_{0} ),(m_{0} = 1,2, \ldots ,8)\) are then fitted as a three-order polynomial function as

$$\overline{\theta }_{{m_{0} }} (f_{0} ){ = }\beta_{{m_{0} ,0}} + \beta_{{m_{0} ,1}} f_{0} + \beta_{{m_{0} ,2}} f_{0}^{2} + \beta_{{m_{0} ,3}} f_{0}^{3}$$
(36)

The coefficients \(\beta_{{m_{0} ,i}}\) are estimated as shown in Table 7. The comparisons of the outputs of the identified model and the real system under rotating speed \(\Omega { = [1080,1140,1200]}\;{\text{rev/}}\min\)are presented in Figs. 11 and 12. It can be found that the proposed identification approach can provide a reliable model for the underlying system, while the identified NMSE were 0.009, 0.0032, and 0.0015, respectively.

Table 7 Results for the parameters \(\beta_{{m_{0} ,i}}\) in (34)
Full size table
Fig. 11
figure 11

Comparison of system output in the time domain: a case 1 (\(\Omega { = 1080}\;{\text{rev/}}\min\)); b case 2 (\(\Omega { = 1140}\;{\text{rev/}}\min\)); c case 3 (\(\Omega { = 1200}\;{\text{rev/}}\min\))

Full size image
Fig. 12
figure 12

Comparison of system output in the frequency domain: a case 1 (\(\Omega { = 1080}\;{\text{rev/}}\min\)); b case 2 (\(\Omega { = 1140}\;{\text{rev/}}\min\)); c case 3 (\(\Omega { = 1200}\;{\text{rev/}}\min\))

Full size image

6 Conclusions

The frequency sweep system identification approach is proposed for the identification of the dynamic parametrical model for the rotor-bearing system, on the basis of the identification approach for the traditional NARX model with a physical parameter. The corresponding frequency domain version modeling framework, containing the physical parameter and frequency sweep data sets are derived. In this study, the PRESS-based EFOR algorithm is introduced to accomplish the model structure detection, by shifting the application of the algorithm from single-input multiple-output scenarios to single-input single-output scenarios corresponding to different physical parameter values.

The numerical examples of the bolted joint rotor system and the experimental application both demonstrate the feasibility of the proposed identification approach to the dynamic parametrical modeling of the rotor system. Hence, the new identification approach can be regarded as a means by which to enrich the method for the NARX model-based dynamic parametrical modeling, and can be extended to the application of any other sinusoidal excitation structures. Based on the cases reported in this paper, the proposed approach has the potential to be used in industrial scenarios, to represent the underlying systems, and reveals rules for physical parameters that affect dynamic behaviors. Moreover, revealing fundamental and interesting information to the user, by reproducing the system output in the time domain and then mapping to the frequency domain. The proposed system identification method is originated in the control theory, which is only dependent on the system input and output. Therefore, the proposed approach has the potential to be applied to the modeling of rotor systems with other types of joints.