Numerical analysis for the non-Newtonian flow over stratified stretching/shrinking inclined sheet with the aligned magnetic field and nonlinear convection

Abstract

In the existence of an aligned magnetic field over the inclined shrinking/stretching stratified sheet in a non-Darcy porous medium, the two-dimensional boundary layer flow of an upper-convected Maxwell fluid is analyzed. The heat transfer effects are acknowledged by using the nonlinear convection. The system of partial differential equations, which administrates the distinctive properties of flow and heat transfer, is depleted into ordinary differential equations with the use of similarity variables. The governing equations are determined numerically by utilizing the shooting technique. The response of varied implicated parameters on velocity, skin friction, and temperature accounts is inspected graphically and displayed in the table. It is noted that local inertia coefficient is accountable for the reduction in the velocity profile and the aligned magnetic field has the opposite relation for the shrinking and stretching sheet.

1 Introduction

The investigation of fluid properties on different geometries and surfaces is one of the significant topics discussed by the researchers as it involves numerous industrial and technological aspects, like expulsion, wire drawing, generation of glass fiber, assembling of elastic sheets, cooling of immense metallic plates, etc. [1]. The boundary layer flow past a persistent solid panel flowing with consistent speed was examined by Sakiadis [2] for the first time. In the past few decades, a critical consideration has been given to the non-Newtonian fluids flowing over the stretched surface. The significance of non-Newtonian fluids in countless engineering and technological applications can never be contradicted. The extensive area of applications consists of aerodynamic, emission of plastic films, liquid film condensation process, annealing and copper wires thinnings, etc. [3]. In the food industry, mayonnaise, starch suspension, fruit juices, alcoholic beverages, yogurt, and syrups are common examples of non-Newtonian fluids. Apart from the viscous liquids, a noticeable difficulty in the mathematical framing of these liquids is that all the attributes of these fluids’ structures cannot be displayed by a single constitutive equation. That is why analysts proposed certain non-Newtonian fluid models in the literature. These models are divided as a differential, rate, and integral types. Maxwell model falls within the category of rate-type fluids, and it highlights the fluid relaxation time phenomenon. Harris [4] pioneering work, which presented the 2D flow of upper-convected Maxwell fluid, motivated the followers to explore further possibilities in this regard. Many scientists have considered the transfer of heat and boundary layer flow in the multiple forms due to the stretching sheet for the upper-convected Maxwell fluid [5,6,7].

Heat transfer is a working area of exploration in fluid dynamics over the past few decades. There are countless industrial applications of heat and mass transfer such as in the asphalt and concrete industry for concrete warming and hot blend paving and in the chemical industry for the atomic reactor, in food industry like meat and poultry preparing, snack foods, in cloth industries, pipe and plastic industries, electric and electronic devices and steam generators, glass fiber generation, streamlined expulsion of plastic sheets, glass blowing, etc. Crane [8] was the first to examine the continuous two-dimensional flow in a steady fluid induced by a stretching sheet and to develop an exact analytical solution. The heat transfer features were explored by Chen and Char [9] above a persistent stretching area among varying surface temperatures. Gupta and Gupta [10] studied the heat and mass transition referred to suction or blowing over the stretching panel. The spearheading work of Crane has been expanded by many researchers involving the importance of heat transfer flow [11,12,13,14,15,16,17,18,19].

Material containing pores in fluid dynamics is called a porous medium. The porous medium is typically a liquid-filled biological application. Due to its broad usage, liquid flow and transport procedures via porous formations are a subject of great concern in many scientific and technical fields. In manufacturing and agricultural processes for instance condensers (for cooling condensers, utilized as a heat exchanger) and gas turbines (used for cooling gas turbine blades), catalytic plants (utilized for decreasing poisonous quality of depleting emanations from automobiles engines), geothermal energy systems and geophysics, the study of the porous medium plays a vital role. In particular, the porous media are very beneficial in the fermentation processes, storage of grains, groundwater contamination, water motion in petroleum reservoirs, gasoline generation, ground-water frameworks, fossil fuel beds, retrieval apparatus, depleting radioactive waste units, power conserving areas, petroleum assets, thermal storage, and other many more. In the high-velocity systems, liquid flow through porous media is a challenging area for the researchers. The non-Darcian porous model is the improved figure of the old Darcian model that assimilates concurrent features of inertial tortuosity drag and boundary features. In 1856, Henry Darcy, a French engineer, developed the flow of heterogeneous liquids via a porous medium during his precious work on fluid flow through the sand beds. The classical Darcy law is ineffective when an account is taken of inertia and boundary characteristics at a high flow rate. The work was then expanded in 1901 by the Dutch scientist named Philippes Forchheimer. To evaluate the inertia and boundary characteristics, Forchheimer [20] integrated a square velocity element at Darcian speed to predict the essence of boundary layer flow and inertia. For the high Reynolds number, this feature is indeed credible. Muskat [21] then named the factor “Forchheimer phrase.” Pal and Mondal [22] developed a fluid model with impacts of Darcy–Forchheimer on a stretching panel. Ganesh et al. [23] inspected the adequacy of Darcy–Forchheimer hydromagnetic nanofluid flow in the direction of stretching/shrinking panel and the existence of thermal stratification, Ohmic dissipation, second-order velocity slip, and viscous dissemination impacts. Gireesha et al. [24] researched the hydromagnetic flow of viscous liquid with viscous dissipation and thermal radiation in a non-Darcian hydrophobic medium. Rashidi et al. [25] found the streamwise Darcy–Brinkman–Forchheimer liquid flow and heat transfer model for the magnetohydrodynamics. Ahmed [26] used Bejan’s thermal lines to evaluate infused non-Darcy hydrophobic medium with natural and forced convection in two-sided lid-driven enclosures. Because of the nonlinear stretching sheet, Hayat et al. [27] additionally investigated the Darcy–Forchheimer mobility of viscoelastic nanofluids. Kang et al. [28] recently analyzed the boundary conditions of Neumann for a standardized Darcy–Forchheimer framework.

Magnetohydrodynamics (MHD) is the region of the magnetic characteristics of electrically conductive liquids. The word MHD was first introduced by Hannes Alfen. Magnetohydrodynamic MHD flow analyses are very common in the industry and even have implementations in various fields such as petroleum production and metallurgical procedures. The characteristics of the final result rely heavily on the cooling speed engaged in these procedures, and the required final product characteristics can be regulated with the use of electrically conductive liquids and magnetic field. However, other electrically conductive liquids such as enriched uranium, molten metals, arsenic copper alloys, biochemical fluids, engine oils, and other grades have various features in the nonattendance as well as in the magnetic field view [29]. The heat transfer flow features dramatically altered as the magnetic field applied manipulates the elevated fluid molecules and rearranges their composition within the flow. Hayat et al. [30] inspected the nanofluid flows with convective circumstances and MHD impacts. Hsiao [31] researched the viscous and elastic MHD liquid flow in a mixed convection form, past a porous wedge. The MHD mixed convection flow of viscoelastic fluid is investigated by Hisao [32] with Ohmic dissipation across a stretching plate. Ganji and Malvandi [33] measured the natural heat transfer of nanofluid within a longitudinal framework, in the presence of a uniform magnetic field. Recently Raju et al. [34] addressed the impacts of associated magnetic fields on a continuous two-dimensional flux over a vertical stretching layer. They discovered that a rise in the aligned angle reduces the velocity profile and improves the temperature of the fluid.

Inspiring from above-cited research areas and their industrial applications, the core determination of the present work is the analysis of Maxwell fluid’s nonlinear mixed convective flow over the non-Darcian porous media in the existence of an aligned magnetic field. Further, we have used stratified inclined shrinking/stretching panel and no such research has been dealt with the best of our knowledge until now. The problem is tackled by the nonlinear shooting method as we have coupled nonlinear differential boundary value problems. After drawing the graphs and tables, the nature of different parameters on the profiles of the temperature and velocity in addition to Nusselt number and the skin friction coefficient is determined

2 Mathematical formulation

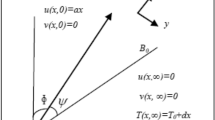
A continuous, laminar upper-convected Maxwell fluid flowing through the two-dimensional stratified shrinking/stretching inclined sheet with inclination angle $\alpha$ which is being stretched along the x-axis with velocity $u_{w}(x)=ax$, is contemplated as presented in Fig. 1. An aligned magnetic force field $B_{0}$ with acute angle $\gamma$ with the direction of y-axis is applied. The temperature at the wall is $T_{f}=T_{0}+a_{1}x$ and away from the surface is $T_{\infty }=T_{0}+d_{1}x$. The induced magnetic field is ignored because of the movement of the electrically conductive fluid. Nonlinear mixed convection through the non-Darcian porous medium is utilized to elaborate a porous media result for the transfer of the heat.

For the boundary layer flow, the governing equations of continuity, momentum and the temperature are defined as [35]:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} =0, \end{aligned}$$

(1)

$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\lambda \left[ \begin{array}{l} u^{2}\frac{\partial ^{2}u}{\partial x^{2}}+v^{2}\frac{\partial ^{2}u}{\partial y^{2}} \\ +2uv\frac{\partial ^{2}u}{\partial x\partial y}\end{array} \right] =v\frac{\partial ^{2}u}{\partial y^{2}}-\frac{\sigma B_{0}^{2}}{\rho }\sin ^{2}\left( \gamma \right) \left( u+\lambda v\frac{\partial u}{\partial y} \right) \nonumber \\&\quad +g\left[ \beta _{1}\left( T-T_{\infty }\right) +\beta _{2}\left( T-T_{\infty }\right) ^{2} \right] \cos (\alpha ) -\frac{v}{K}u-Fu^{2}, \end{aligned}$$

(2)

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y} =\frac{k}{ \rho c_{p}}\frac{\partial ^{2}T}{\partial y^{2}}, \end{aligned}$$

(3)

where, in Eqs. (1)–(3), u and v are the components of velocity along the x- and y-axes, respectively, K porous medium permeability, g gravitational acceleration, $F=\frac{C_{b}}{\sqrt{K}}$ symbolizes the coefficient of inertia of porous material, $\beta _{1}$ and $\beta _{2}$ are the linear and nonlinear components of thermal expansion, respectively, $C_{b}$ symbolizes drag coefficient and $T_{\infty }$ ambient liquid temperature. It is worthy to mention here that $+g\left[ \beta _{1}\left( T-T_{\infty }\right) +\beta _{2}\left( T-T_{\infty }\right) ^{2} \right] \cos (\alpha )$ appears due to nonlinear convection and $-\frac{v}{K} u-Fu^{2}$ is because of the non-Darcian porous medium. Further, we have taken the impact of thermal stratification over the inclined sheet. The boundary conditions for the governing equations are as follows:

$$\begin{aligned} \left. \begin{aligned}&u =\epsilon u_{w}, \quad v=v_{0},\quad T=T_{f}=T_{0}+a_{1}x,\quad \text {at}\quad y=0, \\&u \rightarrow 0,\quad T\rightarrow T_{\infty }=T_{0}+d_{1}x,\quad \text {as}\quad \text {y}\rightarrow \infty , \end{aligned} \right\} \end{aligned}$$

(4)

where, in (4), $v_{0}$ symbolizes mass flux velocity, $T_{f}$ and $T_{0}$ represent heated liquid temperature and reference temperature, respectively, and $a_{1}$ and $d_{1}$ are dimensional constants. Next, we pursue for the similarity solution of the above equations based on boundary conditions (4) by proposing the following similarity transformation first:

$$\begin{aligned} \left. \begin{aligned}&\omega =\sqrt{vxu_{w}\left( x\right) }f\left( \zeta \right) =\sqrt{av}xf\left( \zeta \right) , \\&\zeta =\sqrt{\frac{u_{w}\left( x\right) }{vx}}y=\left( \frac{a}{v}\right) ^{\frac{1}{2}}y, \\&\theta \left( \zeta \right) =\frac{T-T_{\infty }}{T_{f}-T_{0}}, \end{aligned} \right\} \end{aligned}$$

(5)

where $\zeta$ is the similarity variable. The ordinary coupled boundary value problem is achieved as:

$$\begin{aligned}&f^{\prime \prime \prime }+ff^{\prime \prime }+\beta \left( 2ff^{\prime }f^{\prime \prime }-f\text {}^{2}f^{\prime \prime \prime } \right) +M\sin ^{2}\left( \gamma \right) \left[ \beta ff^{\prime \prime }-f^{\prime } \right] \nonumber \\&\quad +\delta \left( 1+\beta _{t}\theta \right) \theta \cos (\alpha ) -\lambda _{1} f^{\prime }-\left( 1+Fr\right) f^{\prime }\text { }^{2} =0, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{1}{\Pr }\theta ^{\prime \prime }+f\text {}\theta ^{\prime }-f^{\prime } \theta -f^{\prime }S_{1} =0, \end{aligned}$$

(7)

and the boundary conditions are as follows:

$$\begin{aligned} \left. \begin{aligned}&f^{\prime } \left( 0\right) =\epsilon ,\quad f\left( 0\right) =S,\quad \theta \left( 0\right) =1-S_{1},\quad \text {at} \quad \zeta =0, \\&f^{\prime }\left( \zeta \right) \rightarrow 0,\quad \theta \left( \zeta \right) \rightarrow 0,\quad \text {as} \quad \zeta \rightarrow \infty , \end{aligned} \right\} \end{aligned}$$

(8)

in the above equations, primes denote differentiation corresponding to $\zeta$, $\beta$ and M are dimensionless Maxwell fluid parameter and the magnetic parameter, $\delta$ and $\beta _{t}$ represent the mixed convection parameter and nonlinear convection parameter, $\lambda _{1}$ symbolizes porosity parameter, Fr local inertia coefficient, $\mathrm{Pr}$ Prandtl number, $S_{1}$ the thermal stratification parameter, $\epsilon$ the stretching/shrinking parameter with $\epsilon >0$ for stretching and $\epsilon <0$ for the shrinking case, S is the parameter of suction/injection with $S>0$ for suction and $S<0$ for injection, and these are described as:

$$\begin{aligned}&\delta =\frac{\mathrm{Gr}_{x}}{{\mathrm{Re}}_{x}^{2}},\quad \beta _{t}=\frac{\beta _{2}\left( T_{f}-T_{0}\right) }{\beta _{1}},\quad \lambda _{1}=\frac{\nu }{Ka} ,\quad Fr=\frac{C_{b}}{\sqrt{K}}x, \\&\mathrm{Gr}_{x}=g\beta _{1}\frac{\left( T_{f}-T_{0}\right) x^{3}}{\nu ^{2}},\quad {\mathrm{Re} }_{x}=\frac{xu_{w}}{\nu },\quad u_{w}=ax, \quad \mathrm{Pr} =\frac{\mu c_{p}}{k}, \\&\beta =\lambda a, \quad M=\sigma \frac{B_{0}^{2}}{\rho a},\quad \mu =\rho \nu , \quad S_{1}=\frac{d_{1}}{a_{1}}, \end{aligned}$$

where $\mathrm{Gr}_{x}$ is the Grashof number and $\mathrm{Re}_{x}=u_{w}(x)x/\nu$ symbolizes local Reynolds number. For operational objectives, the skin friction coefficient $C_{f}$ and the local Nusselt number $\mathrm{Nu}_{x}$ can be determined by the functions $f\left( \zeta \right)$ and $\theta \left( \zeta \right)$, respectively, as:

$$\begin{aligned} C_{f}=\frac{\tau _{w}}{\rho u_{w}^{2}(x)/2}, \mathrm{Nu}_{x}=\frac{xq_{w}}{ k(T_{w}-T_{\infty })} \end{aligned}$$

(9)

whereas $\tau _{w}=\mu \left( \partial u / \partial y\right) _{y=0}$ is shear stress and $q_{w}=-k\left( \partial T/\partial y\right) _{y=0}$ is heat flux at the surface. Using similarity transformation (5), we acquire

$$\begin{aligned} \frac{1}{2}C_{f}\mathrm{Re}_{x}^{1/2}=f^{\prime \prime } (0), \mathrm{Nu}_{x}/{\mathrm{Re}} _{x}^{1/2}=-\theta ^{\prime } (0), \end{aligned}$$

(10)

Table 1 Numerical values of Skin friction when $\mathrm{Pr} = 1, M = 0, S = 0, \epsilon = 1.0$ (stretching case) and comparison with previous work

Table 2 Numerical values of skin friction when $\mathrm{Pr} = 1, M = 2, \beta = 0, \epsilon = -1.0$ (shrinking case) and comparison with previous work

Fig. 1

Geometry for the flow under discussion

Fig. 2

Impact of $\gamma$ on velocity $\epsilon = 1$

Fig. 3

Impact of $\gamma$ on velocity $\epsilon = -1$

Fig. 4

Impact of $\beta$ on velocity for $\epsilon =1$

Fig. 5

Impact of $\beta$ on velocity for $\epsilon =-1$

Fig. 6

Impact of $\delta$ on temperature

Fig. 7

Impact of $\delta$ on velocity

Fig. 8

Impact of Fr on velocity

Fig. 9

Impact of $\beta _{t}$ on velocity profile

Fig. 10

Impact of $\mathrm{Pr}$ on temperature

Fig. 11

Impact of $\lambda _{1}$ on temperature

Fig. 12

Impact of $\alpha$ on velocity

Fig. 13

Impact of $S_{1}$ on temperature

Fig. 14

Impact of $\epsilon$ on temperature profile

Fig. 15

Impact of S on temperature

Fig. 16

Impact of M and $\beta$ on the Nusselt number

Fig. 17

Impact of $\mathrm{Pr}$ and $S_{1}$ on the Nusselt number

3 Solution methodology

Boundary value problems (6), (7) cannot be easily solved analytically because these ordinary differential equations (ODEs) are nonlinear and coupled equations. So, for the sake of numerical solution, the shooting method has been considered. The fourth-order Runge–Kutta method and Newton’s method are essential aspects of the shooting method to find the solution of nonlinear differential equations of the first order. Let us use the following notations to get the first-order ordinary differential equations as:

$$\begin{aligned} f=y_{1},\;f^{\prime }=y_{1}^{\prime }=y_{2},\; f^{\prime \prime }=y_{2}^{\prime }=y_{3},\text { \ }\theta =y_{4},\; \theta ^{\prime }=y_{4}^{\prime }=y_{5} \end{aligned}$$

(11)

By using notations (11), we get the following IVP:

$$\begin{aligned} \left. \begin{aligned}&y_{1}^{\prime } =y_{2} \\&y_{2}^{\prime }=y_{3} \\&y_{3}^{\prime } =\frac{-y_{1}y_{3}-2\beta y_{1}y_{2}y_{3}-M\sin ^{2}\left( \gamma \right) \left[ \beta y_{1}y_{3}-y_{2}\right] -\delta \left( 1+\beta _{t}y_{4}\right) y_{4}\cos (\alpha )+\lambda _{1} y_{2}+\left( 1+Fr\right) y_{2}^{2}}{\left( 1-\beta y_{1}^{2}\right) } \\&y_{4}^{\prime } =y_{5} \\&y_{5}^{\prime } =\left( y_{2}y_{4}+y_{2}S_{1}-y_{1}y_{5}\right) \mathrm{Pr} \end{aligned}\right\} \nonumber \\ \end{aligned}$$

(12)

and essential initial condition (8) takes the form as

$$\begin{aligned} y_{1}\left( 0\right) =S,\quad y_{2}\left( 0\right) =\epsilon ,\quad y_{3}\left( 0\right) =c,\quad y_{4}\left( 0\right) =1-S_{1},\quad y_{5}\left( 0\right) =d, \end{aligned}$$

(13)

where c and d are our initial guesses. To achieve the desired results of the aforementioned system numerically, we have altered the domain $\left[ 0,\infty \right)$ by bounded domain $\left[ 0,\zeta _{\infty }\right]$, where $\zeta _{\infty }$ is a relevant finite positive real number. It is chosen in such a way that after its specific value, which is usually in between [5, 7], there is no specific alteration on obtained results. In (12) and (13), the missing initial conditions c and d are to be selected such that

$$\begin{aligned} y_{2}\left( \zeta _{\infty },c,d\right) =0,\qquad y_{4}\left( \zeta _{\infty },c,d\right) =0. \end{aligned}$$

Such estimates are modified by the scheme of the Newton’s method. The algorithmic pattern repeats until the condition below is fulfilled

$$\begin{aligned} \max \left\{ \left| y_{2}\left( \zeta _{\infty },c_{n},d_{n}\right) \right| ,y_{4}\left( \zeta _{\infty },c_{n},d_{n}\right) \right\} <\chi \end{aligned}$$

wherein the tolerance is $\chi$ $>0$. We have fixed $\chi =10^{-5}$ for all computations in this article. The code is verified in limiting case as shown in Tables 1 and 2, with the results of previous articles.

4 Results and discussion

This section aims at examining the numerical results shown in the form of tables and graphs. The analyses were made for various values of factors $\beta$, M, $\mathrm{Pr}$, S, $\epsilon$, $\gamma$, Fr, $\delta$, $\beta _{t}$, $\lambda _{1}$ and $S_{1}$, and the effect of all such specifications on temperature and velocity profiles is also described in detail. In all these figures, we have considered $0 \le \beta \le 0.15,\, 0.6 \le \mathrm{Pr} \le 1.2,\, \pi /6 \le \gamma \le \pi /2,\, 0.1 \le \beta _{t} \le 1.5,\, 0.0 \le M \le 3.0, 0.1 \le \lambda \le 1.0,\, 0.1 \le Fr \le 1.0, \, 0.1 \le S_{1} \le 0.7,\, 0.1 \le \delta \le 0.7, \, 2.0 \le S \le 2.6, \, \pi /6 \le \alpha \le \pi /2,\, -1.0 \le \epsilon \le 1.0,$ unless specified.

Table 3 Numerical results of skin friction coefficient and Nusselt number for various values of $\gamma$, S, $\mathrm{Pr}$, M, $\beta$, Fr, $\beta _{t}$, $\lambda _{1}$, $S_{1}$, $\delta$ and $\epsilon$

The effect of aligned angle $\gamma$ can be observed in Fig. 2 for the velocity profile against the stretching case $\epsilon = 1$. It can be observed that when $\gamma$ escalates, the fluid’s velocity is demolished. The cause of this behavior is that an enhancement in the aligned angle escalates the magnetic field, resulting in an opposite force to the flow generation. That force is termed as the Lorentz force, which decreases the solidity of the momentum boundary layer. In Fig. 3 the influence of aligned angle on the shrinking surface momentum profile, $\epsilon = -1$, is demonstrated. It is observed that when $\gamma$ is boosted, this enhances the speed of the flow for the shrinking sheet. The effect on the velocity profile for the dimensionless Maxwell parameter, when $\epsilon = 1$, is displayed in Fig. 4. It can be recognized that by raising the value of the Maxwell parameter, velocity profile declines. In fact, the amount of the Maxwell parameter determines the nature of the liquid. At $\beta = 0$ the fluid becomes Newtonian, and by rising the values of $\beta$, it ultimately attains the non-Newtonian shear thickening nature and viscosity increases that lower fluid’s velocity. The curves of $f^\prime (\zeta )$ are given in Fig. 5 for various values of the dimensionless Maxwell parameter as $\epsilon =-1$. Here, raising the magnitude of the Maxwell parameter improves both the speed and associated stiffness of the boundary layer. Figure 6 shows the effects of the $\delta$, mixed convection parameter on the temperature domain. This figure shows that significant differences in the parameter of the mixed convection impart comparatively small changes in dimensionless temperature. So, whenever the mixed convection parameter $\delta$ increases, the temperature profile decreases. From Fig. 7, as the mixed convective factor $\delta$ raises, the velocity of $f^\prime (\zeta )$ increases dramatically for the shrinking case. This occurs because the buoyancy force enhances due to higher $\delta$. Figure 8 characterizes the $f^\prime (\zeta )$ deviations for various measurements of the local inertia coefficient Fr. The greater Fr indicates that the porosity of the medium enhances which is responsible for the reduction in fluid speed and the thickness of the momentum boundary layer. This decrement is very nominal for the shrinking case. The $f^\prime$($\zeta$) curves for different values of the nonlinear convection function are plotted in Fig. 9. When there is an increment in $\beta _{t}$, a mounting velocity is noted. Figure 10 shows the Prandtl number’s attitude on the thermal profile. Here $\theta (\zeta )$ and the related thermal layer thickness decline for greater $\mathrm{Pr}$. In consideration of an inverse relationship between the thermal diffusivity and the Prandtl number value, larger $\mathrm{Pr}$ results in the reduction of diffusiveness of temperature. This decrease in thermal diffusivity shows a drop in temperature and thermal layer strength. Figure 11 determines the relationship between the temperature $\theta (\zeta )$ and porosity parameter $\lambda _{1}$. For bigger $\lambda _{1}$, $\theta (\zeta )$ enhanced. The physical presence of porous content enhances the counteraction to fluid movement, which creates inclination in the temperature of the fluid. When the angle of inclination of the stretching sheet is enhanced, it is found that the fluid’s speed is decreased for the shrinking surface and this observation is noted from Fig. 12. The influence of $S_{1}$ on $\theta (\zeta )$ is shown in Fig. 13. When the thermal stratification parameter $S_{1}$ is increased, the difference in temperature between surface and atmosphere decreased. This notable temperature differential causes the temperature profile to decrease. Figure 14 sketches stretching/shrinking parameter $\epsilon ^{\prime }s$ impact on $\theta (\zeta )$. Lesser shrinking causes a decrement in the temperature profile. Figure 15 exhibits the impact of the suction/injection parameter S on the profile of temperature. It is shown that the temperature profile decreases as S goes up. In Fig. 16, the influence of the M magnetic parameter and the $\beta$ dimensionless Maxwell parameter can be seen on the Nusselt number. It can be viewed that when M and $\beta$ increase, the Nusselt number decreases. Because of an increase in the magnetic parameter M, the temperature of the fluid is elevated which means that now the heat flux rate for the higher magnetic parameter is diminished. Figure 17 sketches the influence of the Prandtl number and S1 thermal stratification factor on the Nusselt number. It is observed through the graph that the higher $\mathrm{Pr}$ increases the Nusselt number. A reverse relation is noticed in the case of $S_{1}$, and transfer of heat decreased for the escalating thermal stratification function. In Table 3, the numerical results related to the skin coefficient and the Nusselt number are discussed for different physical parameters. The rise in the magnetic parameter M and suction/injection speed S is noted to improve the local coefficient of skin friction and local Nusselt number. The outcome is that the increment in the aligned angle $\gamma$, Prandtl number $\mathrm{Pr}$, Maxwell parameter $\beta$, the nonlinear thermal variable $\beta _{t}$, porosity parameter $\lambda _{1}$ and mixed convection variable $\delta$ results escalation in the Nusselt number and skin friction coefficient. Moreover, the Nusselt number and skin friction coefficient have the inverse relation with the increasing local inertia coefficient Fr and the thermal stratification variable $S_{1}$. And the shrinking of the sheet has the inverse relation only with the skin friction coefficient.

5 Concluding remarks

In this paperwork, we have examined the numerical study of the aligned magnetic field in the direction of heat and flow transmission of upper-convected Maxwell fluid (UCM) with nonlinear convection in a Darcian porous media across stretching/shrinking sheet. The governing nonlinear partial differential equations (PDEs) of momentum and temperature are restricted to coupled ODEs by implementing a compatible similarity conversion. The shooting method is used in the intention to reach the solution. For the influence of suitable specifications, the value of different physical parameters under consultation on dimensionless velocity and temperature is demonstrated graphically. The main findings are as follows:

• The enhancement in the magnetic parameter and the suction/injection parameter escalates the local skin friction coefficient and the local Nusselt number.

• The elevated angle of inclination of the magnetic field strengthens the coefficient of skin friction and Nusselt number.

• Velocity decreases for the mounting inclination angle of the sheet.

• Local inertia coefficient is accountable for the velocity profile reduction.

• Aligned magnetic field has the opposite relation for the shrinking and stretching sheet.