A new numerical approach to the solution of PDEs with optimal accuracy on irregular domains and Cartesian meshes—Part 1: the derivations for the wave, heat and Poisson equations in the 1-D and 2-D cases

Abstract

A new numerical approach for the time-dependent wave and heat equations as well as for the time-independent Poisson equation on irregular domains has been developed. Trivial Cartesian meshes and simple 9-point stencil equations with unknown coefficients are used for 2-D irregular domains. The calculation of the coefficients of the stencil equations is based on the minimization of the local truncation error of the stencil equations and yields the optimal order of accuracy. The treatment of the Dirichlet and Neumann boundary conditions in the new approach is related to the development of high-order boundary conditions with the stencils that include the same or a smaller number of grid points compared to that for the regular 9-point internal stencils. At similar 9-point stencils, the accuracy of the new approach is two orders higher than that for the linear finite elements. The numerical results for irregular domains in Part 2 of the paper also show that at the same number of degrees of freedom, the new approach is even much more accurate than the quadratic and cubic finite elements with much wider stencils. Similar to our recent results on regular domains, the order of the accuracy of the new approach for the Poisson equation on irregular domains with square Cartesian meshes is higher than that with rectangular Cartesian meshes. The new approach can be directly applied to other partial differential equations.

1 Introduction

The development of numerical techniques for an accurate solution of partial differential equations (PDEs) on complex domains is an active area of research. The finite element method, the finite volume method, the isogeometric elements, the spectral elements and similar techniques represent very powerful tools for the solution of PDE for a complex geometry. However, the generation of non-uniform meshes for a complex geometry is not simple and may lead to the decrease in accuracy of these techniques if ‘bad’ elements (e.g., elements with small angles) appear in the mesh. Moreover, the conventional derivation of discrete equations for these techniques (e.g., based on the Galerkin approaches) does not lead to the optimal accuracy. For example, it has been shown in many publications on wave propagation that at the same width of the stencil equations of a semi-discrete system for regular rectangular domains with uniform meshes, the accuracy of the conventional linear finite elements can be improved from order two to order four (e.g., see [1, 14,15,16, 31,32,33, 40, 42, 46, 51, 59] and others), and the accuracy of the conventional high-order finite and isogeometric elements can be improved from order 2p to order $2p+2$ where p is the element order (e.g., see [2, 47, 56,57,58]). However, the improvement in the order of accuracy for the high-order elements in [2, 47, 56,57,58] is not optimal. In our papers [21, 23, 28], the order of accuracy of the high-order elements on rectangular domains has been improved to 4p, and this order is optimal at a given width of stencil equations.

There is a significant number of publications related to the numerical solution of different PDEs on irregular domains with uniform embedded meshes. For example, we can mention the following fictitious domain numerical methods that use uniform embedded meshes: the embedded finite difference method, the cut finite element method, the finite cell method, the Cartesian grid method, the immersed interface method, the virtual boundary method, the embedded boundary method, etc, e.g., see [3,4,5, 7,8,9,10,11, 13, 17,18,19, 34,35,39, 41, 43,44,45, 48,49,50, 52,53,55, 60] and many others. The main objective of these techniques is to simplify the mesh generation for irregular domains as well as to mitigate the effect of ‘bad’ elements. For example, the techniques based on the finite element formulations (such as the cut finite element method, the finite cell method, the virtual boundary method and others) yield the $p+1$ order of accuracy even with small cut cells generated by the complicated irregular boundary (e.g., see [7, 41, 44, 48, 49, 53, 55] and many others). The main advantage of the embedded boundary method developed in [34, 37,38,39, 45] is the use of a simple Cartesian mesh. The boundary conditions or fluxes in these techniques are interpolated using the Cartesian grid points, and this leads to the increase in the stencil width for the grid points located close to the boundary. (However, the numerical techniques developed in [34, 37,38,39, 45] provide just the second order of accuracy for the global solution.) Therefore, the development of robust numerical techniques for the solution of PDEs on irregular domains that provide an optimal and high order of accuracy is still a challenging problem.

A new numerical approach suggested in this paper is the generalization of our previous numerical algorithms developed for the improvement of accuracy of linear and high-order finite element techniques for wave propagation problems and heat transfer problems for regular rectangular domains with uniform meshes. For example, in [20,21,22, 31,32,33] we have improved the accuracy of the linear finite elements and the high-order isogeometric elements used for wave propagation from order 2p to order 4p where p is the order of the polynomial basis functions. These techniques have been based on the reduction of the numerical dispersion error. Because the numerical dispersion error is based on the existence of exact and numerical harmonic solutions for systems of partial differential equations and its discrete counterpart, then the application of these approaches was limited to wave propagation problems for regular rectangular domains with uniform meshes only. (The numerical dispersion error is defined on uniform meshes.) In [21, 23, 28], we have improved the accuracy of the linear finite elements and the high-order isogeometric elements for time-dependent and time-independent heat transfer problems for regular rectangular domains with uniform meshes. In contrast to the use of the numerical dispersion error, the approach in [21, 23, 28] was based on the minimization of the order of the local truncation error and did not require the existence of exact and numerical harmonic solutions. However, the use of uniform meshes in [21, 23, 28] reduces the application of the technique to rectangular domains and significantly restricts the value of the proposed approach. Moreover, in our paper [21] it was shown that the direct application of some techniques with improved accuracy on uniform meshes (e.g., the MIR techniques in [14, 31, 59]) to non-uniform meshes leads to a significant degradation in the order of accuracy (e.g., by three orders for the wave equation). In this paper, we show that the approach based on the minimization of the local truncation error is very general and can be applied to different partial differential equations on complex irregular domains. We will call this approach as the optimal local truncation error method (OLTEM).

The idea of the proposed OLTEM is very simple. We start the development of a new numerical technique by assuming the stencil equations of a discrete or semidiscrete system of equations used for the solution of a system of partial differential equations. A stencil equation is a linear combination of the numerical values of the function (for a discrete system) or the function and its derivatives (for a semidiscrete system) at a number of grid points where the coefficients of the stencil equations are assumed to be unknown. These unknown coefficients are determined by the minimization of the order of the local truncation error for each stencil equation. This procedure includes a Taylor series expansion of the unknown exact solution at the grid points and its substitution into the stencil equation. As a result, we obtain the local truncation error in the form of a Taylor series. At this point, no information about partial differential equations is used. Then, the corresponding partial differential equations are applied at the grid points in order to exclude some partial derivatives in the expression for the local truncation error. Finally, the unknown coefficients of the stencil equation are calculated from a small local system of algebraic equations obtained by equating to zero the lowest terms in the Taylor series expansion of the local truncation error. The coefficients of the stencil equations are similarly calculated for the regular stencils located far from the boundary and for the cut stencils located close to the boundary. Then, a fully discrete or semidiscrete global system can be easily solved. The main advantages of the new approach are a high optimal accuracy and the simplicity of the formation of a discrete (semi-discrete) system of equations for irregular domains. The order of accuracy of the new approach cannot be improved without adding new grid points into the stencil equation. As a mesh, the grid points of a uniform rectangular (square) Cartesian mesh as well as the points of the intersection of the boundary of a complex irregular domain with the horizontal, vertical and diagonal grid lines of the uniform Cartesian mesh are used, i.e., in contrast to the finite element meshes, a trivial mesh is used with the new approach. Changing the width of the stencil equations, different linear and high-order numerical techniques can be developed.

We should mention that the OLTEM can be also used for the improvement of accuracy of the existing numerical techniques. Usually, many known numerical techniques finally reduce to a system of algebraic equations with respect to the unknown numerical solution at the grid points (or they can be often rewritten in this form). The coefficients of the final system of algebraic equations are defined by the corresponding numerical technique and in many cases do not yield the optimal accuracy. Therefore, the coefficients of the stencil equations for the corresponding numerical techniques can be recalculated by the minimization of the order of the local truncation error as described above. For example, using this idea, in [21, 23, 28] we have improved the accuracy of the linear finite elements and the high-order isogeometric elements for time-dependent and time-independent heat transfer problems on regular domains with uniform meshes. In [25, 27] we have developed 2-D 9-point and 25-point stencils for the time-dependent and time-independent elasticity on regular domains with uniform meshes that are similar to those for quadrilateral linear and quadratic finite elements. For these problems, the 9-point stencils provide the optimal second order of accuracy, while the 25-point stencils provide the 10th order of accuracy for the time-independent elasticity and the 6th order of accuracy for the time-dependent elasticity.

In this paper, we present the development of the new numerical approach for the time-dependent wave and heat equations as well as for the time-dependent Poisson equation in the general case of irregular domains in the 1-D and 2-D cases. Wave propagation in an isotropic homogeneous medium is described by the following scalar wave equation in domain $\Omega$:

$$\begin{aligned} \frac{\partial ^2 u}{\partial t^2} - c^2 \nabla ^2 u = f. \end{aligned}$$

(1)

Similarly, the heat equation in domain $\Omega$ can be written as:

$$\begin{aligned} \frac{\partial u}{\partial t} - a \nabla ^2 u = f. \end{aligned}$$

(2)

The Poisson equation in domain $\Omega$ has the following form:

$$\begin{aligned} \nabla ^2 u = f. \end{aligned}$$

(3)

In Eqs. (1)–(3), c is the wave velocity, a is the thermal diffusivity, $f (\mathbf{x}, t)$ is the loading (source) term, and u is the field variable. The Neumann boundary conditions $\mathbf{n} \cdot \bigtriangledown u = g_1$ on $\Gamma ^t$ and the Dirichlet boundary conditions $u=g_2$ on $\Gamma ^u$ are applied, where $\mathbf{n}$ is the outward unit normal on $\Gamma ^t$, and $\Gamma ^t$ and $\Gamma ^u$ denote the boundaries with the Neumann and Dirichlet boundary conditions, respectively. The initial conditions are $u (\mathbf{x}, t=0) = g_3$, $v (\mathbf{x}, t=0) = \frac{\mathrm{d}u}{\mathrm{d}t} (\mathbf{x}, t=0) =g_4$ in $\Omega$ for the wave equation and $u (\mathbf{x}, t=0) =g_3$ in $\Omega$ for the heat equation where $g_i$ ($i=1,2,3,4$) are the given functions.

Remark 1

The time and the right-hand side in Eqs. (1) and (2) can be rescaled as $\bar{t}= c t$, $\bar{f}=f/c^2$ and $\bar{t}= a t$, $\bar{f}=f/a$, respectively. In this case, the material parameters c and a will not be presented in the rescaled Eqs. (1) and (2). However, in order to keep the derivation of the right-hand side for the numerical technique without confusions, we will use the original notations given by Eqs. (1) and (2). For the rescaled Eqs. (1) and (2), the formulas presented below in the paper can be easily modified by putting $c=a=1$.

According to the new approach, we assume that the stencil equation for the wave and heat equations after the space discretization with a rectangular Cartesian mesh can be written as an ordinary differential equation:

$$\begin{aligned} \sum \limits _{i=1}^{L} \left( h^2 m_i \frac{\mathrm{d}^n u^{\mathrm{num}}_i}{\mathrm{d}t^n} + \bar{c} {k_i} u^{\mathrm{num}}_{i}\right) = \bar{f}, \end{aligned}$$

(4)

where $u^{\mathrm{num}}_i$ and $\frac{d^n u^{\mathrm{num}}_i}{dt^n}$ are the numerical solution for function u and its time derivative at the grid points, $m_i$ and $k_i$ are the unknown coefficients to be determined, L is the number of the grid points included into a stencil, $\bar{f} (t)$ is the discretized loading term (see the next sections), $n=2$ and $\bar{c}=c^2$ for the wave equation and $n=1$ and $\bar{c}=a$ for the heat equation, h is the mesh size along the $x-$ axis. The stencil equation for the Poisson equation after the space discretization can be written as an algebraic equation:

$$\begin{aligned} \sum \limits _{i=1}^{L} {k_i} u^{\mathrm{num}}_{i} = \bar{f}. \end{aligned}$$

(5)

Many numerical techniques such as the finite difference method, the finite element method, the finite volume method, the isogeometric elements, the spectral elements, different meshless methods and others can be finally reduced to Eqs. (4) and (5) with some specific coefficients $m_i$ and $k_i$ for the wave, heat and Poisson equations. In order to demonstrate a new technique, below we will assume a 3-point stencil in the 1-D case and a 9-point stencil in the 2-D case that correspond to the width of the stencils for the linear quadrilateral finite elements on Cartesian meshes. However, the stencils with any width can be used with the suggested approach.

Let us introduce the local truncation error used with the new approach. The replacement of the numerical values of the function $u^{\mathrm{num}}_i$ and its time derivatives $\frac{\mathrm{d}^n u^{\mathrm{num}}_i}{\mathrm{d}t^n}$ at the grid points in Eq. (4) by the exact solution $u_{i}$ and $\frac{\mathrm{d}^n u_i}{\mathrm{d}t^n}$ to the wave or heat equation, Eqs. (1) or (2), leads to the residual of this equation called the local truncation error e in space for the semidiscrete equation, Eq. (4):

$$\begin{aligned} e = \sum \limits _{i=1}^{L} \left( h^2 {m_i} \frac{\mathrm{d}^n u_i}{\mathrm{d}t^n}+ \bar{c} {k_i} u_{i} \right) - \bar{f}. \end{aligned}$$

(6)

Calculating the difference between Eqs. (6) and (4), we can get

$$\begin{aligned} e =\sum \limits _{i=1}^{L} \left\{ h^2 {m_i} \left[ \frac{\mathrm{d}^n u_i}{\mathrm{d}t^n} - \frac{\mathrm{d}^n u^{\mathrm{num}}_{i}}{\mathrm{d}t^n}\right] + \bar{c} {k_i} \left[ u_{i} - u^{\mathrm{num}}_{i}\right] \right\} = \sum \limits _{i=1}^{L} \left( h^2 {m_i} \bar{e}_i^v + \bar{c} {k_i} \bar{e}_i\right) , \end{aligned}$$

(7)

where $\bar{e}_i = u_{i} - u^{\mathrm{num}}_{i}$ and $\bar{e}_i^v = \frac{\mathrm{d}^n u_i}{\mathrm{d}t^n} - \frac{\mathrm{d}^n u^{\mathrm{num}}_{i}}{\mathrm{d}t^n}$ are the errors of function u and its time derivatives at the grid points i. As can be seen from Eq. (7), the local truncation error e is a linear combination of the errors of the function u and its time derivatives at the grid points i which are included into the stencil equation. The local truncation error e for Eq. (5) can be obtained from Eqs. (4)–(7) with $m_i=0$ and $\bar{c} = 1$.

Remark 2

The analysis and improvement of the error in space, Eq. (6), is considered in the paper. Therefore, for the numerical examples in Part II, a sufficiently small size of time steps is used for the time integration of Eq. (4). In this case, the error in time can be neglected and the numerical error is related to the space-discretization error only. However, Part II also includes a numerical example showing the effect of the size of time increments on the total error for the new approach and for FEM (see Fig. 18 in Part II).

In Sect. 2 we consider the development of the new numerical approach for the 1-D wave equation that also includes new high-order boundary conditions on conforming and non-conforming Cartesian meshes. In Sect. 3 we extend it to irregular domains with Cartesian meshes in the 2-D case. The new technique is uniformly derived for the 2-D wave and heat equations. In Sect. 4 we show that along with the time-dependent wave and heat equations, the new approach can be similarly developed for the time-independent Poisson equation. The numerical examples are presented in Part 2 of the paper [12]. For the derivation of many analytical expressions presented below, we use the computational program “Mathematica.” We should also mention that the suggested approach can be extended to the 3-D case (see [24, 30]) as well as to other partial differential equations (see [26, 27, 29]).

2 A new numerical approach for the 1-D wave equation (with zero load $f=0$ in Eq. (1))

In the 1-D case, we consider the wave equation only. The derivations and the coefficients of the stencil equation for the heat equation are exactly the same as those for the wave equation (this is explicitly demonstrated in the 2-D case).

2.1 The determination of the coefficients of the stencil equation

Fig. 1

The spatial locations of the degrees of freedom $u_{i}$ ($i = 1, 2, 3, 4,\ldots$) for a non-conforming uniform mesh in the vicinity of the left end of the 1-D domain

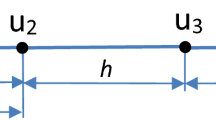
Let us consider a 1-D bounded domain and a Cartesian mesh with a mesh size h. In the case of non-conforming uniform grids when the grid points do not coincide with the boundary, the first grid points that are located outside the physical domain are moved to the boundary of the physical domain. Therefore, the size of the first and the last cells of the mesh can be different from the sizes of other cells, e.g., see the first four grid points in the vicinity of the left end of the 1-D domain in Fig. 1. For example, the size of the first cell in Fig. 1 equals $\xi h$ where the coefficient $0 \le \xi \le 1$ is defined by the location of the physical domain with respect to the Cartesian mesh. A 3-point stencil is assumed. In this case, Eq. (4) can be explicitly rewritten as follows:

$$\begin{aligned} h^2 \left( {m_1} {\ddot{u}^{\mathrm{num}}_{A-1}}+{m_2} {\ddot{u}^{\mathrm{num}}_{A}}+{m_3}{\ddot{u}^{\mathrm{num}}_{A+1}}\right) + c^2\left( {k_1} {u^{\mathrm{num}}_{A-1}}+{k_2} {u^{\mathrm{num}}_{A}}+{k_3}{u^{\mathrm{num}}_{A+1}}\right) = 0, \end{aligned}$$

(8)

where the case of zero loading $f = \bar{f} = 0$ is considered, $A=2,3,\ldots ,N-1$ (N is the total number of the grid points), the coefficients $m_i$ and $k_i$ ($i=1,2,3$) are to be determined from the minimization of the local truncation error. It is sufficient to derive the coefficients of the stencil for the degree of freedom $u_2$ ($A=2$) because the coefficients of the stencils for other degrees of freedom can be obtained from the formulas for $A=2$ (just changing the value of the coefficient $\xi$ related to the length of the first cell; see Fig. 1). To derive the coefficients $m_i$ and $k_i$ ($i=1,2,3$) in Eq. (8) at $A=2$, let us expand the exact solution $u_i$ and its time derivative $\frac{\partial ^2 u_i}{\partial t^2}$ at the grid point i ($i=A-1,A+1$) into a Taylor series at small $h \ll 1$ as follows (see Fig. 1 for the locations of $u_i$):

$$\begin{aligned} w_{A - 1}= & {} w_A - \frac{\partial w_A}{\partial x} \xi h + \frac{\partial ^2 w_A}{\partial x^2} \frac{(\xi h) ^2}{2!} - \frac{\partial ^3 w_A}{\partial x^3}\frac{(\xi h) ^3}{3!} + \frac{\partial ^4 w_A}{\partial x^4} \frac{(\xi h) ^4}{4!} + \cdots . \end{aligned}$$

(9)

$$\begin{aligned} w_{A + 1}= & {} w_A + \frac{\partial w_A}{\partial x} h + \frac{\partial ^2 w_A}{\partial x^2} \frac{h^2}{2!} + \frac{\partial ^3 w_A}{\partial x^3}\frac{h^3}{3!} + \frac{\partial ^4 w_A}{\partial x^4} \frac{h^4}{4!} + \cdots , \end{aligned}$$

(10)

where $w = u$ and $w = \frac{\partial ^2 u}{\partial t^2}$. The exact solution to Eq. (1) also meets the following equations at point A with the coordinates $x = x_A$ and $y = y_A$:

$$\begin{aligned} \frac{\partial ^2 u_A}{\partial t^2} - c^2 \frac{\partial ^2 u_A}{\partial x^2}= & {} 0, \end{aligned}$$

(11)

$$\begin{aligned} \frac{\partial ^{j+2} u_A}{\partial x^{j} \partial t^2} - c^2 \frac{\partial ^{j+2} u_A}{\partial x^{j + 2}}= & {} 0, \end{aligned}$$

(12)

where the case of zero loading $f = 0$ is considered and $j=1, 2, 3, 4,\ldots$. Equation (12) is obtained by the differentiation of Eq. (11) with respect to $x^{j}$. Replacing the numerical solution in Eq. (8) by the exact solution (similar to Eq. (6)) and using Eqs. (9)–(10) with $w = u$ and $w = \frac{\partial ^2 u}{\partial t^2}$ as well as Eqs. (11)–(12), we get a Taylor series of the local truncation error in space for the new approach:

$$\begin{aligned} e= & {} {c}^2 \left[ u_A ( {k_1}+ {k_2}+ {k_3})- {h} \frac{\partial u_A}{\partial x} (-\xi {k_1}+ {k_3}) +\frac{1}{2} {h}^2 \frac{\partial ^2 u_A}{\partial x^2} \left( \xi ^2 {k_1} + {k_3}+2({m_1}+ {m_2}+ {m_3})\right) \right. \nonumber \\&-\frac{1}{6} {h}^3 \frac{\partial ^3 u_A}{\partial x^3} \left( -\xi ^3 {k_1}+ {k_3}+6(-\xi {m_1}+ {m_3})\right) +\frac{1}{24} {h}^4 \frac{\partial ^4 u_A}{\partial x^4} \left( \xi ^4 {k_1} + {k_3}+12 (\xi ^2 {m_1}+{m_3})\right) \nonumber \\&+\frac{1}{120} {h}^5 \frac{\partial ^5 u_A}{\partial x^5} \left( -\xi ^5 {k_1} + {k_3} +20 (-\xi ^3 {m_1}+{m_3}) \right) +\frac{1}{720} {h}^6 \frac{\partial ^6 u_A}{\partial x^6} \left( \xi ^6 {k_1}+{k_3}+30 (\xi ^4 {m_1}+ {m_3})\right) \nonumber \\&\left. +\frac{1}{5040} { {h}^7 \frac{\partial ^7 u_A}{\partial x^7} \left( -\xi ^7 {k_1}+{k_3} +42 (-\xi ^5 {m_1}+ {m_3})\right) }\right] +O\left( {h}^{8}\right) . \end{aligned}$$

(13)

Due to the use of Eqs. (11) and (12), the local truncation error in Eq. (13) does not include the time derivatives. Equating the first five coefficients with the smallest orders of h in Eq. (13) to zero, we get a linear system of five algebraic equations:

$$\begin{aligned}&{k_1}+ {k_2}+ {k_3} = 0, \qquad -\xi {k_1}+ {k_3} = 0, \qquad \xi ^2 {k_1} + {k_3}+2({m_1}+ {m_2}+ {m_3}) = 0,\\&-\xi ^3 {k_1}+ {k_3}+6(-\xi {m_1}+ {m_3}) = 0, \qquad \xi ^4 {k_1} + {k_3}+12 (\xi ^2 {m_1}+{m_3}) = 0. \end{aligned}$$

Solving this system, we can find the following coefficients $m_i$ and $k_i$ ($i=1,2,3$) of the stencil Eq. (8) that yield the minimum local truncation error:

$$\begin{aligned} {m_1}= & {} -\frac{(-1 + \xi + \xi ^2)}{(1 + \xi ) (1 + 3 \xi + \xi ^2)} a_1 , \qquad {m_2}= a_1 , \qquad {m_3}= \frac{\xi (1 + \xi - \xi ^2)}{(1 + \xi ) (1 + 3 \xi + \xi ^2)} a_1, \nonumber \\ {k_1}= & {} -\frac{12 a_1}{1 + 4 \xi + 4 \xi ^2 + \xi ^3}, \qquad {k_2}= \frac{12 a_1}{1 + 3 \xi + \xi ^2}, \qquad {k_3}= -\frac{12 \xi a_1}{1 + 4 \xi + 4 \xi ^2 + \xi ^3}, \end{aligned}$$

(14)

where $a_1$ is an arbitrary coefficient. For the other degrees of freedom with $A=3,4,\ldots ,N-2$ that correspond to the uniform grid, the coefficients $m_i$ and $k_i$ ($i=1,2,3$) of the stencil equations can be obtained from Eq. (14) at $\xi =1$ and they are:

$$\begin{aligned} {m_1}= & {} \frac{a_1}{10}, \qquad {m_2}= a_1 \,, \qquad {m_3}= \frac{a_1}{10}, \nonumber \\ {k_1}= & {} -\frac{6 a_1}{5}, \qquad {k_2}= \frac{12 a_1}{5}, \qquad {k_3}= -\frac{6 a_1}{5}. \end{aligned}$$

(15)

Inserting the coefficients $m_i$ and $k_i$ ($i=1,2,3$) for the new approach (see Eq. (14)) into Eq. (13), we get the following local truncation error:

$$\begin{aligned} e_{\mathrm{new}}= & {} - \frac{(-1 + \xi ) \xi (2 + \xi ) (1 + 2 \xi ) c^2 h^5 a_1 \frac{\partial ^{5} u_A }{\partial x^{5}}}{30 (1 + \xi (3 + \xi ))} +\frac{ \xi (3 + (-1 + \xi ) \xi (2 + \xi ) (-1 + 3 \xi )) c^2 h^6 a_1 \frac{\partial ^{6} u_A }{\partial x^{6}}}{120 (1 + \xi (3 + \xi ))} \nonumber \\&-\frac{(-1 + \xi ) \xi (1 + (-1 + \xi ) \xi ) (5 + \xi (12 + 5 \xi )) c^2 h^7 a_1 \frac{\partial ^{7} u_A }{\partial x^{7}}}{840 (1 + \xi (3 + \xi ))} + O(h^{8}) \, \end{aligned}$$

(16)

for the stencil equation for the degree of freedom $u_2$ ($A=2$) located close to the boundary with the coefficient $\xi$ that can be different from unity, and

$$\begin{aligned} e_{\mathrm{new}}^{\mathrm{unif}} = \frac{c^2 a_1 }{20 } \frac{\partial ^{6} u_A }{\partial x^{6}} h^{6} + O(h^{8}) \, \end{aligned}$$

(17)

for the regular stencil equations for the grid points located far from the boundary with $\xi =1$ ($A=3,4,\ldots ,N-2$). It should be mention that small distances from the grid points to the boundary (or small $\xi \ll 1$) do not decrease the accuracy of the new approach. Moreover, at small $\xi \ll 1$, the accuracy is higher than that at $\xi \approx 0.5$; see Fig. 2 for the variation of the leading term of the local truncation error in Eq. (16) as a function of $\xi$.

In the final semidiscrete system, there are only two stencils (Eq. (8) at $A=2$ and $A=N-1$) with the 5th order of the local truncation error, see Eq. (16), and $N-4$ stencils (Eq. (8) at $A=3,4,\ldots ,N-2$) with the 6th order of the local truncation error, see Eq. (17). These stencils provide the 4th order of accuracy of the entire numerical solution at mesh refinement for a large number N of the grid points.

Fig. 2

The variation of the leading term $Coef_1 = - \frac{(-1 + \xi ) \xi (2 + \xi ) (1 + 2 \xi ) }{30 (1 + \xi (3 + \xi ))}$ in Eq. (16) as a function of $\xi$ (see Fig. 1)

It is interesting to mention that for the conventional linear finite elements that also have a 3-point stencil, the local truncation error is:

$$\begin{aligned} e_{FE} = \frac{c^2 (1+3 \xi ^2) h^4}{12 } \frac{\partial ^4 u_A}{\partial x^{4}} + O(h^{5}) \, \end{aligned}$$

(18)

for a degree of freedom $u_2$ of a non-uniform mesh shown in Fig. 1. As can be seen from Eq. (18), the local truncation errors for the linear finite elements have the same orders on non-uniform ($\xi \ne 1$) and uniform ($\xi =1$) meshes. These stencils provide the second order of accuracy of the entire finite element solution at mesh refinement for a large number N of the grid points.

2.2 Boundary conditions

The application of the boundary conditions at the left and right ends of the 1-D domain is similar. Therefore, we show this application for the left end only.

2.2.1 Dirichlet boundary conditions

The application of the Dirichlet boundary conditions in the new approach is trivial and similar to that for the finite elements. We simply use $u_1^{\mathrm{num}} = g_2(t)$ (and, as a consequence, $\ddot{u}_1^{\mathrm{num}} = \ddot{g}_2(t)$) in the stencil equation, Eq. (8), at $A=2$, i.e., the Dirichlet boundary conditions are exactly imposed. Here, $g_2(t)$ is a given function of time t that describes the Dirichlet boundary conditions. The final semidiscrete system of equations includes $N-2$ equations given by Eq. (8) with $A=2,\ldots ,N-1$ and the two Dirichlet boundary conditions for the degrees of freedom $u_1^{\mathrm{num}}$ and $u_N^{\mathrm{num}}$.

2.2.2 Neumann boundary conditions (with the inclusion of boundary degrees of freedom)

For the imposition of the Neumann boundary conditions, we will show two possible approaches. The first approach is based on an additional stencil equation for the boundary grid point $u_1$, and the degree of freedom $u_1$ is included into the stencil equation. We assume that this stencil has the same form as that for the grid point $u_2$ given by Eq. (8) at $A=2$ with nonzero right-hand side term $f_1$:

$$\begin{aligned} h^2 \left( {m_1} {\ddot{u}^{\mathrm{num}}_{1}}+{m_2} {\ddot{u}^{\mathrm{num}}_{2}}+{m_3}{\ddot{u}^{\mathrm{num}}_{3}}\right) + c^2\left( {k_1} {u^{\mathrm{num}}_{1}}+{k_2} {u^{\mathrm{num}}_{2}}+{k_3}{u^{\mathrm{num}}_{3}}\right) = f_1, \end{aligned}$$

(19)

where $f_{1}$ is the load term for the Neumann boundary conditions that will be defined later. The difference in the derivation of the coefficients $m_i$ and $k_i$ of the stencil Eqs. (8) and (19) consists in the fact that for the stencil Eq. (19) we use a Taylor series for $u_2$ and $u_3$ as well as for their time derivatives in the vicinity of the first grid point (in contrast to Eqs. (9)–(12)):

$$\begin{aligned} w_{2}= & {} w_1 + \frac{\partial w_1}{\partial x} \xi h + \frac{\partial ^2 w_1}{\partial x^2} \frac{(\xi h) ^2}{2!} + \frac{\partial ^3 w_1}{\partial x^3}\frac{(\xi h) ^3}{3!} + \frac{\partial ^4 w_1}{\partial x^4} \frac{(\xi h) ^4}{4!} + \cdots . \end{aligned}$$

(20)

$$\begin{aligned} w_{3}= & {} w_1 + \frac{\partial w_1}{\partial x} (\xi +1)h + \frac{\partial ^2 w_1}{\partial x^2} \frac{[(\xi +1)h]^2}{2!} + \frac{\partial ^3 w_1}{\partial x^3}\frac{[(\xi +1)h]^3}{3!} + \frac{\partial ^4 w_1}{\partial x^4} \frac{[(\xi +1)h]^4}{4!} + \cdots , \end{aligned}$$

(21)

where $w = u$ and $w = \frac{\partial ^2 u}{\partial t^2}$. For a sufficiently smooth solution, the exact solution $u_1(x=x_1,t)$ to Eq. (1) at the boundary also meets Eqs. (11) and (12) with $A=1$. Replacing the numerical solution in Eq. (19) by the exact solution (similar to Eq. (6)) and using Eqs. (20)–(21) with $w = u$ and $w = \frac{\partial ^2 u}{\partial t^2}$ as well as Eqs. (11)–(12) with $A=1$, we get a Taylor series of the local truncation error in space for the new approach:

$$\begin{aligned} e= & {} {c}^2 \left\{ \left[ u_1 ({k_1}+{k_2}+{k_3}) +\frac{1}{2} h^2 \frac{\partial ^2 u_1}{\partial x^2} (\xi ^2 ({k_2}+{k_3})+2 \xi {k_3}+{k_3}+2 ({m_1}+{m_2}+{m_3}))\right. \right. \nonumber \\&+\frac{1}{24} h^4 \frac{\partial ^4 u_1}{\partial x^4} (\xi ^4 {k_2}+12 \xi ^2 {m_2}+(\xi +1)^4 {k_3}+12 (\xi +1)^2 {m_3}) \nonumber \\&+\frac{1}{720} h^6 \frac{\partial ^6 u_1}{\partial x^6} (\xi ^6 {k_2}+30 \xi ^4 {m_2}+(\xi +1)^6 {k_3}+30 (\xi +1)^4 {m_3}) \nonumber \\&+\frac{ h^8 \frac{\partial ^8 u_1}{\partial x^8} (\xi ^8 {k_2}+56 \xi ^6 {m_2}+(\xi +1)^8 {k_3}+56 (\xi +1)^6 {m_3})}{40320} \nonumber \\&\left. +\frac{h^{10} \frac{\partial ^{10} u_1}{\partial x^{10}} (\xi ^{10} {k_2}+90 \xi ^8 {m_2}+(\xi +1)^{10} {k_3}+90 (\xi +1)^8 {m_3})}{3628800}\right] \nonumber \\&+ \left[ h (\xi ({k_2}+{k_3})+{k_3}) \frac{\partial u_1}{\partial x} +\frac{1}{6} h^3 \frac{\partial ^3 u_1}{\partial x^3} (\xi ^3 ({k_2}+{k_3})+3 \xi ^2 {k_3}+3 \xi ({k_3}+2 ({m_2}+{m_3}))+{k_3}+6 {m_3}) \right. \nonumber \\&+\frac{1}{120} h^5 \frac{\partial ^5 u_1}{\partial x^5} (\xi ^5 {k_2}+20 \xi ^3 {m_2}+(\xi +1)^5 {k_3}+20 (\xi +1)^3 {m_3}) \nonumber \\&+\frac{ h^7 \frac{\partial ^7 u_1}{\partial x^7} (\xi ^7 {k_2}+42 \xi ^5 {m_2}+(\xi +1)^7 {k_3}+42 (\xi +1)^5 {m_3})}{5040} \nonumber \\&\left. \left. +\frac{ h^9 \frac{\partial ^9 u_1}{\partial x^9} (\xi ^9 {k_2}+72 \xi ^7 {m_2}+(\xi +1)^9 {k_3}+72 (\xi +1)^7 {m_3})}{362880} - f_1/c^2\right] \right\} +O\left( {h}^{11}\right) . \end{aligned}$$

(22)

Due to the use of Eqs. (11) and (12), the local truncation error in Eq. (22) does not include the time derivatives. From now, we will use the Neumann boundary conditions at the left boundary:

$$\begin{aligned} \frac{\partial u_1}{\partial x} (x_1,t) = g_1 (t), \end{aligned}$$

(23)

where $g_1 (t)$ is a given function of time t. Taking the even derivatives of Eq. (23) with respect to time, we can express the odd spatial derivatives of the solution $u_{1} (x_1,t)$ with respect to x at the left boundary in terms of the known boundary conditions $g_1 (t)$. For example,

$$\begin{aligned} u_{xtt} (x_1,t) = c^2 u_{xxx} (x_1,t) = (g_1)_{tt} (t), \end{aligned}$$

(24)

where for the first equality in Eq. (24), the second derivative with respect to time is replaced by the second derivative with respect to space using the partial differential equation, Eq. (1), indices x and t designate the corresponding partial derivatives with respect to x and t. Equating to zero the expression in the second square brackets of Eq. (22), we define the load vector $f_1$ for the stencil equation, Eq. (19), that can be expressed in terms of the given Neumann boundary conditions at the left boundary as follows:

$$\begin{aligned} f_1 \,= & {} \, {c}^2 \left[ h (\xi ({k_2}+{k_3})+{k_3}) \frac{\partial u_1}{\partial x}\right. \nonumber \\&+\frac{1}{6} h^3 \frac{\partial ^3 u_1}{\partial x^3} \left( \xi ^3 ({k_2}+{k_3})+3 \xi ^2 {k_3}+3 \xi ({k_3}+2 ({m_2}+{m_3}))+{k_3}+6 {m_3}\right) \nonumber \\&+\frac{1}{120} h^5 \frac{\partial ^5 u_1}{\partial x^5} \left( \xi ^5 {k_2}+20 \xi ^3 {m_2}+(\xi +1)^5 {k_3}+20 (\xi +1)^3 {m_3}\right) \nonumber \\&+\frac{ h^7 \frac{\partial ^7 u_1}{\partial x^7} \left( \xi ^7 {k_2}+42 \xi ^5 {m_2}+(\xi +1)^7 {k_3}+42 (\xi +1)^5 {m_3}\right) }{5040} \nonumber \\&\left. +\frac{ h^9 \frac{\partial ^9 u_1}{\partial x^9} \left( \xi ^9 {k_2}+72 \xi ^7 {m_2}+(\xi +1)^9 {k_3}+72 (\xi +1)^7 {m_3}\right) }{362880} \right] \nonumber \\ \,= & {} \, {c}^2 h (\xi ({k_2}+{k_3})+{k_3}) g_1(t) \nonumber \\&+\frac{1}{6} h^3 \frac{\mathrm{d}^2 g_1 (t)}{\mathrm{d}t^2} \left( \xi ^3 ({k_2}+{k_3})+3 \xi ^2 {k_3}+3 \xi ({k_3}+2 ({m_2}+{m_3}))+{k_3}+6 {m_3}\right) \nonumber \\&+\frac{1}{120{c}^2} h^5 \frac{\mathrm{d}^4 g_1 (t)}{\mathrm{d}t^4} \left( \xi ^5 {k_2}+20 \xi ^3 {m_2}+(\xi +1)^5 {k_3}+20 (\xi +1)^3 {m_3}\right) \nonumber \\&+\frac{ h^7 \frac{\mathrm{d}^6 g_1 (t)}{\mathrm{d}t^6} \left( \xi ^7 {k_2}+42 \xi ^5 {m_2}+(\xi +1)^7 {k_3}+42 (\xi +1)^5 {m_3}\right) }{5040 {c}^4} \nonumber \\&+\frac{ h^9 \frac{\mathrm{d}^8 g_1 (t)}{\mathrm{d}t^8} \left( \xi ^9 {k_2}+72 \xi ^7 {m_2}+(\xi +1)^9 {k_3}+72 (\xi +1)^7 {m_3}\right) }{362880 {c}^6}. \end{aligned}$$

(25)

Now, equating to zero the first five coefficients in the first square brackets of Eq. (22) with the smallest even orders of h, we get a linear system of five algebraic equations. Solving this system, we can find the following coefficients $m_i$ and $k_i$ ($i=1,2,3$) of the stencil equation, Eq. (19), for the new approach:

$$\begin{aligned} m_1 \,= & {} \, a_1, \qquad m_{2}\, = \, -\frac{(\xi +1)^4 (4 \xi ^2+26 \xi +13) a_1}{(2 \xi +1) (48 \xi ^4+96 \xi ^3-212 \xi ^2-260 \xi -65)}, \nonumber \\ m_{3}\,= & {} \, \frac{\xi ^4 (4 \xi ^2-18 \xi -9) a_1}{(2 \xi +1) (48 \xi ^4+96 \xi ^3-212 \xi ^2-260 \xi -65)}, \nonumber \\ k_{1}\,= & {} \, \frac{12 (32 \xi ^6+96 \xi ^5+8 \xi ^4-144 \xi ^3-166 \xi ^2-78 \xi -13) a_1}{\xi ^2 (\xi +1)^2 (48 \xi ^4+96 \xi ^3-212 \xi ^2-260 \xi -65)}, \nonumber \\ k_{2}\,= & {} \, -\frac{12 (\xi +1)^4 (29 \xi ^2-26 \xi -13) a_1}{\xi ^2 (2 \xi +1) (48 \xi ^4+96 \xi ^3-212 \xi ^2-260 \xi -65)}, \nonumber \\ k_{3}\,= & {} \, \frac{12 \xi ^4 (29 \xi ^2+84 \xi +42) a_1}{(\xi +1)^2 (2 \xi +1) (48 \xi ^4+96 \xi ^3-212 \xi ^2-260 \xi -65)}, \end{aligned}$$

(26)

where $a_1$ is an arbitrary coefficient. Inserting the coefficients $m_i$ and $k_i$ ($i=1,2,3$) from Eq. (26) into Eqs. (25) and (22), we get the following load term $f_1$ and local truncation error $e_{\mathrm{new}}$ for the stencil, Eq. (19), related to the Neumann boundary conditions with the new approach:

$$\begin{aligned} f_1 \,= & {} \, a_1 \left[ -\frac{12 (7 \xi (\xi +1) (5 \xi (\xi +1) (\xi ^2+ \xi -4)-13)-13) {c^2} h g_1(t)}{ \xi (\xi +1) (2 \xi +1) (4 \xi (\xi +1) (12 \xi (\xi +1)-65)-65)} \right. \nonumber \\&-\frac{ \xi (\xi +1) (5 \xi (\xi +1) (2 \xi (\xi +1)-13)-13) h^3 \frac{\mathrm{d}^2 g_1 (t)}{\mathrm{d}t^2}}{(2 \xi +1) (4 \xi (\xi +1) (12 \xi (\xi +1)-65)-65)} \nonumber \\&+\frac{\xi ^3 (\xi +1)^3 (3 \xi (\xi +1)-26) h^5 \frac{\mathrm{d}^4 g_1 (t)}{\mathrm{d}t^4}}{30 (2 \xi +1) (4 \xi (\xi +1) (12 \xi (\xi +1)-65)-65) {c^2}} \nonumber \\&-\frac{\xi ^4 (\xi +1)^4 (2 \xi (\xi +1)-21) h^7 \frac{\mathrm{d}^6 g_1 (t)}{\mathrm{d}t^6}}{840 (2 \xi +1) (4 \xi (\xi +1) (12 \xi (\xi +1)-65)-65) {c}^6} \nonumber \\&\left. + \frac{\xi ^4 (\xi +1)^4 (5 (\xi -3) \xi (\xi +1) (\xi +4)-12) h^9 \frac{\mathrm{d}^8 g_1 (t)}{\mathrm{d}t^8}}{30240 (2 \xi +1) (4 \xi (\xi +1) (12 \xi (\xi +1)-65)-65) {c}^{10}} \right] \end{aligned}$$

(27)

and

$$\begin{aligned} e_{\mathrm{new}} = \frac{\xi ^4 (\xi +1)^4 (4 \xi (\xi +1) (4 \xi (\xi +1)-51)-51) {c^2} h^{10} {a_1} \frac{\partial ^{10} u_1 }{\partial x^{10}}}{604800 (4 \xi (\xi +1) (12 \xi (\xi +1)-65)-65)} + O(h^{11}), \end{aligned}$$

(28)

i.e., the local truncation error in space for the stencil, Eq. (19), related to the Neumann boundary conditions is even smaller than that for the regular 3-point stencils of the internal degrees of freedom considered in the previous Sect. 2.1 (see Eq. (17)). It should be mention that small distances from the grid points to the boundary (or small $\xi \ll 1$) do not decrease the accuracy of the new approach. Moreover, at small $\xi \ll 1$, the accuracy is higher than that at $\xi$ close to 1; see Fig. 3 for the variation of the leading term of the local truncation error in Eq. (28) as a function of $\xi$.

Fig. 3

The variation of the leading term $Coef_2 = \frac{\xi ^4 (\xi +1)^4 (4 \xi (\xi +1) (4 \xi (\xi +1)-51)-51) }{604800 (4 \xi (\xi +1) (12 \xi (\xi +1)-65)-65)}$ in Eq. (28) as a function of $\xi$ (see Fig. 1)

The final semidiscrete system of equations includes $N-2$ equations given by Eq. (8) with $A=2,\ldots ,N-1$, Eq. (19) for the left end and the equation similar to Eq. (19) for the right end. (These last two equations include the Neumann boundary conditions.)

Remark 3

Due to Eqs. (26) and (27), the same multiplier $a_1$ included into the left- and right-hand sides of the stencil equation, Eq. (19), can be canceled (or it can be taken $a_1=1$).

2.2.3 Neumann boundary conditions (without the inclusion of boundary degrees of freedom)

In contrast to the approach for the Neumann boundary conditions described in Sect. 2.2.2, the second approach is based on a uniform mesh without the inclusion of the boundary degrees of freedom into stencil equations. This technique can be derived from the previous technique in Sect. 2.2.2 as follows. The boundary degree of freedom $u_1$ is not included in calculations. Instead of the two stencil equations, Eq. (8) at $A=2$ and Eq. (19), we will use just one stencil equation, Eq. (19), with $m_1=k_1=0$. Repeating the derivations presented in the previous Sect. 2.2.2 with $m_1=k_1=0$ and equating to zero the first three coefficients in the first square brackets of Eq. (22) with the smallest even orders of h, we get a linear system of three algebraic equations. Solving this system, we can find the following coefficients $m_i$ and $k_i$ ($i=2,3$) of the stencil equation, Eq. (19), for the new approach:

$$\begin{aligned} m_1 \,= & {} \, 0, \qquad m_{2}\, = \,a_1 , \qquad m_{3}\, = \, \frac{(-4 \xi ^2+2 \xi +1) a_1}{4 \xi ^2+10 \xi +5}, \nonumber \\ k_1 \,= & {} \, 0 , \qquad k_{2}\, = \, \frac{12 a_1}{4 \xi ^2+10 \xi +5}, \qquad k_{3}\, = \, -\frac{12 a_1}{4 \xi ^2+10 \xi +5}, \end{aligned}$$

(29)

where $a_1$ is an arbitrary coefficient. Inserting the coefficients $m_i$ and $k_i$ ($i=1,2,3$) from Eq. (29) into Eqs. (25) and (22), we get the following load term $f_1$ and local truncation error $e_{\mathrm{new}}$ for the stencil Eq. (19) related to the Neumann boundary conditions with the new approach:

$$\begin{aligned} f_1 \,= & {} \, a_1 \left[ -\frac{12 {c^2} h g_1(t)}{2 \xi (2 \xi +5)+5} -\frac{(2 \xi (\xi +1)-1) h^3 \frac{d^2 g_1 (t)}{dt^2}}{2 \xi (2 \xi +5)+5} +\frac{(2-5 \xi (\xi (3 \xi (\xi +2)+1)-2)) h^5 \frac{d^4 g_1 (t)}{dt^4}}{30 (2 \xi (2 \xi +5)+5) {c^2}} \right. \nonumber \\&-\frac{(1-7 \xi (\xi +1) (\xi ^2+a-1) (2 \xi (\xi +1)+1)) h^7 \frac{d^6 g_1 (t)}{dt^6}}{168 (2 \xi (2 \xi +5)+5) {c}^6} \nonumber \\&\left. \quad \frac{(1-3 \xi (\xi (7 \xi (\xi ^2 (\xi +2) (\xi (\xi +2)+2)-2)-10)-3)) h^9 \frac{d^8 g_1 (t)}{dt^8}}{6048 (2 \xi (2 \xi +5)+5) {c}^{10}} \right] \, \qquad \end{aligned}$$

(30)

and

$$\begin{aligned} e_{\mathrm{new}} = \frac{(2 \xi +1) (4 \xi (\xi (4 \xi (\xi +2)+1)-3)-3) {c^2} h^{6} {a_1} \frac{\partial ^{6} u_1 }{\partial x^{6}}}{120 (2 \xi (2 \xi +5)+5)} + O(h^{7}), \end{aligned}$$

(31)

i.e., the order of the local truncation error in space for the stencil Eq. (19) related to the Neumann boundary conditions and given by Eq. (31) is comparable with that for the 3-point stencils of the internal degrees of freedom considered in Sect. 2.1 (see Eq. (17)). It should be mention that small distances from the grid points to the boundary (or small $\xi \ll 1$) do not decrease the accuracy of the new approach. Moreover, at small $\xi \ll 1$, the accuracy is higher than that at $\xi$ close to 1; see Fig. 4 for the variation of the leading term of the local truncation error in Eq. (31) as a function of $\xi$.

Fig. 4

The variation of the leading term $Coef_3 = \frac{(2 \xi +1) (4 \xi (\xi (4 \xi (\xi +2)+1)-3)-3) }{120 (2 \xi (2 \xi +5)+5)}$ in Eq. (31) as a function of $\xi$ (see Fig. 1)

The final semidiscrete system of equations includes $N-4$ stencil equations given by Eq. (8) with $A=3,\ldots ,N-2$, Eq. (19) for the left end and the equation similar to Eq. (19) for the right end. (These last two equations include the Neumann boundary conditions.) The degrees of freedom $u_1^{\mathrm{num}}$ and $u_N^{\mathrm{num}}$ are not included in the final global system. The values of the unknown function at these grid points can be found by an extrapolation after the solution of the final system of equations.

Remark 4

Due to Eqs. (29) and (30), the same multiplier $a_1$ included into the left- and right-hand sides of the stencil equation, Eq. (19), can be canceled (or it can be taken $a_1=1$).

3 A new numerical approach for the 2-D wave and heat equations

3.1 Zero load $f=0$ in Eqs. (1) and (2)

Fig. 5

The spatial locations of the degrees of freedom $u_{i,j}$ ($i = A-1, A, A+1$, $j = B-1, B, B+1$) that contribute to the 9-point uniform stencil for the internal degree of freedom $u_{A,B}$ located far from the boundary

Fig. 6

The spatial locations of the degrees of freedom $u_{i,j}$ ($i = A-1, A, A+1$, $j = B-1, B, B+1$) that contribute to the 9-point non-uniform stencil for the internal degree of freedom $u_{A,B}$ located close to the boundary with the Dirichlet boundary conditions

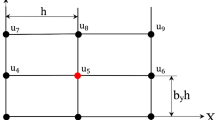
Here, we present 9-point uniform stencils that will be used for the internal grid points located far from the boundary and 9-point non-uniform stencils that will be used for the grid points located close to the boundary with the Dirichlet boundary conditions. (The case of the Neumann boundary conditions will be considered separately in Sect. 3.3.2.) Let us consider a 2-D bounded domain and a rectangular Cartesian mesh with a mesh size h where h is the size of the mesh along the x-axis and $b_y h$ is the size of the mesh along the y-axis ($b_y$ is the aspect ratio of the mesh); see Figs. 5 and 6. The 9-point stencil considered here is similar to that for the 2-D linear quadrilateral finite elements. The spatial locations of the 8 degrees of freedom that are close to the internal degree of freedom $u_{A,B}$ and contribute to the 9-point stencil for this degree of freedom are shown in Fig. 5 for the case when the boundary and the Cartesian mesh are matched or when the degree of freedom $u_{A,B}$ is located far from the boundary. In the case of non-conforming grids when the grid points do not coincide with the boundary, the first grid points that are located outside the physical domain are moved to the boundary of the physical domain as shown in Fig. 6. In order to find the boundary points that are included into the stencil for the degree of freedom $u_{A,B}$ (see Fig. 6), we join the central point $u_{A,B}$ with the 8 closest grid points, i.e., we have eight straight lines along the $x-$ and $y-$axes and along the diagonal directions (the dashed lines) of the grid; see Fig. 6. If any of these lines intersects the boundary of the domain, then the corresponding grid point (designated as $\circ$) should be moved to the boundary. (The new location is designated as $\bullet$.) This means that for all internal points located within the domain, we use the 9-point uniform (see Fig. 5) or non-uniform (see Fig. 6) stencil. To describe the coordinates of the boundary points shown in Fig. 6 we introduce 8 coefficients $0 \le d_i \le 1$ ($i=1,2,\ldots ,8$) as follows (see also Fig. 6):

$$\begin{aligned} x_{A-1,B-1} \,= & {} \, x_{A,B} - d_1 h, \qquad y_{A-1,B-1} \, = \, y_{A,B} - d_1 b_y h, \qquad \nonumber \\ x_{A,B-1} \,= & {} \, x_{A,B}, \qquad y_{A,B-1} \, = \, y_{A,B} - d_2 b_y h, \qquad \nonumber \\ x_{A+1,B-1} \,= & {} \, x_{A,B} + d_3 h, \qquad y_{A+1,B-1} \, = \, y_{A,B} - d_3 b_y h, \qquad \nonumber \\ x_{A-1,B} \,= & {} \, x_{A,B} - d_4 h, \qquad y_{A-1,B} \, = \, y_{A,B}, \qquad \nonumber \\ x_{A+1,B} \,= & {} \, x_{A,B} + d_5 h, \qquad y_{A+1,B} \, = \, y_{A,B}, \qquad \nonumber \\ x_{A-1,B+1} \,= & {} \, x_{A,B} - d_6 h, \qquad y_{A-1,B+1} \, = \, y_{A,B} + d_6 b_y h, \qquad \nonumber \\ x_{A,B+1} \,= & {} \, x_{A,B}, \qquad y_{A,B+1} \, = \, y_{A,B} + d_7 b_y h, \qquad \nonumber \\ x_{A+1,B+1} \,= & {} \, x_{A,B} + d_8 h , \qquad y_{A+1,B+1} \, = \, y_{A,B} + d_8 b_y h. \end{aligned}$$

(32)

If for a specific geometry of the domain some grid points designated in Fig. 6 as $\circ$ are located inside the domain, then these grid points should not be moved and the coordinates of these points can be also determined by Eq. (32) with the corresponding coefficients $d_i$ equal to unity ($d_i = 1$). Equation (4) for the 9-point uniform (see Fig. 5) or non-uniform (see Fig. 6) stencil can be explicitly rewritten as follows:

$$\begin{aligned}&h^2 \left\{ m_1 \frac{\mathrm{d}^n u^{\mathrm{num}}_{(A-1),(B-1)}}{\mathrm{d}t^n} + m_2 \frac{\mathrm{d}^n u^{\mathrm{num}}_{A,(B-1)}}{\mathrm{d}t^n} + m_3 \frac{\mathrm{d}^n u^{\mathrm{num}}_{(A+1),(B-1)}}{\mathrm{d}t^n} + {m_4} \frac{\mathrm{d}^n u^{\mathrm{num}}_{(A-1),B}}{\mathrm{d}t^n} + {m_5} \frac{\mathrm{d}^n u^{\mathrm{num}}_{A,B}}{\mathrm{d}t^n}\right. \nonumber \\&\left. \quad + m_6 \frac{\mathrm{d}^n u^{\mathrm{num}}_{(A+1),B}}{\mathrm{d}t^n} + m_7 \frac{\mathrm{d}^n u^{\mathrm{num}}_{(A-1),(B+1)}}{\mathrm{d}t^n} + m_8 \frac{\mathrm{d}^n u^{\mathrm{num}}_{A,(B+1)}}{\mathrm{d}t^n} + m_9 \frac{\mathrm{d}^n u^{\mathrm{num}}_{(A+1),(B+1)}}{\mathrm{d}t^n}\right\} \nonumber \\&\quad +\bar{c} \left\{ k_1 u^{\mathrm{num}}_{(A-1),(B-1)} + k_2 u^{\mathrm{num}}_{A,(B-1)} + k_3 u^{\mathrm{num}}_{(A+1),(B-1)} + {k_4} u^{\mathrm{num}}_{(A-1),B} + {k_5} u^{\mathrm{num}}_{A,B}\right. \nonumber \\&\left. \quad + k_6 u^{\mathrm{num}}_{(A+1),B} + k_7 u^{\mathrm{num}}_{(A-1),(B+1)} + k_8 u^{\mathrm{num}}_{A,(B+1)} + k_9 u^{\mathrm{num}}_{(A+1),(B+1)} \right\} \, = \, \bar{f}_{A,B}, \end{aligned}$$

(33)

where $\bar{f}_{A,B} = 0$ in the case of zero load $f=0$ in Eqs. (1) and (2), the unknown coefficients $m_i$ and $k_i$ ($i=1,2,\ldots ,9$) are to be determined from the minimization of the local truncation error, the superscript n in the time derivative in Eq. (33) and the material parameter $\bar{c}$ are $n=1$ and $\bar{c}=a$ for the heat equation as well as $n=2$ and $\bar{c}=c^2$ for the wave equation. For the calculation of the local truncation error, let us expand the exact solution $u_{j,l}$ ($j = A-1, A, A+1$ and $l = B-1, B, B+1$) and its time derivatives into a Taylor series at small $h \ll 1$ as follows:

$$\begin{aligned} w_{A + i, B + j}= & {} w_{A,B} + \frac{\partial w_{A,B}}{\partial x} (i h d_{ij}) + \frac{\partial w_{A,B}}{\partial y} ( j h d_{ij}) + \frac{\partial ^2 w_{A,B}}{\partial x^2} \frac{(i h d_{ij})^2}{2!} \nonumber \\&+ \frac{\partial ^2 w_{A,B}}{\partial x \partial y} \frac{(i h d_{ij})( j h d_{ij})}{2!} + \frac{\partial ^2 w_{A,B}}{\partial y^2} \frac{(j h d_{ij})^2}{2!} \qquad \nonumber \\&+ \frac{\partial ^3 w_{A,B}}{\partial x^3} \frac{(i h d_{ij})^3}{3!} + \frac{\partial ^3 w_{A,B}}{\partial y \partial x^2} \frac{(i h d_{ij})^2 ( j h d_{ij})}{3!}\nonumber \\&+ \frac{\partial ^3 w_{A,B}}{\partial y^2 \partial x} \frac{(i h d_{ij}) ( j h d_{ij})^2}{3!} + \frac{\partial ^3 w_{A,B}}{\partial y^3} \frac{( j h d_{ij})^3}{3!} + \cdots \end{aligned}$$

(34)

where $w = u$ and $w = \frac{\partial ^n u}{\partial t^n}$ as well as $i,j= -1,0,1$, and there is no summation over the repeated indexes i and j in Eq. (34). For convenience, the coefficients $d_i$ ($i=1,2,\ldots ,8$) in Eq. (32) are designated as $d_{ij}$ ($i,j=-1,0,1$) in Eq. (34) with the following correspondence between $d_i$ and $d_{ij}$:

$$\begin{aligned} d_{-1,-1}= & {} d_1 , \qquad d_{0,-1} = d_2 , \qquad d_{1,-1} = d_3 , \qquad d_{-1,0} = d_4 , \qquad \\ \nonumber d_{1,0}= & {} d_5 , \qquad d_{-1,1} = d_6, \qquad d_{0,1} = d_7 , \qquad d_{1,1} = d_8. \end{aligned}$$

(35)

The exact solution $u_{A,B}$ to Eqs. (1) or (2) meets the following equations:

$$\begin{aligned} \frac{\partial ^n u_{A,B}}{\partial t^n} - \bar{c} \nabla ^2 u_{A,B}= & {} 0, \end{aligned}$$

(36)

$$\begin{aligned} \frac{ \partial ^{i+j+n} u_{A,B}}{\partial x^{i} \partial y^{j} \partial t^n} - \bar{c} \frac{\partial ^{i+j} \nabla ^2 u_{A,B}}{\partial x^{i} \partial y^{j}}= & {} 0, \end{aligned}$$

(37)

with $i,j=0, 1, 2, 3, 4,\ldots$. Replacing the numerical solution in Eq. (33) by the exact solution (similar to Eq. (6)) and using Eq. (34) with $w = u$ and $w = \frac{\partial ^n u}{\partial t^n}$ as well as Eqs. (35)–(37), we get a Taylor series of the local truncation error in space for the new approach:

$$\begin{aligned} e= & {} \bar{c} \left\{ b_1 u_{A,B} + h \left( b_2 \frac{\partial u_{A,B} }{\partial x} + b_3 \frac{\partial u_{A,B} }{\partial y}\right) + \frac{h^2}{2} \left( b_4 \frac{\partial ^{2} u_{A,B} }{\partial x^{2}} + b_5 \frac{\partial ^{2} u_{A,B} }{\partial x \partial y} + b_6 \frac{\partial ^{2} u_{A,B} }{\partial y^{2}}\right) \right. \nonumber \\&+ \frac{h^3}{6} \left( b_7 \frac{\partial ^{3} u_{A,B} }{\partial x^{3}} + b_8 \frac{\partial ^{3} u_{A,B} }{\partial x^{2} \partial y} + b_9 \frac{\partial ^{3} u_{A,B} }{\partial x \partial y^{2}}+ b_{10} \frac{\partial ^{3} u_{A,B} }{\partial y^{3}}\right) \nonumber \\&+ \frac{h^4}{24} \left( b_{11} \frac{\partial ^{4} u_{A,B} }{\partial x^{4}} + b_{12} \frac{\partial ^{4} u_{A,B} }{\partial x^{3} \partial y} + b_{13} \frac{\partial ^{4} u_{A,B} }{\partial x^{2} \partial y^{2}} + b_{14} \frac{\partial ^{4} u_{A,B} }{\partial x \partial y^{3}}+ b_{15}\frac{\partial ^{4} u_{A,B} }{\partial y^{4}}\right) \nonumber \\&+ \frac{h^5}{120} \left( b_{16} \frac{\partial ^{5} u_{A,B} }{\partial x^{5}} + b_{17} \frac{\partial ^{5} u_{A,B} }{\partial x^{4} \partial y} + b_{18} \frac{\partial ^{5} u_{A,B} }{\partial x^{3} \partial y^{2}} + b_{19} \frac{\partial ^{5} u_{A,B} }{\partial x^{2} \partial y^{3}} + b_{20} \frac{\partial ^{5} u_{A,B} }{\partial x \partial y^{4}} + b_{21} \frac{\partial ^{5} u_{A,B} }{\partial y^{5}}\right) \nonumber \\&+ \frac{h^6}{720} \left( b_{22} \frac{\partial ^{6} u_{A,B} }{\partial x^{6}} + b_{23} \frac{\partial ^{6} u_{A,B} }{\partial x^{5}\partial y} + b_{24} \frac{\partial ^{6} u_{A,B} }{\partial x^{4}\partial y^{2}} + b_{25} \frac{\partial ^{6} u_{A,B} }{\partial x^{3}\partial y^{3}} + b_{26} \frac{\partial ^{6} u_{A,B} }{\partial x^{2} \partial y^{4}}\right. \nonumber \\&\left. \left. + b_{27} \frac{\partial ^{6} u_{A,B} }{\partial x \partial y^{5}} + b_{28} \frac{\partial ^{6} u_{A,B} }{\partial y^{6}}\right) \right\} + O({h}^{7}) \end{aligned}$$

(38)

with the coefficients $b_p$ ($p=1,2,\ldots ,28$) given in “Appendix A.” Due to the use of Eqs. (36) and (37), the local truncation error in Eq. (38) does not include the time derivatives. In order to improve the order of the local truncation error in Eq. (38) at small $h \ll 1$, we will equate to zero the coefficients $b_p$ in Eq. (38) for the smallest orders of h. If we equate to zero the first 15 coefficients $b_p = 0$ ($p=1,2,\ldots ,15$) in Eq. (38), then, at least, we could obtain the fifth order of the local truncation error. However, for a rectangular mesh with $b_y \ne 1$, the corresponding system of 15 algebraic equations for some particular cases (e.g., when three or four points of the 9-point regular stencil are located outside the physical domain and we have a non-uniform stencil with $d_4 \ne 1$, $d_6 \ne 1$, $d_7 \ne 1$ and $d_8 \ne 1$, see Fig. 6) can be analytically solved with the help of Mathematica. These solutions show that all coefficients $k_i$ in this stencil equation are zeros, i.e., these solutions are inappropriate. Therefore, the maximum possible order of the local truncation error for a non-uniform stencil, Eq. (38), on a rectangular mesh corresponds to the fourth order. (This can be done by equating to zero the first 10 coefficients $b_p = 0$ ($p=1,2,\ldots ,10$) in Eq. (38).) Fortunately, for square meshes with $b_y = 1$, the solutions of the system of 14 algebraic equations $b_p = 0$ ($p=1,2,\ldots ,11,13,14,15$) for the cases when five points of the 9-point regular stencil are located outside the physical domain (e.g., for non-uniform stencils with $d_4 \ne 1$, $d_5 \ne 1$, $d_6 \ne 1$, $d_7 \ne 1$, $d_8 \ne 1$ or $d_1 \ne 1$, $d_4 \ne 1$, $d_6 \ne 1$, $d_7 \ne 1$, $d_8 \ne 1$; see Fig. 6) can be analytically solved with the help of Mathematica. The substitution of these solutions in the expression for coefficient $b_{12}$ (see “Appendix A”) yields $b_{12} = 0$, i.e., all 15 coefficients $b_p = 0$ ($p=1,2,\ldots ,15$) are zero in these cases. Therefore, for square meshes the new approach with the non-uniform stencils for a very general geometry (the five points of the 9-point regular stencil can be located outside the physical domain) yields, at least, the fifth order of the local truncation error. The case of square Cartesian meshes with $b_y = 1$ will be considered below for the wave and heat equations.

In order to zero the coefficients $b_p$ ($p =1,2,\ldots , 15$) and minimize the values of the coefficients $b_p$ ($p =16,17,\ldots , 21$) for the fifth and sixth orders of the local truncation error, we use the following procedure. First, let us zero the following coefficients $b_p$:

$$\begin{aligned} b_p =0, \qquad p=1,2,\ldots ,11,13,15, \end{aligned}$$

(39)

and

$$\begin{aligned} b_{12} + b_{14} = 0, \end{aligned}$$

(40)

The use of Eq. (40) instead of equating a single coefficient $b_p$ (as in Eq. (39)) allows a symmetric form of the local truncation error in Eq. (38) with respect to x and y.

Then, for the coefficients $b_p$ related to the fifth and sixth orders of the local truncation error, we use the least square method with the following residual R:

$$\begin{aligned} R = \sum \limits _{p=16}^{21} b_p^2 + h_1 \sum \limits _{p=22}^{28} b_p^2, \end{aligned}$$

(41)

where $h_1$ is the weighting factor to be selected (e.g., the numerical experiments show that $h_1 = 1$ yields accurate results). The inclusion of the sixth-order terms is explained by the fact that for uniform square meshes, the fifth-order terms do not provide a sufficient number of equations for the calculation of the coefficients $m_i$ and $k_i$ ($i=1,2,\ldots ,9$). In order to minimize the residual R with the constraints given by Eqs. (39)–(40), we can form a new residual $\bar{R}$ with the Lagrange multipliers $\lambda _p$:

$$\begin{aligned} \bar{R} = \sum \limits _{p=16}^{21} b_p^2 + h_1 \sum \limits _{p=22}^{28} b_p^2 + \sum \limits _{p=1}^{11} \lambda _p b_p + \lambda _{12}(b_{12} + b_{14}) + \lambda _{13}b_{13} + \lambda _{14}b_{15}. \end{aligned}$$

(42)

The residual $\bar{R}$ is a quadratic function of coefficients $m_i$ and $k_i$ ($i=1,2,\ldots ,9$) and a linear function of the Lagrange multipliers $\lambda _p$, i.e., $\bar{R}= \bar{R}(m_i, k_i, \lambda _p)$. In order to minimize the residual $\bar{R}(m_i, k_i, \lambda _p)$, the following equations based on the least square method for the residual $\bar{R}$ can be written down:

$$\begin{aligned} \frac{\partial R}{\partial m_i}= & {} 0, \qquad \frac{\partial R}{\partial k_i} =0, \qquad i=1,2,\ldots ,9, \end{aligned}$$

(43)

$$\begin{aligned} \frac{\partial R}{\partial \lambda _p}= & {} 0, \qquad p=1,2,\ldots ,14, \qquad \end{aligned}$$

(44)

where equation $\frac{\partial R}{\partial m_{5}} =0$ should be replaced by $m_{5} =1$ (because for the homogeneous stencil equation, Eq. (33), with $\bar{f}_{A,B} = 0$ one of the coefficients $m_i$ and $k_i$ ($i=1,2,\ldots ,9$) can be arbitrary selected, e.g., $m_{5} =1$). Equations (43) and (44) form a system of 32 linear algebraic equations with respect to 18 unknown coefficients $m_i$ and $k_i$ ($i=1,2,\ldots ,9$) and 14 Lagrange multipliers $\lambda _p$ ($p=1,2,\ldots ,14$). Solving these linear algebraic equations numerically, we can find the coefficients $m_i$, $k_i$ ($i=1,2,\ldots ,9$) for the 9-point non-uniform stencils.

Remark 5

To estimate the computation costs of the solution of 32 linear algebraic equations formed by Eqs. (43) and (44), we solved $10^6$ such systems with the general MATLAB solver on a simple student laptop computer (Processor: Intel (R) Core(TM) i5-4210U CPU @ 1.70 GHz 2.40 GHz). The computation ’wall’ time was $T=1216 s$ for $10^6$ systems or the average time for one system was 0.001216s. Because the coefficients $m_i$ and $k_i$ ($i=1,2,\ldots ,9$) are independently calculated for different non-uniform stencils, the computation time of their calculation for different grid points can be significantly reduced on modern parallel computers. This means that for large global systems of equations, the computation time for the calculation of the coefficients $m_i$ and $k_i$ ($i=1,2,\ldots ,9$) is very small compared to that for the solution of the global system of equations.

Remark 6

The coefficients $m_i$ and $k_i$ ($i=1,2,\ldots ,9$) calculated according to the above-mentioned procedure lead to a non-symmetric global system of semidiscrete equations. Non-symmetric global matrices are also reported for other numerical techniques with Cartesian meshes on irregular domains, e.g., see [6].

For the limit case of uniform stencils with $d_i=1$ ($i=1,2,\ldots ,8$) and square meshes, the coefficients $m_i$ and $k_i$ ($i=1,2,\ldots ,9$) can be calculated analytically with the help of Mathematica and are equal to those obtained by the modified integration rule technique for uniform stencils in [23, 59]:

$$\begin{aligned} m_1 \,= & {} \, m_3 \, = \, m_7 \, = \, m_9 \, = \, a_1/ 100 , \qquad m_2 \, = \, m_4 \, = \, m_6 \, = \, m_8 \, = \, a_1/ 10, \qquad m_5 \, = \, a_1 , \nonumber \\ k_1 \,= & {} \, k_3 \, = \, k_7 \, = \, k_9 \, = \, - 6 a_1/ 25 , \qquad k_2 \, = \, k_4 \, = \, k_6 \, = \, k_8 \, = \, -24 a_1/ 25, \qquad k_5 \, = \, 24 a_1/5, \end{aligned}$$

(45)

where $a_1$ is an arbitrary coefficient.

By the substitution of $m_i$ and $k_i$ ($i=1,2,\ldots ,9$) from Eq. (45) for the uniform stencil in the formulas for the coefficients $b_p$ (see “Appendix A”), we can find that $b_p = 0$ for $p=1,2,\ldots ,21$ and the local truncation error for the uniform stencil on square meshes is:

$$\begin{aligned} e_{\mathrm{new}} = \frac{3 a_1 \bar{c} h^{6}}{500 } \left[ \frac{\partial ^{6} u_{A,B} }{\partial x^{6}} + \frac{\partial ^{6} u_{A,B} }{\partial y^{6}}\right] + O(h^{7}). \end{aligned}$$

(46)

The new approach with square Cartesian meshes provides the fifth order of the local truncation error for the non-uniform stencils and the sixth order of the local truncation error for the uniform stencils (see Eq. (46)). For the conventional linear finite elements on uniform square meshes, the local truncation error is (see [23])

$$\begin{aligned} e_{\mathrm{conv}}^{\mathrm{lin}} = \frac{\bar{c} h^4}{12} \left( \frac{\partial ^4 u_{A,B}}{\partial x^{4}} + \frac{\partial ^4 u_{A,B}}{\partial y^{4}}\right) + O(h^{6}), \end{aligned}$$

(47)

i.e., for the 9-point stencils the new approach improves the local truncation error in space by two orders compared to that for the conventional linear elements on uniform square meshes.

3.2 Nonzero load $f \ne 0$ in Eqs. (1) and (2)

The inclusion of nonzero loading term f in the partial differential equations, Eqs. (1) and (2), leads to the nonzero term $\bar{f}_{A,B}$ in the stencil equation, Eq. (33) (similar to Eq. (4)). The expression for the term $\bar{f}_{A,B}$ can be calculated from the procedure used for the derivation of the local truncation error in the case of zero loading function.

In case of nonzero loading function ($f(\mathbf{x}, t) \ne 0$), Eqs. (36) and (37) for the exact solution at $x=x_A$ and $y=y_B$ can be modified as follows:

$$\begin{aligned} \frac{\partial ^n u_{A,B}}{\partial t^n} - \bar{c} \nabla ^2 u_{A,B}= & {} f(x_A, y_B, t),\end{aligned}$$

(48)

$$\begin{aligned} \frac{\partial ^{(i+j+n)} u_{A,B}}{\partial x^{i} \partial y^{j} \partial t^n} - \bar{c} \frac{\partial ^{(i+j)} \nabla ^2 u_{A,B}}{\partial x^{i} \partial y^{j}}= & {} \frac{\partial ^{(i+j)} f(x_A, y_B, t)}{\partial x^{i} \partial y^{j}}. \end{aligned}$$

(49)

Then, replacing the numerical solution in Eq. (33) with nonzero $\bar{f}_{A,B}$ by the exact solution (similar to Eq. (6)) and using Eq. (34) with $w = u$ and $w = \frac{\partial ^n u}{\partial t^n}$ as well as Eqs. (35), (48) and (49), we get a Taylor series of the local truncation error in space $e_f$ for the new approach:

$$\begin{aligned} e_f= & {} e - \left[ \bar{f}_{A,B} - \left\{ h^2 f_{A,B} (m_{1}+m_{2}+m_{3}+m_{4}+m_{5}+m_{6}+m_{7}+m_{8}+m_{9})\right. \right. \nonumber \\&+h^3 \left( b_y\frac{\partial f_{A,B} }{\partial y} (-d_{1} m_{1}-d_{2} m_{2}-d_{3} m_{3}+d_{6} m_{7}+d_{7} m_{8}+d_{8} m_{9}) \right. \nonumber \\&\left. +\frac{\partial f_{A,B} }{\partial x} \left( -d_{1} m_{1}+d_{3} m_{3}-d_{4} m_{4}+d_{5} m_{6}-d_{6} m_{7}+d_{8} m_{9}\right) \right) \nonumber \\&+\frac{1}{2} h^4\left( b_y^2 \frac{\partial ^2 f_{A,B} }{\partial y^2} \left( d_{1}^2 m_{1}+d_{2}^2 m_{2}+d_{3}^2 m_{3}+d_{6}^2 m_{7}+d_{7}^2 m_{8}+d_{8}^2 m_{9}\right) \right. \nonumber \\&+\frac{\partial ^2 f_{A,B} }{\partial x^2} \left( d_{1}^2 m_{1}+d_{3}^2 m_{3}+d_{4}^2 m_{4}+d_{5}^2 m_{6}+d_{6}^2 m_{7}+d_{8}^2 m_{9}\right) \nonumber \\&\left. +2 b_y\frac{\partial ^2 f_{A,B} }{\partial x \partial y} \left( d_{1}^2 m_{1}-d_{3}^2 m_{3}-d_{6}^2 m_{7}+d_{8}^2 m_{9}\right) \right) \nonumber \\&+\frac{1}{6} h^5 \left( b_y^3 \frac{\partial ^3 f_{A,B} }{\partial y^3} \left( d_{1}^3 (-m_{1})-d_{2}^3 m_{2}-d_{3}^3 m_{3}+d_{6}^3 m_{7}+d_{7}^3 m_{8}+d_{8}^3 m_{9}\right) \right. \nonumber \\&+\frac{\partial ^3 f_{A,B} }{\partial x^3} \left( d_{1}^3 (-m_{1})+d_{3}^3 m_{3}-d_{4}^3 m_{4}+d_{5}^3 m_{6}-d_{6}^3 m_{7}+d_{8}^3 m_{9}\right) \nonumber \\&+3b_y\left( b_y\frac{\partial ^3 f_{A,B} }{\partial x \partial y^2} (d_{1}^3 (-m_{1})+d_{3}^3 m_{3}-d_{6}^3 m_{7}+d_{8}^3 m_{9}) \right. \nonumber \\&\left. \left. +\frac{\partial ^3 f_{A,B} }{\partial x^2 \partial y} \left( d_{1}^3 (-m_{1})-d_{3}^3 m_{3}+d_{6}^3 m_{7}+d_{8}^3 m_{9}\right) \right) \right) \nonumber \\&+\frac{1}{24} h^6 \left( b_y^4 \frac{\partial ^4 f_{A,B} }{\partial y^4} \left( d_{1}^4 m_{1}+d_{2}^4 m_{2}+d_{3}^4 m_{3}+d_{6}^4 m_{7}+d_{7}^4 m_{8}+d_{8}^4 m_{9}\right) \right. \nonumber \\&+\frac{\partial ^4 f_{A,B} }{\partial x^4}\left( d_{1}^4 m_{1}+d_{3}^4 m_{3}+d_{4}^4 m_{4}+d_{5}^4 m_{6}+d_{6}^4 m_{7}+d_{8}^4 m_{9}\right) \nonumber \\&+4 b_y^3 \frac{\partial ^4 f_{A,B} }{\partial x \partial y^3} \left( d_{1}^4 m_{1}-d_{3}^4 m_{3}-d_{6}^4 m_{7}+d_{8}^4 m_{9}\right) \nonumber \\&+6 b_y^2 \frac{\partial ^4 f_{A,B} }{\partial x^2 \partial y^2} \left( d_{1}^4 m_{1}+d_{3}^4 m_{3}+d_{6}^4 m_{7}+d_{8}^4 m_{9}\right) \nonumber \\&\left. \left. \left. +4 b_y\frac{\partial ^4 f_{A,B} }{\partial x^3 \partial y} \left( d_{1}^4 m_{1}-d_{3}^4 m_{3}-d_{6}^4 m_{7}+d_{8}^4 m_{9}\right) \right) +\cdots \right\} \right] , \qquad \end{aligned}$$

(50)

where e is the local truncation error in space given by Eq. (38) for zero loading function, $f_{A,B}$ designates function f(x, y, t) calculated at $x=x_A$ and $y=y_B$. Equating to zero the expression in the square brackets in the right-hand side of Eq. (50), we will get the expression for $\bar{f}_{A,B}$:

$$\begin{aligned} \bar{f}_{A,B}= & {} h^2 f_{A,B} (m_{1}+m_{2}+m_{3}+m_{4}+m_{5}+m_{6}+m_{7}+m_{8}+m_{9}) \nonumber \\&+h^3 (b_y\frac{\partial f_{A,B} }{\partial y} (-d_{1} m_{1}-d_{2} m_{2}-d_{3} m_{3}+d_{6} m_{7}+d_{7} m_{8}+d_{8} m_{9})\nonumber \\&+\frac{\partial f_{A,B} }{\partial x} (-d_{1} m_{1}+d_{3} m_{3}-d_{4} m_{4}+d_{5} m_{6}-d_{6} m_{7}+d_{8} m_{9})) \nonumber \\&+\frac{1}{2} h^4 (b_y^2 \frac{\partial ^2 f_{A,B} }{\partial y^2} (d_{1}^2 m_{1}+d_{2}^2 m_{2}+d_{3}^2 m_{3}+d_{6}^2 m_{7}+d_{7}^2 m_{8}+d_{8}^2 m_{9})\nonumber \\&+\frac{\partial ^2 f_{A,B} }{\partial x^2} (d_{1}^2 m_{1}+d_{3}^2 m_{3}+d_{4}^2 m_{4}+d_{5}^2 m_{6}+d_{6}^2 m_{7}+d_{8}^2 m_{9})\nonumber \\&+2 b_y\frac{\partial ^2 f_{A,B} }{\partial x \partial y} (d_{1}^2 m_{1}-d_{3}^2 m_{3}-d_{6}^2 m_{7}+d_{8}^2 m_{9}))\nonumber \\&+\frac{1}{6} h^5 (b_y^3 \frac{\partial ^3 f_{A,B} }{\partial y^3} (d_{1}^3 (-m_{1})-d_{2}^3 m_{2}-d_{3}^3 m_{3}+d_{6}^3 m_{7}+d_{7}^3 m_{8}+d_{8}^3 m_{9}) \nonumber \\&+\frac{\partial ^3 f_{A,B} }{\partial x^3} (d_{1}^3 (-m_{1})+d_{3}^3 m_{3}-d_{4}^3 m_{4}+d_{5}^3 m_{6}-d_{6}^3 m_{7}+d_{8}^3 m_{9}) \nonumber \\&+3 b_y(b_y\frac{\partial ^3 f_{A,B} }{\partial x \partial y^2} (d_{1}^3 (-m_{1})+d_{3}^3 m_{3}-d_{6}^3 m_{7}+d_{8}^3 m_{9}) \nonumber \\&+\frac{\partial ^3 f_{A,B} }{\partial x^2 \partial y} (d_{1}^3 (-m_{1})-d_{3}^3 m_{3}+d_{6}^3 m_{7}+d_{8}^3 m_{9}))) +\frac{1}{24} h^6 (b_y^4 \frac{\partial ^4 f_{A,B} }{\partial y^4} (d_{1}^4 m_{1}+d_{2}^4 m_{2}+d_{3}^4 m_{3}\nonumber \\&+d_{6}^4 m_{7}+d_{7}^4 m_{8}+d_{8}^4 m_{9}) \nonumber \\&+\frac{\partial ^4 f_{A,B} }{\partial x^4}(d_{1}^4 m_{1}+d_{3}^4 m_{3}+d_{4}^4 m_{4}+d_{5}^4 m_{6}+d_{6}^4 m_{7}+d_{8}^4 m_{9})\nonumber \\&+4 b_y^3 \frac{\partial ^4 f_{A,B} }{\partial x \partial y^3} (d_{1}^4 m_{1}-d_{3}^4 m_{3}-d_{6}^4 m_{7}+d_{8}^4 m_{9}) \nonumber \\&+6 b_y^2 \frac{\partial ^4 f_{A,B} }{\partial x^2 \partial y^2} (d_{1}^4 m_{1}+d_{3}^4 m_{3}+d_{6}^4 m_{7}+d_{8}^4 m_{9}) \nonumber \\&+4 b_y\frac{\partial ^4 f_{A,B} }{\partial x^3 \partial y} (d_{1}^4 m_{1}-d_{3}^4 m_{3}-d_{6}^4 m_{7}+d_{8}^4 m_{9})) + \cdots \end{aligned}$$

(51)

as well as we get the same local truncation errors $e_f = e$ for zero and nonzero loading functions. This means that the coefficients $m_i$ and $k_i$ of the stencil equations are first calculated for zero load $f = 0$ as described in Sect. 3.1. Then, the nonzero loading term $\bar{f}_{A,B}$ given by Eq. (51) is used in the stencil equation, Eq. (33).

3.3 Boundary conditions

3.3.1 Dirichlet boundary conditions

Similar to the 1-D case in Sect. 2.2.1, the application of the Dirichlet boundary conditions in the new approach is trivial and similar to that for the finite elements. We simply equate the boundary degrees of freedom of the uniform and non-uniform stencils (see Figs. 5 and 6) to the values of a given function $g_2(x,y,t)$ at the corresponding boundary points, i.e., the Dirichlet boundary conditions are exactly imposed. Here, $g_2(x,y,t)$ describes the Dirichlet boundary conditions. The final global discrete system of equations includes the 9-point uniform and non-uniform stencil equations (see Figs. 5 and 6) for all internal grid points that are located inside the domain as well as the Dirichlet boundary conditions at the boundary points.

Remark 7

The imposition of the Dirichlet boundary conditions at any boundary point means that the stencil coefficients at this boundary point are multiplied by the known values of function u and its time derivatives and are moved to the right-hand side of the stencil equation. Therefore, the left-hand side of the stencil equation in this case includes the unknown function u and its time derivative at the Cartesian grid points. (There are no unknowns at the boundary points, and the boundary points contribute to the right-hand side of the stencil equation only.) This also means that the 9-point non-uniform stencils shown in Fig. 6 actually include less than 9 Cartesian grid points.

Remark 8

The proposed technique yields accurate results for the non-uniform stencils even with very small coefficients $d_i \ll 1$; see the numerical examples in Part II. However, the new technique allows also to exclude very small coefficients $d_i \ll 1$ from calculations. For example, if $d_i \ll \hbox {tol}$ for some internal point (see Fig. 6) where tol is a small tolerance (e.g., $\hbox {tol} = 10^{-3}$), then the non-uniform stencil for this internal point can be removed from the global system of equations and this point can be moved to the boundary and treated as the boundary point for other stencils. In this case, the corresponding coefficients $d_i$ for this point in other stencils can be slightly greater than one. According to the derivations in the previous section, all equations will be valid also for $d_i > 1$. The numerical experiments with a small tolerance $\hbox {tol} = 10^{-3}$ show that if the point with very small coefficients $d_i \ll 1$ is moved to the boundary, then the coefficients $d_i$ for this point in other stencils can be taken as $d_i = 1$ without introducing any significant errors.

3.3.2 Neumann boundary conditions (with no inclusion of boundary degrees of freedom)

Fig. 7

The spatial locations of the degrees of freedom $u_{i,j}$ ($i = A-1, A, A+1$, $j = B-1, B, B+1$) that contribute to the 8-point cut stencils for the internal degrees of freedom $u_{A,B}$ and $u_{A,B+1}$ located close to the boundary with the Neumann boundary conditions. $\bullet$ designates the 8 points contributing to the stencil equation

In this section, we show that a high accuracy of the new approach with the Neumann boundary conditions in the 2-D case can be developed with a cut stencil that includes less than 9 grid points. Here, we show that the 8-point cut stencil can be used for the imposition of the Neumann boundary conditions at the upper boundary. (The cases of the left, lower and right boundaries can be considered by the rotation of this stencil through angles $90^o$, $180^o$ and $270^o$, respectively.) This stencil includes the internal grid points of a uniform Cartesian mesh only. Similar to the Neumann boundary conditions in the 1-D case presented in Sect. 2.2.3, the boundary points with the Neumann boundary conditions are included into the right-hand side of the 8-point cut stencil. For the time-dependent wave and heat equations, we use three boundary points with the coordinates $x_i, y_i$, $i=1,2,3$ (see Fig. 7 and Eq. (52) ). The stencil equations should be formed for all grid points located within the actual domain. For any internal grid point located far from the boundary, we use the 9-point stencil; see Fig. 5. For the 9-point regular stencil for the grid point $u_{A,B}$ shown in Fig. 7 and located close to the boundary, one grid point $u_{A-1,B+1}$ is cut by the boundary. Therefore, for this grid point, we use the 8-point stencil shown in Fig. 7. The case when the boundary cuts the grid point $u_{A+1,B+1}$ (instead of the grid point $u_{A-1,B+1}$) can be treated similarly. For the 9-point regular stencil for the grid point $u_{A,B+1}$ shown in Fig. 7 and located close to the boundary, the boundary cuts four grid points $u_{A-1,B+1}$, $u_{A-1,B+2}$, $u_{A,B+2}$ and $u_{A+1,B+2}$. In this case, for the grid point $u_{A,B+1}$, we use the same 8-point stencil as that for the grid point $u_{A,B}$. However, in order to have linear independent stencil equations for the grid points $u_{A,B+1}$ and $u_{A,B}$, we will select different locations of the boundary points used for these stencils (with the different coordinates $x_i, y_i$, $i=1,2,3$). If for the 9-point regular stencil for the grid point $u_{A,B+1}$ the boundary cuts one grid point $u_{A,B+2}$, or two grid points $u_{A-1,B+2}$ and $u_{A,B+2}$, or three grid points $u_{A-1,B+2}$, $u_{A,B+2}$ and $u_{A+1,B+2}$ (or three grid points $u_{A-1,B+1}$, $u_{A-1,B+2}$ and $u_{A,B+2}$), then the same 8-point stencil as that for the grid point $u_{A,B+1}$ shown in Fig. 7 is used, i.e., the 8-point stencils will be used for all grid points close to the boundary where the boundary cuts the grid points of the 9-point regular stencil. Equation (4) for the 8-point stencil (see Fig. 7) can be explicitly written as follows:

$$\begin{aligned}&h^2 \left\{ m_1 \frac{d^n u^{\mathrm{num}}_{(A-1),(B-1)}}{dt^n} + m_2 \frac{d^n u^{\mathrm{num}}_{A,(B-1)}}{dt^n} + m_3 \frac{d^n u^{\mathrm{num}}_{(A+1),(B-1)}}{dt^n} + {m_4} \frac{d^n u^{\mathrm{num}}_{(A-1),B}}{dt^n} + {m_5} \frac{d^n u^{\mathrm{num}}_{A,B}}{dt^n}\right. \nonumber \\&\left. \qquad + m_6 \frac{d^n u^{\mathrm{num}}_{(A+1),B}}{dt^n} + m_8 \frac{d^n u^{\mathrm{num}}_{A,(B+1)}}{dt^n} + m_9 \frac{d^n u^{\mathrm{num}}_{(A+1),(B+1)}}{dt^n} \right\} \nonumber \\&\qquad +\,\bar{c} \left\{ k_1 u^{\mathrm{num}}_{(A-1),(B-1)} + \,k_2 u^{\mathrm{num}}_{A,(B-1)} + \,k_3 u^{\mathrm{num}}_{(A+1),(B-1)} + \,{k_4} u^{\mathrm{num}}_{(A-1),B} + \,{k_5} u^{\mathrm{num}}_{A,B}\right. \nonumber \\&\left. \qquad + k_6 u^{\mathrm{num}}_{(A+1),B} + \,k_8 u^{\mathrm{num}}_{A,(B+1)} + k_9 u^{\mathrm{num}}_{(A+1),(B+1)}\right\} \nonumber \\&\quad = \, \left[ \bar{c} h (l_1 g_1(x_1,y_1,t)+l_2 g_1(x_2,y_2,t)+l_3 g_1(x_3,y_3,t))\right] +\, \bar{f}_{A,B}, \end{aligned}$$

(52)

where $\bar{f}_{A,B} = 0$ in the case of zero load $f=0$ in Eqs. (1) and (2), the unknown coefficients $m_i$, $k_i$ ($i=1,2,\ldots ,6,8,9$) and $l_i$ ($i=1,2,3$) are to be determined from the minimization of the local truncation error, the expression in the square brackets in the right-hand side of Eq. (52) represents the Neumann boundary conditions at three boundary points with the coordinates $x_i, y_i$, $i=1,2,3$ ($x_{A-1,B+1} \le x_i \le x_{A+1,B+1}$, see Fig. 7), the superscript n for the time derivative in Eq. (52) and the material parameter $\bar{c}$ are $n=1$ and $\bar{c}=a$ for the heat equation as well as $n=2$ and $\bar{c}=c^2$ for the wave equation. For convenience, the left-hand side of Eq. (52) is written similar to that of Eq. (33) with $k_7=m_7=0$.

Remark 9

Only 18 out of the 19 coefficients $m_i$, $k_i$ ($i=1,2,\ldots ,6,8,9$) and $l_i$ ($i=1,2,3$) in Eq. (52) can be considered as unknown coefficients. This can be explained as follows: In the case of zero load $f=0$ and $\bar{f}_{A,B} = 0$, Eq. (52) can be rescaled by the division of the left and right sides of Eq. (52) by any scalar $a_1$. For example, let us select $a_1=m_5$. In this case, the rescaled coefficients ${\bar{m}}_i$, ${\bar{k}}_i$ ($i=1,2,\ldots ,6,8,9$) and ${\bar{l}}_i$ ($i=1,2,3$) of the stencil equation are: ${\bar{m}}_i = m_i/m_5$ ($i=1,2,3,4,6,8,9$), ${\bar{m}}_5=1$, ${\bar{k}}_i = k_i/m_5$ ($i=1,2,\ldots ,6,8,9$) and ${\bar{l}}_i = l_i/m_5$ ($i=1,2,3$), i.e., there are only 18 unknown rescaled coefficients. The case of nonzero load $\bar{f}_{A,B} \ne 0$ can be similarly treated because the term $\bar{f}_{A,B}$ is a linear function of the coefficients $m_i$ (see Eq. (51)).

Remark 10

In the numerical simulations in Part 2 of the paper, we use the uniform spacing $h_1 = h/32$ for the boundary points along the x-axis ($x_{i+1} = x_i + h_1$ with $i=1,2$; see Fig. 7) with the following x-coordinate of the first point: (a) $x_1 = x_{A-1,B} + h_1$ in the case when the boundary cuts one grid point $u_{A-1,B+1}$; (b) $x_1 = x_{A,B} - h_1$ in the case when the boundary cuts one grid point $u_{A,B+2}$ or three grid points $u_{A-1,B+2}$, $u_{A,B+2}$ and $u_{A+1,B+2}$ as well as in the case of the conforming mesh; (c) $x_1 = (x_{A,B}+ x_{A+1,B})/2 - h_1$ in the case when the boundary cuts four grid points $u_{A-1,B+1}$, $u_{A-1,B+2}$, $u_{A,B+2}$ and $u_{A+1,B+2}$ or three grid points $u_{A-1,B+1}$, $u_{A-1,B+2}$ and $u_{A,B+2}$ or two grid points $u_{A-1,B+2}$ and $u_{A,B+2}$. The numerical results show that with this selection of the boundary points we have stable numerical solutions.

The local truncation error of the stencil equation, Eq. (52), at any time t can be written down by the replacement of the numerical solution in Eq. (52) by the exact solution as follows:

$$\begin{aligned} e \,= & {} \, h^2 \left\{ m_1 \frac{d^n u_{(A-1),(B-1)}}{dt^n} +\, m_2 \frac{d^n u_{A,(B-1)}}{dt^n} + \,m_3 \frac{d^n u_{(A+1),(B-1)}}{dt^n} + \,{m_4} \frac{d^n u_{(A-1),B}}{dt^n} + \,{m_5} \frac{d^n u_{A,B}}{dt^n}\right. \nonumber \\&\left. +\, m_6 \frac{d^n u_{(A+1),B}}{dt^n} +\, m_8 \frac{d^n u_{A,(B+1)}}{dt^n} + \,m_9 \frac{d^n u_{(A+1),(B+1)}}{dt^n}\right\} \nonumber \\&+\,\bar{c} \left\{ k_1 u_{(A-1),(B-1)} +\, k_2 u_{A,(B-1)} +\, k_3 u_{(A+1),(B-1)} +\, {k_4} u_{(A-1),B} +\, {k_5} u_{A,B}\right. \nonumber \\&\left. +\, k_6 u_{(A+1),B} +\, k_8 u_{A,(B+1)} +\, k_9 u_{(A+1),(B+1)}\right\} \nonumber \\&- \,\, \left[ \bar{c} h \left( l_1 \left( n_{11} \frac{\partial u(x_1 , y_1) }{\partial x} + n_{21} \frac{\partial u(x_1 ,y_1) }{\partial y}\right) + l_2 \left( n_{12} \frac{\partial u(x_2 ,y_2) }{\partial x} + n_{22} \frac{\partial u(x_2 ,y_2) }{\partial y}\right) \right. \right. \nonumber \\&\left. \left. +\, l_3 \left( n_{13} \frac{\partial u(x_3 ,y_3) }{\partial x} + n_{23} \frac{\partial u(x_3 ,y_3) }{\partial y}\right) \right) \right] , \end{aligned}$$

(53)

where $n_{1i}$ and $n_{2i}$ ($i=1,2,3$) are the x- and y-components of the unit normal vector ${\mathbf{n}}_i$ at the boundary point i (see Fig. 7), function u(x, y, t) in Eq. (53) corresponds to the exact solution, the Neumann boundary conditions in the right-hand side of Eq. (52) are expressed in terms of the function u(x, y, t) and are moved to the left-hand side of Eq. (53). Next, using the following notations for the coordinates of the boundary points (see Fig. 7):

$$\begin{aligned} x_i = x_{A,B} + \alpha _i h, \qquad y_i = y_{A,B} + \beta _i h, \end{aligned}$$

(54)

with the coefficients $\alpha _i$ ($-1 \le \alpha _i \le 1$), $\beta _i$, $i= 1,2,3$, let us expand the expression in the square brackets of Eq. (53) (that corresponds to the Neumann boundary conditions) into a Taylor series at small $h \ll 1$ as follows:

$$\begin{aligned} \frac{\partial u(x_{A,B} + \alpha _i h , y_{A,B} + \beta _i h)}{\partial z}= & {} \frac{\partial u_{A,B} }{\partial z} + \frac{\partial ^2 u_{A,B}}{\partial z \partial x} (\alpha _i h )\nonumber \\&+ \frac{\partial ^2 u_{A,B}}{\partial z \partial y} ( \beta _i h) + \frac{\partial ^3 u_{A,B}}{\partial z \partial x^2} \frac{(\alpha _i h)^2}{2!} + \frac{\partial ^3 u_{A,B}}{\partial z \partial x \partial y} \frac{(\alpha _i h)( \beta _i h)}{2!} \nonumber \\&+ \frac{\partial ^3 u_{A,B}}{\partial z \partial y^2} \frac{(\beta _i h)^2}{2!} + \frac{\partial ^4 u_{A,B}}{\partial z \partial x^3} \frac{(\alpha _i h)^3}{3!} + \frac{\partial ^4 u_{A,B}}{\partial z \partial y \partial x^2} \frac{(\alpha _i h)^2 ( \beta _i h)}{3!}\nonumber \\&+ \frac{\partial ^4 u_{A,B}}{\partial z \partial y^2 \partial x} \frac{(\alpha _i h) ( \beta _i h)^2}{3!} + \frac{\partial ^4 u_{A,B}}{\partial z \partial y^3} \frac{( \beta _i h)^3}{3!} + \cdots \end{aligned}$$

(55)

with $\frac{\partial u}{\partial z} = \frac{\partial u}{\partial x}$, $\frac{\partial u}{\partial z} = \frac{\partial u}{\partial y}$. Using Eq. (34) with $w = u$, $w = \frac{\partial ^n u}{\partial t^n}$ and $d_{ij}=1$, Eqs. (36), (37), (55), we get the following form of the local truncation error in space e from Eq. (53):

$$\begin{aligned} e= & {} \bar{c} \left\{ b_1 u_{A,B} + h \left( b_2 \frac{\partial u_{A,B} }{\partial x} + b_3 \frac{\partial u_{A,B} }{\partial y}\right) + \frac{h^2}{2} \left( b_4 \frac{\partial ^{2} u_{A,B} }{\partial x^{2}}+ b_5 \frac{\partial ^{2} u_{A,B} }{\partial x \partial y} + b_6 \frac{\partial ^{2} u_{A,B} }{\partial y^{2}}\right) \right. \nonumber \\&+ \frac{h^3}{6} \left( b_7 \frac{\partial ^{3} u_{A,B} }{\partial x^{3}} + b_8 \frac{\partial ^{3} u_{A,B} }{\partial x^{2} \partial y} + b_9 \frac{\partial ^{3} u_{A,B} }{\partial x \partial y^{2}} + b_{10} \frac{\partial ^{3} u_{A,B} }{\partial y^{3}}\right) \nonumber \\&+ \frac{h^4}{24} \left( b_{11} \frac{\partial ^{4} u_{A,B} }{\partial x^{4}} + b_{12} \frac{\partial ^{4} u_{A,B} }{\partial x^{3} \partial y} + b_{13} \frac{\partial ^{4} u_{A,B} }{\partial x^{2} \partial y^{2}} + b_{14} \frac{\partial ^{4} u_{A,B} }{\partial x \partial y^{3}} + b_{15}\frac{\partial ^{4} u_{A,B} }{\partial y^{4}}\right) \nonumber \\&+ \frac{h^5}{120} \left( b_{16} \frac{\partial ^{5} u_{A,B} }{\partial x^{5}} + b_{17} \frac{\partial ^{5} u_{A,B} }{\partial x^{4} \partial y} + b_{18} \frac{\partial ^{5} u_{A,B} }{\partial x^{3} \partial y^{2}} + b_{19} \frac{\partial ^{5} u_{A,B} }{\partial x^{2} \partial y^{3}} + b_{20} \frac{\partial ^{5} u_{A,B} }{\partial x \partial y^{4}} + b_{21} \frac{\partial ^{5} u_{A,B} }{\partial y^{5}}\right) \nonumber \\&\left. + \frac{h^6}{720} \left( b_{22} \frac{\partial ^{6} u_{A,B} }{\partial x^{6}} + b_{23} \frac{\partial ^{6} u_{A,B} }{\partial x^{5}\partial y} + b_{24} \frac{\partial ^{6} u_{A,B} }{\partial x^{4}\partial y^{2}} + b_{25} \frac{\partial ^{6} u_{A,B} }{\partial x^{3}\partial y^{3}} + b_{26} \frac{\partial ^{6} u_{A,B} }{\partial x^{2} \partial y^{4}} + b_{27} \frac{\partial ^{6} u_{A,B} }{\partial x \partial y^{5}} + b_{28} \frac{\partial ^{6} u_{A,B} }{\partial y^{6}}\right) \right\} \end{aligned}$$

(56)

with the coefficients $b_p$ ($p=1,2,\ldots ,28$) given in “Appendix A.” Due to the use of Eqs. (36) and (37), the local truncation error in Eq. (56) does not include the time derivatives. In order to improve the order of the local truncation error in Eq. (56) at small $h \ll 1$, we equate to zero the coefficients $b_p$ in Eq. (56) for the smallest orders of h. The stencil equation, Eq. (52), includes 19 unknown coefficients $m_i$, $k_i$ ($i=1,2,\ldots ,6,8,9$) and $l_i$ ($i=1,2,3$), but only 18 of them can be considered as unknown coefficients; see Remark 9. Therefore, we can zero 18 coefficients $b_p$ in Eq. (56). As can be seen from Eq. (56), this will lead to the fifth order of the local truncation error. In order to minimize the leading terms of the local truncation error, we use the following procedure. First, we can zero the first 15 coefficients $b_p = 0$ ($p=1,2,\ldots ,15$) in Eq. (56) (this provides the fifth order of the local truncation error), and then, we can minimize the coefficients $b_p$ ($p=16,17,\ldots ,21$) that define the leading terms of the local truncation error. From this procedure, we can find the unknown coefficients $m_i$, $k_i$ ($i=1,2,\ldots ,6,8,9$) and $l_i$ ($i=1,2,3$) of the stencil equation, Eq. (52). Symbolic computations with the Mathematica software show that the 14 algebraic equations $b_p = 0$ ($p=1,2,\ldots ,11,13,14,15$) can be analytically solved for $k_i$ ($i=1,2,\ldots ,6,8,9$) and $m_i$ ($i=2,3,\ldots ,6,8,9$) in terms of $m_1$, $m_5$ and $l_i$ ($i=1,2,3$) and are given in the attached file ’m-k-coeff.pdf’ where the coefficients $m_5$ can be taken as $m_5=1$ after rescaling; see Remark 9. The remaining unknown coefficients $m_1$ and $l_i$ ($i=1,2,3$) can be found from the minimization of the leading terms of the local truncation error at the constraint $b_{12}=0$. Let us consider the least square method with the following residual:

$$\begin{aligned} R = b_{16}^2 + b_{17}^2 + b_{18}^2 + b_{19}^2 + b_{20}^2 + b_{21}^2 + \lambda b_{12}, \end{aligned}$$

(57)

where $\lambda$ is the Lagrange multiplier. With the help of the formulas given in “Appendix A” and the attached file ’m-k-coeff.pdf’, the right-hand side of Eq. (57) can be expressed as a quadratic function of $m_1$ and $l_i$ ($i=1,2,3$) and a linear function of $\lambda$, i.e., $R= R(m_1, l_1, l_2, l_3, \lambda )$. In order to minimize the residual $R(m_1, l_1, l_2, l_3, \lambda )$, the following five equations based on the least square method for the residual R can be written down:

$$\begin{aligned}&\frac{\partial R}{\partial m_1} =0, \qquad \frac{\partial R}{\partial l_1} =0 , \qquad \frac{\partial R}{\partial l_2} =0 , \nonumber \\&\quad \frac{\partial R}{\partial l_3} =0 , \qquad \frac{\partial R}{\partial \lambda } =0, \end{aligned}$$

(58)

where the explicit form of these linear algebraic equations is given in the attached file ’Derivatives.pdf.’ Solving the 5 linear algebraic equations (see Eq. (58)), we can find the coefficients $m_1$, $l_i$ ($i=1,2,3$) as well as the coefficients $k_i$ ($i=1,2,\ldots ,6,8,9$) and $m_i$ ($i=2,3,\ldots ,6,8,9$) with the help of the formulas given in the attached files ’m-k-coeff.pdf’ and ’Derivatives.pdf.’ As can be seen, the 8-point cut stencil with the Neumann boundary conditions yields the same fifth order of the local truncation error as the non-uniform 9-point stencil with the Dirichlet boundary conditions in Sect. 3.1.

Remark 11

For some simple cases, the 5 linear algebraic equations (see Eq. (58)) can be solved analytically. In this case, the leading terms $b_p$ ($p=16,17,\ldots ,21$) of the local truncation error are the rational functions of the $x_i$ and $y_i$ coordinates ($i=1,2,3$) of the boundary points and the components of the unit normal vectors $n_{1i}$ ($i=1,2,3$) for the boundary points. (The components $n_{2i}$ can be expressed in terms of $n_{1i}$.) If the denominators of these rational functions are nonzero for all $x_i$, $y_i$ and $n_{1i}$, then the leading terms $b_p$ ($p=16,17,\ldots ,21$) are bounded. The numerical results show that in this case we have stable numerical solutions. A more comprehensive study of the imposition of the optimal boundary conditions (including the number and location of the boundary points) will be considered in the future. We should also mention that a simpler way of the imposition of the Neumann boundary conditions is considered in our papers [29, 30].

4 A new numerical approach for the 2-D Poisson equation

4.1 Zero load $f=0$ in Eq. (3)

The derivation of the new approach for the Poisson equation is similar to that for the wave and heat equations in Sect. 3. The 9-point uniform and non-uniform stencils introduced in Section 3.1 (see Figs. 5 and 6) will be used with the new approach for the internal grid points located far from the boundary and for the grid points located close to the boundary with the Dirichlet boundary conditions. (The case of the Neumann boundary conditions will be considered separately in Sect. 4.3.2.) The stencil equation for the degree of freedom $u^{\mathrm{num}}_{A,B}$ of the time-independent Poisson equation can be obtained from Eq. (33) with $\bar{c}=1$ and $m_i= 0$ for $i=1,2,\ldots ,9$) as follows:

$$\begin{aligned}&k_1 u^{\mathrm{num}}_{(A-1),(B-1)} + \,k_2 u^{\mathrm{num}}_{A,(B-1)} +\, k_3 u^{\mathrm{num}}_{(A+1),(B-1)} + \,{k_4} u^{\mathrm{num}}_{(A-1),B} + \,{k_5} u^{\mathrm{num}}_{A,B} \nonumber \\&\quad + k_6 u^{\mathrm{num}}_{(A+1),B} +\, k_7 u^{\mathrm{num}}_{(A-1),(B+1)} + \,k_8 u^{\mathrm{num}}_{A,(B+1)} + \,k_9 u^{\mathrm{num}}_{(A+1),(B+1)} \, = \, \bar{f}_{A,B}, \end{aligned}$$

(59)

where $\bar{f}_{A,B} = 0$ in the case of zero load $f=0$ in Eq. (3), the unknown coefficients $k_i$ ($i=1,2,\ldots ,9$) are to be determined from the minimization of the local truncation error. The exact solution $u_{A,B}$ to the Poisson equation, Eq. (3), with $f=0$ at $x=x_A$ and $y=y_B$ meets the following equations:

$$\begin{aligned} \frac{\partial ^2 u_{A,B}}{\partial x^2}= & {} - \frac{\partial ^2 u_{A,B}}{\partial y^2} , \end{aligned}$$

(60)

$$\begin{aligned} \frac{ \partial ^{(i+2j)} u_{A,B}}{\partial y^{i} \partial x^{2j} }= & {} (-1)^j \frac{\partial ^{(i+2j)} u_{A,B}}{\partial y^{(i+2j)}}, \end{aligned}$$

(61)

$$\begin{aligned} \frac{ \partial ^{(i+2j-1)} u_{A,B}}{\partial y^{i} \partial x^{(2j-1)} }= & {} (-1)^j \frac{\partial ^{(i+2j-1)} u_{A,B}}{\partial y^{(i+2j-1)} \partial x}, \end{aligned}$$

(62)

with $i=0, 1, 2, 3, 4,\ldots$ and $j=1, 2, 3, 4,\ldots$. The right-hand sides of Eqs. (61) and (62) are obtained by the replacement of the second x-derivative in the left-hand sides of Eqs. (61) and (62) by the second y-derivative using Eq. (60). For the calculation of the local truncation error, we also use Eq. (32) with Eqs. (34) and (35). Replacing the numerical solution in Eq. (59) by the exact solution (similar to Eq. (6)) and using Eq. (34) with $w = u$ as well as Eqs. (60)–(62), we get a Taylor series of the local truncation error in space for the new approach:

$$\begin{aligned} e= & {} b_1 u_{A,B} + h \left( b_2 \frac{\partial u_{A,B} }{\partial x} + b_3 \frac{\partial u_{A,B} }{\partial y}\right) + \frac{h^2}{2} \left( b_4 \frac{\partial ^{2} u_{A,B} }{\partial x \partial y}+b_5 \frac{\partial ^{2} u_{A,B} }{\partial y^{2}}\right) \nonumber \\&+ \frac{h^3}{6} \left( b_6 \frac{\partial ^{3} u_{A,B} }{\partial x \partial y^{2}} + b_{7} \frac{\partial ^{3} u_{A,B} }{\partial y^{3}}\right) + \frac{h^4}{24} \left( b_{8} \frac{\partial ^{4} u_{A,B} }{\partial x \partial y^{3}}+ b_{9}\frac{\partial ^{4} u_{A,B} }{\partial y^{4}}\right) \nonumber \\&+ \frac{h^5}{120} \left( b_{10} \frac{\partial ^{5} u_{A,B} }{\partial x \partial y^{4}} + b_{11} \frac{\partial ^{5} u_{A,B} }{\partial y^{5}}\right) + \frac{h^6}{720} \left( b_{12} \frac{\partial ^{6} u_{A,B} }{\partial x \partial y^{5}} + b_{13} \frac{\partial ^{6} u_{A,B} }{\partial y^{6}}\right) + O({h}^{7}) \end{aligned}$$

(63)

with the coefficients $b_p$ ($p=1,2,\ldots ,13$) given in “Appendix A.” Due to the use of Eqs. (60)–(62), the local truncation error in Eq. (63) does not include the second- and higher-order partial derivatives with respect to x. In order to improve the order of the local truncation error in Eq. (63) at small $h \ll 1$, we equate to zero the coefficients $b_p$ in Eq. (63) for the smallest orders of h. The stencil equation, Eq. (59), includes 9 coefficients $k_i$ ($i=1,2,\ldots ,9$), but only 8 of them can be considered as unknown coefficients; the explanation is similar to that for the wave (heat) equation in Remark 9. Therefore, we zero 8 coefficients $b_p$ ($p=1,2,\ldots ,7,9$) in Eq. (63). Taking the scaling coefficient $k_5=a_1=1$, from the 8 linear algebraic equations $b_p = 0$ ($p=1,2,\ldots ,7,9$), all coefficients $k_i$ ($i=1,2,\ldots ,9$) of the stencil equation, Eq. (59), can be numerically found for the new approach. As can be seen from Eq. (63), this leads to the fourth order of the local truncation error for rectangular meshes with $b_y \ne 1$. However, we would like to mention that for square meshes with $b_y = 1$, the coefficient $b_8=0$; see “Appendix A” and the attached file ’b-coeff.pdf.’ This means that the order of the local truncation error on square meshes is five (see Eq. (63) with $b_p=0$ for $p=1,2,\ldots ,9$) and is one order higher than that on rectangular meshes. Below, we present the analytical solution of a system of algebraic equations $b_p = 0$ for $p=1,2,\ldots ,7,9$ in the case of the 9-point uniform stencil with $d_i = 1$ ($i=1,2,\ldots ,8$). In this case, the coefficients $k_i$ ($i=1,2,\ldots ,9$) of the stencil equation, Eq. (59), and the local truncation error e (see Eq. (63)) are:

$$\begin{aligned} {k_1}= & {} -\frac{a_1}{20}, \qquad {k_2}= \frac{\left( b_y^2-5\right) {a_1}}{10 \left( b_y^2+1\right) }, \qquad {k_3}= -\frac{a_1}{20}, \qquad {k_4}= \frac{\left( 1-5 b_y^2 \right) {a_1}}{10 \left( b_y^2+1\right) }, \qquad {k_5}= a_1, \nonumber \\ {k_6}= & {} \frac{\left( 1-5 b_y^2 \right) {a_1}}{10 \left( b_y^2+1\right) }, \qquad {k_7}= -\frac{a_1}{20}, \qquad {k_8}= \frac{\left( b_y^2-5\right) {a_1}}{10 \left( b_y^2+1\right) }, \qquad {k_9}= -\frac{a_1}{20} \end{aligned}$$

(64)

and

$$\begin{aligned} e = a_1 \left[ \frac{h^6}{400} b_y^2 \left( -1 + b_y^2\right) \frac{\partial ^{6} u_{A,B} }{\partial y^{6}} + \frac{h^8}{100800} b_y^2 \left( 11 - 32 b_y^2 + 11 b_y^4\right) \frac{\partial ^{8} u_{A,B} }{\partial y^{8}}\right] + O({h}^{10}), \end{aligned}$$

(65)

where $a_1$ is an arbitrary coefficient (we can take $a_1 = 1$). As can be seen from Eq. (65), on the square meshes with $b_y = 1$, the local truncation error for the 9-point uniform stencil is two orders higher than that on rectangular meshes (see also our paper [23]).

For the conventional linear finite elements on uniform rectangular meshes, the local truncation error is (e.g., see [23]):

$$\begin{aligned} e_{\mathrm{conv}}^{\mathrm{lin}}= & {} \frac{\left( b_y + b_y^3\right) {h}^4}{12} \frac{\partial ^4 u_{A,B}}{\partial y^{4}} + \frac{b_y \left( -1 + b_y^4\right) h^{6}}{90 } \frac{\partial ^{6} u_{A,B} }{\partial y^{6}} \nonumber \\&+ \frac{b_y \left( 1 + b_y^2\right) \left( 25 - 67 b_y^2 + 25 b_y^4\right) h^{8}}{60480} \frac{\partial ^{8} u_{A,B} }{\partial y^{8}} + O({h}^{10}). \end{aligned}$$

(66)

As can be seen from Eq. (66), the order of the local truncation error for the linear finite elements is four on rectangular and square meshes, i.e., compared to conventional linear elements, the new approach improves the local truncation error in space by two orders on uniform rectangular meshes and by four orders on uniform square meshes.

4.2 Nonzero load $f \ne 0$ in Eq. (3)

The inclusion of nonzero loading term f in the partial differential equation, Eq. (3), leads to the nonzero term $\bar{f}_{A,B}$ in the stencil Eq. (59) (similar to Eq. (5)). The expression for the term $\bar{f}_{A,B}$ can be calculated from the procedure similar to that for the wave (heat) equation in Sect. 3.2 and is given in the attached file ’RHS-Poisson.pdf.’ Similar to Sect. 4.1, the coefficients of the stencil equations are first calculated for zero load $f = 0$. Then, the nonzero loading term $\bar{f}_{A,B}$ given in the attached file ’RHS-Poisson.pdf’ is used in the stencil equation, Eq. (59). The expressions for the local truncation error are the same for zero and nonzero loading functions.

4.3 Boundary conditions

4.3.1 Dirichlet boundary conditions

Similar to Sect. 3.3.1, the application of the Dirichlet boundary conditions in the new approach is trivial and similar to that for the finite elements. We simply equate the boundary degrees of freedom of the uniform and non-uniform stencils (see Figs. 5 and 6) to the values of a given function $g_2(x,y)$ at the corresponding boundary points, i.e., the Dirichlet boundary conditions are exactly imposed; see also Remark 7 in Sect. 3.3.1. Here, $g_2(x,y)$ describes the Dirichlet boundary conditions. The final global discrete system of algebraic equations includes the 9-point uniform and non-uniform stencil equations (see Figs. 5 and 6) for all internal grid points that are located inside the domain as well as the Dirichlet boundary conditions at the boundary points.

4.3.2 Neumann boundary conditions (with no inclusion of boundary degrees of freedom)

Here, we show that the 8-point cut stencil used in Sect. 3.3.2 for the grid points close to the boundary in the case of the wave (heat) equation can be also used for the imposition of the Neumann boundary conditions for the Poisson equation. Similar to Sect. 3.3.2, we consider this stencil at the upper boundary (the stencils at the left, lower and right boundaries can be considered by the rotation of this stencil through angles $90^{\circ }$, $180^{\circ }$ and $270^{\circ }$, respectively). Similar to Sect. 3.3.2, the boundary points with the Neumann boundary conditions are included into the right-hand side of the 8-point cut stencil. For the time-independent Poisson equation, we use four boundary points with the coordinates $x_i, y_i$, $i=1,2,3,4$ (see Fig. 7 and Eq. (67) below). The stencil equations should be formed for all grid points located within the actual domain. For any internal grid point located far from the boundary, we use the 9-point stencil; see Fig. 5. For the 9-point regular stencil for the grid point $u_{A,B}$ shown in Fig. 7 and located close to the boundary, one grid point $u_{A-1,B+1}$ is cut by the boundary. Therefore, for this grid point, we use the 8-point stencil shown in Fig. 7. The case when the boundary cuts the grid point $u_{A+1,B+1}$ (instead of the grid point $u_{A-1,B+1}$) can be treated similarly. For the 9-point regular stencil for the grid point $u_{A,B+1}$ shown in Fig. 7 and located close to the boundary, the boundary cuts four grid points $u_{A-1,B+1}$, $u_{A-1,B+2}$, $u_{A,B+2}$ and $u_{A+1,B+2}$. In this case, for the grid point $u_{A,B+1}$, we use the same 8-point stencil as that for the grid point $u_{A,B}$. However, in order to have linear independent stencil equations for the grid points $u_{A,B+1}$ and $u_{A,B}$, we select different locations of the boundary points used for these stencils (with the different coordinates $x_i, y_i$, $i=1,2,3,4$). If for the 9-point regular stencil for the grid point $u_{A,B+1}$ the boundary cuts one grid point $u_{A,B+2}$, or two grid points $u_{A-1,B+2}$ and $u_{A,B+2}$, or three grid points $u_{A-1,B+2}$, $u_{A,B+2}$ and $u_{A+1,B+2}$ (or three grid points $u_{A-1,B+1}$, $u_{A-1,B+2}$ and $u_{A,B+2}$), then the same 8-point stencil as that for the grid point $u_{A,B+1}$ shown in Fig. 7 is used, i.e., the 8-point stencils are used for all grid points close to the boundary where the boundary cuts the grid points of the 9-point regular stencil. Equation (4) for the 8-point stencil (see Fig. 7) can be explicitly written as follows:

$$\begin{aligned}&k_1 u^{\mathrm{num}}_{(A-1),(B-1)} + k_2 u^{\mathrm{num}}_{A,(B-1)} + k_3 u^{\mathrm{num}}_{(A+1),(B-1)} + {k_4} u^{\mathrm{num}}_{(A-1),B} + {k_5} u^{\mathrm{num}}_{A,B} \nonumber \\&\qquad +\, k_6 u^{\mathrm{num}}_{(A+1),B} + k_8 u^{\mathrm{num}}_{A,(B+1)} + k_9 u^{\mathrm{num}}_{(A+1),(B+1)} \nonumber \\&\quad = \, [ h (l_1 g_1(x_1,y_1)+l_2 g_1(x_2,y_2)+l_3 g_1(x_3,y_3)+l_4 g_1(x_4,y_4)] + \bar{f}_{A,B}, \end{aligned}$$

(67)

where $\bar{f}_{A,B}$ is zero $\bar{f}_{A,B} = 0$ in the case of zero load $f=0$ in Eq. (3), the unknown coefficients $k_i$ ($i=1,2,\ldots ,6,8,9$) and $l_i$ ($i=1,2,3,4$) are to be determined from the minimization of the local truncation error, the expression in the square brackets in the right-hand side of Eq. (67) represents the Neumann boundary conditions at four boundary points with the coordinates $x_i, y_i$, $i=1,2,3,4$ ($x_{A-1,B+1} \le x_i \le x_{A+1,B+1}$, see Fig. 7). For convenience, the left-hand side of Eq. (67) is written similar to that of Eq. (59) with $k_7=0$.

Remark 12

Only 11 out of 12 coefficients $k_i$ ($i=1,2,\ldots ,6,8,9$) and $l_i$ ($i=1,2,3,4$) in Eq. (67) can be considered as unknown coefficients with the rescaled coefficient $k_5=1$. This can be explained similar to that in Remark 9.

Remark 13

In the numerical simulations in Part 2 of the paper, we use the uniform spacing $h_1 = h/32$ for the boundary points along the x-axis ($x_{i+1} = x_i + h_1$ with $i=1,2,3$; see Fig. 7) with the following x-coordinate of the first point: a) $x_1 = x_{A-1,B} + h_1$ in the case when the boundary cuts one grid point $u_{A-1,B+1}$; b) $x_1 = x_{A,B} - 1.5 h_1$ in the case when the boundary cuts one grid point $u_{A,B+2}$ or three grid points $u_{A-1,B+2}$, $u_{A,B+2}$ and $u_{A+1,B+2}$ as well as in the case of the conforming mesh; c) $x_1 = (x_{A,B}+ x_{A+1,B})/2 - 1.5 h_1$ in the case when the boundary cuts four grid points $u_{A-1,B+1}$, $u_{A-1,B+2}$, $u_{A,B+2}$ and $u_{A+1,B+2}$ or three grid points $u_{A-1,B+1}$, $u_{A-1,B+2}$ and $u_{A,B+2}$ or two grid points $u_{A-1,B+2}$ and $u_{A,B+2}$. The numerical results show that with this selection of the boundary points we have stable numerical solutions.

The local truncation error of the stencil equation, Eq. (67), can be written down by the replacement of the numerical solution in Eq. (67) by the exact solution as follows:

$$\begin{aligned} e \,= & {} \, k_1 u_{(A-1),(B-1)} + \,k_2 u_{A,(B-1)} +\, k_3 u_{(A+1),(B-1)} + \,{k_4} u_{(A-1),B} + \,{k_5} u_{A,B} \nonumber \\&+\, k_6 u_{(A+1),B} + \,k_8 u_{A,(B+1)} + \,k_9 u_{(A+1),(B+1)} \nonumber \\&- \, h \left[ l_1 \left( n_{11} \frac{\partial u(x_1 , y_1) }{\partial x} + n_{21} \frac{\partial u(x_1 ,y_1) }{\partial y}\right) + l_2 \left( n_{12} \frac{\partial u(x_2 ,y_2) }{\partial x} + n_{22} \frac{\partial u(x_2 ,y_2) }{\partial y}\right) \right. \nonumber \\&\left. +\, l_3 \left( n_{13} \frac{\partial u(x_3 ,y_3) }{\partial x} + n_{23} \frac{\partial u(x_3 ,y_3) }{\partial y}\right) + l_4 (n_{14} \frac{\partial u(x_4 ,y_4) }{\partial x} + n_{24} \frac{\partial u(x_4 ,y_4) }{\partial y})\right] , \end{aligned}$$

(68)

where $n_{1i}$ and $n_{2i}$ ($i=1,2,3,4$) are the x- and y-components of the unit normal vector ${\mathbf{n}}_i$ at the boundary point i (see Fig. 7), function u(x, y) in Eq. (68) corresponds to the exact solution, the Neumann boundary conditions in the right-hand side of Eq. (67) are expressed in terms of the function u(x, y) and are moved to the left-hand side of Eq. (68).

Using Eq. (34) with $w = u$ and $d_{ij}=1$, Eqs. (60)–(62), we get the following form of the local truncation error in space e from Eq. (68):

$$\begin{aligned} e= & {} b_1 u_{A,B} + h \left( b_2 \frac{\partial u_{A,B} }{\partial x} + b_3 \frac{\partial u_{A,B} }{\partial y}\right) \nonumber \\&+ \frac{h^2}{2} \left( b_4 \frac{\partial ^{2} u_{A,B} }{\partial x \partial y} +b_5 \frac{\partial ^{2} u_{A,B} }{\partial y^{2}}\right) \nonumber \\&+ \frac{h^3}{6} \left( b_6 \frac{\partial ^{3} u_{A,B} }{\partial x \partial y^{2}} + b_{7} \frac{\partial ^{3} u_{A,B} }{\partial y^{3}}\right) + \frac{h^4}{24} \left( b_{8} \frac{\partial ^{4} u_{A,B} }{\partial x \partial y^{3}}\right. \nonumber \\&\left. + b_{9}\frac{\partial ^{4} u_{A,B} }{\partial y^{4}}\right) \nonumber \\&+ \frac{h^5}{120} \left( b_{10} \frac{\partial ^{5} u_{A,B} }{\partial x \partial y^{4}} + b_{11} \frac{\partial ^{5} u_{A,B} }{\partial y^{5}}\right) + \frac{h^6}{720} \left( b_{12} \frac{\partial ^{6} u_{A,B} }{\partial x \partial y^{5}}\right. \nonumber \\&\left. + b_{13} \frac{\partial ^{6} u_{A,B} }{\partial y^{6}}\right) + O({h}^{7}) \end{aligned}$$

(69)

with the coefficients $b_p$ ($p=1,2,\ldots ,13$) given in “Appendix A.” For the derivation of Eq. (69), we also used Eqs. (54) and (55) with $\frac{\partial u}{\partial z} = \frac{\partial u}{\partial x}$ and $\frac{\partial u}{\partial z} = \frac{\partial u}{\partial y}$. Due to the use of Eqs. (60)–(62), the local truncation error in Eq. (69) does not include the second- and higher-order partial derivatives with respect to x.

In order to improve the order of the local truncation error in Eq. (69) at small $h \ll 1$, we equate to zero the coefficients $b_p$ in Eq. (69) for the smallest orders of h. The stencil equation, Eq. (67), includes 12 coefficients $k_i$ ($i=1,2,\ldots ,6,8,9$) and $l_i$ ($i=1,2,3,4$), but only 11 of them can be considered as unknown coefficients; see Remark 12. Therefore, we zero 11 coefficients $b_p$ ($i=1,2,\ldots ,11$) in Eq. (69). Taking the scaling coefficient $k_5=a_1=1$, from the 11 linear algebraic equations $b_p = 0$ ($p=1,2,\ldots ,11$), all coefficients $k_i$ ($i=1,2,\ldots ,6,8,9$) and $l_i$ ($i=1,2,3,4$) of the stencil equation, Eq. (67), can be numerically found for the new approach. As can be seen from Eq. (69), this leads to the sixth order of the local truncation error for rectangular $b_y \ne 1$ and square $b_y = 1$ meshes. As can be seen, the 8-point cut stencil with the Neumann boundary conditions yields the sixth order of the local truncation error.

Remark 14

For some simple cases, the 11 linear algebraic equations $b_p = 0$ ($p=1,2,\ldots ,11$) can be solved analytically. In this case, the leading terms $b_p$ ($p=12,13$) of the local truncation error are the rational functions of the $x_i$ and $y_i$ coordinates ($i=1,2,3,4$) of the boundary points and the components of the unit normal vectors $n_{1i}$ ($i=1,2,3,4$) for the boundary points (the components $n_{2i}$ can be expressed in terms of $n_{1i}$). If the denominators of these rational functions are nonzero for all $x_i$, $y_i$ and $n_{1i}$, then the leading terms $b_p$ ($p=12,13$) are bounded. The numerical results show that in this case we have stable numerical solutions. A more comprehensive study of the imposition of the optimal boundary conditions (including the number and location of the boundary points) will be considered in the future. We should also mention that a simpler way of the imposition of the Neumann boundary conditions is considered in our papers [29, 30].

5 Concluding remarks

Most of the numerical techniques for the solution of partial differential equations finally reduce to a system of discrete or semi-discrete equations. However, in many cases the corresponding stencil equations of these systems do not provide an optimal accuracy. The idea of the new approach consists in the direct optimization of the coefficients of the stencil equations and is based on the minimization of the order of the local truncation error. The form and width of the stencil equations in the new approach are assumed (e.g., as it is assumed for the finite-difference method) or can be selected similar to those for known numerical technique. (In this case, the accuracy of the known numerical techniques can be significantly improved by the modification of the coefficients of the stencil equations.) Another idea of the new approach is the use of simple Cartesian meshes for complex irregular domains. In the considered paper, the new approach has been applied to the space discretization of the time-dependent wave and heat equations as well as of the time-independent Poisson equation. 3-point stencils in the 1-D case and 9-point stencils in the 2-D case that are similar to those for the linear quadrilateral finite elements are considered in the paper. The main advantages of the suggested technique can be summarized as follows:

• The idea of the minimization of the order of the local truncation error of stencil equations can be easily and efficiently applied to the development of new numerical techniques with optimal accuracy as well as to the accuracy improvement of known numerical methods. The new approach can be equally applied to regular and irregular domains. In contrast to many fictitious domain numerical methods, the new approach uses the exact Dirichlet and Neumann boundary conditions at the actual boundary points without their interpolation using the Cartesian grid points.

• In contrast to the finite-difference techniques with the stencil coefficients calculated through the approximation of separate partial derivatives, the entire partial differential equation is used for the calculation of the stencil coefficients in the new approach. This leads to the optimal accuracy of the proposed technique.

• At the similar 9-point 2-D stencils, the accuracy of the new approach is two orders higher than that for the linear finite elements. This means that at a given accuracy, the new approach significantly reduces the computation time compared to that for the linear finite elements.

• Similar to our recent results for regular domains in [23], the order of accuracy of the new approach for the Poisson equation on irregular domains with square Cartesian meshes is higher than that with rectangular Cartesian meshes.

• The treatment of the Dirichlet and Neumann boundary conditions in the new approach is related to the development of high-order boundary conditions with the stencils that include the same or smaller number of grid points compared to that for the regular 9-point internal stencils. For example, the numerical boundary conditions for the Cartesian meshes developed in [34, 37,38,39] include stencils with a greater number of grid points but yield a much smaller order of accuracy compared with that for the proposed technique.

• In contrast to the finite elements, spectral elements, isogeometric elements and other similar techniques used for irregular domains, the new approach uses trivial Cartesian meshes that requires practically negligible computation time for their preparation.

• The new approach does not require time-consuming numerical integration for finding the coefficients of the stencil equations, e.g., as for the high-order finite, spectral and isogeometric elements. For the new technique, the coefficients of the stencil equations for the grid points located far from the boundary are calculated analytically. For the grid points located close to the boundary (with non-uniform and cut stencils), the coefficients of the stencil equations are calculated numerically by the solution of a very small local systems of linear algebraic equations.

• In contrast to the finite element techniques, a large difference in distances between the boundary and Cartesian grid points used in the same stencil does not lead to the degradation of accuracy. This is very important for the application of the new approach to irregular domains.

• It has been shown that the wave and heat equations can be uniformly treated with the new approach. The order of the time derivative in these equations does not affect the coefficients of the stencil equations of the semi-discrete systems.

In the future, we plan to consider the stencils with a larger numbers of grid points for a higher order of accuracy (similar to the high-order finite elements or to the high-order finite-difference techniques), to consider a mesh refinement with uniform Cartesian meshes using special stencils for the transition from a fine mesh to a coarse mesh, to apply the proposed technique to other partial differential equations, to consider nonlinear problems (e.g., by analysis of the local truncation error for nonlinear stencils obtained by known approaches and by optimization of their stencil coefficients), to solve real-world problems with the new approach.

Appendix A: The coefficients \(b_p\) used in Eqs. (38), (56), (63) and (69)

The first five coefficients $b_i$ ($i=1,2,\ldots ,5$) used in Eqs. (38), (56), (63) and (69) are presented below. All coefficients $b_i$ used in these formulas are given in the attached file ’b-coeff.pdf’

Equation (38):

$$\begin{aligned} b_1= & {} (k_1 + k_2 + k_3 + k_4 + k_5 + k_6 + k_7 + k_8 + k_9), \nonumber \\ b_2= & {} (-d_1 k_1 + d_3 k_3 - d_4 k_4 + d_5 k_6 - d_6 k_7 + d_8 k_9), \nonumber \\ b_3= & {} b_y (-d_1 k_1 - d_2 k_2 - d_3 k_3 + d_6 k_7 + d_7 k_8 + d_8 k_9), \nonumber \\ b_4= & {} (d_1^2 k_1 + d_3^2 k_3 + d_4^2 k_4 + d_5^2 k_6 + d_6^2 k_7 + d_8^2 k_9\nonumber \\&+ 2 (m_1 + m_2 + m_3 + m_4 + m_5 + m_6 + m_7 + m_8 + m_9)), \nonumber \\ b_5= & {} 2 b_y (d_1^2 k_1 - d_3^2 k_3 - d_6^2 k_7 + d_8^2 k_9), \nonumber \\&\ldots \qquad \end{aligned}$$

(A.1)

Equation (56):

$$\begin{aligned} b_{1} \,= & {} \, (k_{1}+k_{2}+k_{3}+k_{4}+k_{5}+k_{6}+k_{8}+k_{9}), \nonumber \\ b_{2} \,= & {} \, - (k_{1}-k_{3}+k_{4}-k_{6}-k_{9}+l_1 n_{11}+l_2 n_{12}+l_3 n_{13}), \nonumber \\ b_{3} \,= & {} \, - (k_{1}+k_{2}+k_{3}-k_{8}-k_{9}+l_1 n_{21}+l_2 n_{22}+l_3 n_{23}), \nonumber \\ b_{4} \,= & {} \, \frac{1}{2} (k_{1}+k_{3}+k_{4}+k_{6}+k_{9}+2 m_{1}+2 m_{2}+2 m_{3}+2 m_{4}+2 m_{5}+2 m_{6}+2 m_{8}+2 m_{9} \nonumber \\&-2 \alpha _{1} l_1 n_{11}-2 \alpha _{2} l_2 n_{12}-2 \alpha _{3} l_3 n_{13}),\nonumber \\ b_{5} \,= & {} \, (k_{1}-k_{3}+k_{9}-\beta _1 l_1 n_{11}-\beta _2 l_2 n_{12}-\beta _3 l_3 n_{13}-\alpha _{1} l_1 n_{21}-\alpha _{2} l_2 n_{22}-\alpha _{3} l_3 n_{23}),\nonumber \\&\ldots \end{aligned}$$

(A.2)

Equation (63):

$$\begin{aligned} b_1 \,= & {} \, (k_1 + k_2 + k_3 + k_4 + k_5 + k_6 + k_7 + k_8 + k_9) , \nonumber \\ b_2 \,= & {} \, (-d_1 k_1 + d_3 k_3 - d_4 k_4 + d_5 k_6 - d_6 k_7 + d_8 k_9), \nonumber \\ b_3 \,= & {} \, b_y (-d_1 k_1 - d_2 k_2 - d_3 k_3 + d_6 k_7 + d_7 k_8 + d_8 k_9), \nonumber \\ b_4 \,= & {} \, 2 b_y (d_1^2 k_1 - d_3^2 k_3 - d_6^2 k_7 + d_8^2 k_9), \nonumber \\ b_5 \,= & {} \, (d_1^2 (-1 + b_y^2) k_1 - d_3^2 k_3 - d_4^2 k_4 - d_5^2 k_6 - d_6^2 k_7 - d_8^2 k_9 \nonumber \\&+ b_y^2 (d_2^2 k_2 + d_3^2 k_3 + d_6^2 k_7 + d_7^2 k_8 + d_8^2 k_9)),\nonumber \\&\ldots \end{aligned}$$

(A.3)

Equation (69):

$$\begin{aligned} \ b_{1} \,= & {} \, k_{1}+k_{2}+k_{3}+k_{4}+k_{5}+k_{6}+k_{8}+k_{9}, \nonumber \\ b_{2} \,= & {} \, -k_{1}+k_{3}-k_{4}+k_{6}+k_{9}+{l_1} n_{11}+{l_2} n_{12}+{l_3} n_{13}+{l_4} n_{14}, \nonumber \\ b_{3} \,= & {} \, -b_y (k_{1}+k_{2}+k_{3}-k_{8}-k_{9})+{l_1} n_{21}+{l_2} n_{22}+{l_3} n_{23}+{l_4} n_{24}, \nonumber \\ b_{4} \,= & {} \, b_y (k_{1}-k_{3}+k_{9}+{\beta _1} {l_1} n_{11}+{l_1} n_{11}+{\beta _2} {l_2} n_{12}+{l_2} n_{12}+{\beta _3} {l_3} n_{13}+{l_3} n_{13}+{\beta _4} {l_4} n_{14} \nonumber \\&+{l_4} n_{14})+({\alpha _1}-1) {l_1} n_{21}+{\alpha _2} {l_2} n_{22}-{l_2} n_{22}+{\alpha _3} {l_3} n_{23}-{l_3} n_{23}+{\alpha _4} {l_4} n_{24}-{l_4} n_{24}, \nonumber \nonumber \\ b_{5} \,= & {} \, \frac{1}{2} ((k_{2}+k_{3}+k_{8}+k_{9}) b_y^2+2 (({\beta _1}+1) {l_1} n_{21}+({\beta _2}+1) {l_2} n_{22}+{\beta _3} {l_3} n_{23}+{l_3} n_{23}+{\beta _4} {l_4} n_{24} \nonumber \\&+{l_4} n_{24}) b_y+(b_y^2-1) k_{1}-k_{3}-k_{4}-k_{6}-k_{9}-2 {\alpha _1} {l_1} n_{11}+2 {l_1} n_{11}-2 {\alpha _2} {l_2} n_{12} \nonumber \\&+2 {l_2} n_{12}-2 {\alpha _3} {l_3} n_{13}+2 {l_3} n_{13}-2 {\alpha _4} {l_4} n_{14}+2 {l_4} n_{14}), \nonumber \\&\ldots \end{aligned}$$

(A.4)