1 Introduction

The surface/interface effects due to the internal defects in the materials were not incorporated in the classical solution. These effects would, however, have a dramatic influence on the mechanical properties of the materials when the sizes of the internal defects are at nano-length scales and need to be explicitly addressed [9, 19, 23].

Atomistic models were used successfully to simulate the nano-mechanical problems involving fracture and related issues [1,2,3]. Nevertheless, direct micro-computation at atom scale, even at molecule scale, takes up huge computational resources, and thus it is rather difficult for simulating mechanical behavior of a bulk material with common size. An alternative numerical method involved with less computation is to model the crack as set of contiguous cracked particles for removing the additional unknowns introduced in the cracking-particle method [16, 17].

Continuum model reflecting surface/interface effects has the advantages of minor calculation and better calculating stability, and therefore it captures the attention of many researchers. Gurtin and Murdoch [7] firstly presented the mathematical exposition on surface elasticity and established the “surface/interface effect model.” Later, the model has been widely used in the problems with surface/interface effects.

Extensive investigations have been reported on interface effects of nano-inhomogeneity. Luo et al. [13] investigated the interaction between a screw dislocation and an elliptical nanoscale inhomogeneity in an infinite matrix by applying conformal mapping technique to convert an elliptical nanoscale inhomogeneity into a ring nanoscale one. Using the complex variable function method, Ou et al. [15] derived analytically the stresses in a coated nano-inhomogeneity material and the image forces acting on the screw dislocation. By means of the complex potential functions expanded in Laurent series, Shodja et al. [20] studied the elastic behavior of an edge dislocation positioned outside of a nanoscale elliptical inhomogeneity, and the elastic modulus and surface tension of the interface were incorporated.

As contrast, few analyses have been published to this date on surface effects of the nano-crack. In the research of mode-III line crack problem, Kim et al. [10] found that the stresses with surface effects were always dependent on the crack length. Recently, the interaction between a nanoscale crack incorporating surface elasticity and a screw dislocation was investigated by Wang and Fan [22].

Self-evidently, exactly evaluating physical fields such as stresses, displacements and stress intensity factor of nano-cracks (SIFNCs) is based on the finite-form solution. However, the results in all the literature published by other researchers so far including surface effects of the nano-cracks were expressed in the form of infinite series and therefore none of them has obtained the SIFNCs.

In this paper, the finite-form solution was obtained for the problem of an elastic body weakened by a straight nano-crack and disturbed by a screw dislocation in the mode-III deformation. At first, the Gurtin–Murdoch [8] surface model was used to incorporate the surface effects and the stress boundary equations were integrated over the crack boundary and reduced to single one. The reduced boundary equation was then mapped to image region via the conformal mapping technique and converted into a first-order differential equation by the Muskhelishvili [14] method together with the Cauchy’s integral formula. After inverse mapping, the finite-form solution for the anti-plane problem was established. The results from the present solution were compared with other solutions and the singularity at the crack tip was discussed.

2 Basic formulation

In the linearly elastic, homogeneous and isotropic (bulk) solids, the equilibrium equation and the constitute relation in the absence of the body force read

$$\begin{aligned} \sigma _{{ij'j}} =0, \quad \sigma _{ij} =\lambda \delta _{ij} \varepsilon _{kk} +\mu \varepsilon _{ij} \end{aligned}$$
(1)

where \(\lambda \) and \(\mu \) are the Lamé constants.

In the anti-plane problem, the nonzero components are the stresses \(\tau _{xz} , \tau _{yz} \) and the out-plane displacement w. From (1) we have

$$\begin{aligned} \tau _{xz} =\mu \frac{\partial w}{\partial x}, \quad \tau _{yz} =\mu \frac{\partial w}{\partial y} \end{aligned}$$
(2)

In the Gurtin and Murdoch [7] surface elasticity model, the equilibrium equations are expressed as

$$\begin{aligned}&\left\| {\sigma _{\alpha \beta } n_j } \right\| +\sigma _{\beta \alpha '\beta }^\mathrm{s} =0 \end{aligned}$$
(3)
$$\begin{aligned}&\left\| {\sigma _{ji} n_i n_j } \right\| =\sigma _{\alpha \beta }^\mathrm{s} k_{\alpha \beta } \end{aligned}$$
(4)

and the constitute relation on the isotropic surface is given by

$$\begin{aligned} \sigma _{\alpha \beta }^\mathrm{s} =\sigma _0 \delta _{\alpha \beta } +2(\mu ^\mathrm{s}-\sigma _0 )\varepsilon _{\alpha \beta }^\mathrm{s} +(\lambda ^\mathrm{s}+\sigma _0 )\varepsilon _{\gamma \gamma } \delta _{\alpha \beta } \end{aligned}$$
(5)

where \(\lambda ^\mathrm{s}\) and \(\mu ^\mathrm{s}\) are the Lamé constants for the isotropic surface, the superscript s represents the surface, and \(\sigma _{\alpha \beta }^\mathrm{s} \) is the surface stress tensor. \(\sigma _0 \) stands for the surface tension, \(k_{\alpha \beta } \) is the curvature tensor of the surface, and \(\left\| {*} \right\| \) represents the jump across the surface.

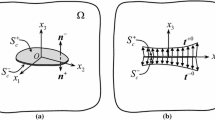
Consider a homogeneous infinite elastic body which occupies the infinite plane (z-plane) and contains a straight-line crack of the length 2a in nanoscale as shown in Fig. 1. Here \(z=x+\hbox {i}y\) is the complex variable. A screw dislocation with the Burgers vector \(b_{z}\) is located at an arbitrary point \(z_0 =x_0 +\hbox {i}y_0 \), and the uniform loads of anti-plane shear stresses, \(\tau _1 \) and \(\tau _2 \), are exerted at the infinite boundary (drawn as dash lines)

Fig. 1
figure 1

The nanoscale crack and the screw dislocation

Full size image

For the anti-plane problem, the out-plane displacement and the stresses in z-plane can be represented by a complex potential function \(\vartheta _1 (z)\) as

$$\begin{aligned}&w(z)=\hbox {Re}[\vartheta _1 (z)] \end{aligned}$$
(6)
$$\begin{aligned}&\tau _{xz} -\hbox {i}\tau _{yz} =\mu {\vartheta }_{1}^{\prime } (z) \end{aligned}$$
(7)

in which the prime indicates the derivative with respect to the variable in the bracket.

From (3) and (4), the boundary conditions for the upper and lower crack faces in z-plane can be written as [10]

$$\begin{aligned}&\hbox {i}\mu [{\vartheta }_{1}^{\prime } (z)-\overline{{\vartheta }_{1}^{\prime } (z)} ]^{+}=-(\mu ^\mathrm{s}-\sigma _0 )[{\vartheta }_{1}^{\prime \prime } (z)+\overline{{\vartheta }_{1}^{\prime \prime } (z)} ]^{+} \end{aligned}$$
(8a)
$$\begin{aligned}&\hbox {i}\mu [{\vartheta }_{1}^{\prime } (z)-\overline{{\vartheta }_{1}^{\prime } (z)} ]^{-}=(\mu ^\mathrm{s}-\sigma _0 )[{\vartheta }_{1}^{\prime \prime } (z)+\overline{{\vartheta }_{1}^{\prime \prime } (z)} ]^{-} \end{aligned}$$
(8b)

where the symbols “\(+\)” and “−” denote the upper and lower crack faces for \(y>0\) and \(y<0\) as shown in Fig. 1.

Now the stress boundary equations (8a) and (8b) are integrated over the boundary of the crack. Probably worthy to be reminded that the route of the integration should be taken as a loop instead of a line segment, the variable increases from left end to the right end for integrating over the upper part of the loop, while it is from right end to the left end for the lower part integration of the loop. This convention will also be used in the later loop integral calculations.

The integration of the boundary equations (8a) and (8b) leads to the following equation

$$\begin{aligned} \frac{\mu }{\hbox {i}}[\vartheta _1 (z)-\overline{\vartheta _1 (z)} ]=(\mu ^\mathrm{s}-\sigma _0 )[{\vartheta }_{1}^{\prime } (z)+\overline{{\vartheta }_{1}^{\prime } (z)} ],\quad z\in L \end{aligned}$$
(9)

In this way, the original boundary problem expressed by two equations (8a) and (8b), is reduced to one equation (9), and easy to be calculated by using Cauchy integrals of the complex function theory.

The following complex function pair is used to simplify the geometry of the problem

$$\begin{aligned} z=\omega (\zeta )=\frac{a}{2}\left( {\zeta +\frac{1}{\zeta }} \right) , \quad \zeta =\omega ^{-1}(z)=\frac{z}{a}\left[ {1+\sqrt{1-\left( {\frac{a}{z}} \right) ^{2}}} \right] \end{aligned}$$
(10)

where \(\zeta =\xi +\hbox {i}\eta \) is the complex variable of the position in \(\zeta \)-plane.

Fig. 2
figure 2

The \(\zeta \)-plane after transformation

Full size image

The mapping function pair (10) maps the whole z-plane (the physical region in Fig. 1) into \(\zeta \)-plane (the image region in Fig. 2), while the nano-crack in z-plane is mapped onto an orifice of unit radius in \(\zeta \)-plane. Equation (9) in \(\zeta \)-plane becomes

$$\begin{aligned} \frac{\mu }{\hbox {i}}[\vartheta (\zeta )-\overline{\vartheta (\zeta )} ]=(\mu ^\mathrm{s}-\sigma _0 )\left[ {\frac{{\vartheta }'(\zeta )}{{\omega }'(\zeta )}+\frac{\overline{{\vartheta }'(\zeta )} }{\overline{{\omega }'(\zeta )}}} \right] ,\quad \zeta \in \gamma \end{aligned}$$
(11)

3 Problem: a screw dislocation disturbance

3.1 Solution

When an infinity plane (z-plane) with a nano-crack and a screw dislocation (the Burgers vector \(b_{z})\) is subjected to uniform loads \({{\tau }}_{1}\) and \({{\tau }}_{2}\) at infinity, the complex potential function \(\vartheta _1 (z)\) can be expressed as

$$\begin{aligned} \vartheta _1 (z)=\varGamma z+\frac{b_z }{2{\pi \hbox {i}}}\ln (z-z_0 )+\vartheta _{10} (z) \end{aligned}$$
(12)

where \(\varGamma ={(\tau _1 -\hbox {i}\tau _2 )}/\mu , \vartheta _{10} (z)\) is an unknown analytic function in domain \(S^{+}\) (Fig. 1). The potential function \(\vartheta _1 (z)\) satisfies the stress conditions \(\tau _{xz} =\tau _1\) and \(\tau _{yz} =\tau _2 \) at infinity only if the value of the analytic function \(\vartheta _{10} (z)\) vanishes at infinity, i.e.,

$$\begin{aligned} \mathop {\lim }\limits _{z\rightarrow \infty } \vartheta _{10} (z)=0 \end{aligned}$$
(13)

Besides, the analytic function \(\vartheta _{10} (z)\) should fulfill the crack-boundary condition. The following conformal mapping technique is used to find the function \(\vartheta _{10} (z)\).

On the image plane, the complex potential function can be written as [5, 14]

$$\begin{aligned} \vartheta (\zeta )=\frac{\varGamma a}{2}\left( {\zeta +\frac{1}{\zeta }} \right) +\frac{b_z }{2\pi \hbox {i}}\left[ {\ln \left( {-\frac{a}{2\zeta _0 }} \right) +\ln (\zeta -\zeta _0 )+\ln \left( {\frac{1}{\zeta }-\zeta _0 } \right) } \right] +\vartheta _0 (\zeta ) \end{aligned}$$
(14)

where \(\vartheta _0 (\zeta )\) is an analytic function in domain \(s^{+}\) (Fig. 2), and

$$\begin{aligned} \zeta _0 =\frac{1}{a}\left( {z_0 +\sqrt{z_0^2 -a^{2}}} \right) \end{aligned}$$
(15)

With inserting (14) and (10) into (11), the boundary condition on the unit circle in \(\zeta \)-plane becomes [5]

$$\begin{aligned}&\frac{\mu }{\hbox {i}}[\vartheta _0 (\sigma )-\overline{\vartheta _0 (\sigma )} ]-(\mu ^\mathrm{s}-\sigma _0 )\left[ {\frac{{\vartheta }_{0}^{\prime } (\sigma )}{{\omega }'(\sigma )}+\frac{\overline{{\vartheta }_{0}^{\prime } (\sigma )} }{\overline{{\omega }'(\sigma )} }} \right] =\frac{\hbox {i}\mu (\varGamma -\bar{{\varGamma }})a}{2}\left( {\sigma +\frac{1}{\sigma }} \right) \nonumber \\&\quad +\,\frac{\mu b_z }{2\pi }\left[ {\ln \left( {\frac{a^{2}}{4\zeta _0 \bar{{\zeta }}_0 }} \right) +\ln (\sigma -\zeta _0 )+\ln (\sigma -\bar{{\zeta }}_0 )+\ln \left( {\frac{1}{\sigma }-\zeta _0 } \right) +\ln \left( {\frac{1}{\sigma }-\bar{{\zeta }}_0 } \right) } \right] \nonumber \\&\quad -\,(\mu ^\mathrm{s}-\sigma _0 )\frac{\hbox {i}b_z }{\pi a}\left\{ {\frac{1}{\zeta _0 -1/{\zeta _0 }}\left[ {\frac{\zeta _0 }{\sigma -\zeta _0 }-\frac{1}{\zeta _0 (\sigma -1/{\zeta _0 )}}} \right] -\frac{1}{\bar{{\zeta }}_0 -1/{\bar{{\zeta }}_0 }}\left[ {\frac{\bar{{\zeta }}_0 }{\sigma ^{-1}-\bar{{\zeta }}_0 }-\frac{1}{\bar{{\zeta }}_0 (\sigma -1/{\bar{{\zeta }}_0 )}}} \right] } \right\} \nonumber \\&\quad +\,(\mu ^\mathrm{s}-\sigma _0 )(\varGamma +\bar{{\varGamma }}) \quad (\sigma \in \gamma ) \end{aligned}$$
(16)

It falls into a problem to find an analytic function \(\vartheta _0 (\zeta )\) satisfying the boundary condition (16).

In \(\zeta \)-plane, for any function \(f(\zeta )\) which is analytic in \(s^{+}\), the value of the function at any point \(\zeta \) in \(s^{+}\) can be expressed as the Cauchy’s integral over a closed boundary \(\gamma \) [14]

$$\begin{aligned} \frac{1}{2\pi \hbox {i}}\mathop {\oint }\limits _{\gamma } {\frac{f(\sigma )}{\sigma -\zeta }\hbox {d}\sigma } =-f(\zeta )+f(\infty ) \end{aligned}$$
(17)

Now both sides of (16) are integrated over \(\gamma \) (the boundary of the unit circle) and then the Cauchy’s integral formula (17) is applied; this leads to the following first-order differential equation for the function \(\vartheta _0 (\zeta )\) in domain \(s^{+}\)

$$\begin{aligned} \frac{{\vartheta }_{0}^{\prime } (\zeta )}{{\omega }'(\zeta )}+\frac{\hbox {i}\mu }{\mu ^\mathrm{s}-\sigma _0 }\vartheta _0 (\zeta )=q(\zeta ) \end{aligned}$$
(18)

where

$$\begin{aligned} q(\zeta )=q_\varGamma (\zeta )+q_b (\zeta ) \end{aligned}$$
(19)

and

$$\begin{aligned} q_\varGamma (\zeta )= & {} \frac{\mu a\varGamma }{(\mu ^\mathrm{s}-\sigma _0 )\zeta } \end{aligned}$$
(20a)
$$\begin{aligned} q_b (\zeta )= & {} \frac{\mu b_z }{2\pi (\mu ^\mathrm{s}-\sigma _0 )}\left[ {\ln (\zeta _0 \bar{{\zeta }}_0 )-\ln \left( {\frac{1}{\zeta }-\zeta _0 } \right) -\ln \left( {\frac{1}{\zeta }-\bar{{\zeta }}_0 } \right) } \right] \nonumber \\&-\frac{\hbox {i}b_z }{\pi a}\left[ {\frac{1}{(\zeta _0^2 -1)(\zeta -1/{\zeta _0 )}}-\frac{1}{(\bar{{\zeta }}_0^2 -1)(\zeta -1/{\bar{{\zeta }}_0 )}}} \right] \end{aligned}$$
(20b)

Two functions, \(q_\varGamma (\zeta )\) and \(q_b (\zeta )\) in (19), are non-homogeneous terms corresponding to \(\varGamma \) and \(b_{z}\), which represent the stress loads \({{\tau }}_{1}\), \({{\tau }}_{2}\) at infinity and the screw dislocation at \(\zeta _{0}\), respectively.

In this manner, the boundary condition (16) is converted via the Cauchy’s integral formula into a first-order differential equation (18) for the unknown function \(\vartheta _0 (\zeta )\). According to Einar Hille [4] (Chapter 5, Eq. (5.17)), the solution of (18) is derived as

$$\begin{aligned} \vartheta _0 (\zeta )=\exp \left[ {-\frac{\hbox {i}\mu \omega (\zeta )}{\mu ^\mathrm{s}-\sigma _0 }} \right] \int _{\mathrm {i}\infty }^\zeta {q(s)\exp \left[ {\frac{\hbox {i}\mu \omega (s)}{\mu ^\mathrm{s}-\sigma _0 }} \right] } \cdot {\omega }'(s)\hbox {d}s \end{aligned}$$
(21)

It can be verified that the function \(\vartheta _0 (\zeta )\) expressed by (21) is the solution of (18) solely by substituting the former into the latter. Similarly, the potential function \(\vartheta (\zeta )\) in (14) with its analytic part (21) surely satisfies the boundary condition (11).

The unknown analytic function \(\vartheta _{10} (z)\) in (12) is then obtained by

$$\begin{aligned} \vartheta _{10} (z)=\vartheta _0 [\omega ^{-1}(z)] \end{aligned}$$
(22)

It is easy to check that the value of the right side of (21) approaches zero as \(\zeta \rightarrow \hbox {i}\infty \) and thus the analytic function \(\vartheta _{10} (z)\) in (22) satisfies the boundary condition (13) at infinity.

After determination of the function \(\vartheta _{10} (z)\), the displacement w and stresses \({{\tau }}_{xz}\), \({{\tau }}_{yz}\) can be obtained from (6) and (7).

Specially, when the surface effects are neglected, i.e., \(\mu ^\mathrm{s}=0, \sigma _0 =0\), and \(\vartheta _1^*(z)\) is used to represent the potential function for this case, the boundary equation (9) reduces to

$$\begin{aligned} \vartheta _1^{*} (z)-\overline{\vartheta _1^{*} (z)} =0 \end{aligned}$$
(23)

Equation (23) is the boundary condition for the classical elastic problem in z-plane. Similarly, the boundary condition (11) in \(\zeta \)-plane becomes

$$\begin{aligned} \vartheta ^{{*}}(\zeta )-\overline{\vartheta ^{{*}}(\zeta )} =0 \end{aligned}$$
(24)

in which \(\vartheta ^{*}(\zeta )\) denotes the potential function without the surface effects. Performing similar derivation, we then obtain the complex potential function for this case as follows:

$$\begin{aligned} \vartheta ^{*}(\zeta )=\frac{\varGamma a}{2}\zeta +\frac{\bar{{\varGamma }}a}{2\zeta }+\frac{b_z }{2\pi \hbox {i}}\left[ {\ln \left( {\frac{a\zeta _0 \bar{{\zeta }}_0 }{2}} \right) +\ln (\zeta -\zeta _0 )-\ln \left( {\zeta -\frac{1}{\bar{{\zeta }}_0 }} \right) +\ln \zeta } \right] \end{aligned}$$
(25)

After removing the constant terms irrelevant to stresses, Eq. (25) represents the same solution as that derived by Muskhelishvili [14].

3.2 Stress field and SIFNCs

In order to obtain the stress distribution near the crack tip and SIFNCs, substituting (22), (21), (12) and (10) into (7), we have

$$\begin{aligned} \tau _{xz} -\hbox {i}\tau _{yz}= & {} \mu \varGamma -\frac{\hbox {i}\mu b_z }{\pi a}\cdot \frac{1}{\zeta _0 -1/{\zeta _0 }}\left[ {\frac{\zeta _0 }{\zeta -\zeta _0 }-\frac{1}{\zeta _0 (\zeta -1/{\zeta _0 )}}} \right] \nonumber \\&+\mu q(\zeta )-\frac{\hbox {i}\mu ^{2}}{\mu ^\mathrm{s}-\sigma _0 }\exp \left[ {-\frac{\hbox {i}\mu \omega (\zeta )}{\mu ^\mathrm{s}-\sigma _0 }} \right] \int _{\mathrm {i}\infty }^\zeta {q(s)\exp \left[ {\frac{\hbox {i}\mu \omega (s)}{\mu ^\mathrm{s}-\sigma _0 }} \right] \cdot {\omega }'(s)\hbox {d}s} \end{aligned}$$
(26)

For the classical case in which the surface effects are not incorporated, substituting (25) and (10) into (7) yields

$$\begin{aligned} \tau _{xz}^*-\hbox {i}\tau _{yz}^*=\mu \left\{ {\varGamma +\frac{2\hbox {i}\varGamma }{\zeta ^{2}-1}-\frac{\hbox {i}b_z }{\pi a}\left[ {\frac{\zeta }{(\zeta -\zeta _0 )(\zeta -1/{\zeta _0 })}+\frac{1}{\zeta _0 \zeta (\zeta -1/{\zeta _0 })}+\frac{1}{\bar{{\zeta }}_0 \zeta (\zeta -1/{\bar{{\zeta }}_0 })}} \right] } \right\} \end{aligned}$$
(27)

The formula for the stress intensity factor (SIF) is given by [21]

$$\begin{aligned} K_{\mathrm {III}} =\hbox {i}\mu \sqrt{2\pi }\mathop {\lim }\limits _{\zeta \rightarrow \zeta _t } \sqrt{\omega (\zeta )-\omega (\zeta _t )}\Theta (\zeta )e^{{\hbox {i}\alpha }/2} \end{aligned}$$
(28)

in which \(\zeta _t =\omega ^{-1}(z_t )\) is the position coordinate of the crack tip in \(\zeta \)-plane, \(\Theta (\zeta )={{\vartheta }'(\zeta )}/{{\omega }'(\zeta )}\), \(\alpha \) is the angle between the crack tangent vector at the crack tip and the vector of the real axis Re(z), i.e., \(\alpha =\mathop {\lim }\limits _{z\rightarrow z_t } \left. {\arg (z-z_t )} \right| _{z\in \varGamma _C } \), where \(\left. {(L)} \right| _{\varGamma _C } \) (\({\varGamma }_{C}\) is in z-plane) denotes the crack extension line starting from the crack tip.

When the crack surface effects are incorporated, substituting (21), (14) and (10) into (28), and note \(\zeta _t =1\), we have

$$\begin{aligned} K_{\mathrm {III}} =\hbox {i}\mu \sqrt{2\pi }\mathop {\lim }\limits _{\zeta \rightarrow 1+0} \sqrt{\omega (\zeta )-\omega (1)}\Theta (\zeta )=0 \end{aligned}$$
(29)

As the comparison, for the classical case where the crack surface effects are excluded, substituting (25) and (10) into (28) yields

$$\begin{aligned} K_{\mathrm {III}}^{*}= & {} \hbox {i}\mu \sqrt{2\pi }\mathop {\lim }\limits _{\zeta \rightarrow 1+0} \sqrt{\omega (\zeta )-\omega (1)}\frac{[\vartheta ^{{*}}(\zeta )]'}{{\omega }'(\zeta )} \nonumber \\= & {} \hbox {i}\mu \sqrt{\pi a}\left[ {\frac{\varGamma -\bar{{\varGamma }}}{2}+\frac{b_z }{2\pi \hbox {i} a}\left( {\frac{1}{1-\zeta _0 }-\frac{1}{1-1/{\bar{{\zeta }}_0 }}+1} \right) } \right] \end{aligned}$$
(30)

which has non-trivial value.

By reducing the non-standard boundary condition for incorporation of the surface effects and solving the Cauchy singular integro-differential equation numerically, Kim et al. [10] developed a complete solution for traction-free mode-III problem. They asserted that the stress singularity at the crack tip is eliminated when the surface effects are incorporated. However, further investigation showed that the incorporation of the surface effects in Kim et al. [10] model alleviates the square-root stress/strain singularity to being weaker logarithmic [24]. In their later work, Kim et al. [11] suggested that the different set of the employed end-point conditions results in the two cases, (1) eliminating completely the classical stress singularity at the crack tip when the end-point conditions exceed the maximum number, and (2) diminishing the strong square-root singularity to the weaker logarithmic one for the end-point conditions in admissible number.

Wang and Fan [22] investigated the interaction between a nano-crack and a screw dislocation in mode-III deformation. They argued that the stress singularity at the crack tip exhibits two types depending on the location of the screw dislocation, i.e., being the logarithmic plus square root (dislocation is not on real axis) or the logarithmic only (dislocation is on real axis).

As so far, in all the already published literature for the nano-crack incorporating the surface effects in mode-III deformation, the stresses were expressed in infinite series together with the auxiliary conditions to find the solution. However, the singularity at the crack tip is, at least partially, dependent on the form of the series employed in analysis.

In present formalism, firstly the boundary equations are established and integrated over the crack boundary, and the cracked region is mapped from z-plane onto \(\zeta \)-plane for simplifying the boundary geometry. Then the equation of the boundary problem is converted into a first-order differential equation in \(\zeta \)-plane after Cauchy’s integral formula is performed. The differential equation is solved and the solution is mapped back to z-plane thereafter. In this manner, it is unnecessary to preset the solution form and auxiliary conditions to bound the stresses at the crack tip. In other words, in our process, the range of the stresses (finite or infinite) at the crack tip is assumed to be unknown previously. The derived finite-form solution (26) shows that the stresses at the crack tip are indeed finite and the stress singularity is removed completely. As a result, the SIFNC will be trivial (\(K_{\mathrm {III}} =0)\).

3.3 Image forces

Now the stresses generated by the screw dislocation in an uncracked infinite elastic body are subtracted from (26) and (27) respectively, and then taking limit \(z\rightarrow z_0 \), the perturbation stresses due to the dislocation read [12]

$$\begin{aligned} {\tilde{\tau }}_{xz} (z_0 )-\hbox {i}{\tilde{\tau }}_{yz} (z_0 )=\mathop {\lim }\limits _{z\rightarrow z_0 } \left[ {\tau _{xz} (z_0 )-\hbox {i}\tau _{yz} (z_0 )-\frac{\mu b_z }{2\hbox {i}\pi (z-z_0 )}} \right] \end{aligned}$$
(31)

where \(z-z_0 \) can be expressed by \(\zeta _{0}\)

$$\begin{aligned} z-z_0 =\frac{a}{2}\left( {\zeta -\zeta _0 +\frac{1}{\zeta }-\frac{1}{\zeta _0 }} \right) \end{aligned}$$
(32)

Consider the physical process: in an infinite body there is a dislocation which is in stable state, and then an operation is performed that a crack is generated and the loads are exerted at infinity. The perturbing stresses, which are resulted from such an operation and act at the position of the dislocation, thus might be understood as the increment of the stresses.

Substituting (26) and (27) into (31) results in the stress fields for both cases of including and excluding surface effects, respectively

$$\begin{aligned} {\tilde{\tau }}_{xz} (z_0 )-\hbox {i}{\tilde{\tau }}_{yz} (z_0 )= & {} \mu [\varGamma +q(\zeta _0 )] \nonumber \\&-\frac{\hbox {i}\mu ^{2}}{\mu ^\mathrm{s}-\sigma _0 }\exp \left[ {-\frac{\hbox {i}\mu \omega (\zeta _0 )}{\mu ^\mathrm{s}-\sigma _0 }} \right] \int _{\mathrm {i}\infty }^{\zeta _0 } {q(s)\exp \left[ {\frac{\hbox {i}\mu \omega (s)}{\mu ^\mathrm{s}-\sigma _0 }} \right] \cdot {\omega }'(s)\hbox {d}s} \end{aligned}$$
(33)
$$\begin{aligned} {\tilde{\tau }}_{xz}^*(z_0 )-\hbox {i}{\tilde{\tau }}_{yz}^*(z_0 )= & {} \mu \left\{ {\varGamma +\frac{2\hbox {i}\varGamma }{\zeta _0^2 -1}-\frac{\hbox {i}b_z }{\pi a}\left[ {\frac{1}{\zeta _0 (\zeta _0^2 -1)}+\frac{1}{\zeta _0 (\bar{{\zeta }}_0 \zeta _0 -1)}} \right] } \right\} \end{aligned}$$
(34)

The Peach–Koehler formula for the image forces reads [6]

$$\begin{aligned} f_x -\hbox {i}f_y =\hbox {i}b_z [{\tilde{\tau }}_{xz} (z_0 )-\hbox {i}{\tilde{\tau }}_{yz} (z_0 )] \end{aligned}$$
(35)

When the screw dislocation in z-plane is located at x-axis, and \(z_0 =x_0 >a\), the corresponding coordinate of the screw dislocation in \(\zeta \)-plane is expressed as

$$\begin{aligned} \zeta _0 =\frac{x_0 }{a}\left[ {1+\sqrt{1-\left( {\frac{a}{x_0 }} \right) ^{2}}} \right] =\xi _0 \end{aligned}$$
(36)

Therefore \(\zeta _0 \) is a real constant. Substituting (33) and (34) into (35) respectively, the image forces in x-axis direction due to the screw dislocation for the cases of including and excluding surface effects, respectively, become

$$\begin{aligned} f_x -\hbox {i}f_y= & {} \hbox {i}\mu b_z \left\{ {\varGamma +q(\zeta _0 )-\frac{\hbox {i}\mu }{\mu ^\mathrm{s}-\sigma _0 }\exp \left[ {-\frac{\hbox {i}\mu \omega (\zeta _0 )}{\mu ^\mathrm{s}-\sigma _0 }} \right] \int _{\mathrm {i}\infty }^{\zeta _0 } {q(s)\exp \left[ {\frac{\hbox {i}\mu \omega (s)}{\mu ^\mathrm{s}-\sigma _0 }} \right] \cdot {\omega }'(s)\hbox {d}s} } \right\} \end{aligned}$$
(37)
$$\begin{aligned} f_x^*-\hbox {i}f_y^*= & {} \hbox {i}\mu b_z \left[ {\varGamma +\frac{2\hbox {i}\varGamma }{\zeta _0^2 -1}-\frac{2\hbox {i}b_z }{\pi a\zeta _0 (\zeta _0^2 -1)}} \right] \end{aligned}$$
(38)

4 Numerical results and discussion

In this section, the influence of the surface effects is further analyzed and discussed by using numerical calculations. The surface parameters for the nano-crack were suggested as [18]

$$\begin{aligned} \mu ^\mathrm{s}=161.73\;\hbox {J/m}^{2}, \quad \sigma _0 =1.3\;\hbox {J}/\hbox {m}^{2}, \quad \mu =168\;\hbox {GPa} \end{aligned}$$

4.1 Problems with dislocation disturbance

(1) Stress field and comparison with other solution

The stress field at the crack tip evaluated by the present analysis is compared with that from Kim et al. [10]. The case analyzed by Kim et al. [10] can be considered as a simplified one of the present analysis, in which the loads were taken as \({{\tau }}_{1} = 0, {{\tau }}_{2} \ne 0\) and \(b_{z} = 0\) in the relevant equations above. In this case, Eq. (26) reduces to

$$\begin{aligned} \tau _{xz} -\hbox {i}\tau _{yz} =-\hbox {i}\tau _2 -\frac{\mu a\tau _2 }{(\mu ^\mathrm{s}-\sigma _0 )\zeta }+\frac{\hbox {i}\mu ^{2}a\tau _2 }{(\mu ^\mathrm{s}-\sigma _0 )^{2}}\exp \left[ {-\frac{\hbox {i}\mu \omega (\zeta )}{\mu ^\mathrm{s}-\sigma _0 }} \right] \int _{\mathrm {i}\infty }^\zeta {\frac{1}{s}\exp \left[ {\frac{\hbox {i}\mu \omega (s)}{\mu ^\mathrm{s}-\sigma _0 }} \right] \cdot {\omega }'(s)\hbox {d}s} \end{aligned}$$
(39)
Fig. 3
figure 3

Dimensionless stress versus surface effects at crack tip for \(\tau _1 =0, \tau _2 =0.1\mu \) and \(z=x=a+0, S_e ={({\mu }^\mathrm{s}-\sigma _0 )}/{\mu a}\)

Full size image

The comparison between the results from the present analysis and those by Kim et al. [10] is plotted in Fig. 3 where the loads at infinity in present analysis are the same as that in Kim et al. [10], i.e., \({{\tau }}_{1} = 0, {{\tau }}_{2} = 0.1{\mu }\), and the parameter \(S_e ={(\mu ^\mathrm{s}-\sigma _0 )}/{\mu a}\) represents the effects of the surface contribution. Both the results indicate that the dimensionless stress \({{\tau }}_{yz }/{\mu }\) decreases gradually as \(S_{e}\) increases. There is, however, significant difference near the start point \(S_{e} = 0\) where the results by present solution are much higher than that from Kim et al. [10]. The reason for this difference may be that Kim et al. [10] expressed the solution in the form of infinite series so that their formula can only evaluate the stress approximately when \(S_{e}\) tends to be zero, while the present solution can calculate the stress accurately since the formulation is in finite form.

The phenomenon that the stress decreases with increasing \(S_{e}\) is also observed in the following figures.

(2) Influence of the surface effects on the stress distribution

The classical counterpart corresponding to (39) can be obtained by taking \(\tau _1 =0\) and \(b_z =0\) in (27), which yields

$$\begin{aligned} \tau _{xz}^*-\hbox {i}\tau _{yz}^*=-\hbox {i}\tau _2 \cdot \frac{\zeta ^{2}+1}{\zeta ^{2}-1} \end{aligned}$$
(40)

Since the crack length a is inversely proportional to \(S_{e}\), the influence of the surface effects is dependent on the crack length a. The numerical results of the dimensionless stress \({{\tau }}_{yz}/{\mu }\) versus the ratio x / a for \({{\tau }}_{1} = 0, {{\tau }}_{2} = 0.1{\mu }\) and \(S_{e} = 0.1, S_{e} = 0.05, S_{e} = 0.01\) are plotted in Fig. 4, and the results from classical case (40) in which the influence of surface effects is not incorporated are also plotted for comparison. It is seen that with increase in the ratio x / a, the dimensionless stresses for all cases decrease while the results incorporating the surface effects are always lower than those of the classical solution.

Fig. 4
figure 4

Dimensionless stress field \({{\tau }}_{yz}/{\mu }\) versus the ratio x / a for different \(S_{e}\) and \({{\tau }}_{1}=0, {{\tau }}_{2}=0.1{\mu }, z=x, S_e ={(\mu ^\mathrm{s}-\sigma _0 )}/{\mu a}\)

Full size image

The significant difference appears near \(x/a = 1\), and the influence of surface effects weakens with the decrease in \(S_{e}\), i.e., the increase in crack length according to the formula \(S_e ={(\mu ^\mathrm{s}-\sigma _0 )}/{\mu a}\). Different from the classical solution where the shear stress tends to be infinite at the crack tip, the shear stress from the present analysis with surface effects is a finite value. It is also seen that the stress evaluated by (39) approaches that of the classical solution as \(S_{e}\) approaches zero.

Fig. 5
figure 5

Dimensionless image force \({f_x \pi a}/{\mu b_z^2}\) versus the ratio \(x_0 /a, S_e ={(\mu ^\mathrm{s}-\sigma _0 )}/{\mu a}\)

Full size image

(3) Influence of surface effects on the image forces

The image forces from the present solution are compared with those by Wang and Fan [22] in this section. Wang and Fan [22] calculated the image forces in the case without shear stress at infinity and a screw dislocation at point \(z_{0}\), which is located on the x-axis and \(z_0 =\bar{{z}}_0 =x_0 >a\). For this case, the image forces expressed by (37) and (38) reduce to

$$\begin{aligned} f_x -\hbox {i}f_y= & {} \hbox {i}\mu b_z \left\{ {q_b (\zeta _0 )-\frac{\hbox {i}\mu }{\mu ^\mathrm{s}-\sigma _0 }\exp \left( {-\frac{\hbox {i}\mu z_0 }{\mu ^\mathrm{s}-\sigma _0 }} \right) \int _{\mathrm {i}\infty }^{\zeta _{0} } {q_b (s)\exp \left[ {\frac{\hbox {i}\mu \omega (s)}{\mu ^\mathrm{s}-\sigma _0 }} \right] \cdot {\omega }'(s)\hbox {d}s} } \right\} \end{aligned}$$
(41)
$$\begin{aligned} f_x^*-\hbox {i}f_y^*= & {} \frac{2\mu b_z^2 }{\pi a\zeta _0 (\zeta _0^2 -1)} \end{aligned}$$
(42)

The numerical results of the dimensionless image force \({f_x \pi a}/{\mu b_z^2 }\) versus the relative position \(x_{0}/a\) of the screw dislocation for the cases of \(S_{e} = 1, S_{e} = 0.5, S_{e} = 0.1\) and \(S_{e} = 0.001\) are shown in Fig. 5a. It is seen that:

  1. 1.

    For the cases with and without the surface effects, the variation trend of the image forces \({f_x \pi a}/{\mu b_z^2 }\) for both cases is similar; however, the magnitude of the former force is always less than that of the later one.

  2. 2.

    The influence of the surface effects is localized, and the magnitude of the image force \({f_x \pi a}/{\mu b_z^2 }\) approaches zero with the increase in the ratio \(x_{0}/a\).

  3. 3.

    The image force is negative and its magnitude increases as the ratio \({x_0 }/a\) decreases; hence, the crack always attracts the dislocation.

  4. 4.

    From the formula \(S_e ={(\mu ^\mathrm{s}-\sigma _0 )}/{\mu a}\) where \(S_{e}\) is inversely proportional to the crack length a, the magnitude of the image force \({f_x \pi a}/{\mu b_z^2}\), therefore, increases with the decrease in \(S_{e}\). This means that when the surface effects descend progressively, the image force approaches that of the classical case in which the influence of surface effects is not incorporated, e.g., the image force is approximately equal to that from classical elastic theory for \(S_{e} = 0.001\).

The image forces evaluated by present article and those from Wang and Fan [22] are compared in Fig. 5b in which only the results corresponding to \(S_{e} = 1\) and \(S_{e} = 0.001\) are plotted for explicit. It shows that the results from two solutions are in agreement with each other.

5 Conclusions

A solution for the nano-crack problem with surface effects in mode-III deformation was proposed. The potential function was calculated via the conformal mapping technique. At first, the boundary equations were integrated over the crack boundary and reduced to single one, and the physical domain was mapped onto \(\zeta \)-plane by the mapping function. Then Muskhelishvili’s method was applied in \(\zeta \)-plane and the reduced boundary equation was converted into a first-order differential equation after carrying out the Cauchy integrals. Next, the unknown analytic function in z-plane was obtained via the inverse mapping.

Compared to other solutions published in the literature for nano-crack in mode-III deformation, the present solution was expressed in finite form instead of the infinite series. This makes it possible to evaluate the stresses at the crack tip exactly. Different from analyses by others, the solution in the present method was derived without pre-settings such as the solution form and the auxiliary conditions for the stress limitation at the crack tip. The results from the present solution showed that the stresses at the crack tip are indeed finite and the stress singularity is completely removed when the surface effects are incorporated, which leads to the conclusion that the stress intensity factor for the nano-crack in mode-III deformation is zero. This is against the classic elastic fracture theory but reasonable in the nature.

When the surface effects were incorporated, the numerical results showed that the magnitudes of the stresses and the image forces near the crack tip are always less than those from the classical solution. As the crack length increases, the reduction of the stresses and the image forces due to the surface effects decreases, and the results approach that by the classical elastic theory.