1 Introduction

Microelectromechanical systems (MEMS) are microscale devices or miniature embedded systems involving one or more components that enable higher-level functionality. MEMS have a characteristic length scale between 1 mm and \(1\;\upmu \hbox {m}\). Similarly, Nanoelectromechanical systems (NEMS) are nanoscale devices. NEMS have a characteristic length scale between 1 nm and \(100\;\upmu \hbox {m}\) [1, 6, 12, 13, 30]. The micro- and nanodevices are widely used in engineering industries, communications, defense systems, health care, information technology, environmental monitoring, etc. [12, 13, 21]. Fabrication of the MEMS and NEMS rapidly increases from year to year. Therefore modeling, simulation and mathematical analysis are very important for optimizing process of their fabrication and further safety exploration.

At the beginning of MEMS developments, the majority of research has been directed toward methods of fabrication with little presented on modeling and simulation. Hence, researchers had been using simple mathematical models and analytical methods based on crude approximations or complicated FEM-based models using software that are not geared for MEMS. The result of either approach was simulation results that contradict or in disagreement with the laboratory data [11, 15, 29, 31, 35, 47]. Therefore, there is a great need for creation of new relatively simple and adequate mathematical models and methods for MEMS and NEMS simulation. Indeed, right mathematical models and simulation tools allow designers to develop devices of higher quality and improved features based on robust knowledge gained from simulation results, reducing the design time and cost. They also allow designers to optimize the performance of existing devices and design novel devices. This is one of the biggest advantages of simulation tools. They increase our knowledge and help us gain solid understanding of the behavior of MEMS and NEMS devices and the natural phenomena associated with them. Because MEMS and NEMS touch on so many application areas, the ideal simulation tool must follow, suite and provide a vast range of coupled multiphysical effects. In reality, no single tool caters to all the needs of the MEMS community. Hence, MEMS developers, designers and researchers have to develop new mathematical models and appropriate simulation tools for that task. That is why scientists have been actively discussing the possibility of application methods of classical mechanics to micro- and nanoobjects. In the references [9, 17, 18, 27], it was shown that in spite of the fact that the mechanical characteristics corresponding to nanosize structure elements such as beams and plates can differ from mechanical characteristics corresponding to structures of the same material, which have “normal” geometrical sizes, classical elasticity can be extended to the micro- and nanoscale. In application of the continuum mechanics theory to micro- and nanoscale objects have to be taken into account the physical phenomenon that can occur in such structures and devices [4, 5, 10, 15, 37, 39, 40, 49].

Thermal actuation is the most widely used in various MEMS-based applications due to the simplicity of the fabrication process, favorable scaling laws, ability to develop large forces, low power consumption and possibility of integration with a standard integrated circuit environment [11, 20, 22, 32, 34, 43]. Thermally actuated MEMS are a special class of MEMS that use thermal expansion force as the driving mechanism in sensing and actuation. They are currently used in automotive electronics, medical equipment, smart portable electronics, hard disk drives and computer peripherals, etc., as transistors, switches, micromirrors, accelerometers, pressure sensors, micropumps, moving valves and microgrippers [6, 21, 22, 26, 28, 38, 47, 50]. Thermally actuated MEMS also find applications in the characterization of the material properties of thin films, such as elastic constants and residual stresses. Additional information and comprehensive review of modeling of thermally actuated MEMS can be found in [1, 6, 7, 15, 21, 26, 30, 33, 37, 48], etc.

In many cases, the MEMS and NEMS structures and devices are exposed to high temperature. As it is reported in [11, 19, 20, 43], temperature in thermal actuators reaches values \(300\hbox {--}600\;^{\circ }\hbox {C}\) and even can exceed the value \(900\;^{\circ }\hbox {C}\) [14, 29, 31, 45]. Therefore, thermal analysis and optimization of such structures are very important. In the case if temperature is distributed irregularly or deformation caused by temperature field are restricted, thermomechanical loading in the same way as mechanical loading can cause significant stress concentrations and in some circumstances can result in structural destruction or even failure [5, 16, 30, 37, 40, 42, 46]. This clearly shows the importance of accurate stress analysis of thermal loaded MEMS and NEMS structures. Therefore, development of new mathematical models and simulation tools for MEMS and NEMS represents an essential need for designers and researchers to advance the technology to the next levels.

Many MEMS and NEMS structures and devices can be considered as thin-walled structures that are exposed to high-temperature fields and are in thermal contact with other structural elements and massive bases through thin heat-conducting layers. Often in the analysis and simulation of such devices, classic models based on Euler–Bernoulli or Timoshenko hypothesis give an inaccurate result. For accurate analysis and simulation of such structures and devices, high-order theories may be more preferable. These theories are based on expansion of the stress–strain and temperature field components into polynomial series in terms of thickness. It was proposed by Cauchy and Poisson and at that time was not popular. Significant extension and development of that method were done by Kil’chevskii [26]. Vekua has used Legendre polynomials for the expansion of the equations of elasticity and reduction of the 3-D problem to 2-D one [44]. Such an approach has significant advantages because Legendre polynomials are orthogonal and as result obtained equations are simpler. This approach was extended and applied to dynamical thermoelasticity in [16, 36]. More applications and recent developments in the theory of thin-walled structures can be found in [2, 3, 24, 35, 41].

The approach based on the use of Legendre polynomials series expansion has been applied to thermoelastic contact problems of plates and shells when mechanical and thermal conditions are changed during deformation in our previous publications [24, 51–59]. The mathematical formulation, differential equations and contact conditions for the cases of plates and axisymmetric cylindrical shells have been developed in [24, 52]. Then, proposed approach and methodology were further developed and extended to non-stationary processes in [51, 53], thermal and mechanical contact of plates and shells with rigid bodies through heat-conducting layer in [58], thermoelasticity of the laminated composite materials with possibility of delamination and mechanical and thermal contact in temperature field in [55], the pencil-thin nuclear fuel rods modeling in [54], electrostatically actuated MEMS in [58] and functionally graded shells in [56, 59]. Analysis and comparison with classical theory of thermoelasticity of plated and shells have been done in [57].

In this paper, an approach based on expansion of the 2-D equations of thermoelasticity and heat conductivity into Fourier series in terms of Legendre polynomials has been developed and applied to high-order theory of beams. For that purpose, we expand functions that describe stress–strain and temperature state of thermoelastic body into Fourier series in terms of Legendre polynomials with respect to thickness and find corresponding relations of thermoelasticity and heat conductivity for Fourier coefficients of those expansions. Then, using techniques developed in our previous publications, we find system of differential equations and boundary conditions for Fourier coefficients. Case of first and second approximation theory is considered in more detail, and all relations and equations are explicitly presented. An essential new feature of the approach proposed here is taking into account the change of the conditions of heat exchange between the beam and solid foundation during the beam deformation. As a result of such approach, the equations of elasticity and heat conductivity become coupled and nonlinear even for statically applied mechanical and thermal load. For the numerical solution of the developed equations, the FEM implemented in the commercial software COMSOL Multiphysics and MATLAB have been used. Developed models used for thermoelastic analysis of the MEMS have been done using developed first- and second-order theories. Comparative analysis of the results obtained with and without considering influence of the beam deformation during thermal load has been done.

2 The thermally based MEMS/NEMS, their design and simulation

Exploration of the MEMS and NEMS rapidly increases from year to year. The MEMS and NEMS are a process technology used to create tiny integrated devices or systems that combine mechanical and electrical components. They are fabricated using integrated circuit (IC) batch processing techniques and can range in size from a few nanometers to millimeters. These devices (or systems) have the ability to sense, control and actuate on the micro-/nanoscale and generate effects on the macroscale. In the most general form, MEMS/NEMS consist of mechanical nanodevices, microdevices and structures, such as: transducers, sensors, actuators, valves, pumps, flow channels, gears, turbines, different engines, mechanically functional structures and other electronic devices all integrated onto the same silicon chip [1, 6, 12, 13, 21, 26, 30, 33, 42].

A transducer is a device that transforms one form of signal or energy into another form. The term transducer can therefore be used to include both sensors and actuators and is the most generic and widely used term in MEMS/NEMS. A sensor is a device that measures information from a surrounding environment and provides an electrical output signal in response to the parameter it measured. It detects changes in the system environment by measuring mechanical, thermal, magnetic, chemical or electromagnetic information or phenomena. An actuator is a type of device for moving or controlling a mechanism or system. It is operated by a source of energy, typically electric or thermal current, hydraulic or pneumatic pressure and converts that energy into an action. It can create a force to manipulate itself, other mechanical devices, or the surrounding environment to perform some useful function.

Because of their small size, light weight, high resolution, enhanced performance and reliability and low cost, MEMS/NEMS have been applied in automotive and aerospace systems, health care, chemical and biomedical engineering, environmental monitoring and control, instrumentation, communication, computers, etc. They promise to revolutionize measurements of extremely small displacement and extremely weak forces, particularly at the molecular level. For example, NEMS devices can be so small that hundreds of them can be fit in the same space as one single microdevice that performs the same function.

In this study, we concentrated mostly on thermal and thermoelastic phenomena problems involving heat transfer at the micro- and nanoscale. A large number of such MEMS/NEMS are based on thermal and thermoelectric principles. They use thermoelastic and thermoelectric phenomena for sensor or actuator operation. Thermal-based sensors are also often used to measure non-thermal measurements. It appears that multifunctional transducers for radiation, pressure, position, level, flow or biological and chemical reactions can all be constructed on the basis of temperature or temperature-difference sensors. Hence, complex micro- and nanosystems for utilization in above-mentioned areas of application all contain thermally based micro- and nanodevices, such as sensors, actuators, resistors, converters.

Thermoresistors are devices for temperature measurement that use the temperature sensitivity of electrical conductive materials like metals or semiconductors. The dependence of the resistivity of these materials on temperature has been intensively investigated, so that by measuring the resistance, the temperature can be deduced directly from database. Thermoelectric sensors and actuators are based on the thermoelectric effects, which consists in the direct conversion of temperature differences to electric voltage and vice versa. A thermoelectric device creates voltage when there is a different temperature on each side. Conversely, when a voltage is applied to it, it creates a temperature difference. Widely used thermoelectric actuators are bimorphs, bent-beam and chevron-type actuators. The crucial feature of such devices is the high thermal insulation of “hot” contacts, which can be performed by etching thin suspended membranes or preparing cantilever beams. Some of the thermoactuators are based on volumetric expansion of gas or liquid. They can be used for various actuation processes, for example, to produce valves that can sustain differential pressures. Micromirrors also can be actuated thermoelectrically, and they have extensive application in optical switches, displays and many other areas optoelectronics.

Because of all above temperature changes must therefore be analyzed carefully when designing a MEMS/NEMS working on thermomechanical principle, not only for sensitivity optimization but also for reliability purposes. Therefore, development of new mathematical models and simulation tools for MEMS/NEMS is very important task for designers and researchers to advance the development and production of the devices to the high level. Because MEMS/NEMS touch on so many application areas, the ideal simulation tool must follow suite and provide a vast range of coupled multidomain physical effects. In reality, no single tool caters to all the needs of the MEMS/NEMS community. Hence, MEMS/NEMS designers carry the burden to find the appropriate tools and strategy for their task. In this situation, researchers had been using simple mathematical models and analytical methods based on crude approximations or complicated FEM-based models using commercial software that are not geared for MEMS/NEMS simulation. The result of either approach was simulation results that contradict or in disagreement with the laboratory data. It is because simple mathematical models cannot take into account all multiphysical phenomenons and commercial FEM software usually designed for general purposes, and it badly suit to address particular problems that appear in MEMS/NEMS simulation. Therefore, there is a great need for creating new relatively simple and adequate mathematical models and methods for MEMS/NEMS simulation. Indeed, right mathematical models and simulation tool allow designers to develop devices of higher quality and improved features based on robust knowledge gained from simulation results, reducing the design time and cost. They also allow designers to optimize the performance of existing devices and design novel devices. This is one of the biggest advantages of simulation tools. They increase our knowledge and help us gain solid understanding of the behavior of MEMS/NEMS devices and the natural phenomena associated with them. Because MEMS/NEMS touch on so many application areas, the ideal simulation tool must follow suite and provide a vast range of coupled multiphysical effects. In reality, no single tool caters to all the needs of the MEMS/NEMS community. Hence, MEMS/NEMS developers, designers and researchers have to develop new mathematical models and appropriate simulation tools for that task.

Many thermally based MEMS/NEMS devices as structural elements can be considered as beams exposed to high-temperature fields and interact with other structural elements and rigid supports through thin heat conducting layers. Temperature change causes deformation of the structural elements and as result change of the heat-conducting layer thickness. This causes a change in the conditions of heat exchange and temperature distribution. Unfortunately, existing mathematical models of the MEMS/NEMS devises do not consider all multiphysical phenomenons that occur. In this study, we develop mathematical models of the thermally based MEMS and NEMS devices that more accurately take into account mentioned above heat exchange conditions.

3 2-D formulation

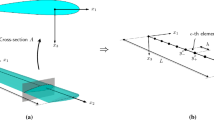
Let us consider a linear elastic beam in 2-D Euclidian space domain \(V=\Omega \times [-h,h]\) with a smooth boundary \(\partial V\). Here 2h is thickness of the beam, \(\Omega =[0,L]\) is the middle line of the beam, L its length and b its width. Boundary of the beam \(\partial V\) can be presented in the form \(\partial V=S\cup \Omega ^{+}\cup \Omega ^{-}\), where \(\Omega ^{+}\) and \(\Omega ^{-}\) are the upper and lower sides and S is a sheer side. The beam is situated on a rigid foundation with an initial gap \(h_{0}\) in the temperature field. There is a heat-conducting medium in the gap between the foundation and the beam. The medium does not resist the beam deformation, and heat exchange between the foundation and the beam is due to the thermal conductivity of the medium. We assume that gap \(h_0\) is commensurable with the beam displacements which are assumed to be small.

Thermodynamic state of the plane beam as 2-D thermoelastic body is defined by stress \(\sigma _{ij} \) and \(\varepsilon _{ij} \) strain tensors with components \(\{\sigma _{11} ,\sigma _{22} ,\sigma _{12}\}\) and \(\{\varepsilon _{11} ,\varepsilon _{22} ,\varepsilon _{12} \}\), respectively, and displacements \(u_{i}\), traction \(p_{i} \) and body forces \(b_{i} \) vectors with components \(\{u_{1} ,u_{2} \}\), \(\{p_{1} ,p_{2}\}\) and \(\{b_{1} ,b_{2} \}\) and \(\theta \), \(\chi \), the temperature and specific strength of the internal heat sources, respectively. These quantities are not independent; they are related by equations of linear thermoelasticity.

The equations of equilibrium have the form

$$\begin{aligned} \frac{\partial \sigma _{11} }{\partial x_{1} }+\frac{\partial \sigma _{12}}{\partial x_{2} }+b_{1}= & {} 0 \nonumber \\ \frac{\partial \sigma _{21} }{\partial x_{1} }+\frac{\partial \sigma _{22}}{\partial x_{2} }+b_{2}= & {} 0 \end{aligned}$$
(1)

The Cauchy relations have the form

$$\begin{aligned} \varepsilon _{11}=\frac{\partial u_{1} }{\partial x_{1}},\quad \varepsilon _{22}=\frac{\partial u_{2} }{\partial x_{2}},\quad \varepsilon _{12}=\frac{\partial u_{1} }{\partial x_{2}}+\frac{\partial u_{2} }{\partial x_{1} }. \end{aligned}$$
(2)

The stress \(\sigma _{ij} \) tensor, tensor of deformation \(\varepsilon _{ij}\) and temperature \(\theta \) are related by Hooke’s law

$$\begin{aligned} \sigma _{ij}=c_{ijkl}\varepsilon _{kl}-\beta _{ij}\theta ,\quad c_{ijkl} =c_{jikl}=c_{jilk}=c_{klij},\quad \beta _{ij}=\beta _{ji} \end{aligned}$$
(3)

where \(c_{ijkl}\) and \(\beta _{ij}\) are elastic modulus and the coefficients of linear thermal expansion. In the isotropic case

$$\begin{aligned} c_{ijkl}=\lambda \delta _{ij}\delta _{kl}+\mu (\delta _{ik}\delta _{jl} +\delta _{il}\delta _{kj} ),\quad \beta _{ij}=(\mu +3\lambda )\alpha _{T}\delta _{ij} \end{aligned}$$
(4)

where \(\lambda \) and \(\mu \) are the Lame constants, \(\alpha _{T}\) are the coefficients of linear thermal expansion and \(\delta _{ij}\) is a Kronecker delta tensor.

It is important to mention that in the case of the rods and beams in order to take into account Poisson’s effect one has to use the modified Lame constants in the form

$$\begin{aligned} \lambda =\frac{2E\nu }{1-\nu ^{2}},\quad \mu =\frac{E}{2(1+\nu )} \end{aligned}$$
(5)

The differential equations of equilibrium for the displacement vector components may be presented in the form

$$\begin{aligned} A_{ij}u_{j}+A_{i}\theta +b_{i}=0 \end{aligned}$$
(6)

with

$$\begin{aligned}&\displaystyle A_{ij}=c_{ijkl}\frac{\partial }{\partial x_{k}}\frac{\partial }{\partial x_l},\quad A_{i}=\beta _{ij}\frac{\partial }{\partial x_j }, \nonumber \\&\displaystyle A_{ij}=\mu ^{2}\delta _{ij} \frac{\partial }{\partial x_{k} }\frac{\partial }{\partial x_{k} }+(\lambda +\mu )\frac{\partial }{\partial x_{i} }\frac{\partial }{\partial x_j },\quad A_{i}=(\mu +3\lambda )\alpha _{T} \frac{\partial }{\partial x_{i}} \end{aligned}$$
(7)

in anisotropic and isotropic case, respectively.

On the boundary of the body \(\partial V\), it is necessary to establish boundary conditions. We consider the mixed mechanical boundary conditions in the form

$$\begin{aligned} u_{i} (\mathbf{x})= & {} \phi _{i} (\mathbf{x}),\quad \forall \mathbf{x}\in \partial V_u,\nonumber \\ p_{i} (\mathbf{x})= & {} \sigma _{ij} (\mathbf{x})n_j (\mathbf{x})=P_{ij} [u_j (\mathbf{x})]=\psi _{i} (\mathbf{x}),\quad \forall \mathbf{x}\in \partial V_p \end{aligned}$$
(8)

The differential operator \(P_{ij} :u_j \rightarrow p_{i}\) is referred to as the stress operator. It transforms the displacements into the tractions. For homogeneous anisotropic and isotropic media, they have the forms

$$\begin{aligned} P_{ij}=c_{ikjl} n_{k} \frac{\partial }{\partial x_l }\quad \hbox {and}\quad P_{ij}=\lambda \delta _{ij} n_{k} \frac{\partial }{\partial x_{k} }+\mu \left( {n_{i}\frac{\partial }{\partial x_j }+n_j \frac{\partial }{\partial x_{i}}}\right) \end{aligned}$$
(9)

respectively. Here \(n_{i}\) are the components of the outward unit normal vector, and \(\partial _n =n_{i} \partial _{i}\) is the derivative in the direction of the vector \(\mathbf{n}(\mathbf{x})\) normal to the surface \(\partial V_p\).

We assume that heat distributes in the beam and in the heat-conducting media according to Fourier low

$$\begin{aligned} q_{i}=\lambda _{ij}\frac{\partial \theta }{\partial x_j} \end{aligned}$$
(10)

Here \(q_{i}\) is a vector of thermal flow, and \(\lambda _{ij}\) is the tensor of coefficients of thermal conductivity of the body. In the isotropic case

$$\begin{aligned} \lambda _{ij}=\delta _{ij}\lambda _{T}, \end{aligned}$$
(11)

where \(\lambda _{T}\) is the coefficients of thermal conductivity of the body.

Then, linear equations for heat conductivity for the beam as 2-D body have the form

$$\begin{aligned} \lambda _{ij}\frac{\partial }{\partial x_{i} }\frac{\partial \theta }{\partial x_j }-\chi =0,\;\hbox { or }\;\lambda _{T} \Delta \theta -\chi =0, \,\forall \mathbf{x}\in V \end{aligned}$$
(12)

in anisotropic and isotropic cases, respectively. Here \(\Delta =\delta _{ij}\frac{\partial }{\partial x_{i} }\frac{\partial }{\partial x_j}\) is Laplace operator.

The temperature distribution within the heat-conducting medium is described by the equations of heat conductivity

$$\begin{aligned} \lambda _{ij}^{*} \frac{\partial }{\partial x_{i} }\frac{\partial \theta _*}{\partial x_j }-\chi _*=0,\;\hbox { or }\;\lambda _{T}^{*} \Delta \theta -\chi =0, \,\forall \mathbf{x}\in V^{{*}} \end{aligned}$$
(13)

Here \(\lambda _{ij}^{*}\) is the tensor of coefficients of thermal conductivity of the heat-conducting medium. In the isotropic case

$$\begin{aligned} \lambda _{ij}^{*} =\delta _{ij} \lambda _{T}^{*} , \end{aligned}$$
(14)

where \(\lambda _{T}^{*} \) is the coefficients of thermal conductivity of the heat-conducting medium.

Boundary conditions for temperature and heat flux may be presented in one of the following forms

$$\begin{aligned} \theta =\theta ^{b}, \forall \mathbf{x}\in \partial V_{\theta },q_{i} =q_{i}^{b}, \forall \mathbf{x}\in \partial V_q \;\hbox { or }\;n_{i} \lambda _{ij} \frac{\partial \theta }{\partial x_j}+\beta \left( {\theta -\theta ^{b}}\right) =0, \end{aligned}$$
(15)

where \(\theta ^{b}\) and \(q_{i}^{b}\) denote prescribed temperature and thermal flux on the boundary, respectively, \(\lambda _{ij}\) is the tensor of coefficients of thermal conductivity of the body and coefficient \(\beta \) depends on thermal properties of surroundings.

We assume that the lower part of the boundary \(\Omega ^{-}\) is in thermal contact with foundation through the heat-conducting layer and classical thermal contact conditions with heat conducting taking place. It means that temperature and thermal flux of the beam and media on contact area are equal. Therefore, conditions of heat conductivity through the heat-conducting medium have the form

$$\begin{aligned} \theta _{*} =\theta ,\quad \lambda _{ij}^{*} n_{k} \frac{\partial \theta _{*}}{\partial x_{k} }=\lambda _{ij} n_{k} \frac{\partial \theta }{\partial x_{k}} \end{aligned}$$
(16)

where \(\theta _{*}\) is a temperature and \(\lambda _{ij}^{*}\) is the tensor of coefficients of thermal conductivity of the heat-conducting layer.

In some cases, under action of mechanical load and temperature field lower side \(\Omega ^{-}\) of the beam can be in unilateral mechanical contact with the rigid foundation. In this case, the area of close mechanical contact \(\partial V_{e}\) and contact forces are not known in advance. Therefore, unilateral mechanical contact conditions have the form of inequalities [2]

$$\begin{aligned} u_{n}=\ge h_{0}, q_{n} \ge 0, (u_{n}-h_{0})q_{n}=0,\quad \forall \mathbf{x}\in \partial V_{e} \end{aligned}$$
(17)

and thermal conditions (16) are transformed into the form

$$\begin{aligned} q_{\theta }=\alpha _{e}(\theta -\theta _{*}),\quad \forall \mathbf{x}\in \partial V_{e} \end{aligned}$$
(18)

where \(q_{\theta }\) is the heat flux passing across the close mechanical contact area, \(\alpha _{e}\) is the coefficient of the contact surface thermal conductivity.

Now the problem consists in join solution of the equations of thermoelasticity (6) and heat conductivity (12) and (13) with boundary conditions (8) and (15). In the case when close mechanical contact takes place, the unilateral contact conditions (17) and thermal conditions (18) have to be satisfied. Analysis of the problem encounters mathematical difficulties caused by the dimension of the problem, as well as by its nonlinearity. The problem can be partially simplified considering thin-walled bodies. In this case, we can reduce the dimension of the problem.

4 1-D formulation

We expand the physical parameters that describe the thermodynamical state of the beam into the Legendre polynomials series along the coordinate \(x_{3}\). Such expansion can be done because of any function f(p), which is defined in domain \(-1\le p\le 1\) and satisfies Dirichlet’s conditions (continuous, monotonous and having finite set of discontinuity points), can be expanded into Legendre series according to formulas

$$\begin{aligned} f(p)=\sum \limits _{k=0}^{\infty } a_{k} P_{k} (p)\;\;\hbox { where }a_n =\frac{2k+1}{2}\int \limits _{-1}^1 f(p)P_{k} (p)dp\; \end{aligned}$$
(19)

Any function of more than one independent variable can also be expanded into Legendre series with respect to, for example, variable \(x_3 \in [-1,1]\), but first the new normalized variable \(\omega =x_3 /h\in [-1,1]\) has to be introduced. Taking into account (19), we have

(20)

where

$$\begin{aligned} \sigma _{ij}^{k}(x_{1})= & {} \frac{2k+1}{2h}\int \limits _{-h}^{h} \sigma _{ij}(x_{1}, x_{2})P_{k} (\omega )\mathrm{d}x_{2},\quad \varepsilon _{ij}^k (x_{1})=\frac{2k+1}{2h}\int \limits _{-h}^{h} \varepsilon _{ij} (x_{1}, x_{2})P_{k} (\omega )\mathrm{d}x_{2}, \nonumber \\ u_{i}^{k}(x_{1})= & {} \frac{2k+1}{2h}\int \limits _{-h}^{h} u_{i} (x_{1}, x_{2})P_{k} (\omega )\mathrm{d}x_{2}, \quad \theta ^{k}(\mathbf{x}_{\alpha }) =\frac{2k+1}{2h}\int \limits _{-h}^{h} {\theta (\mathbf{x}_{\alpha }, x_{2} )P_{k} (\omega )\mathrm{d}x_{2}}. \end{aligned}$$
(21)

Substituting these expansions in Eqs. (1)–(7) and (10)–(12) and taking into account that

$$\begin{aligned} \frac{2k+1}{2h}\int \limits _{-h}^h {\frac{\partial \sigma _{ij} }{\partial x_{1} }P_{k} (\omega )\mathrm{d}x_{2} } =\frac{\partial \sigma _{ij}^k }{\partial x_{1} },\quad \frac{2k+1}{2h}\int \limits _{-h}^h {\frac{\partial u_{i} }{\partial x_{1} }P_{k} (\omega )\mathrm{d}x_{2} } =\frac{\partial u_{i}^k }{\partial x_{1} },\quad \frac{2k+1}{2h}\int \limits _{-h}^{h} {\frac{\partial \theta }{\partial x_{1} }} P_{k} (\omega )\mathrm{d}x_{2} =Q_{2}^k\nonumber \\ \end{aligned}$$
(22)

and

$$\begin{aligned} \frac{2k+1}{2h}\int \limits _{-h}^h {\frac{\partial \sigma _{i2} }{\partial x_{2} }P_{k} (\omega )\mathrm{d}x_{2} }= & {} \underline{\sigma _{i2}^k },\quad \underline{\sigma _{i2}^k }=-\frac{2k+1}{h}\left( {\sigma _{i2}^{k-1} +\sigma _{i2}^{k-3} +...} \right) , \nonumber \\ \frac{2k+1}{2h}\int \limits _{-h}^h {\frac{\partial u_{i} }{\partial x_{2} }P_{k} (\omega )\mathrm{d}x_{2}}= & {} \underline{u_{i}^k},\quad \underline{u_{i}^k }=\frac{2k+1}{h}\left( {u_{i}^{k+1} +u_{i}^{k+3} +...} \right) , \nonumber \\ \frac{2k+1}{2h}\int \limits _{-h}^h {\frac{\partial ^{2} \theta }{\partial x_{2} }} P_{k} (\omega )\mathrm{d}x_{2}= & {} \underline{Q_{2}^k },\quad \underline{Q_{2}^k }=-\frac{2k+1}{h}\left( {Q_{2}^{k-1} +Q_{2}^{k-3} +...} \right) \end{aligned}$$
(23)

we obtain corresponding relations for Legendre polynomials series coefficients.

Then, the differential equations of thermoelasticity of the beam (6) are transformed into the 1-D form

$$\begin{aligned} \mathbf{L}_u \cdot \mathbf{u}+\mathbf{L}_\theta \cdot {\varvec{\uptheta }}+\mathbf{f}=0 \end{aligned}$$
(24)

where matrix differential operators \(\mathbf{L}_u \) and \(\mathbf{L}_{\theta }\) and vectors \(\mathbf{u}\), \({\varvec{\uptheta }}\), and \(\mathbf{f}\) have the form

$$\begin{aligned} \mathbf{L}_u =\left| {{\begin{array}{lllll} L_{11}^{00}&{}\; L_{12}^{00}&{}\; \cdots &{}\;L_{11}^{0n}&{}\;L_{12}^{0n} \\ L_{21}^{00}&{}\;L_{22}^{00}&{}\;\cdots &{}\;L_{21}^{0n}&{}\;L_{22}^{nn} \\ \vdots &{}\;\vdots &{}\;\cdots &{}\;\vdots &{}\;\vdots \\ L_{11}^{n0}&{}\;L_{12}^{n0}&{}\;\cdots &{}\;L_{11}^{nn} &{}\; L_{12}^{nn} \\ L_{21}^{n0}&{}\;L_{22}^{n0}&{}\;\cdots &{}\;L_{21}^{nn} &{}\;L_{22}^{nn} \\ \end{array}}}\right| ,\quad \mathbf{L}_\theta =\mathbf{E}\cdot \left| {{\begin{array}{l} L_{1}^{0} \\ L_{2}^{0} \\ \vdots \\ L_{1}^{n} \\ L_{2}^{n} \\ \end{array}}} \right| ,\quad \mathbf{u}=\left| {{\begin{array}{l} u_{1}^{0} \\ u_{2}^{0} \\ \vdots \\ u_{1}^{n} \\ u_{2}^{n} \\ \end{array}}} \right| ,\quad {\varvec{\uptheta }}=\left| {{\begin{array}{l} \theta _{1}^{0} \\ \theta _{2}^{0} \\ \vdots \\ \theta _{1}^{n} \\ \theta _{2}^{n} \\ \end{array}}} \right| ,\quad \mathbf{f}=\left| {{\begin{array}{l} f_{1}^{0} \\ f_{2}^{0} \\ \vdots \\ f_{1}^{n} \\ f_{2}^{n} \\ \end{array}}} \right| \end{aligned}$$
(25)

The differential equations of the beam heat conductivity (12) are transformed into the 1-D form

$$\begin{aligned} \mathbf{L}_{\theta \theta }\cdot {\varvec{\uptheta }}+\mathbf{Q}+{\varvec{\upchi }}=0 \end{aligned}$$
(26)

where matrix differential operators \(\mathbf{L}_{\theta \theta }\) and vectors \(\mathbf{Q}\), and \({\varvec{\upchi }}\) have the form

$$\begin{aligned} \mathbf{L}_{\theta \theta } =\left| {{\begin{array}{lll} L^{0}&{}\; \cdots &{}\; 0 \\ \vdots &{}\; \cdots &{}\; \vdots \\ 0&{}\; \cdots &{}\;L^{n} \\ \end{array}}}\right| =\mathbf{E}\cdot \left| {{\begin{array}{l} L^{0} \\ \vdots \\ L^{n} \\ \end{array}}}\right| , \quad \mathbf{Q}=\left| {{\begin{array}{l} Q_{2}^{0}\\ \vdots \\ Q_{2}^{n} \\ \end{array}}}\right| ,\quad {\varvec{\upchi }}=\left| {{\begin{array}{l} \bar{{\chi }}^{0} \\ \vdots \\ \bar{{\chi }}^{n} \\ \end{array}}} \right| \; \end{aligned}$$
(27)

In (24) and (26), components of the vectors \(\mathbf{f}\) and \({\varvec{\upchi }}\), respectively, have the form

$$\begin{aligned} f_{i}^{k}=\frac{2k+1}{h}\left[ {\sigma _{i2}^{+}-(-1)^{k}\sigma _{i2}^{-}}\right] -b_{i}^{k}\quad \hbox {and}\quad \bar{{\chi }}^{k} =\frac{2k+1}{h}\left[ {Q_{2}^{+} -\left( {-1} \right) ^{k}Q_{2}^{-}}\right] +\frac{\chi ^{k}}{\lambda _0} \end{aligned}$$
(28)

The boundary conditions at the sheer sides (8) and (15) can be easily transformed into 2-D form. Applying expansion into Legendre polynomials series, we obtain boundary conditions for coefficients of the expansion in the form

$$\begin{aligned} p_{i}^{k} (x_{1})= & {} \psi _{i}^{k},\, \forall x_{1} \in \partial \Omega _p; \quad u_{i}^{k} (x_{1})=\phi _{i}^{k},\,\forall x_{1} \in \partial \Omega _{u}, \nonumber \\ \theta ^{k}= & {} \theta _{b}^{k},\, \forall \mathbf{x}\in \partial \Omega _{\theta };\quad q_{i}^{k}=Q_{i}^{k}, \forall x_{1} \in \partial \Omega _{q} \end{aligned}$$
(29)

Here \(\psi _{i}^{k} (x_{1})\hbox { and }\phi _{i}^k (x_{1})\) are coefficients of the expansion Legendre polynomials of the displacement and traction vector components.

Surface forces and displacements on upper and lower sides of the beam are calculated in the form

$$\begin{aligned} \sum _{k=0}^{\infty }p_{i}^{k}= & {} p_{i}^{+}, \;\sum _{k=0}^{\infty } (-1)^{k}u_{i}^{k} =u_{i}^{+}, \;\forall x_{2} \in \Omega ^{+},\nonumber \\ \sum _{k=0}^{\infty }(-1)^{k}p_{i}^{k}= & {} p_{i}^{-}, \;\sum _{k=0}^{\infty }{u_{i}^k}=u_{i}^{-}, \;\forall x_{2} \in \Omega ^{-}\;, \nonumber \\ \sum _{k=0}^{\infty }\theta ^{k}= & {} \theta ^{+}, \;\sum _{k=0}^{\infty } (-1)^{k}q_{i}^{k}=Q_{i}^{+}, \; \forall \mathbf{x}\in \Omega ^{+} \;, \nonumber \\ \sum _{k=0}^{\infty }(-1)^{k}\theta ^{k}= & {} \theta ^{-} , \;\sum _{k=0}^{\infty }{q_{i}^{k}}=Q_{i}^{-}, \;\forall \mathbf{x}\in \Omega ^{-}. \end{aligned}$$
(30)

We used here relations for Legendre polynomials \(P_{k} (1)=1\) and \(P_{k} (-1)=(-1)^{k}\).

The coefficients of Legendre polynomials series for temperature and its derivative with respect to \(x_{2}\) are related by equation

$$\begin{aligned} \frac{2\theta _{i}^k }{h}=\frac{Q_{i}^{k-1} }{2k-1}-\frac{Q_{i}^{k+1} }{2k+3},\quad (k=1,\ldots ,n) \end{aligned}$$
(31)

As it was shown in [51], unilateral mechanical contact conditions cannot be formulated for coefficients of Legendre polynomial series due to their nonlinearity. Thermal contact conditions depend on thermal boundary conditions on upper side \(\Omega ^{+}\) and foundation and also on order of polynomial approximation of the temperature in the beam and heat-conducting layer. For some specific cases, they will be considered in next sections.

Thus, we obtain infinite set of 1-D differential equations for coefficients of the Legendre polynomials series expansion (24) and (26) with corresponding boundary (29) and contact conditions. In order to simplify the problem, we have to construct approximate theory and keep only finite set of members in the expansions (20)–(21). Order of the approximation depends on assumption regarding thickness distribution of the thermodynamical parameters of the beam. We consider here the case of relatively small thickness in comparison with length of the beam. Therefore, we can keep only two and three members in polynomial expansion (20). In this case, we will get first- and second-order approximation equations for thermoelasticity of beam.

5 First-order approximation

In this case, only the first two terms of the Legendre polynomials series expansions (20) have to be taken into account. Then, the parameters, which describe the thermodynamical state of the beam, have the form

(32)

In this particular case, equations of thermoelasticity and heat conductivity have the same form as (24) and (26), respectively, but matrix operators (25) and (27) now have simpler form

$$\begin{aligned}&\displaystyle \mathbf{L}_u =\left| {{\begin{array}{llll} L_{11}^{00}&{}\; 0&{}\; 0&{}\;L_{12}^{01} \\ 0&{}\; L_{22}^{00}&{}\; L_{12}^{01} &{}\; 0 \\ 0&{}\; L_{12}^{01}&{}\; L_{11}^{11} &{}\; 0 \\ L_{21}^{10}&{}\; 0&{}\; 0&{}\; L_{22}^{11}\\ \end{array}}}\right| ,\quad \mathbf{L}_\theta =\mathbf{E}\cdot \left| {{\begin{array}{l} L_{1}^{0}\\ L_{2}^{0}\\ L_{1}^{1} \\ L_{2}^{1} \\ \end{array} }} \right| ,\quad \mathbf{u}=\left| {{\begin{array}{l} {u_{1}^{0} } \\ {u_{2}^{0} } \\ {u_{1}^1 } \\ {u_{2}^1 } \\ \end{array} }} \right| ,\quad {\varvec{\uptheta }}=\left| {{\begin{array}{l} {\theta _{1}^{0} } \\ {\theta _{2}^{0} } \\ {\theta _{1}^1 } \\ {\theta _{2}^1 } \\ \end{array}}}\right| ,\quad \mathbf{f}=\left| {{\begin{array}{l} f_{1}^{0} \\ f_{2}^{0} \\ f_{1}^{1}\\ f_{2}^{1}\\ \end{array} }} \right| \end{aligned}$$
(33)
$$\begin{aligned}&\displaystyle \mathbf{L}_{\theta \theta } =\left| {{\begin{array}{ll} L^{0}&{}\; 0 \\ 0&{}\; L^{1} \\ \end{array}}} \right| ,\quad \mathbf{Q}=\left| {{\begin{array}{l} Q_{2}^{0} \\ Q_{2}^{1} \\ \end{array} }} \right| ,\quad {\varvec{\upchi }}=\left| {{\begin{array}{l} {\bar{\chi }}^{0} \\ {\bar{\chi }}^{1} \\ \end{array}}} \right| \end{aligned}$$
(34)

where

$$\begin{aligned} L_{11}^{00}= & {} (\lambda +2\mu )\frac{\partial ^{2}}{\partial x_{1}^{2} },\quad L_{12}^{01} =\lambda \frac{1}{h}\frac{\partial }{\partial x_{1} },\quad L_{22}^{00} =\mu \frac{\partial ^{2}}{\partial x_{1}^{2}},\quad L_{21}^{01} =\frac{\mu }{h}\frac{\partial }{\partial x_{1}},\nonumber \\ L_{12}^{10}= & {} -\frac{3\mu }{h}\frac{\partial }{\partial x_{1}}, \quad L_{11}^{11} =\left( {\lambda +2\mu } \right) \frac{\partial ^{2}}{\partial x_{1}^{2}}-\mu \frac{3}{h^{2}},\quad L_{21}^{10} =-\frac{3\lambda }{h}\frac{\partial }{\partial x_{1} }, \quad L_{22}^{11} =\mu \frac{\partial ^{2}}{\partial x_{1}^{2}}-\left( {\lambda +2\mu }\right) \frac{3}{h^{2}}\nonumber \\ L^{0}= & {} \lambda _{T} \frac{\partial ^{2}}{\partial x_{1}^{2} }-\frac{3\lambda _{T}}{h^{2}},\quad L^{1} =\lambda _{T} \frac{\partial ^{2}}{\partial x_{1}^{2}}-\frac{15\lambda _{T} }{h^{2}} \end{aligned}$$
(35)

Parameters \(Q_{2}^{0} \) and \(Q_{2}^1 \) can be calculated using Eqs. (23) and (31) and heat-conducting conditions on upper and lower sides of the beam and conditions of heat exchange through heat conduction layer. For specific case of temperature set on upper side of the beam \(\theta ^{+}(x_{1})\) and foundation \(\theta ^{-}(x_{1})\), respectively, and contact conditions through heat conduction layer, we have

$$\begin{aligned} Q_{2}^{0}= & {} \frac{1}{2h}(\theta ^{+}-T_{k}),\quad Q_{2}^1 =\frac{3}{2h}\left( {\theta ^{+}+T_{k}} \right) -\frac{3\theta ^{1}}{2h},\quad Q_{2}^{2} =5Q_{1}^{0} -\frac{5}{h}\theta ^{1}, \end{aligned}$$
(36)
$$\begin{aligned} T_{k}= & {} \frac{\lambda _{T} (h_{0}-u_{2})\left( {3\theta ^{+}+6\theta ^{0}-10\theta ^{1}}\right) +\lambda _{T}^{*} h\theta ^{-}}{9\lambda _{T} (h_{0}-u_{2})+\lambda _{T}^{*}h} \end{aligned}$$
(37)

Here \(u_{2} (x_{1} )\) is calculated using representation (32) for the displacements.

Thus, we obtained the 1-D system of differential equations which is called the first approximation theory of thermoelasticity and heat conductivity of beam. Together with corresponding boundary conditions and conditions of thermal and mechanical contact, it can be used for the stress–strain and temperature calculation for the beam.

6 Second-order approximation

In the second-order approximation, first three terms of the Legendre polynomials series have to be taken into account. In this case, the parameters, which describe the stress–strain state of the shell, can be presented in the form

(38)

In this particular case, equations of thermoelasticity and heat conductivity have the same form as (24) and (26), respectively, but matrix operators (25) and (27) now have simpler form

$$\begin{aligned}&\displaystyle \mathbf{L}_u=\left| {{\begin{array}{llllll} L_{11}^{00}&{}\; 0&{}\; 0&{}\; L_{12}^{01}&{}\; 0&{}\; 0 \\ 0&{}\; L_{22}^{00}&{}\;L_{21}^{01}&{}\; 0&{}\; 0&{}\; 0 \\ 0&{}\; L_{12}^{10}&{}\;L_{11}^{11}&{}\; 0&{}\; 0&{}\; L_{12}^{12} \\ L_{21}^{10} &{}\; 0&{}\; 0\;&{} L_{22}^{11} &{}\; 0&{}\; 0 \\ 0&{}\; 0&{}\; 0&{}\; L_{12}^{21} &{}\; 0&{}\; L_{12}^{22} \\ 0&{}\; 0&{}\; L_{21}^{21} &{}\; L_{21}^{12} &{}\; 0&{}\; L_{22}^{22} \\ \end{array}}} \right| ,\quad \mathbf{L}_\theta =\mathbf{E}\cdot \left| {{\begin{array}{l} L_{1}^{0} \\ L_{2}^{0}\\ L_{1}^{1} \\ L_{2}^{1} \\ L_{1}^{2} \\ L_{2}^{2} \\ \end{array}}}\right| ,\quad \mathbf{u}=\cdot \left| {{\begin{array}{l} u_{1}^{0}\\ u_{2}^{0}\\ u_{1}^{1} \\ u_{2}^{1}\\ u_{1}^{2}\\ u_{2}^{2}\\ \end{array}}}\right| ,\quad {\varvec{\uptheta }}=\left| {{\begin{array}{l} \theta _{1}^{0} \\ \theta _{2}^{0} \\ \theta _{1}^{1}\\ \theta _{2}^{1}\\ \theta _{1}^{2} \\ \theta _{2}^{2}\\ \end{array} }} \right| ,\quad \mathbf{f}=\cdot \left| {{\begin{array}{l} f_{1}^{0} \\ f_{2}^{0}\\ f_{1}^{1}\\ f_{2}^{1}\\ f_{1}^{2}\\ f_{2}^{2}\\ \end{array}}} \right| \end{aligned}$$
(39)
$$\begin{aligned}&\displaystyle \mathbf{L}_{\theta \theta }=\left| {{\begin{array}{lll} L^{0}&{}\; 0&{}\; 0 \\ 0&{}\;L^{1}&{}\; 0 \\ 0&{}\; 0&{}\; L^{2}\\ \end{array}}}\right| ,\quad \mathbf{Q}=\left| {{\begin{array}{l} Q_{2}^{0}\\ Q_{2}^{1} \\ Q_{2}^{2} \\ \end{array}}} \right| ,\quad {\varvec{\upchi }}=\left| {{\begin{array}{l} \bar{{\chi }}^{0} \\ \bar{{\chi }}^{1} \\ \bar{{\chi }}^{2} \\ \end{array}}}\right| \end{aligned}$$
(40)

where

$$\begin{aligned} L_{11}^{00}= & {} (\lambda +2\mu )\frac{\partial ^{2}}{\partial x_{1}^{2} }, \quad L_{12}^{01} =\frac{\lambda }{h}\frac{\partial }{\partial x_{1} }, \quad L_{22}^{00} =\mu \frac{\partial ^{2}}{\partial x_{1}^{2} },\quad L_{21}^{01} =\frac{\mu }{h}\frac{\partial }{\partial x_{1} },\nonumber \\ L_{12}^{10} u_{2}^{0}= & {} -\frac{3\mu }{h}\frac{\partial u_{2}^{0} }{\partial x_{1} }, \quad L_{11}^{11}=(\lambda +2\mu )\frac{\partial ^{2}}{\partial x_{1}^{2} }-\frac{3\mu }{h^{2}}, \quad L_{12}^{12} =\frac{3\lambda }{h}\frac{\partial }{\partial x_{1} },\nonumber \\ L_{21}^{10}= & {} -\frac{3\lambda }{h}\frac{\partial }{\partial x_{1}},\quad L_{22}^{11} =\mu \frac{\partial ^{2}}{\partial x_{1}^{2} }-\frac{3(\lambda +2\mu )}{h^{2}},\nonumber \\ L_{22}^{21}= & {} -\frac{5\lambda }{h}\frac{\partial }{\partial x_{1}},\quad L_{11}^{22}=(\lambda +2\mu )\frac{\partial ^{2}}{\partial x_{1}^{2} }-\frac{15\mu }{h^{2}},\nonumber \\ L_{21}^{21}= & {} -\frac{5\lambda }{h}\frac{\partial }{\partial x_{1}},\quad L_{21}^{21} =-\frac{5\lambda }{h}\frac{\partial }{\partial x_{1}}, \quad L_{22}^{22} =\mu \frac{\partial ^{2}}{\partial x_{1}^{2} }-\frac{15(\lambda +2\mu )}{h^{2}},\nonumber \\ L^{0}= & {} \lambda _{T}\frac{\partial ^{2}}{\partial x_{1}^{2} }-\frac{5\lambda _{T}}{h^{2}},\quad L^1 =\lambda _{T} \frac{\partial ^{2}}{\partial x_{1}^{2} }-\frac{15\lambda _{T} }{h^{2}},\quad L^{2} =\lambda _{T} \frac{\partial ^{2}}{\partial x_{1}^{2} }-\frac{35\lambda _{T}}{h^{2}} \end{aligned}$$
(41)

Parameters \(Q_{2}^{0} \) and \(Q_{2}^1 \) can be calculated using Eqs. (23) and (31) and heat-conducting conditions on upper and lower sides of the beam and conditions of heat exchange through heat conduction layer. For specific case of temperature set on upper side of the beam \(\theta ^{+}(x_{1})\) and foundation \(\theta ^{-}(x_{1} )\), respectively, and contact conditions through heat conduction layer, we have

$$\begin{aligned}&\displaystyle Q_{2}^{0}=\frac{1}{2h}\left( {\theta ^{+}-T_{k}} \right) ,\quad Q_{2}^1 =\frac{3}{2h}\left( {\theta ^{+}+T_{k} } \right) -\frac{3\theta ^{1}}{2h},\quad Q_{2}^{2} =\frac{5}{2h}\left( {\theta ^{+} -T_{k} )} \right) -\frac{5}{h}\theta ^{1},\nonumber \\&\displaystyle Q_{2}^3=\frac{7}{2h}\left( \theta ^{+} +T_{k}\right) -\frac{7}{h}\left( \theta ^{2}+\theta ^{0}\right) \end{aligned}$$
(42)

Here \(T_{k} \) is calculated by (37) and \(u_{2} (x_{1} )\) is calculated using representation (38) for the displacements.

Thus, we obtained the 1-D system of differential equations which is called the second approximation theory of thermoelasticity and heat conductivity of beam. Together with corresponding boundary conditions and conditions of thermal and mechanical contact, it can be used for the stress–strain and temperature calculation for the beam.

7 Thermoelastic analysis of microbeams

Let us consider an elastic microbeam of the length 2l, width b and thickness 2h, which is settled above the rigid foundation with an initial gap \(h_0 \) in the thermal field as it is shown in Fig. 1. There is a heat-conducting medium in the gap between the foundation and the beam. The medium does not resist the beam deformation, and heat exchange between the foundation and the beam is due to the thermal conductivity of the medium. We assume that the gap \(h_0\) is commensurable with the beam displacements which are assumed to be small.

Fig. 1
figure 1

Microbeam settles above the rigid foundation in the thermal field

Full size image

It is important to mention that systems of differential equations of thermoelasticity (33) and (39) and heat conductivity (34) and (40), respectively, are coupled. Their connectedness is not the one usually related to dynamical thermoelasticity. We consider stationary problem, and here the connectedness of the corresponding equations is caused by change of the heat-conducting conditions during the microbeam deformations. One can see that in the equations of heat conductivity (34) and (40) is presented member function \(u_{2} (x_{1})\) that is deflection of the microbeam. The presence of the function \(u_{2} (x_{1})\) in the equation (37) turns the problem into nonlinear one.

For solution of the problem, we use iterative algorithm developed in [51, 53]. In the first step of iteration, we assume that deflection of the microbeam \(u_{2} (x_{1} )=0\). In this case, we have traditional uncoupled problem of thermoelasticity and heat conductivity. For that uncoupled problem, any analytical or numerical method can be used and corresponding equations of thermoelasticity and heat conductivity can be solved independently. We refer below to this case as uncoupled or traditional formulation. In the next step of iterations, we substitute in (37) deflection \(u_{2} (x_{1})\) obtained from the solution of the problem in previous step of iteration. Our previous and this research shows that in the problems under consideration algorithm is convergent and convergence is fast enough.

In this study the differential equations of thermoelasticity (33) and (39) and heat conductivity (34) and (40) we solve numerically using finite element method (FEM). All calculations and post-processing analysis have been done using commercial software MATLAB and COMSOL Multiphysics. We performed finite element analysis with COMSOL Multiphysics. We used PDE mode with coefficient form impute module. The differential equations (33), (34) and (39), (40) are presented in the form convenient for COMSOL Multiphysics input. In 1-D PDE coefficient module are used finite elements of Lagrange type from linear to quantic order. Also in COMSOL Multiphysics there is option for mesh refinement. For details we refer to the corresponding software manuals. Our numerical experiments show that for the problem under consideration FEM has good convergence and use of quadratic elements with one mesh refinement gives accurate results. Obtained using embedded in COMSOL Multiphysics FEM tools date then have been transferred to MATLAB environment for further analysis, visualizations and comparison with results obtained using Euler–Bernoulli theory.

For convenience we introduce the coordinate \(\hat{{x}}_{1} =x_{1}/l\). For numerical calculations and analysis, we consider the simply supported microbeam with the following physical and geometrical parameters presented in Table 1.

Table 1 Properties of investigated microbeam
Full size table

Below we perform thermoelastic analysis of simply supported microbeam using first-order and second-order approximation theories for the following two problems. Our analysis show that distribution and values of the displacements and temperature calculated using first-order and second-order theories for relatively thin microbeam differ not much. As soon as thickness of the microbeam increases, difference of the results obtained using first-order and second-order theories also increase and for \(h/l>0.2\) becomes greater.

7.1 On the outer side of microbeam and foundation set the temperature \(\theta ^{+}=550\;^{\circ }\hbox {C},\;\theta ^{-}=0\;^{\circ }\hbox {C}\)

In this case deflection of the microbeam directed up \(u_{2} >0\) and initial gap \(h_0\) increase during the microbeam deformation. In Table 2, we presented results of calculation performed using traditional approach (in our case first iteration) and presented in here coupled theory. In columns 2–7 are presented deflection \(u_{2}\), stresses \(\sigma _{11}\) and temperature \(\theta \) distributions calculated in the midpoint of the microbeam on top and bottom sides. Upper values correspond to calculations using traditional uncoupled theory, and lower values correspond to calculations using coupled theory presented here. Analysis of the presented data shows that results obtained using two above-mentioned approaches are different and some time difference is significant. We consider that coupled theory presented here is more consistent with physical processes occurring at the microbeam deformation in temperature field with taking into account heat conductivity through thin heat-conducting layer.

Table 2 Deflection \(u_{2}\), stresses \(\sigma _{11}\) and temperature \(\theta \) in the midpoint
Full size table

Distribution of the Legendre coefficients of the displacements \(u_{2}^k (x_{1} )\) and temperature \(\theta ^{k}(x_{1} )\) is presented in Table 1, and data are presented in Fig. 2. Surfaces of the displacements \(u_{2} (x_{1} ,x_{2} )\), stresses \(\sigma _{11} (x_{1}, x_{2})\) and temperature \(\theta (x_{1} ,x_{2} )\) distribution are presented in Fig. 3. Calculations have been done using coupled approach proposed here and second-order theory of microbeam.

Fig. 2
figure 2

Legendre coefficients of the displacements \(u_{2}^k (x_{1})\) and temperature \(\theta ^{k}(x_{1} )\)

Full size image
Fig. 3
figure 3

Surfaces of the displacements \(u_{2} (x_{1} ,x_{2})\), stresses \(\sigma _{11} (x_{1}, x_{2})\) and temperature \(\theta (x_{1} ,x_{2})\) distribution

Full size image

7.2 On the outer side of microbeam and foundation set the temperature \(\theta ^{+}=30\;^{\circ }\hbox {C},\;\theta ^{-}=170\;^{\circ }\hbox {C}\)

In this case, deflection of the microbeam happens downward \(u_{2} <0\) and initial gap \(h_{0}\) decreases during the microbeam deformation. In Table 3, we presented results of calculation performed using traditional approach (in our case first iteration) and coupled theory presented here. In columns 2–7 are presented deflection \(u_{2}\), stresses \(\sigma _{11}\) and temperature \(\theta \) distributions calculated in the midpoint of the microbeam on top and bottom sides. Upper values correspond to calculations using traditional uncoupled theory, and lower values correspond to calculations using coupled theory presented here. Analysis of the presented data shows that results obtained using two above-mentioned approaches are different, and sometimes difference is significant. Once again we consider that coupled theory presented here is more consistent with physical processes occurring at the microbeam deformation in temperature field with taking into account heat conductivity through thin heat-conducting layer.

Table 3 Deflection \(u_{2}\), stresses \(\sigma _{11}\) and temperature \(\theta \) in the midpoint
Full size table

Distribution of the Legendre coefficients of the displacements \(u_{2}^k (x_{1} )\) and temperature \(\theta ^{k}(x_{1} )\) is presented in Table 1, and data are presented in Fig. 4. Surfaces of the displacements \(u_{2} (x_{1} ,x_{2} )\), stresses \(\sigma _{11} (x_{1} ,x_{2})\) and temperature \(\theta (x_{1} ,x_{2} )\) distribution are presented in Fig. 5. Calculations have been done using coupled approach proposed here and second-order theory of microbeam.

Fig. 4
figure 4

Legendre coefficients of the displacements \(u_{2}^k (x_{1})\) and temperature \(\theta ^{k}(x_{1})\)

Full size image
Fig. 5
figure 5

Surfaces of the displacements \(u_{2} (x_{1} ,x_{2})\), stresses \(\sigma _{11} (x_{1} ,x_{2})\) and temperature \(\theta (x_{1}, x_{2})\) distribution

Full size image

In order to simplify situation, we chose for calculations data presented in Table 2 geometric parameters of the microbeam and temperature so as to avoid mechanical contact of microbeam and foundation. The cases of unilateral mechanical contact have been considered in our previous publications using classical theory. We are planning to consider unilateral mechanical contact in frame of high-order theory in further publications, taking into account that this problem has many applications in MEMS and NEMS design and simulation.

8 Conclusions

A high-order theory for homogeneous thermoelastic beams has been developed and applied for thermal and stress–strain analysis of the MEMS/NEMS structures and devices. The proposed approach is based on the expansion of the 2-D equations of elasticity into Fourier series in terms of Legendre polynomials. Starting from the 2-D equations of thermoelasticity and heat conductivity, the stress and strain tensors, the displacement, traction, body force vectors and temperature have been expanded into Fourier series in terms of Legendre polynomials in the thickness coordinate. Therefore, all equations of thermoelasticity and heat conductivity including Hooke’s and Fourier’s laws have been transformed to the corresponding equations for the series expansion coefficients. The system of differential equations in terms of the displacements and temperature and corresponding boundary conditions for the expansion coefficients has been obtained. The first- and second-order approximations of the exact shell theory have been considered in more detail. All necessary equations and their expansion coefficients have been derived explicitly, and the corresponding boundary-value problems have been formulated. In the approach proposed here, there is essential new method of taking into account the change of the thermal conditions between the beam and solid foundation during the beam deformation.

As a result it leads to the coupled nonlinear system of the equations of elasticity and heat conductivity even for statically applied mechanical and thermal load. For the numerical solution of the formulated problems, the FEM implemented in the commercial software COMSOL Multiphysics and MATLAB have been used. Developed models have been used for thermomechanical analysis and modeling MEMS structures and devices. Numerical calculations show that in many situations for accurate thermal and stress–strain analysis of the MEMS and NEMS structures and devices subjected to high-temperature thermal contact conditions proposed here that take into account deformation of the beam during thermal loading have to be used. Classical thermal contact conditions are not acceptable in such because they cannot take into account physical processes related to deformation and heat exchange.