Mechanistic study on lung cancer mortality after radon exposure in the Wismut cohort supports important role of clonal expansion in lung carcinogenesis

Abstract

Lung cancer mortality after radon exposure in the Wismut cohort was analyzed using the two-stage clonal expansion (TSCE) model. A total of 2996 lung cancer deaths among the 58,695 male workers were observed during the follow-up period between 1946 and 2003. Adjustment to silica exposure was performed to find a more accurate estimation of the risk of radon exposure. An additional analysis with the descriptive excess relative risk (ERR) model was carried out for comparison. The TSCE model that best describes the data is nonlinear in the clonal expansion with radon exposure and has a saturation level at an exposure rate of $d_{\mathrm{r}}\simeq 100\,\text{WLM}{/}\text{yr}$. The excess relative risk decreases with age and shows an inverse exposure rate effect. In comparison with the ERR model, the TSCE model predicts a considerably larger risk for low exposures rates below $50\,\text{WLM}{/}\text{yr}$. Comparison to other mechanistic studies of lung cancer after exposure to alpha particles using the TSCE model reveals an extraordinary consistency in the main features of the exposure response, given the diversity in the characteristics of the cohorts and the exposure across different studies. This suggests that a nonlinear response mechanism in the clonal expansion, with some level of saturation at large exposure rates, may be playing a crucial role in the development of lung cancer after alpha particle irradiation.

Introduction

Exposure to radon and its progeny has been recognized as a cause of lung cancer for many decades. This association between radon exposure and lung cancer was established after analyses of health effects of miners who worked in environments with high concentrations of radon (BEIR 1999). Some of the radon decay products (also called progeny or daughters) decay in the lungs after inhalation and emit densely ionizing alpha particles. Radon emanates from the soil, water and building materials, becoming trapped in homes. Although typical residential radon exposures may be a factor of 10 or 100 smaller than the exposures received by miners, understanding how radon acts on the development of lung cancer is a general population health concern.

The Wismut cohort is the worldwide largest uranium miner cohort. The workers of the Wismut company exposed to radon and its progeny were exposed chiefly working underground or in uranium ore processing facilities. Different aspects of the lung cancer caused by radon inhalation in the Wismut cohort have been studied in detail before (Grosche et al. 2006; Kreuzer et al. 2010a, b; Walsh et al. 2010). Apart from radon, Wismut workers were also exposed to external gamma radiation, long-lived radionuclides, arsenic, fine dust and silica, which are all considered to be carcinogenic agents. Among these possible confounders, only adjustment due to silica dust exposure was found to be significant in the Wismut miners (Sogl et al. 2012), and therefore, corrections due to silica exposure were performed in the current study to allow for more accurate predictions of radon lung cancer risk. The analyses of lung cancer in the Wismut cohort mentioned above were generally performed using descriptive models and Poisson regression techniques. Unfortunately, no smoking information for the Wismut workers was available in the current study. It is noted, however, that in a nested case–control study of the cohort with limited smoking information the radon-related lung cancer risks were very similar with and without smoking adjustment (Schnelzer et al. 2010).

In the current analysis, the two-stage clonal expansion model (TSCE) (Moolgavkar and Knudson 1981; Moolgavkar 1983; Moolgavkar and Luebeck 1990) was used. In the TSCE model, it is assumed that in a specific organ there is a large number of target cells susceptible to malignant transformation. One of these target cells undergoes two mutations and clonal expansion during the intermediate stage before it develops a tumor. Thus, the model distinguishes three specific processes on a cell’s pathway to cancer: initiation, clonal expansion and transformation. The TSCE model has been widely used to analyze epidemiological data and allows explicit examination of the effect of radiation on these processes. To verify the risk estimates obtained here with the TSCE model, an additional analysis was performed for comparison using the excess relative risk model (ERR).

There have already been previous studies of the Wismut cohort or studies in which the Wismut cohort formed part of a pool of uranium miners cohorts, using mechanistic models (Dillen et al. 2011; Heidenreich et al. 2012), and also studies which included mechanistic analyses of other uranium miners cohorts (Luebeck et al. 1999a; Leenhouts 1999; Little et al. 2002; Heidenreich et al. 2004; Brugmans et al. 2004; Eidemüller et al. 2012). Other important studies of lung cancer among uranium miners included the Colorado (Schubauer-Berigan et al. 2009), Czech (Tomasek 1999), French (Vacquier et al. 2008) and Eldorado (Lane et al. 2010) cohort studies. In an extensive 11 underground miners study (Lubin et al. 1994), a joint analysis of the above-mentioned plus other miners cohorts was performed.

In the present work, lung cancer mortality among the Wismut workers is analyzed using the mechanistic TSCE model of carcinogenesis. The influence of radon exposure on the different steps in the carcinogenic process of lung cancer is evaluated, with special emphasis on the clonal expansion rate. The model was adjusted to silica dust exposure, a known lung cancer confounder. Risk estimates for different exposure scenarios were derived and compared to those obtained with excess relative risk models. Finally, the results are compared to those of other mechanistic studies on lung cancer after alpha particle exposure. Common mechanisms across different studies were found.

Materials and methods

The Wismut Cohort

The cohort studied here includes 58,695 workers employed by the Wismut company between 1946 and 1989 to extract the uranium ore in the mountains of Saxony and Thuringia, former East Germany. The cohort members in this study were all males born after 1899. They were employed at least for 180 days and had silica dust exposure records. Workers were considered to be at risk from the date of first employment until their date of death, loss of follow-up or the end of the follow-up period, that is on the December 31,2003. The total number of person years is 2011,873. In total, 2996 lung cancer deaths occurred, which in combination with the large number of workers and long duration of the follow-up gives a very strong statistical power. For a more detailed description of the cohort see, Kreuzer et al. (2010a) and references therein.

Radon and silica exposure

The exposure to radon was estimated retrospectively using a job-exposure matrix (JEM). According to each work place and type of job, the JEM gives annual values of exposures to radon, external gamma radiation and long-lived radionuclides (Lehmann et al. 1998). The mean cumulative radon exposure is 280 Working Level Month (WLM),¹ with a maximum exposure of 3, 224 WLM. The Wismut cohort workers were exposed at a young age and were exposed to radon for a relatively long period. The average age at first exposure is about 25 years, whereas the average duration of exposure is 11 years.

Apart from exposure data on gamma radiation and long-lived radionuclides, there is available data on the exposure to silica, fine and arsenic dust. Silica and fine dust exposures are highly correlated because the silica dust is part of the total measured fine dust exposure. Hence, fine dust is excluded from the analysis. A previous study of this cohort has found that exposure to silica results in a significant lung cancer risk (Sogl et al. 2012). The inclusion of the gamma radiation, long-lived radionuclides and arsenic, however, did not confound the radon risk (Walsh et al. 2010). Thus, only radon and silica were considered in the current analysis. Information on the silica dust is given by a second JEM (Dahmann et al. 2008). The exposures are given in units of dust-years. A silica dust-year is defined as exposure by $1 {\mathrm{mg}}\ {\mathrm{m}}^{-3}$ over 220 shifts of 8 hours.

Occupational safety measures, and in particular radiation protection measures, were lacking in the early years of the mine just after the end of World War II. Wet drilling and appropriate ventilation were subsequently introduced decreasing notably the miners radon and dust exposure. For these early years, no radon measurements were performed and exposure was estimated retrospectively. Figure 1 shows the pronounced decrease in radon and silica dust with calendar year, after 1955.

Fig. 1

Cohort average annual radon and silica dust exposure

The TSCE model

The two-stage clonal expansion model (TSCE) used here has been widely used as standard mechanistic model for carcinogenesis (Kai et al. 1997; Luebeck et al. 1999a; Kaiser et al. 2012; Eidemüller et al. 2012). In addition to independent estimates of the risk that can be compared to those obtained with other more traditional epidemiological models, the TSCE model provides indications of possible biological processes during the development of cancer. Furthermore, it can be used as a simple prototype to model carcinogenesis, that may be replaced by an improved and perhaps more complex model, once more precise biological information on the development of a certain cancer type is available, e.g., for colon cancer (Little and Li 2007; Luebeck et al. 2013; Kaiser et al. 2014).

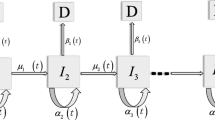
A sketch of the TSCE model with its two stages and the clonal expansion phase is shown in Fig. 2. A cell can be initiated with rate $\nu$, i.e., receive mutational changes that result in a growth advantage. Initiated cells may divide into two initiated cells with rate $\alpha$, die (or differentiate) with an inactivation rate $\beta$, or divide asymmetrically into an initiated cell and a malignant cell with rate $\mu$. After a lag time $t_{\mathrm{lag}}$ the malignant cell develops into a malignant tumor. The rates $\nu$ and $\mu$ describe rate-limiting events in the process of carcinogenesis, e.g., mutations of driver genes (Vogelstein et al. 2013). Implicit in the model is the assumption that initiation follows a nonhomogeneous Poisson process with intensity $N_{\mathrm{s}}\nu$, where $N_{\mathrm{s}}$ is the number of susceptible cells. In general, the pool of susceptible healthy cells divide symmetrically or inactivate at certain given rates $\alpha _{\mathrm{s}}$ and $\beta _{\mathrm{s}}$, and initiation occurs during asymmetrical cell division the same way as transformation takes place with an initiated cell. For very large $N_{\mathrm{s}}$ and very small mutation rate $\nu$, however, the nonhomogeneous Poisson process assumption is justified insofar as $\alpha _{\mathrm{s}}\ge \beta _{\mathrm{s}}$ (Tan 1991).

Fig. 2

Sketch of the different stages and processes leading to a malignant tumor in a TSCE model. The model includes two rate-limiting steps and a phase of clonal expansion

The parameters $\alpha$, $\beta$, $\nu$ and $\mu$, are however unidentifiable, and thus, they cannot be determined from the data alone (Heidenreich 1996; Heidenreich et al. 1997). These parameters may vary without modifying the survival function and hazard, and hence keeping the likelihood constant. They are therefore not uniquely determined by the epidemiological data. This is a consequence of the mathematical structure of the model, and it leads to infinite confidence intervals for the non-identifiable parameters (Raue et al. 2009, 2010). One can in principle remove this non-identifiability by using suitable constraints on the parameters. One such constraint often used is assuming that the mutation rates $\mu$ and $\nu$ are equal. The alternative to constrain the parameter space used here is to define a set of identifiable parameters. An identifiable parameter is a parameter that can be determined from the survival function alone and has a finite confidence interval. Leaving the spontaneous transformation rate undetermined (i.e., allowing it to vary freely), one can define the following set of three parameters (Eidemüller et al. 2010):

$$\begin{aligned} X= N_{\mathrm{s}} \nu \mu _0, \end{aligned}$$

(1)

$$\begin{aligned} \gamma= \alpha -\beta -\mu, \end{aligned}$$

(2)

$$\begin{aligned} \delta= \alpha \mu _0, \end{aligned}$$

(3)

where $\gamma$ is the clonal expansion rate and $\delta$ is a parameter proportional to the division rate $\alpha$. $\mu _0$ is the transformation rate at person’s birth. The three identifiable parameters above as well as the transformation rate $\mu$ can in principle be time dependent for the baseline and vary with attained age and year. For the time-dependent $\mu$, the parameter ratio $m(a)=\mu (a){/}\mu _0$ is used. Other parametrizations, which can be expressed in terms of these identifiable parameters, are possible. The choice of the identifiable parameters above allows to directly compare the results obtained in the present study for the estimated parameters with those obtained in other studies using the TSCE model (see Comparison of TSCE model parameters in Sect. 4).

The baseline hazard in the cohort data is well described by constant X, $\delta$ and m parameters (i.e $m=1$), and a clonal expansion rate for the baseline $\gamma _{\mathrm{b}}$ that varies as a function of attained age a and calendar year y. In the model that best fits the data, the calendar year dependence of $\gamma _{\mathrm{b}}$ is quadratic with a maximum at $y_{\rm c}=1951$. On the other hand, $\gamma _{\mathrm{b}}$ remains constant with age until about an age of $a_0=48\,\text{yr}$ when it starts to decrease exponentially. That is

$$\begin{aligned} \gamma _{\mathrm{b}}(a,y)=\gamma _{\rm b}(a)\left[ 1-b_{\rm y}(y-y_{\rm c})^2\right] \;, \end{aligned}$$

(4)

where $\gamma _{\mathrm{b}}(a)$ is given by

$$\begin{aligned} \gamma _{\mathrm{b}}(a)={\left\{ \begin{array}{ll} \gamma _0, &{}\quad \text {if}\quad a\le a_{\rm c}.\\ \gamma _0\;{\mathrm{e}}^{-b_{\rm a}\left(a-a_{\rm c}\right)}, &{}\quad \text {otherwise}, \end{array}\right.} \end{aligned}$$

(5)

where the fit parameters $\gamma _0$, $b_{\rm y}$, $b_{\rm a}$ are greater than zero and $b_{\rm y}$ is small enough such that $\gamma$ is always positive. The parameter values of $y_{\rm c}$ and $a_{\rm c}$ are also estimated, but rather than allowing these parameters to vary continuously to find the maximum likelihood, they were varied step-wise by increments of one year.

The exposure response in the TSCE model was studied by checking the influence of radon and silica on the identifiable parameters X, $\gamma$ and m. Variations in the $\gamma$ and m parameters with exposure correspond to changes in the clonal expansion and transformation processes in the TSCE model. X is proportional to $N_{\mathrm{s}}\cdot \nu$ because $\mu _0$ is a constant. Therefore, changes in X correspond to changes in the total rate of creation of initiated cells since $\nu$ is the initiation rate per cell. Ultimately considering that healthy cells endeavor to maintain the lung tissue homeostasis, one can assume that $N_{\mathrm{s}}$ remains practically constant once the development of a person during the early young age has concluded.

Tumor initiators induce heritable alterations in the cellular DNA and gene function of the target cell. These alterations result from mutations through different mechanisms (e.g., a break in one or both DNA strands, adduct formation, etc.), and the corresponding endpoints are often linearly related to dose (Portier and Edler 2009; Neumann 2009). Therefore, linear responses in the parameter X with exposure were tested as well as simple nonlinear responses to check for possible deviations from linearity. Mutagenic agents may also induce the progression of a benign tumor of initiated cells to a malignant neoplasm (Barrett 1993). Consequently, exposure response functions similar to those used in initiation were checked in successive fits for the parameter m. On the other hand, there is evidence that a substantial number of carcinogenic agents do not involve direct interaction with DNA (WHO 2007). Such non-genotoxic carcinogens act by “inducing sustained proliferation, either directly through a trophic stimulus or indirectly by inducing a proliferative response as a consequence of cell death” (Felter et al. 2011). The promoting agents often show nonlinear dose–responses, and a non-observable-effect level (NOEL), i.e., no detectable response below some critical value, has been determined in many cases (Neumann 2009). Another important characteristic of non-genotoxic agents is that they need to be active during a certain period of time to have an effect. This is the case because of the low spontaneous or induced initiation rates, and also because of the reversible effects of these agents (Felter et al. 2011). Therefore, it is helpful to perform a categorical analysis of the exposure response in $\gamma$ to evaluate the form of dose–response relationship. Ultimately, a carcinogen may exhibit both genotoxic and non-genotoxic characteristics, and therefore, the exposure response was checked simultaneously in X, $\gamma$ and $m$ for radon and silica.

Initially, only radon was considered with different alternatives tested on initiation, clonal expansion and transformation. A categorical analysis of $\gamma$ on different exposure rates suggests a significant saturation level at radon exposures greater than about $100\,\text{WLM}$ (see Fig. 4). Among different possible curves displaying this behavior, a linear leveling of the clonal expansion with radon exposure rate fitted the data best. In this model, $\gamma$ is given by

$$\begin{aligned} \gamma =\gamma _{\mathrm{b}}\left(a,y\right) \left(1+f_{\mathrm{r}}\right) \,, \end{aligned}$$

(6)

where $f_{\mathrm{r}}$ is the radon exposure response factor which depends on the annual radon exposure rate $d_{\mathrm{r}}$ as follows,

$$\begin{aligned} f_{\mathrm{r}}\left(d_{\mathrm{r}}\right) =r_1\left(1-{\mathrm{e}}^{-r_2d_{\mathrm{r}}{/}r_1}\right). \end{aligned}$$

(7)

In the expression above, $r_1$ determines the saturation level for large exposure rates, and $r_2$ the linear slope for small exposure rates, $f_{\mathrm{r}}=r_2\cdot d_{\mathrm{r}}+O(d_{\mathrm{r}}^2)$.

An alternative model with radiation response in the initiation stage resulted in much worse fits (see results section); linear, linear-quadratic and linear-exponential forms were analyzed,

$$\begin{aligned} X_{ln}= X_{\mathrm{b}}\left(1+r_Xd_{\mathrm{r}}\right) \,, \end{aligned}$$

(8)

$$\begin{aligned} X_{lq}= X_{\mathrm{b}}\left(1+r_{X1}d_{\mathrm{r}}+r_{X2}\,d_{\mathrm{r}}^2\right) \,, \end{aligned}$$

(9)

$$\begin{aligned} X_{lk}= X_{\mathrm{b}}\left(1+r_{X1}d_{\mathrm{r}}\,\mathrm{e}^{-r_{X2}d_{\mathrm{r}}}\right) \,, \end{aligned}$$

(10)

where $X_{\mathrm{b}}$ denotes the baseline parameter. The third model above, $X_{lk}$, is motivated by the possibility that high exposure rates of alpha particles may cause injury severe enough to “kill” the target cell. Compared to exposure responses in initiation, i.e, those obtained just with $X_{ln}$, $X_{lq}$ and $X_{lk}$ above, linear and linear-quadratic responses in the transformation parameter result in deviances that were several hundred deviance points larger.

Models with silica response in initiation, clonal expansion and transformation were added to the best model without silica, the model given in Eqs. (6) and (7), and fitted to the data. That is

$$\begin{aligned} X= & {} X_{\mathrm{b}}\left(1+f_{\mathrm{s}}\right) \,, \end{aligned}$$

(11)

$$\begin{aligned} \gamma= & {} \gamma _{\mathrm{b}}\left(1+f_{\mathrm{r}}+f_{\mathrm{s}}\right) \,, \end{aligned}$$

(12)

$$\begin{aligned} \mu= & {} \mu _{\mathrm{b}}\left(1+f_{\mathrm{s}}\,\right) , \end{aligned}$$

(13)

where for the silica response factor $f_{\mathrm{s}}$ linear, linear-quadratic and linear spline functions of the annual silica exposure rates were analyzed. A model with an interaction term in $\gamma$ between radon and silica exposure, $\gamma =\gamma _{\mathrm{b}}(1+f_{\mathrm{r}}+f_{\mathrm{s}}+\epsilon f_{\mathrm{r}}f_{\mathrm{s}})$, was also fitted but it did not significantly improve the fit. The model that best describes the data is a function of silica exposure $f_{\mathrm{s}}(d_{\mathrm{s}})$ acting on the clonal expansion rate $\gamma$ that is linear above the exposure rate $d_{\rm c}$

$$\begin{aligned} f_{\mathrm{s}}\left(d_{\mathrm{s}}\right) ={\left\{ \begin{array}{ll} 0, &{} \text {if}\quad d_{\mathrm{s}}\le d_{\rm c}.\\ r_{\rm s}(d_{\mathrm{s}}-d_{\rm c}), &{} \text {otherwise}, \end{array}\right.} \end{aligned}$$

(14)

with

$$\begin{aligned} \gamma = \gamma _{\mathrm{b}}\left(1+f_{\mathrm{r}}+f_{\mathrm{s}}\right) \,. \end{aligned}$$

(15)

$d_{\mathrm{s}}$ denotes the annual exposure to silica dust concentrations expressed in $\mathrm{mg{/}m^3}$. Models with a silica effect on transformation gave much worse fits than those with a silica effect on initiation.

To this final model, the different radon responses in initiation used before were added to ensure that the additional initiation parameters are still not significant once the adjustment for silica was done. The same check for an additional silica response in initiation with linear, linear-quadratic and linear spline functions was performed. In this case also, the additional parameters were not significant.

The ERR model

To build an appropriate TSCE model, it is helpful to have a descriptive model as a reference. Here, the exposure response to radon and silica found in Walsh et al. (2010) and Sogl et al. (2012) was used, with the only addition of an extra parameter to describe the time since median exposure covariate.

The baseline used here has been specifically built for this cohort. For the baseline hazard, the following model was used,

$$\begin{aligned} h_{\mathrm{b}}\left(a,y\right) = 10^{-5}\times \mathrm{e}^{\Psi (a,y)}, \end{aligned}$$

(16)

where

$$\begin{aligned} \Psi \left(a,y\right)&= \psi _0+\psi _1\mathrm{ln}\frac{a}{60} \nonumber \\&+\,\psi _2\mathrm{ln}^2\left(\frac{a}{a_{\rm c}}\right) \Theta \left(a-a_{\rm c}\right) \nonumber \\&+\,\phi _2 \left(y-y_{\rm c}\right) ^2. \end{aligned}$$

(17)

In the equation above, y denotes the calendar year, and $y_{\rm c}$ the location of the maximum of the quadratic function in y. $\psi _0$, $\psi _1$, $\psi _2$ and $\phi _2$ are parameter values, which were estimated. $\Theta \left(a -a_{\rm c}\right)$ represents a step function located at an age $a_{\rm c}$. As for the TSCE model, the parameter values of $y_{\rm c}$ and $a_{\rm c}$ were varied step-wise by increments of one year.

The excess relative risk (ERR) of radon exposure for vanishing silica exposure is defined as $\mathrm{ERR}\left(a,D,x_i\right) =h\left(a,D,x_i\right) {/}h_{\mathrm{b}}\left(a\right) -1$, where $h_{\mathrm{b}}$ denotes the baseline rate, a is the attained age, D is the cumulative radon exposure (typically time-lagged) and $x_i$ represent a definite number of confounders and effect modifiers of the actual radon exposure.

When there is more than one risk factor, as in the case here with the radiation and silica dust exposure, the combined effect of the different exposures can in principle modify the effect of radon in an additive or multiplicative way. Here, both possibilities were checked and, in agreement with Sogl et al. (2012), the additive model resulted in a statistically better fit. Then, the hazard function may be written as

$$\begin{aligned} h = h_{\mathrm{b}} [1+\text {ERR}_r (D,a,t_\mathrm{sme},d_\mathrm{avg}) +\mathrm{ERR_{\rm s}}(\hbox {sil})]. \end{aligned}$$

(18)

In the equation above, $\mathrm{ERR_r}$ is the radon excess relative risk, which depends on the cumulative dose D and the following covariates: attained age a, $t_\mathrm{sme}$ representing time since median exposure and the exposure rate $d_\mathrm{avg}$. D is time-lagged $D\equiv D\left(a-\tau _\mathrm{lag}\right)$. $t_\mathrm{sme}$ is a function of attained age a, and it is estimated with respect to the time-lagged cumulative dose at a definite age $D(a-\tau _\mathrm{lag})$. The exposure rate $d_\mathrm{avg}$ used here is defined as the total time-lagged cumulative dose divided by the total duration at each year of attained age assuming 11 working months per year. This definition which represents an average exposure rate is similar to the one used in Tomasek et al. (2008) and Walsh et al. (2010).

This type of model called exposure-age-concentration model for the radon risk has been used by the BEIR VI committee to analyze different uranium miners data sets (BEIR 1999). An alternative model for the radon risk used in the BEIR VI report, the exposure-age-duration model, describes the Wismut data worse and has not been used here (Walsh et al. 2010). $\mathrm{ERR_{\rm s}}$ is the silica excess relative risk. As in the uranium miner data sets analyzed by BEIR VI (1999) and other more recent studies, a time lag $\tau _\mathrm{lag}$ of 5 years was used. From now on, D is used to denote the time-lagged exposure.

The exposure response for radon that best fits the data is linear (Walsh et al. 2010). The radon exposure effect on the risk decreases exponentially with attained age a and exposure rate $d_\mathrm{avg}$. In the case of $t_\mathrm{sme}$, the statistical fit is 4.6 deviance points better when the decrease is linear-quadratic rather than exponential. The radon exposure risk is given by

$$\begin{aligned} \mathrm{ERR}_{\mathrm{r}}&= \beta _{\mathrm{r}}D\times [1+\alpha _{t1}(t_\mathrm{sme}-11) +\alpha _{t2}(t_\mathrm{sme}-11)^2]\nonumber \\&\quad *\,\mathrm{e}^{-\alpha _{\rm a}(a-44)-\alpha _r(d_\mathrm{avg}-2.7)} \;, \end{aligned}$$

(19)

where the model-centering constants 44 years of age, 11 years since median exposure and 2.7 WL of exposure rate, are typical values for the Wismut cohort. The parameter $\beta _{\mathrm{r}}$ represents the ERR per unit of radon exposure, adjusted for silica exposure, of a person with these typical values for the modifier covariates.

The silica exposure response, after adjusting for radon, has the form of a linear increase above the cumulative exposure $\hbox {sil}_\mathrm{c}$, similar to Sogl et al. (2012),

$$\begin{aligned} \mathrm{ERR}_{\mathrm{s}}\hbox {(sil)}={\left\{ \begin{array}{ll} 0, &{}\quad \text {if}\quad \hbox {sil} \le \hbox {sil}_\mathrm{c}.\\ \beta _{\mathrm{s}}(\hbox {sil}-\hbox {sil}_\mathrm{c}), &{}\quad \text {otherwise}, \end{array}\right.} \end{aligned}$$

(20)

where sil is the silica dust exposure in dust-years.

Statistical analysis

The parameter estimates $\alpha _j$ for the hazard function $h(t;\alpha _j)$ for a definite model are obtained by maximizing the total likelihood, which is the product of all individual likelihoods in the cohort. Taking the parameters to be piece-wise constant on a definite number of intervals allows the TSCE model to be solved analytically simplifying the estimation of the hazard, the likelihood construction and the numerical optimization (Moolgavkar and Luebeck 1990; Heidenreich et al. 1997). The optimization was performed using the Minuit2 minimization package (James 1994). The best model is selected according to the likelihood ratio test or the Akaike information criterion, denoted by AIC, depending on whether the model is nested or not.² The confidence intervals for the parameters given here are Wald-type at $2\sigma$ confidence level. In addition to the likelihood method, the integrated hazard, which gives the estimated number of cases, was compared here with the observed cases for different categories of the covariates.

Results

The TSCE model that describes best the data is a model with a linear-leveling exposure response in the clonal expansion, as in Eq. (7). The ERR model used here is very similar to the models analyzed in Walsh et al. (2010) and Sogl et al. (2012), except for a possible quadratic $t_\mathrm{sme}$ decay of the excess risk in Eq. (19), and therefore, the results are not presented in detail here.

Table 1 compares the deviances and AIC differences ($\Delta _i$) resulting from the optimization of models with different exposure response in the initiation stage X and a linear-leveling clonal expansion rate $\gamma$. The silica exposure adjustment is not included here. Setting $\gamma =\hbox {constant}$ w.r.t. exposure rate $d_{\mathrm{r}}$, and allowing an effect of $d_{\mathrm{r}}$ only on initiation, one sees that the resulting fit is much worse than that using the $\gamma (a,y,d_{\mathrm{r}})$ model without an effect of radiation on X. On the other hand, if one considers a more complex model with the radiation affecting both $\gamma$ and X, the additional parameters corresponding to X are not significant according to the likelihood ratio test and yield large relative errors in the 300–400 % range. The values of $\Delta _i$ and their respective weights $\omega _i$ indicate that an effect of radon on initiation, however much weaker than the dominant $\gamma (d_{\mathrm{r}})$, cannot be ruled out.

Table 1 Comparing TSCE models for different radon response without silica

To adjust for the silica exposure, two more parameters had to be added in either the ERR or TSCE models. Table 2 shows the number of parameters, deviance and excess cases predicted by the models. In both the ERR and TSCE model, the silica adjustment was highly significant. In the ERR model, 13 parameters were found to be significant in this analysis. Among these 13 parameters, 6 were used for the baseline, 5 to describe the radon response and 2 for the silica dust exposure. In the TSCE model, amidst the 11 parameters used in the likelihood analysis, 7 were used in the baseline, 2 describe the radon response and another 2 the silica dust exposure. In terms of deviance, the ERR model is about 16 points smaller with two more overall parameters. Thus, there might be an indication that the radon exposure response is more complex than what the TSCE model suggests. Nevertheless, when the observed and expected number of cases across different exposure categories are compared for the two models in Table 3, the two extra parameters of the ERR model do not seem to improve substantially the fit to the data.

Table 2 Best ERR and TSCE models with silica

Table 3 Observed and expected number of deaths for different radon exposure categories

The maximum likelihood estimates for the parameters of the ERR and TSCE model and their corresponding 95 % Wald type confidence intervals are shown in Table 4. Parameters without error bars have been minimized in a step-wise fashion when the hazard is not a smooth function of the parameter, or when, as in the case of $y_{\rm c}$, one is not really interested in relatively small differences. In either the ERR or TSCE models, the $y_{\rm c}$ value gives the maximum rates with calendar year. The exposure response on $\gamma$ is discussed in detail in the following section, together with consequences for the radiation risk. The silica exposure response is linear in the cumulative silica exposure above $\hbox {sil}_\mathrm{c}=10\,\mathrm{mg}{/}\mathrm{m}^3\,\hbox {yrs}$ for the descriptive model (Sogl et al. 2012). Similarly, in the TSCE model the response is linear in the silica dust exposure rate above concentrations of $d_\mathrm{c}=0.92\, \mathrm{mg}{/}\mathrm{m}^3$ during a working year.

Table 4 Maximum likelihood estimates of the ERR and TSCE models

Discussion

Mortality rates at old age

The observed lung cancer mortality rates in the Wismut cohort reach a maximum at about an age of 70 and then remain practically constant. This pronounced flattening of the hazard curve is typical of spontaneous lung cancer mortality rates.

In the ERR model, to get a flatter curve at old age one needs to modify the typical quadratic baseline rate, i.e, $h_{\mathrm{b}}\propto \hbox {exp}(\psi _0+\psi _1\hbox {ln}a+\psi _2\hbox {ln}^2a)$, by using a step function in the quadratic term see Eq. (17). The result is a much better description of the cohort’s hazard at old age, as can be seen in Fig. 3 and in the fact that the addition of the extra parameter $a_{\rm c}$ results in a deviance 26 points smaller. This is the case because below an age of about 60 years a good approximation to the baseline rates is linear in a log-scale. That is

$$\begin{aligned} \hbox {ln} h_{\mathrm{b}}\propto \psi _0+\psi _1\hbox {ln}a , \quad \text {for}\,a\,\lesssim\, 60. \end{aligned}$$

(21)

Fig. 3

Above, the cohort’s average total and baseline hazards are shown for different ERR and TSCE models. On the upper left the hazard curve resulting from the ERR model with and without a step function in the quadratic age is compared. Below the TSCE model with a decaying clonal expansion with age is shown. On the right the average rates for the best fitting ERR and TSCE models found in this study are compared. The 95 % confidence intervals for the observed hazard are estimated according to Schoenberg (1983)

A very similar behavior of the hazard was found in the TSCE model. In this case, a decrease with age in the clonal expansion rate is necessary to get a good description of the observed data. As Fig. 3 shows, the TSCE model with $\gamma$ constant with age fails dramatically to describe the observed rates at old age. The addition of two parameters, $b_\mathrm{a}$ and $a_\mathrm{c}$, reduced the deviance by about 30 points, see Eq. (5). The $b_\mathrm{a}$ parameter represents the decay rate with age of the clonal expansion and results in a decrease of $\gamma$ to half its value in 24 years from an age of $a_\mathrm{c}=48$ years. The same decrease pattern with age was found in the uranium workers of Eldorado (Eidemüller et al. 2012). The value for the base rate $\gamma _{\mathrm{b}}$ is similar, but the decrease rate is faster than in the present study. A similar decay features in analyses using the so-called Two-Mutation Carcinogenesis model (TMC) (Brugmans et al. 2004; Dillen et al. 2011). In this model, however, which differs from the TSCE model in how it deals with the unidentifiability of the parameters, radiation does not act on the clonal expansion. In other TSCE mechanistic studies of radon exposure, although $\gamma$ remains constant with age, similar base rates for $\gamma _{\mathrm{b}}$ were found (see “Comparing TSCE model parameters” below).

The decay of the clonal expansion rate with age in the TSCE model and the leveling of the lung mortality rates at old age may reflect the fact that (stem) cells loose regenerative potential with age leading to a significant net decline of cell pool renewal at old age. In addition, there are indications that there is a strong association between cancer risk and the total number of (stem) cell divisions, the tissue types with more divisions of their self-renewing cells having more lifetime cancer risk (Tomasetti and Vogelstein 2015). In this context, it is not surprising to find a relation between the clonal expansion decay with old age and a leveling of the cancer rates.

Calendar year dependence

In the ERR model, the natural logarithm of baseline hazard depends quadratically on calendar year [see Eq. (17)]. The year center $y_{\rm c}$ used in the present work is 1985, which gives the lowest deviance, and marks the maximum of the hazard with year. Using a quadratic birth year dependence instead of a quadratic calendar year dependence does not improve the fit, resulting in larger values for the deviance. For the TSCE model, a decrease in the clonal expansion with calendar year [see Eq. (4)] results in the lowest deviance. The calendar year dependence is again quadratic with a maximum at $y_{\rm c}=1951$, so effectively spontaneous rates were larger at the beginning of the mining activity and decreased by about $20\,\%$ within the following 40 years. As in the case of the ERR model, a birth year effect cannot be observed in the data.

It is noted, however, that in previous mechanistic studies of radon exposure among uranium miners, a birth year effect was found (Luebeck et al. 1999a; Little et al. 2002; Heidenreich et al. 2004; Dillen et al. 2011; Heidenreich et al. 2012; Eidemüller et al. 2012). Typically the parameter X was a function of the birth year (Luebeck et al. 1999a; Little et al. 2002; Heidenreich et al. 2004, 2012), though in Little et al. (2002); it was the number of susceptible cells $N_{\mathrm{s}}$ which changed explicitly with birth year, while it was the transformation rate $\mu$ in the Eldorato cohort (Eidemüller et al. 2012). Birth year trends are often thought to be associated with smoking and other lifestyle factors. Even when there is explicit smoking information, however, as in the Colorado miners, a residual trend with birth year is still present in the data (Luebeck et al. 1999a). Unfortunately, for the Wismut cohort there is no smoking information for the whole cohort and therefore its effect cannot be evaluated.

Notwithstanding the influence of smoking in this cohort, large background cell clonal expansion rates during the early years of the Wismut company are compatible with dietary deficiencies of the German population during the last years and in the aftermath of World War II. Note that deficient intake of vitamin A and its precursors has been associated with increased risk of lung cancer (Diet, Nutrition and Cancer 1982). In particular, vitamin A plays a vital role as an anti-inflammatory agent ensuring normal epithelial differentiation and growth (Reifen 2002), and its deficient intake has been an argument to justify high background clonal expansion rates in mechanistic studies (Hazelton et al. 2001). Between the maximum of background mortality rates with calendar year, which occurs in 1985 according to the ERR model, and the maximum clonal expansion rates for $\gamma$ in 1951, there are about 30 years. This “delay” reflects the need of a cell to acquire further cancer capabilities and develop to a full tumor (Hanahan and Weinberg 2000, 2011).

Radon exposure response

An effect of radon exposure on the clonal expansion of intermediate cells has been found in most of the mechanistic analyses of uranium miners data using the TSCE model (Luebeck et al. 1999a; Little et al. 2002; Heidenreich et al. 2004, 2012; Eidemüller et al. 2012). The effect of radon on the clonal expansion has been found in other studies of occupational exposure to alpha radiation too, specifically in the Mayak cohort studies of plutonium-induced lung cancer (Jacob et al. 2005, 2007; Zöllner et al. 2015). In all of the studies cited above, the radon exposure rate was found to act on the clonal expansion in a nonlinear way. In the present analysis, a linear-leveling functional form for $\gamma (d_{\mathrm{r}})$ as in Eqs. (6, 7) fitted well the data. Accounting for the effect of silica dust, the radon effect on $\gamma$ decreased, but the functional form remained the same. Figure 4 shows $\gamma$ as a function of radon exposure rate with and without adjustment for silica dust. With adjustment for silica dust, the saturation level decreases substantially while the linear response does not vary largely. The inhalation of silica dust has an effect on the clonal expansion for exposure rates larger than about $d_{\rm c}\simeq 1\,\mathrm{mg}{/}\mathrm{m}^3\,\text{yr}$. This corresponds roughly to an exposure of $0.02\,\mathrm{mg}{/}\mathrm{m}^3$ during a 40-h working week.³

Fig. 4

Clonal expansion rate relative to the baseline rate vs the annual exposure rate in 1951

In some of the uranium miners cohorts, an additional radon effect on initiation was found in the data (Heidenreich et al. 2012; Luebeck et al. 1999a; Little et al. 2002; and Heidenreich et al. 2004). In the present analysis, a $\gamma$ decreasing with attained age is, however, more significant (see Table 1). On the other hand, no effect of radon on transformation has been found, which is consistent with previous radon TSCE model studies. The similarities and disagreements between different analyses using the TSCE model are explored in more detail below after having discussed the risk estimation.

Soluble factors, such as e.g., the transforming growth factor β1 (TGF-β1), produced after alpha particle irradiation have been associated with increased cell proliferation and the bystander effect in vitro (Iyer and Lehnert 2000). It is possible then that the nonlinear radon exposure response in $\gamma (d)$ might be the consequence of a bystander effect. In Eidemüller et al. (2012), a similar radon exposure response was found for the Eldorado uranium workers. It was argued that for low radon exposure rates only a small fraction of the target cells could be hit by an alpha particle and that the exposure response could be transmitted by the hit cells to their neighboring cells via a bystander effect. For higher exposure rates more cells could be exposed, leading to saturation. It was estimated that for exposure rates larger than 20 WLM/year, a significant proportion of target cells could be hit by alpha particles during one cell cycle, leading to saturation. The saturation level obtained in the current work is somewhat larger, but still consistent with this estimate.

Increased clonal growth of initiated cells after radon exposure has been also found in studies with biophysical models. For example, in Balashazy et al. (2009), Madas and Balashazy (2011) and Madas and Vargas (2014) detailed radon exposure patterns for the bronchial epithelium were modeled for radon exposure conditions characteristic of homes and uranium mines. It was found that local deposition of inhaled radon progeny can concentrate in hot spots, leading to locally high doses and a high probability of multiple hits per cell by alpha particles. Thus, the activity deposition could be highly nonlinear, potentially inducing local inflammation effects. Note that increased clonal expansion rates were proposed as an important mechanism for mutation induction, although apart from affecting the growth of mutant clones in the lungs, radon had also an effect on initiation and transformation.

Potential mechanisms in the mediation of the bystander effect are oxidative and inflammatory responses, which are considered to be critical in the occurrence of non-targeted effects after radiation exposure (Sprung et al. 2015). There is growing evidence associating the development of various cancer types to inflammation (Qian and Pollard 2010). Persistent inflammation produces a mutagenic and growth-stimulating microenvironment supporting cancer development (Mantovani et al. 2008). Indeed, the connection of lung squamous cell carcinoma in former uranium miners with high levels of radon exposure and IL-6 promoter variants, which play a central role in many inflammatory and immunological processes, suggests that radon may be leading to cancer through persistent pulmonary inflammation (Leng et al. 2010). In the case of silica exposure, Borm et al (2011) also argue that the most likely mechanism of crystalline silica to support cancer development is an inflammation-driven secondary genotoxicity. Experimental data in rats suggest that persistent inflammation produces oxidants causing injury and the proliferation of lung epithelial cells [see also IARC 1997 Silica Monograph (IARC 1997)]. The existence of a NOEL seems to be related to the level of exposure that impairs alveolar particle clearance which results in inflammatory responses (Borm et al. 2011). It is not surprising then that the radon response does not result in an exposure threshold, since the short half-life of the radon progeny compared to typical lung clearance rates prevents the decay products to be cleared before they cause damage (BEIR 1999).

Risk estimates and effect modification

The magnitude of the lung cancer radon risk can vary substantially with the exposure scenario. In the ERR model, the hazard depends explicitly on the effect modifiers age, time since median exposure and exposure rate. Effect modification in the TSCE model is built-in in the dynamics of the model. To compare the exposure response to radon in both models and to give accurate estimates for the risk, one needs to specify the exposure scenario.

Table 5 shows the quartiles and average values for the lifetime radon exposure and other covariates relevant for the exposure scenario. These quartiles indicate the distribution of the covariates and the values that are best represented in the data. The ERR for different exposure scenarios are shown in Fig. 5. In all these hypothetical scenarios, the person’s birth year is 1930, the silica exposure is set to zero and the exposure is assumed to be homogeneously distributed throughout the years, so that the exposure rate is constant. As shown in the left panel of Fig. 5, radon risk decreases with attained age. Below the 25 % quartile, at attained ages of 50 years and younger, the ERR model yields larger values for $\mathrm{ERR}_{\mathrm{r}}{/}\text{WLM}$ in comparison with the TSCE model. It may be that the increase in $\mathrm{ERR}_{\mathrm{r}}\mathrm{{/}\text{WLM}}$ in the ERR model below the median cancer death age is unrealistic. The $\mathrm{ERR}_{\mathrm{r}}{/}\mathrm{\text{WLM}}$ curve in the TSCE model is considerably less steep and may provide a much more plausible extrapolation from the central cohort values than the ERR/WLM from the ERR model.⁴ Between the attained ages of 50 and 80 years, the ERR and TSCE model risk estimates are closer for large than for small exposure rates.

Fig. 5

Radon ERR versus attained age for different exposure scenarios. Age at median exposure is 26 years and silica exposure is set to zero in all of the curves. In the left panel the gray (or red color) curves correspond to the ERR model, the black (or blue) to the TSCE model. In the right panel the black (or blue) and gray (or red) lines represent the 4 and 8 years duration of radon exposure, respectively, for the TSCE model. Error bars, shown only for the 25 and 100 $\text{WLM}{/}\text{yr}$ rates, are 1$\sigma$ and are based on the uncertainty of the parameters and their correlations

Table 5 Quartiles for covariates of interest

There is an inverse dose rate effect identified by both models (Brenner and Hall 1990). This effect was consistently observed in the analysis of the 11 underground miners studies (Lubin et al. 1994) and was explicitly or implicitly used by the BEIR VI committee in their models.⁵ Nevertheless, the inverse dose rate effect may only be present at relatively high exposure rates, as studies of the Czech and French cohort (Tomasek and Placek 1999; Rogel et al. 2002; Tomasek et al. 2008) and animal studies seem to imply (Cross 1992). Other analyses suggest no exposure rate effect below cumulative exposures of 50 WLM (Lubin et al. 1995). It has been argued that the uncertainties involved in WL and WLM estimations, which are typically large in the initial years of mining, could at least partially produce an apparent inverse dose rate artifact (Lubin et al. 1995). In the left panel of Fig. 5, risk estimates for different radon exposure rates are shown. There is a clear increasing risk per unit exposure trend with decreasing exposures rates in both models. The uncertainty of the risk estimates increase with decreasing exposure rates. Thus, it is difficult to justify in this analysis an exposure rate effect below rates of about 50–25 WLM/year for the TSCE model, which would be in agreement with Tomasek and Placek (1999) and Tomasek et al. (2008). Note, however, that in the ERR model the $1\sigma$ confidence intervals are broader and the exposure rate effect is less pronounced, resulting in a clear exposure rate effect at larger rates. In the present model, the inverse dose rate effect is related to the saturation level in the clonal expansion: as the $\gamma (d_{\mathrm{r}})$ curve flattens, the effectiveness of the radon exposure decreases. High dose rate saturation by multiple track traversals during the cell cycle has been proposed to explain the inverse dose rate effect (Rossi and Kellerer 1986; Brenner et al. 1993), but as already mentioned above the saturation could be mediated by bystander effects as well.

In the right panel of Fig. 5, the effect of duration of radon exposure in the TSCE model is shown. The $\mathrm{ERR}_{\mathrm{r}}{/}\mathrm{WLM}$ given the same exposure rate increases with duration of exposure. This is not very surprising as a protracted duration of exposure gives an extended time for the clonal expansion of initiated cells (Moolgavkar and Luebeck 1990). As in the case of the exposure rate, the duration effect is stronger at larger exposure rates becoming negligible below $50\,\text{WLM}{/}\mathrm{year}$, given the uncertainty in the estimation of the risk. An increased $\mathrm{ERR}_{\mathrm{r}}{/}\mathrm{WLM}$ with duration of radon exposure has been also observed in the pooled study of 11 underground miners cohorts, and in the independent analysis of most of the single studies (Lubin et al. 1994). The ERR model used in the present work, the so-called exposure-age-concentration model, does not depend on duration of exposure.

Estimated values of the cohort average excess relative and absolute risk for the ERR and TSCE models are shown in Table 6. The values given in the table are estimates per 100 WLM of radon exposure. At about the median cancer death age of the cohort, $a\sim 65$ years, the estimated risk values are very similar for both models. For young attained ages, however, the ERR model gives substantially larger risk compared to the TSCE model, whereas at 75 and older, risks from the ERR model are moderately larger.

A limitation of the present study is the lack of complete smoking information. Thus, the effect of smoking on lung cancer risk from radon cannot be evaluated here. However, information on smoking was collected within a nested case–control study where the resulting radon-related lung cancer risks, calculated with and without adjustment for smoking, were very similar (Schnelzer et al. 2010). This appears to be a common pattern in the case of uranium miners cohorts, perhaps because most of the miners smoked. Analysis of the individual and combined data of the Czech, French and German case–control studies confirmed that smoking does not seem to be confounding radon risk (see Leuraud et al. (2011) and references therein).

Table 6 Cohort average excess relative and absolute risk per 100$\text{WLM}$ with attained age for the ERR and TSCE models

Comparison of TSCE model parameters to those of other mechanistic studies

In Table 7, the values of the baseline parameters $\gamma _{\mathrm{b}}$ and $X_{\mathrm{b}}$ obtained in our analysis are compared to those found in other TSCE model studies. Of particular interest is the linear regime for small exposures, and the saturation level (when there is one), which can also be found in Table 7. All studies deal with the effect of occupational alpha radiation exposure on lung cancer. The majority of these analyses comprehend uranium workers and radon exposure, but two studies of the Mayak workers exposed to plutonium were also included. The current study is the only study using the mechanistic TSCE model (or related stochastic models of carcinogenesis) that we are aware of, in which silica exposure is included to adjust for the lung cancer risk after radon exposure.⁶ Mining and the related milling of ores results in occupational exposure to silica dust for most of the different occupations and mines (IARC 1997), and therefore, the parameter estimates in Table 7 except from those of the current study may be liable to adjustment. As discussed below, the missing adjustment for silica or fine dust exposure may partially explain larger saturation levels of $\gamma$ found in radon miner studies. In general, the most recent analysis of a specific cohort corresponds to a longer follow-up and therefore its estimated parameters should be considered more accurate. If the value of a parameter does not vary much between different studies or follow-up periods, it is a strong indication that this parameter may be describing an important general mechanism in lung carcinogenesis. The list of cohorts selected in Table 7 is not exhaustive, given the several cohort analyses that have been left out of this table. Nevertheless, we believe that it represents well the agreements and variability between the results from different TSCE studies. Analyses not included in Table 7 are cited along the text below when relevant.

Table 7 Comparison of TSCE model parameters for different studies

The agreement of the estimated value for the baseline clonal expansion $\gamma _{\mathrm{b}}$ is remarkably good. Whenever smoking information is available, as in the Colorado (Luebeck et al. 1999a) and Mayak workers studies (Jacob et al. 2007; Zöllner et al. 2015), the $\gamma _{\mathrm{b}}$ shown in the table contains the smoking contribution $\gamma _{\mathrm{s}}$ added to the actual baseline rate. It is in the range $\gamma _{\mathrm{s}}=0.04{\text {--}}0.08\ \text{yr}^{-1}$. The high values obtained for the base rates $\gamma _{\mathrm{b}}\sim 0.13{\text {--}}0.16\ \text{yr}^{-1}$ in the rest of studies imply that the smoking contribution is included in the baseline value. This is plausible given that most workers smoked. Note that the $\gamma _{\mathrm{b}}$ of our preferred model depends on attained age and calendar year. However, the effect of these parameters on the value of $\gamma _{\mathrm{b}}$ is small: setting the base rate constant the model yields $\gamma _{\mathrm{b}}=0.14\ \text{yr}^{-1}$.

A saturation level of the exposure response in the clonal expansion has been found in many mechanistic studies on lung cancer and alpha radiation. The saturation level in the current Wismut study, $\gamma _\mathrm{sat}=0.3\text{yr}^{-1}$, is in very good agreement with the result from the pool of the French and German cohort (Heidenreich et al. 2012). The beginning of the follow-up used in the Fr/Ge2012 study for the German cohort is 1955, just when wet drilling was introduced and the annual exposures of radon and silica dropped dramatically. Thus, it is remarkable that the present estimation for $\gamma _\mathrm{sat}$ agrees so well with that for the Fr/Ge2012 after adjusting for silica. Incidentally, the calendar year 1955 marks the beginning of annual dust exposures below $1\,\mathrm{mg}{/}\mathrm{m}^3-\mathrm{year}$, which is essentially the value for the exposure rate $d_{\rm c}$ found in the current study [see Eq. (14) and Table 4].

The saturation level for $\gamma$ in the Mayak workers is larger than that found in Ge2015 and Fr/Ge2012. In the latest analysis, the estimate decreased to $\gamma _\mathrm{sat}=0.44\,\text{yr}^{-1}$ and has a $2\sigma$ region adjacent to our result of $\gamma _\mathrm{sat}\simeq 0.30\pm 0.05\,\text{yr}^{-1}$. Considerably larger values, $\gamma _\mathrm{sat}\sim 1\,\text{yr}^{-1}$, were obtained in the Ca2012 study, the Czech cohort (Heidenreich et al. 2012) and in the Colorado workers analysis performed by Little et al. (2002). These values are about a factor of 3 or 4 larger than the present Ge2015 estimate, but it is possible that after a potential correction for silica (or fine dust) they will be more compatible with our results. Even when a clear saturation level has not been found, a considerable flattening of the $\gamma (d_{\mathrm{r}})$ curve for high exposure rates was obtained (Luebeck et al. 1999a; Eidemüller et al. 2012). In view of these studies, some sort of saturation in the clonal expansion of initiated cells at high exposure rates is evident.

The parameter $\gamma _{\mathrm{r}}$, defined by $\gamma \simeq \gamma _{\mathrm{b}}+\gamma _{\mathrm{r}} d_{\mathrm{r}}+O(d_{\mathrm{r}}^2)$, represents the slope of clonal expansion for low exposure rates. Related to this quantity is $d_\mathrm{l}$, defined as the exposure rate at which the derivative of $\gamma (d_{\mathrm{r}})$ decreases to 14 % of its initial value. Above $d_\mathrm{l}$ the response becomes relatively flat. All studies show a strong relative flattening of the response curve at high exposures rates, even in analyses without an actual saturation level. For the linear-leveling form of $\gamma$ in Eqs. (6) and (7), $\gamma _{\mathrm{r}}=\gamma _{\mathrm{b}}r_2$ and $d_\mathrm{l}\simeq 2r_1{/}r_2$. There is fair agreement between the different estimates for $\gamma _{\mathrm{r}}$, except for the Fr/Ge2012 and the Ca2012 cohorts. These two studies give similar results, roughly an order magnitude larger than the others. As a consequence, their $\gamma (d_{\mathrm{r}})$ curves saturate or flatten considerably at much smaller exposure rates than those of the other studies. Common in the Fr/Ge2012 and Ca2012 analyses is that the average exposure is about $100\,{\text{WLM}}$ or less, i.e., considerably smaller than in the other cohorts. It is possible that the large $\gamma _{\mathrm{r}}$ values obtained in these two studies represent a stronger response at low exposures rates $d_\mathrm{l}=10{\text {--}}15\,\text{WLM}{/}\text{yr}$, which analyses of cohorts with more statistics concentrated at higher exposures rates fail to reproduce. This observation agrees with an analysis performed in the present study (not shown here) by excluding workers in the cohort by different upper bounds on the total cumulative exposure, which gave larger values for $\gamma _{\mathrm{r}}$ as one reduces the upper limit. Larger risks at low exposures have been observed in the Wismut cohort (Kreuzer et al. 2015) and in other uranium miners analyses (e.g., see Tomasek et al. 2008).

In the case of the workers exposed to plutonium, the estimated $\gamma _{\mathrm{r}}$ agrees very well with the results of the present study, given the uncertainty levels. Note that for this comparison, a conversion factor of 8.9 mSv per WLM of radon exposure was used. This value was derived from a stochastic airway generation model (Winkler-Heil and Hofman 2007), and it is between the $5.7\ \mathrm{mSv}{/}\text{WLM}$ used in UNSCEAR reports (UNSCEAR 2000) and a larger value of $21.1\,\mathrm{mSv}{/}\text{WLM}$, derived in more recent calculations with new dosimetric models (ICRP 2010).

The parameter $X_{\mathrm{b}}$, the product of initiation and transformation rate, shows a larger variation between the studies than the other parameters discussed above. This is expected since the clonal expansion rate $\gamma$ is the parameter that can be determined with highest precision in the TSCE model. Nevertheless, the values obtained in the other studies shown in Table 7 indicate that the value estimated here, $X_{\mathrm{b}}\sim 8\times 10^{-8}\text{yr}^{-2}$, is well within one order of magnitude of the estimated value in the latest follow-up.

Conclusion

Lung cancer mortality in the Wismut cohort was analyzed with the mechanistic TSCE model, and the results were compared to those obtained with the ERR model. Results for different exposure scenarios are shown in Fig. 5, and cohort averaged risk estimates are presented in Table 6. In all models, risk decreases substantially with increasing age and the risk per unit of exposure with increasing exposure rate. However, due to the complex interplay between the different exposure modifiers, the results show a significant model uncertainty. For large exposure rates of about 100 WLM/yr, the excess relative risk is similar for the TSCE and ERR models, while for smaller rates the TSCE model predicts higher risk, as shown in the left panel of Fig. 5. For the median age of cancer death, about 65 years, the cohort average risk of both types of models is similar; however, the ERR models predict a stronger dependence of risk on attained age, in particular for smaller ages (see Table 6).

The TSCE model has a very significant exposure response in the clonal expansion $\gamma$. The response has a linear-leveling form with a saturation level at about $100\text{WLM}{/}\mathrm{yr}$. The nonlinear exposure rate response in $\gamma$ seems to be a very solid result. A similar response was found in the majority of TSCE studies of lung cancer among miners exposed to radon and in studies of workers exposed to other sources of alpha radiation, such as the Mayak workers after plutonium exposure. Such response could be the consequence of a bystander effect (Eidemüller et al. 2012). A detailed comparison of the results of the different TSCE studies reveals an extraordinary agreement of the baseline clonal expansion rate of $\gamma _{\mathrm{b}}\sim 0.13{\text {--}}0.16\text{yr}^{-1}$. In addition, the saturation level reached by the clonal expansion rate with large exposure rates is very consistent in the different TSCE studies. The linear response for small exposure rates, $\gamma _{\mathrm{r}}$, shows more variation. As discussed, this could be a consequence of different exposure levels of the studies.

The increase in clonal expansion rates may be due to permanent low-grade inflammation by exposure to radon and silica (or fine dust) during an extensive period of time, which in turn may be the major cause of increased lung cancer risk for the uranium miners. Persistent inflammation may assist the clonal growth of intermediate cells by supplying growth and survival factors to their microenvironment, which sustain proliferative signals and limit cell death, respectively. This is considered to be an “enabling characteristic” that allows cells to acquire the functional capabilities to become cancer cells (Hanahan and Weinberg 2011). Noteworthy is that the Scientific and Regulatory Policy Committee (SRPC) recognizes cell proliferation as crucial in the mode of action for many carcinogens and calls for more efforts in the interpretation and use of cell proliferation data in the assessment of cancer risk (Wood et al. 2015).

Transfer of risk from miners to domestic exposure situations is a very complex task and beyond the scope of the current work (ICRP 2010); it is, however, interesting to look at risk modifiers at low exposures typical in the domestic environment. An important issue for risk assessment and lifetime risk estimates is the potential dependence of the ERR on attained age or time since exposure. Miner studies have been performed that only included miners with low radon exposure, low radon exposure rates and good assessment of dosimetry. In Tomasek et al. (2008), a decrease in risk with time since exposure and age at exposure has been observed, whereas in Kreuzer et al. (2015) no significant dependence of risk on time since exposure was found due to lack of statistical power. One can investigate the age dependence of risk with a mechanistic TSCE model for a typical domestic exposure. For example, using a constant exposure rate of 0.44 WLM/year starting at age 40 until age 65 with a total of 11 WLM at age 65 (ICRP 2010), the TSCE model predicts a decrease in ERR per dose with attained age of about 25 % per decade. This decrease is a consequence of radiation acting on the clonal expansion rate. Although the value of 25 % may depend on the exposure scenario, the decrease in ERR with age is a general characteristic of the radiation action.

The TSCE model is the most often used biologically based model. It allows to capture the complex dynamics of cancer development despite its limited number of parameters and provides robust risk estimates. The consistency of TSCE parameters across different studies indicates that the dynamics of cancer development and the exposure response are captured in a realistic way. Remarkably, the application of the TSCE model for plutonium exposure in the Mayak workers (Jacob et al. 2007; Zöllner et al. 2015) results in a similar exposure response as in the radon studies. This suggests similar mechanistic effects of both types of alpha particles being active. More complex stochastic models adding an additional step to the TSCE model have been used to describe the radon exposure response in uranium miner studies (Little et al. 2002) and in the Mayak workers (Zöllner et al. 2015), improving the goodness of fit compared to that obtained with the TSCE model. In neither of these cases there was evidence that the addition of a step results in radon acting differently to the way it does in the TSCE model. With available information on lung cancer subtypes, it might be possible to develop more specific lung cancer models, e.g., using information from TCGA analyses (Network The Cancer Genome Atlas Research 2014, 2012). In this case, different lung cancer subtypes would develop through different pathways, each pathway having different baseline parameters and susceptibility to radiation (Kaiser et al. 2014). The current work should provide a basis for such possible future developments.