Peristaltic flow of Phan-Thien-Tanner fluid: effects of peripheral layer and electro-osmotic force

Abstract

The two-layered electro-osmotic peristaltic flow of Phan-Thien-Tanner (PTT) fluid in a flexible cylindrical tube is analyzed. The core (inner) layer fluid satisfies the constitutive equation of PTT fluid model and the peripheral (outer) layer is characterized as a Newtonian fluid. For each region, the two-dimensional conservation equations for mass and momentum with electro-osmotic body forces are transformed from the fixed frame to the moving frame of reference. These equations are further simplified by invoking the constraints of long wavelength and low Reynolds number. Closed-form expressions for velocity and stream function are derived and then employed to investigate the pressure variations, trapping, interface region, and reflux for a variety of the involved parameters. The analysis reveals that the reflux and trapping can be restrained by appropriately tuning the electro-kinetic slip parameter and Deborah number. Further, the pumping efficacy can also be improved by adjusting the rheological and the electro-kinetic effects. These results may be helpful for improving the performance of the microfluidic peristaltic pump.

Introduction

Peristaltic mechanism is involved in manufacturing of several devices of modern era. Few examples are: heart-lung machine, dialysis machine, diabetic pumps, devices used in food manufacturing, paper industries and pharmaceutical productions. Existing literature indicates that numerous theoretical approaches have been carried out in the past to understand the physics of this mechanism (Shapiro et al. 1969; Raju and Devanathan 1972; Siddiqui and Schwarz 1994; Rao and Mishra 2004; Tripathi 2011; Ali and Hayat 2008; Hayat et al. 2009; Ali et al. 2010; Hayat and Ali 2006; Hayat et al. 2017a, 2017b; Mekheimer 2004). The fundamental focus of such studies was to investigate the various aspects of pumping, trapping, and reflux phenomena. Apart from that, attempts have also been made to optimize the wave shape of peristaltic pumping (Walker and Shelley 2010), to include the solid mechanics of the tube wall in peristaltic wall pumping of a viscous fluid (Takagi and Balmforth 2011a) and to derive a model of peristaltic pumping of rigid objects suspended in a fluid-filled elastic tube (Takagi and Balmforth 2011b).

In some physiological ducts such as the esophagus, ureter, and small blood vessels, it is observed that the structure of the wall pumping the fluid is coated with a fluid of different characteristics than the fluid being pumped out. In order to properly recognize the influence of coated fluid on transport properties, the single-fluid model should be extended to a two-fluid model by considering a different viscosity fluid in the peripheral layer. Motivated by this fact, Shukla et al. (1980) probed the effects of peripheral layer viscosity on the peristaltic transport in both channel and axisymmetric geometries for a presumed interface shape. Brasseur et al. (1987) revised the analysis of Shukla et al. (1980) for a case when interface is determined as a part of the solution. Following Brasseur et al. (1987), Rao and Usha (1995) examined the pumping of two immiscible Newtonian fluids in circular tube geometry and emphasized the trapping under co-pumping conditions and the detachments of the trapped bolus from the centerline. The simplified model of Shukla et al. (1980) was also extended by Srivastava and Saxena (1995) by taking the Casson fluid in the center region of a cylindrical tube. Misra and Pandey (1999) followed the approach of Brasseur et al. (1987) and presented the analytical results for peristaltic flow of power-law fluid in a channel with a peripheral layer. The effects of a porous medium in the model Brasseur et al. (1987) were incorporated by Mishra and Rao (2005). Vajravelu et al. (2006) utilized the Herschel-Bulkley constitutive equation to characterize the fluid in the core region and highlighted the influence of yield stress in peristaltic transport of two immiscible fluids through a channel. The analysis of Rao and Usha (1995) was extended by Vajravelu et al. (2009) to the flow of Casson fluid in the core region and a viscous fluid in the peripheral region in a tube with permeable wall. Peristaltic flow of the Bigham fluid in contact with the viscous fluid was analyzed by Narahari and Sreenadh (2010) and Prabakaran et al. (2013). More recently, Kavitha et al. (2017) investigated the peristaltic flow of the Jeffery fluid in an inclined channel with a peripheral layer and reported the variations in the shape of the interface with respect to the Jeffery parameter. It is important to mention that all the studies mentioned above are valid under the constraints of the long wavelength and low Reynolds number. An important aspect highlighted in these studies is that for prescribed wall movement, a larger viscosity fluid in the peripheral layer dramatically increases the pumped volume flow rate compared with the single-fluid pump for a fixed pressure head. Thus, the presence of a greater viscosity peripheral layer could lead to amplification in the peristaltic flow. This observation gives further motivation to identify alternative means that could result in the augmentation of peristaltic flow. One such idea, which is precisely the augmentation of the peristaltic flow through electro-osmotic forces, was presented by Chakraborty (2006). The model investigated by Chakraborty (2006) was a singled-layered peristaltic flow model. Several attempts have been made in the literature to extend this model. These attempts are briefly reviewed below. Jayavel et al. (2019) investigated the flow of the Williamson fluid in a tapered channel driven by electro-osmosis and peristalsis. Unsteady electro-osmotic peristaltic flow in the presence of transverse magnetic field has been simulated by Tripathi et al. (2016). Goswami et al. (2016) explored the simultaneous effects of a thin peripheral layer and electro-osmotic body force on the peristaltic flow of power-law fluid through a circular tube. The analysis of Goswami et al. (2016) is a direct extension of the work by Usha and Rao (1995). Tripathi et al. (2018a) investigated the electro-osmotic peristaltic transport of an aqueous nano-fluid in a wavy micro-channel with Joule heating and buoyancy effects. The simultaneous effects of buoyancy, peristaltic motion, and electro-osmosis on an unsteady flow of a Newtonian fluid in a micro-channel have been examined by Tripathi et al. (2017). The flow of Jeffrey fluid in an asymmetric channel induced by electro-osmosis and peristaltic activity has been investigated by Tripathi et al. (2018b). Narla and Tripathi (2019) discussed the two-layer electro-osmotic transport in a curved channel by considering the viscous fluid in both regions. Electro-osmotic peristaltic flow of a Jeffrey fluid model in a tapered channel induced by asymmetric zeta potential at the walls of the channel has been analyzed by Narla et al. (2018). Chaube et al. (2018) investigated the inertia-free peristaltic flow of a power-law aqueous solution in a mirco-channel under the influence of electro-kinetic body force. Jayavel et al. (2019) examined the peristaltic transport of pseudoplastic aqueous nano-liquids in a micro-channel under the effects of an electric field. The pseudoplastic aqueous liquid has been modeled by tangent hyperbolic equation. It is important to mention that several theoretical studies are also available in the literature on electro-osmotic flow of single and two-layered fluids through a non-deformable channel or tube. In this regard, Afonso et al. (2009) analytically examined the combined effects of pressure and electro-kinetic force by applying the Debye-Huckel assumption. The electro-osmotic flow on nano-scale was discussed by Zhao and Yang (2013), in which they theoretically analyzed electro-kinetic influences on a non-Newtonian power-law fluid through a cylindrical micro-channel. Zhao et al. (2013) examined key properties of a non-steady flow of Oldroyd-B fluid in a capillary under the effect of electro-kinetic force. Afonso et al. (2013) analytically tackled the two-fluid electro-kinetic flow of viscoelastic liquid in a cylindrical tube. Ferras et al. (2014) probed electro-kinetic effects in the annular flow of the viscoelastic fluid and provided both numerical and analytical illustration of the solution of the problem.

Motivated by above attempts, our objective is to analyze the electro-osmotic peristaltic flow of a two-fluid system in which the outer Newtonian core surrounds a non-Newtonian core characterized by the Phan-Thien-Tanner (PTT) model. The PTT model exhibits three non-Newtonian effects, namely, shear-thinning, viscoelastic, and time relaxation effects and hence much advantageous than the power-law model. It is also an established fact that bio-fluid such as blood, chyme, and spermatic fluid exhibit both shear-thinning and viscoelastic properties and hence can better be characterized by PTT equation instead of power-law equation. Similarly, the use of a PTT model shall also make the applicability of the present analysis to the transport of polymeric fluid in the industry by means of electro-osmotic peristaltic pumps. The usage of the PTT model in modeling of several flows can be seen through the refs (Oliveira and Pinho 1999; Hayat et al. 2010; Ferras et al. 2012). The remaining part of the paper is organized as follows.“Constitutive equations” section describes the constitutive equation of PTT fluid model. The mathematical formulation and solution of the flow problem are described in the “Problem formulation and its solution” section. The graphical interpretation of the computational results is provided in the “Results and discussion” section. The present study is concluded in the “Deductions” section.

Constitutive equations

The constitutive equations for the Phan-Thien-Tanner (PTT) fluid model are (Oliveira and Pinho 1999; Hayat et al. 2010; Ferras et al. 2012):

$$ \Big\{{\displaystyle \begin{array}{l}\mathbf{T}=-p\mathbf{I}+\boldsymbol{\uptau} \\ {}f\left( tr\left(\boldsymbol{\uptau} \right)\right)\boldsymbol{\uptau} +\kappa {\boldsymbol{\uptau}}^{\nabla }=2\mu \mathbf{D}\\ {}{\boldsymbol{\uptau}}^{\nabla }=\frac{\partial \boldsymbol{\uptau}}{\partial t}+\left(\mathbf{u}.\nabla \right)\boldsymbol{\uptau} -\boldsymbol{\uptau} {\left(\nabla \mathbf{u}\right)}^{\mathrm{T}}-\left(\nabla \mathbf{u}\right)\boldsymbol{\uptau} \end{array}} $$

(1)

where p is the pressure, κ is the relaxation time, τ is an extra-stress tensor, D is the deformation rate tensor, tr is the trace, I is the identity tensor, τ^∇ is the Oldroyd’s upper-convected derivative, T is the Cauchy stress tensor, and μ is the dynamic viscosity. The function f is defined as:

$$ \mathrm{Linearized}\ \mathrm{PTT}\ \left(\mathrm{LPTT}\right):\kern0.5em f\left(\mathrm{tr}\left(\boldsymbol{\uptau} \right)\right)\boldsymbol{\uptau} =1+\frac{\varepsilon \kappa}{\mu}\left(\mathrm{tr}\left(\boldsymbol{\uptau} \right)\right), $$

(2)

$$ \mathrm{Exponential}\ \mathrm{PTT}\ \left(\mathrm{EPTT}\right):\kern0.5em f\left(\mathrm{tr}\left(\boldsymbol{\uptau} \right)\right)\boldsymbol{\uptau} =\exp \left(\frac{\varepsilon \kappa}{\mu}\left(\mathrm{tr}\left(\boldsymbol{\uptau} \right)\right)\right). $$

(3)

Problem formulation and its solution

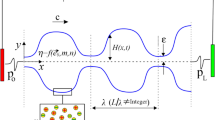
The physical sketch of the problem under consideration is shown in Fig. 1. It describes the flow of a bio-fluid due to combined action of the electro-osmotic force and the peristaltic movement of the tube wall. Within the tube, two different regions can be identified; the region near to the wall of the tube is the peripheral (outer) region and the central core is the core (inner) region. The charged surface of the tube is neutralized through equal and opposite ions in the polar liquid inside the tube. The charged surface attracts the counter-ions in the polar liquid to form a thin layer adjacent to it. Thus, this layer of immobile counter-ions is designated as a stern layer. A thicker layer of moving counter-ions develops adjacent to the stern layer. The combination of the aforementioned two layers is known as the electric double layer (EDL). Now, when a DC potential difference is applied along the axis at the inlet and outlet, an electric field is produced that exerts a body force on the opposite ions of the EDL, and as a result of which, EDL moves along the channel dragging the neutral core. Next, our aim is to compute the flow fluid generated by both electro-kinetic body force and peristaltic movement of the wall.

Fig. 1

Geometry of the flow problem

The basic equations necessary to formulate the flow problem are:

$$ \mathrm{Momentum}\ \mathrm{equation}:\kern0.5em \rho \left(\frac{Du}{Dt}\right)=\nabla .\mathbf{T}+{\mathbf{F}}_e, $$

(4)

$$ \mathrm{Continuity}\ \mathrm{equation}:\kern0.5em \left(\frac{\partial \rho }{\partial t}\right)+\nabla .\left(\rho u\right)=0, $$

(5)

where ρ is the density, F_e is the electro-kinetic body force, and D/Dt is the material derivative. The inner core region (0 ≤ r ≤ R₁(z, t)) is filled with a fluid characterized by the PTT model for which the stress tensor is given by Eqs. (1)–(3).

In the peripheral region (R₁(z, t) ≤ r ≤ R₀(z, t)), the stress tensor is defined as:

$$ \mathbf{T}=-p\mathbf{I}+\boldsymbol{\uptau}, $$

where

$$ \boldsymbol{\uptau} =2{\mu}_2\mathbf{D}. $$

(6)

In the above relation, R₁ is the function defining the interface between inner and outer regions, μ₁ and μ₂ are the viscosities of the fluids in the inner and outer regions, respectively, and R₀ is the radius of the conduit. The velocity field for axisymmetric incompressible flow under investigation is defined as:

$$ \mathbf{u}=\left[u\left(r,z,t\right),0,w\left(r,z,t\right)\right]. $$

(7)

Invoking Eq. (7) into Eqs. (4) and (5), one gets

$$ \frac{1}{r}\frac{\partial (ru)}{\partial r}+\frac{\partial w}{\partial z}=0, $$

(8)

$$ \kern0.50em \rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}\right)=-\frac{\partial p}{\partial r}+\left[\frac{1}{r}\frac{\partial \left(r{\tau}_{rr}\right)}{\partial r}+\frac{\partial {\tau}_{rz}}{\partial z}-\frac{\tau_{\theta \theta}}{r}\right], $$

(9)

$$ \rho \left(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right)=-\frac{\partial p}{\partial z}+\left[\frac{1}{r}\frac{\partial \left(r{\tau}_{rz}\right)}{\partial r}+\frac{\partial {\tau}_{zz}}{\partial z}\right]+{F}_e. $$

(10)

When the system is connected to the external electric field E_z, the fluid experiences a body force given by Hunter 1981:

$$ \kern0.50em {F}_e={\rho}_e{E}_z, $$

(11)

where ρ_e stands for the total ionic concentration and is the sum of ionic charge concentrations for core(ρ_ec) and peripheral(ρ_eN)regions, respectively. In a frame (r, z) which is fixed relative to the peristaltic wave, the flow phenomenon is unsteady and wall deformation is a function of time. However, the flow become steady and wall appears stationary in a frame moving with wave speed U. This frame designated as $\left(\overline{r},\overline{z}\right)$ is known as the wave frame. The conversion between both frames is achieved through the transformations:

$$ \overline{r}\to r,\overline{p}\to p,\overline{u}\to u,\overline{z}\to z- Ut,\overline{w}\to w-U. $$

Using the above transformations, Eqs. (8)–(10) and stress components for the both regions take the following form:

$$ \frac{1}{\overline{r}}\frac{\partial \left(\overline{r}\overline{u}\right)}{\partial \overline{r}}+\frac{\partial \overline{w}}{\partial \overline{z}}=0, $$

(12)

$$ \rho \left(\overline{u}\frac{\partial \overline{w}}{\partial \overline{r}}+\overline{w}\frac{\partial \overline{w}}{\partial \overline{z}}\right)=-\frac{\partial \overline{p}}{\partial \overline{z}}+\left[\frac{1}{\overline{r}}\frac{\partial \left(\overline{r}{\overline{\tau}}_{rr}\right)}{\partial \overline{r}}+\frac{\partial {\overline{\tau}}_{zz}}{\partial \overline{z}}-\frac{{\overline{\tau}}_{\theta \theta}}{\overline{r}}\right], $$

(13)

$$ \rho \left(\overline{u}\frac{\partial \overline{w}}{\partial \overline{r}}+\overline{w}\frac{\partial \overline{w}}{\partial \overline{z}}\right)=-\frac{\partial \overline{p}}{\partial \overline{z}}+\left[\frac{1}{\overline{r}}\frac{\partial \left(\overline{r}{\overline{\tau}}_{rr}\right)}{\partial \overline{r}}+\frac{\partial {\overline{\tau}}_{rz}}{\partial \overline{z}}\right]+{F}_e. $$

(14)

Stress equations for the core region:

$$ f\left( tr\left(\overline{\tau}\right)\right){\overline{\tau}}_{rr}+\kappa \left\{\left(\overline{u}\frac{\partial }{\partial \overline{r}}+\overline{w}\frac{\partial }{\partial \overline{z}}\right){\overline{\tau}}_{rr}-2\left(\frac{\partial \overline{u}}{\partial \overline{r}}{\overline{\tau}}_{rr}+\frac{\partial \overline{u}}{\partial \overline{z}}{\overline{\tau}}_{rz}\right)\right\}=2{\mu}_1\frac{\partial \overline{u}}{\partial \overline{r}}, $$

(15)

$$ f\left( tr\left(\overline{\tau}\right)\right){\overline{\tau}}_{r\theta}+\kappa \left\{\left(\overline{u}\frac{\partial }{\partial \overline{r}}+\overline{w}\frac{\partial }{\partial \overline{z}}\right){\overline{\tau}}_{r\theta}-\frac{\overline{u}}{\overline{r}}{\overline{\tau}}_{r\theta}-\frac{\partial \overline{u}}{\partial \overline{r}}{\overline{\tau}}_{r\theta}-\frac{\partial \overline{u}}{\partial \overline{z}}{\overline{\tau}}_{z\theta}\right\}=0, $$

(16)

$$ f\left( tr\left(\tau \right)\right){\overline{\tau}}_{rz}+\kappa \left\{\left(\overline{u}\frac{\partial }{\partial \overline{r}}+\overline{w}\frac{\partial }{\partial \overline{z}}\right){\overline{\tau}}_{rz}-\frac{\partial \overline{w}}{\partial \overline{r}}{\overline{\tau}}_{rr}-\left(\frac{\partial \overline{w}}{\partial \overline{z}}+\frac{\partial \overline{u}}{\partial \overline{r}}\right){\overline{\tau}}_{rz}-\frac{\partial \overline{u}}{\partial \overline{z}}{\overline{\tau}}_{zz}\right\}={\mu}_1\left(\frac{\partial \overline{u}}{\partial \overline{z}}+\frac{\partial \overline{w}}{\partial \overline{r}}\right), $$

(17)

$$ f\left( tr\left(\overline{\tau}\right)\right){\overline{\tau}}_{\theta \theta}+\kappa \left\{\left(\overline{u}\frac{\partial }{\partial \overline{r}}+\overline{w}\frac{\partial }{\partial \overline{z}}\right){\overline{\tau}}_{\theta \theta}-2\frac{\overline{u}}{\overline{r}}{\overline{\tau}}_{\theta \theta}\right\}=2{\mu}_1\frac{\overline{u}}{\overline{r}}, $$

(18)

$$ f\left( tr\left(\overline{\tau}\right)\right){\overline{\tau}}_{\theta z}+\kappa \left\{\left(\overline{u}\frac{\partial }{\partial \overline{r}}+\overline{w}\frac{\partial }{\partial \overline{z}}\right){\overline{\tau}}_{\theta z}-\frac{\overline{u}}{\overline{r}}{\overline{\tau}}_{\theta z}-\frac{\partial \overline{w}}{\partial \overline{r}}{\overline{\tau}}_{\theta r}-\frac{\partial \overline{w}}{\partial \overline{z}}{\overline{\tau}}_{\theta z}\right\}=0, $$

(19)

$$ f\left( tr\left(\overline{\tau}\right)\right){\overline{\tau}}_{zz}+\kappa \left\{\left(\overline{u}\frac{\partial }{\partial \overline{r}}+\overline{w}\frac{\partial }{\partial \overline{z}}\right){\overline{\tau}}_{zz}-2\frac{\partial \overline{w}}{\partial \overline{r}}{\overline{\tau}}_{rz}-2\frac{\partial \overline{w}}{\partial \overline{z}}{\overline{\tau}}_{zz}\right\}=2{\mu}_1\frac{\partial \overline{w}}{\partial \overline{z}}. $$

(20)

Stress equations for the peripheral region:

$$ {\overline{\tau}}_{r r}=2{\mu}_2\frac{\partial \overline{u}}{\partial \overline{r}},\kern0.5em {\overline{\tau}}_{r z}={\overline{\tau}}_{z r}={\mu}_2\left(\frac{\partial \overline{u}}{\partial \overline{z}}+\frac{\partial \overline{w}}{\partial \overline{r}}\right),\kern0.5em {\overline{\tau}}_{\theta \theta}={\mu}_2\frac{\overline{u}}{\overline{r}},\kern0.5em {\overline{\tau}}_{z z}=2{\mu}_2\frac{\partial \overline{w}}{\partial \overline{z}},{\overline{\tau}}_{r\theta}={\overline{\tau}}_{\theta r}={\overline{\tau}}_{\theta z}={\overline{\tau}}_{z\theta}=0. $$

(21)

Employing the dimensionless variables Goswami et al. (2016):

$$ \left.{\displaystyle \begin{array}{l}{r}^{\ast }=\frac{\overline{r}}{r_0},{z}^{\ast }=\frac{\delta\ \overline{z}}{r_0},{u}^{\ast }=\frac{\overline{u}}{\left(\delta\ U\right)},{w}^{\ast }=\frac{\overline{w}}{U},{t}^{\ast }=\frac{\delta\ U}{r_0}\overline{t},\\ {}{p}^{\ast }=\frac{\delta\ {r}_0}{\upmu_1U}\overline{p},\mathit{\operatorname{Re}}=\frac{\rho_cU{r}_0}{\upmu_1},{\tau}^{\ast }=\frac{r_0}{\upmu_1U}\overline{\tau},{F_e}^{\ast }=\frac{-{F}_e{r}_0^2}{\varepsilon_N\xi {E}_z}, De=\frac{\kappa U}{r_0}.\end{array}}\right\} $$

(22)

Equations (12)–(21)after dropping the bars reduce to:

Core region:

$$ \frac{1}{r}\frac{\partial \left(r{u}_c\right)}{\partial r}+\frac{\partial {w}_c}{\partial z}=0, $$

(23)

$$ {\delta}^2\left[\delta Re\left({u}_c\frac{\partial {u}_c}{\partial r}+{w}_c\frac{\partial {u}_c}{\partial z}\right)\right]=-\frac{\partial p}{\partial r}+\delta \left[\left(\frac{1}{r}\frac{\partial \left(r\ {\tau}_{rr}\right)}{\partial r}+\frac{\delta \partial {\tau}_{rz}}{\partial z}\right)-\frac{\tau_{\theta \theta}}{r}\right], $$

(24)

$$ {\delta}^2\left[\delta Re\left({u}_c\frac{\partial {w}_c}{\partial r}+{w}_c\frac{\partial {w}_c}{\partial z}\right)\right]=-\frac{\partial p}{\partial z}+\left[\left(\frac{1}{r}\frac{\partial \left(r\ {\tau}_{rz}\right)}{\partial r}\right)\right]+\frac{\epsilon_N{\upmu}_r{U}_E\kern0.50em }{\epsilon_c}{\rho}_{ec}, $$

(25)

$$ f\left( tr\left(\tau \right)\right){\mu}_1{\tau}_{rr}+ De\left\{\begin{array}{l}\left(\delta {u}_c\frac{\partial }{\partial r}+\delta {w}_c\frac{\partial }{\partial z}\right){\mu}_1{\tau}_{rr}-\\ {}2\left[\delta \frac{\partial }{\partial r}\left({u}_c\right){\mu}_1{\tau}_{rr}+{\delta}^2\frac{\partial }{\partial z}\left({u}_c\right){\mu}_1{\tau}_{rz}\right]\end{array}\right\}=2{\mu}_1\delta \frac{\partial }{\partial r}\left({u}_c\right), $$

(26)

$$ f\left( tr\left(\tau \right)\right){\mu}_1{\tau}_{rz}+ De\left\{\begin{array}{l}\left(\delta {u}_c\frac{\partial }{\partial r}+\delta {w}_c\frac{\partial }{\partial z}\right){\mu}_1{\tau}_{rz}-{\mu}_1\frac{\partial {w}_c}{\partial r}{\tau}_{rr}\\ {}-\left(\delta \frac{\partial {w}_c}{\partial z}+\delta \frac{\partial {u}_c}{\partial r}\right){\mu}_1{\tau}_{rz}-\delta {\mu}_1\frac{\partial {u}_c}{\partial z}{\tau}_{zz}\end{array}\right\}={\mu}_1\left({\delta}^2\frac{\partial {u}_c}{\partial z}+\frac{\partial {w}_c}{\partial r}\right), $$

(27)

$$ f\left( tr\left(\tau \right)\right){\mu}_1{\tau}_{r\theta}+ De\left\{\begin{array}{l}\left(\delta {u}_c\frac{\partial }{\partial r}+\delta {w}_c\frac{\partial }{\partial z}\right){\mu}_1{\tau}_{r\theta}-\delta \left({u}_c\right){\mu}_1{\tau}_{r\theta}-\\ {}\delta {u}_c\frac{\partial {u}_c}{\partial r}{\tau}_{r\theta}-{\delta}^3{u}_c\frac{\partial {u}_c}{\partial z}{\mu}_1{\tau}_{z\theta}\end{array}\right\}=0, $$

(28)

$$ f\left( tr\left(\tau \right)\right){\mu}_1{\tau}_{\theta \theta}+ De\left\{\left(\delta {u}_c\frac{\partial }{\partial r}+\delta {w}_c\frac{\partial }{\partial z}\right){\mu}_1{\tau}_{\theta \theta}-2\delta \left({u}_cU\right){\mu}_1{\tau}_{\theta \theta}\right\}=2{\mu}_1\delta {u}_c, $$

(29)

$$ f\left( tr\left(\tau \right)\right){\mu}_1{\tau}_{zz}+ De\left\{\begin{array}{l}\left(\delta {u}_c\frac{\partial }{\partial r}+\delta {w}_c\frac{\partial }{\partial z}\right){\mu}_1{\tau}_{zz}-2{\mu}_1{\tau}_{rz}\left(\frac{\partial {w}_c}{\partial r}\right)\\ {}-2{\mu}_1\delta {\tau}_{zz}\left(\frac{\partial {w}_c}{\partial z}\right)\end{array}\right\}={\mu}_1\delta \frac{\partial {w}_c}{\partial z}. $$

(30)

$$ \Big\{{\displaystyle \begin{array}{l}\mathrm{Linearized}\ \mathrm{PTT}:f\left(\mathrm{tr}\left(\tau \right)\right)=1+\varepsilon De\left({\tau}_{zz}\right),\\ {}\mathrm{Exponential}\ \mathrm{PTT}:f\left(\mathrm{tr}\left(\tau \right)\right)=\exp \left(\varepsilon De\left({\tau}_{zz}\right)\right).\end{array}} $$

(31)

Peripheral region:

$$ \frac{1}{r}\frac{\partial \left(r{u}_N\right)}{\partial r}+\frac{\partial {w}_N}{\partial z}=0, $$

(32)

$$ {\delta}^2\left[\delta Re\left({u}_N\frac{\partial {u}_N}{\partial r}+{w}_N\frac{\partial {u}_N}{\partial z}\right)\right]=-\frac{\partial p}{\partial r}+\delta \left[\left(\frac{1}{r}\frac{\partial \left(r\ {\tau}_{rr}\right)}{\partial r}+\frac{\delta \partial {\tau}_{rz}}{\partial z}\right)-\frac{\tau_{\theta \theta}}{r}\right], $$

(33)

$$ {\delta}^2\left[\delta Re\left({u}_N\frac{\partial {w}_N}{\partial r}+{w}_N\frac{\partial {w}_N}{\partial z}\right)\right]=-\frac{\partial p}{\partial z}+\left[\left(\frac{1}{r}\frac{\partial \left(r\ {\tau}_{rz}\right)}{\partial r}\right)\right]+\frac{\epsilon_N{\upmu}_r{U}_E\kern0.50em }{\epsilon_c}{\rho}_{ec}, $$

(34)

$$ {\tau}_{r r}=2{\mu}_r\delta \frac{\partial {u}_N}{\partial r},\kern0.5em {\tau}_{r z}={\tau}_{z r}={\mu}_r\left({\delta}^2\frac{\partial {u}_N}{\partial z}+\frac{\partial {w}_N}{\partial r}\right),\kern0.5em {\tau}_{\theta \theta}={\mu}_r\delta \frac{u_N}{r},\kern0.5em {\tau}_{z z}=2{\mu}_r\delta \frac{\partial {w}_N}{\partial z},{\tau}_{r\theta}={\tau}_{\theta r}={\tau}_{\theta z}={\tau}_{z\theta}=0. $$

(35)

The subscripts c and N are used to differentiate between the core and peripheral regions. The parameter µ_r = µ₂/µ₁ is the viscosity ratio between the two regions. The parameter De is the Deborah number and is a measure of the elasticity in the fluid. On the other hand, the parameter ϵ is the measure of the extensional property of the fluid. It is evident that variations of De have stronger impact than similar variations of ϵ because of the manner in which both parameters appear in the analysis. The combined effects of ϵ and De can be felt via a single parameter b = ε^1/2 De which gives a measure of both elastic and extensional properties of the fluid. At this stage, we make use of long wavelength (δ ≪ 1) and low Reynolds number (Re ≪ 1) constraints to get the following equations for each region.

Core region:

$$ \Big\{{\displaystyle \begin{array}{l}0=-\frac{\partial p}{\partial z}+\left[\left(\frac{1}{r}\frac{\partial \left(r\ {\tau}_{rz}\right)}{\partial r}\right)\right]+\frac{\upmu_r{U}_E\kern0.50em }{\epsilon_r}{\rho}_{ec},\\ {}0=-\frac{\partial p}{\partial r},\end{array}} $$

(36)

$$ \mathrm{Linearized}\ \mathrm{PTT}:\kern0.5em \Big\{{\displaystyle \begin{array}{l}\left(1+\varepsilon De{\tau}_{z z}\right){\tau}_{r z}=\left(\frac{\partial {w}_c}{\partial r}\right),\\ {}\left(1+\varepsilon De{\tau}_{z z}\right){\tau}_{z z}=2\ De\left(\frac{\partial {w}_c}{\partial r}\right){\tau}_{r z},\\ {}{\tau}_{r r}={\tau}_{\theta \theta}={\tau}_{z\theta}={\tau}_{r\theta}=0,\end{array}} $$

(37)

$$ \mathrm{Exponential}\ \mathrm{PTT}:\kern0.5em \Big\{{\displaystyle \begin{array}{l}\exp \left(\varepsilon De{\tau}_{z z}\right){\tau}_{r z}=\left(\frac{\partial {w}_c}{\partial r}\right),\\ {}\mathit{\exp}\left(\varepsilon De{\tau}_{z z}\right){\tau}_{z z}=2 De\left(\frac{\partial {w}_c}{\partial r}\right){\tau}_{r z},\\ {}{\tau}_{r r}={\tau}_{\theta \theta}={\tau}_{z\theta}={\tau}_{r\theta}=0,\end{array}} $$

(38)

where U_E =  − ϵ_NξE_z/µ₂ is the electro-kinetic slip velocity and ϵ_c and ϵ_N stand for dielectric constants corresponding to the inner and outer regions, respectively.

Peripheral region:

$$ \Big\{{\displaystyle \begin{array}{l}0=-\frac{\partial p}{\partial z}+\left[\left(\frac{1}{r}\frac{\partial \left(r\ {\tau}_{rz}\right)}{\partial r}\right)\right]+{U}_E\frac{\upmu_r\kern0.50em }{\epsilon_r}{\rho}_{ec},\\ {}0=-\frac{\partial p}{\partial r},\\ {}{\tau}_{rz}={\mu}_r\left(\frac{\partial {w}_N}{\partial r}\right).\end{array}} $$

(39)

From the set of Eqs. (38) and (39), a simple manipulation gives:

$$ \Big\{{\displaystyle \begin{array}{l}\mathrm{Linearized}\ \mathrm{PTT}:\left(1+2{b}^2{\tau^2}_{rz}\right){\tau}_{rz}=\frac{\partial {w}_c}{\partial r},\\ {}\mathrm{Exponential}\ \mathrm{PTT}:\exp \left(2{b}^2{\tau^2}_{rz}\right){\tau}_{rz}=\frac{\partial {w}_c}{\partial r}.\end{array}} $$

(40)

The appropriate dimensionless boundary conditions for the model under consideration are:

$$ \frac{\partial {w}_c}{\partial r}=0, atr=0;\kern1em \left(\mathrm{centerline}\ \mathrm{symmetry}\right) $$

(41)

$$ {w}_c={w}_N\;\mathrm{and}\;{\left({\tau}_{rz}\right)}_N={\left({\tau}_{rz}\right)}_c\;\mathrm{at}\;r={R}_1;\left(\mathrm{continuity}\ \mathrm{of}\ \mathrm{shear}\ \mathrm{stress}\ \mathrm{and}\ \mathrm{velocity}\ \mathrm{of}\ \mathrm{the}\ \mathrm{fluid}\ \mathrm{at}\ \mathrm{the}\ \mathrm{interface}\right) $$

(42)

$$ {w}_N=-1\;\mathrm{at}\;r={R}_0;\left(\mathrm{no}-\mathrm{slip}\ \mathrm{condition}\ \right) $$

(43)

In Eqs. (36) and (39), we drop the electro-osmotic body force term by incorporating the well-known artifice from the electro-kinetic literature. Through this artifice, the plug velocity of electro-osmotic flow can be equivalently achieved either by taking into account the body force term in the governing (momentum) equation or observing the effects of this term in the boundary in the form of slip condition based on electro-osmotic slip velocity. In our problem, we shall drop the electro-osmotic body force term from the momentum equation with an appropriate modification of no-slip boundary condition at the tube wall. This procedure is already used by Goswami et al. (2016). In this way, our problem is now governed by the following equations and boundary conditions.

Core region:

$$ \Big\{{\displaystyle \begin{array}{l}0=-\frac{\partial p}{\partial z}+\left[\left(\frac{1}{r}\frac{\partial \left(r\ {\tau}_{rz}\right)}{\partial r}\right)\right],\\ {}0=-\frac{\partial p}{\partial r}\end{array}} $$

(44)

$$ \Big\{{\displaystyle \begin{array}{l}\mathrm{Linearized}\ \mathrm{PTT}:\left(1+2{b}^2{\tau^2}_{rz}\right){\tau}_{rz}=\frac{\partial {w}_c}{\partial r},\\ {}\mathrm{Exponential}\ \mathrm{PTT}:\exp \left(2{b}^2{\tau^2}_{rz}\right){\tau}_{rz}=\frac{\partial {w}_c}{\partial r}.\end{array}} $$

(45)

$$ \frac{\partial {w}_c}{\partial r}=0, atr=0; $$

(46)

Peripheral region:

$$ \Big\{{\displaystyle \begin{array}{l}0=-\frac{\partial p}{\partial z}+\left[\left(\frac{1}{r}\frac{\partial \left(r\ {\tau}_{rz}\right)}{\partial r}\right)\right],\\ {}0=-\frac{\partial p}{\partial r},\\ {}{\tau}_{rz}={\mu}_r\left(\frac{\partial {w}_N}{\partial r}\right).\end{array}} $$

(47)

$$ {\displaystyle \begin{array}{l}\frac{\partial {w}_N}{\partial r}=0, atr=0;\\ {}{w}_N={U}_E-1, atr={R}_0.\end{array}} $$

(48)

In order to adopt stream function formulation, it is appropriate to define:

$$ u=-\frac{\partial {\psi}^{\ast }}{\partial z},w=-\frac{1}{r}\frac{\partial {\psi}^{\ast }}{\partial r}. $$

(49)

The stream functions in fixed and moving frames are related to each other by the relation $\psi ={\psi}^{\ast }-\frac{r^2}{2}$. Employing the definition of stream function, equations and boundary condition governing the flow read:

$$ \mathrm{Linearized}\ \mathrm{PTT}:\kern0.5em \frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial \psi }{\partial r}\right)=\frac{r}{2}\ \frac{\partial p}{\partial z}+\frac{\ {b}^2}{4}\ {\left(\frac{\partial p}{\partial z}\right)}^3\ {r}^3,0\le r\le {R}_1 $$

(50)

$$ \mathrm{Exponential}\ \mathrm{PTT}:\kern0.5em \frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial \psi }{\partial r}\right)=\exp \left(\frac{\ {b}^2}{2}\ {\left(\frac{\partial p}{\partial z}\right)}^2\ {r}^2\right)\frac{r}{2}\ \frac{\partial p}{\partial r},0\le r\le {R}_1 $$

(51)

$$ \frac{\partial p}{\partial z}=\frac{1}{r}\frac{\partial }{\partial r}\left[\left(r{\upmu}_r\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial \psi }{\partial r}\right)\right)\right],{R}_1\le r\le {R}_0 $$

(52)

$$ \psi =0,\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial \psi }{\partial r}\right)=0 atr=0, $$

(53)

$$ \psi =q/2,\partial \psi /\partial r=\left({U}_E-1\right){R}_0 atr={R}_0, $$

(54)

$$ \psi ={q}_1/2, atr={R}_1. $$

(55)

In the above equations, q and q₁ stand for volume flow rate over the outer and the inner cross-sections, respectively. Solving Eqs. (50)–(52) with boundary conditions (Eqs. (53) and (54)), the stream function (ψ) for each region appears as:

For linearized PTT model:

$$ \psi =\Big\{{\displaystyle \begin{array}{l}\frac{r^2}{2}\left\{\left({U}_E-1\right)+\frac{\ {b}^2}{48}{\left(\frac{\partial p}{\partial z}\right)}^3\left[{r}^4-3{R_1}^4\right]+\frac{1}{8}\frac{\partial p}{\partial z}\left\{{r}^2-2{R_1}^2\right\}+\frac{1}{4{\upmu}_r}\frac{\partial p}{\partial z}\left\{{R_1}^2-{R_0}^2\right\}\right\},0\le r<{R}_1\\ {}\frac{r^2}{2}\left({U}_E-1\right)+\left(\frac{q}{2}-\left({U}_E-1\right)\frac{{R_0}^2}{2}\right)+\frac{1}{4{\upmu}_r}\frac{\partial p}{\partial z}{\left({r}^2-{R_0}^2\right)}^2,{R}_1\le r\le {R}_0\end{array}} $$

(56)

For exponential PTT model:

$$ \psi =\Big\{{\displaystyle \begin{array}{l}\frac{1}{2{b}^4{\left(\frac{\partial p}{\partial z}\right)}^2}\frac{\partial p}{\partial z}\left[\exp \left({b}^2{\left(\frac{\partial p}{\partial z}\right)}^2\frac{r^2}{2}\right)-1\right]+\frac{r^2}{2}\left(\begin{array}{l}\left({U}_E-1\right)+\frac{1}{4{\upmu}_r}\frac{\partial p}{\partial z}\left({R_1}^2-{R_0}^2\right)\\ {}-\frac{1}{2{b}^2{\left(\frac{\partial p}{\partial z}\right)}^2}\frac{\partial p}{\partial z}\exp \left({b}^2{\left(\frac{\partial p}{\partial z}\right)}^2\frac{{R_1}^2}{2}\right)\end{array}\right),0\le r<{R}_1\\ {}\frac{r^2}{2}\left({U}_E-1\right)+\left(\frac{q}{2}-\left({U}_E-1\right)\frac{{R_0}^2}{2}\right)+\frac{1}{4{\upmu}_r}\frac{\partial p}{\partial z}{\left({r}^2-{R_0}^2\right)}^2,{R}_1\le r\le {R}_0\end{array}} $$

(57)

From the above expressions and Eq. (49), the axial velocity corresponding to the inner and outer regions for both linearized and exponential PTT fluid models becomes:

For linearized PTT model:

$$ w\left(r,z\right)=\Big\{{\displaystyle \begin{array}{l}\left({U}_E-1\right)+\frac{\ {b}^2}{16}{\left(\frac{\partial p}{\partial z}\right)}^3\left[{r}^4-{R_1}^4\right]+\frac{1}{4}\frac{\partial p}{\partial z}\left\{{r}^2-{R_1}^2\right\}+\frac{1}{4{\upmu}_r}\frac{\partial p}{\partial z}\left\{{R_1}^2-{R_0}^2\right\},0\le r\le {R}_1\\ {}\left({U}_E-1\right)+\frac{1}{4{\upmu}_r}\frac{\partial p}{\partial z}\left({r}^2-{R_0}^2\right),{R}_1\le r\le {R}_0\end{array}} $$

(58)

For exponential PTT model:

$$ w\left(r,z\right)=\Big\{{\displaystyle \begin{array}{l}\frac{1}{2{b}^2{\left(\frac{\partial p}{\partial z}\right)}^2}\frac{\partial p}{\partial z}\left[\exp \left({b}^2{\left(\frac{\partial p}{\partial z}\right)}^2\frac{r^2}{2}\right)-\exp \left({b}^2{\left(\frac{\partial p}{\partial z}\right)}^2\frac{{R_1}^2}{2}\right)\right]\\ {}+\left({U}_E-1\right)+\frac{1}{4{\upmu}_r}\frac{\partial p}{\partial z}\left\{{R_1}^2-{R_0}^2\right\},0\le r\le {R}_1\\ {}\left({U}_E-1\right)+\frac{1}{4{\upmu}_r}\frac{\partial p}{\partial z}\left({r}^2-{R_0}^2\right),{R}_1\le r\le {R}_0\end{array}} $$

(59)

The function characterizing wall deformation in dimensionless is:

$$ {R}_o(z)=1+{\phi}_{oc}\sin \left(2\pi z\right), $$

where ϕ_oc is the occlusion parameter.

The solution of the considered problem is still incomplete because of two unknowns R₁ and ∂p/∂z appearing in the Eqs. (56) and (57). In order to obtain these unknowns, a semi-analytical approach (Goswami et al. 2016) is used. Invoking the boundary condition (Eq. (55)) yields:

$$ \frac{q_1}{2}=\frac{{R_1}^2}{2}\left({U}_E-1\right)+\left(\frac{q}{2}-\left({U}_E-1\right)\frac{{R_0}^2}{2}\right)+\frac{1}{16{\upmu}_r}\frac{\partial p}{\partial z}{\left({R_1}^2-{R_0}^2\right)}^2. $$

(60)

In order to eliminate q₁, we set R₀ = 1 and R₁ = k at z = 0 in Eq. (60), to get

$$ \frac{q_1}{2}=\frac{k^2}{2}\left({U}_E-1\right)+\left(\frac{q}{2}-\left({U}_E-1\right)\frac{1}{2}\right)+\frac{1}{16{\upmu}_r}{P}_0{\left({k}^2-1\right)}^2. $$

(61)

Eliminating q₁ from Eqs. (60) and (61), we get

$$ \frac{k^2}{2}\left({U}_E-1\right)+\left(\frac{q}{2}-\left({U}_E-1\right)\frac{1}{2}\right)+\frac{1}{16{\upmu}_r}{P}_0{\left({k}^2-1\right)}^2=\frac{{R_1}^2}{2}\left({U}_E-1\right)+\left(\frac{q}{2}-\left({U}_E-1\right)\frac{{R_0}^2}{2}\right)+\frac{1}{16{\upmu}_r}\frac{\partial p}{\partial z}{\left({R_1}^2-{R_0}^2\right)}^2 $$

(62)

where the term P₀ is define as P₀ = (∂p/∂z)|_z = 0. In this way, q₁ is replaced by another unknown P₀. Now, there are three unknowns to be determined i.e., P₀, R₁ , and ∂p/∂z. Thus, there must be three equations relating these unknowns for a unique solution. One of the three required equations is available in Eq. (62), while the other two equations can be obtained by equating the stream functions given in Eqs. (56) and (57) at the interface. This gives:

$$ \mathrm{Linearized}\ \mathrm{PTT}:\kern0.5em \frac{b^2}{48}{\left(\frac{\partial p}{\partial z}\right)}^3{R_1}^6+\frac{1}{16}\frac{\partial p}{\partial z}{R_1}^4+\frac{1}{16{\upmu}_r}\frac{\partial p}{\partial z}\left({R_0}^4-{R_1}^4\right)+\frac{q}{2}-\left({U}_E-1\right)\frac{{R_0}^2}{2}=0, $$

(63)

$$ {\displaystyle \begin{array}{l}\mathrm{Exponential}\ \mathrm{PTT}:\frac{1}{2{b}^2{\left(\partial p/\partial z\right)}^2}\partial p/\partial z\left[\exp \left({b}^2{\left(\partial p/\partial z\right)}^2\frac{{R_1}^2}{2}\left(\frac{{R_1}^2}{2}-1/{b}^2{\left(\partial p/\partial z\right)}^2\right)\right)+1/{b}^2{\left(\partial p/\partial z\right)}^2\right]\\ {}+\frac{q}{2}-\left({U}_E-1\right)\frac{{R_0}^2}{2}+\frac{1}{16{\upmu}_r}\frac{\partial p}{\partial z}\left({R_0}^4-{R_1}^4\right)=0,\end{array}}, $$

(64)

Setting R₀ = 1and R₁ = katz = 0, the above expressions become:

$$ \mathrm{Linearized}\ \mathrm{PTT}:\frac{\ {b}^2}{48}{P_0}^3{k}^6+\frac{1}{16}{P}_0{k}^4+\frac{1}{16{\upmu}_r}{P}_0\left(1-{k}^4\right)+\frac{q}{2}-\left({U}_E-1\right)\frac{1}{2}=0. $$

(65)

$$ {\displaystyle \begin{array}{l}\mathrm{Exponential}\ \mathrm{PTT}:\frac{1}{b^2{\left({P}_0\right)}^2}{P}_0\left[\exp \left(\frac{k^2}{2}\left(\frac{k^2}{2}-1/{b}^2{\left({P}_0\right)}^2\right)\right)+1/{b}^2{\left({P}_0\right)}^2\right]\\ {}+\frac{q}{2}-\left({U}_E-1\right)\frac{1}{2}+\frac{1}{16{\upmu}_r}{P}_0\left\{1-{k}^4\right\}=0,\end{array}} $$

(66)

Eqs. (62)–(66) are solved numerically using the bisection technique at each axial station z to obtain the values of P₀, R₁, and ∂p/∂z for both linearized and exponential PTT fluid models. Mathematica 8.1 has been used for producing the numerical results. It is mentioned that Eqs. (62), (63), and (65) for LPTT model can be reduced to the following polynomial equation in R₁:

$$ {A}_{14}{R}_1^{14}+{A}_{12}{R}_1^{12}+{A}_{10}{R}_1^{10}+{A}_8{R}_1^8+{A}_6{R}_1^6+{A}_4{R}_1^4+{A}_2{R}_1^2+{A}_0=0. $$

(67)

The coefficients of the above polynomial are defined in the Appendix. A further simplification of the interface polynomial for limiting case b = 0 yields:

$$ {\displaystyle \begin{array}{l}\left[\left({k}^2\left({\upmu}_r-1\right)+1\right)\left({U}_E-1\right)\left({\upmu}_r-1\right)\right]{R_1}^6+\left[\begin{array}{l}\left({k}^2\left({\upmu}_r-1\right)+1\right)\left\{\begin{array}{l}\left({k}^2+{R_0}^2-1\right)\left({U}_E-1\right)\left({\upmu}_r-1\right)\\ {}+\left(q-\left({U}_E-1\right){R_0}^2\right)\end{array}\right\}\\ {}+\left({\left({k}^2-1\right)}^2\left({U}_E-1\right)\left({\upmu}_r-1\right)-q\right)\end{array}\right]{R_1}^4\\ {}-{R_0}^2\left({k}^2\left({\upmu}_r-1\right)+1\right)\left[2q-\left({U}_E-1\right){R_0}^2\right]{R_1}^2+\left[\left({k}^2\left({\upmu}_r-1\right)+1\right)\left({k}^2-1\right)\left({U}_E-1\right)+q\right]+{\left({k}^2-1\right)}^2\left[\left({U}_E-1\right)-q\right]=0\end{array}} $$

In the absence of the electro-kinetic slip velocity U_E, the above polynomial is further simplified to the interface polynomial equation reported by Rao and Usha (1995)). In contrast, it is tedious to setup a polynomial equation of interface for EPTT model.

Results and discussion

Analysis of interface region

Parameter b is the measure of the non-Newtonian shear-thinning behavior of the core region fluid. Greater values of this parameter correspond to the enhanced shear-thinning effects of the inner (core) region fluid. The parameter μ_r is the ratio of the viscosity of the outer (peripheral) region and the core region. Three cases arise depending on the values of μ_r. The situation when the viscosity of the core (inner) region is greater than the viscosity of the outer (peripheral) region is represented by taking μ_r < 1. When both regions have equal viscosities, then μ_r = 1. Similarly, μ_r > 1 corresponds to the situation when the viscosity of the outer (peripheral) region is greater than the viscosity of the inner (core) region. The remaining important parameter in the problem is denoted by U_E and is known as the electro-kinetic slip velocity. Naturally, each of the abovementioned parameters affect the interface shape, pumping features, reflux, and trapping. In order to quantify such effects, Fig. 2 a–c are prepared. Figure 2 shows that an increase in the viscosity ratio leads to an increase in the vertical force exerted on the fluid present in a peripheral layer region in the crest region. Further, the peripheral fluid in the trough region experiences an increased vertically downward force with increasing the viscosity ratio. In such an arrangement, the interface curves for μ_r < 1 and μ_r = 1 lies in between the interface curves for μ_r < 1 and μ_r > 1. In contrast, the peripheral fluid in the upper half of the wave (crest) region experiences an increased vertically downward force with increasing U_E. While the peripheral fluid in the lower half of the wave (trough) region is acted upon an increased upward force with increasing the electro-kinetic slip velocity. A similar variation in the interface is noted with increasing parameter b as observed with raising parameter μ_r. However, the peripheral fluid in the upper half of the wave (crest) region is less sensitive to an increase in parameter b in comparison with the peripheral fluid in the lower half of the wave (trough) region for which the effects of b are much pronounced. As a result, the interface curves for b = 4 shows larger deviation from the corresponding interface curves for b = 0.1. Such a deviation is attributed to enhance shear thinning in viscosity for larger values of parameter b and the greater deformation gradients in the trough region.

Fig. 2

The behavior of the interface region with respect to µ_r, U_E and b

A comparison between the predictions of the linear PTT model and the exponential PTT model is presented in Fig. 3a–c. It is observed that the results of both models are in excellent correlation for smaller values of parameter b. However, the deviation between the results of both models amplifies as parameter b increases. Therefore, we have presented the subsequent results only for EPTT model.

Fig. 3(a–c)

Comparison between the results of linear and exponential PTT models

Pressure expression and graphical discussion

From Eq. (62), the expression of pressure rise ∂p/∂z in the tube is given by:

$$ \frac{\partial p}{\partial z}=\frac{16{\upmu}_r}{{\left({R_1}^2-{R_0}^2\right)}^2}\left\{\frac{1}{2}\left({U}_E-1\right)\left({k}^2-{R_1}^2+{R_0}^2-1\right)+\frac{1}{16{\upmu}_r}{P}_0{\left({k}^2-1\right)}^2\right\}. $$

(68)

The change in the pressure gradient across one wavelength is achieved by integrating Eq. (68). Thus on integrating Eq. (68), we get:

$$ \varDelta p=16{\upmu}_r\underset{0}{\overset{\lambda }{\int }}\left\{\left(\frac{1}{2}\left({U}_E-1\right)\left({k}^2-{R_1}^2+{R_0}^2\right)+\frac{1}{16{\upmu}_r}{P}_0{\left({k}^2-1\right)}^2\right)/{\left({R_1}^2-{R_0}^2\right)}^2\right\} dz. $$

(69)

The volume flux in moving and fixed frame of references is linked through with the following expression:

$$ {Q}_S=2\underset{0}{\overset{R_0}{\int }}\left(w+1\right)r\ dr=q+{R}_0^2. $$

The above expression after time averaging over a complete period gives $Q=\frac{1}{T_P}{Q}_S\ dt=q+\left(1+\frac{\phi^2}{2}\right)$,

The solution of Eq. (69) is achieved through numerical integration and the profiles of ΔP₀(=ΔP|_Q = 0) versus ϕ_oc are demonstrated in Fig. (4). Special attention is given to seek the influence of the involved parameters such as, U_E, μ_r, and the rheological parameter b on the pressure rise at zero volume flow rate. It is observed that both electro-kinetic slip velocity (U_E) and viscosity ratio (μ_r) amplify the pressure rise at zero volume flow rate. The amplification with raising U_E is maximum at lower occlusion values and least when occlusion parameter approaches unity. On the other hand, increase in ΔP₀ with increasing μ_r is observed over the complete range of occlusion parameter. Contrary to effects of U_E and μ_r, an increase in the fluid rheological parameter b causes a decrement in the pressure required to produce zero volume flow rate. Again, this decrease is a consequence of enhanced shear thinning in the viscosity of the fluid in the inner (core) region for higher values of b.

Fig. 4

The variation in pumping characteristic with respect to U_E, μ_r and b

Trapping phenomena

Trapping corresponds to the formation of eddying regions in the flow domain. Such regions enclose a volume of fluid which is usually known as bolus in the literature. The bolus is transported along the tube via the peristaltic activity with the speed of wave. Its formation is linked with the bulk momentum of the flow. The zones of low bulk momentum are more vulnerable to the bolus formation in comparison with the region where bulk movement is high. Figures 5, 6, 7, and 8 indicate the influence of electro-kinetic slip velocity on the trapping phenomena in both the core and peripheral (outer) regions. It is evident that the area of trapping bolus reduces and the bolus eventually disappears with raising the electro-kinetic slip velocity. In contrast, raising parameter b results in an increase in the area and circulation of the trapped bolus. Similar results are obtained with increasing the viscosity ratio μ_r. Another important aspect is to find the trapping limit on the normalized volume flow rate for a given set of the involved parameters. To do so, we have plotted the normalized volume flow rate (Q/Q_Δp = 0) versus the ϕ_oc for different values of b and U_E. In fact, the values of stream function lies between 0 and Q where ψ = 0 is the center streamline while ψ = Q represents the boundary wall. In order to obtain the pair (ϕ_oc, Q/Q_Δp = 0), the first step is to locate a sub-region in the flow domain {0 ≤ ϕ_oc ≤ 1 : 0 ≤ Q/Q_Δp = 0 ≤ 1} where ψ changes its sign from negative to positive. In the next step, a suitable iterative technique is deployed to obtain the exact value of the pair (ϕ_oc, Q/Q_Δp = 0) at which the transition takes place. The region above a specific curve in each figure is the region of trapping. It is noted that the trapping region expands with raising the values of the parameter b while it narrows down with enhancing the electro-kinetic slip velocity.

Fig. 5

The streamline behavior in the inner region for k = 0.4, b = 0.1, μ_r = 10, ϕ_oc = 0.75, Q = 0 and the outer region for k = 0.8, b = 0.1, μ_r = 1, ϕ_oc = 0.75, Q = 4. The dashed line curve corresponds to the interface

Fig. 6

Effect of b on trapping for k = 0.4, μ_r = 0.1, ϕ_oc = 0.6, Q = 0.6, U_E = 0

Fig. 7

The trapping phenomenon for viscosity ratio when k = 0.4, b = 0.1, ϕ_oc = 0.75, Q = 0.1, U_E = 0

Fig. 8

Trapping limit against b and U_E·

Reflux interpretation

The phenomenon which estimates the net flow of fluid in a complete wave cycle is known as reflux. This is due to an unfavorable pressure rise across the tube or backward motion of the fluid elements within the tube. In both regions, the reflux phenomena is strongly dependent on the emerging parameters, for example, viscosity ratio, electro-kinetic slip velocity, and b. In the earlier analysis, Brasseur et al. (1987)) estimated the amount of reflux through the quantity (Q − Q_ψ)/Q during a wave cycle, where Q_ψ is given by the relation (Rao and Mishra 2004)

$$ {Q}_{\psi }=2\psi +\underset{0}{\overset{1}{\int }}{r}^2 dz. $$

(70)

Equation (70) arises as a consequence of transforming the expression ${Q}_{\psi^{\ast }}=2\underset{0}{\overset{r\left({\psi}^{\ast },z\right)}{\int }} rwdr$ from the fixed frame to the wave frame and then averaging over one period of wave. The quantity ${Q}_{\psi^{\ast }}$ is the average volumetric flow rate between the axis of the tube and a streamline ψ^∗ = constant in the fixed frame. The quantity (Q − Q_ψ)/Q is such that 1 < (Q − Q_ψ)/Q < 0 because 0 < Q_ψ/Q < 1. However, it may happen that Q_ψ/Q takes values greater than unity from some values of ψ^∗ thereby indicating that the flow domain has some kind of backward motion or reflux. An analytical expression for reflux condition can be obtained by treating the integral appearing in Eq. (70) analytically. However, the indicated integration is difficult to perform analytically due to the complicated nature of stream function given by Eq. (57). In the limiting case when b = 0, it turns out that for reflux to occur one must have (Rao and Usha 1995)

$$ -\underset{0}{\overset{1}{\int }}\frac{8\mu \left(q+{R_0}^2\right) dz}{{R_0}^4+\left(\mu -1\right){R_1}^4}\ge 0. $$

For the case when b ≠ 0, numerical quadrature is used to calculate the values of ${Q}_{\psi^{\ast }}\left(={Q}_{\psi }/Q\right)$ for given values of ψ^∗. The curves ${Q}_{\psi^{\ast }}$ verses ψ^∗ are plotted in Fig. 9. Fig. 9 depicts that reflux is enhanced by raising the parameter b while it reduces with increase in the electro-kinetic slip velocity.

Fig. 9

(a–b) The reflux phenomenon against different combinations of viscosity ratio, electro-kinetic slip velocity, and parameter b

Deductions

In the present article, the electro-osmotic peristaltic flow of PTT fluid model in contact with the Newtonian in a tube is investigated. The governing equations are simplified by using well-known approximations of long wavelength and low Reynolds number. The main focus of this study is to highlight the effects of electro-kinetic slip velocity and PTT model parameters on pressure rise per wavelength, interface region, trapping, and reflux phenomena. The information about these phenomena is important for both physiological and industrial application of peristaltic transport. Our study reveals that both trapping and reflux can be controlled either by increasing the strength of the applied electric field or by exploiting the viscoelastic and extensional characteristics of the core region fluid. In fact, it turns out that in order to avoid trapping and reflux the non-dimensional number b which provides a measure of both the extensional (measured by ϵ) and the elastic (measured by De) characteristics of the core fluid must be kept small. This observation also advocates for carrying out a complete rheological characterization of the material in the core region. In contrast, the efficiency of the pumping can be improved by taking the lower values of the non-dimensional group b associated with the core region fluid or by regulating the strength of the applied electric field.

The analysis presented here can be extended to three layered electro-osmotic flow. The efforts are under way in this direction and would be communicated soon. It is worthy to mention that the studies on three layered electro-osmotic peristaltic flow carried out by (Tripathi et al., 2017a, b, 2018a, b, c) would serve as a starting point for this research.

Appendix

Here, we provide the values of coefficients appearing in the interface polynomial Eq. (67):

$$ {A}_{14}=\left({U}_E-1\right)\left({\mu}_r-1\right), $$

$$ {A}_{12}=\frac{1}{24{\mu}_r}\left(3{\left(-1+{k}^2\right)}^2{P}_0\left(-1+{\mu}_r\right)+8{\mu}_r\left(3\left(-1+{k}^2+q+{U}_E-{k}^2{U}_E\right)+3\left(-1+{k}^2\right)\left({U}_E-1\right){\mu}_r-64{b}^2{\left({U}_E-1\right)}^3{\mu}_r^3+3{R}_0^2\left({U}_E-1\right)\left(-6+5{\mu}_r\right)\right)\right), $$

$$ {A}_{10}=\frac{1}{2{\mu}_r}\left({\left(-1+{k}^2\right)}^2{P}_0\left(-{R}_0^2\left(-1+{\mu}_r\right)+16{b}^2{\left({U}_E-1\right)}^2{\mu}_r^3\right)+2{\mu}_r\left({R}_0^2\left(4-4{k}^2-6q+15{R}_0^2\left({U}_E-1\right)+4\left(-1+{k}^2\right){U}_E\right)-2{R}_0^2\left(-2+2{k}^2+5{R}_0^2\right)\left({U}_E-1\right){\mu}_r+64{b}^2\left(-1+{k}^2+{R}_0^2\right){\left({U}_E-1\right)}^3{\mu}_r^3\right)\right), $$

$$ {A}_8=\frac{1}{8{\mu}_r}\left(-8{b}^2{\left(-1+{k}^2\right)}^4{P}_0^2\left({U}_E-1\right){\mu}_r^2+{\left(-1+{k}^2\right)}^2{P}_0\left(-5{R}_0^4+6{R}_0^4{\mu}_r-128{b}^2\left(-1+{k}^2+{R}_0^2\right){\left({U}_E-1\right)}^2{\mu}_r^3\right)+8{\mu}_r\left(5{R}_0^4\left(-1+{k}^2+3q-4{R}_0^2\left({U}_E-1\right)+{U}_{\mathrm{E}}-{k}^2{U}_{\mathrm{E}}\right)+2{R}_0^4\left(-3+3{k}^2+5{R}_0^2\right)\left({U}_E-1\right){\mu}_r-64{b}^2{\left(-1+{k}^2+{R}_0^2\right)}^2{\left({U}_E-1\right)}^3{\mu}_r^3\right)\right), $$

$$ {A}_6=\frac{1}{24}\left({b}^2{\left(-1+{k}^2\right)}^6{P}_0^3-480q{R}_0^6+24{b}^2{\left(-1+{k}^2\right)}^4{P}_0^2\left(-1+{k}^2+{R}_0^2\right)\left({U}_E-1\right){\mu}_r+12{\left(-1+{k}^2\right)}^2{P}_0\left(-{R}_0^6+16{b}^2{\left(-1+{k}^2+{R}_0^2\right)}^2{\left({U}_E-1\right)}^2{\mu}_r^2\right)+8\left({U}_E-1\right)\left(45{R}_0^8-3{R}_0^6\left(-4+4{k}^2+5{R}_0^2\right){\mu}_r+64{b}^2{\left(-1+{k}^2+{R}_0^2\right)}^3{\left({U}_E-1\right)}^2{\mu}_r^3\right)\right), $$

$$ {A}_4=\frac{1}{8{\mu}_r}{R}_0^8\left({\left(-1+{k}^2\right)}^2{P}_0\left(5+{\mu}_r\right)+8{\mu}_r\left(5-5{k}^2+15q+{R}_0^2\left({U}_E-1\right)\left(-6+{\mu}_r\right)+{\mu}_r-{k}^2{\mu}_r+\left(-1+{k}^2\right){U}_E\left(5+{\mu}_r\right)\right)\right), $$

$$ {A}_2=\frac{1}{2{\mu}_r}{R}_0^{10}\left(-{\left(-1+{k}^2\right)}^2{P}_0-2\left(4-4{k}^2+6q-{R}_0^2\left({U}_E-1\right)+4\left(-1+{k}^2\right){U}_E\right){\mu}_r\right), $$

$$ {A}_0=\frac{1}{8{\mu}_r}{R}_0^{12}\left({\left(-1+{k}^2\right)}^2{P}_0+8\left(1-{k}^2+q+\left(-1+{k}^2\right){U}_E\right){\mu}_r\right). $$

From Eq. (65), the real solution of P₀ can be obtained by employing Cardan-Tartaglia formula of algebraic cubic equation as follows:

$$ {P}_0=-\frac{B}{S}+\frac{S}{A}, $$

where $S={\left(-d+\sqrt{A^3{B}^3+{d}^2}\right)}^{\frac{1}{3}}$,

with d = 12(q − (U_E − 1))A²,  B = 1 + (μ_r − 1)k⁴ and A = b²μ_rk⁶.