1 Introduction

Indian Summer Monsoon Rainfall (ISMR) is a major component of the Asian summer monsoon, which covers almost 80% of Indian total annual rainfall, from June to September (Jain and Kumar 2012). The occurrences of short term heavy rainfall events during monsoon can cause losses to human life, infrastructure, industry, agriculture and ecosystem at an unprecedented scales, e.g. Flood in Mumbai during 2005 (Kumar et al. 2008), Flood in Kedarnath during 2013 (Mishra et al. 2014), etc. India is the 3rd worst affected country by weather related disasters and it can be attributed to both higher occurrences of extremes and high population (UNISDR 2015). Global warming due to increased greenhouse gas emissions causes the changes in the behaviour of the extreme precipitation all over the world (Trenberth et al. 2005). Global studies indicate that the magnitude and frequency of the extreme precipitation will increase in the future, even in the regions where total precipitation is unchanged or decreased (IPCC 2007). Recent studies (Allen and Ingram 2002; Held and Soden 2006) show that the increase in the mean precipitation with increasing temperature is around 2% K-1, while the extremes are not energetically constrained and would increase at a greater rate under the warming scenario (Muller and Gormann 2011). The precipitation extremes are projected to increase at a larger rate than that of the mean precipitation in most part of the globe under the warmer climate due to the abundant availability of water vapour. This can be explained by the Clacuius–Clapeyron (C–C) relation, which states 7.5% increase in precipitation per degree C increase in temperature. Changes in the magnitudes and frequency of extremes in future have been assessed using the General Circulation Models (GCMs) by Kharin and Zwiers (2000) and others (Kharin et al. 2007; Min et al. 2009; Wetterhall et al. 2009; Wasko and Sharma 2015). However, there are some recent studies which indicated that the increase in precipitation extremes in a warming environment exhibits a super C–C relation, especially in the case of hourly precipitation (Drobinski et al. 2016; Westra et al. 2014; Mishra et al. 2012; Lenderink and van Meijgaard 2010). The multi-model projections from GCMs on global monsoon depict significant increase in its intensity in the future (Kitoh et al. 2013; Lee and Wang 2014) and also its sensitivity to global warming (Kitoh et al. 2013). Hence the severity of ISMR is expected to increase with increase in the global warming (Sharmila et al. 2015) leading to detrimental effect on country’s agricultural activities and economy. Thus proper understanding and efficient projection of ISMR and its extremes have a significant influence on the India’s water resources and management policies (Mall et al. 2006; Archer et al. 2010).

The ISMR extremes have gained the attention of scientific research community due to its enormous complexities. There are numerous observational studies performed to understand the behaviour of the extremes over India, which revealed conflicting conclusions about the nature of changes in ISMR extremes. For instance, Goswami et al. (2006) showed significant increase in the frequency and magnitude of precipitation extremes, with decrease in moderate precipitation in Central India by spatially aggregating the gridded precipitation data. This conclusion is further supported by Rajeevan et al. (2008). However, follow-up studies (Krishnamurthy et al. 2009; Ghosh et al. 2009, 2012) pointed some of the limitations of these analyses, which include heterogeneity of Central Indian precipitation with spatial non-uniformity in trend and failure in field significance test. On the other hand, the fine resolution analysis of ISMR extremes revealed increasing trend of spatial heterogeneity (Ghosh et al. 2012). The debates on the space–time variation of Indian monsoon rainfall extremes with the relative contributions from large scale circulation (Goswami et al. 2006; Rajeevan et al. 2008) and local influences, such as urbanization (Kishtawal et al. 2010; Vittal et al. 2013; Shastri et al. 2014) still exist. In a very recent study, Mondal and Mujumdar (2014) reported that no spatially uniform pattern exists in Indian rainfall extremes. However, there is a general consensus that on a spatial aggregate scale there is an increase in extremes with statistically significant increase in spatial variability. The hypothesis, which is not yet explored, is that if such patterns exist in future projections of monsoon rainfall under greenhouse warming.

GCMs are useful tools, which are being used extensively by the researchers to understand the present and future changes in the precipitation in case of both mean and extremes. There are also several studies existing on Indian monsoon, which are largely focusing on the mean precipitation (Gadgil and Sajani 1998; Hu et al. 2000; Lal et al. 2001; May 2002; Wang et al. 2004; Kripalani et al. 2007; Turner et al. 2007; Stowasser et al. 2009; Sharmila et al. 2015; Sarathi et al. 2015), with considerable uncertainty across multiple GCM projections. However, relatively fewer studies have focused on examining the projected changes of ISMR extremes (Turner and Slingo 2009a, b). The studies mentioned above, directly utilized the GCM data to analyze the projections of ISMR; however, coarse resolution simulations by GCMs may not suitable for simulating regional precipitation. Regional climate model outputs of Indian monsoon have been rarely used to understand the characteristics of future extremes. This is partially due to the inability of models in simulating the extremes, though some of them may be good for other characteristics such as climatology or seasonality. Revadekar et al. (2011) and Rao et al. (2014) conducted studies on projection of ISMR extremes by using RCM known as PRECIS (Providing REgional Climates for Impacts Studies), which showed increase in extremes towards the end of twenty-first century. However, the parent model was one of the old generation climate model from CMIP3 suite and the analyses do not consider inter-model uncertainty. Mishra et al. (2014) have evaluated the dynamic downscaling simulations from Coordinated Regional Climate Downscaling Experiment (CORDEX) with CMIP5 models as parent models and have not found any value addition with respect to the parent GCM. They have also concluded that the regional simulations of extremes are inadequate for climate change adaptation. In addition, a recent study by Singh et al. (2016) revealed that the regional models do not add value to the ISMR projections including extremes. Salvi et al. (2013) and Shashikanth et al. (2013) have developed statistical downscaling model with kernel regression for fine resolution projection of Indian monsoon; however, such downscaling model was unable to capture the extremes. The other recently reported statistical downscaling algorithms include beta regression (Sohom et al. 2016), K-nearest neighbourhood (Sharif and Burn 2006, 2007; Goyal et al. 2011, 2013; King et al. 2015), maximum entropy bootstrapping (Srivastav and Simonovic 2014), Hidden Markov Model (Mehrotra and Sharma 2005, 2010), geostatistical approaches (Jha et al. 2015) etc. The inability of both state of art dynamic and statistical regional models in simulating ISMR extremes makes it a potential area of research and here we attempt to address the same. The other issue associated with extremes is the analysis of tail which needs special statistical treatment through application of Extreme Value Theory (EVT) (Kharin and Zwiers 2000; Kharin et al. 2007; Khan et al. 2007; Vittal et al. 2013); however majority of the studies on Indian monsoon (Goswami et al. 2006; Revadekar et al. 2011 and Rao et al. 2014) have not really utilized this tool for a strong statistical support. Here, in the present study we modify the state-of-art statistical downscaling model (Kannan and Ghosh 2013; Salvi et al. 2013) for better simulations of regional rainfall extremes; characterize extremes by applying EVT with Annual Maxima/Block maxima (AM/BM) (Ghosh et al. 2012) and Peak over Threshold (PoT) (Vittal et al. 2013; Coles 2001) approaches. We further compute the statistically significant changes in extremes during future considering the uncertainty in parameters of extreme value distributions by using multiple GCMs from CMIP5 suites.

The current paper is organized as follows. The selection of the GCMs and the data details are discussed in Sect. 2. The methodology and list of models are also provided in Sect. 2. A discussion of the various results obtained in the study is presented in Sect. 3. Finally, a summary, followed by concluding remarks, are presented in Sect. 4.

2 Data and methods

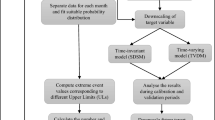
We first use the conventional statistical downscaling (Supplementary Fig. S1) (Kannan and Ghosh 2013; Salvi et al. 2013) for projection of Indian summer monsoon rainfall (ISMR). Here, in the present study, we focus on rainfall during JJAS (June–September, Indian summer monsoon) time period only. The model is then further modified to capture the extremes (Fig. 1). Extremes are characterized with extreme value theory. Brief overview of different steps and data used for the same are presented in the following subsections.

Fig. 1
figure 1

Modified Downscaling Algorithm for simulations/ projections of precipitation extremes

Full size image

2.1 Statistical downscaling

Statistical downscaling involves development of statistical relationship between synoptic scale circulation pattern and regional precipitation, which is further applied to the bias corrected synoptic circulation patterns projected by GCMs. The synoptic scale climate variables forming the circulation pattern are known as predictors. Following Shashikanth et al. (2013), Salvi et al. (2013) and Kannan and Ghosh (2013), here, we use wind velocities in both U and V directions, temperature at surface and 500 hPa, specific humidity at 500 hPa and mean sea level pressure (MSLP) as predictors. We follow the state of art transfer function based statistical downscaling where kernel regression (Supplementary Fig. S1) is used as a transfer function (Kannan and Ghosh 2013; Salvi et al. 2013). The methodology is applied separately to seven meteorologically homogeneous zones (Parthasarathy et al. 1995) in India (Supplementary Fig. S2).

We first develop the statistical relationship between predictors and predictand. We use National Centers for Environmental Prediction/ National Center for Atmospheric Research (NCEP/ NCAR) reanalysis data (Kalnay et al. 1996) as predictor and the gridded rainfall provided by Asian Precipitation—highly-resolved observational data integration towards evaluation (APHRODITE) (Yatagai et al. 2012) as predictand for establishing the relationship. The relationship involves multiple statistical steps, such as Principal Component Analysis (PCA) for reduction of dimensionality of predictors; Classification and Regression Tree (CART) for estimation of rainfall states representing spatial patterns of precipitation and Kernel Regression (KR) at individual grid conditional on derived state to simulate gridded precipitation. Details of the methodology with the domain of predictors are reported in Salvi et al. (2013).

We apply the derived relationship to the GCM simulated synoptic scale climate variables. The GCMs used for the present study are developed by Norway climate center (NCC) formerly BCCR (Bjerknes centre for Climate Research, Norway), CCCma (Canadian Center for Climate Modelling Analysis), MIROC-medium resolution (Model for Interdisciplinary Research on Climate), MRI (Meteorological Research Institute, Japan), and MPI (Max Plank Institute, Germany). The GCMs used in the present work are from CMIP5 suite. The GCMs are selected based on their capability to simulate the Indian monsoon (Kripalani et al. 2007). In addition to this, Bayesian analysis with statistically downscaled projections assigns higher weigtages to the GCMs BCCR, MRI and MPI for the India monsoon (Shashikanth et al. 2014). The GCM simulated variables have systematic departure (bias) with respect to observe NCEP/NCAR reanalysis data. For the current study, quantile based transformation method, proposed by Li et al. (2010) is used for bias correction. The daily precipitations are simulated by applying the derived relationship to bias corrected GCM simulations.

2.2 Modified downscaling for precipitation extremes

One of the key limitation as reported in state-of-art regional climate modelling with statistical downscaling is that they fail to simulate extremes, since the regression based methods aim to simulate the expected value of predictand, given a circulation pattern (Wilby et al. 2004; Benestad 2010). This is true for Indian monsoon and is reported in Salvi et al. (2013). To simulate the extremes, we modify the algorithm (Fig. 1), and the new method involves a twofold approach, first, the identification of extreme days and then the use of robust regression for simulating extreme precipitation amount. As extreme precipitation data set is mostly associated with the outliers, we apply robust regression.

Robust Regression (RR) is mostly implemented when non-normal or outliers are observed in the data set. The linear least square estimate performs badly in the presence of unusual data (extremes), where the residuals do not follow a normal distribution. If the distribution of errors is asymmetric and prone to outliers, the model assumptions will no longer remain valid, and also the parameter estimates, confidence intervals, and other computed statistics will become unreliable (Huber 1972). Therefore, robust regression is employed which is not as vulnerable as least squares to heavy tailed data. The most general method for robust regression is M-estimation (Huber 1972; Fox 2002), where, M stands for “maximum likelihood type”. It assigns weight to each data point automatically and iteratively using a process called Iteratively Reweighted Least Squares (IRLS). In the first iteration, each point is assigned equal weight and model coefficients are estimated using ordinary least squares. The weights are then recomputed with least weight assigned to the data point deviating maximum from model prediction. Model coefficients are recomputed and the process continues until the values of the coefficient estimates converge within a specified tolerance (Huber 1972; Fox 2002).

However, RR being a modified linear regression method may not perform well for highly non-linear relationship. In such scenario, the nonlinear kernel regression may perform better. Hence, for downscaling of rainfall extremes we apply both KR and RR, to select the best one for individual grid.

2.3 Extreme value analysis

For analysis of extremes on the observed and simulated gridded monsoon precipitation over India, we apply Extreme Value Theory (EVT) (Coles 2001), which infers the tail behaviour of a population on the basis of well-grounded statistical theory (Ghosh et al. 2012). The two commonly used EVT methods are Block Maxima (BM) (Annual/ seasonal Maxima for hydro-meteorological applications) using generalized extreme value distribution (GEV) and peak over threshold (PoT) using Generalized Pareto Distribution (GPD).

The BM approach involves extraction of maxima values from a block of a year or a season (here, monsoon season, JJAS). These maxima values are then fitted to Generalized Extreme Value (GEV) distribution. The BM method is preferable with long historical record or long range of data (Kharin et al. 2007). The details of fitting the GEV distribution to annual/block maxima are described in the Coles (2001). The details of GEV distributions are explained below:

Suppose ‘x’ represents the annual/block maxima of daily precipitation in a given series, then the GEV distribution is defined by (Coles 2001; Katz et al. 2002);

$$F\left( {x;\mu ,\alpha ,\xi } \right) = \left\{ {\begin{array}{*{20}{l}} {\exp \left\{ { - {{\left[ {1 - \frac{{\xi \left( {x - \mu } \right)}}{\alpha }} \right]}^{ - \frac{1}{\xi }}}} \right\}} \\ {1 + \xi \left( {x - \mu } \right)/\alpha> 0 \xi \ne 0} \\ {\exp \left\{ { - \exp \left[ { - \frac{{\left( {x - \mu } \right)}}{\sigma }} \right]} \right\} \xi = 0} \end{array}} \right.$$
(1)

GEV distribution has three parameters namely location (µ), scale parameter (α) and shape parameter (ξ). In the present work the maximum likelihood estimation (MLE) technique is used to estimate the parameters. However, for small data sets the parameters may be unstable (Martins and Stedinger 2000; Wang et al. 1990). This may be considered as a limitation of the present work. The positive, negative and zero values of shape parameters guide to three different cases of GEV distribution namely Frechet, Weibull and Gumbel distribution respectively.

The goodness of fit is estimated using Kolomogorov–Smirnov (K-S) (5% level significance) test and if the test fails an empirical distribution is fitted instead of GEV. The fitted GEV parameters are used to estimate 30 year return level. The return level/ period (RLN) is defined as a particular value expected to exceed once in every N year (here, 30 year) with probability of 1/N in any given year (Khan et al. 0.2007).

$${F^{ - 1}}\left( {1 - p;\mu ,\alpha ,\xi } \right) = \left\{ {\begin{array}{l} {\mu - \left( {\alpha /\xi } \right)\left\{ {1 - {{\left[ { - \ln \left( {1 - p} \right)} \right]}^{ - \xi }}} \right\} \xi \ne 0} \\ {\mu - \alpha \ln \left[ { - \ln \left( {1 - p} \right)} \right] \xi = 0} \end{array}} \right.$$
(2)

On the other hand, a nonparametric Gaussian kernel distribution was fitted to those grids where KS test failed for GEV.

The main weakness of block maxima method is that it does not consider multiple occurrences of an extreme event over a particular threshold (Katz et al. 2005; Coles 2001; Vittal et al. 2013). The PoT method considers all the extreme events exceeding a threshold and here we consider 95 percentile rainfall at individual grids as the threshold for that grid. The clusters of maximas of rainfall are identified when the daily rainfall is above the respective threshold for successive days, and clusters are separated when there is at least a single day between them with rainfall lower than the threshold. The maximas from clusters of rainfall values exceeding these thresholds are then fitted to GP distribution. The expression for GPD is provided below:

$$F\left( {x;{\text{ }}\mu ,{\text{ }}\alpha ,{\text{ }}\xi } \right) = \left\{ \begin{gathered} 1 - {\left( {1{\text{ }} + {\text{ }}\xi {\text{ }}\left( {y/\sigma } \right)} \right)^{ - 1/{\text{ }}\xi }} \hfill \\ 1{\text{ }} + {\text{ }}\xi {\text{ }}\left( {y/\sigma } \right) \xi \ne {\text{ }}0 \hfill \\ 1 - {\text{ }}e{\text{ }} - y/\sigma \xi = 0 \hfill \\ \end{gathered} \right.,$$
(3)

where, y > 0, with σ > 0 is a scale parameter and is a shape parameter. The shape of GPD assumes three possible types depending upon the shape parameter ξ = 0, known as exponential distribution; ξ > 0 Pareto distribution and ξ < 0 beta distribution (Katz et al. 2005). The parameters are obtained using maximum likelihood estimation and goodness of fit is estimated using KS test at 5% significance level. The extreme values are expressed as return levels/periods (RLN) (Coles 2001; Vittal et al. 2013).

$$RL_{N} = \left\{ \begin{array}{*{20}l} u + \frac{\sigma }{\xi }\left[ {(Nn_{y} \zeta _{u} )^{\xi } - 1} \right],\;\xi \ne 0 \hfill \\ u + \sigma \log (Nn_{y} \zeta _{u} ),\;\xi = 0 \hfill \\ \end{array} \right..$$
(4)

One of the key assumptions in PoT is that the fitted rainfall values should be independent. Here we examine the independence using lbqtest (Ljung-Box 1978). Further information regarding the PoT can be obtained from Coles (2001), Vittal et al. (2013) and Madsen et al. (1997). However, Cunnane et al. (1973) reported that PoT and BM models are of similar efficiency when a relatively high threshold is used for the PoT series.

2.4 Computing changes in extremes with significance

Fitting of distribution to a sample is characterized by uncertainty and hence computing the changes in return levels derived from distribution needs to be tested for statistical significance. Resampling is an approach for estimating parameter uncertainties (Efron and Tibshirani 1993; Davison and Hinkley 1997). It generates the confidence intervals for return levels which are used to compute statistical significance (Dupuis and Field 1998; Kharin and Zweirs 2005; Kharin et al. 2007).

The changes in the 30-year return levels that are subjected to the uncertainty resulting from the fitting of distribution are evaluated with bootstrapping approach. Following Kharin and Zwiers (2005), the extremes are sub-sampled (with repetition) 1000 times. These new samples are used to re-estimate the extreme distribution parameters and the corresponding return quantiles. The difference between (future and historical values) two return level estimates is said to be statistically significant at 20% when their confidence bands have less than 60% overlap (Kharin and Zwiers 2005).

3 Results and discussion

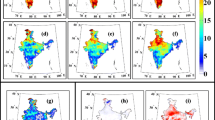
We apply the conventional statistical downscaling and evaluate its performance for Indian monsoon mean and extremes over the historic period (1981–2000). The results are presented in Fig. 2. For mean ISMR, we observe both the statistically downscaled evaluation runs (from reanalysis) and GCM simulations perform well, specifically in capturing the spatial patterns (Fig. 2a–c). We further evaluate the same for extremes using both the methods, viz., Block Maxima (BM) and Peak over Threshold (PoT) (Fig. 2d–i). The errors are computed in terms of 30 years return levels and are observed to be even as high as 80–100% at many locations. The discrepancy between BM and PoT suggests the existence of multiple extremes other than the maxima in a season that significantly affects the extreme rainfall quantiles corresponding to return levels. Figure 2 shows similar spatial pattern of return levels from BM and PoT, however; there are significant discrepancies at multiple locations. These attribute to the existence of multiple statistically impactful extremes other than seasonal maxima. Such differences are also reported for other regions (Adamowski 2000). This shows the necessity of special treatment for extremes in downscaled climate simulations/ projections.

Fig. 2
figure 2

The rainfall simulations based on methodology developed by Salvi et al. (2013). Mean ISMR (a–c) is well captured by the downscaling model with the predictors from NCEP/NCAR reanalysis and GCMs. However, simulations of extreme rainfall with Block Maxima (BM) and Peak over Threshold (PoT) (e, h) approaches indicate high absolute percentage errors (f, i)

Full size image

To apply specific algorithms to the rainfall extremes, the first step would be the identification of extreme days. We compute the 95 percentile rainfall values for individual grids from the conventionally downscaled simulations separately and identify the extreme days based on them. The detection of extreme days is evaluated with Heidke Skill Score (HSS). The score is around 15% for majority of the locations (Fig. 3) and this has been considered as a reasonable value for climate simulations (Maity and Nagesh Kumar 2008).

Fig. 3
figure 3

The detection of extreme days as evaluated with the Heidke skill score (HSS)

Full size image

We apply the modified approach to these extremes days. As mentioned in Sect. 2.2, the best regression at stage 2 is not necessarily the RR, and there are locations where KR is doing better (Supplementary Fig. S3). We select the best among KR and RR for individual grids and then apply the extreme value analysis for the evaluation. Here, we find RR performs better for 58% (2894 nodes) of nodes, while KR performs better for the rest. Hence, we have made a grid specific selection of methods. This step is performed independently to all the grids. The results show (Fig. 4) significant decrease in the absolute percentage errors in terms of 30 years return levels. The results of the absolute percentage errors across nodes for all India (Supplementary Table T1(a)) and zone wise for the NCEP/NCAR simulated extremes (Supplementary Table T1(b)) show the maximum percentage nodes lie within 5% error.

Fig. 4
figure 4

Spatial variation of the simulated extreme rainfall corresponding to 30 years return period and the absolute errors with respect to observed data. The extreme rainfall is simulated by modified downscaling algorithm using NCEP/NCAR predictors. a Spatial map of 30 year return level (30RL) intensity estimated by BM approach and its absolute errors (b). Similarly the analysis is further carried with PoT approach, where (c) depicts the spatial variation of the 30 years extreme precipitation with absolute errors (d)

Full size image

Further, we have performed a cross validation of our model with different combinations as presented in Supplementary Table T2. The total 40 years data is split into 4 parts each with 10 years data, viz., 1961–1970 (A), 1971–1980 (B), 1981–1990 (C) and 1991–2000 (D). For e.g. AD-BC combination denotes that the model is trained for A and D period (1961–1970 and 1991–2000) and tested for B and C (1971–1980 and 1981–1990) period for the projections of extremes using modified statistical downscaling model with NCEP/NCAR predictors. Similarly the results for other combinations are obtained and presented in the (Supplementary Fig. S4). The results indicate satisfactory performance for above mentioned combinations except for AD (Training) -BC (Testing) combination where we observe absolute percentage being slightly high in some regions.

We present the scatter plots where the errors for conventional and modified downscaling methods are presented (Fig. 5). Each of the points in the scatter plot represents each grid. For both BM and PoT, the errors have been reduced significantly. The improvements are more in BM method, compared to PoT and probably this is because of the errors in identification of extreme days. PoT considers all the extreme days and hence the errors are slightly more than those of BM; however the performance is still better than the conventionally downscaled simulations. The discrepancy in the results between BM and PoT needs to be further explored with a detailed sensitivity analysis and may be considered as the potential area of future research. To check the reliability and also to compare with the results obtained from the GEV distributions, we have now performed the PoT with the thresholds 97.5 and 99 percentile. However, by changing the threshold, the discrepancies between the results from PoT and BM cannot be reduced (Supplementary Fig. S5). Further at the same time, we observe that 94% of nodes are not violating the IID assumption at 5% significance level, when 95 percentile rainfalls is considered as threshold. Hence, we perform the rest of the analysis with 95 percentile rainfall as threshold and this may be considered as limitation of the present work. The discrepancy between the results obtained from BM and PoT is one of the limitations of the present model.

Fig. 5
figure 5

Scatter plots of absolute errors for simulated extreme precipitation from modified downscaling method conventional downscaling Method. The results are obtained for both BM (a) and PoT approaches (b)

Full size image

We apply the modified downscaling algorithms to the CMIP5 GCMs, and present the ensemble mean of 30 years return levels in Fig. 6. The model captures high return levels at the Western Ghats when applied to the GCM simulations. High return levels are also observed over some of the regions of North East India. However, the plots are spotty with high quantiles at few locations in the central India. The error diagram shows that the percentage deviations of simulated extremes from observed are within permissible limits. We also performed the analysis for 10 year return period to understand the spatial pattern of errors with respect to 30 year return period. We found the similarity in the spatial pattern both in 10 and 30 years return levels, however, the errors are high in later case, mainly due to the extrapolation (Supplementary Fig. S6). Nonetheless, it should be noted that the main motivation of the present work is to develop the methodology for extreme downscaling especially for ISMR. Once the methodology is developed any return levels can further be computed based on the sample size availability.

Fig. 6
figure 6

Same as Fig. 4, when the bias corrected predictors are used from historic simulations of CMIP5 models

Full size image

The proposed method does not really consider the association among predictors while correcting the bias. The predictors have significant correlation among themselves and this cannot be taken care with the methodology proposed by Li et al. (2010). Impacts of such limitation will be more significant for extremes. This is required to be incorporated with the approach suggested by Mehrotra and Sharma (2015) in the present model. This is a potential area of future research. We apply the same to the future (2081–2100) projections of GCM simulations. We keep the threshold for the future as same to the 95 percentile of the current climate. This is to deal with the possible large changes in the future.

Selection of predictors have remained a major challenge in statistical downscaling and there have been a recent development in the literature on the same. Here, we have employed such a method by using partial weight to the predictors, as described in Sharma et al. (2016) for the projections of extremes. This study uses the non parametric predictive model using Partial Informational Correlation (PIC) and Partial Weights (PW) model. Non parameter Prediction (NPRED) identifies predictors using PIC and predicts the response using a k-nearest neighbor regression formulation based on a PW based weighted Euclidean distance. The results from this formulation show similar performance (Supplementary Fig S7) to the same obtained with the proposed model. However, such an approach may add value in other regions and should be employed.

We present the spatial variations of historic and future return quantiles (multi-model mean) as obtained for India and Central India with their respective PDFs (Fig. 7). The Block Maxima (BM) method shows increase in the spatial average of projected return levels in future for both the cases, India and Central India. This is consistent with the observed trends as concluded in Goswami et al. (2006). However the PoT does not show any significant difference between the historic and future period in spatial average of return levels. Both the methods show increase in the standard deviation of return levels, which denotes the increase in spatial variability. This is consistent with the observed characteristics as analyzed by Ghosh et al. (2012). The increase in spatial variability is less for PoT compare to BM in Central India.

Fig. 7
figure 7

PDFs, standard deviation and box plots of the 30 years extreme precipitation for historical (1981–2000) and future (2081–2100) periods for All India and Central India (as considered in Goswami et al. 2006). Both BM and PoT are used to compute the 30 years extreme precipitation. The spatial variability of extremes are presented with PDFs for All India using Block Maxima (a), and PoT (d) and for Central India using Block Maxima (g), and PoT (j). The blue solid vertical lines represent the mean for historical, and the magenta lines represent the mean for future. The standard deviations resulting from the spatial variations for all the four cases are plotted in (b), (e), (h) and (k). The corresponding box plots are presented in (c), (f), (i) and (l)

Full size image

We also present the changes in return levels as obtained with BM method for future with respect to the same for historic (Fig. 8). We show the changes which are significant at 20% level with less than 60% overlap (Vittal et al. 2016) between the uncertainty bands of historic and future extremes. The results show spatially non-uniform changes in extremes for all the downscaled GCM simulations, which are consistent with the observed data (Ghosh et al. 2012). We also present results with 80% overlap (10% confidence level) in Supplementary Fig. S8 and Supplementary Fig. S9 for both BM and PoT approaches. The spatial patterns remain the same. We present the zone wise distribution of changes in rainfall in Supplementary Table T3 for both BM and PoT approaches. Here, we find increase in extremes over majority of the locations in Central India and the grids which are showing increasing changes are clustered together. This observation is consistent across all the GCMs. We find almost similar number of grid points has undergone positive and negative changes in return levels for multi-model mean, though Fig. 7 shows increase in spatial average for multi-model mean. This attributes to the statistically non-significant changes that were considered in computing the average in Fig. 7 as well to the very high magnitude of changes in the increasing grid points than those of the decreasing grid points. This points to the necessity of using extreme value theory with statistical significance in analysis of extremes rather than simple count based approaches with a low sample of rare events. We also find that a significant area in the North – East India will receive fewer extremes in future period (2081–2100) compared to historical period (1981–2000) and this has significant implications considering the highest rainfall occurrences over this area at present.

Fig. 8
figure 8

The Changes in 30 year RL extreme precipitation during historical (198–2000) and future (2081–2100) for BM approach for each of the GCMs considered in the study. Following the bootstrap approach, the changes in 30RL is estimated at 20% significance level. The pie chart inside the maps represents the percentages of the total grids with statistically significant positive, negative and no change respectively

Full size image

We present the projected changes in return levels as obtained with PoT and find similar spatially non-uniform changes as those obtained with BM (Fig. 9). Here we find that the increase is less compared to BM. The differences in the results obtained from BM and PoT show that seasonal or Block maxima probably do not present the extremes occurring in the entire season and consideration of such cases needs PoT approach. In the results from the PoT method, the increasing grid points are observed to be clustered in the Central India, which is very similar to that obtained from BM.

Fig. 9
figure 9

Same as Fig. 8, but with PoT approach

Full size image

It should be noted that local factors such as urbanization (Shastri et al. 2015), deforestation play major role in the changing pattern of precipitation and such forcing are not considered in the present work. Changing patterns of extremes make the extreme value analysis non-stationary, which may need a special treatment such as Generalized Additive Models for Location, Scale and Shape (GAMLSS) (Villarini et al. 2009, 2010) and such an approach has not been applied here. Downscaling for extremes with its extreme value analysis with GAMLSS may be considered as a potential area for future research.

4 Summary and conclusions

Projections of rainfall extremes are a major research challenge in climate science which is even more difficult for ISMR. Here we find the conventional statistical downscaling fails to simulate the characteristics of extremes because the transfer function (regression) can model the expected quantity, but not the higher quantiles. We develop 2-stage regression, where an extra regression is applied only for extreme days after the conventional downscaling. The outliers in the regression are taken care by robust regression, whereas the nonlinearity is addressed with kernel regression. The developed model captures well the extremes along with its spatial variability. The return levels of extremes are obtained with statistically rigorous extreme value theory where both BM and PoT are used. The future projections show spatially non-uniform changes in extreme rainfall with increase in spatial variability. Similar changes are also observed in recent periods (Ghosh et al. 2012) and hence this characteristic of downscaled projections is consistent with the recent observed trend. Furthermore, we find increase in the spatial average of extremes for India and Central India as computed with BM, which is consistent with observed trend (Goswami et al. 2006). We also find that the PoT approach does not show distinct increase of extremes. Testing of statistical significance with bootstrapping to address uncertainty in fitting of distribution shows the increasing grid points are clustered together mostly in the Central Indian belt and possibly result into increase in extremes for the same region. However, spatial non-uniformity in statistically significant changes of extremes is distinctly visible in India during 2081–2100, as compared to the historic period. Though the present study is a successful attempt to downscale the rainfall extreme for Indian monsoon, however, there are some limitations that can be addressed in future. The first limitation is: The Statistical downscaling (SD) model firstly establishes relationship between reanalysis predictors and predictand (observed extreme rainfall) during the historical period. The same established relation is used for future projections for the GCM simulated synoptic scale climate predictors. This statistical relationship, extracted from historical data remains unaltered, despite non-stationary change in climate (Salvi et al. 2016). It is true that the performance of the proposed model needs to be tested in a non-stationary climate and the design of experiments proposed by Salvi et al. (2016) may be used for the same. The increase in extremes during future may not be visible in the projections possibly due to the failure of the model in a non-stationary climate; however at the same time it should also be noted that dependence of the intensification of Indian monsoon extremes on warming of land and sea surface is weak (Vittal et al. 2016). This deserves a detailed analysis and should be a potential area of future research. Further, the non-stationarity in the distribution parameters fitted to simulated data set has not been considered. The second limitation is that the local effects such as impacts of deforestation and urbanization have not been considered in this study. Incorporation of local changes has been practiced in dynamic downscaling framework by coupling with a land surface model; however, incorporating them in statistical framework remains a challenge and may also be considered as a potential scope for future research.