Small Matchings Extend to Hamiltonian Cycles in Hypercubes

Abstract

Ruskey and Savage asked the following question: does every matching of a hypercube $Q_{n}$ for $n\ge 2$ extend to a Hamiltonian cycle of $Q_{n}$? Fink confirmed that the question is true for every perfect matching, thus solved Kreweras’ conjecture. In this paper we prove that every matching of at most $3n-10$ edges can be extended to a Hamiltonian cycle of $Q_{n}$ for $n\ge 4$.

1 Introduction

The $n$-$dimensional$ $hypercube$ $Q_{n}$ is a graph whose vertex set consists of all binary strings of length $n$, with two vertices being adjacent whenever the corresponding strings differ in just one position.

It is well known that $Q_{n}$ is Hamiltonian for every $n\ge 2$. This statement dates back to 1872 [9]. Since then, the research on Hamiltonian cycles in hypercubes satisfying certain additional properties has received considerable attention.

A set of edges in a graph $G$ is called a matching if no two edges have an end-vertex in common. A matching is perfect if it covers all of $V(G)$. Ruskey and Savage [12] asked the following question: does every matching of $Q_{n}$ for $n\ge 2$ extend to a Hamiltonian cycle of $Q_{n}$? Kreweras [11] conjectured that every perfect matching of $Q_{n}$ for $n\ge 2$ can be extended to a Hamiltonian cycle of $Q_{n}$. Fink [4, 6] solved the conjecture. Also, Fink in [4] pointed out that Ruskey and Savage’s question is true for $n=2,3,4$.

Gregor [7] strengthened Fink’s result and obtained that given a partition of the hypercube into subcubes of nonzero dimensions, every perfect matching of the hypercube can be extended on these subcubes to a Hamiltonian cycle if and only if it interconnects them.

A complementary problem of Hamiltonian cycles in $Q_{n}$ avoiding given matchings has been already settled for arbitrary matchings by Dimitrov et al. [2]. In particular, the authors in [2] proved that $Q_{n}$ has a Hamiltonian cycle faulting a perfect matching $M$ if and only if $Q_{n}-M$ is connected.

The $matching$ $graph$ $\mathcal {M}(G)$ of a graph $G$ has a vertex set of all perfect matchings of $G$, with two vertices being adjacent whenever the union of the corresponding perfect matchings forms a Hamiltonian cycle of $G$. Fink [5, 6] proved that the matching graph $\mathcal {M}(Q_{n})$ of the $n$-dimensional hypercube is bipartite and connected for $n\ge 4$. This proved Kreweras’ conjecture [11] that the graph $M_{n}$ is connected, where $M_{n}$ is obtained from $\mathcal {M}(Q_{n})$ by contracting all vertices of $\mathcal {M}(Q_{n})$ which correspond to isomorphic perfect matchings.

The following result obtained by Dvořák implied that Ruskey and Savage’s question is true for every matching of at most $2n-3$ edges. A forest is $linear$ if each component of it is a path.

Lemma 1.1

[3] For $n\ge 2$, let $E\subseteq E(Q_{n})$ with $|E|\le 2n-3$. Then there exists a Hamiltonian cycle of $Q_{n}$ containing $E$ if and only if the subgraph induced by $E$ is a linear forest.

In a bipartite graph $G$, a set $S\subseteq V(G)$ is $deficient$ if $|N(S)|<|S|$. A matching $M$ (with vertex set $U$) is $k$-$suitable$ if $G-U$ has no deficient set of size less than $k$. Vandenbussche and West [14] proved that every $k$-suitable matching of at most $k(n-k)+\frac{(k-1)(k-2)}{2}$ edges for $k\le n-3$ and every induced matching can be extended to a perfect matching of $Q_{n}$, so can be extended to a Hamiltonian cycle of $Q_{n}$ by Fink’s result quoted above.

Ruskey and Savage’s question has been resolved for perfect matchings only, while the general case is still widely open. In this paper, we consider this question and obtain the following result.

Theorem 1.2

For $n\ge 4$, let $M$ be a matching of $Q_{n}$ with $|M|\le 3n-10$. Then there exists a Hamiltonian cycle containing $M$ in $Q_{n}$.

The rest of this paper is organized as follows. In Sect. 2 we introduce some conclusions about path partitions of $Q_{n}$. The main result is proved in Sect. 3.

2 Path Partitions of $Q_{n}$

This section is devoted to auxiliary results about path partitions which are applied in the constructions of Hamiltonian cycles in the main result. First, we introduce some necessary definitions.

The vertex and edge sets of a graph $G$ are denoted by $V(G)$ and $E(G)$ respectively. For a vertex $v\in V(G)$ and a set $E\subseteq E(G)$, let $G-v$ denote the subgraph of $G$ induced by $V(G){\setminus }\{v\}$, let $G-E$ denote the graph with vertices $V(G)$ and edges $E(G){\setminus } E$, let $\langle E\rangle$ denote the subgraph of $G$ induced by $E$ and let $N(v)$ denote the set $\{u\in V(G)\mid uv\in E(G)\}$. The distance of vertices $u$ and $v$ is denoted by $d(u,v)$. The distance $d(u,xy)$ of a vertex $u$ and an edge $xy$ is defined by $d(u,xy):=\min \{d(u,x),d(u,y)\}$ and the distance $d(uv,xy)$ of edges $uv$ and $xy$ is defined by $d(uv,xy):=\min \{d(u,xy),d(v,xy)\}$. For a vertex $u=(\delta _{1},\delta _{2},\ldots ,\delta _{n})\in V(Q_{n})$, we define the $parity$ of $u$ by $p(u)=(-1)^{|\{i\in [n]\mid \delta _{i}=1\}|}$. Note that vertices of each parity form bipartite sets of $Q_{n}$. Consequently, $p(u)=p(v)$ if and only if $d(u,v)$ is even.

An edge in $Q_{n}$ is called an $i$-$dimensional$ $edge$ if its endvertices differ in the $i$th position. The set of all $i$-dimensional edges of $Q_{n}$ is denoted by $E_{i}$. Let $[n]$ denote the set $\{1,2,\ldots ,n\}$. For any given $j\in [n]$, let $Q_{n-1}^{0,j}$ and $Q_{n-1}^{1,j}$, with the superscript $j$ being omitted when the context is clear, be two $(n-1)$-dimensional subcubes of $Q_{n}$ induced by all the vertices with the $j$th positions being 0 or 1, respectively. Clearly, $Q_{n}-E_{j}=Q_{n-1}^{0}\cup Q_{n-1}^{1}$, we say that $Q_{n}$ is decomposed into two $(n-1)$-dimensional subcubes $Q_{n-1}^{0}$ and $Q_{n-1}^{1}$ by $E_{j}$. For $\delta \in \{0,1\}$, any vertex $u\in V(Q_{n-1}^{\delta })$ has in $Q_{n-1}^{1-\delta }$ a unique neighbor, denoted by $u_{1-\delta }$ and for any edge $e=uv\in E(Q_{n-1}^{\delta })$, $e_{1-\delta }$ denotes the edge $u_{1-\delta }v_{1-\delta }\in E(Q_{n-1}^{1-\delta })$. Given $M\subseteq E(Q_{n})$, let $M_{\delta }:=M\cap E(Q_{n-1}^{\delta })$.

Lemma 2.1

[13] For $n\ge 2$, let $e$ and $f$ be two disjoint edges in $Q_{n}$. Then $Q_{n}$ can be decomposed into two $(n-1)$-dimensional subcubes such that one contains $e$ and the other contains $f$.

A $path$ $partition$ of a graph $G$ is a set of vertex-disjoint paths that cover all vertices of $G$. Given a set $E$ of edges, a path $P$ $passes$ $through$ $E$ if $E\subseteq E(P)$. Similarly, a set $\{P_{i}\}_{i=1}^{k}$ of paths $passes$ $through$ $E$ if $E\subseteq \bigcup _{i=1}^{k}E(P_{i})$. We use $P_{uv}$ to denote a path between vertices $u$ and $v$.

First, let us recall the following classical result, originally obtained by Havel in [10].

Lemma 2.2

[10] Let $x,y\in V(Q_{n})$ such that $p(x)\ne p(y)$. Then there exists a Hamiltonian path between $x$ and $y$ in $Q_{n}$.

Lemma 2.3

[3] For $n\ge 2$, let $x,y\in V(Q_{n})$ and $e\in E(Q_{n})$ such that $p(x)\ne p(y)$ and $e\ne xy$. Then there is a Hamiltonian path of $Q_{n}$ between $x$ and $y$ passing through edge $e$.

Lemma 2.4

For $n\ge 4$, let $e$ and $f$ be two disjoint edges in $Q_{n}$ and $x,y\in V(Q_{n})$ such that $p(x)\ne p(y)$ and $xy\notin \{e,f\}$. Then there is a Hamiltonian path of $Q_{n}$ between $x$ and $y$ passing through $\{e,f\}$.

Proof

By Lemma 2.1, $Q_{n}$ can be decomposed into subcubes $Q_{n-1}^{0}$ and $Q_{n-1}^{1}$ such that $e\in E(Q_{n-1}^{0})$ and $f\in E(Q_{n-1}^{1})$. Without loss of generality, assume that $x\in V(Q_{n-1}^{0})$.

If $y\in V(Q_{n-1}^{0})$, since $p(x)\ne p(y)$ and $xy\ne e$, by Lemma 2.3 there is a Hamiltonian path $P_{xy}$ of $Q_{n-1}^{0}$ passing through edge $e$. Let $uv\in E(P_{xy}){\setminus }\{e\}$ such that $u_{1}v_{1}\ne f$ and using Lemma 2.3 again, there is a Hamiltonian path $P_{u_{1}v_{1}}$ of $Q_{n-1}^{1}$ passing through $f$. Then the desired Hamiltonian path of $Q_{n}$ is induced by edges of $(E(P_{xy})\cup E(P_{u_{1}v_{1}})\cup \{uu_{1},vv_{1}\}){\setminus }\{uv\}$.

If $y\in V(Q_{n-1}^{1})$, choose a vertex $w\in V(Q_{n-1}^{0})$ such that $p(x)\ne p(w)$ and $xw\ne e, yw_{1}\ne f$. Note that as $|\{w\in V(Q_{n-1}^{0})\mid p(x)\ne p(w)\}|=2^{n-2}>2$ for $n\ge 4$, this is always possible. Since $p(w_{1})=p(x)\ne p(y)=p(w)$, by Lemma 2.3 there exist Hamiltonian paths $P_{xw}$ of $Q_{n-1}^{0}$ and $P_{w_{1}y}$ of $Q_{n-1}^{1}$ passing through $e$ and $f$, respectively. Hence the desired Hamiltonian path of $Q_{n}$ is induced by edges of $E(P_{xw})\cup \{ww_{1}\}\cup E(P_{w_{1}y})$. $\square$

Lemma 2.5

[3] For $n\ge 2$, let $x,y,u,v$ be pairwise distinct vertices of $Q_{n}$ such that $p(x)\ne p(y)$ and $p(u)\ne p(v)$. Then (i) there exists a path partition $\{P_{xy},P_{uv}\}$ of $Q_{n}$; (ii) moreover, in the case when $d(x,y)=1$, path $P_{xy}$ can be chosen such that $P_{xy}=xy$, unless $n=3$, $d(u,v)=1$ and $d(xy,uv)=2$.

Lemma 2.6

For $n\ge 5$, let $uv$ and $f$ be two disjoint edges in $Q_{n}$ and $x,y\in V(Q_{n}){\setminus }\{u,v\}$ such that $p(x)\ne p(y)$ and $xy\ne f$. Then there exists a Hamiltonian path between $x$ and $y$ passing through edge $f$ in $Q_{n}-\{u,v\}$.

Proof

By Lemma 2.1, $Q_{n}$ can be decomposed into subcubes $Q_{n-1}^{0}$ and $Q_{n-1}^{1}$ such that $uv\in E(Q_{n-1}^{0})$ and $f\in E(Q_{n-1}^{1})$.

If $x,y\in V(Q_{n-1}^{0})$, since $n-1\ge 4$, by Lemma 2.5 there is a Hamiltonian path $P_{xy}$ in $Q_{n-1}^{0}-\{u,v\}$. Let $st\in E(P_{xy})$ such that $s_{1}t_{1}\ne f$ and apply Lemma 2.3 to find a Hamiltonian path $P_{s_{1}t_{1}}$ passing through $f$ in $Q_{n-1}^{1}$. Then the desired Hamiltonian path in $Q_{n}-\{u,v\}$ is induced by edges of $(E(P_{xy})\cup E(P_{s_{1}t_{1}})\cup \{ss_{1},tt_{1}\}){\setminus }\{st\}$.

If $x\in V(Q_{n-1}^{0})$ and $y\in V(Q_{n-1}^{1})$, choose a vertex $w\in V(Q_{n-1}^{0})$ such that $p(x)\ne p(w)$ and $w\notin \{u,v\},w_{1}y\ne f$. Note that as $|\{w\in V(Q_{n-1}^{0})\mid p(x)\ne p(w)\}|\ge 2^{n-2}\ge 8$ for $n\ge 5$, this is always possible. Since $p(w_{1})=p(x)\ne p(y)=p(w)$, by Lemmas 2.5 and 2.3 there exist a Hamiltonian path $P_{xw}$ in $Q_{n-1}^{0}-\{u,v\}$ and a Hamiltonian path $P_{w_{1}y}$ passing through $f$ in $Q_{n-1}^{1}$. Then the desired Hamiltonian path in $Q_{n}-\{u,v\}$ is induced by edges of $E(P_{xw})\cup E(P_{w_{1}y})\cup \{ww_{1}\}$.

If $x,y\in V(Q_{n-1}^{1})$, apply Lemma 2.3 to find a Hamiltonian path $P_{xy}$ passing through $f$ in $Q_{n-1}^{1}$. Since $|E(P_{xy}){\setminus }\{f\}|\ge 2^{n-1}-2>4$, there exists an edge $wt\in E(P_{xy}){\setminus }\{f\}$ such that $\{w_{0},t_{0}\}\cap \{u,v\}=\emptyset$. Since $n-1\ge 4$, by Lemma 2.5 there is a Hamiltonian path $P_{w_{0}t_{0}}$ in $Q_{n-1}^{0}-\{u,v\}$. Then the desired Hamiltonian path in $Q_{n}-\{u,v\}$ is induced by edges of $(E(P_{w_{0}t_{0}})\cup E(P_{xy})\cup \{w_{0}w,t_{0}t\}){\setminus }\{wt\}$. $\square$

A set $\{\{a_{i},b_{i}\}\}_{i=1}^{k}$ of pairs of distinct vertices of $Q_{n}$ is called a $balanced$ $pair$ $set$ if $\sum _{i=1}^{k}(p(a_{i})+p(b_{i}))=0$.

Lemma 2.7

[1] For $n\ge 4$, let $x,y,u,v$ be pairwise distinct vertices of $Q_{n}$ such that $p(x)=p(y)\ne p(u)=p(v)$. Then there exists a path partition $\{P_{xy},P_{uv}\}$ of $Q_{n}$.

Lemma 2.8

[8] For $n\ge 1$, let $\{\{a_{i},b_{i}\}\}_{i=1}^{k}$ be a balanced pair set in $Q_{n}$ such that $2k-|\{a_{i}b_{i}\}_{i=1}^{k}\cap E(Q_{n})|<n$. Then there exists a path partition $\{P_{a_{i}b_{i}}\}_{i=1}^{k}$ of $Q_{n}$.

Let $P=v_{1}v_{2}\ldots v_{i}\ldots v_{j}\ldots v_{k}$ be a path, we use $P[v_{i},v_{j}]$ to denote the subpath $v_{i} \ldots v_{j}$ of $P$ from $v_{i}$ to $v_{j}$. For an edge $e$, we use $V(e)$ to denote the set of two endvertices of $e$ and for a matching $M$, let $V(M):=\bigcup _{e\in M}V(e)$.

Lemma 2.9

For $n\ge 5$, let $e\in E(Q_{n})$ and $x,y,u,v\in V(Q_{n})$ be pairwise distinct vertices such that $p(x)\ne p(y)$, $p(u)\ne p(v)$ and $\{u,v\}\cap V(e)=\emptyset$. Then there exists a path partition $\{P_{xy},P_{uv}\}$ of $Q_{n}$ passing through edge $e$.

Proof

If $xy=e$, by Lemma 2.5 there exists a path partition $\{P_{xy}=xy,P_{uv}\}$ of $Q_{n}$, and hence the conclusion holds. So in what follows we shall assume that $xy\ne e$. Without loss of generality we may assume $y\notin V(e)$ and $p(y)=p(v)\ne p(x)=p(u)$. Since $d(x,u)\ge 2$, there exists $j\in [n]$ such that $x\in V(Q_{n-1}^{0})$, $u\in V(Q_{n-1}^{1})$ and $e\notin E_{j}$. If $x\in V(e)$, then $e\in E(Q_{n-1}^{0})$. If $x\notin V(e)$, then without loss of generality we may assume $e\in E(Q_{n-1}^{0})$.

First, we suppose $v\in V(Q_{n-1}^{0})$. Since $p(x)\ne p(v)$ and $xv\ne e$, by Lemma 2.3 there is a Hamiltonian path $P_{xv}$ passing through edge $e$ in $Q_{n-1}^{0}$. If $y\in V(Q_{n-1}^{0})$, let $w$ be the neighbor of $y$ such that $w\in V(P_{xv}[y,v])$. Since $y\notin V(e)$, we have $yw\ne e$. Since $p(w_{1})=p(y)\ne p(u)$, by Lemma 2.2 there is a Hamiltonian path $P_{w_{1}u}$ in $Q_{n-1}^{1}$. Then $\{P_{xv}[x,y],$ $\langle E(P_{xv}[v,w])\cup \{ww_{1}\}\cup E(P_{w_{1}u})\rangle \}$ is the desired path partition of $Q_{n}$. If $y\in V(Q_{n-1}^{1})$, since $|E(P_{xv}){\setminus }\{e\}|=2^{n-1}-2>4$ for $n\ge 5$, there exists an edge $st\in E(P_{xv}){\setminus }\{e\}$ such that $\{s_{1},t_{1}\}\cap \{u,y\}=\emptyset$. Assume that $s$ lies on $P_{xv}[x,t]$, which means that $s$ is closer to $x$ on $P_{xv}$ than $t$. Since $p(s_{1})\ne p(t_{1}), p(y)\ne p(u)$ and $n-1\ge 4$, using Lemma 2.5 in case $p(s_{1})\ne p(y)$ or Lemma 2.7 in case $p(s_{1})=p(y)$, there exists a path partition $\{P_{s_{1}y},P_{t_{1}u}\}$ of $Q_{n-1}^{1}$. Then $\{\langle E(P_{xv}[x,s])\cup \{ss_{1}\}\cup E(P_{s_{1}y})\rangle ,$ $\langle E(P_{xv}[v,t])\cup \{tt_{1}\}\cup E(P_{t_{1}u})\rangle \}$ is the desired path partition of $Q_{n}$.

Next, we consider $v\!\in \! V(Q_{n-1}^{1})$. If $y\!\in \! V(Q_{n-1}^{0})$, by Lemmas 2.3 and 2.2 there exist Hamiltonian paths $P_{xy}$ of $Q_{n-1}^{0}$ passing through $e$ and $P_{uv}$ of $Q_{n-1}^{1}$, then $\{P_{xy},P_{uv}\}$ is the desired path partition of $Q_{n}$. If $y\in V(Q_{n-1}^{1})$, since $|\{w\in V(Q_{n-1}^{1}){\setminus }\{u\}\mid p(w)=p(u)\}|\ge 2^{n-2}-1>1$, there exists a vertex $w\in V(Q_{n-1}^{1}){\setminus }\{u\}$ such that $p(w)=p(u)$ and $xw_{0}\ne e$. Note that then $p(x)=p(u)=p(w)\ne p(y)=p(v)=p(w_{0})$. By Lemma 2.3 there is a Hamiltonian path $P_{xw_{0}}$ passing through $e$ in $Q_{n-1}^{0}$ and by Lemma 2.5 there exists a path partition $\{P_{wy},P_{uv}\}$ of $Q_{n-1}^{1}$. Then $\{\langle E(P_{xw_{0}})\cup \{w_{0}w\}\cup E(P_{wy})\rangle ,$ $P_{uv}\}$ is the desired path partition of $Q_{n}$. $\square$

Lemma 2.10

Let $ux,vy\in E(Q_{4})$ be two disjoint edges and $e\in E(Q_{4})$ such that $\{u,v\}\cap V(e)=\emptyset$ and $xy\ne e$. Then there exists a path partition $\{P_{ux},P_{vy}\}$ of $Q_{4}$ passing through edge $e$.

Proof

By Lemma 2.1, $Q_{4}$ can be decomposed into $Q_{3}^{0}$ and $Q_{3}^{1}$ by some $E_{j}$ such that $ux\in E(Q_{3}^{0})$ and $vy\in E(Q_{3}^{1})$. If $e\in E_{j}$, let $e=ww_{1}$. Since $xy\ne e=ww_{1}$, by symmetry, we may assume that $x\ne w$. Since $|\{s\in V(Q_{3}^{0})\mid p(s)\ne p(w)\}|=4$, there exists a vertex $s\in V(Q_{3}^{0})$ such that $p(s)\ne p(w)$ and $s\notin \{u,x\}$, $s_{1}\ne v$. By Lemma 2.5 there exists a path partition $\{P_{ux},P_{ws}\}$ of $Q_{3}^{0}$. Since $v\ne w_{1}$ and $v\ne s_{1}$, we have $w_{1}s_{1}\ne vy$. Since $p(w_{1})\ne p(s_{1})$, by Lemma 2.3 there exists a Hamiltonian path $P_{w_{1}s_{1}}$ of $Q_{3}^{1}$ passing through $vy$. Then $\{P_{ux},$ $\langle (E(P_{w_{1}s_{1}})\cup E(P_{ws})\cup \{ww_{1},ss_{1}\}){\setminus }\{vy\}\rangle \}$ is the desired path partition of $Q_{4}$. If $e\notin E_{j}$, by symmetry, we may assume that $e\in E(Q_{3}^{0})$. Since $p(u)\ne p(x), p(v)\ne p(y)$ and $ux\ne e$, by Lemmas 2.3 and 2.2 there exist Hamiltonian paths $P_{ux}$ of $Q_{3}^{0}$ passing through $e$ and $P_{vy}$ of $Q_{3}^{1}$. Then $\{P_{ux},P_{vy}\}$ is the desired path partition of $Q_{4}$. $\square$

Lemma 2.11

For $n\ge 4$, let $M$ be a matching of $Q_{n}$ with $|M|\le 2n-8$ and $ux,vy\in E(Q_{n})$ be two disjoint edges such that $\{u,v\}\cap V(M)=\emptyset$ and $xy\notin M$. Then there exists a path partition $\{P_{ux}^{'},P_{vy}^{'}\}$ of $Q_{n}$ passing through $M$.

Proof

We prove the lemma by induction on $n$. The lemma holds for $n=4$ by Lemma 2.5. Assume that the lemma holds for $n-1(\ge 4)$, we are to show it holds for $n(\ge 5)$.

Select $j\in [n]$ such that $|(M\cup \{ux,vy\})\cap E_{j}|$ is as small as possible. Since $|M\cup \{ux,vy\}|\le 2n-6$, we have $|(M\cup \{ux,vy\})\cap E_{j}|\le 1$. If $|(M\cup \{ux,vy\})\cap E_{j}|=1$, since $|(M\cup \{ux,vy\})\cap E_{i}|\ge 1$ for any $i\in [n]$, there are at least six possibilities of such $j$ and therefore, moreover, we can choose $j$ such that $(M\cup \{ux,vy\})\cap E_{j}=M\cap E_{j}:=\{ww_{1}\}$ and $\{x,y\}\cap \{w,w_{1}\}=\emptyset$. Decompose $Q_{n}$ into $Q_{n-1}^{0}$ and $Q_{n-1}^{1}$ by $E_{j}$. Since $\{ux,vy\}\subseteq E(Q_{n-1}^{0})\cup E(Q_{n-1}^{1})$, by symmetry, we may assume that $ux\in E(Q_{n-1}^{0})$.

Case 1. Suppose $vy\in E(Q_{n-1}^{1})$.

If $M\cap E_{j}=\emptyset$, since $M_{0}\cup \{ux\}$ and $M_{1}\cup \{vy\}$ are both linear forests of at most $2(n-1)-5$ edges, by Lemma 1.1 there exist Hamiltonian cycles $C_{0}$ of $Q_{n-1}^{0}$ and $C_{1}$ of $Q_{n-1}^{1}$ containing $M_{0}\cup \{ux\}$ and $M_{1}\cup \{vy\}$, respectively. Then $\{C_{0}-ux,C_{1}-vy\}$ is the desired path partition of $Q_{n}$.

If $M\cap E_{j}=\{ww_{1}\}$, since $\{u,v\}\cap V(M)=\emptyset$ and $\{x,y\}\cap \{w,w_{1}\}=\emptyset$, we have $\{u,v,x,y\}\cap \{w,w_{1}\}=\emptyset$. By symmetry, we may assume that $|M_{0}|\ge |M_{1}|$. Since $|N(w_{1})\cap V(Q_{n-1}^{1})|=n-1>3$ for $n\ge 5$ and $p(v)\ne p(y), p(u)\ne p(x)$, there exists a vertex $s\in N(w_{1})\cap V(Q_{n-1}^{1})$ such that $s\notin \{v,y\}, s_{0}\notin \{u,x\}$ and $sy\notin M_{1}$. Then $w_{1},s,v,y$ are pairwise distinct vertices satisfying $\{w_{1},v\}\cap V(M_{1})=\emptyset$, $w_{1}s,vy\in E(Q_{n-1}^{1})$ and $sy\notin M_{1}$. Since $|M_{0}|+|M_{1}|\le 2n-9$ and $|M_{0}|\ge |M_{1}|$, we have $|M_{1}|\le n-5\le 2(n-1)-8$ and therefore by the induction hypothesis, there exists a path partition $\{P_{w_{1}s},P_{vy}\}$ of $Q_{n-1}^{1}$ passing through $M_{1}$. Since $M_{0}$ is a matching, $\{u,w\}\cap V(M_{0})=\emptyset$ and $u,x,w,s_{0}$ are pairwise distinct vertices, we obtain that $M_{0}\cup \{ux,ws_{0}\}$ is a linear forest of at most $2(n-1)-5$ edges and therefore by Lemma 1.1, there is a Hamiltonian cycle $C_{0}$ containing $M_{0}\cup \{ux,ws_{0}\}$ in $Q_{n-1}^{0}$. Then $\{P_{ux}^{'}:=\langle (E(C_{0})\cup E(P_{w_{1}s})\cup \{ww_{1},s_{0}s\}){\setminus }\{ux,ws_{0}\}\rangle ,$ $P_{vy}^{'}:=P_{vy}\}$ is the desired path partition of $Q_{n}$.

Case 2. Suppose $vy\in E(Q_{n-1}^{0})$.

Claim 1 If there is a path partition $\{P_{ux},P_{vy}\}$ of $Q_{n-1}^{0}$ passing through $M_{0}$, then we can construct a path partition $\{P_{ux}^{'},P_{vy}^{'}\}$ of $Q_{n}$ passing through $M$.

If $M\cap E_{j}=\{ww_{1}\}$, without loss of generality, assume that $w\in V(P_{ux})$. Select a neighbor $t$ of $w$ on $P_{ux}$. Since $M$ is a matching and $ww_{1}\in M$, we have $\{wt,w_{1}t_{1}\}\cap M=\emptyset$. If $M\cap E_{j}=\emptyset$, without loss of generality, assume that $|E(P_{ux})|\ge |E(P_{vy})|$, then $|E(P_{ux})|\ge 2^{n-2}-1$. Since $|E(P_{ux}){\setminus } M_{0}|-|M_{1}|\ge 2^{n-2}-1-(2n-8)\ge 5$ for $n\ge 5$, we can choose an edge $wt\in E(P_{ux}){\setminus } M_{0}$ with $w_{1}t_{1}\notin M_{1}$. In both cases, $M_{1}\cup \{w_{1}t_{1}\}$ is a linear forest of at most $2(n-1)-5$ edges. By Lemma 1.1 there is a Hamiltonian cycle $C_{1}$ containing $M_{1}\cup \{w_{1}t_{1}\}$ in $Q_{n-1}^{1}$. Then $\{P_{ux}^{'}:=\langle (E(P_{ux})\cup E(C_{1})\cup \{ww_{1},tt_{1}\}){\setminus }\{wt,w_{1}t_{1}\}\rangle ,$ $P_{vy}^{'}:=P_{vy}\}$ is the desired path partition of $Q_{n}$. Claim 1 is proved.

If $|M_{0}|\le 2(n-1)-8$, by the induction hypothesis, there exists a path partition $\{P_{ux},P_{vy}\}$ of $Q_{n-1}^{0}$ passing through $M_{0}$. Then the lemma holds by Claim 1. So in what follows it suffices to consider the case that $|M_{0}|\ge 2n-9$. Since $|M|\le 2n-8$, we have $|M_{1}|\le 1$. We distinguish two subcases to consider.

Subcase 2.1. $M_{1}=\emptyset$. Since $M_{0}\cup \{ux,vy\}$ is a linear forest of at most $2(n-1)-4$ edges, by Lemma 1.1 there is a Hamiltonian cycle $C_{0}$ containing $M_{0}\cup \{ux,vy\}$ in $Q_{n-1}^{0}$. Observe that $C_{0}-\{ux,vy\}$ is a disjoint union of two paths $P_{u}$ and $P_{x}$ with endvertices $u$ and $x$, respectively. If $M\cap E_{j}=\{ww_{1}\}$, since $\{u,v,x,y\}\cap \{w,w_{1}\}=\emptyset$, without loss of generality, we may assume that $w\in V(P_{u})$. Let $t$ be a neighbor of $w$ on $P_{u}$. Since $M$ is a matching and $ww_{1}\in M$, we have $wt\notin M$. Since $xy\notin M$ and $v\notin V(M)$, there exists an edge $sr\in E(P_{x}){\setminus } M$. If $M\cap E_{j}=\emptyset$, since $\{u,v\}\cap V(M)=\emptyset$ and $xy\notin M$, there exist edges $wt\in E(P_{u}){\setminus } M$ and $sr\in E(P_{x}){\setminus } M$.

Without loss of generality, assume that $w\in V(P_{u}[u,t])$ and $s\in V(P_{x}[x,r])$. Since $p(w_{1})\ne p(t_{1})$ and $p(s_{1})\ne p(r_{1})$, using Lemma 2.5 in case $p(w_{1})\ne p(s_{1})$ or Lemma 2.7 in case $p(w_{1})=p(s_{1})$, there exists a path partition $\{P_{w_{1}s_{1}},P_{t_{1}r_{1}}\}$ of $Q_{n-1}^{1}$. Then $\{P_{ux}^{'}:=\langle E(P_{u}[u,w])\cup E(P_{x}[x,s])$ $\cup \{ww_{1},ss_{1}\}\cup E(P_{w_{1}s_{1}})\rangle ,$ $P_{vy}^{'}:=\langle (E(P_{u}){\setminus } E(P_{u}[u,t]))\cup (E(P_{x}){\setminus } E(P_{x}[x,r]))$ $\cup \{tt_{1},rr_{1}\}\cup E(P_{t_{1}r_{1}})\rangle \}$ is the desired path partition of $Q_{n}$.

Subcase 2.2. $|M_{1}|=1$. Since $|M_{0}|\ge 2n-9$ and $|M|\le 2n-8$, we have $|M_{0}|=2n-9$ and $M\cap E_{j}=\emptyset$. If $n=5$, since $|M_{0}|=1$, by Lemma 2.10 there is a path partition $\{P_{ux},P_{vy}\}$ of $Q_{n-1}^{0}$ passing through $M_{0}$ and therefore, the lemma holds by Claim 1. If $n\ge 6$, since $|M_{0}|=2n-9\ge 3$, there exists an edge $wt\in M_{0}$ such that $\{x,y\}\cap \{w,t\}=\emptyset$. Apply the induction to find a path partition $\{P_{ux},P_{vy}\}$ of $Q_{n-1}^{0}$ passing through $M_{0}{\setminus }\{wt\}$. If $wt\in E(P_{ux})\cup E(P_{vy})$, then $\{P_{ux},P_{vy}\}$ is a path partition of $Q_{n-1}^{0}$ passing through $M_{0}$ and therefore, the lemma holds by Claim 1. If $wt\notin E(P_{ux})\cup E(P_{vy})$, without loss of generality, we may assume that $w\in V(P_{ux})$.

If $t\in V(P_{ux})$, let $s,r$ be neighbors of $w,t$ on $P_{ux}$, respectively, such that exactly one of $s$ and $r$ lies on $P_{ux}[w,t]$ and $s_{1}r_{1}\notin M_{1}$. Since $\{u,x\}\cap \{w,t\}=\emptyset$, this is always possible. Since $p(s_{1})\ne p(r_{1})$, by Lemma 2.3 there is a Hamiltonian path $P_{s_{1}r_{1}}$ passing through $M_{1}$ in $Q_{n-1}^{1}$. Then $\{P_{ux}^{'}:=\langle (E(P_{ux})\cup E(P_{s_{1}r_{1}})\cup \{wt,ss_{1},rr_{1}\}){\setminus }\{sw,rt\}\rangle ,$ $P_{vy}^{'}:=P_{vy}\}$ is the desired path partition of $Q_{n}$.

If $t\in V(P_{vy})$, without loss of generality, assume that $|E(P_{ux})|\ge |E(P_{vy})|$, then $|E(P_{ux})|\ge 2^{n-2}-1$. Choose a vertex $b\in V(P_{ux}){\setminus }\{w\}$ such that $p(b)=p(w)$ and $b\notin V(M_{0})$. Since $|\{b\in V(P_{ux}){\setminus }\{w\}\mid p(b)=p(w)\}|\ge 2^{n-3}-1\ge (2n-9)+4$ for $n\ge 6$, there are at least four ways to choose such $b$. Let $a$ be the neighbor of $b$ such that $a\in V(P_{ux}[b,w])$. Then, moreover, we can choose $b$ such that $a_{1}\notin V(M_{1})$. Since $b\notin V(M_{0})$, we have $ba\notin M_{0}$. Let $r$ be the neighbor of $w$ on $P_{ux}$ such that $w$ lies on $P_{ux}[r,a]$ and let $s$ be a neighbor of $t$ on $P_{vy}$ such that $s_{1}\notin V(M_{1})$. Since $\{u,v,x,y\}\cap \{w,t\}=\emptyset$, this is always possible. Then in $Q_{n-1}^{1}$, $p(r_{1})\ne p(b_{1}), p(s_{1})\ne p(a_{1})$ and $\{s_{1},a_{1}\}\cap V(M_{1})=\emptyset$. Since $n-1\ge 5$, by Lemma 2.9 there exists a path partition $\{P_{r_{1}b_{1}},P_{s_{1}a_{1}}\}$ of $Q_{n-1}^{1}$ passing through $M_{1}$. Since $M$ is a matching and $wt\in M$, we have $\{wr,ts\}\cap M=\emptyset$. Hence $\{P_{ux}^{'}:=\langle (E(P_{ux}){\setminus } E(P_{ux}[r,b]))\cup \{rr_{1},bb_{1}\}\cup E(P_{r_{1}b_{1}})\rangle ,$ $P_{vy}^{'}:=\langle (E(P_{vy})\cup E(P_{ux}[w,a])\cup E(P_{s_{1}a_{1}})\cup \{wt,aa_{1},ss_{1}\}){\setminus }\{st\}\rangle \}$ is the desired path partition of $Q_{n}$. $\square$

3 Proof of Theorem 1.2

We prove the theorem by induction on $n$. The theorem holds for $4\le n\le 7$ by Lemma 1.1. Suppose that the theorem holds for $n-1(\ge 7)$. We are to show that it holds for $n(\ge 8)$. Since $|M|\le 3n-10$, there exists $j\in [n]$ such that $|M\cap E_{j}|\le 2$. Decompose $Q_{n}$ into subcubes $Q_{n-1}^{0}$ and $Q_{n-1}^{1}$ by $E_{j}$ such that $|M_{0}|\ge |M_{1}|$. When $|M\cap E_{j}|=1$, let $M\cap E_{j}=\{uu_{1}\}$; when $|M\cap E_{j}|=2$, let $M\cap E_{j}=\{uu_{1},vv_{1}\}$.

Claim 1

If there exists a Hamiltonian cycle $C_{0}$ containing $M_{0}$ in $Q_{n-1}^{0}$, then we can construct a Hamiltonian cycle containing $M$ in $Q_{n}$.

If $M\cap E_{j}=\{uu_{1}\}$, select a neighbor $v$ of $u$ on $C_{0}$. Since $M$ is a matching and $uu_{1}\in M$, we have $\{uv,u_{1}v_{1}\}\cap M=\emptyset$. If $M\cap E_{j}=\emptyset$, since $|E(C_{0})|-(|M_{0}|+|M_{1}|)\ge 2^{n-1}-(3n-10)>1$ for $n\ge 8$, there exists an edge $uv\in E(C_{0}){\setminus } M_{0}$ such that $u_{1}v_{1}\notin M_{1}$. If $M\cap E_{j}=\{uu_{1},vv_{1}\}$ and $d_{C_{0}}(u,v)=1$, then $uv\in E(C_{0}){\setminus } M_{0}$ and $u_{1}v_{1}\notin M_{1}$. In all cases, $M_{1}\cup \{u_{1}v_{1}\}$ is a linear forest with $|M_{1}\cup \{u_{1}v_{1}\}|\le \frac{3n-10}{2}+1 <2(n-1)-3$ for $n\ge 8$. By Lemma 1.1 there exists a Hamiltonian cycle $C_{1}$ containing $M_{1}\cup \{u_{1}v_{1}\}$ in $Q_{n-1}^{1}$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(C_{1})\cup \{uu_{1},vv_{1}\}){\setminus }\{uv,u_{1}v_{1}\}$.

If $M\cap E_{j}=\{uu_{1},vv_{1}\}$ and $d_{C_{0}}(u,v)>1$, let $x,y$ be neighbors of $u,v$ on $C_{0}$, respectively, such that $x\ne y$ and $x_{1}y_{1}\notin M_{1}$. Since $\{u_{1},v_{1}\}\cap V(M_{1})=\emptyset$ and $|M_{1}|\le \frac{3n-12}{2}\le 2(n-1)-8$ for $n\ge 8$, by Lemma 2.11 there exists a path partition $\{P_{u_{1}x_{1}},P_{v_{1}y_{1}}\}$ of $Q_{n-1}^{1}$ passing through $M_{1}$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{u_{1}x_{1}})\cup E(P_{v_{1}y_{1}})$ $\cup \{uu_{1},vv_{1},xx_{1},yy_{1}\}){\setminus }\{ux,vy\}$. Claim 1 is proved.

Claim 2

Let $xy\in M_{0}$ and moreover, when $|M\cap E_{j}|\ge 1$, let $xy$ be such that $d(u,xy)\ne 1$. Let $C_{0}$ be a Hamiltonian cycle of $Q_{n-1}^{0}$ containing $M_{0}{\setminus }\{xy\}$. If $xy\notin E(C_{0})$ and $|M\cap E_{j}|+|M_{1}|\le 2$, then we can construct a Hamiltonian cycle containing $M$ in $Q_{n}$.

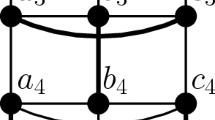
If $M\cap E_{j}=\emptyset$, then $|M_{1}|\le 2$. Let $s$ and $r$ be neighbors of $x$ and $y$ on $C_{0}$, respectively, such that one of the paths between $x$ and $y$ on $C_{0}$ contains $s$ and the other contains $r$. If $s_{1}r_{1}\notin M_{1}$, since $p(s_{1})\ne p(r_{1})$, by Lemma 2.4 there is a Hamiltonian path $P_{s_{1}r_{1}}$ passing through $M_{1}$ in $Q_{n-1}^{1}$, then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{s_{1}r_{1}})\cup \{xy,ss_{1},rr_{1}\}){\setminus }\{xs,yr\}$. If, however, $s_{1}r_{1}\in M_{1}$, since $|E(C_{0}){\setminus } M_{0}|-|M_{1}|\ge 2^{n-1}-(3n-10)>4$, there exists an edge $wt\in E(C_{0}){\setminus } M_{0}$ such that $\{w,t\}\cap \{s,r\}=\emptyset$ and $w_{1}t_{1}\notin M_{1}$. Using Lemma 2.6 in case $|M_{1}|=2$ or Lemma 2.5 in case $|M_{1}|=1$, there is a Hamiltonian path $P_{w_{1}t_{1}}$ passing through $M_{1}{\setminus } \{s_{1}r_{1}\}$ in $Q_{n-1}^{1}-\{s_{1},r_{1}\}$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{w_{1}t_{1}})$ $\cup \{xy,ss_{1},rr_{1},s_{1}r_{1},$ $ww_{1},tt_{1}\}){\setminus }\{xs,yr,wt\}$, see Fig. 1.

Fig. 1

A Hamiltonian cycle containing $M$ in $Q_{n}$ when $M\cap E_{j}=\emptyset$ and $s_{1}r_{1}\in M_{1}$ in Claim 2

If $M\cap E_{j}=\{uu_{1}\}$, then $|M_{1}|\le 1$. Select a neighbor $v$ of $u$ on $C_{0}$ such that $v_{1}\notin V(M_{1})$, then $\{u_{1},v_{1}\}\cap V(M_{1})=\emptyset$. If $M\cap E_{j}=\{uu_{1},vv_{1}\}$ and $d_{C_{0}}(u,v)=1$, note that then $M_{1}=\emptyset$. In the above two cases, since $u$ is not adjacent to $x$ or $y$ on $C_{0}$, we can choose neighbors $s,r$ of $x,y$ on $C_{0}$, respectively, such that one of the paths between $x$ and $y$ on $C_{0}$ contains $s$ and the other contains $r$ and $\{s,r\}\cap \{u,v\}=\emptyset$. Since $p(s_{1})\ne p(r_{1})$ and $p(u_{1})\ne p(v_{1})$, using Lemma 2.5 in case $M_{1}=\emptyset$ or Lemma 2.9 in case $|M_{1}|=1$, there exists a path partition $\{P_{s_{1}r_{1}},P_{u_{1}v_{1}}\}$ of $Q_{n-1}^{1}$ passing through $M_{1}$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{s_{1}r_{1}})\cup E(P_{u_{1}v_{1}})$ $\cup \{xy,ss_{1},rr_{1},uu_{1},vv_{1}\}){\setminus }\{xs,yr,uv\}$.

If $M\cap E_{j}=\{uu_{1},vv_{1}\}$ and $d_{C_{0}}(u,v)>1$, then $M_{1}=\emptyset$. Select neighbors $w,t$ of $x,y$ on $C_{0}$, respectively, such that one of the paths between $x$ and $y$ contains $w$ and the other contains $t$. Note that there are two ways to choose such $w$ and $t$. Since $Q_{n}$ is bipartite and $p(x)\ne p(y)$, the neighbors of $x$ on $C_{0}$ and neighbors of $y$ on $C_{0}$ are disjoint, so, moreover, we can choose $w,t$ such that $v\notin \{w,t\}$. Since $u$ is not adjacent to $x$ or $y$ on $C_{0}$, we have $\{u,v\}\cap \{w,t\}=\emptyset$. Choose neighbors $s,r$ of $u,v$ on $C_{0}$, respectively, such that $s\ne r$ and $\{s,r\}\cap \{w,t\}=\emptyset$. Since $d_{C_{0}}(u,v)>1$, this is always possible. Note that then $s,r,u,v,w,t$ are pairwise distinct vertices and $p(w_{1})\ne p(t_{1}),p(u_{1})\ne p(s_{1}),p(v_{1})\ne p(r_{1})$. Since $\{\{w_{1},t_{1}\},\{u_{1},s_{1}\},\{v_{1},r_{1}\}\}$ is a balanced pair set and $n-1>6$, by Lemma 2.8 there exists a path partition $\{P_{w_{1}t_{1}},P_{u_{1}s_{1}},P_{v_{1}r_{1}}\}$ of $Q_{n-1}^{1}$. Hence the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{w_{1}t_{1}})$ $\cup E(P_{u_{1}s_{1}})\cup E(P_{v_{1}r_{1}})$ $\cup \{xy,uu_{1},vv_{1},rr_{1},ss_{1},$ $ww_{1},tt_{1}\}){\setminus }\{xw,yt,us,vr\}$. Claim 2 is proved.

Claim 3

Let $xy$ and $wt$ be two edges of $M_{0}$. Moreover, when $|M\cap E_{j}|\ge 1$, let $xy,wt$ be such that $d(u,xy)\ne 1$ and $d(u,wt)\ne 1$. Let $C_{0}$ be a Hamiltonian cycle of $Q_{n-1}^{0}$ containing $M_{0}{\setminus }\{xy,wt\}$. If $\{xy,wt\}\cap E(C_{0})=\emptyset$ and $|M\cap E_{j}|+|M_{1}|\le 1$, then we can construct a Hamiltonian cycle containing $M$ in $Q_{n}$.

Since $\{xy,wt\}\cap E(C_{0})=\emptyset$, there are two possibilities up to isomorphism, see Fig. 2. Let $a,b,c,d$ be neighbors of $x,y,w,t$ on $C_{0}$, respectively, see Fig. 2. Note that $a,b,c,d$ are not arbitrarily chosen neighbors of $x,y,w,t$ on $C_{0}$. Their order on the cycle is specified as depicted on Fig. 2. Also, it may happen that $a=w$ or $d=y$ on Fig. 2(1), or even some of $a=w,b=t,c=y,d=x$ on Fig. 2(2), while the constructions described below are still valid.

Fig. 2

Two possibilities of $\{xy,wt\}$ and neighbors of $x,y,w,t$ in Claim 3

If $M\cap E_{j}=\{uu_{1}\}$, then $M_{1}=\emptyset$. Observe that $a,b,c$ and $d$ are pairwise distinct. Since $u$ is adjacent to none of $\{x,y,w,t\}$ on $C_{0}$, we have $u\notin \{a,b,c,d\}$. Let $v$ be a neighbor of $u$ on $C_{0}$ such that $v\notin \{a,b,c,d\}$. If $\{xy,wt\}$ is as on Fig. 2(1), let $z_{1},z_2,z_3,z_4$ denote the vertices $a_{1},b_{1},c_{1},d_{1}$, respectively. If $\{xy,wt\}$ is as on Fig. 2(2), let $z_1,z_2,z_3,z_4$ denote the vertices $a_{1},c_{1},b_{1},d_{1}$, respectively. Since $p(a_{1})\ne p(b_{1})$ and $p(c_{1})\ne p(d_{1})$, we have $\{\{z_1,z_2\},\{z_3,z_4\},\{u_{1},v_{1}\}\}$ is a balanced pair set. Since $n-1>6$, by Lemma 2.8 there exists a path partition $\{P_{z_1z_2},P_{z_3z_4},P_{u_{1}v_{1}}\}$ of $Q_{n-1}^{1}$. Hence the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{z_1z_2})\cup E(P_{z_3z_4})\cup E(P_{u_{1}v_{1}})$ $\cup \{xy,wt,aa_{1},bb_{1},cc_{1},dd_{1},uu_{1},vv_{1}\})$ ${\setminus }\{xa,yb,wc,td,uv\}$.

It remains to settle the case $M\cap E_{j}=\emptyset$. We distinguish two cases to consider. Note that $|M_{1}|\le 1$.

Case 1. Suppose $\{xy,wt\}$ is as on Fig. 2(1). If $\{a_{1},b_{1}\}\cap V(M_{1})=\emptyset$ or $\{c_{1},d_{1}\}\cap V(M_{1})=\emptyset$, using Lemma 2.5 in case $M_{1}=\emptyset$ or Lemma 2.9 in case $|M_{1}|=1$, there exists a path partition $\{P_{a_{1}b_{1}},P_{c_{1}d_{1}}\}$ of $Q_{n-1}^{1}$ passing through $M_{1}$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{a_{1}b_{1}})\cup E(P_{c_{1}d_{1}})$ $\cup \{xy,wt,aa_{1},bb_{1},cc_{1},dd_{1}\})$ ${\setminus }\{xa,yb,wc,td\}$, see Fig. 3. Otherwise, $|\{a_{1},b_{1}\}\cap V(M_{1})|=|\{c_{1},d_{1}\}\cap V(M_{1})|=1$. Note that in this case, $|M_{1}|=1$. Let $M_{1}=\{e\}$.

Fig. 3

A Hamiltonian cycle containing $M$ in $Q_{n}$ when $\{xy,wt\}$ is as on Fig. 2(1) and $\{a_{1},b_{1}\}\cap V(M_{1})=\emptyset$ or $\{c_{1},d_{1}\}\cap V(M_{1})=\emptyset$

If $a_{1}d_{1}=e$ or $b_{1}c_{1}=e$, since $p(a_{1})\ne p(b_{1})$ and $p(c_{1})\ne p(d_{1})$, we have $p(a_{1})\ne p(d_{1})$ and $p(b_{1})\ne p(c_{1})$. Since $\{b_{1},c_{1}\}\cap V(e)=\emptyset$ or $\{a_{1},d_{1}\}\cap V(e)=\emptyset$, by Lemma 2.9, there is a path partition $\{P_{a_{1}d_{1}},P_{b_{1}c_{1}}\}$ of $Q_{n-1}^{1}$ passing through $e$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{a_{1}d_{1}})\cup E(P_{b_{1}c_{1}})$ $\cup \{xy,wt,aa_{1},bb_{1},cc_{1},$ $dd_{1}\}){\setminus }\{xa,yb,wc,td\}$. If $a_{1}c_{1}=e$, let $d^{*}$ be the neighbor of $t$ on $C_{0}$ distinct with $d$. Since $Q_{n}$ is bipartite and $p(w)\ne p(t)$, we have $p(d^{*})\ne p(c)$, and therefore, $d^{*}\ne c$. Since $p(c_{1})=p(b_{1})\ne p(a_{1})=p(d^{*}_{1})$, by Lemma 2.5 there is a path partition $\{P_{a_{1}c_{1}}=a_{1}c_{1}=e,P_{b_{1}d^{*}_{1}}\}$ of $Q_{n-1}^{1}$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{a_{1}c_{1}})\cup E(P_{b_{1}d^{*}_{1}})$ $\cup \{xy,wt,aa_{1},bb_{1},cc_{1},$ $d^{*}d^{*}_{1}\}){\setminus }\{xa,yb,wc,td^{*}\}$, see Fig. 4. If $b_{1}d_{1}=e$, this case is isomorphic to the case $a_{1}c_{1}=e$.

Fig. 4

A Hamiltonian cycle containing $M$ in $Q_{n}$ when $\{xy,wt\}$ is as on Fig. 2(1) and $a_{1}c_{1}=e$

Case 2. Suppose $\{xy,wt\}$ is as on Fig. 2(2). Since $p(w)\ne p(t)$, we have $p(x)=p(w)$ or $p(x)=p(t)$, without loss of generality, we may assume that $p(x)=p(t)$, then $p(x)=p(t)\ne p(w)=p(y)$ and $p(a_{1})=p(d_{1})\ne p(c_{1})=p(b_{1})$.

If $\{a_{1},c_{1}\}\cap V(M_{1})=\emptyset$ or $\{b_{1},d_{1}\}\cap V(M_{1})=\emptyset$, using Lemma 2.5 in case $M_{1}=\emptyset$ or Lemma 2.9 in case $|M_{1}|=1$, there exists a path partition $\{P_{a_{1}c_{1}},P_{b_{1}d_{1}}\}$ of $Q_{n-1}^{1}$ passing through $M_{1}$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{a_{1}c_{1}})\cup E(P_{b_{1}d_{1}})$ $\cup \{xy,wt,aa_{1},bb_{1},cc_{1},dd_{1}\})$ ${\setminus }\{xa,yb,wc,td\}$, see Fig. 5.

Fig. 5

A Hamiltonian cycle containing $M$ in $Q_{n}$ when $\{xy,wt\}$ is as on Fig. 2(2) and $\{a_{1},c_{1}\}\cap V(M_{1})=\emptyset$ or $\{b_{1},d_{1}\}\cap V(M_{1})=\emptyset$

Otherwise, $|\{a_{1},c_{1}\}\cap V(M_{1})|=|\{b_{1},d_{1}\}\cap V(M_{1})|=1$. In this case, $|M_{1}|=1$. Let $M_{1}=\{e\}$. Since $p(a_{1})=p(d_{1})\ne p(c_{1})=p(b_{1})$, we have $a_{1}b_{1}=e$ or $c_{1}d_{1}=e$.

If $d_{C_{0}}(t,y)=1$, since $p(a_{1})\ne p(c_{1})$ and $a_{1}c_{1}\ne e$, by Lemma 2.3 there exists a Hamiltonian path $P_{a_{1}c_{1}}$ of $Q_{n-1}^{1}$ passing through $e$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{a_{1}c_{1}})\cup$ $\{xy,wt,aa_{1},cc_{1}\}){\setminus }\{xa,wc,yt\}$. If $d_{C_{0}}(t,y)\ne 1$, then let $d^{*}$ be the neighbor of $t$ on $C_{0}$ distinct with $d$. Since $p(t)\ne p(y)$ by the above assumption, we have $p(d^{*})\ne p(b)$, and therefore, $d^{*}\ne b$. Observe that $a,b,c,d$ and $d^{*}$ are distinct. When $a_{1}b_{1}=e$, we have $\{c_1,d^{*}_1\}\cap V(e)=\emptyset$. When $c_{1}d_{1}=e$, we have $\{a_1,b_1\}\cap V(e)=\emptyset$. Since $p(d^{*}_{1})=p(t)\ne p(w)=p(c_{1})$, by Lemma 2.9 there exists a path partition $\{P_{a_1b_1},P_{c_1d^{*}_1}\}$ of $Q_{n-1}^1$. Then the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{a_{1}b_{1}})\cup E(P_{c_{1}d^{*}_{1}})$ $\cup \{xy,wt,aa_{1},bb_{1},cc_{1},d^{*}d^{*}_{1}\})$ ${\setminus }\{xa,yb,wc,td^{*}\}$, see Fig. 6. Claim 3 is proved.

Fig. 6

A Hamiltonian cycle containing $M$ in $Q_{n}$ when $\{xy,wt\}$ is as on Fig. 2(2) and $|\{a_{1},c_{1}\}\cap V(M_{1})|=|\{b_{1},d_{1}\}\cap V(M_{1})|=1$, $d_{C_{0}}(t,y)\ne 1$

If $|M_{0}|\le 3n-13=3(n-1)-10$, by the induction hypothesis there exists a Hamiltonian cycle $C_{0}$ containing $M_{0}$ in $Q_{n-1}^{0}$ and therefore, the theorem holds by Claim 1. If $|M_{0}|=3n-12$, choose an edge $xy\in M_{0}$. Since $|M_{0}|=3n-12>(n-1)+1$ for $n\ge 8$, moreover, in the case when $|M\cap E_{j}|\ge 1$, we may choose $xy$ such that $d(u,xy)\ne 1$. Apply the induction to find a Hamiltonian cycle $C_{0}$ containing $M_{0}{\setminus }\{xy\}$ in $Q_{n-1}^{0}$. If $xy\in E(C_{0})$, then $C_{0}$ is a Hamiltonian cycle of $Q_{n-1}^{0}$ containing $M_{0}$ and therefore, the theorem holds by Claim 1. If $xy\notin E(C_{0})$, since $|M\cap E_{j}|+|M_{1}|\le 2$, the theorem holds by Claim 2. If $|M_{0}|=3n-11$, then $|M\cap E_{j}|+|M_{1}|\le 1$. Let $xy,wt$ be two edges of $M_{0}$. Since $|M_{0}|=3n-11>(n-1)+2$, moreover, in the case when $|M\cap E_{j}|\ge 1$, we can choose $xy,wt$ such that $d(u,xy)\ne 1$ and $d(u,wt)\ne 1$. Apply the induction to find a Hamiltonian cycle $C_{0}$ containing $M_{0}{\setminus }\{xy,wt\}$ in $Q_{n-1}^{0}$. Using Claim 1 in case $\{xy,wt\}\subseteq E(C_{0})$, or Claim 2 in case $|\{xy,wt\}\cap E(C_{0})|=1$, or Claim 3 in case $\{xy,wt\}\cap E(C_{0})=\emptyset$, the theorem holds.

Fig. 7

Four possibilities when $\{xy,wt,sr\}\cap E(C_{0})=\emptyset$ up to isomorphism

If $|M_{0}|=3n-10$, then $M\cap E_{j}=\emptyset =M_{1}$. Let $xy,wt,sr\in M_{0}$. Apply the induction to find a Hamiltonian cycle $C_{0}$ containing $M_{0}{\setminus }\{xy,wt,sr\}$ in $Q_{n-1}^{0}$. If $\{xy,wt,sr\}\cap E(C_{0})\ne \emptyset$, the conclusion holds by Claim 1–3. If, however, $\{xy,wt,sr\}\cap E(C_{0})=\emptyset$, there are four possibilities up to isomorphism, see Fig. 7. Let $a,b,c,d,m,n$ be neighbors of $x,y,w,t,s,r$ on $C_{0}$, respectively, see Fig. 7. Since $M$ is a matching and $xy,wt,sr\in M_{0}$, we have $a,b,c,d,m,n$ are pairwise distinct vertices and $\{xa,yb,wc,td,sm,rn\}\cap M=\emptyset$. If $\{xy,wt,sr\}$ is as on Fig. 7(1) or (3), let $z_1,z_2,z_3,z_4,z_5,z_6$ denote the vertices $a_{1},b_{1},c_{1},d_{1},m_{1},n_{1}$, respectively. If $\{xy,wt,sr\}$ is as on Fig. 7(2), let $z_1,z_2,z_3,z_4,z_5,z_6$ denote the vertices $a_{1},m_{1},b_{1},n_{1},c_{1},d_{1}$, respectively. If $\{xy,wt,sr\}$ is as on Fig. 7(4), let $z_1,z_2,z_3,z_4,z_5,z_6$ denote the vertices $a_{1},c_{1},b_{1},n_{1},d_{1},m_{1}$, respectively.

Since $p(a_{1})\!\ne \!p(b_{1})$, $p(c_{1})\!\ne \!p(d_{1})$ and $p(m_{1})\!\ne \!p(n_{1})$, we have $\{\{z_1,z_2\},\{z_3,z_4\},$ $\{z_5,z_6\}\}$ is a balanced pair set. Since $n-1>6$, by Lemma 2.8 there exists a path partition $\{P_{z_1z_2},P_{z_3z_4},$ $P_{z_5z_6}\}$ of $Q_{n-1}^{1}$. Hence the desired Hamiltonian cycle of $Q_{n}$ is induced by edges of $(E(C_{0})\cup E(P_{z_1z_2})\cup E(P_{z_3z_4})\cup E(P_{z_5z_6})$ $\cup \{xy,wt,sr,aa_{1},bb_{1},cc_{1},dd_{1},mm_{1},nn_{1}\})$ ${\setminus }\{xa,yb,wc,td,sm,rn\}$.

The proof of Theorem 1.2 is complete.