Adaptive Kriging-based method with learning function allocation scheme and hybrid convergence criterion for efficient structural reliability analysis

Abstract

Structural reliability analysis poses significant challenges in engineering practices, leading to the development of various state-of-the-art approximation methods. Active learning methods, known for their superior performance, have been extensively investigated to estimate the failure probability. This paper aims to develop an efficient and accurate adaptive Kriging-based method for structural reliability analysis by proposing a novel learning function allocation scheme and a hybrid convergence criterion. Specifically, the novel learning function allocation scheme is introduced to address the challenge of no single learning function universally outperforms others across various engineering contexts. Six learning functions, including EFF, H, REIF, LIF, FNEIF, and KO, constitute a portfolio of alternatives in the learning function allocation scheme. The hybrid convergence criterion, combining the error-based stopping criterion with a stabilization convergence criterion, is proposed to terminate the active learning process at an appropriate stage. Moreover, an importance sampling algorithm is leveraged to enable the proposed method with the capability to deal with rare failure events. The efficiency and accuracy of the proposed method are demonstrated through four numerical examples and one engineering case.

1 Introduction

Structural reliability analysis is crucial in the design and assessment of various engineering structures. Uncertainties arising from material properties, operation conditions, and cognitive deficiencies are prevalent in engineering practice [1,2,3], which can be represented as the random vector X = [X₁, X₂, …, X_n]. The primary objective of structural reliability analysis is to quantify the effects of these uncertainties by calculating the failure probability associated with the performance function. Given the joint probability density function (JPDF) ${f}_{{\varvec{X}}}({\varvec{x}})$, the analytical expression for estimating the failure probability is defined as a multi-dimensional integral:

$$\begin{array}{c}{P}_{f}={\text{P}}{\text{r}}{\text{o}}{\text{b}}\left[\text{g}\left({\varvec{x}}\right)\le 0\right]=\int_{{\text{g}}\left({\varvec{x}}\right)\le 0}{f}_{{\varvec{X}}}\left({\varvec{x}}\right)dx\end{array}$$

(1)

where ${\text{g}}\left({\varvec{x}}\right)$ represents the performance function, also known as the limit-state function. The failure domain of the system is denoted as ${\text{g}}\left({\varvec{x}}\right)\le 0$, while ${\text{g}}\left({\varvec{x}}\right)>0$ denotes the safe domain.

The difficulty in directly integrating Eq. (1) over a specific random space has led to the development of various reliability analysis methods [4,5,6,7]. These methods are typically classified into three categories. The first category includes approximate analytical methods such as the first-order reliability method (FORM) [8] and the second-order reliability method (SORM) [9]. These methods express the performance function mathematically as a linear or quadratic Taylor expansion at the most probable failure point (MPP)10. However, applying these methods to highly complex and non-linear performance functions in engineering applications may be inappropriate. To address this issue, simulation methods–the second category–offer an advanced alternative. Monte Carlo simulation (MCS) is renowned for its simplicity, robustness, and unbiasedness. However, MCS is computationally impractical for problems with low failure probabilities; for instance, if the failure probability is 10^−k, the required number of samples reaches 10^k+2. Different variance-reduction methods, such as importance sampling (IS) [11], directional simulation (DS) [12], subset simulation (SS) [13], line sampling (LS) [14], and asymptotic sampling (AS) [15], have been developed to mitigate this issue. Despite their computational efficiency, these advanced simulation methods remain costly when dealing with implicit performance functions, such as those defined by complex finite element models.

In recent decades, surrogate-based methods have emerged to significantly reduce computational burdens in structural reliability analysis. Commonly used surrogate methods include response surface method (RSM) [16, 17], support vector machine (SVM) [18,19,20], polynomial chaos expansion (PCE) [21,22,23], Kriging model [24,25,26], and artificial neural networks (ANN) [27, 28]. Surrogate methods construct an easy-to-evaluated proxy to predict the region near the limit state surface (LSS) using the Design of Experiments (DoE) containing informative samples. However, improper DoE size can lead to overfitting or underfitting, incurring additional computational costs or deteriorating the failure probability evaluation, respectively. With advances in machine learning, adaptive Kriging-based learning methods have gained extensive attention. The Kriging model offers superior performance by providing a mean prediction and quantifying the estimation variance. Starting from the initial DoE, the Kriging model is adaptively refined using informative samples identified by the learning function during the enrichment process, with convergence criteria employed to terminate the active learning process at the appropriate step. The value of the coefficient of variation for the failure probability is used as an index for augmenting the size of the candidate sample pool, leading to a reliable estimation of failure probability.

The adaptive Kriging Monte Carlo simulation (AK-MCS) [29] and the efficient global reliability analysis (EGRA) [30] are two of the pioneering works in surrogate-based active learning methods. For low failure probabilities, integrating adaptive Kriging with advanced simulation methods has led to algorithms such as AK-IS [31], AK-SS [32], AK-DRIS [33], Meta-IS-AK [34], Meta-DIS-AK [35], IDGN-IS [36], and BAL-LS-LP [37]. Building upon these methods, research on active learning functions and convergence criteria has advanced significantly over the last decade. On the one hand, apart from the well-known learning functions such as the U function [29] and EFF function [30], other effective learning functions have been developed by leveraging different angles. Specifically, Shi et al. [38] developed the Folded Normal based Expected Improvement Function (FNEIF) to well determine the points in the vicinity of the LSS. Khorramian and Oudah [39] introduced the Kriging occurrence (KO) and weighted KO (WKO) learning functions to evaluate the occurrence probability of the Kriging prediction in a prescribed region. Peng et al. [40] proposed the sample-based expected uncertainty reduction (SERU) learning function to appraise the uncertainty in estimating the failure probability when a new sample is selected. Using the quasi-posterior variance in Bayesian active learning, Dang et al. [41] presented a novel learning function, known as the panelized quasi posterior variance contribution (PQPVC), which can be employed in parallel computing with the multi-point strategy. Other learning functions, such as H [42], LIF [43], REIF [44], PAEFF [45], FELF [46], and IEAK [47], have also been proposed to identify new informative samples. On the other hand, as an essential component in active learning, the convergence criterion aims to terminate the active learning process based on appropriate principles. A prescribed threshold for the learning function is commonly defined as the convergence criterion. For instance, Echard et al. [29] employed min U $\ge$ 2 as the convergence criterion, indicating that the probability of mistaking the sign of the Kriging prediction is less than 2.3%. However, this type of convergence criterion may lead to the generation of unnecessary functional calls. To address this issue, the stabilization level of a specific indicator has been used as an alternative termination criterion, e.g., Hong et al. [48] proposed a convergence criterion by detecting the stabilization of the predicted failure probability. Considering the relative error of the estimated failure probability, Wang and Shafieezadeh [49, 50] developed an error-based stopping criterion (ESC), which was further improved in [51, 52] to enhance computational efficiency. More recently, Dang et al. [37, 53] introduced a novel convergence criterion based on the coefficient of variation of the posterior failure probability in a Bayesian active learning framework. It is anticipated that further advancements in learning functions and convergence criteria will emerge, enhancing the performance of surrogate-based active learning methods.

Although previous studies have significantly advanced active learning methods for structural reliability analysis, no single learning function universally outperforms others across different engineering problems without specific prior information [54]. Hence, identifying the most suitable function in the active learning process remains challenging. Inspired by the greedy algorithm in reinforcement learning [55], this paper proposes an innovative allocation scheme to select the learning function from a portfolio of functions. The informative sample identified by the chosen function should be near the LSS and at a certain distance from the existing DoE. Additionally, the JPDF is another influential factor in the active learning process and may need to be considered in formulating the learning function. Therefore, the reward in the proposed allocation scheme will be formulated considering these desirable features to more effectively identify informative samples. Moreover, a novel hybrid convergence criterion, incorporating both error and stabilization of the estimated failure probability, is tailored to terminate the active learning process at an appropriate stage. Specifically, the coefficient of variation of the reliability index is used as the stabilization indicator, while the error-based stopping criterion quantifies the accuracy level of the estimation. Furthermore, the FORM-based IS method [31] will be leveraged to enable the proposed method to deal with rare failure events more efficiently. These advancements contribute to the establishment of an adaptive Kriging method that is applicable to problems of varying complexities.

The remainder of the paper is structured as follows: Section 2 provides a detailed overview of the proposed method. Section 3 illustrates the implementation procedures. Section 4 validates the efficiency, accuracy, and robustness of the proposed method through four numerical examples and one engineering problem. Section 5 discusses the efficacy of the critical components of the proposed method. Finally, conclusions are drawn in Section 6.

2 The proposed method

With its inherent ability to provide predictions based on Gaussian processes, Kriging is a widely used surrogate modeling technique in engineering applications. For the sake of completeness, the basic theory of Kriging is introduced in Appendix A. This section presents a novel adaptive Kriging-based method that combines an active learning function allocation scheme with a hybrid convergence criterion. Key contributions and novelties of this study include an innovative learning function allocation scheme, inspired by reinforcement learning principles to address the multi-armed bandit (MAB) problem [55]. This scheme automatically identifies the optimal learning function from a portfolio of functions, enhancing the selection process and ensuring the identification of the most informative samples near the LSS and at an appropriate distance from the existing DoE. Additionally, a hybrid convergence criterion that integrates an error-based stopping criterion (ESC) with a new stabilization convergence criterion is proposed, ensuring that the active learning process is terminated at an appropriate stage, balancing both the stabilization and accuracy of the estimated failure probability. Furthermore, the FORM-based importance sampling (IS) method is leveraged to efficiently handle rare failure events. It is noted that other more advanced IS methods can also be integrated with the proposed method. In the sequel, the three key ingredients of the proposed method will be introduced.

2.1 Learning function allocation scheme

As an essential component for enriching the DoE, the active learning function has gained extensive attention over the past decade. However, no single learning function is conclusively accredited as the optimal choice for diverse engineering problems. One learning function may perform better in certain aspects while underperforming in others. To simultaneously exploit the merits and mitigate the deficiencies of various learning functions, this study proposes a novel learning function allocation scheme inspired by the greedy algorithm, a classical approach to solving the MAB problem in reinforcement learning. Specifically, consider N independent slot machines, each with its reward ${r}_{j}$ (i.e., ${j} = \, 1, \, 2, \, ..., \, {N})$ when the arm of the slot machine is pulled. The intrinsic property of the greedy algorithm is to seek the best slot machine that possesses the largest cumulative reward ${R}_{j}({\text{t})}$ over t rounds. In structural reliability analysis, the slot machine is considered analogous to the learning function, while the corresponding reward indicates the potential to enhance the performance of the current Kriging model. Accordingly, the learning function that contributes the most to the development of the Kriging model at the current stage is chosen, and the DoE is enlarged based on the new identified sample by this learning function.

In this work, six representative learning functions (i.e., EFF, H, REIF, LIF, FNEIF, and KO) are considered the portfolio in this learning function allocation scheme. Inspired by the U learning function, it is noted that the informative samples tend to be situated near the LSS and exhibit considerable uncertainties. In structural reliability analysis, the fitting degree of the LSS is a significant concern in determining the accuracy of the evaluated failure probability. Therefore, a normalized reward indicator based on the Kriging prediction, as expressed in Eq. (2), is applied to enhance the probability of samples proximate to the LSS. An exponential form is adopted to avoid over-weighting when the Kriging prediction equals 0.

$$\begin{array}{c}{r}_{{j}_{1}}^{*}\left(t\right)={\text{exp}}\left(-\left|\frac{{\widehat{\mu }}_{j}\left(t\right)}{{\widehat{\mu }}_{\text{max}}\left(t\right)}\right|\right), j={1}, \, {2}, \, ... , \, {6}\end{array}$$

(2)

where ${\widehat{\mu }}_{j}\left(t\right)$ is the Kriging prediction at the jth candidate sample ${{\varvec{x}}}_{j}\left(t\right)$ on the current round t, and ${\widehat{\mu }}_{\text{max}}\left(t\right)$ is the maximum one among the six Kriging predictions. The value of the reward ${r}_{{j}_{1}}^{*}\left(t\right)$ is large when the discrepancy between the Kriging prediction and the LSS is approximately 0, and vice versa.

Based on the spatial correlation and stationarity in Kriging, it is recognized that the uncertainty of regions denoted by the estimated variance is large when increasing the distance from these regions to the DoE. Furthermore, incorporating the influence of the distance can control the density of sampling points in the DoE and eliminate the local clustering. A widely used metric called the Euclidean distance is employed to determine the distance as follows:

$$\begin{array}{c}{\widehat{d}}_{j}\left(t\right)=\text{exp}\left(\sqrt{{\left({{\varvec{x}}}_{j}(t)-{{\varvec{x}}}_{\text{D}}^{i}(t)\right)}^{{T}}\left({{\varvec{x}}}_{j}(t)-{{\varvec{x}}}_{\text{D}}^{i}(t)\right)}\right), i={1}, \, {2}, \, ...\end{array}$$

(3)

where ${\widehat{d}}_{j}\left(t\right)$ is the distance between ${{\varvec{x}}}_{j}\left(t\right)$ and the existing DoE on the current round t, and ${{\varvec{x}}}_{\text{D}}^{i}(t)$ is the ith sample within the existing DoE. In this study, a normalized Euclidean distance with an exponential form in Eq. (4) is integrated as an indicator for the learning function reward. The sample with a large distance possesses a high probability of being added to the DoE.

$$\begin{array}{c}{r}_{{j}_{2}}^{*}\left(t\right)={\text{exp}}\left(\frac{{\widehat{d}}_{j}\left(t\right)-{\widehat{d}}_{\text{min}}\left(t\right)}{{\widehat{d}}_{\text{max}}\left(t\right)-{\widehat{d}}_{\text{min}}\left(t\right)}\right), j={1}, \, {2}, \, ..., \, {6}\end{array}$$

(4)

where ${\widehat{d}}_{\text{min}}\left(t\right)$ and ${\widehat{d}}_{{\text{m}}{\text{ax}}}\left(t\right)$ denote the minimum and maximum Euclidean distance, respectively.

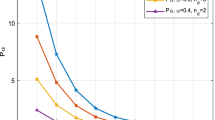
The JPDF is another critical factor influencing the selection of informative samples. To investigate the impact of integrating JPDF into the learning function for the failure probability estimation, the performance function from Example 2 in Section 4 is used. The results for the rare failure event (Case 2 in Table 2) and the non-rare failure event (Case 1 in Table 2) are illustrated in Figs. 1 and 2, respectively. Scenario 1 presents the results obtained without integrating the JPDF, while Scenario 2 shows the results with the JPDF incorporated. It is observed that for the rare failure event, both scenarios exhibit acceptable accuracy, but Scenario 1 achieves higher accuracy than Scenario 2. In addition, Scenario 2 requires 10 more functional calls than Scenario 1, indicating that incorporating the JPDF increases computational burdens and slightly reduces accuracy for rare failure events. Conversely, for non-rare failure events, one can see that incorporating the JPDF accelerates the convergence rate of the algorithm while maintaining accuracy. This phenomenon could be attributed to the fact that the introduction of the JPDF into the learning function will partially prioritize points with large JPDF values, which is beneficial for non-rare failure events. However, for rare failure events, points in the tail region of the JPDF are favored, thus the use of the JPDF will introduce adverse effects on the learning process. Therefore, it is recommended to consider the influence of the JPDF only for non-rare failure events.

Fig. 1

Reliability analysis results with different scenarios for rare failure events

Fig. 2

Reliability analysis results with different scenarios for non-rare failure events

Accordingly, the expression for the individual learning function reward ${r}_{j}^{*}\left(t\right)$ at round t, which incorporates the Kriging prediction, the distance metric, and the JPDF, is introduced as follows:

$$\begin{array}{c}{r}_{j}^{*}\left(t\right)=\left\{\begin{array}{c}{r}_{{j}_{1}}^{*}\left(t\right)\bullet {r}_{{j}_{2}}^{*}\left(t\right)\bullet {f}_{{\varvec{X}}}(t), \, \, \, {\text{for non -\!-\!- rare failure events}}\\ {r}_{{j}_{1}}^{*}\left(t\right)\bullet {r}_{{j}_{2}}^{*}\left(t\right), \, \, \, {\text{for rare failure events}}\end{array}\right.\end{array}$$

(5)

where ${f}_{{\varvec{X}}}(t)$ denotes the JPDF of the jth candidate sample ${{\varvec{x}}}_{j}\left(t\right)$ at round t. In this study, once the estimated failure probability falls below a threshold (e.g., ${P}_{f}^{*}$ = 5 $\times$ 10^–5) three consecutive iterations, the problem will be automatically categorized as a rare failure event.

Similar to the greedy algorithm, the learning function allocation scheme prioritizes the function with the maximal cumulative reward over t rounds. However, notable discrepancies in the predicted individual rewards for these learning functions may arise during the initial stages of Kriging construction. This means that the cumulative rewards for one or two particular learning functions may become excessively large due to their superior contribution to establishing the Kriging model. Consequently, other potentially more suitable learning functions may struggle to be selected in subsequent iterations. Therefore, normalizing the individual reward to the maximum, as shown in Eq. (6), is an efficient strategy to mitigate this issue.

$$\begin{array}{c}{r}_{j}\left(t\right)=\frac{{r}_{j}^{*}\left(t\right)}{{r}_{\text{max}}^{*}\left(t\right)}\end{array}$$

(6)

In the end, the new sample ${{\varvec{x}}}_{\text{new}}(t)$ identified by the learning function with the highest cumulative reward at the current round, as defined in Eq. (7), is iteratively added to the DoE. The detailed procedures of the active learning function allocation scheme are summarized in Algorithm 1. It is worth noting that this allocation scheme is not limited to six learning functions. It also possesses the flexibility to include or exclude additional learning functions from the portfolio as required.

$$\begin{array}{c}{R}_{j}\left(t\right)={\sum\nolimits}_{i=1}^{t}{r}_{j}(i), i={1}, \, {2}, \, .., \, t\end{array}$$

(7)

Algorithm 1

Active learning function allocation scheme

2.2 Hybrid convergence criterion

In structural reliability analysis, an effective convergence criterion is crucial for terminating the active learning process efficiently and accurately. The development of convergence criterion generally encompasses three different aspects: the threshold of the learning function, the accuracy of the failure probability, and the stabilization of a prescribed indicator. Relying solely on the learning function’s prescribed value for convergence can be conservative, leading to additional calls to the performance function. To address this issue, an error-based stopping criterion (ESC) has been introduced in [49, 50], which quantifies the accuracy of the failure probability. The relative error ${\epsilon }_{\text{r}}$ of the failure probability is mathematically expressed as follows:

$$\begin{array}{c}{\epsilon }_{\text{r}}=\left|\frac{{P}_{f}-{\widehat{P}}_{f}}{{P}_{f}}\right|\approx \left|\frac{{P}_{f}^{\text{MCS}}-{\widehat{P}}_{f}^{\text{MCS}}}{{P}_{f}^{\text{MCS}}}\right|=\left|\frac{\frac{{N}_{f}}{{N}_{\text{MCS}}}-\frac{{\widehat{N}}_{f}}{{N}_{\text{MCS}}}}{\frac{{N}_{f}}{{N}_{\text{MCS}}}}\right|=\left|1-\frac{{\widehat{N}}_{f}}{{N}_{f}}\right|\end{array}$$

(8)

where ${P}_{f}$ serves as the benchmark for the failure probability, evaluated through the crude MCS. ${\widehat{P}}_{f}$ represents the predicted failure probability derived from the Kriging model, ${N}_{\text{MCS}}$ denotes the number of candidate points in MCS, ${N}_{f}$ is the number of points in the failure domain identified by the actual performance function, and ${\widehat{N}}_{f}$ is defined as the number of points within the failure domain predicted by the Kriging model. Accordingly, the ESC is given as follows:

$$\begin{array}{c}{\epsilon }_{\text{r}}\le {\text{max}}\left(\left|\left(\frac{{\widehat{N}}_{f}}{{\widehat{N}}_{f}-{\widehat{N}}_{sf}^{u}}-1\right)\right|,\left|\left(\frac{{\widehat{N}}_{f}}{{\widehat{N}}_{f}+{\widehat{N}}_{fs}^{u}}-1\right)\right|\right)={\epsilon }_{\text{max}}\le {\epsilon }_{1}\end{array}$$

(9)

where ${\epsilon }_{1}$ is a predefined threshold, ${\widehat{N}}_{fs}$ represents the number of samples in the failure domain ${\boldsymbol{\Omega }}_{\text{f}}$ that are erroneously classified as samples in the safe domain by the Kriging model. Conversely, ${\widehat{N}}_{sf}$ denotes the number of samples in safe domain ${\boldsymbol{\Omega }}_{\text{s}}$ that are incorrectly identified in the failure domain by the Kriging model. ${\widehat{N}}_{sf}^{u}$ and ${\widehat{N}}_{fs}^{u}$ are the upper bounds of ${\widehat{N}}_{sf}$ and ${\widehat{N}}_{fs}$, respectively. In this study, the bootstrap confidence estimation method presented in [51] is utilized.

The ESC has been demonstrated to be effective and robust in active learning [49,50,51], but it may introduce unnecessary functional calls, particularly when the failure probability has stabilized but the ESC is not yet satisfied [1]. To mitigate this issue, we propose a hybrid convergence criterion that integrates the ESC with a stabilization convergence criterion. In engineering practice, the reliability index ${\beta}$ is commonly used to describe the reliability of structures under various uncertainties. Therefore, the coefficient of variation ${c}_{\text{v}}$ of the reliability index over the last m iterations is employed to quantitatively measure the stability of the estimated result. The proposed stabilization convergence criterion is mathematically expressed as follows:

$$\begin{array}{c}{c}_{\text{v}}=\frac{{\sigma }_{\widehat{\beta }}}{{\mu }_{\widehat{\beta }}}\le {c}_{\text{th}}\end{array}$$

(10)

where ${\mu }_{\widehat{\beta }}$ and ${\sigma }_{\widehat{\beta }}$ are defined as the mean value and the standard deviation of the reliability index over the last m iterations, respectively, and ${c}_{\text{th}}$ denotes the threshold of the criterion. The analytical expressions of ${\mu }_{\widehat{\beta }}$ and ${\sigma }_{\widehat{\beta }}$ are given as follows:

$$\begin{array}{c}{\mu }_{\widehat{\beta }}=\frac{1}{m}\sum_{i={n}_{\beta }-m+1}^{{n}_{\beta }}{\widehat{\beta }}^{(i)}\end{array}$$

(11)

$$\begin{array}{c}{\sigma }_{\widehat{\beta }}=\sqrt{\frac{1}{m}\sum_{i={n}_{\beta }-m+1}^{{n}_{\beta }}{\left({\widehat{\beta }}^{(i)}-{\mu }_{\widehat{\beta }}\right)}^{2}}\end{array}$$

(12)

where ${n}_{\beta }$ represents the ${n}_{\beta }$th iteration step with ${n}_{\beta }\ge m$, and ${\widehat{\beta }}^{(i)}$ presents the ith value of the estimated reliability index. Based on the authors’ numerical experience, setting m = 10 can achieve a good trade-off between accuracy and efficiency.

Therefore, one of the convergence criteria in the proposed method is formulated by incorporating the ESC in Eq. (9) and the stabilization convergence criterion in Eq. (10) as follows:

$$\begin{array}{c}\left\{\begin{array}{c}{\text{max}}\left(\left|\left(\frac{{\widehat{N}}_{f}}{{\widehat{N}}_{f}-{\widehat{N}}_{fs}^{u}}-1\right)\right|,\left|\left(\frac{{\widehat{N}}_{f}}{{\widehat{N}}_{f}+{\widehat{N}}_{sf}^{u}}-1\right)\right|\right)={\epsilon }_{\text{max}}\le {\epsilon }_{2}\\ {c}_{\text{v}}\le {c}_{\text{th}}\end{array}\right.\end{array}$$

(13)

where the threshold ${\epsilon }_{2}$ in Eq. (13) is set larger than ${\epsilon }_{1}$ in Eq. (9) to ensure that the active learning process is both effective and efficient by allowing for an appropriate termination when the stabilization convergence criterion is achieved, thus saving computational resources while maintaining the desired level of accuracy. In other words, the proposed hybrid convergence criterion consists of two independent criteria, i.e., the original ESC in Eq. (9) and the criterion defined in Eq. (13), and the active learning process will be terminated when either of them is satisfied.

2.3 Importance sampling for rare failure events

For the adaptive Kriging-based learning method with MCS, it is indicated that a recommended sample size for problems with a failure probability of 10^−k is at least 10^k+2, contributing to prohibitively computational burdens when dealing with rare failure events (e.g., when the failure probability is smaller than 10^–5). To address this issue, two prominent variance-reduction techniques, denoted as IS and SS, are commonly integrated into the adaptive Kriging-based learning method as efficient and accurate estimation algorithms in structural reliability analysis. In this study, the IS technique is implemented for rare failure events. Furthermore, a threshold distinguishing rare and non-rare failure events is set as ${P}_{f}^{*}$ = 5 $\times$ 10^–5. Once the estimated failure probability falls below the threshold three consecutive times, this problem is automatically categorized as a rare failure event, and the IS technique is activated. Given an IS density function ${h}_{{\varvec{X}}}({\varvec{x}})$, the failure probability can be reformulated as:

$$\begin{array}{c}{P}_{f}=\int {I}_{F}\left({\varvec{x}}\right){f}_{{\varvec{X}}}\left({\varvec{x}}\right)d{\varvec{x}}=\int {I}_{\text{F}}\left({\varvec{x}}\right)\frac{{f}_{{\varvec{X}}}\left({\varvec{x}}\right)}{{h}_{{\varvec{X}}}\left({\varvec{x}}\right)}{h}_{{\varvec{X}}}\left({\varvec{x}}\right)d{\varvec{x}}={\text{E}}_{h}\left[\frac{{{I}_{\text{F}}\left({\varvec{x}}\right)f}_{{\varvec{X}}}\left({\varvec{x}}\right)}{{h}_{{\varvec{X}}}\left({\varvec{x}}\right)}\right]\end{array}$$

(14)

where ${I}_{\text{F}}({\varvec{x}})$ is the indicator function (i.e., ${I}_{\text{F}}\left({\varvec{x}}\right)={1}$ when $\text{g}\left({\varvec{x}}\right)\le {0}$ and ${I}_{\text{F}}\left({\varvec{x}}\right)={0}$ otherwise), and ${\text{E}}_{h}(\bullet )$ is the expectation operator with respect to the ${h}_{{\varvec{X}}}({\varvec{x}})$. By generating N_IS independent samples from the ${h}_{{\varvec{X}}}({\varvec{x}})$, the failure probability can be evaluated as follows:

$$\begin{array}{c}{P}_{f}\approx {\widehat{P}}_{f}=\frac{1}{{N}_{\text{IS}}}\sum\limits_{i=1}^{{N}_{\text{IS}}}\frac{{f}_{{\varvec{X}}}\left({{\varvec{x}}}_{i}\right)}{{h}_{{\varvec{X}}}\left({{\varvec{x}}}_{i}\right)}{I}_{\text{F}}\left({{\varvec{x}}}_{i}\right), i=1, 2,\dots ,{N}_{\text{IS}}\end{array}$$

(15)

In contrast to the crude MCS, the IS technique enhances the likelihood of samples falling into the failure domain, thereby substantially accelerating the convergence speed. However, determining the optimal IS density function, i.e., ${h}_{\text{opt}}\left({\varvec{x}}\right)={I}_{F}\left({\varvec{x}}\right){f}_{{\varvec{X}}}({\varvec{x}})/{P}_{f}$, is challenging due to the unknown failure probability ${P}_{f}$. An essential module of the IS technique is to ascertain the IS density function ${h}_{{\varvec{X}}}({\varvec{x}})$, which controls the accuracy and efficiency of the adaptive Kriging-based learning methods. In this work, the FORM-based importance sampling method [31] is adopted to approximate the optimal IS density function ${h}_{\text{opt}}\left({\varvec{x}}\right)$. It is noted that other more advanced IS methods can also be integrated with the proposed method. Initially, the MPP is defined by the FORM method. Subsequently, the IS density function ${h}_{{\varvec{X}}}({\varvec{x}})$ is modeled as a normal distribution centered at the approximative MPP. The standard deviation is set to 0.1 in this paper, but alternative values can be selected to tighten or broaden the conditioning [5]. Additionally, to exploit the computational resources, the samples whose responses are evaluated by the true performance function using the FORM method can be added to the initial DoE. For the IS technique, the variance and associated coefficient of variation of the failure probability can be calculated as follows:

$$\begin{array}{c}{\text{V}}{\text{a}}{\text{r}}_{\text{IS}}\approx \frac{1}{{N}_{\text{IS}}}\left(\frac{1}{{N}_{\text{IS}}}\sum_{i=1}^{{N}_{\text{IS}}}{\left({I}_{\text{F}}\left({{\varvec{x}}}_{i}\right)\frac{{f}_{{\varvec{X}}}\left({{\varvec{x}}}_{i}\right)}{{h}_{{\varvec{X}}}\left({{\varvec{x}}}_{i}\right)}\right)}^{2}-{\left({\widehat{P}}_{f}\right)}^{2}\right)\end{array}$$

(16)

$$\begin{array}{c}{\text{CoV}}_{{\widehat{P}}_{f}}=\frac{\sqrt{{\text{Va}}{\text{r}}_{\text{IS}}}}{{\widehat{P}}_{f}}\end{array}$$

(17)

3 The implementation procedures

The proposed method starts with a small number of the DoE and progressively refines the Kriging model through the iterative DoE enrichment. In this work, a novel learning function allocation scheme is proposed to enrich the DoE, and a hybrid convergence criterion is introduced to stop the updating process at an appropriate stage. The overall implementation procedures of the proposed method are briefly outlined as follows:

Step 1: Initialize the parameters used in the proposed method.

Step 2: Generate the candidate sample pool S using the Sobol sequence. The initial size of the S is set as N = 1 $\times$ 10⁵.

Step 3: Generate the initial DoE using Latin hypercube sampling (LHS). Unless specified otherwise, the initial DoE size N₀ is taken as ${{N}}_{0}={\text{max}}\{12, \, {2}{\text{n}}+ \text{2} \}$, where n denotes the dimensionality of the input variables.

Step 4: Calibrate the Kriging model. Utilize the DACE toolbox [56] to establish the Kriging model based on the DoE.

Step 5: Determine whether it is a rare failure event. Once the estimated failure probability ${\widehat{P}}_{f}$ falls below the threshold three consecutive times, the problem is automatically categorized as a rare failure event, and then the individual reward can be determined according to Eq. (5). The default configuration designates each problem as a non-rare failure event.

Step 6: Select the new sample ${{\varvec{x}}}_{\text{new}}$ to enrich the DoE. The allocation scheme in Algorithm 1 is used to identify the new sample, and the corresponding response is computed by the performance function.

Step 7: Evaluate the hybrid convergence criterion. Upon satisfaction of any of the convergence criteria in Eq. (9) and Eq. (13), terminate the active learning process and proceed to Step 8. If not, augment the DoE with the new sample, i.e., $\mathcal{D}=\mathcal{D}\cup {{\varvec{x}}}_{\text{new}}$. Repeat Steps 4–7 until the convergence criterion is satisfied.

Step 8: Calculate the coefficient of variation of the failure probability. The sample size N in the candidate sample pool S must be sufficient. If the value of the coefficient of variation exceeds 0.05, the sample size should be enlarged (e.g., $\Delta$ N $=$ 10⁵), then repeat Steps 4–8 until the requirement is satisfied. Otherwise, proceed to Step 9.

$$\begin{array}{c}{\text{CoV}}_{{\widehat{P}}_{f}}=\sqrt{\frac{1-{\widehat{P}}_{f}}{N{\widehat{P}}_{f}}}<0.05\end{array}$$

(18)

Step 9: End of the algorithm with the final failure probability estimation.

4 Numerical examples

This section evaluates the accuracy, efficiency, and robustness of the proposed method through four numerical examples and one practical engineering case. Section 4.1 begins with a series system of four branches. In this case, a parameter analysis is performed to investigate the effects of different thresholds $\epsilon$₁, c_th, and $\epsilon$₂ in the hybrid convergence criterion. Subsequently, Section 4.2 examines the dynamic response of a nonlinear oscillator, focusing on varying magnitudes of the failure probability to elucidate the method’s performance. Section 4.3 introduces two high-dimensional mathematical problems, and Section 4.4 addresses a modified Rastrigin function characterized by non-convex and scattered gaps in failure domains. Finally, a practical engineering scenario of a single tower cable-stayed bridge is investigated to evaluate the applicability of the proposed method. These examples cover a wide range of characteristics pertinent to structural reliability analysis, including multiple failure regions, low failure probabilities, high nonlinearity, high dimensionality, and finite element modelling.

To quantitatively assess accuracy and efficiency, three major metrics are examined: (1) The relative error ${\epsilon }_{{\widehat{P}}_{f}}$ comparing the failure probability ${\widehat{P}}_{f}^{\text{MCS}}$ obtained via MCS with ${\widehat{P}}_{f}$ from different methods; (2) The CPU time, with all results of structural reliability analysis conducted on a computer equipped with an InterI CITM) i-7-9700 CPU Processor @ 3.00 GHz with 32.0 RAM; (3) The number N_call of functional calls. Additionally, the reliability index $\beta$, in conjunction with the failure probability ${\widehat{P}}_{f}$, serves as a direct measure of the reliability for each example. The results in each example are averaged over 50 independent runs to consider the randomness in each simulation. The results obtained by the proposed method are compared with those derived from MCS, AKMCS + U, AKMCS + EFF, adaptive Kriging-based MCS methods with U and EFF learning functions under the hybrid convergence criterion (referred to as HCC + U and HCC + EFF), and other state-of-the-art methods whenever possible.

4.1 Example 1: A series system with four branches

The first example involves a series system with four branches, commonly used as a benchmark to assess the performance of structural reliability analysis methods [29, 57,58,59]. The performance function of this system is given as follows:

$$\begin{array}{c}g\left({x}_{1},{x}_{2}\right)=\text{min}\left\{\begin{array}{c}3+0.1\times {\left({x}_{1}-{x}_{2}\right)}^{2}-\frac{{x}_{1}+{x}_{2}}{\sqrt{2}}\\ 3+0.1\times {\left({x}_{1}-{x}_{2}\right)}^{2}+\frac{{x}_{1}+{x}_{2}}{\sqrt{2}}\\ \genfrac{}{}{0pt}{}{\left({x}_{1}-{x}_{2}\right)+\frac{6}{\sqrt{2}}}{-\left({x}_{1}-{x}_{2}\right)+\frac{6}{\sqrt{2}}}\end{array}\right.\end{array}$$

(19)

where ${x}_{1}$ and ${x}_{2}$ are two independent input variables following the standard normal distribution. A comprehensive parameter analysis is conducted to determine the appropriate values of the thresholds $\epsilon$₁, c_th, and $\epsilon$₂ in the hybrid convergence criterion. Subsequently, the performance of the proposed method in structural reliability analysis is evaluated in comparison with other active learning algorithms.

4.1.1 Effects of the thresholds in the hybrid convergence criterion

In the proposed method, determining appropriate thresholds in the hybrid convergence criterion is crucial to balancing efficiency, accuracy, and robustness. Small threshold values may increase computational costs, while large values may cause premature termination of the algorithm. Therefore, a parameter analysis is conducted to quantitatively assess the performance of different thresholds.

To begin with, the influence of different ranges for $\epsilon$₁ and $\epsilon$₂ is investigated under a fixed value of c_th = 0.001. The results of structural reliability analysis under various threshold combinations are shown in Fig. 3, averaged over 100 independent runs to consider the randomness. It is observed that the performance of the convergence criterion is particularly susceptible to $\epsilon$₁, as specified in Eq. (9). An optimal trade-off between accuracy and efficiency is illustrated in a prescribed range of $\epsilon$₁ $\in$ [0.005, 0.01], without apparent change pattern when the value of $\epsilon$₂ varies from 0.1 to 0.5. As $\epsilon$₁ decreases, the number of functional calls increases. In addition, half of the algorithm terminations are governed by Eq. (9) when $\epsilon$₁ is set to 0.01. Values larger or smaller than this prescribed threshold can jeopardize the balance, contributing to the convergence criterion being predominantly influenced by either Eq. (9) or Eq. (13). Therefore, for an ideal balance of accuracy and efficiency, $\epsilon$₁ = 0.01 and $\epsilon$₂ = 0.3 are recommended.

Fig. 3

Effects of different thresholds $\epsilon$₁ and $\epsilon$₂ in the hybrid convergence criterion

With $\epsilon$₁ = 0.01 and $\epsilon$₂ = 0.3, the results under different values of c_th are illustrated in Fig. 4. It is observed that c_th = 0.001 emerges as an explicit value distinguishing different dispersion tendencies. Specifically, when c_th exceeds 0.001, a significant tendency of dispersion from the reference result is observed, with a maximum relative error of 2.59%. On the contrary, the dispersion remains stable for c_th values smaller than 0.001. Based on these observations, a constraint of c_th $\in$ [0.0001, 0.001] is suggested. Within the specified interval, the number of functional calls and the CPU time decrease as c_th increases. To hold a judicious equilibrium among accuracy, efficiency, and robustness, c_th is set to 0.001. Therefore, the recommended thresholds for the hybrid convergence criterion are $\epsilon$₁ = 0.01, c_th = 0.001, and $\epsilon$₂ = 0.3.

Fig. 4

Effects of different thresholds c_th in the hybrid convergence criterion

4.1.2 Comparisons with other advanced methods

This subsection evaluates the performance of the proposed method against several state-of-the-art methods, e.g., AKMCS + U [29], AKMCS + EFF [30], PRBFM [57], ALK-iRPl2 [58], and ALK-PBA [59]. The results are summarized in Table 1. Additionally, results from HCC + U and HCC + EFF are included to validate the efficacy of the hybrid convergence criterion. The reference result, obtained using MCS with a sample size of 1 × 10⁶, yields a failure probability of 4.416 $\times$ 10^–3 and a coefficient of variation of 1.5% [29].

Table 1 Results of structural reliability analysis for Example 1

All methods demonstrate an acceptable level of precision in evaluating the failure probability, with relative errors consistently smaller than 3.00%. The comparative analysis reveals that HCC + U and HCC + EFF exhibit noteworthy enhancements in computational efficiency compared to AK-MCS + U and AKMCS + EFF, marked by a reduction in functional calls of approximately 65%. This underscores the efficacy of the hybrid convergence criterion in reducing computational costs. In addition, a trade-off between computational efficiency and accuracy is observed, as evidenced by a marginal loss of precision in HCC + U and HCC + EFF. Despite requiring more functional calls, HCC + U and HCC + EFF exhibit lower CPU time compared to the proposed method. This is attributed to the additional computational expenses caused by the estimation of the learning function allocation scheme. However, improvements in CPU time are deemed negligible in engineering scenarios characterized by implicit and intricate numerical simulations, such as finite element models, which may consume hours of computation for each simulation.

Furthermore, the proposed method offers superior accuracy in evaluating the failure probability, while requiring fewer functional calls compared to other surrogate-based active learning methods. Notably, it surpasses both ALK-iRPl2 and ALK-PBA in performance while achieving higher precision than PRBFM with nearly identical functional calls. Therefore, the proposed method exhibits excellent performance in balancing accuracy and efficiency.

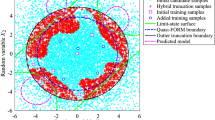
The converged Kriging model in an independent run is illustrated in Fig. 5. One can see that the initial candidate samples in the DoE (green hexagrams) are distributed across the random space, and the subsequently added samples (blue triangles) are uniformly situated in proximity to the LSS without forming the local clustering. Through the strategic allocation of those informative samples in the DoE, the Kriging model successfully captures the shape of the LSS. Despite a minor decrease in fitting precision in areas of low probability densities, particularly at the four corners of the LSS, the model effectively maintains high accuracy in calculating the failure probability, which equals 4.400 $\times$ 10^–3. This result indicates that these regions have negligible impacts on the estimation in structural reliability analysis.

Fig. 5

The converged Kriging model in an independent run of the proposed algorithm for Example 1

4.2 Example 2: Dynamic response of a nonlinear oscillator

As depicted in Fig. 6, a single degree of freedom nonlinear oscillator is considered in this example. The performance function of the system is mathematically expressed as follows [1, 33, 60, 61]:

$$\begin{array}{c}g\left(m,{k}_{1},{k}_{2},r,{t}_{1},{F}_{1}\right)=3r-\left|\frac{2{F}_{1}}{m{\omega }_{0}^{2}}\text{sin}\left(\frac{{\omega }_{0}{t}_{1}}{2}\right)\right|\end{array}$$

(20)

where ${\omega }_{0}=\sqrt{\frac{{k}_{1}+{k}_{2}}{m}}$ represents the frequency of this system. The statistical information of the random variables is listed in Table 2. It is assumed that all random variables are independently and normally distributed. In this study, three different distribution parameters of F₁ are considered to evaluate the performance of the proposed method with respect to different magnitudes of the failure probability, i.e., 10^–2, 10^–6, and 10^–8.

Fig. 6

Nonlinear oscillator subjected to a rectangular load pulse

Table 2 Statistical information of the random variables for Example 2

4.2.1 Structural reliability analysis for Case 1

Taking the results obtained by MCS as the reference, the failure probability of 2.859 $\times$ 10^–2 is obtained with a sample size of 1 $\times$ 10⁶. Furthermore, a comparative analysis is conducted between the results by AK-MCS + U and AK-MCS + EFF and those obtained by HCC + U and HCC + EFF. Additionally, the results of AKSE [1], AK-DRIS [33], AK-MSS [60], and AWL-MCS [61] are compared with those produced by the proposed method. All results are summarized in Table 3.

Table 3 Results of structural reliability analysis for Case 1 in Example 2

For the adaptive Kriging algorithms with U and EFF learning functions, there are substantial discrepancies in the required functional calls after introducing the hybrid convergence criterion. Specifically, for AK-MCS + U and HCC + U, the number of functional calls is reduced from 129.7 to 43.9, accompanied by a significant decrease in CPU time. Moreover, the relative error of these two methods is consistently smaller than 0.2%, highlighting the efficacy of the hybrid convergence criterion in terms of both efficiency and accuracy. Compared with AK-MSS and AWL-MCS, the proposed method provides the most accurate estimation of the failure probability with the highest efficiency. Furthermore, the results of the proposed method, along with those of AKSE and AK-DRIS, closely align with the reference result while requiring fewer functional calls, marking them as attractive options for structural reliability analysis. However, it should be noted that AK-DRIS may impose significant CPU burdens as it employs the Markov Chain Monte Carlo method to generate the candidate sample pool. In summary, the proposed method achieves an excellent trade-off between accuracy and efficiency.

4.2.2 Structural reliability analysis for Case 2 and Case 3

Two cases with different low failure probabilities are examined in the subsection to investigate the efficacy and applicability of the proposed method in addressing rare failure events. In these cases, the simulation method switches from MCS to IS once the estimated failure probability is smaller than the predefined threshold ${P}_{f}^{*}$ for three consecutive iterations. An additional 15 calls to the performance function are produced by the FORM to determine the MPP, after which the IS density function is derived as a normal distribution centered on the MPP. With total consumptions of 1.8 $\times$ 10⁸ and 9 $\times$ 10¹⁰ functional calls, the reference results for Cases 2 and 3 are estimated to be 9.090 $\times$ 10^–6 and 1.550 $\times$ 10^–8, respectively. The results by AKIS + U, AKIS + EFF, HCC + U, HCC + EFF, AKSE-IS [1], AK-DRIS [33], AK-ARBIS [62], and AK-coupled SS [63] are summarized in Tables 4 and 5 for comparison.

Table 4 Results of structural reliability analysis for Case 2 in Example 2

Table 5 Results of structural reliability analysis for Case 3 in Example 2

Regarding Case 2, it is noteworthy that the relative error values for all investigated methods are less than 1.0%, confirming their accuracy. However, the computational efficiency is different, particularly for the AK-IS methods with U and EFF learning functions, which exhibit higher demands in functional calls and CPU time compared to HCC + U and HCC + EFF. This underscores the efficacy of the hybrid convergence criterion as a reliable means to terminate the algorithm. Among the various advanced methods evaluated, the proposed method stands out for its superior efficiency in achieving the second most accurate failure probability estimation. Furthermore, in Case 3, the proposed method provides an accurate failure probability with the fewest functional calls. Therefore, the efficacy and applicability of the proposed method in tackling rare failure events are elucidated based on these cases.

4.3 Example 3: high-dimensional mathematical problems

This example considers two high-dimensional mathematical problems to investigate the performance of the proposed method. Specifically, Case 1 is a linear high-dimensional problem with the following performance function [1, 29, 64]:

$$\begin{array}{c}g\left({\varvec{x}}\right)=n+3\sigma \sqrt{n}-\sum\limits_{i=1}^{n}{x}_{i},i={1}, \, {2}, \, ..., \, n\end{array}$$

(21)

where ${x}_{\text{i}}$ represents the independent normal random variables with a mean of $\mu$ = 1 and a standard deviation of $\sigma$ = 0.2. Case 2 is a non-linear high-dimensional problem, and the corresponding mathematical expression is given by [1]:

$$\begin{array}{c}g\left({\varvec{x}}\right)={\mu }^{3}+0.01\sum\limits_{i=1}^{n-1}{x}_{i}^{3}-{x}_{n}^{2},i={1}, \, {2}, \, ..., \, n\end{array}$$

(22)

where ${x}_{\text{i}}$ denotes the independent random variables following the lognormal distribution with a mean of $\mu$ = 3 and a standard deviation of $\sigma$ = 0.8. The dimensionality n of both cases is defined as 20. The initial sample size of both cases is taken as 12.

The reference results obtained by MCS for these two cases are 1.357 $\times$ 10^–3 and 4.439 $\times$ 10^–3, with sample sizes of 1 $\times$ 10⁷ and 1 $\times$ 10⁶, respectively. The results obtained by the proposed method are compared with those by AKMCS + U, AKMCS + EFF, HCC + U, HCC + EFF, and AKSE [1]. All results are summarized in Tables 6 and 7. In Case 1, HCC + U and HCC + EFF estimate the failure probability with considerable improvements compared to the AK-MCS methods, with reductions of 71.8% and 67.1% in functional calls, respectively. These methods, along with the proposed method, also exhibit higher accuracy and efficiency compared to their adaptive Kriging counterparts. Similarly, in Case 2, the application of the hybrid convergence criterion greatly enhances computational efficiency, reducing functional calls by approximately 70% for the AK-MCS methods. Therefore, the proposed method can effectively balance accuracy and efficiency for these two high-dimensional cases. Additionally, it is noted that more functional calls are required in Case 2, but the associated CPU time is less than that in Case 1. This discrepancy arises because the initial sample size in Case 1 does not satisfy the requirement of the coefficient of variation for the failure probability, thereby necessitating an expansion of the candidate sample pool and consequently increasing the CPU time.

Table 6 Results of structural reliability analysis for Case 1 in Example 3

Table 7 Results of structural reliability analysis for Case 2 in Example 3

4.4 Example 4: A modified Rastrigin function

The fourth example involves a modified Rastrigin function characterized by numerous non-convex failure domains and represents a highly nonlinear and intricate problem. The performance function is expressed as follows [1, 29, 65]:

$$\begin{array}{c}g\left({x}_{1},{x}_{2}\right)=10-\sum\limits_{i=1}^{2}\left({x}_{i}^{2}-5\text{cos}\left(2{\pi}{x}_{i}\right)\right)\end{array}$$

(23)

where the two input variables ${x}_{1}$ and ${x}_{2}$ follow independent standard normal distributions. The reference failure probability calculated by MCS is 7.308 $\times$ 10^–2 using a sample size of 6 $\times$ 10⁴ [29]. Incorporating the identical framework of the AK-MCS methods, but terminated by the hybrid convergence criterion, is used to investigate the efficacy of the proposed convergence criterion for this problem. The results obtained by the proposed method are compared with those from AKSE [1] and AK-SEUR-MCS [65], as detailed in Table 8.

Table 8 Results of structural reliability analysis for Example 4

Traditional AK-MCS methods using U and EFF learning functions require substantial computational costs, i.e., exceeding 560 functional calls, to accurately estimate the failure probability. Integrating the hybrid convergence criterion can notably reduce computational costs, but the precision is compromised for the U learning function, which has a relative error of 4.42%. This suggests that combining the U learning function with the hybrid convergence criterion may not be advisable for this problem. In addition, the proposed method exhibits a relative error below 1.0% with a consumption of 276.0 functional calls, presenting comparable performance to that of AKSE and AK-SEUR-MCS. Figure 7 depicts the final Kriging model in a random simulation of the algorithm with 250 functional calls, leading to the failure probability estimation of 7.249 $\times$ 10^–2. The fitting performance in the inner regions is excellent, albeit undesirable in the outer regions. Nevertheless, the precision of the failure probability estimation is high, as the outer regions with the extremely small probability density contribute negligibly to the failure probability.

Fig. 7

The converged Kriging model in a random simulation of the proposed method for Example 4

4.5 Example 5: A single tower cable-stayed bridge

This example evaluates the performance of the proposed method in accurately and efficiently estimating the failure probability within a practical engineering scenario, i.e., a single tower cable-stayed bridge, as illustrated in Fig. 8a [1, 33, 66]. The bridge configuration features a total of 12 pairs of parallel steel wire cables and one bridge tower consolidated with the beam. The bridge spans 160 m (112 m + 48 m), with a tower height of 66 m. For a realistic assessment of the bridge's structural response, a 3D finite element model is constructed using ANSYS at a real scale, as depicted in Fig. 8b. This model incorporates shell elements for simulating the bridge deck, beam elements for modeling the bridge tower, and link elements for establishing the cables. Vehicle loads are considered concentrated loads. The model involves seven independent input variables, including the modulus of elasticity of concrete (E₁) and steel (E₂), the density of concrete (D₁) and steel (D₂), and the corresponding vehicle loads at the front wheels (F₁), middle wheels (F₂), and rear wheels (F₃). The statistical properties of these input variables are summarized in Table 9. The performance function is expressed as a mathematical function based on the maximum displacement of the bridge:

$$\begin{array}{c}g\left({E}_{1},{E}_{2},{D}_{1},{D}_{2},{F}_{1},{F}_{2},{F}_{3}\right)={\Delta }_{\text{limit}}-\left|{\Delta }_{\text{max}}\right|\end{array}$$

(24)

where ${\Delta }_{\text{limit}}$, taken as 30 cm, is the allowed displacement of the bridge, and ${\Delta }_{\text{max}}$ denotes the maximum displacement of the bridge, which is derived from ANSYS.

Fig. 8

A single tower cable-stayed bridge: a side view of the bridge; b the finite element model [1]

Table 9 Statistical information of random variables for Example 5

The reference result calculated by MCS is 6.732 $\times$ 10^–2 using a sample size of 1 $\times$ 10⁵ [1]. The results obtained from AKMCS + U, AKMCS + EFF, HCC + U, HCC + EFF, AKSE [1], and AK-DRIS [33] are summarized in Table 10, along with the results of the proposed method. It is observed that the use of the hybrid convergence criterion can greatly enhance the computational efficiency, i.e., both the functional calls and CPU time are reduced, without significantly compromising the accuracy. Moreover, compared with AKSE and AK-DRIS, the proposed method exhibits a good trade-off between accuracy and efficiency in tackling this engineering problem.

Table 10 Results of structural reliability analysis for Example 5

5 In-depth discussion

According to the five numerical examples discussed in Section 4, the excellent performance of the proposed method in structural reliability analysis is demonstrated. The primary contributions of this study are two folds: the learning function allocation scheme and the hybrid convergence criterion. Therefore, a comprehensive analysis is essential to thoroughly investigate the feasibility and necessity of these two key components.

5.1 Comparisons with the single learning function

This study introduces a novel learning function allocation scheme, acknowledging that no single learning function universally outperforms others across various problems. To underscore the importance and feasibility of this scheme, the performance of the proposed method (referred to as AK) is compared with that of the adaptive Kriging-based methods employing the individual learning function (e.g., FNEIF, LIF, REIF, H, EFF, and KO). Additionally, to illustrate the efficacy of the greedy algorithm, another scenario (designated as Rand) that randomly selects the best sample from the candidates identified by these learning functions is involved. All results are illustrated in Fig. 9, along with reference results obtained by MCS in each subfigure. For all cases, the Rand scenario exhibits satisfactory accuracy, suggesting that the random selection can produce an acceptable estimation of the failure probability when the candidates are the informative samples selected by the learning functions. However, for some nonlinear and engineering problems (e.g., Examples 3–5), additional computational burdens are generated compared with the proposed algorithm. For instance, the Rand scenario requires approximately 300 more functional calls than the proposed method in Example 4, highlighting that the greedy algorithm achieves a more effective balance between accuracy and computational efficiency than the random selection.

Fig. 9

Results of structural reliability analysis using different learning functions

The proposed allocation scheme is tailored to leverage the unique characteristics of each learning function, allowing for the adaptive determination of the most appropriate learning function. As illustrated in Fig. 9, the proposed algorithm demonstrates commendable performance in structural reliability analysis across diverse problems. The application of the learning function allocation scheme ensures high accuracy and efficiency. For instance, in Fig. 9e, learning functions REIF, H, and EFF deliver accurate failure probability estimations, but require considerable computational resources (over 600 functional calls), whereas the KO learning function achieves lower computational costs at the expense of accuracy. By leveraging the properties of these learning functions, the results of the proposed method matches or even exceeds the performance of each individual learning function, providing a failure probability of 7.238 $\times$ 10^–2 using 276.0 functional calls. Therefore, the proposed learning function allocation scheme offers a robust alternative for balancing accuracy and efficiency, demonstrating superior performance compared to both the single learning function and the random selection scheme.

5.2 Comparisons with different convergence criteria

In this study, the performance of the proposed method using different convergence criteria is investigated. Specifically, the results by the hybrid convergence criterion (Scenario 1), the ESC in Eq. (9) (Scenario 2), and the stabilization convergence criterion in Eq. (10) (Scenario 3) are displayed in Fig. 10, and the reference result from MCS is shown in each subfigure. It is observed that the Scenario 3 in subfigures (d) and (e) exhibits low accuracy in estimating the failure probability, demonstrating that sole reliance on the stabilization convergence criterion may lead to premature convergence. On the contrary, as depicted in Fig. 10c–f, Scenario 2 exhibits high precision in estimating the failure probability, but it comes at considerable computational expenses in terms of functional calls. This demonstrates that the ESC may require additional functional calls when the failure probability estimation has stabilized. However, compared with these two convergence criteria, the hybrid convergence criterion can achieve an excellent balance between accuracy and efficiency for all the investigated cases.

Fig. 10

Results of structural reliability analysis using different convergence criteria

6 Conclusions

This paper introduces an efficient and accurate Kriging-based method for structural reliability analysis by incorporating a novel learning function allocation scheme and a hybrid convergence criterion. Inspired by reinforcement learning, the allocation scheme iteratively determines the most suitable learning function from a portfolio of options, thereby enhancing the active learning process. The hybrid convergence criterion that integrates an error-based stopping criterion (ESC) with a new stabilization convergence criterion ensures the appropriate termination of the proposed method. The efficacy of the proposed method is investigated through four numerical examples, characterized by multiple failure regions, low failure probabilities, high nonlinearity, and high dimensionality, as well as through the analysis of a single tower cable-stayed bridge. The results indicate that the proposed method successfully balances accuracy and efficiency. Additionally, the necessity and feasibility of both the allocation scheme and the hybrid convergence criterion are discussed. The main conclusions drawn from this study are as follows:

• (1) The innovative learning function allocation scheme addresses the challenge of determining suitable learning functions for diverse engineering problems effectively, achieving an optimal trade-off between accuracy and efficiency.

• (2) The hybrid convergence criterion demonstrates excellent performance in terms of efficiency and accuracy, significantly reducing unnecessary functional calls associated with the ESC and preventing premature of the algorithm due to the stabilization convergence criterion.

The integration of the FORM-based importance sample (IS) method effectively mitigates issues related to rare failure events. However, challenges persist in identifying the MPP using FORM in highly nonlinear scenarios and/or with multiple failure domains, potentially affecting the performance. Additionally, while the proposed method shows promising results for problems with up to 20 dimensions, its applicability to extremely high-dimensional scenarios, such as those exceeding 100 dimensions, remains limited. Therefore, further exploration of advanced simulation methods and dimension reduction strategies is recommended to enhance the overall efficacy of the proposed method.

Appendices

Appendix A: Basic theory of Kriging

The mathematical expression of the Kriging model is given as follows [67]:

$$\begin{array}{c}{\text{g}}\left({\varvec{x}}\right)=f{\left({\varvec{x}}\right)}^{{T}}{\varvec{\beta}} +Z\left({\varvec{x}}\right)\end{array}$$

(25)

where ${\varvec{f}}{\left({\varvec{x}}\right)}^{T}=\left[{f}_{1}\left({\varvec{x}}\right),{f}_{2}\left({\varvec{x}}\right),\dots ,{f}_{m}\left({\varvec{x}}\right)\right]$ denotes the regression functions, and ${{\varvec{\beta}}}^{T}=[{\beta }_{1},{\beta }_{2},\dots ,{\beta }_{m}]$ serves as the regression coefficients. $Z\left({\varvec{x}}\right)$ is a zero-mean stationary Gaussian process with the covariance function:

$$\begin{array}{c}{\text{C}}{\text{o}}{\text{V}}\left(Z\left({{\varvec{x}}}_{i}\right),Z\left({{\varvec{x}}}_{j}\right)\right)={\sigma }^{2}R\left({{\varvec{x}}}_{i},{{\varvec{x}}}_{j};{\varvec{\theta}}\right), i,j=1,2,\dots ,N\end{array}$$

(26)

where ${\sigma }^{2}$ is the variance of the Gaussian process, ${{\varvec{x}}}_{i}$ and ${{\varvec{x}}}_{j}$ are the points from the DoE with a sample size of $N$. $R({{\varvec{x}}}_{i},{{\varvec{x}}}_{j};{\varvec{\theta}})$ is the correlation function determined by hyper-parameters ${\varvec{\theta}}={\left[{\theta }_{1},{\theta }_{2},\dots ,{\theta }_{d}\right]}^{T}$. This study will adopt the Gaussian correlation function with the following mathematical expression:

$$\begin{array}{c}R\left({{\varvec{x}}}_{i},{{\varvec{x}}}_{j};{\varvec{\theta}}\right)=\prod_{k=1}^{d}\text{exp}\left(-{\theta }_{k}{\left|{x}_{i}^{k}-{x}_{j}^{k}\right|}^{2}\right)\end{array}$$

(27)

where $d$ is the dimensionality of the random variables, ${\theta }_{k}$ represents the correlation hyper-parameter in the $k$th dimension, ${x}_{i}^{k}$ and ${x}_{j}^{k}$ are the $k$th components of the input variables ${{\varvec{x}}}_{i}$ and ${{\varvec{x}}}_{j}$, respectively.

Given a DoE with $N$ training points, i.e., $\mathcal{X}={\left[{{\varvec{x}}}_{1},{{\varvec{x}}}_{2},\dots ,{{\varvec{x}}}_{N}\right]}^{T}$ with ${{\varvec{x}}}_{i}\in {\mathbb{R}}^{d}$ and the corresponding responses $\mathcal{Y}={\left[{y}_{1},{y}_{2},\dots ,{y}_{N} \right]}^{T}$ with ${y}_{i}=\text{g}\left({{\varvec{x}}}_{{\varvec{i}}}\right)\in {\mathbb{R}}$, the regression coefficients ${\varvec{\beta}}$ and the variance ${\sigma }^{2}$ of the Gaussian process can be estimated as follows:

$$\begin{array}{c}\widehat{{\varvec{\beta}}}={\left({{\varvec{F}}}^{{T}}{{\varvec{R}}}^{-1}{\varvec{F}}\right)}^{-1}{{\varvec{F}}}^{{T}}{{\varvec{R}}}^{-1}{\varvec{Y}}\end{array}$$

(28)

$$\begin{array}{c}{\widehat{\sigma }}^{2}=\frac{1}{N}{\left({\varvec{Y}}-{\varvec{F}}\widehat{{\varvec{\beta}}}\right)}^{{{T}}}{{\varvec{R}}}^{-1}\left({\varvec{Y}}-{\varvec{F}}\widehat{{\varvec{\beta}}}\right)\end{array}$$

(29)

where ${\varvec{F}}$ is the matrix with ${F}_{ij}={f}_{j}\left({{\varvec{x}}}_{i}\right),\boldsymbol{ }i=1,2,\dots ,N$, $j=1,2,\dots ,m$, and ${\varvec{R}}$ denotes the correlation matrix prescribed as ${R}_{ij}=R\left({{\varvec{x}}}_{i},{{\varvec{x}}}_{j};{\varvec{\theta}}\right),\boldsymbol{ }i,j=1,2,\dots ,N$. The hyper-parameters ${\varvec{\theta}}$ are determined via the maximum-likelihood estimation as follows:

$$\begin{array}{c}\widehat{{\varvec{\theta}}}=\underset{{\varvec{\theta}}\in {{\varvec{D}}}_{{\varvec{\theta}}}}{\text{arg min}}\left[\left[\text{log}(\text{det}{\varvec{R}})+N\text{log}\left(2{\pi}{\sigma }^{2}\right)+N\right]\right]\end{array}$$

(30)

Consequently, the best linear unbiased prediction of the response at an unknown point ${{\varvec{x}}}^{{*}}$ follows a Gaussian distribution with mean ${\mu }_{\widehat{\text{g}}}({{\varvec{x}}}^{{*}})$ and variance ${\sigma }_{\widehat{\text{g}}}^{2}\left({{\varvec{x}}}^{{*}}\right)$:

$$\begin{array}{c}{\mu }_{\widehat{\text{g}}}\left({{\varvec{x}}}^{{*}}\right)=f{\left({{\varvec{x}}}^{{*}}\right)}^{{T}}\widehat{{\varvec{\beta}}}+r{\left({{\varvec{x}}}^{{*}}\right)}^{{{T}}}{{\varvec{R}}}^{-1}\left({\varvec{Y}}-{\varvec{F}}\widehat{{\varvec{\beta}}}\right)\end{array}$$

(31)

$$\begin{array}{c}{\sigma }_{\widehat{\text{g}}}^{2}\left({{\varvec{x}}}^{{*}}\right)={\widehat{\sigma }}^{2}\left(1-{{\varvec{r}}}^{{{T}}}\left({{\varvec{x}}}^{{*}}\right){{\varvec{R}}}^{-1}{\varvec{r}}\left({{\varvec{x}}}^{{*}}\right)+{{\varvec{u}}}^{{{T}}}\left({{\varvec{x}}}^{{*}}\right){\left({{\varvec{F}}}^{{{T}}}{{\varvec{R}}}^{-1}{\varvec{F}}\right)}^{-1}{\varvec{u}}\left({{\varvec{x}}}^{{*}}\right)\right)\end{array}$$

(32)

where ${\varvec{u}}\left({{\varvec{x}}}^{{*}}\right)={{\varvec{F}}}^{{{T}}}{{\varvec{R}}}^{-1}{\varvec{r}}\left({{\varvec{x}}}^{{*}}\right)-{\varvec{f}}({{\varvec{x}}}^{{*}})$, and ${\varvec{r}}({{\varvec{x}}}^{{*}})$ represents the correlation vector between the prediction point ${{\varvec{x}}}^{{*}}$ and those in the DoE ${{\varvec{x}}}_{i}$, $i=1,2,\dots ,N$, e.g., ${r}_{i}=R\left({{\varvec{x}}}^{{*}},{{\varvec{x}}}_{i};{\varvec{\theta}}\right).$

Appendix B: Brief review of learning functions

Selecting an appropriate learning function is essential for accurately and efficiently enriching the DoE in structural reliability analysis. Leveraging statistical insights from the Kriging model, various learning functions have undergone extensive developments over the years. This section provides a brief overview of the six functions in the proposed learning function allocation scheme, namely EFF, FNEIF, KO, H, LIF, and REIF. In general, the strategy to identify a candidate sample in these learning functions is categorized into three fundamental principles. (1) Approximation to Design Region: Selection of samples that facilitate the approximation of the design region, such as the LSS or areas characterized by the lower and upper bounds of the LSS; (2) Maximum Contribution to Failure Probability: Identification of samples that contribute the most to mitigating the disparity between the predicted and actual failure probability; (3) Maximum Uncertainty or Probability in Desired Region: Priority to samples that possess the highest uncertainty or probability in the desired region.

(1) EFF

The expected feasibility function (EFF) is introduced as an intuitive metric to quantitively measure the degree to which the real response is near the LSS or a prescribed region. High uncertainties and proximities to these regions result in large values of the EFF learning function. Consequently, the sample that maximizes EFF is added to the DoE. The specific expression of the EFF is given as [30]:

$$\begin{array}{c}{\text{E}}{\text{F}}{\text{F}}\left({\varvec{x}}\right)={\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)\left[2\Phi \left(\frac{-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{-{\upepsilon }_{\text{EFF}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{{\upepsilon }_{\text{EFF}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]-\\ {\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)\left[2\upphi \left(\frac{-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\upphi \left(\frac{-{\upepsilon }_{\text{EFF}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\upphi \left(\frac{{\upepsilon }_{\text{EFF}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]+\\ {\epsilon }_{\text{EFF}}\left[\Phi \left(\frac{{\upepsilon }_{\text{EFF}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{-{\upepsilon }_{\text{EFF}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]\end{array}$$

(33)

(2) FNEIF

To quantify the improvement in approximating the LSS of the Kriging model, the Folded Normal based Expected Improvement Function (FNEIF) is proposed in [38]. The sample with the highest value of the FNEIF learning function is utilized to improve the Kriging model. Leveraging the properties of the folded normal distribution, the analytical expression of FNEIF is derived as follows:

$$\begin{array}{c}{\text{F}}{\text{N}}{\text{E}}{\text{I}}{\text{F}}\left({\varvec{x}}\right)=\left\{\begin{array}{c}2{\sigma }_{f}\left({\varvec{x}}\right)\left[\Phi \left(\frac{2{\sigma }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{-2{\sigma }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]+\\ {\mu }_{f}\left({\varvec{x}}\right)\left[\begin{array}{c}\Phi \left(\frac{{\mu }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{-{\mu }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\\ \Phi \left(\frac{2{\sigma }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)+\Phi \left(\frac{-2{\sigma }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-1\end{array}\right]+\\ {\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)\left[\phi \left(\frac{{\mu }_{f}\left({\varvec{x}}\right)+{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)+\phi \left(\frac{{\mu }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]+\\ {\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)\left[\Phi \left(\frac{{\mu }_{f}\left({\varvec{x}}\right)+{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{{\mu }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right], 2{\sigma }_{f}\left({\varvec{x}}\right)\ge {\mu }_{f}\left({\varvec{x}}\right)\\ 2{\sigma }_{f}\left({\varvec{x}}\right)\left[\Phi \left(\frac{2{\sigma }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{-2{\sigma }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]-{\mu }_{f}\left({\varvec{x}}\right)+\\ {\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)\left[\phi \left(\frac{{\mu }_{f}\left({\varvec{x}}\right)+{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)+\phi \left(\frac{{\mu }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]+\\ {\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)\left[\Phi \left(\frac{{\mu }_{f}\left({\varvec{x}}\right)+{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{{\mu }_{f}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right], 2{\sigma }_{f}\left({\varvec{x}}\right)<{\mu }_{f}\left({\varvec{x}}\right)\end{array}\right.\end{array}$$

(34)

(3) KO

The KO learning function [39] is proposed to assess the probability of the Kriging prediction occurring in the desired region. The sample with the highest value of KO, as expressed in Eq. (35), is considered the optimal alternative to enrich the DoE, thereby enhancing the precision of the Kriging model.

$$\begin{array}{c}{\text{K}}{\text{O}}\left({\varvec{x}}\right)=\Phi \left(\frac{\overline{\text{g} }\left({\varvec{x}}\right)+{\epsilon }_{\text{KO}}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{\overline{\text{g} }\left({\varvec{x}}\right)-{\epsilon }_{\text{KO}}\left({\varvec{x}}\right)-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\end{array}$$

(35)

(4) H

Using information entropy, the H learning function is formulated to effectively characterize the uncertainty of the Kriging predictions within the region proximate to the LSS. In structural reliability analysis, the desired region is specifically defined as the area fluctuating around the LSS, and the sample with the highest H value is selected by the active learning process. The analytical expression of the H learning function is derived as follows [42]:

$$\begin{array}{c}{\text{H}}\left({\varvec{x}}\right)=\left|\begin{array}{c}\text{ln}\left(\sqrt{2{\pi}}{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)+\frac{1}{2}\right)\left[\Phi \left(\frac{{\upepsilon }_{\text{H}}+{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)-\Phi \left(\frac{-{\upepsilon }_{\text{H}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]-\\ \left[\frac{{\upepsilon }_{\text{H}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{2}\phi \left(\frac{{\upepsilon }_{\text{H}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)+\frac{{\upepsilon }_{\text{H}}+{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{2}\phi \left(\frac{-{\upepsilon }_{\text{H}}-{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]\end{array}\right|\end{array}$$

(36)

(5) LIF

The LIF learning function, denoted as the least improvement function, is introduced to quantify the reduction in uncertainty for the predicted failure probability when a new point is added to the DoE. By reducing the difference between the predicted and actual failure probability, the uncertainty decreases, and the value of LIF increases. Consequently, a sample with the maximum LIF value is identified as the optimal choice to update the Kriging model. Incorporating the statistical information from the Kriging model and the JPDF, the specific formula of LIF is given as follows [43]:

$$\begin{array}{c}{\text{L}}{\text{I}}{\text{F}}\left({\varvec{x}}\right)=\left\{\begin{array}{c}\Phi \left(-\text{U}\left({\varvec{x}}\right)\right)f\left({\varvec{x}}\right)\left({\mu }_{\widehat{\text{g}}}^{n}\left({\varvec{x}}\right)+\sum_{m=1}^\frac{n}{2}{C}_{n}^{2m}{\mu }_{\widehat{\text{g}}}^{n-2m}\left({\varvec{x}}\right){\sigma }_{\widehat{\text{g}}}^{2m}\left({\varvec{x}}\right)\left(2m-1\right)!!\right), n \, {\text{i}}{\text{s}} \, {\text{even}}\\ \Phi \left(-\text{U}\left({\varvec{x}}\right)\right)f\left({\varvec{x}}\right)\left(\sqrt{\frac{2}{\pi}}\sum_{\text{m=0}}^{n}{C}_{n}^{m}{\mu }_{\widehat{\text{g}}}^{n-m}\left({\varvec{x}}\right){\sigma }_{\widehat{\text{g}}}^{m}\left({\varvec{x}}\right){\int }_{-\frac{{\mu }_{\widehat{\text{g}}}\left({{\varvec{x}}}_{0}\right)}{{\sigma }_{\widehat{\text{g}}}\left({{\varvec{x}}}_{0}\right)}}^{+\infty }{t}^{m}{\text{exp}}\left(-\frac{{t}^{2}}{2}\right)dt\right), n \, {\text{i}}{\text{s}} \, {\text{uneven}}\end{array}\right.\end{array}$$

(37)

(6) REIF

The REIF learning function, referred to as the active reliability-based expected improvement function, is proposed to facilitate the accurate approximation of the LSS [44]. Within the candidate sample pool, the sample that maximizes REIF is identified to optimize the fitting precision of the LSS. Considering the properties of the folded-normal distribution, the expression of REIF is given as follows:

$${\text{REIF}}\left({\varvec{x}}\right)={\text{E}}\left[\omega {\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)-\left|\widehat{\text{g}}\left({\varvec{x}}\right)\right|\right]=\omega {\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)-{\text{E}}\left[\left|\widehat{\text{g}}\left({\varvec{x}}\right)\right|\right]\begin{array}{c}={\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)\left[1-2\Phi \left(\frac{{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)\right]+{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)\left[\omega -\sqrt{\frac{2}{\pi}}{\text{exp}}\left(-\frac{1}{2}{\left(\frac{{\mu }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}{{\sigma }_{\widehat{\text{g}}}\left({\varvec{x}}\right)}\right)}^{2}\right)\right]\end{array}$$

(38)