1 Introduction

Computational fluid dynamics (CFD) has made great progress in recent decades and has been widely applied in a variety of industries, including the aerospace industry [1], automotive engineering [2], electro-thermal simulation [3], physical simulation [4] and others. In the CFD workflow, finite mesh generation is a crucial procedure that significantly influences simulation efficiency and accuracy [5]. Degenerate mesh elements with undesired qualities such as large or small angles or poor shapes can induce ill-conditioning of the matrix system and decrease convergence rate. Many automatic methods have been proposed to generate finite meshes. However, the meshes required for CFD simulation are closely tied to the physical problems. The meshes generated by automatic methods may not assure acceptable qualities [6]. Therefore, after the mesh generation process, the professionals usually need to check and evaluate mesh qualities, which is time-consuming and tedious work. The manual evaluation remarkably extends the CFD workflow.

Many metrics have been introduced in mesh generation to evaluate mesh quality. For example, aspect ratio, the inner angle of a triangle element, skewness, Jacobian ratio, and other metrics are applied to evaluate two-dimensional meshes. Volumetric skew and volumetric collapse are commonly used metrics to assess tetrahedral meshes in three dimensions [7]. The above metrics are widely adopted by the automatic mesh generation methods to guide the generating process. However, those quality metrics are flawed and can only be utilized to assess mesh quality in a limited way: on the one hand, most metrics are element-based, meaning that they are applied as a scalar function to a finite mesh element. Thus, it represents local features instead of regional or global features. Their thresholds are usually based on the professionals’ subjective experience. On the other hand, some metrics may have no bearing on the accuracy of computations. Knupp [8] investigates the relationship between commonly used mesh quality metrics with industry, the truncation error, and interpolation error. Their results show that some mesh quality metrics may have no connection with the errors. For these two reasons, the mesh quality metrics are primarily utilized to detect defective mesh elements and guide the automatic mesh generation and postprocessing.

With the development of graphics processing unit (GPU) and accessibility to big data, deep learning has been applied in various domains, including computational vision, natural language processing, and machine translation [9]. The deep learning method can learn an abstract function which maps the input data to some target. The method interactively optimizes the model’s parameters through the gradient descent algorithm. In recent years, graph neural networks (GNNs) have shown the ability to perform deep learning on graph data. They have been successfully applied to issues involving graph data as input, such as node classification, graph classification, network embedding [10]. In this paper, we utilize GNN to evaluate the mesh quality without human involvement. We introduce a preprocessing algorithm for transforming mesh data to graph data that can be applied for meshes of different topologies. We also propose a deep graph neural network, GMeshNet, to evaluate the mesh qualities by categorizing meshes by pre-defined classes. The main contributions of our work are as follows:

  1. 1.

    We introduce two graph representation schemes for meshes, and a novel, sparse-implemented preprocessing algorithm to transform CFD mesh data to graph data. The algorithm is applicable to different meshes, such as structured meshes or unstructured meshes.

  2. 2.

    We propose a deep graph neural network, GMeshNet, for the mesh quality evaluation. The network can utilize the topology of the meshes to guide the mesh evaluation.

  3. 3.

    We validate GMeshNet on the real world mesh datasets NACA-Market [11] and NACA6510. It achieves high performance in detecting and recalling distorted meshes. The experiment results show the effectiveness of our proposed network.

The remainder of this paper is organized as follows. We present related work on mesh quality metrics and mesh evaluation methods with machine learning in Sect. 2. In Sect. 3, we introduce our data transform algorithm and our network. In Sect. 4, we evaluate our proposed network on the mesh benchmark datasets, NACA-Market and NACA6510. We conclude and discuss future work in Sect. 5.

2 Related work

Over the years, mesh quality evaluation has been studied in many different methods. Since it is difficult to define an evaluation function to take the entire mesh as input, mesh evaluation usually adopts element-based mesh quality metrics, which are formulated by scalar functions. Many mesh quality metrics have been proposed and widely applied in the industry for structure meshes with different topological structure. Li et al. [7] summarizes various commonly used mesh quality metrics for both two-dimensional and three-dimensional meshes. Warp angle, for example, is an angular quality metric used to evaluate the skewness of the finite element. For triangular mesh, it is defined as

$$\begin{aligned} \theta _{\text{ skew } }=90^{\circ }-\min \left( \alpha _{1}, \alpha _{2}, \alpha _{3}\right) \end{aligned}$$
(1)

where \(\alpha _{1}\), \(\alpha _{2}\), \(\alpha _{3}\) is the smaller crossing angle between the triangular mesh element’s center lines and medians. Jacobian Ratio, defined as Eq. (2), evaluates how far an element’s shape deviates from its ideal shape.

$$\begin{aligned} J_{\mathrm {R}}=\frac{\Vert {\varvec{J}}\Vert _{\min }}{\Vert {\varvec{J}}\Vert _{\max }} \end{aligned}$$
(2)

where \(\Vert {\varvec{J}}\Vert _{\min }\) and \(\Vert {\varvec{J}}\Vert _{\max }\) are the minimum and maximum Jacobian determinants of finite elements. Sarrate et al. [12] proposes a new approach for representing triangular mesh elements in a bound domain, which can graphically depict triangular meshes. Nie et al. [13] discusses several quality metrics for tetrahedral mesh, and shows the inconsistent simulation results when adopting different metrics. Kwok and Chen [14] develop a mesh quality metric for hexahedral and wedge elements based on the aspect ratio, the warping factor, and Jacobian determinants. It exhibits an explicit correlation with the solution errors. Since the lack of mathematical theory for quality metrics, Knupp [15] places the quality metrics in an algebraic framework and provides a method of constructing, classifying and evaluating mesh quality metrics. Knupp [16] specifies essential properties that a quality metric should satisfy, as well as explicit formulas for constructing different quality metrics for various mesh elements. Despite their wide applications in the industry, those quality metrics are usually employed to detect defective mesh elements. Besides this, their thresholds are often ambiguous and highly subjective. Using different mesh quality metrics may even lead to different simulation results.

Aside from those element-based mesh quality metrics, a lot of effort has been put into evaluating mesh quality with machine learning method. We divide those works into two families. One adopts traditional machine learning methods, which use feature engineering to construct input. The other utilizes the deep learning methods, which allow the network to extract needed features on its own. The support vector machine is the most popular linear model for classification and regression problems before the rise of deep learning [17]. The algorithm creates a hyperplane in feature space and classifies data by separating them into different subspaces. Support Vector Regression (SVR) is the regression model based on the same idea. Chetouani [18] evaluates 3D mesh quality (those meshes are used in computer vision instead of CFD) with the SVR model. It combines specified mesh quality metrics and geometric attributes as input features and then employs the SVR to predict the quality scores. Sprave and Drescher [19] consider the neighborhoods of a mesh element by evaluating and aggregating the values of its neighborhoods’ quality metrics. Feedforward neural networks (FNNs) and extremely randomized trees (ExtraTrees) are used to classify mesh elements. As can be seen, such methods are not end-to-end algorithms, as they take mesh quality metrics rather than mesh geometric attributes as input. Also, determining appropriate quality metrics as input features is difficult.

With the development of GPU and the availability of big data, the deep learning method can now solve many problems that were previously difficult for machines to address. By deepening and widening the network, deep neural networks (DNNs) can extract high-level features from the raw input data independently. DNNs can perform classification under diverse application environments, such as text classification, image classification, speech recognition, etc [9]. Convolutional neural networks (CNNs) [20] are commonly used in computer vision tasks such as image classification [20], target detection [21], target segmentation [22], etc. GridNet [11] and MVE-Net [23] develop CNN-based mesh quality evaluation models based on the similar data representation between two-dimensional structural meshes and the grid data. The models take the geometric attributes of mesh elements as input features. The experimental results on structured mesh show that neural networks can evaluate mesh quality in an end-to-end manner. However, such CNN-based models are challenging to apply to three-dimensional meshes or unstructured meshes. It is difficult to represent a three-dimensional mesh with a two-dimensional grid without losing information.

Graph neural networks (GNNs) have shown their ability to handle graph data structures. They have been successfully applied in many environments, including traffic prediction [24], recommender systems [25], molecular properties prediction [26] and social influence prediction [27]. Because of the enormous success of CNNs in computer vision, a lot of effort has been put into redefining convolution and pooling operation on graphs. There are two types of convolutions on graphs, spectral convolution [28] and spacial convolution [29]. The former represents node features in the spectral domain with Fourier transform on the graph. The latter aggregates the neighbors’ features of the node to generate the hidden features. In classification tasks, convolution layers are used to extract features from raw input data, whereas pooling layers are adopted to reduce input size and widen the receptive field. The node clustering methods [30] learn a cluster assignment matrix to coarsen the nodes and the graph structure. The node drop methods [31] score every node and then perform the pooling by dropping a percentage of nodes.

Taken together, we can see that traditional mesh quality metrics have limited usage. Traditional machine learning methods for evaluating mesh quality rely heavily on the manual construction of mesh features, which is not an end-to-end approach. While the CNN-based mesh quality evaluating methods have shown promising results on 2D structured meshes, it cannot be extended to other mesh types. In summary, this paper proposes a novel mesh quality evaluation network based on GNN. The proposed method can be applied to different types of meshes and be performed in an end-to-end manner.

3 Proposed method

In this paper, we define mesh evaluation as a graph classification task under supervised learning. Through a pre-processing algorithm, we transform the meshes into graph data and construct the input features. The GMeshNet takes the graph data as input and predicts the mesh quality by classifying it into pre-defined classes.

3.1 Mesh preprocessing algorithm

The input of GNNs is graph data. However, the mesh is usually stored by a set of point coordinates or mesh elements. To apply GNNs on meshes, a graph-based representation of the mesh is required. In this part, we propose two graph representation schemes for mesh data. Furthermore, we introduce an algorithm with sparse implementation to transform the mesh data into graph data. The main advantage of our algorithm is that it can be applied to meshes with different topologies.

A graph is pair of \(G=\left( V,E\right)\), where \(V=\{v_i\Vert i\in N\}\) is the set of vertices (N is the number of the vertices) and \(E=\{e_{ij}\Vert e_{ij}=\left( v_i,v_j\right) \;\left( v_i,v_j\right) \in V^2\}\) is the set of edges. For an undirected graph, \(e_{ij}\) is identical to \(e_{ji}\). The finite element mesh is made up of nodes and elements. In this paper, we present two schemes for representing mesh as a graph. The element-based graph treats mesh elements as vertices and the adjacencies of mesh elements as edges of the graph. The point-based graph treats mesh nodes as vertices and the adjacencies of nodes as edges of the graph. Using the graph representation, we can represent a mesh with its input feature matrix X and adjacency matrix A. The former represents the features of the vertices (mesh nodes or elements), while the latter represents the topology of the mesh. Figure 1 depicts the two representation schemes for a structured mesh.

Next, we introduce the algorithm for constructing the input feature matrix X and the adjacency matrix A from the raw mesh file format. For the purpose of this paper, we mainly talk about the preprocessing algorithm of the structured quadrilateral mesh. It is easy to expand to other types of meshes. In this paper, we illustrate our algorithms with the file format which stores the point coordinates of each mesh element.

Fig. 1
figure 1

Left: Mesh nodes correspond to vertices on the graph. The adjacency of vertices corresponds to the adjacency of nodes. For example, vertex 5 is adjacent to vertex 2, 4, 6 and 8. Right: Mesh elements are treated as vertices on the graph. Two elements are adjacent if and only if they share one edge. For instance, element 3 is adjacent to element 1, 4

Full size image

3.1.1 The point-based graph

The adjacencies of mesh nodes located in the same element are easily accessible. However, one node may appear in different elements which are stored separately in the mesh file. The key point is how to get the full adjacencies of one node. The main idea is to get the index of the same node in different elements, obtain adjacency and drop duplicated nodes in different elements. We construct \(X_p\in {\mathbb {R}}^{4N\times 3}\) by stacking the coordinates of mesh elements’ nodes, where N is the number of the mesh elements, and \({X_p}_{[i,\cdot ]}\) is the node i coordinates. We have duplicated nodes in different elements, meaning that for some i, j we have \({X_p}_{[i,\cdot ]}={X_p}_{[j,\cdot ]}\). We use \(A_p\in {\mathbb {R}}^{4N\times 4N}\) to represent the adjacency of nodes in the same element. To get the adjacency of the nodes in separate elements, a matrix \(A_s\) is defined as

$$\begin{aligned} \begin{aligned} A_{s}&=[a_{ij}] \in \mathbb {R}^{4N \times 4N}, \\ \text {where}\ a_{ij}&=\left\{ \begin{aligned} 1&\ ,\text {if}\ {X_{p}}_{[i,\cdot ]}={X_{p}}_{[j,\cdot ]}\\ 0&\ ,\text {otherwise} \end{aligned} \right. \end{aligned} \end{aligned}$$
(3)

Intuitively, \(a_{ij}=1\) means that node i and node j are the same node. Then the adjacencies of the nodes in different elements can be attained by

$$\begin{aligned} A_n=A_pA_s \end{aligned}$$
(4)
$$\begin{aligned} A_n'={\text {Reformat}}(A_n) \end{aligned}$$
(5)

The first Eq. (4) computes the adjacencies of the nodes in different elements. The Reformat operation sets the element of a matrix to one if it is greater than one. To avoid losing adjacent relationships when dropping duplicated nodes, we need to ensure that if node i is adjacent to node j, then node i is adjacent to the duplicated nodes of node j. Such operation can be done by

$$\begin{aligned} A_{d}=A_{s}A_{n}^{\prime } ,\ A_{d}^{\prime }={\text {Reformat}}\left( A_{d}\right) \end{aligned}$$
(6)

The final step is dropping duplicated nodes in \(X_p\) and \(A_d'\). Let \(duplicated\_idx=\{j\Vert a_{ij}=1,i<j\}\) denotes the index set of duplicated nodes to be dropped. Then the no duplicated node index is \({idx}=\{i\Vert i\in \left[ 1,4N\right] ,i\in {\mathbb {Z}}\}-{duplicated\_idx}\). Finally, the input feature matrix X and adjacency matrix A are generated by

$$\begin{aligned} X=X_{p[i d x,\cdot ]}, A=A_{d[i d x, i d x]}^{\prime } \end{aligned}$$
(7)
Fig. 2
figure 2

Element i and j share one edge. Each element can obtain the adjacencies of the identical nodes on the other elements. The lines show the connection between the elements. Thus, in this case the connection strength of the two elements is 8

Full size image
Fig. 3
figure 3

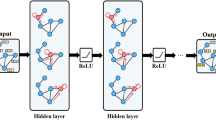
The proposed network for mesh quality evaluation. Through preprocessing, the mesh is represented with the input feature matrix X and the adjacency matrix A. The network learns the features of the mesh and then predicts the mesh quality by classifying it into predefined categories. The GraphConv layer extracts features with message passing among the vertices. The GraphPooling layer coarsens the graph by scoring the nodes the retaining the most valuable vertices

Full size image

3.1.2 The element-based graph

In this representation, we treat mesh elements as vertices. Two elements are adjacent if and only if the two elements share one edge, i.e., the two elements have more than one same point coordinates. The input feature matrix \(X\in {\mathbb {R}}^{N\times d}\) is obtained directly from the raw mesh files, where N is the number of mesh elements and d is the number of element features. We still need a way to construct adjacency relations between mesh elements. Suppose that S is the element assignment matrix, which is define as \(S=\left[ s_{ij}\right] \in {\mathbb {R}}^{N_p\times N}\), where \(N_p\) is the number of the nodes, and \(s_{ij}\) equals to one if node i in element j, otherwise equals to zero. Also let \(A_p\in {\mathbb {R}}^{N_p\times N_p}\) be the adjacency matrix of the point-based representation. Then we can obtain the adjacency matrix denoting the strength between two elements:

$$\begin{aligned} A_{e}=S^TA_pS \end{aligned}$$
(8)

If two elements share one edge, the strength between the elements is 8. The connection strength is illustrated in Fig. 2. So, the item of final adjacency matrix A is

$$\begin{aligned} A_{[i, j]}=\left\{ \begin{array}{l}1, \text{ if } A_{e[i, j]}=8 \\ 0, \text{ otherwise } \end{array}\right. \end{aligned}$$
(9)

The above preprocessing algorithms are implemented with sparse matrixes. For a structure two-dimensional mesh with 30,400 elements, it only takes 0.79 s to preprocess a mesh into a graph. It can be further optimized by rearranging the index order of the nodes or the elements. After obtaining X and A, Min–Max Normalization is adopted to regularize the input feature matrix.

3.2 Network architecture

Typically, a mesh may have a large number of elements. To extract high-level features from low-level features, we design a deep graph neural network. As shown in Fig. 3 our GMeshNet mainly consists of graph convolutional layers, graph pooling layers, and Jumping connections. The graph convolution layers aggregate the features of the elements on the graph layer-by-layer. And the graph pooling layer reduces the size of the graph and expands the graph convolution receptive field. Moreover, we employ Jumping connection to aggregate information under different hierarchical representations. Finally, an MLP classifies data into different classes.

3.3 Graph convolution layers

Similar to CNNs, spatial GNNs extract hidden features of vertices on the graph by aggregating the features of neighbors. Depending on the aggregation method, there are many different graph convolution operations. Since different neighbors may have different influences on the hidden features of the vertice, we adopt GAT [29] as the convolutional layer. It assigns different weights to different vertices in the neighborhood. Specifically, the inputs of the h th graph convolution are the feature matrix, \(X_h=\left[ x_1^{hT},x_2^{hT},...,x_N^{hT}\right] \in {\mathbb {R}}^{N\times m}\), and the adjacency matrix, \(A_h\in {\mathbb {R}}^{N\times N}\) , where N is the number of the vertices, m is the dim of input features, \(x_i^h\) is the features of vertice i in layer h. It then produces a new feature matrix \(X_h^\prime \in {\mathbb {R}}^{N\times n}\) as the input of the pooling layer, where n is the dim of output features. Suppose the weight between vertice i and vertice j is \(\alpha _{ij}\), then the hidden features of the vertice i are attained by

$$\begin{aligned} {{x}_{i}^{h}}'=\sigma \left( \sum _{j \in {\mathcal {N}}_{i}} \alpha _{i j} {\mathbf {W}} {x}_{j}^{h}\right) \end{aligned}$$
(10)

where \(\sigma\) is the ReLU function, W is the transform matrix and \({\mathcal {N}}_{i}\) is the indexes of neighbours of vertice i. To sum up, GAT performs as

$$\begin{aligned} X_{h}'=GAT(X_{h},A_h) \end{aligned}$$
(11)

As the GNN gets deeper and deeper, it suffers from over-smoothing [32]. Over-smoothing leads to possible degradation of the performance of the network as it gets deeper and deeper. To avoid this, we adopt residual connection, which is proposed by Li et al. [33] and Li et al. [34], to tackle this problem. We computer the \(X_{h+1}^{res}\) instead of \(X_{h+1}\) and let the input feature dim equal to output feature dim to enable addition between residuals and original input matrix. Additionally, LayerNorm [35] and activation function \(\sigma\) are performed before the graph convolution. Figure 3 shows the structure of the graph convolution layers.

$$\begin{aligned} \begin{aligned} X_{h}'&=X_{h}^{\text {res}}+X_{h} \\&={\text {GAT}}(\sigma ({\text {LayerNorm}}(X_{h})),A_h)+X_{h} \end{aligned} \end{aligned}$$
(12)

3.4 Pooling layers

The mesh may consist of millions of mesh elements. By pooling the graph into smaller sizes, the network could learn local features from mesh elements and reduce its parameters and computing overhead. Due to a large number of mesh elements, it is inefficient to perform node-cluster pooling methods (e.g. DiffPool [30]) since they require to compute the assignment matrix. Therefore, we adopt SAGPool [36] , implemented with sparse operations, to pool the graph data.

More specifically, the SAGPool first obtains the self-attention scores \(Z\in {\mathbb {R}}^N\) of the nodes by Graph Convolution. Further top \(\lceil kN\rceil\) vertices are selected based on the value of Z, where \(k\in (0,1]\) is the pooling ratio. Finally, the reconstructed feature matrix \({X^\prime _h}\) and adjacency matrix \(A_h\) are obtained by

$$\begin{aligned} {idx}= & {} {\text {top}}-{\text {rank}}(Z,\lceil k N\rceil ) \nonumber \\ Z_{ \text {mask }}= & {} Z_{[{idx}]},X^{\prime }_h=X_{h[{idx},:]}'\nonumber \\ X_{h+1}= & {} X^{\prime }_h \odot Z_{ \text {mask }},\ A_{h+1}=A_{h [{idx}, {idx}]} \end{aligned}$$
(13)

3.5 Jumping connection

To classify the graph, we need a representation of the entire graph. The commonly used graph representation methods are global average readout operation and global maximum readout operation. The former utilizes the average features of all vertices as graph representation, while the latter uses the maximum features of all vertices. To enhance the robustness of the algorithm, we concatenate the above two representations together. The readout operation is

$$\begin{aligned} g_h=[\text {global\_avg\_pool}(X_h),\text {global\_max\_pool}(X_h)]^T \end{aligned}$$
(14)

where the two pooling operations output representations in \({\mathbb {R}}^n\).

Additionally, to consider graph representations under different levels, we apply JK-Net [37] to concatenate graph representations under different levels. The effectiveness of the JK-Net and the analysis of different connect in JK-Net are demonstrated with experiments. The final representation is then input to an MLP with SoftMax output for classification. Between fully connected layers, BatchNorms [38] are adopted to stable the training process.

Fig. 4
figure 4

Examples of meshes in NACA-Market [11] and NACA6510 dataset

Full size image

4 Experiments

In this section, we evaluate our proposed GMeshNet on the real mesh benchmark datasets, NACA-Market and NACA6510. In Sect. 4.1, we introduce the datasets and the features of the input. Section 4.2 demonstrates the training procedures. The results of the network are discussed in Sect. 4.3. Furthermore, we discuss the effect of hyper-parameters and structures of the Network on the performance in the last section.

4.1 Datasets

We evaluate GMeshNet on two mesh benchmark datasets, NACA-Market and NACA6510. NACA-Market [11] is a two-dimensional structured mesh dataset proposed for the mesh quality evaluation task. It has a total of 10240 meshes with different sizes. The distorted meshes are generated by modifying points and lines of the well-shaped mesh. Meshes are classified into eight types depending on their smoothness, orthogonality, and spacing distribution. We verify the mesh quality with CFD solver in terms of solution accuracy and convergence speed. Figure 4 shows some examples of meshes with different properties. To illustrate the generalization performance of our network under different airfoils, we used the same method to construct the NACA6510 dataset (a total of 1024 meshes) from the NACA6510 airfoil, which is shown in Fig. 4e. In experiments, we choose the element-based representation to represent mesh. We leave the point-based representation for future work because it performs poorly in the experiments. Some insights are provided in Sect. 4.4.3 to explain the difficulties of learning from point-based representation. The edge length, the maximum angle and the area of the mesh element are adopted as vertices features.

4.2 Training procedures

During our training, 10% of the meshes are used as testing data to get the final accuracy of the network. 10% of the meshes are employed for validation in training. The remaining meshes are adopted as the training data. We select AMSGrad [39] with a initial learning rate of 1e-2 as the optimizer, and manually adjust the learning rate in the trainning . We use cross-entropy as the loss function and add L2 regularization with 1e-4 weight decay for the NACA-Market dataset and 5e-4 for the NACA6510 dataset. The batch size is set to 32. For all pooling layers, the pooling ratio is set to 0.78. The experiments are carried out on two RTX Titan GPUs.

4.3 Network evaluation results

Table 1 Confusion matrix of the GMeshNet on NACA-market
Full size table
Table 2 Recall and accuracy of different networks
Full size table

First, we evaluated the accuracy of the network on the test set of the NACA-Market. The classification results of different types of meshes are shown in Table 1. O, S, D denote the orthogonality, smoothness, and distribution density of the mesh, respectively. N-O represents the meshes of poor orthogonality, and N-OD represents the meshes poor orthogonality and distribution. The W represents meshes with good qualities. From the experiment results, we can see that GMeshNet achieves high accuracy on the dataset. For mesh with good qualities, the network achieves the highest accuracy with 99.22%. The network can easily classify the meshes with poor orthogonality and distribution. For different types of meshes, the accuracy rate is all above 85%, which demonstrates the effectiveness of GMeshNet for mesh quality evaluation.

Second, we utilize recall on NACA-Market test set to evaluate the ability of GMeshNet to identify defects of the mesh. In the experiment, we calculate the recall based on the orthogonality, smoothness and distribution of the mesh. Recall indicates the percentage of bad meshes identified by the network out of all bad meshes. For example, the recall of the N-O meshes is defined as

$$\begin{aligned} {\text {recall}}_{\text {{N-O}}}=\frac{\text {{N-O} meshes identified by the network}}{\text {all {N-O} meshes }} \end{aligned}$$
(15)
Table 3 Recall and accuracy of GMeshNet on the NACA6510 dataset
Full size table
Fig. 5
figure 5

Visualization of discrimination results on NACA-Market with ICEM. Figure 5a–c, shows that our network can discriminate the defective meshes in agreement with the traditional metrics. However, for some meshes (such as mesh in Fig. 5d) that are actually flawed, our network can correctly classify them but the traditional mesh quality evaluation metrics fail

Full size image

Table 2 shows the results of recalling a different kind of defects. From Table 2, we can see that GMeshNet can retrieve almost all bad meshes. Meshes of poor orthogonality and poor distribution can be easily distinguished with the accuracy of 99.81% and 99.21%, respectively. In comparison with GridNet [11], GMeshNet has comparable performance in terms of recall. As for the overall accuracy, GMeshNet has 1.11% improvement. But more importantly, GMeshNet has the ability to train on all types of meshes rather than structure meshes.

Third, we also validate our network by comparing it with the widely used CFD-preprocessing software ICEM CFD, which utilizes traditional metrics to evaluate mesh qualities. As shown in Fig. 5, we can see that the proposed method can correctly discriminate meshes with poor distribution, poor smoothness or poor orthogonality. Furthermore, the network is superior to traditional quality metrics. Figure 5d depicts a defective mesh which has poor-distribution. However, the ICEM CFD misclassifies it as a well-shaped mesh. In contrast, our proposed network successfully detects it, which shows the effectiveness of the proposed network compared with traditional metrics.

Fourth, to illustrate the generalization performance of the network, we validate the network on a different airfoil mesh dataset, NACA6510. The experimental results are shown in Table 3. We can see that the network can also achieve satisfying accuracy and recall when the airfoil changes, which shows the ability of the network to learn patterns of meshes with different airfoils. We can also observe that due to overfitting on the small-scale NACA6510 dataset, the performance is slightly inferior to that on NACA-Market.

In summary, our proposed GMeshNet can evaluate the mesh quality with both high accuracy and recall, has a better discriminative ability compared to traditional metrics and can be applied to different meshes.

Table 4 Test accuracy for different hyper-parameters
Full size table

4.4 Analysis of hyper-parameters

In this part, we discuss the effect of hyper-parameters on the performance. For the mesh evaluation tasks, selecting the appropriate hyper-parameters is beneficial to the network performance, and can reduce the computational and storage overhead. We only discuss the hyper-parameters that have a large impact on the network performance. Due to the long training time of the model on the whole dataset, we perform hyper-parameter experiments on a subset (1024 meshes of the same size) of the dataset. In the experiments, we fix other parameters and change the depth of the network and the pooling ratio of the pooling layers. The experimental results are shown in Table 4.

4.4.1 Depth of the network

As the number of network layers deepens, the performance of the network improves to some extend. The average accuracy of the 16-layer network has a 2.99% improvement than the average accuracy of the 4-layer network. However, A deeper network is not necessarily better than a shallower network. We can see that the 8-layer networks with 0.7 pooling ratio achieve the best performmance. A shallow network with a suitable pooling rate may be better than a deep network with an inappropriate pooling rate. In addition, a appropriate number of network layers can also reduce the sensitivity of the network to the pooling rate. We can see that the performance of the network is less sensitive to the pooling rate when the network depth is 25 or 32.

Table 5 Experimental results of the JK-Net aggregation schemes
Full size table
Table 6 Experimental results of the different GraphConv
Full size table

4.4.2 Pooling ratio

The other important hyper-parameter is the pooling ratio k. Intuitively, the pooling ratio determines what percentage of vertices are left after pooling. A larger k helps to preserve the information of the graph, while a smaller k helps to quickly reduce the size of the graph resulting to a smaller network depth. We can see that the optimal pooling ratio is related to the network depth. For 4-layer or 16-layer networks, the performance is better at the pooling ratio of 0.5. While for 8-layer networks, the appropriate pooling ratios is 0.7. 25-layer networks and 32-layer networks achieve best result at a pooling ratio of 0.3 and 0.9. On average, 0.5 is an appropriate pooling rate for networks of different depths. This experience can help us to set the pooling ratio at the beginning of constructing the mesh evaluation network.

4.4.3 Representation scheme

In Sect. 3.1 we propose two different representations, but in our experiments, we only used the element-based representation. In fact, we experimented with both representations, but the point-based representation fails to achieve satisfactory results even for simple discrimination tasks (such as train on 256 samples). We believe that the reason for this is that the point-based representation loses the information of the mesh elements. The mesh quality depends in large part on the shape of the mesh elements. However, in the point-based scheme mesh nodes become the basic units for feature learning. Because of the stochastic of neural networks, we cannot constrain how the network learns, for example, let it learn the norm of the vector which is obtained by subtracting the coordinates of two points. Thus, the graph convolution layers may not capture the edge features. However, we believe that the information about the element edges of meshes is important for network to determine mesh quality. Future work includes the use of convolution layers utilizing edge features, so that point-based representations can also achieve satisfactory results.

4.5 The analysis of network structure

In this section, we illustrate the effectiveness of JK-Net and the effect of the graph convolution layer on the network performance. The purpose of JK-Net is to consider the graph representation under different hierarchies in the network. In JK-Net, we can use different schemes to aggregate graph representations, such as as concatenation and max pooling. We test the effect of JK-Net on the performance in different aggregation schemes, including without JK-Net, with max pooling scheme and with concatenation scheme. The results are shown in Table 5. We can see that not using JK-Net the network has a large degradation in performance. Compared with the max pooling scheme, the concatenation scheme can achieve higher accuracy.

In addition to JK-Net, we also compare the effect of adopting different graph convolutions on the network performance. We select classical graph convolutions for the experiment, including GCN [28], GraphSAGE [40], GAT [29]. The experimental results are shown in Table 6. We can see that the network based on GAT achieves better train and test accuracy, which indicates that using that type of convolutions makes the network have better learning ability. However, the choice of the graph convolution layer has less impact on the performance of the network. In summary, we recommend GAT as the graph convolution for feature learning on the mesh.

5 Conclusion

The mesh quality is of great importance for the accuracy of CFD simulations. However, the widely used mesh quality metrics based on mesh elements have limited usage. The mesh quality evaluation still relies on manual work. To tackle this problem, we introduce graph neural network into the mesh quality evaluation. Firstly, we define two graph-based representations for meshes, and propose algorithms with sparse-implementation to transform any type of mesh into the graph. Secondly, a deep graph neural network, GMeshNet, is designed for mesh quality evaluation. We evaluate our network on NACA-Market and NACA0012 mesh datasets. The experimental results show the feasibility of the GNN-based network for mesh evaluation tasks for different meshes.

Future work includes extending the classification of the whole mesh to the classification of mesh elements. However, performances for the meshes with different working conditions (such as when Reynolds number and angle of attack change) and topological structures still need to be investigated in future work. By considering the flow field features and working condition features, we believe that GNN can deal with different meshes as we have shown when the airfoil changes. Moreover, we will focus on applying the GNN-based networks to more fields in CFD, including mesh generation, mesh optimization, and others.