Abstract
In the target matrix optimization paradigm (TMOP), it has long been understood that one must create a set of target matrices before the mesh can be optimized. But there is still no general method to create correct, effective targets in response to a specific mesh quality improvement goal. The TMOP literature describes how certain sets of target matrices can be used to control the shape or size of mesh elements, but those examples address only a fraction of the problems that can occur in mesh quality improvement and were not derived from a general framework for target matrix construction. In this work, a general method of target construction is introduced based on an independent set of geometric parameters that are intrinsic to the Jacobian matrices upon which TMOP is based. The parameters enable a systematic approach to target definition and construction. The approach entails two parts. The first part defines correspondences between available primary data (stuff about the mesh and/or the physical solution) and secondary data (e.g., a field of error estimates). Once the correspondences are established, the primary data are processed into intermediate field data existing on mesh sample points. The second part creates a model that represents the values of the geometric target parameters as functions of the secondary data. The model is then tested numerically to establish model constants and effectiveness. This systematic approach to target construction is illustrated in a set of examples to show how it can be applied to common problems in mesh optimization such as equalization of geometric properties, preservation of existing good quality, and adaptation of the mesh to the physical solution. The result is a systematic method of target construction for TMOP that can be applied to a wide variety of planar and volume mesh quality improvement tasks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mesh quality may be defined as those features of a mesh that impact simulation robustness, accuracy, and efficiency. Features such as mesh resolution, the spatial distribution of the nodes, mesh geometry, mesh smoothness, mesh topology, the type of elements in the mesh, and order of the element basis functions (if any) can all be considered to be aspects of mesh quality. In any simulation, the practitioner should be concerned with the quality of the meshes they are using. The quality of meshes can, in some cases, be assessed visually, through the use of mesh diagnostics, and/or values of quality metrics. In other cases, a mesh quality issue is noticed through the examination of the numerical solution. If a quality issue is identified by any of these means, one most likely will want to consider methods for improving the mesh quality. Mesh optimization via node movement strategies such as the target matrix optimization paradigm (TMOP) is one option [15] that is considered in detail here. Other node-movement options include [1, 7, 10, 19, 20, 23,24,25,26].
1.1 Introduction to mesh quality improvement
Mesh generation is a numerical procedure used to create meshes on a given physical domain. Often, these meshes lack sufficient quality according to one measure or another. In mesh quality improvement (MQI), one presupposes the existence of an initial mesh whose quality is to be improved, through various methods. Two basic categories of mesh quality improvement methods are mesh topology changes and node movement. In general, the term “mesh optimization” is often used interchangeably with the term “mesh quality improvement” and can include both topology changes and node movement. However, for our purposes, we refer to mesh optimization as a numerical optimization method in which the initial mesh vertex coordinates are changed (thus creating node movement) to minimize an objective function that is a function of the coordinates and which represents a measure of global mesh quality.
A considerable number of mesh optimization methods have been proposed over the years. One of the more famous methods is the variational method leading to the Winslow smoothing procedure [25]. In this procedure, the Euler–Lagrange equations of the variational principle consist of a homogenous, quasi-linear, second order elliptic set of partial differential equations. The method yields smooth, non-inverted meshes on any given physical domain. The method has been extended to multi-block structured and finite element meshes.
Winslow is an example of an unweighted optimization method (i.e., a method that does not employ problem-specific weightings). Unweighted mesh optimization methods essentially provide a “generic” mesh optimization method in which details of the mesh improvement problem are not taken into account. There is only one solution to the Winslow equations, and thus only one optimal mesh exists for a given domain. If the Winslow mesh lacks sufficient quality with respect to a particular application, there is nothing one can do. To address this issue, many mesh optimization methods introduce weighting functions to create weighted methods that can potentially control the properties of the optimal mesh. In the case of Winslow, for example, weighting functions P and Q convert the set of elliptic equations to a set of Poisson equations [24]. By selecting appropriate forms and values for the weighting functions, one can control additional properties of the mesh in addition to smoothness (e.g., clustering mesh vertices toward a particular point in the domain).
Ever since the introduction of such weightings, a major issue in mesh optimization has been to find weighting functions and values that achieve the desired quality improvement. To this point, success has been rather mixed, and so efforts continue to strengthen this aspect of mesh optimization. This situation was a major motivation for the creation of the target matrix optimization paradigm. To address the full range of situations in which the issue of mesh quality arises, TMOP introduces weighting functions in the form of target matrices, which, unlike P and Q, have a well understood geometric meaning. A major thrust in TMOP is to include not only the targets within the metrics, but to describe the entire process of target matrix construction, in which one starts with a specific mesh quality improvement problem and proceeds through various steps until a full set of target matrices has been determined, prior to numerical optimization. This article summarizes what is currently known about the targets and this procedure.
The main contribution in this paper, which is an abridged version of [16], is to provide a methodology for creating a set of target matrices suitable for a particular simulation. As there are many different simulations and simulation types, many different target sets are needed to cover all the different potential simulations. There is currently a gap in the mesh optimization literature, because it fails to explain how one can systematically create such targets given any individual application; the methodology proposed in this paper is intended to fill this gap. As such, this work is a methodology paper, not a computational algorithms paper. The output of the methodology, when applied to a particular application, is an approach to creating a set of target matrices. The approach must then be implemented in code and tried. As such, the need to provide numerical confirmation of every target set suggested in this paper is not critical. It is not mesh optimization using a particular set of targets that needs to be demonstrated here, but only that the proposed methodology is reasonable and well designed. This is demonstrated by the examples given in Sect. 3.5.
1.2 Introduction to the target matrix optimization paradigm
The basic objects and concepts used in the target matrix optimization paradigm (TMOP) are reviewed in order to set the stage for this study on target construction (see also [15]). The main ingredients of TMOP are (1) the sample point concept, (2) the active Jacoban matrix, (3) the target matrix, and (4) the local quality metric(s).
1.2.1 Sample points
TMOP assumes that, for each mesh element, there is a map from a logical element to the physical element. The basis of the map is specified prior to optimization, and can be low order (i.e., first order) or high order (order greater than first). A sample point is a fixed point within the logical element at which we wish to measure local quality. Prior to mesh optimization, a set of sample points within the logical element is selected and remains fixed throughout the optimization procedure. This set of sample points could be, for example, the set of Gaussian integration points within the element. The sample points can be assigned a global index k so that \((\xi _k,\eta _k)\) indicates the kth sample point within a 2D mesh. Each sample point of a planar mesh has a corresponding location \((x_k,y_k)\) in physical space. Unlike the logical coordinates, the coordinates of the physical sample points may change during the optimization procedure when a node movement strategy is applied. Sample points enable one to measure both the quality of elements and the quality within elements. This is critical, because quality can vary within, for example, hexahedral elements and in high-order elements.
1.2.2 Active matrices
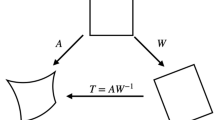
At every sample point, TMOP requires both an active and a target matrix. For planar meshes, the active matrix is a \(2 \times 2\) matrix and has four elements.Footnote 1 A volume mesh requires the active matrix to be \(3 \times 3\), with nine elements. The active matrix is denoted by A and the active matrix at sample point k (a global index) is \(A_k\). In general, the active matrix can vary from one sample point to the next. The active matrix represents the Jacobian of the map from the logical element to a physical element of the active mesh. The active matrix is a function of the nodal coordinates of the element and thus changes during the mesh optimization procedure. An important goal of mesh optimization is to ensure that, in the optimal mesh, \({\text {det}}(A)>0\) at each sample point. Occasionally, we make use of the notation \(A=\left[ \mathbf{a}_1, \mathbf{a}_2 \right] \) in which the two vectors \(\mathbf{a}_1\) and \(\mathbf{a}_2\) are the column vectors of \(A_{2 \times 2}\) or \(A=\left[ \mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3 \right] \) when A is \(3 \times 3\). The collection of active matrices \(\{ \mathcal A \}\) is the set of all active matrices in the mesh; thus \(A_k \in \{ \mathcal A \}\) for all k. We call \(\{ \mathcal A \}\) the active matrix set. In general, \(A_k\) changes as the mesh is optimized, which is why the terminology “active matrix” is used.
1.2.3 Target matrices
TMOP requires that, for every sample point k, at which \(A_k\) exists, a corresponding target matrix \(W_k\) be defined at the same sample point. If A is a \(d_1 \times d_2\) matrix, then so is W. Unlike the active matrix, the target matrix does not change during mesh optimization. In general, the target matrix can vary from one sample point to the next. Each target matrix is defined prior to mesh optimization. The target matrix represents the ideal Jacobian matrix toward which the active matrix will evolve during the mesh optimization procedure. A fundamental assumption we make is that, by construction, \({\text {det}}(W)>0\) (and therefore, \(W^{-1}\) exists). This ensures that the target matrix represents a location in the mesh at which the ideal Jacobian determinant is positive. Occasionally, we make use of the notation \(W=\left[ \mathbf{w}_1, \mathbf{w}_2 \right] \) in which the two vectors \(\mathbf{w}_1\) and \(\mathbf{w}_2\) are the column vectors of \(W_{2 \times 2}\) or \(W=\left[ \mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3 \right] \) when W is \(3 \times 3\). With this approach, there is no essential difference between targets for low order meshes and targets for high-order meshes. Targets can provide a specific problem-dependent definition of mesh quality.
The collection of target matrices \(\{ \mathcal W \}\) is the set of all target matrices in the mesh; thus \(W_k \in \{ \mathcal W \}\) for all k. We call \(\{ \mathcal W \}\) the target matrix set. The target matrix set need not be self-consistent (i.e, the set does not necessarily imply that a corresponding mesh exists). In mesh optimization this is not a major difficulty because the objective function implicitly defines a compromise between inconsistent sets of targets (e.g., as in least squares methods). However, the more the targets can be made to correspond to a mesh that exists, the more the optimization will improve quality. This is one reason why the target construction phase is so important. The target matrix set is defined prior to the beginning of the mesh optimization procedure. In general, the set will be different for every particular mesh and every mesh quality improvement goal. Target Matrix Set “smoothness” (however, that is defined) is necessary if the optimal mesh is to be smooth.
1.2.4 Local quality metrics
To measure mesh quality, TMOP uses local quality metrics. Local quality metrics are functions from a matrix to a scalar. The value of a local quality metric is measured at sample points of the mesh. Two common forms of local quality metrics are \(\mu =\mu (T)\) and \(\nu =\nu (A,W)\), with \(T=AW^{-1}\) the weighted Jacobian matrix. The values of these metrics are \(\mu _k = \mu (T_k)\) and \(\nu _k = \nu (A_k,W_k)\), where k is the global sample point index. Local quality metrics in TMOP do not measure mesh quality in an absolute sense. Rather, through the target matrix mechanism, the metrics measure quality relative to the set of targets provided (i.e., the targets constructed essentially define mesh quality in geometric terms).
1.2.5 Sets of matrices
Certain sets of matrices in connection with TMOP have been defined previously. The main matrix set with which we are concerned is \(\mathcal{M}_d\), the set of \(d \times d\) matrices with real elements. The cases \(d=2\) and \(d=3\) are important in planar and volume meshing, respectively. The following subsets of \(\mathcal{M}_d\) also play an important role: \(\mathcal{M}_d^s\), the set of singular matrices, \(\mathcal{M}_d^{\sim s} = \mathcal{M}_d \setminus \mathcal{M}_d^s\), the set of non-singular matrices, \(\mathcal{M}_d^p\), the set of matrices whose determinant is positive, and \(\mathcal{M}_d^d\), the set of degenerate matrices.
Definition 1
A matrix \(X \in M_d\) is degenerate if one or more of its column vectors is zero. Define \(\mathcal{M}_d^{\sim d}\) to be the set of non-degenerate matrices.
Clearly, \(\mathcal{M}_d^d \subset \mathcal{M}_d^s\).
1.3 Development of the target matrix paradigm
Methods for mesh quality improvement via node movement must, in some fashion, define relations between a definition of mesh quality and the mesh geometry. For example, if mesh quality is defined to be a solution-adapted mesh, then various solution-based quantities such as gradient, Hessian, flow-vectors, error estimates, etc. must be connected to the mesh geometry (i.e., to volume, shape, and orientation). The exact manner in which these relations are made varies from one MQI method to the next.
While the target matrix optimization paradigm has been studied for some time, the theory outlined in Sect. 1.2 is incomplete, particularly with regard to a general description of how the connection between mesh quality and mesh geometry is made for each of the mesh quality improvement goals listed in Ref. [16]. This article is a major step in filling this gap.
Various analytic relationships between planar mesh geometry and the Jacobian matrix are explored in Sect. 2 in order to understand how they can be exploited in target construction. Due to lack of space, the case of volume meshes whose vertices lie in \(\mathfrak {R}^3\) and \(A \in \mathcal{M}_3\) is not presented in this article. The volume case has been fully worked out in [16]. Section 2.1 defines a standard set of scalar geometric parameters that can be derived from any mesh consisting of triangular and/or quadrilateral elements. Section 2.2 shows how one defines the target matrix given the values of these geometric parameters. Section 2.3 deals with the problem of extracting the standard parameters from a given active matrix so that local quality metrics may be evaluated. Finally, Sect. 2.4 gives a matrix decomposition of the Jacobian matrix in terms of “size,” “shape,” and “orientation” factors.
Prior to numerical optimization of the active mesh, one must endow the targets at every sample point with numerical values by some algorithm. In the case that no algorithm is available, one must be devised. The process by which this is done, described in Sect. 3, is called target construction. There are three phases in target construction, beginning with formulating a strategy that takes into account the mesh simulation and context (Sect. 3.1.1), continuing with a determination on which geometric parameters are the most important to control (Sect. 3.1.2), and finally, establishing correspondences between primary data and particular geometric parameters (Sect. 3.1.3). In the second phase of target construction, one identifies sources of primary data and devises algorithms for converting the primary data to secondary data. Secondary data consist of either mesh functionals (Sect. 3.2.1) or simulation functionals (Sect. 3.2.2). In the final stage of target construction, one develops various models relating the functionals to values of the target geometric parameters (Sects. 3.3.1, 3.3.2). In Sect. 3.5, examples of target construction are provided that illustrate how the construction of targets depends on the mesh quality improvement goal.
2 Relations between matrices and geometric parameter sets
A standard set of geometric parameters that are meaningful in mesh quality are defined. The parameters are related to the elements of any \(2 \times 2\) matrix. When considering the active matrix A, the parameters describe the geometry of the tangent vectors to the mapping at the sample point within the active mesh. When considering the target matrix W, the parameters represent the local geometry of the target mesh at the sample point. Various relationships between the TMOP matrices and their geometric parameters are important in measuring geometric mesh quality and in constructing the target matrices.
Planar meshes contain two-dimensional mesh elements such as triangles, quadrilaterals, or polygons. While planar meshes can exist in both \(\mathfrak {R}^2\) and \(\mathfrak {R}^3\), it shall be assumed in this paper that a planar mesh belongs to \(\mathfrak {R}^2\). Any planar mesh in \(\mathfrak {R}^3\) can be transformed into a planar mesh in \(\mathfrak {R}^2\). Each triangular or quadrilateral element in \(\mathfrak {R}^2\) has a mapping from a two-dimensional logical space to points within the element. The boundaries of the physical elements can be curved in the high order element case. Rather than try to characterize the quality of a planar element directly, TMOP first measures local quality at sample points within the element. The set of sample points within an element can then be combined via some averaging technique to create an element quality metric. The present section, however, is concerned with the definition and construction of targets at a given sample point of a planar mesh element.
Before elaborating on the active and target matrices, it is useful to gather together some important geometry-related facts about square matrices with real elements. Geometry is emphasized because mesh quality improvement generally involves controlling geometric properties of a given mesh.
2.1 Geometric parameters for meshes in \(\mathfrak {R}^2\)
At a given sample point in a 2D mesh element, there exists the two tangent vectors to the element mapping. From the two tangent vectors, various geometric quantities can be defined: the lengths of the two tangents, the angle between them, the two angles between the tangents and the x-axis, the aspect ratio, and the area of the parallelogram between the two tangents. We refer to these parameters as length (\(\ell _1\), \(\ell _2\)), skew angle (\(\phi \)), orientation (\(\theta \), \(\theta ^\prime \)), aspect ratio (\(\rho \)), and area/volume (\(\upsilon \)). There are various relations between these quantities:
It is also useful to define a “size” quantity \(\zeta \) by
We will call these quantities the first order geometric parameters of planar mesh quality. In general, at every sample point, the value of each parameter can be different from its value at another sample point (e.g., area will differ from one sample point to the next).
Due to the relations above, only four of the parameters are needed to create a parameter set \(\mathbf{p}_2\) in which each of the parameters in \(\mathbf{p}_2\) is fully independent of the others in the set. We elect to define \(\mathbf{p}_2 \in \mathfrak {R}^4\) as follows:
We call \(\mathbf{p }_2\) the standard independent geometric parameter set for planar mesh quality. The components of \(\mathbf{p}_2\) are size, orientation, skew, and aspect ratio. The non-standard parameters may be calculated from the parameters in \(\mathbf{p}_2\). If \(\zeta >0\), then the standard geometric parameters are well-defined. In general, the values of the standard parameters can have the following ranges: \(0 \le \zeta \), \(-\pi < \theta \le \pi \), \(-\pi < \phi \le \pi \), and \(0 \le \rho \). Define the subset \(\mathcal{P}\) of \(\mathfrak {R}^4\) by the Cartesian product
Then, in general, \(\mathbf{p}_2 \in \mathcal{P}\).
The two tangent vectors at a sample point can thus be used to define the standard geometric parameter set at the sample point. We use the notation
to indicate the values of the standard parameters at sample point k.
The Jacobian of the element map is a matrix whose columns consist of the tangent vectors. Since the parameters reflect the geometry of the tangent vectors, the geometry can also be associated with the Jacobian matrix. In fact, the Jacobian matrix must be a function of the parameters. This observation is exploited in the next few sections.
From the definition of a degenerate matrix, it is clear that a matrix in \(M_2\) (such as the Jacobian) is degenerate if and only if \(\zeta =0\).
If the values of the standard parameters are obtained from the active matrix, one can indicate this by the notation \((\zeta _A, \theta _A, \phi _A, \rho _A)\). Likewise, if they are related to the target matrix, the notation \((\zeta _W, \theta _W, \phi _W, \rho _W)\) indicates this. Where the context is clear, the subscripts are not used.
2.2 A parametric definition of the \({ \mathbf{2} \times 2}\) target matrix
The target matrix W is a matrix which is constructed prior to mesh optimization in such a manner that \(W \in M_2^p\). In that case, \(\zeta _W>0\) and the geometric parameters are all well defined. The target matrix is expressed in terms of the target parameters as
Equation 1 is called the standard parameterization of W.
With \(W \in M_2^p\), the range of the parameter values is restricted to a subset \(\mathcal{P}_W \subset \mathcal{P}\). Equation (1) shows that there exists a mapping \(\mathbf{F}\) from the set \(\mathcal{P}_W\) to the matrix set \(M_2^p\). For the purpose of target matrix construction, the ranges of the geometric parameters is restricted to \(0 < \zeta \) and \(0< \phi < \pi \). These restrictions guarantee that \({\text {det}}(W) = \zeta \sin \phi >0\) (the target mapping is non-singular) and that \(0< \rho < \infty \). Therefore, the set \(\mathcal{P}_W\) is
The target matrix W can be usefully represented parametrically, as in equation 1, given parameters \(\zeta \), \(\theta \), \(\phi \), and \(\rho \). When \(\mathbf{p}_2 \in \mathcal{P}_W\), one can replace \(\zeta \) in (1) with \(\frac{\upsilon }{\sin \phi }\) if one wants to specify the target in terms of the area/volume parameter. Values of these parameters must be supplied at every sample point in order to construct the set \(\{ \mathcal W \}\) prior to mesh quality assessment and improvement. The process of determining these values is called target parameter construction; this process is discussed in the Sect. 3.
2.3 Parameter extraction from the \(2 \times 2\) active matrix
A slightly different situation holds for the active matrix, because A is not constructed; rather, it is given by the mesh. That is, the geometric parameters of A, which can be denoted by \(\mathbf{p}_2 (A) \equiv (\zeta _A,\theta _A, \phi _A, \rho _A)\), are implicitly defined by the mesh, both before and during mesh optimization. These four geometric parameters, which are referred to as the active geometric parameters, are a measure of existing geometric mesh quality, whereas the four target parameters are a statement of desired geometric quality. With respect to the active matrix, then, the question is given A, find \(\mathbf{p}_2(A)\). This is called the extraction problem.
Because A is given, it is not guaranteed that \(A \in M_2^p\). If it were, the method described in the previous section can be used to find the active parameters. Unfortunately, the most that can be said is that \(A \in M_2\). The active matrix could be degenerate, singular, or have a negative determinant, particularly if it corresponds to a poor quality initial mesh. If A is degenerate, then \(\zeta _A=0\), \(\phi _A\) is undefined, and possibly \(\theta _A\) and \(\rho _A\) are as well. On the other hand, if A is non-degenerate, all four geometric parameters exist. Therefore, given A non-degenerate, it is possible to extract \(\mathbf{p}_2(A)\) from A, using one extraction function for each geometric parameter (see [16] for the explicit functions). The extraction functions for the active mesh have domain \(M_2^{\sim d}\) and result in a point \(\mathbf{p}_2 (A)\) in the set
Extraction is used in TMOP for (1) assessing geometric quality of the active mesh, (2) evaluating mesh quality metrics, and (3) target matrix construction. Only (3) is relevant to this article so further discussion of this topic in relation to TMOP is left to a future article.
2.4 Parametric factors of the \(2 \times 2\) target matrix
Given \(W \in M_2^p\), the parametric representation of W in Eq. 1 has the following matrix factorization (or decomposition):
where
Equation 2 is called the parametric factorization of \(W_{2 \times 2}\). Notice that each factor is a function of a single geometric parameter. The matrix \(R(\theta )\) is called the orientation matrix; R is a rotation matrix [i.e., \({\text {det}}(R)=1\), \(R^t R = I\)]. The matrix \(Q(\phi )\) is called the skew matrix; Q is upper triangular with unit column vectors. The matrix \(D(\rho )\) is called the aspect ratio matrix; D is diagonal, with unit determinant. Taking the determinant of both sides of the factorization relation, one finds \(\upsilon = \zeta \sin \phi \), as expected.
Define the shape matrix S by \(S \equiv QD\) and the shape+size matrix U by \(U=\sqrt{\zeta } \, S\). Thus
The matrix S is upper triangular with determinant equal to \(\sin \phi \). The matrix U is upper triangular with determinant \(\upsilon \). Except for W itself, these matrices are referred to as incomplete target matrices.
The active matrix, when non-degenerate, may also be factored similarly, to produce factors, \(R_A\), \(Q_A\), \(D_A\), \(S_A\), and \(U_A\), as needed. The incomplete matrix factors are used in some TMOP local quality metrics, to be discussed in a future article. Target construction may require the construction of one or more of the incomplete factors rather than all of W.
3 The target construction methodology
A standard set of geometric parameters (volume, skew, aspect ratio, orientation) has been identified for both planar and volume meshes. The active and target matrices A and W form a pair at each sample point of the mesh. Likewise, the active and target geometric parameters form a pair at each sample point. The active parameters are determined by the active mesh; they can be extracted from the active matrix. The main focus of this section is the assignment of the target parameter values that indicate the target mesh quality towards which the active parameter values will evolve during mesh optimization via node movement. The target parameter values (and perhaps the target matrix) are assigned prior to initiating the optimization procedure.
A critical issue in TMOP is to understand, in a general way, how to assign values to the target mesh parameters. In the ideal situation, one can use either a published method to assign the values or an existing algorithm in a mesh optimization code. If neither is available, one can consider developing their own method for assigning the target parameter values. This section describes the process by which a new method for assigning the target parameter values can be developed.Footnote 2 We call this process Target Construction (or target parameter construction).
Definition 2
Target Construction is a process by which one develops a numerical algorithm that takes primary data and converts it into values of the target parameters at every mesh sample point.Footnote 3 The process takes into account the mesh quality improvement goal, facts about the mesh, and the simulation. The resulting numerical algorithm is called a Target Construction Method.
One can, of course, develop a target construction method without following the process to be described. However, a general description of the target construction process should help those who wish to create an effective method appropriate to the given mesh quality improvement goal and the problem context.
At present, there are only a few proven target construction methods, e.g., “shape improvement” (Example I in Sect. 3.5.1.1) and “shape improvement with size equalization” (Example II in the same section). In the long term, one or more target construction methods for each of the mesh quality improvement goals listed in section 1.1 of [16] are envisioned. In this vision, the practitioner with a mesh quality issue would be able to consult the list of quality improvement goals to find an appropriate target construction method that they could use directly or adapt to their specific problem. In the meantime, barring the existence of an appropriate target construction method, one must devise their own method. The purpose of this section is to assist and encourage the development of new methods.
Three sequential phases within target construction are proposed: (1) target construction strategy, (2) secondary data algorithms, and (3) target parameter model development.
3.1 Target construction strategy
In the first phase of target construction, one develops an overall target construction strategy to determine the mesh quality improvement goal and to sketch an approach to the problem of assigning appropriate values of the target parameters. It is assumed that at this point the practitioner has assessed the quality of their meshes, found them lacking, and determined a mesh quality improvement goal. The practitioner has determined that there is no appropriate target construction method that already exists and has decided to develop a new method. In developing a strategy, one determines the relevant target parameters and how they will be treated, and examines the available primary data.
Strategy development itself entails a number of sub-phases that are described in Sects. 3.1.1–3.1.3. These sub-phases are referred to as context assessment, parameter control decision, and correspondence chain description, respectively.
3.1.1 Mesh and simulation context assessment
As background information for the target construction process, it is helpful to determine the mesh and simulation context. This information can bear on the approach selected at various stages in the target construction process.
The mesh context concerns basic facts about the initial mesh to be optimized. Basic information needed to characterize the mesh context includes the spatial dimension of the object on which the mesh resides, the type of mesh (e.g., structured or unstructured), and the type of elements (e.g., simplicial or non-simplicial). In addition, one should consider information concerning number of mesh elements, mesh connnectivity, and whether or not the initial mesh is inverted or tangled.
The simulation context concerns basic facts about the simulation code and the particular simulation. This includes, for example, physics type, physical boundary conditions, and discretization method. Obtaining answers to these questions before engaging in target construction is a good idea, because it can clarify the optimization goal, identify possible sources of primary data, and assist in target model development.
3.1.2 Target parameter control decision
As noted previously, there are four groups of target parameters: volume, orientation, shape, and aspect ratio.Footnote 4 In the volume mesh case, there are several target parameters within each of these groups. In this phase of developing a target construction strategy, one decides which target parameter groups will be controlled and which will not. Parameters within a particular parameter group are controlled if values of the target parameters in the group are or will be assigned (at all the sample points) in target construction.Footnote 5 If, on the other hand, values are not assigned for a particular parameter group, then the group is not controlled.
It would seem at first thought that one would always want to control all four parameter groups to achieve the highest mesh quality. The four groups are often not equally important, however. Volume is perhaps the most important parameter, closely followed by skew. Aspect ratio is important if the physics of the problem is anisotropic or if it is isotropic. Control over orientation is probably the least often required. Overall, the relative importance of the groups depends on the particular simulation at hand and on the mesh optimization goal. In addition, assigning values at every mesh sample point to a parameter or parameter group can be challenging, especially when the physics does not dictate that the parameter needs to be controlled. Thus, it is fortunate that there exist mesh quality metrics that allow one to abstain from controlling a particular parameter group if desired. In some cases, abstaining on one parameter group may allow better control over another parameter group. One cannot abstain on too many parameters at once, however, so a balance between controlling and abstaining is needed.
The decision to control or not control the parameter groups can be represented by a sequence of four letters, one for each of the groups (i.e., volume, orientation, skew, and aspect ratio). Each group can be assigned only the letters C or A, standing for “control” and “abstain” (i.e., not control). There are \(2^4=16\) possible combinations of these letters, yielding 16 possible decisions one can make. If one wants to control volume and shape, for example, the control decision is represented as \(C-A-C-C\). The control decision determines (1) which target parameter groups need to be assigned values in target construction, (2) an associated (incomplete) target matrix, and (3) the metric type.Footnote 6 Continuing the example, if the control decision is \(C-A-C-C\), then one will need to assign values to the target parameters \(\upsilon \), \(\phi \), and \(\rho \) at each sample point of the mesh. Items (2) and (3) are intertwined. Metric type refers to local quality metrics that control only the parameters one has decided to control; in the example of \(C-A-C-C\), one controls the volume parameter, and thus the required metric type is a “volume + shape” metric. Volume + shape metrics are functions of the active and target parameters \((\upsilon _A,\upsilon _W)\), \((\phi _A,\phi _W)\) and \((\rho _A,\rho _W)\). Some volume + shape metrics are directly functions of these parameters, while others can be expressed in terms of the volume + size matrices \(U_A\) and \(U_W\). Due to lack of space, this topic is discussed in detail elsewhere [17].
Therefore, how does one make the cision? Basically, the decision is made in light of the identified mesh quality improvement goal, the mesh and simulation context, and the available primary data. If, for example, the mesh quality improvement goal is to improve the shape of the mesh elements, then one needs to control the skew and aspect ratio parameters. Such a goal tacitly implies that the volume and orientation parameters are not particularly important (except for keeping the volume positive), and thus one can abstain on those parameters. The control decision for “shape” improvement is thus \(A-A-C-C\). In general, one might wish to abstain on a parameter group, because (1) it is unimportant with respect to the mesh quality improvement goal or (2) it is important but there is no primary data that can be converted into appropriate values of the particular parameter. By abstaining on a particular parameter group, the optimization procedure should be able to produce an optimal mesh more in tune with the controlled parameters (and the quality improvement goal) than otherwise. Although a control decision always results in one of the four-letter combinations of A and C, the decision should be restricted so that the corresponding metric type is one of the effective types mentioned above.Footnote 7 In nearly all instances, one will want to control the skew parameter because it directly impacts the local volume (which one wants to be positive). Thus, the 16 4-letter combinations is effectively reduced to 8.
Once the control decision has been made, one need consider only the controlled parameter groups in the rest of the target construction process.
3.1.3 Establishing data correspondences
As noted earlier, target construction results in an algorithm (or series of algorithms) that takes data and converts it into values of the target parameters. As an preliminary step, one frequently first converts the data into “intermediate” data and subsequently converts the intermediate data into target parameter data.
Definition 3
Primary data consist of geometric data and simulation data that is accessible from the simulation state prior to target construction and which is useful in constructing targets. See Table 1 for examples.
Definition 4
Secondary data primarily consists of data that is computed from the primary data and can be considered as functionals of the primary data. See Table 2 for examples.
Definition 5
Tertiary (or Parameter) Data consists of data corresponding to values of the controlled target parameters over the set of sample points. Parameter data is computed from Secondary Data.
Primary data refer to data that comes mainly from the simulation, the simulation state, or even a priori knowledge concerning the simulations. Primary data generally comes from two kinds of sources: (1) geometric sources and (2) simulation sources. Geometric data sources consist of items that are largely independent of any physical information and independently of the simulation that is to be performed. This includes information and data concerning the physical and computational domain, the mesh type, the mesh topology, element type, the coordinates of the initial mesh, and the coordinates of any reference meshes. Simulation data sources consist of items that are available from physical information and the simulation itself. Simulation data can be used as primary data for target matrix construction at the beginning of the simulation or as the simulation proceeds, while geometric data are generally available prior to the simulation. An exception to the latter might be the case in which the domain deforms with time.
3.1.3.1 Geometric primary and secondary data
There are three potential sources of geometric primary data. First, there is the contextual information described in Sect. 3.1.1. Information concerning significant mesh subregions, domain size or aspect ratio, and whether the mesh is dynamic or static may be important.
The second potential source of geometric primary data (and one which is often neglected) is the initial mesh. The initial mesh contains primary data such as that listed in Table 1. From these quantities, one can calculate secondary data: the area or volume of the computational domain and thus an average local or cell area/volume. From the boundary discretization, one can determine a boundary parameterization or arclength. From element type, one can determine the isotropic element shape (skew and aspect ratio). One can also compute the initial mesh Jacobian matrix (and determinant) at every sample point. From that one can extract values of the initial mesh active geometric parameters. One can calculate the initial mesh quality using various metrics. One can calculate mesh statistics (e.g., average, minimum, maximum, variance) on such quantities as length or area/volume. One can compute a local “sizing” function [22]. The initial mesh can thus be used to calculate a wealth of secondary data valuable in constructing target matrices.
The third potential source of geometric primary data is a reference mesh, i.e., a mesh whose connectivity can be put into a one-to-one correspondence with the initial mesh. Reference meshes can be obtained from (1) the initial or computational mesh at an earlier time in the simulation (applies to moving mesh or deforming domain problems) or (2) a mesh generated “from scratch” on a similar domain with the same mesh topology (applies mainly to structured meshes). As with the initial mesh, the vertex coordinates of the reference mesh can be used to calculate secondary data such as the reference Jacobian matrix and to calculate reference mesh statistics on length or area/volume.
3.1.3.2 Simulation primary and secondary data
The physical simulation creates primary data such as that shown in Table 2. Other fields can be obtained from the coefficients of the governing partial differential equations. Each type of physics simulation will have its own set of primary data that can perhaps help determine the input parameters in the target matrix set.
As Table 2 shows, the primary data present in the simulation can be further processed to create secondary data. From symmetric-matrix data, one can obtain real eigenvectors and eigenvalues, which, in turn are useful for determining directions and aspect ratios. From vector fields, one obtains directions and lengths. Primary solution data can be used to recover the solution Hessian matrix and to create spatially dependent a posteriori error estimates. The literature describes many different methods for creating some types of secondary data (e.g., Hessian recovery methods [8], a posteriori error estimates [27], and interpolation error [5, 9]).
3.1.3.3 Correspondences between primary, secondary, and parameter data
The primary and secondary data mentioned in Tables 1 and 2 identifies only what kinds of data can potentially be of use in target construction. One needs in addition to identify the specific primary data and the specific secondary data that will be used in target construction. Specifying primary or secondary data include determining the form of the data and the locations of the data on the mesh or physical domain.
Beyond identification of the specific primary and secondary data that will be used, one needs to determine a correspondence chain between the primary and target data.
Definition 6
A Correspondence Chain is a mapping that identifies, for a controlled target parameter, (1) the specific secondary data that will be used to compute the controlled parameter data and (2) the specific primary data that will be used to compute the specific secondary data.
One correspondence chain is needed for each target parameter that is to be controlled. As an example, one might define a correspondence chain between a particular simulation density field (the primary data), a particular error estimator (the intermediate data), and the volume parameter. In this example, the local volume in the optimal mesh is to be adapted to the simulation densify field.
Note that, if multiple correspondence chains are needed, one is free to choose the primary data sources for each chain independently of what the primary data is in a different chain. For example, the skew angles can be constructed from the primary data “element type” while the area/volume parameter can be constructed from primary data consisting of the initial mesh vertex coordinates. At the same time, the direction parameter group could be constructed from primary data corresponding to a simulation-produced vector field. Flexibility in terms of mixing and matching data sources is quite important in being able to find appropriate values for the target parameters.
3.1.3.4 The PIE decision
When creating correspondence chains that identify specific data, it is helpful to keep in mind what can be referred to as the PIE decision. For each of the parameter groups, one has basically four options in defining how the group will be constructed. The four options are (P) preserve, (I) improve, (E) equalize, or (A) abstain. In the preserve option, one seeks to retain the quality present in the initial mesh, with respect to the given input parameter. Thus, the specific primary data in the correspondence chain will be the initial mesh if one chooses the preserve option. In the improve option, the parameter group is constructed so as to improve upon the quality existing in the initial mesh because the existing initial mesh quality is inadequate (with respect to the given parameter). In the equalize option, the parameter group is constructed by assigning a value that is constant over all sample points.Footnote 8 In this way, quantities such as area, volume, or size can be equalized over the mesh. Strictly speaking, one would do this only in an attempt to improve the quality of the mesh with respect to the given parameter group, so equalization can be viewed as a special case of the improve option. Finally, the abstain option is used when there is no good primary data source for creating acceptable values for a given parameter group. This option was discussed in Sect. 3.1.2.
As an example, consider the area/volume parameter group. In r-adaptivity, one often seeks to adapt (improve) mesh quality by varying the area/volume of mesh elements according to some scalar quantity such as an a posteriori error estimate. In mesh generation, one often equalizes cell area/volume in the absence of any specific knowledge about the particular physical simulation that the mesh will facilitate. In some mesh quality improvement problems, the area/volume of mesh elements has already been adapted to the solution; in that case, one wants the area/volume construction procedure to preserve the existing area/volume, i.e., not obliterate it during mesh optimization. Finally, it is often the case in mesh generation in the absence of simulation information to be indifferent or neutral to element area/volume, as in shape optimization. In this case, one abstains from controlling the area/volume parameter. One also abstains when there is no relevant primary data for the construction of the parameter group.
The “preserve” option, if selected, usually calls for extracting values of geometric parameters from the reference mesh, so the latter becomes the specific primary data in the correspondence chain. The “equalize” option most often calls for constants available or computable from mesh and simulation data. The skew parameter is very often determined by the isotropic element data; this would fall under the equalize option. “Improve” is the most difficult option to achieve since it often requires model development. These options are illustrated in Sect. 3.3.
In the PIE decision, one assigns to each correspondence chain (representing one target parameter) either P, I, or E. Including the control/abstain option there are, in theory, \(4^4 = 256\) possible PIE combinations that can be made, ranging from P-P-P-P (preserve everything) to A-A-A-A (abstain from all). In practice, the number of useful combinations is probably much smaller. Nevertheless, the large number of combinations provides a great deal of flexibility.
Finally, note that most often if a particular set of PIE decisions is made, it usually applies to every sample point of the mesh. For example, if one chooses to preserve the area parameter, one wants to preserve it at every mesh sample point. However, in some cases it may be desirable to preserve area on one set of sample points and to equalize it on the remaining sample points. The flexibility to do this should be available in any general optimization code.
Having identified the mesh and simulation context, made the parameter control decision, and established the necessary correspondence chains, one now has a complete target construction strategy. Note that a correspondence chain defines only the mapping between the various levels of data; it does not tell one how the data is to be converted. The latter question is addressed in Sect. 3.2.
3.2 Primary to secondary data conversion algorithms
The purpose of the algorithms mentioned in this section is to convert primary mesh or simulation data into values of one or more mesh or solution functionals over the mesh. The correspondence chains determine exactly which primary data and which secondary data will be the input and output of each algorithm needed in this phase. The secondary data must ultimately be defined at the mesh sample points. If not, then the interpolation of the secondary data to the sample points must be done in the target parameter calculation phase. The algorithms in this section provide examples as to how the primary data are converted.
3.2.1 Algorithms for mesh functionals
Examples of primary mesh data include mesh connectivity, vertex or nodal coordinates, and element types. Examples of secondary mesh data include isotropic element coordinates, the Jacobian matrix of a reference mesh, and mesh statistics. Algorithms for calculating the latter are described next.
3.2.1.1 Isotropic element coordinates from element type. This subsection covers a rather trivial but important example. The most commonly used mesh elements are the triangle, quadrilateral, tetrahedron, hexahedron, triangular prism, and pyramid.
Definition.
An isotropic element, as the term is used here, is defined as a straight-sided element for which all angles within a given face are equal. The isotropic forms of the first four element types are the equilateral triangle, the square, the equilateral tetrahedron, and the cube. Isotripc elements define the targeted shape of an element but not its size or orientation. They are used if the application has isotropic physics or in lieu of detailed knowledge of what element shape is best for the given application.
The primary data in this example are the element type. If the mesh is a hybrid mesh then each element will likely have a flag associated with it that tells the element type; this flag is the primary data. If the mesh consists of only one element type, then one has (in principle) just one flag per mesh. Given the element type, one can define (as secondary data) the vertex coordinates of the isotropic element (see Table 3).Footnote 9 Isotropic elements need not have unit edge lengths. However, in terms of defining vertex coordinates for the isotropic element, assuming unit edge length is convenient. Thus, the vertex coordinates in the table have been defined for isotropic elements with unit edge lengths. Note that there is no conversion algorithm involved in this example, only a look-up table. One can, of course, provide their own definition of the coordinates of an isotropic element. From the coordinates of an isotropic element, one can calculate the corresponding target skew and aspect ratio parameters, but this activity does not conceptually belong to the calculation of secondary data this latter activity is discussed in Sect. 3.3.1). Coordinates for the isotropic 3D element types can be found in [16].
3.2.1.2 Reference mesh Jacobian from a reference mesh. A reference mesh is a mesh that exists and has the same topology (connectivity) as the mesh that is to be optimized. An important example of a reference mesh is the initial mesh; this is the mesh whose quality is to be improved via optimization. Another example of a reference mesh occurs in deforming domain problems: in that context, the reference mesh can be the active mesh at some earlier time in the deformation process. In yet another example of a reference mesh, one may be able to use a moving mesh at an earlier time as the reference mesh. In many optimization problems, the initial mesh has quality that is, in part, adequate or compatible with the optimization goal. When that is the case, we can use the local Jacobian matrices of the reference mesh to calculate all or part of the target matrix. Suppose the element mapping has the form
with N the number of element nodes (or control points), \(\mathbf{c}_n\) the coordinates of the nth node in the reference mesh, and \(\phi _n\) the nth basis function. Then the element reference Jacobian matrix at the point \((\xi _1,\xi _2,\xi _3)\) has elements
The element reference Jacobian matrix at the sample points can be found by evaluation of the above at the logical sample points.
In this example of primary to secondary data conversion, the reference mesh nodal coordinates are the primary data and the reference mesh Jacobian matrix (which can be considered to be a mesh functional) is the secondary data. Once the reference mesh Jacobian is calculated, one can use it to compute values of the target parameters at the sample points. This latter step converts secondary data into parameter data and is discussed in Sect. 3.3.1.
3.2.2 Algorithms for simulation functionals
Primary data related to the simulation are commonly available in the form of scalar and vector fields for the dependent variables in the PDE, along with PDE coefficients related to material properties. This data can be used to compute secondary data (i.e., solution/simulation functionals) such as gradients, flux, Hessians, error indicators, interpolation error, and a posteriori error estimates. Methods for doing so are better known to the simulation community than to the meshing community. Here we provide only some Refs. to methods for converting simulation primary data into secondary simulation data. For gradient recovery methods, see Refs. [6, 11, 18, 27]. For an introduction to Hessian recovery methods, see Refs. [8, 12, 21]. For interpolation error, see Refs. [3, 4, 9].
3.3 Target parameter model development
The final phase of target construction is concerned with the conversion of secondary data into target parameter data. Because the final phase often entails devising an ad hoc model of target parameter behavior as a function of secondary data, complete with arbitrary constants whose values must be determined, it is referred to as target parameter model development. As an example, one might wish to devise a model that relates local a posteriori error estimates to the target volume parameter \(\upsilon \). Clearly, in that case, one wants a function that decreases monotonically as the error increases. Beyond that, it is often unclear what type of function or model is most useful, so numerical experiments may be warranted. In such cases, model development is clearly an art, not a science.
Each correspondence chain identified in the first phase pairs some specific secondary data with specific geometric target parameters, so multiple models may be necessary, one for each chain. On the other hand, there are cases in which models do not need to be developed because the relationship between the geometric parameter and the secondary data is unambiguous. This is especially true when the secondary data consists of mesh functionals.
3.3.1 Converting mesh functionals to parameter data
Three examples are given in which secondary data in the form of mesh functionals is converted into values of target parameters.
3.3.1.1 Skew and aspect ratio parameters from isotropic element coordinates
Isotropic elements can be used to find target parameter values for the skew and aspect ratio groups, but not the volume or orientation groups. The secondary data in this case consists of the coordinates of the isotropic element (see Table 3). For the triangle element, let (u, v) be a point in the isotropic triangle. For \(0 \le \xi \le 1\) and \(0 \le \eta \le 1 - \xi \), the points in the triangle are
with \((u_k, v_k)\) the isotropic element coordinates at vertex \(k=0,1,2\) (see Table 3). In that case, the Jacobian matrix corresponding to the isotropic element is
The skew angle \(\phi \) is found by extracting it from the ideal Jacobian matrix:
Then \(\sin \phi = \frac{\sqrt{3}}{2}\) and \(\phi = \frac{\pi }{3}\). Since all the lengths in the equilateral triangle are equal, the aspect ratio parameter is \(\rho =1\). Proceeding similarly for the unit square element, one finds \(\cos \phi = 0\), \(\sin \phi = 1\), and \(\phi =\frac{\pi }{2}\). Note that the Jacobian matrix of these isotropic elements is a constant over the element, thus so are the skew and aspect ratio parameters.
Of course, in this example, the computation of the isotropic skew and aspect ratio parameters does not change from mesh to mesh or from problem to problem. One can simply use the results given in this section as the target values of the skew and aspect ratio parameters, going directly from the element type indicator to the target values. See [16] for a description of the isotropic skew and aspect ratio parameters for the 3D element types.
3.3.1.2 Target parameter values from a reference mesh Jacobian
Another example of using mesh functionals to find target parameter values is that of using a reference mesh (see Sect. 3.2.1). The secondary data in this example are the set of Jacobian matrices that can be computed at the sample points of the reference mesh. Values of the target parameters can be found by applying extraction functions to the reference mesh Jacobian, as described in Sect. 2.3.
As an example, in many optimization problems the initial mesh has quality that is, in part, adequate or compatible with the optimization goal. When that is the case, one can use the local Jacobian matrices of the reference mesh to calculate all or part of the target matrix. Let \(A_{\text {ref}}\) be the Jacobian matrix of the reference mesh at some given sample point (or just A when the context is clear). Then, if one wants to create values at every sample point for the area or volume parameter \(\upsilon \) from the reference mesh, then simply let \(\upsilon = \upsilon _{A_{\text {ref}}}\). Using these values as target parameter values implies that one finds the corresponding reference mesh values acceptable, or that one wants to preserve those values in the optimal mesh to be created.
Note that the target parameters calculated from the reference mesh may not always satisfy the requirements of a valid target matrix input parameter. For example, if the reference mesh has poor quality, one might encounter sample point locations for which \(\ell _i = \ell _i (A_{\text {ref}}) = 0\) or for which \(\upsilon =\upsilon (A_{\text {ref}}) \le 0\). If the reference mesh contains such points, the reference mesh cannot be used, at least not at the sample points where these issues occur. Thus the reference mesh should have good quality, at least with respect to the target parameters of interest.
In the reference mesh example of target matrix input parameter construction, the reference mesh vertex coordinates are the primary data, the reference Jacobian matrix is the secondary data, and the target parameter data extracted from the matrix is the final parameter data.
3.3.1.3 Reference mesh statistics
As a third example of converting secondary mesh data into target parameter values, consider again the Jacobian matrix computed on the reference (or initial) mesh. For any given geometric target parameter p, one can form the set
\(\{ p_k \}\) of values over the set of reference mesh sample points by using the extraction functions. Then, given values \(\{ p_k \}\), one can calculate parameter statistics over the sample points: the average,
the minimum,
the maximum,
the standard deviation,
and other statistics.
Mesh statistics can be useful in target parameter model development. An important example occurs in the area or volume equalization problem where the goal is to create equal area or volume elements throughout the mesh. In that case, the local area parameter \(\upsilon \) should be constant, so one can set \(\upsilon = \bar{\upsilon }_{\text {ref}}\) at all sample points. In this example, the vertex coordinates of the reference mesh are the primary data, and the reference mesh Jacobian and the parameter values calculated therefrom are the secondary data. The final parameter data is based on a model that relates a mesh statistic (or, more generally, some function of a mesh statistic) to a set of target parameter values.
3.3.2 Converting simulation functionals to parameter data
This topic is illustrated with an example in which the model is relatively simple. Suppose one wants to adapt a 2D quadrilateral mesh to the principal axes of the permeability tensor K (a symmetric, positive definite matrix) in a subsurface Darcy flow simulation. The first column of the active Jacobian matrix is to be aligned with the principal flow direction to improve simulation accuracy. The mesh spacing in that direction should be small compared to the normal direction. The primary data are the permeability tensor K. The secondary data consist of the unit eigen-pairs of K; let those be referred to as \((\lambda ,\mathbf{e})\) and \((\lambda ^\perp ,\mathbf{e}^\perp )\), with \(\mathbf{e}=(\cos u, \sin u)\) and \(\mathbf{e}^\perp =(-\sin u, \cos u)\) and u the angle between the x-axis and the direction of \(\mathbf{e}\). Define the ratio \(r \equiv \left( \frac{1}{\lambda } \right) \lambda ^\perp \). If \(r \le 1\), align the first column of the active matrix with \(\mathbf{e}\), so the orientation, skew, and aspect ratio target parameters can be chosen to be \(\theta = u\), \(\phi =\frac{\pi }{2}\), and \(\rho = \frac{1}{r}\). On the other hand, if \(r > 1\), align the first column of the active matrix with \(\mathbf{e}^\perp \), so the orientation, skew, and aspect ratio target parameters can be chosen to be \(\theta = u + \frac{\pi }{2}\), \(\phi =\frac{\pi }{2}\), and \(\rho = r\).
Three of the four target parameters were defined in the Darcy flow example above. If the permeability tensor is not a constant, then the orientation and aspect ratio parameters will vary from one sample point to the next. The remaining target parameter, corresponding to the volume \(\upsilon \), can also be defined using the tensor. It is reasonable to expect that the local mesh volume would be a function of the determinant of K, i.e., \(\upsilon = \upsilon (\lambda \,\lambda ^\perp )\). Here is where model development is needed. It seems clear that the volume should be a decreasing function of the determinant, because a relatively large determinant means greater flows and thus requires smaller element areas. Many functions, of course, satisfy this condition − for example,
and
with constants \(\upsilon _o\), a to be determined. Both functions obey \(\upsilon =\upsilon _o\) when the determinant is zero and monotonically decrease to zero as the determinant approaches infinity. Two issues arise in this kind of model development: (1) what is a good functional form and (2) what values should be given to the constants? From experience, the answer to the first question seems to be that the particular functional form is often not critical, as long as it is monotonically decreasing. However, in practice, trying several functional forms is advisable. Answering the second question generally requires numerical experimentation using the simulation of interest. In this example, a PDE coefficient matrix and its eigenvalues/vectors were used as the secondary data. Other sources of secondary data that might be useful in a simulation were given in Table 2.
In this Darcy flow example, there are four correspondence chains, one for each of the four geometric parameters associated with meshes in \(\mathfrak {R}^2\). All four chains began with the permeability tensor K over the domain as the primary data. The first chain connects K to the secondary data \({\text {det}}(K)\) and then to the volume parameter \(\upsilon \). Since in this chain, there was no use of a reference mesh nor of any constant data, the chain is an “improve” chain with respect to the PIE decision. The second chain connects K to the secondary data consisting of the eigenvectors \((\mathbf{e},\mathbf{e}^\perp )\) of K. The second chain then connects the secondary data to values of the orientation parameter \(\theta \); this chain is also an “improve” chain. The third chain is built upon the fact that the eigenvectors of K are orthogonal, suggesting that the skew angle should be that of the isotropic quadrilateral element, i.e., \(\frac{\pi }{2}\). In this case, one can say that the primary data is K, the secondary data are the isotropic angle in a quadrilateral element, and the final parameter data are the skew angle. The chain uses the “equalize” option since the target skew angle is constant over the mesh. The last chain is built upon the idea that the ratio of the eigenvalues of K suggest an appropriate value for the aspect ratio parameter. In this case, one can say that the primary data are K, the secondary data consist of the eigenvalues of K, and the final parameter data is the aspect ratio parameter. The chain uses the “improve” option since the target aspect ratio is non-constant and does not come from a reference mesh. In summary, the four chains correspond to a PIE decision of the form I-I-E-I.
3.3.3 Summary of the model development phase
In the model development phase, one defines the way in which the secondary data in each correspondence chain will be converted into values of a particular target parameter. There are many ways in which this can be done, and one is limited only by one’s ingenuity. The values should all be defined over the set of mesh sample points. Once the parameter values have all been determined, one can further compute various target matrices if needed by the local quality metric.
3.4 Summary of the target parameter construction process
The three phases in target construction are (1) strategy development, (2) secondary data algorithm development/application, and (3) parameter data model development. Although each stage has been carefully described in some detail, target construction is not envisioned as a formal process. Rather, the description is intended only to guide those seeking to define values of the required target parameters that are appropriate to a particular mesh quality improvement goal. Although other mesh optimization methods have used target parameters of various sorts, this is the first time that methods for assigning values to these parameters has been systematically described. There are no guarantees that the target construction process will result in an adequate optimal mesh or that the mesh quality improvement goal will be reached. However, at least there is now a rational approach to the problem of assigning values of target parameters that can be systematically employed in the future. As noted earlier, in the long term, this could result in a library of target construction algorithms available to the general community.
3.5 Target construction examples for planar meshes
The target construction methodology described in Sects. 3.1–3.4 is illustrated by ten examples in this section. For simplicity of presentation, the examples are in the context of planar meshes in \(\mathfrak {R}^2\); most of the examples can be extended to volume meshes without great difficulty. The examples illustrate how a construction method, aimed at a particular mesh quality improvement problem, is created using the methodology outlined above. Some of the construction methods have been previously presented in the TMOP literature, but this is the first time, they are explained in the context of the target construction methodology. The seven examples in Sect. 3.5.1 illustrate parameter construction based on geometric primary and secondary data, while the three examples in Sect. 3.5.2 illustrate parameter construction based in part on simulation data. Numerical confirmation of the specific construction methods is shown either by numerical examples or by citation of the literature. Given the large variety of mesh contexts, quality improvement problems, primary data types, primary-to-secondary data conversion algorithms, and model development opportunities, many more target construction methods are possible.
Mesh quality improvement begins with an initial mesh and ends with an optimized mesh. To improve the initial mesh, one must construct the target parameter values. As noted in Sect. 3.1, the parameter values are ultimately determined by primary and secondary data. If the data used to construct the parameter values is strictly geometric in nature (i.e., does not originate from a physical simulation), then the data will be defined at logical locations associated with the mesh. As the mesh moves within the domain during the optimization procedure, the data moves along with it. On the other hand, if some of the data used to construct the parameter values is obtained from the simulation, the data will most likely be defined at physical locations associated with the domain. As the mesh moves within the domain during the optimization procedure, the simulation data do not move with it. In this case, the physical parameter data must be interpolated (or advected) to logical locations in the mesh. The interpolation or advection of data occurs during the optimization step and therefore has nothing to do with the target parameter construction process, which occurs prior to optimization. Therefore, target parameter construction does not depend on whether or not one uses geometric or physical data in the target (one can mix and match the different types as needed). That said, the final values of the target parameters to be constructed must be located at logical locations within the mesh called sample points, because that is where the active and target matrices reside. In the examples below, it is assumed that interpolation of the data to sample points has taken place at some stage of the primary–secondary–tertiary data processing; this topic is not discussed further in the examples.
In the examples that follow, reference is made to certain metric types. One outcome of the parameter control decision is to define the type of metric that should be used in the optimization procedure. For example, if the parameter control decision is \(A-A-C-C\), then one must use a metric whose type is skew + aspect ratio (i.e., shape). There are eight metric types that can potentially arise [17]. Of these, only 3–4 metric types have been demonstrated to reliably yield acceptable optimal meshes. The parameter control decision is thus constrained with those limitations in mind. In the examples of 2D target construction below, some of the viable metric types are referred to even though they are not defined in this document due to lack of space.
3.5.1 Target parameter construction using geometric data
The target construction examples in this section use only geometric data, i.e., data obtained from the problem domain or the mesh. The mesh context for all these examples is assumed to be that of a conformal, unstructured mesh in \(\mathfrak {R}^2\) consisting of triangle and/or quadrilateral elements (either low or high order).
Example I
Equalize isotropic shape.
The mesh quality improvement goal in this example is to create a set of target parameters and matrices that can be used to create an optimized mesh in which element shape is closer to the isotropic element shape. With shape improvement as the goal, and shape defined as skew + aspect ratio, it is clear that the parameter control decision is \(A-A-C-C\). Since only skew and aspect ratio (i.e., shape) are to be controlled, metric type shape must be used. Furthermore, because the shape is to be the same at every sample point, the PIE decision is \(A-A-E-E\). The primary data in this problem are element type and also the isotropic element vertex coordinates given in Table 3. The secondary data are the Jacobian matrix on the isotropic element. Finally, the parameter data consist of the values \(\phi = \frac{\pi }{3}\) and \(\rho =1\) if the element is a triangle and \(\phi =\frac{\pi }{2}\), \(\rho =1\) if the element is a quadrilateral (see Sect. 3.3.1 on how this is determined).
Shape metrics are functions of the parameters \(\phi \) and \(\rho \) only, i.e., they must not also depend on the volume and orientation parameters. In some cases, shape metrics are defined in terms of the shape matrix
Inserting \(\phi =\frac{\pi }{3}\), \(\rho =1\) for the isotropic triangle, the shape matrix is
For the isotropic quadrilateral, \(S_{\text {quad}}\) is the identity matrix. For an all-triangle mesh, \(S_{\text {tri}}\) will be used at every sample point. For an all-quadrilateral mesh, \(S_{\text {quad}}\) will be used at every sample point. For a hybrid triangle-quad mesh, one uses either \(S_{\text {tri}}\) or \(S_{\text {quad}}\) at a given sample point, depending on the local element type.
Example II
Equalize isotropic shape and equalize local volume.
The mesh quality improvement goal in this example is to create a set of target parameter values that will encourage the optimized mesh to have elements whose shape corresponds to the isotropic element and whose volume is nearly constant. The control decision is \(C-A-C-C\) and, therefore, the metric type is volume + shape. The associated incomplete target matrix is \(U=\sqrt{\zeta } S\). The PIE decision is E-A-E-E and, therefore U will be the same at all sample points. The previous example showed how to construct S, so here only assignment of \(\zeta \) values need be considered. In general, volume and size are related in 2D by \(\upsilon = \zeta \sin \phi \). To equalize the volume over the sample points, set the target \(\upsilon \) equal to the average value of \(\upsilon \) on the initial mesh; this is an example of using the mesh statistics approach described in Sect. 3.3.1.3. Since \(\phi \) is known from the element type, one can find values of \(\zeta \) from \(\phi \) and \(\upsilon \). The primary data for the volume parameter is the initial mesh and mapping. From that, one calculates, as secondary data, the set of initial mesh Jacobians and determinants. The target parameter data \(\upsilon \) is just the average of the determinants over the sample points.
Example III
Equalize isotropic shape and preserve local volume.
This example is similar to the previous except that, instead of equalizing volume, the goal is to preserve the initial mesh local volume at each sample point. Clearly this goal only makes sense if the set of local volumes of the initial mesh are all positive. The control decision is again \(C-A-C-C\), but now the PIE decision is P-A-E-E. The shape matrix is constructed as in Example I. The target value of \(\upsilon \) is determined by setting it to the determinant of the initial mesh Jacobian matrix at the given sample point. Thus \(\upsilon \) is not a constant over the mesh, but rather varies with sample point. The primary and secondary data for the volume parameter is the same in the previous example, while the target parameter data for \(\upsilon \) is computed as described in Sect. 3.3.1.2, with the initial mesh as the reference mesh.
Example IV
Equalize local volume.
In this example, the goal is to equalize only volume (cell area). The control decision is \(C-A-A-A\); a volume metric is required and the incomplete target is simply \(\upsilon \) equal to a constant. The constant is simply the average of the volume parameters in the initial mesh.
Example V
Equalize Isotropic Skew and Equalize Local Volume.
In this example, the mesh quality improvement goal is to equalize volume and skew. The control decision is thus \(C-A-C-A\); in turn, this requires a volume + skew metric and the incomplete target matrix \(\sqrt{\zeta } Q\). The PIE decision is \(E-A-E-A\), with \(\phi \) determined by the isotropic angle and \(\zeta \) found from setting the target volume parameter to the average of the volume parameters in the initial mesh. Alternatively, the PIE decision could be \(P-A-E-A\) and the volume would be based on the initial mesh volumes at each sample point. That would preserve the initial mesh volumes.
Numerical confirmation of Examples I–V.
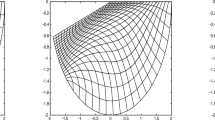
Examples I–V, each having a different constructed target, are used in conjunction with a metric of the appropriate type to confirm numerically that the examples work as expected. All the confirmation tests used the same initial mesh (with first-order elements). The initial mesh is optimized once for each example, giving the optimal meshes shown in Fig. 1.
In Example I, the cells in the optimal mesh are closer to being squares (the shape of the isotropic quadrilateral element). The skew angles are generally closer to 90 degrees and the aspect ratios closer to 1 compared to the initial mesh. The area of the cells has changed compared to the initial mesh, some getting larger and some smaller, because the volume parameter is not controlled. Orientation has also changed. The metric was the shape metric
In Example II, both the cell area and cell shape parameters are controlled. Cell areas are more nearly equal compared to the initial mesh and the shape is generally improved although not as much as in Example I. Of course, the areas in the optimal mesh are not exactly equal.. The metric used in Example II was the shape+volume metric
In Example III, shape is improved while the cell areas in the initial mesh are more or less preserved. This example also used \(\mu _9\), but with a different set of targets. In Example IV, only area is equalized. Cell areas in the optimal mesh are nearly equal, but cells have considerable skew because the skew parameter was not controlled. The metric used in Example IV was the volume metric
In Example V, the area and skew parameters are controlled, but not the aspect ratio parameter. Compared to the initial mesh cell areas are more nearly equal, Compared to the other optimal meshes, the aspect ratios in the example 3 optimal mesh are further from 1 because the aspect ratio parameter was not controlled. The composite area + skew metric used was
While the differences in these optimal meshes are subtle, they do confirm our theoretical expectations. The meshes differ, not only because different quality metrics were used, but because different targets were used.
Numerical confirmation of Examples I–V. Upper Left: Initial Mesh. Upper middle: Example I. Equalize shape, \(\mu _2\). Upper right: Example II. Equalize shape, equalize area, \(\mu _9\). Lower left: Example III. Equalize shape, preserve area, \(\mu _9\). Lower middle: Example IV, equalize area, \(\mu _{56}\). Lower right: Example III. Equalize skew, equalize area. Area + skew metric, \(\gamma =0.50\)
Example VI
Preserve a good mesh on a deforming domain.
In this example the physical domain changes with time during a simulation due to various forces exerted on the domain. It is assumed that the boundary of the domain is known at the beginning of each time step. It is also assumed that at the previous time step the mesh has acceptable quality and includes non-constant features such as anisotropy, biasing, clustering vertices, and perhaps other features. The goal is to create target matrices such that the optimized mesh (to be used at the next time step) resembles the mesh at the previous time step and thus preserves the non-constant features. There are several variations on this theme, depending on the physical problem and the particular features one wishes to preserve. In TMOP, this is again described by the parameter control and PIE decisions.
In the simplest situation, one wishes to preserve all of the features of the mesh at the previous time step (i.e., the initial mesh). That is, the goal is to preserve shape, size, and orientation of the previous mesh, corresponding to the PIE decision \(P-P-P-P\). In that case, the full target matrix W is needed. The preservation option requires the use of the initial mesh as the reference mesh, with Jacobian \(A_{\text {ini}}\). Values of the reference Jacobian are found from the mesh at the previous time step. Thus, one constructs the set of target matrices at each sample point by setting \(W = A_{\text {ini}}\). Because all of W is used in this situation, one must use metric type volume + orientation + shape (VOS). The primary data in this example can be considered to be the mesh at the previous time step, the secondary data are \(\{ A_{\text {ini}} \}\), and the final data is \(W=A_{\text {ini}}\).
A variation on the previous example would be to change the PIE decision to \(P-P-E-P\), in which the isotropic skew angles replace the angles from the reference mesh.
Another situation that occurs in practice is the need to preserve everything except volume. This occurs, for example, when the size of the domain is rapidly increasing or decreasing with time. In this case, one can either abstain on volume (giving \(A-P-P-P\)) or one can recalculate the local volume at each sample point as time passes. In the former, the mesh at the earlier time is the reference mesh, and one would calculate the matrix \(R(A_{\text {ref}}) \, S(A_{\text {ref}})\) from the reference mesh and use that as the incomplete target matrix, along with a orientation + shape (OS) metric. Volume would not be controlled and should change automatically as needed, with this selection. In the latter possibility, the PIE decision is \(I-P-P-P\), in which data must be found for the size factor \(\zeta \) (or, equivalently the volume factor \(\upsilon \)). One way to do this would be to compute the total volume of the domain (V), both at the previous and at the current time steps (\(n, n+1\)). This requires the use of the mesh at time step n and the mesh at time step \(n+1\). The latter mesh conforms to the updated domain boundary and is considered the initial mesh in the optimization procedure for time step \(n+1\). Then, at each sample point, let
Since, in two dimensions, \(\upsilon = \zeta \, \sin \phi \), one has \(\upsilon ^n = \zeta ^n \sin \phi ^n\) and \(\upsilon ^{n+1} = \zeta ^{n+1} \sin \phi ^n\). In the latter, one can use \(\phi ^n\) in place of \(\phi ^{n+1}\) because the intention is to preserve the skew angle. Thus
This approach would only work well if the domain volume is changing uniformly. In the \(I-P-P-P\) case, one must use a VOSA (volume + orientation + shape) metric, with \(W^n = \zeta ^{n+1} \, R(A_{\text {ref}}) \, S(A_{\text {ref}})\).
See [14] for examples of target construction for the deforming domain problem.
Example VII
Increase a short edge length.
Suppose that in two dimensions, at some sample point, the edge that defines \(\ell _2\) in the initial mesh is unacceptably small. Let \(\ell _{\text {min}}>0\) be the smallest acceptable edge length in the mesh and assume \(\ell _2 < \ell _{\text {min}}\). The goal is to construct the target parameters such that in the optimized mesh the small edge length \(\ell _2\) at the same sample point has been increased. Let the new edge length be \(\ell _2 + \Delta \ell _2\). At the same time, let’s preserve the length \(\ell _1\) at the same sample point, i.e., there should be no change in \(\ell _1\) as a result of the mesh optimization. In fact, let \(f \ge 1\) be a user input and let us suppose that we desire \(\ell _2 + \Delta \ell _2 = f \, \ell _{\text {min}}\) after optimization.
Recall that in two dimensions, \(\zeta = \ell _1 \, \ell _2\) and \(\rho = \frac{\ell _2}{\ell _1}\). Thus,
Then, since a goal is to preserve \(\ell _1\),
and thus \(\rho \, \Delta \zeta = \zeta \, \Delta \rho \), or
This means that, for some \(\beta \ne 0\), one needs \(\Delta \zeta = \beta \, \zeta \) and \(\Delta \rho = \beta \, \rho \).
Furthermore,
from which one finds
So, if \(\beta >0\), then \(\Delta \ell _2 > 0\) and the length of the small edge will increase under optimization. Finally, in terms of f and \(\ell _{\text {min}}\),
with \(\beta > 0\).
Therefore, in this target construction method, one first writes the target matrix in the parametric form in Equation 2.2. For the given sample point at which the small edge occurred, set \(\theta = \theta _{\text {init}}\) and \(\phi =\phi _{\text {init}}\) from the initial mesh. Then replace \(\zeta \) in the target with \(\zeta + \Delta \zeta = (1 + \beta ) \, \zeta _{\text {init}}\) and replace \(\rho \) in the target with \(\rho + \Delta \rho = (1 + \beta ) \, \rho _{\text {init}}\) (where \(\beta \) is given in the last formula above, with \(\ell _2\) the value of \(\ell _2\) on the initial mesh). A metric of type VOSA preserves orientation and skew, while improving size and aspect ratio with the revised target matrix. The PIE decision is thus \(I-P-P-I\).
In practice, one can find every sample point in the initial mesh at which \(\ell _2 < \ell _{\text {min}}\) and construct the target accordingly.
Of course, it may happen that at some sample points \(\ell _1 < \ell _{\text {min}}\). In that case, let’s preserve \(\ell _2\) and increase \(\ell _1\). That is, set
and
Then,
and
From the first relation, for \(\beta \ne 0\), \(\Delta \zeta = \beta \, \zeta \) and \(\Delta \rho = - \beta \, \rho \) is a solution. (The alternative solution, \(\Delta \zeta = - \beta \, \zeta \) and \(\Delta \rho = \beta \, \rho \) will be discussed momentarily.) From the second relation,
Here, \(\beta > 0\), but while \(\zeta \) will be increased, \(\rho \) will be decreased. In that case, \(\ell _1\) is increased but \(\ell _2\) is preserved. The alternative solution gives
Here, \(\beta < 0\). Then, from the alternative solution, one sees that \(\Delta \zeta > 0\) and \(\Delta \rho < 0\). Therefore, in the alternative solution, \(\zeta \) will be increased and \(\rho \) will be decreased. Thus, the alternative solution gives the same result as the original solution, i.e. \(\ell _1\) is increased but \(\ell _2\) is preserved.
Finally, this scheme does not guarantee that in the optimal mesh all edge lengths will be greater than \(\ell _{\text {min}}\). It only encourages it. If the scheme fails to give the needed improvement, one could consider (1) decreasing the value of f (while keeping it greater than 1) or (2) choosing \(I-A-P-I\) in the PIE decision to provide more flexibility to the mesh optimization. That would require a volume + shape (VS) metric.
3.5.2 Target parameter construction using simulation data
In these examples, one or more of the target parameter values is defined in physical space, while others are defined in logical space. Thus, some parameters will be interpolated (or advected) while others will not.
Example VIII
Adapt local volume to a set of local error estimates.
Suppose that, as primary data, one has values of the dependent variable in a simulation at the sample points of the initial mesh (the one just prior to optimization). Suppose, in addition, that the primary data is processed to give secondary data consisting of values \(\{ e_j \}\) of some scalar error estimator at the sample points. From the secondary data, compute, as final data, the values of the local area parameters \(\{ \upsilon _j \}\) at the sample points. To do this, a function \(\upsilon = \upsilon (e)\) is used to convert the local errors into local areas. With such a function, one can find \(\upsilon _j = \upsilon (e_j)\). Finally, convert the local volumes to local sizes \(\{ \zeta _j \}\) by the usual formulas in 2D or 3D, if needed.
Assume, for the moment, that one has such a function. Next, the parameter control decision must be made. It has already been decided to adapt the local volume to the error, so the decision must have the form \(C-X-X-X\), with X to be determined. Let us abstain from controlling orientation, but try to control shape. This gives \(C-A-C-C\) for the parameter control decision, so one needs a volume + shape metric and the incomplete matrix U (see Sect. 2.4). Since the volume parameter is to be adapted to the error estimates, the PIE decision has the form \(I-A-X-X\). It is reasonable to assume that in most cases, the skew decision will be to equalize the skew angles, so that angles in the adapted mesh will be close to the isotropic angle.Footnote 10 For the aspect ratio parameter, it might be best to choose \(X = P\) (i.e., to preserve existing aspect ratios), especially if the initial mesh contains high-aspect ratio elements. So, the final PIE decision is \(I-A-E-P\).
With the \(I-A-E-P\) choice, one need only interpolate the values of the local volume during the optimization procedure. The other parameters are computed in the usual fashion on the initial mesh and do not need to be updated during optimization.
The remaining question is how to create an adequate function \(\upsilon (e)\). To begin, define a non-dimensional error parameter, given by
with \(e_{\text {min}} = \min _j \{ e_j \}\) and \(e_{\text {max}} = \max _j \{ e_j \}\). Then \(0 \le E \le 1\) and
Let \(\upsilon (e) = \tilde{\upsilon } (E) \). There are many functions \(\tilde{\upsilon }(E)\) that may suffice for adapting the mesh to the error, so let us first mention some basic requirements on \(\tilde{\upsilon }\). The first requirement is that \(\tilde{\upsilon }(E) > 0\) for \(0 \le E \le 1\). This guarantees that the targets have positive local volume. The second requirement is that \(\tilde{\upsilon }\) should be a strictly decreasing function of E because larger errors require smaller local volumes in the adapted mesh. A third requirement is that
where \(\upsilon _A\) is the local volume in the initial mesh.
To proceed further, define the change in the volume at point j to be
Substituting this relation into the third requirement on \(\tilde{\upsilon }\), the requirement on \(\Delta \tilde{v}\) is
From the second requirement on \(\tilde{\upsilon }\), one sees that \(\Delta \tilde{\upsilon }\) must be a decreasing function of E because for E near 1, the change in volume must be negative, while for E near 0, the change in volume must be positive. In addition, let’s require that \(\Delta \tilde{\upsilon } (E) =0\) at \(E=\bar{E}\), where the latter is the average of the \(\{ E_j \}\). Finally, from the first requirement on \(\tilde{\upsilon }\),
for every j. Because the function \(\Delta \tilde{\upsilon }\) is decreasing, its minimum value occurs at \(E=1\). Thus \(\left( \Delta \tilde{\upsilon } \right) _j \ge \Delta \tilde{\upsilon } (1)\). Therefore, it is sufficient to require
The simplest function to satisfy these requirements would be a linear function in E. Therefore, assume that \(\Delta \tilde{\upsilon }\) has the form
Since it is required that \(\Delta \tilde{\upsilon } (\bar{E})=0\), \(b = - a \, \bar{E}\) and thus
Since this is supposed to be a decreasing function, one needs \(a < 0\). Further
Assuming \(\left( \upsilon _A \right) _j > 0\) for all j, the first requirement on \(\Delta \tilde{\upsilon }\),
is satisfied when
Therefore, the range of a must be constrained to
Finally, note that with this model,
Thus the constraint on the sum of the deltas is automatically satisfied for any a.
The final value of the constructed volume parameter is
with “a” a user input parameter in the specified range.
Of course, many other functional forms for \(\Delta \tilde{\upsilon }\) satisfying the requirements may be more suitable for adapting to the local error. For example, if \(\Delta E = E - \bar{E}\), functions of the form \(a \, \Delta E + b \, (\Delta E)^3\) or \(\tan \left( \Delta E \right) \) may work better because they are less sensitive to small \(\Delta E\) but change rapidly with larger \(\Delta E\). To determine that, however, requires an actual simulation with error values available.
Example IX
Adapting to a material indicator function.
In the ICF problem described in earlier work, the domain was a quarter circle that was meshed by a multi-block structured quadrilateral mesh consisting of three blocks. In the outer part of the mesh, one had azimuthal symmetry. The goal in the problem was to create values for the target parameters (the target matrix in particular) so that the mesh would be adapted to one or more material layers at distances \(r_1\) and \(r_2\) from the center of the circular domain. The suggested target matrix for one layer was
with
and with user parameters \(0 < f \le 1\) and \(\sqrt{2}< a< b < 3\). Notice that the target matrix here is a function of position in physical space and \(\rho = \rho (r)\). With this target matrix, the optimized mesh is adapted to the material layers by creating high-aspect-ratio cells in the ring at distance \(r = \sqrt{x^2+y^2}\) from the circle center. The shape metric \(\mu _2\) was used in optimizing the objective function.
In terms of the construction method presented in this document, the parameter control decision is to abstain or not abstain on each of the four geometric parameters in 2D. Since a shape metric was used, it is clear that the decision must have been \(A-A-C-C\). In PIE, the decision was \(A-A-E-I\). The skew angle in the target is the isotropic skew angle for a quadrilateral element (\(\frac{\pi }{2}\)) and the aspect ratio parameter defined as above. Thus, the correct shape matrix in this problem is
With the isotropic skew angle, the skew matrix Q becomes the identity matrix. Thus \(S=D\). The aspect ratio matrix D can be written
Since shape metrics are invariant to scaling, using the matrix W above is equivalent to using S above. As seen previously, using S in place of T in \(\mu _2\) gives the same result.
Now consider the more general two-dimensional, two-material problem in which one is given a discrete material indicator function \(\iota _j\) with \(0 \le \iota _j \le 1\) at physical points \((x_j,y_j)\) in the initial mesh. The goal is to adapt the local mesh volume to the two materials it contains. Clearly, one needs to control volume and skew. Without additional information, it makes sense to abstain on the orientation parameter. In the ICF problem just described, aspect ratio was controlled instead of volume. This was because thin mesh layers at distance r were desired. In the more general problem here, no such assumption is made, and thus it is better to control volume instead of aspect ratio. It seems that, in the absence of additional information, there are three potential approaches to aspect ratio: (1) set aspect ratio to 1, (2) abstain on aspect ratio, or (3) preserve aspect ratio. The PIE decision is \(I-A-E-E\), \(I-A-E-A\), or \(I-A-E-P\), respectively. The resulting metric types are VS (volume + shape), VQ (volume + skew), and VS, respectively. The choice between the three approaches depends on whether one believes that the simulation will produce high-aspect ratio elements or not; if it might, then option (1) should be avoided. Additionally, if one believes that the aspect ratio in the optimized mesh should not be too different from the aspect ratios in the initial mesh, then option (3) is a viable approach. If one expects the aspect ratios to change a lot between the initial and optimal meshes, then option (2) is the best choice.
Finding the values for the skew and aspect ratios is easy once one of the three options above is selected. Next, concentrate on finding a model for the volume parameter, given the material indicator. Suppose that \(\iota =1\) means that locally the only material present is material 1 and \(\iota =0\) means that locally only material present is material 2. Furthermore, assume that one wants the local volume of material 1 to decrease monotonically with \(\iota \) [and therefore the local volume of material 2 (which is \(1-\iota \)) should increase monotonically with \(\iota \)]. Suppose that \(\upsilon _{\text {ini}}^{(1)}\) is the local volume of material 1 in the initial mesh and \(\upsilon _{\text {opt}}^{(1)}\) is the local volume of material 1 in the optimal mesh (at the same physical location). Assume that \(\upsilon _{\text {init}}^{(1)}>0\) at all locations. Write \(\upsilon _{\text {opt}}^{(1)} = \upsilon _{\text {ini}}^{(1)} + \Delta \upsilon \). It seems reasonable to require that \(\Delta \upsilon < 0\) if and only if \(\iota > \frac{1}{2}\). The simplest model for \(\Delta \upsilon \) is
with the requirement \(0< m < 2 \, \upsilon _{\text {ini}}^{(1)}\) to ensure that \(\upsilon _{\text {opt}}^{(1)}>0\) at all locations. The value of m would be a user input parameter.
With this model, the target volume parameter is fully defined. The maximum range of \(\upsilon _{\text {opt}}^{(1)}\) is \(0< \upsilon _{\text {ini}}^{(1)} - \frac{m}{2}< \upsilon _{\text {opt}}^{(1)}< \upsilon _{\text {ini}}^{(1)} + \frac{m}{2} < 2 \, \upsilon _{\text {ini}}^{(1)}\). Other models for \(\Delta \upsilon \) can, of course, be developed.
Example X
Alignment of mesh lines to a smooth vector field.
The term “alignment” in meshing has been defined in the past by saying that two vectors in \(\mathfrak {R}^3\) are aligned if their cross product is zero [2]. The equivalent in two dimensions is to say that the area enclosed by the two vectors is zero. With this definition, if \(\mathbf{u}\) and \(\mathbf{v}\) are aligned, then \(\mathbf{u} = \lambda \mathbf{v}\), with \(\lambda \) a real number. In TMOP, however, an alternative definition of alignment is used based on target terminology. Recall that \(\theta \) is the angle between the x-axis and the first column vector of any non-degenerate matrix. In TMOP, two vectors in \(\mathfrak {R}^2\) are aligned if their orientation angle with respect to the x-axis is the same. This definition of alignment is used, because it is more consistent with the target construction approach. With the TMOP definition, if \(\mathbf{u}\) and \(\mathbf{v}\) are aligned, then \(\mathbf{u} = \lambda \mathbf{v}\), with \(\lambda > 0\). In two dimensions, one can write \(\theta _\mathbf{u} = \theta _\mathbf{v}\) when the two vectors are aligned.
In this example, suppose, for the sake of clarity, that one has an initial quadrilateral mesh with globally structured mesh topology. In addition let there be, as primary or secondary data, a discrete vector field \(\{ \mathbf{v}_j \}\) defined at points \((x_j,y_j)\) in the physical domain (j is a global index) and possibly at some discrete time \(t_n\). The vector field is processed into a final discrete vector field by interpolating it to the sample points of the mesh (if not already located there). It is assumed that the underlying continuum vector field is “smooth” (i.e., there are no abrupt changes in direction or length between nearby sample points). Further assume that the vector field is non-self intersecting. The feasibility of aligning mesh lines with a vector field depends heavily on the orientation of the vector field with respect to the domain/mesh boundary. If the boundary vertices are allowed to move, better alignment can be achieved, but this is not always possible.
The goal in the alignment problem is to assign values to the target orientation parameters such that the first column (vector) of the active matrix is aligned with \(\mathbf{v}\) at every sample point. Controlling only the orientation parameter will lead to poor mesh quality with respect to the other geometric parameters, thus some of the additional parameters need to be controlled. Suppose then that the parameter control decision is \(C-C-C-A\). Leaving aspect ratio undefined provides some flexibility to the optimizer so that perhaps the alignment can be more effective. Given this decision, the metric type must be VOQ (volume + orientation + skew).
The PIE decision in this example is \(P-I-E-A\) (i.e., preserve initial volume, improve orientation, and equalize the skew angle). From this, one has directly that \(\upsilon = \upsilon (A_{\text {init}})\) and \(\phi = \phi _{\text {iso}}\). Since \(\phi _{\text {arch}} = \frac{\pi }{2}\) for a quadrilateral element (and thus \(\sin \phi _{\text {arch}}= 1\)), the size parameter is \(\zeta = \upsilon \), so \(\zeta \) is also preserved.
Recall that in two dimensions, \(\theta (A)\) is the angle between the x-axis and the mesh vector \(\mathbf{a}_1\) and \(\theta (W)\) is the angle between the x-axis and the target column vector \(\mathbf{w}_1\). The challenge is to define values for the orientation parameter \(\theta (W)\) at every sample point. The most straightforward thing to do is to set \(\theta (W) = \theta _\mathbf{v}\), where the latter is the orientation of the vector \(\mathbf{v}\) with respect to the x-axis, at the given sample point. Doing so should make \(\theta (A) \sim \theta _\mathbf{v}\) in the optimal mesh provided the mesh topology allows it. However, if the goal is to create alignment on a wide class of smooth vector fields, one cannot just try to align \(\mathbf{a}_1\) with \(\mathbf{v}\) at every sample point. Doing so could produce a very poor quality mesh with some vector fields. It may be better, for example, to align \(-\mathbf{a}_1\) with \(\mathbf{v}\) at some sample points and to align to \(\mathbf{a}_1\) at others. It may also be better to try to align \( \pm \mathbf{a}_1^\perp \) with \(\mathbf{v}\) at other sample points.Footnote 11 The decision as to which of these vectors should be aligned with \(\mathbf{v}\) has to be made at every sample point. Since there are many sample points, an automatic way of making the decision is needed. One way to do this goes as follows. Given \(\mathbf{a}_1\) from the initial mesh and the non-zero vector \(\mathbf{v}\) at the same location, compute the corresponding unit vectors \(\hat{\mathbf{a}}_1\) and \(\hat{\mathbf{v}}\). Then evaluate the two quantities \(c \equiv \hat{\mathbf{v}} \cdot \hat{\mathbf{a}}_1\) and \(s \equiv {\text {det}} \left( \hat{\mathbf{v}}, \hat{\mathbf{a}}_1 \right) \). Then the alignment decision is made as follows:
-
1.
If \(c \ge \frac{1}{\sqrt{2}}\), then align \(\mathbf{a}_1\) with \(\mathbf{v}\) by setting \(\cos \theta _\mathbf{w} = \frac{v_x}{\mid \mathbf{v} \mid }\) and \(\sin \theta _\mathbf{w} = \frac{v_y}{\mid \mathbf{v} \mid }\).
-
2.
If \(c \le -\frac{1}{\sqrt{2}}\), then align \(-\mathbf{a}_1\) with \(\mathbf{v}\) by setting \(\cos \theta _\mathbf{w} = -\frac{v_x}{\mid \mathbf{v} \mid }\) and \(\sin \theta _\mathbf{w} = -\frac{v_y}{\mid \mathbf{v} \mid }\).
-
3.
If \(s > \frac{1}{\sqrt{2}}\), then align \(\mathbf{a}_1^\perp \) with \(\mathbf{v}\) by setting \(\cos \theta _\mathbf{w} = \frac{v_y}{\mid \mathbf{v} \mid }\) and \(\sin \theta _\mathbf{w} = -\frac{v_x}{\mid \mathbf{v} \mid }\).
-
4.
If \(s < -\frac{1}{\sqrt{2}}\), then align \(-\mathbf{a}_1^\perp \) with \(\mathbf{v}\) by setting \(\cos \theta _\mathbf{w} = -\frac{v_y}{\mid \mathbf{v} \mid }\) and \(\sin \theta _\mathbf{w} = \frac{v_x}{\mid \mathbf{v} \mid }\).
That completes the definition of the three target parameters \(\zeta \), \(\theta \), \(\phi \) for this alignment problem. One might wonder why we do not try to align the second column vector of A (i.e., \(\mathbf{a}_2\)) with \(\mathbf{v}\) in this scheme. The main reason is that the orientation of \(\mathbf{a}_2\) is not directly used in target construction (because its orientation is \(\theta +\phi \)). Additionally, \(\phi = \phi _{arch}\) has already been specified so that, by controlling \(\theta \) and \(\phi \), one is already controlling the orientation of \(\mathbf{a}_2\). Notice also that in this scheme, the target parameters are fully defined prior to optimization. This is why \(\mathbf{a}_1\) from the initial mesh is used to make the alignment decision in the construction of the orientation parameter. Experience has shown that trying to update target parameters during the optimization procedure can lead to convergence and non-uniqueness issues. Finally, note once again that, because the vector field is associated with a position in physical space, the target parameters must be updated via interpolation or by an advection scheme during the optimization procedure. An example of a target construction method for mesh alignment can be found in Ref. [13].
3.5.3 The “Delta” method of target parameter construction
Previously, the task of assigning values to the geometric target parameters has been described as a process in which a function takes the primary data and converts it to data for the parameter at each sample point. While this remains valid, there is another way to think about this process. Suppose, instead, that one starts with the initial mesh, whose set of Jacobians is \(\{ A_{i} \}\). One can evaluate each of the non-abstained parameters on the sample points of the initial mesh, giving \(\zeta _i = \zeta (A_{i})\), \(\theta _i = \theta (A_{i})\), and so on. Define the initial target parameter set as \(\{ \zeta _i, \theta _i, \phi _i, \rho _i \}\) (or, if one has an actual target matrix \(W_i = W(\zeta _i, \theta _i, \phi _i, \rho _i)\). Using this data in the optimization will, of course, result in an optimal mesh identical to the initial mesh. However, if any of this data is changed, one will have new or partly new target data and a different optimal mesh will result. As an example, suppose \(\zeta _i\) is changed to \(\zeta _o\) (where o stands for optimal). Let \(\zeta _o = \zeta _i + \Delta \zeta \). Then the challenge is to define \(\Delta \zeta \) (at every sample point). Thus, the final target matrix (if there is one) can be expressed as either \(W=W(\zeta _o, \theta _o, \phi _o, \rho _o)\) or as \(W = W(\zeta _i + \Delta \zeta , \theta _i + \Delta \theta , \phi _i + \Delta \phi , \rho _i + \Delta \rho )\). In theory, it is possible that for some parameters and some problems it will be easier to define \(\zeta _o\) directly and in others it will be easier to define \(\Delta \zeta \). In practice it will often be easier to define the values \(\zeta _o\), \(\upsilon _o\), and perhaps \(\rho _o\) in terms of \(\Delta \zeta \), \(\Delta \upsilon \), and \(\Delta \rho \). On the other hand, it is probably easier to specify the angle parameters \(\theta _o\) and \(\phi _o\) directly, rather than in terms of \(\Delta \theta \) and \(\Delta \phi \). An example of the ‘Delta’ method in target construction was seen in Example VI.
4 Summary and conclusion
The Target Matrix Optimization Paradigm is a methodology for mesh quality improvement that uses optimization to find optimal locations of mesh vertices and nodes. The TMOP methodology is general in that it can be applied to a wide variety of mesh quality improvement problems, rather being limited to just one situation. An important feature of TMOP is the use of target matrices (or target parameters) to define the local geometric properties of the desired optimal mesh.
Section 2 investigated the relationship between \(2 \times 2\) matrices and a standard set of geometric parameters representing local volume, orientation, skew, and aspect ratio. With certain restrictions, the relationship between the matrices and the parameters can be represented as a one-to-one, onto map. Given the matrix, one can find the geometric parameters; this process is called parameter extraction. Given the geometric parameters, one can find the corresponding matrix. In the context of TMOP, the matrices represent Jacobian matrices of the element mapping at the mesh sample points. Thus, one can say that the geometric parameters represent the first order geometric quality of the mesh (qualities such as curvature cannot be described by the Jacobian matrix). Given the active mesh, i.e., the mesh that is being optimized, one can find its active Jacobian matrices. In turn, one can extract values of the geometric parameters from the active matrices. These values are useful in the assessment of mesh quality and in the evaluation of local quality metrics in the optimization procedure. On the other hand, given the values of the target geometric parameters, one can find the target matrix. While the idea of matrices having geometric content is not new, the contribution in Sect. 2 is to identify a standard set of geometric parameters based on the Jacobian matrix that can be used in target construction.
In TMOP, every local quality metric is defined in terms of a set of active and corresponding target parameters. The active parameter values are extracted from the active mesh while the target parameter values are defined prior to the mesh optimization procedure. Section 3 describes the process in TMOP by which new target construction algorithms can be devised. This process is broken into three phases: that of developing a construction strategy, developing algorithms for converting primary to secondary data, and developing models for converting secondary data into final target parameter data. In developing the strategy, one begins with a mesh quality improvement goal that is appropriate for the application. Next, one considers the mesh and simulation context. In the target parameter control decision phase, one decides whether to control or abstain on each geometric parameter. The fact that one can abstain on a parameter means, in general, that (1) values of the corresponding target parameters need not be assigned and (2) there may be increased improvement in the parameters that are controlled. This flexibility gives greater freedom in the design of mesh optimization algorithms. Finally, correspondence chains are defined that associate specific primary, secondary, and target data to one another so that the flow between data types is well-defined. In the next phase of target construction, one determines how the primary data in each correspondence chain will be converted into secondary data (i.e., into mesh or solution functionals). The determination consists of identifying particular existing algorithms that are suitable for the conversion or, in some cases, devising an entirely new algorithm. Examples of such algorithms include a posteriori error estimation, Hessian or gradient recovery methods, or other techniques used in mesh adaptivity. In the last phase, one determines how the secondary data in each correspondence chain will be converted into values of the target parameters at every mesh sample point. Determination may consist of a straightforward direct conversion of the data (as in the case of skew parameters defined by the isotropic element) or may require the development of an ad-hoc model that consists of an analytic formula or function relating, for example, the determinant of a matrix to the local mesh volume parameter. Model development mainly consists of determining the best functional form, as well as selecting (via numerical experiment) the best values of any constants contained within the model. With the completion of the target construction process, one has a complete description of the data and algorithms that will be used to assign values to the target parameters in order to address the mesh quality improvement goal. This description, along with corresponding software, yields a target construction method.
In the ideal situation, target construction is not needed because there already exists an appropriate target construction method corresponding to the mesh quality improvement goal, mesh context, and simulation context. If this is not the case, then one may engage in the target construction process. It is hoped that, over the long term, a library of target construction algorithms will be developed and made available so that the need to engage in target construction becomes gradually less. Various examples of target construction for both planar and volume meshes were presented in Sect. 3.
Much of the existing mesh optimization literature focuses on the definition or selection of quality metrics and/or the numerical optimization procedure. Many of the proposed quality metrics do not make use of targets. For methods that do include targets, the most glaring gap is the lack of discussion on how to construct a set of targets that are suitable for the particular application at hand. The description of target construction in this report is thus considered to fill a major gap in the mesh optimization literature.
Of course, not all mesh quality improvement problems can be solved simply by proper construction of the target matrix. On the one hand, target construction is an essential step in mesh quality improvement; with this document there is finally a clear exposition of this topic. On the other hand, we still lack firm solutions to a number of the listed mesh quality improvement problems, especially in view of the large number of contexts in which they may occur. In addition to target construction, the solution to these problems may include (1) choosing or defining a quality metric having the right metric type and that can produce unique optimal meshes, (2) choosing the right objective function template, (3) constructing proper trade-off coefficients, and (4) employing other techniques such as the use of a different metric in different parts of the domain or adding other terms to the basic objective function.
Notes
The active matrix is \(3 \times 2\) for a mesh on some surface.
It is expected that, over time, more and more methods for assigning target parameter values will be developed so that one will not have to develop a new method each time a mesh is to be optimized.
We shall discuss what we mean by primary data in Sect. 3.1.3.
For 2D meshes, each parameter group has one parameter. For 3D meshes, some parameter groups contain more than one variable. For example, while in 2D, there is only one skew parameter \(\phi \), in 3D there are three skew parameters \(\phi _1,\phi _2, \phi _3\) that form the skew group.
If one wants to control a particular parameter within a parameter group, one will usually want to control all the other parameters in the group as well. There may be the rare occasions where one wants to control only some of the parameters within a group.
An extensive discussion of ‘metric type’ and how it is determined by the control decision can be found in [17].
It is recognized that, in more complex situations, the mesh quality improvement goal may require one to make multiple control decisions, for example, one for each sub-region of the physical domain.
The term “equalize” is used to mean “making the values of a geometric parameter equal at all sample points of the mesh.” Equalize is a special case of “equi-distribution” in which the product of a geometric parameter and a scalar weight is made the same over all sample points. Non-trivial equi-distribution is included under the “improve” option of PIE.
These coordinates are not unique, but uniqueness is not needed for the present purpose.
In some rare instances, one might wish to choose \(Y = I\), if one has some a priori knowledge about the skew angles.
If \(\mathbf{w}\) is a non-zero vector in \(\mathfrak {R}^2\), then we use the notation \(\mathbf{w}^\perp \) to indicate the vector that is perpendicular to \(\mathbf{w}\) and obeys \({\text {det}} \left[ \mathbf{w}, \mathbf{w}^\perp \right] > 0\).
References
Brackbill J, Saltzman J (1981) Adaptive zoning for singular problems in two dimensions. J Comput Phys 46:342–368
Brackbill J (1993) An adaptive grid with directional control. J Comput Phys 108:38–50
Cao W (2007) An interpolation error estimate on anisotropic meshes in \(\Re ^n\) and optimal meshes for mesh refinement. SIAM J Numer Anal 45(6):2368–2391
Chen L, Sun P, Xu J (2007) Optimal anisotropic meshes for minimizing interpolation errors in \(L^p\)-norm. Math Comput 76:179–204
Coulaud O, Loseille A (2016) Very high order anisotropic metric-based mesh adaptation in 3D. Procedia Eng 163:353–365
Du L, Yan N (2001) Gradient recovery type a posteriori error estimate for finite element approximation on non-uniform meshes. Adv Comput Math 14(2):175–193
Dvinsky A (1991) Adaptive grid generation from harmonic maps on Riemannian manifolds. J Comput Phys 95(2):450–476
Guo H, Zhang Z, Zhao R (2017) Hessian recovery for finite element methods. Math Comput 86(306):1671–1692
Hetmaniuk U, Knupp P (2008) A mesh optimization algorithm to decrease the maximum error in finite element computations. In: Proceedings of the 17th international meshing roundtable, pp 533–550
Huang W, Russell R (2011) Adaptive moving meshes. In: Bloch A, Epstein CL, Goriely A, Greengard L (eds) Applied mathematical sciences series, vol 174. Springer, New York
Ilyas M, Lamichhane B, Meylan M (2017) A gradient recovery method based on an oblique projection and boundary modification. ANZIAM J 58:C38–C45
Kamenski L, Huang W (2014) How a nonconvergent recovered Hessian works in mesh adaptation. SIAM J Numer Anal 52(4):1692–1708
Knupp P (1995) Mesh generation using vector fields. J Comput Phys 119:142–148
Knupp P (2007) Updating meshes on deforming domains. Commun Numer Methods Eng 24(6):467–476
Knupp P (2012) Introducing the target matrix paradigm for mesh optimization via node movement. Eng Comput 28(4):419–429
Knupp P (2019) Target formulation and construction in mesh quality improvement. LLNL-TR-795097, Lawrence Livermore National Laboratory, Livermore, CA
Knupp P (2020) Metric type in the target-matrix mesh optimization paradigm, LLNL-TR-817490. Lawrence Livermore National Laboratory, Livermore, CA
Lakkis O, Pryer T (2012) Gradient recovery in adaptive finite-element methods for parabolic problems. IMA J Numer Anal 32(1):246–278
Leng J, Zhang Y, Xu G (2013) A novel geometric flow approach for quality improvement of multi-component tetrahedral meshes. Comput Aided Des 45(10):1182–1197
Liseikin V (1999) Grid generation methods. Springer, Berlin
Lipnikov K, Vassilveski Y (2007) Analysis of Hessian recovery methods for generating adaptive meshes. In: Proceedings of the 15th international meshing roundtable, pp 163–171
Quadros WR, Vyas V, Brewer M, Owen SJ, Shimada K (2005) A computational framework for generating sizing function in assembly meshing. In: Hanks BW (eds) Proceedings of the 14th international meshing roundtable. Springer, Berlin, Heidelberg
Steinberg S, Roache P (1986) Variational grid generation. Numer Methods PDEs 2:71–96
Thompson J, Thames F, Mastin C (1974) Automatic numerical grid generation of boundary-fitted curvilinear coordinates for field containing any number of arbitrary two-dimensional bodies. J Comput Phys 15:299–319
Winslow A (1967) Numerical solution of the quasilinear Poisson equations in a non-uniform triangle mesh. J Comput Phys 2:149–172
Zhang Y, Bajaj C, Xu G (2009) Surface smoothing and quality improvement of quadrilateral/hexahedral meshes with geometric flow. J Commun Numer Methods Eng 25(1):1–18
Zienkiewicz O, Zhu J (1992) The superconvergence patch recovery and a posteriori error estimates, part I. Int J Numer Methods Eng 33:1331–1364
Acknowledgements
The author would like to thank members of the ETHOS team: Veselin Dobrev, Tzanio Kolev, Ketan Mittal, and Vladimir Tomov. Funding was supported by Lawrence Livermore National Laboratory (B615479).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Dihedral LLC Support provided by the ETHOS project, LLNL Subcontract B615479.
Rights and permissions
About this article
Cite this article
Knupp, P. A target construction methodology for mesh quality improvement. Engineering with Computers 38, 4451–4474 (2022). https://doi.org/10.1007/s00366-022-01653-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-022-01653-2