Multidirectional grading influence on static/dynamic deflection and stress responses of porous FG panel structure: a micromechanical approach

Abstract

This is the first time the multidirectional-graded porous panel structure modeled numerically using an equivalent single-layer higher-order polynomial model considering the cubic variation of extensional displacement to maintain the necessary stress/strain. The effect of porosity (even and uneven distributions) and variable grading patterns also included achieving the generality. Further, the deflection and stress values, the proposed bidirectional functionally graded (2D-FG) structure, are predicted under the variable loadings, i.e. static and dynamic. Three different types of grading pattern, i.e. power-law, exponential and sigmoid are introduced by varying the material constituents along their principal material axes (longitudinal and transverse). The current numerical solutions (deflection and stress) are obtained through a customized computer code (prepared in MATLAB), under the influences of the static and time-dependent loadings utilizing the higher-order finite element formulations. The dynamic deflections are obtained through the constant acceleration type Newmark’s time-integration steps. The predicted result accuracy is checked by comparing the previously published values in literature and different simulation models (ANSYS and ABAQUS). Besides, the batch input technique is adopted for the simulation material models for both the ANSYS and ABAQUS. Moreover, the python scripting is adopted first time to modify ABAQUS input files for the present 2D graded structure. The influential structure input parameter (power-law exponents, thickness ratio, aspect ratio, end conditions, geometry and curvature ratio) is varied to compute a few final responses (deflection and stress data) of multidirectional FG structure via the derived mathematical model and the final understandings listed the details.

1 Introduction

The functionally graded materials (FGMs) are nonhomogeneous composite materials usually made from the combination of metals and ceramics. The smooth and continuous variation of the material properties in the FGM is achieved by gradually varying the volume fraction of constituent materials from one surface to another, to eliminate the interface problems like debonding and delamination. In present work, the variation in the properties of the FGM is achieved mathematically using different distribution patterns, i.e. power-law, exponential and sigmoid [1]. Also, the porosity type of defect may reduce the stiffness as well as structural strength and consequent performance of the component. Therefore, the present mathematical model includes even and uneven type of porosity distribution [2] to know its effect on the final deflection and stress responses.

Now, to check the recent investigations in the field of FGMs, some relevant articles are reported here. The three-dimensional (3D) deformation of the simply supported thick FG plate under thermoelastic loading is presented in [3]. A third-order shear deformation theory (TSDT) is utilized in [4] to perform static deformation analysis of a simply supported FG plate. The large deflection analysis of the SSSS graded plate under pressure loading is performed in [5] using the finite strip method. The semi-analytical elasticity solutions for static deflection and thermal deformations of the 2D-FGM beam with various support conditions are presented in [6] utilizing the state space-based differential quadrature method (DQM). The static deflection and free vibration results of the open cylindrical shell made of 2D-FGM are analyzed in [7] utilizing a 2D-generalized DQM. The static bending responses of the FG plate are computed in [8] by employing the HSDT kinematics. The buckling analysis of FG plate is performed in [9] using an HSDT-based finite strip method. The bending responses of FG and laminated composite shells and panels are computed in [10] by employing the generalized DQM in association with the first-order shear deformation theory (FSDT). Static deflection responses of FG plates resting on elastic foundation under the hygro-thermo-mechanical loading are evaluated in [11] using a four-variable refined plate theory. The nonlinear thermal instability of shape memory alloy (SMA) reinforced sandwich (FG/SMA/FG) structures, i.e. moving sandwich plates with constant speed and the geometrically imperfect sandwich cylindrical shells is investigated in [12, 13] utilizing TSDT and von Karman geometrical nonlinearity. A new sinusoidal shear deformation theory is utilized in [14] for flexural analysis of FG nano-plates resting on elastic foundation. The thermoelastic deflection and stress responses of simply supported FG sandwich plates are computed in [15] using Carrera unified formulation (CUF). Nonlinear deflection responses of thick 2D-FG variable thickness plate resting on the nonlinear elastic foundation are evaluated in [16] using generalized DQM in association with HSDT and von Karman nonlinearity. TSDT kinematics is used in [17] for flexure and buckling analysis of 2D-FG plates. Bending and stress responses of 2D-FG circular beams are computed in [18] using Euler–Bernoulli beam theory (EBBT) under the action of various loading functions. Further, a non-uniform rational B-spline (NURBS) functions are used in [19] to compute the free vibrational frequency characteristics of a 2D-FG Timoshenko beam. The effect of different material combinations on the mechanical behavior of sandwich plates under high-temperature environment is presented in [20] utilizing the finite element method (FEM) and the FSDT. Static bending characteristics of 2D-FG microbeams subjected to uniformly distributed load (UDL) under different end support conditions are studied in [21] using the quasi-3D theory based on modified couple stress theory (MCST). Natural frequency, buckling and static deflection responses of FG plates were evaluated in [22] via moving Kriging interpolation meshfree method combined with the HSDT kinematics. Similarly, the TSDT kinematics is adopted in [23] for the evaluation of the frequency responses of the 2D-FG beams subjected to various support conditions. A meshless total Lagrangian corrective smoothed particle method is used in [24] for flexural analysis of 2D-FG beams. A quasi-3D beam theory in conjunction with MCST is utilized in [25] for frequency analysis of FG microbeams. The EBBT and Eringen’s nonlocal theory (ENT) is utilized combinedly in [26] to perform the natural frequency analysis of the rotating 2D-FG nano-beams.

In addition, a few more literatures are reported here concerning the dynamic analysis of the graded structure. A 3D thermomechanical deformation of a simply supported FG rectangular plate subjected to time-dependent thermal loads is presented in [27]. The HSDT, normal deformable plate theory and a meshless local Petrov–Galerkin (MLPG) method are utilized in [28] to perform the static deflection and free and forced vibration analyses of thick FG plate. The 3D dynamic responses of simply supported FG and multi-layered magneto-electro-elastic plate are evaluated in [29] using a modified Pagano’s method. The transient thermoelastic responses of two-phase FGMs are obtained in [30] using the asymptotic expansion homogenization scheme and the FEM. The time-dependent thermo-electro-mechanical creep behavior of a thick hollow rotating cylinder made of radially polarized piezoelectric material is investigated in [31] using a semi-analytical technique based on Mendelson’s method of the successive elastic solution. A 3D static and dynamic analysis of thick FG plates based on the MLPG method is performed in [32]. Also, the dynamic, free vibration and bending deflections responses of the doubly curved FGM panel are performed in [33, 34] utilizing the lower-order polynomial kinematic model, i.e. the FSDT. The earlier kinematic model was adopted in [35] to predict the deflections under the static and the dynamic loadings of the FG plate structure by combining the NURBS-based FEM. Further, the FGMs and laminated composite structure time-dependent flexural and stress characteristics are reported in [36] using a refined 8-node shell element. The dynamic analysis of the bidirectionally graded Timoshenko beam under the movable load is carried out in [37] using the Timoshenko beam theory (TBT) and the EBBT. One-dimensional CUF is combined with the mode superposition method in [38] to study the dynamic characteristics of the laminated structure. A quasi-3D HSDT-based nonlocal elasticity theory is used in [39] for the investigation of dynamic characteristics of FG nanoplates. Dynamic deflection responses of the 2D-FG sandwich beam under moving point load are computed in [40] using the FSDT kinematics. The nonlinear dynamic responses of 2D-FG beams are reported in [41] based on the TBT including von Karman nonlinearity. Also, a finite element model in conjunction with CUF is employed in [42] for the dynamic characterization of the composite metamaterials. A CUF is employed in [43] to investigate the large deflection and post-buckling load values of the composite plate. The nonlinear equilibrium analysis of the U-shaped 2D lattice structure is presented in [44] utilizing CUF. Further, Green–Lagrange nonlinearity in the framework of CUF has been adopred to compute the nonlinear frequencies of thin structure considering the large displacement in [45]. The effect of fiber orientation path on the buckling, free vibration and static analysis of variable angle tow panels is studied in [46]. The influence of fiber misalignments on the buckling performance of variable stiffness composites is presented in [47] by employing layerwise models.

Similarly, a few completed research relevant to the porous structures is discussed in this paragraph. The thermal buckling load parameter of 2D-FG porous microbeams is investigated in [48] using EBBT and MCST and generalized DQM. The flexural bending of porous FG nano-beams under the hygro-thermo-mechanical loading is carried out in [49] via ENT. The buckling load parameter of graded porous sandwich nanoplates is studied in [50] utilizing a higher-order nonlocal strain gradient theory. The static bending, buckling and natural frequencies of porous 2D-FG plates are investigated in [51] considering the isogeometric modeling technique in the framework of the FSDT. The eigenvalue (linear and nonlinear) responses of the rotating 2D-FG porous micro-beams are computed in [52] using TBT and the geometrical distortion modeled via von Karman nonlinearity in association with MCST. The two-dimensional-graded porous plate structures reinforced with eccentrically stiffener dynamic responses are computed in [53]. The model is derived using the von Karman nonlinear strain and the FSDT displacement field kinematics under the moving load.

The extensive reviews of the past contributions indicate that most of them follow the power-law (PWL) type of grading pattern and information related to the SIG and the EXP kind are too small. Also, a few articles focused on the modeling and computation of structural responses considering the porosity type of defects within the graded structure. Additionally, the research related to the grading in different directions is also limited in number. Therefore, the present work aims to develop an inclusive material model mathematically comprising various grading patterns (PWL, SIG and EXP) along with two different directions (longitudinal and thickness), types of porosity and distribution (even and uneven through-thickness) for the computation of structural responses (flexural strength and stress). Also, the model is generic to take care the influences of geometrical shapes (plate, cylindrical, elliptical, spherical and hyperbolic) on the static and dynamic deflection responses of 2D-FG panel structure under the variable loading intensities. To achieve the desired objective, the necessary governing equation is formulated mathematically in association with displacement type isoparametric finite element (FE) technique and Newmark’s integration scheme. The solutions are predicted through an in-house MATLAB code using the prepared mathematical formulation and a few simulation models via the available commercial FE tools (ANSYS and ABAQUS). Moreover, the simulation model input parameter files are prepared through the batch techniques (ANSYS parametric language code, APDL and python scripting for ABAQUS). The present finite element formulation validity established by comparing the results with previously published data. The derived model comprehensiveness is discussed by solving altered numerical examples through the influential input parameters, i.e., power-law exponents, thickness ratio, aspect ratio, end conditions, geometrical shapes and curvature ratio, on the flexural and stress data of the 2D-FG structure under static and time-dependent loadings.

2 Mathematical formulation

2.1 Material properties of FGM

The effective property of 2D-FG material calculation is provided by considering the material grading along with the thickness (X₃-axis) and longitudinal directions (X₁-axis). The variations of elastic properties are achieved via a Voigt’s micromechanical model in conjunction with the individual volume fractions each material constituent. The expressions for three types of grading pattern, i.e. PWL, EXP and SIG are presented in the following subsections for the numerical computation of bidirectional material properties.

2.1.1 PWL-FGM

A bidirectional elastic property variation [54] according to PWL grading along the transverse and length directions can be written as:

$$ P\left( {X_{1} ,X_{3} } \right) = \left( {P^{\text{c}} - P^{\text{m}} } \right)V_{{f_{\text{c}} }} + P^{\text{m}} . $$

(1)

Now, the desired porosity comprising even and uneven type of distribution patterns [54] are represented by the Eqs. (2) and (3), respectively.

$$ P\left( {X_{1} ,X_{3} } \right) = \left( {P^{{\text{c}}} - P^{{\text{m}}} } \right)V_{{f_{{\text{c}}} }} + P^{{\text{m}}} \, - 0.5\lambda \times \left( {P^{{\text{c}}} + P^{{\text{m}}} } \right), $$

(2)

$$ P\left( {X_{1} ,X_{3} } \right) = \left( {P^{{\text{c}}} - P^{{\text{m}}} } \right)V_{{f_{{\text{c}}} }} + P^{{\text{m}}} \, - 0.5\lambda \times \left( {P^{{\text{c}}} + P^{{\text{m}}} } \right)\left( {1 - \frac{{2\left| {X_{3} } \right|}}{h}} \right), $$

(3)

where, $P\left( {X_{1} ,X_{3} } \right)$ is the required final property (Poisson’s ratio, modulus of elasticity and density) of the 2D-FG structure in the X₁ and X₃ directions, and P^m and P^c are the respective properties of the metal and ceramic constituents. Also, ‘X₁’ and ‘X₃’ denote the random point in the length and transverse direction, ‘n_x’ and ‘n_z’ represent power exponents along the length and thickness direction, ‘λ’ and ‘h’ are the porosity index and the thickness, respectively. Also, the ceramic and metal volume fractions are represented as $V_{{f_{{\text{c}}} }} = \left( {0.5 + \frac{{X_{3} }}{h}} \right)^{{n_{z} }} \left( {\frac{{X_{1} }}{a}} \right)^{{n_{x} }}$ and $V_{{f_{{\text{m}}} }} = 1 - V_{{f_{{\text{c}}} }}$, respectively.

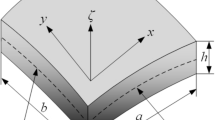
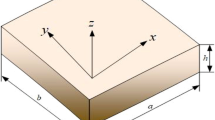
Now, the geometry of the bidirectional FG panel is shown in Fig. 1 whereas the material grading along the length and thickness direction is shown in Fig. 2. Also, Fig. 3 shows the porosity distributions patterns (even and uneven) whereas Fig. 4 represents the variation of ceramic volume fraction along the length and thickness direction of the FG structure according to PWL-FGM method.

Fig. 1

The geometry of the FGM panel with bidirectional grading

Fig. 2

Material grading along the length and thickness direction

Fig. 3

Porosity distribution along the thickness direction

Fig. 4

Variation of ceramic volume fraction of PWL-FGM in the length and thickness directions for n_z = n_x = 2

2.1.2 SIG-FGM

The variation of properties of bidirectional-graded structural panel is obtained using the extended PWL-FGM steps to achieve the SIG kind of pattern distributions and presented in following Eqs. (4) and (5).

$$ P\left( {X_{1} ,X_{3} } \right) = \left( {P^{{\text{c}}} - P^{{\text{m}}} } \right)\left[ {1 - 0.5\left( {1 - \frac{{2X_{3} }}{h}} \right)^{{n_{z} }} } \right]\left( {\frac{{X_{1} }}{a}} \right)^{{n_{x} }} + P^{{\text{m}}} \quad {\text{for}}\quad 0 \le X_{3} \le h/2. $$

(4)

$$ P\left( {X_{1} ,X_{3} } \right) = \left( {P^{\text{c}} - P^{\text{m}} } \right)\left[ {0.5\left( {1 + \frac{{2X_{3} }}{h}} \right)^{{n_{z} }} } \right]\left( {\frac{{X_{1} }}{a}} \right)^{{n_{x} }} + P^{\text{m}} \,\,for\,\, - h/2 \le X_{3} \le 0 $$

(5)

Now, the effect of porosity distribution patterns (even and uneven kind) on the effective material properties of SIG-FGM structure is obtained using the subsequent steps as shown in the below equations:

$$ P\left( {X_{1} ,X_{3} } \right) = \left( {P^{\text{c}} - P^{\text{m}} } \right)\left[ {1 - 0.5\left( {1 - \frac{{2X_{3} }}{h}} \right)^{{n_{z} }} } \right]\left( {\frac{{X_{1} }}{a}} \right)^{{n_{x} }} + P^{\text{m}} - 0.5\lambda \times \left( {P^{\text{c}} + P^{\text{m}} } \right)\,\,\,for\,\,0 \le X_{3} \le \frac{h}{2} $$

(6)

$$ P\left( {X_{1} ,X_{3} } \right) = \left( {P^{\text{c}} - P^{\text{m}} } \right)\left[ {0.5\left( {1 + \frac{{2X_{3} }}{h}} \right)^{{n_{z} }} } \right]\left( {\frac{{X_{1} }}{a}} \right)^{{n_{x} }} + P^{\text{m}} - 0.5\lambda \times \left( {P^{\text{c}} + P^{\text{m}} } \right)\,\,\,\,{\text{for}}\,\, - \frac{h}{2} \le X_{3} \le 0, $$

(7)

$$ P\left( {X_{1} ,X_{3} } \right) = \left( {P^{\text{c}} - P^{\text{m}} } \right)\left[ {1 - 0.5\left( {1 - \frac{{2X_{3} }}{h}} \right)^{{n_{z} }} } \right]\left( {\frac{{X_{1} }}{a}} \right)^{{n_{x} }} + P^{\text{m}} - 0.5\lambda \times \left( {P^{\text{c}} + P^{\text{m}} } \right)\,\,\left( {1 - \frac{{2\left| {X_{3} } \right|}}{h}} \right)\,\,\,\,{\text{for}}\,\,0 \le X_{3} \le \frac{h}{2}, $$

(8)

$$ P\left( {X_{1} ,X_{3} } \right) = \left( {P^{\text{c}} - P^{\text{m}} } \right)\left[ {0.5\left( {1 + \frac{{2X_{3} }}{h}} \right)^{{n_{z} }} } \right]\left( {\frac{{X_{1} }}{a}} \right)^{{n_{x} }} + P^{\text{m}} - 0.5\lambda \times \left( {P^{\text{c}} + P^{\text{m}} } \right)\,\left( {1 - \frac{{2\left| {X_{3} } \right|}}{h}} \right)\quad {\text{for}} - \frac{h}{2} \le X_{3} \le 0. $$

(9)

The bidirectional variation in the volume fraction of ceramic constituent for SIG-FGM is presented in Fig. 5.

Fig. 5

Variation of ceramic volume fraction of SIG-FGM in the length and thickness directions for n_z = n_x = 2

2.1.3 EXP-FGM

In this subsection, the material property of the 2D-FG structure using EXP distribution pattern is described by the equation given below as:

$$ P\left( {X_{1} ,X_{3} } \right) = P^{\text{c}} \times {\text{e}}^{{ - \frac{1}{2}\ln \left( {\frac{{P^{\text{c}} }}{{P^{\text{m}} }}} \right)\left( {1 - \frac{{2X_{3} }}{h}} \right)\left( {\frac{{X_{1} }}{a}} \right)}} . $$

(10)

Similarly, the material properties of EXP-FGM in association with the porosity distribution patterns of even and uneven kind are calculated using the Eqs. (11) and (12) as:

$$ P\left( {X_{1} ,X_{3} } \right) = P^{\text{c}} \times {\text{e}}^{{\left( { - \frac{1}{2}\ln \left( {\frac{{P^{\text{c}} }}{{P^{\text{m}} }}} \right)\left( {1 - \frac{{2X_{3} }}{h}} \right)\left( {\frac{{X_{1} }}{a}} \right) - 0.5\lambda \times \ln \left( {\frac{{P^{\text{c}} }}{{P^{\text{m}} }}} \right)} \right)}} , $$

(11)

$$ P\left( {X_{1} ,X_{3} } \right) = P^{\text{c}} \times {\text{e}}^{{\left( { - \frac{1}{2}\ln \left( {\frac{{P^{\text{c}} }}{{P^{\text{m}} }}} \right)\left( {1 - \frac{{2X_{3} }}{h}} \right)\left( {\frac{{X_{1} }}{a}} \right) - 0.5\lambda \times \ln \left( {\frac{{P^{\text{c}} }}{{P^{\text{m}} }}} \right)\left( {1 - \frac{{2\left| {X_{3} } \right|}}{h}} \right)} \right)}} . $$

(12)

Now, the ceramic volume fraction distribution using EXP-FGM method in the length and thickness directions is presented in Fig. 6.

Fig. 6

Variation of ceramic volume fraction of EXP-FGM in the length and thickness direction

2.2 Displacement field kinematics

The geometrical dimension (refer to Fig. 1) of a 2D-FG panel, i.e. the length (a), width (b) and thickness (h) are along its principal material axes (X₁, X₂ and X₃), respectively. Also, the radii of curvatures at the mid-plane of the panel along their principal material directions are denoted by R_X1 and R_X2. The material displacement field model has been expressed below using the HSDT polynomial [55,56,57]:

$$ \left. \begin{gathered} X_{{11}} = X_{{11_{0} }} + X_{3} \psi _{x} + X_{3}^{2} X_{{11_{0} }}^{*} + X_{3}^{3} \psi _{x}^{*} \hfill \\ X_{{22}} = X_{{22_{0} }} + X_{3} \psi _{y} + X_{3}^{2} X_{{22_{0} }}^{*} + X_{3}^{3} \psi _{y}^{*} \hfill \\ X_{{33}} = X_{{33_{0} }} \hfill \\ \end{gathered} \right\}, $$

(13)

where, $X_{{11}} ,\,\,X_{{22}} ,\,\,X_{{33}}$ and $X_{{11_{0} }} ,\,X_{{22_{0} }} ,\,X_{{33_{0} }}$ are the global and mid-plane displacement fields in the X₁, X₂, and X₃ directions, respectively. $\psi _{x} ,\,\psi _{y}$ are the rotations of transverse normal about X₂, and X₁ axes, respectively. The higher-order terms of Taylor’s series expansion are denoted by $X_{{11_{0} }}^{*} ,\,\,X_{{22_{0} }}^{*} ,\,\,\psi _{x}^{*} ,\,\,\psi _{y}^{*}$ while $X_{3}^{2}$ and $X_{3}^{3}$ are the square and cubic thickness coordinates, respectively.

Now, the strain–displacement relation of the 2D-FG model is presented in Green–Lagrange sense as [58]

$$ \left\{ \varepsilon \right\} = \varepsilon _{l} = \left\{ \begin{gathered} \overline{X} _{{11,X_{1} }} \\ \overline{X} _{{22,X_{2} }} \\ \overline{X} _{{11,X_{2} }} + \overline{X} _{{22,X_{1} }} \\ \overline{X} _{{11,X_{3} }} + \overline{X} _{{33,X_{1} }} \\ \overline{X} _{{22,X_{3} }} + \overline{X} _{{33,X_{2} }} \\ \end{gathered} \right\} = \left\{ \begin{gathered} \varepsilon _{{X_{1} X_{1} }} \hfill \\ \varepsilon _{{X_{2} X_{2} }} \hfill \\ \gamma _{{X_{1} X_{2} }} \hfill \\ \gamma _{{X_{1} X_{3} }} \hfill \\ \gamma _{{X_{2} X_{3} }} \hfill \\ \end{gathered} \right\}\,, $$

(14)

where, $\varepsilon _{l}$ denotes linear strain tensor and.

$$ \begin{aligned} & \overline{X} _{{11,X_{1} }} = \frac{{\partial X_{{11}} }}{{\partial X_{1} }} + \frac{{X_{{33}} }}{{R_{{X_{1} }} }};\,\overline{X} _{{11,X_{2} }} = \frac{{\partial X_{{11}} }}{{\partial X_{2} }};\,\,\overline{X} _{{11,X_{3} }} = \frac{{\partial X_{{11}} }}{{\partial X_{3} }}; \\ & \overline{X} _{{22,X_{1} }} = \frac{{\partial X_{{22}} }}{{\partial X_{1} }};\,\overline{X} _{{22,X_{2} }} = \frac{{\partial X_{{22}} }}{{\partial X_{2} }} + \frac{{X_{{33}} }}{{R_{{X_{2} }} }};\,\,\overline{X} _{{22,X_{3} }} = \frac{{\partial X_{{22}} }}{{\partial X_{3} }}; \\ & \overline{X} _{{33,X_{1} }} = \frac{{\partial X_{{33}} }}{{\partial X_{1} }} - \frac{{X_{{11}} }}{{R_{{X_{1} }} }};\,\overline{X} _{{33,X_{2} }} = \frac{{\partial X_{{33}} }}{{\partial X_{2} }} - \frac{{X_{{22}} }}{{R_{{X_{2} }} }}. \\ \end{aligned} $$

Further, the linear strain tensor can be expressed in the form:

$$ \left\{ {\varepsilon _{l} } \right\} = \left\{ \begin{gathered} \varepsilon _{{X_{1} }}^{0} \hfill \\ \varepsilon _{{X_{2} }}^{0} \hfill \\ \varepsilon _{{X_{1} X_{2} }}^{0} \hfill \\ \varepsilon _{{X_{1} X_{3} }}^{0} \hfill \\ \varepsilon _{{X_{2} X_{3} }}^{0} \hfill \\ \end{gathered} \right\} + X_{3} \left\{ \begin{gathered} k_{{X_{1} }}^{1} \hfill \\ k_{{X_{2} }}^{1} \hfill \\ k_{{X_{1} X_{2} }}^{1} \hfill \\ k_{{X_{1} X_{3} }}^{1} \hfill \\ k_{{X_{2} X_{3} }}^{1} \hfill \\ \end{gathered} \right\} + X_{3}^{2} \left\{ \begin{gathered} k_{{X_{1} }}^{2} \hfill \\ k_{{X_{2} }}^{2} \hfill \\ k_{{X_{1} X_{2} }}^{2} \hfill \\ k_{{X_{1} X_{3} }}^{2} \hfill \\ k_{{X_{2} X_{3} }}^{2} \hfill \\ \end{gathered} \right\} + X_{3}^{3} \left\{ \begin{gathered} k_{{X_{1} }}^{3} \hfill \\ k_{{X_{2} }}^{3} \hfill \\ k_{{X_{1} X_{2} }}^{3} \hfill \\ k_{{X_{1} X_{3} }}^{3} \hfill \\ k_{{X_{2} X_{3} }}^{3} \hfill \\ \end{gathered} \right\}, $$

(15)

or

$$ \left\{ {\varepsilon _{l} } \right\} = \left[ {T_{l} } \right]\left\{ {\overline{{\varepsilon _{l} }} } \right\} = \left\{ {\varepsilon ^{0} } \right\} + X_{3} \left\{ {k^{1} } \right\} + X_{3}^{2} \left\{ {k^{2} } \right\} + X_{3}^{3} \left\{ {k^{3} } \right\}, $$

(16)

where, $\left[ {T_{l} } \right]_{{5 \times 20}}$ denotes linear thickness coordinate matrix and $\left\{ {\overline{{\varepsilon _{l} }} } \right\}_{{20 \times 1}}$ denotes mid-plane strain vector.

Next, the generalized form of the stress–strain relation [55] for the bidirectional FG structure is written as:

$$ \left\{ \sigma \right\} = \left\{ \begin{gathered} \sigma _{{_{{X_{1} X_{1} }} }} \hfill \\ \sigma _{{_{{X_{2} X_{2} }} }} \hfill \\ \tau _{{_{{X_{1} X_{2} }} }} \hfill \\ \tau _{{_{{X_{1} X_{3} }} }} \hfill \\ \tau _{{_{{X_{2} X_{3} }} }} \hfill \\ \end{gathered} \right\}\, = = \left[ Q \right]\left\{ \varepsilon \right\} = \left[ {\begin{array}{*{20}c} {\frac{E}{{1 - \mu ^{2} }}} & {\frac{{E \times \mu }}{{1 - \mu ^{2} }}} & 0 & 0 & 0 \\ {\frac{{E \times \mu }}{{1 - \mu ^{2} }}} & {\frac{E}{{1 - \mu ^{2} }}} & 0 & 0 & 0 \\ 0 & 0 & {\frac{E}{{2\left( {1 + \mu } \right)}}} & 0 & 0 \\ 0 & 0 & 0 & {\frac{E}{{2\left( {1 + \mu } \right)}}} & 0 \\ 0 & 0 & 0 & 0 & {\frac{E}{{2\left( {1 + \mu } \right)}}} \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon _{{_{{X_{1} X_{1} }} }} \hfill \\ \varepsilon _{{_{{X_{2} X_{2} }} }} \hfill \\ \gamma _{{_{{X_{1} X_{2} }} }} \hfill \\ \gamma _{{_{{X_{1} X_{3} }} }} \hfill \\ \gamma _{{_{{X_{2} X_{3} }} }} \hfill \\ \end{gathered} \right\}, $$

(17)

where, stress and strain vectors are denoted by {σ} and {ε}, respectively, whereas [$\bar{Q}$] denotes the reduced stiffness matrix.

After obtaining the stress and strain values of the FG structure, the total strain energy can be calculated using the below expression

$$ U = \frac{1}{2}\int\limits_{{ - h/2}}^{{h/2}} {\left( {\iint {\left\{ \varepsilon \right\}^{T} \left\{ \sigma \right\}}{\text{d}}X_{1} {\text{d}}X_{2} } \right)} {\text{d}}X_{3} , $$

(18)

Further, the energy functional can be rearranged by putting Eqs. (16) and (17) in Eq. (18) as:

$$ U = \frac{1}{2}\iint {\left\{ {\overline{{\varepsilon _{l} }} } \right\}^{T} \left[ D \right]\left\{ {\overline{{\varepsilon _{l} }} } \right\}}{\text{d}}X_{1} {\text{d}}X_{2} , $$

(19)

here,

$$ \left[ D \right] = \int\limits_{{ - h/2}}^{{h/2}} {\left[ {T_{l} } \right]^{T} \left[ Q \right]} {\text{d}}X_{3} . $$

Also, the expression of kinetic energy for the FG model can be obtained using the relation given below as:

$$ T_{{\text{e}}} = \frac{1}{2}\int\limits_{v} {\rho \left\{ {\dot{\delta }} \right\}^{T} } \left\{ {\dot{\delta }} \right\}{\text{d}}V, $$

(20)

$$ T_{{\text{e}}} \, = \frac{1}{2}\int\limits_{A} {\left( {\int_{{ - 0.5h}}^{{0.5h}} {\left\{ {\dot{\delta }_{0} } \right\}^{T} } \left[ f \right]^{T} \rho \left[ f \right]\left\{ {\dot{\delta }_{0} } \right\}{\text{d}}X_{3} } \right)} {\text{d}}A\, = \frac{1}{2}\int\limits_{A} {\left\{ {\dot{\delta }_{0} } \right\}^{T} } \left[ m \right]\left\{ {\dot{\delta }_{0} } \right\}{\text{d}}A, $$

(21)

where, ρ denotes mass density, the velocity vector is denoted by $\left\{ {\dot{\delta }} \right\}$ and [m] denotes elemental inertia matrix, which is given by

$$ \left[ m \right] = \int\limits_{{ - h/2}}^{{h/2}} {\left[ f \right]^{T} } \rho \left[ f \right]{\text{d}}X_{3} . $$

2.3 Finite element formulation

The nine-noded (nine degrees of freedom each node) isoparametric quadrilateral Lagrangian element is utilized for the modeling of a proposed mathematical model. The finite element representation for mid-plane displacement vector with the help of shape functions [59] is expressed as:

$$ \left\{ {\delta _{0} } \right\} = \sum\limits_{{i = 1}}^{9} {\left[ N \right]} \left\{ {\delta _{{0_{i} }} } \right\}, $$

(22)

where, [N] denotes shape function, $\left\{ {\delta _{{0_{i} }} } \right\}$ denotes ith node mid-plane displacement vector, which can be written as:

$$ \left\{ {\delta _{{0_{i} }} } \right\} = \left\{ {X_{{11_{{0_{i} }} }} \,X_{{22_{{0_{i} }} }} X_{{33_{{0_{i} }} }} \,\psi _{{x_{i} }} \,\psi _{{y_{i} }} X_{{11_{{0_{i} }} }}^{*} X_{{22_{{0_{i} }} }}^{*} \,\psi _{{x_{i} }}^{*} \,\psi _{{y_{i} }}^{*} } \right\}^{T} . $$

Thus allowing the mid-plane strain vector to be expressed as:

$$ \left\{ {\overline{{\varepsilon _{l} }} } \right\} = \left[ B \right]\left\{ {\delta _{{0_{i} }} } \right\}, $$

(23)

where, [B]_20×9 is the product of the differential operators and shape functions.

Next, the expression for work done due to the mechanical load (q) applied externally is given by:

$$ W = \int\limits_{A} {\left\{ {\delta _{0} } \right\}^{T} } q{\text{d}}A, $$

(24)

$$ W = \left\{ {\delta _{0} } \right\}^{T} \left\{ F \right\}, $$

(25)

where, q and {F} are the load intensity and the corresponding force vector, respectively.

Also, the mass [M] and stiffness matrix [k] can be expressed as

$$ \left[ M \right] = \iint {\left[ N \right]^{T} \left[ N \right]\rho }{\text{d}}X_{1} {\text{d}}X_{2} , $$

(26)

$$ \left[ k \right] = \iint {\left[ B \right]^{T} \left[ D \right]\left[ B \right]}{\text{d}}X_{1} {\text{d}}X_{2} . $$

(27)

2.4 Governing equation

The variational form of the total energy functional is used to compute the static bending responses of the FG structure. The structural equilibrium equation in the final form is expressed below as:

$$ \delta \Pi = \delta (U - W) = 0, $$

(28)

where, δ and п denote variation symbol and the total energy functional, respectively. The total stiffness, displacement and force vectors are used to rearrange the equation into a matrix form as:

$$ \left[ K \right]\left\{ {\delta _{0} } \right\} = \left\{ F \right\} $$

(29)

where, [K] denotes the global stiffness matrix.

Now, the time-dependent bending values are evaluated usually by solving the static equilibrium equation at a particular time (t) comprising damping and inertia forces [60]. The damping and inertia forces are the functions of velocity and acceleration, respectively. The damping effect is not considered in the present work; thus, the governing equilibrium equation for the time-dependent analysis of the current system is given below as:

$$ \left[ M \right]\ddot{\delta }_{0} + \left[ k \right]\delta _{0} = \left[ F \right], $$

(30)

where, $\ddot{\delta }_{0}$ denotes the acceleration vector.

Further, the total time (T) integrated with the time interval of Δt utilizing the Newmark’s technique to solve the expression of transient analysis. Also, the necessary transient equation is obtained using the Newmark's integration parameters (α, φ and β₀ to β₇) as in [60]. The effective stiffness matrix at any particular time instant (t) is given by

$$ \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right] = \left[ k \right] + \beta _{0} \left[ M \right]. $$

(31)

Likewise, the effective load matrix considering the increment of time step $t + \Delta t$ is given by:

$$ {}^{{t + \Delta t}}\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} } \right] = {}^{{t + \Delta t}}\left[ F \right] + \left[ M \right]\left( {\beta _{0} ^{t} \delta _{0} + \beta _{2} ^{t} \dot{\delta }_{0} + \beta _{3} ^{t} \ddot{\delta }_{0} } \right). $$

(32)

Also, the expressions to calculate the displacement, velocity and acceleration are given in the below equations:

$$ \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} } \right]^{{t + \Delta t}} \delta _{0} = {}^{{t + \Delta t}}\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} } \right], $$

(33)

$$ {}^{{t + \Delta t}}\dot{\delta }_{0} = {}^{t}\dot{\delta }_{0} + \beta _{6} ^{t} \ddot{\delta }_{0} + \beta _{7} ^{{t + \Delta t}} \ddot{\delta }_{0} , $$

(34)

$$ {}^{{t + \Delta t}}\ddot{\delta }_{0} = \beta _{0} \left( {{}^{{t + \Delta t}}\delta _{0} - {}^{t}\delta _{0} } \right) - \beta _{2} ^{t} \dot{\delta }_{0} - \beta _{3} ^{t} \ddot{\delta }_{0} . $$

(35)

To compute the static and dynamic bending and stress values, different kinds of boundary conditions are utilized and presented in the below lines:

• Clamped:

$X_{{11_{0} }} = X_{{22_{0} }} = X_{{33_{0} }} = \psi _{x} = \psi _{y} = X_{{11_{0} }}^{*} = X_{{22_{0} }}^{*} = \psi _{x}^{*} = \psi _{y}^{*} = 0$ for both X₁ = 0, a and X₂ = 0, b.

• Simply supported:

$X_{{22_{0} }} = X_{{33_{0} }} = \psi _{y} = X_{{22_{0} }}^{*} = \psi _{y}^{*} = 0$ at X₁ = 0, a and

$X_{{11_{0} }} = X_{{33_{0} }} = \psi _{x} = X_{{11_{0} }}^{*} = \psi _{x}^{*} = 0$ at X₂ = 0, b

Also, the combination of the clamped and simply supported end conditions helped to achieve a few more end conditions which are used in present work and mentioned below:

• CCCC: all sides are clamped.

• SCSC: two opposite sides (X₂ = 0, b) are clamped whereas X₁ = 0, a are simply supported

• CFCF: two opposite sides (X₁ = 0, a) are clamped whereas X₂ = 0, b are free.

• SSSS: all sides simply supported.

2.5 Procedure for simulation modeling (ANSYS and ABAQUS)

In the present analysis, the bending and stress responses of the 2D-FGM are computed under the static and dynamic loadings for the verification purpose only. In this regard, the simulation softwares, i.e. ANSYS and ABAQUS are used to prepare a bidirectional FG model. A batch input technique method is used in ANSYS whereas the input method using python coding is utilized in the ABAQUS. For the development of the FG model, a shell element has been utilized with six degrees of freedom at each node. Also, the ANSYS and ABAQUS adopt FSDT kinematics for the modeling of the structural component. The procedure for the development of the bidirectional-graded model is presented below in detailed using three major sub-steps.

Step 1 Preprocessing

In this step, the required geometrical input data, i.e. length, width and thickness for the development of the 2D-FG model have been given. Also, to achieve the smooth variation of the material properties through the thickness, the finite number of layers (≤ 100) is defined here. The properties of metals and ceramics have also been provided here as per the defined relations.

Step 2 Solution

In the second step, the required load and the necessary boundary conditions have been applied to the structure.

Step 3 Postprocessing

Lastly, the bending and stress responses under static and dynamic loading conditions for the bidirectional-graded structure are evaluated via the inbuilt solution technique available in ANSYS and ABAQUS. Additionally, a few Python scripts related to batch input file prepared for modification in the ABAQUS platform are provided in Appendix 1.

3 Results and discussion

After the successful development of the higher-order finite element formulation, a home-made computer code has been prepared for the evaluation of the structural responses. To check the accuracy of this model, a convergence and verification study has been carried out. Also, the bending and stress data of the bidirectional-graded structure under the influence of several design parameters, i.e., power-law exponents, thickness ratio, aspect ratio, end conditions, geometry and curvature ratio are computed considering static and dynamic loading conditions.

3.1 Convergence and verification

The convergence and verification of the present higher-order FE model are checked in this subsection by evaluating the static and dynamic results. For convergence study, the static and dynamic bending responses of the SSSS bidirectional FG plate made of Alumina (Al₂O₃) and Aluminum (Al) are computed and presented in Figs. 7 and 8, respectively. It can be seen from the figures that the (6 × 6) mesh is sufficient for the computation of the static and dynamic responses. The material properties of the Al₂O₃ and Al constituents are given below:

Fig. 7

Convergence (Static bending responses) of bidirectional SSSS PWL-FGM panel (a/b = 1, h = 0.1, n_x = n_z = 2, R = 1)

Fig. 8

Convergence (time-dependent bending responses) of bidirectional PWL-FGM SSSS plate (a/b = 1, h = 0.01, n_x = n_z = 2)

Ceramic-Al₂O₃: E^c = 380 GPa; ρ^c = 380 kg/m³; µ^c = 0.3

Metal-Al: E^m = 70 GPa; ρ^c = 2700 kg/m³; µ^m = 0.3.

Also, the non-dimensional form used for the computation of deflection responses is:

$$ \bar{w} = \frac{{10wE^{{\text{c}}} h^{3} }}{{qa^{4} }}, $$

(36)

where, w denotes the central deflection and q denotes the load intensity (1 N/m²).

Now, the verification of the current bidirectional FG model is presented here by comparing the current bending and stress data with the previously published and simulation data (ANSYS and ABAQUS). In the first case, the non-dimensional deflection responses of the bidirectional square FG plate for different values of power-law exponents (n_x and n_z) are computed for SSSS boundary condition under the UDL (1 N/m²) and matched with Do et al. [17], and the simulation (ANSYS and ABAQUS) results (Table 1). The verification study shows that the current deflection values are very close to the published as well as simulation data and the percentage difference between the deflection values is very small. For the calculation of static deflection data, the graded plate made of three different materials is used with the following material properties.

Table 1 Effect of power-law exponents (n_z and n_x) on the non-dimensional deflection responses of SSSS bidirectional FG plate (a/b = 1, h = 0.1)

Modulus of elasticity: E¹ = 205.1 GPa, E² = 70 GPa, E³ = 151 GPa.

Poisson’s ratio: µ¹ = µ² = µ³ = 0.3

Also, the non-dimensional form used here is expressed as: $\bar{w} = \frac{{10wE^{3} h^{3} }}{{qa^{4} }}$.

Further, the verification for non-dimensional stress responses is presented in Table 2, by comparing the current values with the published data [61] and the simulation results. It can be seen from the table that the present results are very close to the published data and the simulation values and the percentage difference between the stress responses are negligible (≤ 3.622%). For the computation of the stress values, a UDL (1 N/m²) is applied on the Al₂O₃-Al power-law graded plate under SSSS conditions. The non-dimensional form used in this case is given below:

$$ \overline{{\sigma _{x} }} = \frac{{\sigma _{x} h}}{{qa}}\left( {\frac{a}{2},\frac{b}{2},\frac{h}{2}} \right), $$

(37)

where, σ_x is the actual stress.

Table 2 Effect of power exponent (n_z) on the non-dimensional stress values of SSSS FG plate (a/b = 1, h = 0.01)

Additionally, the time-dependent bending results of the SSSS graded plate are computed by applying a UDL (5 N/cm²) and matched with the published data [36] and the simulation results, i.e. ANSYS and ABAQUS (Fig. 9). It can be seen from the verification that the responses computed using MATLAB are very close to the published and the simulation results. The input parameters used in this case of verification are:

Fig. 9

Time-dependent bending responses of SSSS FG square plate (a/b = 1, h = a/100, n_z = 10)

E^c = 151 GPa, E^m = 70 GPa, µ^c = µ^m = 0.3 and ρ^c = ρ^m = 8 × 10^–6 N s²/cm⁴.

3.2 Parametric study

The convergence and verification show that the static and dynamic results (deflection ad stress) of the bidirectional-graded structure considering porosity can be calculated with the required accuracy utilizing the present model. Hence, few examples are discussed in the subsections below to study the effect of different input parameters (power-law exponents, thickness ratio, aspect ratio, end conditions, geometry and curvature ratio) on the static and dynamic responses of the graded structures. For this purpose, alumina (Al₂O₃) and aluminum (Al) are used as ceramic and metal constituents of the bidirectional FG structure, respectively. The details of the material properties of Al₂O₃-Al constituents are provided in Sect. 3.1.

3.3 Static analysis

In this subsection, the static deflection and stress results of the bidirectional-graded structure are presented in the non-dimensional form by applying a UDL (1 N/m²). The non-dimensional form used for the computation of deflection responses is given in Eq. (36) whereas the stresses can be converted into the non-dimensional form using the following expressions:

$$ \overline{{\sigma _{x} }} = \frac{{\sigma _{x} \times h}}{{q \times a}};\quad \overline{{\sigma _{y} }} = \frac{{\sigma _{y} \times h}}{{q \times a}}\quad {\text{and}}\quad \overline{{\tau _{{xy}} }} = \frac{{\tau _{{xy}} \times h}}{{q \times a}}. $$

Now, the influence of the power exponents on the dimensionless bending responses of the bidirectional FG structure is presented (Table 3) considering various kind of porosity distribution patterns (even and uneven). It is observed from the results that the increase in the exponent value reduces the structural stiffness and the deflection results follow an upward slope. This is because the volume fraction of metal within the graded structure increases with increase in power exponent. This, in turn, lowers the structural stiffness and allows the panel to deflect more. Also, when the power-law exponent in the transverse direction is equal to one (n_z = 1), the deflection observed for SIG-FGM and PWL-FGM is same for all other input parameters. Further, it is well known that the overall stiffness of the structure may reduce due to the porosity, therefore, an increase in porosity index increases deflection parameter.

Table 3 Effect of Power-law exponents (n_z and n_x) on the non-dimensional bending responses of bidirectional SSSS porous FG cylindrical panel (a/b = 1, h = 0.1, R = 1)

In the second example, the non-dimensional deflection responses of the bidirectional porous FG plate are computed and presented in Table 4, for CCCC boundary condition considering various aspect ratio values (b/a = 0.5, 1, 2). The overall stiffness of the present FG panel is decreased with an increase in the aspect ratio because stiffness and length are inversely related. Therefore, the non-dimensional bending data follow an upward slope when the aspect ratio increases. It can also be seen from the table that the maximum deflection values are observed in PWL-FGM case while compared to the SIG-FGM and EXP-FGM.

Table 4 Effect of aspect ratio (b/a) on the dimensionless bending responses of CCCC bidirectional porous FG plate (a = 1, h = 0.1, n_x = n_z = 2)

Further, the effect of various end conditions (SCSC, CCCC, CFCF and SSSS) on the dimensionless deflection values of the bidirectional spherical panel considering porosities (even and uneven) is presented in Table 5. The relative displacement of the clamped structure is lower than the other structures. Therefore, the minimum deflection is observed in the CCCC condition whereas the maximum deflection is observed in the SSSS case.

Table 5 Effect of boundary conditions on the non-dimensional bending values of the bidirectional porous FG spherical panel (a/b = 1, h = 0.1, n_x = n_z = 2, R = 1)

Now, the influence of the thickness ratio (a/h) on the dimensionless stress values of the bidirectional FG hyperbolic panel is presented in Table 6 considering SSSS boundary condition and variable porosity distribution patterns. The overall stiffness of the structure is reduced with the reduction in thickness and therefore the corresponding stress values are increasing, which can also be observed from the results presented in Table 6.

Table 6 Effect of thickness ratio (a/h) on the stress responses of bidirectional SSSS porous FG hyperbolic panel (a = 0.1, b = 0.05, n_x = n_z = 2, R = 1)

Next, the non-dimensional stress results of the SSSS bidirectional FG porous structure are presented in Table 7 considering various geometrical shapes (cylindrical, spherical and elliptical). It is clear from the table that the maximum stresses induced in the spherical panels whereas the minimum stress values are observed in the cylindrical case.

Table 7 Effect of geometry on the dimensionless stress responses of SSSS porous 2D-FG structure (a = 0.1, b = 0.05, h = 0.01 n_x = n_z = 2, R = 1)

3.4 Dynamic analysis

In this subsection, the bending and stress responses of the bidirectional-graded structure are computed under the action of a UDL (1 N/m²). In the first example, the effect of various geometrical shapes (cylindrical, elliptical and spherical) on the time-dependent bending data of the bidirectional porous FG SSSS panel is shown in Figs. 10, 11 and 12 for PWL-FGM, SIG-FGM and EXP-FGM, respectively. It can be seen from the figures that the maximum deflection is observed in cylindrical structures whereas the minimum deflection is observed in spherical panels. Also, the deflection observed in the porous FG structures is more than that of the FG structure without porosity.

Fig. 10

Effect of geometrical shapes on the time-dependent central deflection of the PWL-FGM panel (a/b = 1, h = 0.01, R = 10, n_z = n_x = 2)

Fig. 11

Effect of geometrical shapes on the time-dependent central deflection of the SIG-FGM panel (a/b = 1, h = 0.01, R = 10, n_z = n_x = 2)

Fig. 12

Effect of geometrical shapes on the time-dependent central deflection of the EXP-FGM panel (a/b = 1, h = 0.01, R = 10)

Also, the effect of boundary conditions (CCCC, SCSC and CFCF) on the transient bending responses of the bidirectional-graded hyperbolic panel is shown for PWL-FGM in Fig. 13, for SIG-FGM in Fig. 14 and for EXP-FGM in Fig. 15. The results indicate the minimum deflections for the clamped boundaries while the maximum under the CFCF kind of end support, respectively, irrespective of the assigned known structure material and/or geometry-related input variables.

Fig. 13

Effect of boundary conditions on the time-dependent central deflection of the PWL-FGM hyperbolic panel (a/b = 1, h = 0.01, R = 10, n_z = n_x = 2)

Fig. 14

Effect of boundary conditions on the time-dependent central deflection of the SIG-FGM hyperbolic panel (a/b = 1, h = 0.01, R = 10, n_z = n_x = 2)

Fig. 15

Effect of boundary conditions on the time-dependent central deflection of the EXP-FGM hyperbolic panel (a/b = 1, h = 0.01, R = 10)

Next, the effect of curvature ratio (R/a) on the dimensionless stress values of the bidirectional cylindrical FG panels is presented in different graphs, i.e. Figure 16 (PWL-FGM), Fig. 17 (SIG-FGM) and Fig. 18 (EXP-FGM), respectively. The results show that the bending responses are following an upward path for the greater values of the curvature ratio. This is because the flexural stiffness of the curved structure is more than that of the flat structure, which shows high deflection. The non-dimensional form used here is expressed below as:

$$ \overline{{\sigma _{{xx}} }} = \frac{{\sigma _{{xx}} \times h^{2} }}{{q \times a^{2} }}. $$

Fig. 16

Effect of curvature ratio (R/a) on the time-dependent stress of the PWL-FGM cylindrical panel (a/b = 1, h = 0.01, n_z = n_x = 2)

Fig. 17

Effect of curvature ratio (R/a) on the time-dependent stress of the SIG-FGM cylindrical panel (a/b = 1, h = 0.01, n_z = n_x = 2)

Fig. 18

Effect of curvature ratio (R/a) on the time-dependent stress of the EXP-FGM cylindrical panel (a/b = 1, h = 0.01)

4 Conclusion

The deflection and stress values of the bidirectional FG structure are evaluated numerically under the static and dynamic loading conditions and utilizing an HSDT model including the porosity effect. The Newmark’s constant acceleration time-integration scheme is utilized to derive the necessary governing equation. An isoparametric FE formulation is used for the evaluation of static and dynamic responses via own MATLAB-based computer code. The correctness of the model has been checked by matching the present results with the simulation results and the published data. The verification study indicates the correctness of the present higher-order FE model. A parametric study is then carried out to study the influence of various design parameters on the structural responses of the bidirectional-graded model. Based on this study, a few important outcomes are listed below in a pointwise manner:

• The SIG-FGM structure shows stiffer characteristics among all three types of FGMs, hence, show least deflection and stress values, whereas the PWL-FGM is a most flexible one which shows highest deflection and stress results when the effect of porosity is not considered.

• Conversely, the porosity shows the least effect on the EXP-FGM, i.e., under the influence of porosity, the deflection and stresses observed in the EXP-FGM are least. In this case, also, the maximum stress and deflection results are obtained for the PWL-FGM.

• The PWL-FGM and SIG-FGM show same results when the power exponent in the thickness direction is equal to one i.e. n_z = 1.

• The uneven porosity distribution pattern shows a lesser variation in the results (deflection and stress) when compare it to the even type of porosity distribution.

• Various design parameters (power-law exponents, thickness ratio, aspect ratio, end conditions, geometry and curvature ratio) show a considerable effect on the deflection and stress values of the bidirectional porous FG structure.