1 Introduction

Problems with multimaterial, multiphase and fluid structure interactions arise in many engineering applications such as solid combustion, droplet evaporation, flow-driven projectile, blood flow through flexible arteries, flow-induced vibration, to name a few. Figure 1 shows two such problems. In such problems a common and important feature is that the interface evolves in time. Therefore, the geometry or spatial domain must be updated based on the interactions, for example, between an object and the surrounding fluid (i.e., between projectile and air) in the projectile case or between two phases (i.e., liquid and gas) in the droplet case.

Two types of mesh-based approaches are commonly used for evolving geometry problems: explicit interface tracking, which is also referred to as front tracking, and implicit interface capturing. These approaches employ different frames to describe and simulate the transport equations of the material, namely the Lagrangian/material, the Eulerian/fixed or an arbitrary Lagrangian–Eulerian (ALE) [12, 24, 26] frame. In the case of an interface capturing approach, the interface is represented implicitly in the material/volumetric mesh that is typically fixed based on the Eulerian frame. Commonly used interface capturing methods include the level set [35, 45, 48], phase field [2, 5] and immersed boundary [36] methods. On the contrary, in an interface tracking method the evolving interface is explicitly represented in the underlying discretization at all times. Interface tracking method can be achieved by using any of the three frames involving a fixed or a moving mesh. Commonly used interface tracking methods include interface embedding methods [19, 49], interface reconstruction procedures based on volume-of-fluid and moment-of-fluid [6, 14, 44], interface enrichment approaches based on XFEM [8] and methods using interface-fitted mesh based on the Lagrangian or an ALE frame [10, 11, 17, 28, 37, 51].

Fig. 1
figure 1

Two examples of the evolving geometry problem with a fluid–structure interaction and b multiphase interaction (two instances of time are shown in each example)

Full size image

A major advantage of implicit interface capturing is that topological changes in the interface are relatively easy to incorporate, even when they occur frequently (e.g., a large number of droplets interacting with each other causing topological changes). The major drawback of implicit methods is the ad-hoc treatment of interface conditions as well as constitutive laws and equations of state in the so-called blending region around the interface. In contrast, interface tracking allows for a direct treatment of the interface physics including discontinuities and steep normal gradients. However, topological changes are more complex to manage in interface tracking.

We present an interface tracking approach that employs an ALE frame along with an interface-fitted conforming hybrid/mixed mesh with anisotropic layered elements. In such an approach the geometry of the computational domain must be updated at every instance as dictated by the analysis to properly represent the current state of the interface in terms of its location, shape and topology. We note that the current paper does not include general topological changes. The additional functions needed for topological changes in the geometry are under development. Further, the mesh must also be updated at every instance to remain consistent with the evolving geometry (including the interface). One way to update the mesh is to regenerate it entirely based on the updated geometry. Another option is to apply local mesh modifications. Regenerating or modifying a mesh and using this altered mesh in the analysis code at each time step is computationally expensive (i.e., mesh regeneration or modification and re-initialization of data structures within the analysis code are time consuming). In contrast to mesh regeneration or modification, mesh motion can be used as the geometry evolves, based on the motion and deformation of the interface, while keeping the mesh connectivity the same (as well as the size of the data structures related to the mesh in the analysis code). Thus, mesh motion is efficient to use.

Several mesh motion methods have been proposed in the previous research, such as mesh elasticity analogy [13, 34, 47, 52], spring analogy [4, 7, 15, 53] and target-matrix paradigm [31].

Large motion and deformation in the geometry occur in many problems of interest. For example, a projectile moving from one end of the cannon to the other or droplets shirking significantly in volume due to phase change. For problems with large motion and deformation in the geometry, mesh motion alone is not sufficient while mesh regeneration or modification alone is computationally expensive. Thus, a combination of mesh motion and regeneration/modification is required in such problems [3, 10, 16, 21, 22, 25, 28, 33, 37, 50].

We have developed an approach that employs a combination of mesh motion and modification (instead of mesh regeneration) to be efficient. In our approach, mesh motion is based on mesh elasticity analogy and mesh modification is based on local cavity-based operations (e.g., see [32, 39, 43]) that offers specific advantages such as local solution transfer and parallelization. A mesh size field (e.g., see [32]), which describes the desired mesh resolution over the domain, is used to automatically trigger and drive mesh modification. The mesh size field is either prescribed, computed based on an error estimator, or a combination of the two.

In summary, the novelty of the current approach is that it updates both the geometry and mesh, where the mesh is updated automatically such that it remains consistent with the evolving geometry and maintains the structure and resolution of the highly anisotropic layered elements. This paper is organized as follows. Section 2 describes the overall simulation workflow and components. Section 3 discusses the details of the geometry and mesh updates. Results and discussion are presented in Sect. 4. Section 5 provides closing remarks.

2 Overall simulation workflow

Fig. 2
figure 2

Simulation components for interface tracking

Full size image

The parallel interface tracking approach developed in this work is based on three primary simulation components or libraries. These components are shown in Fig. 2 and include a pre-processor, a solver, and a model and mesh adaptor. These three components are coupled/linked using a “driver” code. Further, all the components operate in parallel to target practical problems of interest.

The pre-processor converts input data (including mesh-related data) into a solver-suitable format and uses data streams to pass it to the solver. In addition to physics computation, the solver includes sub-components for mesh motion, error estimation and mesh modification trigger (to indicate that the mesh topology must be modified). These three additional sub-components operate efficiently within the solver because of the direct access to the necessary data needed for them, especially in a parallel distributed-memory environment. The third component of model and mesh adaptor updates the geometric model, applies mesh modification and performs dynamic mesh partitioning to maintain parallel load balance. The solver uses data streams to pass the necessary information to the adaptor. These data streams include: (1) the current interface location and mesh coordinates to update the shape information in the geometry and mesh, and (2) the mesh size and solution fields to drive mesh modification and perform solution transfer.

Several of the sub-components have been developed in earlier works not involving interface tracking. For example, in-memory based coupling [46] is used between all components (instead of a file-based coupling), which is crucial to be performant on parallel computers. The pre-processor and solver use data streams for in-memory coupling as mentioned above, while the adaptor uses well-defined functional interfaces (or application programming interfaces, APIs), see [46] for details. The solver employs an ALE finite element formulation [54] for the physics computation, while the error estimation is performed using an explicit variational multiscale (VMS)-based error estimator [23].

In this paper, we focus our attention on new developments made related to parallel interface tracking. Details of the geometry and mesh updates are discussed in the next section, while the trigger for mesh modification along with the parallel programming model and mesh partition are discussed in this section.

2.1 Trigger for mesh modification

Geometry updates in the current problems of interest only involve shape changes and thus, can be performed at the necessary frequency (e.g., at every time step). However, mesh updates also include modification or connectivity changes that are time consuming. Thus, it is desirable to apply mesh modification at a lower frequency, i.e., not at every time step, and a mechanism is needed that can trigger mesh modification only when necessary.

Two criteria are used to trigger mesh modification. If either criterion is met then mesh modification is executed. Both criteria rely on the mesh size field. In this study, the mesh size field is determined at each time step, which is relatively inexpensive. It is either prescribed based on the current state of the geometry (i.e., it evolves in time with the geometry), computed based on an error estimator, or a combination of the two.

The first criterion is based on mesh resolution and a mesh modification is triggered when the current mesh resolution is not satisfactory with respect to the mesh size field at the given time step. This idea has been developed before and commonly used in an adaptive transient simulation (e.g., see [38]), and we follow the same in this work.

The second criterion targets mesh quality and requires element shape quality to be above a threshold. Several element shape quality measures are available in the literature. Note that it is necessary to use a signed quality measure such that any inverted/invalid element is detected by a negative value. In this work, we use a normalized mean ratio in the transformed/metric space defined by the given mesh size field (e.g., see [32]). It can attain a maximum value of 1 for an element with the “best” shape (e.g., a regular tetrahedron). We note that any other suitable measure of the element shape quality can be used. Mesh modification is triggered when the shape quality measure for any element in the mesh is below the threshold value. The current procedure is summarized in Algorithm 1, where \(\gamma ^M\) denotes the shape quality measure in the metric space while the subscripts e and 0 are used to denote an element value and the threshold value, respectively. For the current choice of element shape quality measure, 0.3 is used as the threshold value.

figure a

2.2 Parallel programming model and mesh partition

The current parallel programming model builds upon earlier work by extending it to include interface tracking. It relies on each simulation component using the same parallel mesh partition (e.g., see [27]) and thus, ensures that all simulation steps are efficiently performed in parallel. In this model, the mesh is partitioned into the desired number of parts and message passing interface (MPI) [20] is used such that each part is associated with a MPI rank or process. Hybrid parallel programming including data parallelism will be considered in the future.

The underlying parallel mesh database provides APIs to query the necessary information related to the inter-part boundaries, specifically each mesh entity on the inter-part boundaries (including mesh vertices, edges and faces in 3D) has multiple copies since it is duplicated on all residing parts. These copies are stored as remote copies in each residing part (e.g., see [27]). These APIs are directly used by the model and mesh adaptor to operate in parallel as discussed in the next section. Similarly, these APIs are used in the pre-processor to build parallel communication structures used by the solver.

In the pre-processor, owner relationship is established among remote copies of any given mesh entity at inter-part boundary such that one copy is assigned as the owner and in-charge of communication between all the copies. In the solver, owner relationship is used to device a two-pass communication strategy to perform physics computation in parallel (see [40, 41] for details). Sub-components of mesh motion and error estimation follow the same form of parallel computation. This is the primary reason why these sub-components currently reside in the solver component. However, our workflow is flexible enough to accommodate instances when these sub-components are defined outside of the solver.

Parallel interface tracking is supported by imposing two constraints on the parallel mesh partition. These constraints ensure that the overall parallelization strategy and communication structures used in each component remain the same with and without interface tracking. The first constraint is applied to support parallel discontinuous interpolation/solution for physically discontinuous fields at the interface such as density and the normal component of velocity. The second constraint is applied to support parallel mesh updates of highly anisotropic layered elements around the interface. Each constraint is imposed by forming sets of related elements around the interface and enforcing the elements within any related set to be assigned to the same part during mesh partitioning. We note that due to the locality of any constrained element set, the parallel load balance is not altered for practical problems of interest.

Fig. 3
figure 3

A 2D schematic showing a portion of the distributed mesh on three parts, \(P_0\), \(P_1\) and \(P_2\), that consist of discontinuous interpolation and layered elements at the interface (an artificial gap is introduced at the interface and inter-part boundaries for clarity)

Full size image

In the case of a discontinuous interpolation at the interface, the degrees-of-freedom on each side of the interface are different. Any mesh face on the interface is duplicated into two images and each image is used by the corresponding mesh region (i.e., on each side of the interface). Note that lower dimensional mesh entities, i.e., vertices and edges, can have more than two images for cases involving interactions between more than two materials at a physical location. Further note that the geometric compatibility between all images of each mesh entity on the interface is ensured during mesh motion and modification, as discussed in the next section. The diffusive term in the current finite element formulation couples the degrees-of-freedom of the two mesh regions sharing a mesh face on the interface (see [54] for details). Thus, a macro element is formed based on the two mesh regions/elements around the interface, as shown in Fig. 3. Each macro element containing two mesh elements is defined as an element set that is constrained to be on the same part during parallel mesh partitioning. This ensures that the parallel interactions between degrees-of-freedom remain the same to a parallel case with no interface and thus, the two-pass communication strategy mentioned above is applicable in physics computation involving parallel interface tracking.

Element sets are also defined for the highly anisotropic layered elements around the interface to ensure their desired structure, shape and resolution are maintained during mesh motion and modification. In this case, as shown in Fig. 3, an element set is defined based on a layered stack which contains all the elements through the layered height/thickness. Layered stacks on each side of the interface are considered separately. Note that the parallelization details of the model and mesh adaptor are discussed in the next section.

In summary, two types of element sets are defined around the interface. One based on macro elements and the other based on layered stacks. An overlap can occur between different element sets. In such a situation, a superset containing all the relevant element sets is constructed and enforced to be on the same part during mesh partitioning. Note that the maximum possible overlap can be forced or limited to be local in nature such that the parallel load balance is not altered for practical problems of interest. For example, the maximum possible overlap can be forced to the most common situation which includes a macro element and two layered stacks from each side of the interface. This can be attained by a meshing process that ensures any mesh region around the interface only has one mesh face on the interface. It is also important to note that the current (two) types of element sets provide flexibility to target a wide variety of problems. For example, some problems may not require macro elements (e.g., free surface problems) in which case element sets based on macro elements will not be present, or may not require layered elements (e.g., due to lack of anisotropy) in which case element sets based on layered stacks will not be present, while in a parallel setting some problems may not involve macro elements on some part of the interface and may not require layered elements on some part of the interface.

3 Geometry and mesh updates

3.1 Geometry updates

The computational domain is defined using a boundary representation-based geometric model. Such a domain definition includes a set of topological entities, each having shape information associated with them. Interface motion can result in shape and/or topological changes in the geometry. As mentioned above, we currently focus on problems where the geometry undergoes shape changes while the topology remains fixed. There are two classes of shape changes. One class where a rigid body motion is involved. The second class includes arbitrary deformations.

For problems involving a rigid body motion, a parametric representation is employed for the geometry (i.e., based on a CAD system), while in cases involving arbitrary deformations a parametric description is not suitable and therefore, a discrete representation is used (e.g., based on a triangulation).

In the case of a parametric geometry, the update is applied to the relevant objects or region entities in the geometry, e.g., when a projectile slides through the cannon. Parallelization is straightforward in this case and is achieved by storing the entire geometry in each MPI rank/process and updating the shape of the geometry in each process. We note that a parallel partition may be required for a parametric geometric model with millions of geometric entities and will be considered in the future.

For problems involving arbitrary deformations, we currently use the evolving interface mesh to define and update the discrete geometric representation. Parallelization is achieved based on the partitioning of the interface mesh. It is also important to note that the relation of the mesh entities to the geometric model entities is maintained. By doing this it is possible to employ methods that enrich the shape information for the discrete geometry beyond that defined by linear/straight-sided mesh facets. For example, methods like subdivision surfaces can potentially be used to account for the local curvature [50]. Shape enrichment is particularly useful in case of a discrete geometry when applying mesh modification at the interface.

3.2 Mesh updates

The mesh must be updated to remain consistent with the geometric model at every instance. In this study, the mesh is updated by mesh motion, or by mesh modification when indicated by the trigger. Mesh modification is based on local cavity-based operations including non-manifold cases and layered elements [32, 39, 42, 50]. For parallel mesh modification based on local cavity-based operations see [1, 43]. For interface tracking, we employ the same parallel mesh modification procedures including at the interface. This is made possible with the two constraints applied on parallel mesh partition, as discussed in Sect. 2.2. In this paper, we focus our attention on mesh motion.

Mesh motion is divided into four steps each covering a specific set of geometric and mesh entities: moving geometric entities, static geometric entities, layered elements, and tetrahedral elements. These steps are coupled with the mesh modification trigger to maintain mesh quality and validity, where the updated mesh is checked after applying all the four steps and is accepted/used only if it is deemed acceptable by the trigger. Otherwise the mesh state is reverted to the prior state (i.e., before applying mesh motion) and a mesh modification is triggered. Further, parallelization in each step is achieved by moving together all the copies of each mesh entity at the inter-part boundaries, which ensures geometric compatibility at the inter-part boundaries. Each mesh motion step is discussed below.

3.2.1 Moving geometric entities

In the present study, a certain set of geometric entities are attributed to undergo a motion; specifically a set of geometric faces, edges and vertices are allowed to move. The motion for these moving geometric entities is computed as part of the physics computation, e.g., as part of a rigid body motion or of an arbitrarily deforming interface. Motion of each mesh entity residing on these geometric entities is set to be the same as that of the geometric entity. This motion is used as the input to drive the other three steps in mesh motion. We recall that for an interface supporting discontinuous interpolation, all images of each mesh entity on the interface move together ensuring geometric compatibility at the interface.

3.2.2 Static geometric entities

Mesh motion for each mesh entity residing on the static geometric entities, i.e., geometric faces, edges and vertices that are fixed, is computed such that the mesh entity is constrained to remain on the geometric entity. This is achieved in two steps. In the first step, we use the linear mesh elasticity analogy (including Jacobian-based stiffening [47]) to displace mesh entities without any constraints; given the input on mesh motion from the moving geometric entities discussed above. In the second step, updated locations from the first step (which can be off from the curved geometric entities) are projected back onto the geometric entities by employing a local search procedure based on gradient descent. The projected locations are used to move the mesh entities residing on the static geometric entities. Essentially, during mesh motion the mesh on the static geometric entities is constrained to move/slide on the geometry. This feature provides a great deal of flexibility in mesh motion and enables the use of mesh motion alone (without any mesh modification) for long durations. We note that in many problems of interest, absence of this feature may result in mesh modification at every time step. Figure 4 shows a translating and rotating projectile in a cannon. The projectile translates axially from the back/closed end to the open end by a distance approximately equal to its length. It rotates in the counter clockwise sense by 34.5\(^\circ\) as shown by the 4 differently colored quadrants of the projectile. For this demonstration, a uniform tetrahedral mesh is used and the total motion is applied in about 250 steps; remarkably only mesh motion is used. The mesh on the projectile surface moves with it while the mesh on the cannon walls is constrained to slide on it and the interior tetrahedral volume mesh is free to move in all three directions as part of the fourth step discussed below.

Fig. 4
figure 4

Mesh motion for a translating and rotating projectile in a cannon (half of the mesh is shown with a cut through the center plane and translucent cannon walls)

Full size image

3.2.3 Layered elements

Many problems of interest exhibit relatively strong gradients in certain directions as compared with other directions, such as a shear layer near the wall in a viscous flow or high temperature variations in the normal direction at a burning interface. In such cases, highly anisotropic layered elements are desired near the appropriate boundaries/interfaces.

Pre-defined meshes with layered elements near the walls have been utilized in previous studies ([18, 29, 30]). However, a procedure is needed that tightly controls the anisotropic layered elements around evolving geometry entities. The current approach maintains the desired structure, shape and resolution of the anisotropic layered elements during mesh motion. As noted earlier, mesh modification for layered elements is based on earlier works [39, 42, 43]. Mesh motion based on the linear mesh elasticity approach is not robust in maintaining or explicitly controlling the structure, shape and resolution of the anisotropic layered elements. Therefore, we have developed an explicit repositioning method for the layered elements that employs connectivity of the growth curves. Note that mesh motion for the rest of the interior mesh containing tetrahedral elements is discussed below, while transition elements between layered and tetrahedral elements move accordingly from each side. This does not require any additional consideration for a linear/straight-sided mesh.

Fig. 5
figure 5

Schematic of a growth curve

Full size image

We first define a growth curve (see Fig. 5). It is a collection or stack of mesh edges defined along the local normal direction to the boundary/interface. At an interface, growth curves on each side are treated differently. The mesh vertex on the boundary/interface from which a growth curve originates is called the base vertex. The direction of a growth curve is called the growth direction.

Currently, a growth curve is geometrically graded and defined by four parameters: the first layer thickness \(t_l^{(1)}\), growth ratio \(r_l\), total number of layers \(n_l\) and growth direction or local unit normal vector \(\varvec{n}\). The first three parameters (\(t_l^{(1)}\), \(r_l\), \(n_l\)) are either prescribed or computed adaptively [9]. The fourth parameter \(\varvec{n}\) is calculated based on the current shape of the evolving boundary/interface. For a given mesh vertex on the boundary/interface, the local unit normal vector \(\varvec{n}\) is computed by a weighted average of the unit normal vector of mesh faces on the boundary/interface around this mesh vertex. In case of a distributed/partitioned mesh, the two-pass communication strategy (see Sect. 2.2) is used to computed the local unit normal vector along the growth direction.

First, the thickness of the ith layer in a growth curve is computed as:

$$\begin{aligned} t_l^{(i)} = r_l^{i-1} t_l^{(1)} = r_l t_l^{(i-1)} \qquad i=2,3,\ldots ,n_l. \end{aligned}$$
(1)

Subsequently, the position of each vertex on a growth curve is given by:

$$\begin{aligned} \varvec{x}^{(i)} = \varvec{x}^{(i-1)} + t_{l}^{(i)} \varvec{n} = \varvec{x}^{(i-1)} + r_l^{i-1} t_l^{(1)} \varvec{n}, \end{aligned}$$
(2)

where \(\varvec{x}\) is the coordinate of a vertex. The superscript (i) indicates it is the ith vertex on a growth curve, where \(i = 0\) implies the base vertex on the evolving boundary/interface.

This procedure requires the connectivity of a growth curve, where all the mesh vertices on each growth curve are maintained in a list. In case of a distributed/partitioned mesh, a growth curve is allowed to be at the inter-part boundary. However, the entire growth curve (or layered stack) is constrained to be together on any residing part(s) as discussed in Sect. 2.2 (i.e., the list of vertices on a growth curve is complete on any given part). Figure 6 shows a partitioned growth curve for mesh motion of layered elements in a distributed/partitioned mesh. This allows the explicit repositioning for each growth curve to be applied independently on each part assuming that the position of the base vertex and the four growth-curve parameters, including local unit normal vector, are available on each part. The position of the top most vertex in case of a partitioned growth curve is also ensured to be consistent among all residing parts by using the two-pass communication strategy (see Sect. 2.2).

Fig. 6
figure 6

A partitioned growth curve

Full size image

3.2.4 Tetrahedral elements

After applying the three mesh motion steps described above, all that is remaining is the mesh motion for the interior mesh containing tetrahedral elements. It is performed using the linear mesh elasticity approach including Jacobian-based stiffening [47]. The input to this fourth step is provided by the mesh motion or displacement computed in the above three steps.

3.3 Summary of geometry and mesh updates

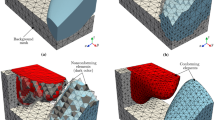
We summarize this section with a demonstration of the entire geometry and mesh update process. A 9-grain case is used where the grains translate and shrink in a closed chamber. We note that the interface motion is prescribed in this demonstration. In Fig. 7, three meshes, including anisotropic layered elements at the interface, are shown at two instances of time (\(t=t_0\) and \(t_1\)). Each mesh consists of about 1 million elements. Mesh motion is applied on the initial mesh at time \(t=t_0\) to obtain a mesh at time \(t=t_1\), see Fig. 7b. In the mesh after motion, two aspects are important to note: (1) the structure, shape and resolution of the layered mesh is maintained, and (2) the elements become too distorted in between the grains (see the zoomed view on the right column in Fig. 7b). We note that the mesh motion is exaggerated in this case to clearly show the distorted elements. Further, a mesh modification is applied at time \(t=t_1\) to obtain a mesh with the desired quality, see Fig. 7c.

Fig. 7
figure 7

Mesh updates based on a combination of mesh motion and modification (including layered elements) for a 9-grain case; a cut through the mesh is shown along with a zoomed view on the right column

Full size image

4 Numerical results and discussion

Two problems that demonstrate the utility of the current interface tracking approach are considered. The first one involves 6 droplets undergoing phase change with arbitrary deformation. The second one includes a rigid projectile moving/translating down the barrel.

4.1 Droplets with phase change

Fig. 8
figure 8

Center plane of the 6-droplet case at the beginning

Full size image

In this section, we present a problem involving 6 droplets undergoing phase change from denser liquid to lighter gas inside a chamber. In this problem, predicting the exponential rise of pressure and temperature in the chamber is typically of interest and thus, fully 3D transient simulations of phase change process is performed (see [54] for more details). Figure 8 shows the center plane of the problem with 6 droplets in an adiabatic cylindrical chamber with no-slip walls. At the beginning, each droplet is a 2 mm long circular cylinder with hemispherical end caps of 0.5 mm radius. The phase change rate is governed by the Vieille’s law:

$$\begin{aligned} u_p = a (p^+)^n, \end{aligned}$$
(3)

where \(p^+\) is the pressure of the surrounding gas, while the exponent is set to be \(n=0.7\) and the pre-factor to be \(a=7.9\text {e}-5\) \(\text {m}/(\text {s}\text {Pa}^n)\). The initial pressure of the closed chamber is set to be 1 atm. As the droplets undergo phase change from denser phase to lighter phase, the pressure increases and speeds up the phase change rate in return. Discontinuous interpolations are utilized at the interface to model the phase change. Further, layered elements are used on both sides of the interface.

Fig. 9
figure 9

Mesh cut (top row), and solution fields (bottom row), around one of the 6 droplets at three instances of time, \(t=t_0\), \(t_1\) and \(t_2\), where time \(t=t_0\) is near the beginning while at times \(t=t_1\) and \(t_2\) mesh modification is triggered

Full size image

Figure 9 shows meshes and solution fields around one of the droplets at three instances of time (\(t=t_0\), \(t_1\) and \(t_2\)). A cut through the mesh is shown, where the change in droplet size/volume is clear between the first and last instances. Solution fields of velocity magnitude and temperature are shown, where at each instance the former is shown in the left half of the droplet and the latter in the right half. Time \(t=t_0\) is near the beginning while \(t=t_1\) and \(t_2\) are instances when mesh modification is triggered. Thus, there are two mesh and solution states at times \(t=t_1\) and \(t_2\); one after mesh motion (only) and the other after mesh modification. In this case, the mesh size field is prescribed to be finer near the interface and is based on the current state of the geometry (i.e., it evolves in time with the geometry). Note that the structure, shape and resolution of the anisotropic layered elements are maintained during mesh motion and modification. The overall mesh quality is maintained to be above the threshold value of 0.3 based on the trigger for mesh modification discussed in Sect. 2.1. Further, the solution fields are well resolved, especially at the interface including discontinuity in the normal component of the velocity and steep normal gradient of the velocity and temperature fields.

4.2 Projectile with rigid motion

A finned projectile inside a pressurized cannon is considered next. In this case, the projectile velocity and flow field at the exit of the cannon are of interest (e.g., to design a muzzle brake). Figure 10 shows the problem setup for this case, where high pressure and temperature is set at the left/closed end of the cannon. The high pressure pushes the projectile towards the open end. The projectile is considered to be a rigid object which is 711 mm long and has 8 fins. It translates axially along the tube. The inner length of the cannon is 2000 mm, while its inner diameter and thickness are 120 mm and 10 mm, respectively. The outer boundary (not shown) is set as outflow and placed at a sufficiently long distance away from the cannon. On all the walls, no-slip and zero heat flux conditions are set, where no-slip condition due to the projectile is given precedence at the contact between projectile and inner side of the cannon. Since we are primarily interested in the projectile motion and gaseous flow, material inside the projectile and cannon walls are not included in the current simulation.

Fig. 10
figure 10

Setup of the projectile case

Full size image

A stabilized finite element method for pressure-primitive variables is used along with a discontinuity capturing operator (see [54] for more details). The projectile starts at 20 mm from the left inner side of the cannon and moves about a distance of 1270 mm in a duration of 6 ms such that it reaches near the exit of the cannon. Two mesh size fields are used in this case. One that is prescribed to be finer near the projectile and is based on the current state of the geometry (i.e., it evolves in time with the geometry). The other is computed adaptively using a VMS-based error estimator.

We first focus our attention on the geometry-based prescribed mesh size field. Evolution of the geometry and mesh is shown in Fig. 11 at six different instances of time as the projectile moves from the closed end to the open end of the cannon. A cut through the mesh is shown. A zoomed view near the projectile nose is shown for all six instances at the top while a zoomed view near a fin is shown at the bottom. The mesh refinement around the projectile is maintained as dictated by the geometry-based prescribed mesh size field. Similarly, a finer mesh is maintained near the tip of the fins. Figure 12 shows the parallel mesh partition at the same instances. Here different colors indicate different parts. Throughout the simulation, the partitioned mesh consists of about 13.5 million elements in total on 256 parts.

Figure 13 shows the minimum mesh quality over time. It is clear that the threshold value is satisfied throughout the simulation. Note that the rate of mesh modification becomes relatively higher towards the end of the simulation, which is expected as the projectile reaches the exit of the cannon and a topological change in the geometry is imminent.

Fig. 11
figure 11

Mesh at six different instances of time (cut view)

Full size image
Fig. 12
figure 12

Parallel mesh partition at six different instances of time (cut view)

Full size image
Fig. 13
figure 13

Minimum mesh quality over time (the dashed line indicates the threshold value that is used to trigger mesh modification and solid dots are used to indicate the instances when mesh modification is applied)

Full size image

Figure 14 shows the normalized projectile velocity over time. The maximum projectile velocity is roughly 330 m/s, which is reached near the exit of the cannon.

Fig. 14
figure 14

Normalized projectile velocity with time

Full size image

Figures 15 and 16 show the Mach number and numerical Schlieren at four different instances of time. The precursor wave in front of projectile is clearly formed at time \(t=2.5\) ms and it propagates out of the cannon by time \(t=3.5\) ms. In the later two instances of \(t=4.5\) ms and 5.5 ms, the barrel shock is clearly formed and at the last instance a complex shock structure is observed near the exit of the cannon. These features are common for a case with a fast moving projectile in a cannon.

Fig. 15
figure 15

Mach number at four different instances of time (cut view), for clarity only ambient air region is shown

Full size image
Fig. 16
figure 16

Numerical Schlieren at four different instances of time (cut view), for clarity only ambient air region is shown

Full size image

Next we focus our attention on the simulation employing the error-based mesh size field. In the initial instances, the error-based adapted mesh is similar to the mesh based on the prescribed mesh size field, where some additional refinements are observed near the exit of the cannon as the precursor wave propagates out of the cannon (e.g., at time \(t=3.5\) ms). However, with the formation of the barrel shock by time \(t=4.5\) ms and a complex shock structure by time \(t=5.5\) ms, the error-based adapted mesh focuses the resolution in the shock regions. The total number of elements reaches a maximum of about 8.5 million in the error-based adapted mesh, while the total number of elements is about 13.5 million elements for the mesh based on the prescribed mesh size field. Figures 17 and 18 show a cut view of the mesh zoomed near the exit of the cannon at two instances of \(t=4.5\) ms and 5.5 ms. Meshes based on both types of the mesh size field are presented to clearly show the utility of the error-based mesh adaptation. Figures 19 and 20 show a zoomed view of the Mach number near the exit of the cannon at the same two instances. As expected, the complex shock structure is resolved crisply on the error-based adapted mesh and thus, leads to a higher accuracy.

Fig. 17
figure 17

Comparison of mesh near the exit (cut view) with prescribed (upper) and error-based (lower) mesh size fields at time \(t=4.5\) ms

Full size image
Fig. 18
figure 18

Comparison of mesh near the exit (cut view) with prescribed (upper) and error-based (lower) mesh size fields at time \(t=5.5\) ms

Full size image
Fig. 19
figure 19

Comparison of Mach number near the exit (cut view) with prescribed (upper) and error-based (lower) mesh size fields at time \(t=4.5\) ms

Full size image
Fig. 20
figure 20

Comparison of Mach number near the exit (cut view) with prescribed (upper) and error-based (lower) mesh size fields at time \(t=5.5\) ms

Full size image

5 Closing remarks

We presented a parallel interface tracking approach for evolving geometry problems. In our approach, the computational domain is defined using a boundary representation-based geometric model that is updated as dictated by the analysis. An interface-fitted conforming hybrid/mixed mesh with anisotropic layered elements is used. The mesh is updated to be consistent with the updated geometry at every instance. Mesh is updated using a combination of mesh motion and mesh modification. Mesh modification is triggered automatically only when necessary. Further, during mesh motion and modification the desired structure, shape and resolution of the anisotropic layered elements at interface are maintained. All steps are performed on partitioned meshes on distributed-memory parallel computers.

We demonstrated our approach on two problems with large motion or deformation in the geometry. The first problem involved 6 droplets undergoing phase change with arbitrary deformation. The second problem included a rigid projectile moving/translating down the cannon, where an error-based adapted mesh was shown to provide a highly accurate solution. In the future, we plan to consider topological changes in the geometry as well as hybrid parallel programming including data parallelism.