On the vibration of nanobeams with consistent two-phase nonlocal strain gradient theory: exact solution and integral nonlocal finite-element model

Abstract

Recently, it has been proved that the common nonlocal strain gradient theory has inconsistence behaviors. The order of the differential nonlocal strain gradient governing equations is less than the number of all mandatory boundary conditions, and therefore, there is no solution for these differential equations. Given these, for the first time, transverse vibrations of nanobeams are analyzed within the framework of the two-phase local/nonlocal strain gradient (LNSG) theory, and to this aim, the exact solution as well as finite-element model are presented. To achieve the exact solution, the governing differential equations of LNSG nanobeams are derived by transformation of the basic integral form of the LNSG to its equal differential form. Furthermore, on the basis of the integral LNSG, a shear-locking-free finite-element (FE) model of the LNSG Timoshenko beams is constructed by introducing a new efficient higher order beam element with simple shape functions which can consider the influence of strains gradient as well as maintain the shear-locking-free property. Agreement between the exact results obtained from the differential LNSG and those of the FE model, integral LNSG, reveals that the LNSG is consistent and can be utilized instead of the common nonlocal strain gradient elasticity theory.

1 Introduction

Due to paradoxical behaviors [1,2,3,4] of the common differential nonlocal elasticity [5,6,7,8] which has been widely utilized by researchers to consider the size effects for studying the mechanics of nano structures [9,10,11,12,13,14,15], other size-dependent elasticity theories such as stress-driven integral nonlocal [16, 17] and two-phase local/nonlocal have been recently attracted the attentions of the nano-mechanic researchers.

Although, some valuable efforts [18, 19] have been made to resolve the weakness of the differential nonlocal, it has been indicated [20, 21] that using the differential form of nonlocal elasticity instead of its integral form is allowable only in a few certain cases in which satisfying additional constitutive boundary conditions (CBCs), resulted from this transformation, is possible.

It should be noted that the integral form of nonlocal elasticity has been seldom used in the past years [22,23,24], while after presentation of Ref.[20], a significant growth occurs in applying the integral form of nonlocal theory. Due to this fact, the basic integral form of pure nonlocal elasticity has been directly employed to probe into the static bending [25], vibration characteristics, and buckling [26] of Euler–Bernoulli nanobeams without any paradoxes. In these two works, the Laplace transform method has been applied to present an analytical solution which has led to some comments [27] and replies [28] about the correctness of the proposed exact solution. In addition, the integral nonlocal finite-element method (FEM) has been employed to examine the nonlocal characteristics of Euler–Bernoulli nanobeams [29,30,31]. Also, the vibration frequency shifts resulted from the attached mass on a cantilever carbon-nanotube sensor [32] have been predicted by the integral nonlocal FEM. To analyze the nonlocal static bending of Timoshenko nanobeams [33], an integral nonlocal FEM model has been constructed using a higher order beam element with eight nodes to avoid the shear-locking effect. Along these works, it can be pointed to the papers in which the isogeometric analysis [34,35,36] as well as FEM [37, 38] have been developed within the framework of the integral nonlocal and strain gradient elasticity theories.

Applying two-phase local/nonlocal elasticity, for considering the nonlocal effects in nanostructures, has been recently proposed by researchers due to its advantages over the common differential nonlocal. Being paradox free, compatibility between the results extracted from the differential form with those obtained by the integral form, and compatibility between the order of the differential governing equations and the number of boundary conditions are some of these advantages. However, it is noted that employing two-phase elasticity instead of the differential nonlocal increases the complexity of the problems, so that finding efficient solutions is now an important challenge.

On the basis of the two-phase elasticity, nonlocal bending analysis of nanobeams has been performed and associated exact solutions have been presented for the Euler–Bernoulli [39] and Timoshenko nanobeams [40]. Also, different mechanical characteristics of nanostructures such as axial, torsional, and transverse vibrations of nanorods [41], nanobeams [42, 43], and double nanobeams system [44] have been evaluated by developing the exact solutions [41,42,43] as well as numerical methods such as FEM [43] and generalize differential quadrature method (GDQM) [44]. To utilize the advantages of two-phase elasticity, size dependence of elastic medium and axial loads, resulted from the thermal expansion and nonlinear van-Karman strain, has been considered by two-phase elasticity and their influences on the linear [45] and nonlinear [46] vibrations of nanobeams have been investigated. In addition, by combination of surface and two-phase elasticity theories, the damping vibrations of local/nonlocal nanobeams [47] have been studied. Assessment of the complex natural frequencies obtained by exact solution indicated that using the local/nonlocal theory eliminates the paradoxes in both of the real and imaginary parts of vibration frequencies. Also, size-dependent coupled flexural–axial vibrations of cantilevered mass nanosensors [48] have been investigated by two-phase elasticity to prevent the paradoxical behavior due to applying differential nonlocal on clamped-free beams.

In addition to the common differential nonlocal, the nonlocal strain gradient elasticity, introduced by Lim et al. [49], has been widely utilized [50,51,52] by researchers to explore on the size-dependent mechanics of various nanostructures. For instance, wave propagation [49, 53,54,55], longitudinal vibration [56], bending, buckling, and transverse vibrations [57, 58] of nanobeams and nanoplates have been comprehensively studied in the recent years by using this theory.

Here, it is essential to express that the nonlocal strain gradient is resulted from the combination of integral nonlocal theory with the strain gradient one and its differential form has been considered in most works without paying attention to this fact that the transformation of integral nonlocal strain gradient to a differential form is allowable if the CBCs related to this conversion can be satisfied. This common negligence leads to significant differences [59] between the results of the differential nonlocal strain gradient and those that have been extracted by the integral nonlocal strain gradient. Despite the suggestion [60] of satisfying the CBCs, resulted from conversion of the integral nonlocal strain gradient to the differential form, instead of the higher order boundary conditions related to the strain gradient theory, inconsistency of this theory has been proved [61, 62] and it has been shown that achieving to correct results from the differential nonlocal strain gradient is impossible, and therefore, using the common differential form of nonlocal strain gradient theory is not correct. To present more explanations about this issue, it should be said that the order of the differential governing equations derived by the nonlocal strain gradient is less than the number of all boundary conditions and these differential equations have no solution at all. To resolve these issues, the two-phase local/nonlocal strain gradient (LNSG) theory has been utilized to extract the closed-form solutions for the static deflections of nanorods subjected to a tensional force [63] and, for studying the size-dependent longitudinal vibrations of nano-scaled rods [64].

According to these facts, in this work, free transverse vibrations of nanobeams are analyzed on the basis of the LNSG, for the first time. By transformation of the integral form of LNSG to the equal differential form, the differential equations associated with the LNSG Euler–Bernoulli and Timoshenko nanobeams as well as all mandatory CBCs are derived, and then, the exact solutions are presented by satisfying all BCs. In addition, by introducing a new higher order shear-locking-free beam element and using the basic integral form of LNSG, the FE model of LNSG Timoshenko nanobeams is constructed with the aim of preventing shear-locking effect without increasing the complexity of the integral nonlocal strain gradient FE model. It is shown that employing the LNSG makes it possible to obtain solvable differential equations with the order equal to the number of all mandatory BCs. Also, compatibly between the exact results obtained by solving the differential LNSG with those of the integral LNSG FE model reconfirms the consistency of the LNSG theory.

2 Problem formulation

To apply the LNSG elasticity for recognizing the size-dependent vibration characteristics of nanobeams, the differential governing equations, all constitutive boundary conditions, and exact solutions will be derived using the equal differential form of LNSG. To provide a comprehensive study, the formulations associated with the Euler–Bernoulli beam theory (EBT) as well as Timoshenko beam theory (TBT) are presented in the following.

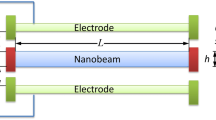
Furthermore, the finite-element model of LNSG Timoshenko beam is constructed using a new efficient higher order locking-free beam element and direct use of the integral form of LNSG. To this aim, a beam is assumed with the length of L and cross section with the height of h and width of b which they are respectively located along the x-, z-, and y-directions of the Cartesian coordinates, see Fig. 1.

Fig. 1

Schematic of problem

2.1 Two-phase local/nonlocal strain gradient

First, the corresponding local/nonlocal stress relations of LNSG nanobeams are presented as follow using the local stresses, $\sigma_{{{\text{kl}}}}^{{{\text{local}}}}$, due to local strains, and the higher order ones, $\sigma_{{{\text{kl}}}}^{{1\;\,{\text{local}}}}$, resulted from the strain gradient [63, 64]:

$$\begin{gathered} \sigma _{{{\text{kl}}}} \left( x \right) = \zeta _{1} \sigma _{{{\text{kl}}}}^{{{\text{local}}}} \left( x \right) + \zeta _{2} \int\limits_{L} {\alpha \left( {\left| {x - x^{\prime}} \right|,k} \right)\sigma _{{{\text{kl}}}}^{{{\text{local}}}} \left( {x^{\prime}} \right)dx^{\prime}} \hfill \\ \sigma _{{{\text{kl}}}}^{1} \left( x \right) = \zeta _{1} \sigma _{{{\text{kl}}}}^{{1\;\,{\text{local}}}} \left( x \right) + \zeta _{2} \int\limits_{L} {\alpha \left( {\left| {x - x^{\prime}} \right|,k} \right)\sigma _{{{\text{kl}}}}^{{1\;\,{\text{local}}}} \left( {x^{\prime}} \right)dx^{\prime}} \hfill \\ \zeta _{1} > 0,\,\zeta _{2} > 0\,,\,\,\zeta _{1} + \,\zeta _{2} = 1\,\,{\text{and}}\,\alpha \left( {\left| {x - x^{\prime}} \right|,k} \right) = \frac{1}{{2k}}e^{{ - \frac{{\left| {x - \bar{x}} \right|}}{k}}} , \hfill \\ \end{gathered}$$

(1)

where $\zeta_{1}$, $\zeta_{2}$, and k, indicate the local phase fraction factor, nonlocal phase fraction factor, and nonlocal parameter, respectively. In addition, $\alpha \left( {\left| {x - x^{\prime}} \right|,k} \right)$ is nonlocal kernel function. Also, it has been shown [42, 65] that the following integral equation, i.e., Eq. (2), can be replaced with an equal differential equation, i.e., Eq. (3), by satisfying essential CBCs, i.e., Eq. (4):

$$\Re \left( x \right) = \Im \left( x \right) + C\int_{0}^{L} {e^{{\vartheta \left| {x - \overline{x}} \right|}} } \Im \left( {\overline{x}} \right)d\overline{x}.$$

(2)

$$\Re^{\prime\prime}\left( x \right) - \upvartheta ^{2} \Re \left( x \right) = \Im^{\prime\prime}\left( x \right) + \vartheta \left( {2C - \vartheta } \right)\Im \left( x \right).$$

(3)

$$\begin{gathered} \Re^{\prime}\left( x \right) + \vartheta \,\Re \left( x \right) = \Im^{\prime}\left( x \right) + \vartheta \Im \left( x \right)\,\,\,{\text{at}}\,x = 0 \hfill \\ \Re^{\prime}\left( x \right) - \vartheta \,\Re \left( x \right) = \Im^{\prime}\left( x \right) - \vartheta \Im \left( x \right)\,\,\,{\text{at}}\,x = L. \hfill \\ \end{gathered}$$

(4)

2.2 Governing equations of EBT

To extract the equations governed on the EBT within the framework of the LNSG, the displacement field is considered as follows:

$$u_{1}^{E} = - z\frac{{\partial w^{E} \left( {x,t} \right)}}{\partial x},\,\,u_{2}^{E} = w^{E} \left( {x,t} \right),\,\,u_{3}^{E} = 0,$$

(5)

where $u_{1}^{E} ,\,u_{2}^{E} ,\,\,{\text{and}}\,\,u_{3}^{E}$ are the deflections in the x-, y-, and z-directions, respectively. Also, the superscript “E” refers to the EBT and $w^{E} \left( {x,t} \right)$ is the transverse displacement of the neutral axis. Next, the axial strain related to the EBT is presented:

$$\varepsilon_{xx}^{E} = - z\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }}.$$

(6)

According to Eq. (1), the LNSG stress–strain relations can be obtained for EBT:

$$\begin{gathered} \sigma_{xx}^{E} = \zeta_{1} E\varepsilon_{xx}^{E} + \frac{{\left( {1 - \zeta_{1} } \right)}}{2k}E\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \varepsilon_{xx}^{E} (\overline{x})d\overline{x} \hfill \\ \sigma_{xx}^{E1} = l_{m}^{2} \zeta_{1} E\varepsilon_{xx,x}^{E} + \frac{{l_{m}^{2} \left( {1 - \zeta_{1} } \right)}}{2k}E\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \varepsilon_{xx,x}^{E} (\overline{x})d\overline{x}, \hfill \\ \end{gathered}$$

(7)

where l_m and E indicate the length scale of the strain gradient and Young modulus, respectively. By employing the integration by parts method, the variation of the strain potential is written as:

$$\begin{gathered}\updelta U^{E} = \int\limits_{V} {\left[ {\sigma_{xx}^{E}\updelta \varepsilon_{xx}^{E} + \sigma_{xx}^{E1}\updelta \varepsilon_{xx,x}^{E} } \right]} dAdx \hfill \\\updelta U^{E} = \int\limits_{V} {\left( {\sigma_{xx}^{E} - \frac{d}{dx}\sigma_{xx}^{E1} } \right)\updelta \varepsilon_{xx}^{E} } dAdx + \left[ {\int\limits_{A} {\sigma_{xx}^{E1}\updelta \varepsilon_{xx}^{E} } dA} \right]_{0}^{L} \hfill \\ t_{xx}^{E} = \sigma_{xx}^{E} - \frac{d}{dx}\sigma_{xx}^{E1} ;\,\,\,\left. {\sigma_{xx}^{E1}\updelta \varepsilon_{xx}^{E} } \right|_{0}^{L} = 0. \hfill \\ \end{gathered}$$

(8)

According to Eq. (8), it can be expressed that the stress of LNSG is resulted from the $\sigma_{xx}^{E}$ and the first derivative of the $\sigma_{{_{xx} }}^{E1}$ by satisfying the strain gradient boundary conditions, i.e., $\left. {\sigma_{xx}^{E1}\updelta \varepsilon_{xx}^{E} } \right|_{0}^{L} = 0$. Given this, the LNSG bending moment of EBT is obtained as Eq. (9) in which A and I stand for the area and the moment of inertia of cross section, respectively:

$$\begin{gathered} M^{E} = - \zeta_{1} EI\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }} - \frac{{\zeta_{2} }}{2k}EI\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{{\partial^{2} w^{E} }}{{\partial \overline{x}^{2} }}d\overline{x} \hfill \\ + \zeta_{1} EIl_{m}^{2} \frac{{\partial^{4} w^{E} }}{{\partial x^{4} }} + \frac{{\zeta_{2} }}{2k}EIl_{m}^{2} \frac{d}{dx}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{{\partial^{3} w^{E} }}{{\partial \overline{x}^{3} }}d\overline{x}} \right]. \hfill \\ \end{gathered}$$

(9)

To transform this complex differential-integral equation, i.e., Eq. (9), into an equal differential form, it is essential to rewrite this equation with the help of the procedure presented in [63]. Therefore, the following relation is considered:

$$\begin{gathered} \frac{d}{dx}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{{\partial^{3} w^{E} }}{{\partial \overline{x}^{3} }}d\overline{x}} \right] = - \frac{2}{k}\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }} + \frac{1}{{k^{2} }}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{{\partial^{2} w^{E} }}{{\partial \overline{x}^{2} }}d\overline{x}} \right] + \hfill \\ + \frac{1}{k}\left( {\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }}\left( 0 \right)e^{{ - \frac{x}{k}}} + \frac{{\partial^{2} w^{E} }}{{\partial x^{2} }}\left( L \right)e^{{\frac{x - L}{k}}} } \right). \hfill \\ \end{gathered}$$

(10)

And, to summarize the following equations, Eq. (11) is presented:

$$\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }}\left( 0 \right) = St_{1}^{E} ,\,\,\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }}\left( L \right) = St_{2}^{E} .$$

(11)

Now, by applying Eqs (10) and (11), Eq. (9) can be rewritten as Eq. (12):

$$\begin{gathered} M^{E} = - EI\left( {\zeta_{1} + \frac{{\left( {1 - \zeta_{1} } \right)l_{m}^{2} }}{{k^{2} }}} \right)\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }} - \hfill \\ \frac{EI}{{2k}}\left( {1 - \frac{{l_{m}^{2} }}{{k^{2} }}} \right)\left( {1 - \zeta_{1} } \right)\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{{\partial^{2} w^{E} }}{{\partial \overline{x}^{2} }}d\overline{x} + \zeta_{1} EIl_{m}^{2} \frac{{\partial^{4} w^{E} }}{{\partial x^{4} }} \hfill \\ + \frac{{\left( {1 - \zeta_{1} } \right)}}{{2k^{2} }}EI\,l_{m}^{2} \left( {St_{1}^{E} e^{{ - \frac{x}{k}}} + St_{2}^{E} e^{{\frac{x - L}{k}}} } \right). \hfill \\ \end{gathered}$$

(12)

Here, the following relations are represented:

$$\begin{gathered} \mu_{1}^{E} = EI\left( {\zeta_{1} + \frac{{\left( {1 - \zeta_{1} } \right)l_{m}^{2} }}{{k^{2} }}} \right),\,\mu_{2}^{E} = \frac{EI}{{2k}}\left( {1 - \frac{{l_{m}^{2} }}{{k^{2} }}} \right)\left( {1 - \zeta_{1} } \right) \hfill \\ \mu_{3}^{E} = - \zeta_{1} EIl_{m}^{2} ,\,\mu_{4}^{E} = - \frac{EI}{2}\frac{{l_{m}^{2} }}{{k^{2} }}(1 - \zeta_{1} ),\,\,\,\mu_{5}^{E} = St_{1}^{E} e^{{ - \frac{x}{k}}} + St_{2}^{E} e^{{\frac{x - L}{k}}} . \hfill \\ \end{gathered}$$

(13)

Now, Eq. (12) can be rewritten by utilizing Eq. (13):

$$\frac{{M^{E} }}{{\mu_{1}^{E} }} + \frac{{\mu_{3}^{E} }}{{\mu_{1}^{E} }}\frac{{\partial^{4} w^{E} }}{{\partial x^{4} }} - \frac{{\mu_{4}^{E} }}{{\mu_{1}^{E} }}\mu_{5}^{E} = - \frac{{\partial^{2} w^{E} }}{{\partial x^{2} }} - \frac{{\mu_{2}^{E} }}{{\mu_{1}^{E} }}\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{{\partial^{2} w^{E} }}{{\partial \overline{x}^{2} }}d\overline{x}.$$

(14)

It can be seen that Eq. (14) is obtained in the form of Eq. (2), and therefore, the equal differential form of this integral–differential equation can be generated using Eq. (3):

$$\frac{1}{{\mu_{1}^{E} }}\frac{{\partial^{2} M^{E} }}{{\partial x^{2} }} + \frac{{\mu_{3}^{E} }}{{\mu_{1}^{E} }}\frac{{\partial^{6} w^{E} }}{{\partial x^{6} }} - \frac{1}{{k^{2} }}\left[ {\frac{{M^{E} }}{{\mu_{1}^{E} }} + \frac{{\mu_{3}^{E} }}{{\mu_{1}^{E} }}\frac{{\partial^{4} w^{E} }}{{\partial x^{4} }}} \right] = - \frac{{\partial^{4} w^{E} }}{{\partial x^{4} }} + \frac{1}{k}\left( {\frac{{2\mu_{2}^{E} }}{{\mu_{1}^{E} }} + \frac{1}{k}} \right)\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }}.$$

(15)

In addition, as previously mentioned, it is essential to satisfy the CBCs associated with the LNSG bending moment of EBT if Eq. (14) is replaced with Eq. (15). Therefore, according to the Eqs.(4) and (5), two CBCs can be extracted from Eq. (14):

$$\begin{gathered} \frac{1}{{\mu_{1}^{E} }}\frac{{\partial M^{E} }}{\partial x} + \frac{{\mu_{3}^{E} }}{{\mu_{1}^{E} }}\frac{{\partial^{5} w^{E} }}{{\partial x^{5} }} - \frac{{\mu_{4}^{E} }}{{\mu_{1}^{E} }}\frac{{\partial \mu_{5}^{E} }}{\partial x} - \frac{1}{k}\left[ {\frac{{M^{E} }}{{\mu_{1}^{E} }} + \frac{{\mu_{3}^{E} }}{{\mu_{1}^{E} }}\frac{{\partial^{4} w^{E} }}{{\partial x^{4} }} - \frac{{\mu_{4}^{E} }}{{\mu_{1}^{E} }}\mu_{5}^{E} } \right] = - \frac{{\partial^{3} w^{E} }}{{\partial x^{3} }} + \frac{1}{k}\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }}\,\,at\,x = 0 \hfill \\ \frac{1}{{\mu_{1}^{E} }}\frac{{\partial M^{E} }}{\partial x} + \frac{{\mu_{3}^{E} }}{{\mu_{1}^{E} }}\frac{{\partial^{5} w^{E} }}{{\partial x^{5} }} - \frac{{\mu_{4}^{E} }}{{\mu_{1}^{E} }}\frac{{\partial \mu_{5}^{E} }}{\partial x} + \frac{1}{k}\left[ {\frac{{M^{E} }}{{\mu_{1}^{E} }} + \frac{{\mu_{3}^{E} }}{{\mu_{1}^{E} }}\frac{{\partial^{4} w^{E} }}{{\partial x^{4} }} - \frac{{\mu_{4}^{E} }}{{\mu_{1}^{E} }}\mu_{5}^{E} } \right] = - \frac{{\partial^{3} w^{E} }}{{\partial x^{3} }} - \frac{1}{k}\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }}\,\,at\,x = L. \hfill \\ \end{gathered}$$

(16)

In this step, the equilibrium equations of EBT are represented:

$$\begin{gathered} \frac{{\partial^{2} M^{E} }}{{\partial x^{2} }} - m_{1} \frac{{\partial^{2} w^{E} }}{{\partial t^{2} }} = 0 \hfill \\ Q^{E} = \frac{{\partial M^{E} }}{\partial x} \hfill \\ m_{1} = \rho A, \hfill \\ \end{gathered}$$

(17)

where $\rho$ is the mass density. Next, the first part of Eq. (17) is substituted into Eq. (15) and the LNSG bending moment of EBT is obtained. Also, the shear force of EBT, which should be utilized for satisfying the boundary conditions related to the beams with free ends, is written using the second part of Eq. (17):

$$\begin{gathered} M^{E} = k^{2} \mu_{3}^{E} \frac{{\partial^{6} w^{E} }}{{\partial x^{6} }} - \left( {\mu_{3}^{E} - k^{2} \mu_{1}^{E} } \right)\frac{{\partial^{4} w^{E} }}{{\partial x^{4} }} \hfill \\ - \left( {2\mu_{2}^{E} k + \mu_{1}^{E} } \right)\frac{{\partial^{2} w^{E} }}{{\partial x^{2} }} + k^{2} m_{1} \frac{{\partial^{2} w^{E} }}{{\partial t^{2} }} \hfill \\ \hfill \\ Q^{E} = k^{2} \mu_{3}^{E} \frac{{\partial^{7} w^{E} }}{{\partial x^{7} }} - \left( {\mu_{3}^{E} - k^{2} \mu_{1}^{E} } \right)\frac{{\partial^{5} w^{E} }}{{\partial x^{5} }} \hfill \\ - \left( {2\mu_{2}^{E} k + \mu_{1}^{E} } \right)\frac{{\partial^{3} w^{E} }}{{\partial x^{3} }} + k^{2} m_{1} \frac{{\partial^{3} w^{E} }}{{\partial x\partial t^{2} }}. \hfill \\ \end{gathered}$$

(18)

Now that the differential form of the LNSG bending moment is available, it is possible to obtain the differential governing equation of EBT by substituting the first part of Eq. (18) into the first part of Eq. (17):

$$\begin{gathered} k^{2} \mu_{3}^{E} \frac{{\partial^{8} w^{E} }}{{\partial x^{8} }} - \left( {\mu_{3}^{E} - k^{2} \mu_{1}^{E} } \right)\frac{{\partial^{6} w^{E} }}{{\partial x^{6} }} \hfill \\ - \left( {2\mu_{2}^{E} k + \mu_{1}^{E} } \right)\frac{{\partial^{4} w^{E} }}{{\partial x^{4} }} + k^{2} m_{1} \frac{{\partial^{4} w^{E} }}{{\partial x^{2} \partial t^{2} }} - m_{1} \frac{{\partial^{2} w^{E} }}{{\partial t^{2} }} = 0. \hfill \\ \end{gathered}$$

(19)

Also, the CBCs presented in Eq. (16) should be obtained in term of w^E by substituting the differential form of M^E, Eq. (18), into Eq. (16).

2.3 Governing equations of TBT

To derive the TBT governing equations using the LNSG elasticity theory, the displacements of Timoshenko beams are written in terms of the transverse, w^T(x,t), and rotational deflections, $\phi \left( {x,t} \right)$, of the neutral axis:

$$u_{1}^{T} = z\phi \left( {x,t} \right),\,\,u_{2}^{T} = w^{T} \left( {x,t} \right),\,\,u_{3}^{T} = 0.$$

(20)

Also, the nonzero strains are achieved using Eq. (20):

$$\varepsilon_{xx}^{T} = z\frac{\partial \phi }{{\partial x}},\,\gamma_{xz} = \frac{{\partial w^{T} }}{\partial x} + \phi .$$

(21)

By utilizing Eq. (1) as well as Eq. (21), the stress–strain relations corresponding to the TBT can be obtained as follows:

$$\begin{gathered} \sigma_{xx}^{T} = \zeta_{1} E\varepsilon_{xx}^{T} + \frac{{\left( {1 - \zeta_{1} } \right)}}{2k}E\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \varepsilon_{xx}^{T} (\overline{x})d\overline{x} \hfill \\ \sigma_{xx}^{T1} = l_{m}^{2} \zeta_{1} E\varepsilon_{xx,x}^{T} + \frac{{l_{m}^{2} \left( {1 - \zeta_{1} } \right)}}{2k}E\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \varepsilon_{xx,x}^{T} (\overline{x})d\overline{x} \hfill \\ \sigma_{xz} = \zeta_{1} G\gamma_{xz} + \frac{{\left( {1 - \zeta_{1} } \right)}}{2k}G\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \gamma_{xz} (\overline{x})d\overline{x} \hfill \\ \sigma_{xz}^{1} = l_{m}^{2} \zeta_{1} G\gamma_{xz,x} + \frac{{l_{m}^{2} \left( {1 - \zeta_{1} } \right)}}{2k}G\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \gamma_{xz,x} (\overline{x})d\overline{x}. \hfill \\ \end{gathered}$$

(22)

Here, G shows the shear modulus. In this step, variations of the strain potential are written using the integration by parts method:

$$\begin{gathered}\updelta U^{T} = \int\limits_{V} {\left[ {\sigma_{xx}^{T}\updelta \varepsilon_{xx}^{T} + \sigma_{xx}^{T1}\updelta \varepsilon_{xx,x}^{T} + \sigma_{xz}\updelta \gamma_{xz} + \sigma_{xz}^{1}\updelta \gamma_{xz,x} } \right]} dAdx \hfill \\\updelta U^{T} = \int\limits_{V} {\left( {\sigma_{xx}^{T} - \frac{d}{dx}\sigma_{xx}^{T1} } \right)\updelta \varepsilon_{xx}^{T} } dAdx + \int\limits_{V} {\left( {\sigma_{xz} - \frac{d}{dx}\sigma_{xz}^{1} } \right)\updelta \gamma_{xz} } dAdx \hfill \\ + \left[ {\int\limits_{A} {\sigma_{xx}^{T1}\updelta \varepsilon_{xx}^{T} } dA} \right]_{0}^{L} + \left[ {\int\limits_{A} {\sigma_{xz}^{1}\updelta \gamma_{xz} } dA} \right]_{0}^{L} \hfill \\ \hfill \\ t_{xx}^{T} = \sigma_{xx}^{T} - \frac{d}{dx}\sigma_{xx}^{T1} ;\,\,\,\left. {\sigma_{xx}^{T1}\updelta \varepsilon_{xx}^{T} } \right|_{0}^{L} = 0 \hfill \\ t_{xz} = \sigma_{xz} - \frac{d}{dx}\sigma_{xz}^{1} ;\,\,\,\left. {\sigma_{xz}^{1}\updelta \gamma_{xz} } \right|_{0}^{L} = 0. \hfill \\ \end{gathered}$$

(23)

According to Eq. (21), Eq. (22), and Eq. (23), the LNSG bending moment and shear force of Timoshenko nanobeams are generated as Eq. (24):

$$\begin{gathered} M^{T} = \zeta_{1} EI\frac{\partial \phi }{{\partial x}} + \frac{{\zeta_{2} }}{2k}EI\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{\partial \phi }{{\partial \overline{x}}}d\overline{x} \hfill \\ - \zeta_{1} EIl_{m}^{2} \frac{{\partial^{3} \phi }}{{\partial x^{3} }} - \frac{{\zeta_{2} }}{2k}EIl_{m}^{2} \frac{d}{dx}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{{\partial^{2} \phi }}{{\partial \overline{x}^{2} }}d\overline{x}} \right] \hfill \\ \hfill \\ Q^{T} = \zeta_{1} K_{s} GA\left( {\frac{{\partial w^{T} }}{\partial x} + \phi } \right) + \frac{{\zeta_{2} }}{2k}K_{s} GA\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \left( {\frac{{\partial w^{T} }}{{\partial \overline{x}}} + \phi } \right)d\overline{x} \hfill \\ - \zeta_{1} K_{s} GAl_{m}^{2} \left( {\frac{{\partial^{3} w^{T} }}{{\partial x^{3} }} + \frac{{\partial^{2} \phi }}{{\partial x^{2} }}} \right) - \frac{{\zeta_{2} }}{2k}K_{s} GAl_{m}^{2} \frac{d}{dx}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \left( {\frac{{\partial^{2} w^{T} }}{{\partial \overline{x}^{2} }} + \frac{\partial \phi }{{\partial \overline{x}}}} \right)d\overline{x}} \right]. \hfill \\ \end{gathered}$$

(24)

Here, K_s is the shear correction factor. In this step, the following relations are presented:

$$\begin{gathered} \frac{d}{dx}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{{\partial^{2} \phi }}{{\partial \overline{x}^{2} }}d\overline{x}} \right] = - \frac{2}{k}\frac{\partial \phi }{{\partial x}} + \frac{1}{{k^{2} }}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{\partial \phi }{{\partial \overline{x}}}d\overline{x}} \right] + \hfill \\ + \frac{1}{k}\left( {\frac{\partial \phi }{{\partial x}}\left( 0 \right)e^{{ - \frac{x}{k}}} + \frac{\partial \phi }{{\partial x}}\left( L \right)e^{{\frac{x - L}{k}}} } \right) \hfill \\ \end{gathered}$$

(25)

$$\begin{gathered} \frac{d}{dx}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \left( {\frac{{\partial^{2} w^{T} }}{{\partial \overline{x}^{2} }} + \frac{\partial \phi }{{\partial \overline{x}}}} \right)d\overline{x}} \right] = - \frac{2}{k}\left( {\frac{{\partial w^{T} }}{\partial x} + \phi } \right) \hfill \\ + \frac{1}{{k^{2} }}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \left( {\frac{{\partial w^{T} }}{{\partial \overline{x}}} + \phi } \right)d\overline{x}} \right] + \hfill \\ + \frac{1}{k}\left( {\left( {\frac{{\partial w^{T} }}{\partial x} + \phi } \right)\left( 0 \right)e^{{ - \frac{x}{k}}} + \left( {\frac{{\partial w^{T} }}{\partial x} + \phi } \right)\left( L \right)e^{{\frac{x - L}{k}}} } \right). \hfill \\ \end{gathered}$$

(26)

Next, to brevity, it is assumed that:

$$\begin{gathered} \frac{\partial \phi }{{\partial x}}\left( 0 \right) = St_{1}^{T} ,\,\,\frac{\partial \phi }{{\partial x}}\left( L \right) = St_{2}^{T} \hfill \\ \left( {\frac{{\partial w^{T} }}{\partial x} + \phi } \right)\left( 0 \right) = St_{3}^{T} ,\,\,\left( {\frac{{\partial w^{T} }}{\partial x} + \phi } \right)\left( L \right) = St_{4}^{T} . \hfill \\ \end{gathered}$$

(27)

Substituting Eq. (27) into Eqs. (25), (26) and then into Eq. (24) gives:

$$\begin{gathered} M^{T} = EI\left( {\zeta_{1} + \frac{{\left( {1 - \zeta_{1} } \right)l_{m}^{2} }}{{k^{2} }}} \right)\frac{\partial \phi }{{\partial x}} + \hfill \\ \frac{EI}{{2k}}\left( {1 - \frac{{l_{m}^{2} }}{{k^{2} }}} \right)\left( {1 - \zeta_{1} } \right)\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{\partial \phi }{{\partial \overline{x}}}d\overline{x} - \zeta_{1} EIl_{m}^{2} \frac{{\partial^{3} \phi }}{{\partial x^{3} }} \hfill \\ - \frac{{\left( {1 - \zeta_{1} } \right)}}{{2k^{2} }}EI\,l_{m}^{2} \left( {St_{1}^{T} e^{{ - \frac{x}{k}}} + St_{2}^{T} e^{{\frac{x - L}{k}}} } \right) \hfill \\ \hfill \\ Q^{T} = K_{s} GA\left( {\zeta_{1} + \frac{{\left( {1 - \zeta_{1} } \right)l_{m}^{2} }}{{k^{2} }}} \right)\gamma_{xz} + \hfill \\ \frac{{K_{s} GA}}{2k}\left( {1 - \frac{{l_{m}^{2} }}{{k^{2} }}} \right)\left( {1 - \zeta_{1} } \right)\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \left( {\frac{{\partial w^{T} }}{{\partial \overline{x}}} + \phi } \right)d\overline{x} - \zeta_{1} K_{s} GAl_{m}^{2} \left( {\frac{{\partial^{3} w^{T} }}{{\partial x^{3} }} + \frac{{\partial^{2} \phi }}{{\partial x^{2} }}} \right) \hfill \\ - \frac{{\left( {1 - \zeta_{1} } \right)}}{{2k^{2} }}K_{s} GA\,l_{m}^{2} \left( {St_{3}^{T} e^{{ - \frac{x}{k}}} + St_{4}^{T} e^{{\frac{x - L}{k}}} } \right). \hfill \\ \end{gathered}$$

(28)

Here, to facilitate, the following symbols are introduced:

$$\begin{gathered} \mu_{1}^{T} = EI\left( {\zeta_{1} + \frac{{\left( {1 - \zeta_{1} } \right)l_{m}^{2} }}{{k^{2} }}} \right),\,\mu_{2}^{T} = \frac{EI}{{2k}}\left( {1 - \frac{{l_{m}^{2} }}{{k^{2} }}} \right)\left( {1 - \zeta_{1} } \right) \hfill \\ \mu_{3}^{T} = - \zeta_{1} EIl_{m}^{2} ,\,\mu_{4}^{T} = - \frac{EI}{2}\frac{{l_{m}^{2} }}{{k^{2} }}(1 - \zeta_{1} ),\,\,\,\mu_{5}^{T} = St_{1}^{T} e^{{ - \frac{x}{k}}} + St_{2}^{T} e^{{\frac{x - L}{k}}} \hfill \\ \hfill \\ \eta_{1} = K_{s} GA\left( {\zeta_{1} + \frac{{\left( {1 - \zeta_{1} } \right)l_{m}^{2} }}{{k^{2} }}} \right),\,\eta_{2} = \frac{{K_{s} GA}}{2k}\left( {1 - \frac{{l_{m}^{2} }}{{k^{2} }}} \right)\left( {1 - \zeta_{1} } \right) \hfill \\ \eta_{3} = - \zeta_{1} K_{s} GAl_{m}^{2} ,\eta_{4} = - \frac{{K_{s} GA}}{2}\frac{{l_{m}^{2} }}{{k^{2} }}(1 - \zeta_{1} ),\,\,\,\eta_{5} = St_{3}^{T} e^{{ - \frac{x}{k}}} + St_{4}^{T} e^{{\frac{x - L}{k}}} . \hfill \\ \end{gathered}$$

(29)

By employing the symbols presented in Eq. (29), Eq. (28) is rewritten as follows:

$$\begin{gathered} \frac{{M^{T} }}{{\mu_{1}^{T} }} - \frac{{\mu_{3}^{T} }}{{\mu_{1}^{T} }}\frac{{\partial^{3} \phi }}{{\partial x^{3} }} - \frac{{\mu_{4}^{T} }}{{\mu_{1}^{T} }}\mu_{5}^{T} = \frac{\partial \phi }{{\partial x}} + \frac{{\mu_{2}^{T} }}{{\mu_{1}^{T} }}\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \frac{\partial \phi }{{\partial \overline{x}}}d\overline{x} \hfill \\ \frac{{Q^{T} }}{{\eta_{1} }} - \frac{{\eta_{3} }}{{\eta_{1} }}\frac{{\partial^{2} \gamma_{xz} }}{{\partial x^{2} }} - \frac{{\eta_{4} }}{{\eta_{1} }}\eta_{5} = \gamma_{xz} + \frac{{\eta_{2} }}{{\eta_{1} }}\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} } \gamma_{xz} d\overline{x}. \hfill \\ \end{gathered}$$

(30)

Now, according to the transformation procedure presented in Eq. (2) and Eq. (3), the equal differential form of Eq. (30) can be obtained as follows:

$$\begin{gathered} \frac{1}{{\mu_{1}^{T} }}\frac{{\partial^{2} M^{T} }}{{\partial x^{2} }} - \frac{{\mu_{3}^{T} }}{{\mu_{1}^{T} }}\frac{{\partial^{5} \phi }}{{\partial x^{5} }} - \frac{1}{{k^{2} }}\left[ {\frac{{M^{T} }}{{\mu_{1}^{T} }} - \frac{{\mu_{3}^{T} }}{{\mu_{1}^{T} }}\frac{{\partial^{3} \phi }}{{\partial x^{3} }}} \right] = \frac{{\partial^{3} \phi }}{{\partial x^{3} }} - \frac{1}{k}\left( {\frac{{2\mu_{2}^{T} }}{{\mu_{1}^{T} }} + \frac{1}{k}} \right)\frac{\partial \phi }{{\partial x}} \hfill \\ \hfill \\ \frac{1}{{\eta_{1} }}\frac{{\partial^{2} Q^{T} }}{{\partial x^{2} }} - \frac{{\eta_{3} }}{{\eta_{1} }}\frac{{\partial^{4} \gamma_{xz} }}{{\partial x^{4} }} - \frac{1}{{k^{2} }}\left[ {\frac{{Q^{T} }}{{\eta_{1} }} - \frac{{\eta_{3} }}{{\eta_{1} }}\frac{{\partial^{2} \gamma_{xz} }}{{\partial x^{2} }}} \right] = \frac{{\partial^{2} \gamma_{xz} }}{{\partial x^{2} }} - \frac{1}{k}\left( {\frac{{2\eta_{2} }}{{\eta_{1} }} + \frac{1}{k}} \right)\gamma_{xz} . \hfill \\ \end{gathered}$$

(31)

Also, the essential CBCs should be derived using Eq. (4). Therefore:

$$\begin{gathered} \frac{1}{{\mu_{1}^{T} }}\frac{{\partial M^{T} }}{\partial x} - \frac{{\mu_{3}^{T} }}{{\mu_{1}^{T} }}\frac{{\partial^{4} \phi }}{{\partial x^{4} }} - \frac{{\mu_{4}^{T} }}{{\mu_{1}^{T} }}\frac{{\partial \mu_{5}^{T} }}{\partial x} - \frac{1}{k}\left[ {\frac{{M^{T} }}{{\mu_{1}^{T} }} - \frac{{\mu_{3}^{T} }}{{\mu_{1}^{T} }}\frac{{\partial^{3} \phi }}{{\partial x^{3} }} - \frac{{\mu_{4}^{T} }}{{\mu_{1}^{T} }}\mu_{5}^{T} } \right] = \frac{{\partial^{2} \phi }}{{\partial x^{2} }} - \frac{1}{k}\frac{\partial \phi }{{\partial x}}\,\,at\,x = 0 \hfill \\ \frac{1}{{\mu_{1}^{T} }}\frac{{\partial M^{T} }}{\partial x} - \frac{{\mu_{3}^{T} }}{{\mu_{1}^{T} }}\frac{{\partial^{4} \phi }}{{\partial x^{4} }} - \frac{{\mu_{4}^{T} }}{{\mu_{1}^{T} }}\frac{{\partial \mu_{5}^{T} }}{\partial x} + \frac{1}{k}\left[ {\frac{{M^{T} }}{{\mu_{1}^{T} }} - \frac{{\mu_{3}^{T} }}{{\mu_{1}^{T} }}\frac{{\partial^{3} \phi }}{{\partial x^{3} }} - \frac{{\mu_{4}^{T} }}{{\mu_{1}^{T} }}\mu_{5}^{T} } \right] = \frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \frac{1}{k}\frac{\partial \phi }{{\partial x}}\,\,at\,x = L \hfill \\ \hfill \\ \frac{1}{{\eta_{1} }}\frac{{\partial Q^{T} }}{\partial x} - \frac{{\eta_{3} }}{{\eta_{1} }}\frac{{\partial^{3} \gamma_{xz} }}{{\partial x^{3} }} - \frac{{\eta_{4} }}{{\eta_{1} }}\frac{{\partial \eta_{5} }}{\partial x} - \frac{1}{k}\left[ {\frac{{Q^{T} }}{{\eta_{1} }} - \frac{{\eta_{3} }}{{\eta_{1} }}\frac{{\partial^{2} \gamma_{xz} }}{{\partial x^{2} }} - \frac{{\eta_{4} }}{{\eta_{1} }}\eta_{5} } \right] = \frac{{\partial \gamma_{xz} }}{\partial x} - \frac{1}{k}\gamma_{xz} \,\,at\,x = 0 \hfill \\ \frac{1}{{\eta_{1} }}\frac{{\partial Q^{T} }}{\partial x} - \frac{{\eta_{3} }}{{\eta_{1} }}\frac{{\partial^{3} \gamma_{xz} }}{{\partial x^{3} }} - \frac{{\eta_{4} }}{{\eta_{1} }}\frac{{\partial \eta_{5} }}{\partial x} + \frac{1}{k}\left[ {\frac{{Q^{T} }}{{\eta_{1} }} - \frac{{\eta_{3} }}{{\eta_{1} }}\frac{{\partial^{2} \gamma_{xz} }}{{\partial x^{2} }} - \frac{{\eta_{4} }}{{\eta_{1} }}\eta_{5} } \right] = \frac{{\partial \gamma_{xz} }}{\partial x} + \frac{1}{k}\gamma_{xz} \,\,at\,x = L. \hfill \\ \end{gathered}$$

(32)

Now, the equilibrium equations associated with the TBT are written:

$$\begin{gathered} \frac{{\partial Q^{T} }}{\partial x} - m_{1} \frac{{\partial^{2} w^{T} }}{{\partial t^{2} }} = 0 \hfill \\ \frac{{\partial M^{T} }}{\partial x} - Q^{T} - m_{2} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} = 0 \hfill \\ m_{1} = \rho A,\,\,m_{2} = \rho I. \hfill \\ \end{gathered}$$

(33)

In this step, by performing some mathematical manipulations on Eq. (33) to extract the second derivate of M^T and Q^T, and substituting them into Eq. (31), the LNSG bending moment as well as the LNSG shear force of TBT can be achieved in differential form:

$$\begin{gathered} M^{T} = - k^{2} \mu_{3}^{T} \frac{{\partial^{5} \phi }}{{\partial x^{5} }} + \left( {\mu_{3}^{T} - k^{2} \mu_{1}^{T} } \right)\frac{{\partial^{3} \phi }}{{\partial x^{3} }} \hfill \\ + \left( {2\mu_{2}^{T} k + \mu_{1}^{T} } \right)\frac{\partial \phi }{{\partial x}} + k^{2} \left( {m_{2} \frac{{\partial^{3} \phi }}{{\partial t^{2} \partial x}} + m_{1} \frac{{\partial^{2} w^{T} }}{{\partial t^{2} }}} \right) \hfill \\ \hfill \\ Q^{T} = - k^{2} \eta_{3} \left( {\frac{{\partial^{5} w^{T} }}{{\partial x^{5} }} + \frac{{\partial^{4} \phi }}{{\partial x^{4} }}} \right) + \left( {\eta_{3} - k^{2} \eta_{1} } \right)\left( {\frac{{\partial^{3} w^{T} }}{{\partial x^{3} }} + \frac{{\partial^{2} \phi }}{{\partial x^{2} }}} \right) \hfill \\ + \left( {2\eta_{2} k + \eta_{1} } \right)\left( {\frac{{\partial w^{T} }}{\partial x} + \phi } \right) + k^{2} m_{1} \frac{{\partial^{3} w^{T} }}{{\partial t^{2} \partial x}}. \hfill \\ \end{gathered}$$

(34)

Now, it is possible to extract the LNSG governing equations of Timoshenko nanobeams by substituting Eq. (34) into Eq. (33). These equations are written as follows by applying the symbols introduced in Eq. (29):

$$\begin{gathered} - m_{1} \frac{{\partial^{2} w^{T} }}{{\partial t^{2} }} + K_{s} GA\frac{\partial \phi }{{\partial x}} + K_{s} GA\frac{{\partial^{2} w^{T} }}{{\partial x^{2} }} + k^{2} m_{1} \frac{{\partial^{4} w^{T} }}{{\partial t^{2} \partial x^{2} }} \hfill \\ - \left( {K_{s} GAl_{m}^{2} + K_{s} GA\zeta_{1} k^{2} } \right)\left( {\frac{{\partial^{4} w^{T} }}{{\partial x^{4} }} + \frac{{\partial^{3} \phi }}{{\partial x^{3} }}} \right) \hfill \\ + K_{s} GAl_{m}^{2} \zeta_{1} k^{2} \left( {\frac{{\partial^{6} w^{T} }}{{\partial x^{6} }} + \frac{{\partial^{5} \phi }}{{\partial x^{5} }}} \right) = 0 \hfill \\ \hfill \\ K_{s} GA\left( {\left( {l_{m}^{2} + \zeta_{1} k^{2} } \right)\frac{{\partial^{3} w^{T} }}{{\partial x^{3} }} - \frac{{\partial w^{T} }}{\partial x} - l_{m}^{2} \zeta_{1} k^{2} \frac{{\partial^{5} w^{T} }}{{\partial x^{5} }}} \right) - m_{2} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} - K_{s} GA\phi \hfill \\ + \left( {EI + K_{s} GA\left( {l_{m}^{2} + \zeta_{1} k^{2} } \right)} \right)\frac{{\partial^{2} \phi }}{{\partial x^{2} }} + k^{2} m_{2} \frac{{\partial^{4} \phi }}{{\partial t^{2} \partial x^{2} }} \hfill \\ - \left( {K_{s} GAl_{m}^{2} \zeta_{1} k^{2} + EI\left( {l_{m}^{2} + \zeta_{1} k^{2} } \right)} \right)\frac{{\partial^{4} \phi }}{{\partial x^{4} }} + EIk^{2} l_{m}^{2} \zeta_{1} \frac{{\partial^{6} \phi }}{{\partial x^{6} }} = 0. \hfill \\ \end{gathered}$$

(35)

Similarly, the CBCs should be obtained in terms of $w^{T}$ and $\phi$ by replacing the Eq. (34) into Eq. (32):

2.4 Exact solution

To achieve the exact solution of the Eq. (19), which is related to the EBT, as well as the solution of the governing equations corresponding to the TBT, i.e., Eq. (35), the separation of variables method is employed and non-dimensional parameters are introduced as follows:

$$\begin{gathered} w^{E} \left( {x,t} \right) = W^{E} \left( x \right)e^{i\omega t} \,\,\,for\,EBT \hfill \\ \hfill \\ \left\{ {\begin{array}{*{20}c} {w^{T} \left( {x,t} \right) = W^{T} \left( x \right)e^{i\omega t} } \\ {\phi \left( {x,t} \right) = \Phi \left( x \right)e^{i\omega t} } \\ \end{array} } \right.\,for\,TBT \hfill \\ \hfill \\ \overline{x} = \frac{x}{L},\,\overline{W}_{E} = \frac{{W^{E} }}{L}\,\overline{W}_{T} = \frac{{W^{T} }}{L} \hfill \\ \Gamma_{1} = \frac{k}{L},\,\,\Gamma_{2} = \frac{{m_{1} L^{2} }}{{m_{2} }},\,\,\Gamma_{3} = \,\frac{EI}{{K_{s} GAL^{2} }},\,\Gamma_{4} = \,\frac{{l_{m} }}{L},\,\,\lambda = \omega L^{2} \sqrt {\frac{{m_{1} }}{EI}} , \hfill \\ \end{gathered}$$

(36)

where $\omega$ and $\lambda$ show the dimensional and non-dimensional vibration frequencies, respectively.

2.4.1 EBT

In the first step, Eq. (19) is rewritten in the non-dimensional form:

$$\lambda^{2} \overline{W}_{E}^{{}} - \overline{W}_{E}^{(4)} + \Gamma_{4}^{2} \overline{W}_{E}^{(6)} - \Gamma_{1}^{2} \left( {\lambda^{2} \overline{W}_{E}^{\prime \prime } - \zeta_{1} \overline{W}_{E}^{(6)} + \zeta_{1} \Gamma_{4}^{2} \overline{W}_{E}^{(8)} } \right) = 0.$$

(37)

Next, the non-dimensional bending moment and shear force as well as two CBCs related to the EBT should be presented. Therefore:

$$\begin{gathered} \overline{M}_{E} = - \overline{W}_{E}^{\prime \prime } + \Gamma_{4}^{2} \overline{W}_{E}^{(4)} - \Gamma_{1}^{2} \left( {\lambda^{2} \overline{W}_{E} - \zeta_{1} \overline{W}_{E}^{(4)} + \zeta_{1} \Gamma_{4}^{2} \overline{W}_{E}^{(6)} } \right) \hfill \\ \overline{Q}_{E} = - \overline{W}_{E}^{(3)} + \Gamma_{4}^{2} \overline{W}_{E}^{(5)} - \Gamma_{1}^{2} \left( {\lambda^{2} \overline{W}_{E}^{\prime } - \zeta_{1} \overline{W}_{E}^{(6)} + \zeta_{1} \Gamma_{4}^{2} \overline{W}_{E}^{(7)} } \right) \hfill \\ \end{gathered}$$

(38)

$$\begin{gathered} \left( \begin{gathered} \left( {\zeta_{1} - 1} \right)\Gamma_{4}^{2} \overline{W}_{E}^{\prime \prime } - \left( {\zeta_{1} - 1} \right)\Gamma_{1} \Gamma_{4}^{2} \overline{W}_{E}^{(3)} - \left( {\zeta_{1} - 1} \right)\Gamma_{1}^{2} \left( {\overline{W}_{E}^{\prime \prime } - \Gamma_{4}^{2} \overline{W}_{E}^{(4)} } \right) \hfill \\ + \left( {\zeta_{1} - 1} \right)\Gamma_{1}^{3} \left( {\overline{W}_{E}^{(3)} - \Gamma_{4}^{2} \overline{W}_{E}^{(5)} } \right) + \Gamma_{1}^{4} \left( {\lambda^{2} \overline{W}_{E} - \zeta_{1} \overline{W}_{E}^{(4)} + \zeta_{1} \Gamma_{4}^{2} \overline{W}_{E}^{(6)} } \right) \hfill \\ - \Gamma_{1}^{5} \left( {\lambda^{2} \overline{W}_{E}^{\prime } - \zeta_{1} \overline{W}_{E}^{(5)} + \zeta_{1} \Gamma_{4}^{2} \overline{W}_{E}^{(7)} } \right) - \overline{W}_{E}^{\prime \prime } \left( { - \Gamma_{4}^{2} + \zeta_{1} \Gamma_{4}^{2} } \right) \hfill \\ \end{gathered} \right) = 0\,\,\,at\,\overline{x} = 0 \hfill \\ \hfill \\ \left( \begin{gathered} \left( {\zeta_{1} - 1} \right)\Gamma_{4}^{2} \overline{W}_{E}^{\prime \prime } + \left( {\zeta_{1} - 1} \right)\Gamma_{1} \Gamma_{4}^{2} \overline{W}_{E}^{(3)} - \left( {\zeta_{1} - 1} \right)\Gamma_{1}^{2} \left( {\overline{W}_{E}^{\prime \prime } - \Gamma_{4}^{2} \overline{W}_{E}^{(4)} } \right) \hfill \\ - \left( {\zeta_{1} - 1} \right)\Gamma_{1}^{3} \left( {\overline{W}_{E}^{(3)} - \Gamma_{4}^{2} \overline{W}_{E}^{(5)} } \right) + \Gamma_{1}^{4} \left( {\lambda^{2} \overline{W}_{E} - \zeta_{1} \overline{W}_{E}^{(4)} + \zeta_{1} \Gamma_{4}^{2} \overline{W}_{E}^{(6)} } \right) \hfill \\ + \Gamma_{1}^{5} \left( {\lambda^{2} \overline{W}_{E}^{\prime } - \zeta_{1} \overline{W}_{E}^{(5)} + \zeta_{1} \Gamma_{4}^{2} \overline{W}_{E}^{(7)} } \right) + \overline{W}_{E}^{\prime \prime } \left( {\Gamma_{4}^{2} - \zeta_{1} \Gamma_{4}^{2} } \right) \hfill \\ \end{gathered} \right) = 0\,\,\,at\,\overline{x} = 1. \hfill \\ \end{gathered}$$

(39)

Now, the general solution of Eq. (37), which is an eight-order differential equation with constant coefficients, can be considered as follows:

$$\overline{W}_{E} \left( {\overline{x}} \right) = \sum\limits_{i = 1}^{8} {C_{i} e^{{R_{i} \overline{x}}} } ,$$

(40)

where R_i are the roots of the following equation and C_i are unknown coefficients which can be extracted by satisfying all boundary conditions:

$$\lambda^{2} - \Gamma_{1}^{2} \lambda^{2} D^{2} - D^{4} + \left( {\Gamma_{4}^{2} + \Gamma_{1}^{2} \zeta_{1} } \right)D^{6} - \Gamma_{1}^{2} \Gamma_{4}^{2} \zeta_{1} D^{8} = 0.$$

(41)

Here, according to the higher order boundary conditions associated with the strain gradient, i.e., $\left. {\sigma_{xx}^{E1}\updelta \varepsilon_{xx}^{E} } \right|_{0}^{L} = 0$, the following boundary conditions must be satisfied:

$$\begin{gathered} \partial_{{\overline{x},\overline{x}}} \overline{W}_{E} = 0\,\,or\,\,\sigma_{xx}^{1} = 0 \to \zeta_{1} \partial_{{\overline{x},\overline{x},\overline{x}}} \overline{W}_{E} + \frac{{(1 - \zeta_{1} )}}{{2\Gamma_{1} }}\mathop \smallint \limits_{0}^{1} e^{{ - \frac{y}{{\Gamma_{1} }}}} \partial_{y,y,y} \overline{W}_{E} \,{\text{d}}y = 0\,at\,\overline{x} = 0 \hfill \\ \partial_{{\overline{x},\overline{x}}} \overline{W}_{E} = 0\,\,or\,\,\sigma_{xx}^{1} = 0 \to \zeta_{1} \partial_{{\overline{x},\overline{x},\overline{x}}} \overline{W}_{E} + \frac{{(1 - \zeta_{1} )}}{{2\Gamma_{1} }}\mathop \smallint \limits_{0}^{1} e^{{ - \frac{1 - y}{{\Gamma_{1} }}}} \partial_{y,y,y} \overline{W}_{E} \,{\text{d}}y = 0\,at\,\overline{x} = 1. \hfill \\ \end{gathered}$$

(42)

Finally, the vibration frequencies of the LNSG Euler–Bernoulli nanobeams can be obtained by constructing the constant coefficients matrix and find the values of $\lambda$ which lead to zero determinant. It is helpful to be mentioned that there are eight boundary conditions including four geometrical or natural, two CBCs, Eq. (39), and two boundary conditions due to the strain gradient, Eq. (42).

2.4.2 TBT

The non-dimensional governing equations of TBT, Eq. (35), are rewritten as follows:

$$\begin{gathered} \Phi^{\prime } + \overline{W}_{T}^{\prime \prime } + \lambda^{2} \Gamma_{3} (\overline{W}_{T} - \Gamma_{1}^{2} \overline{W}_{T}^{\prime \prime } ) - \hfill \\ \left( {\zeta_{1} \Gamma_{1}^{2} + \Gamma_{4}^{2} } \right)\left( {\Phi^{(3)} + \overline{W}_{T}^{(4)} } \right) + \zeta_{1} \Gamma_{1}^{2} \Gamma_{4}^{2} \left( {\Phi^{(5)} + \overline{W}_{T}^{(6)} } \right) = 0 \hfill \\ \hfill \\ \frac{1}{{\Gamma_{2} }}\left( \begin{gathered} \lambda^{2} \Gamma_{3} \left( { - \Phi + \Gamma_{1}^{2} \Phi^{\prime \prime } } \right) + \hfill \\ \Gamma_{2} \left( {\Phi + \overline{W}_{T}^{\prime } - \left( {\zeta_{1} \Gamma_{1}^{2} + \Gamma_{3} + \Gamma_{4}^{2} } \right)\Phi^{\prime \prime } - \left( {\zeta_{1} \Gamma_{1}^{2} + \Gamma_{4}^{2} } \right)\overline{W}_{T}^{(3)} } \right) \hfill \\ \end{gathered} \right) + \hfill \\ \left( \begin{gathered} \left( {\zeta_{1} \Gamma_{1}^{2} \Gamma_{3} + \zeta_{1} \Gamma_{1}^{2} \Gamma_{4}^{2} + \Gamma_{3} \Gamma_{4}^{2} } \right)\Phi^{(4)} \hfill \\ + \zeta_{1} \Gamma_{1}^{2} \Gamma_{4}^{2} \overline{W}_{T}^{(5)} - \zeta_{1} \Gamma_{1}^{2} \Gamma_{3} \Gamma_{4}^{2} \Phi^{(6)} \hfill \\ \end{gathered} \right) = 0. \hfill \\ \end{gathered}$$

(43)

In addition, the LNSG bending moment and shear force should be represented in dimensionless form:

$$\begin{gathered} \overline{M} = \left( {\Phi^{\prime } - \Gamma_{4}^{2} \phi^{(3)} } \right) - \frac{{\Gamma_{1}^{2} }}{{\Gamma_{2} }}\left( {\lambda^{2} \Phi^{\prime } + \Gamma_{2} \left( {\lambda^{2} \overline{W}_{T} + \zeta_{1} \Phi^{(3)} - \zeta_{1} \Gamma_{4}^{2} \Phi^{(5)} } \right)} \right) \hfill \\ \hfill \\ \overline{Q} = \Phi + \left( {1 - \lambda^{2} \Gamma_{1}^{2} \Gamma_{3} } \right)\overline{W}_{T}^{\prime } - \left( {\zeta_{1} \Gamma_{1}^{2} + \Gamma_{4}^{2} } \right)\Phi^{\prime \prime } - \left( {\zeta_{1} \Gamma_{1}^{2} - \Gamma_{4}^{2} } \right)\overline{W}_{T}^{(3)} \hfill \\ + \zeta_{1} \Gamma_{1}^{2} \Gamma_{4}^{2} \Phi^{(4)} + \zeta_{1} \Gamma_{1}^{2} \Gamma_{4}^{2} \overline{W}_{T}^{(5)} . \hfill \\ \end{gathered}$$

(44)

Similarly, the non-dimensional form of all CBCs is obtained and pretend in Appendix. Afterward, using the derivative operator as $D^{n} \equiv \partial^{n} /\partial x^{n}$, the matrix form of Eq. (43) is presented:

$$\left[ {\begin{array}{*{20}c} \begin{gathered} \zeta_{1} \Gamma_{1}^{2} \Gamma_{4}^{2} D^{6} - \left( {\zeta_{1} \Gamma_{1}^{2} + \Gamma_{4}^{2} } \right)D^{4} \hfill \\ + \left( {1 - \lambda^{2} \Gamma_{1}^{2} \Gamma_{3} } \right)D^{2} + \lambda^{2} \Gamma_{3} \hfill \\ \end{gathered} & {\zeta_{1} \Gamma_{1}^{2} \Gamma_{4}^{2} D^{5} + \left( { - \zeta_{1} \Gamma_{1}^{2} - \Gamma_{4}^{2} } \right)D^{3} + D} \\ {\zeta_{1} \Gamma_{1}^{2} \Gamma_{4}^{2} D^{5} + \left( { - \zeta_{1} \Gamma_{1}^{2} - \Gamma_{4}^{2} } \right)D^{3} + D} & \begin{gathered} \hfill \\ \,\, - \zeta_{1} \Gamma_{1}^{2} \Gamma_{3} \Gamma_{4}^{2} D^{6} + \hfill \\ \left( {\zeta_{1} \Gamma_{1}^{2} \Gamma_{3} + \zeta_{1} \Gamma_{1}^{2} \Gamma_{4}^{2} + \Gamma_{3} \Gamma_{4}^{2} } \right)D^{4} + \hfill \\ \,\,\frac{{\left( { - \zeta_{1} \Gamma_{1}^{2} \Gamma_{2} + \lambda^{2} \Gamma_{1}^{2} \Gamma_{3} - \Gamma_{2} \Gamma_{3} - \Gamma_{2} \Gamma_{4}^{2} } \right)}}{{\Gamma_{2} }}D^{2} \hfill \\ + \frac{{\Gamma_{2} - \lambda^{2} \Gamma_{3} }}{{\Gamma_{2} }} \hfill \\ \end{gathered} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\overline{W}_{T} } \\ \Phi \\ \end{array} } \right\} = 0.$$

(45)

Now, taking the determinant of the coefficients matrix of Eq. (45) gives:

$$\begin{gathered} \left( { - \zeta_{1}^{2} \Gamma_{1}^{4} \Gamma_{3} \Gamma_{4}^{4} } \right)D^{12} + \left( {2\zeta_{1} \Gamma_{1}^{2} \Gamma_{3} \Gamma_{4}^{2} \left( {\zeta_{1} \Gamma_{1}^{2} + \Gamma_{4}^{2} } \right)} \right)D^{10} + \hfill \\ \frac{{\Gamma_{3} }}{{\Gamma_{2} }}\left( { - 4\zeta_{1} \Gamma_{1}^{2} \Gamma_{2} \Gamma_{4}^{2} - \Gamma_{2} \Gamma_{4}^{4} + \zeta_{1} \Gamma_{1}^{4} \left( {\lambda^{2} \Gamma_{4}^{2} + \Gamma_{2} \left( { - \zeta_{1} + \lambda^{2} \Gamma_{3} \Gamma_{4}^{2} } \right)} \right)} \right)D^{8} \hfill \\ - \frac{{\Gamma_{3} }}{{\Gamma_{2} }}\left( \begin{gathered} - 2\Gamma_{2} \Gamma_{4}^{2} + \zeta_{1} \lambda^{2} \Gamma_{1}^{4} \left( {1 + \Gamma_{2} \left( {\Gamma_{3} + \Gamma_{4}^{2} } \right)} \right) + \hfill \\ \Gamma_{1}^{2} \left( {\left( {1 + \zeta_{1} } \right)\lambda^{2} \Gamma_{4}^{2} + \Gamma_{2} \left( { - 2\zeta_{1} + \left( {1 + \zeta_{1} } \right)\lambda^{2} \Gamma_{3} \Gamma_{4}^{2} } \right)} \right) \hfill \\ \end{gathered} \right)D^{6} + \hfill \\ \frac{{\Gamma_{3} }}{{\Gamma_{2} }}\left( \begin{gathered} \Gamma_{1}^{4} \left( {\zeta_{1} \lambda^{2} \Gamma_{2} - \lambda^{4} \Gamma_{3} } \right) + \lambda^{2} \Gamma_{4}^{2} + \Gamma_{2} \left( { - 1 + \lambda^{2} \Gamma_{3} \Gamma_{4}^{2} } \right) + \hfill \\ \left( {1 + \zeta_{1} } \right)\lambda^{2} \Gamma_{1}^{2} \left( {1 + \Gamma_{2} \left( {\Gamma_{3} + \Gamma_{4}^{2} } \right)} \right) \hfill \\ \end{gathered} \right)D^{4} + \hfill \\ \frac{{\lambda^{2} \Gamma_{3} }}{{\Gamma_{2} }}\left( { - 1 - \Gamma_{1}^{2} \left( {\left( {1 + \zeta_{1} } \right)\Gamma_{2} - 2\lambda^{2} \Gamma_{3} } \right) - \Gamma_{2} \left( {\Gamma_{3} + \Gamma_{4}^{2} } \right)} \right)D^{2} + \hfill \\ \lambda^{2} \Gamma_{3} \left( {1 - \frac{{\lambda^{2} \Gamma_{3} }}{{\Gamma_{2} }}} \right) = 0. \hfill \\ \end{gathered}$$

(46)

It is worth noting that, as can be seen from Eq. (46), the order of corresponding governing differential equation of LNSG Timoshenko nanobeam is 12 which is equal to the total number of boundary conditions including 4 natural or geometric BCs, 4 BCs related to the strain gradient, and 4 CBCs relevant to the transformation of integral equations to differential ones. Accordingly, the exact solution of Eq. (43) can be obtained by satisfying all boundary conditions. Therefore, the general solution of this differential equation is considered as follows:

$$\begin{gathered} \overline{W}_{T} \left( {\overline{x}} \right) = \sum\limits_{i = 1}^{12} {C_{i} e^{{R_{i} \overline{x}}} } \hfill \\ \Phi \left( {\overline{x}} \right) = \sum\limits_{i = 1}^{12} {\alpha_{i} C_{i} e^{{R_{i} \overline{x}}} } , \hfill \\ \end{gathered}$$

(47)

in which $C_{i}$ are constant coefficients, $R_{i}$ are the roots of Eq. (46) and:

$$\alpha_{i} = \frac{{ - \lambda^{2} \Gamma_{3} + R_{i}^{2} \left( { - 1 + \lambda^{2} \Gamma_{1}^{2} \Gamma_{3} } \right) - \zeta_{1} R_{i}^{6} \Gamma_{1}^{2} \Gamma_{4}^{2} + R_{i}^{4} \left( {\zeta_{1} \Gamma_{1}^{2} + \Gamma_{4}^{2} } \right)}}{{R_{i} \left( { - 1 + \zeta_{1} R_{i}^{2} \Gamma_{1}^{2} } \right)\left( { - 1 + R_{i}^{2} \Gamma_{4}^{2} } \right)}}.$$

(48)

As previously mentioned and also, it can be seen from the Eq. (23), the higher order boundary conditions related to the strain gradient, i.e., $\left. {\sigma_{kl}^{1}\updelta \varepsilon_{kl} } \right|_{0}^{L} = 0$, must be satisfied. Owing this, it is essential to be considered that:

$$\begin{gathered} \partial_{{\overline{x}}} \Phi = 0\,\,or\,\,\sigma_{xx}^{1} = 0 \to \zeta_{1} \partial_{{\overline{x},\overline{x}}} \Phi + \frac{{(1 - \zeta_{1} )}}{{2\Gamma_{1} }}\mathop \smallint \limits_{0}^{1} e^{{ - \frac{y}{{\Gamma_{1} }}}} \partial_{y,y} \Phi \,{\text{d}}y = 0\,at\,\overline{x} = 0 \hfill \\ \partial_{{\overline{x}}} \Phi = 0\,\,or\,\,\sigma_{xx}^{1} = 0 \to \zeta_{1} \partial_{{\overline{x},\overline{x}}} \Phi + \frac{{(1 - \zeta_{1} )}}{{2\Gamma_{1} }}\mathop \smallint \limits_{0}^{1} e^{{ - \frac{1 - y}{{\Gamma_{1} }}}} \partial_{y,y} \Phi \,{\text{d}}y = 0\,at\,\overline{x} = 1 \hfill \\ \hfill \\ \Phi + \partial_{{\overline{x}}} \overline{W}_{T} = 0\,\,or\,\,\,\sigma_{xz}^{1} = 0 \to \zeta_{1} \left( {\partial_{{\overline{x}}} \Phi + \partial_{{\overline{x},\overline{x}}} \overline{W}_{T} } \right) + \frac{{(1 - \zeta_{1} )}}{{2\Gamma_{1} }}\mathop \smallint \limits_{0}^{1} e^{{ - \frac{y}{{\Gamma_{1} }}}} \left( {\partial_{y} \Phi + \partial_{y,y} \overline{W}_{T} } \right)\,{\text{d}}y = 0\,at\,\overline{x} = 0 \hfill \\ \Phi + \partial_{{\overline{x}}} \overline{W}_{T} = 0\,\,or\,\,\,\sigma_{xz}^{1} = 0 \to \zeta_{1} \left( {\partial_{{\overline{x}}} \Phi + \partial_{{\overline{x},\overline{x}}} \overline{W}_{T} } \right) + \frac{{(1 - \zeta_{1} )}}{{2\Gamma_{1} }}\mathop \smallint \limits_{0}^{1} e^{{ - \frac{1 - y}{{\Gamma_{1} }}}} \left( {\partial_{y} \Phi + \partial_{y,y} \overline{W}_{T} } \right)\,{\text{d}}y = 0\,at\,\overline{x} = 1. \hfill \\ \end{gathered}$$

(49)

Now, by satisfying all 12 BCs, the coefficients matrix is constructed, and then, its determinant should be set equal to zero for extracting the characteristic equation.

Finally, the vibration frequencies of LNSG Timoshenko beams are obtained by solving this equation by employing numerical ways such as the method presented in Reference [66]. It is helpful to note that to prevent ill-conditioning, all elements of each column of the coefficients matrix are divided by the norm of that column.

2.5 Local/nonlocal strain gradient finite-element model

First of all, it should be noted that the present FEM of LNSG is constructed using the basic integral form of the LNSG Timoshenko beam and no transformation is implemented on the integral equation. Also, to create an efficient shear-locking-free beam element, the shear strain is considered as an independent degree of freedom and the order of element is set in such a way that the derivative of the strains related to the strain gradient is not neglected. Therefore, the rotation of cross section is rewritten as follows by this assumption that $\gamma = - \gamma_{xy}$:

$$\phi (x,t) = - \left( {\frac{\partial w}{{\partial x}} + \gamma } \right).$$

(50)

Now, according to Eq. (21), Eq. (22), and Eq. (50), the strain potential energy, per length, of the LNSG Timoshenko nanobeam can be expressed:

$$\begin{gathered} \overline{U} = \frac{1}{2}\int\limits_{A} {\left[ {\sigma_{xx}^{T} \varepsilon_{xx}^{T} + \sigma_{xx}^{T1} \varepsilon_{xx,x}^{T} + \sigma_{xz} \gamma_{xz} + \sigma_{xz}^{1} \gamma_{xz,x} } \right]} dA \hfill \\ \overline{U} = \zeta_{1} \overline{U}^{L} + \left( {1 - \zeta_{1} } \right)\overline{U}^{NL} \hfill \\ \hfill \\ \alpha = EI,\,\,\beta = K_{s} GA \hfill \\ \hfill \\ \overline{U}^{L} = \frac{\alpha }{2}\left[ {\left( {\frac{\partial \gamma }{{\partial x}} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} + l_{m}^{2} \left( {\frac{{\partial^{2} \gamma }}{{\partial x^{2} }} + \frac{{\partial^{3} w}}{{\partial x^{3} }}} \right)^{2} } \right] + \frac{\beta }{2}\left( {\gamma^{2} + l_{m}^{2} \left( {\frac{\partial \gamma }{{\partial x}}} \right)^{2} } \right) \hfill \\ \hfill \\ \overline{U}^{NL} = \frac{\alpha }{4k}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} \left( {\frac{\partial \gamma }{{\partial \overline{x}}} + \frac{{\partial^{2} w}}{{\partial \overline{x}^{2} }}} \right)} d\overline{x}} \right]\left( {\frac{\partial \gamma }{{\partial x}} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \hfill \\ + \frac{\alpha }{4k}\left[ {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} l_{m}^{2} \left( {\frac{{\partial^{2} \gamma }}{{\partial \overline{x}^{2} }} + \frac{{\partial^{3} w}}{{\partial \overline{x}^{3} }}} \right)} d\overline{x}} \right]\left( {\frac{{\partial^{2} \gamma }}{{\partial x^{2} }} + \frac{{\partial^{3} w}}{{\partial x^{3} }}} \right) \hfill \\ \,\, + \frac{\beta }{4k}\left( {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} \gamma \left( {\overline{x}} \right)} d\overline{x}} \right)\gamma \left( x \right) \hfill \\ \, + \frac{\beta }{4k}\left( {\int_{0}^{L} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} l_{m}^{2} \frac{\partial \gamma }{{\partial \overline{x}}}} d\overline{x}} \right)\frac{\partial \gamma }{{\partial x}}. \hfill \\ \end{gathered}$$

(51)

In which the superscripts “L” and “NL” stand for the local and nonlocal cases, respectively. Now, a two-node beam element with five degrees of freedom per node is introduced as Fig. 2 for jth element. In fact, to consider the influences of strain gradient, the higher order form of the beam element proposed in Reference [43] is considered.

Fig. 2

Two-node beam element with five degrees of freedom per node

Due to independency of the shear strain from the transverse displacement, the shape functions of them can be easily derived as follow. These shape functions are presented as functions of x which is the axial distance from the beginning of the beam:

$$\begin{gathered} \left\{ {N_{{5\,j - 4}}^{w} ,N_{{5\,j - 3}}^{w} ,N_{{5\,j - 2}}^{w} ,N_{{5\,j - 1}}^{w} ,N_{{5\,j}}^{w} ,N_{{5\,j + 1}}^{w} ,N_{{5\,j + 2}}^{w} ,N_{{5\,j + 3}}^{w} ,N_{{5\,j + 4}}^{w} ,N_{{5\,j + 5}}^{w} } \right\} = \hfill \\ \left\{ \begin{gathered} - \frac{{\left( {l_{{e_{j} }}^{2} + 3l_{{e_{j} }} (x - x_{j} ) + 6(x - x_{j} )^{2} } \right)\left( {x - l_{{e_{j} }} - x_{j} } \right)^{3} }}{{l_{{e_{j} }}^{5} }}, \hfill \\ - \frac{{\left( {l_{{e_{j} }} + 3\left( {x - x_{j} } \right)} \right)\left( {x - x_{j} } \right)\left( {x - l_{{e_{j} }} - x_{j} } \right)^{3} }}{{l_{{e_{j} }}^{4} }}, \hfill \\ - \frac{{\left( {x - x_{j} } \right)^{2} \left( {x - l_{{e_{j} }} - x_{j} } \right)^{3} }}{{2l_{{e_{j} }}^{3} }},0,0, \hfill \\ \frac{{\left( {10l_{{e_{j} }}^{2} - 15l_{{e_{j} }} (x - x_{j} ) + 6(x - x_{j} )^{2} } \right)\left( {x - x_{j} } \right)^{3} }}{{l_{{e_{j} }}^{5} }}, \hfill \\ \frac{{\left( { - 4l_{{e_{j} }}^{2} + 7l_{{e_{j} }} (x - x_{j} ) - 3(x - x_{j} )^{2} } \right)\left( {x - x_{j} } \right)^{3} }}{{l_{{e_{j} }}^{4} }}, \hfill \\ \frac{{(x - x_{j} )^{3} \left( {x - l_{{e_{j} }} - x_{j} } \right)^{2} }}{{2l_{{e_{j} }}^{3} }},0,0 \hfill \\ \end{gathered} \right\} \hfill \\ \left\{ {N_{{5\,j - 4}}^{\gamma } ,N_{{5\,j - 3}}^{\gamma } ,N_{{5\,j - 2}}^{\gamma } ,N_{{5\,j - 1}}^{\gamma } ,N_{{5\,j}}^{\gamma } ,N_{{5\,j + 1}}^{\gamma } ,N_{{5\,j + 2}}^{\gamma } ,N_{{5\,j + 3}}^{\gamma } ,N_{{5\,j + 4}}^{\gamma } ,N_{{5\,j + 5}}^{\gamma } } \right\} = \hfill \\ \left\{ \begin{gathered} 0,0,0,1 - \frac{{3(x - x_{j} )^{2} }}{{l_{{e_{j} }}^{2} }} + \frac{{2(x - x_{j} )^{3} }}{{l_{{e_{j} }}^{3} }},(x - x_{j} ) - \frac{{2(x - x_{j} )^{2} }}{{l_{{e_{j} }} }} + \frac{{(x - x_{j} )^{3} }}{{l_{{e_{j} }}^{2} }} \hfill \\ 0,0,0,\frac{{3(x - x_{j} )^{2} }}{{l_{{e_{j} }}^{2} }} - \frac{{2(x - x_{j} )^{3} }}{{l_{{e_{j} }}^{3} }}, - \frac{{(x - x_{j} )^{2} }}{{l_{{e_{j} }} }} + \frac{{(x - x_{j} )^{3} }}{{l_{{e_{j} }}^{2} }} \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered}$$

(52)

Now, for the jth element, it can be written as:

$$\begin{gathered} w_{j} (x) = \sum\limits_{n = 5j - 4}^{5j + 5} {N_{n}^{w} a_{n} } \hfill \\ \gamma_{j} (x) = \sum\limits_{n = 5j - 4}^{5j + 5} {N_{n}^{\gamma } a_{n} } , \hfill \\ \end{gathered}$$

(53)

where a_n are the degrees of freedom that are illustrated in Fig. 2. In this step, the nonlocal strain gradient potential energy of the jth element which is resulted from the contribution of the ith element is written as Eq. (54):

$$\begin{gathered} U_{ji}^{NL} = \frac{\alpha }{4k}\int_{{x_{j} }}^{{x_{j + 1} }} {\left[ {\int_{{x_{i} }}^{{x_{i + 1} }} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} \left( {\frac{{\partial \gamma_{i} }}{{\partial \overline{x}}} + \frac{{\partial^{2} w_{i} }}{{\partial \overline{x}^{2} }}} \right)} d\overline{x}} \right]} \left( {\frac{{\partial \gamma_{j} }}{\partial x} + \frac{{\partial^{2} w_{j} }}{{\partial x^{2} }}} \right)dx \hfill \\ + \frac{\alpha }{4k}\int_{{x_{j} }}^{{x_{j + 1} }} {\left[ {\int_{{x_{i} }}^{{x_{i + 1} }} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} l_{m}^{2} \left( {\frac{{\partial^{2} \gamma_{i} }}{{\partial \overline{x}^{2} }} + \frac{{\partial^{3} w_{i} }}{{\partial \overline{x}^{3} }}} \right)} d\overline{x}} \right]\left( {\frac{{\partial^{2} \gamma_{j} }}{{\partial x^{2} }} + \frac{{\partial^{3} w_{j} }}{{\partial x^{3} }}} \right)dx} \hfill \\ \,\, + \frac{\beta }{4k}\int_{{x_{j} }}^{{x_{j + 1} }} {\left( {\int_{{x_{i} }}^{{x_{i + 1} }} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} \gamma_{i} \left( {\overline{x}} \right)} d\overline{x}} \right)\gamma_{j} \left( x \right)dx} \hfill \\ \, + \frac{\beta }{4k}\int_{{x_{j} }}^{{x_{j + 1} }} {\left( {\int_{{x_{i} }}^{{x_{i + 1} }} {e^{{ - \frac{{\left| {x - \overline{x}} \right|}}{k}}} l_{m}^{2} \frac{{\partial \gamma_{i} }}{{\partial \overline{x}}}} d\overline{x}} \right)\frac{{\partial \gamma_{j} }}{\partial x}dx} \hfill \\ \alpha = EI,\,\,\beta = K_{s} GA. \hfill \\ \end{gathered}$$

(54)

As can be seen from Eq. (54), due to integral nonlocal stress, all elements are coupled with together. Given this, three different types of nonlocal strain gradient stiffness element are defined according to the location of jth element relative to the ith element position. Therefore:

$$\begin{gathered} for\,j > i\, \hfill \\ m = 5i - 4,5i - 3,...,5i + 4,5i + 5 \hfill \\ n = 5j - 4,5j - 3,...,5j + 4,5j + 5 \hfill \\ knl_{mn}^{ij} = \int_{{x_{j} }}^{{x_{j + 1} }} {\left[ {\frac{\alpha }{2k}\int_{{x_{i} }}^{{x_{i + 1} }} {e^{{ - \frac{{x - \overline{x}}}{k}}} \left( {\frac{{\partial^{2} N_{m}^{w} }}{{\partial \overline{x}^{2} }} + \frac{{\partial N_{m}^{\gamma } }}{{\partial \overline{x}}}} \right)d\overline{x}} } \right]} \left( {\frac{{\partial^{2} N_{n}^{w} }}{{\partial x^{2} }} + \frac{{\partial N_{n}^{\gamma } }}{\partial x}} \right)dx \hfill \\ + \int_{{x_{j} }}^{{x_{j + 1} }} {\left[ {\frac{\beta }{2k}\int_{{x_{i} }}^{{x_{i + 1} }} {e^{{ - \frac{{x - \overline{x}}}{k}}} \left( {N_{m}^{\gamma } } \right)d\overline{x}} } \right]} \left( {N_{n}^{\gamma } } \right)dx \hfill \\ + \int_{{x_{j} }}^{{x_{j + 1} }} {\left[ {\frac{{l_{m}^{2} \alpha }}{2k}\int_{{x_{i} }}^{{x_{i + 1} }} {e^{{ - \frac{{x - \overline{x}}}{k}}} \left( {\frac{{\partial^{3} N_{m}^{w} }}{{\partial \overline{x}^{3} }} + \frac{{\partial^{2} N_{m}^{\gamma } }}{{\partial \overline{x}^{2} }}} \right)d\overline{x}} } \right]} \left( {\frac{{\partial^{3} N_{n}^{w} }}{{\partial x^{3} }} + \frac{{\partial^{2} N_{n}^{\gamma } }}{{\partial x^{2} }}} \right)dx \hfill \\ + \int_{{x_{j} }}^{{x_{j + 1} }} {\left[ {\frac{{l_{m}^{2} \beta }}{2k}\int_{{x_{i} }}^{{x_{i + 1} }} {e^{{ - \frac{{x - \overline{x}}}{k}}} \left( {\frac{{\partial N_{m}^{\gamma } }}{{\partial \overline{x}}}} \right)d\overline{x}} } \right]} \left( {\frac{{\partial N_{n}^{\gamma } }}{\partial x}} \right)dx. \hfill \\ \end{gathered}$$

(55)

$$\begin{gathered} For\,j = i \hfill \\ m = 5i - 4,5i - 3,...,5i + 4,5i + 5 \hfill \\ n = 5i - 4,5i - 3,...,5i + 4,5i + 5 \hfill \\ knl_{mn}^{ii} = \int_{{x_{i} }}^{{x_{i + 1} }} {\left[ {\frac{\alpha }{2k}\left( {\int_{{x_{i} }}^{x} {e^{{ - \frac{{x - \overline{x}}}{k}}} \left( {\frac{{\partial^{2} N_{m}^{w} }}{{\partial \overline{x}^{2} }} + \frac{{\partial N_{m}^{\gamma } }}{{\partial \overline{x}}}} \right)d\overline{x}} } \right)} \right]} \left( {\frac{{\partial^{2} N_{n}^{w} }}{{\partial x^{2} }} + \frac{{\partial N_{n}^{\gamma } }}{\partial x}} \right)dx \hfill \\ + \int_{{x_{i} }}^{{x_{i + 1} }} {\left[ {\frac{\alpha }{2k}\left( {\int_{x}^{{x_{i + 1} }} {e^{{\frac{{x - \overline{x}}}{k}}} \left( {\frac{{\partial^{2} N_{m}^{w} }}{{\partial \overline{x}^{2} }} + \frac{{\partial N_{m}^{\gamma } }}{{\partial \overline{x}}}} \right)d\overline{x}} } \right)} \right]} \left( {\frac{{\partial^{2} N_{n}^{w} }}{{\partial x^{2} }} + \frac{{\partial N_{n}^{\gamma } }}{\partial x}} \right)dx \hfill \\ + \int_{{x_{i} }}^{{x_{i + 1} }} {\left[ {\frac{\beta }{2k}\left( {\int_{{x_{i} }}^{x} {e^{{ - \frac{{x - \overline{x}}}{k}}} \left( {N_{m}^{\gamma } } \right)d\overline{x} + \int_{x}^{{x_{i + 1} }} {e^{{\frac{{x - \overline{x}}}{k}}} \left( {N_{m}^{\gamma } } \right)d\overline{x} + } } } \right)} \right]} \left( {N_{n}^{\gamma } } \right)dx \hfill \\ + \int_{{x_{i} }}^{{x_{i + 1} }} {\left[ {\frac{{l_{m}^{2} \alpha }}{2k}\left( {\int_{{x_{i} }}^{x} {e^{{ - \frac{{x - \overline{x}}}{k}}} \left( {\frac{{\partial^{3} N_{m}^{w} }}{{\partial \overline{x}^{3} }} + \frac{{\partial^{2} N_{m}^{\gamma } }}{{\partial^{2} \overline{x}}}} \right)d\overline{x}} } \right)} \right]} \left( {\frac{{\partial^{3} N_{n}^{w} }}{{\partial x^{3} }} + \frac{{\partial^{2} N_{n}^{\gamma } }}{{\partial x^{2} }}} \right)dx \hfill \\ + \int_{{x_{i} }}^{{x_{i + 1} }} {\left[ {\frac{{l_{m}^{2} \alpha }}{2k}\left( {\int_{x}^{{x_{i + 1} }} {e^{{\frac{{x - \overline{x}}}{k}}} \left( {\frac{{\partial^{3} N_{m}^{w} }}{{\partial \overline{x}^{3} }} + \frac{{\partial^{2} N_{m}^{\gamma } }}{{\partial \overline{x}^{2} }}} \right)d\overline{x}} } \right)} \right]} \left( {\frac{{\partial^{3} N_{n}^{w} }}{{\partial x^{3} }} + \frac{{\partial^{2} N_{n}^{\gamma } }}{{\partial x^{2} }}} \right)dx \hfill \\ + \int_{{x_{i} }}^{{x_{i + 1} }} {\left[ {\frac{{l_{m}^{2} \beta }}{2k}\left( {\int_{{x_{i} }}^{x} {e^{{ - \frac{{x - \overline{x}}}{k}}} \left( {\frac{{\partial N_{m}^{\gamma } }}{{\partial \overline{x}}}} \right)d\overline{x} + \int_{x}^{{x_{i + 1} }} {e^{{\frac{{x - \overline{x}}}{k}}} \left( {\frac{{\partial N_{m}^{\gamma } }}{{\partial \overline{x}}}} \right)d\overline{x} + } } } \right)} \right]} \left( {\frac{{\partial N_{n}^{\gamma } }}{\partial x}} \right)dx. \hfill \\ \end{gathered}$$

(56)

$$\begin{gathered} For\;j < i \hfill \\ m = 5i - 4,\;5i - 3,...,5i + 4,\;5i + 5 \hfill \\ n = 5j - 4,\;5j - 3,...,5j + 4,\;5j + 5 \hfill \\ knl_{{mn}}^{{ij}} = \int_{{x_{j} }}^{{x_{{j + 1}} }} {\left[ {\frac{\alpha }{{2k}}\int\limits_{{x_{i} }}^{{x_{{i + 1}} }} {e^{{\frac{{x - \bar{x}}}{k}}} \left( {\frac{{\partial ^{2} N_{m}^{w} }}{{\partial \bar{x}^{2} }} + \frac{{\partial N_{m}^{\gamma } }}{{\partial \bar{x}}}} \right)d\bar{x}} } \right]} \left( {\frac{{\partial ^{2} N_{n}^{w} }}{{\partial x^{2} }} + \frac{{\partial N_{n}^{\gamma } }}{{\partial x}}} \right)dx \hfill \\ + \int\limits_{{x_{j} }}^{{x_{{j + 1}} }} {\left[ {\frac{\beta }{{2k}}\int\limits_{{x_{i} }}^{{x_{{i + 1}} }} {e^{{\frac{{x - \bar{x}}}{k}}} \left( {N_{m}^{\gamma } } \right)d\bar{x}\left( {N_{n}^{\gamma } } \right)dx} } \right]} \hfill \\ + \int\limits_{{x_{j} }}^{{x_{{j + 1}} }} {\left[ {\frac{{l_{m}^{2} \alpha }}{{2k}}\int\limits_{{x_{i} }}^{{x_{{i + 1}} }} {e^{{\frac{{x - \bar{x}}}{k}}} \left( {\frac{{\partial ^{3} N_{m}^{w} }}{{\partial \bar{x}^{3} }} + \frac{{\partial ^{2} N_{m}^{\gamma } }}{{\partial \bar{x}^{2} }}} \right)d\bar{x}} } \right]} \left( {\frac{{\partial ^{3} N_{n}^{w} }}{{\partial x^{3} }} + \frac{{\partial ^{2} N_{n}^{\gamma } }}{{\partial x^{2} }}} \right)dx \hfill \\ + \int\limits_{{x_{j} }}^{{x_{{j + 1}} }} {\left[ {\frac{{l_{m}^{2} \beta }}{{2k}}\int\limits_{{x_{i} }}^{{x_{{i + 1}} }} {e^{{\frac{{x - \bar{x}}}{k}}} \left( {\frac{{\partial N_{m}^{\gamma } }}{{\partial \bar{x}}}} \right)d\bar{x}} } \right]} \left( {\frac{{\partial N_{n}^{\gamma } }}{{\partial x}}} \right)dx. \hfill \\ \end{gathered}$$

(57)

By adding all of the knl_mn elements which generated by changing i and j from one to the number of applied elements (NE), the total nonlocal strain gradient stiffness matrix, KNSG, can be created.

In the following, the production process of the local strain gradient stiffness matrix, i.e., KLSG, is presented. Substituting Eq. (53) into the local strain potential energy, presented in Eq. (51), and taking the integral over the length of the beam element give the total potential energy due to local part of the jth element:

$$\begin{gathered} U_{j}^{L} = \frac{\alpha }{2}\int_{{x_{j} }}^{{x_{j + 1} }} {\left[ {\left( {\frac{{\partial \gamma_{j} }}{\partial x} + \frac{{\partial^{2} w_{j} }}{{\partial x^{2} }}} \right)^{2} + l_{m}^{2} \left( {\frac{{\partial^{2} \gamma_{j} }}{{\partial x^{2} }} + \frac{{\partial^{3} w_{j} }}{{\partial x^{3} }}} \right)^{2} } \right]dx} \hfill \\ + \frac{\beta }{2}\int_{{x_{j} }}^{{x_{j + 1} }} {\left( {\gamma_{j}^{2} + l_{m}^{2} \left( {\frac{{\partial \gamma_{j} }}{\partial x}} \right)^{2} } \right)dx} . \hfill \\ \end{gathered}$$

(58)

Now, the elements of KLSG matrix, associated with the jth element, can be generated by replacing the shape functions into the Eq. (58) and taking the derivative with respect to the degrees of freedom. Therefore:

$$\begin{gathered} i = j \hfill \\ kl_{mn} = \alpha \int_{{x_{j} }}^{{x_{j + 1} }} {\left( {\frac{{\partial^{2} N_{m}^{w} }}{{\partial x^{2} }} + \frac{{\partial N_{m}^{\gamma } }}{\partial x}} \right)} \left( {\frac{{\partial^{2} N_{n}^{w} }}{{\partial x^{2} }} + \frac{{\partial N_{n}^{\gamma } }}{\partial x}} \right)dx + \beta \int_{{x_{j} }}^{{x_{j + 1} }} {N_{m}^{\gamma } } N_{n}^{\gamma } dx \hfill \\ + l_{m}^{2} \alpha \int_{{x_{j} }}^{{x_{j + 1} }} {\left( {\frac{{\partial^{3} N_{m}^{w} }}{{\partial x^{3} }} + \frac{{\partial^{2} N_{m}^{\gamma } }}{{\partial x^{2} }}} \right)} \left( {\frac{{\partial^{3} N_{n}^{w} }}{{\partial x^{3} }} + \frac{{\partial^{2} N_{n}^{\gamma } }}{{\partial x^{2} }}} \right)dx + l_{m}^{2} \beta \int_{{x_{j} }}^{{x_{j + 1} }} {\frac{{\partial N_{m}^{\gamma } }}{\partial x}} \frac{{\partial N_{n}^{\gamma } }}{\partial x}dx. \hfill \\ \end{gathered}$$

(59)

Finally, to extract the mass matrix, the kinetic energy of jth element is written and then the mass matrix element is obtained as follows:

$$\begin{gathered} T = \int_{{x_{j} }}^{{x_{j + 1} }} {\frac{1}{2}\left( {\rho I\phi_{j}^{2} + \rho Aw_{j}^{2} } \right)dx} \hfill \\ = \int_{{x_{j} }}^{{x_{j + 1} }} {\frac{1}{2}\left( {\rho I\left( {\frac{{\partial w_{j} }}{\partial x} + \gamma_{j} } \right)^{2} + \rho Aw_{j}^{2} } \right)dx} \hfill \\ M_{mn} = \rho I\int_{{x_{j} }}^{{x_{j + 1} }} {\left( {\frac{{\partial N_{m}^{w} }}{\partial x} + N_{m}^{\gamma } } \right)} \left( {\frac{{\partial N_{n}^{w} }}{\partial x} + N_{n}^{\gamma } } \right)dx + \rho A\int_{{x_{j} }}^{{x_{j + 1} }} {N_{m}^{w} } N_{n}^{w} dx. \hfill \\ \hfill \\ \end{gathered}$$

(60)

Here, it is helpful to note that, if the mesh distribution and nanobeam properties are uniform over the length of the nanobeam, the local stiffness and mass element matrices of all elements are similar, and therefore, they can be achieved easily by setting j = 1 in Eq. (59) and Eq. (60).

After generation of KLSG and KNSG matrices, the local/nonlocal strain gradient matrix, KLNSG, can be produced by applying desired local phase fraction factor:

$$KLNSG = \zeta_{1} KLSG + \left( {1 - \zeta_{1} } \right)KNSG.$$

(61)

Since the rotation is not considered as a degree of freedom in the present element, two ways are proposed for satisfying the boundary conditions with $\phi = 0$ and $\partial_{x} \phi = 0$. In the first one, similar to the approach utilized in Ref.[43], the penalty terms should be calculated and added to the total stiffness matrix, and in the second one, it can be considered that $\partial_{x} w = - \gamma$ for $\phi = 0$ and $\partial_{x,x} w = - \partial_{x} \gamma$ for $\partial_{x} \phi = 0$ in the boundaries, and therefore, the column and row associated with the $\gamma$ and $\gamma^{\prime}$ in the boundaries should be, respectively, subtracted from the column and row of $w^{\prime}$ and $w^{\prime\prime}$. Next, columns and rows related to the $\gamma$ and $\gamma^{\prime}$ must be removed.

In the last step, free vibration of LNSG Timoshenko nanobeams can be investigated by solving the following eigenvalue problem:

$$\left( {KLNSG - \omega^{2} M} \right)\left\{ {\begin{array}{*{20}c} {a_{1} } \\ \vdots \\ {a_{dof} } \\ \end{array} } \right\}e^{i\omega t} = 0\,;\,dof = {\text{5NE + 5}}{.}$$

(62)

3 Numerical results and discussion

Before identifying the influences of applying the LNSG elasticity on the size-dependent vibrations of nanobeams, it is essential that the accuracy and correctness of the present formulations and solutions are examined. These assessments and further investigations on vibrations of LNSG nanobeams are performed by considering nanobeams with square cross section, i.e., b = h, and $\rho = 1,E = 1,\,\nu = 0.3\,{\text{and}}\,k_{s} = 5/6$. Furthermore, to conduct a comprehensive study, several boundary conditions including simply supported (SS), clamped-free (CF), and clamped–clamped (CC) are evaluated.

Also, it should be noted that the BCs in which the boundary strains are set equal to zero are shown by “S”, while “F” means that the zero higher order stress is satisfied. For example, “CSCS” stands for a clamped–clamped beam with zero strains at both ends, while “CFCF” refers to a clamped–clamped beam with zero higher order stress in the boundaries.

First of all, in Tables 1, 2, 3, the convergence trend of the present LNSG FEM is checked by comparing the non-dimensional vibration frequencies obtained by the FE model with different number of elements and the exact ones generated by the present exact solutions. The results of Tables 1, 2, 3 are extracted for the LNSG nanobeams with k/L = 0.05 and l_m/L = 0.1.

Table 1 The first four non-dimensional vibration frequencies of two-phase strain gradient SSSS nanobeams, k/L = 0.05, l_m/L = 0.10

Table 2 The first four non-dimensional vibration frequencies of two-phase strain gradient CSFS nanobeams, k/L = 0.05, l_m/L = 0.10

Table 3 The first four non-dimensional vibration frequencies of two-phase strain gradient CSCS nanobeams, k/L = 0.05, l_m/L = 0.10

Now, to compare the results of the exact solutions with the FEM ones in the cases of the boundary conditions with zero higher order stresses, $\sigma_{kl}^{1} = 0$, the first four vibration frequencies related to the SFSF, CFFF, and CFCF beams are computed and listed in Table 4. The FEM results of Table 4 are produced by applying 20 elements. Also, these results are provided by considering h/L = 0.10, k/L = 0.05, $\zeta_{1} = 0.10$, and two different values of l_m/L.

Table 4 The first four non-dimensional frequencies of LNSG nanobeams with SFSF, CFFF, and CFCF boundary conditions. h/L = 0.10, k/L = 0.05, and $\zeta_{1} = 0.10$

Several interesting points can be taken from the results listed in Tables 1, 2, 3, 4. In all boundary conditions, there are good agreements between the FEM outcomes with the exact ones, and this confirms the consistency of LNSG theory, since the exact results are produced by solving the differential governing equations that are derived using the differential form of LNSG, while the FE model is directly constructed by the integral form of LNSG. Furthermore, the present FEM, which is constructed employing a new higher order beam element, maintains its precision in both thin and thick nanobeams. Therefore, it can be concluded that the present LNSG FEM is shear-locking-free and its convergence is desirable. Accordingly, all following results are produced from FEM with applying 20 elements.

In the following, since there is no work on the transverse vibrations of nanobeam with two-phase local/nonlocal strain gradient, the locking-free property and validity of the present FEM are more investigated by doing comparison between the present FEM results corresponding to thin beams with h/L = 0.0001 and Euler–Bernoulli ones reported in the previous works. Therefore, in Table. 5, by assuming l_m/L = 0, the non-dimensional frequencies of two-phase nanobeams, without strain gradient effect, are obtained for different nonlocal parameters and local phase fraction factors and then compared with the similar exact results which have been extracted by the procedure explained in Ref.[42]. Also, in Table 6, by applying a negligible value for local phase fraction factor, $\zeta_{1} \simeq 0.0$, as well as considering h/L = 0.0001 and l_m/L = 0.20, the frequency ratios, defined as Eq. (63), of integral nonlocal strain gradient nanobeams are computed and compared with the results of Ref.[59]:

$${\text{frequency}}\,{\text{ratio}} = \frac{{{\text{Size}}\,{\text{dependent}}\,{\text{frequency}}\,}}{{{\text{Classic}}\,{\text{frequency}}}}.$$

(63)

Table 5 Comparison between the first non-dimensional vibration frequency of the present LNSG Timoshenko nanobeams with h = 0.0001 L and l_m/L = 0 with those of two-phase Euler–Bernoulli nanobeams provided through the exact solution (exact) proposed in Reference[42]

Table 6 Comparison between the first two frequency ratios of the present LNSG Timoshenko nanobeams with h = 0.0001 L, l_m/L = 0.20, and $\zeta_{1} \simeq 0.0$ with those of integral nonlocal strain gradient Euler–Bernoulli nanobeams [59]

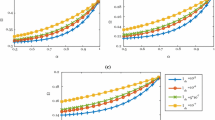
Tables 5 and 6 reveal that the present LNSG FE model of Timoshenko nanobeam is reliable and shear-locking-free, since, even in case of the thin nanobeams, there are good agreements between the present FEM outcomes with the results reported in the previous works. In the following, to identify how the LNSG affects the vibration of nanobeams, the frequency ratio (FR) is calculated in several cases and its variations are respectively plotted in Figs. 3, 4, 5 versus the l_m/k, $\zeta_{1}$, and mode number. In Fig. 3, by considering $\zeta_{1} = 0.01\,{\text{and}}\,k/L = 0.10$, the fundamental FRs of nanobeams with different boundary conditions and thickness ratios are depicted against the values of l_m/k. Figure 3 indicates that by going from the lower values of l_m/k to the higher ones, the FR curves, which are first located below the classic line, rise, and intersect the classic line in a certain value of l_m/k, depending on boundary conditions and thickness ratio. Thus, it can be said that the softening effect of nonlocal parameter is dominant in lower l_m/k, while the stiffening effect of strain gradient becomes more influential in higher l_m/k.

Fig. 3

Influence of $l_{m} /k$ on the fundamental frequency ratios of LNSG nanobeams with different boundary conditions and thickness ratios, $\zeta_{1} = 0.01,\,k/L = 0.10$

Figure. 4

Influence of local phase fraction factor on the fundamental frequency ratios of LNSG nanobeams with different boundary conditions, h/L = k/L = 0.10

Figure. 5

Variations of frequency ratio of thin and thick LNSG nanobeams in different transverse vibration modes: $\zeta_{1} = \,k/L = 0.10$

Also, the differences between the FRs corresponding to zero boundary strains, for example SSSS, with the ones of zero higher order boundary stresses, for example SFSF, are insignificant for small values of l_m/k, while these differences become considerable in higher l_m/k, especially for CF and SS nanobeams. Therefore, it can be concluded that the role of how the boundary conditions associated with strain gradient are satisfied is more important in the cases with higher values of l_m/k.

To identify the influences of local phase fractions factor and strain gradient on the FRs of the LNSG nanobeams, variations of the FRs due to changes of $\zeta_{1}$ are calculated for l_m/L = 0.0 as well as l_m/L = 0.05 and shown in Fig. 4. Evaluations of these results indicate that decreasing effect of nonlocality reduces when the local phase fraction factor grows. Also, considering strain gradient leads to stiffening effects and these effects are more significant in the cases with zero strains in boundaries than those associated with zero higher order boundary stresses. In addition, the clamped–clamped nanobeam shows more sensitivity to size-dependence factors than the other nanobeams, so that the lower value of FRs as well as the higher one occur in this type of nanobeam.

In the following, to study on the role of scale parameters associated with the LNSG on the different vibration modes of nanobeams, in Fig. 5, the FRs of the LNSG thin and thick nanobeams with zero strains in boundaries are displayed from the first to the fifteen mode for constant $\zeta_{1} = \,k/L = 0.10$ and different values of h/L and l_m/L.

From Fig. 5, it is clear that the FRs corresponding to l_m/L = 0 have the values less than one in all boundary conditions and mode numbers. This is due to the softening effect of nonlocal parameter which its effect intensifies in the higher modes. On the other hand, the curves of l_m/L = 0.10 locate above the one and it can be seen that these curves rise by going to the higher modes. Accordingly, it can be said that similar to the nonlocal effect, the role of stain gradient becomes more considerable in higher vibration modes. An interesting behavior can be seen in the cases of l_m/L = 0.05, so that from the first mode up to a specific mode, the role of nonlocality is more than the strain gradient and therefore the FRs show reduction, while after that specific mode, the downward trends have stopped and they can even increase due to the stiffness-hardening effect resulted from the strain gradient. Comparisons between the FRs of thin and thick nanobeams disclose that the FRs of thin beams show uniform manners, while the curves of the beams with h/L = 0.2 have non uniform trends. Also, in most cases, thin nanobeams show more sensitivity to scale parameters than the thick ones, especially in the higher modes.

Finally, to make a comparison between the results of EBT and TBT, the first non-dimensional vibration frequencies of LNSG nanobeams with different boundary conditions are computed by means of the exact solutions and presented in Table 7. These results are extracted for different values of h/L and l_m/L as well as constant values of k/L = 0.05 and $\zeta_{1} = 0.1$. Also, the percent of the difference, Dif. (%), between the outcomes of two beam theories is calculated and presented into Table 7.

Table 7 Comparison between the first non-dimensional frequencies of LNSG nanobeams obtained with different beam theories, k/L = 0.05 and $\zeta_{1} = 0.1$

From Table 7, it can be realized that, in all cases, the EBT produces higher frequencies than the TBT ones and theses differences intensify in the nanobeams with higher thickness ratio and stiffer boundary conditions. It is interesting to note that the difference percent depends on the l_m/L in such a way that, for the CF and CC nanobeams, the higher l_m/L values, the more discrepancy between the outcomes of EBT and TBT appears, while an opposite trend can be observed in the cases of the SS nanobeams.

4 Conclusion

Size-dependent transverse vibrations of Euler–Bernoulli and Timoshenko nanobeams are studied using the LNSG elasticity. The exact solutions and FEM are developed by two different approaches. For exact solutions, the equal differential form of LNSG is utilized to derive the differential governing equations and boundary conditions while the basic integral form of LNSG is employed to create the FE model. In addition, a new higher order shear-locking-free beam element with simple shape functions is proposed to construct a locking-free FE model of LNSG Timoshenko nanobeams. To determine the influences of nonlocality and strain gradient on the vibration of LNSG, several studies have been performed. Evaluating the results shows that:

• The softening effect of nonlocal parameter is dominant in lower l_m/k, while the stiffening effect of strain gradient becomes more influential in higher l_m/k.

• The role of how the boundary conditions associated with the strain gradient are satisfied is more important in the cases with higher values of l_m/k.

• The clamped–clamped nanobeam shows more sensitivity to LNSG size-dependence factors.

• In most cases, thin nanobeams shows more sensitivity to scale parameters than the thick ones, especially in higher modes.

• The present higher order beam element is an efficient, simple, and locking-free beam element which can be utilized in future studies in the problems of the LNSG with more complexity.

Finally, it can be stated that the consistency between the order of governing equations and number of all boundary conditions as well as agreement between the results of equal differential form of LNSG, exact solutions, and those of the integral from FEM prove that the LNSG can be a good alternative to the common nonlocal strain gradient theory which its inconsistency has been proved.

Appendix-A

Non dimensional form of CBCs related to the TBT:

$$\begin{gathered} \frac{1}{{\Gamma_{1}^{2} \Gamma_{2} }}(( - 1 + \zeta_{1} )\Gamma_{2} \Gamma_{4}^{2} \partial_{x} \Phi - ( - 1 + \zeta_{1} )\Gamma_{1} \Gamma_{2} \Gamma_{4}^{2} \partial_{x,x} \Phi - \hfill \\ ( - 1 + \zeta_{1} )\Gamma_{1}^{2} \Gamma_{2} (\partial_{x} \Phi - \Gamma_{4}^{2} \partial_{x,x,x} \Phi ) + ( - 1 + \zeta_{1} )\Gamma_{1}^{3} \Gamma_{2} (\partial_{x,x} \Phi - \Gamma_{4}^{2} \partial_{x,x,x,x} \Phi ) - \hfill \\ \Gamma_{1}^{4} (\lambda^{2} \partial_{x} \Phi + \Gamma_{2} (\lambda^{2} \overline{W}_{T} + \zeta_{1} \partial_{x,x,x} \Phi - \zeta_{1} \Gamma_{4}^{2} \partial_{x,x,x,x,x} \Phi )) + \hfill \\ \Gamma_{1}^{5} (\lambda^{2} \partial_{x,x} \Phi + \Gamma_{2} (\lambda^{2} \partial_{x} \overline{W}_{T} + \zeta_{1} \partial_{x,x,x,x} \Phi - \zeta_{1} \Gamma_{4}^{2} \partial_{x,x,x,x,x,x} \Phi )) + \hfill \\ (\Gamma_{2} \Gamma_{4}^{2} - \zeta_{1} \Gamma_{2} \Gamma_{4}^{2} )\partial_{x} \Phi ) = 0\,\,\,at\,\overline{x} = 0 \hfill \\ \end{gathered}$$

(64)

$$\begin{gathered} \frac{1}{{\Gamma_{1}^{2} \Gamma_{2} }}( - ( - 1 + \zeta_{1} )\Gamma_{2} \Gamma_{4}^{2} \partial_{x} \Phi - ( - 1 + \zeta_{1} )\Gamma_{1} \Gamma_{2} \Gamma_{4}^{2} \partial_{x,x} \Phi + \hfill \\ ( - 1 + \zeta_{1} )\Gamma_{1}^{2} \Gamma_{2} (\partial_{x} \Phi - \Gamma_{4}^{2} \partial_{x,x,x} \Phi ) + ( - 1 + \zeta_{1} )\Gamma_{1}^{3} \Gamma_{2} (\partial_{x,x} \Phi - \Gamma_{4}^{2} \partial_{x,x,x,x} \Phi ) + \hfill \\ \Gamma_{1}^{4} (\lambda^{2} \partial_{x} \Phi + \Gamma_{2} (\lambda^{2} \overline{W}_{T} + \zeta_{1} \partial_{x,x,x} \Phi - \zeta_{1} \Gamma_{4}^{2} \partial_{x,x,x,x,x} \Phi )) + \hfill \\ \Gamma_{1}^{5} (\lambda^{2} \partial_{x,x} \Phi + \Gamma_{2} (\lambda^{2} \partial_{x} \overline{W}_{T} + \zeta_{1} \partial_{x,x,x,x} \Phi - \zeta_{1} \Gamma_{4}^{2} \partial_{x,x,x,x,x,x} \Phi )) + \hfill \\ ( - \Gamma_{2} \Gamma_{4}^{2} + \zeta_{1} \Gamma_{2} \Gamma_{4}^{2} )\partial_{x} \Phi ) = 0\,\,at\,\overline{x} = 1 \hfill \\ \end{gathered}$$

(65)

$$\begin{gathered} \frac{1}{{\Gamma_{1}^{3} }}(( - 1 + \zeta_{1} )\Gamma_{4}^{2} (\Phi + \partial_{x} \overline{W}_{T} ) - ( - 1 + \zeta_{1} )\Gamma_{1} \Gamma_{4}^{2} (\partial_{x} \Phi + \partial_{x,x} \overline{W}_{T} ) - \hfill \\ ( - 1 + \zeta_{1} )\Gamma_{1}^{2} (\Phi + \partial_{x} \overline{W}_{T} - \Gamma_{4}^{2} (\partial_{x,x} \Phi + \partial_{x,x,x} \overline{W}_{T} )) + \hfill \\ ( - 1 + \zeta_{1} )\Gamma_{1}^{3} (\partial_{x} \Phi + \partial_{x,x} \overline{W}_{T} - \Gamma_{4}^{2} (\partial_{x,x,x} \Phi + \partial_{x,x,x,x} \overline{W}_{T} )) - \hfill \\ \Gamma_{1}^{4} (\lambda^{2} \Gamma_{3} \partial_{x} \overline{W}_{T} + \zeta_{1} (\partial_{x,x} \Phi + \partial_{x,x,x} \overline{W}_{T} - \Gamma_{4}^{2} (\partial_{x,x,x,x} \Phi + \partial_{x,x,x,x,x} \overline{W}_{T} ))) + \hfill \\ \Gamma_{1}^{5} (\lambda^{2} \Gamma_{3} \partial_{x,x} \overline{W}_{T} + \zeta_{1} (\partial_{x,x,x} \Phi + \partial_{x,x,x,x} \overline{W}_{T} - \Gamma_{4}^{2} (\partial_{x,x,x,x,x} \Phi + \partial_{x,x,x,x,x,x} \overline{W}_{T} ))) + \hfill \\ (\Gamma_{4}^{2} - \zeta_{1} \Gamma_{4}^{2} )(\Phi + \partial_{x} \overline{W}_{T} ))\, = 0\,\,\,at\,\overline{x} = 0 \hfill \\ \end{gathered}$$

(66)

$$\begin{gathered} \frac{1}{{\Gamma_{1}^{3} }}( - ( - 1 + \zeta_{1} )\Gamma_{4}^{2} (\Phi + \partial_{x} \overline{W}_{T} ) - ( - 1 + \zeta_{1} )\Gamma_{1} \Gamma_{4}^{2} (\partial_{x} \Phi + \partial_{x,x} \overline{W}_{T} ) + \hfill \\ ( - 1 + \zeta_{1} )\Gamma_{1}^{2} (\Phi + \partial_{x} \overline{W}_{T} - \Gamma_{4}^{2} (\partial_{x,x} \Phi + \partial_{x,x,x} \overline{W}_{T} )) + \hfill \\ ( - 1 + \zeta_{1} )\Gamma_{1}^{3} (\partial_{x} \Phi + \partial_{x,x} \overline{W}_{T} - \Gamma_{4}^{2} (\partial_{x,x,x} \Phi + \partial_{x,x,x,x} \overline{W}_{T} )) + \hfill \\ \Gamma_{1}^{4} (\lambda^{2} \Gamma_{3} \partial_{x} \overline{W}_{T} + \zeta_{1} (\partial_{x,x} \Phi + \partial_{x,x,x} \overline{W}_{T} - \Gamma_{4}^{2} (\partial_{x,x,x,x} \Phi + \partial_{x,x,x,x,x} \overline{W}_{T} ))) + \hfill \\ \Gamma_{1}^{5} (\lambda^{2} \Gamma_{3} \partial_{x,x} \overline{W}_{T} + \zeta_{1} (\partial_{x,x,x} \Phi + \partial_{x,x,x,x} \overline{W}_{T} - \Gamma_{4}^{2} (\partial_{x,x,x,x,x} \Phi + \partial_{x,x,x,x,x,x} \overline{W}_{T} ))) + \hfill \\ ( - \Gamma_{4}^{2} + \zeta_{1} \Gamma_{4}^{2} )(\Phi + \partial_{x} \overline{W}_{T} )) = 0\,\,\,at\,\overline{x} = 1. \hfill \\ \end{gathered}$$

(67)