Shifted Chebyshev collocation of the fourth kind with convergence analysis for the space–time fractional advection-diffusion equation

Abstract

The main purpose of this paper is to design a numerical method for solving the space–time fractional advection-diffusion equation (STFADE). First, a finite difference scheme is applied to obtain the semi-discrete in time variable with convergence order $\mathcal {O}(\tau ^{2-\beta })$. In the next, to discrete the spatial fractional derivative, the Chebyshev collocation method of the fourth kind has been applied. This discrete scheme is based on the closed formula for the spatial fractional derivative. Besides, the time-discrete scheme has studied in the $L_{2}$ space by the energy method and we have proved the unconditional stability and convergence order. Finally, we solve three examples by the proposed method and the obtained results are compared with other numerical problems. The numerical results show that our method is much more accurate than existing techniques in the literature.

1 Introduction

Fractional calculus (FC) is extended variants of classical integer-order ones that are produced by replacing fractional integer-order derivatives. Many applications of FC are in the branch of science and engineering such as physics, optimal control, chemistry, economics, polymeric materials and social science [3, 15, 17, 21,22,23,24,25]. Because of FC’s non-local, the solution of fractional differential equations (FDEs), such as the diffusion and reaction-diffusion models, has been considerable attention in the physical environment, statistical mechanics and continuum [1, 7, 8]. These physical models explain the action of the plural movement of microparticles in a material resulting from the random movement of each microparticle. It is also suitable as a topic relevant to the Markov system in mathematics as well as in different fields. These subjects can be explained using the diffusion equations named Brown equations. In the Brownian case, diffusion with an additional field of velocity and diffusion under the influence of a constant field of external force are both based on the equation of advection-dispersion. This is no longer true in the case of anomalous diffusion, i.e., the fractional generalization that varies in the case of advection and carries an external force field in [20]. A straightforward extension of the model of continuous-time random walk results in a fractional advection-dispersion equation (FADE).

Space and time-fractional diffusion equation are two main types of FADEs [13]. In the current paper, we investigate the STFADE, as follows:

$$\begin{aligned} \begin{aligned}&{}_{0}\mathcal {D}_{t} ^{\beta } u(x,t)=a(x,t) {}_{0}\mathcal {D}_{x}^{\alpha } u(x,t)+b(x,t) {}_{0}\mathcal {D}_{x}^{\gamma } u(x,t)+q(x,t),\\&0< x< 1,~~~ 0< t \le T,~~~ 0< \beta , \gamma \le 1,~~~ 1 < \alpha \le 2, \end{aligned} \end{aligned}$$

(1)

where a(x, t) and b(x, t) are known functions and q(x, t) is the source term. An initial condition and the boundary conditions are also assumed:

$$\begin{aligned} u(x, 0)= & {} g(x),\quad 0<x<L,\quad u(0, t)=\mathbf {\upsilon }_{0}(t),\nonumber \\ u(L, t)= & {} \mathbf {\upsilon }_{1}(t), \quad 0<t\le T, \end{aligned}$$

(2)

where ${}_{0}\mathcal {D}_{t} ^{\beta }$ is the right Caputo fractional of the order $\beta$. For $n-1<\vartheta \le n,~ n\in \mathbb {N},$ the left and right Caputo fractional derivative of order $\vartheta$, is defined by

$$\begin{aligned} \begin{aligned}&{}^{C}_{a}{\mathcal {D}}_{x}^{\vartheta }u(x, t)= \frac{1}{\Gamma (n-\vartheta )}\int _{a}^{x}{(x-\tau )^{n-\vartheta -1}}\frac{{\partial }^{n} u(\tau , t) }{\partial {\tau }^{n}}\mathrm{d}\tau ,\\&{}^{C}_{x}{\mathcal {D}}_{b}^{\vartheta }u(x, t)= \frac{(-1)^{n}}{\Gamma (n-\vartheta )}\int _{x}^{b}{(\tau -x)^{n-\vartheta -1}}\frac{{\partial }^{n} u(\tau , t) }{\partial {\tau }^{n}}\mathrm{d}\tau . \end{aligned} \end{aligned}$$

If $n-1<\vartheta <n \in \mathbb {N}$, then we have $\lim _{\vartheta \rightarrow n}{}^{C}_{a}{\mathcal {D}}_{x}^{\vartheta }u(x, t)=\lim _{\vartheta \rightarrow n}{}^{C}_{x}{\mathcal {D}}_{b}^{\vartheta }u(x, t)=\frac{{\partial }^{n} u(x, t) }{\partial {x}^{n}}$. For $a=0$, we introduce the notation $\mathcal {D}^{\vartheta }_{x}$ for the space derivative. Equation (1) is the classical advection-dispersion equation (ADE) in the case of $\beta =\gamma =1$ and $\alpha =2$. We presume that STFADE has a unique and smooth solution under the initial and boundary conditions of relation (2).

In recent years, several methods have been proposed for solving the ADEs. Liu et al. applied the Mellin and Laplace transform for solving the time-fractional ADE in [18]. Moreover, [16] represented practical numerical schemes with variable coefficients on a finite domain to solve the one-dimensional space fractional ADE. Huang and Nie [9] by using Green functions and applying the Fourier–Laplace transforms approximated the STFADE. Momani et al. [12] produced an accurate algorithm for the Adomian decomposition to build a numerical solution of STFADE. Recently, the theorems of existence and uniqueness for STFADE in [10, 19, 23] and collocation method by using the shifted Chebyshev and rational Chebyshev polynomials in [4] are discussed.

The main aim of this paper is to represent a new numerical scheme to solve STFADE. The proposed scheme is founded on a finite difference method and a Chebyshev collocation method of the fourth kind. In Sect. 2, we investigate the time-discrete approach in the convergence and unconditional stability case. Then, we apply the Chebyshev collocation method to discrete the spatial direction and to get a full-discrete plan in Sect. 3. Eventually, we introduce three numerical examples to depict the efficiency of the new manner.

2 The convergence analysis of the time-discrete method

In this section, we obtain the semi-discrete scheme and prove the convergence and stability of the new numerical technique for Eq. (1). To obtain this, we need some preliminaries. Now, we define the functional space

$$\begin{aligned} \mathcal {H}^{n}_{\Omega }(\varphi )=\left\{ \varphi \in L^{2}(\Omega ),~~ \mathcal {D}^{\alpha }_{x}\varphi \in L^{2}(\Omega ),~ \forall ~|\alpha |\le n \right\} , \end{aligned}$$

where $\mathcal {D}^{\alpha }_{x}= \frac{\partial ^{\alpha }}{\partial x^{\alpha }}$ and $L^{2}(\Omega )$ is the Lebesgue integrable in $\Omega$ with the inner product.

$$\begin{aligned} \langle \varphi (x), \psi (x)\rangle =\int _{\Omega }\varphi (x)\psi (x)\mathrm{d}x, \end{aligned}$$

and the standard norm $\Vert u(x)\Vert _{2}=\langle u(x), u(x)\rangle ^{\frac{1}{2}}$. For $\gamma >0$ , the semi-norm and norm for right fractional derivative space $J_\mathrm{R}^{\gamma }$ are defined as follows

$$\begin{aligned} \vert \varphi \vert _{J_\mathrm{R}^{\gamma }}=\Vert {}_{a}\mathcal {D}_{x}^{\gamma }\varphi \Vert _{L^{2}(\mathbb {R})},~~ \Vert \varphi \Vert _{J_\mathrm{R}^{\gamma }}=\left( \Vert \varphi \Vert ^{2}_{L^{2}({\mathbb {R}})}+\Vert {}_{a}\mathcal {D}_{x}^{\gamma }\varphi \Vert ^{2} _{\mathrm{L}^{2}(\mathbb {R})}\right) ^{\frac{1}{2}}, \end{aligned}$$

respectively. Similar to the above relationship for left fractional derivative space $J_\mathrm{L}^{\gamma }$, we have

$$\begin{aligned} \vert \varphi \vert _{J_\mathrm{L}^{\gamma }}=\Vert {}_{x}\mathcal {D}_\mathrm{b}^{\gamma }\varphi \Vert _{\mathrm{L}^{2}(\mathbb {R})},~~ \Vert \varphi \Vert _{J_\mathrm{L}^{\gamma }}=\left( \Vert \varphi \Vert ^{2}_{\mathrm{L}^{2}({\mathbb {R}})}+\Vert {}_{x}\mathcal {D}_\mathrm{b}^{\gamma }\varphi \Vert ^{2} _{\mathrm{L}^{2}(\mathbb {R})}\right) ^{\frac{1}{2}}. \end{aligned}$$

It should be noticed that the notations $J_\mathrm{L}^{\gamma }, J_\mathrm{R}^{\gamma }$ denote the closure of $\mathbb {C}_{0}^{\infty }(\mathbb {R})$ with respect to $\Vert \cdot \Vert _{J_\mathrm{L}^{\gamma }}, \Vert \cdot \Vert _{J_\mathrm{R}^{\gamma }}$, respectively. We define symmetric fractional derivative space $J_\mathrm{S}^{\gamma }$ for $\gamma >0,~\gamma \ne n-\frac{1}{2},~n\in \mathbb {N}$ with the semi-norm and norm

$$\begin{aligned} \vert \varphi \vert _{J_\mathrm{S}^{\gamma }}=\left| \langle {}_{a}\mathcal {D}_{x}^{\gamma }\varphi ,{}_{x}\mathcal {D}_\mathrm{b}^{\gamma }\varphi \rangle \right| _{L^{2}(\mathbb {R})},~~ \Vert \varphi \Vert _{J_\mathrm{S}^{\gamma }}=\left( \Vert \varphi \Vert ^{2}_{\mathrm{L}^{2}({\mathbb {R}})}+\vert \varphi \vert _{J_\mathrm{S}^{\gamma }}^{2}\right) ^{\frac{1}{2}}, \end{aligned}$$

respectively. Let us introduce some lemmas for developing and proving the stability of the numerical solution of (1) that are listed below.

Lemma 1

(See [24].) Assume $\theta$ be non-negative constant, $s_{m}$ and $r_{ k}$ are non-negative sequences that the sequence $\upsilon _{m}$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} \upsilon _{ 0}\le \theta , &{}\theta >0,\\ \upsilon _{ m}\le \theta +\sum \limits _{k=0}^{m-1}r_{k}+\sum \limits _{k=0}^{m-1}s_{k}\upsilon _{m}, &{} m\ge 1, \end{array}\right. } \end{aligned}$$

then $\upsilon _{m}$ satisfies

$$\begin{aligned} \upsilon _{ m}\le \left( \theta +\sum \limits _{k=0}^{m-1}r_{k} \right) \exp \left( \sum \limits _{k=0}^{m-1}s_{k}\right) . \end{aligned}$$

Lemma 2

(See [6, 9].) For any $u, \nu \in \mathcal {H}_{\Omega }^{\frac{\alpha }{2}}$ we have

$$\begin{aligned} \begin{aligned}&\langle {}_{a}\mathcal {D}^{\alpha }_{x}u, {}_{x}{\mathcal {D}}^{\alpha }_\mathrm{b}u\rangle =\cos (\alpha \pi )\Vert {}_\mathrm{a}\mathcal {D}^{\alpha }_{x}u\Vert ^{2}_{\mathrm{L}_{2}(\Omega )}\\&\quad =\cos (\alpha \pi )\Vert {}_{x}\mathcal {D}^{\alpha }_\mathrm{b}u\Vert ^{2}_{\mathrm{L}_{2}(\Omega )}, ~~ \forall \alpha >0,\\&\langle {}_\mathrm{a}\mathcal {D}^{\alpha }_{x}u, \nu \rangle =\left\langle {}_{a}\mathcal {D}^{\frac{\alpha }{2}}_{x}u, {}_{x}\mathcal {D}^{\frac{\alpha }{2}}_\mathrm{b}\nu \right\rangle , \quad \langle {}_{x}\mathcal {D}^{\alpha }_\mathrm{b}u, \nu \rangle \\&\quad =\left\langle {}_{x}\mathcal {D}^{\frac{\alpha }{2}}_\mathrm{b}u, {}_{a}\mathcal {D}^{\frac{\alpha }{2}}_{x}\nu \right\rangle ,~~~~~~\forall \alpha \in (1, 2). \end{aligned} \end{aligned}$$

(3)

Lemma 3

(See [5].) If $\varphi \in J_{L}^{\gamma }, J_{R}^{\gamma }$ and $0<\gamma <\alpha$, then we have

$$\begin{aligned} \begin{aligned}&\Vert \varphi \Vert _{\mathrm{L}^{2}(\mathbb {R})}\le C \vert \varphi \vert _{J_\mathrm{R}^{\gamma }},~~ \vert \varphi \vert _{J_\mathrm{R}^{\gamma }} \le C \vert \varphi \vert _{J_\mathrm{R}^{\alpha }},\\&\Vert \varphi \Vert _{\mathrm{L}^{2}(\mathbb {R})}\le C \vert \varphi \vert _{J_\mathrm{L}^{\gamma }},~~ \vert \varphi \vert _{J_\mathrm{L}^{\gamma }} \le C \vert \varphi \vert _{J_\mathrm{L}^{\alpha }}, \end{aligned} \end{aligned}$$

(4)

where C is constant. The analogous results exist for $u\in J_\mathrm{S}^{\gamma }$ with $\gamma >0, \gamma \ne n-\frac{1}{2}, n\in \mathbb {N}$.

Lemma 4

(See [14].) Let $\beta \in (0,1)$ then the following $\tau ^{2-\beta }$-order of the Caputo derivative approximation formula (CDAF) into each subintervals [0, T] with the uniform step size $\tau =\frac{T}{M}$ such that the node points are $t_{j}=j\tau ,~ j=0, 1, \ldots , M$, holds

$$\begin{aligned} {\mathcal {D}}_{t}^{\beta }u(x,t)=\frac{ \tau ^{-\beta }}{\Gamma (2-\beta )}\sum _{j=0}^{M}\mathcal {S}_{M,j}u(x,t_{j})+\mathcal {O}({ \tau } ^{2-\beta }), \end{aligned}$$

where

$$\begin{aligned} \small {\mathcal {S}_{M,j}= {\left\{ \begin{array}{ll} 1, &{} j=M, \\ (M-j-1)^{1-\beta }-2(M-j)^{1-\beta }+(M-j+1)^{1-\beta }, &{} 1\le j< M,\\ (M-1)^{1-\beta }-(M)^{1-\beta }, &{} j=0. \\ \end{array}\right. }} \end{aligned}$$

Lemma 5

The coefficients $\mathcal {S}_{M,j},~ j=0, 1, \ldots , M$, in the CDAF defined by Lemma 4satisfy the properties:

• 1. $\mathcal {S}_{M,M}=1$,

• 2. $-1<\mathcal {S}_{M,j}<0, ~~j=0, 1,\ldots , M-1$,

• 3. $\left| \sum _{j=1}^{M-1}\mathcal {S}_{M,j}\right| <1$,

• 4. $-2<\mathcal {S}_{M,0}+\sum _{j=1}^{M-1}\mathcal {S}_{M,j}<1.$

Proof

Let $f(x)=(x)^{1-\beta }$, that is strictly increasing for all $x>0$. By using the mean value theorem and describing $f(M-j)=(M-j)^{1-\beta },~ M>j$, we can prove the lemma. We are not going to cover the details here.□

Now, we obtain the semi-discrete form of Eq. (1) at points $\lbrace t _{j} \rbrace _{j=0}^{j=M}$. By using Lemma 4, we can write

$$\begin{aligned}&U^{M}-\mathfrak {a}\tau ^{\beta }\mathcal {D}_{x}^{\alpha }U^{M}-\mathfrak {b}\tau ^{\beta }\mathcal {D}_{x}^{\gamma }U^{M}\nonumber \\&\quad =\sum _{j=0}^{M-1}\mathcal {\overline{S}}_{M,j}U^{j}+\tau ^{\beta }Q^{M}+\tau ^{\beta }\mathfrak {R}^{M},~~\nonumber \\&\qquad 0<\gamma \le 1,~~ 1 < \alpha \le 2, \end{aligned}$$

(5)

where $U^{M}=u(x,t_{M}), Q^{M}=\Gamma (2-\beta )q(x,t_{M}), \mathfrak {a}=\Gamma (2-\beta )a(x,t_{M}), \mathfrak {b}=\Gamma (2-\beta )b(x,t_{M})$ and $\overline{\mathcal{S}}_{M,j}=-{\mathcal{S}}_{M,j}$. The truncation term is $\mathfrak {R}^{M}$ where a positive constant C exists such that $\mathfrak {R}^{M}\le C\mathcal {O}({ \tau } ^{2-\beta })$. By omitting the truncation term, we can get the following numerical approach, in which $U^{M}$ and N are the approximation solution of Eq. (5) and the total number of the points in the x domain, respectively.

$$\begin{aligned} \small {{\left\{ \begin{array}{ll} U^{M}-\fancyscript {a}\tau ^{\beta }\mathcal {D}_{x}^{\alpha }U^{M}-\fancyscript {b}\tau ^{\beta }\mathcal {D}_{x}^{\gamma }U^{M}=\sum _{j=0}^{M-1}\mathcal {\overline{S}}_{M,j}U^{j}+\tau ^{\beta }Q^{M},\\ U^{j}_{0}=u(0,t_{j})=\mathbf {\upsilon }_{0}(t_{j}),~~ U^{j}_{N}=u(1,t_{j})=\mathbf {\upsilon }_{1}(t_{j}), ~j=0, 1,\ldots , M,\\ U^{0}=g(x),\quad 0<x<1. \end{array}\right. }} \end{aligned}$$

(6)

We suppose that in the current section for $x\in [0,1]$, we have $\mathfrak {a}, \mathfrak {b} >0$.

Lemma 6

Let $U^{k}\in \mathcal {H}^{n}_{\Omega }, k=1, 2, \ldots , M$ and $C_{1}, C_{2}\in \mathbb {R}$, be the solution of time discrete (6), then

$$\begin{aligned} \Vert U^{k}\Vert \le C_{1} \Vert U^{0}\Vert +C_{2}\max _{{\begin{matrix} {0\le r\le N}\\ {0\le l\le M}\end{matrix}}}\Vert Q_{r}^{l}\Vert . \end{aligned}$$

Proof

We use the mathematical induction on k to prove the above inequality. For $k=1$, we get

$$\begin{aligned} U^{1}-\mathfrak {a}\tau ^{\beta }\mathcal {D}_{x}^{\alpha }U^{1}-\mathfrak {b}\tau ^{\beta }\mathcal {D}_{x}^{\gamma }U^{1}= \mathcal {\overline{S}}_{1,0}U^{0}+\tau ^{\beta }Q^{1}. \end{aligned}$$

(7)

Multiplying Eq. (7) by $U^{1}$ and integrating on $\Omega$, it results

$$\begin{aligned}&\langle U^{1},U^{1}\rangle -\mathfrak {a} \tau ^{\beta }\langle \mathcal {D}_{x}^{\alpha }U^{1},U^{1}\rangle \nonumber \\&\quad -\mathfrak {b}\tau ^{\beta }\langle \mathcal {D}_{x}^{\gamma }U^{1},U^{1}\rangle =\mathcal {\overline{S}}_{1,0}\langle U^{0},U^{1}\rangle \nonumber \\&\quad +\tau ^{\beta }\langle Q^{1},U^{1}\rangle . \end{aligned}$$

(8)

By using of Lemma 2, the second term of the left-hand side of the above inequality is negative, i.e.,

$$\begin{aligned} \langle {}_{a}\mathcal {D}_{x}^{\alpha }U^{1},U^{1}\rangle= & {} \langle {}_{a}\mathcal {D}_{x}^{\frac{\alpha }{2}}U^{1},{}_{x}\mathcal {D}^{\frac{\alpha }{2}}_{b}U^{1}\rangle \\= & {} \cos \left( \frac{\alpha }{2}\pi \right) \Vert {}_{a}\mathcal {D}_{x}^{\frac{\alpha }{2}}\Vert ^{2}\\= & {} \cos \left( \frac{\alpha }{2}\pi \right) \Vert {}_{x}\mathcal {D}_{b}^{\frac{\alpha }{2}}\Vert ^{2}<0,~~\forall ~1<\alpha \le 2. \end{aligned}$$

Regarding Lemmas 2 and 3 for the third term of left-hand side Eq. (8), one can obtain

$$\begin{aligned} \langle {}_{a}\mathcal {D}_{x}^{\gamma }U^{1},U^{1}\rangle= & {} \left\langle {}_{a}\mathcal {D}_{x}^{\frac{\gamma }{2}}U^{1},{}_{x}\mathcal {D}^{\frac{\gamma }{2}}_{b}U^{1}\right\rangle \\\le & {} C \left\langle {}_{a}\mathcal {D}_{x}^{\frac{\alpha }{2}}U^{1},{}_{x}\mathcal {D}^{\frac{\alpha }{2}}_{b}U^{1}\right\rangle <0. \end{aligned}$$

The aforesaid relation and by using Lemma 5 can be rewritten as

$$\begin{aligned} \Vert U^{1} \Vert \le \mathcal {\overline{S}}_{1,0}\Vert U^{0} \Vert +\tau ^{\beta }\max _{0\le r\le N}\Vert Q_{r}^{1} \Vert \le \Vert U^{0} \Vert +\max _{0\le r\le N}\Vert Q_{r}^{1} \Vert . \end{aligned}$$

Now, assume that the induction principle is true for all $k=1, 2, \ldots , M-1$,

$$\begin{aligned} \Vert U^{k} \Vert \le \Vert U^{0} \Vert +\max _{0\le r\le N}\Vert Q_{r}^{k} \Vert . \end{aligned}$$

Multiplying Eq. (6) by $U^{M}$ and integrating on $\Omega$, it follows that

$$\begin{aligned}&\langle U^{M},U^{M}\rangle -\mathfrak {a} \tau ^{\beta }\langle \mathcal {D}_{x}^{\alpha }U^{M},U^{M}\rangle -\mathfrak {b}\tau ^{\beta }\langle \mathcal {D}_{x}^{\gamma }U^{M},U^{M}\rangle \nonumber \\&\qquad =\sum _{j=0}^{M-1}\mathcal {\overline{S}}_{M,j}\langle U^{j},U^{M}\rangle +\tau ^{\beta }\langle Q^{M},U^{M}\rangle . \end{aligned}$$

(9)

From Lemmas 2, 3 and 5 and using the Cauchy–Schwarz inequality, we deduce the following relation

$$\begin{aligned} \begin{aligned}&\Vert U^{M}\Vert \le \sum _{j=0}^{M-1}\mathcal {\overline{S}}_{M,j}\Vert U^{j}\Vert +\max _{0\le r\le N}\Vert Q_{r}^{M}\Vert = \mathcal {\overline{S}}_{M,0} \Vert U^{0}\Vert \\&\quad +\sum _{j=1}^{M-1}\mathcal {\overline{S}}_{M,j}\Vert U^{j}\Vert +\max _{0\le r\le N}\Vert Q_{r}^{M}\Vert \\&\le \mathcal {\overline{S}}_{M,0} \Vert U^{0}\Vert +\sum _{j=1}^{M-1}\mathcal {\overline{S}}_{M,j}\left( \Vert U^{0}\right. \Vert \\&\quad \left. +\max _{0\le r\le N}\Vert Q_{r}^{j}\Vert \right) +\max _{0\le r\le N}\Vert Q_{r}^{M}\Vert \\&\le \left( \mathcal {\overline{S}}_{M,0} +\sum _{j=1}^{M-1}\mathcal {\overline{S}}_{M,j} \right) \Vert U^{0}\Vert +\sum _{j=1}^{M-1}\mathcal {\overline{S}}_{M,j}\max _{0\le r\le N}\Vert Q_{r}^{j}\Vert \\&+\max _{0\le r\le N}\Vert Q_{r}^{M}\Vert \le C_{1} \Vert U^{0}\Vert +C_{2}\max _{{\begin{matrix} {0\le r\le N}\\ {0\le l\le M}\end{matrix}}}\Vert Q_{r}^{l}\Vert , \end{aligned} \end{aligned}$$

(10)

where $C_{1}$ and $C_{2}$ are constants. This concludes the proof of Lemma 6.□

Theorem 1

Assume $U^{M}\in \mathcal {H}^{n}_{\Omega }$ is the solution of semi-discrete scheme (6). Then, system (6) is unconditionally stable.

Proof

We suppose that $\widehat{U}^{j}, j=1, 2, \ldots , M$, is the solution of scheme (6) with the initial condition $\widehat{U}^{0}=u(x, 0)$. Then, given the error $\varepsilon ^{j}=U^{j}-\widehat{U}^{j}$, Eq. (5) is converted as follows

$$\begin{aligned} \varepsilon ^{M}-\mathfrak {a}\tau ^{\beta }\mathcal {D}_{x}^{\alpha }\varepsilon ^{M}-\mathfrak {b}\tau ^{\beta }\mathcal {D}_{x}^{\gamma }\varepsilon ^{M}=\sum _{j=0}^{M-1}\mathcal {\overline{S}}_{M,j}\varepsilon ^{j}, \end{aligned}$$

(11)

from Lemma 6 and the above relation, we have

$$\begin{aligned} \Vert \varepsilon ^{j}\Vert \le C \Vert \varepsilon ^{0}\Vert , \quad j=1, 2, \ldots , M, \end{aligned}$$

which completes the proof of the unconditional stability.

Theorem 2

If $\varepsilon ^{k}=U^{k}-\widehat{U}^{k}, ~k=1, 2, \ldots , M$, be the errors to Eq. (6), then the time-discrete scheme is convergent with the convergence order $\mathcal {O}({ \tau })$.

Proof

From Eq. (5), we get the following round-off error equation

$$\begin{aligned} \varepsilon ^{k}-\mathfrak {a}\tau ^{\beta }\mathcal {D}_{x}^{\alpha }\varepsilon ^{k}-\mathfrak {b}\tau ^{\beta }\mathcal {D}_{x}^{\gamma }\varepsilon ^{k}=\sum _{j=0}^{k-1}\mathcal {\overline{S}}_{k,j}\varepsilon ^{j}+\tau ^{\beta }\mathfrak {R}^{k}. \end{aligned}$$

(12)

There is a positive constant C where $\mathfrak {R}^{M}\le C\mathcal {O}({ \tau } ^{2-\beta })$.

With multiplying Eq. (12) by $\varepsilon ^{k}$ and integrating, we get the following relation

$$\begin{aligned}&\langle \varepsilon ^{k},\varepsilon ^{k}\rangle -\mathfrak {a}\tau ^{\beta }\langle \mathcal {D}_{x}^{\alpha }\varepsilon ^{k},\varepsilon ^{k}\rangle -\mathfrak {b}\tau ^{\beta }\langle \mathcal {D}_{x}^{\gamma }\varepsilon ^{k},\varepsilon ^{k}\rangle \\&\quad =\sum _{j=0}^{k-1}\mathcal {\overline{S}}_{k,j}\langle \varepsilon ^{j},\varepsilon ^{k}\rangle +\tau ^{\beta } \langle \mathfrak {R}^{k},\varepsilon ^{k}\rangle . \end{aligned}$$

Using the Cauchy–Schwarz inequality, Lemmas 2, 3 and 5, we can write the following inequality

$$\begin{aligned} \begin{aligned} \Vert \varepsilon ^{k}\Vert&\le \sum _{j=0}^{k-1}\mathcal {\overline{S}}_{k,j}\Vert \varepsilon ^{j}\Vert +\tau ^{\beta } \Vert \mathfrak {R}^{k}\Vert \\&\le \mathcal {\overline{S}}_{k,k-1}\Vert \varepsilon ^{k-1}\Vert +\sum _{j=0}^{k-2}\mathcal {\overline{S}}_{k,j}\Vert \varepsilon ^{j}\Vert +\tau ^{\beta } \Vert \mathfrak {R}^{k}\Vert \\&\le \Vert \varepsilon ^{k-1}\Vert +\sum _{j=0}^{k-2}\mathcal {\overline{S}}_{k,j}\Vert \varepsilon ^{j}\Vert +\tau ^{\beta } \Vert \mathfrak {R}^{k}\Vert , \end{aligned} \end{aligned}$$

or in the equivalent form, we can get

$$\begin{aligned} \Vert \varepsilon ^{k}\Vert -\Vert \varepsilon ^{k-1}\Vert \le \sum _{j=0}^{k-2}\mathcal {\overline{S}}_{k,j}\Vert \varepsilon ^{j}\Vert +\tau ^{\beta } \Vert \mathfrak {R}^{k}\Vert , \end{aligned}$$

Summing the above equation for k form 1 to M and since $\Vert \varepsilon ^{0}\Vert =0$, we get

$$\begin{aligned} \Vert \varepsilon ^{M}\Vert \le \sum _{k=1}^{M} \sum _{j=0}^{k-2}\mathcal {\overline{S}}_{k,j}\Vert \varepsilon ^{j}\Vert +\tau ^{\beta } \sum _{k=1}^{M}\Vert \mathfrak {R}^{k}\Vert , \end{aligned}$$

by changing index, the above relation simply can be rewritten as

$$\begin{aligned} \Vert \varepsilon ^{M}\Vert \le \sum _{k=0}^{M-2} \mathcal {\overline{S}}_{M,k}\Vert \varepsilon ^{k}\Vert +\tau ^{\beta }\sum _{k=0}^{M-1} \Vert \mathfrak {R}^{k+1}\Vert . \end{aligned}$$

We will write on the other hand

$$\begin{aligned} \Vert \varepsilon ^{M}\Vert \le \Vert \varepsilon ^{M}\Vert +\mathcal {\overline{S}}_{M,M-1}\Vert \varepsilon ^{M-1}\Vert&\le \sum _{k=0}^{M-1} \mathcal {\overline{S}}_{M,k}\Vert \varepsilon ^{k}\Vert \\&+\tau ^{\beta }\sum _{k=0}^{M-1} \Vert \mathfrak {R}^{k+1}\Vert . \end{aligned}$$

Now, using Lemmas 1 and 5 we gain

$$\begin{aligned} \begin{aligned} \Vert \varepsilon ^{M}\Vert&\le \left( \tau ^{\beta }\sum _{k=0}^{M-1} \Vert \mathfrak {R}^{k+1}\Vert \right) \exp \left( \sum _{k=0}^{M-1} \mathcal {\overline{S}}_{M,k}\right) \\&\le \left( \tau ^{\beta }\sum _{k=0}^{M-1} \Vert \mathfrak {R}^{k+1}\Vert \right) \exp \left( 2\right) \\&\le \left( \frac{T}{\tau ^{1-\beta }} \max _{1\le k\le M}\Vert \mathfrak {R}^{k}\Vert \right) \exp \left( 2\right) \le C_{T} \mathcal {O}(\tau ) , \end{aligned} \end{aligned}$$

where $C_{T}$ is a constant. The proof is finished.□

3 Space-discrete method

In this section, we employ the Chebyshev collocation method to discrete the space direction and obtain a full-discrete scheme of (5). Firstly, we define some notations and get the closed form of the fractional derivative of the Chebyshev polynomials of fourth kind (CPFK) that have applications in the current section.

Definition 1

The Jacobi polynomials $J_{i}^{(r , s)}(x)$ are orthogonal polynomials with respect to the Jacobi weight function $\omega ^{(r , s)}(x)=(1-x)^{r}(1+x)^{s}$ in interval $[-1, 1]$ as follows

$$\begin{aligned} J^{(r , s)}_{i}= & {} \frac{\Gamma (r +i +1)}{i! \Gamma (r +s +i+1)}\sum _{m=0}^{i}\left( {\begin{array}{c}i\\ m\end{array}}\right) \frac{\Gamma (r +s +i+m+1)}{\Gamma (r +m+1)}\\&\times \left( \frac{x-1}{2}\right) ^{m}. \end{aligned}$$

By the analytical form of the Jacobi polynomials, the CPFK $\mathcal {W}_{i}(x)$ of degree i can be restated as below

$$\begin{aligned} \begin{aligned} \mathcal {W}_{i}(x)&=\frac{2^{2i}}{\left( {\begin{array}{c}2i\\ i\end{array}}\right) }J_{i}^{\left( \frac{1}{2},\frac{-1}{2}\right) }(x) =\frac{2^{2i-2} \Gamma (i+0.5)}{i(2i-2)!} \sum _{k=0}^{i-1}\\&\quad \sum _{\xi =0}^{k}\frac{(-1)^{\xi } 2^{-k} \Gamma (i+k) i!}{(i-k-1)! \Gamma (k+1.5) (k-\xi )! \xi !}\times x^{k-\xi }\\&={I}_{i}\sum _{k=0}^{i-1}\sum _{\xi =0}^{k}{\Gamma }_{i, k, \xi }\times x^{k-\xi },\quad x\in [-1, 1], \quad i=1, 2, \ldots , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {I}_{i}= & {} \frac{2^{2i-2}\Gamma (i+0.5)}{i(2i-2)!},~~{\Gamma }_{i, k,3\xi }\\= & {} \frac{(-1)^{\xi } 2^{-k} \Gamma (i+k) i!}{(i-k-1)! \Gamma (k+1.5) (k-\xi )! \xi !}. \end{aligned}$$

For using these polynomials on the interval [0, 1], we define the shifted CPFK (SCPFK) $\mathcal {W}_{i}^{*}(x)=\mathcal {W}_{i}(2x-1)$ by the change of variable. The analytic form of SCPFK as follows

$$\begin{aligned} \mathcal {W}_{i}^{*}(x)= & {} {I}_{i}\sum _{k=0}^{i-1}\sum _{\xi =0}^{k}{\Gamma }_{i, k, \xi }\times {2}^{k}\times x^{k-\xi },\nonumber \\&\qquad \quad x\in [0, 1], \quad i=1, 2, \ldots . \end{aligned}$$

(13)

These polynomials are orthogonal in the interval [0, 1] with respect to the following inner product

$$\begin{aligned} \langle \mathcal {W}_{i}^{*}(x), \mathcal {W}_{j}^{*}(x)\rangle= & {} \int _{0}^{1}\sqrt{\frac{1-x}{x}}\mathcal {W}^{*}_{i}(x)\mathcal {W}^{*}_{j}(x)\mathrm{d}x\\= & {} {\left\{ \begin{array}{ll} 0, &{} i\ne j, \\ \frac{\pi }{2} , &{} i =j. \end{array}\right. } \end{aligned}$$

The square-integrable function g(x) in the interval [0, 1] can be expanded in series of SCPFK as

$$\begin{aligned} g(x)=\sum _{i=0}^{\infty }w_{i}\mathcal {W}^{*}_{i}(x), \quad x\in [0, 1], \end{aligned}$$

where the coefficients $v_{i}, i=0, 1, 2, \ldots ,$ are defined by

$$\begin{aligned} w_{i}= & {} \frac{2}{\pi }\int _{0}^{1}\sqrt{\frac{1-x}{x}}g(x)\mathcal {W}^{*}_{i}(x)\mathrm{d}x, \nonumber \\ w_{i}= & {} \frac{1}{\pi }\int _{-1}^{1}\sqrt{\frac{1-x}{1+x}}g(x)\mathcal {W}_{i}(x)\mathrm{d}x. \end{aligned}$$

(14)

Now, by using the linearity of the Caputo fractional differentiation and Eq. (13) one can get the closed form of the fractional derivative of SCPFK, as the form

$$\begin{aligned} \mathcal {D}_{x}^{\omega }(\mathcal {W}^{*}_{i}(x))= & {} \sum _{k=0}^{i-\lceil \omega \rceil }\sum _{\xi =0}^{k}N_{i, k, \xi }^{\omega ,\lceil \omega \rceil } \nonumber \\&\times x^{k-\xi -\omega +\lceil \omega \rceil },\quad x\in [0, 1],\quad i=0, 1, 2, \ldots , \end{aligned}$$

(15)

where $\lceil \omega \rceil$ denotes the ceiling part of $\omega$ and $N_{i, k, \xi }^{\omega ,\lceil \omega \rceil }$ is given by

$$\begin{aligned} N_{i, k, \xi }^{\omega ,\lceil \omega \rceil }=\frac{(-1)^{\xi }2^{2i}(i)! \Gamma (i +0.5)\Gamma (i+k+\lceil \omega \rceil +1)\Gamma (k-\xi +\lceil \omega \rceil +1)}{\xi ! (2i)! (i-k-\lceil \omega \rceil )! (k+\lceil \omega \rceil -\xi )! \Gamma (k+\lceil \omega \rceil +1.5)\Gamma (k-\xi -\omega +\lceil \omega \rceil +1)}. \end{aligned}$$

Notice that for $i=0, 1, 2, \ldots , \lceil \omega \rceil -1,$ we have $\mathcal {D}_{x}^{\omega }(\mathcal {W}_{i}^{*}(x))=0$. In practice, only the first N-terms of SCPFK are considered in the approximate case. Then we have:

$$\begin{aligned} g(x)=\sum _{i=0}^{N}w_{i}\mathcal {W}^{*}_{i}(x). \end{aligned}$$

(16)

In addition, by means of Caputo fractional differentiation properties and combinations Eqs. (15) and (16), one can obtain

$$\begin{aligned} \mathcal {D}_{x}^{\omega }(g(x))=\sum _{i=\lceil \omega \rceil }^{N}\sum _{k=0}^{i-\lceil \omega \rceil }\sum _{\xi =0}^{k}w_{i} N_{i, k, \xi }^{\omega , \lceil \omega \rceil } x^{k-\xi -\omega +\lceil \omega \rceil },\quad x\in [0, 1]. \end{aligned}$$

(17)

As is discussed in Section 2, the time-discrete scheme is

$$\begin{aligned} U^{M}-\mathfrak {a}\tau ^{\beta }\mathcal {D}_{x}^{\alpha }U^{M}-\mathfrak {b}\tau ^{\beta }\mathcal {D}_{x}^{\gamma }U^{M}=\sum _{j=0}^{M-1}\mathcal {\overline{S}}_{M,j}U^{j}+\tau ^{\beta }Q^{M}. \end{aligned}$$

(18)

To get a full-discrete scheme based on the SCPFK, we apply the following approximate

$$\begin{aligned} \hat{u}(x, t)=\sum _{i=0}^{N}\mathfrak {u}_{i}(t)\mathcal {W}^{*}_{i}(x). \end{aligned}$$

(19)

From Eqs. (17) and (18), we have

$$\begin{aligned} \begin{aligned}&\sum _{i=0}^{N}\mathfrak {u}^{j}_{i}\mathcal {W}^{*}_{i}(x)-\mathfrak {a}\tau ^{\beta } \sum _{i=\lceil \alpha \rceil }^{N}\sum _{k=0}^{i-\lceil \alpha \rceil }\sum _{\xi =0}^{k}\mathfrak {u}_{i}^{j} N_{i, k, \xi }^{\alpha ,\lceil \alpha \rceil } x^{k-\xi -\alpha +\lceil \alpha \rceil }\\&\qquad -\mathfrak {b}\tau ^{\beta } \sum _{i=\lceil \gamma \rceil }^{N}\sum _{k=0}^{i-\lceil \gamma \rceil }\sum _{\xi =0}^{k}\mathfrak {u}_{i}^{j} N_{i, k, \xi }^{\gamma ,\lceil \gamma \rceil } x^{k-\xi -\gamma +\lceil \gamma \rceil }\\&\quad =\sum _{m=0}^{j-1}\sum _{i=0}^{N}\mathcal {\overline{S}}_{j,m}\mathfrak {u}^{m}_{i}\mathcal {W}^{*}_{i}(x)+\tau ^{\beta }Q(x,t_{j}),~~j=0, 1, \ldots , M, \end{aligned} \end{aligned}$$

(20)

where $\mathfrak {u}_{i}^{j}$ is the coefficients in the points of $(x_{i},t_{j})$. For positive integer N, $\lbrace x_{r}\rbrace _{r=1}^{N+1-\lceil \alpha \rceil }$ denote the collocation points that they are the roots of SCPFK $\mathcal {W}_{N+1-\lceil \alpha \rceil }^{*}(x)$. We collocate Eq. (20) with the collocation points $\lbrace x_{r}\rbrace _{r=1}^{N+1-\lceil \alpha \rceil }$ as below

$$\begin{aligned} \begin{aligned}&\sum _{i=0}^{N}\mathfrak {u}^{j}_{i}\mathcal {W}^{*}_{i}(x_{r})-\mathfrak {a}\tau ^{\beta } \sum _{i=\lceil \alpha \rceil }^{N}\sum _{k=0}^{i-\lceil \alpha \rceil }\sum _{\xi =0}^{k}\mathfrak {u}_{i}^{j}N_{i, k, \xi }^{\alpha ,\lceil \alpha \rceil } x_{r}^{k-\xi -\alpha +\lceil \alpha \rceil }\\&\qquad -\mathfrak {b}\tau ^{\beta } \sum _{i=\lceil \gamma \rceil }^{N}\sum _{k=0}^{i-\lceil \gamma \rceil }\sum _{\xi =0}^{k}\mathfrak {u}_{i}^{j} N_{i, k, \xi }^{\gamma ,\lceil \gamma \rceil } x_{r}^{k-\xi -\gamma +\lceil \gamma \rceil }\\&\quad =\sum _{m=0}^{j-1}\sum _{i=0}^{N}\mathcal {\overline{S}}_{j,m}\mathfrak {u}^{m}_{i}\mathcal {W}^{*}_{i}(x_{r})+\tau ^{\beta }Q(x_{r},t_{j}),~~j=0, 1, \ldots , M. \end{aligned} \end{aligned}$$

(21)

By substituting Eq. (19) in Eq. (2), in case of $x=0$ and $x=1$ we obtain the boundary conditions to get on $\lceil \alpha \rceil$ equations as

$$\begin{aligned}&\sum _{i=0}^{N}(-1)^{i}\mathfrak {u}_{i}^{j}={\upsilon }_{0}(t_{j}),\nonumber \\&\sum _{i=0}^{N}(2i+1)\mathfrak {u}_{i}^{j}={\upsilon }_{1}(t_{j}),~~j=0, 1, \ldots , M. \end{aligned}$$

(22)

Equation (21), together with boundary conditions (22), gives $N+1$ of linear algebraic equations which can be determined the unknown $\mathfrak {u}^{j}_{i}, i=0, 1, 2, \ldots , N$, in every step of time j. For obtaining the initial solution $\mathfrak {u}_{i}^{0}$, we use the initial condition $u(x, 0)=g(x)$ combining with Eq. (14).

4 Numerical examples

The main of this section is to give the numerical conclusion of the present method. We checked the stability of the developed method for various values of N and M. We will calculate the computational order (denoted by $\mathcal {C}_{\tau }$) by the following formula

$$\begin{aligned} \mathcal {C}_{\tau }=\frac{\log \left( \frac{E_{1}}{E_{2}}\right) }{\log \left( \frac{{ \tau }_{1}}{{ \tau }_{2}}\right) }, \end{aligned}$$

in which $E_{1}$ and $E_{2}$ are errors corresponding to grids with mesh size ${\tau }_{1}$ and ${\tau }_{2}$, respectively.

Example 1

Consider the following STFADE

$$\begin{aligned}&\frac{{\partial } ^{\beta } u(x, t)}{\partial {t} ^{\beta }}=a(x,t) \frac{{\partial }^{1.8} u(x, t)}{\partial x^{1.8}}+b(x,t) \nonumber \\&\qquad \frac{{\partial }^{\gamma } u(x, t)}{\partial x^{\gamma }}+q(x, t),\\&\qquad ~~ 0< x< 1, \quad 0 < t \le T, \end{aligned}$$

with the known functions $a(x,t)=\Gamma (1.2)x^{1.8}$ and $b(x,t)=0$. The boundary and initial conditions are $u(0, t)=u(1, t)=0$ and $u(x,0)=x^{2}(1-x)$, respectively. The source term is $q(x,t)=3x^{2}e^{-t}(2x-1)$. This problem has exact solution $u(x, t)=x^{2}e^{-t}(1-x)$ in the case of $\beta =1$.

We solve this example based on the approach method and report the results in Tables 1, 2 and 3. In Table 1, the comparison of $L_{\infty }$ between the proposed method and methods described with the Chebyshev estimates solved by the finite difference method in [11], the classical Crank–Nicholson method in [26], the Legendre polynomials in [2], and on the other hand, shifted Chebyshev polynomials for space and rational Chebyshev functions for the time-discrete in [4], are reported at $T=2, T=10$ and $T=50$ for $M=400$ with 5 collocation points in the space domain. The reports show a better estimation of the current method than the methods mentioned. In addition, the absolute error of the presented method (PM) and the method of [4] are compared in Table 2 which indicates our method gives much better than the method [4]. In Table 3, the computational orders with $\beta =0.99$ at $T=1, N = 5, 7$ and different values of M, are shown. From this table, we can conclude that the computational orders are closed to the theoretical order.

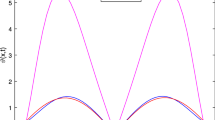
Figure 1 shows the approximation solution and absolute error for $N=3$ and the different values of M at $T=1$. Figure 2 demonstrates the numerical solution at $T=1$ (left panel) and $T=2$ (right panel) with $M=N=5$ and several values of $\beta$. Moreover, Fig. 3 depicts the numerical solution for the different values M and N at $T=1$ with various qualities of $\alpha$, which they display the convergence of the proposed method when $\beta$ and $\alpha$ tend to 1 and 1.8, respectively.

Table 1 Comparison of $L_{\infty }$ with $N=5, M=400$ on interval [0, 1] for Example 1

Table 2 The comparison of the absolute error of the present method with method given in [4] for $N=M=3$ at $T=2$ for Example 1

Table 3 The computational orders, $L_{\infty }$ and $L_{2}$ with $N=5, 7,~M=3, 6, 12, 24, 48$ and $\beta =0.99$ at $T=1$ for Example 1

Fig. 1

Graphs of the absolute error (left-side) and approximate solution (right-side) of Example 1 at $T=1$ and $N=3$

Fig. 2

The numerical solution of Example 1 at $T=1$ (left-side) and $T=2$ (right-side), for $M=N=5$

Fig. 3

The compression of numerical solution for Example 1 at $T=1$, for the different values M, N

Example 2

The smooth initial condition for problem (1) to be considered: homogeneous boundary conditions, $u(x,0)=x^{2}-x^{3}$, the space fractional orders $\alpha =1.8 , \gamma =0.8$ and $a(x,t)=\frac{\Gamma (2.2)}{2}x^{1.8}, b(x,t)=-\frac{\Gamma (3.2)}{2}x^{0.8}$ are known functions. The source term can be achieved corresponding to the exact solution $u(x,t)=x^{2}(1-x)(1+t^{\beta })$ when $\beta =1$.

Table 4 presents a comparison between $L_{\infty }$ and $L_{2}$ for $N=5, 7$ and the various values of M at $T=1$ with $\beta =0.9$, and also investigating this table, we can conclude that the developed method has the order $\mathcal {O}(\tau )$ in the time direction. Figure 4 clearly reveals the absolute error based on the present technique for $N=5$ (left side) and $N=9$ (right side) at $T=1$ with $\beta =0.2$. From this figure, it is clear that the absolute error is decreased when the time step is increased. In Fig. 5, we plotted the numerical solution for values of $\alpha$, $\gamma$ and $\beta =0.2$ based on $M=N=5$ that displays the convergence.

Table 4 The computational orders, $L_{\infty }$ and $L_{2}$ with $N=5, 7,~M=3, 6, 12, 24, 48$ and $\beta =0.9$ at $T=1$ for Example 2

Fig. 4

The absolute error of Example 2 for $N=5$ (left-side) and $N=9$ (right-side), at $T=1, \beta =0.2$

Fig. 5

The numerical solution of Example 2 at $T=1$ for $M=N=5$ with various values $\alpha$ , $\gamma$ and $\beta =0.2$

Example 3

Consider the following STFADE

$$\begin{aligned} \begin{aligned} \frac{{\partial }^{\beta } u(x, t)}{\partial {t}^{\beta }}&=\frac{\Gamma (1.4)}{2}x^{0.6}\frac{{\partial }^{1.6} u(x, t)}{\partial x^{1.6}}\\&\quad +\frac{\Gamma (1.2)}{2}x^{0.8}\frac{{{\partial }^{0.8}} u(x, t)}{\partial {x}^{0.8}}+q(x,t), \quad 0<x<1,\\ u(x, 0)&=x(1-x),~~u(0, t)=0, ~~u(1, t)=0,~~ t>0, \end{aligned} \end{aligned}$$

(23)

where $q(x,t)=exp(-t)(-0.5x+(1+\frac{\Gamma (1.2)}{\Gamma (2.2)})x^{2})$. This example has exact solution $u(x, t)=x(1-x)exp(-t)$ in the case of $\beta =1$.

The results of this problem are listed in Table 5 at various given parameters M and N with $\beta =0.9$. It is shown that the convergence order of the time derivative supports the theoretical result, that is, $\mathcal {O}( \tau )$. Figure 6 depicts the approximate solution at $T=1$ for $M=N=9$ with different values $\alpha$ , $\gamma$ and $\beta =0.9$.

Table 5 The computational orders, $L_{\infty }$ and $L_{2}$ with $N=3, 5,~M=3, 6, 12, 24, 48$ and $\beta =1$ at $T=1$ for Example 3

Fig. 6

The numerical solution of Example 3 at $T=1$ for $M=N=9$ with different values $\alpha$ , $\gamma$ and $\beta =0.9$

5 Conclusion

This paper presented a new numerical scheme for approximating the STFADE. First of all, a finite difference method is utilized to discrete the fractional derivative in time directly with the $\mathcal {O}(\tau ^{2-\beta })$ accuracy. In Lemma 5, the relation of approximating coefficients is stated for establishing the convergence analysis. In Theorem 1, the unconditional stability of the time-discrete scheme is proved by using the energy method and mathematical induction. Moreover, we obtained the linear convergence order in Theorem 2. Also, we applied the Chebyshev collocation method to discrete the space direction and obtain a full-discrete scheme. Finally, the numerical conclusion is illustrated to demonstrate and support the accuracy of the proposed scheme.