1 Introduction

In recent decades, as a consequence of the development in material science and lightweight design, a new class of adaptive structures equipped with piezoelectric materials is introduced in the automotive, aerospace, medical, and scientific areas to produce smart structures. Due to their coupled mechanical and electrical properties, smart materials enable to sense and to adapt their static and dynamic responses. Up to present, the research on intelligent structures is very rich. Investigations content of piezoelectric laminate beams, plates, and shells can be found in the following literature [1,2,3,4,5,6,7,8]. Conventional passive composite, subjected to dynamic loads, are sensitive to vibrations and suffer often from dynamic instabilities. Hence, the use of adaptive and active structures can solve such problems. A series of studies have been carried out to predict the dynamic behavior of piezolaminated structures. Moita et al. [9] developed a single-layer triangular plate/shell element with 18 degrees of freedom to control the structural dynamic response of the piezolaminated thin plate. Furthermore, Saviz et al. [10] studied the free-vibration characteristics of a thick cylindrical shell with piezoelectric layers using the layerwise theory. Later, Saviz and Mohammadpourfard [11] presented a transient analysis of orthotropic laminated cylindrical shells covered by two active layers. The solutions of governing equations were obtained using Galerkin’s finite-element formulation in the radial direction.

Currently, the computational approaches for nonlinear analysis of shell have been developed by many investigators, since structures can endure large deformations and finite rotations. Several researches have been carried out to predict the nonlinear behavior of shell structures under mechanical loading [12,13,14,15,16,17,18,19,20]. However, it is very essential to anticipate the sensing and actuator capabilities of smart shell structures in the range of large deformations [21]. Hence, the effect of static large deformations on the structural behavior of piezolaminated beams is analyzed by [22]. By means of third-order shear deformation theory, the response of smart thin and sandwich plates is predicted by [23] accounting for geometric nonlinearity. Panda and Ray [24] developed an FE model to simulate the nonlinear behavior of smart functionally graded (FG) plates based on von Karman type nonlinearity. Geometrically nonlinear analysis is also investigated by [25] to survey the behavior of adaptive structures. The developed model considers the Kirchhoff shell theory, and it can be used for any arbitrary shape, and mechanical and electrical loadings. Moreover, an improved FSDT theory was used for geometrically nonlinear analysis of piezolaminated shell structures [26]. Several piezolaminated geometries are investigated in the above research using a novel nonlinear smart finite shell element.

Analyses of nonlinear dynamics and control of smart structures have been undertaken by several researchers [27,28,29,30]. Static and dynamic analyses of smart structures undergoing large displacements are also investigated by [31]. Using their finite-element model, they simulated sensor output voltage and piezoelectric actuator based on first-order shear deformation theory (FSDT). A developed shell element is employed in [28,29,30,31] to modal the shape, control vibration, and predict nonlinear transient deformation of smart structures using various shell theories. Schmidt and their co-authors [32,33,34,35] developed an FE shell elements to analyze the geometrically nonlinear behavior of smart thin-walled structures. In their works, authors prove that it is necessary to predict the sensing and actuating capabilities of the piezolaminated structures taking into account their geometrical nonlinearity. Recently, Marinković and Rama [36,37,38,39] used a co-rotational FE formulation to develop a three-node shell element for modeling piezolaminated structures in the nonlinear static and dynamic cases. By presenting several numerical examples, important aspects of modeling shell structures with embedded sensors and actuators are exposed.

Recently, functionally graded materials (FGMs) attracted many researchers to study the linear and nonlinear static, dynamic, free, and forced vibration behavior [40,41,42,43,44,45,46,47,48,49]. These kinds of composite materials are characterized especially by the smooth and continuous variation of its mechanical properties [47]. Therefore, delamination problems caused by interlaminar stresses in the conventional composite are solved. Based on this background, a new category of composites, known as functionally graded carbon nanotube-reinforced composite (FG-CNTRC), is growing nowadays. In fact, the carbon nanotubes (CNTs) are uniformly or randomly distributed in the traditional methods; therefore, the improvement of their special mechanical properties may not be perfect. Recently, the carbon nanotubes aligned in axial direction and functionally graded in the thickness are embedded in a polymer matrix to eliminate the above shortcomings. Recent studies [19, 50,51,52] reported the linear and nonlinear analysis in the static, buckling, and free-vibration behavior of FG-CNT plate and shell structures under purely mechanical loading. Zhang et al. analyzed the vibrations of quadrilateral plate [53, 54] with FG-CNT composite using element-free kp-Ritz method based on FSDT theory. Parametric studies showing the effects of different boundary conditions, geometrical parameters, and types of carbon nanotube distributions are examined. As well as, Lei et al. [55] investigated the dynamic response of FG-CNTRC plates modeled with a macroscopic continuum approach and using the element-free method.

Most of the past studies were focused on the vibration characteristics of passive FG-CNT structures under only mechanical dynamic load. A few studies considered the structural behavior of smart FG-CNT plates and shells. The combination between FG-CNT reinforced materials and piezoelectric materials makes an intelligent structural material [56]. In this context, the optimal shape of FG-CNT composite plates with embedded piezoelectric patches is studied by Zhang et al. [57], using the genetic algorithm to find the optimal displacement feedback control gains and actuator voltages. Moreover, other investigations using FSDT theory were carried out to predict large amplitude vibration of FG-CNTRC annular sector plate covered by two piezolayers. Mohammadzadeh-Keleshteri et al. [58] found two interesting results; the frequencies of the FG-CNTRC sector plate increase when the volume fraction of the CNTs is increasing and the thickness of piezoelectric layers plays an important role in the hardening responses of the global structure. Furthermore, Alibeigloo et al. [59, 60] investigated thermoelastic behavior of CNTRC plate and shell structures embedded in piezoelectric layers using three-dimensional theory of elasticity. Nguyen-Quang et al. [61] proposed an extension of the isogeometric approach for the dynamic response of laminated carbon nanotube-reinforced composite (CNTRC) plates integrated with piezoelectric layers. In this study, the effects of volume fraction of CNT, its graded pattern, and the influence of piezoelectric layers on dynamic behavior of the plate structure were outlined. Recent advances in material science and technology make a new nano-filler material like graphene platelets (GPLs). Very recently, Rao et al. [62, 63] studied the static and forced vibration behavior of the FG-GPLs’ structures bonded with smart layers under piezoelectric and mechanical loads.

By the literature survey, it may be demonstrated that nonlinear transient analysis of smart FG-CNTRC shells is very scarce. Thus, the need to analyze the geometric nonlinear behavior of such structures has had an essential impact on these achievements. In this context, this paper proposes an FE analysis to predict nonlinear dynamic behavior of FG-CNTRC plate and shell structures with embedded piezosensors or/and actuators. A micro-mechanical model based on the developed rule of mixture is used to assess the effective material properties of the FG-CNTRC structures reinforced by single-walled carbon nanotubes (SWCNTs). To insure realistic parabolic transverse shear strain through the shell thickness, an improved FSDT theory is adopted. The electric potential varies linearly through the piezolayers. Assumed natural strain (ANS) method is used to overcome shear locking in the case of thin plate and shell. The performance of the developed nonlinear finite-element formulation, considering large rotation, to predict the transient behavior of piezolaminated structures acting as both actuator or as sensor is examined. It is shown that numerical results agree well with examples, from the literature, considering piezolaminated structures for nonlinear dynamic applications. Furthermore, an exhaustive discussion is presented to offer some new transient results to unearth the influence of the CNT distribution along the layer thickness, CNTs’ volume fractions, as well as geometrical parameters on the dynamic of active FG-CNTRC spherical and cylindrical shells with large rotations.

2 Material properties of smart FG-CNTRC shells

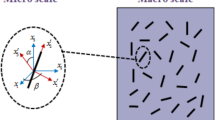
As shown in Fig. 1, a sandwich shell structure composed of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) core and two piezoelectric layers is considered in this study. The FG-CNTRC is made of a mixture from CNTs that are aligned in axial direction and functionally graded in the thickness direction, and a polymeric matrix. A single-walled carbon nanotubes (SWCNTs) is combined with an isotropic matrix polymer poly (m-phenylenevinylene)-co-[(2, 5-dioctoxy-p-phenylene) vinylene] PmPV. Various carbon nanotube distributions such as UD, FG-V, FG-O, and FG-X are investigated in the present analysis.

Fig. 1
figure 1

Schematic of a UD, b FG-V, c FG-X, and d FG-O CNTRC smart shell structure

Full size image

The corresponding volume fractions \(V_{\text{CNT}}^{{}}\) for multifarious CNTs distributions are expressed as:

$$\begin{aligned} V_{\text{CNT}} \left( z \right) = \left\{ {\begin{array}{*{20}l} {V_{\text{CNT}}^{ *} \left( {\text{UD - CNT}} \right)}\vspace{4pt} \hfill \\ {\left( {1 + \frac{2z}{h}} \right)V_{\text{CNT}}^{ *} \left( {\text{FG - V - CNT}} \right)}\vspace{4pt} \hfill \\ {4\frac{\left| z \right|}{h}V_{\text{CNT}}^{ *} \left( {\text{FG - X - CNT}} \right)}\vspace{4pt} \hfill \\ {2\left( {1 - 2\frac{\left| z \right|}{h}} \right)V_{\text{CNT}}^{ *} \left( {\text{FG - O - CNT}} \right)}\vspace{4pt} \hfill \\ \end{array} \left( { - \frac{h}{2} \le z \le \frac{h}{2}} \right)} \right., \end{aligned}$$
(1)

in which \(V_{\text{CNT}}^{ *}\) denotes the total volume fraction of CNTs, given as:

$$V_{\text{CNT}}^{ *} = \frac{{w_{\text{CNT}}^{{}} }}{{\left( {w_{\text{CNT}}^{{}} + \frac{{\rho_{{}}^{\text{CNT}} }}{{\rho_{{}}^{m} }} - \frac{{\rho_{{}}^{\text{CNT}} }}{{\rho_{{}}^{m} }}w_{\text{CNT}}^{{}} } \right)}},$$
(2)

where \(w_{\text{CNT}}^{{}}\) represents the mass fraction of the CNT in the composite structure. \(\rho_{{}}^{\text{CNT}}\) and \(\rho_{{}}^{m}\) are the CNT and matrix mass densities, respectively.

The effective mechanical properties of the FG-CNTR composite can be computed, using an extended rule of mixture, as [33]:

$$\begin{aligned} Y_{{11}}^{{}} & = \eta _{1} V_{{{\text{CNT}}}}^{{}} Y_{{{\text{11}}}}^{{{\text{CNT}}}} + V_{m}^{{}} Y_{m}^{{}} \\ \frac{{\eta _{2} }}{{Y_{{22}}^{{}} }} & = \frac{{V_{{{\text{CNT}}}}^{{}} }}{{Y_{{22}}^{{{\text{CNT}}}} }} + \frac{{V_{m}^{{}} }}{{Y_{m}^{{}} }} \\ \frac{{\eta _{3} }}{{G_{{12}}^{{}} }} & = \frac{{V_{{{\text{CNT}}}}^{{}} }}{{G_{{{\text{12}}}}^{{{\text{CNT}}}} }} + \frac{{V_{m}^{{}} }}{{G_{m}^{{}} }} \\ \rho & = V_{{{\text{CNT}}}}^{{}} \rho _{{}}^{{{\text{CNT}}}} + V_{m}^{{}} \rho _{{}}^{m} \\ \nu _{{12}}^{{}} & = V_{{{\text{CNT}}}}^{{}} \nu _{{{\text{12}}}}^{{{\text{CNT}}}} + V_{m}^{{}} \nu _{{12}}^{m} , \\ \end{aligned}$$
(3)

where \(Y_{ 1 1}^{\text{CNT}}\), \(Y_{ 2 2}^{\text{CNT}}\), \(G_{ 1 2}^{\text{CNT}}\), and \(\nu_{ 1 2}^{\text{CNT}}\) are the elastic constants of the carbon nanotubes; \(Y_{m}^{{}}\), \(G_{m}^{{}}\), and \(\nu_{12}^{m}\) are the elastic properties of the polymer matrix; \(\eta_{1}\), \(\eta_{2}\), and \(\eta_{3}\) denote the CNT efficiency parameters; \(V_{\text{CNT}}^{{}}\) and \(V_{m}^{{}}\) are the volume fraction of CNTs and matrix, respectively, satisfying the following condition [64]:

$$V_{\text{CNT}}^{{}} + V_{m}^{{}} = 1.$$
(4)

3 Piezoelectric enhanced FSDT shell formulation

The developed shell formulation based on the enhanced first-order shear deformation (FSDT) theory is here used to analyze the global characteristics of thick and thin shells. In this approach, a parabolic distribution of the transverse shear strains across the shell thickness is assumed and a zero condition of the transverse shear stresses on the top and bottom surfaces is imposed. Furthermore, the present theory pretends to model accurately the effects of large rotations leading to large deformations. A linear electric potential function in the thickness direction is employed. Nonlinear dynamic analysis of the piezoelectric laminated functionally graded carbon nanotube-reinforced (FG-CNT) composite shells using linear theory of piezoelectricity with nonlinear strain measure is considered.

3.1 Constitutive equations

The linear constitutive relations coupling the mechanical and electrical behavior of the piezolaminated structure can be expressed as:

$$\left[ {\begin{array}{*{20}l} \varvec{S} \\ \varvec{q} \\ \end{array} } \right]_{8 \times 1} = \left[ {\begin{array}{*{20}c} \varvec{C} & { - \varvec{p}^{T} } \\ \varvec{p} & \varvec{k} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c}\varvec{\varepsilon}\\ \varvec{E} \\ \end{array} } \right]_{8 \times 1} ,$$
(5)

in which \(\varvec{S}\), \(\varvec{\varepsilon}\), \(\varvec{q}\), and \(\varvec{E}\) are the second Piola–Kirchhoff stress, Lagrangian strain, electric displacement, and electric field vectors, respectively, and \(\varvec{C}\), \(\varvec{p}\), and \(\varvec{k}\) are the elasticity, dielectric constant, and piezoelectric stress constant matrices, respectively.

3.2 Basic geometry and kinematics

A description of the geometry and kinematics of piezoelectric improved FSDT shell model is concisely developed in this part. According to this theory, each point p of the mid-surface has three displacement, two independent rotational, and one electrical degrees of freedom. To express these degrees of freedom at any point q of the shell structure located at the distance z from the mid-surface, a curvilinear coordinate system \({\varvec{\upxi}} = \left( {\xi ,\eta ,z} \right)\) needs to be introduced at that point. Variables referred to the reference configuration C0 are symbolized by upper case letters and by lower case letters when associated with the current configuration Ct. Vectors are expressed using bold letters.

The mechanical displacement of one point q (see Fig. 2) can be defined, in both initial and deformed state of shell, as:

Fig. 2
figure 2

Geometry of a piezolaminated composite shell

Full size image
$$\begin{array}{*{20}l} {{\mathbf{X}}_{q} \left( {\xi ,\eta ,z} \right) = {\mathbf{X}}_{p} \left( {\xi ,\eta } \right) + z\,{\mathbf{D}}\left( {\xi ,\eta } \right)} \hfill \\ {{\mathbf{x}}_{q} \left( {\xi ,\eta ,z} \right) = {\mathbf{x}}_{p} \left( {\xi ,\eta } \right) + z_{{}} {\mathbf{d}}\left( {\xi ,\eta } \right)} \hfill \\ \end{array} ;\,z \in \left[ { - h/2\,,\,h/2} \right],$$
(6)

where h is the thickness; \({\mathbf{D}}\) is the initial shell director which is perpendicular to the undeformed mid-surface; \({\mathbf{d}}\) represents the director shell vector in the deformed configuration.

3.3 Stress and strain field

In the large deformation case, the strain field \(\varvec{\varepsilon}\) is defined using the Green–Lagrange strain tensor as follows:

$$\left\{ \begin{aligned} \varepsilon_{\alpha \beta }& = e_{\alpha \beta } + z\chi_{\alpha \beta }^{{}} \hfill \\ 2\varepsilon_{\alpha 3} &= \gamma_{\alpha }^{{}} \hfill \\ \end{aligned} \right.,$$
(7)

where \(e_{\alpha \beta }\), \(\chi_{\alpha \beta }^{{}}\), and \(\gamma_{\alpha }^{{}}\) denote the membrane, bending, and transverse shear strains, respectively. In the current state Ct, the variation of the strain measures are expressed as:

$$\left\{ \begin{aligned} \delta e_{\alpha \beta } &= \left( {\varvec{a}_{\alpha } \cdot \delta \varvec{x}_{,\beta } + \varvec{a}_{\beta } \cdot \delta \varvec{x}_{,\alpha } } \right)/2 \hfill \\ \delta \chi_{\alpha \beta }^{{}} &= \left( {\varvec{a}_{\alpha } .\delta \varvec{d}_{,\beta } + \varvec{a}_{\beta } \cdot \delta \varvec{d}_{,\alpha } + \delta \varvec{x}_{,\alpha } \cdot \varvec{d}_{,\beta } + \delta \varvec{x}_{,\beta } \cdot_{{}} \varvec{d}_{,\alpha } } \right)/2 \hfill \\ \delta \gamma_{\alpha }^{{}}& = \varvec{a}_{\alpha } \cdot \delta \varvec{d}_{{}} + \delta \varvec{x}_{,\alpha } \cdot \varvec{d} \hfill \\ \end{aligned} \right.;\quad \alpha ,\beta = 1,\;2.$$
(8)

In matrix form, the membrane, the bending and the shear strains are written as follows:

$${\mathbf{e}} = \left[ {\begin{array}{*{20}c} {e_{11} } \\ {e_{22} } \\ {2e_{12} } \\ \end{array} } \right]\text{;}\quad {\varvec{\upchi}} = \left[ {\begin{array}{*{20}c} {\chi_{11}^{{}} } \\ {\chi_{22}^{{}} } \\ {2\,\chi_{12}^{{}} } \\ \end{array} } \right]\text{;}\quad {\varvec{\upgamma}} = \left[ {\begin{array}{*{20}c} {\gamma_{1}^{{}} } \\ {\gamma_{2}^{{}} } \\ \end{array} } \right].$$
(9)

It should be noted that the FSDT theory developed by Mindlin [65] is adopted to model the kinematics for both thin and moderately thick shell structures. This theory assumes a constant distribution of the transverse shear deformations. However, it is already well known that both transverse strain and stress distributions are parabolic across the thickness and vanishing at points on the top and bottom surfaces of the structure. In this paper, the modified FSDT is introduced to handle the linear distribution of the shear strains by imposing a parabolic function \(f\left( z \right)\) inspired from the high-order shear deformation (HSDT) theory given by [66]. Regarding to the enhanced FSDT, shear strain vector becomes:

$$\delta {\varvec{\upgamma}}^{{_{{}} Z}} = f\left( z \right)\delta {\varvec{\upgamma}}\text{;}\quad f\left( z \right) = \frac{5}{4}\left( {1 - \frac{{4z^{2} }}{{h^{2} }}} \right).$$
(10)

The membrane N, bending \(\varvec{M}\) and shear \(\varvec{T}\) stress resultants are derived through the integration of the stress tensor \(\varvec{S}\) over the thickness. Similarly, the electric displacement resultant \(\bar{\varvec{q}}\) is obtained by integration of the electric displacement \(\varvec{q}\) through the thickness:

$$\begin{aligned} N^{\alpha \beta } & = \int_{ - h/2}^{h/2} { S_{{}}^{\alpha \beta } \varvec{d}z}_{{}} \text{;}\quad M_{{}}^{\alpha \beta } = \int_{{{ - }h / 2}}^{h / 2} {zS_{{}}^{\alpha \beta } \varvec{d}z} \quad \\ T_{{}}^{\alpha } & = \int_{{{ - }h / 2}}^{h / 2} {f\left( z \right)S_{{}}^{\alpha 3} \varvec{d}z_{{}} } \text{;}\quad \overline{\varvec{q}} = \int_{{{ - }h / 2}}^{h / 2} {q \varvec{d}z}_{{}} \text{;}\quad \alpha = 1,2. \\ \end{aligned}$$
(11)

In the matrix form, these quantities can expressed as:

$$\varvec{N} = \left\{ {\begin{array}{*{20}c} {N^{11} } \\ {N^{22} } \\ {N^{12} } \\ \end{array} } \right\}\text{;}\quad \varvec{M} = \left\{ {\begin{array}{*{20}c} {M_{{}}^{11} } \\ {M_{{}}^{22} } \\ {M_{{}}^{12} } \\ \end{array} } \right\}\text{;}\quad \varvec{T} = \left\{ {\begin{array}{*{20}c} {T_{{}}^{1} } \\ {T_{{}}^{2} } \\ \end{array} } \right\}\text{;}\quad \bar{\varvec{q}} = \left[ {\begin{array}{*{20}c} {\bar{q}_{1} } \\ {\bar{q}_{2} } \\ {\bar{q}_{3} } \\ \end{array} } \right].$$
(12)

The membrane N, bending \(\varvec{M}\) and shear \(\varvec{T}\) stress resultants and the electric displacement resultant \(\bar{\varvec{q}}\) as well as the membrane \(\varvec{e}\), bending \(\varvec{\chi}\) and shear \(\varvec{\gamma}\) strains and the electric field \(\varvec{E}_{m}\) (\(\varvec{E}_{m}\) = \(- \varvec{E}\)) are arranged in the following way to obtain a generalized resultant of stress \(\varvec{R}\) and strain \(\varvec{\varSigma}\) vectors:

$$\varvec{R = }\left[ {\begin{array}{*{20}c} N \\ M \\ T \\ {\overline{q} } \\ \end{array} } \right]_{11 \times 1} \text{;}\quad\varvec{\varSigma}= \left[ {\begin{array}{*{20}c} \varvec{e} \\\varvec{\chi}\\\varvec{\gamma}\\ {\varvec{E}_{m} } \\ \end{array} } \right]_{11 \times 1} .$$
(13)

In the case of an elastic constitutive model, the variations in stress resultants \({\varvec{\Delta}}{\mathbf{R}}\) and in strain field \({\varvec{\Delta}}{\varvec{\Sigma}}\) are related in the well-known form:

$${\varvec{\Delta}}{\mathbf{R}} = {\mathbf{H}}_{T} {\varvec{\Delta}}{\varvec{\Sigma}},$$
(14)

with \({\mathbf{H}}_{T}\) is the linear coupling elastic and electric matrix expressed as:

$${\mathbf{H}}_{T} = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}_{{11}} } & {{\mathbf{H}}_{{12}} } & 0 & {{\mathbf{H}}_{{14}} } \\ {} & {{\mathbf{H}}_{{22}} } & 0 & {{\mathbf{H}}_{{24}} } \\ {} & {} & {{\mathbf{H}}_{{33}} } & {{\mathbf{H}}_{{34}} } \\ {\user2{Sym}} & {} & {} & {{\mathbf{H}}_{{44}} } \\ \end{array} } \right]{\text{;}}\left\{ {\begin{array}{*{20}l} {\left( {{\mathbf{H}}_{{11}} ,{\mathbf{H}}_{{12}} ,{\mathbf{H}}_{{22}} } \right) = \int_{{ - h/2}}^{{h/2}} {\left( {1,z,z_{{}}^{2} } \right)\,\user2{C}~~\user2{d}z} } \hfill \\ {{\mathbf{H}}_{{33}} = \int_{{ - h/2}}^{{h/2}} {\left( {f\left( z \right)} \right)^{2} \,\user2{C}_{\tau } \,\user2{d}z} } \hfill \\ {\left( {{\mathbf{H}}_{{14}} ,{\mathbf{H}}_{{24}} } \right) = \int_{{ - h/2}}^{{h/2}} {\left( {1,z} \right)\,\user2{p}_{{}}^{T} \,\user2{d}z} } \hfill \\ {{\mathbf{H}}_{{34}} = \int_{{ - h/2}}^{{h/2}} {f\left( z \right)\,\user2{p}_{\tau }^{T} ~\,\user2{d}z} } \hfill \\ {{\mathbf{H}}_{{44}} = \int_{{ - h/2}}^{{h/2}} {\,\user2{k}\,\user2{d}z} } \hfill \\ \end{array} } \right.,$$
(15)

in which \(\varvec{C}\) and \(\varvec{p}_{{}}^{{}}\) represent the in-plane linear elastic and piezoelectric coupling sub-matrix. \(\varvec{C}_{\tau }\) and \(\varvec{p}_{\tau }\) are the out-of-plane linear elastic and piezoelectric sub-matrices.

3.4 Electrical field

The electric field vector E is computed using the gradient of the electric potential \(\Delta \varphi\) as mentioned:

$$\varvec{E}\text{ = } - \varphi_{{{,\alpha }}} \text{;}\quad \alpha = 1 \ldots 3.$$
(16)

In this research, only transverse electric field \(E_{3}\) is considered and the in-plane electric field \(E_{1}\) and \(E_{2}\) are neglected, since the active layer is considered thin with polarization in the thickness direction. Regarding to this assumption, the electric field can be rewritten as below:

$$\varvec{E}_{m} = - \varvec{E} = - \varvec{B}_{e} \cdot \varphi_{{}} \text{;}\quad \varvec{B}_{e} = \left[ {\begin{array}{*{20}l} 0 & 0 & {\frac{{\partial }}{{{\partial }z}}} \\ \end{array} } \right]^{T} .$$
(17)

3.5 Weak form of the governing equations for piezoelectric laminate shell

The weak form of the governing equations of piezoelectric structures is defined by the following:

$$G = \int_{V} {\left( {S_{{}}^{{\alpha \beta }} \delta \varepsilon _{{\alpha \beta }} \, + S_{{}}^{{3\alpha }} \delta \gamma _{\alpha }^{Z} + \,q_{3} \delta E_{3} } \right)\varvec{d}V} \, - G_{{\rm{ext}}} { = 0}\,{;}\,\quad \alpha ,\beta = 1,2,$$
(18)

where \(G_{{\varvec{ext}}}\) is the external virtual work.

Integrating Eq. (18) through the thickness of the shell and using Eqs. (7), (10), and (11) would lead to:

$$G = \int_{A} {\left( {\varvec{N} \cdot \delta \varvec{e}\, + \varvec{M}.\delta\varvec{\chi}\, + \varvec{T} \cdot \delta\varvec{\gamma}+ \overline{q} \cdot \delta \varvec{E}} \right)\varvec{d}A} \, - G_{{\varvec{ext}}} = 0.$$
(19)

Using Eq. (13), the weak form can be repressed as:

$$G = \int_{A} {\delta\varvec{\varSigma}_{{}}^{T} \varvec{R}_{{}} dA} \, - G_{ext} = 0.$$
(20)

4 Nonlinear finite-element modeling

To predict the nonlinear transient behavior of smart shell structures, an efficient and accurate 4-nodes’ shell element with 6 degrees of freedom per node (\(u,v,w,\theta_{x} ,\theta_{y} ,\varphi\)) is proposed.

5 Discretization of displacement vector

The displacement vector \(\varvec{U}\) \(\left( {\varvec{U} = \varvec{x} - \varvec{X}} \right)\), the director vector d, their incremental quantities, and the electric potential \(\varphi\) are interpolated based on isoparametric shape functions \(N^{I}\) as:

$$\begin{aligned} \varvec{U} = \sum\limits_{I = 1}^{4\,} {N^{I} \varvec{U}_{I} } \text{;}\,\quad \Delta \varvec{U} = \sum\limits_{I = 1}^{4\,} {N^{I} \Delta \varvec{U}_{I} \text{;}\,\quad } \varphi = \sum\limits_{I = 1}^{4\,} {N^{I} \varphi_{I} } \hfill \\ \delta {\mathbf{d}}_{{}} = \sum\limits_{I = 1}^{4\,} {N^{I} \delta {\mathbf{d}}_{I} } \text{;}\,\quad \Delta {\mathbf{d}} = \sum\limits_{I = 1}^{4\,} {N^{I} \Delta {\mathbf{d}}_{I} } , \hfill \\ \end{aligned}$$
(21)

with \(\varvec{U}_{I}\) and \(\varvec{d}_{I}^{{}}\) represent the displacement vector and director vector at the nodal points, respectively.\(N^{I}\) denote the shape functions, which are expressed in two-dimensional parametric space as (see Fig. 3):

Fig. 3
figure 3

Four-node shell element

Full size image
$$N^{I} \left( {\xi ,\eta } \right) = \frac{1}{4}\left( { 1+ \xi^{I} \xi } \right)\left( {1 + \eta^{I} \eta } \right)\text{;}\quad I = 1\ldots 4 .$$
(22)

The curvilinear coordinates are transferred to the Cartesian ones using the Jacobian matrix \({\mathbf{J}}\). The derivations of \(N^{I}\) in the local Cartesian and the local elementary systems can be expressed as:

$$\left[ {\begin{array}{*{20}c} {\bar{N}_{,1}^{I} } \\ {\bar{N}_{,2}^{I} } \\ \end{array} } \right]_{{\left\{ {{\mathbf{n}}_{1}^{0} ,\,{\mathbf{n}}_{2}^{0} ,{\mathbf{n}}_{{}}^{0} } \right\}}} = \left[ {\mathbf{J}} \right]^{ - 1} \left[ {\begin{array}{*{20}c} {N_{,1}^{I} } \\ {N_{,2}^{I} } \\ \end{array} } \right]_{{\left\{ {{\mathbf{A}}_{1}^{{}} ,\,{\mathbf{A}}_{2}^{{}} ,{\mathbf{A}}_{3}^{{}} } \right\}}} ,$$
(23)

where \({\mathbf{n}}^{0}\) denotes the mid-surface normal, in the initial state C0, which can be evaluated by:

$${\mathbf{n}}^{0} = \frac{{{\mathbf{A}}_{1} \wedge {\mathbf{A}}_{2} }}{{\left\| {{\mathbf{A}}_{1} \wedge {\mathbf{A}}_{2} } \right\|}}.$$
(24)

The Jacobian matrix can be expressed as:

$${\mathbf{J}} = \left[ {\begin{array}{*{20}c} {{\mathbf{n}}_{1}^{0} \cdot {\mathbf{A}}_{1} } & {{\mathbf{n}}_{2}^{0} \cdot {\mathbf{A}}_{1} } \\ {{\mathbf{n}}_{1}^{0} \cdot {\mathbf{A}}_{2} } & {{\mathbf{n}}_{2}^{0} \cdot {\mathbf{A}}_{2} } \\ \end{array} } \right].$$
(25)

Note that a spatial description leads to a shell problem with 7 DOF/node and the material description leads to a shell problem with 6 DOF/node. Therefore, the generalized displacement vector \(\delta {\varvec{\Phi}}_{n} =\, \left( {\delta \varvec{x},\delta \varvec{d},\delta \varphi } \right)_{n}\) and the nodal displacement vector \(\delta\varvec{\varGamma}_{n} = \left( {\delta \varvec{x},\delta\varvec{\varTheta},\delta \varphi } \right)_{n}\) are related in the following way using transformation matrix \(\bar{\varvec{\varLambda }}_{K}\):

$$\delta {{\Phi }}_{n} = \varvec{\Pi }_{n} ~\delta \varvec{\Gamma }_{n} {;}\quad \varvec{\Pi }_{n} {\bf{ = }}\rm{diag}\left( {\begin{array}{*{20}l} {\varvec{\Pi }_{1} } & {\varvec{\Pi }_{2} } & {\varvec{\Pi }_{3} } & {\varvec{\Pi }_{4} } \\ \end{array} } \right),$$
(26)

with

$$\varvec{\varPi}_{I} = \left[ {\begin{array}{*{20}c} \varvec{I} & \varvec{0} & \varvec{0} \\ \varvec{0} & {\mathop {\varvec{\varLambda}_{I} }\limits^{\varvec{\_}} } & \varvec{0} \\ 0 & 0 & 1 \\ \end{array} } \right] \text{;}\quad {\bar{\mathbf{\varLambda }}}\,_{I} = {\mathbf{Q}}_{\text{I}} {\tilde{\mathbf{E}}}_{3} \text{;}\quad I = 1 \ldots 4,$$
(27)

where \({\mathbf{d}}_{\text{I}} = {\mathbf{Q}}_{\text{I}} {\mathbf{E}}_{3} \text{;}\,\quad\) \({\mathbf{E}}_{3} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]^{\,t}\), and \(\quad {\mathbf{Q}}_{\text{I}} = \left[ {\begin{array}{*{20}l} {{\mathbf{t}}_{{\text{1I}}} } & {{\mathbf{t}}_{{\text{2I}}} } & {{\mathbf{t}}_{{\text{3I}}} } \\ \end{array} } \right]\) in which, \({\mathbf{t}}_{\text{I}}\) denotes the director vector of the rotation matrix \({\mathbf{Q}}_{\text{I}}\).

5.1 Discretization of strain and electric fields

The discretization of the membrane and bending parts of the strain field, defined in Eq. (8), is given by:

$$\delta {\mathbf{e}} = {\mathbf{B}}_{m} \cdot \delta {\varvec{\Phi}}_{n} ;\quad \delta {\varvec{\upchi}} = {\mathbf{B}}_{b} \cdot \delta {\varvec{\Phi}}_{n} ,$$
(28)

where \({\mathbf{B}}_{m}\) and \({\mathbf{B}}_{b}\) are the membrane and the bending strain–displacement operators, respectively, which are expressed at node I as:denotes the director vector

$$\begin{gathered} {\mathbf{B}}_{m}^{I} = \left[ {\begin{array}{*{20}l} {{\mathbf{B}}_{{mm}}^{I} } & {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]{;}\quad {\mathbf{B}}_{b}^{I} = \left[ {\begin{array}{*{20}l} {{\mathbf{B}}_{{bm}}^{I} } & {{\mathbf{B}}_{{bb}}^{I} } & {\mathbf{0}} \\ \end{array} } \right]{;}\quad I = 1,...,4 \hfill \\ {\mathbf{B}}_{{mm}}^{I} = \left[ {\begin{array}{*{20}c} {{\mathbf{n}}_{1}^{T} \bar{N}_{{,1}}^{I} } \\ {{\mathbf{n}}_{2}^{T} \bar{N}_{{,2}}^{I} } \\ {{\mathbf{n}}_{1}^{T} \bar{N}_{{,2}}^{I} + {\mathbf{n}}_{2}^{T} \bar{N}_{{,1}}^{I} } \\ \end{array} } \right]{;}\quad {\mathbf{B}}_{{bm}}^{I} = \left[ {\begin{array}{*{20}c} {{\mathbf{d}}_{{,1}}^{T} \bar{N}_{{,1}}^{I} } \\ {{\mathbf{d}}_{{,2}}^{T} \bar{N}_{{,2}}^{I} } \\ {{\mathbf{d}}_{{,1}}^{T} \bar{N}_{{,2}}^{I} + {\mathbf{d}}_{{,2}}^{T} \bar{N}_{{,1}}^{I} } \\ \end{array} } \right]{;}\quad {\mathbf{B}}_{{bb}}^{I} = {\mathbf{B}}_{{mm}}^{I} , \hfill \\ \end{gathered}$$
(29)

where \({\mathbf{d}}_{,a}^{{}} = \sum\nolimits_{I = 1}^{4} {\bar{N}_{,a}^{I} \,{\mathbf{d}}_{I}^{{}} } \text{;}\quad \,a = 1,2\). \({\mathbf{n}}_{1}^{{}}\) and \({\mathbf{n}}_{2}^{{}}\) are the vectors of the actual basis that defined as:

$$\varvec{n}_{1}^{{}} = \sum\limits_{I = 1}^{4} {\bar{N}_{{}}^{I} \,\left( {\varvec{X} + \varvec{U}} \right)_{I}^{{}} }_{{}} \text{;}\quad \,\,\varvec{n}_{2}^{{}} = \sum\limits_{I = 1}^{4} {\bar{N}_{{}}^{I} \,\left( {\varvec{X} + \varvec{U}} \right)_{I}^{{}} } \,\,.$$
(30)

The Assumed Natural Strains (ANS) method is adopted in the developed discrete model to avoid locking problems, which may improve the efficiency of the present model in the prediction of nonlinear dynamic behavior. Therefore, the shear strain is expressed as [26]:

$$\delta {\varvec{\upgamma}}_{\xi }^{{}} = \left[ {\begin{array}{*{20}c} {\delta \gamma_{1}^{{}} } \\ {\delta \gamma_{2}^{{}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {1 - \eta } \right)\,\,\delta \gamma_{1}^{{}} \left( B \right) + \left( {1 + \eta } \right)\,\delta \gamma_{1}^{{}} \left( D \right)} \\ {\left( {1 - \xi } \right)\,\delta \gamma_{2}^{{}} \left( A \right) + \left( {1 + \xi } \right)\delta \gamma_{2}^{{}} \left( C \right)} \\ \end{array} } \right],$$
(31)

where \(\gamma_{2}^{{}} \left( A \right)\), \(\gamma_{1}^{{}} \left( B \right)\), \(\gamma_{2}^{{}} \left( C \right)\), and \(\gamma_{1}^{{}} \left( D \right)\) represent, respectively, the strains at middle points of the elements A, B, C, and D (see Fig. 3). The variation of transverse shear strain becomes:

$$\begin{aligned} \delta {\varvec{\upgamma}}_{\xi }^{{}} = {\mathbf{B}}_{s\xi } .\delta {\varvec{\Phi}}_{n} \text{;}\quad \,\,{\mathbf{B}}_{s\xi }^{{}} = \left[ {\begin{array}{*{20}c} {N_{,1}^{1} {\mathbf{d}}_{B}^{{^{T} }} } & {N_{,1}^{2} {\mathbf{A}}_{1B}^{T} } & {\mathbf{0}} & {N_{,1}^{2} {\mathbf{d}}_{B}^{{^{T} }} } & {N_{,1}^{2} {\mathbf{A}}_{1B}^{T} } & {\mathbf{0}} \\ {N_{,2}^{1} {\mathbf{d}}_{A}^{{^{T} }} } & {N_{,2}^{4} {\mathbf{A}}_{2A}^{T} } & {\mathbf{0}} & {N_{,2}^{2} {\mathbf{d}}_{C}^{{^{T} }} } & {N_{,2}^{3} {\mathbf{A}}_{2C}^{T} } & {\mathbf{0}} \\ \end{array} } \right. \hfill \\ \left. {\begin{array}{*{20}c} {N_{,1}^{3} {\mathbf{d}}_{D}^{{^{T} }} } & {N_{,1}^{3} {\mathbf{A}}_{1D}^{T} } & {\mathbf{0}} & {N_{,1}^{4} {\mathbf{d}}_{D}^{{^{T} }} } & {N_{,1}^{3} {\mathbf{A}}_{1D}^{T} } & {\mathbf{0}} \\ {N_{,2}^{3} {\mathbf{d}}_{C}^{{^{T} }} } & {N_{,2}^{3} {\mathbf{A}}_{2C}^{T} } & {\mathbf{0}} & {N_{,2}^{4} {\mathbf{d}}_{A}^{{^{T} }} } & {N_{,2}^{4} {\mathbf{A}}_{2A}^{T} } & {\mathbf{0}} \\ \end{array} } \right]. \hfill \\ \end{aligned}$$
(32)

Hence, the transverse shear strain can be expressed in the local Cartesian system as:

$$\delta {\mathbf{\gamma }} = {\mathbf{B}}_{s} \cdot \delta {\mathbf{\Phi }}_{n} {;}\quad \,\,{\mathbf{B}}_{s} = {\mathbf{J}}^{{ - 1}} {\mathbf{B}}_{{s\xi }}$$
(33)

The electric field varies linearly through the piezolayers’ thickness, and it is assumed constant over an element of these active layers:

$$\begin{aligned} \delta \varvec{E}_{m} = {\mathbf{B}}_{e} .\delta {\varvec{\Phi}}_{n} \text{;}\quad \varvec{B}_{e}^{I} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{B}}_{ee}^{I} } \\ \end{array} } \right]\text{;}\quad \hfill \\ B_{ee}^{I} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{{N^{I} }}{t}} \\ \end{array} } \right]^{T} , \hfill \\ \end{aligned}$$
(34)

where t denotes the thickness of the active layer and \(\varvec{B}_{e}^{I}\) is the discrete electric field-displacement relation.

As a result, the virtual and incremental generalized strain can be represented in approximate form as follows:

$$\Delta {\varvec{\Sigma}} = {\mathbf{B}}.\Delta {\varvec{\Phi}}_{{}} \text{;}\quad \delta {\varvec{\Sigma}} = {\mathbf{B}}.\delta {\varvec{\Phi}}_{{}} \text{;}\quad {\mathbf{B}}^{T} = \left[ {\begin{array}{*{20}c} {\varvec{B}_{m}^{T} } & {{\mathbf{B}}_{b}^{T} } & {{\mathbf{B}}_{s}^{T} } & {{\mathbf{B}}_{e}^{T} } \\ \end{array} } \right].$$
(35)

5.2 Linearization of weak form

The nonlinear shell problem solved by the Newton iterative procedure is established using the weak form directional derivatives in the direction of the increment. The linearized weak form, mentioned in Eq. (19), is given by:

$$G + DG ._{{}} {\varvec{\Delta}}{\varvec{\Phi}} = 0.$$
(36)

It is practical to split the tangent operator into geometric and material parts, denoted by \(D_{G} G ._{{}} {\varvec{\Delta}}{\varvec{\Phi}}\) and \(D_{M} G ._{{}} {\varvec{\Delta}}{\varvec{\Phi}}\), respectively:

$$DG ._{{}} {\varvec{\Delta}}{\varvec{\Phi}} = D_{G} G ._{{}} {\varvec{\Delta}}{\varvec{\Phi}} \, + \, D_{M} G ._{{}} {\varvec{\Delta}}{\varvec{\Phi}}.$$
(37)

5.2.1 Material part

The material part of the tangent operator, obtained by the variation in the stress resultants, can be written as follows:

$$D_{M} G._{{}} {\varvec{\Delta}}{\varvec{\Phi}} = \int_{A} { \, \delta {\varvec{\Sigma}}^{T} {\varvec{\Delta}}{\mathbf{R}}dA} .$$
(38)

Using Eq. (35), the internal virtual work becomes:

$$G_{int} = \delta {\varvec{\Phi}}_{n}^{T} \int_{A} {B^{T} {\mathbf{R}}dA} = \delta {\varvec{\Phi}}_{n}^{T} \int_{A} {B^{T} H_{T} B dA} .$$
(39)

The material stiffness matrix is inferred from Eq. (39).

$$K_{M} = \int_{A} { B^{T} H_{T} B dA} = \left[ {\begin{array}{*{20}c} {K_{m}^{uu} } & {K_{m}^{u\varphi } } \\ {K_{m}^{\varphi u} } & {K_{m}^{\varphi \varphi } } \\ \end{array} } \right],$$
(40)

where

$$\begin{aligned} K_{M}^{uu} &= \int_{A} { B_{u}^{T} C_{{}} B_{u}^{{}} dA}_{{}} \text{;}\quad K_{M}^{u\varphi } = \int_{A} { B_{u}^{T} p_{{}}^{T} B_{e} dA} \hfill \\ K_{M}^{\varphi u} &= \int_{A} { B_{e}^{T} p_{{}} B_{u}^{{}} dA}_{{}} \text{;}\quad K_{M}^{\varphi \varphi } = \int_{A} {B_{e}^{T} k_{{}}^{{}} B_{e} dA\text{;}\quad } B_{u}^{T} = \left[ {\begin{array}{*{20}l} {{\mathbf{B}}_{m}^{T} } & {{\mathbf{B}}_{b}^{T} } & {{\mathbf{B}}_{s}^{T} } \\ \end{array} } \right]. \hfill \\ \end{aligned}$$
(41)

5.2.2 Geometrical part

The geometrical part of the tangent operator is obtained by the variation of the virtual strain and keeping constant the stress resultants:

$$D_{G} G ._{{}} {\varvec{\Delta}}{\varvec{\Phi}} = \int_{A} {\left( {{\mathbf{\Delta \delta \varSigma }}^{T} \cdot_{{}} {\mathbf{R}}} \right){\text{d}}A = }_{{}} \delta {\varvec{\Phi}}_{n}^{\varvec{T}} \cdot_{{}} \varvec{K}_{\varvec{G}} \cdot_{{}} {\varvec{\Delta}}{\varvec{\Phi}}_{n} ,$$
(42)

where the geometric tangent matrix \(\varvec{K}_{\varvec{G}}\) is detailed in [26].

The generalized tangent stiffness matrix of an element is given as the following:

$$\varvec{K}_{T} \varvec{ = K}_{M} + \varvec{K}_{\varvec{G}} .$$
(43)

After nodal transformation, Eq. (26), the global material stiffness matrix can be computed by:

$$\varvec{K} =\varvec{\varPi}_{n}^{T} \varvec{K}_{T}\varvec{\varPi}_{n} .$$
(44)

5.3 Nodal updates

Considering large deformations of the shell structures, the generalized displacement vector at node ‘I’ is updated as seen in Table 1.

Table 1 The nodal updates
Full size table

6 Transient analysis of nonlinear formulation

Kinetic energy of smart shell structure is expressed in the discrete form as:

$$T = \delta\varvec{\varGamma}_{n}^{T} \,{\mathbf{M}}\,\varvec{\ddot{\varGamma }}_{n} ,$$
(45)

where \(\delta\varvec{\varGamma}\) and \(\varvec{\ddot{\varGamma }}\) are the virtual displacement and acceleration vector at the global level. M denotes the mass matrix. In the current dynamic analysis, a lumped mass matrix is adopted, which is a diagonal matrix based on the assumption that the element mass is lumped on the element nodes. Its expression is given by:

$${\mathbf{M}}_{II} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{1I} } & {{\mathbf{M}}_{2I} } & 0 \\ \end{array} } \right]_{\text{diag}} \text{;}\quad I = 1 \ldots 4,$$
(46)

where

$$\begin{aligned} {\mathbf{M}}_{kI} = \frac{{\int_{{}}^{{}} {\bar{\rho }_{kk} N_{{}}^{I} N_{{}}^{I} dA} \,\int_{{}}^{{}} {\bar{\rho }_{kk} dA} }}{{\int_{{}}^{{}} {\left( {\sum\limits_{{}}^{{}} {\bar{\rho }_{kk} N_{{}}^{I} N_{{}}^{I} } } \right)dA} }}\,\,{\mathbf{I}}_{k} \text{;}\quad k = 1,2\text{;}\quad I = 1..4\, \hfill \\ {\bar{\mathbf{\rho }}} = \int_{ - h/2}^{h/2} {\rho \,\,\left[ {\begin{array}{*{20}c} 1 & z \\ z & {z^{2} } \\ \end{array} } \right]\,} \,dz\text{;}\quad {\mathbf{I}}_{1} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 \\ \end{array} } \right]\text{;}\quad {\mathbf{I}}_{2} = \left[ {\begin{array}{*{20}c} 1 & 1 \\ \end{array} } \right]; \hfill \\ \end{aligned}$$
(47)

\(\rho\) represents the material density varying along the thickness.

Once the computation of the inertia term \(f_{\text{iner}}\) is done, the residual vector \({\mathbb{R}}\) may be deducted:

$${\mathbb{R}}\varvec{ = F} - {\mathbf{M}}\,\varvec{\ddot{\varGamma }}_{n}^{{}} \text{;}\quad f_{\text{iner}} = {\mathbf{M}}\,\varvec{\ddot{\varGamma }}_{n}^{{}} ,$$
(48)

where F is the contribution of either the internal and external work.

The governing equations of motion are solved by Newmark’s method. Indeed, this method allows the direct solution of a second-order differential equation or a system of second-order differential equations without the need of the transformation to a pair of simultaneous first-order differential equations. The method may be applied in various fields of engineering, in particular to the dynamic response systems. It remains to choose values of Newmark parameters β and γ. In the present study, these parameters are chosen as: β = 0.25 and γ = 0.5: the Newmark method is implicit and unconditionally stable, meaning that the method will converge for all time increments. The Newmark’s algorithm is detailed in Appendix A.

The elementary governing equation of motion solved by Newmark’s algorithm is inferred as:

$$\varvec{K}_{{}}^{*} \Delta\varvec{\varGamma}_{n + 1}^{t + \Delta t} \, = {\mathbb{R}}_{n + 1}^{t} \text{;}\quad \varvec{K}_{{}}^{*} = \varvec{K} + \frac{1}{{\beta\Delta t^{2} }}\varvec{M}\varvec{.}$$
(49)

7 Numerical examples and discussion

This section mainly includes the following two parts to ensure the accuracy and the validity of the proposed finite-element analysis model. First, comparison studies with the existing literature are carried out for the nonlinear transient behavior of piezolaminated composite shells. Then, numerical discussions on the nonlinear dynamic analysis of smart FG-CNTRC structures are made mainly to provide some parameterized new results.

7.1 Convergence studies

Convergence studies are carried out on nonlinear transient deflection of isotropic spherical shell, piezolaminated plate, and isotropic semicircular cylindrical shell with surface-bonded active layers to show the validity of the present formulation.

7.1.1 Nonlinear dynamic behavior of passive spherical shell

A clamped passive spherical cap shell is analyzed with consideration of both linear and nonlinear computation. The whole structure is subjected to a concentrated step load, F = 100, located at its mid-span (see Fig. 4). The spherical cap is meshed by 217 nodes and 192 elements with 5 degrees of freedom at each node. Geometric and material properties for this test are R = 4.76, θ = 10.9o, h = 0.01576, H = 0.0859, Y = 107,\(\nu = \text{0.3}\), and ρ = 0.000245 according to [14].

Fig. 4
figure 4

Shallow spherical cap, geometry, and finite-element modeling

Full size image

The response of the structure is observed in a time interval of 250 µs. The time increment is Δt = 0.2 µs. The results for the linear and nonlinear normalized vertical displacements at shell apex obtained with the presented model are compared with those from [14]. The element used by [14] is a higher order solid shell element based on the Enhanced Assumed Strain (EAS). The results for the displacements at shell apex are depicted in Fig. 5 and show very good agreement.

Fig. 5
figure 5

Transient response of the isotropic shallow spherical cap

Full size image

7.1.2 Nonlinear dynamic behavior of active plate

The following example is a two-sided hinged plate, as shown in Fig. 6. It consists of three layers forming a symmetric architecture. The middle layer is made of graphite fiber-reinforced epoxy T300/976. Its material properties are as follows: Y1 = 132.28 GPa, Y2 = 10.76 GPa, G12 = 5.65 GPa, G23 = 3.61 GPa, \(\nu_{12}\) = 0.24 and ρ = 7300 kg/m3. Two PZT G1195 actuators cover the structure. The material and piezoelectric properties of PZT G1195 are Y1 = Y2 = 63 GPa, \(\nu_{12}\) = 0.3, e31 = e32 = 22.86 C/m2 and ρ = 7600 kg/m3. The dimensions of the plate are also shown in Fig. 6. The thicknesses of the mid layer and the active layer are 0.2 mm and 0.15 mm, respectively. The present results are obtained with a 4 × 4 mesh and with an increment time of 10−4 s. The two-actuator layers are subjected to a sinusoidal dynamic voltage excitations expressed as \(\varphi = 300_{{}} \sin \left( {2\pi f_{{}} t} \right)\), where the frequency \(f = 100_{{}} \text{Hz}\). Due to the opposite polarization of the piezo layers, their activation produces internal bending moments over the plate edges.

Fig. 6
figure 6

Two-edge simply supported plate with embedded PZT layers

Full size image

Figure 7 shows the transient response of composite piezolaminated plate under harmonic electric excitation. The present transient center deflection of the plate is compared with those in the existing literature given by [32, 33]. Zhang et al. [33] developed an eight-node piezoelectric coupled shell element with uniformly reduced integration and the nonlinear theory includes fully geometrically nonlinear shell theory with large rotations (LRT56). The finite-rotation theory (FRT) model developed by Rao and Schmidt [32] has 18 internal DOFs for strain field in the enhanced assumed strain (EAS) and 12 internal DOFs for electric field in the an enhanced assumed gradient (EAG). The transient results obtained by the developed element exhibit similar vibration tendencies with those mentioned in [32, 33].

Fig. 7
figure 7

Center deflection of piezolaminated plate over time under harmonic electric excitation

Full size image

7.1.3 Nonlinear dynamic behavior of smart semicircular cylindrical shell

The dynamic simulation of smart semicircular cylindrical shell was proposed by [67] and was further modified by [36]. This smart structure was also studied by Rao and Schmidt [68] to perform three different analyses: linear eigenvalue problem, static analysis of geometrically linear and nonlinear deformations, and simulation of large amplitude vibrations and control with distributed actuators. The curved structure is clamped at one end and free at the other end. The dimensions of the host structure and the piezoceramic layers are displayed in Fig. 8. The host material is considered as a steel metal, whose material properties are given as follows: Y1 = 68.95 GPa, \(\nu_{12}\) = 0.3, and ρ = 7750 kg/m3. The material and piezoelectric properties of PZT are Y1 = Y2 = 63 GPa, \(\nu_{12}\) = 0.3, e31 = e32 = 16.11 C/m2, k33 = 1.65 × 10−8 F/m, and ρ = 7600 kg/m3. The thickness of each active layer is estimated to be 0.254 mm. The semicircular arch is subjected to a step force F = 50 N at the tip point: The piezoelectric layers act as sensor. The transient deflections at tip point at the free end are predicted by the Newmark method with a time-step increment of 10−3 s. The shell is modeled using 16 × 16 mesh. The obtained results in terms of time-hoop/radial displacements at the tip point are compared to those given by [36]. Excellent agreements between both results are observed as depicted in Figs. 9 and 10 for hoop and radial displacements, respectively.

Fig. 8
figure 8

Semicircular cylindrical shell covered with active layers

Full size image
Fig. 9
figure 9

Hoop deflection of the PZT laminated semicircular cylindrical shell over time

Full size image
Fig. 10
figure 10

Radial deflection of the PZT laminated semicircular cylindrical shell over time

Full size image

7.2 New results for smart FG-CNTRC shell structures

After the validation of the developed model via the above convergence studies, the nonlinear dynamic behavior for smart FG-CNTRC shell structures is now simulated to highlight the effect of introduction of CNT reinforcements to such piezolaminated structures. The material properties of CNT composite and polymer matrix are given in Tables 2 and 3.

Table 2 Mechanical properties of SWCNT fibers and PmPV at T = 300 K [69]
Full size table
Table 3 (CNT) efficiency parameters for three different volume fractions [69]
Full size table

7.2.1 Large transient deflection of smart FG-CNTRC spherical shell

Nonlinear transient analysis of FG-CNTRC shallow spherical cap with integrated piezoelectric layers is considered. The same geometrical properties of spherical shell are considered as mentioned earlier in the sub-Sect. 7.1.1. The material and piezoelectric properties of PZT are Y = 63 GPa, \(\nu_{12}\) = 0.3, e31 = e32 = 16.11 C/m2, k33 = 1.65 × 10−8 F/m, and ρ = 7600 kg/m3. The thickness of the each active layer is 1 mm. The structure is exhibited to sudden applied uniform pressure loading of value q0 = − 1 × 106 N/m2.

Figure 11 represents the transient center deflection for uniform (UD) and three-dispersion pattern of CNT: FG-V, FG-O, and FG-X-CNTRC spherical caps and under three values of volume fractions \(\left( {V_{\text{CNT}}^{ *} = 0.11,_{{}} 0.14,_{{}} 0.17} \right)\), respectively. It is intrigued to illustrate that FG-X induces the lowest transient central deflection, while the FG-O has the highest one. For UD and FG-V, they located between FG-X and FG-O. This can be explained by the form of CNT distribution where the reinforcements distributed close to the top and bottom surfaces and are more efficient in the enhancement of the nonlinear dynamic behavior of such structures. In addition, it is noted that the CNT volume fraction has a great influence on the vertical deflection of the FG-CNTRC spherical shell. In fact, when the volume fraction of CNTs decreases, the value of the transverse central deflection increases for each type of distribution. For instance, the value of central deflection of UD distribution decreases about 54% from \(V_{\text{CNT}}^{ *} = 0.11\) to \(V_{\text{CNT}}^{ *} = 0.17\) at t = 0.016 s. The following results demonstrate the effect of CNTs in the transient behavior of the smart spherical shell. Therefore, designer can adjust the form and the volume fraction of CNT to control the vibration phenomenon. Furthermore, Table 4 summarizes the maximum center deflection of the FG-CNT spherical cap with surface-bonded piezolayers to clearly see the differences of results using various CNT distribution patterns and volume fractions.

Fig. 11
figure 11

Nonlinear dynamic responses of FG-CNT spherical cap with surface-bonded piezolayers for various distribution pattern of CNTs and under different volume fraction

Full size image
Table 4 Maximum center deflection of the smart FG-CNT spherical cap
Full size table

Moreover, the influence of variation of radius-to-thickness ratio (R/H) is studied here for the active FG-CNTRC spherical shell (see Fig. 12). Obviously, the central deflection extend with the increasing of the parameter R/H. In fact, for (R/H = 20), the amplitude of transverse deflection does not exceed (8.88 × 10−3 m) for the different distribution pattern of CNTs, while this amplitude reaches (2.16 × 10−1 m) with (R/H = 50). Thereby, the increase of this parameter has a significant effect on nonlinear forced vibrations of such smart FG-CNTRC structures.

Fig. 12
figure 12

Nonlinear dynamic responses of FG-CNT spherical cap with surface-bonded piezolayers for various distribution pattern of CNTs, under volume fraction \(V_{\text{CNT}}^{ *} = 0.11\) and with two different apothem-to-thickness ratios R/H

Full size image

7.2.2 Large transient deflection of smart FG-CNTRC cylindrical shell

Extending the previous analysis in the sub-Sect. 6.1.3 to FG-CNTRCs, large deformations for smart FG-CNTRC semicircular cylindrical shell are studied where the geometrical parameters are the same. This problem was studied by Rao et al. [62] to predict the forced vibration response of FG-Graphene Platelet-reinforced polymer composites laminated with piezoelectric layers. It was found that the GPL distribution and weight fraction of GPLs have a significant effect on the vibration and damping characteristics of the FG-GPL composite cylindrical shell.

Figure 13 represents the nonlinear transient hoop tip deflection for UD and various patterns of CNT dispersion: FG-V, FG-O, and FG-X-CNT cylindrical shell with embedded actuators and under different volume fraction of CNTs \(V_{\text{CNT}}^{ *}\). It is found that FG-X semicircular shell has the lowest transient tip deflection values, while FG-O shell has the highest ones. Furthermore, values of period increase from FG-X curve to FG-O curve. This is due to the fact that reinforcements distributed close to the top and bottom are more efficient than those distributed near the mid-surface, which allow the increase of the stiffness of adaptive FG-CNT shell structures. Furthermore, the effect of CNT fraction volume on the large transverse deformation of the studied semicircular shell under step force at tip point is examined as shown in Fig. 13. It is observed that the enrichment of the polymer matrix PmPV with higher quantities of CNTs results in the decline of nonlinear transient central deflection. This is expected, since, for lower values of volume fraction \(V_{\text{CNT}}^{ *}\), the cylindrical shell loses stiffness.

Fig. 13
figure 13

Large transverse deformation of FG-CNT cylindrical shell with surface-bonded piezolayers for various distribution patterns of CNTs and under different volume fraction

Full size image

The sensitivity of the geometrically nonlinear dynamics to the curvature of the smart FG-CNT shell structure is analyzed in this part. Figure 14 depicts the nonlinear hoop deflection of the FG-CNT semicircular cylindrical shell, considering the volume fraction \(V_{\text{CNT}}^{ *} = 0.14\), for different radius-to-thickness ratio (R/h) values. It should be mentioned that, as the R/h ratio increases, the radius of curvature rises and a cylindrical shell tends to be a flat structure. For all analyzed patterns of CNT dispersion, it is clearly observed that, as the R/h ratio increases, the tip hoop displacement rises, and the piezolaminated shell structure provides a higher stiffness in comparison to the piezolaminated plate structure due to the presence of an initial curvature in its geometry.

Fig. 14
figure 14

Large transverse deformation of FG-CNT cylindrical shell with surface-bonded piezolayers for various distribution patterns of CNTs, under a volume fraction \(V_{\text{CNT}}^{ *} = 0.14\) and with different radius-to-thickness ratio

Full size image

To illustrate the influence of piezoelectric layer thickness tp on the nonlinear dynamic characteristics of FG-CNTRC plates with surface-bonded sensors, tip deflection is depicted in Fig. 15, for various profiles of CNT distribution and under a volume fraction. It is clearly seen from Fig. 15 that as the thickness of PZT layer tp increases, the structure becomes softer, since the volume fraction of PZT is increasing which results in higher deflections, for all patterns of CNT dispersion. Hence, it can be inferred that such geometrical parameter (thickness of active layer) has a significant effect on the nonlinear dynamic behavior of the active FG-CNT structures, which should be carefully considered for the structure design.

Fig. 15
figure 15

Large transverse deformation of FG-CNT cylindrical shell with surface-bonded piezolayers for various distribution patterns of CNTs, under a volume fraction \(V_{\text{CNT}}^{ *} = 0.11\) and with different piezoelectric layer thickness tp

Full size image

8 Conclusion

This paper makes a first attempt to predict geometrically nonlinear dynamic behavior of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) with surface-bonded piezoelectric layers, so as to enrich the existing research results on FG-CNTRC structures. A micro-mechanical model according to the extended rule of mixture is adopted to assess the effective material properties of the FG-CNTRC structures strengthened by SWCNTs. The nonlinear formulation is based on the improved FSDT ensuring realistic parabolic variation of transverse shear strain along the thickness direction. The governing equations of motion are solved using the Newmark’s algorithm coupled with Newton–Raphson iteration. By a variety of numerical examples, the accuracy of the proposed model is verified. Several novel results of smart FG-CNTRC spherical and cylindrical shells are presented. Furthermore, the effects of structure and material parameters are also reported. The obtained results show that CNT with FG-X-CNT distribution is correlated with the lowest nonlinear transverse deflection, while FG-O-CNT distribution exhibits the highest one among the other CNT distributions. Furthermore, it is found that the volume fraction of the carbon nanotubes \(V_{\text{CNT}}^{ *}\) has a significant effect on the structural behavior of the adaptive FG-CNTRC structures.