1 Introduction

Nowadays, numerical methods and algorithms have come to help the engineers and researchers to open the way for solving complex scientific problems such as molecular structural analysis, meteorology and weather forecasting, system dynamics, and many other essential topics. In general, numerical calculations use the practical results of computing to find new ways to analyze problems. In engineering problems, the analysis of structures using modern numerical methods is one of the most widely used problems [1].

More recently, the mechanical and structural analyses of nanostructures due to their widespread applications with the help of modern numerical methods has received much attention [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. Among these numerical methods, the Haar wavelet method [26,27,28] and higher order Haar wavelet method [29, 30] and also differential quadrature method [31,32,33] are among the advanced numerical methods with excellent precision. The wavelet is a special series of functions that are now known as the first wavelet. This series was presented as the simplest type of the wavelet first introduced by Alfred Haar in 1909. Mathematically, the wavelet is a set of fixed piece functions that can approximate a function. Among the published papers, Hein and Feklistova [34] investigated Haar wavelets to study free vibrations of non-uniform and axially functionally graded beams under different boundary conditions. They transformed their equations based on the simplest wavelets. Their results were appropriately matched with the other presented works. Lepik [35] based on the Euler–Bernoulli beam model studied an elastic local beam containing a crack subjected to a longitudinal in-plane load based on the Haar wavelet method. His results proved the high accuracy of the Haar wavelet method. Kirs et al. [36] analyzed dynamically a nonlocal Euler–Bernoulli beam model based on the Haar wavelets. They also carried out three boundary conditions, namely pined–pined, clamped–clamped, and clamped–pined ones.

As it has been seen so far, the properties of materials such as their energy at the nanoscale vary with their large-scale state. However, the size reduction is a physical change, and it is not expected that the basic properties of the material will change with this physical change. This has made the nanoscale more attractive than other scales. Properties such as electrical conductivity, color, mechanical strength, and even weight can be changed at the nanoscale. For example, the conductivity of metals is well known. However, metals can be a semiconductor or even insulated on a nanoscale. Nanomaterials also have a much higher surface-to-volume ratio compared to bulk materials. This is a fundamental property that is extremely important in all processes that occur on the surface of the material (such as reactivity). So it can be stated that nano does not just mean a thousand times smaller than micro. Investigating the mechanical behavior of a nanostructure at the nanoscale is in dire need of a suitable theory that to date elasticity theory of nonlocal of Eringen [37,38,39,40,41,42], couple stress [43, 44] and strain gradient theories [45,46,47,48,49] predict the behavior of nanostructures extensively as a mechanical analysis under different conditions. However, in this study, the size-dependent effects have been described employing the nonlocal strain gradient theory, which is a combination of the Eringen’s nonlocal theory and the second-order Mindlin strain gradient theory, which can well show the effects of size reduction and atomic interaction [50, 51].

More recently, some researchers have focused on the main model of nonlocal strain gradient theory, namely its integral forms [52, 53]. As a matter of fact, both nonlocal and strain gradient terms instead of their differential models have been re-considered in their integral models. They have found that in some beam analyses, the results of differential models may be inconsistent with the integral ones’ results. In addition, in some valuable researches [54, 55], researchers have presented that while considering nonlocal elasticity theory of Eringen or nonlocal strain gradient approach, there have been more appropriate numerical outcomes if the effect of change in the thickness is investigated in the gradients of stress and strain, that is, although the effect of changes in the thickness has been ignored in the strains by researchers, the effect of size-dependent can be crucial in the thickness direction. Of some important conclusions within these studies, they showed that the thickness effect strengthens the c effect of nonlocal strain gradient theory and by ignoring the effect of thickness the stiffness-hardening effect is underestimated. In fact, the stiffness-hardening and stiffness-softening influences are affected by the length to thickness ratio when considering the thickness effect.

This research has come to consider profoundly and comprehensively various advanced numerical approaches, namely Haar wavelet method (HWM), higher order Haar wavelet method (HOHWM) and differential quadrature method (DQM) to analyze a nanobeam under mechanical stability situation. To this, the classical beam model is embedded in the energy formulation to extract the equilibrium equations and the strain gradient nonlocal model reformulates the obtained local equations to implement a nanoscale behavior in the problem. Moreover, the Winkler elastic matrix is assumed to be as an outer effect. Afterward, several diagrams are graphically plotted with the results of the HWM, HOHWM, and DQM for two boundary conditions, namely pined–pined and clamped–clamped ones to show the stability behavior of the modeled nanobeam.

2 Review of the strain gradient model

The stress field as per the first-order nonlocal strain gradient model [19, 50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68] is presented as

$$ \sigma_{xx} = \sigma_{xx}^{\diamondsuit } - \nabla \sigma_{xx}^{*} \,, $$
(1)

where \( \sigma_{xx}^{\diamondsuit } = \int\limits_{0}^{L} {E\alpha \left( {x,\,x^{\prime},\,e_{0} a} \right)} \,\varepsilon^{\prime}_{xx} \left( {x^{\prime}} \right)\,{\text{d}}x^{\prime} \) and \( \sigma_{xx}^{*} = l^{2} \int\limits_{0}^{L} {E\alpha^{*} \left( {x,\,x^{\prime},\,e_{1} a} \right)} \,\varepsilon^{\prime}_{xx,x} \left( {x^{\prime}} \right)\,{\text{d}}x^{\prime} \) denote the classical nonlocal stress tensor and the higher order nonlocal stress tensor, respectively. \( \alpha \left( {x,\,x^{\prime},\,e_{0} a} \right) \) and \( \alpha^{*} \left( {x,\,x^{\prime},\,e_{1} a} \right) \) are the nonlocal kernel, \( \varepsilon_{xx} \) and \( \varepsilon_{xx,x} \) represent the strain and gradient of strain, \( L \) and \( l \) are the length of nanobeam and material length-scale parameter, and \( e_{0} a \), and \( e_{1} a \) are the nonlocal parameters due to the higher order strain gradient stress field. Applying the nonlocal differential operator \( \left( {\ell_{i} = 1 - \left( {e_{i} a} \right)^{2} \nabla^{2} \,,\,i = 0,\,1} \right) \) on the stress field, viz. Eq. (1), the first-order strain gradient model for a one-dimensional elastic material is described as [53]

$$ \begin{aligned} & \left( {1 - (e_{0} a)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\,\left( {1 - (e_{1} a)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\,\sigma_{xx} \\ & \quad = E\,\left( {1 - (e_{1} a)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\,\varepsilon_{xx} - \,El^{2} \,\left( {1 - (e_{0} a)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\,\frac{{\partial^{2} }}{{\partial x^{2} }}\varepsilon_{xx} . \\ \end{aligned} $$
(2)

Considering \( e_{0} = e_{1} \), Eq. (2) is converted into [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68]:

$$ \left( {1 - (e_{0} a)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\,\sigma_{xx} = E\,\left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\,\varepsilon_{xx} . $$
(3)

3 Formulation of proposed model

The displacement field of the Euler–Bernoulli beam at any point may be defined as [37]

$$ u_{1} \left( {x,\,z,\,t} \right) = \,u\,\left( {x,\,t} \right) - z\frac{{\partial w\,\left( {x,\,t} \right)}}{\partial x}, $$
(4a)
$$ u_{2} \left( {x,\,z,\,t} \right) = 0, $$
(4b)
$$ u_{3} \left( {x,\,z,\,t} \right) = w\,\left( {x,\,t} \right), $$
(4c)

where \( u_{1} ,\,u_{2} , \) and \( u_{3} \) represent displacements along \( x,\,y, \) and \( z \) directions, respectively, whereas \( u\,\left( {x,\,t} \right) \) and \( w\,\left( {x,\,t} \right) \) denote axial and transverse deflections of the point on the mid-plane of the beam. Using von Kármán hypothesis, the nonlinear strain–displacement relation may be expressed as

$$ \varepsilon_{xx} = \frac{{\partial u\,\left( {x,\,t} \right)}}{\partial x} - z\frac{{\partial^{2} w\,\left( {x,\,t} \right)}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{{\partial w\,\left( {x,\,t} \right)}}{\partial x}} \right)^{2} . $$
(5)

Hamilton’s principle for the conservative system is presented as

$$ \delta \prod = \int\limits_{{t_{1} }}^{{t_{2} }} {\delta \,\left( {W_{\text{e}} + U} \right)} \,{\text{d}}t, $$
(6)

where \( U \) is the strain energy and \( W_{\text{e}} \) is the work done by the elastic foundation. The variations in strain energy and external work done are given as

$$ \delta U = \int\limits_{0}^{L} {\int\limits_{A} {\sigma_{xx} \delta \varepsilon_{xx} {\text{d}}A\,{\text{d}}x} } = \int\limits_{0}^{L} {\left[ {N_{xx} \frac{\partial \delta u}{\partial x} - M_{xx} \frac{{\partial^{2} \delta w}}{{\partial x^{2} }} + N_{xx} \frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x}} \right]\,} {\text{d}}x, $$
(7)
$$ \delta W_{e} = - \int\limits_{0}^{L} {k_{\text{w}} w\,\delta w} \,{\text{d}}x, $$
(8)

where \( k_{\text{w}} \) is the Winkler modulus, \( \sigma_{xx} \) is the normal stress, \( N = \int\limits_{A} {\sigma_{xx} \,{\text{d}}A} , \) and \( M = \int\limits_{A} {\sigma_{xx} \,z\,{\text{d}}A} \) are axial force and bending moment, respectively. Substituting Eqs. (7) and (8) in Eq. (6) and setting \( \delta \prod = 0 \), we have

$$ \delta \prod = \int\limits_{0}^{t} {\int\limits_{0}^{L} {\left[ {N_{xx} \frac{\partial \delta u}{\partial x} - M_{xx} \frac{{\partial^{2} \delta w}}{{\partial x^{2} }} + N_{xx} \frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x} - k_{\text{w}} w\delta w} \right]\,} {\text{d}}x{\text{d}}t = 0} . $$
(9)

On simplification of Eq. (9) and taking \( N_{xx} = P \), the constitutive relation may be derived as

$$ \frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} - P\frac{{\partial^{2} w}}{{\partial x^{2} }} - k_{\text{w}} w = 0. $$
(10)

Multiplying Eq. (3) by \( z{\text{d}}A \) and integrating over \( A \), we have

$$ M_{xx}^{nl} = \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} M}}{{\partial x^{2} }} - EI\frac{{\partial^{2} w}}{{\partial x^{2} }} + l^{2} EI\frac{{\partial^{4} w}}{{\partial x^{4} }}, $$
(11)

where \( e_{0} \) and \( a \) denote material constant and internal characteristic length, respectively, \( I = \int\limits_{A} {z^{2} {\text{d}}A} \) is the second moment of inertia and \( E \) is Young’s modulus. Inserting Eq. (10) in Eq. (11), the nonlocal bending moment \( M_{xx}^{nl} \) can be changed into

$$ M_{xx}^{nl} = \left( {e_{0} a} \right)^{2} \left( {P\frac{{\partial^{2} w}}{{\partial x^{2} }} + k_{w} w} \right) - EI\frac{{\partial^{2} w}}{{\partial x^{2} }} + l^{2} EI\frac{{\partial^{4} w}}{{\partial x^{4} }}. $$
(12)

Putting Eq. (12) in Eq. (10), and assuming \( w\,\left( {x,\,t} \right) = w_{0} \left( x \right)\sin \omega t \), the governing equation is given as

$$ \begin{aligned} & \left( {e_{0} a} \right)^{2} k_{w} \frac{{{\text{d}}^{2} w_{0} }}{{{\text{d}}x^{2} }} + \left( {e_{0} a} \right)^{2} P\frac{{{\text{d}}^{4} w_{0} }}{{{\text{d}}x^{4} }} - EI\frac{{{\text{d}}^{4} w_{0} }}{{{\text{d}}x^{4} }} \\ & \quad + l^{2} EI\frac{{{\text{d}}^{6} w_{0} }}{{{\text{d}}x^{6} }} - P\frac{{{\text{d}}^{2} w_{0} }}{{{\text{d}}x^{2} }} - k_{\text{w}} w_{0} = 0, \\ \end{aligned} $$
(13)

Now, using \( X = \frac{x}{L}, \) \( W = \frac{{w_{0} }}{L}, \) \( K_{\text{w}} = \frac{{k_{\text{w}} L^{4} }}{EI}, \) \( \hat{P} = \frac{{PL^{2} }}{EI} \) and \( \beta = \frac{l}{L} \) in Eq. (13), the normalizing form of governing equation may be derived as

$$ \beta^{2} \frac{{{\text{d}}^{6} W}}{{{\text{d}}X^{6} }} - \frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }} + \frac{{\left( {e_{0} a} \right)^{2} }}{{L^{2} }}K_{\text{w}} \frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }} - K_{\text{w}} W = \hat{P}\,\left( {\frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }} - \frac{{\left( {e_{0} a} \right)^{2} }}{{L^{2} }}\frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }}} \right). $$
(14)

4 Preliminaries

4.1 Haar wavelet

The Haar function can be expressed as [28,29,30, 35, 36, 69, 70]

$$ h_{i} \,\left( x \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,} \hfill & {{\text{for}}\,\,x \in \left[ {\phi_{1} (i),\,\,\,\phi_{2} (i)} \right]} \hfill \\ { - 1\,\,} \hfill & {{\text{for}}\,\,x \in \left[ {\phi_{2} (i),\,\,\,\phi_{3} (i)} \right]} \hfill \\ 0\hfill & {\text{elsewhere }} \hfill \\ \end{array} \,\,\,\,\,} \right., $$
(15)

where \( i = m + k + 1 \), where \( m = 2^{j} \) and \( k \) denote the maximum number of square waves and the position of the particular square wave in the interval \( \left[ {I_{1} ,\,\,\,I_{2} } \right] \). Also, \( \phi_{1} \left( i \right) = I_{1} + k\frac{{I_{2} - I_{1} }}{{2^{j} }} \)\( \phi_{2} \left( i \right) = I_{1} + \left( {2k + 1} \right)\frac{{I_{2} - I_{1} }}{{2^{j + 1} }} \), and \( \phi_{3} \left( i \right) = I_{1} + \left( {k + 1} \right)\frac{{I_{2} - I_{1} }}{{2^{j} }} \), where \( j \)\( \left( {j = 0,\,1,\, \ldots ,J\,} \right) \) and \( k \)\( \left( {k = 0,\,1,\, \ldots ,\,2^{j} - 1} \right) \) represent the dilatation and translation parameters of the wavelets, respectively. \( J \) is termed as maximal of resolution of the wavelets. The Haar function, presented in Eq. (15) is only valid if \( i \ge 2. \) For \( i = 1 \), \( h_{1} (x) = 1 \) for \( x \in \left[ {I_{1} ,\,\,\,I_{2} } \right] \) and 0 elsewhere.

The \( \kappa \)th integral of the Haar function (for \( i > 1 \)), presented in Eq. (1) can be derived analytically as [28,29,30, 35, 36, 69, 70]

$$ p_{\kappa ,\,i} (t) = \frac{1}{\kappa !}\left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{for }}x \in \left[ {I_{1} ,\,\,\,\phi_{1} (i)} \right)} \hfill \\ {\left( {x - \phi_{1} (i)} \right)^{\kappa } } \hfill & {{\text{for}}\,\,x \in \left[ {\phi_{1} (i),\,\,\,\phi_{2} (i)} \right)} \hfill \\ {\left( {x - \phi_{1} (i)} \right)^{\kappa } - 2\,\left( {x - \phi_{2} (i)} \right)^{\kappa } } \hfill & {{\text{for }}x \in \left[ {\phi_{2} (i),\,\,\,\phi_{3} (i)} \right)} \hfill \\ {\left( {x - \phi_{1} (i)} \right)^{\kappa } - 2\,\left( {x - \phi_{2} (i)} \right)^{\kappa } + \left( {x - \phi_{3} (i)} \right)^{\kappa } } \hfill & {{\text{for }}x \in \left[ {\phi_{3} (i),\,\,\,I_{2} } \right)} \hfill \\ \end{array} } \right.. $$
(16)

For \( i = 1 \), we have \( \phi_{1} = I_{1} \), \( \phi_{2} = \phi_{3} = I_{2} \) and \( p_{\eta ,\,1} (t) = \frac{1}{\eta \,!}\left( {t - S} \right)^{\eta } \).

The collocation points are considered as [29, 35, 70]

$$ x_{k} = I_{1} + \left( {k - 0.5} \right)\frac{{I_{2} - I_{1} }}{{2^{J + 1} }},\quad k = 1,\,2, \ldots ,\,2^{J + 1} . $$
(17)

\( H,\,P_{1} ,\,P_{2} ,\,P_{3} , \ldots ,P_{\kappa } \) are the Haar matrices of dimension \( 2^{J + 1} \) and the elements of these matrices are expressed by \( H\left( {i,\,\,k} \right) = h_{i} (x_{k} ) \) and \( P_{\kappa } \left( {i,\,\,k} \right) = p_{\kappa ,\,i} (x_{k} ) \).

4.2 Differential quadrature method

In the present investigation, Quan and Chang’s [71, 72] version of Differential Quadrature Method has been implemented. According to this approach, the derivatives of any function \( W(X) \) at a given discrete point \( i \) can be expressed as linear sums of functions at discrete grid points, which are demonstrated as [31,32,33]

$$ W^{\prime}_{i} = \sum\limits_{j = 1}^{N} {A_{ij} W_{j} } , $$
(18a)
$$ W^{\prime\prime}_{i} = \sum\limits_{j = 1}^{N} {B_{ij} } W_{j} , $$
(18b)
$$ W^{\prime\prime\prime}_{i} = \sum\limits_{j = 1}^{N} {C_{ij} W_{j} } , $$
(18c)
$$ W_{i}^{IV} = \sum\limits_{j = 1}^{N} {D_{ij} } W_{j} , $$
(18d)
$$ W_{i}^{V} = \sum\limits_{j = 1}^{N} {E_{ij} } W_{j} , $$
(18e)
$$ W_{i}^{VI} = \sum\limits_{j = 1}^{N} {F_{ij} } W_{j} , $$
(18f)

where \( A_{ij} ,B_{ij} ,C_{ij} \), \( D_{ij} \), \( E_{ij} \) and \( F_{ij} \) are the weighting coefficient matrices, and \( N \) is the number of discrete grid points. Chebyshev–Gauss–Lobatto grid points have been used in this study which is defined as [31,32,33]

$$ X_{i} = \frac{1}{2}\left[ {1 - \cos \left( {\frac{i - 1}{N - 1} \cdot \pi } \right)} \right]. $$
(19)

The weighting coefficient matrices can be computed using Lagrange interpolation by the following procedure [31,32,33].

For \( i \ne j, \)

$$ A_{ij} = \frac{1}{{X_{j} - X_{i} }}\prod\limits_{\begin{subarray}{l} k \ne i \\ k \ne j \\ k = 1 \end{subarray} }^{N} {\frac{{X_{i} - X_{k} }}{{X_{j} - X_{k} }}} \,\quad \,i = 1,\,2,\, \ldots ,N\quad j = 1,\,2,\, \ldots ,N $$
(20a)

for \( i = j \)

$$ A_{ii} = \sum\limits_{\begin{subarray}{l} k \ne i \\ k = 1 \end{subarray} }^{N} {\frac{1}{{X_{i} - X_{k} }}} \quad \,i = 1,2, \ldots ,N. $$
(20b)

Other weighting coefficients of higher order derivatives can be produced by performing matrix multiplications as [31,32,33]

$$ B = B_{ij} = \sum\limits_{k = 1}^{N} {A_{ik} A_{kj} } , $$
(21)
$$ C = C_{ij} = \sum\limits_{k = 1}^{N} {A_{ik} B_{kj} } , $$
(22)
$$ D = D_{ij} = \sum\limits_{k = 1}^{N} {A_{ik} C_{kj} } = \sum\limits_{k = 1}^{N} {B_{ik} B_{kj} } , $$
(23)
$$ E = E_{ij} = \sum\limits_{k = 1}^{N} {A_{ik} D_{kj} } = \sum\limits_{k = 1}^{N} {B_{ik} C_{kj} } , $$
(24)
$$ F = F_{ij} = \sum\limits_{k = 1}^{N} {A_{ik} E_{kj} } = \sum\limits_{k = 1}^{N} {B_{ik} D_{kj} } = \sum\limits_{k = 1}^{N} {C_{ik} C_{kj} } . $$
(25)

5 Implementation of HWM, HOHWM, and DQM in the proposed model

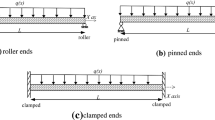
For the investigation of buckling behavior of stain gradient nonlocal beam, pined–pined (P–P), and clamped–clamped (C–C) boundary conditions are taken into consideration which is given as [58]

Pined–pined (P–P):

$$ \begin{aligned} & W\left( 0 \right) = 0,\,\,\frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }}\left( 0 \right) = 0,\,\,\frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }}\left( 0 \right) = 0\quad \\ & \quad {\text{and}}\quad W\left( 1 \right) = 0,\,\,\frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }}\left( 1 \right) = 0,\,\frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }}\left( 1 \right) = 0. \\ \end{aligned} $$
(26)

Clamped–clamped (C–C):

$$ \begin{aligned} & W\left( 0 \right) = 0,\,\,\frac{{{\text{d}}W}}{{{\text{d}}X}}\left( 0 \right) = 0,\,\frac{{{\text{d}}^{3} W}}{{{\text{d}}X^{3} }}\left( 0 \right) = 0\quad \\ & \quad {\text{and}}\quad W\left( 1 \right) = 0,\,\,\frac{{{\text{d}}W}}{{{\text{d}}X}}\left( 1 \right) = 0,\,\frac{{{\text{d}}^{3} W}}{{{\text{d}}X^{3} }}\left( 1 \right) = 0. \\ \end{aligned} $$
(27)

5.1 Haar wavelet method

According to HWM, the highest order derivative of the governing equation, viz. \( \frac{{{\text{d}}^{6} W}}{{{\text{d}}X^{6} }} \) in Eq. (14) can be expressed as [35, 36]

$$ \frac{{{\text{d}}^{6} W}}{{{\text{d}}X^{6} }} = \sum\limits_{i = 1}^{N} {c_{i} h_{i} } = C^{T} H, $$
(28)

where \( N = 2^{J + 1} \). Performing sixth-time integration successively, we have

$$ \frac{{{\text{d}}^{5} W}}{{{\text{d}}X^{5} }}(X) = C^{\text{T}} P_{1} \left( X \right) + d_{1} , $$
(29a)
$$ \frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }}(X) = C^{\text{T}} P_{2} \left( X \right) + d_{1} X + d_{2} , $$
(29b)
$$ \frac{{{\text{d}}^{3} W}}{{{\text{d}}X^{3} }}(X) = c^{\text{T}} P_{3} + d_{1} \frac{{X^{2} }}{2} + d_{2} X + d_{3} , $$
(29c)
$$ \frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }}(X) = C^{\text{T}} P_{4} + d_{1} \frac{{X^{3} }}{6} + d_{2} \frac{{X^{2} }}{2} + d_{3} X + d_{4} , $$
(29d)
$$ \begin{aligned} \frac{{{\text{d}}W}}{{{\text{d}}X}}(X) & = C^{\text{T}} P_{5} + d_{1} \frac{{X^{4} }}{24} + d_{2} \frac{{X^{3} }}{6}, \\ & \quad + d_{3} \frac{{X^{2} }}{2} + d_{4} X + d_{5} \\ \end{aligned} $$
(29e)
$$ \begin{aligned} W(X) & = C^{\text{T}} P_{6} + d_{1} \frac{{X^{5} }}{120} + d_{2} \frac{{X^{4} }}{24} + d_{3} \frac{{X^{3} }}{6.} \\ & \quad + d_{4} \frac{{X^{2} }}{2} + d_{5} X + d_{6} \\ \end{aligned} $$
(29f)

Here \( c = \left( {c_{1} ,\,c_{2} ,\,c_{3} , \ldots c_{N} } \right)^{\text{T}} \) and \( d_{1} ,\,d_{2} ,d_{3} ,\,d_{4} ,\,d_{5} , \) and \( d_{6} \) are integration constants which are different for particular boundary conditions. Substituting Eq. (29) with proper boundary condition, the governing Eq. (14) will be converted into an Eigenvalue problem as

$$ \left[ {\rm K} \right]\left\{ C \right\} = \hat{P}\left[ {\rm B} \right]\left\{ C \right\}, $$
(30)

where the Eigenvalue \( \hat{P} \) is the buckling load parameter.

Theorem 1

Let us assume a square-integrable, finite function \( \varphi (x) = \frac{{{\text{d}}^{n} \phi (x)}}{{{\text{d}}x^{n} }} \) in the interval \( \left[ {0,\,\,1} \right] \) and \( \exists \) \( \kappa \) such that \( \left| {\frac{{{\text{d}}\varphi (x)}}{{{\text{d}}x}}} \right| \le \kappa \), for all \( x \in \left[ {0,\,\,1} \right] \), then the HWM based on the discretized approach is convergent and the order of convergence is computed as two.

Proof

For the proof, one may see an interesting paper [73].□

5.2 Higher order haar wavelet method

From Theorem 1, it is found that the order of convergence of HWM is two. To improve the order of convergence, Majak et al. [30] proposed another approach. According to this technique, we have

$$ \frac{{{\text{d}}^{n + 2\tau } W}}{{{\text{d}}X^{n + 2\tau } }} = C^{\text{T}} H,\,\,\,\,\tau = 1,\,2, \ldots , $$
(31)

where \( n \) is the highest order derivative and \( \tau \) is the extra term which is going to enhance the order of convergence of HOHWM. Assigning \( \tau = 1 \), \( n + 2 \) integration constants will be generated and the extra two integration constants can be handled using the algorithm presented in [30, 74].

Now setting \( \tau = 1 \) and following the procedures of HOHWM, we obtain

$$ \frac{{{\text{d}}^{8} W}}{{{\text{d}}X^{8} }} = \sum\limits_{i = 1}^{N} {c_{i} h_{i} } = C^{\text{T}} H. $$
(32)

Integrating successively, we get

$$ \frac{{{\text{d}}^{6} W}}{{{\text{d}}X^{6} }} = C^{\text{T}} P_{2} \left( X \right) + d_{1} X + d_{2} , $$
(33a)
$$ \frac{{{\text{d}}^{5} W}}{{{\text{d}}X^{5} }}(X) = C^{\text{T}} P_{3} \left( X \right) + d_{1} \frac{{X^{2} }}{2} + d_{2} X + d_{3} , $$
(33b)
$$ \frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }}(X) = C^{\text{T}} P_{4} \left( X \right) + d_{1} \frac{{X^{3} }}{6} + d_{2} \frac{{X^{2} }}{2} + d_{3} X + d_{4} , $$
(33c)
$$ \begin{aligned} \frac{{{\text{d}}^{3} W}}{{{\text{d}}X^{3} }}(X) & = C^{\text{T}} P_{5} \left( X \right) + d_{1} \frac{{X^{4} }}{24} + d_{2} \frac{{X^{3} }}{6} \\ & \quad + d_{3} \frac{{X^{2} }}{2} + d_{4} X + d_{5} , \\ \end{aligned} $$
(33d)
$$ \begin{aligned} \frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }}(X) & = C^{\text{T}} P_{6} \left( X \right) + d_{1} \frac{{X^{5} }}{120} + d_{2} \frac{{X^{4} }}{24} \\ & \quad + d_{3} \frac{{X^{3} }}{6} + d_{4} \frac{{X^{2} }}{2} + d_{5} X + d_{6} , \\ \end{aligned} $$
(33e)
$$ \begin{aligned} \frac{{{\text{d}}W}}{{{\text{d}}X}}(X) & = C^{\text{T}} P_{7} \left( X \right) + d_{1} \frac{{X^{6} }}{720} + d_{2} \frac{{X^{5} }}{120} + d_{3} \frac{{X^{4} }}{24} \\ & \quad + d_{4} \frac{{X^{3} }}{6} + d_{5} \frac{{X^{2} }}{2} + d_{6} X + d_{7} , \\ \end{aligned} $$
(33f)
$$ \begin{aligned} W(X) & = C^{\text{T}} P_{8} \left( X \right) + d_{1} \frac{{X^{7} }}{5040} + d_{2} \frac{{X^{6} }}{720} + d_{3} \frac{{X^{5} }}{120} \\ & \quad + d_{4} \frac{{X^{4} }}{24} + d_{5} \frac{{X^{3} }}{6} + d_{6} \frac{{X^{2} }}{2} + d_{7} X + d_{8} , \\ \end{aligned} $$
(33g)

Here \( C = \left( {c_{1} ,\,c_{2} ,\,c_{3} , \ldots c_{N} } \right)^{T} \) and \( d_{1} ,\,d_{2} ,\,d_{3} ,\,d_{4} ,\,d_{5} ,\,d_{6} ,\,d_{7} \) and \( d_{8} \) are integration constants. Out of these eight constants, six can be obtained from each of the boundary condition, presented in Eqs. (26) and (27) whereas the rest two can also be obtained from the governing equation as

$$ \begin{aligned} & \beta^{2} \frac{{{\text{d}}^{6} W}}{{{\text{d}}X^{6} }}\left( 0 \right) - \frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }}\left( 0 \right) + \frac{{\left( {e_{0} a} \right)^{2} }}{{L^{2} }}K_{w} \frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }}\left( 0 \right) - K_{w} W\left( 0 \right) \\ & \quad = \hat{P}\,\left( {\frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }}\left( 0 \right) - \frac{{\left( {e_{0} a} \right)^{2} }}{{L^{2} }}\frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }}\left( 0 \right)} \right), \\ \end{aligned} $$
(34)
$$ \begin{aligned} & \beta^{2} \frac{{{\text{d}}^{6} W}}{{{\text{d}}X^{6} }}\left( 1 \right) - \frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }}\left( 1 \right) + \frac{{\left( {e_{0} a} \right)^{2} }}{{L^{2} }}K_{w} \frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }}\left( 1 \right) - K_{w} W\left( 1 \right) \\ & \quad = \hat{P}\,\left( {\frac{{{\text{d}}^{2} W}}{{{\text{d}}X^{2} }}\left( 1 \right) - \frac{{\left( {e_{0} a} \right)^{2} }}{{L^{2} }}\frac{{{\text{d}}^{4} W}}{{{\text{d}}X^{4} }}\left( 1 \right)} \right). \\ \end{aligned} $$
(35)

Plugging Eq. (31) in governing Eq. (14) and performing the procedures properly as mentioned in [30, 74], governing Eq. (14) will be converted into a generalized Eigenvalue problem as Eq. (30) where the Eigenvalues represent the buckling load parameters.

5.3 Differential quadrature method

Applying Eqs. (21–25) in Eqs. (26–27), the pined–pined (P–P) and clamped–clamped (C–C) boundary conditions are given as [19]

Pined–pined:

$$ \begin{aligned} \{ W^{\prime}\} & = [\bar{A}]\{ W\} \\ \{ \,W^{\prime\prime}\} & = [A]\,\{ W^{\prime}\} = [A]\,[\bar{A}]\{ W\} = [\bar{B}]\{ W\} \\ \{ \,W^{\prime\prime\prime}\} & = [\bar{A}]\,\{ W^{\prime\prime}\} = [\bar{A}]\,[\bar{B}]\,\{ W\} = [\bar{C}]\,\{ W\} \\ \{ \,W^{IV} \} & = [A]\,\{ W^{\prime\prime\prime}\} = [A]\,[\bar{C}]\,\{ W\} \\ & = [\bar{B}]\,[\bar{B}]\,\{ W\} = [\bar{D}]\,\{ W\} \\ \{ \,W^{V} \} & = [\bar{A}]\,\{ W^{IV} \} = [\bar{A}]\,[\bar{D}]\,\{ W\} \\ & = [\bar{A}]\,[\bar{B}]\,[\bar{B}]\,\{ W\} = [\bar{E}]\,\{ W\} \\ \{ \,W^{VI} \} & = [A]\,\{ W^{V} \} = [A]\,[\bar{E}]\,\{ W\} \\ & = [A]\,[\bar{A}][\bar{B}]\,[\bar{B}]\,\{ W\} = [A]\,[\bar{A}][\bar{D}]\,\,\{ W\} = [\bar{F}]\,\{ W\} . \\ \end{aligned} $$

Clamped–clamped:

$$ \begin{aligned} \{ \,W^{\prime}\} & = [\bar{A}]\,\left\{ W \right\} \\ \{ \,W^{\prime\prime}\} & = [\bar{A}]\,\{ W^{\prime}\} = [\,\bar{A}]\,[\bar{A}]\,\{ W\} = [\bar{B}]\,\{ W\} \\ \{ \,W^{\prime\prime\prime}\} & = [A]\,\{ W^{\prime\prime}\} = [A]\,[\bar{B}]\,\{ W\} = [\bar{C}]\,\{ W\} \, \\ \{ \,W^{IV} \} & = [\bar{A}]\,\{ W^{\prime\prime\prime}\} = [\bar{A}]\,[\bar{C}]\,\{ W\} = [\bar{D}]\,\{ W\} \\ \{ \,W^{V} \} & = [A]\,\{ W^{IV} \} = [A]\,[\bar{D}]\,\{ W\} \\ & = [A]\,[\bar{A}]\,[\bar{C}]\,\{ W\} = [\bar{E}]\,\{ W\} \\ \{ \,W^{VI} \} & = [A]\,\{ W^{V} \} = [A]\,[\bar{E}]\,\{ W\} \\ & = [A]\,[A][\bar{A}]\,[\bar{C}]\,\{ W\} = [\bar{F}]\,\{ W\} , \\ \end{aligned} $$

in which \( A,\,\bar{A},\,\bar{A}_{1} \) and \( \bar{A}_{2} \) are given as

$$ \begin{aligned} A & = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & \cdots & {A_{1,N - 1} } & {A_{1,N} } \\ {A_{21} } & {A_{22} } & \cdots & {A_{2,N - 1} } & {A_{2,N} } \\ \vdots & \vdots & {} & \vdots & \vdots \\ {A_{N1} } & {A_{N2} } & \cdots & {A_{N,N - 1} } & {A_{N,N} } \\ \end{array} } \right]\quad \\ \bar{A} & = \left[ {\begin{array}{*{20}c} 0 & {A_{12} } & \cdots & {A_{1,N - 1} } & 0 \\ 0 & {A_{22} } & \cdots & {A_{2,N - 1} } & 0 \\ \vdots & \vdots & {} & \vdots & \vdots \\ 0 & {A_{N2} } & \cdots & {A_{N,N - 1} } & 0 \\ \end{array} } \right] \\ \bar{A}_{1} & = \left[ {\begin{array}{*{20}c} 0 & {A_{1,2} } & \cdots & {A_{1,N} } \\ 0 & {A_{2,2} } & \cdots & {A_{2,N} } \\ \cdots & \cdots & \cdots & \cdots \\ 0 & {A_{N,2} } & \cdots & {A_{N,N} } \\ \end{array} } \right]\quad \\ \bar{A}_{2} & = \left[ {\begin{array}{*{20}c} {A_{1,1} } & {A_{1,2} } & \cdots & {A_{1,N - 1} } & 0 \\ {A_{2,1} } & {A_{2,2} } & \cdots & {A_{2,N - 1} } & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ {A_{N,1} } & {A_{N,2} } & \cdots & {A_{N - 1,N - 1} } & 0 \\ \end{array} } \right]. \\ \end{aligned} $$

Substituting Eq. (18) along with the above boundary conditions in Eq. (14), a generalized Eigenvalue problem will be formed.

6 Numerical results and discussion

Governing Eq. (14) has been solved by HWM, HOHWM, and DQM as an Eigenvalue problem using MATLAB codes developed by the authors. The critical buckling load parameter \( \left( {\hat{P}_{cr} } \right) \) also has been obtained for pined–pined and clamped–clamped boundary conditions with \( E = 1 \) TPa, \( L = 10 \) nm, and \( h = 1\,{\text{nm}} \).

6.1 Validation

The critical buckling loads, obtained by HWM, HOHWM, and DQM for both the PP and CC boundary conditions are validated with Wang et al. [75] assigning \( K_{\text{w}} = 0 \) and \( \beta = 0 \) whereas other parameters remain same as Wang et al. [75]. The comparisons of results are given in a graphical form which is illustrated in Fig. 1. The graphical results are drawn by varying the nonlocal parameter \( \left( {e_{0} a} \right) \) from 0 to 2 with an increase of 0.5. From Fig. 1, it is revealed that the results obtained by present methods are showing a decent agreement with the reference.

Fig. 1
figure 1

Validation of present results with [75]

Full size image

6.2 Convergence study

Convergence studies are carried out for all the three methods, viz. HWM, HOHWM, and DQM concerning the critical buckling load. In this regard, pined–pined boundary condition has been considered for the study. The critical buckling loads are calculated with \( e_{0} a = 0.5 \), \( K_{\text{w}} = 50 \), \( \beta = 0.2 \), and \( L = 20 \). For HWM, the convergence is attained at \( J = 5 \) whereas, for HOHWM, the same results are obtained at \( J = 2 \). In the case of DQM, the results start converging at \( N = 8 \) or \( J = 2 \). These investigations are noted in Table 1 and Fig. 2. Also, the order of convergence for HWM and HOHWM are calculated based on the formula presented in [76], and it is found that the order of convergence is approximately two and four, respectively. It may also be noted that HOHWM converges as fast as DQM exhibiting its supremacy over HWM.

Table 1 Convergence of critical buckling load parameter \( \left( {\hat{P}_{cr} } \right) \) by HWM, HOHWM, and DQM with \( e_{0} a = 0.5 \), \( K_{\text{w}} = 50 \), \( \beta = 0.2 \) and \( L = 20 \) for pined–pined (P–P) boundary condition
Full size table
Fig. 2
figure 2

Convergence study of HWM, HOHWM, and DQM

Full size image

6.3 Effect of nonlocal parameter

The impacts of nonlocal parameters \( \left( {e_{0} a} \right) \) are noted on the critical buckling load \( \left( {\hat{P}_{cr} } \right) \) and critical buckling load ratio in forms of tabular result and graphical plot. The critical buckling load ratio is defined as the ratio of critical buckling load parameter using nonlocal theory and critical buckling load parameter using classical theory. The results are calculated with \( K_{\text{w}} = 100 \), \( \beta = 0.1 \) and \( L = 10 \). Also, \( J = 8 \) for HWM, \( J = 4 \) for HOHWM, and \( N = 25 \) for DQM are taken in the computation. The nonlocal parameters \( \left( {e_{0} a} \right) \) are varying from 0 to 4 with an increment of 0.5. The results are demonstrated in Table 2 and Figs. 3 and 4. From these results, it is observed that the critical buckling load parameters are decreasing with an increase of \( \left( {e_{0} a} \right) \) for both the boundary conditions and this reduction in critical buckling load is more significant in case of clamped–clamped boundary condition.

Table 2 Effect of \( e_{0} a \) on critical buckling load parameter \( \left( {\hat{P}_{cr} } \right) \) and critical buckling load ratio by HWM, HOHWM and DQM with \( K_{\text{w}} = 100 \), \( \beta = 0.1 \) and \( L = 10 \)
Full size table
Fig. 3
figure 3

a Critical buckling load versus nonlocal parameter, b critical buckling load ratio versus nonlocal parameter

Full size image
Fig. 4
figure 4

Critical buckling load versus strain gradient parameter for PP case

Full size image

6.4 Effect of strain gradient parameter

In this subsection, the response of the strain gradient parameter \( \left( \beta \right) \) on critical buckling load \( \left( {\hat{P}_{cr} } \right) \) has been noted with \( K_{\text{w}} = 200 \), and \( L = 10 \). Critical buckling loads are calculated for different nonlocal parameters \( \left( {e_{0} a} \right) \) by varying strain gradient parameter from 0 to 1 with an increment of 0.2. Critical buckling loads increase with the increase of strain gradient parameters, but this increase is much faster in case of clamped–clamped boundary conditions, which can be illustrated in Table 3 and Figs. 4 and 5. Also, critical buckling load is maximum in the case of classical theory with higher values of strain gradient parameters, and this trend is equal for both the boundary conditions.

Table 3 Effect of \( \beta \) on critical buckling load parameter \( \left( {\hat{P}_{cr} } \right) \) by HWM, HOHWM, and DQM with \( K_{\text{w}} = 200 \), and \( L = 10 \)
Full size table
Fig. 5
figure 5

Critical buckling load versus strain gradient parameter for CC case

Full size image

6.5 Effect of Winkler modulus parameter

The impacts of Winkler modulus parameters \( \left( {K_{\text{w}} } \right) \) on critical buckling loads are studied through this subsection. The results are computed with \( e_{0} a = 1 \), and \( L = 10 \) by HOW, HOHWM, and DQM by considering \( J = 8 \), \( J = 4 \), and \( N = 20 \), respectively. Both the boundary conditions such as PP and CC are considered for the study by changing \( K_{\text{w}} \) from 0 to 500 with an increase of 100 for different values of strain gradient parameters. Both the graphical and tabular results are presented in Figs. 6 and 7, and Table 4. From these results, it can be concluded that the increase of Winkler modulus parameter increases the critical buckling load for both the boundary conditions. Also, this increases much higher in CC boundary condition with higher values of strain gradient parameters.

Fig. 6
figure 6

Critical buckling load versus Winkler modulus parameter for PP case

Full size image
Fig. 7
figure 7

Critical buckling load versus Winkler modulus parameter for CC case

Full size image
Table 4 Effect of \( K_{\text{w}} \) on critical buckling load parameter \( \left( {\hat{P}_{cr} } \right) \) by HWM, HOHWM, and DQM with \( e_{0} a = 1 \), and \( L = 10 \)
Full size table

6.6 Buckling mode shape

Buckling mode shape is essential to predict the buckling characteristics of structural members. In this regard, mode shapes are plotted by considering the PP boundary condition with \( K_{\text{w}} = 100 \), \( \beta = 0.2 \) and \( L = 10 \). Mode shapes are plotted for different nonlocal parameters such as \( e_{0} a = 0,\,e_{0} a = 0.5 \) and \( e_{0} a = 1 \) which can be seen in Fig. 8. From this figure, it is found that the critical buckling loads are affected significantly by varying different scaling parameters.

Fig. 8
figure 8

Critical buckling mode shape for PP boundary condition

Full size image

7 Concluding remarks

Buckling behavior of strain gradient nonlocal beam embedded in Winkler elastic foundation is studied using HWM, HOHWM, and DQM. The validation of the present model is conducted and found to be perfectly agreeing with the previously published article. A convergence study is also performed to exhibit the superiority of the methods. The responses of all the scaling parameters on critical buckling loads are also reported in terms of graphical and tabular results for both the boundary condition such as pined–pined and clamped–clamped. Followings are the main observations regarding the present investigation;

  • The HOHWM and DQM are converging much faster as compared to HWM. The order of convergence of HOHWM is found to be four, whereas the order of convergence of HWM is two.

  • The critical buckling loads are decreasing with an increase of nonlocal parameters for both the boundary condition and this reduction in critical buckling load is more significant in case of clamped–clamped boundary condition.

  • The critical buckling loads increase with the increase of strain gradient parameters, but this increase is much faster in case of clamped–clamped boundary conditions, and the critical buckling load is maximum in case of classical theory with higher values of strain gradient parameters, and this trend remains constant for both the boundary conditions.

  • An increase in Winkler modulus parameter increases the critical buckling load for both the boundary conditions, and this increase is much higher in CC boundary condition with higher values of strain gradient parameters.