1 Introduction

Meshfree particle methods refer to the class of numerical techniques in which, at least, the connectivity constraint of field data points (computational nodes) is alleviated [1]. In the absence of connectivity constraints, the data points can be added, removed or relocated, during the computational process, with greater flexibility and ease compared to traditional mesh-based methods [2]. Owing to this feature, meshfree methods are considered to offer a better solution platform for problems which involve large deformation of boundaries or require adaptive refinement. Meshfree methods have, therefore, been the focus of many researchers in the recent past [3,4,5,6,7,8,9,10].

Radial basis functions (RBFs) are real-valued functions which are used for multivariate data interpolation over scattered data points [5]. The use of multiquadric RBFs for solution of partial differential equations (PDEs) over scattered data points was first proposed by Kansa [11]. Subsequently, a number of RBF-based meshfree methods have been developed including RBF-collocation methods [12] and local RBF methods [13, 14]. RBF-based solution schemes are truly meshfree and their applications were later explored to solve flow problems by a number of researchers [2, 5, 6, 12, 15, 16]. One of the difficulties while solving flow problems with RBFs was that the problem became ill-conditioned by increasing the number of data points in the local support domain. In 2003, Tolstykh and Shirobokov [14] and Shu et al. [13] simultaneously proposed the use of local RBFs for solving flow and structural problems. Local RBF methods compromise on spectral accuracy to result in well-conditioned matrix equations with better accuracy. RBF in finite difference mode (RBF-FD) [14, 17, 18] and RBF-based differential quadrature (RBF-DQ) [13, 16, 19] are two commonly used local RBF methods.

Solution of flow problems involves Navier–Stokes equations which are primarily convective diffusive equations. Such problems become convection dominated at high Reynolds number (\(Re=\rho Uc/\mu\), where \(\rho\) is the flow density, U is the flow velocity, c is the characteristic length and \(\mu\) is the dynamic viscosity). Accurate and stable modeling of convection-dominated flows has always been a challenging task. Without the use of artificial viscosity, upwinding or any other stabilization technique for such problems, most numerical methods result in spurious oscillations which lead to inaccurate and unstable solutions [20]. For such problems, stabilization techniques are very well developed using traditional mesh-based methods. For example, in the finite difference method, the first- and second-order upwind difference schemes [21, 22], quadratic upstream interpolation for convective kinetics (QUICK) [23], hybrid differencing scheme [20], and the power law scheme [24] are some common stabilization techniques. Similarly, in finite element method, a number of stabilization techniques are available which include use of anisotropic balancing diffusion, streamline upwind Petrov–Galerkin [25] and hierarchical basis functions [26].

Development of stabilized solution schemes for convection-dominated flows, using meshfree methods, is still an active area of research [2]. Oñate [10] derived stabilized form of governing equations using balance of convective and diffusive flux. Shu et al. [27] used flux at midpoint between the reference node and its supporting nodes to introduce upwinding effect while using meshfree nodal cloud. Gu and Liu [28] proposed a number of techniques to improve the stabilization of numerical solutions of highly convective flows over meshfree data points. They proposed the use of nodal refinement, local support domain enlargement, use of fully upwind local support domain and adaptive upwind support domain. Kee et al. [29] suggested using least square regularization to introduce stabilization in the radial point collocation method. Fornberg and Lehto [30] proposed the use of a filter mechanism to stabilize the solution of purely convective flows using the RBF-FD method. Chan et al. [31] introduced comet-shaped local support domains for local RBFs to deal with highly convective flows. Javed et al. [2] proposed a stabilized RBF-FD scheme for solving convection-dominated flows. They proposed that the stabilization term emerge naturally by considering higher-order approximation of governing equation during force and momentum balance.

The conventional flow solution schemes using local RBFs do not distinguish between upwind and downwind data points while calculating the RBF weights. RBF weights between two data points are calculated based on the Euclidean distance only resulting in radially symmetric RBF surfaces. The current study proposes the use of upwind skewed radial basis function (USRBF) to introduce upwinding in the solution scheme for convection-dominated flows over meshfree nodes. These upwind-skewed RBFs are obtained by multiplying an upwinding factor with the conventional RBFs. The upwinding factor is a function of flow direction, intensity of convection, size of local support domain, and nodal distribution. The use of USRBFs modifies the weight values such that the necessary artificial diffusion is added only along the flow direction and avoids crosswind diffusion. The performance of the proposed scheme is studied by solving one- and two-dimensional convection–diffusion equation on uniformly and randomly distributed nodes with various convection intensities. The results of the numerical tests show a remarkable improvement in the accuracy and stability of the solution scheme.

The organization of the paper is as follows. A brief introduction to local RBF is presented in Sect. 2. Formulation of the proposed upwind skewed RBFs (USRBFs) is presented in Sect. 3. In Sect. 4, numerical tests are performed using the conventional and proposed schemes, and comparison is made between the results obtained from the two methods. Future work and conclusions are discussed in Sects. 5 and 6, respectively.

Fig. 1
figure 1

Local support domain around data point \(x_{1}\) containing N neighbouring data points

Full size image

2 Local radial basis functions

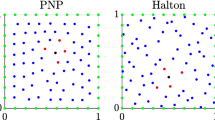
Local radial basis function in finite difference mode (RBF-FD) is a strong-form meshfree method developed independently by Shu et al. [13] and Tolstykh and Shirobokov [14]. Like the finite difference method, RBF-FD approximates the derivatives of a dependent variable, at any spatial location, using linear weighted sum of the values of similar variable at surrounding data point. A support domain is defined around each node, say \(x_{1}\), which constitutes N neighbouring data points as shown in Fig. 1. Classical finite differencing suggests finding the value of the differential operator \({\mathcal {L}}\) of any parameter \({\mathsf {v}}\), at \(x_1\), as the weighted sum of values of \({\mathsf {v}}\) at its neighbouring data points \(x_j~\epsilon~{\mathbf {R}}^d,~j=1,2,\ldots N\) as [3]:

$$\begin{aligned} {\mathcal {L}}{\mathsf {v}}(x_1)=\sum \limits _{j=1}^N \mathbf {W}_{1,j}^{({\mathcal {L}})} {\mathsf {v}}(x_j), \end{aligned}$$
(1)

where \(\mathbf {W}_{1,j}^{({\mathcal {L}})}\) is the weight, at \(x_1\) for \(x_j\), corresponding to the differential operator \({\mathcal {L}}\). Parameter \({\mathsf {v}}\) can also be approximated using standard RBF interpolation over a set of distinct data points \(x_j~\epsilon~{\mathbf {R}}^d,~j=1,2,\ldots N\) as:

$$\begin{aligned} \mathsf {v}(x) \approx s(x) = \sum\limits_{j = 1}^N {{\lambda _j}} \phi (x - {x_j}) + \beta , \end{aligned}$$
(2)

where \(\phi\) is the radial basis function, \(\Vert .\Vert\) is the standard Euclidean norm, and \(\lambda _j\) and \(\beta\) are the expansion coefficients. Some of the common radial basis functions are given in Table 1. Equation (2) can also be expressed in Lagrange form as

$$\begin{aligned} \bar{s}(x)=\sum \limits _{j=1}^{N}{\mathcal {X}}\left( \Vert x-x_j\Vert \right) {\mathsf {v}}\left( x_j\right) , \end{aligned}$$
(3)

where \({\mathcal {X}}\left( \Vert x-x_j\Vert \right)\) satisfies the cardinal conditions as

$$\begin{aligned} {\mathcal {X}}\left( \Vert x_k-x_j\Vert \right) = \left\{ \begin{array}{ll}1, &{} \text {if }k=j\\ 0, &{} \text {if }k\ne j\end{array}\right. \quad k=1,2, \ldots N. \end{aligned}$$
(4)

Applying the differential operator \({\mathcal {L}}\) on Eq. (3) at node \(x_1\) yields:

$$\begin{aligned} {\mathcal {L}}{\mathsf {v}}\left( x_1\right) \approx {\mathcal {L}}\bar{s}\left( x_1\right) =\sum \limits _{j=1}^{N}{\mathcal {L}}{\mathcal {X}}\left( \Vert x_1-x_j\Vert \right) {\mathsf {v}}\left( x_j\right) . \end{aligned}$$
(5)

Using Eqs. (1) and (5), RBF-FD weights \(\mathbf {W}^{({\mathcal {L}})}_{1,j}\) are given by

$$\begin{aligned} \mathbf {W}^{({\mathcal {L}})}_{1,j}={\mathcal {L}}{\mathcal {X}}\left( \Vert x_1-x_j\Vert \right) . \end{aligned}$$
(6)

In practice, these weights are computed by solving the following linear system [32]:

$$\begin{aligned} \left[ \begin{array}{ll}\Phi &{} e\\ e^T &{} 0 \end{array}\right] \left[ \begin{array}{l} W \\ \mu \end{array}\right] =\left[ \begin{array}{l}{\mathcal {L}}\Phi _1\\ 0\end{array}\right] , \end{aligned}$$
(7)

where \(\Phi _{i,j}=\phi \left( \Vert x_j-x_i\Vert \right)\), \(i,j=1,2,\ldots ,N\), e is a row vector of integers from 1 to N, \({\mathcal {L}}\Phi _1\) represents the column vector of \({\mathcal {L}}\phi \left( \Vert x_1-x_i\Vert \right) ,\) and \(\mu\) is a scalar parameter which enforces the condition:

$$\begin{aligned} \sum \limits _{j=1}^N \mathbf {W}_{1,j}^{({\mathcal {L}})}=0. \end{aligned}$$
(8)

Evaluation of Eq. (7) gives weights \(\mathbf {W}_{1,j}^{\mathcal {L}}\) corresponding to all the nodes in the support domain for differential operator \({\mathcal {L}}\). The corresponding weights and values of \({\mathsf {v}}\) are used to approximate \({\mathcal {L}}({\mathsf {v}})\) at \(x_1\).

Table 1 Commonly used radial basis functions (r is the Euclidean distance and \(\sigma\) is the shape parameter)
Full size table
Fig. 2
figure 2

Variation of \(\beta\) with Peclet number ranging from \(10^{-6}\) to \(10^6\)

Full size image
Fig. 3
figure 3

Conventional and upwind skewed RBF surfaces over two-dimensional space

Full size image

3 Formulation of upwind skewed radial basis functions (USRBFs)

To introduce an upwinding effect for solution of convection-dominated problems, upwind-skewed radial basis functions (USRBFs) are proposed. Conventional RBFs produce radially symmetric surfaces as shown in Fig. 3a. USRBFs surfaces (Fig. 3b) are obtained by multiplying the conventional RBFs with an upwinding factor which skews the RBF surfaces in a manner that the data points located at the upwind direction of the reference point will have more weight compared to those at the downwind direction. The proposed upwinding factor \({\mathcal {F}}\) is given by

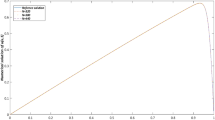
$$\begin{aligned} {{\mathcal {F}}}=1 - \beta \sin \left( \frac{\pi }{2} \frac{{\mathbf{{u} }} \cdot \mathbf{r }}{\left| {\mathbf{{u} }} \right| r_0 } \right) , \end{aligned}$$
(9)

where \({{\mathbf {u}}}\) is the flow velocity, \({{\mathbf {R}}}\) is the position vector from the reference point \({\mathbf {x}} _1\) to the neighbouring point \({\mathbf {x}} _j\) \(({{\mathbf {R}}} ={\mathbf {x}} _j-{\mathbf {x}} _1)\), \(r_0\) is the size of the local support domain, and \(\beta\) is an upwinding parameter which is a function of the nodal distribution Peclet number (Pe) as [2],

$$\begin{aligned} \beta = coth \left( Pe \right) - \frac{1}{Pe}. \end{aligned}$$
(10)

The Peclet number, Pe,  is defined as

$$\begin{aligned} Pe=\frac{\left| {{\mathbf {u}}} \right| (\Delta {s})}{2a}, \end{aligned}$$
(11)

where \(\Delta {s}\) is the average spacing between N data points in the support domain. When \(Pe \rightarrow 0\), \(\beta \rightarrow 0\) corresponding to zero upwinding, and when \(Pe \rightarrow \infty\), \(\beta \rightarrow 1\) corresponding to maximum upwinding in the solution. The relation of \(\beta\) with Pe, shown in Fig. 2, depicts the monotonic increase of \(\beta\) with Peclet number. The upwinding factor \({\mathcal {F}}\) can be multiplied with any conventional RBF and the resulting upwind skewed radial basis functions (USRBF) can be used for calculating the weights of differential operators as mentioned in Sect. 2. In this paper, the RBF-FD method with Inverse multiquadric (IMQ) basis function is considered. RBF with IMQ basis function is given as

$$\begin{aligned} \phi = \frac{1}{\sqrt{r^2 + \sigma ^2}.} \end{aligned}$$
(12)

Using the upwinding factor from Eq. 9, the proposed upwind-skewed inverse multiquadric radial basis function becomes

$$\begin{aligned} \phi = \frac{1}{\sqrt{r^2 + \sigma ^2}} \times \left[ 1 - \beta \sin \left( \frac{\pi }{2} \frac{{\mathbf{{u} }} \cdot \mathbf{r }}{\left| {\mathbf{{u} }} \right| r_0 } \right) \right] . \end{aligned}$$
(13)

The plots of conventional RBF and upwind skewed RBF (USRBF) with IMQ basis functions are shown in Figs. 4 and 5 for 1-D and 2-D domains, respectively. The plots of conventional RBF are symmetric about the center of the RBF, whereas the plots of USRBF are skewed along the flow direction (Fig. 3).

Fig. 4
figure 4

The plots of conventional RBF and upwind skewed RBF (USRBF) with IMQ basis function on domain with \(x\in \left[ -0.5,0.5\right]\), \(x_1 = 0\), \({\mathbf {u}} = 1\), and \(Pe=1000\)

Full size image
Fig. 5
figure 5

Contour plots of conventional RBF and upwind skewed RBF (USRBF) with IMQ basis function on domain with \(\left( x, y \right) \in \left[ -0.5,0.5\right] \times \left[ 0.5, 0.5 \right]\), \(\left( x_1, y_1 \right) = \left( 0, 0 \right)\), \({\mathbf {u}} = [1,1]\), and \(Pe =1000\)

Full size image

Figure 6 shows the weights \((W^x\)) for convection operator \(\mathbf{u} \frac{ {\text {d}}}{{\text {d}}x}\), evaluated using conventional RBF and proposed USRBF on a sample 1-D domain. The weights from conventional RBF are symmetric about the reference node, \(x_{1} = 0\), whereas, the weights from USRBF are skewed toward the flow direction. For example, the weight of the upstream point at \(x = -0.1\) is greater than the weight of downstream point at \(x = 0.1\). Similarly, Fig. 7 shows the weights \((W^{x+y})\) for the convection operator \({{\mathbf {u}}} \cdot \nabla\), evaluated on a sample 2-D domain using conventional and proposed RBFs. It can be observed that USRBF assigns higher weight values to the neighbouring nodes upwind to the reference location. For example, the weight \(W^{x+y}\) of point 1 is greater than the weight \(W^{x+y}\) of point 9, because point 1 lies on the upstream side. Similarly, the weights \(W^{x+y}\) of points 2 and 4 are greater than the weights \(W^{x+y}\) of points 6 and 8 because points 2 and 4 lie on the upstream side. The weights of points on crosswind direction are equal. For example, the weight \(W^{x+y}\) of point 2 and point 4 are equal, because they lie along the crosswind direction. Therefore, upwinding is introduced in the direction of flow only

Fig. 6
figure 6

Comparison of weights \((W^x)\) of convection operator \({\mathbf {u}} \frac{d}{dx}\), evaluated using conventional RBF and proposed USRBF on a sample 1-D domain with \(x\in \left[ -0.5,0.5\right] , x_{1} = 0, {\mathbf {u}}=[1,1]\), and \(Pe=1000\)

Full size image
Fig. 7
figure 7

Comparison of weights \(W^{x+y}\) of convection operator \({{\mathbf {u}}} \cdot \nabla\), evaluated using conventional RBF and proposed USRBF on a sample 2-D domain with \(\left( x, y \right) \in \left[ -0.2, 0.2\right] \times \left[ -0.2, 0.2 \right]\), \(\left( x_{1}, y_{1} \right) = \left( 0, 0 \right)\), \({{\mathbf {u}}} = [1, 1]\), \(Pe =1000\)

Full size image

4 Numerical tests

4.1 1-D test cases

The stability and accuracy of the proposed scheme are tested by solving two different convection–diffusion problems in one-dimensional space using conventional and upwind skewed RBFs, respectively, in finite difference mode. The first problem is a standard convection–diffusion problem with unit source as

$$\begin{aligned} \begin{aligned}&\frac{dT}{dx}-a\frac{d^2T}{dx^2}=1, \quad x\in [0,1] \\&T(0)=1 \quad \hbox {and} \quad T(1)=0 \end{aligned}. \end{aligned}$$
(14)

The exact solution of Eq. (14) is given by [20]

$$\begin{aligned} {T_{\text {exact}}}= -\frac{ e^{ \frac{x-1}{a} } - 1 }{ 1 - e^{ -\frac{1}{a} } }. \end{aligned}$$
(15)

The second problem is a convection–diffusion equation with trigonometric source function,

$$\begin{aligned}&\frac{{dT}}{{dx}} - a\frac{{d}^{2}T}{{dx^{2}}}=a{\pi ^{2}}sin\left( {\pi x} \right) + \pi cos\left( {\pi x} \right) ,\quad x \in [0,1]\nonumber \\&T(0) = 0\quad {{and}}\quad T(1) = 1. \end{aligned}$$
(16)

The exact solution of Eq. (16) is given by [20]

$$\begin{aligned} T_{\text {exact}}=sin \left( \pi x \right) + \left[ \frac{e^{\frac{x}{a} -\frac{1}{a}} - e^{\frac{-1}{a}}}{1-e^{\frac{-1}{a}}} \right] . \end{aligned}$$
(17)

In both the problems, the boundary layer exists near \(x = 1\). The transport velocity appears as the coefficient of dT / dx in the standard equation. In these problems, the transport velocity is set as unity and the diffusion coefficient, a, is varied to vary the intensity of convection. The problem is solved using conventional as well as upwind skewed RBFs. For this purpose, the domain is represented by n computational nodes, each having N nodes in its local support domain. Spatially discretized form of Eq. (14) can be written using RBF-FD, at node i, as [3],

$$\begin{aligned} \sum _{j=1}^{N}\mathbf {W}_{i,j}^{(x)}T_{j}-a \sum _{j=1}^{N}\mathbf {W}_{i,j}^{(xx)}T_{j}=1, \quad x\in [0,1]. \end{aligned}$$
(18)

Discretized equations are formulated at each node in the domain. Subsequently, the set of discretized equations is solved to get the values of T at all computational nodes. The procedure of discretization remains the same for conventional and upwind skewed RBFs. However, the weights are calculated differently using the procedure mentioned in Sects. 2 and 3. A similar procedure is followed for solution of Eq. (16).

Fig. 8
figure 8

Solution of 1-D convection–diffusion equation with unit source function (Eq. 14) at \(0 \le x \le 1\) using \(N=40\) uniformly spaced nodes. Solutions are obtained with conventional and upwind skewed RBFs

Full size image
Fig. 9
figure 9

Solution of 1-D convection–diffusion equation with unit source function (Eq. 14) at \(0 \le x \le 1\) using \(N=40\) randomly spaced nodes. Solutions are obtained with conventional and upwind skewed RBFs

Full size image
Fig. 10
figure 10

Solution of 1-D convection–diffusion equation with trigonometric source function (Eq. 16) at \(0 \le x \le 1\) using \(N=40\) uniformly spaced nodes. Solutions are obtained with conventional and upwind skewed RBFs

Full size image
Fig. 11
figure 11

Solution of 1-D convection–diffusion equation with trigonometric source function (Eq. 16) at \(0 \le x \le 1\) using \(N=40\) randomly spaced nodes. Solutions are obtained with conventional and upwind skewed RBFs

Full size image
Fig. 12
figure 12

Variation of maximum and RMS errors with a for 1-D convection–diffusion equation with unit source function (Eq. 14). Uniformly spaced nodes \(N=40\) at \(0 \le x \le 1\)

Full size image
Fig. 13
figure 13

Variation of maximum and RMS errors with a for 1-D convection–diffusion equation with trigonometric source function (Eq. 16). Uniformly spaced nodes \(N=40\) at \(0 \le x \le 1\)

Full size image

Figures 8, 9, 10, and 11 show the the solutions of Eqs. (14) and (16) using conventional and upwind skewed RBFs along with the exact solutions on uniformly and randomly spaced data point over the 1-D domain. The total number of data points is set as 40 for all cases. The nodal distribution is randomized by adding a noise of the level \(0.1 \Delta x\) in the coordinate locations of uniformly distributed interior nodes. At higher values of diffusion coefficient (e.g., \(a = 10^{-2}\)), the solutions from conventional as well as upwind skewed RBFs produce accurate results. This is because the higher diffusion in the problem does not let instabilities arise even if conventional RBFs are employed. However, as the value of diffusion coefficient, a, decreases, the problem becomes more convection dominated and the solution from conventional RBF starts deviating from the exact solution. For such cases, the solution from USRBF remains stable and accurate. This is because of the upwinding effect introduced by USRBF for the solution of convection-dominated problem.

Figures 12 and 13 show the variation of maximum and root-mean-square (RMS) errors with diffusion parameter (a). For higher diffusion cases, conventional and upwind skwered RBFs produce similar results. However, as the convection term dominates for \(1/a > 110\), and up to \(10^5\), a significant error reduction can be observed from the solutions of USRBF. For large values of 1/a, upwinding becomes necessary to stabilize the solution and is provided by USRBF.

The solution of convective–diffusive problems is sought on 1-D stencil with varying nodal density to study the effect of nodal spacing on error of the solution. The corresponding values of maximum and RMS errors are obtained for conventional and upwind skewed RBFs with different convection intensities. The error plots for problem with unit and trigonometric source functions are shown in Figs. 14 and 15, respectively. The computational advantage of using the proposed USRBF over conventional (symmetric) RBFs can be quantified by comparing the average nodal spacing values \((\Delta {x})\), from conventional and proposed schemes, resulting in the same error values. For example, the solution of Eq. (14) with \(a=10^{-2}\) shown in Fig. 14a depicts that an average nodal spacing value, \(\Delta {x}=0.045,\) is required to achieve a maximum error of 0.1 with conventional RBF. However, the same maximum error is obtained with an average nodal spacing value, \(\Delta {x}=0.09,\) using the proposed USRBFs. Therefore, the proposed scheme requires almost half the computational nodes compared to the conventional scheme for producing result with a maximum error of 0.1 in this case. However, the difference in errors from the two schemes varies with nodal densities and value of diffusion coefficient. The plots in Figs. 14 and 15 depict a declining trend of maximum and RMS errors when nodal spacing \(\Delta x\) is reduced. For higher values of diffusion coefficient, a, and smaller \(\Delta x\), the errors from conventional RBFs are small. In such cases, the advantage of increased nodal density tends to circumvent the errors caused by convection terms even for symmetric RBFs. However, as the value of diffusion coefficient, a, decreases, the convection term dominates. In such cases, error from USRBF is significantly lower than that from conventional (symmetric) RBF schemes. The difference becomes even more pronounced at higher nodal spacing, \((\Delta x)\), when the added advantage of higher nodal density is also absent for conventional RBFs. Therefore, upwind skewed RBFs offer improved accuracy especially for convection-dominated problems and with lower nodal densities.

Fig. 14
figure 14

Variation of maximum and RMS errors with \(\Delta x\) for 1-D convection–diffusion equation with unit source function (Eq. 14) at \(0 \le x \le 1\)

Full size image
Fig. 15
figure 15

Variation of maximum and RMS errors with \(\Delta x\) for 1-D convection–diffusion equation with trigonometric source function (Eq. 16) at \(0 \le x \le 1\)

Full size image

4.2 2-D test cases

The stability and accuracy of the proposed scheme is also tested by solving two convection–diffusion problems over the 2-D plane. The first problem is described by the following equation:

$$\begin{aligned} \frac{\partial T}{\partial x} - a\left( \frac{\partial ^2 T}{\partial x^2} + \frac{\partial ^2 T}{\partial y^2} \right) = 0, \quad \left( x,y\right) \in \left[ 0,1\right] \times \left[ 0,1\right] . \end{aligned}$$
(19)

The exact solution of Eq. (19) is given by [20] as

$$\begin{aligned} \begin{aligned}&T_{\text {exact}}= \frac{\sin (\pi y)}{e^l - e^m} \left( e^{l+mx}-e^{lx+m} \right) ,\\&\hbox {where} \quad l = \frac{\left( a +\sqrt{4 \pi ^2 + a^2} \right) }{2} \quad \hbox {and} \quad m = \frac{\left( a - \sqrt{4 \pi ^2 + a^2}\right) }{2} \end{aligned}. \end{aligned}$$
(20)

The second problem is represented by a convection–diffusion equation with an exponential source term as

$$\begin{aligned} \frac{\partial T}{\partial x} + \frac{\partial T}{\partial y} - a\left( \frac{\partial ^2 T}{\partial x^2} + \frac{\partial ^2 T}{\partial y^2} \right) = \frac{-e^{\frac{\left( x-1\right) \left( y-1\right) }{2a}} \left( x^2+y^2-2\right) }{4a}, \quad \left( x,y\right) \in \left[ 0,1\right] \times \left[ 0,1\right] . \end{aligned}$$
(21)

The exact solution of the problem in Eq. (21) is expressed as [20]

$$\begin{aligned} T_{\text {exact}} = e^{-\left( 1-x\right) \left( 1-y\right) /2a}. \end{aligned}$$
(22)

Dirichlet boundary conditions at the boundaries of the domain are derived from exact solutions of both the problems. For the first 2-D test case, the boundary layer exists near the \(x=1\) edge, and for the second 2-D test case, the boundary layer exists near \(x=1\) and \(y=1\) edges of the domain. Numerical solutions of the problems are sought using inverse multiquadric RBFs over uniformly spaced as well as random particles on a 2-D plane. Randomization of nodes is achieved by introducing noise in the positions of uniformly spaced stencil. A randomized nodal distribution is shown in Fig. 16. Uniform velocity is assumed in all cases for calculation of Peclet number. Therefore, convection intensity is varied by varying the value of diffusion coefficient, a. The problems are solved using conventional RBFs as well as upwind skewed RBFs with varying convection intensities to study the effect of upwinding as the convection intensity increases. Moreover, the effect of changing nodal spacing is also studied for both conventional and upwind skewed RBFs.

Fig. 16
figure 16

Randomized nodal distribution used for solution 2-D convection diffusion problem

Full size image
Fig. 17
figure 17

Solution of 2-D convection–diffusion equation with zero source term (Eq. 19) over \((x, y) \in [0, 1] \times [0, 1]\) using \(N = 40 \times 40\) uniformly spaced nodes. Left column: exact solution, center column: solution using conventional RBF. Right colum: solution using upwind skewed RBF

Full size image
Fig. 18
figure 18

Solution of 2-D convection–diffusion equation with zero source term (Eq. 19) over \((x, y) \in [0, 1] \times [0, 1]\) using \(N = 40 \times 40\) randomly spaced nodes. Left column: exact solution, center column: solution using conventional RBF. Right column: solution using upwind skewed RBF

Full size image
Fig. 19
figure 19

Variation of maximum and RMS errors with a for 2-D convection–diffusion equation with zero source term (Eq. 19) over \((x, y) \in [0, 1] \times [0, 1]\) using \(N = 40 \times 40\) uniformly spaced nodes

Full size image
Fig. 20
figure 20

Variation of maximum and RMS errors with \(\Delta x\) for 2-D convection–diffusion equation with zero source term (Eq. 19) over \((x, y) \in [0, 1] \times [0, 1]\)

Full size image

The results of 2-D convection diffusion equation with zero source term (Eq. 19) on uniformly spaced and randomized stencils are shown in Figs. 17 and 18 respectively. The solutions are obtained with conventional as well as upwind skewed RBFs and are compared with the exact solution at different convection intensities. For higher values of diffusion coefficient (e.g., \((a=10^{-2})\) case), solutions from both conventional and upwind skewed RBFs are accurate and smooth. However, as the diffusion reduces (e.g., \((a=10^{-5})\) case), large perturbations, caused by numerical instabilities, appear with conventional RBFs. These are non-physical perturbation caused by numerical instabilities in convection-dominated problems. These instabilities are more pronounced on random nodal distribution. The results indicate that the solution from USRBF remains free from perturbations. The upwinding introduced by skewed RBFs effectively suppressed the instabilities caused by high convection. The errors of numerical solutions are calculated by comparing the results with the exact solution given by Eq. 20. The curves of maximum and RMS errors for both conventional and upwind skewed RBFs are co-plotted with changing convection intensities in Fig. 19. The plots depict substantially lower error associated with USRBF particularly at higher convection intensities. At lower convection intensity, the errors from the USRBF are almost the same as from conventional RBFs. Maximum and RMS error values are also plotted against varying nodal spacing (\(\Delta x\)) for both conventional and upwind skewed RBFs, at two different values of diffusion parameter, in Fig. 20. At \(a=10^{-5},\) the maximum error from USRBFs is almost 100 times lower than that from conventional RBFs.

The solutions of 2-D convection diffusion equation with non-zero source term (Eq. 21) on uniformly spaced and randomized stencils are shown in Figs. 21 and 22, respectively. Similar trends have been observed from the solutions of zero source term equation (Eq. (21). The variation of maximum and RMS errors with convection intensities is shown in Fig. 23. Similarly, Fig. 24 shows the variation of maximum and RMS errors with nodal spacing \(\Delta x\), over a uniform stencil. At lower convection intensity (\(a=0.01\) case) when the problem becomes diffusion dominated, the errors from USRBFs are slightly lower than those from conventional RBFs. However, when the diffusion parameter drops (\(a=10^{-5}\) case), the errors from the USRBF solution are almost 100 times lower that those from conventional RBFs. USRBF is, therefore, found to provide improved solutions for highly convective problems.

Fig. 21
figure 21

Solution of 2-D convection–diffusion equation with non-zero source term (Eq. 21) over \((x, y) \in [0, 1] \times [0, 1]\) using \(N = 40 \times 40\) uniformly spaced nodes. Left column: exact solution, center column: solution using conventional RBF. Right column: solution using upwind skewed RBF

Full size image
Fig. 22
figure 22

Solution of 2-D convection–diffusion equation with non-zero source term (Eq. 21) over \((x, y) \in [0, 1] \times [0, 1]\) using \(N = 40 \times 40\) randomly spaced nodes. Left column: exact solution, center column: solution using conventional RBF. Right colunm: solution using upwind skewed RBF

Full size image
Fig. 23
figure 23

Variation of maximum and RMS errors with a for 2-D convection–diffusion equation with non-zero source term (Eq. 21) over \((x, y) \in [0, 1] \times [0, 1]\) using \(N = 40 \times 40\) uniformly spaced nodes

Full size image
Fig. 24
figure 24

Variation of maximum and RMS errors with \(\Delta x\) for 2-D convection–diffusion equation with non-zero source term (Eq. 21) over \((x, y) \in [0, 1] \times [0, 1]\)

Full size image

4.3 False diffusion

The upwind schemes smear the distribution of transport properties in a manner that a false diffusion is added to the solution [20]. This effect can be demonstrated by calculating the transport of variable T over a rectangular domain \((x, y) \in [0, 1] \times [0, 1]\) where flow is diagonal to the domain boundaries. A pure convective problem is considered which can be obtained by using removing the diffusion term from Eq. (19) and introducing the boundary conditions \(T(x,0)=T(1,y)=0\) and \(T((0,y)=T(x,1)=100\). Flow velocity is set as \({\mathbf {u}}=[2,2]\). The degree of false diffusion added to the solution is demonstrated by solving the problem using USRBF in finite difference mode and plotting the distribution of transport variable, T, along the diagonal of domain boundaries as shown in Fig. 25. In the absence of any diffusion in the problem, the exact solution follows a step change in the value of T, from 100 to 0, in the middle of the diagonal, to satisfy the boundary conditions. However, the results calculated by USRBF show a smeared profile of T corresponding to a rather gradual change in value from 100 to 0. This is because of the added false diffusion which tends to reduce as the nodal density increases and the numerical solution becomes close to the exact profile of T. The current problem is solved over meshfree nodal cloud with various nodal densities. However, the same problem is solved by [20] and a similar behavior is depicted while solving the problem with the finite volume method.

Fig. 25
figure 25

False diffusion depicted by the solution of Eq. 19 with zero diffusion term and \(T(x,0)=T(1,y)=0\) and \(T((0,y)=T(x,1)=100\). The problem is solved using USRBF in finite difference mode on a stencil of meshfree nodes with three different nodal densities\((10\times 10,~50\times 50,~100\times 100)\). Rectangular domain is used as \((x, y) \in [0, 1] \times [0, 1]\). The flow velocity is \({\mathbf {u}}=[2,2]\)

Full size image

5 Future work

The focus of this research is limited to the development of upwind skewed RBFs and its application in suppressing the spurious perturbations in the solution of convection-dominated problems. However, a lot of research work still needs to be done to fully understand the behavior and effect of free parameters on the performance of the proposed USRBFs. For example, Micchelli’s theorem [33, 34] guarantees the non-singularity of moment matrix, \(\Phi\), for conventional RBFs with MQ, IMQ and exponential basis function in the presence of arbitrary nodal distributions. The study by [33, 34] may be extended to determine the conditions under which the moment matrix of USRBF is non-singular. The shape parameter, \(\sigma\), of conventional RBFs plays an important role in the accuracy of the numerical solutions of ordinary and partial differential equations. In present study, the optimum value of shape function is determined as proposed by [3] for radially symmetric RBFs. However, further study to determine the “optimal” value of shape parameter for USRBFs may be useful. Only linear and steady state problems are considered in this research. Since, almost all real-life flow problems are governed by nonlinear, unsteady Navier–Stokes equation, the proposed scheme should be applied to NS equation, and the results should be compared with data available in literature.

6 Conclusions

An upwind-skewed radial basis functions (USRBF) is proposed and is applied with local radial basis function in finite difference mode (RBF-FD) for stable numerical solutions of highly convective problems over meshfree nodal cloud. Unlike conventional RBFs (which depend upon the spatial location of nodes only), the proposed USRBF takes into account the flow direction and intensity of convection while calculating the RBF weights. In practice, USRBF are obtained by multiplying the conventional RBFs with an upwinding factor. It is observed that for low convection intensities, the solution from USRBF are slightly more accurate than conventional RBFs. However, as the convection intensity increases, conventional RBFs tend to show non-physical perturbations in the solution which ultimately lead to highly erroneous results. The RBFs skewed toward the upwind direction provide more weightage to the nodes at the upwind of reference location. This upwinding effect suppresses the instabilities caused by the convection term and the resulting solution is stabilized. For highly convective problems (diffusion parameter \(a\approx 10^{-5}\) in convection–diffusion problems defined in Sect. 4), the error from the proposed USRBF-based solution scheme is almost 100 times lower than that from conventional RBF-based solutions. Therefore, for highly convective flows, the proposed USRBF provides more accurate and stable solutions as compared to radially symmetric conventional RBFs.