1 Introduction

Literature consists of many experimental and theoretical studies into the prediction of the load-bearing capacity and behavior of piles though the mechanisms have not yet clarified completely for scholars of the field. In case of the piles that are driven into cohesionless soil, the problem is of high complexity and this is because of the sensitive nature of the factors that have impact on the behaviors of the pile. These factors can not only be quantified easily, but also involve extensive uncertainties. These factors include the stress and strain history of the soil, the impacts of soil fabric and compressibility, installation effects, and the difficulty of attaining undisturbed samples of soil.

To address effectively these complexities, the correlations with in situ experiments, e.g., the cone penetration test, the standard penetration test, and the pressure meter, are applied to numerous cases. Such tests show, to some degree, the natural conditions of soil though they suffer from many limitations. For instance, the standard penetration tests have considerably inherent variability, and they do not show the compressibility of the soil. On the other hand, if such tests are correlated with load test data upon a regional basis, instead of employing general correlations, they can deliver acceptable predictions [1, 2].

The limitations of the correlations that are attained with the in situ tests have made the researchers to develop numerous empirical relations between pile capacity and soil parameters in both end-bearing and friction piles, on the basis of load test results. The aim is providing rapid and yet practically accurate estimations regarding the pile capacity. Four of the most popular empirical methods in the literature have been introduced by Meyerhof [3], Coyle and Castello [4], the American Petroleum Institute [5], and Randolph [6]. However, they either oversimplify or inappropriately consider the impacts of given factors. The factors include residual stresses, the stress history, and actual soil parameters that exist following the pile driving operation. The designing recommendations these methods provide for users have an inconsistency with the physical processes that dictate the actual pile capacity [6]. As a result, a substitute method needs to be developed in a way to resolve the uncertainties that we face in the prediction process of the pile load capacity [2].

In recent years, in the geotechnical engineering fields of study, artificial neural networks (ANNs) have been implemented effectively to a variety of applications [7,8,9,10,11,12,13]. A multivariate adaptive regression spline (MARS) approach was used by Samui [14] for the purpose of determining the ultimate capacity of the driven piles that are installed in sands. In MARS, a variety of parameters are used as the input variables, including driven pile area (A), effective vertical stress at the tip of the pile (\(\sigma_{v}^{\prime }\)), soil at the tip of the derived pile (\(\phi_{\text{tip}}\)) and angle of shear resistance of the soil surrounding the shaft (\(\phi_{\text{shaft}}\)), and pile length (L). The pile ultimate bearing capacity is set as the MARS output. Samui [14] compared the results obtained from MARS to those of other ANN-based models, e.g., the generalized regression neural network (GRNN) model. In addition, an equation was eventually proposed on the basis of the proposed MARS. On the other hand, the driven pile bearing capacity in clay was studied by Dzagov and Razvodovskii [15]. Depending on the surrounding soil properties and the length of pile, the driven piles are capable of providing basic characteristics to be recognized as both end bearing and/or friction piles. Having integrated the artificial neural networks (ANNs) and genetic algorithm (GA), Momeni et al. [16] attempted to develop a hybrid model applicable to the prediction of the pile bearing capacity. Literature also contains other AI techniques effectively applied to the prediction of the bearing capacities of a variety of piles by means of ANN [17,18,19], functional networks (FN) [20], relevance vector machines (RVM) [21], support vector machines (SVM) [22], extreme learning machines (ELM) [23], and MARS [20, 24]. ANN has been applied not only to the load-bearing capacity of piles, but also to the prediction of the settlement of piles on the basis of the cone penetration tests (CPT) [25]. On the other hand, ANN suffers from the drawback of poor generalization, which is due to the fact that, during the training process, it attains local minima and it requires iterative learning steps to achieve learning performances of a higher quality.

Moayedi and Jahed Armaghani [26] offered a combination of ANN and imperialism competitive algorithm (ICA) to predict bearing capacity of driven pile. Their results indicated that the performance of ICA–ANN was comparable with higher accuracy in prediction of K of the bearing capacity of driven pile than ANN one.

In other study, Moayedi and Hayati [27] predicted the friction capacity of driven piles through SVM, genetic programming (GP) and adaptive neuro-fuzzy inference system (ANFIS). Performance assessment indicated that the ANFIS possessed superior predictive ability than the GP and SVM models.

The ANFIS model was compared with hybrid ICA–ANN for the prediction of bearing capacity of driven pile in the study conducted by Shaik et al. [28]. They showed the superiority of ICA–ANN over ANFIS in terms of performance measures.

Recently, Harandizadeh et al. [29] presented a hybrid intelligent model based on ANFIS in combination with group method of data handling (GMDH) to predict bearing capacity of driven pile. Then the developed ANFIS–GMDH was optimized by particle swarm optimization (PSO). They compared the performance of proposed model with ANN performance, and indicated the effectiveness of ANFIS–GMDH–PSO model to predict the bearing capacity of driven pile.

This research is mainly aimed to present a new artificial intelligent approach to predict the total bearing capacity of the driven pile that is installed inside the cohesionless soil using support vector regression (SVR) optimized by genetic algorithm (GA). In other words, the main contribution of this study is to propose a new GA-SVR model in the field of driven piles. To the best of our knowledge, no research has developed the GA-SVR model to predict vertical load capacity of driven piles in different timescales as of yet. Additionally, SVR and linear regression models are also used for comparison.

2 Dataset

To develop the models capable of predicting the vertical capacity of piles, the dataset of Darrag [1] was used in this study. This database comprises in situ tests carried out on soil together with the pile load test data coming from various parts of the world. In this database, there are input parameters such as \(\phi_{\text{tip}}\), \(\phi_{\text{shaft}}\), L, \(\sigma_{v}^{\prime }\), and A, whereas the output is set to be the total pile capacity (Qm). In the used database, \(\phi_{\text{tip}}\), \(\phi_{\text{shaft}}\), L, \(\sigma_{v}^{\prime }\), A and Qm were varied in the ranges of 31–41, 28–39, 3–47.2 m, 38–475 KN/m2, 0.0061–0.6568 m2 and 75–5604 KN, respectively. In modeling processes of GA-SVR, SVR and linear regression, the datasets were separated into two parts in a random way: training (47 data samples) and testing (12 data samples). A part of datasets used in this study is given in Table 1.

Table 1 A part of datasets used in this study
Full size table

3 Optimizing the SVR parameters by GA

3.1 Support vector regression (SVR)

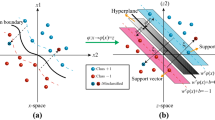
Support vector machines (SVM) have been recognized as a proper tool for predicting aims [30, 31]. The basis of SVM is the principle of structural risk minimization, and it enjoys an acceptable generalization with only a few number of data samples. SVM is actually a generation learning system that has been developed on the basis of developments that occurred in statistical learning theory. It helps researchers to map non-linear form of an n-dimensional input space and change it to a high-dimensional feature space in which, for instance, a linear classifier is applicable. SVM is capable of training the non-linear models on the basis of the principles of structural risk minimization, whose main aim is the minimization of an upper bound of the generalization errors, not the minimization of the empirical errors (as aimed by other neural networks). The basis of such induction principle is the fact that generalization error is bounded by the sum of the empirical error and a confidence interval term, which is dependent upon the Vapnik–Chervonenkis (VC) dimension. In accordance with this principle, SVM can attain an optimal model structure through the establishment of an appropriate balance between the VC confidence interval and the empirical error, which finally results in a generalization performance with a higher quality compared to that of the other ANN [32]. An added bonus of SVM is that its training is an exclusively solvable quadratic optimization problem, and in SVM, the solution complexity is only dependent upon the intricacy of the desired solution, not upon the dimensionality of the input space. As a result, SVM employs a non-linear mapping (on the basis of a kernel function) for the transformation of an input space into a high-dimensional space; then, within such space, it seeks for a non-linear relation between inputs and outputs. Note that SVM enjoys a rigorous theoretical background and, additionally, it is capable of finding global optimal solutions to the problems that have small training samples, non-linearity, high dimension, and local optima. In the beginning, SVM was developed to be applied to the pattern recognition problems [33], and it is only in the recent years that it has demonstrated a high capacity in solving a wide range of problems, e.g., non-linear regression. Support vector regression (SVR) employs the same principles as the SVM for classification, with only a few minor differences such as the margin of tolerance is set in approximation to the SVM which would have been requested from the problem [34]. For more detailed information about the SVR, please refer to [34,35,36,37,38]. Figure 1 shows a view of SVR structure. In this figure, \(a_{i}^{*} - a_{i}\) and B parameters are the weights of support vectors and polarization, respectively.

Fig. 1
figure 1

Structure of the SVR [39]

Full size image

3.2 Model development

To have a high precision and efficiency in estimations made by SVR models, it is of high importance to accurately select the following SVR parameters: the regularization parameter (C), Kernel parameter (\(\gamma\)), and epsilon (\(\varepsilon\)) [40]. The values set for the above-noted parameters have a great impact on the model performance as explained in the following.

The C parameter (or box constraints) designates the penalty of the approximation function. The C value is recommended not to be too small or too large. In case it is too small, it considers an inadequate penalty upon the fitting of the training data, while in case it is selected too large, it can result in overfitting problems upon the training data [40]. The responsibility of the insensitivity loss function (\(\varepsilon\)) is controlling the number of support vectors; this parameter also affects the SVR performance. On the other hand, the \(\gamma\) parameter is for mapping non-linear function into higher dimensional space; in other words, it measures the SVR capacity of handling the problems of non-linearity [40, 41]. This is worth mentioning that numerous studies carried out previously into SVR performance still make use of manual or grid search for the purpose of choosing the hyperparameters of SVR [42]. The problem is that in cases where there is a broad parameter searching range, such approaches get computationally demanding and, at the same time, the achievement of the best parameters is of no guarantee in these approaches. Because of such shortages, researchers have designed some other techniques of searching aiming at solving the optimization problems. Remember that GA is a prevailing global optimization technique first introduced by Holland in 1975. It is highly attractive for scholars of numerous scientific fields because of its outstanding global searching capacity [41,42,43,44]. The present study makes the use of GA to find the optimal combination of SVR parameters. Figure 2 clearly depicts a flowchart of the optimization of SVR hyperparameters by means of GA.

Fig. 2
figure 2

GA-SVR structure [45]

Full size image

3.2.1 The proposed GA-SVR

Here is proposed the GA-SVR model using the MATLAB 2018b platform. The MATLAB SVM toolbox containing SVR was utilized to develop the model. This toolbox was integrated with Global Optimization Toolbox in MATLAB to optimize the parameters of SVR. In a random way, 80% of whole data were classified into training dataset and the remaining 20% were assigned to the testing dataset. In other words, 47 and 12 data samples were used for training and testing parts. The former was applied to developing the proposed model.

In the training process, an algorithm is utilized to establish the functional relationship between the inputs and the corresponding target. Such process is normally done to explore the suitable set of SVR parameters, which decreases the cross-validation errors as far as possible. Before the beginning of model training, a normalization process was done on the training data in a way to make sure that it is computationally efficient. After that, the training data (inputs and target), the SVR parameter range, the population size and the number of generation were inserted into GA. In the present paper, the upper bound and lower bounds of the SVR parameters were specified as C (1e−08, inf), \(\varepsilon\) (1e−6, 8), \(\gamma\) (1e−8, inf), whereas the maximum iteration and the population size were set to 300. Also, the values of 0.8 and 0.25 were assigned for the crossover and mutation rates, respectively, based on trial and error method. When the functional relationships are learnt from the training dataset by the model in a successful way, it is the turn for the testing dataset to be employed for the purpose of validating the precision of the proposed model in its predictions. Table 2 lists the most proper set of SVR parameters that were achieved in the course of model training; they would be utilized later for testing upon the new dataset (testing dataset). Note that, the GA-SVR explained here was trained and tested based on five input parameters, i.e., \(\phi_{\text{tip}}\), \(\phi_{\text{shaft}}\), L, \(\sigma_{v}^{\prime }\), and A. The performance of the proposed GA-SVR model to predict Qm is discussed in Sect. 4.

Table 2 SVR parameters optimized by GA
Full size table

4 Results and discussion

In this study, SVR, and GA-SVR models are used to predict Qm. To demonstrate the effect of input parameters on Qm, the different SVR and GA-SVR models were constructed based on different combinations of input parameters. In other words, six different SVR models and six different GA-SVR models were constructed in this study. The inputs of the mentioned models were according to the following:

  • SVR model 1; inputs: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), L, \(\sigma_{v}^{\prime }\), and A

  • SVR model 2; inputs: \(\phi_{\text{tip}}\), L, \(\sigma_{v}^{\prime }\), and A

  • SVR model 3; inputs: \(\phi_{\text{shaft}}\), L, \(\sigma_{v}^{\prime }\), and A

  • SVR model 4; inputs: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), L, and A

  • SVR model 5; inputs: \(\phi_{\text{shaft}}\), \(\phi_{tip}\), \(\sigma_{v}^{\prime }\), and A

  • SVR model 6; inputs: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), L, and \(\sigma_{v} '\)

  • GA-SVR model 1; inputs: \(\phi_{tip}\), \(\phi_{\text{shaft}}\), L, \(\sigma_{v}^{\prime }\), and A

  • GA-SVR model 2; inputs: \(\phi_{\text{tip}}\), L, \(\sigma_{v}^{\prime }\), and A

  • GA-SVR model 3; inputs: \(\phi_{\text{shaft}}\), L, \(\sigma_{v}^{\prime }\), and A

  • GA-SVR model 4; input: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), L, and A

  • GA-SVR model 5; input: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), \(\sigma_{v}^{\prime }\), and A

  • GA-SVR model 6; inputs: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), L, and \(\sigma_{v}^{\prime } .\)

Apart from the mentioned SVR and GA-SVR models, six different linear regression models were also constructed based on different independent parameters as follows:

  • Linear regression model 1; inputs: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), L, \(\sigma_{v}^{\prime }\), and A

  • Linear regression model 2; inputs: \(\phi_{\text{tip}}\), L, \(\sigma_{v}^{\prime }\), and A

  • Linear regression model 3; inputs: \(\phi_{\text{shaft}}\), L, \(\sigma_{v}^{\prime }\), and A

  • Linear regression model 4; inputs: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), L, and A

  • Linear regression model 5; inputs: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), \(\sigma_{v}^{\prime }\), and A

  • Linear regression model 6; inputs: \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), L, and \(\sigma_{v}^{\prime } .\)

The generally form of linear regression can be formulated as

$$Q_{\text{m}} = X + x_{1} \cdot \phi_{\text{shaft}} + x_{2} \cdot \phi_{\text{tip}} + x_{3} \cdot \sigma_{v}^{\prime } + x_{4} \cdot L + x_{5} \cdot A,$$
(1)

where \(X\), \(x_{1}\)…\(x_{5}\) are the coefficients of equation, and can be determined by SPSS software. Considering the analyses, the following equations were constructed based on different input parameters:

$$Q_{\text{m}} = - \;0.034 + 0.034\phi_{\text{shaft}} + 0.211\phi_{\text{tip}} + 2.460\sigma_{v}^{\prime } - 2.079L + 0.850A,$$
(2)
$$Q_{\text{m}} = - \;0.021 + 0.234\phi_{\text{tip}} + 2.408\sigma_{v}^{\prime } - 2.036L + 0.842A,$$
(3)
$$Q_{\text{m}} = - \;0.025 + 0.172\phi_{\text{shaft}} + 3.022\sigma_{v}^{\prime } - 2.620L + 0.927A,$$
(4)
$$Q_{\text{m}} = - \;0.081 - 0.106\phi_{\text{shaft}} + 0.457\phi_{\text{tip}} + 0.424L + 0.743A,$$
(5)
$$Q_{\text{m}} = - \;0.096 - 0.058\phi_{\text{shaft}} + 0.401\phi_{\text{tip}} + 0.466\sigma_{v}^{\prime } + 0.762A,$$
(6)
$$Q_{\text{m}} = 0.065 - 0.181\phi_{\text{shaft}} + 0.559\phi_{\text{tip}} + 1.371\sigma_{v}^{\prime } - 0.954L.$$
(7)

Note that Eqs. 2–7 were constructed based on normalized inputs and output. From Eq. 2, it can be found that \(Q_{\text{m}}\) has a direct relationship with \(\phi_{\text{shaft}}\), \(\phi_{\text{tip}}\), \(\sigma_{v}^{\prime }\) and A parameters, while it has an indirect relationship with the L parameter. To check the performance of all eighteen models (six SVR, six GA-SVR and six linear regression models), three well-known criteria, namely root mean square error (RMSE), coefficient of determination (R2) and mean absolute error (MAE) were used, which can be expressed as follows [46,47,48,49,50,51,52,53,54,55,56]:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {Qm_{a} - Qm_{p} } \right)^{2} } ,$$
(8)
$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {Qm_{a} - Qm_{p} } \right|,$$
(9)
$$R^{2} = \frac{{\left[ {\mathop \sum \nolimits_{i = 1}^{n} \left( {Qm_{a} - Qm_{\text{mean}} } \right)^{2} } \right] - \left[ {\mathop \sum \nolimits_{i = 1}^{n} \left( {Qm_{a} - Qm_{p} } \right)^{2} } \right]}}{{\left[ {\mathop \sum \nolimits_{i = 1}^{n} \left( {Qm_{a} - Qm_{\text{mean}} } \right)^{2} } \right]}},$$
(10)

where \(Qm_{a} \;\;{\text{and}}\;\; Qm_{p}\) are the actual and predicted Qm values, and n is the number of total data (here 59 data). A value closer to one for R2, and closer to zero for RMSE and MAE indicates a better model. The values of R2, RMSE and MAE obtained from linear regression, SVR and GA-SVR models are given in Table 3. It is worth mentioning that in the analysis of the predictive models, we only consider the results of the testing phase. According to Table 3, among the linear regression models, model 1 has the lowest MAE and RMSE values, while model 3 has the highest R2 value. Also, among the SVR models, model 1 has the lowest MAE and RMSE values, and the highest R2 value. On the other hand, GA-SVR model 1 has also the lowest MAE and RMSE values, and the highest R2 value among the other GA-SVR models. Considering all predictive models, it can be seen that model 1 of GA-SVR with R2 of 0.980, RMSE of 0.017 and MAE of 0.017 has the best performance compared to SVR and linear regression models, as bolded in Table 3. In other words, the results confirm the ability of GA to improve SVR results. Based on Table 3, model 6 of linear regression, SVR and GA-SVR models have the worst performance among the other models. In other words, when A, as an input parameter, was removed from the modeling, the highest RMSE and MAE, and the lowest R2 values were obtained. Consequently, the A parameter can be considered as the most effective parameter to predict Qm. According to Table 3, model 3 among the linear regression models, model 1 among the SVR models, and model 1 among the GA-SVR models have the highest R2 values in testing phase. For a better view, the R2 values obtained from the mentioned models are shown in Figs. 3, 4, and 5. From these figures, it was found that the GA-SVR possessed superior predictive ability than the SVR and linear regression models, since a very close agreement (R2 = 0.980) between the measured and the predicted values of Qm was obtained.

Table 3 Obtained RMSE, R2 and MAE values from the predictive models
Full size table
Fig. 3
figure 3

Actual vs. predicted Qm values using model 3 of linear regression models

Full size image
Fig. 4
figure 4

Actual vs. predicted Qm values using model 1 of SVR models

Full size image
Fig. 5
figure 5

Actual vs. predicted Qm values using model 1 of GA-SVR models

Full size image

5 Conclusion

Achieving a high-precision model to predict vertical load capacity of driven piles is an important task in geotechnical field. This study investigates the ability of GA-SVR model to predict vertical load capacity of driven piles in cohesionless soils. Additionally, the SVR and linear regression models were also employed and their results were compared to GA-SVR results. In modeling processes of GA-SVR, SVR and linear regression models, \(\phi_{\text{tip}}\), \(\phi_{\text{shaft}}\), L, \(\sigma_{v}^{\prime }\), and A were adopted as the input parameters, while Qm was the output parameter. In total, 59 data samples were used in the modeling, categorized to training and testing parts. To check the effect of each input parameters on Qm, the different GA-SVR, SVR and linear regression models were constructed based on different combinations of input parameters. Accordingly, eighteen different models (six GA-SVR models, six SVR models and six linear regression models) were developed to predict Qm. After training and testing processes, the performance of the models was evaluated and compared using three common statistical performance metrics, namely R2, RMSE and MAE. According to the obtained results, it was demonstrated that the accuracy of the GA-SVR was higher compared with SVR and linear regression models. In other words, GA-SVR model with R2 of 0.980 can predict Qm better than the SVR and linear regression models with R2 of 0.912 and 0.625, respectively. From the results of this study, it can be concluded that the GA was an excellent optimization algorithm to improve the performance of SVR and has the potential to generalize. As a recommendation, other optimization algorithms such as Flower Pollination Algorithm, Gravitational Search Algorithm, Imperialistic Competitive Algorithm and Locust Swarm Algorithm may be trialed as well to optimize SVR model.