Applications of two numerical methods for solving inverse Benjamin–Bona–Mahony–Burgers equation

Abstract

In this paper, two numerical techniques are presented to solve the nonlinear inverse generalized Benjamin–Bona–Mahony–Burgers equation using noisy data. These two methods are the quartic B-spline and Haar wavelet methods combined with the Tikhonov regularization method. We show that the convergence rate of the proposed methods is $\textit{O}(k^2+h^3)$ and $\textit{O}\left( \frac{1}{M}\right)$ for the quartic B-spline and Haar wavelet method, respectively. In fact, this work considers a comparative study between quartic B-spline and Haar wavelet methods to solve some nonlinear inverse problems. Results show that an excellent estimation of the unknown functions of the nonlinear inverse problem has been obtained.

1 Introduction

Nonlinear phenomena play important roles in applied mathematics, physics and also in engineering problems [1]. As said in [2], many phenomena in engineering and applied sciences are modeled by nonlinear evolution equations, such as: solid-state physics [3], fluid mechanics [4], chemical kinetics [5], plasma physics, population models [6], nonlinear optics and etc. Analytical exact solutions to nonlinear partial differential equation (PDE) play an important role in nonlinear science, especially they may provide us much physical information and more insight into the physical aspects of the problem and may lead to further applications. A variety of powerful methods, such as inverse scattering method [7], exp-function method [8], homotopy perturbation method [9], $(G'/G)$-expansion method [10] were used for obtaining explicit traveling and solitary wave solutions of nonlinear evolutions equation. The knowledge of closed form solutions of the nonlinear partial differential equations facilitates the testing of numerical solvers, aids in the stability analysis of solutions and conduces to a better understanding of nonlinear phenomena that these equations model [11]. But, the research of exact solution for the nonlinear partial differential equations is very difficult. Therefore, numerical methods are useful for solving these equations. The mathematical model of propagation of small amplitude long waves in nonlinear dispersive media is described by the following Benjamin–Bona–Mahony–Burgers equation [12],

$$\begin{aligned}&u_{t}-u_{xxt}-\alpha u_{xx}+\beta u_{x}+uu_{x}=f(x,t),\qquad (x,t)\in [0,L]\times [0,t_f],\nonumber \\&u(0,t)=u(L,t)=0,\qquad t\in [0,t_f],\nonumber \\&u(x,0)=u_0(x),\qquad x\in [0,L], \end{aligned}$$

(1.1)

where $\alpha >0$ and $\beta$ are constants, and f is a given forcing term. In the physical case, the dispersive effect of (1.1) is the same as the Benjamin–Bona–Mahony (BBM) equation, while the dissipative effect is the same as the burger equation, and which is an alternative model for the Korteweg-de Vries-Burger (KdVB) equation [13]. As mentioned in [14], the (BBM) equation is used in the analysis of the surface waves of long wavelength in liquids, hydro-magnetic wave in cold plasma, acoustic-gravity waves in compressible fluids and acoustic waves in harmonic crystals. The Eq. (1.1) is solved using different numerical methods such as numerical methods based on either finite elements [15], finite difference [16], Adomian decomposition scheme [17], cubic B-spline collocation method, [18] and quadratic B-spline finite element method [19].

In this paper, we consider the nonlinear inverse generalized Benjamin–Bona–Mahony–Burger equation to the following form

$$\begin{aligned} u_{t}-u_{xxt}- u_{xx}+ u_{x}+uu_{x}=f(x,t),\,\,\,\, (x,t)\in [0,1]\times [0,t_f], \end{aligned}$$

(1.2)

with initial condition

$$\begin{aligned} u(x,0)=p(x),\,\,\,\,\,x\in [0,1], \end{aligned}$$

(1.3)

boundary conditions

$$\begin{aligned}&u(0,t)=g_1(t),\qquad t\in [0,t_f], \end{aligned}$$

(1.4)

$$\begin{aligned}&u(1,t)=g_2(t),\qquad t\in [0,t_f], \end{aligned}$$

(1.5)

where p(x) and f(x, t) are continuous known functions and $t_f$ represents the final time, while the functions $g_{1}(t)$, $g_{2}(t)$, and u(x, t) are unknown which remain to be determined.

The core of applied mathematical models is made up of partial differential equations [20]. These models can be divided into two general classifications as direct and inverse problems. Today, the literature on both analytical and numerical methods for the solution of direct problems, even for multi-dimensional cases, is well extended. While for the inverse problems, this matter still remains poorly developed. Inverse problems in physics often belong to the class of ill-posed problems. Inverse problems are encountered in many branches of engineering and science. In one particular branch, parabolic initial and boundary value problems in one dimension have been studied by several authors [21,22,23,24,25,26,27,28,29]. Mathematically speaking, in these problems, apart from the both issues of existence and uniqueness of the solution that appear extremely difficult to be shown, there is also the issue of stability to deal with, i.e., the continuous dependence of the solution on input data [30].

The key note in the approximate solution of the inverse problems is the requirement to identify the right-hand side, leading coefficients and parameters and some initial and boundary conditions of time-dependent or stationary equations. On the other hand, since a wide area of the sciences and engineering phenomena is modeled by these problems, the main intent is to draw attention to the use of more applicable and accurate algorithms that make it possible to determine the unknown function using some given observation at accessible parts of the domain of the problem. Producing more accurate methods for inverse problems rests on the development and examination of numerical methods for boundary value problems formulated for basic equations in mathematical physics [20]. On top of that, in the past few decades, a great deal of interest has been directed towards the determination of unknown coefficients which represent physical quantities, for example, the conductivity of a medium, in second-order equations, especially to parabolic equations. As an example for application of inverse problems in modeling the stationary equations, we can point to the process of reconstructing the mass distribution in the problems of potential theory formulated by Laplace equation, if a mass distribution is not known but its potential outside a certain ball is given and the goal is finding this mass distribution [31]. Besides, inverse boundary value problems can be used in modeling the diffusion processes like denoting the concentration of a chemical or temperature in the context of the heat conduction problems [22, 32]. Also for determination of source parameter in the wave equation, we refer the interested reader to [33]. In this paper, we design two numerical methods for solving inverse Benjamin–Bona–Mahony equations of the form (1.2)–(1.5). Collocation method based on a quartic B-spline basis functions and Haar wavelet method.

We know that B-splines have some special features, which are useful in numerical work. One feature is that the continuity conditions are inherent, other special features of B-splines are that they have small local support, i.e., each B-spline function is only non-zero over a few mesh sub-intervals, so that the resulting matrix for the discretization equation is tightly banded. Due to their smoothness and capability to handle local phenomena, B-spline offer distinct advantages. In combination with collocation, this significantly simplifies the solution procedure of differential equations. There is a great reduction of the numerical effort, because there is no need to calculate the integrals (like in variational methods) to form the final set of algebraic equations, which substitutes the given set of nonlinear differential equations. Unlike some previous techniques using various transformations to reduce the equation into simpler equation, the current method does not require extra effort to deal with the nonlinear terms. Therefore, the equations are solved easily and elegantly using the present method. This method also has additional advantages over some rival techniques, such as ease of use and computational cost effectiveness to find solutions of the given nonlinear evolution equations. In the present work, the combination of the quartic B-spline collocation method in space with finite difference in time and the Tikhonov regularization method for solving ill-conditioned system provides an efficient explicit solution with high accuracy and minimal computational effort for the problem represented by (1.2)–(1.5).

Wavelet methods have been applied for solving partial differential equations from beginning of the early 1990s. Among all the wavelet families the Haar wavelets have been given more attention. They are made up of pairs of piecewise constant functions and are therefore mathematically the simplest of all the wavelet families. A good feature of the Haar wavelets is also the possibility to integrate these wavelets analytically in arbitrary times. A drawback of these wavelets is their discontinuity. Hence, the absence of the derivatives in the breaking points makes impossible, the direct usage of these wavelets for solving PDEs. The Haar wavelets are very efficient tools for solving the nonlinear systems in physics, biology, chemical reactions and fluid mechanics [34,35,36,37]. Furthermore, Celik in [38] used the Haar wavelets approximation method based on approximating the truncated double Haar wavelets series to obtain magnetohydrodynamic flow equations in a rectangular duct in presence of transverse external oblique magnetic. Ray [39] used the operational matrix of Haar wavelet method for solving Bagley–Torvik equation. Ray and Patra [40] proposed an efficient numerical method for solving nonlinear damped Van der Pol equation based on the Haar wavelets. In the field of numerical solution of the inverse problems, Pourgholi et al. [41,42,43,44] have used the Haar wavelet method for the solution of a variety of PDEs.

The rest of the paper is organized as follows: in Sect. 2, quartic B-spline collocation scheme is explained and in Subsect. 2.1 and 2.2 the method is applied to solve problem (1.2)–(1.5). The uniform convergence of the method is proved in Subsect. 2.3. The Haar wavelet method for solving the nonlinear inverse problem (1.2)–(1.5), and the convergence analysis of this method is described in Sect. 3. In Sect. 4 numerical experiment is conducted to demonstrate the viability and the efficiency of the proposed methods computationally. A summary is given at the end of the paper in Sect. 5.

2 Quartic B-spline collocation method

In this Section we solve the nonlinear inverse problem (1.2)–(1.5) with the over-specified conditions

$$\begin{aligned}&u(a,t)=h_{1}(t),\qquad t\in [0,t_f], \end{aligned}$$

(2.1)

$$\begin{aligned}&u_x(a,t)=h_{2}(t),\qquad t\in [0,t_f], \end{aligned}$$

(2.2)

$$\begin{aligned}&u_{xx}(a,t)=h_{3}(t), \qquad t\in [0,t_f], \end{aligned}$$

(2.3)

where $0<a<1$ is a fixed point.

The solution domain $x\in [0,1]$ is partitioned into a mesh of uniform length $h=x_{i+1}-x_{i}$ by the knots $x_i$ where $i=0,1,\cdots ,N-1$ such that $\varDelta ={0=x_0<x_1<\cdots <x_N=1}$ be the partition in [0, 1]. B-splines are the unique nonzero splines of smallest compact support with knots at $x_0<x_1<\cdots <x_N$. We define the quartic B-spline $B_i(x)$ for $i=-2,0,\cdots ,N+1$ by the following relation [45]

$$\begin{aligned} B_i(x)= \frac{1}{h^4} {\left\{ \begin{array}{ll} (x-x_{i-2})^4, &{} x\in [x_{i-2},x_{i-1}),\\ (x-x_{i-2})^4-5(x-x_{i-1})^4, &{} x\in [x_{i-1},x_{i}),\\ (x-x_{i-2})^4-5(x-x_{i-1})^4+10(x-x_i)^4, &{} x\in [x_{i},x_{i+1}),\\ (x_{i+3}-x)^4-5(x_{i+2}-x)^4, &{} x\in [x_{i+1},x_{i+2}),\\ (x_{i+3}-x)^4, &{} x\in [x_{i+2},x_{i+3}),\\ 0, &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(2.4)

It can be easily seen that the set of functions $\varGamma =\{B_{-2}(x), B_{-1}(x), B_{0}(x),\cdots , B_{N+1}(x)\}$ is linearly independent on [0, 1], thus $\varTheta =\text {Span}(\varGamma )$ is a subspace of $C^{2}[0,1]$ and $\varTheta$ is $(N+4)$-dimensional. Let us consider $U_m(x,t)\in \varTheta$ is the B-spline approximation to the exact solution u(x, t) in the form

$$\begin{aligned} U_{m}(x,t)=\sum _{i=-2}^{m+1}c_i(t)B_i(x), \end{aligned}$$

(2.5)

where $c_i(t)$ are time-dependent quantities to be determined from the boundary and over-specified conditions and collocation form of the differential equations. The values of $B_i(x)$ and its derivatives may be tabulated as in Table 1.

Table 1 Values of $B_i(x)$ and its derivatives at the nodal points

Using approximate function (2.5) and quartic B-spline (2.4), the approximate values at the knots of U(x) and its derivatives up to third order are determined in terms of the time parameters $c_m$ as

$$\begin{aligned} U_m=&c_{m+1}+11c_m+11c_{m-1}+c_{m-2}, \end{aligned}$$

(2.6)

$$\begin{aligned} U'_m=&(4/h)(c_{m+1}+3c_{m}-3c_{m-1}-c_{m-2}), \end{aligned}$$

(2.7)

$$\begin{aligned} U''_m=&(12/h^2)(c_{m+1}-c_m-c_{m-1}+c_{m-2}), \end{aligned}$$

(2.8)

$$\begin{aligned} U'''_m=&(24/h^3)(c_{m+1}-3c_m+3c_{m-1}-c_{m-2}), \end{aligned}$$

(2.9)

2.1 Temporal discretization

Let us consider a uniform mesh $(x_i,t_n)$ to discretize the region $[0,1]\times [0,t_f]$ where $x_i=ih$, $i=0,1,2,\cdots ,N$ and $t_n=nk$, $n=0,1,\cdots ,$ where h and k are mesh sizes in the space and time directions, respectively.

At first we discretize the problem in time variable using the following finite difference approximation with uniform step size k

$$\begin{aligned} u_{t}^{n}\cong \frac{\delta _t}{k(1-\gamma \delta _t)}u^{n}, \quad n\ge 0, \quad \gamma \ne 1, \end{aligned}$$

(2.10)

where $\delta _{t}u^{n}=u^{n+1}-u^{n}$, $u^n=u(x,t_n)$ and $u^0=u(x,0)=p(x)$. Substituting the above approximation in to Eq. (1.2) and discretizing in time variable we have

$$\begin{aligned} \frac{\delta _t}{k(1-\gamma \delta _t)}u^{n}-\frac{\delta _t}{k(1-\gamma \delta _t)}u_{xx}^{n}=u_{xx}^{n}-u_{x}^{n}-(uu_x)^n+f(x,t_n), \end{aligned}$$

(2.11)

so

$$\begin{aligned} \frac{\delta _t}{k(1-\gamma \delta _t)}\left[ u^{n}-u_{xx}^{n}\right] =u_{xx}^{n}-u_{x}^{n}-(uu_x)^n+f(x,t_n), \end{aligned}$$

(2.12)

thus, we have

$$\begin{aligned}&\left[ u^{n+1}-u^n-u_{xx}^{n+1}+u_{xx}^{n}\right] =k \left[ u_{xx}^n-u_x^n-(uu_x)^n+f(x,t_n)\right] \nonumber \\&\quad -k\gamma \left[ u_{xx}^{n+1}-u_{xx}^n-u_x^{n+1}+u_x^{n}-(uu_x)^{n+1}+(uu_x)^n \right. \nonumber \\&\quad \left. +f(x,t_{n+1})-f(x,t_n)\right] . \end{aligned}$$

(2.13)

To linearized the nonlinear term $(uu_x)^{n+1}$ we use the linearization form given by Rubin and Graves [46]

$$\begin{aligned} (uu_x)^{n+1}=u^{n+1}u_x^n+u^nu_x^{n+1}-(uu_x)^n. \end{aligned}$$

(2.14)

Putting values from Eq. (2.14) in (2.13) we get

$$\begin{aligned}&u^{n+1}-u_{xx}^{n+1}+k\gamma \left[ u_{xx}^{n+1}-u^{n+1}u_x^n-u^nu_x^{n+1}-u_x^{n+1}+f(x,t_{n+1})\right] \nonumber \\&\quad =u^{n}-u_{xx}^n+k \left[ u_{xx}^n-u_x^n-u^nu_x^n+f(x,t_n)\right] \nonumber \\&\qquad -k\gamma \left[ -u_{xx}^n+u_x^n+2u^nu_x^n-f(x,t_n)\right] , \end{aligned}$$

(2.15)

thus

$$\begin{aligned}&\theta _1 u^{n+1}+\theta _2 u_{xx}^{n+1}+\theta _3 u_x^{n+1}= u^n+\theta _4 u_{xx}^n+\theta _5 u_x^n \nonumber \\&\quad +\theta _6 u^{n}u_x^{n}+\theta _7 f(x,t_n)+\theta _8f(x,t_{n+1}), \end{aligned}$$

(2.16)

where

$$\begin{aligned}&\theta _1=1-k\gamma u_x^n, \qquad \theta _2=k\gamma -1, \qquad \theta _3=-k\gamma (u^n+1), \qquad \theta _4=-1+k(1+\gamma ), \\&\theta _5=-k(1+\gamma ), \qquad \theta _6=-k(1+2\gamma ), \qquad \theta _7=k(1+\gamma ), \qquad \theta _8=-k\gamma . \end{aligned}$$

Substituting the approximate solution U for u and putting the values of the nodal values U, its derivatives using Eqs. (2.6)–(2.8) at the knots in Eq. (2.16) yield the following difference equation with the variable c

$$\begin{aligned} A^{*}c_{i-2}^{n+1}+B^{*} c_{i-1}^{n+1}+C^{*} c_{i}^{n+1}+D^{*} c_{i+1}^{n+1}=H(x_i,t_n)+H(x_i,t_{n+1}), \end{aligned}$$

(2.17)

where

$$\begin{aligned} A^{*}=&\theta _1+\left( \frac{12}{h^2}\right) \theta _2-\left( \frac{4}{h}\right) \theta _3, \\ B^{*}=&11\theta _1-\left( \frac{12}{h^2}\right) \theta _2-\left( \dfrac{12}{h}\right) \theta _3,\\ C^{*}=&11\theta _1+\left( \frac{12}{h^2}\right) \theta _2+\left( \frac{12}{h}\right) \theta _3,\\ D^{*}=&\theta _1+\left( \frac{12}{h^2}\right) \theta _2+\left( \frac{4}{h}\right) \theta _3,\\ H(x_i,t_n)=&(c_{i+1}^{n}+11c_{i}^{n}+11c_{i-1}^{n}+c_{i-2}^{n})\\&+\theta _4\left( \frac{12}{h^2}\right) (c_{i+1}^{n}-c_{i}^{n}-c_{i-1}^{n}+c_{i-2}^{n})\nonumber \\&+\theta _5\left( \frac{4}{h}\right) (c_{i+1}^{n}+3c_{i}^{n}-3c_{i-1}^{n}-c_{i-2}^{n})\nonumber \\&+\theta _6\left( \frac{4}{h}\right) (c_{i+1}^{n}+11c_{i}^{n}+11c_{i-1}^{n}+c_{i-2}^{n})(c_{i+1}^{n}+3c_{i}^{n}-3c_{i-1}^{n}-c_{i-2}^{n}) \nonumber \\&+\theta _7 f(x_i,t_n), \qquad 0\le i \le N \\ H(x_i,t_{n+1})=&\theta _8 f(x_i,t_{n+1}), \qquad 0\le i \le N. \end{aligned}$$

The system (2.17) consists of $(N+1)$ linear equations in $(N+4)$ unknowns

$$\begin{aligned}(c_{-2},c_{-1},c_{0},\cdots ,c_N,c_{N+1})^T.\end{aligned}$$

To obtain a unique solution to this system the over-specified conditions (2.1)–(2.3) are required.

Let $a=x_s$, $1\le s \le N-1$, so we have

$$\begin{aligned}&u(x_s,t)=h_{1}(t),\qquad t\in [0,t_f], \end{aligned}$$

(2.18)

$$\begin{aligned}&u_x(x_s,t)=h_{2}(t), \qquad t\in [0,t_f], \end{aligned}$$

(2.19)

$$\begin{aligned}&u_{xx}(x_s,t)=h_{3}(t), \qquad t\in [0,t_f], \end{aligned}$$

(2.20)

expanding u in terms of approximate quartic B-spline formula from (2.6)–(2.8) at $x_s$ putting $m=s$ we get

$$\begin{aligned}&c_{s+1}^{n+1}+11c_{s+2}^{n+1}+11c_{s+3}^{n+1}+c_{s+4}^{n+1}=h_1(t_{n+1}), \end{aligned}$$

(2.21)

$$\begin{aligned}&\left( \frac{4}{h}\right) (c_{s+4}^{n+1}+3c_{s+3}^{n+1}-3c_{s+2}^{n+1}-c_{s+1}^{n+1})=h_2(t_{n+1}), \end{aligned}$$

(2.22)

$$\begin{aligned}&\left( \frac{12}{h^2}\right) (c_{s+4}^{n+1}-c_{s+3}^{n+1}-c_{s+2}^{n+1}+c_{s+1}^{n+1})=h_3(t_{n+1}), \end{aligned}$$

(2.23)

thus, the system (2.17) is changed to a system of $(N+4)$ linear equations in $(N+4)$ unknowns, given by

$$\begin{aligned} AC=D, \end{aligned}$$

(2.24)

where

$$\begin{aligned}&A[1,s+1]=A[1,s+4]=1, \\&A[1,s+2]=A[1,s+3]=11,\\&A[2,s+1]=-A[2,s+4]=-4/h, \\&A[2,s+2]=-A[2,s+3]=-12/h,\\&A[N+4,s+1]=A[N+4,s+4]=12/h^2, \\&A[N+4,s+2]=A[N+4,s+3]=-12/h^2, \end{aligned}$$

thus

$$\begin{aligned} A= & {} \begin{pmatrix} 0 &{} \cdots &{}&{} 1 &{} 11 &{} 11 &{}1 &{}&{} \cdots &{} 0 \\ 0 &{} \cdots &{}&{} -\frac{4}{h} &{} -\frac{12}{h} &{} \frac{12}{h} &{}\frac{4}{h} &{}&{} \cdots &{} 0 \\ A^{*} &{} B^{*} &{} C^{*} &{}D^{*} &{} &{} &{} &{} &{} &{}\vdots \\ &{} A^{*} &{} B^{*} &{} C^{*} &{}D^{*} &{} &{} &{} &{} \\ &{} &{} \cdots &{}\cdots &{}\cdots &{} &{} &{}&{}\\ &{} &{} &{} \cdots &{} \cdots &{} \cdots &{} &{}&{}\\ &{} &{} &{} &{} &{} A^{*} &{} B^{*} &{} C^{*} &{}D^{*} \\ \vdots &{} &{} &{} &{} &{} &{} A^{*} &{} B^{*} &{} C^{*} &{}D^{*} \\ 0 &{} \cdots &{}&{} \frac{12}{h^2} &{} -\frac{12}{h^2} &{} -\frac{12}{h^2} &{}\frac{12}{h^2} &{} &{}\cdots &{} 0 \\ \end{pmatrix},\\ {C}= & {} \begin{pmatrix} {c_{-2}^{(n+1)}}\\ {c_{-1}^{(n+1)}}\\ {c_{0}^{(n+1)}}\\ {c_{1}^{(n+1)}}\\ \vdots \\ {c_{s}^{(n+1)}}\\ \vdots \\ {c_{N-1}^{(n+1)}}\\ {c_{N}^{(n+1)}}\\ {c_{N+1}^{(n+1)}}\\ \end{pmatrix}, \\ D= & {} \begin{pmatrix} {D_{-2}^{(n)}}\\ {D_{-1}^{(n)}}\\ {D_{0}}^{(n)}\\ {D_{1}^{(n)}}\\ \vdots \\ {D_{s}^{(n)}}\\ \vdots \\ {D_{N-1}}^{(n)}\\ {D_{N}}^{(n)}\\ {D_{N+1}}^{(n)}\\ \end{pmatrix},\\&D_{-2}^{(n)}=h_1(t_{n+1})\\&D_{-1}^{(n)}=h_2(t_{n+1}),\\&D_{i}^{(n)}=H(x_i,t_n)+H(x_i,t_{n+1}),\quad 0\le i\le N,\\&D_{N+1}^{(n)}=h_3(t_{n+1}). \end{aligned}$$

A is ill-conditioned matrix, thus we solved this system (2.24) by the Tikhonov regularization method [25].

2.2 The initial state

The initial vector $c^0$ can be obtained from the initial condition (1.3) and over-specified conditions (2.1)–(2.3) as the following expressions

$$\begin{aligned}&u(x_i,t_0)=c_{i+1}^0+11c_{i}^0+11c_{i-1}^0+c_{i-2}^0=p(x_i), \qquad 0\le i \le N,\\&u(x_s,t_0)=c_{s+1}^0+11c_{s}^0+11c_{s-1}^0+c_{s-2}^0=h_1(t_0),\\&u_x(x_s,t_0)=\left( \frac{4}{h}\right) (c_{s+4}^{0}+3c_{s+3}^{0}-3c_{s+2}^{0}-c_{s+1}^{0})=h_2(t_0),\\&u_{xx}(x_s,t_0)=\left( \frac{12}{h^2}\right) (c_{s+4}^{0}-c_{s+3}^{0}-c_{s+2}^{0}+c_{s+1}^{0})=h_3(t_0). \end{aligned}$$

This yields a $(N+4)\times (N+4)$ system of equations, of the form

$$\begin{aligned} \varLambda C^0=\rho , \end{aligned}$$

(2.25)

where

$$\begin{aligned}&\varLambda [1,s+1]= \varLambda [1,s+4]=1, \\&\varLambda [1,s+2]= \varLambda [1,s+3]=11, \\&\varLambda [2,s+1]=- \varLambda [2,s+4]=-4/h, \\&\varLambda [2,s+2]=- \varLambda [2,s+3]=-12/h,\\&\varLambda [N+4,s+1]= \varLambda [N+4,s+4]=12/h^2, \\&\varLambda [N+4,s+2]= \varLambda [N+4,s+3]=-12/h^2, \end{aligned}$$

thus

$$\begin{aligned} \varLambda= & {} \begin{pmatrix} 0 &{} \cdots &{}&{} 1 &{} 11 &{} 11 &{}1 &{}&{} \cdots &{} 0 \\ 0 &{} \cdots &{}&{} -\frac{4}{h} &{} -\frac{12}{h} &{} \frac{12}{h} &{}\frac{4}{h} &{}&{} \cdots &{} 0 \\ 1 &{} 11 &{} 11 &{}1 &{} &{} &{} &{} &{} &{}\vdots \\ &{} 1 &{} 11 &{} 11 &{}1 &{} &{} &{} &{} \\ &{} &{} \cdots &{}\cdots &{}\cdots &{} &{} &{}&{}\\ &{} &{} &{} \cdots &{} \cdots &{} \cdots &{} &{}&{}\\ &{} &{} &{} &{} &{} 1 &{} 11 &{} 11 &{}1 \\ \vdots &{} &{} &{} &{} &{} &{} 1 &{}11 &{} 11 &{}1 \\ 0 &{} \cdots &{}&{} \frac{12}{h^2} &{} -\frac{12}{h^2} &{} -\frac{12}{h^2} &{}\frac{12}{h^2} &{} &{}\cdots &{} 0 \\ \end{pmatrix}, \\ C^0= & {} \begin{pmatrix} {c_{-2}^0}\\ {c_{-1}^0}\\ {c_{0}}^0\\ {c_{1}}^0\\ \vdots \\ {c_{s}}^0\\ \vdots \\ {c_{N-1}}^0\\ {c_{N}}^0\\ {c_{N+1}}^0\\ \end{pmatrix},\\ \rho= & {} \begin{pmatrix} h_1(t_0)\\ h_2(t_0)\\ p(x_{0})\\ p(x_{1})\\ \vdots \\ p(x_{s})\\ \vdots \\ p(x_{N-1})\\ p(x_{N})\\ h_3(t_0)\\ \end{pmatrix}.\end{aligned}$$

The solution of (2.25) can be found by the Tikhonov regularization method.

2.3 Convergence analysis

Let $u(x)=u(x,t_{n+1})$ be the exact solution of the Eq. (1.2) in $t=t_{n+1}$ with the over-specified conditions (2.1)–(2.3) and initial condition (1.3) and also $U(x)=\sum \nolimits _{i=-2}^{N+1}c_iB_i(x)$ be the B-spline collocation approximation to u(x). Due to round off errors in computations we assume that $\widehat{U}(x)$ be the computed spline for U(x) so that $\widehat{U}(x)=\sum \nolimits _{i=-2}^{N+1}\hat{c}_iB_i(x)$ where $\widehat{C}=(\hat{c}_{-2},\hat{c}_{-1},\hat{c}_{0},\hat{c}_{1},\cdots ,\hat{c}_N,\hat{c}_{N+1})$. To estimate the error $\Vert u(x)-U(x)\Vert _{\infty }$ we must estimate the errors $\Vert u(x)-\widehat{U}(x)\Vert _{\infty }$ and $\Vert \widehat{U}(x)-U(x)\Vert _{\infty }$ separately. Following (2.24) for $\widehat{U}$ we have

$$\begin{aligned} A\widehat{C}=\widehat{D}, \end{aligned}$$

(2.26)

where

$$\begin{aligned}\widehat{D}=(h_1(t_{n+1}),h_2(t_{n+1}),\hat{\omega }_{0},\hat{\omega }_{1},\cdots ,\hat{\omega }_{N},h_3(t_{n+1})),\end{aligned}$$

and

$$\begin{aligned} \hat{\omega }_{i}=&(\hat{c}_{i+1}^{n}+11\hat{c}_{i}^{n}+11\hat{c}_{i-1}^{n}+\hat{c}_{i-2}^{n})\\&+\theta _4\left( \frac{12}{h^2}\right) (\hat{c}_{i+1}^{n}-\hat{c}_{i}^{n}-\hat{c}_{i-1}^{n}+\hat{c}_{i-2}^{n})\\&+\theta _5\left( \frac{4}{h}\right) (\hat{c}_{i+1}^{n}+3\hat{c}_{i}^{n}-3\hat{c}_{i-1}^{n}-\hat{c}_{i-2}^{n})\\&+\theta _6\left( \frac{4}{h}\right) (\hat{c}_{i+1}^{n}+11\hat{c}_{i}^{n}+11\hat{c}_{i-1}^{n}+\hat{c}_{i-2}^{n})(\hat{c}_{i+1}^{n}+3\hat{c}_{i}^{n}-3\hat{c}_{i-1}^{n}-\hat{c}_{i-2}^{n})\\&+\theta _7 f(x_i,t_n)+\theta _8 f(x_i,t_{n+1}). \end{aligned}$$

Subtracting (2.26) and (2.24) we have

$$\begin{aligned} A(C-\widehat{C})=(D-\widehat{D}), \end{aligned}$$

(2.27)

first we need to recall a Theorem.

Theorem 2.1

Suppose that $f(x)\in C^{5}[0,1]$and $|f^{5}(x)|\le L$, $\forall \, x\in [0,1]$and $\varDelta =\{0=x_{0}<x_{1}<\cdots <x_{N}=1\}$is the equality spaced partition of [0, 1] with step size h. If $S_{\varDelta }(x)$is the unique spline function interpolate f(x) at nodes $x_{0},x_{1},\cdots ,x_{N}\in \varDelta$, then there exist a constant $\lambda _{j}\le 2$such that $\forall x\in [0,1]$,

$$\begin{aligned} \Vert f^{j}(x)-S_{\varDelta }^{j}(x)\Vert \le \lambda _{j}Lh^{5-j},\,\,\,j=0,1,2,3,4, \end{aligned}$$

(2.28)

where $\Vert .\Vert$represents the $\infty$-norm.

Proof

For the proof see [47]. $\square$

Now, we want to find a bound on $\Vert D-\widehat{D}\Vert _{\infty }$ first. We have

$$\begin{aligned} |D(x_i)-\widehat{D}(x_{i})|= & {} \left| \omega \left( x_i,U(x_i), {U^{\prime }(x_i)},{U^{\prime \prime }}(x_i) \right) \right. \\&\left. -\omega \left( x_i,\widehat{U}(x_i),{\widehat{U}}^{\prime }(x_i), {\widehat{U}}^{\prime \prime }(x_i)\right) \right| , \end{aligned}$$

by following theorem (2.1) and [48] (page 218) we obtain

$$\begin{aligned} \Vert D-\widehat{D}\Vert _{\infty }&\le M \left( |U(x)-\widehat{U}(x)|+|U^{\prime }(x)-{\widehat{U}}^{\prime }(x)| +|U^{\prime \prime }(x)-{\widehat{U}}^{\prime \prime }(x)| \right) \nonumber \\&\le ML\lambda _{0}h^{5}+ML\lambda _{1}h^{4}+L\lambda _{2}h^{3}, \end{aligned}$$

(2.29)

where $\Vert \omega ^{\prime \prime }(z)\Vert _{\infty }\le M$. Thus we can rewrite (2.29) as follows

$$\begin{aligned} \Vert D-\widehat{D}\Vert _{\infty }\le M_{1}h^{3}, \end{aligned}$$

(2.30)

where $M_{1}=ML(\lambda _{0}h^{2}+\lambda _{1}h+\lambda _{2})$. The matrix A in (2.27) is an ill-conditioned matrix, thus by Tikhonov regularization solution [25], we have

$$\begin{aligned} (C-\widehat{C})=[A^{T}A+\alpha (R^{(2)})^{T}R^{2}]^{-1}A^{T}(D-\widehat{D}), \end{aligned}$$

(2.31)

taking the infinity norm and then using (2.30) we find

$$\begin{aligned} \Vert C-\widehat{C}\Vert _{\infty }\le \Vert [A^{T}A+\alpha (R^{(2)})^{T}R^{2}]^{-1}A^{T}\Vert _{\infty }\Vert D-\widehat{D}\Vert _{\infty }\le M_{2}h^{3}, \end{aligned}$$

(2.32)

where $M_{2}=M_{1} \Vert [A^{T}A+\alpha (R^{(2)})^{T}R^{2}]^{-1}A^{T}\Vert _{\infty }$. Now, we will be able to prove the convergence of our present method. Therefore, we recall a following lemma first

Lemma 2.1

The B-splines $\{B_{-2},B_{-1},B_{0},\cdots ,B_{N+1}\}$ satisfy the following inequality

$$\begin{aligned} \left| \sum _{i=-2}^{N+1}B_i(x)\right| \le 35, \quad (0\le x\le 1). \end{aligned}$$

(2.33)

Proof

We know that

$$\begin{aligned} \left| \sum _{i=-2}^{N+1}B_i(x)\right| \le \sum _{i=-2}^{N+1}|B_i(x)|,\quad (0\le x\le 1). \end{aligned}$$

(2.34)

At any node $x_i$, we have

$$\begin{aligned} \sum _{i=-2}^{N+1}|B_i|=|B_{i-2}|+|B_{i-1}|+|B_{i}|+|B_{i+1}|=24<35, \end{aligned}$$

(2.35)

also, we have

$$\begin{aligned} |B_{i-2}(x)|\le 11,\quad |B_{i-1}(x)|\le 11, \quad |B_{i}(x)|\le 11, \quad x_{i-1}\le x \le x_i, \end{aligned}$$

(2.36)

similarly,

$$\begin{aligned} |B_{i-3}(x)|\le 1,\quad |B_{i+1}(x)|\le 1, \quad x_{i-1}\le x \le x_i. \end{aligned}$$

(2.37)

Now for point $x_{i-1}\le x \le x_i$, we have

$$\begin{aligned} \sum _{i=-2}^{N+1}|B_i(x)|=|B_{i-3}|+|B_{i-2}|+|B_{i-1}|+|B_{i}|+|B_{i+1}|\le 35. \end{aligned}$$

(2.38)

Hence, this proves the lemma. $\square$

Now, observe that we have

$$\begin{aligned}U(x)-\widehat{U}(x)=\sum _{i=-2}^{N+1}(c_{i}-\hat{c}_{i})B_i(x),\end{aligned}$$

thus taking the infinity norm and using (2.32) and (2.33) we get

$$\begin{aligned} \Vert U(x)-\widehat{U}(x)\Vert _{\infty }= & {} \left\| \sum _{i=-2}^{N+1} (c_{i}-\hat{c}_{i})B_i(x)\right\| _{\infty } \nonumber \\\le & {} \Vert (c_{i}-\hat{c}_{i})\Vert _{\infty } \left| \sum _{i=-2}^{N+1}B_i(x)\right| \le 35M_{2}h^{3}, \end{aligned}$$

(2.39)

Theorem 2.2

Let u(x) be the exact solution of the equation (1.2) with the over-specified conditions (2.1)–(2.3) and initial condition (1.3) and also U(x) be the B-spline collocation approximation to u(x) then the method has second order convergence

$$\begin{aligned}\Vert u(x)-U(x)\Vert \le \varOmega h^3,\end{aligned}$$

where $\varOmega =\lambda _{0}L h^{2}+35M_{2}$is some finite constant.

Proof

From theorem (2.1) we have

$$\begin{aligned} \Vert u(x)-\widehat{U}(x)\Vert \le \lambda _{0}L h^{5}, \end{aligned}$$

(2.40)

thus substituting from (2.39) and (2.40) we have

$$\begin{aligned} \Vert u(x)-U(x)\Vert \le \Vert u(x)-\widehat{U}(x)\Vert +\Vert \widehat{U}(x)-U(x)\Vert \le \lambda _{0}L h^{5}+35M_{2}h^{3}=\varOmega h^3, \end{aligned}$$

(2.41)

where $\varOmega =\lambda _{0}L h^{2}+35M_{2}$. $\square$

Theorem 2.3

The time discretization process (2.10) that we use to discretize equation (1.2) in time variable is of the two order convergence.

Proof

See [49]. $\square$

We suppose that u(x, t) is the solution of Eq. (1.1) and U(x, t) be the approximate solution by our present method then we have

$$\begin{aligned}\Vert u(x,t_n)-U(x,t_n)\Vert \le \rho (k^2+h^3),\end{aligned}$$

($\rho$ is some finite constant), thus the order of convergence of our process is $\textit{O}(k^2+h^3)$.

3 Haar wavelet method

The aim of this Section is to describe a new modification of the Haar wavelet method for solving the nonlinear inverse problem (1.2)–(1.5) with the over-specified conditions

$$\begin{aligned}&u(a,t)=h_{1}(t),\qquad t\in [0,t_f], \end{aligned}$$

(3.1)

$$\begin{aligned}&u_x(a,t)=h_{2}(t), \qquad t\in [0,t_f], \end{aligned}$$

(3.2)

where $0<a<1$ is a fixed point.

3.1 Function approximation

It is known that any integrable function $u(x) \in L^2([0,1))$ can be expanded by the Haar series with an infinite number of terms [41],

$$\begin{aligned}&u(x)=\sum _{i=1}^{\infty }c_{i}h_i(x),\qquad c_i=2^j \int _{0}^{1} u(x) h_{i}(x) \,dx, \\&\quad i=2^{j}+k+1,\,\,\,j\ge 0,\,\,\, 0\le k <2^{j}. \end{aligned}$$

Specially $c_1=\int _{0}^{1} u(x)\,dx$. So

$$\begin{aligned} u(x)=c_1h_1(x)+\sum _{j=0}^{\infty }\sum _{k=0}^{2^j-1}c_{2^{j}+k+1}h_{2^{j}+k+1}(x). \end{aligned}$$

If u(x) is piecewise constant function or can be approximated as piecewise constant functions during each subinterval, then u(x) will be terminated at finite term, which we show it with $u_J(x)$ as follows:

$$\begin{aligned} u_J(x)\cong c_1h_1(x)+\sum _{j=0}^{J}\sum _{k=0}^{2^j-1}c_{2^{j}+k+1}h_{2^{j}+k+1}(x)=C_{M}^TH_{M}(x), \end{aligned}$$

(3.3)

where the coefficient $C_{M}^T$ and the Haar function vectors $H_{M}(x)$ are defined as

$$\begin{aligned}C_{M}^T=\left( c_{1},c_{2},\cdots ,c_{M} \right) ,\qquad \qquad H_{M}(x)= \left( h_1(x),h_2(x),\cdots ,h_{M}(x) \right) ^T.\end{aligned}$$

3.2 Convergence analysis of the Haar wavelet method

In this part, we present the error analysis for our proposed scheme. To analyze the convergence of our method, we assume that $u_J(x)$ is approximation solution of u(x). The corresponding error at J-th level of u(x) is defined as

$$\begin{aligned}e^u_J(x)=u(x)-u_J(x).\end{aligned}$$

So we have

$$\begin{aligned} e^u_J(x)=\sum _{j=J+1}^{\infty } \sum _{k=0}^{2^j-1}c_{2^{j}+k+1}h_{2^{j}+k+1}(x), \end{aligned}$$

Now, we state and prove the following convergence theorem.

Theorem 3.1

Suppose that u(x) satisfies the Lipschitz condition on [0, 1],  that is,

$$\begin{aligned} \exists \, \kappa >0,\,\forall \,x_1,x_2 \in [0,1]\,:\,|u(x_1)-u(x_2)|\le \kappa |x_1-x_2|. \end{aligned}$$

(3.4)

Then the error bound for $\Vert {e^u_J}\Vert _{2}$is obtained as

$$\begin{aligned}\Vert {e^u_J}\Vert _{2} \le \sqrt{\frac{1}{3}}\frac{\kappa }{M}.\end{aligned}$$

Also, the Haar wavelet method will converge in the sense that $e^u_J(x)$goes to zero as M goes to infinity. Moreover, the convergence is of order one, that is,

$$\begin{aligned}\Vert {e^u_J}\Vert _{2}=\textit{O}\left( \frac{1}{M}\right) .\end{aligned}$$

Proof

We compute $\Vert {e^u_J}\Vert _{2}^{2}$ as the following:

$$\begin{aligned} \Vert {e^u_J}\Vert _{2}^{2}=&\int _{0}^{1} \left( \sum _{j=J+1}^{\infty } \sum _{k=0}^{2^j-1}c_{2^{j}+k+1}h_{2^{j}+k+1}(x) \right) ^2 \mathrm{d}x \\ =&\int _{0}^{1}\left( \sum _{j=J+1}^{\infty } \sum _{k=0}^{2^j-1}c_{2^{j}+k+1}h_{2^{j}+k+1}(x)\right) \\&\times \left( \sum _{l=J+1}^{\infty } \sum _{q=0}^{2^l-1}c_{2^l+q+1}h_{2^l+q+1}(x)\right) \mathrm{d}x \\ =&\sum _{j=J+1}^{\infty }\sum _{k=0}^{2^j-1}\sum _{l=J+1}^{\infty } \sum _{q=0}^{2^l-1}c_{2^j+k+1}c_{2^l+q+1}\\&\times \left( \int _{0}^{1}h_{2^j+k+1}(x)h_{2^l+q+1}(x) \mathrm{d}x\right) . \end{aligned}$$

For as much as,

$$\begin{aligned} \int _{0}^{1}h_{i_1}(x)h_{i_2}(x)\,\mathrm{d}x={\left\{ \begin{array}{ll} 2^{-j},&{} i_1=i_2,\\ 0,&{} i_1 \ne i_2, \end{array}\right. } \end{aligned}$$

we have

$$\begin{aligned}\Vert {e^u_J}\Vert _{2}^{2}=\sum _{j=J+1}^{\infty }\sum _{k=0}^{2^j-1}\frac{1}{2^j}\,c^{2}_{2^j+k+1}.\end{aligned}$$

Since $c_{2^j+k+1}=2^j\int _{0}^{1}u(x)h_{2^j+k+1}(x) \mathrm{d}x$, according to the Haar wavelet functions,

$$\begin{aligned} h_i(x)= {\left\{ \begin{array}{ll} 1, &{} x\in [\frac{k}{m},\frac{k+0.5}{m}),\\ -1, &{} x\in [\frac{k+0.5}{m},\frac{k+1}{m}),\\ 0, &{}\text {elsewhere}, \end{array}\right. } \end{aligned}$$

we can write

$$\begin{aligned}c_{2^j+k+1}=2^j \left( \int _{\frac{k}{2^j}}^{\frac{k+0.5}{2^j}}u(x) \mathrm{d}x-\int _{\frac{k+0.5}{2^j}}^{\frac{k+1}{2^j}}u(x) \mathrm{d}x \right) .\end{aligned}$$

Now, using the mean value theorem for integral, we can conclude

$$\begin{aligned}\exists \,x_1 \in \left[ \frac{k}{2^j},\frac{k+0.5}{2^j}\right] , \,\,\,\,x_2 \in \left[ \frac{k+0.5}{2^j},\frac{k+1}{2^j}\right] , \end{aligned}$$

such that

$$\begin{aligned}\int _{\frac{k}{2^j}}^{\frac{k+0.5}{2^j}}u(x) \mathrm{d}x=\frac{1}{2^{j+1}}u(x_1),\qquad \int _{\frac{k+0.5}{2^j}}^{\frac{k+1}{2^j}}u(x)\mathrm{d}x=\frac{1}{2^{j+1}}u(x_2).\end{aligned}$$

Thus, we can compute $c_{2^j+k+1}$ as follows:

$$\begin{aligned} c_{2^j+k+1}&=2^j\left( \frac{1}{2^{j+1}}u(x_1)-\frac{1}{2^{j+1}}u(x_2)\right) \\&=\frac{1}{2}\left( u(x_1)-u(x_2)\right) \\&\le \frac{\kappa }{2} \left( x_1-x_2 \right) \\&\le \frac{\kappa }{2^{j+1}}. \end{aligned}$$

The first inequality is obtained with regard to relation (3.4). On the other hand, we have

$$\begin{aligned} \Vert {e^u_J}\Vert _{2}^{2}&=\sum _{j=J+1}^{\infty }\sum _{k=0}^{2^j-1}\frac{1}{2^j}\,c^{2}_{2^j+k+1}\\&\le \sum _{j=J+1}^{\infty }\sum _{k=0}^{2^j-1}\frac{1}{2^j} \,\frac{\kappa ^2}{2^{2j+2}}\\&=\frac{\kappa ^2}{4} \sum _{j=J+1}^{\infty }4^{-j}=\frac{\kappa ^2}{3}4^{-J-1}. \end{aligned}$$

Since $M=2^{J+1}$, we obtain

$$\begin{aligned}\Vert {e^u_J}\Vert _{2}^{2} \le \frac{\kappa ^2}{3}M^{-2}.\end{aligned}$$

Therefore, the error bound can be expressed as

$$\begin{aligned}\Vert {e^u_J}\Vert _{2} \le \sqrt{\frac{1}{3}}\frac{\kappa }{M}.\end{aligned}$$

So, the Haar wavelet method will be convergent, i.e.,

$$\begin{aligned}\lim _{J\rightarrow \infty }e^u_J(x)=0.\end{aligned}$$

Moreover, the convergence is of order one, that is,

$$\begin{aligned}\Vert {e^u_J}\Vert _{2}=\textit{O}\left( \frac{1}{M}\right) ,\end{aligned}$$

and the proof is complete. $\square$

3.3 Overview of the method

In this part, we first present our method based on the Haar wavelet method for solving the nonlinear inverse problem (1.2)–(3.2). Now, Let us divide the interval $[0,t_f]$ into N equal parts of length $\varDelta t=\frac{t_f}{N}$ and denote $t_s=(s-1)\varDelta t$, $s=1,2,\cdots ,N-1$. We assume that $\dot{u}''$ can be expanded in terms of Haar wavelets as,

$$\begin{aligned} \dot{u}''(x,t)\cong c^s_1h_1(x)+\sum _{j=0}^{J}\sum _{k=0}^{2^j-1}c^s_{2^{j}+k+1}h_{2^{j}+k+1}(x)=C_{M}^TH_{M}(x), \end{aligned}$$

(3.5)

where . and $'$ mean differentiation with respect to t and x, respectively. Integrating Eq. (3.5) one time with respect to t from $t_s$ to t, twice with respect to x from a to x, and using the over-specified conditions (3.1) and (3.2), we obtain

$$\begin{aligned} u''(x,t)=&(t-t_s)C^T_MH_M(x)+u''(x,t_s), \end{aligned}$$

(3.6)

$$\begin{aligned} u'(x,t)=&(t-t_s)C^T_M \left[ P_MH_M(x)-P_MH_M(a)\right] \nonumber \\&+u'(x,t_s)+h_2(t)-h_2(t_s), \end{aligned}$$

(3.7)

$$\begin{aligned} u(x,t)=&(t-t_s)C^T_M \left[ Q_MH_M(x)-Q_MH_M(a)-(x-a)P_MH_M(a)\right] +u(x,t_s)\nonumber \\&+ \left[ h_1(t)-h_1(t_s) \right] +(x-a) \left[ h_2(t)-h_2(t_s) \right] . \end{aligned}$$

(3.8)

Now, individual differentiation of Eq. (3.8), one time with respect to t, yield

$$\begin{aligned} \dot{u}(x,t)=&C^T_M \left[ Q_MH_M(x)-Q_MH_M(a)-(x-a)P_MH_M(a) \right] \nonumber \\&+h'_1(t)+(x-a)h'_2(t), \end{aligned}$$

(3.9)

where H, P, and Q are obtained from [41]. With discretizing the results by assuming $x\rightarrow x_l$, $t\rightarrow t_{s+1}$ and using notation $T=t_{s+1}-t_s$, Eqs. (3.5)–(3.9) are changed as follows,

$$\begin{aligned} \dot{u}''(x_l,t_{s+1})=&C_{M}^TH_{M}(x_l), \end{aligned}$$

(3.10)

$$\begin{aligned} u''(x_l,t_{s+1})=&TC^T_MH_M(x_l)+u''(x_l,t_s), \end{aligned}$$

(3.11)

$$\begin{aligned} u'(x_l,t_{s+1})=&TC^T_M \left[ P_MH_M(x_l)-P_MH_M(a) \right] \nonumber \\&+u'(x_l,t_s)+h_2(t_{s+1})-h_2(t_s), \end{aligned}$$

(3.12)

$$\begin{aligned} u(x_l,t_{s+1})=&TC^T_M \left[ Q_MH_M(x_l)-Q_MH_M(a)-(x_l-a)P_MH_M(a) \right] +u(x_l,t_s)\nonumber \\&+ \left[ h_1(t_{s+1})-h_1(t_s) \right] \nonumber \\&+(x_l-a) \left[ h_2(t_{s+1})-h_2(t_s) \right] , \end{aligned}$$

(3.13)

$$\begin{aligned} \dot{u}(x_l,t_{s+1})=&C^T_M \left[ Q_MH_M(x_l)-Q_MH_M(a)-(x_l-a)P_MH_M(a)\right] \nonumber \\&+h'_1(t_{s+1})+(x_l-a)h'_2(t_{s+1}). \end{aligned}$$

(3.14)

In the following scheme

$$\begin{aligned}&\dot{u}(x_l,t_{s+1})-\dot{u}''(x_l,t_{s+1})-u''(x_l,t_{s+1})\nonumber \\&\quad +u'(x_l,t_{s+1})+u(x_l,t_{s+1})u'(x_l,t_{s+1})=f(x_l,t_{s+1}). \end{aligned}$$

(3.15)

To linearize the nonlinear term $u(x_l,t_{s+1})u'(x_l,t_{s+1})$ we use the linearization form given by Rubin and Graves [46],

$$\begin{aligned} u(x_l,t_{s+1})u'(x_l,t_{s+1})=&u(x_l,t_{s+1})u'(x_l,t_{s})\nonumber \\&+u(x_l,t_{s})u'(x_l,t_{s+1})-u(x_l,t_{s})u'(x_l,t_{s}). \end{aligned}$$

(3.16)

By putting (3.16) in Eq. (3.15) we have,

$$\begin{aligned}&\dot{u}(x_l,t_{s+1})-\dot{u}''(x_l,t_{s+1})-u''(x_l,t_{s+1}) + \left( 1+u(x_l,t_{s})\right) u'(x_l,t_{s+1})\nonumber \\&\quad +u(x_l,t_{s+1})u'(x_l,t_{s})=f(x_l,t_{s+1}) +u(x_l,t_{s})u'(x_l,t_{s}). \end{aligned}$$

(3.17)

Substituting Eqs. (3.10)–(3.14) into Eq. (3.17), we obtain

$$\begin{aligned}&C^T_M \left[ \left[ 1+Tu'(x_l,t_s) \right] \left[ Q_MH_M(x_l)-Q_MH_M(a)-(x_l-a)P_MH_M(a)\right] \right. \nonumber \\&\quad - (1+T)H_M(x_l)\nonumber \\&\quad \left. +T \left[ 1+u(x_l,t_s) \right] \left[ P_MH_M(x_l)-P_MH_M(a)\right] \right] = f(x_l,t_{s+1})\nonumber \\&\quad - \left[ h'_1(t_{s+1})+(x_l-a)h'_2(t_{s+1})\right] +u''(x_l,t_s)\nonumber \\&\quad - \left[ 1+u(x_l,t_s)\right] \left[ u'(x_l,t_s)+h_2(t_{s+1}) -h_2(t_s) \right] \nonumber \\&\quad -u'(x_l,t_s) \left[ h_1(t_{s+1})-h_1(t_s)+(x_l-a) \left[ h_2(t_{s+1})-h_2(t_s)\right] \right] \end{aligned}$$

(3.18)

From the Eq. (3.18), a system of M linear equations in the M unknown coefficients is obtained. This system can be written in the matrix vector form as follows

$$\begin{aligned} AX=B. \end{aligned}$$

(3.19)

To solve the system of linear equation (3.19) and calculated the wavelet coefficients $C^T_M$, we use the Tikhonov regularization method [25]. Finally, putting the calculated wavelet coefficients into the Eq. (3.13), we can successively calculate the approximate solutions for $l=1,2,\cdots ,M$ and $s=1,2,\cdots ,N$, as follows:

$$\begin{aligned} u(0,t_{s+1})=&g_1(t_{s+1})=TC^T_M \left[ aP_MH_M(a)-Q_MH_M(a)\right] \\&+u(0,t_s)+ \left[ h_1(t_{s+1})-h_1(t_s) \right] -a \left[ h_2(t_{s+1})-h_2(t_s)\right] ,\\ u(1,t_{s+1})=&g_2(t_{s+1})=TC^T_M \left[ Q_MH_M(1)-Q_MH_M(a)-(1-a)P_MH_M(a)\right] \\&+u(1,t_s)\\&+ \left[ h_1(t_{s+1})-h_1(t_s)\right] +(1-a) \left[ h_2(t_{s+1})-h_2(t_s) \right] ,\\ u(x_l,t_{s+1})=&TC^T_M \left[ Q_MH_M(x_l)-Q_MH_M(a)-(x_l-a)P_MH_M(a)\right] \\&+u(x_l,t_s) \\&+ \left[ h_1(t_{s+1})-h_1(t_s)\right] \\&+(x_l-a) \left[ h_2(t_{s+1})-h_2(t_s)\right] . \end{aligned}$$

4 Numerical illustrations

In this Section, the quartic B-spline collocation and Haar wavelet method are employed to obtain the numerical solutions for unknown boundary conditions in the problem (1.2)–(1.5). Numerical example is discussed in this Section to demonstrate the accuracy of the presented methods described in Sects. 2 and 3 for solving the nonlinear inverse problem (1.2)–(1.5) and these numerical results are compared with together.

In an inverse problem, there are two sources of error in the estimation. The first source is the unavoidable bias deviation (deterministic error) and the second one is the variance due to the amplification of measurement errors (stochastic error). The global effect of deterministic and stochastic errors is considered in the mean squared error or the total error [50]. Therefore, we compare the exact and the approximate solutions by considering the total error S defined by

$$\begin{aligned}&S_{g_1}= \left[ \frac{1}{N-1}\sum ^{N}_{s=1} \left( g_1(t_{s+1})-g_1^*(t_{s+1}) \right) ^{2} \right] ^{\frac{1}{2}}, \\&S_{g_2}= \left[ \frac{1}{N-1}\sum ^{N}_{s=1}\left( g_2(t_{s+1})-g_2^*(t_{s+1}) \right) ^{2} \right] ^{\frac{1}{2}}, \end{aligned}$$

where N is the number of estimated values, $g_1$ and $g_2$ are the exact values, $g_1^*$ and $g_2^*$ are the estimated values.

To illustrate the performance of the methods and justify the accuracy and efficiency of the proposed methods, we also offer the infinity-norm of absolute error for $0\le x \le 1$ and $0\le t \le t_f$.

$$\begin{aligned}&L_{\infty }^{g_1}=||g_1(t) -g_1^*(t)||_{\infty }=\max |g_1(t) -g_1^*(t)|,\\&L_{\infty }^{g_2}=||g_2(t) -g_2^*(t)||_{\infty }=\max |g_2(t) -g_2^*(t)|, \end{aligned}$$

also,

$$\begin{aligned}&L_{\infty }^{u}=||u(x,t) -u^*(x,t)||_{\infty }=\max |u(x,t)-u^*(x,t)|, \end{aligned}$$

where, $u^*(x,t)$ is the estimated value of u(x, t).

In the following numerical example, we take $a=0.2$, $t_f=1$, $\varDelta t=0.01$, and the noisy data (input data+0.001$\times$rand(1)).

Example 4.1

In this example, we solve the nonlinear inverse problem (1.2)-(1.5) satisfying,

$$\begin{aligned}u_{t}-u_{xxt}- u_{xx}+ u_{x}+uu_{x}=f(x,t),\end{aligned}$$

with given data

$$\begin{aligned}&u(x,0)=sech(x), \\&f(x,t)=\frac{2\cosh (x-t) + 5\sinh (x-t) -\sinh (x-t)\cosh (x-t)- \cosh ^3(x-t) - \sinh ^3(x-t)}{\cosh ^4(x-t)}. \end{aligned}$$

The exact solutions of this problem are,

$$\begin{aligned}&u(x,t)=sech(x-t),\qquad 0\le x \le 1, \,\, 0\le t \le 1,\\&u(0,t)=g_1(t)=sech(-t), \qquad 0\le t \le 1,\\&u(1,t)=g_2(t)=sech(1-t), \qquad 0\le t \le 1. \end{aligned}$$

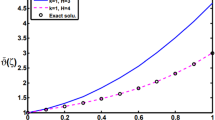
The numerical results of the unknown boundary conditions u(0, t) and u(1, t) are reported in Tables 2 and 3, respectively. To clarify the accuracy of the present method, the corresponding graphical illustration are presented in Figures 1 and 2. The obtained numerical solutions for u(x, t) at point $x=0.1$ is given in Table 4. Also, the graphical illustration of the comparison between exact and numerical solutions u(x, t) are presented in Figures 3 and 4.

Table 2 The comparison between exact and numerical solutions for $g_{1}(t)$ using the quartic B-spline collocation and Haar wavelet method in Example 4.1, when $N=100$ and $M=32$, respectively

Table 3 The comparison between exact and numerical solutions for $g_{2}(t)$ using the quartic B-spline collocation and Haar wavelet method in Example 4.1, when $N=100$ and $M=32$, respectively

Fig. 1

The comparison between the exact and numerical solutions (using quartic B-spline method) of (a) u(0, t) and (b) u(1, t) for Example 4.1

Fig. 2

The comparison between the exact and numerical solutions (using Haar wavelet method) of (a) u(0, t) and (b) u(1, t) for Example 4.1

Table 4 The comparison between exact and numerical solutions for u(0.1, t) using the quartic B-spline collocation and Haar wavelet method in Example 4.1, when $N=100$ and $M=32$, respectively

Fig. 3

Plot of variation u(x, t) (using quartic B-spline method) when $N=100$ in Example 4.1

Fig. 4

Plot of variation u(x, t) (using Haar wavelet method) at collocation points $x_l$ when $M=32$ in Example 4.1

5 Conclusion

The quartic B-spline and Haar wavelet method have been employed to estimate unknown boundary conditions were proposed for the nonlinear inverse generalized Benjamin–Bona–Mahony–Burgers Eqs. (1.2)–(1.5). Since in both methods, the coefficients matrix is usually ill-conditioned, hence to regularize the resultant ill-conditioned linear system of equations, we have applied the Tikhonov regularization method to obtain a stable numerical approximation to the solution. The convergence rate of the proposed methods have been discussed and shown that it is $\textit{O}(k^2+h^3)$ and $\textit{O}\left( \frac{1}{M}\right)$ for the quartic B-spline and Haar wavelet method, respectively. Numerical comparisons have been made between the implementations of the quartic B-spline and Haar wavelet method. The numerical results showed that the quartic B-spline has the best performance. More precisely, it is the most accurate, stable and fastest in comparison with Haar wavelet method. Generally, the obtained numerical solutions by the presented methods are in excellent agreement with the exact solutions. The strong point of the quartic B-spline method is its easy and simple computation with low-storage space and cost. These results are obtained in the MATLAB 7.10 (R2010a) and is tested on a personal computer with intel(R) core(TM)2 Duo CPU and 4GB RAM.