Nested strong orthogonal arrays

Abstract

Nested space-filling designs are popular for conducting multiple computer experiments with different levels of accuracy. Strong orthogonal arrays (SOAs) are a special type of space-filling designs which possess attractive low-dimensional stratifications. Combining these two kinds of designs, we propose a new type of design called a nested strong orthogonal array. Such a design is a special nested space-filling design that consists of two layers, i.e., the large SOA and the small SOA, where they enjoy different strengths, and the small one is nested in the large one. The proposed construction method is easy to use, capable of accommodating a larger number of columns, and the resulting designs possess better stratifications than the existing nested space-filling designs in two dimensions. The construction method is based on regular second order saturated designs and nonregular designs. Some comparisons with the existing nested space-filling designs are given to show the usefulness of the proposed designs.

1 Introduction

Computer experiments with different levels of accuracy are prevalent in many business, engineering and scientific applications. To solve this issue, there are various nested designs used in multifidelity computer experiments. Qian (2009) proposed an approach to constructing nested Latin hypercube designs. Additionally, several classes of nested Latin hypercube designs with exact or near orthogonality have been proposed, such as those by Li and Qian (2013); Yang et al. (2014) and Yang et al. (2016). Besides preserving the univariate stratification properties of Latin hypercube designs, designs with multi-dimensional stratification properties are more desirable for computer experiments. Motivated by orthogonal array (OA)-based Latin hypercube designs in Tang (1993); Qian et al. (2009) proposed nested space-filling designs. With the help of nested orthogonal arrays (NOAs) and nested difference matrices in which a subarray in rows is also a difference matrix after level-collapsing, Qian et al. (2009) constructed nested space-filling designs with two layers. Sun et al. (2014) constructed space-filling designs with more than two layers based on group projection which is a decomposition of Galois fields. The nested designs mentioned above are all symmetric, Qian et al. (2014) proposed asymmetric nested lattice samples by randomizing asymmetric NOAs where different axes are divided at different scales of fineness.

Complex mathematical models encoded in computer programs are extensively utilized to study real-world systems. Conducting equivalent physical experiments would require more time and be more expensive. Since a large computer program at various levels of sophistication often leads to significantly different computational times. In practice, it has been widely used to conduct multiple experiments with varying degrees of accuracy or fidelity. For example, one code employs finite element analysis, while the other relies on the finite difference method. Finite element analysis and finite difference method are both numerical techniques used for solving differential equations; see (Reddy 2019) for details. Finite element analysis approximates the solution as a finite sum of functions defined on the discretized space. Finite difference method discretizes space and seeks values of the solution function at mesh points. These two codes vary in their numerical approaches and grid resolutions, leading to one accurate but slow version and another rougher but quicker version. For simplicity of presentation, Qian et al. (2009) refers to these experiments as the high-accuracy experiment and the low-accuracy experiment, respectively. The corresponding designs are described as nested space-filling designs for running computer codes with two levels of accuracy. A pair of nested space-filling designs, $H_{2}\subset H_{1}$, consists of two designs where the smaller design is employed for the more accurate yet more expensive code, and the larger design is used for the less accurate but less expensive code. It is guided by three principles:

Economy::

the number of points in $H_{2}$ is smaller than the number of points in $H_{1}$;

Nested relationship::

$H_{2}$ is nested within $H_{1}$, that is, $H_{2}\subset H_{1}$;

Space-filling::

both $H_{2}$ and $H_{1}$ achieve uniformity in low dimensions.

The aim of this article is to propose and develop appropriate designs for this context.

He and Tang (2013) introduced the SOAs for computer designs. They pointed out that Latin hypercube designs based on SOAs of strength t are more space-filling than comparable OA-based Latin hypercube designs in all g dimensions for any $2 \le g \le t-1$. He and Tang (2014) characterized the SOAs of strength 3. Shi and Tang (2020) constructed strength-three SOAs that enjoy some of the stratifications of strength-four SOAs. To address the problem where the SOAs of strength 3 require large run sizes, He et al. (2018) proposed the SOAs of strength $2+$ which still retain the two-dimensional stratifications of the former, but make the run sizes more economical. Zhou and Tang (2019) considered the column-orthogonal SOAs of strength $2+$ and $3-$. The main difference between the SOAs of strength 3 and $3-$ lies in the number of levels, i.e., the former has $s^3$ levels, while the latter has $s^2$ levels. To increase the number of levels in SOAs of strength $2+$, Li et al. (2022) proposed the SOAs of strength $2*$, which have the better space-filling properties in one and two dimensions.

Inspired by SOAs and nested space-filling designs, we propose a new class of design called a nested strong orthogonal array (NSOA). This is a special type of SOA that contains a smaller SOA as a subset after level collapsing. In this paper, we focus on two projection methods, $\delta$ and $\phi$, to collapse levels. For each projection method, we provide deterministic and theory-guided search methods to construct NSOAs with different parameters. Compared with the existing nested space-filling designs, the proposed NSOAs have several advantages. (i) Under projection $\delta$, with the same number of columns, the constructed SOA $H_{1}$ has significantly fewer runs, and $H_{2}$ exhibits better stratification in low dimensions. For the same run sizes of $H_{2}$, the constructed design $H_{2}$ has better stratification, and $H_{1}$ can have more columns and fewer runs. This benefit comes with a trade-off: the stratification of $H_{1}$ is slightly inferior to existing designs. (ii) Under projection $\phi$, for the same run sizes of $H_{1}$ and $H_{2}$, our $H_{1}$ and $H_{2}$ show better stratification and may have even more columns. Our main construction results are as follows. For projection $\delta$, we can construct $H_{1}$ and $H_{2}$ with $n_{1}$ and $n_{2}$ runs and $m$ columns, where $(n_{1}, n_{2}, m) = (2^{k+2}, 2^{k+1}, 2^k - 1)$ ($k \ge 2$) and $(2\,s^k, s^k, (s^{k-1} - 1)/(s - 1))$ ($k, s \ge 3$). More generally, we can construct $H_{1}$ and $H_{2}$ using nonregular OAs, where $(n_{1}, n_{2}, m) = (2n, n, m)$ with $n$ and $m$ being the numbers of runs and columns in a nonregular OA, respectively. For example, we have a type of nonregular OAs with $n = 4\lambda$ and $m = 4\lambda - 1$ ($\lambda \ge 1$). For projection $\phi$, we can use a recursive method to construct $H_{1}$ and $H_{2}$ with $(n_{1}, n_{2}, m) = (2^{k+1}, 2^k, 5 \cdot 4^\lambda )$ and $(2^{k+1}, 2^k, 10 \cdot 4^\lambda )$ ($k \ge 4, \lambda \ge 1$).

Here is a brief preview of the paper. Section 2 introduces some preliminaries and definitions. Section 3 gives some constructions for the NSOAs in different cases. Section 4 serves to some comparisons with the existing nested space-filling designs. Conclusions are provided in Sect. 5.

2 Preliminaries

An $N\times k$ matrix whose jth column has $s_{j}$ levels from $\{0,1,\dots ,s_{j}-1\}$ is said to be an OA of strength t if for every $N\times t$ subarray, all possible level combinations occur equally often. We denote such an array by OA$(N,k,s_{1}\times \dots \times s_{k},t)$. When $s_{1}=\dots =s_{k}=s$, the array is symmetric and denoted by OA(n, m, s, t). An $n\times m$ matrix with entries from $\{0, 1,\dots , s^{t}-1\}$ is called an SOA of strength t, denoted by SOA$(n,m,s^{t},t)$, if any subarray of g columns ($1\le g\le t$) can be collapsed into an OA$(n, g, s^{u_{1}}\times \dots \times s^{u_{g}},g)$ for any positive integers $u_{1},\dots ,u_{g}$ with $u_{1} +\dots + u_{g}= t$, where collapsing into $s^{u_{j}}$ levels is done using $\lfloor a/s^{t-u_{j}}\rfloor$ for $a\in \{0, 1,\dots , s^{t}-1\}.$

An SOA$(n, m, s^{3},3)$ achieves stratifications on $s^{2}\times s$ and $s\times s^{2}$ grids in two dimensions, and $s\times s\times s$ grids in three dimensions. An $n\times m$ matrix with entries from $\{0,1,...,s^2-1\}$ is called an SOA of strength $2+$, denoted by SOA$(n,m,s^2,2+)$, if any two-column subarray can be collapsed into an OA$(n,2,s^2\times s,2)$ and an OA$(n,2,s\times s^2,2)$. If any three columns of SOA$(n,m,s^2,2+)$ can be collapsed into an OA(n, 3, s, 3), we denote this array by SOA$(n,m,s^2,3-)$. An $n\times m$ matrix with entries from $\{0,1,...,s^{3}-1\}$ is called an SOA of strength $2*$, denoted by SOA$(n,m,s^3,2*)$, if any two-column subarray can be collapsed into an OA$(n,2,s^{2}\times s,2)$ and an OA$(n,2,s\times s^{2},2)$.

For any prime s and integer $u>1$, there exists a Galois field of order $s^{u}$, denoted by GF$(s^{u})$. Throughout the paper, let $s_{1}=s^{u_{1}}$ and $s_{2}=s^{u_{2}}$ be two powers of the same prime s with integers $u_{1}>u_{2}\ge 1$. We consider two projection methods that collapse the levels from F to G. One is called the truncation projection, denoted by $\delta$. The element of $F=$ GF$(s_{1})$ can be denoted as f(x) with an irreducible polynomial $p_{1}(x)$ and the element of $G=$ GF$(s_{2})$ can be denoted as g(x) with an irreducible polynomial $p_{2}(x)$. For any $f(x)=a_{0}+a_{1}x+\cdots +a_{u_{2}-1}x^{u_{2}-1}+\cdots +a_{u_{1}-1}x^{u_{1}-1}\in F$, the truncation projection $\delta$ is defined by $\delta (f(x))=a_{0}+a_{1}x+\cdots +a_{u_{2}-1}x^{u_{2}-1} \in G$. The other one is the general level-collapsing method used in the SOAs defined by $\left\lfloor a/s^{u_{1}-u_{2}}\right\rfloor \in G= \{0, 1,\dots , s^{u_{2}}-1\}$, where $a\in F = \{0, 1,\dots , s^{u_{1}}-1\}.$ We denote this mapping by $\phi$. The elements of F and G in a Galois field will be adaptively represented according to their respective level-collapsing methods. For a matrix A, we define $\delta (A)$ and $\phi (A)$ to be the matrices with each entry performed by the projection $\delta$ and $\phi$, respectively.

3 Construction methods

In this section, we will construct several kinds of NSOAs with different strengths under two projections $\delta$ and $\phi$. First of all, we give a formal definition of NSOAs.

Definition 1

Let $H_{1}$ be an SOA$(n_{1},m,s_{1}$, $t_{1})$ and $H_{2}$ be a subarray of $H_{1}$ with $n_{2}$ runs. If the projection $\delta$ (or $\phi$) collapses the $s_{1}$ levels of $H_{2}$ into $s_{2}$ levels and $\delta (H_{2})$ (or $\phi (H_{2})$) is an SOA$(n_{2},m,s_{2},t_{2})$, then the design $H_{1}$, or more accurately $(H_{1},H_{2})$, is called an NSOA, denoted by NSOA$((n_{1},n_{2}),m$, $(s_{1},s_{2}),(t_{1},t_{2}))$. In other words, a small SOA, $\delta (H_{2})$ (or $\phi (H_{2})$), is nested in the large SOA $H_{1}$.

Throughout the paper, under the projection $\delta$, we consider to construct an NSOA$((n_{1},n_{2})$, $m,(s^{3},s^{2}), (t_{1},t_{2}))$ through

$$\begin{aligned} H_{1}=s^2A+sB+C, \quad \delta (H_{2})=sB^{'}+C^{'}, \end{aligned}$$

(1)

where

$$\begin{aligned} A=\begin{pmatrix} A^{'}\\ A^{''} \end{pmatrix}, B=\begin{pmatrix} B^{'}\\ B^{''}\end{pmatrix}, C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}. \end{aligned}$$

(2)

Theorem 1

Under the projection $\delta$, an NSOA$((n_{1},n_{2}),m$, $(s^{3},s^{2}),(2*$, $2+))$, $(H_{1},H_{2})$, can be constructed through (1) if and only if $(a_{i},a_{j},b_{i})$ and $(a_{i},b_{i},c_{i})$ are two OA$(n_{1},3,s,3)$s and $(b^{'}_{i},b^{'}_{j},c^{'}_{i})$ is an OA$(n_{2},3,s,3)$.

Next, we provide a sufficient condition for the design ($H_{1},H_{2}$) to achieve the three-dimensional stratifications on $s\times s\times s$ grids.

Theorem 2

Under the condition of Theorem 1 and the projection $\delta$, if A is an OA$(n_{1},3,s,3)$, an NSOA$\left( (n_{1},n_{2}),m,(s^{3},s^{2}),(3,2+)\right)$ can be constructed through (1); Further, if $B^{'}$ is an OA$(n_{2},3,s,3)$, an NSOA$((n_{1},n_{2}),m,(s^{3},$ $s^{2}), (3,3-))$ can be constructed through (1).

3.1 NSOA $((n_{1},n_{2}),m,(8,4),(2*,2+))$

First of all, for the case of $s=2$, we consider to construct NSOA$((n_{1},n_{2}),m$, $(8,4),(2*,2+))$ using regular two-level designs. Block and Mee (2003) introduced second order saturated (SOS) designs to be two-level fractional factorial designs in which all degrees of freedom are used to estimate main effects and two-factor interactions. He et al. (2018) applied the SOS designs to construct SOAs. Let S be a regular saturated design with $2^{k}$ runs and $2^{k}-1$ columns consisting of $k\ge 4$ independent columns, denoted by $a_{1}, \ldots , a_{k_{1}}, b_{1}, \ldots , b_{k_{2}}$, and all their interaction columns, where $k_{1} \ge 2, k_{2} \ge 2$ and $k_{1}+k_{2}=k$. Then m columns of S form a regular $2^{m-p}$ design C with $p = m-k$. The set of columns that are not in C is called the complementary design of C, denoted by $\overline{C}= S\backslash C$. Since S is regular, for any $a, b\in S$ with $a\ne b$, we have $ab\in S$, where ab stands for the interaction column of a and b. Throughout the paper, all SOS designs are regular. There is a conventional description if C is a regular SOS design, i.e., for any $d\in \overline{C}$, there exist a, $b\in C$ such that $d=ab$.

Consider two subsets P and Q of S, where P consists of $a_{1}, \ldots , a_{k_{1}}$ and all their interaction columns and Q consists of $b_{1}, \ldots , b_{k_{2}}$ and all their interaction columns. He et al. (2018) provided the following four constructions of SOS designs using P and Q.

Construction 1: $C_{1}=P \cup Q$.

Construction 2: $C_{2}=\left( P \backslash \left\{ a_{1}\right\} \right) \cup \left( Q \backslash \left\{ b_{1}\right\} \right) \cup \left\{ a_{1} b_{1}\right\}$.

Construction 3: $C_{3}=\left( P \backslash \left\{ a_{1}\right\} \right) \cup \left( a_{1} Q\right)$.

Construction 4: $C_{4}=\left( b_{1} P\right) \cup \left( a_{1} Q \backslash \left\{ a_{1} b_{1}\right\} \right)$.

Theorem 1 of He et al. (2018) showed that an SOA of strength $2+$ can be constructed through $D=2A+B$, where the columns of A and B are selected from S, if and only if $\overline{A}$ is an SOS design. In the notation of (1) and (2), a natural consideration requires $\overline{B^{'}}$ to be an SOS design if we select $A^{'}$, $A^{''}$ and $B^{''}$ such that the NSOA can achieve stratifications on $2\times 4$ and $4\times 2$ grids. Meanwhile, $A^{'}$ is disjoint with $B^{'}$ and $A^{'}$ is disjoint with $B^{''}$. Thus, we use Algorithm 1 to construct the NSOAs.

Algorithm 1

   

Step 1.:

Let G and $\overline{G}$ be two SOS designs, where the number of columns in G is less than that in $\overline{G}$. Let $B^{'}=G$.

Step 2.:

For any $b_{j}^{'}\in G$, find $b_{j}^{''}\in G$ such that $b_{j}^{'}b_{j}^{''}=a_{j}^{'}\in \overline{G}$ and $a_{i}^{'}\ne a_{j}^{'}$. Take $A^{'}=\{a_{1}^{'},\dots ,a_{m}^{'}\}\subset \overline{G}$ and $B^{''}=\{b_{1}^{''},\dots ,b_{m}^{''}\}$.

Step 3.:

For any $b_{j}^{'}\in G$, find $c_{j}^{'}, d_{j}^{'} \in \overline{G}$ such that $b_{j}^{'}=c_{j}^{'}d_{j}^{'}$. For any $b_{j}^{''}\in G$, find $c_{j}^{''}, d_{j}^{''} \in \overline{G}$ such that $b_{j}^{''}=c_{j}^{''}d_{j}^{''}$. Take $C^{'}=\{c_{1}^{'},\dots ,c_{m}^{'}\}$ and $C^{''}=\{c_{1}^{''},\dots ,c_{m}^{''}\}$.

Step 4.:

Let $A^{''}=A^{'}+1$, where $A^{'}+1$ is the matrix obtained by adding 1 (mod 2) to all the entries of $A^{'}$. Define

$$\begin{aligned} A=\begin{pmatrix} A^{'}\\ A^{''} \end{pmatrix}, B=\begin{pmatrix} B^{'}\\ B^{''}\end{pmatrix}, C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}. \end{aligned}$$

(3)

Let $H_{1}=4A+2B+C$ and $H_{2}=4A{'}+2B^{'}+C^{'}$.

In Step 1 of Algorithm 1, it should be noted that we need a special type of SOS design to construct the NSOAs. As we will see below, the SOS designs $C_{1}, C_{2}, C_{3}$ and $C_{4}$ are exactly the designs we need as G. Furthermore, we provide a new SOS design $C_{5}$ and its complementary design $\overline{C_{5}}$ as G, which also meets the requirement and can result in the NSOAs with more columns.

In Step 2 of Algorithm 1, it is worth noting that $B^{''}$ may have identical columns, and the condition that G is an SOS design guarantees the existence of $A^{'}$ and $B^{''}$. Note that, if G is an SOS design, any column $a_{j}^{'}$ from $\overline{G}$ can be represented by the interaction of two columns $b_{j}^{'}$ and $b_{j}^{''}$ from G. Taking a subset of $\overline{G}$ as $A^{'}$, we can always obtain $B^{'}$ with distinct columns. Thus, in turn, for given $B^{'}$, we can obtain the corresponding $A^{'}$ and $B^{''}$.

The following lemma gives the resolution of an SOS design if its complementary design is also an SOS design.

Lemma 1

If $\overline{G}$ and G are regular two-level SOS designs, then $\overline{G}$ has resoluntion III or V.

Theorem 3

Let $H^{''}=4A^{''}+2B^{''}+C^{''}$. The $H_{2}$, $H^{''}$and $\delta (H_{2})$ constructed through Algorithm 1 achieve $4\times 2$ and $2\times 4$ stratifications in two dimensions.

Corollary 1

If $H_{1}$ and $H_{2}$ are constructed through Algorithm 1, then $H_{1}$ achieves stratifications on $s^{3}$ grids in one dimension and $\delta (H_{2})$ achieves stratifications on $s^{2}$ grids in one dimension.

Combining Theorem 3 with Corollary 1, we have the following results.

Theorem 4

Given an SOS design with n runs and m factors, if its complementary design is also an SOS design, then an NSOA$((2n,n),m,(8,4),(2*$, $2+))$, $(H_{1},H_{2})$, can be constructed through Algorithm 1, where $H_{1}$ is an SOA(2n, m, $8,2*)$ and $\delta (H_{2})$ is an SOA$(n,m,4,2+)$ with $H_{2}$ being a submatrix of $H_{1}$.

Reviewing the aforementioned Constructions 1–4 of SOS designs, we obtain the following properties of them.

Corollary 2

Designs $\overline{C_{1}}$, $\overline{C_{2}}$, $\overline{C_{3}}$ and $\overline{C_{4}}$ are SOS designs.

Corollary 3

The numbers of factors in $C_{1}$, $C_{2}$, $C_{3}$ and $C_{4}$ are less than those in $\overline{C_{1}}$, $\overline{C_{2}}$, $\overline{C_{3}}$ and $\overline{C_{4}}$, respectively.

Corollaries 2 and 3 show that the SOS designs by Constructions 1–4 are exactly what we need in Step 1 of Algorithm 1. Algorithm 1 not only provides a procedure to search for NSOAs but also can be regarded as the conditions that we need to verify. As shown below, we give a deterministic method to obtain $A^{'}$ and $B^{''}$ in Step 2 of Algorithm 1 instead of using a searching algorithm.

Remark 1

Let the interactions in the P and Q be arranged from low to high order and sorted from small to large by subscript.

• (i) For Construction 1, $B^{'}=(P\ \vdots \ Q)=(p_{1},p_{2},\dots ,p_{2^{k_{1}}-1}\ \vdots \ q_{1},q_{2},\dots$, $q_{2^{k_{2}}-1})$. For $k_{1}=k_{2}$, we may choose $B^{''}=(q_{2},\dots ,q_{2^{k_{2}}-1},q_{1}$ $\vdots$ $p_{2},\dots ,p_{2^{k_{1}}-1}$, $p_{1})$; For $k_{1}> k_{2}$, we may choose $B^{''}=(q_{2},q_{3},\dots ,q_{2^{k_{1}}-1},q_{1},q_{2},q_{3},\dots ,q_{2^{k_{1}}-1}$, $q_{1},q_{2},\dots \ \vdots \ p_{1},\dots ,p_{2^{k_{2}}-1})$. Then $a_{j}^{'}=b_{j}^{'}b_{j}^{''}$. For $k_{1}< k_{2}$, it is similar.

• (ii) For Construction 2, $B^{'}=(P \backslash \left\{ a_{1}\right\} \ \vdots \ Q \backslash \left\{ b_{1}\right\} \ \vdots \ a_{1} b_{1})=(p_{1},p_{2},\dots$, $p_{2^{k_{1}}-2}\ \vdots \ q_{1},$ $q_{2},\dots$, $q_{2^{k_{2}}-2}\ \vdots \ a_{1} b_{1})$. For $k_{1}= k_{2}$, we may choose $B^{''}=(a_{1}b_{1},q_{1},\dots , q_{2^{k_{1}}-3}\ \vdots \ p_{1},\dots ,$ $p_{2^{k_{1}}-2}\ \vdots \ p_{2})$. For $k_{1}> k_{2}$, we may choose $B^{''}=(a_{1}b_{1},q_{1},\dots , q_{2^{k_{2}}-2},q_{1},\dots , q_{2^{k_{2}}-2},q_{1},\dots \ \vdots$ $p_{1},\dots ,p_{2^{k_{2}}-2}\ \vdots \ p_{2})$. Then $a_{j}^{'}=b_{j}^{'}b_{j}^{''}$. For $k_{1}< k_{2}$, it is similar.

• (iii) For Construction 3, $B^{'}=(P \backslash \left\{ a_{1}\right\} \ \vdots \ a_{1} Q)=(p_{1},\dots , p_{2^{k_{1}}-2}\ \vdots \ a_{1}q_{1},\dots$, $a_{1}q_{2^{k_{2}}-1})$. For $k_{1}\le k_{2}$, we may choose $B^{''}=(a_{1}q_{1},\dots ,a_{1}q_{2^{k_{1}}-2}\ \vdots \ p_{2},p_{3},\dots$, $p_{2^{k_{1}}-2},p_{1},p_{2},p_{3},p_{2^{k_{1}}-2},$ $p_{1},p_{2},p_{3}\dots ,)$. Then $a_{j}^{'}=b_{j}^{'}b_{j}^{''}$. For $k_{1}> k_{2}$, it is similar.

• (iv) For Construction 4, $B^{'}=(b_{1}P\ \vdots \ a_{1}Q\backslash \{a_{1}b_{1}\})=(b_{1}p_{1},\dots , b_{1}p_{2^{k_{1}}-1}\ \vdots \$ $a_{1}q_{1},\dots ,$ $a_{1}q_{2^{k_{2}}-2})$. For $k_{1}\ge k_{2}$, we may choose $B^{''}=(a_{1}q_{2},a_{1}q_{3},\dots , a_{1}q_{2^{k_{2}}-2}, a_{1}q_{1}, a_{1}q_{2}, a_{1}q_{3},\dots ,$ $a_{1}q_{2^{k_{2}}-2},a_{1}q_{1}, a_{1}q_{2},a_{1}q_{3} , \dots \ \vdots \ b_{1}p_{1},\dots , b_{1}p_{2^{k_{2}}-2})$. Then $a_{j}^{'}=b_{j}^{'}b_{j}^{''}$. For $k_{1}< k_{2}$, it is similar.

In Cheng et al. (2021), the SOS design with fewer columns is desired to obtain the SOA with more columns. But here we prefer to the SOS design with the number of columns as close to half that of the saturated design S as possible, because the complementary design of the SOS design is also required to be an SOS design.

Table 1 NSOA $((32,16),7,(8,4),(2*,2+))$ in Example 1

Let P consist of $a_{1}, \ldots , a_{k-2}$ and all their interaction columns, Q consist of $b_{1}, b_{2}$ and $b_1b_2$, $P^{*}$ consist of $a_{2}, \ldots , a_{k-2}$ and all their interaction columns, and $P^{**}$ consist of $a_{1}, a_{3},\ldots , a_{k-2}$ and all their interaction columns. We give the following construction.

Construction 5: $C_{5}=P\cup Q\cup \left( b_{1}P^{*}\right) \cup \left( b_{2}P^{**}\right)$.

Lemma 2

Design $C_{5}$ from Construction 5 is an SOS design of $n=2^{k}$ runs and $2^{k-1}$ factors, and its complementary design $\overline{C_{5}}$ is also an SOS design of $n=2^{k}$ runs and $2^{k-1}-1$ factors for $k\ge 4$.

Remark 2

For Construction 5, we take $B^{'}=\overline{C_{5}}$. When $k>4$, the columns of $B^{'}$ can be classified into three types: (i) $B^{'}_{1}=\{a_{1}b_{1},a_{2}b_{2},a_{1}a_{2}b_{1}$, $a_{1}a_{2}b_{2},a_{1}b_{1}b_{2},a_{2}b_{1}b_{2},a_{1}a_{2}b_{1}b_{2}\}$; (ii) $B^{'}_{1}E$ consisting of all interaction columns between $B^{'}_{1}$ and E in total $7( 2^{k-4}-1)$ columns, where $E=\{e_{1},e_{2},\dots ,e_{2^{k-4}-1}\}$ is a set of $a_{3}, \ldots , a_{k-2}$ and all their interaction columns; (iii) $b_{1}b_{2}E$. For (i) and (ii), we may take $\{a_{1}a_{2}b_{1},a_{1}a_{2}b_{2}$, $a_{2}b_{1}b_{2},a_{1}b_{1}b_{2},a_{2}b_{1}b_{2},$ $a_{2}b_{2},a_{1}a_{2}b_{1}\}$ as the corresponding columns in $B^{''}$. For (iii), we may take $\{e_{2},\dots ,e_{2^{k-4}-1},$ $e_{1}\}$ as the corresponding columns in $B^{''}$. For $k=4$, we may take $B^{''}=\{a_{1}a_{2}b_{1},a_{1}a_{2}b_{2}$, $a_{2}b_{1}b_{2},a_{1}b_{1}b_{2},a_{2}b_{1}b_{2},a_{2}b_{2},a_{1}a_{2}b_{1}\}$. Then, we have $a_{j}^{'}=b_{j}^{'}b_{j}^{''}$.

Applying these SOS designs from Constructions 1–5 to Algorithm 1, we can obtain the NSOAs $D_{1},D_{2},D_{3},D_{4}$ and $D_{5}$, respectively.

Theorem 5

Under the projection $\delta$, design $D_{1}$ is an NSOA$((2^{k_{1}+k_{2}+1}-1,2^{k_{1}+k_{2}}),2^{k_{1}}+2^{k_{2}}-2,(8,4),$ $(2*,2+))$, designs $D_{2},D_{3}$ and $D_{4}$ are all an NSOA$( (2^{k_{1}+k_{2}+1}-1,2^{k_{1}+k_{2}}),2^{k_{1}}+2^{k_{2}}-3,(8,4),(2*,2+))$, for $k_{1} \ge 2$ and $k_{2} \ge 2$; Design $D_{5}$ is an NSOA$((2^{k+1}-1,2^{k}),2^{k-1}-1,(8,4),(2*,2+))$ for $k\ge 4$ and its number of columns reaches the maximum value.

Example 1

Let $(e_{1},e_{2},e_{3},e_{4})$ be a full $2^{4}$ factorial design of 16 runs and $C_{5}=\{e_{1},e_{2},e_{1}e_{2},e_{3}$, $e_{4},e_{3}e_{4},e_{2}e_{3},e_{1}e_{4}\}$ be an SOS design. Take $A^{'}=\{e_{2},e_{1},e_{1}e_{4},e_{2}e_{3},e_{1}e_{2},$ $e_{3},e_{4}\}$, $B^{'}=\overline{C_{5}}=\{e_{1}e_{3},e_{2}e_{4}$, $e_{1}e_{2}e_{3},$ $e_{1}e_{2}e_{4},e_{1}e_{3}e_{4}, e_{2}e_{3}e_{4},e_{1}e_{2}e_{3}e_{4}\}$, $B^{''}=\{e_{1}e_{2}e_{3},$ $e_{1}e_{2}e_{4},e_{2}e_{3}e_{4},e_{1}e_{3}e_{4},$ $e_{2}e_{3}e_{4},e_{2}e_{4},$ $e_{1}e_{2}e_{3}\}$, $C^{'}=\{e_{1},e_{2},e_{1}e_{2},e_{1}e_{2},e_{1},e_{3}e_{4},e_{2}e_{3}\}$ and $C^{''}=\{e_{1}e_{2},e_{1}e_{2},e_{2},e_{3}e_{4}$, $e_{3}e_{4},e_{3}$, $e_{1}e_{2}\}$. Let

$$\begin{aligned} A=\begin{pmatrix} A^{'}\\ A^{'}+1\ \end{pmatrix}, B=\begin{pmatrix} B^{'}\\ B^{''}\end{pmatrix}, C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}. \end{aligned}$$

(4)

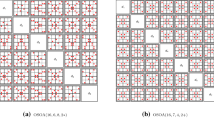
Then design $H_{1}=s^2A+sB+C$ is an NSOA$((32,16),7,(8,4),(2*,2+))$, as shown in Table 1, where design $H_{2}$, i.e., a subarray of $H_{1}$, is listed in first 16 rows of Table 1 and $\delta (H_{2})=sB^{'}+C^{'}$ is an SOA$(16,7,4,2+)$. Figure 1 presents bivariate projections of $\delta (H_{2})$ and $H_{1}$, where the red points correspond to $H_{2}$ and all points correspond to $H_{1}$. We can see that both of them achieve stratifications on $2 \times 4$ and $4 \times 2$ grids in two dimensions.

Fig. 1

Bivariate projections of $\delta (H_{2})$ in (a) and $H_{1}$ in (b)

3.2 NSOA $((n_{1},n_{2}),m,(8,4),(3,t))$ for $t=2+$ and $3-$

In Step 1 of Algorithm 1, we need an SOS design with its complementary design still being an SOS design. However, not all SOS designs have this property. Taking $k_{2}=1$ in Construction 1 as an example, $P\cup \{b_{1}\}$ is an SOS design with $2^{k_{1}+1}$ runs and $2^{k_{1}}$ factors, but its complementary design is not an SOS design. To distinguish from $C_{1}$ in Construction 1, we denote $C_{6}=P\cup \{b_{1}\}$. If we weaken this condition, we can use the following algorithm to obtain an NSOA.

Algorithm 2

Step 1.:

Let $\overline{G}$ be an SOS design and the number of columns in G is less than $2^{k-1}-1$. Let $B^{'}=G$. Find $a_{j}^{'}$ such that $A^{'}=\{a_{1}^{'},\dots ,a_{m}^{'}\}\subset \overline{G}$ and $a_{j}^{'}b_{j}^{'}\in \overline{A^{'}}$.

Step 2.:

For any $b_{j}^{''}\in B^{''}$, take $b_{j}^{''}=a_{j}^{'}b_{j}^{'}$.

Step 3.:

For any $b_{j}^{'}\in G$, find $c_{j}^{'}, d_{j}^{'} \in \overline{G}$ such that $b_{j}^{'}=c_{j}^{'}d_{j}^{'}$ and $c_{j}^{'}\ne b_{j}^{''}$. Take $C^{'}=\{c_{1}^{'},\dots ,c_{m}^{'}\}$. For any $c_{j}^{''}$, find $c_{j}^{''}$ such that $c_{j}^{''}\ne a_{j}^{'}$ and $c_{j}^{''}\ne b_{j}^{'}$. Take $C^{''}=\{c_{1}^{''},\dots ,c_{m}^{''}\}$.

Step 4.:

Let $A^{''}=A^{'}+1$. Define

$$\begin{aligned} A=\begin{pmatrix} A^{'}\\ A^{''} \end{pmatrix}, B=\begin{pmatrix} B^{'}\\ B^{''}\end{pmatrix}, C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}. \end{aligned}$$

(5)

Let $H_{1}=s^2A+sB+C$ and $H_{2}=s^2A^{'}+sB^{'}+C^{'}$.

Theorem 6

Given an SOS design with n runs and m factors, an NSOA((2n, n), m,  $(8,4),(2*,2+))$, ($H_{1},H_{2}$), can be constructed by Algorithm 2, where $H_{1}$ is an SOA(2n, m,  $8,2*)$ and $\delta (H_{2})$ is an SOA$(n,m,4,2+)$ with $H_{2}$ being a submatrix of $H_{1}$.

In Step 1 of Algorithm 2, if $\overline{A^{'}}$ is an SOS design, we can always find such $a_{j}^{'}$ satisfying the condition of Algorithm 2. The following lemma gives a sufficient condition to obtain the NSOAs.

Lemma 3

Under the projection $\delta$, if $\overline{A^{'}}$ and $\overline{B^{'}}$ are two different SOS designs, then an NSOA$((n_{1},n_{2})$, m, (8, 4), $(2*,2+))$ can be constructed from Algorithm 2. Further, if $A^{'}$ is an OA of strength 3, then design ($H_{1},H_{2}$) is an NSOA$((n_{1},n_{2}),m,(8,4)$, $(3,2+))$. If $B^{'}$ is also an OA of strength 3, then design ($H_{1},H_{2}$) is an NSOA$((n_{1},n_{2}),$ m, (8, 4), $(3,3-))$.

Note that $A^{'}$ is disjoint with $B^{'}$, where $A^{'}$ and $B^{'}\in S$. If $\overline{A^{'}}$ and $\overline{B^{'}}$ are two different SOS designs, then both $A^{'}$ and $B^{'}$ can be regarded as projections of different SOS designs. Inspired by this fact, we provide a deterministic construction of an NSOA$((n_{1},n_{2}),m,(8,4),(3,2+))$ as follows.

Let $A^{'}=\overline{C_{6}}=b_{1}P=\{a_{1},a_{2},a_{3},\dots ,a_{2^{k_{1}}-1}\}$ be an OA of strength 3, $B^{'}=P$, $B^{''}=\{b_{1},\dots ,b_{1}\}$ and $C^{'}=C^{''}=\{a_{2},a_{3},\dots ,a_{2^{k_{1}}-1},a_{1}\}$. Then both $\overline{A^{'}}$ and $\overline{B^{'}}$ are an SOS design. From Theorems 1 and 2, we have the following result.

Theorem 7

Under the projection $\delta$, an NSOA$((2^{k_{1}+2},2^{k_{1}+1})$, $2^{k_{1}}-1,(8,4),(3,2+))$ can be constructed for $k_{1}\ge 2$. Moreover, its number of columns reaches the maximum value.

Example 2

Let $(e_{1},e_{2},e_{3})$ be a full $2^{3}$ factorial design and $C_{6}=\{e_{1},e_{2},e_{1}e_{2},e_{3}\}$ be an SOS design. Take $A^{'}=\overline{C_{6}}=\{e_{1}e_{3},e_{2}e_{3},e_{1}e_{2}e_{3}\}$, $B^{'}=\{e_{1},e_{2},e_{1}e_{2}\}$, $B^{''}=\{e_{3},e_{3},e_{3}\}$ and $C^{'}=C^{''}=\{e_{2}e_{3},e_{1}e_{2}e_{3},e_{1}e_{3}\}$. Let

$$\begin{aligned} A=\begin{pmatrix} A^{'}\\ A^{'}+1 \end{pmatrix}, B=\begin{pmatrix} B^{'}\\ B^{''}\end{pmatrix}, C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}. \end{aligned}$$

(6)

Then $H_{1}=s^2A+sB+C$ is an SOA$(16,3,2^3,3)$ and $\delta (H_{2})=sB^{'}+C^{'}$ is an SOA$(8,3,2^2,2+)$.

Example 3

Let $(e_{1},e_{2},e_{3},e_{4})$ be a full $2^{4}$ factorial design and $C_{6}=\{e_{1},e_{2},e_{3},e_{1}e_{2},e_{1}e_{3},e_{2}e_{3}$, $e_{1}e_{2}e_{3},e_{4}\}$ be an SOS design. Take $A^{'}=\overline{C_{6}}=\{e_{1}e_{4},e_{2}e_{4},e_{3}e_{4},$ $e_{1}e_{2}e_{4},$ $e_{1}e_{3}e_{4},e_{2}e_{3}e_{4},e_{1}e_{2}e_{3}e_{4}\}$, $B^{'}=\{e_{1},e_{2},e_{3},$ $e_{1}e_{2}, e_{1}e_{3},e_{2}e_{3},e_{1}e_{2}e_{3}\}$, $B^{''}= \{e_{4},\dots ,e_{4}\}$ and $C^{'}=C^{''}=\{e_{2}e_{4},e_{3}e_{4},e_{1}e_{2}e_{4}$, $e_{1}e_{3}e_{4},e_{2}e_{3}e_{4}, e_{1}e_{2}e_{3}e_{4},$ $e_{1}e_{4}\}$. Let

$$\begin{aligned} {A=\begin{pmatrix} A^{'}\\ A^{'}+1 \end{pmatrix}, B=\begin{pmatrix} B^{'}\\ B^{''}\end{pmatrix}, C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}.} \end{aligned}$$

(7)

Then $H_{1}=s^2A+sB+C$ is an SOA$(32,7,2^3,3)$ and $\delta (H_{2})=sB^{'}+C^{'}$ is an SOA$(16,7,2^2,2+)$. If we pick out $\{e_{1},e_{2},e_{3},e_{1}e_{2}e_{3}\}$ from $B^{'}$ as a new $B^{'}$, and pick out the corresponding $A^{'}$, $B^{''}$, $C^{'}$ and $C^{''}$, then $(H_{1},H_{2})$ is an NSOA((32, 16), $4,(8,4),(3,3-))$ under the projection $\delta$.

Next, we consider the constructions of NSOAs using nonregular OAs.

Theorem 8

Let $G=(g_{1},\dots ,g_{m})$ be an OA(n, m, 2, 2).

• (1) For an odd number m, if we let

  $$\begin{aligned}&A=\begin{pmatrix} A^{'}\\ A^{''} \end{pmatrix}=\begin{pmatrix} 0_{n}& g_{1}& \dots & g_{(m-1)/2} \\ 0_{n}& g_{1}+1& \dots & g_{(m-1)/2}+1 \\ 1_{n}& g_{1}+1& \dots & g_{(m-1)/2}+1 \\ 1_{n}& g_{1}& \dots & g_{(m-1)/2} \end{pmatrix}, \\&B=\begin{pmatrix} B^{'}\\ B^{''} \end{pmatrix}=\begin{pmatrix} g_{(m+1)/2}& \dots & g_{m} \\ g_{(m+1)/2}+1& \dots & g_{m}+1\\ g_{(m+1)/2}+1& \dots & g_{m}+1\\ g_{(m+1)/2}& \dots & g_{m} \end{pmatrix}, \quad C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}=\begin{pmatrix} 0_{n\times (m+1)/2}\\ 1_{n\times (m+1)/2}\\ 0_{n\times (m+1)/2}\\ 1_{n\times (m+1)/2} \end{pmatrix}, \end{aligned}$$

  then $H_{1}=4A+2B+C$ is an SOA$(4n,(m+1)/2,8,3)$ and $\delta (H_{2})$ is an SOA$(2n,(m+1)/2,4,2+)$ with $H_{2}=4A^{'}+2B^{'}+C^{'}$ being a submatrix of $H_{1}$;

• (2) For an even number m, if we let

  $$\begin{aligned}&A=\begin{pmatrix} A^{'}\\ A^{''} \end{pmatrix}=\begin{pmatrix} g_{1}& \dots & g_{m/2} \\ g_{1}+1& \dots & g_{m/2}+1\\ g_{1}+1& \dots & g_{m/2}+1\\ _{1}& \dots & g_{m/2} \end{pmatrix},\\&B=\begin{pmatrix} B^{'}\\ B^{''} \end{pmatrix}=\begin{pmatrix} g_{m/2+1}& \dots & g_{m} \\ g_{m/2+1}+1& \dots & g_{m}+1\\ g_{m/2+1}+1& \dots & g_{m}+1\\ g_{m/2+1}& \dots & g_{m} \end{pmatrix}, \quad C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}=\begin{pmatrix} 0_{n\times m/2}\\ 0_{n\times m/2}\\ 1_{n\times m/2}\\ 1_{n\times m/2} \end{pmatrix}, \end{aligned}$$

  then $H_{1}=4A+2B+C$ is an SOA(4n, m/2, 8, 3) and $\delta (H_{2})$ is an SOA(2n, m/2, 4,  $2+)$ with $H_{2}=4A^{'}+2B^{'}+C^{'}$ being a submatrix of $H_{1}$.

Theorem 9

Let $G=(g_{1},\dots ,g_{m})$ be an OA(n, m, 2, 3). If we let

$$\begin{aligned}&A=\begin{pmatrix} A^{'}\\ A^{''} \end{pmatrix}=\begin{pmatrix} g_{1}& \dots & g_{m-1} \\ g_{1}+1& \dots & g_{m-1}+1 \end{pmatrix},\\&B=\begin{pmatrix} B^{'}\\ B^{''} \end{pmatrix}=\begin{pmatrix} g_{1}& \dots & g_{m-1} \\ g_{1}& \dots & g_{m-1} \end{pmatrix},\ C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}=\begin{pmatrix} g_{m}& \dots & g_{m} \\ g_{m}& \dots & g_{m} \end{pmatrix}, \end{aligned}$$

then $H_{1}=4A+2B+C$ is an SOA$(2n,m-1,8,3)$ and $\delta (H_{2})$ is an SOA$(n,m-1,4,2+)$ with $H_{2}=4A^{'}+2B^{'}+C^{'}$ being a submatrix of $H_{1}$.

Theorems 8 and 9 utilize OAs of strength 2 and 3 to construct the NSOAs, respectively. According to the various sizes of OAs with different strengths, Theorems 8 and 9 provide flexible run sizes for the NSOAs.

The following results introduce easy-to-use methods for constructing large designs by doubling the existing small designs.

Firstly, we can construct a large SOA of strength 2+ based on a small SOA of strength 2+. Let D be an SOA$(n,m,4,2+)$ constructed by $D=2A+B$. Let

$$\begin{aligned} A^{'}=\begin{pmatrix} A& A\\ A& A+1 \end{pmatrix},B^{'}=\begin{pmatrix} B& B\\ B& B \end{pmatrix}. \end{aligned}$$

(8)

Lemma 4

For $A^{'}$ and $B^{'}$ in (8), we have that $D^{'}=2A^{'}+B^{'}$ is an SOA$(2n,2m,4,2+)$.

Secondly, we can construct a large SOA of strength $2*$ or 3 based on a small SOA of strength $2*$ or 3, respectively. Let D be an SOA$(n,m,8,2*)$ or SOA(n, m, 8, 3) constructed by $D=4A+2B+C$. Let

$$\begin{aligned} A^{'}=\begin{pmatrix} A& A\\ A& A+1 \end{pmatrix},B^{'}=\begin{pmatrix} B& B\\ B& B \end{pmatrix},C^{'}=\begin{pmatrix} C& C\\ C& C \end{pmatrix}. \end{aligned}$$

(9)

Lemma 5

For $A^{'}$, $B^{'}$ and $C^{'}$ in (9), we have that $D^{'}=4A^{'}+2B^{'}+C^{'}$ is an SOA$(2n,2m,8,2*)$ or SOA(2n, 2m, 8, 3).

Combining Lemmas 4 and 5, we can obtain some new NSOAs from the existing ones. Let $(H_{1},H_{2})$ be an NSOA$\left( (n_{1},n_{2}),m,(8,4),(2*,2+)\right)$ or NSOA$\big ((n_{1},n_{2}),m,(8,4),(3,2+)\big )$ constructed by $H_{1}=4A+2B+C$, where $A=((A^{'})^{T},(A^{''})^{T})^{T}$, $B=((B^{'})^{T},$ $(B^{''})^{T})^{T}$, $C=((C^{'})^{T},(C^{''})^{T})^{T}$ and $H_{2}=4A^{'}+2B^{'}+C^{'}$. Let

$$\begin{aligned}&\widetilde{A}=\begin{pmatrix} \widetilde{A^{'}}\\ \widetilde{A^{''}} \end{pmatrix}=\begin{pmatrix}\begin{pmatrix} 0& 0\\ 0& 0 \end{pmatrix}\oplus A^{'}\\ \begin{pmatrix} 0& 0\\ 0& 1 \end{pmatrix}\oplus A^{'} \end{pmatrix},\ \widetilde{B}=\begin{pmatrix} \widetilde{B^{'}}\\ \widetilde{B^{''}} \end{pmatrix}=\begin{pmatrix}\begin{pmatrix} 0& 0\\ 0& 1 \end{pmatrix}\oplus B^{'}\\ \begin{pmatrix} 0& 0\\ 0& 1 \end{pmatrix}\oplus B^{''} \end{pmatrix},\\\nonumber&\widetilde{C}=\begin{pmatrix} \widetilde{C^{'}}\\ \widetilde{C^{''}} \end{pmatrix}=\begin{pmatrix}\begin{pmatrix} 0& 0\\ 0& 0 \end{pmatrix}\oplus C^{'}\\ \begin{pmatrix} 0& 0\\ 0& 0 \end{pmatrix}\oplus C^{''} \end{pmatrix}, \end{aligned}$$

(10)

where $\oplus$ is Kronecker sum.

Theorem 10

If there exists an NSOA$\left( (n_{1},n_{2}),m,(8,4),(2*,2+)\right)$ or NSOA$\left( (n_{1},n_{2}),\right. \left. m,(8,4),(3,2+)\right)$, then $(\widetilde{H_{1}},\widetilde{H_{2}})$ under the projection $\delta$ becomes an NSOA$((2n_{1},2n_{2})$, 2m, (8, 4),  $(2*,2+))$ or NSOA(( $2n_{1},2n_{2}),2m,(8,4),(3,2+))$, which is constructed by $\widetilde{H_{1}}=4\widetilde{A}+2\widetilde{B}+\widetilde{C}$ and $\widetilde{H_{2}}=4\widetilde{A^{'}}+2\widetilde{B^{'}}+\widetilde{C^{'}}$, where $\widetilde{A}$, $\widetilde{B}$ and $\widetilde{C}$ are given in (10).

From Theorem 10, we can construct a large NSOA from a small one. An illustrative example is given to show the idea.

Example 4

Let $(H_{1},H_{2})$ be an NSOA$((32,16),7,(8,4),(2*,2+))$ constructed by $H_{1}=4A+2B+C$ and $H_{2}=4A^{'}+2B^{'}+C^{'}$, where $A=((A^{'})^{T},(A^{'}+1)^{T})^{T}$, $B=((B^{'})^{T},(B^{''})^{T})^{T}$ and $C=((C^{'})^{T},(C^{''})^{T})^{T}$, as shown in Example 1. For ease of explanation, $H_{1}$ can be represented as

$$\begin{aligned} H_{1}=\begin{pmatrix} H_{2}\\ H_{3} \end{pmatrix}, \end{aligned}$$

where $H_{3}=4(A^{'}+1)+2B^{''}+C^{''}$. We can construct a larger NSOA$((64,32),14,(8,4),(2*,2+))$, $(\widetilde{H_{1}},\widetilde{H_{2}})$, from the existing $(H_{1},H_{2})$ by (10), which is given by

Then $\widetilde{H_{1}}$ can achieve stratifications on $2\times 4$ and $4\times 2$ grids, and $\delta (\widetilde{H_{2}})$ can achieve stratifications on $2\times 4$ and $4\times 2$ grids.

3.3 NSOA $((n_{1},n_{2}),m,(8,4),(2*,2+))$ with stratifications on $4\times 4$ grids

In Sect. 3.1, we have presented the construction of an NSOA$((n_{1},n_{2}),m,(8,4),(2*,2+))$ under the projection $\delta$. In this subsection, we aim to construct an NSOA$((n_{1},n_{2}), m,(8,4),(2*,2+))$ with finer stratifications on $4\times 4$ grids in all two-dimensions under the projection $\phi$. The following algorithm provides a general framework for the construction.

Algorithm 3

Step 1.:

Let G be an SOS design of $2^{k}$ runs based on k independent factors $e_{1},\dots ,e_{k}$. Find $a^{'}_{i}\in \overline{G}$, $b^{'}_{i}, b^{''}_{i} \in G$ such that $a^{'}_{i}=b^{'}_{i}b^{''}_{i}$ and $b^{'}_{i}\ne b^{'}_{j}$, $b^{''}_{i}\ne b^{''}_{j}$. Take $A^{'}=\{a_{1}^{'},\dots ,a_{m}^{'}\}$ with $A^{'}\subseteq \overline{G}$, $B^{'}=\{b_{1}^{'},\dots ,b_{m}^{'}\}$ and $B^{''}=\{b_{1}^{''},\dots ,b_{m}^{''}\}$.

Step 2.:

Let $A=(0,1)^{T}\oplus A^{'}=\{a_{1},\dots ,a_{m}\}$ and $B=(0,0)^{T}\oplus B^{'}=\{b_{1},\dots ,b_{m}\}.$

Step 3.:

Find $c_{i}$ such that $(a_{i},b_{i},c_{i})$ is an OA$(2^{k+1},m,2,3)$, and let $C=\{c_{1},\dots ,c_{m}\}=(C^{'},C^{''})^{T}$.

Step 4.:

Let $H_{1}=4A+2B+C$ and $H_{2}=4A{'}+2B^{'}+C^{'}$.

Theorem 11

An NSOA$((2^{k+1},2^{k}),m,(8,4),(2*,2+))$, $(H_{1},H_{2})$, can be constructed through Algorithm 3, where $H_{1}$ is an SOA$(2^{k+1},m,8,2*)$ achieving stratifications on $4\times 4$ grids in all two-dimensions, and $\phi (H_{2})$ is an SOA$(2^{k},m,4,2+)$ with $H_{2}$ being a submatrix of $H_{1}$.

Remark 3

In Step 3 of Algorithm 3, the selection of $c_{i}$ can take the half of locations corresponding with $(\alpha ,\beta )$ in the columns $(a_{i},b_{i})$ as 0, and the other half of locations as 1, where $\alpha ,\beta \in \{0,1\}$. In total, we can obtain sixteen different C in Step 3, and $H_{2}$ may be an SOA$(2^{k},m,4,2+)$ without the level-collapsing for a certain C.

Example 5

Let $(e_{1},e_{2},e_{3},e_{4})$ be a full $2^{4}$ factorial design and $G=\{e_{1},e_{2},e_{3},e_{4},e_{1}e_{2},$ $e_{3}e_{4},e_{1}e_{4}$, $e_{2}e_{3}e_{4}\}$ be an SOS design. Take

$$\begin{aligned} A^{'}= & \{e_{1}e_{3},e_{2}e_{4},e_{2}e_{3},e_{1}e_{2}e_{4},e_{1}e_{2}e_{3}e_{4},e_{1}e_{3}e_{4},e_{1}e_{2}e_{3}\}, \\ B^{'}= & \{e_{1},e_{2},e_{3},e_{4},e_{1}e_{2},e_{3}e_{4},e_{1}e_{4}\}, \quad B^{''}=\{e_{3},e_{4},e_{2},e_{1}e_{2},e_{3}e_{4},e_{1},e_{2}e_{3}e_{4}\},\\ A= & (0,1)^{T}\oplus A^{'}, \quad B=(0,0)^{T}\otimes B^{'} \quad \textrm{and} \quad C=(0_{16\times 5}^{T},J_{16\times 5}^{T})^{T}, \end{aligned}$$

where J is the $u\times v$ matrix of ones. Then $H_{1}=4A+2B+C$ listed in Table 2 is an SOA$(32,7,8,2*)$, which achieves stratifications on $4\times 4$ grids in all two dimensions and 8 grids in all one dimension, as shown in Fig. 2. Design $H_{2}=4A^{'}+2B^{'}+C^{'}$, a subarray of $H_{1}$, consists of the first 16 runs in Table 2 and is an SOA$(16,7,4,2+)$ even without level-collapsing. Figure 2 shows its stratifications on $2\times 4$ and $4\times 2$ grids in all two dimensions. On the other hand, we can regard $H_{1}$ as an augmented design for $H_{2}$, which not only increases the number of levels from 4 to 8 but also strengthens the stratifications from on $2\times 4$ and $4\times 2$ grids to $4\times 4$ grids in all two dimensions. Such a design is extremely useful for sequential experiments.

Table 2 $H_{1}$ in Example 5

Fig. 2

Bivariate projections of $H_{1}$ and $H_{2}$, where $H_{1}$ consists of the red points and black crosses and $H_{2}$ consists of the red points

Furthermore, we provide a sufficient condition to guarantee that $\phi (H_{2})$ can also achieve stratifications on $4\times 4$ grids in all two dimensions.

Theorem 12

Besides $b_{i}^{'}\ne b_{j}^{''}$ in Step 1 of Algorithm 3, an NSOA$((2^{k+1},2^{k})$, m, (8, 4),  $(2*,2+))$, $(H_{1},H_{2})$, can be constructed through Algorithm 3, where $H_{1}$ is an SOA$(2^{k+1},$ $m,8,2*)$ and $\phi (H_{2})$ is an SOA$(2^{k},m,4,2+)$ with $H_{2}$ being a submatrix of $H_{1}$. Meanwhile, both $H_{1}$ and $\phi (H_{2})$ achieve stratifications on $4\times 4$ grids in all two dimensions.

Example 6

Let $(e_{1},e_{2},e_{3},e_{4})$ be a full $2^{4}$ factorial design and $G=\{e_{1},e_{2},e_{3},e_{4},e_{1}e_{2}$, $e_{3}e_{4},e_{1}e_{2}e_{3}$, $e_{1}e_{2}e_{4},e_{2}e_{3}e_{4},e_{1}e_{3}e_{4}\}$ be an SOS design. Take

$$\begin{aligned} A^{'}= & \{e_{1}e_{3},e_{1}e_{4},e_{2}e_{3},e_{2}e_{4},e_{1}e_{2}e_{3}e_{4}\},\\ B^{'}= & \{e_{1}e_{2}e_{3},e_{1}e_{3}e_{4},e_{2}e_{3}e_{4},e_{1}e_{2}e_{4},e_{1}e_{2}\}, \quad B^{''}=\{e_{2},e_{3},e_{4},e_{1},e_{3}e_{4}\}.\\ A= & (0,1)^{T}\oplus A^{'}, B=(0,0)^{T}\otimes B^{'} \quad \textrm{and} \quad C=(0_{16\times 5}^{T},J_{16\times 5}^{T})^{T}, \end{aligned}$$

where J is the $u\times v$ matrix of ones. Then $H_{1}=4A+2B+C$ is an SOA(32, $5,8,2*)$ and $H_{2}=4A^{'}+2B^{'}+C^{'}$, consisting of the first 16 runs in $H_{1}$, is an SOA$(16,5,4,2+)$. They both achieve stratifications on $4\times 4$ grids in all two dimensions.

We next present a recursive construction of NSOA$((2^{k+1},2^{k}),m,(8,4)$, $(2*,2+))$, $(H_{1},H_{2})$, where $H_{1}$ can achieve stratifications on $4\times 4$ grids in all two dimensions and $\phi (H_{2})$ can achieve stratifications on $2\times 4$ and $4\times 2$ grids in all two dimensions. Let $A_{k}^{'}$ and $B_{k}^{'}$ with $2^{k}$ runs and m columns satisfy the conditions in Algorithm 1. Then $A_{k+1}^{'}$ and $B_{k+1}^{'}$ with $2^{k+1}$ runs and 2m columns can be constructed by defining

$$\begin{aligned} A_{k+1}^{'}=\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}\oplus A_{k}^{'},\ B_{k+1}^{'}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}\oplus B_{k}^{'}, \end{aligned}$$

and

$$\begin{aligned} A_{k+1}=(0,1)^{T}\oplus A_{k+1}^{'},\ B_{k+1}=\begin{pmatrix} 0_{2} & 0_{2} \\ 0_{2} & 1_{2} \end{pmatrix}\oplus B_{k}^{'}. \end{aligned}$$

Similarly, the $C_{k+1}$ can be constructed according to Remark 3.

Theorem 13

Under the projection $\phi$, suppose that an NSOA((2n, n), m, (8, $4),(2*,2+))$, $(H_{1},H_{2})$, is available, where $H_{1}$ and $\phi (H_{2})$ both achieve stratifications on $4\times 4$ grids in all two dimensions. Then an NSOA$((4n, 2n), 2m, (8, 4), (2*, 2+))$, $(\tilde{H_{1}}, \tilde{H_{2}})$, can be constructed, where $\tilde{H_{1}}$ achieves stratifications on $4 \times 4$ grids in all two dimensions.

The proof of Theorem 13 is similar to those of Theorems 11 and 12. Essentially, designs $A_{k+1}$ and $B_{k+1}$ in Theorem 13 are obtained by doubling $A_{k}$ and $B_{k}$. Next, we give another recursive construction via doubling $A_{k}$ and $B_{k}$ twice such that both $\tilde{H_{1}}$ and $\delta (H_{2})$ achieve stratifications on $4\times 4$ grids in all two dimensions.

If $A_{k}^{'}$ and $B_{k}^{'}$ based on k independent factors $e_{1}, \dots , e_{k}$ satisfy the condition in Theorem 12, then $A_{k+2}^{'}$ and $B_{k+2}^{'}$ based on $k+2$ independent factors $e_{1}, \dots , e_{k+2}$ that also satisfy the condition in Theorem 12 can be constructed by

$$\begin{aligned} A_{k+2}^{'}= & \{A_{k}^{'},e_{k+1}A_{k}^{'},e_{k+2}A_{k}^{'},e_{k+1}e_{k+2}A_{k}^{'}\},\\ B_{k+2}^{'}= & \{B_{k}^{'},e_{k+2}B_{k}^{'},e_{k+1}e_{k+2}B_{k}^{'},e_{k+1}B_{k}^{'}\}, \end{aligned}$$

and

$$A_{k+2}=(0,1)^{T}\oplus A_{k+2}^{'},\ B_{k+2}=(0,0)^{T}\oplus B_{k+2}^{'}.$$

Similarly, the $C_{k+2}$ can be constructed according to Remark 3.

Theorem 14

Under the projection $\phi$, suppose that an NSOA((2n, n), m, (8, $4),(2*,2+))$, $(H_{1},H_{2})$, is available, where $H_{1}$ and $\phi (H_{2})$ both achieve stratifications on $4\times 4$ grids in all two dimensions. Then an NSOA((8n, 4n), 4m, $(8,4),(2*,2+))$, $(\tilde{H_{1}},\tilde{H_{2}})$, can be constructed, where $\tilde{H_{1}}$ and $\phi (\tilde{H_{2}})$ both achieve stratifications on $4\times 4$ grids in all two dimensions.

3.4 NSOA $((n_{1},n_{2}),m,(s^3,s^2),(2*$, $2+))$ for $s\ge 3$

This subsection will focus on the construction of NSOA$((n_{1}, n_{2}), m, (s^3, s^2), (2*, 2+))$ for any prime power $s \ge 3$.

Let $e_{1},\dots ,e_{k}$ denote the k independent columns of a regular saturated design S with $s^{k}$ runs and $(s^{k}-1)/(s-1)$ factors of s levels. We denote $e_{1}^{u_{1}}\cdots e_{k}^{u_{k}}$ as the interaction column $u_{1}e_{1}+\cdots + u_{k}e_{k}$, where $u_{j}\in \{0,1,\dots ,s-1\}$ are not all zero and the first nonzero element in $(u_{1},\dots , u_{k})$ is 1.

Algorithm 4

Step 1.:

Select $m= (s^{k-1}-1)/(s-1)$ different interaction columns from S as $B^{'}=\{b_{1}^{'},\dots ,b_{m}^{'}\}$, where each column has the form of $e_{1}e_{2}^{u_{2}}\cdots e_{k}^{u_{k}}$ such that at least one $u_{j}$ equals $\omega _{s-1}$.

Step 2.:

Let $B^{''}=\{b^{'}_{2},\dots ,b^{'}_{m},b^{'}_{1}\}$.

Step 3.:

If $u_{p},\dots , u_{q}=\omega _{s-1}$ in $b_{i}^{'}$ and $b_{i}^{''}$, we take $c^{'}_{i}$ and $c^{''}_{i}=e_{p}\cdots e_{q}$.

Step 4.:

Select m different interaction columns from S which have the form of $e_{2}e_{3}^{u_{3}}\cdots e_{k}^{u_{k}}$, and then rearrange these columns as $A^{'}=\{a_{1}^{'},\dots ,a_{m}^{'}\}$ such that $a_{i}^{'}\ne c^{'}_{i}$ and $a_{i}^{'}\ne c^{''}_{i}$.

Step 5.:

Let $A^{''}=A^{'}+1\ (\textrm{mod}\ s)$ and take

$$\begin{aligned} A=\begin{pmatrix} A^{'}\\ A^{''} \end{pmatrix}, B=\begin{pmatrix} B^{'}\\ B^{''}\end{pmatrix}, C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}. \end{aligned}$$

(11)

Let $H_{1}=s^2A+sB+C$ and $H_{2}=s^2A^{'}+sB^{'}+C^{'}$.

Theorem 15

For any $k\ge 3$ and any prime power $s\ge 3$, an NSOA$((2s^{k},s^{k})$, $(s^{k-1}-1)/(s-1),(s^{3},s^{2}),(2*,2+))$, $(H_{1},H_{2})$, can be constructed by Algorithm 4 under the projection $\delta$.

Example 7

For $s=k=3$, let $e_{1},\ldots ,e_{k}$ denote the k independent columns of an $s^{k}$ full factorial design. Take $A^{'}=\{e_{2}e_{3},e_{3},e_{2},e_{2}e_{3}^{2}\}$, $B^{'}=\{e_{1}e_{2}^{2},e_{1}e_{2}^{2}e_{3},e_{1}e_{2}^{2}e_{3}^{2},e_{1}e_{2}e_{3}^{2}\}$, $C^{'}=\{e_{2},e_{2},e_{2}e_{3},e_{3}\}$, $B^{''}=\{e_{1}e_{2}^{2}e_{3},e_{1}e_{2}^{2}e_{3}^{2}$, $e_{1}e_{2}e_{3}^{2},e_{1}e_{2}^{2}\}$ and $C^{''}=\{e_{2},e_{2}e_{3},e_{3},e_{2}\}$. Let

$$\begin{aligned} A=\begin{pmatrix} A^{'}\\ A^{'}+1 \end{pmatrix}, B=\begin{pmatrix} B^{'}\\ B^{''}\end{pmatrix}, C=\begin{pmatrix} C^{'}\\ C^{''} \end{pmatrix}. \end{aligned}$$

(12)

Then $H_{1}=s^2A+sB+C$ is an SOA$(54,4,3^3,2*)$ and $\delta (H_{2})=sB^{'}+C^{'}$ is an SOA$(27,4,3^2,2+)$ with $H_{2}=s^2A^{'}+2B^{'}+C^{'}$ being a submatrix of $H_{1}$.

Remark 4

Let $H^{''}=s^{2}A^{''}+sB^{''}+C^{''}$. In Algorithm 4, we have that both $\delta (H_{2})=sB^{'}+C^{'}$ and $\delta (H^{''})=sB^{''}+C^{''}$ are an SOA($s^{k}$,$(s^{k-1}-1)/(s-1),s^{2}, 2+)$. Further, design $H_{1}$ can be regarded as a sliced strong orthogonal array which can be partitioned into two small SOAs after the level-collapsing.

4 Comparisons with the existing nested space-filling designs

This section provides comparisons between NSOAs and NOAs. We mainly compare the designs with respect to the numbers of runs and columns, as well as two- and three-dimensional stratifications.

Our comparisons primarily focus on the NOAs constructed in Sun et al. (2014) in terms of two-dimensional stratifications since they encompass most scenarios presented in the existing literature. In addition, the large design in the nested space-filling design has more design points than the small one, making it natural to expect the large design to have better stratifications, as discussed in Qian et al. (2009). They wish the large design to achieve stratifications in three dimensions, which is especially attractive for the three-way interactions in the response. Thus, we also compare the proposed designs with the NOAs in Qian et al. (2009) in terms of the three-dimensional stratifications. The OAs required for Theorems 3, 4 and 5 in Sun et al. (2014), as well as Lemma 1 in Qian et al. (2009), can be found in the OA library maintained by Dr. N.J.A. Sloane, available at http://neilsloane.com/oadir/index.html.

Table 3 Comparisons between NSOA$((2^{k+1},2^{k}),m,(8,4),(2*,2+))$’s and NOAs for the case of $s=2$

Table 3 shows the two-dimensional stratifications of the NSOA$((2^{k+1},2^{k})$, m, (8, 4),  $(2*,2+))$ with the different runs and columns. Firstly, when comparing NSOA$^1$ with NOA$^3$, it is evident that NSOA$^1$ requires fewer runs in $H_{1}$ to have the same number of columns, making it more economical. The trade-off is that NSOA$^1$ sacrifices the stratifications of $H_{1}$ and requires more runs in $H_{2}$. Taking the nested space-filling design with 15 columns as an example, the run size of NSOA$^1$ in $H_{1}$ is less than that of NOA$^3$ (64 vs. 256). Although the $H_{1}$ in NOA$^3$ achieves stratifications on $4\times 4$ grids, which is superior to NSOA$^1$ achieving stratifications on $2\times 4$ and $4\times 2$ grids, the $H_{2}$ in NSOA$^1$ can achieve finer $2\times 4$ and $4\times 2$ grids, in comparison with NOA$^3$ achieving stratifications on $2\times 2$ grids. In practice, it is reasonable to prefer $H_{2}$ with better stratifications as it is often used for high-accuracy experiments. Secondly, when comparing NSOA$^2$ with NOA$^4$, given the same number of runs in $H_{1}$ and $H_{2}$, the number of columns in NSOA$^2$ is similar to or even greater than that in NOA$^4$. Notably, the $H_{2}$ in NSOA$^2$ can achieve better stratifications, including $2\times 4$ and $4\times 2$ grids, or even $4\times 4$ grids, while the $H_{2}$ in NOA$^4$ only achieves stratifications on $2\times 2$ grids. Taking $H_{1}$ of 128 runs and $H_{2}$ of 64 runs as an example, we can see that NSOA$^2$ has 20 columns while NOA$^4$ only has 18 columns. Meanwhile, the $H_{2}$ in NSOA$^2$ achieves stratifications on $4\times 4$ grids, whereas NOA$^4$ only achieves stratifications on $2\times 2$ grids.

Table 4 tabulates the three-dimensional stratifications of NSOAs and NOAs. The NOA$^5$, as discussed in Qian et al. (2009), only offers three-dimensional stratifications in $H_{1}$, whereas the NOA$^6$, mentioned in Sun et al. (2014), displays different three-dimensional stratifications between $H_{1}$ and $H_{2}$. In comparison with the NOAs, the NSOA$((2^{k+1},2^{k}),m,(8,4),(3$, $2+))$ and NSOA$((2^{k+1},2^{k}),m,(8,4)$, $(3,3-))$ can accommodate more columns and have a satisfactory space-filling property. For example, the NSOA$^7$ with 64 runs in $H_{1}$ has 15 or 8 columns, which surpasses the NOAs having at most 5 columns. When comparing NSOA$^7$ with NOA$^6$, although the $H_{1}$ in NOA$^6$ achieves stratifications on $4\times 4\times 4$ grids, superior to NSOA$^7$ achieving stratifications on $2\times 4$, $4\times 2$ and $2\times 2\times 2$ grids, the $H_{2}$ in NSOA$^7$ achieves stratifications on $2\times 4$ and $4\times 2$ grids, outperforming NOA$^6$ achieving stratifications on $2\times 2$ grids in two dimensions, and also features more number of columns. Moreover, comparing NSOA$^7$ with NOA$^5$ reveals that $H_{2}$ in NOA$^5$ cannot achieve three-dimensional stratifications and has fewer number of columns than NSOA$^7$.

Table 4 Comparisons between NSOAs and NOAs in three dimensions

Table 5 outlines the two-dimensional stratifications of NSOA$((n_{1},n_{2})$, $m,(s^3,s^2),$ $(2*,2+))$ with different numbers of runs and columns for cases of $s\ge 3$. Similar to the scenario with $s=2$, NSOAs outperform NOAs in terms of run size and the number of columns. Although the stratifications of $H_{1}$ in NSOAs are slightly less favorable than those in NOAs, the stratifications of $H_{2}$ in NSOAs surpass those of NOAs. Taking $s=3$ as an example, when $H_{2}$ has the same 243 runs, NOA$^{10}$ accommodates 30 columns whereas NSOA$^8$ has 40 columns, and the run size of $H_{1}$ in NSOA$^8$ is fewer than that of NOA$^{10}$ (486 vs. 729). Furthermore, when comparing scenarios where both NSOA and NOA have 40 columns, the run size of NSOA$^8$ is fewer than that of NOA$^9$ (486 vs. 729).

Table 5 Comparisons between NSOAs and NOAs for the case of $s\ge 3$

5 Conclusion remarks

In this paper, we proposed a new class of design called the nested strong orthogonal array (NSOA), which can enjoy more columns, more economic run sizes and better stratifications. We utilize two projections, $\delta$ and $\phi$, to collapse the levels of the nested design from $s^{3}$ to $s^{2}$, ensuring that the small design nested within the large SOA is still an SOA after the level-collapsing. The large and small SOAs exhibit distinct strengths. We detail the constructions for NSOA$((n_{1},n_{2}),m,(s^3,s^2)$, $(2*,2+))$, NSOA$((n_{1},n_{2}),m,(8,4)$, $(3,2+))$ and NSOA$((n_{1},n_{2}),m,(8,4),(3,3-))$ under projection $\delta$, as well as NSOA$((n_{1},n_{2}),m,(8,4),(2*,2+))$ with stratifications on $4\times 4$ grids under projection $\phi$. To summarize, the space-filling properties of the proposed nested designs, $H_{2}\subset H_{1}$, by deterministic constructions are as follows: $H_{1}$ can achieve stratifications on $2\times 2\times 2$, $s\times s^2$ and $s^2\times s$ grids (for a prime power $s \ge 2$); $\delta (H_{2})$ can achieve stratifications on $s\times s^2$ and $s^2\times s$ grids (for a prime power $s \ge 2$); $H_{1}$ and $\phi (H_{2})$ can achieve stratifications on $2\times 4$, $4\times 2$ and $4\times 4$ grids. Our approaches not only provide algorithms for obtaining NSOAs but also develop direct algebraic construction methods derived from regular and nonregular designs. Algorithms 1, 2, and 3 provide general theory-guided searches to obtain various designs. However, the search process is relatively time-consuming, as we have to select the columns one by one. Assuming the larger number of columns in G and $\overline{G}$ is d, the complexity of the search in Algorithms 1, 2, and 3 is $O(d^2)$. Thus, we also provide direct algebraic construction methods to obtain NSOAs. Moreover, the resulting large designs can be constructed from the existing small designs. The proposed NSOAs are suitable for experiments with different accuracies. Compared with NOAs, the proposed NSOAs offer a superior number of columns and maintain desirable stratifications in both two and three dimensions.

For future research, at least two issues are worth to be studied. Firstly, it is possible to delve into the use of truncation projection, a specific type of subgroup projection, to construct NSOAs with more than two layers. Secondly, in this paper, we only focused on the cases where $H_{1}$ has $s^{3}$ levels and $\delta (H_{2})$ (or $\phi (H_{2})$) has $s^{2}$ levels. A potential extension is to investigate more general scenarios where $s_{1}=s^{u_{1}}$ and $s_{2}=s^{u_{2}}$ with $u_{1}-u_{2}\ge 1$.

Appendix: proofs

Proof of Theorem 1

According to He et al. (2018), the condition that $(b^{'}_{i},b^{'}_{j},c^{'}_{i})$ forms an OA$(n_{2},3$, s, 3) is both necessary and sufficient for constructing SOAs of strength 2+, $\delta (H_{2})$. Furthermore, $(a_{i},a_{j},b_{i})$ being an OA$(n_{1},3,s,3)$ is essential for achieving $s^{2}\times s$ and $s\times s^{2}$ stratifications in two dimensions. Additionally, $(a_{i},b_{i},c_{i})$ being an OA$(n_{1},3,s,3)$ ensures the incorporation of $s^{3}$ levels in the $H_{1}$.

Proof of Lemma 1

It can be verified that for any column $b_{j}\in \overline{G}$, there exist $b_{j_{1}},b_{j_{2}},b_{j_{3}},b_{j_{4}}\in \overline{G}$ such that $b_{j}=b_{j_{1}}b_{j_{2}}$ or $b_{j}=b_{j_{1}}b_{j_{2}}b_{j_{3}}b_{j_{4}}$.

Proof of Theorem 3

Note that $\delta (H_{2})=2B^{'}+C^{'}$. Since $a_{i}^{'}b_{i}^{'}=b_{i}^{''}\in G$ and $a_{j}^{'}\in \overline{G}$, $(a_{i}^{'},b_{i}^{'},a_{j}^{'})$ is an OA of strength 3. The property of orthogonality is preserved upon permuting the levels of the columns; hence, $(a_{i}^{'},b_{j}^{'},a_{j}^{'})$, $(a_{i}^{''},b_{i}^{''},a_{j}^{''})$ and $(a_{i}^{''},b_{j}^{''},a_{j}^{''})$ are also OAs of strength 3. As a result, both $H_{2}$ and $H^{''}$ achieve stratifications on $4\times 2$ and $2\times 4$ grids in two dimensions. Given that $\overline{G}$ is an SOS design, for any $b_{i}^{'}\in G$, there exist $c_{i}^{'},d_{i}^{'}\in \overline{G}$ such that $b_{i}^{'}=c_{i}^{'}d_{i}^{'}$. Consequently, $(b_{i}^{'},b_{j}^{'},c_{i}^{'})$ and $(b_{i}^{'},b_{j}^{'},c_{j}^{'})$ are OA of strength 3. Therefore, $\delta (H_{2})$ achieves stratifications on $s^{2}\times s$ and $s\times s^{2}$ grids in two dimensions.

Proof of Corollary 1

Since $a_{j}^{'}b_{j}^{'}=b_{j}^{''}\in G$ and $c_{j}^{'}\in \overline{G}$, it follows that $(a_{j}^{'},b_{j}^{'},c_{j}^{'})$ is an OA of strength 3. The orthogonality is maintained when permuting the levels of the columns. Similarly, $(a_{j}^{''},b_{j}^{''},c_{j}^{''})$ is also an OA of strength 3. Therefore $(a_{j},b_{j},c_{j})$ is an OA of strength 3, leading to $H_{1}$ achieving stratifications on $s^{3}$ grids in one dimension. It is evident that $\delta (H_{2})$ achieves stratifications on $s^{2}$ grids in one dimension.

Proof of Theorem 4

We define $A=\{a_{1},\ldots ,a_{m}\}$, $B=\{b_{1},\ldots ,b_{m}\}$ and $C=\{c_{1},\ldots ,c_{m}\}$. According to Theorem 1 in He et al. (2018), $\delta (H_{2})$ is an SOA$(n,m,s^2,2+)$. Given that $(a_{i}^{'},b_{i}^{'},a_{j}^{'})$, $(a_{i}^{'},b_{j}^{'},a_{j}^{'})$, $(a_{i}^{''},b_{i}^{''},a_{j}^{''})$ and $(a_{i}^{''},b_{j}^{''},a_{j}^{''})$ are OAs of strength 3, it follows that $(a_{i},b_{i},a_{j})$ and $(a_{i},b_{j},a_{j})$ are OAs of strength 3. Consequently, $H_{1}$ achieves stratifications on $s^{2}\times s$ and $s\times s^{2}$ grids in two dimensions. Combining Corollary 1, $H_{1}$ is an SOA$(2n,m,s^3,2*)$.

Proof of Corollary 2

We only prove that $\overline{C_{1}}$ is an SOS design, and the proofs for $\overline{C_{2}}$, $\overline{C_{3}}$ and $\overline{C_{4}}$ are similar. Initially, we acknowledge that the situation $k_{1} = k_{2} = 2$ is met. We proceed by assuming a scenario where $C_{1}=P\cup Q$ and $\overline{C_{1}}$ is an SOS design, where P consists of independent columns $a_{1}, \ldots , a_{k_{1}}$ and all their interaction columns, and Q consists of independent columns $b_{1}, \ldots , b_{k_{2}}$ and all their interaction columns. The objective is to verify that $\overline{C_{1}^{'}}$ is an SOS design when independent columns $a_{1}, \ldots , a_{k_{1}}, a_{k_{1}+1}$ and all their interaction columns form $P^{'}$, and $C_{1}^{'}=P^{'}\cup Q$. Then $\overline{C_{1}^{'}}$ and $C_{1}^{'}$ have the following expressions:

$$\begin{aligned} \overline{C_{1}^{'}}=a_{k_{1}+1}Q\cup a_{k_{1}+1}\overline{C_{1}}\cup \overline{C_{1}},\quad C_{1}^{'}=C_{1}\cup \{a_{k_{1}+1}\}\cup a_{k_{1}+1}P. \end{aligned}$$

For any column $d\in \{a_{k_{1}+1},a_{k_{1}+1}P\}$, if $d=a_{k_{1}+1}$, then there must exist columns $e\in a_{k_{1}+1}\overline{C_{1}}$ and $f\in \overline{C_{1}}$ such that $e\cdot f=d$; If $d\in a_{k_{1}+1}P$, then there must exist columns $e\in a_{k_{1}+1}\overline{C_{1}}$ and $f\in \overline{C_{1}}$ such that $e\cdot f=d$, or there exist $g\in a_{k_{1}+1}Q$ and $f\in \overline{C_{1}}$ such that $g\cdot f=d$.

Proof of Corollary 3

Design $C_{1}$ has $n=2^{k}$ runs and $m=2^{k_{1}}+2^{k_{2}}-2$ factors, while $C_{2},C_{3},C_{4}$ have $n =2^{k}$ runs and $m=2^{k_{1}}+2^{k_{2}}-3$ factors, where $k_{1}\ge 2$, $k_{2}\ge 2$, and $k_{1}+k_{2}=k\ge 4$. We denote the number of factors in $\overline{C_{1}}$, $\overline{C_{2}}$, $\overline{C_{3}}$ and $\overline{C_{4}}$ as $m^{'}$. Since the number of columns in $C_{1}$ is more than that in $C_{2}-C_{4}$, we just need to prove $m<m^{'}$ in $C_{1}$. For $k_{1}\ge 2$ and $k_{2}\ge 2$, $m^{'}-m=2^{k}-1-2m=2^k-2^{k_{1}+1}-2^{k_{2}+1}+3=(2^{k_{1}}-2)(2^{k_{2}}-2)-1>0$, then we complete the proof.

Proof of Lemma 2

First of all, it is clear that the result is true for $k=4$. Assuming that the regular saturated design S, based on k independent columns, has already been established, we aim to prove the case for $k+1$. Let $P^{'}$ consist of independent columns $a_{1}, \ldots , a_{k-1}$ and all their interaction columns. Then $C_{5}^{'}=P\cup Q\cup \left( b_{1}P^{*}\right) \cup \left( b_{2}P^{**}\right)$, and denote its complementary design as $\overline{C_{5}^{'}}$. $C_{5}^{'}$ and $\overline{C_{5}^{'}}$ have the following expressions:

$$\begin{aligned} C_{5}^{'}=C_{5}\cup a_{k-1}\{C_{5}\backslash b_{1}b_{2}\}\cup \{a_{k-1}\},\quad \overline{C_{5}^{'}}=\overline{C_{5}}\cup a_{k-1}\overline{C_{5}}\cup \{a_{k-1}b_{1}b_{2}\}. \end{aligned}$$

For any column $d\in \{a_{k-1}\overline{C_{5}},a_{k-1}b_{1}b_{2}\}$, if $d\in a_{k-1}\overline{C_{5}}$, then $a_{k-1}d\in \overline{C_{5}}$. Given that $C_{5}$ is an SOS design, it follows that $a_{k-1}d=e\cdot f$ for some $e\in C_{5}\backslash \{b_{1}b_{2}\}$ and $f\in C_{5}$. Therefore, $d=a_{k-1}e\cdot f$, where $a_{k-1}e\in a_{k-1}\{C_{5}\backslash b_{1}b_{2}\}\subset C_{5}^{'}$ and $f\in C_{5}\subset C_{5}^{'}$. If $d=a_{k-1}b_{1}b_{2}$, then $a_{k-1}b_{1}\in a_{k-1}\{C_{5}\backslash b_{1}b_{2}\}\subset C_{5}^{'}$ and $b_{2}\in C_{5}\subset C_{5}^{'}$. Consequently, $C_{5}^{'}$ is an SOS design.

For any column $d\in \{a_{k-1}\{C_{5}\backslash b_{1}b_{2}\},a_{k-1}\}$, if $d=a_{k-1}$, then there exists an $e\in \overline{C_{5}}\subset \overline{C_{5}^{'}}$ such that $a_{k-1}=e\cdot ea_{k-1}$ with $ea_{k-1}\in \{a_{k-1}\overline{C_{5}}\}\subset \overline{C_{5}^{'}}$. If $d\in a_{k-1}\{C_{5}\backslash b_{1}b_{2}\}$, then $a_{k-1}d\in C_{5}\backslash \{b_{1}b_{2}\}$. Since $\overline{C_{5}}$ is an SOS design, it follows that $a_{k-1}d=e\cdot f$ for some $e,f\in \overline{C_{5}}$. Therefore, $d=a_{k-1}e\cdot f$, where $a_{k-1}e\in \{a_{k-1}\overline{C_{5}}\}\subset C_{5}^{'}$ and $f\in \overline{C_{5}}\subset C_{5}^{'}$. Consequently, $\overline{C_{5}}$ is an SOS design.

Proof of Theorem 6

Given that $a_{j}^{'}b_{j}^{'}\in \overline{A^{'}}$ and $a_{i}^{'}\in A^{'}$, then $(a_{i}^{'},a_{j}^{'},b_{j}^{'})$ is an OA of strength 3. Since $a_{j}^{'}b_{j}^{''}=b_{j}^{'}\in G$ and $a_{i}^{'}\in \overline{G}$, $(a_{i}^{'},a_{j}^{'},b_{j}^{''})$ is also an OA of strength 3. The orthogonality is preserved after permuting the levels of the columns, making $(a_{i}^{''},a_{j}^{''},b_{j}^{''})$ an OA of strength 3. Consequently, $(a_{i},a_{j},b_{j})$ is an OA of strength 3. For a given SOS design $\overline{G}$, $(b_{i}^{'},b_{j}^{'},c_{j}^{'})$ is an OA of strength 3. With $a_{j}^{'}b_{j}^{'}=b_{j}^{''}$ and $c_{j}^{'}\ne b_{j}^{''}$, so $(a_{j}^{'},b_{j}^{'},c_{j}^{'})$ is an OA of strength 3. Similarly, $a_{j}^{'}b_{j}^{''}=b_{j}^{'}$ and $c_{j}^{''}\ne b_{j}^{'}$, so $(a_{j}^{'},b_{j}^{''},c_{j}^{''})$ is an OA of strength 3. Permuting the levels of the columns does not change the orthogonality, hence $(a_{j}^{''},b_{j}^{''},c_{j}^{''})$ is an OA of strength 3. Therefore, $(a_{j},b_{j},c_{j} )$ is an OA of strength 3. By Theorem 1, the design ($H_{1},H_{2}$), constructed by Algorithm 2, is an NSOA$\left( (2n,n),m,(8,4),(2*,2+)\right)$.

Proof of Theorem 11

After applying the level-collapsing operation by [a/2], each column in $H_{2}$ becomes $2a_{i}^{'}+b_{i}^{'}$. Given that $a^{'}_{i}b^{'}_{i}=b^{''}_{i}\in G$ and $a^{'}_{j}\in \overline{G}$, we have that $(a^{'}_{i},a^{'}_{j},b^{'}_{i})$ is an OA$(2^{k},3,2,3)$. Thus, $H_{2}$ is an SOA$(2^{k},m,4,2+)$ after the level-collapsing by [a/2] for $a=0,1,\dots , 7$. We take $E_{i}=1_{2}\otimes e_{i}$, for $i=1,\dots ,k$, and $E_{k+1}=(0_{2^{k}}^{T},1_{2^{k}}^{T})^{T}$. The $2^{k}-1$ column in S, denoted by $X_{k}$, consists of $E_{1},\dots ,E_{k}$ and all their interactions. Consequently, we have $A\subseteq X_{k}E_{k+1}$ and $B\subseteq X_{k}$. Therefore, $(a_{i},b_{i},a_{j},b_{j})$ is an OA$(2^{k+1},4,2,4)$ because the following three facts: (1) $a_{i}b_{i}\in X_{k}E_{k+1}$, so $a_{i}b_{i}\ne b_{j}$; (2) $a_{i}^{'}b_{i}^{'}=b_{i}^{''}\ne a_{j}^{'}$, thus $a_{i}b_{i}\ne a_{j}$; (3) $a_{i}^{'}b_{i}^{'}=b_{i}^{''}\ne b_{j}^{''}=a_{j}^{'}b_{j}^{'}$, therefore $a_{i}b_{i}\ne a_{j}b_{j}$. On the other hand, $(a_{i},b_{i},c_{i})$ is an OA$(2^{k+1},m,2,3)$. Consequently, $H_{1}$ is an SOA$(2^{k+1},m,8,2*)$ and achieves stratifications on $4\times 4$ grids in all two dimensions.

Proof of Theorem 12

Given that $a_{i}^{'}b_{i}^{'}=b_{i}^{''}\ne b_{j}^{'}$, $b_{i}^{''}\ne b_{j}^{''}=a_{j}^{'}b_{j}^{'}$, and $b_{i}^{''}\ne a_{j}^{'}$, we have that $(a_{i}^{'},a_{j}^{'},b_{i}^{'},b_{j}^{''})$ is an OA$(2^{k},4,2,4)$. Therefore, $H_{2}$ achieves stratifications on $4\times 4$ grids in all two dimensions after the level-collapsing by [a/2] for $a=0,1,\dots , 7$.

Proof of Theorem 15

Given that the interaction $a_{j}^{'}+\lambda _{l}b_{j}^{'}$ includes the term $e_{1}$ and $a_{j}^{'}+\lambda _{l}b_{j}^{'}\ne a_{i}^{'}$, for $l=\{0,\omega _{1},\dots$, $\omega _{s-1}\}$, we have that $(a_{i}^{'},a_{j}^{'},b_{j}^{'})$ is an OA of strength 3. Similarly, $(a_{i}^{''},a_{j}^{''},b_{j}^{''})$ is also an OA of strength 3. Since the interaction $b_{j}^{'}+\lambda _{l}c_{j}^{'}$ does not include the term $e^{u_{p}},\dots , e^{u_{q}}$ for $u_{p}=\cdots =u_{q}=\omega _{s-1}$ and $b_{j}^{'}+\lambda _{l}c_{j}^{'}\ne b_{i}^{'}$, we have that $(b_{i}^{'},b_{j}^{'},c_{j}^{'})$ is an OA of strength 3. Similarly, $(b_{i}^{''},b_{j}^{''},c_{j}^{''})$ is an OA of strength 3. The interaction $a_{i}^{'}c_{i}^{'}$ does not include the term $e_{1}$, and $a_{i}^{'}c_{i}^{'}\ne b_{i}^{'}$, so $(a_{i}^{'},b_{i}^{'},c_{i}^{'})$ is an OA of strength 3. Similarly, $(a_{i}^{''},b_{i}^{''},c_{i}^{''})$ is an OA of strength 3. By Theorem 1, we obtain an NSOA$((2s^{k},s^{k}),m=(s^{k-1}-1)/(s-1),(s^{3},s^{2}),(2*,2+))$ for $k\ge 3$.