1 Introduction

In the general setup of shock models, the system is assumed to subject shocks that occur randomly over time and they are usually defined by the help of renewal processes whose interarrival times represent the times between successive shocks. The literature includes various kind of shock models such as an extreme shock model, cumulative shock model, and run shock model (see, e.g. Sumita and Shanthikumar 1985; Gut 1990; Mallor and Omey 2001).

Assume that a system is subjected to external shocks that arrive according to a renewal process \(N(t)\) defined by

$$\begin{aligned} N(t)=\sup \left\{ n:S_{n}\le t\right\} , \end{aligned}$$

where \(S_{n}=\sum \nolimits _{i=1}^{n}X_{i}\) is the time of the \(n\)th shock and the interarrival times between two successive shocks, \(X_{i}, i=1,2,\ldots \) are independent random variables with common cumulative distribution function (cdf) \(F\) (\(F(0)=0\)).

According to the \(\delta \)-shock model, the system fails when the time between two consecutive shocks falls below a fixed threshold \(\delta \) (Wang and Zhang 2001; Li and Kong 2007; Li and Zhao 2007; Eryilmaz 2012, 2013). That is, if \(X_{n}>\delta ,\) the system can recover before the \(n\)th shock, and does not fail; if \(X_{n}\le \delta \), the system fails. Therefore the lifetime of system is defined by the following compound random variable

$$\begin{aligned} T=\sum \limits _{i=1}^{N}X_{i}, \end{aligned}$$

where \(N\) is the waiting time for the first interarrival time which is less than a threshold \(\delta ,\) i.e.

$$\begin{aligned} \left\{ N=n\right\} \quad \text{ iff } \left\{ X_{1}>\delta ,\ldots ,X_{n-1}>\delta ,X_{n}\le \delta \right\} . \end{aligned}$$

This \(\delta \)-shock model has a potential application in various fields such as inventory, insurance and system reliability. In insurance, the random variables \(X_{i},i=1,2,\ldots \) represent the interclaim times. In the model of a queueing system, \(X_{i}\) is the waiting time between the arrivals of consecutive customers. Thus a relevant problem might be of interest in the fields such as economics and operational research.

Recently, Ma and Li (2010) have introduced and studied a censored \(\delta \)-shock model. According to this model, the lifetime of the system is defined by the random variable

$$\begin{aligned} \bar{T}=\sum \limits _{i=0}^{\bar{N}}X_{i}+\delta , \end{aligned}$$

where

$$\begin{aligned} \left\{ \bar{N}=n\right\} \quad \text{ iff } \left\{ X_{1}<\delta ,\ldots ,X_{n}<\delta ,X_{n+1}\ge \delta \right\} , \end{aligned}$$

with \(X_{0}\equiv 0.\)

So far in the literature, the above mentioned shock models have been studied only for the case when \(N(t)\) is a Poisson process, i.e. the interarrival times between successive shocks follow exponential distribution. However, there might be a situation that the time between shocks has an arbitrary distribution such as uniform, gamma and weibull. In the present paper we study the random variables \(T\) and \(\bar{T}\) when the shocks occur according to a renewal process whose interarrival times follow uniform distribution. The uniform distribution is useful when we wish to observe the first order effects of stochastic variation. That is, it is a useful distribution when we want to show the main differences between deterministic and stochastic models. For the queueing systems and renewal processes with uniform interarrival times see, e.g. Rosberg (1987) and Kao (1997). In particular, we obtain the first two moments of the corresponding random variables for general \(F.\) The survival functions of \(T\) and \(\bar{T}\) are explicitly derived when the interarrival distribution \(F\) is uniform distribution function on \((0,a).\)

2 Results for \(\delta \)-shock model

If the interarrival times between two successive shocks, \(X_{i},\) \(i=1,2,\ldots \) are independent random variables with common cdf \(F,\) then the probability mass function of the random variable \(N\) is

$$\begin{aligned} P\left\{ N=n\right\} =(\bar{F}(\delta ))^{n-1}F(\delta ), \end{aligned}$$
(1)

for \(n=1,2,\ldots \).

Lemma 1

For a sequence of interarrival times \(X_{1},X_{2},\ldots \) with common cdf \(F,\)

$$\begin{aligned} P\left\{ T>t\right\} =\sum \limits _{n=1}^{\infty }(\bar{F}(\delta ))^{n-1}\int \limits _{0}^{\delta }P\left\{ S_{n-1}^{*}>t-x\right\} dF(x), \end{aligned}$$
(2)

where \(S_{n}^{*}\) is the \(n\)th arrival time of a renewal process whose interarrival times have the cdf

$$\begin{aligned} F_{\delta }^{*}(x)=\frac{F(x)-F(\delta )}{1-F(\delta )}, \end{aligned}$$

for \(x>\delta \).

Proof

By conditioning on \(N\),

$$\begin{aligned} P\left\{ T>t\right\}&= P\left\{ \sum \limits _{i=1}^{N}X_{i}>t\right\} \\&= \sum \limits _{n=1}^{\infty }P\left\{ S_{n}>t,X_{1}>\delta ,\ldots ,X_{n-1}>\delta ,X_{n}\le \delta \right\} \end{aligned}$$

Because \(S_{n}=S_{n-1}+X_{n}\) and \(X_{n}\) is independent of \(S_{n-1}\) one obtains

$$\begin{aligned}&P\left\{ S_{n}>t,X_{1}>\delta ,\ldots ,X_{n-1}>\delta ,X_{n}\le \delta \right\} \\&\quad =\int \limits _{0}^{\delta }P\left\{ S_{n-1}>t-x,X_{1}>\delta ,\ldots ,X_{n-1}>\delta \right\} dF(x)\\&\quad =P\left\{ X_{1}>\delta ,\ldots ,X_{n-1}>\delta \right\} \\&\qquad \times \int \limits _{0}^{\delta }P\left\{ S_{n-1}>t-x\mid X_{1}>\delta ,\ldots ,X_{n-1}>\delta \right\} dF(x). \end{aligned}$$

The conditional distribution of \(S_{n-1}\) given \(\left\{ X_{1}>\delta ,\ldots ,X_{n-1}>\delta \right\} \) is same with the distribution of the sum of \( n-1\) independent random variables having truncated cdf

$$\begin{aligned} F_{\delta }^{*}(x)=P\left\{ X_{1}\le x\mid X_{1}>\delta \right\} =\frac{F(x)-F(\delta )}{1-F(\delta )}, \end{aligned}$$

for \(x>\delta \), that is

$$\begin{aligned} P\left\{ S_{n-1}>t-x\mid X_{1}>\delta ,\ldots ,X_{n-1}>\delta \right\} =P\left\{ S_{n-1}^{*}>t-x\right\} , \end{aligned}$$

where \(S_{n-1}^{*}=\sum \nolimits _{i=1}^{n}X_{i}^{*}\) and \(F_{\delta }^{*}(x)=P\left\{ X_{i}^{*}\le x\right\} ,i=1,2,\ldots ,n\). Thus the proof is completed. \(\square \)

In the following we obtain the first two moments of \(T\).

Proposition 1

For a sequence of interarrival times \(X_{1},X_{2},\ldots \) with common cdf \(F,\)

$$\begin{aligned} E(T)=\frac{E(X_{1})}{F(\delta )}, \end{aligned}$$

and

$$\begin{aligned} E(T^{2})&= \left( \frac{1-F(\delta )}{F(\delta )}\right) E(X_{1}^{2}\mid X_{1}>\delta )+E(X_{1}^{2}\mid X_{1}\le \delta ) \\&+2\left( \frac{1-F(\delta )}{F(\delta )}\right) ^{2}\left[ E(X_{1}\mid X_{1}>\delta )\right] ^{2} \\&+2\left( \frac{1-F(\delta )}{F(\delta )}\right) \left[ E(X_{1}\mid X_{1}>\delta )E(X_{1}\mid X_{1}\le \delta )\right] . \end{aligned}$$

Proof

Since the event \(\left\{ N=n\right\} \) is independent of \( X_{n+1},X_{n+2},\ldots \) for all \(n=1,2,\ldots \) the random variable \(N\) is a stopping time for \(X_{1},X_{2},\ldots \) Thus from Wald’s equation we readily have

$$\begin{aligned} E(T)=E(N)E(X_{1})=\frac{E(X_{1})}{F(\delta )}. \end{aligned}$$

For the second moment, by conditioning on \(N,\)

$$\begin{aligned} E(T^{2})\!=\!\sum \limits _{n=1}^{\infty }E\left( \left( \sum \limits _{i=1}^{n}X_{i}\right) ^{2}\mid N\!=\!n\right) P\left\{ N\!=\!n\right\} . \end{aligned}$$
(3)

It is clear that

$$\begin{aligned} E\left( \left( \sum \limits _{i=1}^{n}X_{i}\right) ^{2}\mid N\!=\!n\right) =\sum \limits _{i=1}^{n}E(X_{i}^{2}\mid N\!=\!n)\!+\!2\underset{1\le i<j\le n}{ \sum \sum }E(X_{i}X_{j}\mid N\!=\!n).\quad \end{aligned}$$
(4)

By the definition of \(N,\)

$$\begin{aligned} \sum \limits _{i=1}^{n}E(X_{i}^{2}\mid N=n)=(n-1)E(X_{1}^{2}\mid X_{1}>\delta )+E(X_{n}^{2}\mid X_{n}\le \delta ), \end{aligned}$$
(5)

and

$$\begin{aligned}&\underset{1\le i<j\le n}{\sum \sum }E(X_{i}X_{j} \mid N=n)=\genfrac(){0.0pt}0{n-1 }{2}\left[ E(X_{1}\mid X_{1}>\delta )\right] ^{2} \nonumber \\&\quad +(n-1)E(X_{1} \mid X_{1}>\delta )E(X_{n}\mid X_{n}\le \delta ). \end{aligned}$$
(6)

Using (5) and (6) in (4) and then via (3) one obtains

$$\begin{aligned} E(T^{2})&= (E(N)-1)E(X_{1}^{2}\mid X_{1}>\delta )+E(X_{1}^{2}\mid X_{1}\le \delta ) \\&+E\left[ (N-1)(N-2)\right] \left[ E(X_{1}\mid X_{1}>\delta )\right] ^{2} \\&+2(E(N)-1)\left[ E(X_{1}\mid X_{1}>\delta )E(X_{1}\mid X_{1}\le \delta ) \right] \end{aligned}$$

and the results follows noting that \(E\left[ (N-1)(N-2)\right] =2\frac{ (1-F(\delta ))^{2}}{F^{2}(\delta )}\). \(\square \)

As it can be seen from Lemma 1, the derivation of the survival function of \( T \) needs to determine the distribution of the sum \(S_{n}^{*}\) of \(n\) independent random variables having the cdf \(F_{\delta }^{*}(x).\) Obviously, this is not an easy task except for some special cases. In the following we evaluate (2) when \(F\) is uniform on \((0,a)\) for \(a>\delta .\)

Theorem 1

For a sequence of interarrival times \(X_{1},X_{2},\ldots \) having uniform distribution on \((0,a)\) (\(a>\delta \)),

$$\begin{aligned} P\left\{ T>t\right\} =\sum \limits _{n=2+\left[ \frac{t-\delta }{a}\right] }^{1+\left[ \frac{t}{\delta }\right] }\left( 1-\frac{\delta }{a}\right) ^{n-1}\int \limits _{\max (0,t-(n-1)a)}^{\min (\delta ,t-(n-1)\delta )}\frac{1}{a}P\left\{ S_{n-1}^{*}>t-x\right\} dx \end{aligned}$$
$$\begin{aligned} +\sum \limits _{n=1+\left[ \frac{t}{\delta }\right] }^{\infty }\left( 1-\frac{ \delta }{a}\right) ^{n-1}\left\{ \frac{\delta -\max (0,t-(n-1)\delta )}{a} \right\} , \end{aligned}$$

for \(t>\delta ,\) and \(P\left\{ T>t\right\} =1-\frac{t}{a}\) for \(t\le \delta ,\) where

$$\begin{aligned} P\left\{ S_{n}^{*}>t\right\}&= \frac{1}{(a-\delta )^{n}(n-1)!} \sum \limits _{k=0}^{n}(-1)^{k}\left( {\frac{n}{k}} \right) \frac{1}{n}\left\{ \left[ n(a-\delta )-k(a-\delta )\right] ^{n}\right. \\&\left. -\left[ \max (t-n\delta ,k(a-\delta ))-k(a-\delta )\right] ^{n}\right\} , \end{aligned}$$

for \(t>n\delta \) and \(P\left\{ S_{n}^{*}>t\right\} =1\) if \(t\le n\delta .\)

Proof

If \(F\) is uniform on \((0,a)\) (\(a>\delta \)), then \(F_{\delta }^{*}\) is a uniform distribution function defined on \((\delta ,a).\) Thus \(S_{n}^{*}\) is the sum of \(n\) independent uniform random variables defined on \((\delta ,a).\) Equivalently, we can write

$$\begin{aligned} P\left\{ S_{n}^{*}>t\right\} =P\left\{ \sum \limits _{i=1}^{n}Y_{i}>t-n\delta \right\} , \end{aligned}$$

where \(Y_{i}\)s are uniformly distributed random variables on \((0,a-\delta )\) . From Theorem 1 of Sadooghi-Alvandi et al. (2009) the density function of \( \sum \nolimits _{i=1}^{n}Y_{i}\) is

$$\begin{aligned} f(s)=\frac{1}{(a-\delta )^{n}(n-1)!}\sum \limits _{k=0}^{n}(-1)^{k}\left( {\frac{n}{k}} \right) \left[ (s-k(a-\delta ))_{+}\right] ^{n-1}, \end{aligned}$$
(7)

for \(n\ge 2\) and \(0<s<n(a-\delta ),\) where \(x_{+}=\max (0,x).\) Using (7) the survival function of \(S_{n}^{*}\) is obtained as

$$\begin{aligned} P\left\{ S_{n}^{*}>t\right\}&= \int \limits _{t-n\delta }^{n(a-\delta )}f(s)ds\\&= \frac{1}{(a-\delta )^{n}(n-1)!}\sum \limits _{k=0}^{n}(-1)^{k}\left( {\frac{n}{k}} \right) \frac{1}{n}\left\{ \left[ n(a-\delta )-k(a-\delta )\right] ^{n}\right. \\&\left. -\left[ \max (t-n\delta ,k(a-\delta ))-k(a-\delta )\right] ^{n}\right\} , \end{aligned}$$

for \(t>n\delta \) and \(P\left\{ S_{n}^{*}>t\right\} =1\) if \(t\le n\delta .\)

Because \(P\left\{ S_{n-1}^{*}>t-x\right\} =1\) if \(t-x\le (n-1)\delta \) the integral in (2) can be evaluated as

$$\begin{aligned} \int \limits _{0}^{\delta }P\left\{ S_{n-1}^{*}>t-x\right\} dF(x)&= \int \limits _{\max (0,t-(n-1)\delta )}^{\delta }\frac{1}{a} dx\\&+\int \limits _{\max (0,t-(n-1)a)}^{\min (\delta ,t-(n-1)\delta )}\frac{1}{a }P\left\{ S_{n-1}^{*}>t-x\right\} dx. \end{aligned}$$

Thus we obtain

$$\begin{aligned} P\left\{ T>t\right\} =\sum \limits _{n=2+\left[ \frac{t-\delta }{a}\right] }^{1+\left[ \frac{t}{\delta }\right] }\left( 1-\frac{\delta }{a}\right) ^{n-1}\int \limits _{\max (0,t-(n-1)a)}^{\min (\delta ,t-(n-1)\delta )}\frac{1 }{a}P\left\{ S_{n-1}^{*}>t-x\right\} dx \end{aligned}$$
$$\begin{aligned} +\sum \limits _{n=1+\left[ \frac{t}{\delta }\right] }^{\infty }\left( 1-\frac{ \delta }{a}\right) ^{n-1}\left\{ \frac{\delta -\max (0,t-(n-1)\delta )}{a} \right\} , \end{aligned}$$

for \(t>\delta ,\) and \(P\left\{ T>t\right\} =1-\frac{t}{a}\) for \(t\le \delta \) \(\square \)

Proposition 2

For a sequence of interarrival times \(X_{1},X_{2},\ldots \) having uniform distribution on \((0,a)\),

$$\begin{aligned} E(T)=\frac{a^{2}}{2\delta }, \end{aligned}$$

and

$$\begin{aligned} E(T^{2})&= \frac{(a-\delta )\left[ 3(a+\delta )^{2}+(a-\delta )^{2}\right] }{12\delta }+\frac{\delta ^{2}}{3} \\&+\frac{(a-\delta )^{2}(a+\delta )^{2}}{2\delta ^{2}}+\frac{(a-\delta )(a+\delta )}{2}. \end{aligned}$$

Proof

The proofs are immediate since the conditional random variables \(\left( X_{1}\mid X_{1}>\delta \right) \) and \(\left( X_{1}\mid X_{1}\le \delta \right) \) have uniform distributions on \((\delta ,a)\) and \((0,\delta ) \), respectively. \(\square \)

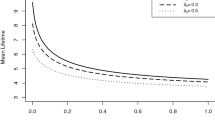
Although the survival function of \(T\) is given as series of terms involving integrals, it can be computed numerically using mathematical packages. In Table 1, we compute \(P\left\{ T>t\right\} \) for selected values of \(\delta \) and \(t\) when \(F\) is uniform on \((0,1)\). Table 2 includes the mean time to failure of the system (\(E(T)\)) and \(Var(T)\) for different choices of \(a\) and \(\delta .\)

Table 1 Survival function of \(T\) for unit uniform distribution
Full size table
Table 2 Mean and variance of \(T\)
Full size table

2.1 Estimation problem

Because the random variables \(X_{i},i=1,2,\ldots \) represent the interarrival times between successive events (claims, arrivals, failures etc.) the system failure occurs if the waiting time between two successive events is below a threshold parameter \(\delta \). That is, the system cannot recover if the length between two successive occurrences is below \(\delta \). In most cases, we only observe the system’s lifetime and the data between the occurrences of the events is not recorded. In this framework, the problem of estimating threshold parameter \(\delta \) from system’s lifetime data might be interesting from statistical point of view. If \(t_{1},\ldots ,t_{n}\) represent the lifetime data based on \(n\) independent systems, then using Proposition 2 we can obtain the moment estimators of the parameters \(a\) and \(\delta \) by solving

$$\begin{aligned} E(T)=\frac{a^{2}}{2\delta }=\frac{1}{n}\sum \limits _{i=1}^{n}t_{i}, \end{aligned}$$

and

$$\begin{aligned} E(T^{2})&= \frac{(a-\delta )\left[ 3(a+\delta )^{2}+(a-\delta )^{2}\right] }{12\delta }+\frac{\delta ^{2}}{3} \\&+\frac{(a-\delta )^{2}(a+\delta )^{2}}{2\delta ^{2}}+\frac{(a-\delta )(a+\delta )}{2}=\frac{1}{n}\sum \limits _{i=1}^{n}t_{i}^{2}. \end{aligned}$$

Similar estimation problems have been considered in Xu and Li (2004) and Li et al. (2007).

3 Results for censored \(\delta \)-shock model

If the interarrival times between two successive shocks, \(X_{i},\) \(i=1,2,\ldots \) are independent random variables with common cdf \(F,\) then the probability mass function of the random variable \(\bar{N}\) is

$$\begin{aligned} P\left\{ \bar{N}=n\right\} =(F(\delta ))^{n}(1-F(\delta )), \end{aligned}$$

for \(n=0,1,\ldots \) and

$$\begin{aligned} E(\bar{N})=\frac{F(\delta )}{1-F(\delta )}, \quad Var(\bar{N})=\frac{ F(\delta )}{(1-F(\delta ))^{2}}. \end{aligned}$$

Lemma 2

Let \(X_{1},X_{2},\ldots \) be a sequence of interarrival times with common cdf \(F.\) Then for \(t\ge \delta \)

$$\begin{aligned} P\left\{ \bar{T}>t\right\} =\sum \limits _{n=1}^{\infty }P\left\{ \bar{S} _{n}>t-\delta \right\} (F(\delta ))^{n}(1-F(\delta )), \end{aligned}$$

where \(\bar{S}_{n}\) is the \(n\)th arrival time of a renewal process whose interarrival times have the cdf

$$\begin{aligned} G_{\delta }(x)=\left\{ \begin{array}{c@{\quad }c} \frac{F(x)}{F(\delta )} &{} if\;x<\delta \\ 1 &{} if\;x\ge \delta \end{array} \right. , \end{aligned}$$

and \(P\left\{ \bar{T}>t\right\} =1\) for \(t<\delta .\)

Proof

By conditioning on the value of \(\bar{N},\)

$$\begin{aligned} P\left\{ \bar{T}>t\right\} =P\left\{ \bar{T}>t,\bar{N}=0\right\} +\sum \limits _{n=1}^{\infty }P\left\{ \bar{T}>t,\bar{N}=n\right\} . \end{aligned}$$

If \(t\ge \delta ,\) then \(P\left\{ \bar{T}>t,\bar{N}=0\right\} =0\) and hence

$$\begin{aligned} P\left\{ \bar{T}>t\right\}&= \sum \limits _{n=1}^{\infty }P\left\{ S_{n}>t-\delta ,\bar{N}=n\right\} \\&= \sum \limits _{n=1}^{\infty }P\left\{ S_{n}>t-\delta \mid X_{1}<\delta ,\ldots ,X_{n}<\delta \right\} (F(\delta ))^{n}(1-F(\delta )), \end{aligned}$$

for \(t\ge \delta .\) The proof follows since the distribution of \(\left\{ S_{n}\mid X_{1}<\delta ,\ldots ,X_{n}<\delta \right\} \) is same with the distribution of \(\bar{S}_{n}\) which is the sum of \(n\) independent random variables having common cdf \(G_{\delta }\). \(\square \)

Remark 1

The distribution of \(\bar{T}\) is neither discrete nor continuous since \(P\left\{ \bar{T}=\delta \right\} =P\left\{ \bar{N} =0\right\} =1-F(\delta )>0.\)

Proposition 3

Let \(X_{1},X_{2},\ldots \) be a sequence of interarrival times with common cdf \(F.\) Then

$$\begin{aligned} E(\bar{T})=\frac{F(\delta )}{(1-F(\delta ))}E(X_{1}\mid X_{1}<\delta )+\delta , \end{aligned}$$
(8)

and

$$\begin{aligned} Var(\bar{T})=\frac{F(\delta )}{(1-F(\delta ))}Var(X_{1}\mid X_{1}<\delta )+ \frac{F(\delta )}{(1-F(\delta ))^{2}}\left[ E(X_{1}\mid X_{1}<\delta )\right] ^{2}.\qquad \end{aligned}$$
(9)

Proof

By the definition of \(\bar{T},\)

$$\begin{aligned} E(\bar{T})=E\left( \sum \limits _{i=1}^{\bar{N}}X_{i}\right) +\delta \end{aligned}$$

By conditioning on \(\bar{N},\)

$$\begin{aligned} E\left( \sum \limits _{i=1}^{\bar{N}}X_{i}\right)&= \sum \limits _{n=1}^{\infty }nE(X_{1}\mid X_{1}<\delta )P\left\{ \bar{N} =n\right\} \nonumber \\&= E(X_{1}\mid X_{1}<\delta )E(\bar{N}) \end{aligned}$$
(10)

which completes the proof of (8).

$$\begin{aligned} Var(\bar{T})=Var\left( \sum \limits _{i=1}^{\bar{N}}X_{i}\right) =E\left( \sum \limits _{i=1}^{\bar{N}}X_{i}\right) ^{2}-\left[ E\left( \sum \limits _{i=1}^{\bar{N}}X_{i}\right) \right] ^{2}. \end{aligned}$$
(11)

We have

$$\begin{aligned} E\left( \sum \limits _{i=1}^{\bar{N}}X_{i}\right) ^{2}=\sum \limits _{n=1}^{\infty }E\left( \left( \sum \limits _{i=1}^{n}X_{i}\right) ^{2}\mid \bar{N}=n\right) P\left\{ \bar{N} =n\right\} , \end{aligned}$$

where

$$\begin{aligned} E\left( \left( \sum \limits _{i=1}^{n}X_{i}\right) ^{2}\mid \bar{N}=n\right) =nE(X_{1}^{2}\mid X_{1}<\delta )+n(n-1)\left[ E(X_{1}\mid X_{1}<\delta ) \right] ^{2}. \end{aligned}$$

Simple manipulations yield

$$\begin{aligned} E\left( \sum \limits _{i=1}^{\bar{N}}X_{i}\right) ^{2}=E(\bar{N} )Var(X_{1}\mid X_{1}<\delta )+E(\bar{N}^{2})\left[ E(X_{1}\mid X_{1}<\delta ) \right] ^{2}. \end{aligned}$$
(12)

Thus the proof of (9) is completed using (10) and (12) in (11). \(\square \)

Theorem 2

For a sequence of interarrival times \(X_{1},X_{2},\ldots \) having uniform distribution on \((0,a)\) (\(a>\delta \))\(,\)

$$\begin{aligned} P\left\{ \bar{T}>t\right\}&= \left( 1-\frac{\delta }{a}\right) \sum \limits _{n=1}^{\infty }\sum \limits _{k=0}^{n}(-1)^{k}\genfrac(){0.0pt}0{n}{k}\frac{ 1}{n!a^{n}} \\&\times \left\{ \left( \max (t-\delta ,k\delta )-k\delta \right) ^{n}-\delta ^{n}(n-k)^{n}\right\} , \end{aligned}$$

for \(t\ge \delta \) and \(P\left\{ \bar{T}>t\right\} =1\) for \(t<\delta .\)

Proof

If \(F\) is uniform on \((0,a)\) (\(a>\delta \)), then \(G_{\delta }\) is a uniform distribution function defined on \((0,\delta ).\) Thus \(\bar{S} _{n}\) is the sum of \(n\) independent uniform random variables defined on \( (0,\delta )\) and its pdf is

$$\begin{aligned} f_{\bar{S}_{n}}(s)=\frac{1}{\delta ^{n}(n-1)!}\sum \limits _{k=0}^{n}(-1)^{k} \left( {\frac{n}{k}} \right) \left[ (s-k\delta )_{+}\right] ^{n-1}, \end{aligned}$$

for \(n\ge 2\) and \(0<s<n\delta .\) Therefore the required result is obtained using

$$\begin{aligned} P\left\{ \bar{S}_{n}>t-\delta \right\} =\int \limits _{t-\delta }^{n\delta }f_{\bar{S}_{n}}(s)ds=\frac{1}{n}\left\{ \left( \max (t-\delta ,k\delta )-k\delta \right) ^{n}-\delta ^{n}(n-k)^{n}\right\} \end{aligned}$$

in Lemma 2. \(\square \)

The following result can be immediately obtained using Proposition 3 since the conditional random variable \((X_{1}\mid X_{1}<\delta )\) has uniform distribution on \((0,\delta ).\)

Proposition 4

For a sequence of interarrival times \(X_{1},X_{2},\ldots \) having uniform distribution on \((0,a)\),

$$\begin{aligned} E(\bar{T})=\frac{\delta (2a-\delta )}{2(a-\delta )}, \quad Var(\bar{T})= \frac{\delta ^{3}(4a-\delta )}{12(a-\delta )^{2}}, \end{aligned}$$

for \(a>\delta .\)

4 Summary and Conclusions

In this paper, we have studied \(\delta \)-shock and censored \(\delta \)-shock models for uniformly distributed interarrival times. In particular, we have obtained explicit expressions for the survival functions of the corresponding lifetime random variables. Our derivations are mainly based on the distribution of the sum of independent uniform random variables. We have also obtained expressions for the first two moments of the lifetime random variables for an arbitrary interarrival time distribution.

The study of \(\delta \)-shock and censored \(\delta \)-shock models for general interarrival distribution will be among our future research problems. On the other hand, the statistical estimation problem mentioned in Sect. 2.1 can also be studied extensively using other estimation methods.