Clustering Large Datasets by Merging K-Means Solutions

Abstract

Existing clustering methods range from simple but very restrictive to complex but more flexible. The K-means algorithm is one of the most popular clustering procedures due to its computational speed and intuitive construction. Unfortunately, the application of K-means in its traditional form based on Euclidean distances is limited to cases with spherical clusters of approximately the same volume and spread of points. Recent developments in the area of merging mixture components for clustering show good promise. We propose a general framework for hierarchical merging based on pairwise overlap between components which can be readily applied in the context of the K-means algorithm to produce meaningful clusters. Such an approach preserves the main advantage of the K-means algorithm—its speed. The developed ideas are illustrated on examples, studied through simulations, and applied to the problem of digit recognition.

1 Introduction

Cluster analysis is the area of unsupervised learning with the objective of grouping data in such a way that observations within each group have similar characteristics but groups themselves are relatively distinct. Such groups of data points are commonly called clusters. As follows from this description, the notion of a cluster is subjective and can vary not only based on the nature of the data but also analysis goals. In the most traditional understanding of the word, clusters present group objects heavily populated with observations and separated from each other by substantial gaps in the density of data points. The more clear the density gap, the more distinct (or well-separated) clusters are. There exist a wide variety of clustering methods. Among procedures most popular in statistical literature, there are hierarchical agglomerative and divisive algorithms (Sneath 1957; Ward 1963), K-means (MacQueen 1967) and K-medoids (Kaufman and Rousseeuw 1990) algorithms, and model-based clustering (Fraley and Raftery 2002).

Hierarchical algorithms rely on the notion of the object dissimilarity and vary according to the rules of measuring distances among objects. Such rules are commonly called linkages. The single linkage (Sneath 1957) measures the closeness of groups based on the distance between two nearest neighboring objects that belong to the groups. It is well-known for the so-called chaining effect that is helpful in detecting well-separated clusters (in the sense of separation by substantial gaps in the density of data points) of arbitrary shapes (see, e.g., page 685 in Johnson and Wichern 2007). On the other hand, the use of this linkage should not be recommended if the goal is to identify groups with a considerable overlap. Ward’s linkage (Ward 1963) is one potential candidate in such a situation. This rule aims at minimizing the increase in the error sum of squares associated with merging and tends to produce compact clusters of roughly elliptical shapes (see, e.g., page 693 in Johnson and Wichern 2007). Ward’s linkage is a reasonable choice when the goal is the detection of compact clusters in the presence of substantial overlap.

Model-based clustering employs the notion of finite mixture models (McLachlan and Peel 2000) with every mixture component modeling a particular group of data. Model-based clustering methods show great flexibility in modeling heterogeneity in data due to their ability to incorporate distributions of essentially all forms. Under this setting, clusters are allowed to have various levels of separation, skewness, modality, etc. The specific form of a cluster is completely defined by the properties of a mixture component associated with it.

Despite excellent performance demonstrated in experiments and applications, model-based clustering is a rather sophisticated tool that requires that the functional form of mixture components is known in advance. Michael and Melnykov (2016) studied how the performance of the method changes with varying complexity of datasets and showed that as the dimensionality and size of the data increases the performance also decreased. This will limit its application in the case of clustering massive datasets.

With no doubt, K-means is one of the most well-known and widely used clustering algorithms. While proposed around the middle of the last century, even nowadays a substantial amount of literature is devoted to studying the algorithm and its properties (Steinley and Brusco 2007; Celebi et al. 2012; Melnykov and Melnykov 2014; Aletti and Micheletti 2017). The main reasons justifying its popularity among practitioners are computational speed and intuitive nature. K-means represents the class of partitional clustering algorithms (Celebi 2015) and, in its most traditional form, aims at minimizing the objective function ${\sum }_{i = 1}^{n} {\sum }_{k = 1}^{K} I(z_{i} = k)||\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k}||^{2}$ over membership labels z₁,z₂,…,z_n and cluster mean vectors μ₁,μ₂,…,μ_K, where y₁,y₂,…,y_n is the observed dataset consisting of n data points, K is the number of clusters, and $I(\mathcal {A})$ is an indicator function yielding 1 if the condition $\mathcal {A}$ is true and producing 0 otherwise. Thus, K-means minimizes the within cluster sum of squares which is accomplished through an iterative two-step procedure. At the first step of the b th iteration, the partitioning $z_{1}^{(b)}, z_{2}^{(b)}, \ldots , z_{n}^{(b)}$ is obtained according to the rule $z_{i}^{(b)} = \arg \min _{k}||\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k}^{(b-1)}||$, i.e., based on the proximity of y_i to the current cluster centers measured in terms of Euclidean distances. At the second step, cluster means are recalculated according to the following formula:

$$ \boldsymbol{\mu}_{k}^{(b)} = \frac{{\sum}_{i = 1}^{n} I(z_{i}^{(b)} = k)\boldsymbol{y}_{i}}{{\sum}_{i = 1}^{n} I(z_{i}^{(b)} = k)}. $$

(1)

The algorithm is terminated when a stable partitioning solution is obtained yielding the estimated partitioning vector $\hat z_{1}, \hat z_{2}, \ldots , \hat z_{n}$ and mean estimates $\hat {\boldsymbol {\mu }}_{1}, \hat {\boldsymbol {\mu }}_{2}, \ldots , \hat {\boldsymbol {\mu }}_{K}$.

Despite the general attractiveness and popularity of the K-means algorithm, there are numerous issues and restrictions that have to be taken into consideration before applying the algorithm. K-means is designed to show good performance on spherical clusters with approximately the same volume and spread of points. Three examples illustrating the performance of K-means in various scenarios are provided in Fig. 1. In each case, there are two well-separated clusters that may differ in shape or size. 95% confidence ellipsoids and different colors represent the true groupings, while plotting characters illustrate the solution obtained by the algorithm. In plot (a), there are many observations from the elongated cluster that are mistakenly combined into a common group with data points from the smaller cluster. This effect can be explained by the use of Euclidean distances to measure the proximity of observations to cluster centers. When cluster shapes deviate from being spherical, K-means should be applied with extra caution. In the meantime, the sphericity itself does not necessarily lead to finding good partitionings. As we can see from plot (b), several observations from the edge of the cluster with larger volume are misclassified implying that the presence of spherical clusters is still insufficient for the successful use of K-means. Finally, plot (c) highlights the ideal conditions, under which the K-means algorithm is expected to perform best. There are two spherical clusters of approximately the same volume and spread of data points. The considered illustrations suggest that practitioners should be very careful with the use of K-means as the ideal conditions necessary for the good performance of the algorithm are very restrictive and often unrealistic.

Fig. 1

a–c Illustrative examples: solutions provided by the K-means algorithm. Colors represent different groups, ellipsoids denote corresponding 95% confidence regions, and plotting characters illustrate the partitioning obtained by K-means

One possibility to relax the imposed restrictions is to employ a more general distance metric such as the Mahalanobis one. Then, K-means has the same flavor as the algorithm based on Euclidean distances, but involves calculating distances by $\sqrt {(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})^{T}\boldsymbol {\Sigma }^{-1}_{k}(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})}$, where Σ_k is the covariance matrix associated with the k th data group. For more details on this version of K-means, we refer the reader to a paper by Melnykov and Melnykov (2014). Unfortunately, due to such a modification, K-means loses much of its original appeal due to the necessity to initialize, estimate, and invert covariance matrices Σ_k for k = 1,2,…,K. An interesting approach to covariance matrix estimation based on double shrinkage method was considered in Aletti and Micheletti (2017). In general, we can conclude that K-means in its traditional form lacks flexibility to provide good solutions unless in most trivial situations. On the other hand, more complex versions of K-means might provide better options at a higher cost. In this paper, we propose an alternative approach to clustering through K-means that makes the algorithm applicable in a much broader range of problems.

Some motivation behind the proposed approach can be found in the analysis of dataset Crabs (Campbell and Mahon 1974) by means of the popular model-based clustering R package mclust (Fraley and Raftery 2006) which employs Gaussian mixture models with different covariance matrix structures. There are four classes in this dataset. One hundred observations represent Blue crabs, while the other hundred data points represent Orange crabs. Each of these two species are further divided into male and female subgroups of equal sizes. The dataset is known to be difficult for clustering. Hennig (2010) explained the challenges by model misspecifications, Bouveyron and Brunet (2014) referred to dimensionality issues, and Melnykov (2013) blamed the problem of initialization. An interesting observation can be made as a result of running mclust: among all models, the software chooses the one with nine Gaussian components with covariance matrices of the same shape, orientation, and volume. This nine-component mixture was preferred over many other sophisticated models, including those with unequal covariance matrices. This example suggests that at least sometimes it might be reasonable to fit the data with multiple trivial components instead of using few complicated ones. This conclusion can be joined with the idea of merging components that are located so close to each other that they are likely to model the same cluster. The idea of merging mixture components for model-based clustering was recently considered by several authors (Baudry et al. 2010; Finak and Gottardo 2016; Melnykov 2016). This approach serves as an effective remedy in many cases when the existence of the one-to-one correspondence between clusters and mixture components is not a reasonable assumption. The technique considered in this paper is based on the connection established between model-based clustering and K-means. This connection allows measuring the degree of overlap between components of a K-means solution that is necessary for deciding which groups have to be merged. It provides an effective remedy for K-means that considerably extends the area of possible applications of this popular algorithm. One of its main advantages is the applicability to clustering massive datasets.

The rest of the paper is organized as follows. Section 2 focuses on necessary preliminaries in finite mixture modeling as well as merging mixture components. Section 3 establishes the connection between K-means and model-based clustering and develops an approach for merging solutions obtained by K-means. It also introduces a new visualization tool called the overlap map. Section 4 investigates the performance of the developed technique in various situations. An application to digit recognition is considered in Section 5. A discussion is given in Section 6. An appendix is supplied to show other extensions of the current methodology and other supplementary material.

2 Finite Mixture Modeling and Model-Based Clustering

Let Y₁,Y₂,…,Y_n be a simple random sample of size n consisting of p-dimensional observations. Assume that Y_i is distributed according to a finite mixture model, i.e., it follows a distribution of the form

$$ g(\boldsymbol{y}|\boldsymbol{\Psi}) = \sum\limits_{k = 1}^{K} \tau_{k} f_{k}(\boldsymbol{y}|\boldsymbol{\vartheta}_{k}), $$

(2)

where τ_k represents the mixing proportion of the k th mixture component f_k with the parameter vector 𝜗_k, K is the total number of components, and $\boldsymbol {\Psi } = (\tau _{1}, \tau _{2}, \ldots , \tau _{K-1}, {\boldsymbol {\vartheta }_{1}^{T}}, {\boldsymbol {\vartheta }_{2}^{T}}, \ldots , {\boldsymbol {\vartheta }_{K}^{T}})^{T}$ is the complete parameter vector. Mixing proportions are subject to restrictions τ_k > 0 and ${\sum }_{k = 1}^{K} \tau _{k} = 1$. The functional form of f_k is pre-specified and most commonly chosen to follow the multivariate normal distribution. Then, mixture (2) can be written as

$$ g(\boldsymbol{y}|\boldsymbol{\Psi}) = \sum\limits_{k = 1}^{K} \tau_{k} \phi_{p}(\boldsymbol{y}|\boldsymbol{\mu}_{k}, \boldsymbol{\Sigma}_{k}), $$

where ϕ_p(y|μ_k,Σ_k) represents the p-variate Gaussian probability density function with mean vector μ_k and covariance matrix Σ_k. The parameter vector Ψ is usually unknown and can be estimated through various procedures, among which maximum likelihood estimation is the most popular. The form of the corresponding likelihood function typically does not allow deriving closed-form solutions for parameter estimates. As a result, the maximization is usually carried out by means of an iterative procedure called the expectation-maximization (EM) algorithm (Dempster et al. 1977).

The EM algorithm is a standard instrument for handling problems with missing information. In the finite mixture modeling framework, membership labels of observations denoted as z₁,z₂,…,z_n can be assumed known.

The EM algorithm maximizes the conditional expectation of the complete-data log likelihood function given observed data. In the mixture modeling setting, this expectation, commonly known as the Q-function, is given by

$$ Q(\boldsymbol{\Psi}|\boldsymbol{\Psi}^{(b-1)}) = \sum\limits_{i = 1}^{n} \sum\limits_{k = 1}^{K} \pi_{ik}^{(b)}\left[\log\tau_{k} + \log f_{k}(\boldsymbol{y}_{i}| \boldsymbol{\vartheta}_{k})\right], $$

(3)

where $\pi _{ik}^{(b)} = E\{I(Z_{i} = k)| \boldsymbol {y}_{i}, \boldsymbol {\Psi }^{(b-1)}\}$ is the posterior probability that y_i belongs to the k th mixture component. As shown in McLachlan and Peel (2000), the E-step reduces to updating posterior probabilities by means of the expression

$$ \pi_{ik}^{(b)} = \frac{\tau_{k}^{(b-1)} f_{k}(\boldsymbol{y}_{i}| \boldsymbol{\vartheta}_{k}^{(b-1)})}{{\sum}_{k^{\prime} = 1}^{K} \tau_{k^{\prime}}^{(b-1)} f_{k^{\prime}}(\boldsymbol{y}_{i}| \boldsymbol{\vartheta}_{k^{\prime}}^{(b-1)})}. $$

(4)

In the case of p-variate Gaussian mixtures, the above can be written as

$$ \pi_{ik}^{(b)} = \frac{\tau_{k}^{(b-1)} \phi_{p}(\boldsymbol{y}_{i}| \boldsymbol{\mu}_{k}^{(b-1)}, \boldsymbol{\Sigma}_{k}^{(b-1)})}{{\sum}_{k^{\prime} = 1}^{K} \tau_{k^{\prime}}^{(b-1)} \phi_{p}(\boldsymbol{y}_{i}| \boldsymbol{\mu}_{k^{\prime}}^{(b-1)}, \boldsymbol{\Sigma}_{k^{\prime}}^{(b-1)})} $$

(5)

and the M-step is provided by the following expressions:

$$ \tau_{k}^{(b)} = \frac1n \sum\limits_{i = 1}^{n} \pi_{ik}^{(b)}, \quad \quad \boldsymbol{\mu}_{k}^{(b)} = \frac{{\sum}_{i = 1}^{n} \pi_{ik}^{(b)}\boldsymbol{y}_{i}}{{\sum}_{i = 1}^{n} \pi_{ik}^{(b)}}, \quad \quad \boldsymbol{\Sigma}_{k}^{(b)} = \frac{{\sum}_{i = 1}^{n} \pi_{ik}^{(b)}(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)})(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)})^{T}}{{\sum}_{i = 1}^{n} \pi_{ik}^{(b)}}. $$

Iterations of the EM algorithm produce a non-decreasing sequence of likelihood values.

Upon the convergence of the EM algorithm at some iteration b^⋆, the maximum likelihood estimate $\hat {\boldsymbol {\Psi }} = \boldsymbol {\Psi }^{(b^{\star })}$ and estimated posterior probabilities $\hat \pi _{ik} = \pi _{ik}^{(b^{\star })}$ are obtained.

Model-based clustering has a connection with finite mixture modeling through the Bayes decision rule $\tilde z_{i} = \arg \max _{k} \pi _{ik}$, where $\tilde z_{i}$ is the membership label for y_i obtained by the rule. It is assumed that each component can adequately fit exactly one group of data and thus the one-to-one correspondence between mixture components and clusters is formed. This relationship is very appealing from the interpretation point of view as each cluster can be seen as a sample from a particular component distribution. When one-to-one correspondence between mixture components and clusters is not valid, i.e., when more than one component is needed for adequate modeling of a data group, merging components for clustering is one of several possible remedies. The underlying idea is based on the assumption that several components located close to each other, and thus overlapping, model a particular group of data points. Subject to desired cluster characteristics, this assumption is not always true, but can often be rather effective.

Indeed, a good measure of the closeness of mixture components is required. Melnykov (2016) recommends using pairwise misclassification probabilities and suggests employing the pairwise overlap between mixture components $\omega _{kk^{\prime }}$ defined as the sum of two misclassification probabilities $\omega _{k|k^{\prime }}$ and $\omega _{k^{\prime }|k}$, where $\omega _{k^{\prime }|k}$ for Gaussian mixtures is given by

$$ \omega_{k^{\prime}|k} = \text{Pr}\left[\tau_{k}\phi_{p}(\boldsymbol{Y}|\boldsymbol{\mu}_{k}, \boldsymbol{\Sigma}_{k}) < \tau_{k^{\prime}} \phi_{p}(\boldsymbol{Y}|\boldsymbol{\mu}_{k^{\prime}}, \boldsymbol{\Sigma}_{k^{\prime}}) | \boldsymbol{Y} \sim \phi_{p}(\boldsymbol{y} | \boldsymbol{\mu}_{k}, \boldsymbol{\Sigma}_{k})\right]. $$

Maitra and Melnykov (2010) showed that in the general case this probability can be calculated as

$$ \omega_{k^{\prime}|k} = \text{Pr}\left[\sum\limits_{j = 1 \atop j: \lambda_{j} \ne 1}^{p} (\lambda_{j} - 1)U_{j} + 2\sum\limits_{j = 1 \atop j: \lambda_{j} = 1}^{p} \delta_{j}W_{j} \le \sum\limits_{j = 1 \atop j: \lambda_{j} \ne 1}^{p} \frac{\lambda_{j}{\delta_{j}^{2}}}{\lambda_{j} - 1} - \sum\limits_{j = 1 \atop j: \lambda_{j} = 1}^{p} {\delta_{j}^{2}} + \log\frac{{\tau_{k}^{2}}|\boldsymbol{\Sigma}_{k^{\prime}}|}{\tau_{k^{\prime}}^{2} |\boldsymbol{\Sigma}_{k}|}\right], $$

(6)

where $\delta _{j} = {\boldsymbol {\gamma }_{j}^{T}} \boldsymbol {\Sigma }_{k}^{-\frac 12}(\boldsymbol {\mu }_{k} - \boldsymbol {\mu }_{k^{\prime }})$, λ₁,λ₂,…,λ_p and γ₁,γ₂,…,γ_p are the eigenvalues and eigenvectors of the matrix $\boldsymbol {\Sigma }_{k}^{\frac 12} \boldsymbol {\Sigma }_{k^{\prime }}^{-1} \boldsymbol {\Sigma }_{k}^{\frac 12}$, respectively, U_js are independent non-central χ² random variables with one degree of freedom and noncentrality parameter ${\lambda _{j}^{2}}{\delta _{j}^{2}}/(\lambda _{j} - 1)^{2}$, and W_js are independent standard normal random variables, independent of U_js.

Several special cases of result (6) based on particular forms of covariance matrices can be derived. If covariance matrices are assumed to be unequal and spherical, i.e., $\boldsymbol {\Sigma }_{k} \ne \boldsymbol {\Sigma }_{k^{\prime }}$ with $\boldsymbol {\Sigma }_{k} = {\sigma _{k}^{2}}\boldsymbol {I}$ and $\boldsymbol {\Sigma }_{k^{\prime }} = \sigma _{k^{\prime }}^{2}\boldsymbol {I}$, Eq. 6 reduces to

$$ \omega_{k^{\prime}|k} = \text{Pr}\left[U \le \frac{\sigma_{k^{\prime}}^{2}}{{\sigma_{k}^{2}} - \sigma_{k^{\prime}}^{2}}\left( \frac{(\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}})^{T}(\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}})}{{\sigma_{k}^{2}} - \sigma_{k^{\prime}}^{2}} + \log\frac{{\tau_{k}^{2}}\sigma_{k^{\prime}}^{2p}}{\tau_{k^{\prime}}^{2} \sigma_{k}^{2p}}\right)\right], $$

(7)

where U is a non-central χ² random variable with p degrees of freedom and noncentrality parameter $(\boldsymbol {\mu }_{k} - \boldsymbol {\mu }_{k^{\prime }})^{T}(\boldsymbol {\mu }_{k} - \boldsymbol {\mu }_{k^{\prime }}) {\sigma _{k}^{2}} / ({\sigma _{k}^{2}} - \sigma _{k^{\prime }}^{2})^{2}$. If covariance matrices are assumed to be equal, i.e., $\boldsymbol {\Sigma }_{k} = \boldsymbol {\Sigma }_{k^{\prime }} \equiv \boldsymbol {\Sigma }$, the following result is obtained:

$$ \omega_{k^{\prime}|k} = {\Phi}\left( -\frac12 \sqrt{(\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}})^{T}\boldsymbol{\Sigma}^{-1}(\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}})} + \frac{\log\frac{\tau_{k^{\prime}}}{\tau_{k}}}{\sqrt{(\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}})^{T}\boldsymbol{\Sigma}^{-1}(\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}})}}\right), $$

(8)

where Φ(⋅) represents the cumulative distribution function of the standard normal random variable. Finally, if covariance matrices are equal and spherical, i.e., $\boldsymbol {\Sigma }_{k} = \boldsymbol {\Sigma }_{k^{\prime }} \equiv \sigma ^{2}\boldsymbol {I}$, expression (8) can be simplified further:

$$ \omega_{k^{\prime}|k} = {\Phi}\left( -\frac{1}{2\sigma} \Vert\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}}\Vert + \frac{\sigma\log\frac{\tau_{k^{\prime}}}{\tau_{k}}}{\Vert\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}}\Vert}\right). $$

(9)

Expressions for $\omega _{k | k^{\prime }}$ necessary for the calculation of $\omega _{kk^{\prime }} = \omega _{k^{\prime }|k} + \omega _{k | k^{\prime }}$ are obtained similarly.

3 Merging K-Means Solutions

Some similarity between the EM and K-means algorithms can be noticed. Both algorithms aim at optimizing partitionings, which is fulfilled by means of iterative procedures involving a parameter estimation step. In the course of the EM algorithm, fuzzy classifications for observations are obtained in the form of posterior probabilities calculated at the E-step. On the other hand, K-means provides hard assignments at each iteration. In Celeux and Govaert (1992), the authors showed that the traditional K-means algorithm based on Euclidean distances that minimizes the within cluster variability can be seen as the so-called classification EM (CEM) algorithm applied to a mixture of Gaussian components with equal spherical covariance matrices and equal mixing proportions. The CEM algorithm includes an additional classification step incorporated into the procedure right after the E-step and targets maximizing the classification likelihood rather than the original one.

The general formulation of the CEM algorithm is provided below.

E-step

Estimate posterior probabilities $\pi _{ik}^{(b)}$ based on the current parameter vector Ψ^(b− 1) as described in Eq. 4.

C-step

Classify observations into K groups by the rule $z_{i}^{(b)} = \arg \max _{k} \pi _{ik}^{(b)}$.

M-step

Estimate model parameters based on the Q-function given in Eq. 3 with posterior probabilities $\pi _{ik}^{(b)}$ replaced by hard assignments $I(z_{i}^{(b)} = k)$. This modified version will be called the $\tilde Q$-function, i.e.,

$\tilde Q(\boldsymbol {\Psi }|\boldsymbol {\Psi }^{(b-1)}) = {\sum }_{i = 1}^{n} {\sum }_{k = 1}^{K} I(z_{i}^{(b)} = k)\left [\log \tau _{k} + \log f_{k}(\boldsymbol {y}_{i}| \boldsymbol {\vartheta }_{k})\right ]$.

In this paper, we consider four variations of the K-means algorithm and establish the correspondence between them and model-based clustering relying on the CEM algorithm. Recall that according to the Bayes decision rule, y_i is classified to the k th cluster if $\pi _{ik} > \pi _{ik^{\prime }}$ for all k^′ = 1,2,…,k − 1,k + 1,…,K.

Taking into consideration the functional form of posterior probabilities for Gaussian mixtures given in Eq. 5, the inequality $\pi _{ik} > \pi _{ik^{\prime }}$ implies $\tau _{k} \phi _{p}(\boldsymbol {y}_{i}|\boldsymbol {\mu }_{k}, \boldsymbol {\Sigma }_{k}) > \tau _{k^{\prime }} \phi _{p}(\boldsymbol {y}_{i}|\boldsymbol {\mu }_{k^{\prime }}, \boldsymbol {\Sigma }_{k^{\prime }})$. After straightforward manipulations, we conclude that y_i is classified to the k th component if the inequality

$$ (\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k})^{T}\boldsymbol{\Sigma}_{k}^{-1}(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}) < (\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k^{\prime}})^{T}\boldsymbol{\Sigma}_{k^{\prime}}^{-1}(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k^{\prime}}) + \log\frac{{\tau_{k}^{2}}|\boldsymbol{\Sigma}_{k^{\prime}}|}{\tau_{k^{\prime}}^{2}|\boldsymbol{\Sigma}_{k}|} $$

(10)

holds for all k^′ = 1,2,…,k − 1,k + 1,…,K. As we show below, all four versions of K-means can be seen as variations of model-based clustering with specific restrictions following from the comparison of the decision rule for K-means and inequality (10). We discuss K-means solutions from the mixture modeling point of view and thus refer to components rather than clusters detected by the algorithm.

After the connection between the K-means algorithm and model-based clustering is established, we extend it further to formulate merging principles for K-means solutions. To simplify terminology in the following subsections, components with equal covariance matrices are called homoscedastic while those with unequal covariance matrices are called heteroscedastic. In Section 3.1, we consider the simplest version of K-means that is employed in this paper. Three other versions of K-means, their relationship to the overlap and some interesting properties are discussed in Appendix A.

3.1 HoSC-K-Means: K-Means with Homoscedastic Spherical Components

This setting represents the traditional K-means algorithm based on Euclidean distances. By the K-means classification rule, y_i is assigned to the k th component if $\sqrt {(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})^{T}(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})} < \sqrt {(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k^{\prime }})^{T}(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k^{\prime }})}$ holds for all k^′ = 1,2,…,k − 1,k + 1,…,K. It is immediate to see that this inequality is equivalent to decision rule (10) with restrictions Σ₁ = … = Σ_K ≡ σ²I and τ₁ = … = τ_K = 1/K imposed. Thus, HoSC-K-means can be seen as model-based clustering through the CEM algorithm for Gaussian mixtures with homoscedastic spherical components and equal representations. The corresponding $\tilde Q$-function from the CEM algorithm is given by

$$ \tilde Q(\boldsymbol{\Psi}|\boldsymbol{\Psi}^{(b-1)}) = \sum\limits_{i = 1}^{n} \sum\limits_{k = 1}^{K} I(z_{i}^{(b)} = k)\left[\log\frac1K + \log \phi_{p}(\boldsymbol{y}_{i}| \boldsymbol{\mu}_{k}, \sigma^{2}\boldsymbol{I})\right], $$

where the complete parameter vector is $\boldsymbol {\Psi } = ({\boldsymbol {\mu }_{1}^{T}}, {\boldsymbol {\mu }_{2}^{T}}, \ldots , {\boldsymbol {\mu }_{K}^{T}}, \sigma ^{2})^{T}$ with M = Kp + 1 parameters. Mean vectors are calculated at the M-step according to Eq. 1. The common variance σ² is estimated by the expression

$$ (\sigma^{2})^{(b)} = \frac{1}{np}\sum\limits_{i = 1}^{n} \sum\limits_{k = 1}^{K} I(z_{i}^{(b)} = k)(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)})^{T}(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)}). $$

(11)

The overlap under the imposed restrictions can be readily obtained from Eq. 9 and is given by

$$ \omega_{kk^{\prime}} = 2{\Phi}\left( -\frac{\Vert\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}}\Vert}{2\sigma}\right). $$

(12)

This simple formula can be used to assess the level of overlap between components produced by HoSC-K-means and thus to decide which ones should be merged.

3.2 General Framework for DEMP-Based Hierarchical Merging

Directly estimated misclassification probabilities (DEMP) (Hennig 2010; Melnykov 2016) can be conveniently used for measuring the degree of overlap between mixture components (Riani et al. 2015). In the course of hierarchical merging, pairwise misclassification probabilities are calculated between groups of combined components. Melnykov (2016) employed the sum of misclassification probabilities as a linkage function. However, many other functions can be readily used in the considered framework. The choice of a particular linkage should be dictated by the properties of clusters one wants to find.

DEMP-based hierarchical merging of mixture components presents a general framework, where the choice of a particular linkage is driven by the desired properties of clusters. This paper falls into this general framework. In this work, the pairwise overlap is used to measure the closeness of K-means components. In the course of hierarchical merging, we employ single and Ward’s linkages depending on the particular characteristics of clusters sought. The use of relatively simple linkage functions that do not require Monte Carlo simulations as in Melnykov (2016) should be recommended for clustering large datasets. Although all versions of K-means studied in Sections 3.1-Appendix A are viable and can be used in the considered framework, the simplest HoSC-K-means should be preferred for massive data due to its remarkable speed. The combination of HoSC-K-means and effective linkage functions provides the assurance of the speedy performance of the merging algorithm, which from now on we call DEMP-K.

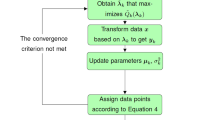
The outline of the proposed hierarchical merging algorithm is as follows.

Outline of the hierarchical merging algorithm:

• 1. Find a K-means solution for some value K such that K > G, where G is the true number of clusters. Some practical guidance on choosing an appropriate values of K and estimation of G is provided in the next section.

• 2. Based on the specific variation of the K-means algorithm, calculate all K(K + 1) misclassification probabilities and corresponding K(K + 1)/2 pairwise overlaps. High pairwise overlaps $\omega _{kk^{\prime }}$ reflect the closeness of the K-means components and thus $1 - \omega _{kk^{\prime }}$ can serve as a dissimilarity measure in the course of traditional hierarchical clustering.

• 3. Based on the particular choice of the linkage function, conduct hierarchical clustering of detected K-means components and find the corresponding tree structure.

• 4. Given a specific value of G, “cut” the tree and identify K-means components that are associated with the same cluster.

• 5. Find the final partitioning by retrieving observations corresponding to each K-means component within detected clusters.

3.3 Practical Implementation

Having the foundation for merging K-means solutions outlined, we focus on other technical details now. One issue concerns choosing a reasonable number of components K for the K-means algorithm. Various methods for selecting K are proposed in literature. One possibility is to employ approximate BIC values calculated based on the connection between K-means and mixture modeling (Goutte et al. 2001). Some other approaches include using various indices (Calinski and Harabasz 1974; Krzanowski and Lai 1985). Our empirical studies show that the specific choice of K is not critical in the considered framework. To illustrate this idea, we conduct a small simulation study. A mixture model with three well-separated skew normal components as in Section 4.2.1 was used to simulate 100 datasets for each sample size n = 10³,10⁴,10⁵,10⁶. K-means solutions were obtained assuming K = 3,…,40 and the proposed merging algorithm DEMP-K was applied. Figure 2 provides relationships between the obtained median of the adjusted Rand index ($\mathcal {A}\mathcal {R}$) and the number of components K for different sample sizes. As we can see, the obtained results are robust to the choice of K. When n = 1000, we observe decrease in $\mathcal {A}\mathcal {R}$ values for K > 30 that can be explained by the detection of some random patterns in skewed clusters. This effect diminishes for higher sample sizes. Another illustration for the robustness of the proposed procedure to the choice of K is provided in Section A.4 of the Appendix A. As the specific choice of the number of components is not critical, one does not have to examine all possible values of K in the search for the best index or BIC value. Intuitively, K has to be large enough to allow adequate filling of clusters of arbitrary shapes with small spheres associated with a K-means solution. A reasonable number can be chosen by the elbow method plotting between cluster variability versus K. The elbow is the point at which the increase in between cluster variability becomes small relative to previous increases. In this paper, we consider K = 5,10,15,… to identify an appropriate K value. The same trend as the one illustrated in Fig. 2 is observed for the other K-means variations. As the main goal of our methodology is to develop tools for fast clustering, from now on, we focus on HoSC-K-means.

Fig. 2

Correspondence between the median adjusted Rand index values obtained as a result of merging K-means solutions with different numbers of components for various sample sizes

When the true number of clusters G is not known, choosing the estimate $\hat G$ is another standalone problem that is beyond the scope of this paper. Here, we outline a couple of possible approaches to the problem and discuss a novel graphical tool that we call an overlap map. One potential approach is to provide some pre-specified overlap threshold value ω^∗ as in Melnykov (2016). Then, the merging process stops when there are no more groups of components that produce the overlap exceeding the threshold level. Another possibility is to employ a visual tool that would simplify the process of making a decision. Melnykov (2016) introduced a graphical display called the quantitation tree which illustrates the merging process and helps detect the best number of groups by the change in color hues associated with the overlap value between merged groups of components. One more method that is based on constructing a tree structure for data groups is considered in Stuetzle and Nugent (2010). The authors develop a graph-based procedure to construct the cluster tree of a nonparametric density estimate. Although the authors do not focus on finding an approach for detecting the best $\hat G$, their paper presents ideas related to our discussion.

In this paper, we propose another tool that we call the overlap map. An example of such a tool, designed to identify well-separated clusters of arbitrary shapes by the use of single linkage, can be found in Fig. 3 (second plot in both rows). The map presents overlap values for all K(K − 1)/2 pairs of components by means of color hues ranging from the pale yellow color for low overlap values to the dark red color for high values. The legend located in the right-hand part of each plot demonstrates the association between overlap values and color hues. The first pair of components included in the plot is reflected by the cell in the lower left corner and is chosen among all pairs according to the highest overlap value produced. The next component added to the display has the highest overlap with one of the components already included in the plot. This process of adding components is repeated until all of them are reflected in the display. The row of color hues located in the bottom of the display serves for choosing the optimal number of clusters $\hat G$ obtained by merging. The color of each cell matches the darkest hue in the corresponding column. Red color hues located next to each other represent a group of components with substantial overlap that are likely to model one cluster. Such groups are usually separated from each other by pale yellow cells associated with considerable gaps. The overlap plot in the first row of Fig. 3 suggests that there are two well-separated groups of points as there is one pale yellow cell separating groups of components with darker hues. The overlap map provides an intuitive instrument for choosing the optimal number of well-separated clusters. On the other hand, this tool somewhat loses its visibility and appeal when the number of components is high.

Fig. 3

Illustrative examples considered in Section 4.1. The first row represents two half-circular clusters and the second row corresponds to the case with two inscribed circular clusters. The first and second columns represent the HoSC-K-means solution and corresponding overlap map, respectively. The third column provides the partitioning result obtained by merging

4 Experimental Validation

In this section, we illustrate the idea of merging HoSC-K-means solutions and provide experimental validation of the proposed approach in various settings.

4.1 Illustrative Examples

The settings considered here include half-circular and inscribed circular clusters. For the purpose of illustration simplicity, we consider bivariate well-separated clusters as provided in Fig. 3.

Half-circular clusters

Consider a setting with two non-globular groups that are presented in the first row of Fig. 3. The total sample size is equal to 1,000.

A 10-group solution obtained by HoSC-K-means is presented in the first plot. The corresponding overlap map suggests that there are two well-separated clusters. The first cluster is obtained by combining components 6, 7, 8, 9, and 10. The second cluster is produced by merging components 1, 2, 3, 4, and 5. As we can see from the overlap map, two closest components from different clusters are the ones with numbers 4 and 10. The corresponding overlap is very small ($\hat \omega _{4,10} < 0.01$) which is reflected by the pale yellow color separating darker color hues. It is worth mentioning that when sample sizes are not very high, local patterns in data can lead to lower overlap values between some components. For example, the overlap between components 8 and 9 ($0.04 < \hat \omega _{8,9} < 0.05$) is not as high as for the other pairs. This effect, already discussed in Section 3.2, is alleviated for datasets with larger sample sizes. The last plot in the first row of Fig. 3 presents the obtained solution: successfully detected clusters are separated by a considerable gap in the density of points.

Inscribed circular clusters

The next setting considered in this section involves one circular cluster inscribed into the other one. The second row of Fig. 3 provides corresponding illustrations.

The first plot shows the 11-component HoSC-K-means solution. The overlap map associated with this solution is provided in the next plot. It clearly suggests the presence of two well-separated clusters. Components 1 to 10 are all merged together based on considerable overlap values. Component 11 is well-separated from the others and is responsible for modeling the inscribed cluster. The obtained grouping is provided in the last plot of Fig. 3.

These simple examples illustrate the proposed idea and demonstrate the utility of overlap maps. Alternative solutions based on 20 HoSC-K-means components along with corresponding overlap maps are provided in Section A.5 of Appendix A.

4.2 Simulation Studies

In this section, we consider three different settings to investigate the performance of the proposed technique and compare it with other clustering procedures. In all cases, clusters are simulated from mixtures of skew normal components using the R package mixsmsn (Prates et al. 2013). The goal of the considered studies is to detect these skewed clusters in various settings. Model parameters and technical details of the simulation studies are provided in Appendix A.6. It is challenging to assess time performance of various clustering methods as procedures can be implemented on different platforms. Therefore, we decided to employ and record computing time for standard functions available in R. The considered methods include spectral clustering (Fiedler 1973; Spielman and Teng 1996) and Nyström approximation (Jain et al. 2013) (both avalable through function specc from the package kernlab), partitioning around medoids (PAM) (Kaufman and Rousseeuw 1990) and Clara Han et al. (2012) (functions pam and clara from the package cluster), hierarchical clustering with Ward’s linkage without squaring dissimilarities (option “ward.D” in function hclust from the package stats; for details on existing variations of the Ward’s algorithm, we refer the reader to Murtagh and Legendre 2014), model-based clustering (Fraley and Raftery 2006) (function Mclust from the package mclust), K-means (MacQueen 1967) (function kmeans from the package stats), entropy-based merging (Baudry et al. 2010), and the proposed method DEMP-K. To read about the specifics of the above-listed clustering procedures, we refer the reader to Han et al. (2012). In all studies of this section, we consider sample sizes n = 10³,10⁴,10⁵,10⁶ and assume that the exact number of clusters is known. In each setting, we simulate 100 datasets. Indeed, the case of n = 10⁶ can be seen as an illustration of rather massive data. The performance of all clustering algorithms is assessed in terms of proportions of correct classifications ($\mathcal {C}\mathcal {P}$), adjusted Rand index ($\mathcal {A}\mathcal {R}$), and computing time ($\mathcal {T}$) (in seconds, run on Fedora 23; Intel(R) Xeon(R) CPU E5-2687W @ 3.10GHz RAM 64Gb). Table 1 provides median and interquartile range values for $\mathcal {C}\mathcal {P}$ and $\mathcal {A}\mathcal {R}$ as well as median values for $\mathcal {T}$. Some clustering algorithms encountered problems with datasets of larger sample sizes (n = 10⁵ and n = 10⁶). The most common issue is the impossibility to allocate the required amount of memory. As a result, only Nyström, Clara, K-means, and DEMP-K methods, designed for clustering massive datasets, can be run in these cases.

Table 1 Results of simulation studies described in Section 4.2.1 (experiment 1), Section 4.2.2 (experiment 2), and Section 4.2.3 (experiment 3)

4.2.1 Experiment 1: Three Well-separated Clusters, Equal Mixing Proportions

The goal of this study is to identify three well-separated bivariate clusters with non-elliptical shapes. A sample dataset is presented in Fig. 4 a. Table 1 provides the results of the corresponding simulation study in the first horizontal block. As we can see, spectral clustering, hierarchical with Ward’s linkage, mclust, entropy-based merging, and DEMP-K show the best performance in terms of $\mathcal {C}\mathcal {P}$ and $\mathcal {A}\mathcal {R}$. Nyström approximation follows closely behind. Spectral clustering is designed to work well in situations with well-separated clusters. mclust shows good performance as ellipsoids associated with mixture components model data adequately due to considerable gaps between groups. Ward’s linkage shows good performance because of the same reason. Expectedly, entropy-based approach performs well: skewed clusters are often modeled with several overlapping Gaussian components that get merged based on the entropy change criterion. As the goal is to find well-separated clusters, we employ the single linkage in DEMP-K and this choice determines the good result obtained. Based on the elbow method, K-means solutions with 20 clusters have been used in DEMP-K. Table 1 suggests that PAM, Clara, and K-means algorithm show similar results but do not perform as well as the procedures mentioned above. This can be explained by the tendency of these algorithms to detect nearly spherical clusters of similar volumes. Hierarchical clustering based on a single linkage is the worst performer in this experiment. Among the four methods that can be run for large datasets, DEMP-K shows a slightly better but also somewhat slower performance compared to Nyström.

Fig. 4

Sample datasets from simulation studies in a Section 4.2.1, b Section 4.2.2, and c Section 4.2.3. The first two datasets are bivariate; plot (c) presents the first two principal components. All datasets considered have a sample size equal to 10,000

4.2.2 Experiment 2: Seven Well-Separated Clusters, Unequal Mixing Proportions

The goal of this experiment is to identify seven well-separated bivariate clusters. Additional clustering complexity has been introduced through severely unequal mixing proportions. In the sample dataset provided in Fig. 4b, nearly half of the data are associated with the large cyan cluster. As a result, other clusters are relatively small in terms of the number of points. In this setting, the best performers in terms of $\mathcal {C}\mathcal {P}$ and $\mathcal {A}\mathcal {R}$ are spectral clustering and DEMP-K based on the single linkage (K equal to 40 by elbow method). Due to the high separation of clusters, this is not unexpected. DEMP-K shows slightly better results. Hierarchical clustering with the average linkage falls just behind these two methods (Appendix A). The performance of Nyström approximation degraded considerably as opposed to that in the previous experiment. mclust also encounters difficulties due to splitting the large cyan cluster into several ones and combining some smaller groups together. Expectedly, the entropy-based merging approach is considerably better than mclust as merging mixture components for clustering works effectively in the considered setting: the large skewed cluster is modeled with several Gaussian components that are combined in the course of the merging procedure. PAM, Clara, and K-means again show relatively similar and not very good performance due to the same reasons as before and unequal cluster sizes. Hierarchical clustering based on Ward’s, single, and complete linkages does not show good performance either. With regard to the four methods that can be run for large datasets, DEMP-K shows substantially better results. $\mathcal {C}\mathcal {P}$ and $\mathcal {A}\mathcal {R}$ are both close to the unity while the other procedures are considerably lower. Specifically, we correctly classify at least 20% of additional data points when we use DEMP-K.

4.2.3 Experiment 3: Three Overlapping Ten-Dimensional Clusters

In the third experiment considered, our goal is considerably different: we aim to identify overlapping compact clusters. To make the situation more challenging, we consider ten-dimensional clusters with two of them having the same mean. The third cluster is located close to the other two as we can see from the first two principal components presented in Fig. 4 c. Clearly, the application of the single linkage is not adequate when we are looking for overlapping clusters. Therefore, per discussion in Section 3.2, we employ Ward’s linkage in the context of the DEMP-K algorithm. By elbow method, K is chosen to be equal to 30.

As we can see, mclust and the entropy-based merging procedure are the best performers in this setting. DEMP-K follows behind the two showing slightly worse results. Comparable results are also obtained by hierarchical clustering with Ward’s linkage. All other procedures perform quite poorly in this difficult setting. Among the four procedures that can be run on large datasets, DEMP-K shows a much better performance.

Results for three additional hierarchical linkages (average, single, and complete) for DEMP-K are given in Table 2. In all considered experiments, we note that DEMP-K with Ward’s linkage performs better than DEMP-K with average, single, or complete linkages. Overall, examples considered in this section demonstrate the broad utility of the developed clustering technique. Depending on the desired properties of clusters such as shape and separation, one has to choose an appropriate linkage function. When sample sizes are not large, there are a few methods that can be successfully used for clustering. For high sample sizes, the use of considered procedures either degrades considerably or is limited by required computing resources. At the same time, the conducted experiments demonstrate that DEMP-K has the potential to show consistently good performance with various sample sizes in all settings considered.

Table 2 Three additional hierarchical clustering methods based on average, single, and complete linkages

5 Application to Digit Recognition

In this section, we apply the developed methodology to the problem of digit recognition. The analyzed dataset was introduced by Alimoglu and Alpaydin (1996) and is publicly available from the University of California Irvine machine learning repository. Forty-four subjects have been asked to write one of the ten digits (0 to 9) in random order using pressure sensitive tablets. The stylus pressure information has been ignored and the collected data represent pairs of coordinates for 8 regularly spaced points located along the pen movement trajectory. To alleviate the translation and scale distortion issues, the collected observations have been normalized. As a result, each written digit can be seen as a sixteen-dimensional observation (eight (x, y) pairs) with coordinate values in the range from 0 to 100. The dataset has a rather moderate sample size of 10,992 that allows us comparing the developed methodology with other clustering techniques, some of which would not be applicable in the case of large datasets. By doing this, we emphasize that although the application of DEMP-K to massive datasets is advantageous, it can also be used in other settings.

It can be noticed that some digits such as 6 can be written in a rather unique way. Due to the conducted normalization at the data pre-processing stage, we can expect roughly spherical dispersions around group means. On the other hand, some other digits can be written in a variety of ways. Figure 5 illustrates 20 realizations of the digit 1. It can be remarked that when the digit is underlined, its image closely resembles that of the digit 2. Similarly, the digit 7 is often crossed by a horizontal line. On the other hand, many people do not cross it. The digit 8 is another complex case as different trajectories can be used to write the same symbol. In such cases, clusters can hardly be assumed spherical. Instead, we can expect that clusters potentially include several subclusters, each with its own mean and roughly spherical dispersion. Under these circumstances, merging subclusters detected by K-means with a sufficiently high number K can lead to a more meaningful clustering solution than those obtained by the competitors. As we discussed in Section 3.2, the choice of the linkage function for hierarchical merging is an important problem. Due to the broad variety of shapes and trajectories used in writing digits, we do not expect to detect well-separated clusters except for some relatively simple cases. As per discussion in Section 3.2, the use of single linkage cannot be recommended in this case and we focus on Ward’s linkage in this application. Due to the nature of the considered problem, the true number of clusters is known to be G = 10. Based on the plot provided in Fig. 9 in Appendix A.7, we choose the number of HoSC-K-means components to be equal to 30. After K = 30, the increase in the proportion of the total variability explained by the between cluster variability is rather minor. Due to the robustness of the proposed procedure, the specific choice of K is not critical.

Fig. 5

Twenty realizations of the digit 1

Table 3 illustrates solutions obtained by the same methods as those considered in Section 4.2. For each partitioning, we provide the classification agreement table (with rows and columns representing true and estimated partitionings, respectively), proportion of correct classifications $\mathcal {C}\mathcal {P}$, adjusted Rand index $\mathcal {A}\mathcal {R}$, and computing time $\mathcal {T}$ in seconds. As we can see, the majority of clustering methods encounter difficulties with clustering at least some digits. This is especially true for 0, 7, and 8. The developed technique based on merging K-means components shows the best performance with $\mathcal {C}\mathcal {P} = 0.843$ and $\mathcal {A}\mathcal {R} = 0.708$. The other methods demonstrate considerably worse results with values varying from $\mathcal {C}\mathcal {P} = 0.554$ and $\mathcal {A}\mathcal {R} = 0.380$ (Nyström clustering) to $\mathcal {C}\mathcal {P} = 0.764$ and $\mathcal {A}\mathcal {R} = 0.588$ (Clara). Entropy-based merging not included in the summary table yielded $\mathcal {C}\mathcal {P} = 0.532$ and $\mathcal {A}\mathcal {R} = 0.329$ with $\mathcal {T} = 1450.61$.

Table 3 Classification agreement tables for 8 clustering methods

From the K-means solution provided in Table 3(g), we can see that clusters representing digits 4 and 6 are identified quite well except for the 88 digits 9 that have been incorrectly assigned to the fourth cluster due to the similarity of the digits 4 and 9. Other clusters are not detected successfully. For example, almost all digits 7 are assigned to data groups containing digits 1 or 2. At the same time, many digits 0 and 8 are combined into a separate cluster. Many similar issues can be also detected after examining the results of other algorithms. On the contrary, Table 3(h) presents a considerably better partitioning obtained by our proposed technique. The most noticeable improvement as opposed to K-means is associated with clusters corresponding to digits 0, 7, and 8. As a result of using DEMP-K instead of K-means, additional 1,930 digits have been identified correctly. The best performing competitor Clara misclassifies 871 digits more than DEMP-K. Figure 6 provides the means of the obtained DEMP-K solution. All digits are easily recognizable except the one representing the digit 8. This effect can be explained by the presence of a high number of digits 1, 5, 8, and 9 assigned to be in the same cluster.

Fig. 6

The means of the 10 data groups obtained by DEMP-K

6 Discussion

We proposed a novel approach for cluster analysis by means of merging components associated with the solution obtained by K-means. This technique falls into a general DEMP-based hierarchical merging framework with various linkages. The main advantage of the developed procedure is in the preserved speed of the K-means algorithm which makes it highly applicable for clustering massive datasets.

The methodology is based on the notion of pairwise overlap which can be instantly calculated for pairs of spherical components with equal covariance matrices. Simulation studies on well-separated and overlapping skewed clusters demonstrate a good promise of the proposed procedure, especially in detecting well-separated clusters of complex shapes. The application of the merging procedure to the problem of digit recognition illustrates that the technique is highly practical even for the cluster analysis of datasets with moderate sample sizes.

Despite the attractiveness of the proposed methodology, there are some challenges the reader should be aware of. If the true number of clusters is unknown, a careful choice of the threshold overlap value, ω^∗ (discussed in Section 3.3), should be made as it will determine which components are to be merged and, in turn, determine how many clusters are obtained. The use of overlap maps can somewhat relax this problem when the goal is to identify well-separated clusters. The linkage choice is extremely important and should be dictated by the desired cluster characteristics. Finally, a reasonable value of K should be chosen for the original K-means algorithm. Fortunately, the developed procedure is rather robust to the choice of K.

Appendix A

1.1 A.1 HoEC-K-means: K-means with Homoscedastic Elliptical Components

This form of the K-means algorithm is based on Mahalanobis distances and assigns y_i to the k th component if inequality $\sqrt {(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})^{T}\boldsymbol {\Sigma }^{-1}(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})} < \sqrt {(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k^{\prime }})^{T}\boldsymbol {\Sigma }^{-1}(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k^{\prime }})}$ holds for all k^′ = 1, 2,…,k − 1,k + 1,…,K. This inequality can be obtained from Eq. 10 by letting Σ₁ = … = Σ_K ≡Σ and τ₁ = … = τ_K = 1/K. Thus, HoEC-K-means can be seen as model-based clustering through the CEM algorithm for Gaussian mixtures with homoscedastic elliptical components and equal proportions. Based on these restrictions, the $\tilde Q$-function is given by

$$ \tilde Q(\boldsymbol{\Psi}|\boldsymbol{\Psi}^{(b-1)}) = \sum\limits_{i = 1}^{n} \sum\limits_{k = 1}^{K} I(z_{i}^{(b)} = k)\left[\log\frac1K + \log \phi_{p}(\boldsymbol{y}_{i}| \boldsymbol{\mu}_{k}, \boldsymbol{\Sigma})\right], $$

where the parameter vector is given by $\boldsymbol {\Psi } = ({\boldsymbol {\mu }_{1}^{T}}, {\boldsymbol {\mu }_{2}^{T}}, \ldots , {\boldsymbol {\mu }_{K}^{T}}, \text {vech}(\boldsymbol {\Sigma })^{T})^{T}$ with vech(Σ) being the vector that consists of unique elements in Σ, namely, vech(Σ)^T = (σ₁₁,…,σ_p1,σ₂₂,…,σ_p2,…,σ_pp). Thus, the total number of parameters is M = Kp + p(p + 1)/2. As before, the k th mean vector is estimated at the M-step according to Eq. 1. The common variance-covariance matrix Σ is estimated by

$$ \boldsymbol{\Sigma}^{(b)} = \frac{1}{n}\sum\limits_{i = 1}^{n} \sum\limits_{k = 1}^{K} I(z_{i}^{(b)} = k)(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)})(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)})^{T}. $$

(13)

Incorporating the above-listed restrictions in Eq. 8, the overlap can be calculated by

$$ \omega_{kk^{\prime}} = 2{\Phi}\left( -\frac12 \sqrt{(\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}})^{T}\boldsymbol{\Sigma}^{-1}(\boldsymbol{\mu}_{k} - \boldsymbol{\mu}_{k^{\prime}})}\right). $$

1.2 A.2 HeSC-K-means: K-means with Heteroscedastic Spherical Components

Under this form of K-means, y_i is assigned to the k th component if inequality $\sqrt {(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})^{T}(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})/{\sigma _{k}^{2}}} < \sqrt {(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k^{\prime }})^{T}(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k^{\prime }})/\sigma _{k^{\prime }}^{2}}$ is satisfied for all k^′ = 1, 2,…,k − 1,k + 1,…,K. This inequality is equivalent to decision rule (10) with the following restrictions: $\boldsymbol {\Sigma }_{1} = {\sigma _{1}^{2}}\boldsymbol {I}, \ldots , \boldsymbol {\Sigma }_{K} = {\sigma _{K}^{2}}\boldsymbol {I}$ and $\tau _{1} = {\sigma _{1}^{p}} / {\sum }_{h = 1}^{K}{{\sigma ^{p}_{h}}}, \ldots , \tau _{K} = {\sigma _{K}^{p}} / {\sum }_{h = 1}^{K}{{\sigma ^{p}_{h}}}$. Thus, HeSC-K-means is equivalent to model-based clustering based on the CEM algorithm for Gaussian mixtures with heteroscedastic spherical components and mixing proportions as provided above. The $\tilde Q$-function from the CEM algorithm in this setting is given by

$$ \tilde Q(\boldsymbol{\Psi}|\boldsymbol{\Psi}^{(b-1)}) = \sum\limits_{i = 1}^{n} \sum\limits_{k = 1}^{K} I(z_{i}^{(b)} = k)\left[\log\frac{{\sigma_{k}^{p}}}{{\sum}_{h = 1}^{K} {\sigma_{h}^{p}}} + \log \phi_{p}(\boldsymbol{y}_{i}| \boldsymbol{\mu}_{k}, {\sigma_{k}^{2}})\right], $$

where $\boldsymbol {\Psi } = ({\boldsymbol {\mu }_{1}^{T}}, {\boldsymbol {\mu }_{2}^{T}}, \ldots , {\boldsymbol {\mu }_{K}^{T}}, {\sigma _{1}^{2}}, {\sigma _{2}^{2}}, \ldots , {\sigma _{K}^{2}})^{T}$ is the parameter vector with M = K(p + 1) parameters. Mean vectors are estimated by Eq. 1 and variance parameters are calculated by the expression

$$ ({\sigma^{2}_{k}})^{(b)} = \frac{{\sum}_{i = 1}^{n} I(z_{i}^{(b)} = k)(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)})^{T}(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)})}{pn\tau_{k}^{(b)}}, $$

(14)

where mixing proportions are estimated by $\tau _{k}^{(b)} = ({\sigma _{k}^{p}})^{(b-1)} / {\sum }_{h = 1}^{K} ({\sigma _{h}^{p}})^{(b-1)}$. Incorporating the above-mentioned restrictions into result (7) leads to calculating the overlap value by

$$ \omega_{kk^{\prime}} = \text{Pr}\left[\chi^{2}_{p,\nu {\sigma_{k}^{2}}} \le \nu\sigma_{k^{\prime}}^{2}\right] + \text{Pr}\left[\chi^{2}_{p,\nu \sigma_{k^{\prime}}^{2}} \le {\nu\sigma_{k}^{2}}\right], $$

where $\nu = (\boldsymbol {\mu }_{k} - \boldsymbol {\mu }_{k^{\prime }})^{T}(\boldsymbol {\mu }_{k} - \boldsymbol {\mu }_{k^{\prime }}) / ({\sigma _{k}^{2}} - \sigma _{k^{\prime }}^{2})^{2}$ and $\chi ^{2}_{p,{\nu \sigma _{k}^{2}}}$ with $\chi ^{2}_{p,\nu \sigma _{k^{\prime }}^{2}}$ are non-central χ² random variables with p degrees of freedom and noncentrality parameters $\nu {\sigma _{k}^{2}}$ and $\nu \sigma _{k^{\prime }}^{2}$, respectively.

1.3 A.3 HeEC-K-means: K-means with Heteroscedastic Elliptical Components

This final variation of K-means assigns y_i to the k th component if inequality $\sqrt {(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})^{T}\boldsymbol {\Sigma }^{-1}_{k}(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k})} < \sqrt {(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k^{\prime }})^{T}\boldsymbol {\Sigma }^{-1}_{k^{\prime }}(\boldsymbol {y}_{i} - \boldsymbol {\mu }_{k^{\prime }})}$ holds for all k^′ = 1, 2,…,k − 1,k + 1,…,K. This inequality can be obtained from the decision rule given in Eq. 10 by imposing restrictions $\tau _{1} = |\boldsymbol {\Sigma }_{1}|^{\frac {1}{2}} / {\sum }_{h = 1}^{K} |\boldsymbol {\Sigma }_{h}|^{\frac {1}{2}}, \ldots , \tau _{K} = |\boldsymbol {\Sigma }_{K}|^{\frac {1}{2}} / {\sum }_{h = 1}^{K} |\boldsymbol {\Sigma }_{h}|^{\frac {1}{2}}$. Thus, HeEC-K-means can be seen as model-based clustering relying on the CEM algorithm for Gaussian mixtures with heteroscedastic elliptical components and mixing weights proportional to the square root of the covariance matrix determinant. The $\tilde Q$-function from the CEM algorithm is given by

$$ \tilde Q(\boldsymbol{\Psi}|\boldsymbol{\Psi}^{(b-1)}) = \sum\limits_{i = 1}^{n} \sum\limits_{k = 1}^{K} I(z_{i}^{(b)} = k)\left[\log\frac{|\boldsymbol{\Sigma}_{k}|^{\frac{1}{2}}}{{\sum}_{h = 1}^{K}|\boldsymbol{\Sigma}_{h}|^{\frac{1}{2}}} + \log \phi_{p}(\boldsymbol{y}_{i}| \boldsymbol{\mu}_{k}, \boldsymbol{\Sigma}_{k})\right], $$

(15)

where $\boldsymbol {\Psi } = ({\boldsymbol {\mu }_{1}^{T}}, {\boldsymbol {\mu }_{2}^{T}}, \ldots , {\boldsymbol {\mu }_{K}^{T}}, \text {vech}(\boldsymbol {\Sigma }_{1})^{T}, \text {vech}(\boldsymbol {\Sigma }_{2})^{T}, \ldots , \text {vech}(\boldsymbol {\Sigma }_{K})^{T})^{T}$. The total number of parameters is M = Kp + Kp(p + 1)/2. It can be shown that the M-step involves updating mean vectors by Eq. 1 and covariance matrices by

$$ \boldsymbol{\Sigma}_{k}^{(b)} = \frac{{\sum}_{i = 1}^{n} I(z_{i}^{(b)} = k)(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)})(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k}^{(b)})^{T}}{n\tau_{k}^{(b)}}, $$

(16)

where $\tau _{k}^{(b)}$ represents the current mixing proportion estimated by $\tau _{k}^{(b)} = |\boldsymbol {\Sigma }_{k}^{{(b-1)}}|^{\frac {1}{2}} / {\sum }_{h = 1}^{K}$$|\boldsymbol {\Sigma }_{h}^{{(b-1)}}|^{\frac {1}{2}}$. Although we do not provide calculations for estimates (11), (13), and (14), the derivation of Eq. 16 is more delicate and is provided below. In order to derive expression (16), $\tilde Q$-function (15) has to be maximized with respect to Σ_k as follows below. From matrix differential calculus, it is known that $\frac {\partial |\boldsymbol {\Xi }|}{\partial \boldsymbol {\Xi }} = |\boldsymbol {\Xi }|(\boldsymbol {\Xi }^{-1})^{T}$ and $\frac {\partial \boldsymbol {A}\boldsymbol {\Xi }^{-1}\boldsymbol {B}}{\partial \boldsymbol {\Xi }} = -(\boldsymbol {\Xi }^{-1}\boldsymbol {B}\boldsymbol {A}\boldsymbol {\Xi }^{-1})^{T}$, where A and B are some matrices of constants and Ξ is an unstructured nonsingular matrix. These two results will be also used in our derivation.

$$ \begin{array}{ll} \frac{\partial \tilde Q(\boldsymbol{\Psi}|\boldsymbol{\Psi}^{(b-1)})}{\partial \boldsymbol{\Sigma}_{k}} & = \frac{\partial}{\partial \boldsymbol{\Sigma}_{k}}\left\{\sum\limits_{i = 1}^{n} \sum\limits_{k = 1}^{K} I(z_{i}^{(b)} = k)\left[\log\frac{|\boldsymbol{\Sigma}_{k}|^{\frac{1}{2}}}{{\sum}_{h = 1}^{K}|\boldsymbol{\Sigma}_{h}|^{\frac{1}{2}}} + \log \phi_{p}(\boldsymbol{y}_{i}| \boldsymbol{\mu}_{k}, \boldsymbol{\Sigma}_{k})\right]\right\}\\ & = -\frac{\partial}{\partial \boldsymbol{\Sigma}_{k}}\left\{\sum\limits_{i = 1}^{n} \sum\limits_{k = 1}^{K} I(z_{i}^{(b)} = k)\left[\log{\sum\limits_{h = 1}^{K}|\boldsymbol{\Sigma}_{h}|^{\frac{1}{2}}} + \frac{1}{2} (\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k})^{T} \boldsymbol{\Sigma}_{k}^{-1} (\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k})\right]\right\}\\ & = -\sum\limits_{i = 1}^{n} \left[\frac{1}{{\sum}_{h = 1}^{K}|\boldsymbol{\Sigma}_{h}|^{\frac{1}{2}}}\frac{\partial |\boldsymbol{\Sigma}_{k}|^{\frac{1}{2}}}{\partial \boldsymbol{\Sigma}_{k}} - \frac12I(z_{i}^{(b)} = k)\boldsymbol{\Sigma}_{k}^{-1}(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k})(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k})^{T}\boldsymbol{\Sigma}_{k}^{-1}\right]\\ & = \frac12\left[-\frac{n|\boldsymbol{\Sigma}_{k}|^{\frac12}\boldsymbol{\Sigma}_{k}^{-1}}{{\sum}_{h = 1}^{K}|\boldsymbol{\Sigma}_{h}|^{\frac{1}{2}}} + \sum\limits_{i = 1}^{n} I(z_{i}^{(b)} = k)\boldsymbol{\Sigma}_{k}^{-1}(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k})(\boldsymbol{y}_{i} - \boldsymbol{\mu}_{k})^{T}\boldsymbol{\Sigma}_{k}^{-1}\right]. \end{array} $$

Setting this derivative equal to zero and letting $\tau _{k} = |\boldsymbol {\Sigma }_{k}|^{\frac 12} / {\sum }_{h = 1}^{K}|\boldsymbol {\Sigma }_{h}|^{\frac {1}{2}}$ yields result (16).

Under considered restrictions, the overlap is calculated as the sum of the misclassification probabilities $\omega _{kk^{\prime }} = \omega _{k^{\prime } | k} + \omega _{k | k^{\prime }}$, where $\omega _{k^{\prime } | k}$ is given by

$$ \omega_{k^{\prime}|k} = \text{Pr}\left[\sum\limits_{j = 1 \atop j: \lambda_{j} \ne 1}^{p} (\lambda_{j} - 1)U_{j} + 2\sum\limits_{j = 1 \atop j: \lambda_{j} = 1}^{p} \delta_{j}W_{j} \le \sum\limits_{j = 1 \atop j: \lambda_{j} \ne 1}^{p} \frac{\lambda_{j}{\delta_{j}^{2}}}{\lambda_{j} - 1} - \sum\limits_{j = 1 \atop j: \lambda_{j} = 1}^{p} {\delta_{j}^{2}}\right] $$

with parameters as described in Eq. 6 and $\omega _{k | k^{\prime }}$ defined similarly.

This version of the K-means algorithm closely resembles the CEM algorithm for the general form of Gaussian mixture models but with mixing proportions of a special form. Recall that the generalized variance for Σ_k is given by $|\boldsymbol {\Sigma }_{k}| = {\prod }_{j = 1}^{p} \lambda _{kj}$, where λ_k1,λ_k2,…,λ_kp are the eigenvalues of Σ_k. The length of the j th axis of the hyperellipsoid corresponding to Σ_k is proportional to $\sqrt {\lambda _{kj}}$ and the volume of hyperellipsoid $V_{\boldsymbol {\Sigma }_{k}}$ is proportional to ${\prod }_{j = 1}^{p} \sqrt {\lambda _{kj}}$. As a result, we conclude that $\tau _{k} = V_{\boldsymbol {\Sigma }_{k}} / {\sum }_{h = 1}^{K} V_{\boldsymbol {\Sigma }_{h}}$, i.e., the restriction imposed on mixing proportions requires that they represent the proportion of the overall volume associated with the k th component. Alternatively, consider the expected size of the k th cluster defined as $n_{k} = {\sum }_{i = 1}^{n} \pi _{ik}$. The log-term in Eq 10 is equal to zero when

$$ \frac{\tau_{k}|\boldsymbol{\Sigma}_{k^{\prime}}|^{\frac{1}{2}}}{\tau_{k^{\prime}}|\boldsymbol{\Sigma}_{k}|^{\frac{1}{2}}} = \frac{n_{k} V_{\boldsymbol{\Sigma}_{k^{\prime}}}}{n_{k^{\prime}} V_{\boldsymbol{\Sigma}_{k}}} = \frac{D_{k}}{D_{k^{\prime}}}, $$

where $D_{k} = n_{k} / V_{\boldsymbol {\Sigma }_{k}}$ can be seen as the “density” of the k th cluster. As a result, we conclude that the HeEC assumption is appropriate when clusters have similar “densities” of data points. Intuitively, such a restriction is often reasonable. At the same time, traditional model-based clustering with unrestricted mixing proportions allows for much higher degrees of modeling flexibility.

1.4 A.4 An Illustration of the Robustness of the Proposed Procedure to the Choice of K

In this example, we repeat an experiment outlined in Section 4.2.3 in a more challenging setting. A mixture model with three ten-dimensional skew-normal components is employed. Two of the components have a very substantial overlap as they share the mean parameter. Under such a setting, the choice of a linkage predetermines the obtained partitioning. If a single linkage is chosen, one cannot expect that clusters associated with the three mixture components will be detected due to the considerable overlap between two components with a common mean. If a Ward’s linkage is selected, approximately elliptical clusters will be produced but the problem of substantial overlap between components will be relaxed. No matter what linkage is chosen, our main question is whether the proposed procedure is sensitive to the choice of the number of K-means components K. 100 datasets are simulated with each size n = 10³, 10⁴, 10⁵, 10⁶. Figure 7 provides the median adjusted Rand index obtained as a result of merging K-means solutions for different numbers K. The first plot represents the performance of the algorithm with the single linkage used. The second plot corresponds to the Ward’s linkage. As we can see, the use of the single linkage produces almost identical results for K ≥ 7 and all considered sample sizes. Thus, the results are very robust to the choice of the initial number of K-means components. As expected, the situation is somewhat more challenging when the Ward’s linkage is used. In this case, hierarchical clustering targets detecting approximately elliptical clusters rather than well-separated ones and we can notice some sample size effect: the results are slightly worse for n = 1000. With regard to the robustness of the procedure to the choice of the number of K-means components, we can notice that roughly the same result is produced after K = 25 for n = 1000 and K = 30 for higher sample sizes. It is worth mentioning here that the considered situation is rather challenging as two ten-dimensional clusters share a common mean. Despite that, the achieved value of the adjusted Rand index is about 0.84–0.85 and corresponding classification agreement is around 94%. It is also worth mentioning that due to high sensitivity of the adjusted Rand index, we observe some slight variation for K ≥ 30 for n = 10⁴, 10⁵, 10⁶. However, this variation is so minor that the maximum difference in the proportion of classification agreements does not exceed 0.003 for any K ≥ 30.

Fig. 7

Correspondence between the median adjusted Rand index values obtained as a result of merging K-means solutions with different numbers of components for various sample sizes

1.5 A.5 Alternative Solutions for Illustrative Examples from Section 4.1

In this section, we present an alternative solution for the HoSC-K-means algorithm with K = 20. Figure 8 demonstrates obtained solutions as well as corresponding overlap maps.

Fig. 8

Illustrative examples considered in Section 4.1. The description is similar to that of Fig. 3. The number of HoSC-K-means components is chosen to be equal to 20

1.6 A.6 Details of the Simulation Studies Considered in Section 4.2

Some technical details associated with the application of the abovementioned clustering methods are as follows below. A Nyström sample to estimate eigenvalues is chosen to be equal to 100 (option “nystrom.sample” in function specc). The number of samples drawn by Clara is 100. The K-means algorithm is initialized by seeding initial cluster centers at random. The results of the algorithm are based on 100 restarts. Finally, mclust is applied assuming the most general form of Gaussian components (i.e., unrestricted in volume, shape, and orientation and denoted as “VVV”). Model parameters for the three experiments considered in Sections 4.2.1-4.2.3 are provided in Table 4.

Table 4 Parameters of the models considered in experiment 1 (Section 4.2.1), experiment 2 (Section 4.2.2), and Experiment 3 (Section 4.2.3)

1.7 A.7 Plot for Selecting the Number of K-means Components in the Pen Written Digits Application Considered in Section 5

Figure 9 shows the relationship between the proportion of the overall variability explained by the between cluster variability and the number of K-means clusters. As we can see, substantial improvements are obtained for K up to the values of 20–25. After K = 30, the increase in the proportion becomes rather marginal. Therefore, we decided to choose K = 30.

Fig. 9

Proportion of the total variability explained by between cluster variability versus the number of K-means clusters