Condorcet winning sets

Abstract

An alternative is said to be a Condorcet winner of an election if it is preferred to any other alternative by a majority of voters. While this is a very attractive solution concept, many elections do not have a Condorcet winner. In this paper, we propose a set-valued relaxation of this concept, which we call a Condorcet winning set: such sets consist of alternatives that collectively dominate any other alternative. We also consider a more general version of this concept, where instead of domination by a majority of voters we require domination by a given fraction $\theta$ of voters; we refer to such sets as $\theta$-winning sets. We explore social choice-theoretic and algorithmic aspects of these solution concepts, both theoretically and empirically.

1 Introduction

When a group of agents is trying to decide on a joint plan, it is often the case that no single alternative is consensual enough to be chosen as the collective decision. For instance, this is the case if consensual alternatives are identified with Condorcet winners, since some profiles do not have Condorcet winners. Similarly, in approval voting, we might view an alternative as consensual if it is approved by all voters: again, in many cases there will be no consensual alternative.

For instance, consider a common practical problem, namely, the choice of a time slot for a departmental seminar. Each faculty member approves of some of the time slots and disapproves of others (based, e.g., on their teaching schedule), so it is natural to make this choice using approval voting. Now, ideally, research seminars in a department should always be held on the same day of the week and at the same time. However, this requirement (R) will have the unfortunate consequence that some members of the department will always miss the research seminar, just because they teach every week at that time. In this case, rather than choosing the time slot acceptable to the highest number of voters, we might instead relax requirement (R) and allow two slots to be chosen, i.e., ask whether there is a set of two slots $\{s,s'\}$ such that every voter approves either $s$ or $s'$. If such a pair exists, then by alternating between $s$ and $s'$, we can ensure that everyone can attend at least some seminars. More generally, we may be interested in a set of slots of minimal cardinality such that every voter approves at least one slot in this set.

In this paper, we extend this approach to the more common model of voting, where voters submit rankings of candidates, and to a weaker notion of collective acceptability. That is, we consider the problem of finding a (minimum-size) set of alternatives such that collectively the voters are happy enough with at least one alternative in the set. Sets of alternatives are thus considered disjunctively. More formally, let $\pi$ be a property of alternatives; then a set of alternatives $Y$ is deemed to satisfy $\pi$ if, in the profile obtained by

• (a) replacing the top alternative from $Y$ in each vote by a new alternative $[Y]$, and

• (b) removing all other elements of $Y$ from each vote,

the property $\pi$ is satisfied by the new alternative $[Y]$. This idea of disjunctive domination is central to the notions we develop in this paper.

Applied to approval voting, and taking $\pi$ to be “being approved by every voter”, this approach reduces to finding a (smallest) subset of alternatives $Y$ such that every voter approves at least one alternative in $Y$, which is equivalent to the well-known hitting set problem (Garey and Johnson 1979). If $\pi$ is defined in terms of the Borda count or, more generally, some scoring function, then this procedure is closely related to the Chamberlin–Courant proportional representation rule (see Sect. 7). If we take $\pi$ to be the Condorcet criterion, we get the following notion: $Y$ is a Condorcet winning set if for every candidate $z$ in X$\setminus$Y, a majority of voters prefer some candidate in $Y$ to $z$; in particular, a Condorcet winner is a Condorcet winning set of size $1$. This concept can be generalized by varying the quota: we say that a set $Y$ is a $\theta$-winning set, $\theta \in [0,1)$, for an $n$-voter profile if for every alternative $x$ not in $Y$, more than $\theta n$ voters prefer some alternative in $Y$ to $x$; Condorcet winning sets correspond to $\theta =\frac{1}{2}$. This relaxation is inspired by viewing collective decision making as a multicriteria optimization problem, where the aim is to select a set of candidates that is as small as possible and dominates all other candidates as strongly as possible.

The goal of this paper is to develop a basic understanding of Condorcet winning sets, and, more generally, $\theta$-winning sets. In Sect. 2 we give the formal definition of a Condorcet winning set and provide some illustrative examples. In Sect. 3 we contrast this new concept with standard tournament solution concepts. Section 4 is concerned with the size of Condorcet winning sets and the problem of efficiently computing Condorcet winning sets of minimum possible size. In Sect. 5 we define and discuss $\theta$-winning sets. We complement our theoretical results with empirical analysis (Sect. 6). Section 7 provides an overview of related work.

2 Condorcet winning sets: definitions and examples

Throughout the paper, we will usually consider elections with a set of candidates (alternatives) $X=\{x_1, \ldots , x_m\}$ and a set of voters $N=\{1, \ldots , n\}$. Each voter $i$ is associated with a linear order $\succ _i$ over $X$, which is called his preference order. If a voter $i$ ranks the candidates as $a\succ b \succ \cdots \succ z$, we will sometimes abbreviate his preference order as $ab\ldots z$. The vector $\langle \succ _1, \ldots , \succ _n\rangle$ of all voters’ preference orders is called a preference profile and is usually denoted by $P$. We will denote the number of voters in a preference profile $P$ by $|P|$. A subprofile of $P$ is a profile obtained from $P$ by removing a subset of $X$ and/or a subset of $N$.

We say that a candidate $x\in X$ beats another candidate $y\in X$ in a pairwise election if a strict majority of voters prefer $x$ to $y$; if exactly half of the voters prefer $x$ to $y$, then $x$ and $y$ are said to be tied. A candidate is said to be a Condorcet winner if she wins in all of her pairwise elections. Clearly, each election has at most one Condorcet winner, but many elections have no Condorcet winners.

We can now formally define Condorcet winning sets.

Definition 1

Given an election over $X$ with a preference profile $P=\langle \succ _1, \ldots , \succ _n\rangle$, a set $Y \subseteq X$ is said to cover an alternative $z\in$ X$\setminus$Y if

$$\begin{aligned} \#\big \{i \in N \mid \exists y \in Y \text {such that } y \succ _i z\big \} > \frac{n}{2}. \end{aligned}$$

We say that $Y$ is a Condorcet winning set if $Y$ covers each alternative in X$\setminus$Y.

An equivalent definition of Condorcet winning sets, which was alluded to in Sect. 1, can be formulated as follows. Given an election with a preference profile $P=\langle \succ _1,\ldots ,\succ _n\rangle$ over $X$ and a set $Y\subseteq X$, we introduce a new alternative $[Y]\not \in X$ and construct a preference profile $P_{[Y]}=\langle \succ '_1,\ldots , \succ '_n\rangle$ over the set of candidates (X$\setminus$Y)$\cup \{[Y]\}$ using the following procedure. For each voter $i$, we construct the vote $\succ '_i$ by identifying the top candidate in $Y$ according to $\succ _i$, replacing it with $[Y]$, and removing all other elements of $Y$ from $\succ _i$. Then $Y$ is a Condorcet winning set if and only if $[Y]$ is a Condorcet winner in $P_{[Y]}$.

Given a $k\in {\mathbb N}$, we will denote by ${ CWS }(P,k)$ the collection of all Condorcet winning sets of size $k$ in a profile $P$; also, we set ${ CWS }(P)=\cup _k { CWS }(P,k)$. For instance, if $P$ has a Condorcet winner $c$, then ${ CWS }(P,1)=\{\{c\}\}$, otherwise, ${ CWS }(P,1)=\emptyset$. Observe that the set family ${ CWS }(P)$ is upwards-closed: if $A\in { CWS }(P)$ and $A\subseteq B$, then $B\in { CWS }(P)$. We say that $A$ is a minimal Condorcet winning set for $P$ if $A \in { CWS }(P)$ and there is no $B \in { CWS }(P)$ such that $B \subset A$. We denote the collection of all minimal Condorcet winning sets in $P$ by ${ CWS }^{\min }(P)$.

Typically, we are interested in winning sets that are as small as possible. Thus, we define the Condorcet dimension $\dim _C(P)$ of a given profile $P$ as the size of the smallest Condorcet winning set for $P$.

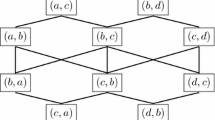
Example 1

Let $X = \{a,b,c,d\}$, $n = 3$, and consider the profile

$$\begin{aligned} P = \langle abcd, cdab, dabc\rangle . \end{aligned}$$

• $\{a,c\}$ covers $d$ (because two voters out of three prefer either $a$ or $c$ to $d$) and $b$ (because every voter prefers either $a$ or $c$ to $b$); thus, $\{a,c\}$ is a Condorcet winning set for $P$. This can also be seen from the fact that $[\{a,c\}]$ is a Condorcet winner of $P_{[\{a,c\}]} = \langle [\{a,c\}]bd, [\{a,c\}]db, d[\{a,c\}]b\rangle$.

• $\{a,b\}$ does not cover $d$, therefore $\{a,b\}$ is not a Condorcet winning set for $P$.

• ${ CWS }(P,2) = \{ \{a,c\}, \{a,d\}, \{b,d\}, \{c,d\} \}$; as ${ CWS }(P,1) = \emptyset$ ($P$ has no Condorcet winner), all these pairs are also minimal Condorcet winning sets. Consequently, $\dim _C(P)=2$.

In Example 1, most of the sets of size $2$ are Condorcet winning sets. We will now provide an example where every set of size $2$ is a Condorcet winning set.

Example 2

Consider a preference profile $P^*$ over a candidate set $X$ that contains a single copy of each of the possible $|X|!$ orderings of the candidates. We claim that $\dim _C(P^*)=2$ and, moreover, every set of size 2 is a Condorcet winning set for $P^*$. Note first that every pairwise election ends in a tie, and therefore $\dim _C(P)>1$. Now, let $n=|X|!$ and consider an arbitrary pair of candidates $Y=\{x, y\}$. There exists a voter $i$ that ranks $x$ first and $y$ last. Pick a candidate $z\in$ X$\setminus$Y. By symmetry, there is a set $S$ of $n/2$ voters that rank $y$ above $z$; moreover, we have $i\not \in S$, since $i$ ranks $y$ last. Hence, the set $S\cup \{i\}$ contains more than $n/2$ voters and $z$ is ranked below $x$ or $y$ by every voter in $S\cup \{i\}$. This implies that $Y$ is a Condorcet winning set for $P^*$.

Furthermore, if the number of voters is large relative to the number of candidates, preference profiles where every set of size $2$ is a Condorcet winning set are very likely to arise under the impartial culture assumption (IC), i.e., if every vote is chosen uniformly at random from the set of all permutations of $X$.

Proposition 1

Let $P$ be an $n$-voter preference profile over a set of candidates $X$, $|X|=m$, obtained by drawing each of the $n$ votes uniformly at random from all permutations of $X$, and let $S=\{a, b\}$ be an arbitrary 2-element subset of $X$. Then with probability at least $1-me^{-n/24}$ the set $S$ is a Condorcet winning set for $P$. Moreover, with probability at least $1-m^3e^{-n/24}/2$ every size-2 subset of $X$ is a Condorcet winning set.

Proof

Consider an arbitrary candidate $c\in$ X$\setminus${a, b}. Any given vote is equally likely to contain any of the six possible permutations of $a$, $b$, and $c$. Therefore, with probability $\frac{2}{3}$ in any given vote either $a$ or $b$ is ranked above $c$. Hence, the expected number of votes where $a$ or $b$ beats $c$ is $\frac{2n}{3}$. By Chernoff bound (see, e.g., Alon and Spencer 1992), the probability that $c$ is ranked above $a$ and $b$ in at least $\frac{n}{2}$ votes is at most $e^{-n/24}$. Thus, by the union bound, the probability that $\{a, b\}$ is not a Condorcet winning set is at most $me^{-n/24}$, and our first claim follows.

To prove the second claim, we observe that the number of size-$2$ subsets of $X$ is bounded from above by $m^2/2$, and apply the union bound again. $\square$

Proposition 1, together with the known bounds on the probability of having a Condorcet winner (see, e.g., Jones et al. 1995), suggests that the notion of a Condorcet winning set is not particularly useful if our goal is to construct a decisive voting correspondence. Indeed, perhaps the most natural voting correspondence inspired by this notion is the mapping $\rho$ defined by $\rho (P)=\cup _{S\in { CWS }^{\min }(P)}S$: given a profile $P$, $\rho$ returns all candidates that belong to some minimal Condorcet winning set for $P$. But $\rho$ can be very far from being decisive: Proposition 1 implies that, under IC, if the number of voters is large relative to the number of candidates, $\rho$ is likely to return (almost) all candidates. Moreover, one can construct elections where the output of $\rho$ contains the Condorcet loser or even a Pareto-dominated alternative. To remedy this, in Sect. 5, we introduce a generalization of Condorcet winning sets, which we refer to as $\theta$-winning sets, and show (empirically) that it produces a much more attractive voting correspondence. However, before we move on to the study of $\theta$-winning sets, we would like to discuss some combinatorial questions pertaining to Condorcet winning sets.

3 Condorcet winning sets vs. dominating sets

Given a profile $P$ over a candidate set $X$, its majority graph $G(P)$ is the directed graph (also called a weak tournament) with the vertex set $X$ that contains a directed edge from $x$ to $y$ if $x$ beats $y$ in their pairwise election. If the number of voters is odd, then for each pair $(x, y)$ either $(x, y)$ or $(y, x)$ is present in the graph, i.e., $G(P)$ is a tournament. A weighted majority graph $G^w(P)$ labels each edge $(x, y)$ with the number of voters that prefer $x$ to $y$. A (weighted) tournament function is a mapping $F$ defined on preference profiles that satisfies $F(P)=F(Q)$ whenever $P$ and $Q$ have the same (weighted) majority graph (see, e.g., Laslier 1997).

There is a certain similarity between the concept of a Condorcet winning set and a classic tournament function, namely, the dominating sets. Recall that a set of vertices $S$ of a directed graph $G=(N, A)$ is called a dominating set if for every vertex $x\in$ N$\setminus$S there exists a vertex $y\in S$ such that the directed edge $(y, x)$ is in $A$. Now, clearly, if $S$ is a dominating set for $G(P)$, then $S$ is a Condorcet winning set for $P$. However, Example 2 shows that the converse is not true: for the preference profile $P^*$ considered in this example, the graph $G(P^*)$ consists of $|X|$ isolated vertices, so the smallest dominating set for $G(P^*)$ is $X$ itself, whereas, as argued in Example 2, every size-$2$ set of candidates is a Condorcet winning set for that profile.

Indeed, a stronger statement is true: the function that outputs all Condorcet winning sets for a given profile is not a (weighted) tournament function, i.e., there exist a set of candidates $X$ and two profiles $P$ and $Q$ over $X$ such that $G^w(P)=G^w(Q)$, but ${ CWS }(P)\ne { CWS }(Q)$. This is shown by the following example.

Example 3

Consider the following pair of four-candidate, three-voter profiles:

$$\begin{aligned} P = \langle abcd, cdba, dabc\rangle , \quad Q = \langle acdb, bcda, dabc\rangle . \end{aligned}$$

The weighted majority graphs for $P$ and $Q$ coincide: $a$ beats $b$ and $c$, $b$ beats $c$, $c$ beats $d$, $d$ beats $a$ and $b$, and in each pairwise election the winner is preferred to the loser by exactly two voters. However, $\{a,b\}$ is a Condorcet winning set for $Q$, but not for $P$.

Note that the preference profile $P$ constructed in Example 3 has an odd number of voters, so this example shows that a Condorcet winning set may fail to be a dominating set even if $G(P)$ is a tournament.

Intuitively, the main difference between Condorcet winning sets and dominating sets is the underlying notion of collective dominance: for Condorcet winning sets it is disjunctive ($S$ dominates $x$ if there are more than $n/2$ voters such that each of these voters prefers some alternative in $S$ to $x$), whereas for dominating sets it is conjunctive ($S$ dominates $x$ if there is an alternative $y\in S$ such that more than $n/2$ voters prefer $y$ to $x$).

This intuition suggests that Condorcet winning sets that are far from being dominating sets are typically sets of alternatives which complement each other.

Example 4

Consider an $n$-voter profile $P$ over the set of candidates $\{x_1, \ldots , x_k, a, b\}$, where $n$ is divisible by $4$, $n/4+1$ voters ranks the candidates as $a x_1 \ldots x_k b$, $n/4$ voters ranks the candidates as $b x_1 \ldots x_k a$, and the remaining voters rank the candidates as $x_1 \ldots x_k ab$. In this profile, the set $\{a, b\}$ is a Condorcet winning set, but it is very far from being a dominating set: for each $i=1, \ldots , k$ it holds that $3n/4-1$ voters prefer $x_i$ to $a$ and $3n/4+1$ voters prefer $x_i$ to $b$.

Conversely, if a Condorcet winning set consists of alternatives that are very similar to each other, it is likely to be a dominating set. For instance, it is not hard to see that if a Condorcet winning set $Y$ is a clone set in the sense of (Tideman 1987) (i.e., for every pair of alternatives $a, b\in Y$ and every alternative $c\in$ X$\setminus$Y it holds that no voter ranks $c$ between $a$ and $b$), then it is also a dominating set.

In Sect. 6, we provide empirical evidence that the collection of Condorcet winning sets of a given election is typically very different from the collection of dominating sets of the majority graph of this election.

4 Condorcet dimension: upper and lower bounds

In this section, we focus on the notion of Condorcet dimension. We have already seen (Proposition 1) that for most profiles their Condorcet dimension is 2 or less. It is therefore interesting to ask whether profiles with a higher Condorcet dimension exist.

4.1 Profiles of Condorcet dimension 1, 2, and 3

Observe that the Condorcet dimension of a given profile $P$ is 1 if and only if $P$ has a Condorcet winner. Thus, it is easy to construct a profile whose dimension exceeds 1: consider, for instance, a Condorcet cycle of size $m$, $m\ge 2$, i.e., an $m$-voter, $m$-candidate preference profile $P_m$, where the $i$th voter places the $j$th candidate in position $i+j-1\mod m$ (e.g., for $m=3$ the Condorcet cycle over the candidate set $X=\{1, 2, 3\}$ is given by $P_3= \langle 123, 231, 312\rangle$). Clearly, $P_m$ has no Condorcet winner, so $\dim _C(P_m)\ge 2$. In fact, it is not hard to see that $\dim _C(P_m)=2$ for every $m\ge 2$: indeed, candidates 1 and $\lfloor m/2\rfloor +1$ form a dominating set in $G(P_m)$ (and hence a Condorcet winning set).

To exhibit a profile of Condorcet dimension 3, we borrow some terminology from linear algebra. Let $A=(a_{ij})$ be a $p$-by-$q$ matrix and let $B=(b_{k\ell })$ be a $p'$-by-$q'$ matrix. Recall that the Kronecker product of $A$ and $B$ is a $pp'$-by-$qq'$ matrix $A\otimes B$ of the form

$$\begin{aligned} \left( \begin{array}{ccc} a_{11}B &{} \dots &{} a_{1q}B \\ \dots &{} \dots &{} \dots \\ a_{p1}B &{} \dots &{} a_{pq}B \end{array} \right) . \end{aligned}$$

Now, any $n$-voter, $m$-candidate preference profile $P$ can be associated with an $m$-by-$n$ matrix $M(P)$: the $i$th entry in the $j$th column of $M(P)$ is the name of the candidate that is ranked in the $i$th position by the $j$th voter. Thus, given a preference profile $P$ over a set of candidates $X$ and a preference profile $Q$ over a set of candidates $Y$, we can define $P\otimes Q$ as a preference profile over the set of candidates $X\times Y$ (i.e., pairs of the form $(x_i, y_j)$, where $x_i\in X$, $y_j\in Y$) that corresponds to the matrix $M(P)\otimes M(Q)$, where we identify the product $x_iy_j$ with the pair $(x_i, y_j)$.

For instance, if $P= \langle 321, 231\rangle$ is a preference profile over $X=\{1, 2, 3\}$ and $Q=\langle 12, 21\rangle$ is a preference profile over $Y=\{1, 2\}$, then the first voter in $P\otimes Q$ has the preference ordering

$$\begin{aligned} (3,1)\succ (3,2)\succ (2,1)\succ (2,2)\succ (1,1)\succ (1,2) \end{aligned}$$

over the candidate set $\{(i, j)\mid i=1, 2, 3,\quad j=1, 2\}$.

We are now ready to present an example of a profile with an odd number of voters whose Condorcet dimension is 3.

Proposition 2

There exists a $15$-candidate profile with an odd number of voters whose Condorcet dimension is $3$.

Proof

Let $X=\{0, 1, 2\}$, $Z=\{0, 1, 2, 3, 4\}$, and consider the profile $P_3\otimes P_5$ over $X\times Z$, where $P_k$, $k\in \{3, 5\}$, is the Condorcet cycle over $\{0, 1, 2, \ldots , k-1\}$. This profile is given in the table below, where we identify the element $(i, j)$ with $5i+j+1$. We claim that $\dim _C(P_3\otimes P_5)=3$.

$v_1$	$v_2$	$v_3$	$v_4$	$v_5$	$v_6$	$v_7$	$v_8$	$v_9$	$v_{10}$	$v_{11}$	$v_{12}$	$v_{13}$	$v_{14}$	$v_{15}$
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
2	3	4	5	1	7	8	9	10	6	12	13	14	15	11
3	4	5	1	2	8	9	10	6	7	13	14	15	11	12
4	5	1	2	3	9	10	6	7	8	14	15	11	12	13
5	1	2	3	4	10	6	7	8	9	15	11	12	13	14
6	7	8	9	10	11	12	13	14	15	1	2	3	4	5
7	8	9	10	6	12	13	14	15	11	2	3	4	5	1
8	9	10	6	7	13	14	15	11	12	3	4	5	1	2
9	10	6	7	8	14	15	11	12	13	4	5	1	2	3
10	6	7	8	9	15	11	12	13	14	5	1	2	3	4
11	12	13	14	15	1	2	3	4	5	6	7	8	9	10
12	13	14	15	11	2	3	4	5	1	7	8	9	10	6
13	14	15	11	12	3	4	5	1	2	8	9	10	6	7
14	15	11	12	13	4	5	1	2	3	9	10	6	7	8
15	11	12	13	14	5	1	2	3	4	10	6	7	8	9

It is immediate that $P_3\otimes P_5$ does not have a Condorcet winner. Now, suppose that $S$ is a Condorcet winning set of size $2$ for $P_3\otimes P_5$. For every $i\in X$, let $T_i=\{(i, j)\mid j\in Z\}$. Assume first that $S\subseteq T_i$ for some $i\in X$; by symmetry we can assume that $S\subseteq T_0$. Then the candidates in $T_2$ are not covered, a contradiction. Thus, we have $|S\cap T_i|=1$, $|S\cap T_j|=1$ for some $i\ne j$; again, by symmetry we can assume that $|S\cap T_0|=1$, $|S\cap T_1|=1$, i.e., $S =\{(0, k), (1, \ell )\}$ for some $k, \ell \in Z$. Now, consider the candidate $(0, k')$, where $k'=k-1\mod 5$. This candidate is ranked below $(0, k)$ in $3$ votes and below $(1, \ell )$ in $5$ votes; moreover, there is exactly one vote where $(0, k')$ is ranked below both $(0, k)$ and $(1, \ell )$, so altogether $(0, k')$ is ranked below $(0, k)$ or $(1, \ell )$ in $7$ votes, i.e., $(0, k')$ is not covered.

Finally, it is easy to see that $P_3\otimes P_5$ has a Condorcet winning set of size $3$: for instance, take any set $S$ such that $S\cap T_i\ne \emptyset$ for $i=0, 1, 2$ or, e.g., the set $\{(0, 0), (0, 2), (1, 0)\}$. $\square$

After the conference version of this paper was published, a number of authors worked on constructing smaller profiles with Condorcet dimension 3. In particular, Laforest (2012) observed that if we do not require the number of voters to be odd, there are subprofiles of $P_3\otimes P_5$ whose Condorcet dimension remains 3. Two such examples have been identified: $P_3\otimes P_4$, where $P_4$ is the Condorcet cycle over $\{0, 1, 2, 3\}$; and the profile obtained from $P_3 \otimes P_5$ by removing even-numbered voters (i.e., $v_2, v_4, \ldots , v_{14}$) and candidates 2 and 3 (Laforest 2012). The former has 12 voters and 12 candidates; the latter has 8 voters and 13 candidates. Geist (2014) has recently obtained an even smaller profile of Condorcet dimension 3: he reduced this question to a satisfiability problem and used a SAT solver to identify a 6-candidate 6-voter profile $P$ with $\dim _C(P)=3$. His proof also shows that no smaller examples exist.

For profiles with an odd number of voters, this question was explored by Cervone and Zwicker (2011), who exhibit a profile $P$ with 11 candidates and 11 voters with $\dim _C(P)=3$; this profile was obtained by computer search and has a more complex structure than our example. More recently, Cervone et al. (2012) have constructed a profile of Condorcet dimension $3$ with even fewer candidates (7), but with 21 voters. We remark that Corollary 1 (see below) implies that every profile with an odd number of voters that has Condorcet dimension 3 or higher has to have at least 7 candidates.

4.2 Searching for profiles of Condorcet dimension 4 or higher

The next natural question is whether there exist profiles whose Condorcet dimension exceeds 3. Intriguingly, we do not have any examples of such profiles: while we do believe that profiles of arbitrarily high dimension exist, we were not able to identify them. We will now discuss some promising approaches to constructing such profiles that nevertheless fail.

First, one might think that by taking a Kronecker product of $s$ sufficiently long Condorcet cycles, we always get a profile of Condorcet dimension $s+1$. However, it turns out that this is not the case: a product of a Condorcet cycle and any profile has Condorcet dimension that does not exceed 3.

Proposition 3

Let $P$ be a Condorcet cycle over the candidate set $X=\{x_1, \ldots , x_m\}$, $m\ge 2$, and let $Q$ be a profile over the candidate set $Y=\{y_1, \ldots , y_k\}$. Then $\dim _C(P\otimes Q)\le 3$.

Proof

Let $y$ be some candidate in $Y$ that is ranked first by some voter in $Q$.

Suppose first that $m=2$. Then $\{(x_1, y), (x_2, y)\}$ is a Condorcet winning set for $P\otimes Q$. Indeed, consider a candidate $(x_1, z)$, $z\ne y$. At least one of the first $|Q|$ voters ranks him below $(x_1, y)$, and the last $|Q|$ voters rank him below $(x_2, y)$. Similarly, candidate $(x_2, z)$, $z\ne y$, is ranked below $(x_1, y)$ by the first $|Q|$ voters, and at least one of the last $|Q|$ voters ranks him below $(x_2, y)$.

Now, suppose that $m>2$. Then the set $S = \{(x_1, y), (x_i, y), (x_m, y)\}$, where $i=\lceil {m}/{2}\rceil$, is a Condorcet winning set for $P\otimes Q$. Indeed, consider any $z = (x_j, y_\ell )\in X\times Y$. If $1 <j \le i$, then $z$ is covered by $(x_1, y)$, if $i <j \le m-1$, then $z$ is covered by $(x_i, y)$, and if $j=1$, then $z$ is covered by $(x_m, y)$. Finally, suppose that $j=m$. Then the first $i|Q|$ voters rank $(x_i, y)$ above $z$. If $m$ is odd, this implies that $z$ is covered by $(x_i, y)$. On the other hand, suppose that $m$ is even. Then if $y_\ell =y$, we have $z\in S$, and otherwise at least one among the last $|Q|$ voters ranks $z$ below $(x_m, y)$, so we are done. $\square$

Another appealing approach is the probabilistic method (Alon and Spencer 1992): one could try to generate a preference profile randomly according to a suitable probability distribution and argue that it has a high Condorcet dimension with non-zero probability. However, Proposition 1 shows that this distribution would have to be more complicated than IC, and we have not been able to identify a suitable distribution.

Finally, one could try to exploit the connection between Condorcet winning sets and dominating sets that was discussed in Sect. 3. Specifically, one could take a tournament in which the smallest dominating set is large and construct an election whose majority graph coincides with this tournament; it seems plausible that this election may have a high Condorcet dimension. The simplest way to construct an election with a given majority graph dates back to McGarvey (1953). In McGarvey’s construction, given a tournament with a vertex set $X$, we fix an order $\succ$ over $X$, and for every edge $(x,y)$ in the tournament we add two votes: in the first vote, $x$ is ranked first, $y$ is ranked second, and the order of all other candidates is given by $\succ$, and in the second vote $y$ is ranked in the last position, $x$ is ranked just above $y$, and other candidates appear in the first $m-2$ positions, in the order given by the reverse of $\succ$. Clearly, the majority graph of the resulting election coincides with the input tournament. However, this construction always produces profiles with Condorcet dimension $2$ or less.

To see this, let $a$ be the first candidate in $\succ$ and let $z$ be the last candidate in $\succ$. We claim that $\{a, z\}$ is a Condorcet winning set. Indeed, consider an arbitrary candidate $x$, and a pair of votes that implements some edge $(s, t)$. If $\{s, t\}$ is disjoint from $\{x, z\}$ then in the first vote in this pair $a$ is ranked above $x$ and in the second vote $z$ is ranked above $x$, so $x$ is dominated in both votes. Otherwise, $x$ is ranked below $a$ or $z$ in at least one of the votes in this pair. If there are at least $4$ candidates, then there is a pair of candidates that is disjoint from $\{x,z\}$ and therefore $x$ is dominated by $\{a, z\}$ in a strict majority of votes. Importantly, this holds even if $x$ beats both $a$ and $z$ in the tournament. This proves our claim. A similar argument shows that the construction used by Alon et al. (2006) to design a tournament with a large dominating set using a small number of voters (which is based on a generalization of McGarvey’s argument) also fails to produce a profile with Condorcet dimension $3$ or higher.

4.3 Upper bounds and computational complexity

While we did not succeed in using the connection between Condorcet winning sets and dominating sets in tournaments to construct a profile with a large Condorcet dimension, we can use this connection to derive an upper bound on the Condorcet dimension. Specifically, Megiddo and Vishkin (1988) show that any tournament on $m$ vertices has a dominating set of size $\lceil \log _2 m \rceil$: the proof proceeds by selecting the vertex with the highest outdegree, which by the pigeonhole principle dominates at least half of the other vertices, deleting this vertex and all vertices dominated by it, and recursively applying the same procedure to the remaining graph. We will now show that this result implies a similar upper bound on the Condorcet dimension; while this is immediate for profiles with an odd number of voters, the case where the number of voters is even (and hence the majority graph is not necessarily a tournament) requires some effort.

Proposition 4

For every $m$-candidate profile $P$ we have $\dim _C(P) \le \lceil \log _2 m \rceil +1$.

Proof

Consider a profile $P$. If $P$ has an odd number of voters, then the graph $G(P)$ is a tournament. Because every dominating set of $G(P)$ is a Condorcet winning set of $P$, and because every tournament on $m$ vertices has a dominating set of size $\lceil \log _2 m \rceil$, it follows that $\dim _C(P)\le \lceil \log _2 m \rceil$.

Now, suppose that $P$ has an even number of voters. Let $x$ be the candidate ranked first by the last voter in $P$, and let $A$ be a minimum-size Condorcet winning set for the profile $P'$ that is obtained from $P$ by removing the last voter. Then $A\cup \{x\}$ is a Condorcet winning set for $P$: for every $z\not \in A\cup \{x\}$, there are at least $|P|/2$ voters in $P'$ who rank some candidate in $A$ above $z$, and the last voter in $P$ ranks $x$ above $z$. Since $P'$ has an odd number of voters, we have $|A|=\dim _C(P')\le \lceil \log _2 m \rceil$. $\square$

We can get a somewhat stronger bound on the size of the smallest dominating set in a tournament by observing that if, at some step of the algorithm, the number of remaining candidates $m$ is even, then at the next step there remain at most $\frac{m}{2}-1$ candidates, and if it is odd, then at the next step there remain at most $\frac{m-1}{2}$ candidates. Define the functions $f$ and $g$ by setting

$$\begin{aligned} f(m) = \left\{ \begin{array}{ll} \frac{m}{2}-1 \quad \text{ if } m \text{ is } \text{ even }\\ \frac{m-1}{2} \quad \text{ if } m \text{ is } \text{ odd } \end{array}\right. \end{aligned}$$

and $g(m) = \min \{k\mid f^k(m) = 0\}$. Then we can strengthen Proposition 4 as follows.

Corollary 1

For every $m$-candidate $n$-voter profile $P$ we have $\dim _C(P) \le g(m)$ if $n$ is odd and $\dim _C(P) \le g(m)+1$ if $n$ is even.

We have $g(1) = g(2) = 1$; $g(3) = \cdots = g(6) = 2$; $g(7) = \cdots = g(14) = 3$. Thus, if we require the number of voters to be odd, to find a profile of Condorcet dimension $4$ or higher we need to consider profiles with $15$ or more candidates.

We can also bound the Condorcet dimension of a given profile in terms of the number of voters. Specifically, for an $n$-voter profile we can obtain a Condorcet winning set of size at most $\lfloor \frac{n}{2}\rfloor +1$ by picking the top candidates of some $\lfloor \frac{n}{2}\rfloor +1$ voters; we emphasize that this holds irrespective of the number of candidates. While this observation is very simple, it can be useful if the number of candidates is much larger than the number of voters.

From the algorithmic perspective, it is natural to ask if we can efficiently compute the Condorcet dimension of a given profile; we will refer to this problem as Condorcet Dimension. Now, if there exists a constant $K$ such that $\dim _C(P) \le K$ for every profile $P$, Condorcet Dimension can be solved in polynomial time by direct enumeration. However, even if this is not the case, and profiles of arbitrarily high dimension do exist, Condorcet Dimension is nevertheless unlikely to be too hard. Indeed, by Proposition 4 we can find a Condorcet winning set by enumerating all subsets of candidates of size $\log _2 m +1$. Thus, Condorcet Dimension can be solved in time ${\mathrm {poly}}(n, m)m^{\log _2 m}$, i.e., it is in the class QP of quasi-polynomial problems.¹ Therefore, Condorcet Dimension is unlikely to be NP-complete, as this would imply QP $=$ NP, and it is strongly believed that QP is strictly contained in NP.

Observe also that Proposition 1 shows that our problem admits an algorithm whose running time is polynomial in expectation under the impartial culture assumption when $n$ is sufficiently large relative to $m$. Namely, given a profile $P$, we pick an arbitrary set of candidates of size $2$, and check if it is a Condorcet winning set for $P$. If this is not the case, we perform the same check for all subsets of candidates of size at most $\lceil \log _2 m \rceil +1$; there are at most $m^{\log _2 m +2}\le e^{(\log _2 m +2)^2}$ such subsets and by Proposition 4 for at least one of them the answer is “yes”. The probability that we execute the second stage is at most $me^{-n/24}$, so the expected running time of this algorithm is polynomial in $n$ and $m$ as long as $n\ge 25(\log _2 m+2)^2$.

5 $\theta$-winning sets

In the definition of a Condorcet winning set, we say that $S$ is a Condorcet winning set if for every candidate $x$ outside of $S$, a majority of voters prefers some candidate in $S$ to $x$. We now generalize this notion by requiring that a given fraction $\theta$ of voters should prefer some candidate in $S$ to $x$.

Definition 2

Given an election over $X$ with a preference profile $P=\langle \succ _1, \ldots , \succ _n\rangle$, a set $Y \subseteq X$ is said to $\theta$-cover an alternative $z\in$ X$\setminus$Y for $\theta \in [0,1)$ if

$$\begin{aligned} \#\big \{i \in N \mid \exists y \in Y \text {such that } y \succ _i z\big \} > \theta n. \end{aligned}$$

For $\theta =1$, we say that a set $Y \subseteq X$ $1$-covers an alternative $z\in$ X$\setminus$Y if

$$\begin{aligned} \#\big \{i \in N \mid \exists y \in Y \text {such that } y \succ _i z\big \} = n. \end{aligned}$$

Given a $\theta \in [0, 1]$, we say that $Y$ is a $\theta$-winning set if $Y$ $\theta$-covers each alternative in $z\in$ X$\setminus$Y.

Clearly, a $\frac{1}{2}$-winning set is a Condorcet winning set.

Just as for Condorcet winning sets, we can reformulate this definition in terms of candidate merging: it is not hard to see that a subset of candidates $Y\subseteq X$ is a $\theta$-winning set for $\theta <1$ if and only if for each $x\in$ X$\setminus$Y it holds that in the preference profile $P_{[Y]}$ (defined in Sect. 2) more than $\theta n$ voters prefer $[Y]$ to $x$. For $\theta =1$, this reformulation is particularly convenient: $Y$ is a $1$-winning set if and only if $[Y]$ is ranked first by all voters in $P_{[Y]}$.

$\theta$-winning sets are quite similar to Condorcet winning sets. In particular, a simple modification of the proof of Proposition 1 gives us the following corollary.

Corollary 2

Let $P$ be a random $n$-voter preference profile over a set $X$, $|X|=m$, generated under the impartial culture assumption, and let $S$ be a $k$-element subset of $X$. Then for every $\varepsilon \in \big (0, \frac{k}{k+1}\big )$ it holds that $S$ is a $\big (\frac{k}{k+1}-\varepsilon \big )$-winning set for $P$ with probability at least $1-m\cdot \exp \big (-\frac{k\varepsilon ^2}{(k+1)n}\big )$.

5.1 Defining voting correspondences via $\theta$-winning sets

The notion of a $\theta$-winning set is useful if we want to define a voting correspondence based on the idea of disjunctive domination. Recall that in Sect. 2 we defined a mapping $\rho (P)=\cup _{S\in { CWS }^{\min }(P)}S$: given a profile $P$, $\rho$ returns all candidates that belong to some minimal Condorcet winning set for $P$. However, we have argued that under the impartial culture assumption every subset of candidates of size two is likely to be a Condorcet winning set, and therefore in the absence of a Condorcet winner this voting correspondence is going to be extremely indecisive. The notion of a $\theta$-winning set provides a natural way to define two families of more decisive voting correspondences using the same approach: First, we can pick a $\theta \in (0, 1]$ and output all candidates that belong to some minimal (or minimum-size) $\theta$-winning set. Alternatively, we can fix the desired size of the winning set (say, $k$), find the largest value of $\theta$ such that there exists a $\theta$-winning set of size $k$, and output all candidates that belong to some such set. A variant of the latter approach is to pick one $\theta$-winning set of size $k$ according to some tie-breaking rule, thus obtaining a committee selection rule (see Sect. 7).

Formally, for every $\theta \in (0, 1]$ and every $k\ge 1$ define ${\mathcal {D}}(P,\theta ,k)$ to be the collection of all $\theta$-winning sets of size $k$. For a fixed $\theta \in (0, 1]$, we let $k(P, \theta )$ be the smallest value of $k$ such that ${\mathcal {D}}(P,\theta ,k) \ne \emptyset$, and define a voting correspondence $D^\theta$ by setting

$$\begin{aligned} D^\theta (P) = \cup _{D\in {\mathcal {D}}(P,\theta ,k(P, \theta ))} D; \end{aligned}$$

note that $D^\theta (P)\ne \emptyset$ for every $\theta \in (0, 1]$. For instance, if $k(P, \theta )=1$, the set $D^\theta (P)$ consists of all candidates that get more than $\theta n$ votes in every pairwise election they participate in. Observe that there is a subtle difference between $D^{\frac{1}{2}}$ and $\rho$: while $\rho$ outputs the union of all minimal Condorcet winning sets, $D^{\frac{1}{2}}$ outputs the union of all minimum-size Condorcet winning sets. Thus, $D^{\frac{1}{2}}$ is a refinement of $\rho$.

To define our second family of voting correspondences, for a given $k\ge 1$, let

$$\begin{aligned} \theta (P, k)=\sup \big \{\theta \mid {\mathcal {D}}(P,\theta ,k)\ne \emptyset \big \}. \end{aligned}$$

Since the definition of a $\theta$-winning set involves a strict inequality, we have

$$\begin{aligned} {\mathcal {D}}\big (P,\theta (P, k),k\big )=\emptyset . \end{aligned}$$

Therefore, we set $\theta '(P, k)=\theta (P, k)-\frac{1}{n}$, where $n$ is the number of voters in $P$, and define a voting correspondence $D_k$ by setting

$$\begin{aligned} D_k(P) = \cup _{D\in {\mathcal {D}}(P,\theta '(P, k),k)} D. \end{aligned}$$

We can replace $\frac{1}{n}$ in the definition of $\theta '(P, k)$ by any sufficiently small value: it is not hard to see that

$$\begin{aligned} D_k(P) = \cap _{0<\varepsilon <\theta (P, k)}\left( \cup _{D\in {\mathcal {D}}(P,\theta (P, k)-\varepsilon ,k)} D\right) . \end{aligned}$$

Indeed, we have $D\in {\mathcal {D}}(P,\theta '(P, k),k)$ if and only if $|D|=k$ and for every $x\not \in D$ more than $\theta '(P, k)n = \theta (P, k)n-1$ voters in $P_{[D]}$ prefer $[D]$ to $x$, or, equivalently, at least $\theta (P, k)n$ voters in $P_{[D]}$ prefer $[D]$ to $x$; clearly, choosing $\varepsilon$ in $(0, \frac{1}{n})$ results in the same criterion, and choosing $\varepsilon$ in $(\frac{1}{n}, \theta (P, k))$ produces a collection of sets that contains ${\mathcal {D}}(P,\theta '(P, k),k)$.

Instead of fixing $k$ in advance, one can set $k=\dim _C(P)$; this ensures that all sets in ${\mathcal {D}}(P,\theta '(P, k),k)$ are Condorcet winning sets. Thus, for this value of $k$ the voting correspondence $D_k$ is a refinement of $D^{\frac{1}{2}}$: while $D^\frac{1}{2}$ outputs the elements of all minimum-size Condorcet winning sets, $D_k$ only considers the “best” Condorcet winning sets of that size. Recall that $D^\frac{1}{2}$ is itself a refinement of $\rho$, and $\rho$ has been shown to be extremely indecisive under the impartial culture assumption; in contrast, $D_k$ for small values of $k$ can be empirically shown to be quite decisive (see Sect. 6).

Interestingly, the voting correspondence $D_1(P)$ is well-known in the social choice literature under a different name: namely, it is simply the Maximin correspondence. We recall that under Maximin, a candidate’s score is the number of votes she gets in her worst pairwise election, i.e., $x$’s score equals $\min _{y\in X\setminus \{x\}}\#\{i\mid x\succ _i y\}$; the Maximin winners are the candidates with the maximum score.

Proposition 5

Given an $n$-voter election with a preference profile $P$, the set

$$\begin{aligned} D_1(P)=\cup _{D\in {\mathcal {D}}(P,\theta '(P, 1),1)} D \end{aligned}$$

is exactly the set of Maximin winners in $P$.

Proof

Let $c$ be a Maximin winner in $P$, and let $s$ be its Maximin score. Then we have $\{c\}\in {\mathcal {D}}(P, \theta , 1)$ for every $\theta <\frac{s}{n}$, and for every alternative $x$ it holds that $\{x\}\not \in {\mathcal {D}}(P, \frac{s}{n}, 1)$. Therefore, $\theta (P, 1) = \frac{s}{n}$ and hence $D_1(P)=\cup _{D\in {\mathcal {D}}(P,\frac{s-1}{n},1)} D$, so $c$ is in $D_1(P)$. Since this is true for every Maximin winner of $P$, the set of all Maximin winners in $P$ is contained in $D_1(P)$. On the other hand, if $d$ is not a Maximin winner, his Maximin score is at most $\frac{s-1}{n}$, so we have $\{d\}\not \in {\mathcal {D}}(P, \theta '(P, 1), 1)$. Since the set family $D(P, \theta '(P, 1), 1)$ consists of singletons only, this completes the proof. $\square$

5.2 Computational complexity

We already know that for $\theta = \frac{1}{2}$ computing a $\theta$-winning set of size $k$ (or deciding that none exists) is unlikely to be NP-hard. This holds a fortiori for every $\theta < \frac{1}{2}$. Also, we can compute a $1$-winning set of size $k$ (or decide that none exists) in linear time: it suffices to count the number of candidates ranked first by at least one voter. However, there are values of $\theta$ for which computing a $\theta$-winning set is computationally difficult. We first state the respective decision problem.

Existence of a $\theta$-winning set of size $k$

Given an $n$-voter, $m$-candidate profile $P$, an integer $k \le m$, and a rational number $\theta \in (0,1]$, decide whether $P$ admits a $\theta$-winning set of size $k$.

Note that in this decision problem $k$ and $\theta$ are both included in the input.

Theorem 1

Existence of a $\theta$-winning set of size $k$ is NP-complete.

Proof

Membership in NP is straightforward. To prove NP-hardness, we will now present a polynomial-time reduction from the Hitting Set problem, which is known to be NP-complete (Garey and Johnson 1979).

Hitting Set

Given a set $C$ of size $r$, a collection $\mathcal{S} = \{S_1, \ldots , S_p\}$ of subsets of $C$, and an integer $s$, decide whether there exist a subset $Y$ of $C$ such that $|Y| \le s$ and $Y \cap S_i \ne \emptyset$ for each $i=1, \ldots , p$.

Without loss of generality, we can assume that $s \le p-3$. In what follows, given a set of alternatives $X$ and two disjoint subsets $Y, Z$ of $X$, we write $\ldots \succ Y\succ Z\succ \ldots$ to denote a vote where all elements of $Y$ are ranked above all elements of $Z$, in an arbitrary order. Given an instance $\langle C, \mathcal{S}, s \rangle$ of Hitting Set with $C = \{c_1, \ldots , c_r\}$, we construct an instance of Existence of a $\theta$-winning set of size $k$ as follows.

• The set of alternatives is $X = C \cup A \cup \{b\}$, where $A=\{a_1, \ldots , a_p\}$.

• The profile $P$ consists of $p^2(p+1)$ votes: $p^2$ votes of type $1$ and $p^3$ votes of type 2. Specifically, for each $i=1, \ldots , p$ we have

  • $p$ type $1$ votes:

    $$\begin{aligned}&S_i \succ a_1\succ A\setminus \{a_1\} \succ X \setminus S_i \succ b\\&S_i \succ a_2\succ A\setminus \{a_2\} \succ X \setminus S_i \succ b\\&\qquad \qquad \ldots \qquad \qquad \qquad \\&S_i \succ a_p\succ A\setminus \{a_p\} \succ X \setminus S_i \succ b \end{aligned}$$

  • $p^2$ type $2$ votes:

    $$\begin{aligned} p^2\quad \text {copies of}\quad a_i \succ b \succ C \succ A \setminus \{a_i\}. \end{aligned}$$

• $\theta = \frac{p}{p+1}-\frac{1}{p^3(p+1)}$. Note that $\frac{p-1}{p}<\theta <\frac{p}{p+1}$.

• $k = s+1$.

We claim that $P$ admits a $\theta$-winning set of size $k$ if and only if $\mathcal S$ admits a hitting set of size $s$.

Let $Y \subseteq C$ be a hitting set of size $s$ for $\mathcal{S}$. Let $Y' = Y \cup \{b\}$. For every $c_j \in C \setminus Y$ it holds that $b$ is ranked above $c_j$ in all votes of type $2$. Therefore the fraction of voters who prefer some element of $Y'$ to $c_j$ is at least $\frac{p^3}{p^2(p+1)} = \frac{p}{p+1} > \theta$. Now consider an arbitrary $a_i$ in $A$. Since $Y$ is a hitting set, some element of $Y$ is ranked above $a_i$ in all votes of type $1$, and $b$ is ranked above $a_i$ in $p^2(p-1)$ votes of type $2$. Thus, some element of $Y'$ is ranked above $a_i$ in at least $p^2 + p^2(p-1) = p^3$ votes, so the fraction of voters who prefer some element of $Y'$ to $a_i$ is at least $\frac{p^3}{p^2(p+1)} = \frac{p}{p+1} > \theta$. Hence, $Y'$ is a $\theta$-winning set of size $k$.

Conversely, suppose that $P$ admits a $\theta$-winning set of size $k$; let $Y'$ be some such set. If $b \notin Y'$, then $b$ is ranked above all elements of $Y'$ in at least $p^2(p-k)$ votes of type $2$, so the fraction of voters who prefer some element of $Y'$ to $b$ is at most

$$\begin{aligned} \frac{p^2k+p^2}{p^2(p+1)} = \frac{k+1}{p+1} \le \frac{p-1}{p+1} < \frac{p-1}{p} < \theta \end{aligned}$$

(recall that we have set $k=s+1$ and assumed $s\le p-3$). Therefore, we have $b\in Y'$. Now, let $A' = Y' \cap A$, $C'=Y'\cap C$. Note that $|A'|\le k<p$, and therefore $A\setminus A'\ne \emptyset$. We will argue that $C'$ is a hitting set for $\mathcal S$.

Indeed, suppose that this is not the case, i.e., there exists an $S_j\in \mathcal S$ such that $S_j\cap C'=\emptyset$. Consider an alternative $a_i \notin A'$. There exists a vote of type $1$ where the candidates from $S_j$ are ranked in top $|S_j|$ positions, followed by $a_i$. In this vote $a_i$ appears above all candidates in $Y'$. Also, there are $p^2$ votes of type $2$ where $a_i$ is ranked first. Thus, the total number of votes where some candidate in $Y'$ is ranked above $a_i$ is at most $p^2(p-1)+p^2-1=p^3-1$, and we have

$$\begin{aligned} \frac{p^3-1}{p^2(p+1)}=\frac{p}{p+1}-\frac{1}{p^3+p^2} < \frac{p}{p+1}-\frac{1}{p^4+p^3}=\theta , \end{aligned}$$

so $Y'$ is not a $\theta$-winning set, a contradiction. $\square$

The reader may have noticed that in Theorem 1 the value of $\theta$ depends on the number of voters. We will now argue that for constant $\theta$ our computational problem is unlikely to be hard, by generalizing the argument for $\theta =\frac{1}{2}$.

Proposition 6

If Existence of a $\theta$-winning set of size $k$ is NP-complete for some constant $\theta \in (0, 1)$, then QP = NP.

Proof

We will argue that for any constant $\theta \in (0, 1)$ our computational problem can be solved in time ${\mathrm {poly}}(n, m)m^{O(\log _2 m)}$, and therefore belongs to the class $\mathsf{QP}$ (see Footnote 1).

Fix a $\theta \in (0, 1)$. Since $\theta <1$, there exists a constant $s$ such that $\theta <\frac{s-1}{s}$. We will argue that any $n$-voter $m$-candidate profile admits a $\theta$-winning set of size $(s-1)\log _\frac{s}{s-1} m$, and therefore a $\theta$-winning set can be found by exhaustive search in time ${\mathrm {poly}}(n, m)m^{\alpha \log _2 m}$, where $\alpha =\frac{s-1}{\log _2\frac{s}{s-1}}$; note that $s$ is a constant, i.e., it does not depend on $n$ and $m$. The proof proceeds by induction on $m$ (with $n$ fixed).

Given an $n$-voter $m$-candidate profile $P$ over a candidate set $X$, we construct a bipartite graph $(L, R, E)$ with parts $L$ and $R$ and the set of edges $E$ as follows. The set $L$ consists of all subsets of $X$ of size $s-1$ (and hence $|L| = {m\atopwithdelims (){s-1}}$) and $R=X$. Further, there is an edge between a subset $A$ and a candidate $a$ if and only if at least $\theta n$ voters rank some candidate in $A$ above $a$.

We claim that $|E|\ge {m\atopwithdelims ()s}$. To see this, consider an arbitrary subset of candidates $B$ of size $s$. There is a candidate $b$ in $B$ that is ranked above all other candidates in $B$ in at most $\frac{n}{s}$ votes. That is, the fraction of voters that prefer some candidate in $B\setminus \{b\}$ to $b$ is at least $1-\frac{1}{s}>\theta$. Therefore, $(B\setminus \{b\}, b)$ is an edge in $E$, and different size-$s$ subsets of $X$ correspond to different edges in $E$. By the pigeonhole principle, there is a vertex $A$ of $L$ that is adjacent to at least ${m\atopwithdelims ()s}/{m\atopwithdelims (){s-1}}=\frac{m-s+1}{s}$ edges. Let $Y=\{a\in X\mid (A, a)\in E\}$, set $X'=X\setminus (Y\cup A)$, and consider the profile $P'=P|_{X'}$. We have $|Y\cup A|>\frac{m}{s}$, so $|X'|\le m\frac{s-1}{s}$, and hence by the inductive hypothesis $P'$ admits a $\theta$-winning set $A'$ of size

$$\begin{aligned} (s-1)\log _\frac{s}{s-1} \left( m\frac{s-1}{s}\right) =(s-1)\log _\frac{s}{s-1}m-(s-1). \end{aligned}$$

As $|A|=s-1$, it follows that $A\cup A'$ is a $\theta$-winning set for $P$ of size $(s-1)\log _\frac{s}{s-1} m$, which is what we wanted to prove. $\square$

5.3 Social choice-theoretic properties

We have argued that the notion of $\theta$-winning set can be used to define two families of voting correspondences: $D_k$ and $D^\theta$. Therefore, it is natural to ask which social choice-theoretic properties are satisfied by these voting correspondences. Since defining new voting correspondences is not the primary motivation of our work, this issue is discussed briefly; a deeper study, perhaps with an axiomatic characterization, would be the topic of another paper. Since $D_1$ is Maximin, we focus on properties satisfied by Maximin; thus, in particular, we do not consider Smith consistency, participation, and clone-proofness, which are all failed by Maximin.

Proposition 7

The following table shows which properties are satisfied by the correspondences $D_k$ and $D^\theta$ (the last two rows refer to the rules obtained by composing $D_k$ and $D^\theta$ with a tie-breaking mechanism). “Y” means that the property is satisfied by $D_k$ (respectively, $D^\theta$) for all values of $k$ (respectively, $\theta$); “N” means that it is failed for at least some values of $k$ (respectively, $\theta$).

	$D_k$	$D^\theta$
Monotonicity	$Y$	$Y$
Reinforcement	$N$	$N$
Condorcet-consistency	$k = 1: Y$	$\theta = \frac{1}{2}: Y$
	$k > 1: N$	$\theta \ne \frac{1}{2}: N$
Efficiency	$k = 1: Y$	$N$
	$k > 1: N$

Proof

Throughout the proof, we will use the following notation. Given a subset of alternatives $S$ and a profile $P$, let

$$\begin{aligned} \theta (P, S)=\sup \{\theta \mid S \in {\mathcal {D}}(P,\theta ,|S|)\} = \sup \{\theta \mid S \text{ is } \text{ a } \theta \text{-winning } \text{ set } \text{ for } P\}. \end{aligned}$$

• Monotonicity Recall that a voting correspondence $R$ is said to be monotone if for every profile $P$ and every alternative $x\in R(P)$ it holds that $x\in R(P')$, where $P'$ is the profile obtained from $P$ by moving $x$ up in the preference ranking of some voter without changing the relative order of the remaining alternatives. We will argue that $D_k$ and $D^\theta$ are monotone for all $k\ge 1$ and all $\theta \in [0, 1]$. Consider a profile $P$, an alternative $x\in D_k(P)$ and a profile $P'$ constructed by moving $x$ up in one of the votes. As $x\in D_k(P)$, $x$ belongs to some $\theta '(P, k)$-winning set $S$. We have $\theta (P',S) \ge \theta (P, S)$, and hence $\theta (P',k) \ge \theta (P, k)$. On the other hand, for every $S'$ such that $|S'| = k$ and $x \notin S'$, we have $\theta (P',S') \le \theta (P, S')$. If $\theta (P',k) > \theta (P, k)$, then all $\theta '(P', k)$-winning sets contain $x$, and therefore $x \in D_k(P')$. On the other hand, if $\theta (P', k) = \theta (P, k)$ then $S\in {\mathcal {D}}(P', \theta '(P', k), k)$ and hence $x \in D_k(P')$. The proof for $D_k$ is complete. The argument for $D^\theta$ is similar. Suppose that $x \in D^\theta (P)$ and $P'$ is defined as above. Then $x$ belongs to some $\theta$-winning set $S$ with $|S|=k(P, \theta )$. Let $k'=k(P', \theta )$. If $k'<k(P, \theta )$, then every $\theta$-winning set of size $k'$ contains $x$, so $x\in D^\theta (P')$. If $k'=k(P, \theta )$, then $x\in S$ implies $x\in D^\theta (P')$.

• Reinforcement Recall that a voting correspondence $R$ is said to satisfy reinforcement if for every pair of profiles $P_1,P_2$ over the same set of alternatives such that $R(P_1)\cap R(P_2)\ne \emptyset$ it holds that $R(P_1)\cap R(P_2)\subseteq R(P_1+P_2)$, where $P_1+P_2$ is the profile obtained by concatenating $P_1$ and $P_2$. For $k = 1$, $D_k$ coincides with Maximin, which is known not to satisfy reinforcement. The respective counterexample $(P_1, P_2)$ can be extended to $k>1$ by employing the following construction. We extend the set of alternatives $X$ by setting $X'=X\cup Z$, where $\{z_1, \ldots , z_{k-1}\}$. We modify each vote in $P_1$ and $P_2$ by inserting the new candidates $z_1, \ldots , z_{k-1}$ in the last $k-1$ positions. Now, let $v_i$, $i=1, \ldots ,k-1$, be an arbitrary vote over $X'$ that ranks $z_i$ first. For each $i=1, \ldots , k-1$ and $j=1, 2$, we add $|P_j|$ copies of $v^i$ to $P_j$; denote the resulting profiles by $P'_1$ and $P_2'$, respectively. Observe that

  $$\begin{aligned} \theta (P'_j, k)=\frac{|P_j|\theta (P_j, 1)+|P_j|(k-1)}{|P_j|k} \quad \text { for } j=1, 2, \end{aligned}$$

  and therefore for $j=1, 2$ we have $\{x\}\in {\mathcal {D}}(P_j, \theta '(P, 1), 1)$ if and only if $\{x\}\cup Z\in {\mathcal {D}}(P_j, \theta '(P, k), k)$. It follows that $D_k(P'_1)=D_1(P_1)\cup Z$, $D_k(P'_2)=D_1(P_2)\cup Z$, and therefore $(P'_1, P'_2)$ is a witness that $D_k$ does not satisfy reinforcement. For $\theta =\frac{1}{2}$, the following example shows that $D^\theta$ does not satisfy reinforcement. Let

  $$\begin{aligned} P_1&= \langle abc, abc, bca, bca, cab, cab\rangle \\ P_2&= \langle acb, acb, bac, bac, cba, cba, cba \rangle . \end{aligned}$$

  Then $\{a,b\}$ is a minimum-size Condorcet winning set for $P_1$ and $P_2$, but not for $P_1 + P_2$, which has $c$ as its Condorcet winner. Again, we can extend this counterexample to many other values of $\theta$ by adding new candidates and voters. For instance, we can introduce a new candidate $d$, modify $P_1$ and $P_2$ by placing $d$ last in each vote, and then add $s$ votes that rank $d$ first to $P_1$ and $s-1$ votes that rank $d$ first to $P_2$; denote the resulting profiles by $P'_1$ and $P'_2$, respectively. We have

  $$\begin{aligned}&\theta (P'_1, \{a, b, d\}) = \frac{s+4}{s+6}, \quad \theta (P'_2, \{a, b, d\}) =\frac{s+3}{s+6},\\&\theta (P'_1, \{c, d\}) = \theta (P'_2, \{c, d\})=\frac{s+2}{s+6}, \quad \theta (P'_1+P'_2, \{c, d\}) =\frac{s+3}{s+6}. \end{aligned}$$

  Consequently, for $s\ge 4$ and $\frac{s+2}{s+6}\le \theta <\frac{s+3}{s+6}$ it holds that $\{a, b, d\}$ is a minimum-size $\theta$-winning set for $P'_1$ and $P'_2$, but the unique minimum-size $\theta$-winning set for $P'_1+P'_2$ is $\{c, d\}$. Since for every $\theta \ge \frac{3}{5}$ we can find a positive integer $s\ge 4$ such that $\frac{s+2}{s+6}\le \theta <\frac{s+3}{s+6}$, it follows that $D^\theta$ does not satisfy reinforcement for every $\theta \ge \frac{3}{5}$.

• Condorcet consistency Recall that a voting correspondence $R$ is said to be Condorcet consistent if, given a profile $P$ that has $x$ as its Condorcet winner, it outputs $\{x\}$. Since $D_1$ coincides with Maximin, it is Condorcet-consistent. Also, if $x$ is a Condorcet winner for $P$ then $D^{\frac{1}{2}}(P) = \{x\}$, therefore $D^{\frac{1}{2}}$ is Condorcet-consistent. However, for $k > 1$ and for $\theta \ge \frac{1}{2}$ the mappings $D_k(P)$ and $D^\theta$ are not necessarily Condorcet-consistent. We give a counterexample that works for $k = 2$ and also for many values of $\theta$; it extends straightforwardly to every even $k\ge 2$. Let $P=\langle acb,acb, bca,bca,cab\rangle$. While $c$ in the Condorcet winner in $P$, we have $D_2(P) = \{a,b\}$. Also, $D^\theta (P) = \{a,b,c\}$ for $\theta \ge \frac{4}{5}$, and $D^\theta (P) = \{a,b\}$ for $\frac{3}{5} \le \theta < \frac{4}{5}$. Note that the Condorcet winner is not even contained in the output of $D_2(P)$ and $D^\theta (P)$ with $\frac{3}{5} \le \theta < \frac{4}{5}$.

• Efficiency Recall that a voting correspondence $R$ is said to be efficient if for every profile $P$ where each voter ranks $a$ above $b$ we have $b\not \in R(P)$. Maximin, i.e., $D_1$, is known to be efficient. However, $D_k$ with $k\ge 2$ is not efficient. To see this, fix a $k\ge 2$, consider a Condorcet cycle over alternatives $X = \{a_1, \ldots , a_{k+1}\}$, and modify it by adding a new alternative $b$ that is ranked right below $a_1$ by every voter. Denote the resulting profile by $P_k$. Let $S = (X\setminus \{a_1, a_2\})\cup \{b\}$. We have $\theta (P_k, S)=\frac{k}{k+1}$, and, moreover, for every set of candidates $S'$ with $|S'|=k$ we have $\theta (P_k, S)\le \frac{k}{k+1}$. Therefore, $\theta (P_k, k)=\frac{k}{k+1}$ and hence $b\in D_k(P_k)$, even though $b$ is dominated by $a_1$. For $k=2$ we obtain

  $$\begin{aligned} P_2 = \langle a_1ba_2a_3, a_2a_3a_1b, a_3a_1ba_2 \rangle , \end{aligned}$$

  and one can check that $\{b, a_3\}\in {\mathcal {D}}(P_2,\theta , k(P_2, \theta ))$ for $\theta \in [\frac{1}{2}, \frac{2}{3})$. This shows that $D^\theta$ is not efficient for $\theta \in [\frac{1}{2}, \frac{2}{3})$. By considering $P_k$ with $k>2$, we can extend this result to other values of $\theta$.

$\square$

Note that, even though $D_k$ and $D^\theta$ do not satisfy reinforcement, the mapping that, given a profile $P$, outputs a $\theta$-winning set for $P$ (for a fixed $\theta$), satisfies a weak form of reinforcement: If $P_1$ and $P_2$ are two profiles over a set of candidates $X$, and $Y$ is a $\theta$-winning set for both $P_1$ and $P_2$, then it is also a $\theta$-winning set for $P_1 + P_2$.

6 Empirical analysis

In this section, we provide an empirical analysis of Condorcet winning sets as well as $\theta$-winning sets under the impartial culture assumption. Our code is available through Bitbucket (https://bitbucket.org/Abdallah/winning-sets/).

In our first experiment, we generate $r$ preference profiles with $m$ voters and $n$ candidates, for various values of $r$, $m$, and $n$, and compute the Condorcet dimension of each profile. In all of our experiments, the Condorcet dimension was either 1 or 2. While this is consistent with Proposition 1, it is remarkable that not even a single profile of a higher dimension has been discovered. The results of our experiments are summarized in Table 1. Note that the probability that the Condorcet dimension of a given profile exceeds 1 is simply the probability of the Condorcet paradox, which has been extensively studied in the social choice literature (see, e.g., Jones et al. 1995). Our results are consistent with those of Jones et al., lending credence to our implementation. Observe also the drastic difference between the columns that correspond to odd and even values of $n$, which is especially pronounced for larger values of $m$.

Table 1 Percentage of profiles with Condorcet dimension 1 and 2

For comparison, we have also computed the size of the smallest dominating set (in what follows, we will refer to it as the DS-dimension) for each of the generated profiles (Table 2). For $m=15$ and $m=50$, we have found a small number of profiles of DS-dimension 5 for $n=10$ and $n=11$; however, for $n\ge 20$ the DS-dimension of all generated profiles was at most 4. For $m=100$ we have found no profiles of DS-dimension 5; while this may appear surprising, note that we considered fewer samples than for $m=15$ or $m=50$.

Table 2 Percentage of profiles with various DS-dimensions

We note that the distribution of the Condorcet dimension is quite different from that of the DS-dimension: for instance, for $m=50$, $n=100$, and $r=10^4$, we obtain that for 989 profiles the smallest dominating set has size 1 (these are exactly the profiles with a Condorcet winner), for 7688 profiles the smallest dominating set has size 2, and for the remaining 1323 profiles the smallest dominating set has size 3. That is, in this experiment, for about $13.2\%$ of the profiles the DS-dimension exceeds the Condorcet dimension. Interestingly, this result seems to indicate that the DS-dimension of a tournament generated under the impartial culture assumption is distributed differently from the DS-dimension a uniformly random tournament, i.e., one where the direction of each edge is chosen uniformly at random. Indeed, for the latter model, it is known that with probability approaching 1 the DS-dimension exceeds $\frac{1}{2}\log _2 m$ (which is $\approx 2.82$ for $m=50$), see, e.g., Lemma 3 in (Scott and Fey 2012). However, comparing these two models in more detail is beyond the scope of our work.

Figure 1 maps the probability that an arbitrary set of candidates of size $k$, $k=1, 2, 3, 4$, is a Condorcet winning set for a 30-candidate election, as a function of the number of voters. We see that for $k>1$ this probability quickly reaches 1.

Fig. 1

Probability that a fixed set of size $k$ is a Condorcet winning set as a function of $n$, for $m = 30$

Figure 2 plots the empirical distribution of $\theta (P, k)$ for $m=30$, $n=100$ and $k=1, 2, 3, 4$. Our results agree with Corollary 2: the values of $\theta (P, k)$ are clustered around $\frac{k}{k+1}$.

Fig. 2

Empirical distribution of $\theta (P,k)$ for $m = 30$ and $n = 100$

Figure 3 shows the empirical distribution of the number of $\frac{2}{3}$-winning sets of size $2$ for $20$ candidates and a varying number of voters. We see that out of $(19\cdot 20)/2$ pairs of candidates, with a high probability, only a few of them are $\frac{2}{3}$-winning sets; in fact, quite often there is just one such set. Recall that we have argued that it is likely that almost all sets of size $2$ are Condorcet winning sets; this means that raising the threshold from $\frac{1}{2}$ to $\frac{2}{3}$ is a powerful method to narrow down the set of winners.

Fig. 3

Empirical distribution of the number of $\frac{2}{3}$-winning sets of size $2$ for $m=20$

However, Fig. 3 shows that there is a non-trivial fraction of profiles with no $\frac{2}{3}$-winning sets of size $2$, i.e., ${\mathcal {D}}(P, \frac{2}{3}, 2)$ may be empty. In contrast, ${\mathcal {D}}(P, \theta '(P, k), k)$ is guaranteed to be non-empty for every $k\ge 1$, so our next experiment investigates whether the associated voting correspondence, i.e., $D_k$, is likely to output a small number of candidates. It turns out that this is indeed the case for $k=2, 3, 4$. Specifically, we plot the empirical distribution of the number of $\theta '(P, k)$-winning sets of size $k$ for $k=2, 3, 4$, for $m=5, m=20$ and $n=50$, $n=500$, $n=5,000$ (see the histograms in Fig. 4). For each value of $k$ we sample 10,000 profiles. It turns out that the number of $\theta '(P, k)$-winning sets is quite small: typically, there are only one or two such sets.

Fig. 4

Empirical distribution of the number of $\theta '(P,k)$-winning sets, $k=2, 3, 4$

7 Related work

There are three streams of research that are closely related to the problems we consider. The first stream deals with the problem of proportional representation, where each voter indicates how well each candidate would represent her, and the goal is to build a committee of a given cardinality that represents every voter. There are approaches to this problem that select a subset of candidates in a disjunctive manner. Specifically, Chamberlin and Courant (1983) propose a method where each voter evaluates a subset of alternatives based on the Borda score of the highest-ranking alternative in this subset: a set $Y$ receives $\max _{y\in Y} s_B(y, i)$ points from a voter $i$, where $s_B(y, i)$ is the number of candidates that $i$ ranks below $y$, and the winning committee of size $k$ is the $k$-element set of candidates with the highest score. Note that, unlike in our work, the committee size $k$ is determined exogenously. Chamberlin and Courant’s method can be generalized to use scoring functions other than Borda’s, and there is a number of papers that explore the computational complexity of finding an optimal committee of a given size, for various scoring functions (Procaccia et al. 2008; Lu and Boutilier 2011; Betzler et al. 2013; Cornaz et al. 2012; Skowron et al. 2013a, b; Yu et al. 2013; Skowron et al. 2013c). Lu and Boutilier also propose a relaxation of Chamberlin and Courant’s approach that allows for tradeoffs between committee size and quality of representation, and show experimental results on real-world data sets. We remark, however, that another classic approach to proportional representation, namely, that of Monroe (1995), is more difficult to interpret disjunctively, as it is based on establishing a many-to-one balanced matching between voters and candidates (for details, see Monroe 1995). Recently, Elkind et al. (2014) identified a number of desirable properties for committee selection rules; an interesting research direction, which we leave for future work, is to verify which of these properties are satisfied by the mapping that, for a given profile $P$ and parameter $k$, outputs a set from ${\mathcal {D}}(P, \theta '(P, k), k)$ using some tie-breaking rule.

A second stream of research has the same starting point as we do, namely, finding a generalization of the notion of a Condorcet winner to sets of alternatives. For instance, Gehrlein (1985) assumes, like us, that individual preferences are given by rankings of the alternatives, and defines a Condorcet committee as a set of alternatives $Y \subseteq X$ such that every alternative in $Y$ beats every alternative in $X \setminus Y$. This method has a conjunctive interpretation, as opposed to the disjunctive interpretation of Condorcet winning sets: $Y$ is a Condorcet committee if for every pair of alternatives $x \in X \setminus Y$ and $y \in Y$ a majority of voters prefers $y$ to $x$. Thus, a Condorcet committee is a Condorcet winning set, but the converse is not necessarily true. As Condorcet committees of size $k$ do not always exist, except for the trivial case $k = m$, Ratliff (2003) suggests to generalize the Dodgson and Kemeny voting rules to sets of alternatives. For instance, the extension of the Dodgson rule computes, for a given subset $Y$, the minimal number of elementary swaps in the votes needed to make $Y$ a Condorcet committee. A different approach is pursued by Fishburn (1981), who proceeds by defining a preference relation on sets of alternatives and looking for a subset that beats any other subset in a pairwise election. These two lines of work are bridged by Kaymak and Sanver (2003), who examine under which condition a Condorcet committee in the sense of Fishburn can be derived from preferences over alternatives. Ratliff (2003) gives further discussion on committee selection. It is not immediately clear whether a Condorcet committee in the sense of Fishburn (1981) and Kaymak and Sanver (2003) is also a Condorcet winning set: the answer depends on the extension function used for lifting the preference relation from alternatives to subsets; for standard extension functions (e.g., ones that compare the sets lexicographically or according to their best element) this is not the case.

The third stream of research concerns dominating sets in tournaments, and, in particular, in tournaments constructed from voters’ preferences (these are known as $n$-majority tournaments): as discussed in Sect. 4.3, for such tournaments the size of the smallest dominating set (and hence the Condorcet dimension of the underlying election) can be bounded in terms of the number of voters. However, the current best upper bound on the DS-dimension of an $n$-voter election is $C_2 n\log n$ for some positive constant $C_2$ (Alon et al. 2006), whereas we have argued that the Condorcet dimension of any such election does not exceed $\frac{n}{2}+1$. Thus, the existing results for $n$-majority tournaments are too weak to provide non-trivial upper bounds on the Condorcet dimension. On the other hand, the current best lower bound on the DS-dimension is sublinear ($C_1n/\log n$ for a positive constant $C_1$), so it does not rule out the possibility of obtaining a sublinear upper bound on the DS-dimension of $n$-majority tournaments; any such result would also provide a better upper bound on the Condorcet dimension.

8 Conclusions

We have defined a framework for defining collectively preferred sets of alternatives that is based on generalizing the Condorcet principle. Such a framework is useful whenever it makes sense to output several alternatives, such as committee elections, multiple recommendations to groups of users (as in Lu and Boutilier 2011), choices of time slots for regular events, etc. A number of questions remain open for future work; perhaps the most pressing of them is whether there exist profiles of Condorcet dimension 4 or higher.