1 Introduction

The acoustic characterization of hydraulic systems is essential to the evaluation of dynamic behavior of industrial circuits during transients, unsteady or unstable operating points.

The goal has to develop a fast, robust and reliable identification methodology of cavitating inducer transfer functions to predict and analyze the POGO phenomenon. It is a current problem in rocket launchers (About et al. 1983; Dordain et al. 1974; Rasumoff and Winje 1973). The whole identification procedure consists in:

  1. (a)

    evaluating the speed of sound in the monophasic or diphasic mediums by using a unique post-treatment (speeds of sound varying from 100 to 1400 m/s).

  2. (b)

    reconstituting flow rate fluctuations by using three pressure sensor measurements.

  3. (c)

    identifying dynamic transfer matrix of different hydraulic components.

The evaluation of the speed of sound is frequently made through the synchronized measurements of three pressure transducers (Lauro and Boyer 1998; Dordain and Marchetti 1974; Margolis and Brown 1976). For example, Shamsborhan et al. (2010) and Testud et al. (2007) have applied this method to evaluate the speed of sound in cavitating flows. They have found a speed of sound around 4 m/s for cavitating flows and 1400 m/s for liquid monophasic flows. Kashima et al. (2012) have applied the three pressure transducers approach to evaluate the flow rate fluctuations in oil pipeline. Using this kind of method, we can estimate speed of sound and flow rate fluctuations, which can be used to estimate system transfer functions as, for example, Dordain and Marchetti (1974). Blommaert (2000) used it to identify the transfer function matrix of a Francis turbine to evaluate its dynamic behavior and to propose an active control to ensure its stability. More recently, Marie-Magdeleine et al. (2012) and Marie-Magdeleine (2013) proposed a kinetic differential pressure method to estimate the speed of sound in order to identify the dynamic transfer matrix of hydraulic components operating in cavitating and non-cavitating flows.

The fundamental differences between those studies are related to the post-treatment of the synchronized pressure signals.

This paper focuses on the analyses of the first part of the global identification procedure presented here above, i.e., on the development of a new process to evaluate the speed of sound in water flow and water/air from three pressure sensors.

The methodology has being carried out and applied in the CREMHyG’s hydro-acoustic test rig, presented in Sect. 2. In this paper, after a review of aspects (Sect. 3), a new processing method to evaluate the speed of sound in both water and water/air flows is proposed in Sect. 4. Finally, Sect. 5 presents the analysis of experimental results, some comparisons with theoretical laws given by Wylie et al. (1993) and Brennen (2005), followed by discussions about the proposed methodology.

2 Experimental study

A scheme of the CREMHyG’s hydro-acoustic test rig is illustrated in Fig. 1 (Marie-Magdeleine 2013).

Fig. 1
figure 1

The hydro-acoustic test rig developed in CREMHyG

Full size image

The test rig is composed of:

  • about 14 m of stainless steel and PVC ducts of ½”,

  • a recirculating pump brand FLYGT type PXN1604 T/P 2”,

  • a steel tank of 1000 l.

The operating conditions can vary from 105 to 5 × 105 Pa in the tank (absolute pressure) and from 0 to 5 l/s. Mean flow rate is measured by an electromagnetic flowmeter Krone model 2100c with an Optiflux 2000 sensor.

The flow is excited by a modulator allowing flow rate fluctuations with amplitudes of about 5 % of the mean discharge and frequencies from 0 to 50 Hz. Figure 2 illustrates the modulator. The fluctuations are generated by the rectilinear movement of a piston, perpendicular to the main pipe. The piston’s diameter is ½” and moved by a Leroy-Somer engine type LSRPM100L with a power of 10 kW.

Fig. 2
figure 2

Picture of the modulator

Full size image

Pressure fluctuations are measured by piezoelectric sensors PCB Piezotronics model S112A22. There are three sections of measurements in the test rig: A, B and C, as indicated in Fig. 4. Each measurement section is composed of three pressure transducers illustrated by Fig. 3. The distance L between the transducers is 0.3 m. The sensors have a sensitivity of 14.5 mV/kPa, a resolution of 0.007 kPa and a measurement range of 345 kPa.

Fig. 3
figure 3

View of the measurement section “A”

Full size image

To study the influence of the void ratio on the speed of the sound, an air injection apparatus has been applied and installed between the measurement’s sections A and C (as indicated in Fig. 4). The principle of the air injector (a Lee jet restrictor illustrated Fig. 5) is the same as the Laval nozzle (sonic gas flow condition at the nozzle). The nozzle section has been calibrated to obtain air mass flow rates of 0.018 ± 0.0005 or 0.030 ± 0.0007 g/s (Fig. 5).

Fig. 4
figure 4

Position of the pressure transducers (A, B, C) of the air injection apparatus and the transparent pipes

Full size image
Fig. 5
figure 5

View of the restrictor (Technical Hydraulic Handbook 2009)

Full size image

Transparent pipes are in Plexiglass and provide qualitative visualization of diphasic flows (Fig. 6).

Fig. 6
figure 6

Example of fluid diphasic flow considered in the study

Full size image

Other control measurements are also available in the test rig:

  • Two temperature Pt100 sensors (for water and ambient temperatures).

  • One Keller sensor type PAA-23 to measure the tank pressure.

  • One absolute pressure sensor Rosemont type 3051 to measure aspiration pressure of the pump.

  • The difference of pressure between pump inlet and outlet measured by a Rosemount sensor type 1151.

3 The method of three sensors

The applied method is based on the utilization of three pressure sensors separated by a distance L. To illustrate the method, an example is given below for an operating point: the mean flow rate is 2 l/s, the pipe pressure is equal to 1 bar, and the excitation frequency of the modulator is 45 Hz.

As indicated in references (Margolis and Brown 1976; Marie-Magdeleine 2013; Marie-Magdeleine et al. 2012; Shamsborhan et al. 2010), the main assumptions considered are:

  • One-dimensional wave propagation in the direction of the pipe

  • Low Mach number

  • Fluctuations of specific mass, pressure and velocity are low compared with their mean values.

In the case of small fluctuations, Allievi’s equations can be written by:

$$\tilde{p}\left( {x,t} \right) = \rho g\left( {A e^{{i \omega \left( {t - \frac{x}{c}} \right)}} + B e^{{i \omega \left( {t + \frac{x}{c}} \right)}} } \right)$$
(1)

and

$$\tilde{v}\left( {x,t} \right) = \frac{g}{c}\left( {A e^{{i \omega \left( {t - \frac{x}{c}} \right)}} - B e^{{i \omega \left( {t + \frac{x}{c}} \right)}} } \right)$$
(2)

where \(\tilde{p}\) is the fluctuation pressure of the liquid in Pascal (Pa), \(\tilde{v}\) is the fluctuation velocity in meter per second (m/s), t is the time in second (s), x denotes a given position on the pipeline in meter (m), ω = 2πf the frequency pulsation in radians per second (rad/s) and c the speed of sound in meter per second (m/s).

Figure 7 gives an example of experimental data obtained for the considered operating point.

Fig. 7
figure 7

Example of pressure fluctuations measured for three pressure sensors in the section A (see Fig. 3)

Full size image

With Eq. (1), we can write the fluctuation for each pressure sensor:

$$P_{1} \left( { - L,t} \right) = \rho g\left( {Ae^{{\frac{ - i\omega L}{c}}} + Be^{{\frac{i\omega L}{c}}} } \right)e^{i\omega t}$$
(3)
$$P_{2} \left( {0,t} \right) = \rho g\left( {A + B} \right)e^{i\omega t}$$
(4)
$$P_{3} \left( {L,t} \right) = \rho g\left( {Ae^{{\frac{i\omega L}{c}}} + Be^{{\frac{ - i\omega L}{c}}} } \right)e^{i\omega t}$$
(5)

If we write \(\frac{{\left( {P_{1} \left( { - L,t} \right) + P_{3} \left( {L,t} \right)} \right)}}{{P_{2} \left( {0,t} \right)}}\), we have the relation

$$\frac{{\left( {P_{1} \left( { - L,t} \right) + P_{3} \left( {L,t} \right)} \right)}}{{P_{2} \left( {0,t} \right)}} = 2\cos \left( {sL} \right)$$
(6)

with \(s = \frac{2 \pi }{\lambda } = \frac{\omega }{c}\) where \(\lambda\) is the wavelength in meter (m), ω the frequency pulsation in radian per second and c the speed of the sound in meter per second.

With Eq. (6), we have:

$$s = \frac{1}{L}{\text{arcos}}\left( {\frac{{P_{1} \left( { - L,t} \right) + P_{3} \left( {L,t} \right)}}{{2P_{2} \left( {0,t} \right)}}} \right)$$
(7)

In the case of liquid monophasic flow, the speed of sound is around 1360 m/s.

In our case, the frequency f varies between 0 and 50 Hz, so 0 ≤ s ≤ 0.23.

Moreover, L = 0.3 m. We have \(0 \le sL < \frac{\pi }{2}\), and then \(0 \le \cos \left( {sL} \right) < 1\).

Thus, (7) can be written

$$s = \frac{1}{L}{\text{arcos}}\left( {\left| {\left| {\frac{{P_{1} \left( { - L,t} \right) + P_{3} \left( {L,t} \right)}}{{2P_{2} \left( {0,t} \right)}}} \right|} \right|} \right)$$
(8)

And using the definition \(c = \frac{\omega }{s}\)

$$c = \frac{\omega L}{{\arccos \left( {\left| {\left| {\frac{{P_{1} \left( { - L,t} \right) + P_{3} \left( {L,t} \right)}}{{2P_{2} \left( {0,t} \right)}}} \right|} \right|} \right)}}$$
(9)

Remark that by taking \(y\left( t \right): = P_{1} \left( { - L,t} \right) + P_{3} \left( {L,t} \right)\) and \(u\left( t \right): = 2P_{2} \left( {0,t} \right)\), we have

$$c = \frac{\omega L}{{\arccos \left( {\left| {\left| {\frac{y\left( t \right)}{u\left( t \right)}} \right|} \right|} \right)}} = \frac{\omega L}{\arccos \left( \gamma \right)}$$
(10)

with

$$\gamma = \left|\left|\frac{y\left( t \right)}{u\left( t \right)}\right|\right|$$
(11)

and \(0 \le \gamma \le 1.\)

4 Estimation of the speed of sound

4.1 The new procedure to evaluate γ

In the proposed method, the algebraic relationship for \(\gamma\) [determined in (11)] can be solved by using the system identification theory. In Landau and Zito (2006), Ljung (1987), we can consider a system like

$$y\left( t \right) = \gamma *u\left( t \right) + \nu$$

with \(y\left( t \right) = P_{1} \left( { - L,t} \right) + P_{3} \left( {L,t} \right)\), \(u\left( t \right) = 2P_{2} \left( {0,t} \right)\) and ν is the measurement noise.

After the frequency analysis of the measured data, the fundamental frequency and its harmonics can be evaluated for each signal.

The relationship (1) can be expressed in frequency domain by:

$$P\left( {x,f} \right) = \rho g \left( {A\left( f \right) e^{ - isx} + B\left( f \right) e^{i sx} } \right)$$
(12)

The measured pressure signals can be written as follows:

$$\left\{ {\begin{array}{*{20}l} {P_{1} \left( { - L,N_{f} } \right) = \rho g\mathop \sum \limits_{n = 1}^{N} \left( {A\left( {n_{f} } \right)e^{i s n L} + B\left( {n_{f} } \right)e^{ - i s n L} } \right) = \mathop \sum \limits_{n = 1}^{N} P_{1} \left( { - L,n_{f} } \right)} \hfill \\ {P_{2} \left( {0,N_{f} } \right) = \rho g\mathop \sum \limits_{n = 1}^{N} A\left( {n_{f} } \right) + B\left( {n_{f} } \right) = \mathop \sum \limits_{n = 1}^{N} P_{2} \left( {0,n_{f} } \right)} \hfill \\ {P_{3} \left( {L,N_{f} } \right) = \rho g\mathop \sum \limits_{n = 1}^{N} A\left( {n_{f} } \right)e^{ - i s n L} + B\left( {n_{f} } \right)e^{i s n L} = \mathop \sum \limits_{n = 1}^{N} P_{3} \left( {L,n_{f} } \right)} \hfill \\ \end{array} } \right.$$
(13)

Each signal contains N harmonics of the fundamental frequency.\(P_{1,2,3} \left( { - L,N_{F} } \right)\) is the frequency representation of \(P_{1,2,3} \left( { - L,t} \right)\).

The relationship (10) can be written in frequency domain by:

$$c = \frac{\omega L}{{\arccos \left( {\left| {\left| {\frac{Y\left( f \right)}{U\left( f \right)}} \right|} \right|} \right)}} = \frac{\omega L}{\arccos \left( \varGamma \right)}$$
(14)

With

$$Y\left( f \right) = P_{1} \left( { - L,N_{f} } \right) + P_{3} \left( {L,N_{f} } \right) = \mathop \sum \limits_{n = 1}^{N} P_{1} \left( { - L,n_{f} } \right) + \mathop \sum \limits_{n = 1}^{N} P_{3} \left( {L,n_{f} } \right)$$
(15)

And

$$U\left( f \right) = 2P_{2} \left( {0,N_{f} } \right) = 2\mathop \sum \limits_{n = 1}^{N} P_{2} \left( {0,n_{f} } \right)$$
(16)

For t = 0, we can write \(\gamma \left( n \right)\) with Eqs. (13) and (14). N is the last harmonic number, and n is the considered harmonic number

$$\varGamma \left( \omega \right) = \left|\left|\frac{{\sum\nolimits_{n = 1}^{N} {\left( {A\left( {\omega n} \right) + B\left( {\omega n} \right)} \right)\left( {e^{isnL} + e^{{ - \left( {isnL} \right)}} } \right) } }}{{\sum\nolimits_{n = 1}^{N} {\left( {A\left( {\omega n} \right) + B\left( {\omega n} \right)} \right) } }} \right|\right|$$
(17)

In this relationship, \(\varGamma\) is evaluated by the summation of the totality of harmonic frequencies. To ensure that \(0 \le \gamma \le 1\), the evaluation of \(\varGamma\) is carried out for each harmonic, as indicated in Table 1.

Table 1 Results of the speed of sound estimation by considering different harmonics
Full size table

In order to extract signal values corresponding to each harmonic, the following filter is applied to treat \(y\left( t \right)\) and \(u\left( t \right)\):

$$H\left( z \right) = \frac{1}{{1 - 2\cos \left( {2\pi fTs} \right)z^{ - 1} + z^{ - 2} }}$$
(18)

where z is the complex variable, T s the sampling time, \(f = f_{\text{exc}} *n\) the cutoff frequency. The fluctuations imposed by the modulator are supposed to be a sum of sinusoids. To reduce the influence of noise and/or vibration problems on experimental data, the polynomial function proposed by (Martinez and Alma 2012) has been applied to model sinusoidal disturbances and provides a reliable data extraction.

After that, the methodology uses a recursive least mean squares approach to estimate γ at each harmonic.

$$\left[ {\begin{array}{*{20}c} {y\left( {t_{\text{ini}} } \right)} \\ {y\left( {t_{\text{ini}} + 1} \right)} \\ \vdots \\ {y\left( {t_{\text{final}} - 1} \right)} \\ {y\left( {t_{\text{final}} } \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {u\left( {t_{\text{ini}} } \right)} \\ {u\left( {t_{\text{ini}} + 1} \right)} \\ \vdots \\ {u\left( {t_{\text{final}} - 1} \right)} \\ {u\left( {t_{\text{final}} } \right)} \\ \end{array} } \right]\gamma$$

For k = t ini to \(t_{\text{final}}\), the next procedure is applied

$$E\left( k \right) = y\left( k \right) - u\left( k \right)*\theta \left( {k - 1} \right)$$
(19)
$$\varXi \left( k \right) = \frac{{\psi \left( {k - 1} \right)}}{{1 + u\left( k \right)\psi \left( {k - 1} \right)u\left( k \right)}}$$
(20)
$$\varPsi \left( k \right) = \varPsi \left( {k - 1} \right) - \left( {\frac{{\varPsi \left( {k - 1} \right)u\left( k \right)u\left( k \right)\varPsi \left( {k - 1} \right)}}{{1 + u\left( k \right)\varPsi \left( {k - 1} \right)u\left( k \right)}}} \right)$$
(21)
$$\theta \left( k \right) = \theta \left( {k - 1} \right) + \varXi \left( k \right)u\left( k \right)E\left( k \right)$$
(22)

The algorithm has to be initialized by taking, \(\theta \left( 0 \right) = 0\) and \(\varPsi \left( 0 \right) = 1000\). At the end \(\gamma \left( n \right) = \theta \left( {t_{\text{final}} } \right)\).\(\Delta \gamma\) is the standard deviation of γ, and \(\Delta \gamma\) can be estimated by using

$$\Delta \gamma = \sqrt {\varPsi \left( {t_{\text{final}} } \right)*\text{var} \left( E \right)}$$
(23)

\(\text{var} \left( E \right)\) is the variance of vector E.

In the considered example, the results obtained (given in Table 1) for \(\varGamma\) by considering a fundamental frequency of 45 Hz do not allow the prediction of the celerity (as \(\varGamma\) is higher than “1,” the \(\arccos \left( \gamma \right)\) and thus the celerity values are not defined).

From this table, it is also worth noting that the estimation of the speed of sound depends on the considered harmonic. The next section presents the proposed approach to select the harmonic allowing for the most reliable estimation of the speed of sound.

4.2 Proposed methodology to select the harmonic

The maximum excitation frequency of the modulator used during experiments is 50 Hz, with a sampling frequency of 1 kHz.

Based on Shannon (or Nyquist) theorem, data can be analyzed between 0 and 500 Hz. Hence, here, the number of possible harmonics \(N \le 10\).

Therefore, by definition, \(c = \frac{\omega }{s}\), and thus, we can write \(c = \frac{n \omega }{n s}\) and we can conclude that the value of the speed of sound could be obtained by using an arbitrary harmonic. For the chosen harmonic n, we have:

$$\gamma \left( n \right) = \frac{{\left( {P_{1} \left( { - L,nf} \right) + P_{3} \left( {L,nf} \right)} \right)}}{{2P_{2} \left( {0,nf} \right)}}$$
(24)

and

$$c\left( n \right) = \frac{n \omega L}{{{\text{arcos}}\left( {\gamma \left( n \right)} \right)}}$$
(25)

Some additional criteria are proposed to choose the best harmonic to evaluate the speed of sound. The objectives are to:

  • Maximize the signal-to-noise ratio by decreasing \(\Delta \gamma\).

  • Minimize the sensitivity of the estimation of “c,” with respect to the estimation of γ by decreasing \(\frac{\partial c}{\partial \gamma }\).

Considering (7), the sensitivity can be obtained as:

$$\frac{\partial c}{\partial \gamma } = \frac{\omega L}{{ \arccos \left( \gamma \right)^{2} \sqrt {1 - \gamma^{2} } }}$$
(26)

In each harmonic:

$$\frac{\partial c\left( n \right)}{\partial \gamma \left( n \right)} = \frac{n\omega L}{{\arccos\left( {\gamma \left( n \right)} \right)^{2} \sqrt {1 - \gamma \left( n \right)^{2} } }}$$
(27)

As illustrated in Fig. 8, a reliable evaluation of “c” needs an accurate estimation of γ. As a matter of fact, when \(\gamma \to 1\), \(\frac{\partial c}{\partial \gamma } \to \infty\) and when \(\gamma \to 0,\,\frac{\partial c}{\partial \gamma } \to 0\).

Fig. 8
figure 8

Evolution of the speed of sound as function of \(\varvec{\gamma}\) values for an excitation frequency of 45 Hz

Full size image

By estimating the standard deviation of c, one obtains:

$$\Delta C = \frac{\partial c}{\partial \gamma }\Delta \gamma$$
(28)

\(\Delta \gamma\) is the standard deviation of γ [given by Eq. (23)]. The relationship (28) takes into account both criteria described above in the two last objectives.The highest accuracy for the estimation of “c” is obtained for low values of \(\Delta C\).

Summarizing the procedure to evaluate the speed of sound:

  1. 1.

    Measure \(P_{1} \left( t \right), P_{2} \left( t \right)\,{\text{and}} \,P_{3} \left( t \right)\) for \(t = t_{\text{ini}}\) to t f every T s second.

  2. 2.

    Compute \(y\left( t \right) = P_{1} \left( t \right) + P_{3} \left( t \right)\) and \(u\left( t \right) = 2 P_{2} \left( t \right)\).

  3. 3.

    Construct the input and output vectors:

    $$U = \left( {\begin{array}{*{20}c} {u\left( {t_{\text{ini}} } \right)} \\ \vdots \\ {u\left( {t_{f} } \right)} \\ \end{array} } \right)\,{\text{and}}\,Y = \left( {\begin{array}{*{20}c} {y\left( {t_{\text{ini}} } \right)} \\ \vdots \\ {y\left( {t_{f} } \right)} \\ \end{array} } \right)$$
  4. 4.

    Filter Y and U with filter \(H\left( z \right)\) [Eq. (18)]

  5. 5.

    Apply the recursive least mean squares approach to evaluate \(\gamma \left( n \right)\, {\text{and}}\,\Delta \gamma \left( n \right)\),

  6. 6.

    Compute the sensitivity, \(\frac{\partial c\left( n \right)}{\partial \gamma \left( n \right)}\), and the estimated speed of sound \(c\left( n \right)\) for each harmonic n using (25) and (26).

  7. 7.

    Choose the best estimation of “c” corresponding to the smallest value of \(\Delta C\left( n \right)\) with Eq. (28).

4.3 Example of application

To illustrate the proposed methodology, an example is given for pipe B, at a considered operating point: mean flow rate of 2.5 l/s, pipe pressure equal to 1.5 bars and flow excitation frequency of 45 Hz. The total duration of acquisition is 10 s with a sampling frequency of 1 kHz. Figure 7 illustrates measured signals. From these signals, we calculate \(u\left( t \right) = 2 P_{2} \left( t \right)\) and \(y\left( t \right) = P_{1} \left( t \right) + P_{3} \left( t \right)\) and we apply the procedure described in the previous section.

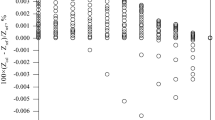
The final results obtained are presented in Table 2. The distribution of the γ value as a function of the acquisition time \(T_{\text{ac}}\) can be analyzed from Fig. 9. For a value of \(T_{\text{ac}}\) of about 10 s, we can observe a good convergence of the γ value. The maximum relative estimation error \(\frac{E\left( k \right)}{y\left( k \right)}\) is smaller than 4 %, observed for the non-converged case. \(\frac{E\left( k \right)}{y\left( k \right)}\) is the ratio between the error of estimation defined in (19) and \(y\left( k \right)\).

Table 2 Results of the speed of the sound obtained for different harmonics
Full size table
Fig. 9
figure 9

Convergence of γ for different harmonics in liquid monophasic flow for an excitation at 45 Hz

Full size image

By considering criteria based on the \(\Delta C\) value and the convergence of level γ, the best solution seems to be obtained with the harmonic of 450 Hz (i.e., the speed of sound would be around 1395 m/s).

This experimental value can be compared to a theoretical estimation given by (Wylie et al. 1993) in the case of liquid monophasic flows. According to that approach, the speed of the sound depends on the duct material and on fluid properties. For thin tubes:

$$c_{\text{fluide}} = \frac{{\sqrt {\frac{K}{\rho }} }}{{\sqrt {1 + \frac{K D}{E e}} }}$$
(29)

with K bulk modulus of fluid, ρ specific mass of the fluid (kg/m3), D internal diameter of the pipe (m), e pipe thickness (m) and E Young’s modulus of the pipe material.

For the considered case, the theoretical speed of sound is about 1360 m/s. We have difference between experimental results and theory lesser than 6 %.

The experimental data concerning measurements in pipes B and C for the considered operating point and other excitation frequencies have been also treated. The main results are illustrated in Table 3. The observed differences between experimental results and the theoretical value are lower than 3 % in mean.

Table 3 Results for \(\bar{Q} = 2.5\,{\text{l/s}}\) and \(\bar{P} = 1.5\) bar
Full size table

5 Analysis of the results

To improve the evaluation and the validation of the method, several experiments at various operating points and excitation frequencies have been carried out for liquid monophasic and diphasic flows. The present paper illustrates results obtained in the measurement sections B and C. It is interesting to note that, according to our experiments, the results obtained in both measurement sections are similar. The presence of the elbow upstream to the measurement section B seems to have no influence over the evaluation of the speed of sound in the pipe.

5.1 Liquid monophasic flow experiments

Table 4 summarizes the results for different operating points (i.e., two flow rates and pipe pressures) in the case of pure water flows. The excitation frequencies are between 45 and 50 Hz.

Table 4 Results for different operating points in liquid monophasic flow
Full size table

These results agree well with the previous analysis, and the methodology proposed to estimate the speed of sound can be considered validated for liquid monophasic flows (i.e., for high values of the speed of sound).

5.2 Diphasic flow experiments

The next step for the methodology validation considered the evaluation of the speed of sound in diphasic flows. Operating points tested are similar to the previous ones. Experiments took into account two values of the air mass flow rates: 0.018 and 0.030 g/s. The air injection apparatus was installed between the measurement sections A and C, so that the flow may be liquid monophasic in A and diphasic in C.

The fluid velocity is around 2 m/s (for 2.5 l/s) and 1.6 m/s (for 2 l/s). The speed of sound in diphasic flow is between 100 and 350 m/s. So the hypothesis of low Mach number considered in Eq. (1) is valid.

5.2.1 Theoretical aspects

Some references in the literature give theoretical approaches to evaluate the speed of sound in diphasic flows. Those approaches consider dispersed homogenous gas in liquid, neglected mass, heat transfers, surface tension influence and the relative movement between gas and liquid.

Based on these assumptions, Jakobsen (1964) proposes the following equation:

$$\frac{1}{{c^{2} }} = \frac{1}{{c_{v}^{2} }}\left[ {\beta^{2} + \frac{{\beta \left( {1 - \beta } \right)\rho_{l} }}{{\rho_{v} }}} \right] + \frac{1}{{c_{l}^{2} }}\left[ {\left( {1 - \beta } \right)^{2} + \frac{{\beta \left( {1 - \beta } \right)\rho_{v} }}{{\rho_{l} }} } \right]$$
(30)

And Nguyen et al. (1981)

$$c = \frac{1}{{\left( {1 - \beta } \right)\sqrt {\frac{1 - \beta }{{c_{l}^{2} }} + \frac{{\beta \rho_{l} }}{{\rho_{v} c_{v}^{2} }}} + \beta \sqrt {\frac{\beta }{{c_{v}^{2} }} + \frac{{\left( {1 - \beta } \right)\rho_{v} }}{{\rho_{l} c_{l}^{2} }}} }}$$
(31)

where β is the void fraction and \(\beta = \frac{{Q_{\text{gas}} }}{{Q_{\text{gas}} + Q_{\text{liquid}} }}\) [Q is the flow rate (m3/s)]; c v is the speed of sound in the gas (m/s); c l is the speed of sound in the liquid (m/s); ρ l is the specific mass of the liquid (kg/m3); ρ v is the specific mass of the gas (kg/m3). Brennen (2005) proposed to write the ρ v and c v in terms of the pressure P and temperature T of the diphasic medium, polytropic index n and R S the constant of perfect gas. The formulas are

$$\rho_{v} = \frac{P}{{R_{s} T}}$$
(32)

and

$$c_{v} = \sqrt {n R_{s} T}$$
(33)

In those approaches, the specific mass of the liquid is considered constant.

5.2.2 Experimental aspects

Figure 10 illustrates measured pressure signals during diphasic experiments. In the pipe A, the flow is a liquid monophasic and the amplitudes of the pressure fluctuations are five times higher than measured in pipes B and C (where the flow is diphasic).

Fig. 10
figure 10

Pressure fluctuations before (A2) and after air injection (C2, B2) with pressure of 1 bar, mean flow at 2 l/s and gas void fraction of 0.6 %

Full size image

Table 5 presents some operating conditions considered in this study, and Fig. 11 gives results obtained for tests carried out with air injections and excitations frequencies varying between 45 and 50 Hz.

Table 5 Operating points in diphasic case
Full size table
Fig. 11
figure 11

Comparison between experimental data and Brennen’s model theory for 1 bar (red) and 1.5 bar (blue)

Full size image

The highest discrepancy between experiments and the theory is about 10 %. The theoretical and experimental evolution of “c” as a function of the void ratio is quite similar. Note that the considered acquisition time in diphasic flow test is enough to obtain a good γ convergence for the low harmonic frequencies, with error \(\frac{E\left( k \right)}{y\left( k \right)}\) of about 5 %.

Taking into account the air mass flow rate accuracy, one can evaluate the relative accuracy of the void ration, which is around 4 %. Consequently, the accuracy of the speed of sound estimated by Brennen’s formula (30) is around 3 %.

6 Conclusions

In this paper, a new post-treatment method to estimate the speed of sound from three pressure measurements has been proposed. The approach has been validated in the case of liquid monophasic and diphasic flows. The method was tested in a test rig developed to study the hydro-acoustic characteristics of hydraulic equipment.

The proposed approach provides a prediction of the speed of sound in the entire range of considered values (i.e., from 100 to 1400 m/s). The mean and the maximum discrepancies between theoretical and experimental values are around 5 % and less than 10 %, respectively, for both liquid monophasic and diphasic cases. The results are in accordance with analytical formulations presented in the literature.

The proposed estimation procedure requires a few numbers of computations, allowing its use in real-time applications.