1 Introduction

The speed of sound is an intensive property whose value depends on the state of the medium through which sound propagates [1]. Nowadays, speed of sound is measured with exceptional accuracy and represents potential source of other (thermodynamic) properties which are measured less accurately. However, in order to derive any other property of the medium from the speed of sound it is necessary to solve a set of nonlinear partial differential equations (PDEs) of the second order [2]. Instead of seeking for a general solution, some researchers suggest various methods of numerical integration for obtaining a particular solution [3,4,5,6,7,8,9,10]. A method which covers a wider domain of solutions, with a fewer and less demanding initial/boundary conditions, may be considered more superior. For example, initial/boundary conditions of Dirichlet type are less demanding than those of Neumann type. Similarly, those composed of volumetric properties (density, compression factor) are less demanding than the ones composed of caloric properties (heat capacity). Therefore, a method using only volumetric initial/boundary conditions of Dirichlet type is desirable. Although the problem is not solvable by numerical integration using only volumetric initial conditions of Dirichlet type, it can be solved using only volumetric boundary conditions of Dirichlet type [11]. However, this approach is not based on numerical integration but rather on discretization. Namely, the set of PDEs is converted into the set of nonlinear algebraic equations by approximating all the derivatives by finite differences. The main disadvantage of this approach is rather huge number of equations (of the order 104). In this paper, an approach based on a cubic spline [12] is used to decrease the number of equations, which are solved as a nonlinear least squares problem by a modified Levenberg–Marquardt algorithm [13,14,15]. Since the values of thermodynamic properties are only locally represented by cubic polynomials, there is no analytical equation of state.

2 Theory

The adiabatic sound wave equation [1]

$$ u^{2} = \left( {\frac{\partial p}{\partial \rho }} \right)_{s} $$
(1)

connects the speed of sound u with thermodynamic properties of a medium through which the wave propagates (p is the pressure, ρ is the density, and s is specific entropy).

Since entropy is not measurable quantity, it can be avoided with the help of the following relation [1]

$$ \left( {\frac{\partial p}{\partial \rho }} \right)_{s} = \frac{{c_{p} }}{{c_{v} }}\left( {\frac{\partial p}{\partial \rho }} \right)_{T} $$
(2)

where T is the temperature, cp is specific heat capacity at constant pressure and cv is specific heat capacity at constant volume.

Combining (1) and (2), one obtains

$$ u^{2} = \frac{{c_{p} }}{{c_{v} }}\left( {\frac{\partial p}{\partial \rho }} \right)_{T} $$
(3)

If cp in (3) is replaced by [1]

$$ c_{p} = c_{v} + \frac{T}{{\rho^{2} }}\left( {\frac{\partial p}{\partial \rho }} \right)_{T}^{ - 1} \left( {\frac{\partial p}{\partial T}} \right)_{\rho }^{2} $$
(4)

one obtains

$$ u^{2} = \left( {\frac{\partial p}{\partial \rho }} \right)_{T} + \frac{T}{{\rho^{2} c_{v} }}\left( {\frac{\partial p}{\partial T}} \right)_{\rho }^{2} $$
(5)

If pressure in (5) is replaced by a less varying compression factor

$$ Z = \frac{pM}{\rho RT} $$
(6)

where M is the molar mass and R is the universal gas constant, after rearrangement one obtains

$$ c_{v} = \frac{R}{M}\left[ {Z + T\left( {\frac{\partial Z}{\partial T}} \right)_{\rho } } \right]^{2} \left[ {\frac{{Mu^{2} }}{RT} - Z - \rho \left( {\frac{\partial Z}{\partial \rho }} \right)_{T} } \right]^{ - 1} $$
(7)

If (7) is coupled with [16]

$$ \left( {\frac{{\partial c_{v} }}{\partial \rho }} \right)_{T} = - \frac{T}{{\rho^{2} }}\left( {\frac{{\partial^{2} p}}{{\partial T^{2} }}} \right)_{\rho } $$
(8)

(3), (7) and (8) may be solved for Z, cv and cp in a rectangular ρ–T domain (supercritical region), respectively. To perform that the values of cv obtained from (7) are partially derived with respect to density, at constant temperature, by a cubic spline. Then, these derivatives are calculated again, but this time from (8). The function which quantifies difference between derivatives obtained in these two different ways is

$$ f = - \frac{T}{{\rho^{2} }}\left( {\frac{{\partial^{2} p}}{{\partial T^{2} }}} \right)_{\rho } - \left( {\frac{{\partial c_{v} }}{\partial \rho }} \right)_{T} $$
(9)

Finally, the objective function is calculated according to

$$ g = \frac{1}{2}\sum {f^{2} } $$
(10)

The aim is to find such values of Z which minimize objective function g. Since functions f are nonlinear with respect to Z, this problem may be solved as a nonlinear least squares problem using a modified Levenberg–Marquardt algorithm.

If p in (8) is replaced by Z, one obtains

$$ \left( {\frac{{\partial c_{v} }}{\partial \rho }} \right)_{T} = - \frac{RT}{M\rho }\left[ {2\left( {\frac{\partial Z}{\partial T}} \right)_{\rho } + T\left( {\frac{{\partial^{2} Z}}{{\partial T^{2} }}} \right)_{\rho } } \right] $$
(11)

If a new variable is introduced

$$ \phi = \frac{\rho }{{\rho_{sat} }} $$
(12)

where ρsat is density of saturated vapor at a given temperature, then, according to calculus,

$$ \left( {\frac{\partial Z}{\partial T}} \right)_{\rho } = \left( {\frac{\partial Z}{\partial T}} \right)_{\phi } - \left( {\frac{\partial Z}{\partial \rho }} \right)_{T} \left( {\frac{\partial \rho }{\partial T}} \right)_{\phi } $$
(13)

and

$$ \left( {\frac{{\partial^{2} Z}}{{\partial T^{2} }}} \right)_{\rho } = \left[ {\frac{\partial }{\partial T}\left( {\frac{\partial Z}{\partial T}} \right)_{\rho } } \right]_{\phi } - \frac{{\partial^{2} Z}}{\partial T\partial \rho }\left( {\frac{\partial \rho }{\partial T}} \right)_{\phi } $$
(14)

So, (7) and (11) become

$$ c_{v} = \frac{R}{M}\left\{ {Z + T\left[ {\left( {\frac{\partial Z}{\partial T}} \right)_{\phi } - \left( {\frac{\partial Z}{\partial \rho }} \right)_{T} \left( {\frac{\partial \rho }{\partial T}} \right)_{\phi } } \right]} \right\}^{2} \left[ {\frac{{Mu^{2} }}{RT} - Z - \rho \left( {\frac{\partial Z}{\partial \rho }} \right)_{T} } \right]^{ - 1} $$
(15)

and

$$\begin{aligned} \left( {\frac{{\partial c_{v} }}{\partial \rho }} \right)_{T} &= - \frac{RT}{M\rho }\left\{ 2\left[ {\left( {\frac{\partial Z}{\partial T}} \right)_{\phi } - \left( {\frac{\partial Z}{\partial \rho }} \right)_{T} \left( {\frac{\partial \rho }{\partial T}} \right)_{\phi } } \right]\right.\\ &\quad + \left. T\left\{ {\left[ {\frac{\partial }{\partial T}\left( {\frac{\partial Z}{\partial T}} \right)_{\rho } } \right]_{\phi } - \frac{{\partial^{2} Z}}{\partial T\partial \rho }\left( {\frac{\partial \rho }{\partial T}} \right)_{\phi } } \right\} \right\} \end{aligned}$$
(16)

respectively. Now, (3), (15) and (16) may be solved for Z, cv and cp in a rectangular ϕ–T domain (subcritical region), respectively. The procedure of solution is the same as the one described for the supercritical region, with

$$\begin{aligned} & f = - \frac{RT}{M\rho }\left\{ 2\left[ {\left({\frac{\partial Z}{\partial T}} \right)_{\phi } - \left({\frac{\partial Z}{\partial \rho }} \right)_{T} \left({\frac{\partial \rho }{\partial T}} \right)_{\phi } } \right]\right. \\ &\left.\qquad + T\left\{ {\left[ {\frac{\partial }{\partial T}\left( {\frac{\partial Z}{\partial T}} \right)_{\rho } } \right]_{\phi } - \frac{{\partial^{2} Z}}{\partial T\partial \rho }\left( {\frac{\partial \rho }{\partial T}} \right)_{\phi } } \right\} \right\} - \left( {\frac{{\partial c_{v} }}{\partial \rho }} \right)_{T} \end{aligned}$$
(17)

and

$$ g = \frac{1}{2}\sum {f^{2} } $$
(18)

2.1 Supercritical Domain

This domain is bounded by two isotherms and two isochores. It is practical, but not necessary, that the lower isochore is in the limit of ideal gas, because along this isochore the compression factor has unique value 1, and the heat capacities are obtained from speed of sound measurements (extrapolated to zero pressure) directly. The temperature and density ranges are divided into several isotherms and several isochores, respectively. Pressures are calculated along each isochore from the Peng–Robinson equation of state [17], and speed of sound values [18,19,20] are specified at these pressures in the form of a less varying quantity F = Mu2/(RT), which is more suitable for interpolation. Several data points of compression factor [18,19,20] are specified along the boundary of the domain. Initial values of compression factor inside the domain are obtained from these boundary values, by a cubic spline interpolation with respect to density.

2.1.1 Algorithm of Solution

  1. 1.

    For the specified set of isotherms and isochores, pressures inside the domain (Tmin < T < Tmax and ρmin < ρ < ρmax) are calculated from compression factors, since they are always known in advance in each iteration. (In the first iteration they are obtained from the boundary values and in all other iterations from a modified Levenberg–Marquardt algorithm.) In any case, this is done by rewriting (6) into

    $$ p = \frac{\rho RTZ}{M} $$
  2. 2.

    Having calculated pressures at different temperatures along each isochore inside the domain, with boundary pressures fixed at their specified values all the time, partial derivatives

    $$ \left( {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial T}}} \right. \kern-0pt} {\partial T}}} \right)_{\rho } $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ρmin < ρ ≤ ρmax), except along ρ = ρmin, since

    $$ \left( {\frac{\partial p}{\partial T}} \right)_{{\rho_{\hbox{min} } = 0}} = 0 $$
  3. 3.

    Partial derivatives of compression factor, with respect to temperature at constant density, are calculated directly from the following relation

    $$ \left( {\frac{\partial Z}{\partial T}} \right)_{\rho } = \frac{M}{\rho RT}\left[ {\left( {\frac{\partial p}{\partial T}} \right)_{\rho } - \frac{p}{T}} \right] $$

    which is obtained by analytical derivation of (6), inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ρmin < ρ ≤ ρmax), except along ρ = ρmin, since

    $$ \left( {\frac{\partial Z}{\partial T}} \right)_{{\rho_{\hbox{min} } = 0}} = 0 $$
  4. 4.

    Since speed of sound values are specified (in the form of F) at pressures calculated from the Peng–Robinson equation of state for the specified set of isotherms and isochores (because true pressures are not known in advance), they are interpolated with respect to pressure using a cubic spline, to pressures from step 1.

  5. 5.

    Having values of compression factor at different densities along each isotherm, partial derivatives

    $$ \left( {{{\partial Z} \mathord{\left/ {\vphantom {{\partial Z} {\partial \rho }}} \right. \kern-0pt} {\partial \rho }}} \right)_{T} $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ρmin ≤ ρ ≤ ρmax).

  6. 6.

    Specific heat capacities at constant volume are calculated from (7)

    $$ c_{v} = \frac{R}{M}\left[ {Z + T\left( {\frac{\partial Z}{\partial T}} \right)_{\rho } } \right]^{2} \left[ {F - Z - \rho \left( {\frac{\partial Z}{\partial \rho }} \right)_{T} } \right]^{ - 1} $$

    inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ρmin < ρ ≤ ρmax).

  7. 7.

    Having interpolated values of F to pressures from step 1, values of speed of sound squared are calculated from

    $$ u^{2} = \frac{FRT}{M} $$
  8. 8.

    Having values of density at different pressures along each isotherm, partial derivatives

    $$ \left( {{{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } \partial }} \right. \kern-0pt} \partial }p} \right)_{T} $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ρmin ≤ ρ ≤ ρmax).

  9. 9.

    Specific heat capacities at constant pressure are calculated from (3)

    $$ c_{p} = c_{v} u^{2} \left( {\frac{\partial \rho }{\partial p}} \right)_{T} $$

    inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ρmin < ρ ≤ ρmax).

  10. 10.

    Having values of pressure at different temperatures along each isochore, partial derivatives

    $$ \left( {{{\partial^{2} p} \mathord{\left/ {\vphantom {{\partial^{2} p} \partial }} \right. \kern-0pt} \partial }T^{2} } \right)_{\rho } $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ρmin < ρ ≤ ρmax), except along ρ = ρmin, since

    $$ \left( {\frac{{\partial^{2} p}}{{\partial T^{2} }}} \right)_{{\rho_{\hbox{min} } = 0}} = 0 $$

    Having values of specific heat capacity at constant volume at different densities along each isotherm, partial derivatives

    $$ \left( {{{\partial c_{v} } \mathord{\left/ {\vphantom {{\partial c_{v} } \partial }} \right. \kern-0pt} \partial }\rho } \right)_{T} $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ρmin ≤ ρ ≤ ρmax).

  11. 11.

    Having calculated derivatives in step 10, values of f are calculated from (9)

    $$ f = - \frac{T}{{\rho^{2} }}\left( {\frac{{\partial^{2} p}}{{\partial T^{2} }}} \right)_{\rho } - \left( {\frac{{\partial c_{v} }}{\partial \rho }} \right)_{T} $$

    inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ρmin < ρ ≤ ρmax), except along ρ = ρmin = 0, because along this isochore, as already stated, the compression factor has unique value 1, and the heat capacities are obtained from speed of sound measurements (extrapolated to zero pressure) directly.

  12. 12.

    Values of f from step 11 are squared (in order to have positive sign) and summed, and the objective function g is then calculated from (10)

    $$ g = \frac{1}{2}\sum {f^{2} } $$
  13. 13.

    If g > 10−4, new values of compression factor are calculated using a modified Levenberg–Marquardt algorithm [21], inside the domain (Tmin < T < Tmax and ρmin < ρ < ρmax).

  14. 14.

    Steps 1 to 13 are repeated as many times as necessary to find such values of compression factor for which g ≤ 10−4.

2.2 Subcritical Domain

This domain is bounded by two isotherms, one isochore and the saturation line. In order to make this domain rectangular, density is replaced by quantity ϕ = ρ/ρsat. The temperature range is divided into several isotherms and ϕ-range into several lines of constant ϕ. Pressures are calculated along each ϕ again from the Peng–Robinson equation of state, and speed of sound values are specified at these pressures again in the form F = Mu2/(RT). Initial and boundary values of compression factor are obtained and specified, respectively, as in the case of the supercritical domain.

2.2.1 Algorithm of Solution

  1. 1.

    For the specified set of isotherms and lines of constant ϕ, densities are calculated from (12)

    $$ \rho = \phi \rho_{sat} $$

    inside the domain (Tmin < T < Tmax and ϕmin < ϕ < ϕmax).

  2. 2.

    For the specified set of isotherms and densities calculated in step 1, pressures inside the domain (Tmin < T < Tmax and ϕmin < ϕ < ϕmax) are calculated from compression factors, since they are always known in advance in each iteration. (In the first iteration they are obtained from the boundary values and in all other iterations from a modified Levenberg–Marquardt algorithm.) In any case, this is done by rewriting (6) into

    $$ p = \frac{\rho RTZ}{M} $$
  3. 3.

    Having values of compression factor at different temperatures along each line of constant ϕ, partial derivatives

    $$ \left( {{{\partial Z} \mathord{\left/ {\vphantom {{\partial Z} \partial }} \right. \kern-0pt} \partial }T} \right)_{\phi } $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin < ϕ ≤ ϕmax), except along ϕ = ϕmin, since

    $$ \left( {\frac{\partial Z}{\partial T}} \right)_{{\phi_{\hbox{min} } = 0}} = 0 $$

    Having values of compression factor at different densities along each isotherm, partial derivatives

    $$ \left( {{{\partial Z} \mathord{\left/ {\vphantom {{\partial Z} \partial }} \right. \kern-0pt} \partial }\rho } \right)_{T} $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin ≤ ϕ ≤ ϕmax).

    Having values of density at different temperatures along line ϕ = 1 (saturation line), derivatives

    $$ {{{\text{d}}\ln \rho_{sat} } \mathord{\left/ {\vphantom {{{\text{d}}\ln \rho_{sat} } {{\text{d}}T}}} \right. \kern-0pt} {{\text{d}}T}} $$

    are estimated from a cubic spline.

  4. 4.

    Partial derivatives of density, with respect to temperature at constant ϕ, are calculated directly from the following relation

    $$ \left( {\frac{\partial \rho }{\partial T}} \right)_{\phi } = \phi \rho \frac{{{\text{d}}\ln \rho_{sat} }}{{{\text{d}}T}} $$

    which is obtained by analytical derivation of (12), inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin < ϕ ≤ ϕmax), except along ϕ = ϕmin, since

    $$ \left( {\frac{\partial \rho }{\partial T}} \right)_{{\phi_{\hbox{min} } = 0}} = 0 $$
  5. 5.

    Partial derivatives of compression factor with respect to temperature at constant density are obtained from those at constant ϕ, according to calculus, as follows

    $$ \left( {\frac{\partial Z}{\partial T}} \right)_{\rho } = \left( {\frac{\partial Z}{\partial T}} \right)_{\phi } - \left( {\frac{\partial Z}{\partial \rho }} \right)_{T} \left( {\frac{\partial \rho }{\partial T}} \right)_{\phi } $$

    inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin < ϕ ≤ ϕmax), except along ϕ = ϕmin, since

    $$ \left( {\frac{\partial Z}{\partial T}} \right)_{{\rho_{\hbox{min} } = \phi_{\hbox{min} } = 0}} = 0 $$
  6. 6.

    For the sake of clarity, it is convenient to introduce new variable a as follows

    $$ a = \left( {\frac{\partial Z}{\partial T}} \right)_{\rho } $$
  7. 7.

    Having values of a at different temperatures along each line of constant ϕ, partial derivatives

    $$ \left( {{{\partial a} \mathord{\left/ {\vphantom {{\partial a} \partial }} \right. \kern-0pt} \partial }T} \right)_{\phi } $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin < ϕ ≤ ϕmax), except along ϕ = ϕmin, since

    $$ \left( {\frac{\partial a}{\partial T}} \right)_{{\phi_{\hbox{min} } = 0}} = 0 $$

    Having values of a at different densities along each isotherm, partial derivatives

    $$ \left( {{{\partial a} \mathord{\left/ {\vphantom {{\partial a} \partial }} \right. \kern-0pt} \partial }\rho } \right)_{T} $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin ≤ ϕ ≤ ϕmax).

  8. 8.

    Partial derivatives of a with respect to temperature at constant density are obtained from those at constant ϕ, according to calculus, as follows

    $$ \left( {\frac{\partial a}{\partial T}} \right)_{\rho } = \left( {\frac{\partial a}{\partial T}} \right)_{\phi } - \left( {\frac{\partial a}{\partial \rho }} \right)_{T} \left( {\frac{\partial \rho }{\partial T}} \right)_{\phi } $$

    inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin < ϕ ≤ ϕmax), except along ϕ = ϕmin, since

    $$ \left( {\frac{\partial a}{\partial T}} \right)_{{\rho_{\hbox{min} } = \phi_{\hbox{min} } = 0}} = 0 $$
  9. 9.

    Since speed of sound values are specified (in the form of F) at pressures calculated from the Peng–Robinson equation of state for the specified set of isotherms and lines of constant ϕ (because true pressures are not known in advance), they are interpolated with respect to pressure using a cubic spline, to pressures from step 2.

  10. 10.

    Specific heat capacities at constant volume are calculated from (7)

    $$ c_{v} = \frac{R}{M}\left[ {Z + T\left( {\frac{\partial Z}{\partial T}} \right)_{\rho } } \right]^{2} \left[ {F - Z - \rho \left( {\frac{\partial Z}{\partial \rho }} \right)_{T} } \right]^{ - 1} $$

    inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin < ϕ ≤ ϕmax).

  11. 11.

    Having values of compression factor at different pressures along each isotherm, partial derivatives

    $$ \left( {{{\partial Z} \mathord{\left/ {\vphantom {{\partial Z} \partial }} \right. \kern-0pt} \partial }p} \right)_{T} $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin ≤ ϕ ≤ ϕmax).

  12. 12.

    Partial derivatives of density, with respect to pressure at constant temperature, are calculated directly from the following relation

    $$ \left( {\frac{\partial \rho }{\partial p}} \right)_{T} = \frac{M}{ZRT}\left[ {1 - \frac{p}{Z}\left( {\frac{\partial Z}{\partial p}} \right)_{T} } \right] $$

    which is obtained by analytical derivation of (6), inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin ≤ ϕ ≤ ϕmax).

  13. 13.

    Having interpolated values of F to pressures from step 2, values of speed of sound squared are calculated from

    $$ u^{2} = \frac{FRT}{M} $$
  14. 14.

    Specific heat capacities at constant pressure are calculated from (3)

    $$ c_{p} = c_{v} u^{2} \left( {\frac{\partial \rho }{\partial p}} \right)_{T} $$

    inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin < ϕ ≤ ϕmax).

  15. 15.

    Having values of specific heat capacity at constant volume at different densities along each isotherm, partial derivatives

    $$ \left( {{{\partial c_{v} } \mathord{\left/ {\vphantom {{\partial c_{v} } {\partial \rho }}} \right. \kern-0pt} {\partial \rho }}} \right)_{T} $$

    are estimated from a cubic spline, inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin ≤ ϕ ≤ ϕmax).

  16. 16.

    Having calculated derivatives in steps 5, 8 and 15, values of f are calculated from (17)

    $$ f = - \frac{RT}{\rho M}\left[ {2\left( {\frac{\partial Z}{\partial T}} \right)_{\rho } + T\left( {\frac{\partial a}{\partial T}} \right)_{\rho } } \right] - \left( {\frac{{\partial c_{v} }}{\partial \rho }} \right)_{T} $$

    inside the domain and along the boundary (Tmin ≤ T ≤ Tmax and ϕmin < ϕ ≤ ϕmax), except along ϕ = ϕmin = 0, because along this line, as already stated, the compression factor has unique value 1, and the heat capacities are obtained from speed of sound measurements (extrapolated to zero pressure) directly.

  17. 17.

    Values of f from step 16 are squared (in order to have positive sign) and summed, and the objective function g is then calculated from (18)

    $$ g = \frac{1}{2}\sum {f^{2} } $$
  18. 18.

    If g > 10−4, new values of compression factor are calculated using a modified Levenberg–Marquardt algorithm [21], inside the domain (Tmin < T < Tmax and ϕmin < ϕ < ϕmax).

  19. 19.

    Steps 1 to 18 are repeated as many times as necessary to find such values of compression factor for which g ≤ 10−4.

3 Results and Discussion

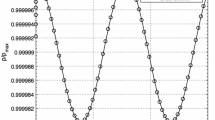
In supercritical domain, a wide range of density/pressure and temperature is covered (see Table 1). The density range exceeds critical point slightly, while temperature range exceeds it several times. The number of isochores, isotherms, speed of sound data points, boundary data points, calculated data points and iterations taken, as well as initial data deviations, is given in Table 3. The speed of sound data points, boundary data points and calculated data points do not include isochore at zero density. The boundary data points consist only of the compression factor and no heat capacities, so the number of calculated heat capacity data points is higher than that of compression factor. The average absolute deviations (AADs) of the calculated data points, with respect to corresponding reference data [18,19,20], are given in Table 5. Comparison of figures for AAD from Table 3 for initial compression factors (obtained from the boundary values by a cubic spline interpolation with respect to density) and those from Table 5 shows that these last are three orders of magnitude smaller. Since the figures from Table 5 are very small, the results obtained are practically in the limits of experimental uncertainties of corresponding direct measurements. Relative deviations of calculated data points are presented graphically in Figs. 1, 2, 3, 4, 5 and 6 for argon, Figs. 13, 14, 15, 16, 17 and 18 for methane and Figs. 25, 26, 27, 28, 29 and 30 for carbon dioxide, as a function of density and temperature. From these pictures and graphs, it can be seen that the deviations tend to increase rapidly when approaching the critical point. This happens because derivatives are approximated less accurately in the vicinity of critical point where thermodynamic surface has the highest curvature. This can be mitigated by increasing the number of isotherms in this area. However, it would demand more boundary data points and more equations to be solved.

In subcritical domain, almost a whole range of density/pressure and temperature is covered (see Table 2). The density range includes the saturation line, while temperature range practically extends from triple to critical point. The number of lines with constant ϕ, isotherms, speed of sound data points, boundary data points, calculated data points and iterations taken, as well as initial data deviations, is given in Table 4. The average absolute deviations (AADs) of the calculated data points, with respect to corresponding reference data [18,19,20], are given in Table 6. Relative deviations of calculated data points are presented graphically in Figs. 7, 8, 9, 10, 11 and 12 for argon, Figs. 19, 20, 21, 22, 23 and 24 for methane and Figs. 31, 32, 33, 34, 35 and 36 for carbon dioxide, as a function of ϕ and temperature.

In order to see how uncertainties in both the boundary conditions and speed of sound data propagate into the final solution, they are perturbed by ± 0.1 %, one at a time, and the results obtained are given in Tables 7, 8, 9 and 10. Tables 5 and 6 show that mean AAD of Z without perturbations is 0.0014 %. When the boundary conditions and speed of sound data are perturbed, this figure increases to 0.0910 % and 0.0041 %, respectively. In the case of cv, corresponding figures are 0.0320 %, 0.3730 % and 0.3113 %, and in the case of cp, they are 0.0572 %, 0.4124 % and 0.2358 %. Therefore, uncertainties in the boundary conditions have more severe effect on the final solution than those in the speed of sound. However, even these results are still in the limits of experimental uncertainties of direct measurements of corresponding properties, especially having in mind the ρ–T–p ranges covered in both the domains.

4 Conclusions

It is possible to solve the adiabatic sound wave equation in gaseous (vapor) phase as a nonlinear least squares problem, on account of volumetric boundary conditions of Dirichlet type only. When the density range reaches the critical point, the upper limit of temperature range is bounded only by the maximum pressure at which the speed of sound data are available. Although the domain of solution is very wide, the number of equations to be solved is only of the order 102, because all the derivatives are obtained from a cubic spline. Accuracy of the results obtained depends on the accuracy of the derivatives estimation, which is in direct correlation with the number of boundary data points. However, this number is rather moderate and experimentally viable, without need for interpolation like in the case of finite differences approximations. This approach is far less sensitive to the accuracy of initial data, in comparison with the numerical integration. It finds solution with AAD of the order 10−3 even if initial data AAD is of the order 100.