Variational fluid flow measurements from image sequences: synopsis and perspectives

Abstract

Variational approaches to image motion segmentation has been an active field of study in image processing and computer vision for two decades. We present a short overview over basic estimation schemes and report in more detail recent modifications and applications to fluid flow estimation. Key properties of these approaches are illustrated by numerical examples. We outline promising research directions and point out the potential of variational techniques in combination with correlation-based PIV methods, for improving the consistency of fluid flow estimation and simulation.

1 Introduction

This paper provides a synopsis of more than two decades research on image motion estimation in the field of image processing and computer vision. It reflects recent collaborations and exchange of ideas between research groups from this field and partners in experimental fluid dynamics. Examples of corresponding projects are the European FET-project “Fluid Image analysis and Description”, ¹ the priority programme on “Image Measurements in Experimental Fluid Dynamics” of the German Science Foundation (DFG), ² and an international symposium on “Experimental Fluid Dynamics, Computer Vision and Pattern Recognition” that held at Schloß Dagstuhl ³ in spring 2007.

Rather than making an attempt to comprehensively review the vast literature, we focus on a concise presentation and classification of essential concepts that we regard as particularly relevant for image analysis in experimental fluid dynamics, with a high potential for future common developments. Likewise, the list of references is by no means exhaustive but includes some key papers as well as links to more recent technical works, containing details that we deliberately omit here in order not to disrupt the main threat of the paper.

The material below complements expositions of established PIV methods based on image correlation (Adrian 2005; Raffel et al. 2007), and also the recent review (Jähne et al. 2007) where variational methods are only briefly mentioned. It also indicates that image processing, visualization and computer vision has become an interdisciplinary field of scientific computing with strong links to various disciplines of applied and computational mathematics. Recent textbooks illustrate this trend (Chan and Shen 2005; Aubert and Kornprobst 2006; Paragios et al. 2005).

This latter trend provides the background and underlines the main message that we intend to convey in this paper. In our opinion, variational methods for fluid flow estimation from image sequences provide a proper framework for consistently combining image measurements with structural constraints due to the underlying continuum mechanics, thus paving the way for bridging the gap between experiments and simulation in the future. The latter community (e.g. Berselli et al. 2006) utilizes concepts closely related to those employed in current research on mathematical image analysis.

Organization. We first outline in Sect. 2 the relation between fluid flow and optical flow. Optical flow models, also called data terms or observation models, are presented for three families of experimental configurations. Then an analysis of the physical assumptions underlying these model-based measurements techniques compared to classical correlation technique is proposed.

Next, we turn in Sect. 3 to basic variational schemes for motion estimation, broadly classified according to the representation of vector fields: local, parametric, non-parametric. Further issues include the underlying assumptions that justify a specific representation, discretization, existence and spatial density of estimates, and complexity of their numerical computation.

Section 4 is devoted to modifications of the basic schemes that are suitable for estimation of fluid flows. These include higher-order regularization in order not to penalize too much high spatial gradients, a basic distributed parameter control setting for directly controlling motion estimation through physical constraints, an outlier handling through using robust norms or semi-norms, a multiresolution scheme to handle large displacements, and an hybrid variational estimation scheme combining the best properties of approaches from PIV and computer vision. This section also exhibits very recent developments, exploiting temporal context in terms of fluid dynamics, for motion estimation. We outline both a short-time estimation scheme that iteratively alternates respective numerical computations, and a more general estimation scheme that embodies in a distributed parameter setting what is well known in engineering for the case of lumped systems. This last approach take a further major step toward an integrated fluid motion “estimation and simulation” framework.

Numerical experiments illustrating various facets of the material presented so far are presented and discussed in Sect. 5.

Finally, we conclude in Sect. 6 and indicate few research directions that show most promise in our opinion: extensions of variational approaches to three-dimensional PIV and the incorporation of turbulence models based on turbulent kinetic energy decay for motion estimation with high spatial resolution.

Notation. $\Upomega\subset {\mathbb{R}}^{2}$ denotes the two-dimensional image section and $\user2{x} \in \Upomega$ any point in it. A recorded image sequence is given in terms of an intensity function

$$ I \colon \Upomega \times [0,T] \to I(\user2{x},t). $$

We denote vector fields with

$$ \user2{w} \colon \Upomega \to \user2{w}(\user2{x}) = (u(\user2{x}), v(\user2{x}))^{\top} = \left(\begin{array}{l}u(\user2{x}) \\ v(\user2{x}) \end{array}\right), $$

where ${\cdot}^\top$ indicates transposition, i.e. the conversion of row-vectors to column-vectors, and vice-versa.

This notation reflects the continuous physical origin of the quantities involved and deliberately ignores the fact that I is given by samples at discrete locations in σ as well as along the time axis t ∈ 0, 1, ... , T. Bridging this gap between numerical computations and the physical world amounts to devise proper discretization schemes that usually do not emerge from signal sampling itself.

2 Optical flow representation

In computer vision, rigid or quasi-rigid body motion estimation methods usually rely on the assumption of the temporal conservation of an invariant derived from the data. These common photometric invariants used for motion estimation are described in Sect. 2.1.2. Geometric invariance deals with particular geometric configurations of the image function such as corners, contours, etc. They define local features that are usually stable over time, but provide only sparse information for motion estimation in sufficiently structured images. For fluid images, however, these features are difficult to define and to extract. Photometric quantities, on the other hand, are more easy to define and to compute, but are not always invariants. This raises the problem of the connection between optical flow and fluid flow. This problem is addressed in Sect. 2.1. The physics-based optical flow equation is given based on the derivation of the projected motion equations. An analysis of the physical assumptions underlying these model-based measurements techniques compared to classical correlation technique is proposed in Sect. 2.2. Optical flow equations alone do not suffice to compute image motion. This badly posed motion estimation problems, called aperture problem, is defined in Sect. 2.3.

2.1 Optical flow and fluid flow

Optical flow is the apparent velocity vector field corresponding to the observed motion of photometric patterns in successive image sequences. This motion is described by the optical flow equation also called observation term or data term. The optical flow equation establishes precisely the link between the spatiotemporal radiance variation from an emitting object in three-dimensional space and its projection onto the image plane. For laser sheet flow visualization, the optical flow equation is the projection of the equation of motion onto the image plane (see Sect. 2.1.1). For volumic flow visualization of three-dimensional flows or for visualization of two-dimensional flows, the optical flow equation has the classical form of the transport equation (see Sect. 2.1.2). Finally, for three-dimensional flow with altimetric or transmittance imagery, the optical flow is derived from the integration of the continuity equation (see Sect. 2.1.3).

2.1.1 3D flow with laser sheet visualization

The relation between fluid flow and optical flow has been described exhaustively by Liu and Shen (2008). The projected motion equations for eleven typical flow visualizations have been carefully derived. Using the underlying governing equation of flow (phase number equation for particulate flow or scalar transport equation), they have shown that the optical flow $\user2{w}$ is proportional to the path-averaged velocity of particles or scalar across the laser sheet and have proposed the following physics-based optical flow equation,

$$ \partial_t I + \varvec{\nabla}^T (I\user2{w})=f(\user2{x},I), $$

(1)

where $f(\user2{x},I)=D\varvec{\nabla}^2I + DcB + c {\bf n}.(N {\bf u})|_{\Upgamma_-}^{\Upgamma_+}$ and D is a diffusion coefficient, c is a coefficient for particle scattering/absorption or scalar absorption, $B=-{\bf n}.\varvec{\nabla} \psi|_{\Upgamma_-}^{\Upgamma_+}-\varvec{\nabla}.(\psi|_{\Upgamma_-}\varvec{\nabla} \Upgamma_-+\psi|_{\Upgamma_+}\varvec{\nabla} \Upgamma_+)$ is a boundary term that is related to the considered transported quantity ψ, and its derivatives coupled with the derivatives of the control surfaces Γ₋, Γ₊ of the laser sheet illuminated volume. Since the control surfaces are planar, there is no particle diffusion by molecular process, and the rate of accumulation of the particle in laser sheet illuminated volume is neglected, the term $f(\user2{x},I) \simeq 0$ and Eq. 1 reads

$$ \partial_t I + \user2{w} \cdot \varvec{\nabla} I + I \hbox{div} \,\user2{w}=0. $$

(2)

In Eqs. 1 and 2, the optical flow $\user2{w}$ is proportional to the path-averaged velocity weighted with a field ψ (scalar concentration or particle number par unit total volume) which is defined as

$$ \user2{w} \propto \frac{\int_{\Upgamma_-}^{\Upgamma_+} \psi \user2{W}_{xy} {\text{d}}z}{\int_{\Upgamma_-}^{\Upgamma_+} \psi {\text{d}}z}, $$

(3)

where $\user2{W}_{xy}$ is the projection of the fluid or particle velocity onto the coordinate plane (x, y).

It should be noted that Eq. 2 corresponds to the integrated continuity equation (ICE) originally proposed by Corpetti et al. (2002) under the assumption that the radiance is proportional to an integral of the fluid density across the measurement volume (see Sect. 2.1.3 for details). Although the ICE model proposed by Corpetti et al. (2006) is theoretically valid only for transmittance imagery, the authors have obtained accurate results for PIV measurements, which are now rigorously justified by the recent derivation of the projected motion equation by Liu and Shen (2008) leading to Eq. 2. The experimental evaluation of this method has shown good agreement with hot-wire measurements for a mixing layer and the wake of a circular cylinder. The numerical examination of the technique with the VSJ standard base image has indicated that the ICE equation provides the best results especially in case of out of plane component (see Sect. 5.1). Close examination of Eq. 2 shows that the physics-based optical flow model is composed of a term $\partial_t I + \user2{w} \cdot \varvec{\nabla} I$ representing brightness constancy, while the term $I \hbox{div}\,\user2{w}$ accounts for the non-conservation of the brightness function due to loss of particles caused by non-null out of plane component.

Note that the above physics-based optical flow equations do not take into account specific phenomenon like for instance spatiotemporal varying illumination of the laser that can easily be included with additional models of brightness variation (Haussecker and Fleet 2001). This issue can also be tackled with robust cost functions presented in Sect. 4.3.

Finally, we point out that the data models described by Eqs. 1 and 2, or 6 and 9 in the following sections, constitute variational models. Their validity cease to hold for long-range displacements. In this case, it is more reliable to use an integrated data model. Assuming a constant velocity of a point between two successive frames, the model defines a first-order differential equation that can be straightforwardly integrated:

$$ \frac{{\text{d}}I(\user2{x}(t),t)}{{\text{d}}t}|_{t=u} = -I(\user2{x}(u),u) \hbox{ div }\, \user2{w}(\user2{x}(u),u) \;\;\forall u\in [t,t+1], $$

leading to the non-linear data model

$$ \forall \user2{x}, I_2(\user2{x}+\user2{d}(\user2{x}))\exp(\hbox{ div }\, \user2{d}(\user2{x}))-I_1(\user2{x})=0, $$

(4)

where $\user2{d}(\user2{x})$ denotes the displacement fields between images $I_1(\user2{x})=I(\user2{x},t)$ and $I_2(\user2{x}+\user2{d})=I(\user2{x}+\user2{d}(\user2{x}),t+1).$ These models are usually linearized around current estimates and embedded into a multiresolution pyramidal image structure (see Sect. 4.4.1).

2.1.2 3D flow with volumic visualization or 2D flow

For laser sheet visualization of two-dimensional incompressible flows, the connection between fluid flow and optical flow is straightforward under the assumption that the laser sheet is perfectly aligned with the flow and/or under the assumption that the field Ψ related to the visualizing medium is constant across the laser sheet. In this context, the out of plane component is zero, the optical flow is proportional to the velocity $\user2{w} \propto \user2{W}_{xy}$, hence is divergence free $\hbox{div}\,\user2{w}=0$ and satisfies the scalar advection-diffusion equation

$$ \partial_t I + \user2{w} \cdot \varvec{\nabla} I =D\varvec{\nabla}^2I. $$

(5)

For volumic visualization of three-dimensional flows, like tomographic reconstruction, the optical flow $\user2{w}$ is a certain average of the velocity field due to the imperfect reconstruction of the three-dimensional image. As a consequence, the connection between fluid flow and optical flow is less straightforward than for the two-dimensional case and is a promising direction for further research (see Sect. 6.2). With a three-dimensional perfect visualization of the flow, the estimated three-dimensional optical flow should obviously obey to the full Navier–Stokes equations, and the evolution of the three-dimensional images should follow a transport equation related to the physical transport law of the observed quantity (e.g. particle, concentration, density, temperature,...). To a first approximation, we will consider in the following that the optical flow $\user2{w},$ associated with three-dimensional flow or two-dimensional flow visualized respectively through volumic data or two-dimensional sheets, satisfies Eq. 5.

For PIV measurements, the diffusion coefficient D = 0, and the physics-based optical flow equation corresponds to well known optical flow constraint equation (OFC) accounting for the brightness constancy assumption,

$$ \partial_t I + \user2{w} \cdot \varvec{\nabla} I=0. $$

(6)

Equation 6 is the linear differential formulation of the matching formulation between two consecutive images also known as the Displaced Frame Difference (DFD):

$$ \forall \user2{x}, I_2(\user2{x}+\user2{d}(\user2{x}))-I_1(\user2{x})=0. $$

(7)

The expression 7 leads to non-linear equations which are always valid irrespective of the displacement range, whereas Eq. 6 is locally valid where the linearization of the intensity function provides a good approximation. This is only the case for small displacements and smooth photometric gradients. Furthermore, the resulting systems are not solvable in photometrically uniform image regions.

In computer vision, for the estimation of rigid or quasi-rigid body motion, other photometric invariants, than the intensity itself, have been proposed like the conservation of the luminance gradient $\varvec{\nabla} I_2(\user2{x}+\user2{d})=\varvec{\nabla} I_1(\user2{x}))$ (Tretiak and Pastor 1984; Brox et al. 2004), or from successive gaussian filtering $g_{\sigma_j}\ast I_2(\user2{x}+\user2{d})=g_{\sigma_j}\ast I_1(\user2{x})$ (Weber and Malik 1995), where * stands for the convolution product.

2.1.3 3D flow with altimetric or transmittance imagery

When the observed luminance function relates to the fluid density, one can rely on the corresponding continuity equation to obtain a meaningful brightness variation model. Neglecting mass exchanges via vertical motions at surface boundaries, we consider the following ICE model (Integrated Continuity Equation):

$$ \partial_t \left(\int \rho {\text{d}}z\right) + \user2{w} \cdot \varvec{\nabla} \left(\int \rho {\text{d}}z\right) + \left(\int \rho {\text{d}}z\right) \hbox{div}\,\user2{w} = 0, $$

(8)

where $\user2{w}$ stands now for a density weighted average of the general 3D motion field along the vertical axis.

This model provides a valid invariance condition for altimetric imagery of compressible flows (Héas et al. 2007a) or for transmittance imagery of compressible fluids (Fitzpatrick 1988). In cases where the assumption I ∝∫ρdz holds, the ice data model provides a way to take into account mass changes observed in the image plan by associating two-dimensional divergence to brightness variations and reads like Eq. 2. For long-range displacements, integration of Eq. 2 gives Eq. 4. This model has been applied to water-vapor and infrared atmospheric satellite images (Corpetti et al. 2002) and to particle images (Corpetti et al. 2006). A similar model has also been defined for Schlieren images (Arnaud et al. 2006). This technique allows to visualize the variation of the fluid density through refraction of a light beam.

Recently, for atmospheric wind measurement applications, this model has been justified—under the assumption of negligible vertical velocities at surface boundaries—through pressure difference image maps (Héas et al. 2007a). The model has been extended to recover the vertical component of velocities, w, at the surface boundaries of altimetric atmospheric pressure layers (Héas and Mémin 2008)

$$ \frac{dh} {dt} + h \hbox{ div }\, \user2{w} = g[\rho w]_{s^-}^{s^+}, $$

(9)

where h corresponds to observed differences of pressure and the lower and upper surface boundaries are denoted by s ⁻ and s ⁺. For long-range displacements, integration of Eq. 9 yields

$$ h_2(\user2{x}+\user2{d}) - h_1(\user2{x})\exp(-\hbox{ div }\, \user2{d}) = g \frac{ [\rho w]_{s^-}^{s^+}} {\hbox{ div }\, \user2{d}} (\exp (\hbox{ div }\, \user2{d}- 1)), $$

(10)

which for vanishing divergence of the horizontal motion fields becomes

$$ h_2(x+\user2{d}(\user2{x})) - h_1(\user2{x}) = g[\rho w]_{s^-}^{s^+}. $$

(11)

2.2 Optical flow and correlation

In this section, we analyse the physical assumptions underlying model-based measurements techniques described above and classical correlation technique. We indicate that the correlation technique involves intrinsic assumptions giving rise to accuracy limits of the method for motion estimation. To provide a simple explanation of this behavior, we shall consider, for simplicity, the DFD model embedded in a local estimation scheme described in Sect. 3.1 and 3.2.

The displacement field between two consecutive images can be determined by minimizing the square of the DFD model

$$ \user2{d}(\user2{x})=\arg\min\limits_{\user2{d}} \sum_{\user2{r}\in{\mathcal W}(\user2{x})}(I_2(\user2{r}+\user2{d})-I_1(\user2{r}))^2 $$

(12)

where ${\mathcal W}(\user2{x})$ is the interrogation window. Since $I_1$ does not depend on $\user2{d}$, the displacement field reads

$$ \user2{d}(\user2{x})=\arg\min\limits_{\user2{d}} \sum_{\user2{r}\in{\mathcal W}(\user2{x})} \left(I_2(\user2{r}+\user2{d})^2 -2I_2(\user2{r}+\user2{d})I_1(\user2{r})\right). $$

(13)

Examination of this equation indicates that the minimization of the square of the DFD model includes the correlation between the displaced image I ₂ and the image I ₁. The displacement field estimated with the DFD is thus equivalent to the displacement field obtained through a correlation maximization when the quantity $\sum_{\user2{r}\in{\mathcal W}(\user2{x})} I_2(\user2{r}+\user2{d})^2$ does not depend on $\user2{d}$. This condition assumes a constant brightness energy contained in the displaced interrogation window whatever the displacement and the point location, i.e.

$$ \forall {\user2{d}}, \sum_{\user2{r}\in{\mathcal W}(\user2{x})} I_2(\user2{r}+\user2{d})^2 \approx \hbox{constant}. $$

(14)

For PIV images, this condition is clearly met for homogeneous particle seeding and sufficiently large interrogation window. Based on a mathematical analysis of the correlation, this conclusion has also been drawn by Gui and Merzkirch (2000) when comparing the square of the DFD, therein called MQD method, with several correlation-based algorithms.

Since Eq. 12 is the ideal physics-consistent measure of fit of the displacement field to the data image—for two-dimensional flow or volumic imagery of three-dimensional flows—the classical correlation provides biased estimations for non-homogeneous particle seeding. The occurrence of this critical phenomenon is locally strengthened when considering small interrogation windows, region with large velocity gradients or scalar image. On the contrary, the square of the DFD intrinsically allows to cope with smaller interrogations areas, high particle density and scalar images. This simple analysis clearly shows that the classical correlation behaves as a poor model which does not take into account the particle image pattern. As a consequence, a correlation goodness of fit exhibits accuracy limits. Furthermore, for laser sheet three-dimensional flows visualization, the correlation “model” hides the effect of intensity variations due to the out of plane component leading to limited achievable accuracy (Nobach and Bodenschatz 2009), whereas the physics-based model 4 take into account this phenomenon.

2.3 Aperture problem

Unlike the non-linear Eqs. 4 and 7, the variational linear Eqs. 2 and 6 do not suffice to compute image motion. For instance, the formulation 6 merely links the temporal variation of the luminance function to the component of the velocity vector normal to the iso-intensity curves (level lines of the image function)

$$\user2{w}(\user2{x})^{\bot}= -\frac{\partial_tI(\user2{x})}{{\|\varvec{\nabla} I(\user2{x})|}}\cdot\frac{\varvec{\nabla}I(\user2{x})}{\|\varvec{\nabla} I(\user2{x})\|}. $$

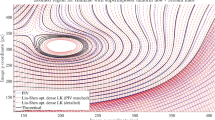
As a consequence, motion estimation of linear moving structures is ill-posed (see Fig. 1). Motion estimation is thus intrinsically linked in a way or another to the definition of windowing functions or to the adjunction of additional spatial constraints or regularization terms. This is referred to in the literature as the aperture problem. Furthermore, we point out that non-linear Eqs. 4 and 7, and the variational Eqs. 2 and 6 do not allow to estimate motion in homogeneous image regions, and are sensitive to noise.

Fig. 1

Schematic illustration of the aperture problem

3 Basic motion estimation schemes

Optical flow equations alone do not suffice to compute image motion. Additional constraints have to be used in order to define well-posed motion estimation problems. The type of these constraints depends on the way motion is represented, parametric or non-parametric, leading to different families of approaches. They include correlation methods and the Lucas Kanade estimator, and optical flow methods. Both families of approaches are described in Sect. 3.1 and 3.2.

3.1 Parametric representation and local or semi-local estimation

Parametric motion representations allow to consider additional relations linking the luminance function to the parameters. These relations are required to hold either on disjoint local spatial supports, or globally on the whole image domain.

3.1.1 Local disjoint spatial supports: correlation, “block matching” and “Lucas and Kanade”

These methods belong to region-based techniques. Their general principle consists in considering a set of windows ${\mathcal W}(\user2{x})$ centered on different points of the image grid. A parametric motion field is then estimated on each of these windows on the basis of a criteria defined classically as the minimization of the negative cross-correlation or as the minimization of a metric like the absolute and the squared differences. A locally constant displacement field is sought over a discrete state space,

$$ \user2{d}(\user2{x})=\arg\min\limits_{\user2{d}} \sum_{\user2{r}\in{\mathcal W}(\user2{x})}{\mathcal C}(I_2(\user2{r}+\user2{d}),I_1(\user2{r})). $$

The similarity functions, ${\mathcal C}$, used usually are the absolute value or the square of the DFD, or correlation functions. The squared differences is commonly used in computer vision for the motion estimation of rigid or quasi-rigid body. It has been suggested by Gui and Merzkirch (1996) for PIV measurements and named minimum quadratic difference (MQD) method. However, as discussed in Sect. 2.1.1, the DFD model, which relies on the brightness constancy assumption, is valid either for three-dimensional flows visualized through volumic data or for two-dimensional flow. For laser sheet three-dimensional flow visualization, this model has to be replaced by the model 4 accounting for particle loss and three-dimensional effects.

3.1.1.1 Correlation

Efficient implementations of the correlation functions are based on the Fast Fourier transform (FFT) and rely on the property that the transform of the correlation of two signals

$$ I_1\circ I_2\equiv\sum\limits_{\user2{r}\in{\mathcal W}(\user2{x})} I_1(\user2{r}) I_2(\user2{r}+\user2{d}) $$

is given by the product of transform of the first signal with the conjugate transform of the second signal

$$ {\mathcal F}(I_1\circ I_2) = {\mathcal F}(I_1) {\mathcal F}^{\ast}(I_2). $$

The correlation function is then computed in the Fourier domain over local windows centered in the same point in both images. Strictly speaking, this approach is only defined for periodic signals. For non-periodic signals, these methods may be sensitive to long-range displacements.

Another correlation method, defined in the phase space, relies on the shift invariance property of the Fourier transform

$$ {\mathcal F}(I(\user2{x} + \user2{w}, t)) = {\mathcal F}(I(\user2{x} + \user2{w}, 0)) \delta (\user2{k}^T\user2{w} + \phi), $$

where δ denotes the Dirac mass and $\user2{k}$ and ϕ designate respectively the spatial and temporal frequencies. This equation shows that a feature moving with a velocity $\user2{w}$ belongs to a subspace of the Fourier domain. For 2D + t image sequences, this is a plane through the origin of the 3D Fourier domain, given by the argument of the δ function

$$ \phi=-\user2{k}^T\user2{w}. $$

The slope of the plane defines the velocity vector: $\user2{w}= -\varvec{\nabla}_{\user2{k}}\phi$. Let us note that the determination of this vector is ambiguous when the signal spectrum does not sufficiently cover the corresponding plane. This is the case when the image signal in the spatial domain is either homogeneous or has a single dominant direction. We retrieve then the aperture problem in the frequency domain.

When both images I ₁ and I ₂ are linked by a global translation and a photometric invariance assumption $(\text{i.e.}, I_1(\user2{x}-\user2{w}_0) =I_2(\user2{x}))$, the Fourier transform of image I ₂ is given by:${\mathcal F}I_2=\hat{I}_2(\user2{k})= \hat{I}_1(\user2{k})\exp(-i\user2{k}^T\user2{w}_0)$ and therefore:

$$ \frac{\hat{I}_2(\user2{k}) \hat{I}^{\ast}_1(\user2{k})}{| \hat{I}_1|^2}=\exp(-i\user2{k}\user2{w}_0). $$

The spatial representation of this normalized spectral correlation coefficient (obtained through inverse Fourier transform) is characterized by a displaced dirac mass $\delta(\user2{x}-\user2{w}_0)$, which allows to determine the displacement $\user2{w}_0$ (Foroosh et al. 2002; Jähne 1993).

Methods based on these principles are largely used for their rapidity and their simplicity. Applications include image indexing, video compression, velocity measurement in experimental fluid mechanics (PIV methods; Adrian 1991), and atmospheric wind field estimation in meteorology. In experimental fluid mechanics, different challenges from 2001 to 2005 have led to very efficient and reliable variations of the technique. The main variations concern Gaussian correlation peak approximation for subpixel accuracy, and refined multipass correlation (Adrian 2005; Raffel et al. 2007).

3.1.1.2 Block matching

A second family methods is based on mean squares brightness conservation 6 and a local parametric motion model of p degrees of freedom defined over a spatial domain. In the case of a linear motion representation defined as $\user2{w}(\user2{x})=P(\user2{x})\user2{\theta}$, where $P(\user2{x})$ is a 2 × p matrix which depends on the chosen parameterization⁴, motion estimation amounts to determine the vector $\widehat{\user2 \theta}$ such that:

$$\widehat{\user2 \theta}=\arg\min_{\user2 \theta}\int\limits_{{\mathcal W}(\user2{x})}g(\user2{x}-\user2{r})\left[\partial_tI(\user2{r}) +\varvec{\nabla} I(\user2{r})^T P(\user2{r})\varvec{\theta}\right]^2 {\text{d}}\user2{r} $$

(15)

where $g(\user2{x})$ is a windowing function, typically a Gaussian, which gives more weight to the window center. This expression may be written as a convolution product in the spatiotemporal domain:

$$ \min_{\user2{v}} \user2{v}^T\left[\underbrace{g_\sigma\ast\left(P^T\varvec{\nabla}_3I \varvec{\nabla}_3 I^T P\right)}_{{\mathcal T}}\right]\user2{v}, $$

(16)

with $\user2{v}=(u,v,1)^T$ and where g _σ stands here for a (2D + t) kernel, and$\varvec{\nabla}_3I$ denotes the spatiotemporal gradients of the luminance function $\left( \varvec{\nabla}_3I \equiv(\partial_xI, \partial_yI, \partial_tI)^T \right).$

3.1.1.3 Lucas and Kanade

For a discrete 2D case and a constant motion model, the least squares solution of the expression 15 constitutes the estimator proposed by Lucas and Kanade (1981):

$$ \begin{aligned}&\user2{w}(\user2{x})=-{\mathcal{T}}^{-1}\int\limits_{{\mathcal{W}}(\user2{x})}g_\sigma(\user2{x}-\user2{r})\partial_tI(\user2{r})\varvec{\nabla}I(\user2{r}) {\text{d}}\user2{r} \\ &\hbox{with}\; {\mathcal{T}}=\int\limits_{{\mathcal{W}}(\user2{x})}g(\user2{x}-\user2{r})\varvec{\nabla}I(\user2{r})\varvec{\nabla} I^T(\user2{r}) {\text{d}}\user2{r}.\end{aligned} $$

(17)

It is easy to see that matrix ${\mathcal T}$ is ill conditioned for small photometric gradients (uniform image regions) or when the photometric contours are structured along a single direction in ${\mathcal W}(\user2{x})$ ($\forall \user2{r}\in {\mathcal W}(\user2{x}), \varvec{\nabla} I(\user2{r})\simeq {\user2 c}$). We retrieve here again the aperture problem (see Sect. 2.3).

This local scheme 17 has been applied to flow field measurements by Okuno and Nakaoka (1991), Sugii et al. (2000) and Yamamoto and Uemura (2009), and called either gradient method or spatiotemporal derivative method. The technique has been extended for the recovery of the velocity fields and its derivative and has been assessed on PIV images by Alvarez et al. (2008).

Solutions to this least squares estimation problem through an eigenvalue analysis (Eq. 16) comprises the so-called structure tensor approaches (Bigün et al. 1991; Jähne 1993). The matrix ${\mathcal T}$ being symmetric, there exists an orthogonal matrix Q such that

$$ \min_{\user2{v}} \user2{v}^T{\mathcal T}\user2{v}= \min_{{\user2 y}} {\user2 y}^TQ^T{\mathcal T}Q {\user2 y} =\min_{{\user2 y}} {\user2 y}^T \Uplambda {\user2 y}, $$

(18)

with ${\user2 y}= Q^T\user2{v}$ and Λ = diag(λ₁, λ₂, λ₃), the diagonal matrix containing the eigenvalues. The solution of Eq. 18 subject to the constraint $\|\user2{v}\|=1$ is given by the eigenvector $\user2{e}^{(\lambda_3)}\equiv\left(e_x^{(\lambda_3)} e_y^{(\lambda_3)} e_t^{(\lambda_3)}\right)^T$ corresponding to the smallest eigenvalue λ₃ ⁵. When the matrix has full rank and is well conditioned, both components of the velocity vector are given by:

$$ \user2{w}(\user2{x})=(u(\user2{x}),v(\user2{x}))= \frac{{\user2 e}^{(\lambda_3)}_{\user2 x}}{e^{(\lambda_3)}_t}. $$

The eigenvalues enable further analysis. For instance, if all three eigenvalues are close to zero, no motion can be estimated. This happens if the spatial support underlying the least squares estimation corresponds to a homogeneous image region. A single eigenvalue different from zero indicates that the luminance gradient has a single dominant spatial direction, and again only the normal velocity vector can be estimated (aperture problem):

$$ \user2{w}^\bot=e_t^{(\lambda_1)}\frac{{\user2 e}_{\user2 x}^{(\lambda_1)}}{\left\|{\user2 e}_{\user2 x}^{(\lambda_1)}\right\|}. $$

Finally, if three eigenvalues are different from zero, there is no coherent apparent motion on the considered support due to a motion discontinuity.

The formulation of the approaches Eqs. 15 and 17 in the Fourier domain leads to a plane regression problem. A set of spatiotemporal directional filters, for instance Gabor filters, enables a direct estimation of the plane parameters (Fleet and Jepson 1990; Heeger 1988; Jähne 1993; Simoncelli 1993; Yuille and Grzywacz 1988).

3.1.2 Globalized local smoothing: Ritz method

The previous techniques comprise local independent motion estimators. While this locality favorably limits error propagation, it prevents taking into account global physical constraints. One way to extend the previous approaches consists in seeking for a solution of the form

$$ \user2{w}_{\phi}(\user2{x})\equiv \sum_{i=1}^N {\user2 c}_i\phi_i(\user2{x}), $$

where the coefficients $\user2{c}_i$ are unknown and the shape functions, $\phi_i(\user2{x})$, are fixed. These functions have compact spatial support and are chosen on a priori grounds of requirements of given application area. The shape function basis should be complete, that is the approximation error $\|\user2{w}_\phi-\user2{w}\|$ converges toward zero for N → ∞.

The method consists in estimating the coefficients $\user2 {c}_i$ by minimizing

$$ J(\user2{w}_{\phi})=\int\limits_\Upomega F\left(\user2{x},\user2{w}_\phi,\frac{\partial \user2{w}_{\phi}} {\partial \user2{x}},\ldots\right) {\rm d}\user2{x} + \int\limits_\Upgamma G(s,\user2{w}_\phi,\cdots){\text{d}}s, $$

(19)

where Ω define the spatial domain with boundary Γ = ∂Ω, in which one seeks for the solution. In the case of a quadratic functional, the minimizer of J with respect to $\user2{c}$ is determined by the following conditions:

$$ \frac{\partial J}{\partial{\user2 c}}=\left[\begin{array}{c} \frac{\partial J}{ {\partial {\user2 c}_1}}\\ \vdots \\ \frac{\partial J}{ {\partial {\user2 c}_N}}\end{array}\right] = K{\user2 c} + \user2{f}=0. $$

If the functional degree with respect to $\user2{w}_\theta$ and its derivative is not larger than 2, the socalled stiffness matrix K is symmetric:

$$ K= \left[\begin{array}{ccc} \frac{\partial^2 J}{{\partial {\user2 c}_1^2}} \cdots &\frac{\partial^2 J}{ {\partial {\user2 c}_N {\user2 c}_1}} \\ \vdots &\vdots \\ \frac{\partial^2 J}{\partial {\user2 c}_1 \partial {\user2 c}_N} \cdots &{\frac{\partial^2 J} {\partial {\user2 c}_N^2}}\end{array}\right] $$

This method has been applied for functions F defined either from the OFC (Srinivasan and Chellappa 1998; Wu et al. 2000) or from the DFD (Musse et al. 1999; Szeliski and Shum 1996). In the former case, the system to be solved is linear, and the shape functions are “cosine window” functions (Srinivasan and Chellappa 1998) and a particular wavelet function basis (Cai-Wang waveletts) defined from B-splines of order 4 (Wu et al. 2000). In the latter case, both methods make use of hierarchical B-splines. As numerical iterative methods were used a Gauss–Newton solver (Musse et al. 1999), a Conjugate Gradient technique (Srinivasan and Chellappa 1998) and the Levenberg–Marquardt method (Szeliski and Shum 1996; Wu et al. 2000). Standard boundary conditions (Dirichlet or Neumann) were associated with those different approaches. Basis functions defined on thin-plate splines (Duchon 1977; Wahba 1990) have been also intensively used in computer vision registration application (Arad et al. 1994; Bookstein 1989) or for medical image applications (Rohr et al. 1999). The main problem of these methods consists to determine an adequate spatial subdivision of the image domain in terms of the basis functions, and to allow for strong discontinuities of the solution that are important in some applications of image sequence processing.

For fluid flow image analysis, an estimator of this kind, relying on the Helmholtz decomposition, has been proposed in Cuzol and Mémin (2005, 2008). An example of the results obtained by the latter estimator is shown in Figs. 12 and 13. The representation on which it relies is further described in Sect. 4.5.2. Let us recall that the Helmholtz decomposition separates the velocity field into a divergent-free and a curl-free component (assuming null boundary conditions at infinity), the solenoidal and irrotational motion components

$$ \user2{w}= \user2{w}_{\rm irr} + \user2{w}_{\rm sol}, $$

(20)

where $\hbox{div} \,\user2{w}= \hbox{div}\,\user2{w}_{\rm irr}$ and $\hbox{curl}\, \user2{w}= \hbox{curl}\,\user2{w}_{\rm sol}$. It is well known that these two fields can be represented by two potential functions, the stream function and the velocity potential

$$ \user2{w}= \varvec{\nabla} \psi + \varvec{\nabla}^\bot \phi. $$

(21)

These potential functions are solutions of two Poisson equations (known for the divergent-free component as the Biot-Savart integral):

$$ \Updelta \psi= -\hbox{curl } \user2{w},\qquad \Updelta\phi= \hbox{div }\, \user2{w}. $$

(22)

As a consequence, they may be expressed by the convolution with the corresponding Green functions. Taking gradients of these convolution products and slightly mollifying the associated singular kernels with Gaussian convolution gives rise to appropriate basis functions for the curl and the divergence, known in the computational fluid dynamics community as vortex particles (Chorin 1973; Cottet and Koumoutsakos 2000; Leonard 1980). The resulting irrotational and solenoidal motion fields are a linear combination of these basis functions. The solenoidal components, for instance, reads

$$ \begin{aligned} {{\bf w}}_{\rm sol}({\bf x})&\approx\sum_{i=0}^{p}\gamma_i K^\perp \ast g_{\varepsilon_i}({\bf z}_i-{\bf x}) \\ &\approx\sum_{i=0}^{p}\gamma_i K^\perp_{\varepsilon_i}({\bf z}_i-{\bf x}), \end{aligned} $$

(23)

where K ^⊥_εi is the kernel function obtained by convolving the orthogonal gradient of the Green kernel, K ^⊥, with a Gaussian function, $g_{\varepsilon_i}$. The coordinates, ${\bf z}_i,$ denotes the location of the ith basis functions. A similar representation of the irrotational component using likewise, source particles and the Biot-Savart integral associated with the divergence map (Eq. 24) can be readily obtained. Using this parameterization together with a photometric model enables to define a least squares estimation problem for the unknown coefficients. The estimation of the basis function parameters, on the other hand, i.e. standard deviation of the gaussian kernel and location of the basis function, is more involved and leads to a non-linear system to be solved numerically. A solution based on a two-stage process is proposed in Cuzol et al. (2007). Code corresponding to this estimator is freely available and can be downloaded on the Web site of the FLUID project (http://www.fluid.irisa.fr).

For fluid flows analysis and fluid motion estimation from image sequences spline basis functions minimizing a second order div–curl constraint (see Eq. 25 Sect. 1) have been proposed (Amodei and Benbourhim 1991; Suter 1994; Isambert et al. 2008). Compared to vortex particles, these basis functions have the drawback to impose strictly an empirical kinematics constraint that is not built from physical considerations.

3.2 Non-parametric representation and non-local estimation

A third basic class of motion estimation schemes considers velocity fields $\user2{w}=(u,v)^{\top}$ as general functions, rather than as individual velocity estimates at discrete locations (Sect. 2.1.2), or as polynomial vector fields defined in a local region (Sect. 3.1). These methods are classically called optical flow or global approaches.

Given an image function $I(\user2{x},t)$, we estimate $\user2{w}$ for an arbitrary but fixed point of time t by minimizing the functional

$$ E(\user2{w}) = \int\limits_{\Upomega} \left\{ (\varvec{\nabla} I \cdot \user2{w} + \partial_{t} I)^{2} + \lambda \left( \|\varvec{\nabla} u\|^{2} + \|\varvec{\nabla} v\|^{2} \right) \right\} {\rm d}\user2{x}. $$

(24)

The variational approach Eq. 24 has been introduced by Horn and Schunck (1981) in the field of computer vision. The objective criterion combines two terms: A so-called data term that enforces the conservation assumption by minimizing the squared norm of the linearized DFD (see Sect. 2.1.2), and a so-called smoothness term or regularizer that enforces spatial smoothness of the minimizing velocity field $\user2{w}$, to a degree as specified by the regularization parameter λ weighting the two terms.

Specific properties of the basic variational approach (Eq. 24) include:

• Under weak conditions, namely, L ²-independence of the two component functions of the spatial image gradient $\varvec{\nabla} I(\user2{x}),$ the functional Eq. 24 is strictly convex (Schnörr 1991). Because the functional additionally is quadratic in $\user2{w},$ discretizing the variational equation

  $$ \frac{{\rm d}}{{\rm d}\tau} E\left(\user2{w} + \tau\tilde{\user2{w}}\right)|_{\tau=0} = 0,\quad \forall \tilde{\user2{w}}, $$

  with piecewise linear finite elements, or the corresponding Euler-Lagrange system of equations with finite differences, yields a sparse linear system that is positive definite. It can be conveniently and efficiently solved using standard iterative numerical techniques.

• The resulting velocity estimate $\user2{w}$ is dense even if the image function I is homogeneous, i.e. $\varvec{\nabla} I \approx 0,$ in some image regions. As before in the two previous subsections, imposing smoothness on the solution is necessary here, too, to obtain a well-defined estimation approach. The non-parametric approach (Eq. 24) is less restrictive, however, than assuming locally constant velocity fields (Sect. 2.1.2), or than prescribing a polynomial form within local regions (Sect. 3.1).

The application of the basic variational approach (Eq. 24) to PIV has been studied in Ruhnau et al. (2005) where more details on the discretization are given. Moreover, in this paper, a multiscale representation of the input image data I obtained by low-pass filtering and subsampling was used to compute long-range motions up to 15 pixels per frame, which is not possible when working with Eq. 24 on the finest sampling grid only (see Sect. 4.4.1 for details on this multiscale representation).

Although providing good results with PIV data, the basic variational approach of Horn and Schunck (1981) was originally proposed for rigid or quasi-rigid motion. Therefore some knowledge of the physics of fluid need to be used to improve the measurement accuracy. For laser sheet visualization of three-dimensional flow, Eq. 2 must be used as a data term. Modifications of the regularization term are addressed in Sect. 4 (higher-order and physics-based regularization) and in Sect. 4.3 robust norms are described for removing outliers and for preserving discontinuities of the velocity fields. Concerning numerical approaches relevant to Eq. 24, we refer to Bruhn et al. (2006) and references therein.

4 Specific motion estimation schemes

The motion estimators presented so far combine a physics-based model of brightness variation related to the observed flow with additional spatial constraints expressed through parametric motion models or smoothness functionals. This last ingredient was mainly designed in the context of rigid luminance patterns that are typical for image sequences of natural scenes.

Regarding fluid flow velocity fields, it is natural to ask for dedicated approaches taking into account physically more plausible smoothing functionals, to provide more accurate velocity measurements. This section addresses these issues.

4.1 Higher-order regularization

Regarding the estimation of fluid flows with spatially varying, strong gradients, an apparent weak point of the basic variational approach (Eq. 24) is the use of first-order derivatives in the regularization term. As a consequence, the value for the parameter λ has to be chosen quite small in order not to underestimate gradients of the flow. On the other hand, this means that data noise influencing the first term in Eq. 24 cannot be effectively suppressed through regularization.

As a remedy, numerous researchers studied higher-order regularizers, in particular terms involving second-order spatial derivatives of the flow, of the form

$$ \int\limits_{\Upomega} \left\{ \|\varvec{\nabla} \hbox{div}\, \user2{w}\|^{2} + \|\varvec{\nabla} \hbox{curl}\, \user2{w}\|^{2} \right\} {\rm d}\user2{x}. $$

(25)

We refer to Corpetti et al. (2002), Yuan et al. (2007) and references to earlier work therein. Further motivation of Eq. 25 is given by the generalized Helmholtz decomposition of the space of square integrable vector fields into gradients and curls (Girault and Raviart, 1986)

$$ L^{2}(\Upomega)^{2} = \varvec{\nabla} H^{1}(\Upomega) \oplus \varvec{\nabla}^{\perp} H_{0}^{1}(\Upomega), $$

(26)

that is valid in two dimensions $\Upomega \subset {\mathbb{R}}^{2}$ if the domain Ω is simply connected. In Eq. 26, the symbol $\varvec{\nabla}^{\perp}$ denotes the vector-valued curl-operator $(\partial_{x_{2}}, -\partial_{x_{1}})^{\top}$ for two-dimensional scalar fields, and H ¹(Ω) denotes the Sobolev space of square integrable functions whose gradients are square integrable as well. H ¹₀ (Ω) denotes the subspace of those functions of H ¹(Ω) that vanish on the boundary ∂Ω.

Using higher-order derivatives has consequences for discretization. Unlike the approach (Eq. 24) where standard textbook schemes apply and lead to numerically stable computations, the regularizer Eq. 25 yields a complex Euler-Lagrange system of equations and natural boundary conditions whose proper discretization is far from being trivial. The decomposition of vector fields $\user2{w} \in L^{2}(\Upomega)^{2}$

into an irrotational and a solenoidal component due to Eq. 26 highlights this issue as well. For example, it is well known from computational fluid dynamics that imposing the incompressibility constraint $\hbox{div}\, \user2{w} = 0$ in connection with standard discretization schemes may result in $\user2{w} = {\bf 0}$, due to the so-called locking effect (cf., e.g., Brezzi and Fortin 1991).

As a consequence, more sophisticated discretizaton schemes have to be applied. Examples include the Mimetic Finite Differences framework developed by Hyman and Shashkov (1997a, 1997b) or alternatively the construction of adequate Finite Element spaces, see Hiptmair (1999) and references therein to earlier work. The primary objective of this line of research is to make hold true orthogonal decompositions of spaces of vector fields and the basic integral identities of vector analysis after discretization. This is an essential prerequisite for stable numerical computations.

Furthermore, vector field decompositions help to analyze variational approaches. For example, it is shown in Yuan et al. (2007) that when using the regularizer (Eq. 25) together with the data term in Eq. 24, one should include an additional boundary term in order to remove an inherent sensitivity against noise in the image data that cannot be regularized by increasing the weight of Eq. 25.

Comparisons of the approaches of Corpetti et al. (2002) and Yuan et al. (2007) with correlation technique are discussed in Sect. 5.1. Results obtained with these higher-order regularization techniques are displayed in Figs. 4, 5, 6 and 7 for particle and scalar images.

4.2 Physical constraints and controlled estimation

The variational approaches Eqs. 24 and 25 are unconstrained. In experimental fluid dynamics, this appears to be unnatural because the flow to be estimated is governed by the Navier–Stokes equation. Consequently, one may ask for approaches that combine flow measurements from image sequences with the constitutive equations of fluid dynamics. This basic problem opens a line of long-term research at the end of which one may expect computational schemes to be available that consistently combine the evaluation of experimental data and simulations.

The reader may argue that physical constraints are less useful in the prevailing two-dimensional measurement scenarios. For example, even the incompressibility condition $\hbox{div}\, \user2{w}=0$ does not strictly hold for flows observed in a planar section through a volume, due to out of plane particle movements. While this is true, it should not hamper to clarify this basic problem that is becoming more and more relevant as soon as novel measurement techniques delivering three-dimensional flow measurements become available.

A basic approach that in some sense provides the simplest setting for a meaningful combination of flow measurements with physical constraints has been recently proposed in Ruhnau And Schnörr (2007). The variational approach comprises the objective functional

$$ \begin{aligned} E(\user2{w}, p, \user2{f}, \user2{g}) =& \int\limits_{\Upomega} \left\{ (\varvec{\nabla} I \cdot \user2{w} + \partial_{t} I)^{2} + \alpha \|\user2{f}\|^{2}\right\} {\rm d}\user2{x} \\ & + \gamma \int\limits_{\partial\Upomega} \|\partial_{\user2 t}\user2{g}\|^{2} {\rm d}s, \end{aligned} $$

(27)

and the constraint system

$$ -\mu \Updelta \user2{w} + \varvec{\nabla} p = \user2{f}\quad \hbox{in } \Upomega, $$

(28a)

$$ \hbox{div} \,\user2{w} = 0 \quad \hbox{in } \Upomega, $$

(28b)

$$ \user2{w} = \user2{g} \quad \hbox{on } \partial\Upomega. $$

(28c)

Estimated flows $\user2{w}$ have to satisfy the Stokes system Eq. 28 and to fit the observed image motion by minimizing the data term (i.e. the first term) in Eq. 27. The connection between the physical constraints and the objective function is established by virtue of distributed vector fields $\user2{f}, \user2{g}$ inside Ω and on the boundary ∂Ω, respectively, that control the estimated flow $\user2{w}$ through the right-hand side of Eq. 28 so as to minimize Eq. 27. Regularization terms of the control variables are included into the objective function, with small weights α and γ, in order to render the whole approach mathematically well posed. $\partial_{{\user2{t}}{\user2{g}}}$ denotes the componentwise tangential derivative of $\user2{g}$ along the boundary ∂Ω.

The following basic observations can be made:

• The approach, Eqs. 27 and 28, is more specific than Eq. 25 (complemented with the same data term), due to the constraint system Eq. 28. This is an advantage if the physical constraints hold true. In fact, if $\user2{w}$ is actually governed by the Stokes equation, the variables $p, \user2{f}$ become physically significant: Pressure and forces can be directly estimated from the image data $I(\user2{x},t)$ (Ruhnau and Schnörr, 2007)

• Using the data term Eq. 6, the approach Eq. 27 was originally devised for two-dimensional flows but may also hold in a physical sense for three-dimensional flow with volumic visualization. In these cases, under the assumptions described in Sect. 2.1.2, the optical flow $\user2{w}$ can satisfy the Stokes Eq. 28;

• In the case of turbulent flow $\user2{w}$ where the Stokes equation is inadequate but the constraint Eq. 28b still holds true, the approach Eqs. 27 and 28 still makes sense. This is because the control variables $\user2{f}, \user2{g}$ are free. While they are no longer physically significant, they still control the flow $\user2{w}$ so as to fit the turbulent measurements observed through the image data, by minimizing Eq. 27. In this connection, we point out that $\user2{f} \propto \Updelta \user2{w}$ in Eq. 28a is proportional to second-order derivatives of $\user2{w}$. As a result, inclusion of $\|\user2{f}\|^{2}$ into Eq. 27 leads to higher-order flow regularization as in Eq. 25, but in a physically more plausible way;

• Finally, observe that the Eq. 28 have the common form used in numerical simulations, and are kept separate from the functional Eq. 27 involving the data. This helps to rely on established numerical schemes developed in both communities.

In Ruhnau and Schnörr (2007), the authors develop a gradient descent scheme for minimizing Eq. 27 subject to the constraints Eq. 28. To compute the gradient, the dependency of the variables $\user2{w}, p$ on the controls $\user2{f},\user2{g}$ has to be taken into account. This can be done by additionally solving an auxiliary system of the same form as Eq. 28. A second major issue is to employ proper discretizations for $\user2{w}$ and p. We refer to Ruhnau and Schnörr (2007), Gunzburger (2003) and Brezzi and Fortin (1991) for details.

4.3 Robust measures

Models of motion estimation described in Sect. 2.1 rely on assumptions that do not strictly hold true. Non-Gaussian noise, changes of illumination, and many other local situations that do not fit well the underlying model provide examples. To handle such deviations in the different energy terms of the functional, it is common to replace the L ² norm by a so-called robust norm

$$ \int\limits_\Upomega \rho(g(\user2{w})){\rm d}\user2{x}. $$

(29)

Such cost functions, originally introduced in the context of robust statistics (Huber 1981), penalize large residual values less than quadratic functions do (Fig. 2).

Fig. 2

Graph of a robust cost function $\left(\rho(x)= 1-{\text{exp}}\left(\frac{x^2}{ {\sigma^2}}\right)\right)$ compared to a quadratic function

Under suitable conditions (mainly concavity of $\Upphi\equiv\rho(\sqrt x)$), it can be shown that any multidimensional minimization problem of the form

$$ \arg\min_{\user2{w}}\int\rho[g(\user2{w})]{\text{d}}\user2{x}, $$

(30)

can be turned into a corresponding dual minimization problem (Huber 1981; Geman and Reynolds 1992)

$$ \arg\min_{\user2{w},z}\int[M z g(\user2{w})^2+\psi(z)]{\rm d}\user2{x}. $$

(31)

This new optimization problem involves additional auxiliary variables acting as weight functions $z(\user2{x})$ with value in the range [0, 1]. Function ψ is a continuously differentiable function, depending on ρ, and $M\equiv\lim_{v\rightarrow 0+}\Upphi'(v).$ Optimization is carried out alternating minimizations with respect to $\user2{w}$ and z. If the function g is affine, minimization with respect to $\user2{w}$ becomes a standard weighted least squares problem. For $\user2{w}$ being fixed, the best weights have the following closed form (Geman and Reynolds 1992):

$$ \hat z(\user2{x})=\frac{\rho'[g(\user2{w})]}{ {2Mg(\user2{w})}}=\frac{1}{{M}}\Upphi'\left[g(\user2{w})^2\right]. $$

(32)

Experimentally, the use of these functions either for the data model or for the regularization term has led to better performance in a range of computer vision application (Black and Rangarajan 1996; Mémin and Pérez 2002). For fluid flows, such functions have been mainly used for the data term (Corpetti et al. 2006; Héas et al. 2007a). They allow to introduce a localized discrepancy measure between the data model and the actual measurements. At points where such a deviation occurs, only the remaining terms of the functional (i.e. regularization) are involved. These functions have been also used together with a classification map to enable the estimation of atmospheric layered data (Héas et al. 2007a). In that case, only data belonging to a predefined layer are taken into account for motion estimation.

4.4 Multiscale estimation

4.4.1 Multiresolution scheme

Velocity measurements from particle image sequence present inherent difficulties for variational methods. The variational formulation is limited to small displacements (smaller than the shortest wavelength present in the image), and therefore is typically embedded into a multiresolution scheme to handle large displacements.

These models are usually linearized around current estimates and embedded into a multiresolution pyramidal image structure obtained from successive low-pass filtering and subsampling of the image sequence (Fig. 3). The estimation process is then incrementally conducted from “coarse to fine” along the multiresolution structure (Bergen et al. 1992; Enkelmann 1988; Mémin and Pérez 1998; Papenberg et al. 2006).

Fig. 3

Coarse-to-fine resolution with multiresolution representation of the images (Heitz et al. 2008)

4.4.2 Correlation-based variational scheme

As mentioned above, the estimation of long-range displacements with optical flow techniques is usually embedded into multiresolution data structures and successive linearizations around the current estimate. These incremental schemes allow to tackle in a Gauss–Newton type manner the non-linear optimization associated with the non-linear integrated brightness constancy assumption, such as the DFD data model. In this scheme, major components of the displacements are computed at coarse resolution levels corresponding to low-pass filtered and subsampled versions of the original images. However, when the motion of thin or small structures differs significantly from the motion of larger regions in their neighborhood, the estimator most likely fails to correctly determine the motion of these high frequency photometric structures. This is particularly true for meteorological images, where for instance mesoscale structures such as cirrus filaments may exhibit large displacements that are completely different from the atmospheric layer motion at a lower altitude. The same problem appears with particle images. Due to the successive down sampling of the image, small particles with large velocities are smoothed out, thus leading to a loss of information and erroneous velocity measurements. As a result, these problems lead to poor performance of traditional multiresolution dense motion estimator.

Correlation techniques have proven to be more robust with respect to the estimation of long-range displacements. Nevertheless, as they rely on parametric spatial motion models, these techniques tend to larger estimation errors in regions with a high motion variability. Furthermore, they provide sparser motion fields that must be interpolated and post-processed in order to compute dense vorticity maps or related differential motion quantities.

In order to benefit from the best properties of both variational dense estimators and correlation techniques, an immediate idea is to combine these two methods. Sugii et al. (2000) combined sequentially cross-correlation technique and local variational approach (Lucas and Kanade method see Sect. 3.1) to achieve high subpixel accuracy with higher spatial resolution. Seemingly, for three-dimensional motion estimation, Alvarez et al. (2009) initialized the estimation with cross-correlation and improved the results with a global variational approach (Horn and Schunck method see Sect. 3.2).

To cope with the multiresolution issue, Héas et al. (2007a) for meteorological satellite images and Heitz et al. (2008) for fluid mechanics particle images, proposed a collaborative correlation-variational approach combining the robustness of correlation techniques with the high spatial density of global variational methods. Both techniques can be formalized as the minimization of the following functional:

$$ \begin{aligned} & \qquad \int\limits_{\Upomega} {\mathcal F}\left(I,\overline{\user2{w}}+\breve{\user2{w}}\right) \\ & \quad + \beta \int\limits_{\Upomega}\sum_{i=1}^{p}h^i g_\sigma(\user2{x}^i- \user2{x})\| \user2{w}_c(\user2{x}^i) - \overline{\user2{w}}\|^2 {\rm d}\user2{x} \\ &+ \alpha \int\limits_\Upomega \|\varvec{\nabla} \hbox{curl}\,\left(\overline{\user2{w}}+\breve{\user2{w}}\right) \|^2+ \|\varvec{\nabla} \hbox{div}\,\left(\overline{\user2{w}}+\breve{\user2{w}}\right) \|^2 {\rm d}\user2{x}, \end{aligned} $$

(33)

where $\overline{\user2{w}}$ denotes the large scale components of the motion, whereas $\breve{\user2{w}}$ represents finer scales. Function ${\mathcal{F}}$ stands for any chosen photometric data model, and $\user2{w}_c$ denotes a finite set of p correlation vectors located at points $\user2{x}^i$. Optimization is carried out in two separate steps. Setting initially to zero the finer motion component, the large-scale components are obtained on the basis of (1) a photometric data model, (2) a goodness of fit term including the correlation vectors that is weighted both by a Gaussian function to spatially enlarge the correlation vector’s influence and a correlation confidence factor, and (3) a second-order div–curl regularizer. Then, in turn, by freezing the large-scale components, the finer scales are estimated on the basis of the div–curl regularizer and the photometric data model. In this second step, the correlations vectors are not anymore involved. Unlike the multiresolution approach, this scheme relies on a single representation of the full resolution data and avoids the use of successive low-pass filtering of the image data.

This technique has been evaluated with synthetic images of particles dispersed in a two-dimensional turbulent flow, and with real-world turbulent wake flow experiments (see Sect. 5.2).

4.5 Utilizing temporal context

The motion estimation techniques described so far only rely on kinematic constraints and provide independent instantaneous motion field measurements for each frame. All these estimates along the time axis are independent from each other, hence consistency of spatiotemporal motion field trajectories cannot be enforced. To do this in a physically plausible way, it is essential to consider motion estimation as a dynamical process along the time-resolved image sequence and to impose corresponding constraints.

Such a process can be set up in two distinct ways. The first approach extends the traditional dense estimation method by adding to the objective functional an additional goodness of fit term comparing the current estimate by the predicted motion based on previous estimates and a specified evolution law. The second approach implements the motion estimation issue as a tracking problem. In this case a sequence of motion fields is estimated using the complete set of image data available. The estimation is formulated as a dynamical filtering problem in order to recover complete velocity field trajectories on the basis of a dynamical law and noisy incomplete image measurements. This strategy can be implemented through a recursive stochastic technique or in terms of a global variational formulation.

In the following sections we explore these two alternatives in some more details and give pros and cons of each of them.

4.5.1 Local temporal context and iterative estimation

A variational approach realizing the first option discussed above has been recently worked out in Ruhnau et al. (2007) for three-dimensional flow with volumic visualization or for the two-dimensional case, in Héas et al. (2007a) for altimetric imagery of three-dimensional flows and in Heitz et al. (2008) for laser sheet three-dimensional flow visualization of particles or scalar.

4.5.1.1 3D flow with volumic visualization or 2D flow

Let [0, T] denote the local time interval between two subsequent frames of the image sequence $I(\user2{x},t)$. The evolution of the flow $\user2{w}$ to be estimated from $I(\user2{x},t)$ is given by the vorticity transport equation

$$ \frac{D}{ {Dt}} v = \partial_{t} v + \user2{w} \cdot \varvec{\nabla} v = \nu \Updelta v,\quad v(\user2{x},0) = v_{0}, $$

(34)

where $v_{0} =\hbox{curl} \,\user2{w}|_{t=0}$ denotes the vorticity of the flow estimated for the first image frame. Solving this equation numerically in the time interval [0, T], that is performing simulation, we compute $v_{T} = v(\user2{x},T)$ and interpret this as an prediction of the vorticity of the flow observed through the second frame of the image sequence $I(\user2{x},t)$ at time t = T.

At time t = T, we have again access to image sequence data. Hence we minimize a motion estimation functional that takes into account the observed data in terms of Eq. 6 and regularizes the flow by comparison with the predicted vorticity v _T .

$$ E(\user2{w}) = \int\limits_{\Upomega} \left\{ (\partial_{t} I +\varvec{\nabla} I \cdot \user2{w} )^{2} + \lambda (v - v_{T})^{2} + \kappa \|\varvec{\nabla} v\|^{2} \right\} {\rm d}\user2{x}, $$

(35a)

$$ \hbox {subject to} \qquad \hbox{ div }\, \user2{w} = 0,\quad \hbox{curl }\user2{w} = v. $$

(35b)

Computing the minimizer $\user2{w},$ we obtain the initialization $v=\hbox{curl} \,\user2{w}$ for Eq. 34, to be solved for the subsequent time interval. For details of the non-trivial discretization of both Eqs. 34 and 35, we refer to Ruhnau et al. (2007).

The following observations can be made:

• Originally proposed for the two-dimensional case, this approach may also hold for volumic three-dimensional flow visualization. In these configurations, under the assumptions described in Sect. 2.1.2, the optical flow $\user2{w}$ estimated with Eq. 35 satisfies the vorticity transport Eq. 34;

• Besides enforcing similarity of $v=\hbox{curl}\, \user2{w}$ and the prediction v _T in Eq. 35, the flow $\user2{w}$ is only regularized through first-order spatial derivatives of vorticity. As a consequence, the variational approach Eq. 35 again generalizes the higher-order regularization approach Eq. 25 in a physically meaningful way;

• Additionally, the iterative interplay between prediction (Eq. 34) and estimation (Eq. 35) utilizes spatiotemporal context in an online manner, because for each computation just two frames of the sequence are used. The “memory” of the overall approach depends on the value of the parameter λ in Eq. 35. This online property is in sharp contrast to the commonly employed way in image processing to exploit spatiotemporal context in a batch-processing mode by treating the time axis as a third spatial variable (Weickert and Schnörr 2001);

• Finally, we point out that the simulation (Eq. 34) and estimation (Eq. 35) are separate processes from the viewpoint of numerical analysis. This keeps the overall design modular and avoids reinventing the wheel.

4.5.1.2 3D flow with laser sheet visualization or altimetric imagery

A different but related technique has been proposed for the recovery of atmospherical motion layer by Héas et al. (2007a) and extended by Heitz et al. (2008) for 2D image sequences of particles dispersed in 3D turbulent flows. In these works, the predicted vorticity is replaced by a predicted velocity, $\user2{w}_p,$ obtained from the numerical integration of a filtered simplified vorticity-divergence formulation of shallow water models. For laser sheet three-dimensional flow visualization, the simplified vorticity-divergence transport equations reads

$$ \left\{\begin{array}{l} v_t+ \user2{w} \cdot \user2{\varvec{\nabla}} v + v \zeta =(\nu_{s}+\nu) \Updelta v\cr \zeta_t+ \user2{w} \cdot \user2{\varvec{\nabla}} \zeta + \zeta^2 - 2 |J|= (\nu_{s} +\nu) \Updelta \zeta, \end{array} \right. $$

(36)

where $\zeta=\hbox{div}\, \user2{w}, |J|$ is the determinant of the Jacobian matrix of variables (u, v), $\nu_{s}=(C\Updelta_x)^2|\user2{x}i|$ is the enstrophy-based subgrid scale model proposed by Mansour et al. (1978), and C the Lilly’s universal constant equal to 0.17.

Here, we minimize a motion estimation functional that takes into account the observed data in terms of Eq. 2 and regularizes the flow by comparison with the predicted velocity $\user2{w}_p,$

$$ \begin{aligned} E(\user2{w}) = & \int\limits_{\Upomega} \left\{( \partial_{t} I + \varvec{\nabla} I \cdot\user2{w} + I \hbox{div}\, \user2{w})^{2} + \lambda \|\user2{w} - \user2{w}_{p}\|^{2} \right. \\ & \quad \left. + \kappa \left(\|\varvec{\nabla} v\|^{2}+\|\varvec{\nabla} \zeta\|^{2}\right) \right\} {\rm d}\user2{x}. \end{aligned} $$

(37)

The prediction term applies here only at a large scale, and the quadratic goodness of fit term only involves a large-scale component of the unknown velocity field. The small-scale unknown components are computed in an incremental setup and depends only on the data model and the smoothing term used in the estimator. This term plays the role of a predictor of a large-scale motion component and thus avoids the use of a multiresolution scheme in order to cope with long-range displacements. Interested readers will find the implementation details and experimental comparison results in Héas et al. (2007a) and in Heitz et al. (2008). The improvements brought by this spatiotemporal regularization are discussed in Sect. 5.3 and shown in Figs. 10 and 11.

Note that as indicated in Sect. 2.1.1, the optical flow $\user2{w}$ estimated with Eq. 37 is proportional to the path-averaged velocity of fluid across the laser sheet and hence does not satisfy exactly the full Navier–Stokes equations. However, in the present approach, since the Navier–Stokes equations have been simplified with shallow flow assumption across the laser sheet, the optical flow $\user2{w}$ satisfies Eq. 36.

4.5.2 Non-local temporal context

In the following sections, we briefly present the two dynamic filtering alternatives that implement a global dynamical consistency of the estimated velocity fields sequences. The first one relies on a stochastic methodology whereas the second one ensues from optimal control theory.

4.5.2.1 Recursive estimation through stochastic filtering

In order to estimate optimally the complete trajectory of an unknown state variable from a sequence of past image frames, we formulate the problem as a stochastic filtering problem. Resorting to stochastic filters consists in modeling the dynamic system to be tracked as an hidden Markov state process. The goal is to estimate the value of the random Markovian process—also called state process and denoted ${\bf x}_{0:n}=\{{\bf x}_t\}_{t\in [0,n]}$—from realizations of the observation process. The set of measurements operated at discrete instants are denoted ${\bf z}_{1:n}=\{{\bf z}_1,{\bf z}_1,...,{\bf z}_n\}$. The system is described by (a) the distribution of the state process at initial time $p({\bf x}_0)$, (b) a probability distribution modeling the evolution (i.e. the dynamics) of the state process $p({\bf x}_k|{\bf x}_{t<k})$ and (c) a likelihood (representing the measurement equation) $p({\bf z}_k|{\bf x}_{k})$ that links the observation to the state. In this framework, the posterior distribution, i.e. the law of the state process knowing the set of observations, carries the whole information on the process to be estimated. More precisely, as tracking is a causal problem, the distribution of interest is the law of the state given the set of past and present observations $p({\bf x}_k|{\bf z}_{1:k})$, known as filtering distribution. The problem of recursively estimating this distribution may be solved exactly through a Bayesian recursive solution, named the optimal filter (Gordon et al. 1993). This solution requires to compute integrals of huge dimension. In the case of linear Gaussian models, the Kalman filter (Anderson and Moore 1979) gives the optimal solution since the distribution of interest $p({\bf x}_k|{\bf z}_{1:k})$ is Gaussian. In the non-linear case, an efficient approximation consists in resorting to sequential Monte Carlo techniques (Arulampalam et al. 2002; Doucet et al. 2000; Gordon et al. 1993). These methods consist in approximating $p({\bf x}_k|{\bf z}_{1:k})$ in terms of a finite weighted sum of Dirac masses centered in elements of the state space, named particles. At each discrete instant, the particles are displaced according to a probability density function named importance function, and the corresponding weights are updated using the system’s equations. A relevant expression of this function for a given problem is essential to achieve an efficient and robust particle filter. Interested readers may found different possible choices in Arnaud and Mémin (2007) and Doucet et al. (2000).

Such a technique has been applied to the tracking of a solenoidal field described as a combination of vortex particles (Cuzol and Mémin 2005, 2008). The motion field in that work is described through a set of random variables ${\bf x}_i, i=1,\ldots,p$:

$$ \user2{w}({\bf x}) \approx \sum_{i=0}^{p}\gamma_i K^\perp_{\epsilon_i^{sol}}\left({\bf x}_i^{sol}-{\bf x}\right), $$

(38)

where $K^\perp_{\epsilon_i}$ is a smoothed Biot-Savart kernel obtained by convolving the orthogonal gradient of the Green kernel associated with the Laplacian operator with a smoothing radial function. The vector ${\bf x}=({\bf x}_i, i=1,\ldots,p)^T$ represents the set of vortex particle locations and the coefficient, γ _i , their strength. The dynamics of these random variables is defined through a stochastic interpretation of the vorticity transport equation Chorin (1973):

$$ d{\bf x}_t=\user2{w}({\bf x}_t)dt + \sigma dB_t, $$

(39)

where B stands for a 2p-dimensional Brownian motion with independent components, and associated with the diffusion coefficient $\sigma=\sqrt{2\nu}$. The evolution of the vortex set, x, between two frame instants k and k + 1 and for a discretization step Δt, is represented by the following Markov transition equation:

$$ p\left({\bf x}^k_j|{\bf x}^k_{j-\Updelta t}\right) \sim {\mathcal N} \left({\bf x}^k_{j-\Updelta t}+\user2{w}\left({\bf x}^k_{j-\Updelta t}\right)\Updelta t,2\nu\Updelta t {\mathbb{I}}_{2p}\right), $$

(40)

where ${\mathbb{I}}_{2p}$ denotes the 2p × 2p identity matrix.

A sample of the trajectories generated between two frames are then weighted according to the likelihood $p({\bf z}_k|{\bf x}_k)$. In this work, this density has been defined in terms of a reconstruction error measurement, ${\bf z}_{k}$, computed from the pair of images (I _k , I _k+1).

The results obtained with this technique for a two-dimensional turbulent flow are discussed in Sect. 5.3 and plotted in Figs. 12 and 13.

4.5.2.2 Global estimation control approach

In this section, we present the second alternative for a dynamical filtering of noisy and incomplete data. This framework ensues from control theories and has been popularized in geophysical sciences where it is known as variational assimilation (Le-Dimet and Talagrand 1986; Lions 1971). Opposite to particle filtering, variational assimilation techniques have the advantage to enable a natural handling of high-dimensional state spaces. Before presenting further the adaptation of such a framework to motion estimation, let us describe the general notions involved.

As previously, the problem we are dealing with consists in recovering a system’s state $\user2{X}(\user2{x},t)$ obeying a dynamical law, given some noisy and possibly incomplete measurements of the state. The measurements, in this context also called observations, are assumed to be available only at discrete points in time. This is formalized, for any location, $\user2{x}$, at time t ∈ [t ₀, t _f ], by the system

$$ \frac{\partial {\user2{X}}}{ {\partial t}}({\user2{x}},t) + {\mathbb{M}} ({\user2{X}}({\user2{x}},t),c(t)) = 0 $$

(41)

$$ \user2{X}(\user2{x},t_0) = \user2{X}_0(\user2{x}) + \varvec{\epsilon}_n(\user2{x}), $$

(42)

where ${\mathbb{M}}$ is a non-linear dynamical operator depending on a control parameter c(t). We assume here that c(t) ∈ C and $\user2{X}(t)\in {\mathcal V}$ are square integrable functions. The term $\user2{X}_0$ is the initial vector at time t ₀, and $\varvec{\epsilon}_n$ is an (unknown) additive control variable of the initial condition. Furthermore, we assume that the measurements of the unknown state, ${\mathcal Y}\in {\mathcal O}$, are available. These observations are measured through the non-linear operator, ${\mathbb{H}}: C\rightarrow {\mathcal O}$. The objective consists then to find an optimal control of low energy that leads to the lowest discrepancy between the measurements and the state variable. This leads to the minimization problem

$$ \begin{aligned} {\mathcal J}(c,\varvec{\epsilon}_n) = &\frac{1}{ {2}}\int\limits_{t_0}^{t_f} \|{\mathcal Y}-{\mathbb{H}}({\user2{X}}(c(t),\varvec{\epsilon}_n,t))||_{R^{-1}}^2{\rm d}t \\ +\quad &\frac{1}{2} \|\varvec{\epsilon}_n ||_{B^{-1}}^2+\frac{1}{ {2}}\int\limits_{t_0}^{t_f}\|c(t)-c_0 ||_{F^{-1}}^2{\rm d}t, \end{aligned} $$

(43)

where c ₀ is some expected value of the parameter. The norms $||. ||_{R^{-1}}, ||.||_{B^{-1}}$ and $||.||_{F^{-1}}$ are induced by the inner products $<R^{-1}\cdot,\cdot>_{\mathcal O},$ $<B^{-1}\cdot,\cdot>_{\mathcal V}$ and $<F^{-1}\cdot,\cdot>_C,$ R, B and F are covariances matrices of the observation space and state space. They are respectively related to the observations, the initial condition of the state variable and to the expected value of the control variable.

Regarding the minimization of the objective function, a direct numerical evaluation of the functional gradient computationally infeasible, because this would require to compute perturbations of the state variables along all the components of the control variables $(\delta c,\delta\varvec{\epsilon}_n)$—i.e. to integrate the dynamical model for all perturbed components of the control variable, which is obviously not possible in practice.

A solution to this problem consists to rely on an adjoint formulation (Le-Dimet and Talagrand 1986; Lions 1971). Within this formalism, the gradient functional is obtained by a forward integration of the dynamical system followed by a backward integration of an adjoint dynamical model. This adjoint model is defined by the adjoint of the discrete scheme associated with the dynamical system.

This technique has been recently applied to the estimation of fluid motion fields (Corpetti et al. 2008; Héas et al. 2007b; Papadakis and Mémin 2008a, 2008b; Papadakis et al. 2007)and to the tracking of closed curves (Papadakis and Mémin 2008b). These works rely either on shallow water dynamical model or on a vorticity–velocity formulation. They associate motion measurements given by external motion estimators (Papadakis and Mémin 2008b) or incorporates directly luminance data (Papadakis et al. 2007; Papadakis and Mémin 2008a). The first case provides a filtering technique that allows improving significantly the observed motion fields. The second technique constitutes a complete autonomous motion estimator that enforces dynamical coherence and a temporal continuous trajectory of the solution. Results obtained with this technique for two-dimensional turbulent flow are shown in Figs. 12 and 13. These approaches, compared to traditional motion estimator, enable to recover accurately a broad range of motion scales.

This technique has been also used recently to recover the parameters of a reduced dynamical system obtained from a POD-Galerkin techniques (D’Adamo et al. 2007). Compared to traditional approaches, this technique allows an improved accuracy and stability of the estimated reduced system. For a flow showing periodic behavior this method allows to denoise experimental velocity fields provided by standard PIV techniques and to reconstruct a continuous trajectory of motion fields from discrete and unstable measurements.

5 Experimental results

In this section, we illustrate various aspects discussed in previous sections by experimental results, obtained for both computer-generated and real datasets. First, in Sect. 5.1, we focus on the effect of using higher-order regularization and robust norms. Next, in Sect. 5.2, we present first results of a variational approach that combines correlation measurements and regularization, as outlined below in Sect. 4.4.2. Finally, in Sect. 5.3, we present results of the currently most advances estimation schemes utilizing temporal context. For further experimental results and their discussion, we refer to the original papers cited in the respective Sects. 4.5 and 4.4.2.

5.1 First- and second-order regularization, robust norms

Throughout this section, we refer the reader to Sects. 2 and 4 for descriptions of the approaches evaluated below.

When the first efforts in correlation technique were proposed for PIV, different approaches based on image analysis were also developed to estimate fluid motion. Among those attempts, Tokumaru and Dimotakis (1995) proposed a semi-local approach (Ritz method see Sect. 3.1.2)—involving a parametric cubic model and insuring a global spatial consistency—appropriate for both scalar and particle images. The integral form (Eq. 7) of the equation of motion (Eq. 6) is employed in this method. Using dynamic programming, Quénot et al. (1998) devised a global approach assuming the conservation of the luminance, with the dense displacement fields estimated being small, rectilinear, uniform, and continuous. The proposed global approach uses the brightness constancy (Eq. 6) as a data term. Dahm et al. (1992) introduced the concept of three-dimensional flow fields measurements based on scalar imaging measurements. The proposed technique based on the direct inversion of the scalar transport equation was later refined in Su and Dahm (1996) with and integral minimization formulation including the scalar transport equation, the continuity equation and a first-order regularization (global approach see Sect. 3.2).

More recently, Ruhnau et al. (2005) evaluated the prototypical variational approach of Horn and Schunck (1981) (see Sect. 3.2) with particle image pairs commonly used in PIV. To estimate long-range motion, they carefully designed a coarse-to-fine implementation. Their experimental evaluation showed that the prototypical approach performs well in noisy real-word applications. Corpetti et al. (2002, 2006) improved this approach by taking into account the features of fluid flows. A data term based on the continuity Eq. 2 was used for estimating the apparent 2D motion of 3D flows, and second-order regularization (see Sect. 4.1) was proposed to enable the estimation of vector fields with pronounced divergent and rotational structures.

Figure 4 presents a comparison of the error for different combinations of data terms (OFC or ICE) and regularization terms (1st order or 2nd order). Corpetti et al. (2006) showed that using the ICE model (2) as a more physically grounded alternative to OFC leads to better results for the case of large out of plane motions. As for the regularization, only the 2nd order div–curl scheme is able to preserve the level of vorticity and divergence. Figure 4 also indicates that a robust norm applied to the data term significantly improves the results (compare approach A2 with approach A3).

Fig. 4

Results from a validation experiment, based on VSJ synthetic images, comparing different combinations of data terms (OFC and ICE) associated with regularization term (1st order or 2nd order), and the influence of using a robust norm. The figure shows the relative L ₁ norm error obtained for eight standard configurations: compared to case 1, cases 2 and 3 yield large and small displacements respectively; cases 4 and 5 have dense and sparse particle concentration respectively; cases 6 and 7 contain constant and large particle size respectively; case 8 exhibits high out of plane velocities. Six algorithms are compared: A1 approach of Quénot et al. (1998); A2 approach of Ruhnau et al. (2005); A3 robust multiresolution-multigrid Horn and Schunck approach of Mémin and Pérez (1998); A4 approach of Corpetti et al. (2006); A5 ICE + 1st order; A6 OFC + 2nd order. The best results are obtained with the ICE data term together with 2nd order div–curl regularization (Corpetti et al. 2006)

5.1.1 Influence of discretization

Using the mimetic finite difference method, Yuan et al. (2007) proposed a novel variational scheme based on a second-order div–curl regularizer that includes the estimation of incompressible flows as a special case. This new scheme has been assessed both for particle and for scalar synthetic image sequences, generated from direct numerical simulations (DNS) of two-dimensional turbulence. Compared to the correlation technique of Lavision (Davis 7.2) and the second-order method of Corpetti et al. (2006), the higher-order approach of Yuan et al. (2007) yields an enlarged dynamic range with accurate measurements at small and large scales. This behaviour is displayed in Fig. 5 showing the better estimated spectrum and the lowest spectrum of the error obtained with the technique of Yuan et al. (2007). This higher accuracy is also observed in Fig. 6 with vorticity maps and vector fields. With scalar image sequences, the differences between the approach of Yuan et al. (2007) and the others is more pronounced, especially at large scales, where as expected the correlation technique completely failed (see Fig. 7).

Fig. 5

Spectrum of the vertical velocity component in a two-dimensional turbulent flow. Top synthetic particle image sequence; Bottom synthetic scalar image sequence. Black line DNS reference; Red symbols correlation approach; Blue symbols Corpetti et al. (2006) approach; Green symbols Yuan et al. (2007) approach. Spectra of the error for the same data are shown in inset

Fig. 6

Vorticity maps and vector fields in a two-dimensional turbulent flow obtained with a synthetic particle image sequence. From top to bottom, correlation approach, Corpetti et al. (2006) approach and Yuan et al. (2007) approach

Fig. 7

Vorticity maps and vector fields in a two-dimensional turbulent flow obtained with a synthetic scalar image sequence. From top to bottom, correlation approach, Corpetti et al. (2006) approach and Yuan et al. (2007) approach

5.1.2 Vector field density

It is interesting to mention that the global variational approaches (see Sect. 3.2) return dense vector fields, i.e. one vector per pixel. From the metrological point of view, this behaviour is expected with scalar images since each pixel exhibits an information of motion; however, it may be surprising for particle-based optical measurements in which the particle image density is roughly of the order of 0.01 particles per pixel. The fact that the global variational techniques provide information of motion beyond the spatial scale associated with the particle density is obtained thanks to the regularization operator involved to tackle the aperture problem. Note that the regularization is conducted from the beginning of the minimization process—on the contrary to the post-processing used with correlation approaches—and complement the information of the data term with spatial or spatiotemporal coherence. In this context, the use of physical models as regularization operators can improve the estimations of the velocity fields down to the smallest scales. In addition, when the regularizer is physically sound, the adjustment of the weighting parameter is inferred with the minimization process (Héas et al. 2009a). The monotonically vanishing error spectra (difference between the estimation and the DNS solution) shown in inset of the Fig. 5 indicate that the dense information is consistent with the reference down to the smallest scales. This behaviour can also be observed in Stanislas et al. (2008) with the results of the third PIV challenge for the global approach of Corpetti et al. (2006). In the following (see Sect. 5.3) it is shown that the use of spatiotemporal regularizer like the Navier–Stokes equations can significantly improve the accuracy on the whole dynamic range.

5.2 Correlation-based variational scheme

The combined correlation-variational scheme proposed by (Heitz et al. 2008) for laser sheet three-dimensional flow visualization, described in Sect. 4.4.2, was evaluated with synthetic images of particles dispersed in a two-dimensional turbulent flow and with real-world turbulent wake flow experiments. Figure 8 shows for particles images, the comparison of results obtained with a multiresolution technique and the collaborative approach. One advantage of the latter method is that, due to the global scheme including regularization, ‘basic’ correlation estimations are sufficient. Furthermore, compared to correlation technique, the combined correlation variational scheme yields dense information as observed in Fig. 9.

Fig. 8

Instantaneous vector field with horizontal velocity color map measured with real images of particles in near the wake of a circular cylinder at Re = 3,900. Top optical-flow approach (Corpetti et al. 2006); Bottom combined correlation-variational approach (Heitz et al. 2008)

Fig. 9

Instantaneous vector field with vorticity colormap measured with real images of particles in the near wake of a circular cylinder at Re = 3,900. Top correlation approach; Bottom combined correlation-variational approach (Heitz et al. 2008)

5.3 Spatiotemporal regularization

Following the route to incorporate explicit physical prior knowledge into variational motion estimation schemes, that was suggested by Ruhnau et al. (2007) in connection with PIV and by Héas et al. (2007a) for satellite imagery, Heitz et al. (2008) adapted and evaluated the latter technique to estimate dynamically consistent large eddy apparent motion of laser sheet 3D turbulent flow visualization (see Sect. 4.5.1 for details of the methods).

Applied on synthetic particle images generated with DNS of two-dimensional turbulent flows, this method enlarges the dynamic range resolved as a function of the time (see in Fig.10 the estimated spectrum). The use of spatiotemporal regularization enhances the accuracy, particularly for noisy image sequences. As observed in Fig. 11, through the map of the deviation from the exact velocity modulus, the technique improves the estimation of the main vortices as a function of the time. As a consequence, this approach is especially well suited for analyzing time-resolved particle image sequences which exhibit noise due to CMOS sensors. Regarding the implementation of this iterative scheme, we point out that the computational costs of the simulation of the dynamic Eq. 34 are negligible in comparison to the variational estimation (Eq. 35).

Fig. 10

Energy spectra showing the enlargement of the dynamic range as a function of the time when using spatiotemporal regularization (Heitz et al. 2008). Spectra of the error for the same data are shown in inset. Measurements obtained with synthetic particle images generated from DNS of two-dimensional turbulent flows

Fig. 11

Results of velocity estimation with spatiotemporal regularization. The analyzed synthetic image sequence is based on a two-dimensional turbulent flow with additive noise simulating the reduction of the power of a virtual laser. From top to bottom: Map of the deviation from the exact velocity modulus for time 1, 2 and 3 (Heitz et al. 2008)

Spatiotemporal consistency of the measurements can be improved with non-local context approaches taking into account the whole image sequence with recursive estimations (see Sect. 4.5.2.).

Cuzol et al. (2007) proposed a non-linear stochastic filter for the tracking of fluid motion. The tracking is based on a low-dimensional representation of the velocity field obtained through a discretization of the vorticity and divergence maps. Beyond the tracking, this method allows to recover a set of consistent velocity fields for a whole sequence and provides an accurate low order representation of the dynamic of fluid flows. The order of the simplified motion estimation is related to the number of vortex particles involved in the estimation.

Papadakis and Mémin (2008b) described a global spatiotemporal variational formulation in order to optimally fuse the information obtained from the data images and the dynamic model. The technique relies on an optimal control approach and consists in a forward integration of the Navier–Stokes equations, followed by a backward integration of an adjoint evolution model. Results obtained with an image sequence of particles dispersed by a turbulent 2D flows are quite impressive. As observed in Figs. 12 and 13, Papadakis and Mémin (2008b) approach outperform other techniques since the whole dynamic range is recovered with this approach. The best results are provided when the image luminance is directly assimilated in the dynamic model, instead of assimilating vector fields previously estimated from image sequences.

Fig. 12

Spectrum of the vertical velocity component measured in particle image sequences generated with DNS of two-dimensional turbulent flow. Black DNS; Red approach of Cuzol et al. (2007); Blue approach of Corpetti et al. (2006); Green, approach of Papadakis and Mémin (2008b). Spectra of the error for the same data are shown in inset

Fig. 13

Vorticity maps and vector fields in a turbulent flow. From top to bottom, Corpetti et al. (2006) approach, Cuzol et al. (2007) approach and Papadakis and Mémin (2008b) approach

Note that the evaluation of the above spatiotemporal regularization techniques have been conducted with image sequences for which the time resolution was ten times the time step of the DNS used to generate the sequence.

6 Conclusion and perspectives

After a brief conclusion, we indicate some promising directions for further research.

6.1 Conclusion

This paper is an attempt to provide an abridged report on variational motion estimation techniques, focusing on techniques that we deem especially relevant for experimental fluid mechanics. After sketching representatives of established basic schemes, we presented modifications that have been developed for the specific case of fluid motion estimation. This latter work indicates the emerging collaboration between two communities, image processing and computer vision, and experimental fluid mechanics.

Yet, in our opinion, this is just the tip of the iceberg regarding the potential for further research. In the following subsections, we indicate few promising research directions. We hope that this paper will stimulate further cooperation along these lines.

6.2 3D-PIV

Recently, Tomographic Particle Image Velocimetry (TomoPIV) (Elsinga et al. 2006) has attracted a lot of interest. Observing projections of particles in a volume of interest with 4–6 cameras, the three-dimensional volume function $I(\user2{x},t),\; \user2{x} \in \Upomega \subset {\mathbb{R}}^{3}$, can be reconstructed with high spatial resolution. A closer look to the currently employed standard algebraic reconstruction techniques shows that there is a potential for improving the trade-off between function reconstruction from a limited amount of noisy data, and increasing the particle density to facilitate subsequent motion estimation (Petra et al. 2009; Petra and Schnörr 2009).

This move to three dimensions plus eventually time will likely enable physics-based models and methods to provide accurate inspection tools for experimental fluid mechanics.

6.3 Turbulence models

Taking seriously the ultimate goal of synergy between experiments and simulation, the question of how to utilize turbulence models in connection with motion estimation naturally appears. To the best of our knowledge, models combining these two worlds in order to improve estimation from real data have not been devised so far.

A promising direction of research concerns ways to incorporate invariants and laws governing the turbulence statistics into a variational estimation scheme. A reasonable approach is to include a regularizing term into the energy functional that enforces quantities derived from the velocity gradient tensor to be smooth. The objective is to preserve the salient enstrophy and dissipation structures that are relevant for characterizing the topology of turbulent regions, like vortex tubes, vortex sheets, and pure straining (Perry and Chong 1987; Chong et al. 1998). Likewise Kolmogorov’s law, describing the statistical structure of turbulence in the inertial range, Héas et al. (2009a) proposed a multiscale estimator based on scaling power laws accounting for the turbulent kinetic energy decay. A spatial regularization properly constraints the solution to behave through scales as a self-similar process via second-order structure function. This enlarges further the dynamic range of the estimates. In contrast to standard approaches, this multiscale regularization presents the valuable advantage of solving the aperture problem while fixing regularizers’ weights at the different scales. Figure 14 shows estimations obtained for real particle images in grid turbulence. In this case, the method is combined with a simple hot-wire measurement providing the real parameters of the power law (Héas et al. 2009b). Results exhibit the ability of this technique to estimate large dynamic ranges and better accuracy than other PIV methods. Note that instead of measuring the parameters with hot-wire anemometry, a promising extension of this approach consists in selecting by Bayesian evidence the most likely scaling law given the image data (Héas et al. 2009c).

Fig. 14

Second-order longitudinal velocity structure functions in the streamwise direction, velocity field and vorticity map estimated for real particle images in grid turbulence with the self-similar regularization method proposed by Héas et al. (2009b). Red HWA measurements; Green proposed method; Blue Horn and Schunck (1981); Purple correlation method; Solid line is ∼ℓ²; Dash line is ∼ℓ^(2/3)