1 Introduction

Understanding the dynamics of moving contact lines for fluids of small viscosity, such as the water–air system on top of hydrophilic and hydrophobic solid surfaces, is important in the analysis of flow and mass transfer in industrial applications. For instance, flow patterns near moving contact lines are the chief concern for the deposition of ultra-thin Langmuir–Blodgett films (Cerro 2003). Flow patterns near a moving contact line can determine a particular mass transfer regime during affinity chromatography (Diaz Martin et al. 2005). Therefore, a basic understanding of the dynamics of moving contact lines will provide a framework to analyze a wide range of phenomena, from coating operations to the performance of packed distillation columns.

There are three basic macroscopic flow patterns in the vicinity of a moving contact line (Huh and Scriven 1971). These flow patterns, shown schematically in Figs. 1 and 2, were qualitatively confirmed experimentally (Savelski et al. 1995) and are further demonstrated here introducing precise measurement of interfacial velocities.

Fig. 1a–c
figure 1

Sketch of streamline patterns near the moving contact line during immersion of a solid surface into a pool of liquid. a A split-injection streamline in the liquid. b A transition pattern. c A split-ejection streamline in the upper fluid

Full size image
Fig. 2a–d
figure 2

Sketch of streamline patterns near a moving contact line during removal of a solid from the liquid pool. a A split-injection streamline in the upper fluid and a rolling motion in the liquid. b A transition pattern. c A split-ejection streamline in the liquid. d A dip-coating flow pattern when a continuous film of liquid is entrained on the solid surface.

Full size image

The patterns shown in Fig. 1 correspond to the immersion of a solid surface into a pool of liquid. In Fig. 1a, the liquid–fluid interface, i.e., the interface between a gas and a liquid or between two liquids, is moving away from the contact line. This flow pattern in the lower fluid is called a split-injection streamline, to signify that the fluid near the contact line is being replenished by fluid coming from the bulk fluid where the split streamline is located. There is a fluid vortex rotating counterclockwise near the solid surface and another vortex running clockwise near the fluid–fluid interface. The drawings show only the upper part of the vortices. In Fig. 1c, the interface is moving towards the contact line. This pattern in the upper fluid is called a split-ejection streamline, to signify that the fluid near the contact line is removed by the flow along the splitting streamline. In the upper fluid, there is a vortex near the solid surface rotating counterclockwise and another vortex near the fluid–fluid interface rotating clockwise. In the lower fluid, there is a single vortex rotating counterclockwise. This motion is called a rolling motion. The intermediate flow pattern shown in Fig. 1b is a transition pattern where both fluids are in rolling motion and the interface between the two fluids is motionless. Notice that, in Fig. 1a, for a split-injection streamline in the lower fluid, the dynamic contact angle between the lower fluid, or liquid, and the solid surface is pictured smaller than 90°; that is, the liquid wets the solid surface. On the other hand, in Fig. 1c, the contact angle for a rolling pattern in the liquid requires a non-wetting fluid, i.e., a contact angle larger than 90°. Transition occurs not necessarily at, but around θDyn≈ 90°.

Flow patterns arising when a solid is removed from a liquid pool are shown in Fig. 2. In Fig. 2a, there is a clockwise rolling pattern in the lower fluid, i.e., the liquid, and a split-injection streamline flow pattern in the upper fluid. The interface is moving away from the contact line and the contact angle in the lower fluid is larger than 90°, i.e., a non-wetting fluid–solid system. Fig. 2c shows a split-ejection streamline pattern in the liquid and a rolling pattern in the upper fluid. The interface moves towards the contact line and the contact angle is smaller than 90°, i.e., a wetting liquid–solid system. Transition, Fig. 2b, occurs about θDyn≈ 90°, and in the transition pattern, both fluids are in a rolling motion and the interface is motionless. Also shown is an additional flow pattern, Fig. 2d, the dip-coating flow pattern. This pattern takes place for totally wetting fluids, i.e., for near-zero contact angles between the liquid and the solid, θDyn≤10°, and is characterized by a film of liquid being entrained on the solid surface. There is no moving contact line in dip-coating flow, but there is a stagnation point, shown here attached to the liquid–fluid interface. The stagnation point can be attached to the free surface, to the solid surface, or it can be inside the liquid film; however, these alternatives to the profile in Fig. 2d will take place only when a surfactant is present at the air–liquid interface. A pattern similar to the dip-coating pattern arises when a solid is immersed into a fluid at high speed. This phenomena has been described elsewhere (Gutoff and Kendrick 1982) and is outside the scope of our experiments.

The hydrodynamic theory of moving contact lines introduced by Huh and Scriven (1971) is based on a Stokes flow formulation leading to the biharmonic equation. Assuming a straight-line configuration of the interface, capillary effects can be neglected. Huh and Scriven’s (1971) hydrodynamic model predicts a rolling pattern in the dense (liquid) phase for almost all dynamic contact angles, i.e., the flow patterns described by Figs. 1c and 2a. The predictions of their model are at variance with our physical observations. The departure of a seemingly sound theory from physical observations configures a hydrodynamic paradox (Birkhoff 1960).

The purpose of this paper is to present a quantitative description of flow patterns and velocity profiles near the moving contact line to fuel the development of more accurate models and to emphasize the fact that small causes can produce large, macroscopic effects.

A computer-aided experimental technique was designed for the precise detection of flow patterns and velocity vectors in the close vicinity of a dynamic contact line. A flat glass slide that moved up and down, outside and inside a liquid pool was the experimental model for the moving contact line. The flow region described by our experiments is approximately 2×2 mm in size and the data is collected as close to 100 μm from the contact line as possible. The flow region marks the outer bounds of the central region of flow (de Gennes et al. 1990) and its outside length scale is the capillary length, \(L_{\text{C}} = \sqrt {\sigma /\rho g.} \) Outside the central region is the outer or external region of flow, where gravity effects are important and flow patterns are influenced by boundary conditions related to the container that holds the liquid. Inside the central region is the proximal region, extending from a few Angstrom to about one micrometer. Our experimental data and conclusions cover only the flow in the central region. However, flow patterns in the central region must be matched to patterns in the proximal and outer regions.

2 Experimental apparatus and procedure

Streamlines and velocity vectors in the vicinity of the dynamic contact line were experimentally determined by means of two-dimensional particle image velocimetry (PIV) technique. A laser beam sheet, approximately 0.2-mm thick, was used to illuminate a nearly two-dimensional section of the flow, perpendicular to the moving solid surface, near the air–water–glass dynamic contact angle. The fluid was sparingly seeded with metallic-coated particles (shape: spherical, density: 2.6 g/cm^3, mean diameter: 12 μm). For the range of velocities obtained during our experiments, the Stokes free-settling velocity of the particles is at least one order of magnitude lower than the fluid velocity. The laser light was scattered by the particles in the fluid phase as the particles passed through the illuminated section and a video camera was used to track and record the motion of particles as a function of time.

2.1 Experimental apparatus

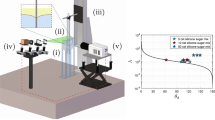
The experimental apparatus consisted of three basic components (see Fig. 3):

  1. 1.

    Laser and optics

  2. 2.

    Video acquisition and recording system

  3. 3.

    Viewing cell, glass slides, and motorized translating system

Fig. 3
figure 3

View of experimental setup showing the laser and optics, the motorized translation mechanism, and the viewing cell with square cross section partly filled with water

Full size image

A sheet of laser beam light was produced using a 20-mW Helium–Neon laser (Uniphase, model 106–1, serial no. 531351) in conjunction with biconvex and cylindrical lenses. A laser beam aligner and micrometer translators were used to precisely position the light sheet within the experimental flow field

A video camera (DAGE-MTI Inc. CCD–72 series solid state camera) with a series of extension rings (Nikon, PK–13, 27.5) and a lens (Nikon, AF MICRO NIKKOR, 60 mm, 1:2.8 D) was focused on the illuminated area (see Fig. 4). The video signal from the video camera was sent simultaneously to two different recording systems, one for analog and the other for digital recording.

Fig. 4
figure 4

Close-up view of flow cell and moving solid surface. The glass slide is in contact with the inside surface of the cell, creating a meniscus and allowing a direct view of the flow field under the interface

Full size image

Experiments were carried out inside a viewing cell with a square cross section (10×10×15 cm) made of 1/8-in-thick glass (see Fig. 4). The side walls of the viewing cell were made of optically flat glass to avoid distortion. Flat glass slides (0.3×2.5×15 cm) were attached to a vertically oriented motor-driven translation stage (Electro-Craft, model no. E552, serial no. 23492) with the capability of moving the slides up and down at pre-set, constant speeds.

2.2 Experimental procedure

During the experiments, a glass slide was moved at constant speed in or out of the rectangular glass cell. The glass slides were either clean or treated to create partially wetting surfaces by immersing the clean and dry slides into diluted solutions of Sigmacote (Sigma-Aldrich, catalog Nr SL-2), which is a special silicone solution in heptane that readily forms a covalent, microscopically thin film on glass. After immersion, the slides were rinsed with deionized water and dried in a stream of dry nitrogen. To avoid the presence of a fluid meniscus on the viewing path, the slide is immersed or removed by moving the glass slide up against the front wall of the rectangular cell (see Fig. 4), creating a meniscus above the fluid surface and giving unobstructed access to the three-phase contact line (Savelski et al. 1995). This effect can be easily confirmed by holding a glass slide, partly submerged in liquid, against the side surface of a beaker. Because of capillarity, the meniscus climbs in the crevice between the slide and the wall and allows us to look at the contact line from “below” the liquid. To avoid three-dimensional edge effects, the sheet of laser beam light is positioned approximately 1 cm away from the glass wall.

3 Video analysis

Video recordings of the experiments were analyzed using a computer program specifically designed to track particles in a two-dimensional space. This program reads any type of AVI video file and returns a text file with the position and velocity vector for each particle in each individual frame.

3.1 Image enhancement

Individual video frames were enhanced to eliminate light reflection from the glass surface. Light reflections were seen as large white spots near the contact line. A mathematical filtering technique was used to separate the particles from the noise caused by the light reflection. An image enhancement technique, convolution, developed by Sun Microsystems (Sun Microsystems 1999) was used to reduce the effect of noise in the images and to sharpen the details of the particles. Based on the actual size of the particle used and the image scale pixel/mm, a kernel of dimension 9×9 pixels was chosen for all analysis of experimental data. Metal particles had an approximate radius of 3 pixels and we added 1 for the particle mask and −1 for the surrounding mask.

3.2 Particle detection

Several publications (Schwarz 1978; Chang et al. 1985a, 1985b; Stellmacher and Obermayer 2000) deal with algorithms specially designed to detect particles in a gray-scale image. Because of programming simplicity, the technique implemented for this work was the one proposed by Chang et al. (1985a, 1985b). A brief description follows. The pixel array is scanned row by row. Only segments of two consecutive rows are in memory at any one time: the previous scanned row and the row undergoing analysis. Each pixel of row 2 is compared to the threshold level. If it is greater than the threshold, the leading edge of a particle image segment is indicated, and the ending edge is subsequently determined (see Fig. 5). The logic criterion for grouping row segments together is based upon the leading and ending edges of particle images. The row previously scanned is used as a reference for the determination of the presence of a new particle on the frame, a particle continued between two rows, or a particle disappearing from the frame. The only purpose of this analytical logic, illustrated in Fig. 5, is to group the particles’ image row segments together; the various parameters of the particle (particle size, mean intensity, and center) have to be determined in the process (Chang et al. 1985a, 1985b).

Fig. 5
figure 5

Classification of image segments by comparing leading and ending edges of adjacent rows

Full size image

3.3 Particle tracking velocimetry technique

There are several particle tracking techniques (PTV) available (Hassan and Canaan 1991; Baek and Lee 1996; Gold et al. 1998; Stellmacher and Obermayer 2000). A two-frame particle tracking algorithm was selected for this work for simplicity (Baek and Lee 1996). The following heuristics were used for matching particle points of two consecutive images (see Fig. 6) separated by a small time interval Δt (Baek and Lee 1996) and are mainly based on the maximum velocity (heuristic 1) and quasi-rigidity conditions (heuristics 2 and 3):

  1. 1.

    Maximum velocity: If a particle is known to have a maximum velocity Um within the flow field, then it can move at most UmΔt between two images with time interval Δt (see Fig. 6a).

  2. 2.

    Small velocity change: Since the seed particles have a finite mass, small velocity changes between exposures are a natural consequence of physical laws (body forces, accelerations, particle settling, shear flow generated lift forces) (see Fig. 6b).

  3. 3.

    Common motion: Spatially coherent objects appear in successive images as regions of points sharing a common motion. That is, a group of particles within a small region show a pattern of similar movement (see Fig. 6c).

  4. 4.

    Consistent match: Two points from one image generally do not match a single point from another image (see Fig. 6d).

Fig. 6a–d
figure 6

Sketch of heuristics used in the detection of particles for the two-frame algorithm

Full size image

3.4 Software implementation

A computer software application was developed to minimize the amount of hand calculations. The software language used was Java, analyzing videos and images using the Java Media Framework and Java Advanced Imaging libraries provided as free software by Sun Microsystems. The software application developed here determines individual frames from a video file and analyzes each frame in search of individual particles. After all the particles in a given frame are located, the application proceeds to match all the particles in consecutive frames.

4 Experimental results

Figure 7 shows an experimental flow pattern determined by the velocity field for an experiment where the solid substrate is treated glass removed from pure water over air. The experimental data points are shown as computer-generated arrows indicating the direction and magnitude of the velocity of particles made visible by a sheet of laser light. This is a digital image generated by placing on it all the experimental data points for one run and can be cleaned by eliminating some of the points. The experimental information resides in computer arrays where the location of the particle and its velocity components are stored.

Fig. 7
figure 7

Computed-generated view of flow field during removal of a solid from the pool of pure water. The lines are the velocity arrows determined using particle image velocimetry. The experiment shown is for ϕ D ≈ 32° and the inclination of the split-ejection streamline is θ≈13°

Full size image

For a given solid–liquid–fluid system and a constant contact angle, experimental data on the liquid–fluid interface velocities show a remarkable constant velocity within a 2-mm distance to the contact line. Interfacial velocities are computed as the modulus of the vector velocities determined using the PIV technique. Figure 8 shows experimental velocities for three different contact angles on a glass–water–air system. Dynamic contact angles were measured in every experiment. Although dynamic contact angles change with solid substrate speed, for the range of speeds of our experiments, dynamic contact angles were constant within experimental error. The glass surfaces were treated to create larger contact angles. Within a distance of about 2 mm to the moving contact line, interface velocities reach a plateau and remain nearly constant up to where it is possible to make a measurement. The data points shown in Fig. 8 are average velocities, computed from several experiments, with error limits within 10%. Outside the 2-mm window, i.e., outside the central region, the velocity at the air–water interface decreases slightly as the particle images moves away from the dynamic contact line.

Fig. 8
figure 8

Experimental liquid–fluid interface velocities as a function of distance to the contact line for three different contact angles

Full size image

The relative interfacial velocity is defined as the ratio of the interface velocity within the 2-mm region to the velocity of the solid substrate:

$$u_{\text{r}} = \frac{{v_{{\text{int}}} }} {{U_{{\text{solid}}} }}$$
(1)

The sign of the velocities is defined by a cylindrical coordinate system centered at the contact line where the origin of the angles is the solid–liquid line. Under this convention, the solid velocity is positive during immersion and negative during removal. In a similar way, if the interface moves towards the contact line, the interface velocity is negative and if it moves away from the contact line, the interface velocity is positive. During immersion, a split-injection streamline pattern (Fig. 1a) results in a positive relative velocity, while a rolling pattern (Fig. 1c) results in a negative relative velocity. During removal, a split-ejection pattern (Fig. 2c) results in a positive relative velocity, while a rolling pattern (Fig. 2a) results in a negative relative velocity. In short, rolling patterns in the liquid phase always result in negative relative velocities and split-streamline patterns in the liquid phase always result in positive relative velocities.

Velocities at the fluid–fluid interface are directly proportional to the actual solid substrate velocity in such a way that relative interfacial velocities are independent of the solid substrate velocity. Figure 9 shows relative velocities for removal at a dynamic contact angle, ϕ D =14.9°. Because dynamic contact angles change very little with solid substrate speed, for the range of speeds used in our experiments, the data shown in Fig. 9 is for the same liquid–air system at different solid substrate velocities. Despite a five-fold change in solid velocity, the relative velocity of the interface and the dynamic contact angle are constant within experimental error.

Fig. 9
figure 9

Experimental liquid–fluid interface relative velocities as a function of the velocity of the solid substrate for a single dynamic contact angle

Full size image

Experimental values of dimensionless interfacial velocities are shown in Fig. 10 as a function of the dynamic contact angle. Experimental velocities were measured for clean and treated glass slides in a water–air system. Some of the experiments are for immersion and some are for the removal of slides from the water bath.

Fig. 10
figure 10

Experimental liquid–fluid interface relative velocities as a function of the dynamic contact angles. Dynamic contact angles are for clean and treated glass slides. The continuous line represents relative velocities computed using the hydrodynamic theory (Huh and Scriven 1971)

Full size image

Regardless of experimental uncertainty in the measured values of velocities and contact angles, Fig. 10 shows a clear functional dependency of dimensionless velocities with dynamic contact angles. Dynamic contact angles were measured as the average tangent to the interface streamline determined from the angle of the velocity vector. By definition, velocities are tangential to the streamlines and the contact angle determined by the interface velocities are just as constant within a 1–2-mm region as the velocities, as shown in Fig. 8.

The solid curve in Fig. 10 shows the theoretical values of the dimensionless interface velocities predicted by Huh and Scriven (1971) for a water–air system at varying dynamic contact angles. For almost the entire range of dynamic contact angles, interfacial velocities predicted by the hydrodynamic theory conform almost exclusively to a rolling pattern in the liquid phase, i.e., they are almost always negative. This prediction was so prevalent in the contact line literature that some authors (e.g., Shikmurzaev 1993) used it as a starting point for their theoretical derivations. The marked discrepancy between apparently sound theoretical derivations and experiments configure a hydrodynamic paradox in the sense of Birkhoff (1960).

4.1 Experimental streamline patterns

Figure 7 showed an experimental flow pattern for a dynamic contact angle of 32°. The velocity of the solid substrate was Usolid=1 mm/s and the capillary number for this flow was NCa=1.4×10−5. The solid line superimposed on the experimental data marks the angle formed by the split-ejection streamline and the solid surface, θ=13°. The actual position of the split streamlines, due to gravity, moves towards the outside of the flow field away from the dynamic contact line, but converges to the fixed angle value in the vicinity of the contact line. The relative velocity of the interface, computed in the region within 1 mm of the contact line, was ur=0.44.

5 Conclusions

There are three important observations to extract from these experiments. First, experimental interface velocities measured using a two-dimensional particle image velocimetry (PIV) technique show a remarkable constant interfacial velocity within a 2-mm distance to the contact line (Fig. 8). The velocity at the fluid–fluid interface changes slightly as one moves away from the vicinity of the contact line, but within a 2-mm distance, the relative velocity of the interface is constant within experimental error. Second, the relative velocity of the interface, defined using Eq. 1, does not depend on the actual velocity of the solid substrate (Fig. 9). Third, the relative interface velocities are clearly a function of the dynamic contact angles (Fig. 10).

The fact that the interface velocity is constant within the central region of flow is important from a theoretical viewpoint. The hydrodynamic theory of the moving contact line (Huh and Scriven 1971; Cox 1986) is based on a series expansion of the velocity field using streamline functions that are solutions to the biharmonic equation:

$$\psi \left( {r,\theta } \right) = \sum\limits_{\lambda \to - \infty }^{\lambda \to \infty } {r^{\lambda + 1} } f_\lambda \left( r \right);\quad u_{\text{r}} = - \frac{1} {r}\frac{{\partial \psi }} {{\partial \theta }};\quad u_\theta = \frac{{\partial \psi }} {{\partial r}}$$
(2)

For a constant velocity at the interface, the only possible streamline of Eq. 2 is λ=0, indicating that this is the dominant eigenvalue in the central region. This eigenvalue also complies with a constant velocity on the solid–liquid and solid–fluid interfaces and was the basis of the hydrodynamic solution developed by Huh and Scriven (1971). Since the dimensionless velocities in Eq. 2 are defined using the velocity of the solid substrate and are independent of the actual substrate velocity for a five-fold change in magnitude, it validates the formulation of the moving contact line problem using the biharmonic equation with no inertial terms considered.

Finally, the dependence of the relative velocity with the dynamic contact angle (Fig. 10) points to the close relationship between the forces that shape the contact angle with the forces that shape the flow patterns near the contact line, and are the key to explaining the failure of the hydrodynamic theory to reproduce experimental data (Fig. 10).