A Study of Flow Patterns Near Moving Contact Lines Over Hydrophobic Surfaces

Abstract

Understanding the flow patterns emerging near the contact line is a primary concern of moving contact line dynamics. A contact line occurs at the intersection of a solid surface with an interface between two immiscible fluids. The moving contact line dynamics can be observed in several flow phenomena, including inkjet printing, spreading of drops across a surface, and tertiary oil recovery, among others. Displacement of the contact line over the solid surface generates flow patterns in both the fluid phases. Based on flow kinematics and boundary conditions (Huh and Scriven, JCIS, 1971; Cox, JFM, 1986), two distinct flow patterns, a rolling motion and a split-streamline motion, occur in one of the fluid phases and the problem is primarily governed by viscosity ratio, $\lambda$, and dynamic contact angle, ${\theta }_{d}$. Most of the existing experimental studies are for obtuse contact angles, ${\theta }_{d}$ > ${90}^{\circ }$ with very low viscosity ratio, $\lambda \ll 1$ and at very low $Re$ (Chen et al., JFM, 1997). The present study aims to obtain flow patterns at low to moderate values of $Re$ and with a relatively higher viscosity ratio using a combination of experiments and simulations. We also present a comparison of our results to existing analytical models.

1 Introduction

A contact line forms at the junction between a solid surface and an interface of two immiscible fluids. Moving contact lines and associated flow patterns in fluid phases are fundamental to several flow configurations, including droplets evaporating and spreading on solid surfaces, inkjet printing, sliding drops on lotus leaves, etc. The motion of the contact line over a solid surface generates different flow patterns in both fluid phases, as shown in Fig. 1. For example, by considering a downward motion of the solid plate into a liquid pool of two immiscible fluids, one can observe three kinematically consistent flow patterns near the moving contact line: (i) A rolling motion in phase B and a split-streamline motion in phase A, where the interface moves toward the contact line, (ii) A split-streamline motion in phase B and a rolling motion in phase A, where the interface moves away from the contact line, and (iii) the rolling motion in both phases A and B with no interface movement.

Fig. 1

The possible flow patterns near the moving contact line: (i) A rolling motion in phase B and a split-streamline motion in phase A, (ii) A split-streamline motion in phase B and a rolling motion in phase A, (iii) The rolling motion in both phases A and B

Moving contact lines have been studied analytically by several researchers. Among them, Huh $\&$ Scriven [1] were the first to mathematically analyze the moving contact line dynamics in the viscous limit considering a flat interface approximation. According to their theory, dynamic contact angle (${\theta }_{d}$) and viscosity ratio ($\lambda$) are key parameters that characterize the flow patterns. A contact angle is defined as an angle between the interface and the solid surface and measured always in phase B. Viscosity ratio $\lambda$ is a ratio of the viscosity of phase A to that of phase B $\left(\lambda = \frac{{\mu }_{A}}{{\mu }_{B}}\right)$. A critical viscosity ratio curve (Fig. 2) separates a rolling from a split-stream line flows on ${\theta }_{d}$ and $\lambda$ plane, with the rolling motion occurring primarily in a more viscous phase. The theory argues that the local solution with a no-slip boundary condition becomes singular as one approaches the contact line.

Fig. 2

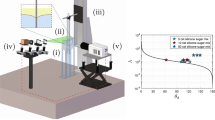
Operating parameter space for experiments and simulations shown in the viscosity ratio and dynamic contact angle plane. Orange-filled circles represent our experiments with water, while unfilled black circles represent simulation, purple-filled circles represent the experiments from Savelski et al. with 50 cSt silicone oil, and the black-filled circle represents the experiment from Chen et al. with 60000 cSt PDMS.

Only a few experimental studies deal with moving contact lines despite their fundamental importance [3,4,5]. Dussan et al. [5] performed experiments with a high viscous drop sliding on an inclined plate. With the help of dye visualizations, they observed a rolling motion at the advancing front of the drop. Using Particle Image Velocimetry (PIV), Chen et al. [3] quantitatively showed a rolling motion in the liquid phase when a solid surface was immersed in a high viscous liquid (PDMS with a viscosity of 60,000 cSt). However, the above experimental studies were at $\lambda \ll 1$ and obtuse dynamic contact angle, where both theory and experiments predict the rolling motion.

In the literature, some studies have also examined interface shape, which is considered an essential characteristic of moving contact line dynamics. A static contact angle and capillary length (${l}_{c}$) determine the static shape of an interface. However, the relative velocity of the substrate affects the contact angle and thereby, the shape of the interface. In the viscous limit, numerous contact angle models [2, 6,7,8,9] such as the Cox-Voinov model, have been reported, which describe a correlation between a macroscopic contact angle and the substrate speed. The Cox-Voinov model connects the microscopic contact angle at the contact line to an apparent contact angle that we observe in experiments.

Specifically for tube shape, Dussan et al. [10] obtained an expression for dynamic interface shape based on two terms, the first from the Cox viscous contact angle model, and the second was static interface shape. Dussan et al. interface shape model agrees with the experimentally determined interface shapes [11, 12]. Nevertheless, the above experiments were conducted at very low $Re$, and for $\lambda \ll 1$.

It is important to note that most of the studies presented above are based on obtuse contact angles, ${\theta }_{d}$ > ${90}^{\circ }$, low viscosity ratios, $\lambda \ll 1$, and low $Re$ [3]. The flow patterns at relatively high viscosity ratios and low to moderate values of $Re$ have not been studied. Therefore, in this study, we use numerical simulations and quantitative experiments to determine the flow patterns and interface shapes at relatively high viscosity ratios. The paper is organized as follows: In Sect. 2, we discuss the experimental, theoretical, and numerical methodologies. We compare the flow fields and other quantitative features in Sect. 3. We summarize our observations and the outcomes of the comparative study in Sect. 4.

2 Methodology

• A. Experimental setup

The experiments have been conducted in a rectangular tank ($100 mm\times 100mm\times 27mm$) made of transparent acrylic to facilitate optical visualization. The illustration of the experimental setup is shown in Fig. 3. The tank is filled with distilled water up to a depth of 80 mm. Prior to the experiment, a clean and surface-treated glass substrate is partially immersed in the liquid bath. A motorized traverse with a stepper motor is used to control the vertical immersion speed of the glass substrate. A DM542 digital micro stepper motor driver is connected to a computer through a data acquisition system from National Instruments. In order to maintain the water level in the tank during immersion, a programmable syringe pump (Model: NE-1010, New Era Pump Systems Inc.) is used to withdraw an equivalent volume from the bottom of the tank. As the liquid partially wets the glass slide, the glass is treated with a hydrophobic coating to control the contact angle over the glass slide. After the coating, the static contact angle over the slides is measured using a contact angle meter (Model: DSA25S, Kruss drop shape analyzer). Typically, the hydrophobic coating results in a high contact angle ($\approx$ ${90}^{\circ }$) over the solid surface. Before every experimental run, the glass slides are cleaned properly in order to avoid contamination. The velocity field near the contact line in the mid-plane of the tank is measured using a two-dimensional PIV. The following sections provide details of the PIV measurement technique and cleaning protocol.

Fig. 3

A schematic illustration of the experimental setup and 2D PIV system. a A linear traverse. b A rectangular tank filled with liquid, c A glass plate, d A combination of laser and sheet optics, e An imaging system (a high-speed camera with a macro lens)

• (1) PIV Measurements

The PIV system consists of a high-speed camera with a macro lens (Model: FASTCAM Nova S9, 1024 pixels $\times$ 1024 pixels), a diode laser (wavelength 532 nm, and power 2W) for illumination, a digital delay generator, and sheet optics. With the combination of biconcave and cylindrical lenses, the sheet optics generate a thin sheet with a thickness of approximately 0.5 mm. The digital delay generator controls the laser pulse width and its synchronization with the high-speed camera. To trace the flow very near the contact line, the distilled water is mixed with polystyrene beads of average diameter 2 $\mu m$. Particle images are acquired at a frame rate ranging from 50 to 1000 frames per second, depending on the speed of the plate. The field of view of the high-speed camera with the macro lens is about 4. 24 mm $\times$ 4.24 mm, which corresponds to a spatial resolution of $\approx$ 4 $\mu$ m/pixel. The images are preprocessed before the PIV analysis, including average background subtraction, image equalization, and masking. The particle images are analyzed using a multi-grid, window deforming PIV algorithm. In addition, since the flow is steady, an ensemble PIV correlation is employed to improve the signal-to-noise ratio in a small interrogation window (16 $\times$ 16 pixels).

• (B) Cleaning procedure

Across all experiments, the same cleaning protocol is used in order to avoid discrepancies. Firstly, the tank and substrates are thoroughly cleaned with distilled water to avoid any dirt buildup. The substrates are dried using a dryer to avoid any kind of water films. To change the contact angle, the plates are treated with hydrophobic spray coating and later cleaned thoroughly with distilled water. Upon completion of the treatment, plates are dried again using a dryer and waited long enough for the plate temperature to reach room temperature.

• 2 Analytical expression for interface shape

In this section, we present analytical expressions for interface shape in a cylindrical coordinate system with the contact point as origin. Here, $r$ is a radial coordinate and $\theta$ is an angle measured from the solid surface. In the viscous limit, the macroscopic dynamic contact angle (${\theta }_{mo}$) and the microscopic dynamic contact angle (${\theta }_{w}$) are related according to the Cox model [2] as

$${\theta }_{mo} = {g}^{-1} \left(g\left({\theta }_{w}\right)+Ca\mathrm{ log}\left(\frac{r}{{l}_{\mathrm{c}}}\right)\right)$$

(1)

where ${l}_{c}$ is the capillary length and $Ca$ is the capillary number (Refer to Nomenclature for definitions). The function g($\theta$) is given as

$$g\left(\theta ,\lambda \right)=\left(\frac{2 sin\theta \left({\lambda }^{2} \left({\theta }^{2}-si{n}^{2}\theta \right)+2 \lambda \left(\theta \left(\pi -\theta \right)+si{n}^{2}\theta \right)+\left({\left(\pi -\theta \right)}^{2}-si{n}^{2}\theta \right)\right)}{\delta }\right)$$

$\delta =\lambda \left({\theta }^{2}-{\mathrm{sin}}^{2} \theta \right)\left(\left(\pi -\theta \right)+\mathrm{sin}\theta \mathrm{cos}\theta \right)+ \left({\left(\pi -\theta \right)}^{2}-{\mathrm{sin}}^{2} \theta \right)\left(\theta -\mathrm{sin\theta cos\theta }\right)$

Based on the above model, Dussan et al. [10] proposed an expression for the shape of an interface. For tube geometry, it is given by.

$$\theta_{mo} = g^{ - 1} \left( {g\left( {\theta_{w} } \right) + Ca{\text{log}}\left( {\frac{r}{{l_{c} }}} \right)} \right) + f_{o} \left( {\frac{r}{{l_{c} }} ;\theta_{w} ;\frac{{R_{T} }}{{l_{c} }},\theta } \right) - \theta_{w}$$

(2)

where ${R}_{T}$ is the outer tube radius. In the above expression, by replacing the static interface expression for a tube with the static interface shape for a flat plate, Shimizu et al. [13], interface shape for a plate is given by.

$$x = {l}_{c}\left(2\mathrm{cos}\frac{{\theta }_{w}}{2} + \mathrm{log}\left|\mathrm{tan}\frac{{\theta }_{w}}{4}\right| - 2\mathrm{cos}\frac{\theta }{2} - \mathrm{log}\left|\mathrm{tan}\frac{\theta }{4}\right|\right)$$

$$y = -2{l}_{c}\mathrm{sin}\frac{\theta }{2}$$

$$f = f_{o} \left( {x,y} \right)$$

(3)

In Eq. 2, the function ${f}_{o}$ is replaced by $f$ for a flat plate, which we refer to as the modified Cox model in this paper.

• 3 Numerical method

The numerical simulations have been performed using COMSOL Multiphysics software®. We considered phase A a passive phase, and flow is solved only in phase B. In a multi-phase simulation, along with the flow parameters, the interface shape also needs to be solved as a part of the solution at each time step. This study uses a moving mesh approach to bind a fine mesh along the interface where surface tension-based boundary conditions are applied. The Navier–Stokes, given by Eqs. 4, 5, are in turn formulated on a moving coordinate system where the movement from the moving mesh equations is solved simultaneously. The passive gas phase only affects the interface curvature and enters the study through the equation, surface tension, and pressure effects.

$$\nabla \cdot \overrightarrow{\mathrm{u}} = 0$$

(4)

$$\rho \frac{{\partial \vec{u}}}{\partial t} + \rho \left( {\vec{u} \cdot \nabla } \right)\vec{u} = \nabla \left( { - pI + \tau } \right) + F_{S.T.}^{\dag } + \hat{g}$$

(5)

The surface tension force $F_{S.T.}^{\dag }$¹ is incorporated by the boundary condition, mentioned in Eq. 6. The last term (surface gradient term) in Eq. 6 disappears as no surfactants or other sources exist to produce any surface tension gradient over the interface in the present study.

$$\widehat{\mathrm{n}}\cdot (-\mathrm{pI}+\uptau ) = -{\mathrm{p}}_{\mathrm{ext}}\widehat{\mathrm{n}} +\upsigma ({\nabla }_{\mathrm{t}}\cdot \widehat{\mathrm{n}} ) -{\nabla }_{\mathrm{t}}\upsigma$$

(6)

$${\overrightarrow{u}}_{mesh}\cdot \widehat{n} = {U}_{Free surface}\cdot \widehat{n}$$

(7)

The equations are solved in the bulk of the domain that constantly undergoes shape change due to the free surface nature of the top wall. The mesh on the interface is constrained to move normal along the interface (Eq. 7).

3 Results

In this section, we present results for air/water/glass systems with a low viscosity ratio ($\lambda =0.02$), obtuse contact angles, and moderate $Re=3.03$. In both experiments and simulations, the speed of the solid surface is maintained at 1 mm/sec. Firstly, we compare theory and experiment, followed by comparisons between simulation and experiment.

• A. A comparison between experiments and theory

Figure 4 shows a streakline image with air/water/glass system at $Re= 3.03$ and $Ca=1.24\times {10}^{-5}$. After the flow reaches a steady state, the maximum intensity of 500 particle images over 2 s is averaged to obtain the streakline image. The solid red line in the Fig. 4 represents the interface between air and water phases.

Fig. 4

A streakline image showing the flow pattern near a moving contact line with air/water/glass system at $Re= 3.03$ and $Ca = 1.24\times {10}^{-5}$. The gray region represents the glass plate that moves down into the liquid. The solid red line represents the interface between the air and water phases. The yellow represents the direction of the flow in water phase

The corresponding vector map obtained from the PIV analysis is shown in Fig. 5. Here, the flow fields are presented in a $x-y$ coordinate system, where the contact point is the origin. From Figs. 4 and 5, it is evident that the flow pattern generated due to the downward motion of the solid substrate produces a rolling motion. In the viscous limit, the theoretical analysis of Huh $\&$ Scriven also predicts the rolling motion for viscosity ratio $\lambda <1$ in the wide range of contact angles. Even though the experiments are performed at moderate $Re= 3.03$, the theory qualitatively agrees with the experiments.

Fig. 5

A velocity vector plot showing the flow pattern at a moving contact line with air/water/glass system at $Re= 3.03$ and $Ca = 1.24\times {10}^{-5}$. Here, the flow fields are presented in the (x, y) coordinate system, where the contact point is taken as the origin. The gray region represents the glass plate. The solid red curve represents the interface shape between air and water phases

A comparison of static interface shape for a flat plate (Eq. 3) to experimental interface shape is given in Fig. 6. To obtain the experimental interface shape, first, the particles from the PIV images are removed by the median filter. The filtered images are averaged and contrast adjusted to enhance the interfaces. Finally, by performing canny edge detection, the location of the interface is determined from the enhanced image. In this case, the static interface comparison is justified since the static interface shape perfectly matches the modified viscous Cox model (see Fig. 7). From Fig. 6, it can be seen that the static interface shape is within ${1}^{\circ }$ deviation from the experimental measurements.

Fig. 6

A comparison of static interface shape for a flat plate to the experimental interface shape for air–water at $Re= 3.03$ and $Ca = 1.24\times {10}^{-5}$

Fig. 7

A comparison of static interface shape to the modified cox interface shape for air–water at $Ca = 1.24\times {10}^{-5}$

• 2 A comparison between experiments and simulations

To the best of our knowledge, this is the first quantitative comparison of experiments to simulations for moving contact line dynamics. Figure 8 shows a velocity vector plot obtained from the simulation at the same parameters as experiments. In line with experiments and theory, the simulation also predicts the rolling motion at $Re=3.03$. A comparison of interface shape from simulation to interface shape from experiments for the air–water system is presented in Fig. 9. As is evident, the simulated interface shape is in good agreement with the experimental interface shape.

Fig. 8

Flow fields in simulation: a rolling motion in air–water at $Re= 3.03$ and $Ca = 1.24\times {10}^{-5}$. Red solid line indicates an interface between air and water phases

Fig. 9

A comparison of interface shape from simulation to the interface shape from experiments with air–water at $Re= 3.03$ and $Ca = 1.24\times {10}^{-5}$

4 Conclusions

In this study, we examine the flow patterns near a moving contact line at relatively high viscosity ratios and moderate values of $Re$, which have never been explored. Both experiments and simulations have been conducted to determine the flow fields near the moving contact line. The results from the experiments are compared to analytical models and numerical simulations. In line with the experiments, both the viscous analysis of Huh $\&$ Scriven and the numerical simulations predict a rolling motion for a low viscosity ratio $\lambda <1$ at obtuse contact angles. It appears that the theory agrees qualitatively with the experiments and the simulation even at moderate $Re=3.03$. In addition, we observe that the interface shapes obtained from the experiment, modified cox model, and numerical simulation are in good agreement. This study provides evidence that the viscous theories can predict flow patterns and quantitative features at high contact angles and even at moderate $Re$.