1 Introduction

Standard textbooks on compressible fluid dynamics explain that a shock wave is formed by an accumulation of overtaking compression waves. The physical mechanism is as follows. When gas is compressed, its density, pressure, and temperature generally increase isentropically, increasing its sound speed and thus the propagation speed of the compression wave. As a result, the speed of compression waves, which propagate into a gas already compressed by precursory waves, exceed that of the precursory waves, and so the compression waves generated later tend to overtake the precursory ones. In a shock tube, this overtaking process occurs continuously since the accelerating contact surface generates compression waves continuously, and the pressure profile at the wavefront steepens to form a shock wave. In other words, it takes some distance to form a shock wave. Actually, in a shock tube, the driven section length must be over some fifty times the tube diameter to obtain a well-developed shock wave. The pressure profiles of underdeveloped shock waves have been measured, but, to the authors’ knowledge, no attempt has been made to visualize the process over which a compression wave grows into a shock wave. In the present paper, we attempt to visualize the shock wave formation process. For this purpose, we devised and applied a method of multiple steps.

Fig. 1 a
figure 1

A plane shock wave propagating over a step-like wedge; b velocity vector diagram

Full size image

An early example of this method lies in a series of experiments carried out by the authors (Adachi et al. 1992). In those experiments, we investigated the shock reflection over multi-guttered wedges to simulate the reflection phenomena over porous media. When the shock wave is incident obliquely on the multi-guttered wedge, a series of compression and rarefaction waves appear, and it is very helpful to interpret the phenomenon physically from the viewpoint of waves. However, with the multi-guttered wedge, the visualized waves were generally complicated because unnecessary rarefaction waves were generated. Considering this drawback, we replaced the multi-guttered wedge by a step-like wedge, which dramatically reduces major rarefaction waves (although it does not eliminate them completely). This method was first applied by Suzuki et al. (1997), in a test to visually clarify the reflected-wave formation process over both concave and convex circular cylindrical wedges. We successfully visualized the formation mechanism of the peculiar reflected wave over a concave wedge as the accumulation of compression waves generated from each step. Later, the same method was applied to the so-called von Neumann reflection of weak shock waves (Kobayashi et al. 1997, 2000a), in which the compressive disturbances generated from a step-like wedge tend to accumulate near the first triple point defined by the intersection of the first disturbance and the incident shock wave front. This result led to an important inference that the flow field around the first triple point might vary as the incident shock proceeds, and that the self-similarity law usually postulated in oblique shock reflection phenomena does not hold. This has been further extended to the ordinary Mach reflection of weak shock waves, and it turns out that non-self-similarity is essential for understanding the so-called von Neumann paradox (Kobayashi et al. 1999).

2 Glancing incidence theory

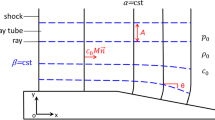
When a plane shock wave propagates over a wedge with a minute (infinitesimal) inclination angle, a weak disturbance issues from the apex of the wedge. This disturbance is so weak that it can be considered to be acoustic. The disturbance propagates at a sound speed relative to the flow behind the incident shock wave (see Fig. 1a). Let the incident shock Mach number be M i and the flow velocity behind the shock wave be u 1, then

$$\frac{{u_{1} }}{{a_{0} }} = \frac{2}{{\kappa + 1}}{\left( {M_{{\text{i}}} - \frac{1}{{M_{{\text{i}}} }}} \right)},$$

where a 0 denotes the sound speed ahead of the incident shock, and κ the specific heat ratio of the medium. When the shock is propagating at speed Us, the incident shock Mach number M i is defined by Us/a 0. The ratio of the sound speed behind the shock to that ahead of the shock is then given by

$$\frac{{a_{1} }}{{a_{0} }} = {\left( {\kappa + 1} \right)}^{{ - 1}} M^{{{\text{ - 1}}}}_{{\text{i}}} {\sqrt {{\left[ {2\kappa M^{2}_{{\text{i}}} - {\left( {\kappa - 1} \right)}} \right]}{\left[ {{\left( {\kappa - 1} \right)}M^{2}_{{\text{i}}} + 2} \right]}} }.$$

From the simple geometrical relation shown in Fig. 1b, we have the well-known formula for glancing incidence angle:

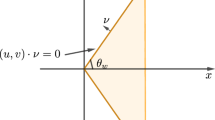
$$\begin{array}{*{20}l} {{\tan \chi _{{\text{g}}} } \hfill} & {{ = \frac{{{\sqrt {a^{2}_{1} - {\left( {U_{{\text{s}}} - u_{1} } \right)}^{2} } }}}{{U_{{\text{s}}} }}} \hfill} \\ {{} \hfill} & {{ = M^{{{\text{ - 2}}}}_{{\text{i}}} {\sqrt {\frac{{{\left[ {{\left( {\kappa - 1} \right)}M^{{\text{2}}}_{{\text{i}}} + 2} \right]}{\left( {M^{{\text{2}}}_{{\text{i}}} - 1} \right)}}}{{{\left( {\kappa + 1} \right)}}}} }{\text{ }}{\text{.}}} \hfill} \\ \end{array} $$

If the wall is not receding but facing the shock front, as shown in Fig. 2a, a head-on collision occurs on the wall, and the disturbance that propagates upstream is stronger than that which propagates downstream. The disturbance strength therefore decreases spatially from the reflected shock wave to the approximate acoustic wave at the triple point.

Fig. 2 a
figure 2

Step-like wedge; b rough-surface wedge

Full size image

3 Triple-point trajectory angle

Oblique reflection occurs when a plane shock wave propagates over a wedge whose slope is θ w with respect to the shock propagation direction. The reflection configuration is roughly either regular or Mach reflection depending on the combination of incident shock Mach number M i and reflecting wedge angle θ w, when the thermodynamic properties of the medium, such as the specific heat ratio κ, are fixed. Although it was found recently that this long-believed statement turns out to be false when the reflecting wedge angle is only slightly below the transition wedge angle θ tr (Henderson et al. 1997, 2001; Kobayashi et al. 2000b), we do not go into details here.

The Mach reflection is composed of three shock waves: the incident shock, the reflected shock, and the Mach stem, and one contact discontinuity called the slipstream. These three shock waves intersect at a point called the triple point, and the slipstream issues from there. The triple point moves along a straight line through the wedge tip (except for the special cases mentioned above). For convenience of comparison with the glancing incidence angle χ g, we define the triple-point trajectory angle χ s as the slope of the straight line connecting the wedge tip and the triple point (conventionally, it is defined by χ s–θ w, the angle made by the triple point trajectory and the wedge surface, in shock-wave literature). Table 1 compares χ g and χ s. The experimental data for χ s are taken from the authors’ own experiment and some of them, but not χ s itself, have already been cited in Kobayashi et al. (1999). The difference between the values is 2° to 3° for M i=1.20 to 1.40, and this is discernible by experiment.

Table 1 Comparison of triple-point trajectory angle and glancing incidence angle
Full size table

When the disturbance at the triple point is intensified, the disturbance propagates faster than the sound speed, which in turn increases in the triple point trajectory angle χ. In the present study, we focus on this angle and use it to estimate the wave development from sound (χ=χ g) to a finite-compression wave, then to shock wave (χ=χ s).

4 Experimental

4.1 Method

The shock tube used in the present study is composed of a driver section (79 mm in diameter and 1200 mm long) and a driven section (3900 mm long with a rectangular cross-section of 65 mm × 30 mm). At the end of the driven section is a test section with a 62 mm × 94 mm optical viewing window on each side. Detailed descriptions of the shock tube and experimental setup are given in our previous papers (for example, Suzuki et al. 1997).

A shadowgraph method was employed to visualize the wave configuration. The light source was a xenon flash lamp with a 180 ns pulse width (nanopulse light NPL-5 and its power supply NP-1A, Sugawara Laboratories, Inc.). The flash lamp was triggered by the output of a pressure gauge (601A, Kistler) nearer to the test section via a digital delay circuit (digital retarder RE-306, Sugawara Laboratories, Inc.). The wave configuration at any desired instant could be photographed by regulating the delay time.

The working gas was air, and the driven section was set at room temperature and atmospheric pressure for each experiment run. The models were step-like wedges with an equivalent slope of 20° and a step width w=2.5 mm and 1.0 mm (Fig. 2a). As a limiting case of step-like wedge when the step width w→0, a rough-surface wedge was used for comparison (Fig. 2b). A piece of #60 sandpaper was pasted on the wedge surface to give surface roughness. The incident shock Mach number M i was 1.20, 1.30 and 1.40. The errors involved in M i were ±0.005.

4.2 Measurement

Figure 3 defines the coordinate system. The tip of the first step is taken as the origin O, and the x-axis is in the direction of the incident shock wave propagation. The y-axis is taken perpendicular to the x-axis.

Fig. 3
figure 3

Definition of coordinate system

Full size image

For the step-like wedge, a compression wave issues at each step, and each compression wave intersects with the incident shock wave. In this case, we regard only the “first” triple point defined by the intersection of the first compression wave and the incident shock. As shown later, the slope of the straight line connecting the wedge tip O and the first triple point T varies as the incident shock proceeds. As a result, angle χ,

$$\chi = \tan ^{{ - 1}} \frac{y}{x},$$

which is defined as the angle made by this straight line and the x-axis, does not represent the physically exact (local) trajectory angle defined as the slope of the tangent to the trajectory. However, we can only measure one set of triple point coordinates for each experiment run, and the results show some scatter due to the error primarily related to the incident shock Mach number. Consequently, the evaluation of the real triple point trajectory angle based on the measured coordinates will necessarily involve some error that cannot be neglected. This error is larger than that for the overall value χ estimated by the straight line OT. Therefore, we evaluated the trajectory angle by the overall value χ rather than the slope of the local tangent.

In reality, the visualized waves have some finite thickness, and so the position of the first triple point involves some ambiguity. In the present measurement, we selected the intersection of the high-pressure side of the incident shock and the (slightly) high-pressure side of the first compression wave as the position of the first triple point. This means χ is generally underestimated. However, when the visualized incident shock wave is too thick, χ will be overestimated. This will be mentioned later.

5 Results and discussion

5.1 Shock reflection over a step-like wedge

Figure 4 shows the shock reflection over a step-like wedge for M i=1.40 and w=2.5 mm. A cylindrical compression wave issues from each step. Close observation of the reflected wave reveals that several compression waves actually accumulate near the triple point. The slipstream from the first triple point is faintly visualized. This means that the strength of the reflected wave is intensified by accumulation, and density and temperature gaps are formed between the two regions bounded by the slipstream. The accumulated reflected wave is therefore already a weak shock wave. Vortices, whose dimensions are the step height s, are generated from the step corners. Energy dissipation due to the vortex generation will diminish as s decreases.

Fig. 4
figure 4

Visualized wave structure over the step-like wedge (M i=1.40, θ w=20°, w=2.5 mm, x=53.1 mm)

Full size image

Figure 5 presents the triple point trajectory for two kinds of step-like wedges, made dimensionless by their step width w. These data show that the first triple point moves approximately along each corresponding straight line through the leading edge. The effect of step width on the energy dissipation due to the vortex generation is not distinct.

Fig. 5
figure 5

Nondimensionalized triple point trajectory for two kinds of step-like wedge

Full size image

Figure 6 presents the overall triple point trajectory angle. On the whole, χ increases rapidly in the early stage (x/w<10), but soon its change becomes very gradual. Some data are already large in the early stage because the visualized incident shock wave was too thick, and, as a result, χ was overestimated. Theoretically, χ cannot be lower than the glancing incidence angle χ g, since the wave propagation speed is not less than the sonic speed. However, some data are lower than the glancing incidence angle for the reason mentioned in the previous section (that χ was underestimated). Within the range of the present experiment, χ does not reach the value for oblique shock wave χ s (Table 1). However, it is expected to approach χ s as x/w increases, except for the error due to underestimation.

Fig. 6
figure 6

Variation of overall triple point trajectory angle for two kinds of step-like wedge

Full size image

5.2 Shock reflection over a rough-surface wedge

If we consider the situation of w<<1, we have a rough-surface wedge (Fig. 2b). The roughness, which corresponds to w in the step-like wedge, is 1 inch/60 ≈ 0.42 mm. Figure 7 shows the reflected wave structure over the rough-surface wedge for M i=1.40. The compression wavelets that cover the region behind the accumulated reflected wave exhibit a surprisingly regular pattern considering the irregularity of the wedge surface.

Fig. 7
figure 7

Visualized reflected wave structure over the rough-surface wedge (M i=1.40, θ w=20°, #=60, x=71.5 mm)

Full size image

Figure 8 presents the triple point trajectory in dimensionless coordinates. The data corresponding to each incident shock Mach number show that the triple point moves along a straight line through the leading edge. The slopes of the least-squares approximation line for Mach number data are 0.5355 (28.16°), 0.5781 (30.03°), and 0.6033 (31.10°). They are quite near the triple point trajectory angle χ for oblique shock reflection (Table 1).

Fig. 8
figure 8

Nondimensionalized triple point trajectory for rough-surface wedge

Full size image

Figure 9 presents the variation of the overall triple-point trajectory angle. In the rough-surface case, the angle is large in the early stage for the same reason as in the step-like wedge case, decreases monotonically toward the oblique shock value χ s, and then remains almost constant. In contrast to the step-like wedge case, the present case has no “first” triple point. We therefore define the location of the triple point as the intersection of the high-pressure side of the incident shock wave and the low-pressure side of the reflected shock wave. Angle χ, thus defined, is considered slightly overestimated. In particular, this overestimation is large at x/w<20 where the visualized incident shock front is thick. For M i=1.20, angle χ decreases almost monotonically over the whole range, demonstrating the opposite tendency to the step-like wedge case. It may be regarded that χ has reached the asymptotic value (χ s) at x/w>100 and that the reflected wave formed by the accumulation of compression wavelets has developed into a shock wave.

Fig. 9
figure 9

Variation of overall triple point trajectory angle for rough-surface wedge

Full size image

6 Conclusions

We conducted a series of experiments using a step-like wedge in order to visualize the shock wave formation process. To estimate the shock formation, we measured the overall triple-point trajectory angle χ defined by the slope of the straight line connecting the wedge tip and the triple point. χ increased from the glancing incidence value χ g toward the oblique shock value χ s. We also conducted an experiment with a rough-surface wedge as the limiting case of a step-like wedge. Qualitatively, we obtained similar results in that the angle χ approaches χ s, although χ was closer to χ s than in the step-like wedge cases. The step-like wedge turns out to be a useful device for generating a series of weak compression waves.