Effects of doping concentrations and position-dependent mass on the nonlinear optical properties of asymmetric double delta-doped GaAs quantum wells

Abstract

This study examines the electronic and optical properties of an asymmetric double delta doped quantum wells structure formed within GaAs. The electronic structure of system is obtained within effective mass and envelope wave function approximations. Optical responses are calculated in the framework of the compact density matrix approach. The roles of distance between wells, varying one well electron concentration, as well as length parameter of position-dependent mass, on the total optical absorption coefficients and the relative refractive index changes are investigated. The findings of this study indicate that prominence of optical coefficients occurs at higher energies for position-dependent mass, compared to constant mass case. Augmented right well electron concentrations lead to blue-shifts on the optical properties not only with constant mass but also with position-dependent mass. However, the increase in the wells’ separation results the absorption peaks to move towards lower energies.

1 Introduction

Nowadays studies on the optical and electronic properties of quantum wells have been conducted on the effect of position-dependent mass (PDM). Newly, the nonlinear optical properties of triple delta-doped GaAs quantum wells with PDM are studied by Tuzemen and co-workers [1]. Delta-doping in III-V semiconductors involves briefly halting crystal growth to deposit dopants before resuming the growth. This technique allows precise control of optical transitions in asymmetric triple δ-doped quantum wells (QWs), enabling tunable properties and advancing optoelectronic device development [2]. The potential profile, wave functions, energy levels, and absorption coefficient (AC) for n-type double δ-doped in GaAs semiconductors are calculated within the Thomas–Fermi (TF) approximation [3,4,5]. The results indicate that the ground and the first excited states are the highest occupied states at short distances between doped layers. The effects of hydrostatic pressure on the linear and nonlinear intersubband optical responses of an asymmetric double delta doped quantum wells (ADDQW) were analyzed using the effective mass approximation and a TF-like model [5]. It was found that hydrostatic pressure causes a redshift in the signal response and reduces the amplitudes of the ACs and refractive index changes (RICs), with the degree of asymmetry in the potential profile further diminishing the RICs [6]. The researchers used the effective mass approximation and a one-dimensional diagonalization method to investigate the conduction band electron states and the linear and nonlinear ACs and RICs in n-type GaAs ADDQWs under an external electric field effect on the growth direction of the homostructure [7]. They found that in the absence of applied electric field when the value of the left-hand side two-dimensional impurity density is fixed, the energy difference for the main intersubband transition is decreasing with an increase in the right-hand side two-dimensional impurity density. With the application of the electric field, the amplitudes of optical resonance peaks of ACs increase significantly. Moreover, it causes greater deviations from the baseline value of GaAs's relative refractive index [7].

The solution of Schrödinger's equation within effective mass approximation for confinement potentials under the influence of non-resonant intense laser fields enables the calculation of the linear and nonlinear ACs and the RICs in an n-type ADDQW [8]. There is a clear interplay between the non-resonant intense laser field application in the growth direction of the structure and the two-dimensional impurity concentration, affecting both the AC and the RICs, in addition to tunability of the confinement potential in n-type double δ-doped QWs [9, 10]. Further, it has recently been demonstrated that a non-resonant, monochromatic laser field and change in the central dopant concentration can modulate ACs and RICs in a triple doped GaAs QW [4, 11, 12]. On the other hand, the separation between the ground and first excited energy levels in a double δ-doped QW increases with the intensity of the laser field, causing an optical blue-shift in intersubband transitions [10, 13].

Asymmetric wells made with different doping concentrations plays an important role in the intersubband transitions. The significant changes in these transitions lead remarkable changes in the optical properties and the optoelectronic devices such as infrared laser amplifiers, high speed electro-optical modulators and photodetectors [12,13,14]. Undoped and Si-delta-doped InGaAs/GaAs QW metal–semiconductor-metal photodetectors are experimentally investigated for their electrical and optical properties [14]. QW photodetectors with interdigitated contacts with delta doping perform better than standard QW photodetectors in the range of 2–6 V. As a result of the electric field created by delta-doping, charge carriers are separated and collected more efficiently, resulting in improved photodetection performance. By appropriately adjusting the separation distance between the double δ-doped QWs, two effects can be achieved: red-shifting, and increase in the intensity of the absorption. A redshift in ACs has been observed with increasing interlayer distance [9]. The structural, electrical, and luminescence properties of quantum-confined InGaAs/GaAs heterostructures, modified by δ-Mn doping of the GaAs barrier have been investigated. Experimental results show that δ-Mn doping enhances electroluminescence intensity and reduces the operating currents of light-emitting diodes [15]. For a single δ-doped QW, the energy difference between the ground and first excited states decreases with increasing doping concentration and the effective width of the doped QW [16]. As a consequence, the resonant peak positions of the total ACs (TACs) and RICs (TRICs) exhibit a red-shift with increasing central doping concentration and effective width of doped QWs [16]. The position of resonances and the amplitude of ACs, as well as RICs, can be adjusted by altering the strength and placement of the doping potential [17, 18]. The optical gain properties of InGaN/GaN QW structures with AlGaN δ-layer are studied using the multiband effective mass theory [19]. When the AlGaN δ-layer increases, the effective separation between QWs also increases. Consequently, the energy levels shift, resulting in higher energy transitions. This phenomenon occurs because the interaction between the QWs diminishes, making each well to act more independently as a single QW. The intersubband linear and nonlinear ACs, as well as the RICs, in modulation-doped GaAs/Al_xGa_1−xAs asymmetric double QWs were examined theoretically. The findings indicate that as the width of the right well decreases, both the TACs and the TRICs shift toward higher energies [20, 21]. It is shown that the laser field, static electric field, asymmetry parameter, varying donor impurity concentrations in the doping layer, and applied hydrostatic pressure can be crucial for engineering the optical properties of QW systems [22,23,24].

In our study, we aim to thoroughly investigate the ACs and RICs in n-type ADDQWs. We will focus on the impacts of varying electron densities and the distances between wells, considering the spatial dependence of the effective mass in these systems. By employing TF approximation derived within the one-dimensional local density functional theory, this approach enables a comprehensive understanding of the confinement potential and optical properties of these ADDQW systems.

2 Theory

ACs and RICs are investigated within n-type ADDQWs. The roles of varying electron densities injected in QWs and the distance between wells are examined while the effective mass of QWs is changing with spatial position. The energy levels and corresponding wave functions of allowed states in the conduction band is modeled with TF approximation derived within the one-dimensional local density functional theory. This approach presents reliable results for δ-doped QWs [25,26,27,28]. The confinement potential of ADDQW systems grown in the $z$ direction can be written as follows:

$$V\left(z\right)=-\frac{{\gamma }^{2}}{{\left(\gamma \left|z+{L}_{W}/2\right|+{z}_{L}\right)}^{4}}-\frac{{\gamma }^{2}}{{\left(\gamma \left|z-{L}_{W}/2\right|+{z}_{R}\right)}^{4}},$$

(1)

where, $\gamma ={e}^{2}{\left(2{m}^{*}\right)}^{3/2}/\left(15\pi \varepsilon {\hslash }^{3}\right)$ and ${z}_{L}={\left[\left(2\varepsilon {\gamma }^{3}\right)/\left(\pi {e}^{2}{N}_{2DL}\right)\right]}^{1/5}$, ${z}_{R}={\left[\left(2\varepsilon {\gamma }^{3}\right)/\left(\pi {e}^{2}{N}_{2DR}\right)\right]}^{1/5}$ are the parameters of local-density TF approximation and includes the electron charge ($e$), electron effective mass (${m}^{*}$), static dielectric constant of the host material ($\varepsilon$) and the reduced Planck’s constant (ħ). ${L}_{w}$ determines the distance between the left (L) and right (R)- side δ-doped layers and ${N}_{2DL}$ and ${N}_{2DR}$ are the number of ionized impurities in the left- and right-hand side $\delta$-doped layers, respectively. One-dimensional time-independent Schrödinger equation for an electron confined within a potential wells system is given as follows:

$$\left[\left(-\frac{d}{dz}\frac{{\hslash }^{2}}{2{m}^{*}\left(z\right)}\frac{d}{dz}\right)+V(z)\right]\varphi \left(z\right)=\text{E}\varphi \left(z\right),$$

(2)

where, ${m}^{*}\left(z\right)$ represents the effective PDM and the dependency of mass to the position is chosen as hyperbolic form as follows:

$${m}^{*}\left(z\right)={m}^{*}{sech}^{2}\left(\frac{\pi z}{d}\right).$$

(3)

This form of PDM is preferred because of the relevance of mass distribution of electron to the soliton profile in condensed matter physics, as discussed in [29, 30]. The parameter $d$ determines the effective length of the mass distribution and ${m}^{*}=0.067 {m}_{0}$ is the effective mass of GaAs at $z=0$ with free electron mass ${m}_{0}.$

The solution of PDM Schrödinger equation is carried out via diagonalization method that offers defining wave function $\varphi \left(z\right)$ in terms of a series of orthonormal base functions with as follows:

$$\varphi \left(z\right)=\sqrt{\frac{2}{{L}_{\infty }}}\sum_{m}{c}_{m}\text{sin}\left(\frac{m\pi z}{{L}_{\infty }}+\frac{m\pi }{2}\right).$$

(4)

These basis functions with an expansion coefficient ${c}_{m}$ are the solutions of a potential well surrounded by infinite barriers within ${L}_{\infty }$ width. While choosing the parameters of diagonalization method we guarantee the walls of infinite well do not affect the results of the energy spectrum of the δ-doped wells. Therefore, the width of well is selected as ${L}_{\infty }=1000 \, nm$ and the size of matrix is taken as $m=200$.

The electronic structure calculation reflects on the evaluation of interested optical properties. Here, the ACs and RICs due to transitions between the lowest two levels are examined with effective PDM while the electron densities of asymmetric wells and the distance between wells are varying. ACs and RICs are functions of the transition energies between first excited state and ground state ($\Delta E={E}_{2}-{E}_{1}$), with amplitudes determined by dipole moment matrix elements (${M}_{ij}=\left|\langle {\varphi }_{i}\left|ez\right|{\varphi }_{j}\rangle \right|$ ($i,j=\text{1,2}$)) of involved wavefunctions. The expressions for the optical coefficients are well known and were derived within density matrix formalism through an iterative procedure. The expressions for linear, third-order nonlinear and total ACs and RICs are defined as follows, respectively [31,32,33,34]:

$${\beta }^{1}\left(\omega \right)=\omega \sqrt{\frac{{\mu }_{0}}{{\varepsilon }_{R}}}\left[\frac{{\left|{M}_{12}\right|}^{2}{\sigma }_{12}\hslash {\Gamma }_{12}}{{\left(\Delta \text{E}-\hslash \omega \right)}^{2}+{\left(\hslash {\Gamma }_{12}\right)}^{2}}\right],$$

(5)

$${\beta }^{3}\left(\omega ,I\right)=-\omega \sqrt{\frac{{\mu }_{0}}{{\varepsilon }_{R}}}\left(\frac{I}{2c{n}_{r}{\varepsilon }_{0}}\right)\frac{{\left|{M}_{12}\right|}^{2}{\sigma }_{12}\hslash {\Gamma }_{12}}{{\left[{\left(\Delta \text{E}-\hslash \omega \right)}^{2}+{\left(\hslash {\Gamma }_{12}\right)}^{2}\right]}^{2}}\left\{4{\left|{M}_{12}\right|}^{2}-\frac{{\left|{M}_{22}-{M}_{11}\right|}^{2}\left[3 {\Delta \text{E}}^{2}-4 \Delta \text{E }\hslash \omega +{\hslash }^{2}\left({\omega }^{2}-{\Gamma }_{12}^{2}\right)\right]}{{\Delta \text{E}}^{2}+{\left(\hslash {\Gamma }_{12}\right)}^{2}}\right\},$$

(6 )

$$\beta \left(\omega ,I\right)={\beta }^{1}\left(\omega \right)+{\beta }^{3}\left(\omega ,I\right),$$

(7)

$$\frac{{\Delta n}^{\left(1\right)}\left(\omega \right)}{{n}_{r}}=\frac{{\sigma }_{12}{\left|{M}_{12}\right|}^{2}}{2{n}_{r}^{2}{\varepsilon }_{0}}\left[\frac{\Delta \text{E}-\hslash \omega }{{\left(\Delta \text{E}-\hslash \omega \right)}^{2}+{\left(\hslash {\Gamma }_{12}\right)}^{2}}\right],$$

(8)

$$\frac{{\Delta n}^{\left(3\right)}\left(\omega ,I\right)}{{n}_{r}}=-\left(\frac{{\sigma }_{12}{\left|{M}_{12}\right|}^{2}}{4{n}_{r}^{2}{\varepsilon }_{0}}\right)\frac{{\mu }_{0}cI}{{\left[{\left(\Delta \text{E}-\hslash \omega \right)}^{2}+{\left(\hslash {\Gamma }_{12}\right)}^{2}\right]}^{2}}\left\{4\left(\Delta \text{E}-\hslash \omega \right){\left|{M}_{12}\right|}^{2}-\frac{{\left|{M}_{22}-{M}_{11}\right|}^{2}}{{\Delta \text{E}}^{2}+{\left(\hslash {\Gamma }_{12}\right)}^{2}}\left[\left(\Delta \text{E}-\hslash \omega \right)\left(\Delta \text{E}\left(\Delta \text{E}-\hslash \omega \right)-{\left(\hslash {\Gamma }_{12}\right)}^{2}\right)-{\left(\hslash {\Gamma }_{12}\right)}^{2}\left(2\Delta \text{E}-\hslash \omega \right)\right]\right\},$$

(9)

$$\frac{\Delta n\left(\omega ,I\right)}{{n}_{r}}=\frac{{\Delta n}^{\left(1\right)}\left(\omega \right)}{{n}_{r}}+\frac{{\Delta n}^{\left(3\right)}\left(\omega ,I\right)}{{n}_{r}}.$$

(10)

The expressions of the optical responses depend on the physical parameters such as angular frequency of the incident photon ($\omega$), carrier density in the system (${\sigma }_{12}$), speed of light in free space ($c$), refractive index of the system (${n}_{r}$), real part of the permittivity (${\varepsilon }_{R}$), intensity of electromagnetic field ($I$), dielectric constant of vacuum (${\varepsilon }_{0}$) and permeability of free space (${\mu }_{0}$). ${\Gamma }_{12}=1/{T}_{12}$ is the damping rate term related with electron lifetime (${T}_{12}$) in the transition, and ${\sigma }_{12}$ is the carrier density in the intersubband transition.

3 Results and discussion

The electronic and optical properties of ADDQW with effective constant mass (CM) and PDM are presented here. The numerical calculations are performed for the conduction band electron of GaAs with the following physical constants and fixed parameters: $e=1.602\times {10}^{-19}$ C, $\hslash =1.056\times {10}^{-34}$ Js, ${\sigma }_{12}=3\times {10}^{22 }\,{\text{m}}^{-3}$, ${n}_{r}=3.53$, ${\mu }_{0}=4\pi \times {10}^{7}\,{\text{Hm}}^{-1}$, ${\varepsilon }_{R}=12.5$, ${\varepsilon }_{0}=8.854\times {10}^{-12}\, {\text{Fm}}^{-1}$, ${T}_{12}=0.14 \text{ps}$, and $I=0.01 \, \text{MW}/{\text{cm}}^{2}$.

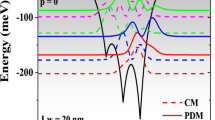
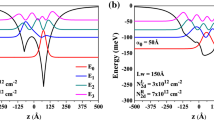
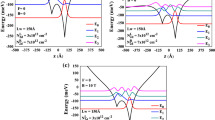
Figure 1 represents the confinement potential distributions of ADDQW and associated wave function probability densities, together with the corresponding energy values obtained with electron’s CM and PDM conditions. The left well includes a doping concentration of $3\times {10}^{12}$ ${\text{cm}}^{-2}$ and that in right well covers $5\times {10}^{12}\, {\text{cm}}^{-2}$ (Fig. 1a), $7\times {10}^{12} \,{\text{cm}}^{-2}$ (Fig. 1b) and $9\times {10}^{12}\, {\text{cm}}^{-2}$ (Fig. 1c). The increase in the electron densities pushes the right well to the lower energies and deepens the confinement potential. Therefore, right well composes greater confinement than left well, and it strengthens with the increase in the doping concentrations. Because of this bigger confinement, the ground state wave function (red curve) localizes at the right well. Huge part of first excited state (blue curve) localizes itself within the left well. Because the energy of the electron in the first excited state is too high to be affected by the depth of the right well. Although the distribution of wave function probabilities is so similar in each concentration, the energy levels differ. Both ground state and first excited state energies shift to lower energies with the augmentation of right well electron concentrations. However, the energy difference between first and ground state, which means transition energy, increases with the increase in the right well electron densities. It should also be noted that energy levels emerge at higher values for PDM, regardless of the change in the confinement profile.

Fig. 1

Confinement potentials of ADDQWs (black curve) and probabilities of the lowest two energy wave functions (colored curves) with fixed left well doping ${N}_{2DL}=3\times {10}^{12}\, {\text{cm}}^{-2}$ and varying right well doping as a ${N}_{2DR}=5\times {10}^{12}\, {\text{cm}}^{-2}$, b ${N}_{2DR}=7\times {10}^{12}\, {\text{cm}}^{-2}$, c ${N}_{2DR}=9\times {10}^{12}\, {\text{cm}}^{-2}$

Figure 2 displays the variation in the transition energies ($\Delta E$) and the occupancy function (${f}_{12}=\left(\Delta E\right)\times {M}_{12}^{*}$) values that are the determinative parameters on the optical coefficients. Figure 2a represents the changes in the $\Delta E$ and ${f}_{12}$ with PDM while the mass length parameter d is varying. The rise of d-parameter causes a decrease in both transition energies and occupancy function values. In addition, augmenting d-parameter of PDM transforms the mass distribution to an effective CM which is heavier than PDM for d < 80 nm for GaAs as given in Ref. [29]. In other words, the electrons will be more energetic for smaller d-values of PDM. Figure 2b presents the changes in $\Delta E$ and ${f}_{12}$ while the distance between wells is increasing. The rising separation of wells causes little changes in the transition energies under CM conditions, but it leads to significant declines in the transition energies for the PDM at $d=20 \text{nm}$. As the distance between the wells increases, the transition energy slightly decreases and then increases for CM, while it significantly decreases for PDM. Conversely, the role of PDM is weak on the ${f}_{12}$ variation when compared to the CM while the distance between wells are going up. The ${f}_{12}$ values firstly decrease slightly and then increase while $d=20 \, \text{ nm}$; however, it sharply declines if the mass is constant. Figure 2c displays the variations in $\Delta E$ and ${f}_{12}$ with changing right well electron concentrations. The transition energies are growing up with increasing electron numbers for both CM and PDM. ${f}_{12}$ factor shows a decreasing attitude with the augmentation of right well electron concentrations.

Fig. 2

Transition energies between the first excited state and ground state (red colored—left scale) and occupancy function values (blue colored—right scale) as a function of d-parameter of PDM (a), separation of wells (b), and varying right well electron concentration (c)

For both $\Delta E$ and ${f}_{12}$ results, the role of PDM slightly lessens for higher asymmetric case.

Figure 3a represents the changes in the TACs versus photon energy with CM and PDM. PDM shifts the TACs to higher photon energies for ADDQW. The blue-shift is greatest at $d=20.0 \, \text{ nm}$ and declines with increasing $d$ values such as $22.5 \, \text{ nm}$, $25.0 \, \text{ nm}$. The amplitudes of TACs rises with PDM and get the highest value for $d=20.0 \, \text{ nm}$. The red-shift in the absorption peaks and reductions in the peak amplitudes with growing d-parameter can be attributed to the $\Delta E$ and ${f}_{12}$ variations as pictured in Fig. 2a. Figure 3b shows the changes in the TAC as a function of incident photon energy while the distance between wells is rising with CM and PDM. When the wells are more separated, TAC moves to the lower photon energies due to the decrease in the transition energy for PDM; while it remains almost same due to the slight change in the transition energy for CM. The TACs occur at higher energies and with greater peaks for PDM than CM for the same wells’ separations. While the mass is changing with position, the absorption peaks firstly decrease and then increase slightly, however the declines with increasing wells separation are significant when the effective mass is constant. In Fig. 3c, we displayed the blue-shifts of TACs as a function of the incident photon energies when the electron concentration in the right well is rising. The shift to higher energies happens not only for the CM but also for the PDM. Nevertheless, the peaks emerge at higher energies and greater amplitudes when the effective mass is changing with position. The change of peak occurrence energies and amplitudes with electron concentration is consistent with the change of transition energies and the occupancy functions displayed in the Fig. 2c, respectively.

Fig. 3

TACs as a function of incident photon energy with varying d-parameter of PDM (a), separation of wells (b), and right well electron density (c)

Table 1 displays the square of off-diagonal dipole moment matrix elements for a fixed left well electron concentration ${N}_{2DL}=3\times {10}^{12} \, {\text{cm}}^{-2}$ and changing right well electron concentration for CM and PDM with varying d-parameter. The declines in the ${M}_{12}^{2}$ matrix are clearly seen with augmented asymmetry for both CM and PDM. Furthermore, the relationship between the square of the dipole moment matrix element and the d-parameter at different electron concentrations are clearly seen in Table 1. Table 2 presents the square of off-diagonal dipole moment matrix elements while the distance between wells is changing for CM and PDM. Although increasing wells separation leads to a decrease in ${M}_{12}^{2}$ for CM case, it causes an increase for PDM case. These tables are introduced to interpret the variations in the peak amplitudes of RICs.

Table 1 Variation of square of off-diagonal dipole moment matrix elements with three different right well electron concentrations for constant mass and position dependent mass while mass length parameter d is varying

Table 2 Variation of square of off-diagonal dipole moment matrix elements with varying well distances for constant mass and position dependent mass while mass length parameter d is varying

Figure 4 represents the changes in the RICs with incident photon energy for both CM and PDM. RICs form at the higher photon energies for PDM than for CM. The peak goes to lower photon energies with increasing d-parameter, as can be guessed from Fig. 2a. The peak amplitude is slightly lower for CM than in the PDM cases and peak amplitudes are so close to each other while the PDM is changing with d-parameter. The reason for these behaviors can be realized from the first row and first column of Table 1, respectively. The role of wells’ separation between asymmetric wells on the RICs is represented in Fig. 4b for both CM and PDM. At any wells’ separation value, RICs peaks occur at higher energies with larger amplitudes for PDM than for CM. Increasing wells separations shifts the RICs peaks to lower energies and for effective CM the peaks occur at almost same photon energy. Although peak amplitude increases with increasing wells separation for PDM, it decreases for CM, in accordance with first and second row of Table 2. The blue-shift in the RICs while the electron concentration within the right well is increasing is shown in Fig. 4c for both CM and PDM. Both CM and PDM display decreasing RICs amplitudes with rising right well electron concentrations. Finally, it should be noted that for any given value of electron concentration, the RICs peaks for PDM occur at higher photon energies with larger amplitudes than for CM.

Fig. 4

RICs as a function of incident photon energies with a varying d-parameter of PDM, b separation of wells, and c one well electron density

4 Conclusion

We have studied on the total absorption coefficient and refractive index changes of an asymmetric double δ-doped quantum wells assuming that the electron effective mass is either constant or position-dependent. Besides, the variations in the mass length parameter, the distance between two δ-doped wells and increasing right well electron concentration are included in the numerical calculations. The electronic properties are obtained by solving the Schrödinger equation with envelope wave function and effective mass approximations. The optical responses are calculated within the compact density matrix approach. The obtained electronic properties show that effective position-dependent mass increases the energy differences between first excited and ground state energies when compared to the constant mass. Therefore, when the effective constant mass is replaced with position-dependent mass both the total absorption coefficient and refractive index changes peaks shift towards higher energies. The increase in the effective mass length parameter (d), leads to red-shifts on these coefficients, but they remain at higher photon energies than the constant mass results. Although position-dependent mass leads to significant changes in the total absorption coefficient peak amplitudes, it causes slight changes on the refractive index changes peaks. The increase in the separation of wells moves the total absorption coefficient and refractive index changes peaks to lower energies while the length parameter of position-dependent mass is increasing. For the same wells’ separations, these peaks emerge at lower photon energies for constant effective mass than position-dependent. The increasing right well electron concentration, which refers the increasing asymmetry, causes blue-shifts with decreasing amplitudes in the total absorption coefficient as well as refractive index changes for both constant mass and position-dependent mass cases. As a summary, the position-dependent mass shifts the total absorption coefficient and refractive index changes to higher energies when compared to the constant mass. We believe the results presented here will be beneficial for the experimental studies with asymmetric double δ-doped wells while the effective mass is varying with position.