1 Introduction

The tunability of energy levels and wavefunctions for carriers in delta-doped quantum wells (DDQWs) and other low-dimensional semiconductor systems are critical for designing optoelectronic devices like quantum cascade lasers, photodetectors, and infrared lasers [1,2,3,4,5,6,7]. The positions of these energies and the spread of wavefunctions depend on the shape of confinement potentials, which can be controlled using growth methods like metal organic vapor deposition (MOVD) and molecular beam epitaxy (MBE). These methods are commonly used for inserting δ-doped layers, creating additional triangular QWs in the quantum structures, enhancing electronic density and altering energy levels and wavefunctions. δ-doping involves introducing silicon atoms into the structure, which, when ionized, create additional triangular QWs and free electrons, leading to new energy levels and wavefunctions. Multiple δ-doped layered structures, such as double, triple, and quadruple DDQWs, offer technological advantages over single DDQWs by reducing active layer thickness. Additionally, δ-doping allows to control over intersubband transitions, crucial for high-power field-effect transistors and infrared photodetectors [8,9,10,11,12,13,14,15,16,17,18,19,20,21].

In recent years, extensive research have focused on δ-doping systems and their impact on the electronic and optical properties of semiconductor structures. These systems have been studied under various external influences, including electric and magnetic fields, intense laser irradiation, as well as changes in hydrostatic pressure and temperature. For example, Gaggero et al. [9] examined temperature effects on electronic properties in a single DDQW, finding mobility ratios consisting with experiments, at different temperatures. Dakhlaoui et al. [22] investigated the optical properties of GaAs semiconductors with triple δ-doped layers, observing combined effects of doping and electromagnetic fields on optical absorption coefficients. Grimalsky explored temperature effects on energy distribution in single δ-doped QWs using a Thomas–Fermi approach, noting its simplicity and accuracy within certain temperature ranges [10]. Rodríguez-Magdaleno and coworkers studied the impacts of electric fields on double asymmetric GaAs DDQWs [23], while Rojas-Briseño et al. [24] analyzed nonlinear optical characteristics of asymmetric double DDQWs with Schottky barriers under electric field. Oubram and collaborators addressed the hydrostatic effects on electronic and optical properties in GaAs DDQWs, demonstrating sensitivity of energy levels and intersubband optical absorptions to applied hydrostatic pressure [25].

Motivated by all the cited works, we aim to analyze in the present paper the influence of hydrostatic pressure, temperature, and position-dependent mass (PDM) on the nonlinear optical properties, including total optical absorption coefficients (TOACs), relative refractive index changes (RRICs), nonlinear optical rectification (NOR), second harmonic generation (SHG), and third harmonic generation (THG) of asymmetric triple δ-doped GaAs quantum wells. To the best of our knowledge, this work is the first one which includes the effects of the position-dependent mass together with the hydrostatic pressure and temperature on the mentioned optical properties. The present work is organized as follows: In the next section, we outline our theoretical approach. In Sect. 3, we present, discuss, and comment our findings, and finally in Sect. 4, we summarize our main conclusions.

2 Theory

In this present work, we examined the effect of applied hydrostatic pressure and temperature on the nonlinear optical properties such as TOACs, RRICs, NOR, SHG, and THG of ATDDQW structure. We put forward this review for two different situations: In the first case, the electron confined in the structure has a constant mass (CM); in the other case, it has a PDM. If we want to write the Hamiltonian of the confined electron in ATDDQW, taking into account the effects of temperature and hydrostatic pressure within the effective mass approach, we obtain the following expression:

$${\mathbf{\mathcal{H}}} = - \frac{{\text{d}}}{{{\text{d}}z}}\frac{{\hbar^{2} }}{{2m\left( {z,p,T} \right)}}\frac{{\text{d}}}{{{\text{d}}z}} + V_{{{\text{ATDDQW}}}} \left( {z,p,T} \right)$$
(1)

where \(P\) and \(T\) express the hydrostatic pressure (in kbar) and the temperature (in Kelvin), respectively. \(m\left(z,p,T\right)\) is the position \(\left(z\right)\), pressure \(\left(p\right)\) and temperature \(\left(T\right)\) dependent electron’s mass value. The confinement potential of the electron is given by \({V}_{\text{ATDDQW}}\left(z,p,T\right)\). Mathematical expression for the electron’s mass depending on the position, pressure and the temperature can be written as,

$$m\left( {z,p,T} \right) = m^{*} \left( {p,T} \right) {\text{sech}}^{2} \left( {\frac{\pi z}{d}} \right)$$
(2)

here the effective length of the PDM distribution is expressed by the d–parameter. \({m}^{*}\left(p,T\right)\) is defined as the effective mass of the electron depending on the pressure and temperature and is computed by the following [26,27,28,29],

$$m^{*} \left( {p,T} \right) = \frac{{m_{0} }}{{1 + 7.51 \times \left[ {\left( {\frac{2}{{E_{g}^{\Gamma } \left( {p,T} \right)}}} \right) + \left( {\frac{1}{{E_{g}^{\Gamma } \left( {p,T} \right) + 0.341}}} \right)} \right]}},$$
(3)

where \({m}_{0}\) shows the value of free electron’s mass. \({E}_{g}^{\Gamma }\left(p,T\right)\) gives us the energy gap (in eV) depended on the hydrostatic pressure and the temperature at \(\Gamma\) point for GaAs [30,31,32,33]:

$$E_{g}^{\Gamma } \left( {p,T} \right) = \left[ {1.519 - \left( {5.405 \times 10^{ - 4} T^{2} } \right)/\left( {T + 204} \right)} \right] + \left( {1.26 \times 10^{ - 2} } \right) p - \left( {3.77 \times 10^{ - 5} } \right) p^{2}$$
(4)

The equality expressing the confinement potential of ATDDQW structure is given below [34]:

$$V_{{{\text{ATDDQW}}}} \left( {z,p,T} \right) = - \frac{{\xi^{2} }}{{\left( {\xi \left| {z - L_{w} /2} \right| + z_{L} } \right)^{4} }} - \frac{{\xi^{2} }}{{\left( {\xi \left| z \right| + z_{M} } \right)^{4} }} - \frac{{\xi^{2} }}{{\left( {\xi \left| {z - L_{w} /2} \right| + z_{R} } \right)^{4} }},$$
(5)

where \({L}_{w}\) gives the horizontal distance between the bottom points of the right and left wells. \({z}_{L}={\left(2{\varepsilon }_{r}{\xi }^{3}/\pi {e}^{2}{N}_{2d}^{L}\right)}^{1/5}\), \({z}_{M}={\left(2{\varepsilon }_{r}{\xi }^{3}/\pi {e}^{2}{N}_{2d}^{M}\right)}^{1/5}\), \({z}_{R}={\left(2{\varepsilon }_{r}{\xi }^{3}/\pi {e}^{2}{N}_{2d}^{R}\right)}^{1/5}\) are delta potential parameters, where \(\xi =\left({e}^{2}{\left(2{m}^{*}\left(p,T\right)\right)}^{3/2}\right)/\left(15\pi {\varepsilon }_{r}{\hslash }^{3}\right)\) and \({\varepsilon }_{r} (={n}_{\text{r}}^{2})\) is the dielectric constant of the structure, where \({n}_{\text{r}}\) is the refractive index of the system. While reduced Planck constant is \(\hslash\), the charge of electron is given by \(e\). \({N}_{2d}^{L}\), \({N}_{2d}^{M}\) and \({N}_{2d}^{R}\) represent \(\delta\) doping concentration in left, mid and right wells, respectively.

After giving the pressure and temperature-dependent expressions of the effective mass and the energy gap, we can write the expressions giving the well width \(\left({L}_{w}(p)\right)\) depending on the pressure and the dielectric constant \(\left({\varepsilon }_{r}(p,T)\right)\) depending on both pressure and temperature are as follows,

$$L_{w} \left( p \right) = L_{w} \left( {1 - \left( {S_{11} + 2S_{12} } \right)p} \right)$$
(6)

here, \({L}_{w}\) expresses the original width of the confinement potential. \({S}_{11}\) and \({S}_{12}\) are GaAs’s elastic constants whose values are \(1.16\times {10}^{-3} {\text{kbar}}^{-1}\) and − \(3.70\times {10}^{-4}{\text{ kbar}}^{-1}\), respectively.

$$\varepsilon_{r} \left( {p,T} \right) = \left\{ {\begin{array}{*{20}c} {12.74e^{{\left( { - 1.67 \times 10^{ - 3} p} \right)}} e^{{\left( {9.4 \times 10^{ - 5} \left( {T - 75.6} \right)} \right)}} , \quad {\text{for}}\; T \le 200 {\text{K}}} \\ {} \\ {13.18e^{{\left( { - 1.73 \times 10^{ - 3} p} \right)}} e^{{\left( {20.4 \times 10^{ - 5} \left( {T - 300} \right)} \right)}} , \quad {\text{for}} \;T > 200 {\text{K}}} \\ \end{array} } \right.$$
(7)

Primarily, we got the solution of the time-independent Schrödinger equation in one dimension. While doing this, we took advantage of the diagonalization method [35], which ensures that the wave functions \(\varphi \left(z\right)\) belonging to the electron are explained in terms of a complete set of orthonormal functions of an infinite barrier potential well, as described in Refs. [36, 37]. This process helps us to get the subband energy levels together with corresponding wave functions (\(\mathcal{H}\varphi \left(z\right)=E\varphi \left(z\right)\), where \(E\) corresponds to the energy eigenvalues). After the computations of eigenvalues and eigenfunctions, we used the compact density matrix method to calculate TOACs, RRICs, NOR, SHG, and THG of the structure. In line with the obtained results, the linear and third-order nonlinear-OACs’ analytical expressions are as follows [38,39,40]:

$$\alpha^{\left( 1 \right)} \left( {\omega , I} \right) = \omega \sqrt {\frac{\mu }{{\varepsilon_{r} \varepsilon_{0} }}} \left[ {\frac{{\left| {M_{10} } \right|^{2} \sigma_{\nu } \hbar \Gamma_{10} }}{{\left( {E_{10} - \hbar \omega } \right)^{2} + \left( {\hbar \Gamma_{10} } \right)^{2} }}} \right],$$
(8)
$$\begin{aligned} \alpha^{\left( 3 \right)} \left( {\omega ,I} \right) = & - 2\omega \sqrt {\frac{\mu }{{\varepsilon_{r} \varepsilon_{0} }}} \left( {\frac{I}{{\varepsilon_{0} n_{{\text{r}}} c}}} \right)\frac{{\left| {M_{10} } \right|^{4} \sigma_{\upsilon } \hbar \Gamma_{10} }}{{\left[ {\left( {E_{10} - \hbar \omega } \right)^{2} + \left( {\hbar \Gamma_{10} } \right)^{2} } \right]^{2} }} \\ & \times \left[ {1 - \frac{{\delta_{01}^{2} }}{{\left| {M_{10} } \right|^{2} }} \frac{{\left( {3E_{10}^{2} - 4E_{10} \hbar \omega + \hbar^{2} \left( {\omega^{2} - \Gamma_{10}^{2} } \right)} \right)}}{{E_{10}^{2} + \left( {\hbar \Gamma_{10} } \right)^{2} }}} \right] \\ \end{aligned}$$
(9)

The summation of Eqs. (8) and (9) equals to the TOAC expression:

$$\alpha \left( {\omega ,I} \right) = \alpha^{\left( 1 \right)} \left( {\omega ,I} \right) + \alpha^{\left( 3 \right)} \left( {\omega ,I} \right)$$
(10)

In these mathematical expressions, \(\omega\) represents the incident photon’s frequency. The speed of light in free space is given as \(c\), \(\mu\) is the medium’s magnetic permeability and \({\sigma }_{\nu }\) shows the intersubband transition electrons’ density. \({\varepsilon }_{0}\) equals to the free space’s dielectric permittivity, \({{\Gamma }_{10}=1/\tau }_{10}\) gives the intersubband relaxation rate term, where \({\tau }_{10}\) is relaxation time. The energy difference between the ground and first excited states is equal to \({E}_{10 }(={E}_{1}-{E}_{0})\). \(I\) defines the incident electromagnetic wave’s intensity. Additionally, \({M}_{ij}\) identifies the electric dipole moment matrix element described as \({M}_{\text{ij}}=\langle {\varphi }_{i}\left(z\right)\left|ez\right|{\varphi }_{j}\left(z\right)\rangle\), where \(i,j=\text{0,1},\text{2,3}\) \(\left({\delta }_{01}=\left|{M}_{00}-{M}_{11}\right|\right)\).

The RRICs is obtained by summation of the linear \(\left({\Delta n}^{\left(1\right)}\left(\omega , I\right)/{n}_{\text{r}}\right)\) and the third-order nonlinear \(\left({\Delta n}^{\left(3\right)}\left(\omega , I\right)/{n}_{\text{r}}\right)\) refractive index changes which are given as follows [41]:

$$\frac{{\Delta n^{\left( 1 \right)} \left( {\omega , I} \right)}}{{n_{{\text{r}}} }} = \frac{{\sigma_{\nu } \left| {M_{10} } \right|^{2} }}{{2n_{{\text{r}}}^{{2}} \varepsilon_{0} }}\left[ {\frac{{E_{10} - \hbar \omega }}{{\left( {E_{10} - \hbar \omega } \right)^{2} + \left( {\hbar \Gamma_{10} } \right)^{2} }}} \right],$$
(11)
$$\begin{aligned} \frac{{\Delta n^{\left( 3 \right)} \left( {\omega ,I} \right)}}{{n_{{\text{r}}} }} = & - \frac{\mu c}{{4n_{{\text{r}}}^{{3}} \varepsilon_{0} }}\frac{{\left| {M_{10} } \right|^{2} \sigma_{\nu } I}} {{\left[ {\left( {E_{10} - \hbar \omega } \right)^{2} + \left( {\hbar {\Gamma }_{10} } \right)^{2} } \right]^{2} }} \times \left[ {4\left( {E_{10} - \hbar \omega } \right)\left| {M_{10} } \right|^{2} - \frac{{\left( {M_{11} - M_{00} } \right)^{2} }} {{E_{10}^{2} + \left( {\hbar \Gamma_{10} } \right)^{2} }}} \right. \\ & \left. \times \left[ {\left( {E_{10} - \hbar \omega } \right)\left( {E_{10} \left( {E_{10} - \hbar \omega } \right) - \left( {\hbar \Gamma_{10} } \right)^{2} } \right) - \left( {\hbar \Gamma_{10} } \right)^{2} \left( {2E_{10} - \hbar \omega } \right)} \vphantom{\frac{{\left( {M_{11} - M_{00} } \right)^{2} }} {{E_{10}^{2} + \left( {\hbar \Gamma_{10} } \right)^{2} }}}\right] \right] \\ \end{aligned}$$
(12)

The equations related to the NOR, SHG, and THG coefficients are given as [42,43,44,45].

$$\chi_{0}^{\left( 2 \right)} = \frac{{4\sigma_{\upsilon } }}{{\varepsilon_{0} \hbar^{2} }}M_{01}^{2} \delta_{01} \frac{{\omega_{01}^{2} \left( {1 + \Gamma_{2} /\Gamma_{1} } \right) + \left( {\omega^{2} + \Gamma_{2}^{2} } \right)\left( {\Gamma_{2} /\Gamma_{1} - 1} \right)}}{{\left[ {\left( {\omega_{01} - \omega } \right)^{2} + \Gamma_{2}^{2} } \right]\left[ {\left( {\omega_{01} + \omega } \right)^{2} + \Gamma_{2}^{2} } \right]}},$$
(13)
$$\chi_{2\omega }^{\left( 2 \right)} = \frac{{\sigma_{\upsilon } }}{{\varepsilon_{0} \hbar^{2} }}\frac{{M_{01} M_{12} M_{20} }}{{\left( {\omega - \omega_{10} - i\Gamma_{3} } \right)\left( {2\omega - \omega_{20} /2 - i\Gamma_{3} } \right)}},$$
(14)
$$\chi_{3\omega }^{\left( 3 \right)} = \frac{{\sigma_{\upsilon } }}{{\varepsilon_{0} \hbar^{3} }}\frac{{{\text{M}}_{01} {\text{M}}_{12} {\text{M}}_{23} {\text{M}}_{30} }}{{\left( {\omega - \omega_{10} - i\Gamma_{3} } \right)\left( {2\omega - \omega_{20} /2 - i\Gamma_{3} } \right)\left( {3\omega - \omega_{30} /3 - i\Gamma_{3} } \right)}},$$
(15)

where \({\omega }_{\text{ij}}=\left({E}_{i}-{E}_{j}\right)/\hslash\) expresses the transition frequency and \({\Gamma }_{i}=1/{T}_{i} \left(i=1, 2, 3\right)\) specifies the relaxation rate relating with the electrons’ transition lifetime.

The physical constants used in our study can be listed as follows: \({L}_{w}=20 \text{nm}\), the total width of the heterostructure is \(100 \text{nm}\), d–parameter is \(30 \text{nm}\) for PDM distribution, doping concentrations from left to right are \({N}_{2d}^{L}=3\times {10}^{12} {\text{cm}}^{-2}\), \({N}_{2d}^{M}=5\times {10}^{12} {\text{cm}}^{-2}\) and \({N}_{2d}^{R}=7\times {10}^{12} {\text{cm}}^{-2}\), respectively, \(\hbar = 1.056 \times 10^{ - 34} {\text{Js}}\), \({\varepsilon }_{0}=8.854\times {10}^{-12} {\text{F m}}^{-1}\), \({\rho }_{\upsilon }=3\times {10}^{22} {m}^{-3}\),\(\text{e}=1.602\times {10}^{-19} \text{C}\), \(I=0.05 \text{MW }{\text{cm}}^{-2}\), \({\tau }_{12}=0.2 \text{ps}\), \({n}_{\text{r}}=3.546\), and \({\Gamma }_{i} \left(i=1, 2, 3\right)\) is \(1\), \(5\) and \(7\) THz, respectively. In addition to these, the changes of some physical constants depending on hydrostatic pressure and temperature are given in Table 1 below.

Table 1 Variations of some physical constants depending on pressure and temperature
Full size table

3 Results and discussion

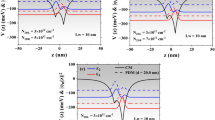
In this section, we present our findings. Figure 1 illustrates the confining potential profile for the ATDDQW structure with wave functions for the ground state and first three excited states. We analyze cases without hydrostatic pressure and temperature, assuming Lw and the total width of the structure as \(20 \text{nm}\) and \(100 \text{nm}\), respectively. The well depths increase from left to right due to varying doping concentrations (\({N}_{2d}^{L}=3\times {10}^{12} {\text{cm}}^{-2}\), \({N}_{2d}^{M}=5\times {10}^{12} {\text{cm}}^{-2}\) and \({N}_{2d}^{R}=7\times {10}^{12} {\text{cm}}^{-2}\)). Dashed lines represent wave functions calculated with CM, where one peak for the ground state and increasing peaks for subsequent excited states. When examining wave functions generated using PDM (solid lines), we note minimal behavioral changes compared to CM, albeit with a slight upward shift. This shift results from reducing position-dependent electron mass, enhancing electron energy, and slightly increasing differences between wave functions.

Fig. 1
figure 1

Potential profile of ATDDQW and the probability density for the envelope wave-functions of the ground and first three excited states in the absence of the effects of temperature and hydrostatic pressure

Full size image

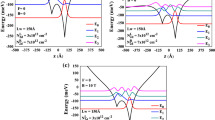
The transition energies between the ground state and the first three excited states, as a function of temperature \(\left(T\right)\) under zero hydrostatic pressure and as a function of hydrostatic pressure \(\left(p\right)\) at \(300\text{ K}\) temperature, are exhibited in Fig. 2a and b, respectively, for CM (dashed line) and PDM (solid line) cases. According to the data obtained, in both cases, the transition energies tend to increase with the increment in temperature (Fig. 2a) for \(p=0\). In the case of PDM, the amounts of increment in transition energies are higher. In Fig. 2b, we kept the temperature constant and examined the changes in transition energies according to the variation of hydrostatic pressure. We observed decreases in transition energies with increasing pressure for both CM (dashed line) and PDM (solid line) cases for \(T=300 \text{K}\). Here, the reduction of transition energies is greater in the PDM case.

Fig. 2
figure 2

For CM (dashed line) and PDM (solid line) cases the transition energies between the ground state and the first, second, and third excited states as a function of the a temperature \(\left(T\right)\) under zero hydrostatic pressure. b Hydrostatic pressure \(\left(p\right)\) at \(300 \text{K}\) temperature

Full size image

We showed the variations in TOAC as a function of the incident photon energy in Fig. 3 in parallel with the parameter values used to generate Fig. 2 for the situations of CM (dashed line) and PDM (solid line). We assume, for Fig. 3a, zero hydrostatic pressure while setting the temperature value to \(0\), \(300 \text{K}\) and \(500 \text{K}\). Figure 3b is produced varying the hydrostatic pressure as \(0\), \(20\text{ kbar}\) and \(30 \text{kbar}\) at \(300 \text{K}\) temperature value. By observing the plotted outcome, it can be clearly seen that TOAC peak positions undergo blueshift/shift to higher energy region (redshift/shift to lower energy region) while increasing (reducing) their amplitudes against augmenting temperature (hydrostatic pressure). It should also be noted that for all conditions, peak positions (peak amplitudes) in the PDM case occur at higher energies (are larger) than in the CM case. We can explain this blueshift and redshift behaviors by the transition energy increases and decreases given in Fig. 2a, b, respectively. Also, the changes of data (with temperature and hydrostatic pressure) related to the value of \(\left({M}_{10}^{2}\times \Delta E\right)\) given in the fourth columns of Tables 2 and 3 for both CM and PDM support the amplitude changes occurring here (Fig. 3a, b).

Fig. 3
figure 3

For CM (dashed line) and PDM (solid line) cases, the variations in TOAC for intersubband transitions as a function of the incident photon energy by changing the value of a temperature for \(p=0\) and b hydrostatic pressure at \(T=300 \text{K}\)

Full size image
Table 2 Changes of dipole matrix elements with temperature \(\left(p=0\right)\)
Full size table
Table 3 Changes of dipole matrix elements with hydrostatic pressure \(\left(T=300 \text{K}\right)\)
Full size table

In Fig. 4, we analyzed TRRICs across incident photon energy under different temperature (for \(p=0\)) and hydrostatic pressure (for \(T=300 \text{K}\)) conditions. Figure 4a illustrates a decrease in TRRICs’ amplitudes, indicating a blueshift with increasing temperature for both CM (dashed line) and PDM (solid line). In Fig. 4b, at \(T=300 \text{K}\) and pressures of \(0, 20 \text{kbar}\), and \(30 \text{kbar}\), we observe a shift of resonant peaks toward lower energies with increasing pressure for both CM and PDM cases. In all scenarios, the resonant peaks for PDM occur at higher energies compared to CM. The variations in transition energies depicted in Fig. 2a, b allow to elucidate the observed blueshift and redshift in Fig. 4a, b, respectively.

Fig. 4
figure 4

For CM (dashed line) and PDM (solid line) cases, the TRRICs as a function of the incident photon energy by changing the value of a temperature for \(p=0\) and b hydrostatic pressure at \(T=300 \text{K}\)

Full size image

In Fig. 5, we illustrate the observed variations in NOR coefficients as a function of incident photon energies under different temperature and pressure conditions. We notice a blueshift phenomenon, where the resonance peaks of NOR coefficients shifted toward higher energy regions while decreasing in amplitude with increasing temperature at zero pressure for both CM and PDM values (Fig. 5a). Conversely, when maintaining a constant temperature of \(300 \text{K}\) and increasing pressure, a redshift occurred. With resonance peaks shifting toward lower energy regions while the amplitudes exhibited an increasing trend for both CM and PDM (Fig. 5b). In all situations, peak positions (and peak amplitudes) for PDM were consistently at higher energies (and smaller) compared to CM. A look at the variations in \({E}_{10}\) and \({M}_{10}^{2} {\delta }_{01}\) from Fig. 2a, b, Tables 2, and 3, for both cases (Fig. 5a, b), reveals a direct explanation for the observed shifts and amplitude changes.

Fig. 5
figure 5

The variations of NOR coefficient as a function of incident photon energy for different values of a temperature \(\left(T\right)\) for \(p=0\) and b hydrostatic pressure \(\left(p\right)\) at \(T=300 \text{K}\)

Full size image

After discussing changes in NOR coefficients, we proceed to analyze how temperature and pressure affect SHG coefficients, as shown in Fig. 6. In both cases, CM (dashed line) exhibits two peaks: a primary resonant peak corresponding to \({E}_{20}/2\) and a secondary peak corresponding to \({E}_{10}\). In contrast, PDM (solid line) shows a distinct primary peak with no secondary peak, attributed to the wider energy range of the \({E}_{20}\) resonance, suppressing the emergence of secondary peak at \({E}_{10}\). Increasing temperature under zero pressure (Fig. 6a) shifts the SHG coefficient peaks to higher energies for both CM and PDM, consistent with \({E}_{20}/2\) behavior (Fig. 2a). Equation (12) shows that the matrix element \(\left({M}_{10}{M}_{12}{M}_{20}\right)\) predominantly influences SHG coefficients, as observed in Table 2. Peak amplitudes decrease accordingly. On the other hand, increasing pressure at constant temperature (Fig. 6b) increases peak amplitudes and shifts peaks to lower energies for both CM and PDM, correlating with \({E}_{20}/2\) decrease (Fig. 2b) and matrix element product \(\left({M}_{10}{M}_{12}{M}_{20}\right)\) increases (see sixth column of Table 3). PDM peaks consistently appear at higher energies than CM peaks. At zero \(p\) and \(T=0 \text{K}\), PDM peak amplitude is larger; at \(300 K\) and zero pressure, CM peak amplitude is larger, while at other conditions, the trend varies.

Fig. 6
figure 6

SHG coefficient’s change as a function of incident photon energy for different values of a temperature \(\left(T\right)\) for \(p=0\) and b hydrostatic pressure \(\left(p\right)\) at \(T=300 \text{K}\)

Full size image

In the last part of our study, we worked on the effects of temperature and pressure changes on THG coefficient for CM (dashed line) and PDM (solid line) in Fig. 7. THG coefficients have main (corresponds to \({E}_{30}/3\)) and secondary (corresponds to \({E}_{20}/2\)) peaks for PDM condition in Fig. 7a, b. In this case, the peak corresponding to \({E}_{10}\) is absent. With increment of temperature (hydrostatic pressure) the positions of main peak move toward to higher (lower) photon energies, with their amplitudes remaining almost constant in Fig. 7a, b. At the same time, THG coefficients have one resonant peak for CM condition. This single peak occurs by the superposition of the main (corresponds to \({E}_{30}/3\)) and secondary (corresponds to \({E}_{20}/2\)) resonant peaks. This superposition phenomenon is the result of the transition energies’ closeness reported in Tables 2 and 3. When Fig. 7a, b is examined for CM value, it can be easily seen that peak positions show blueshift (redshift) with increasing (decreasing) their amplitude values in the case of rising temperature (hydrostatic pressure). It should also be noted that for all conditions, the peak positions (peak amplitudes) in the PDM case are at higher energies (smaller) than in the CM case. The changes of dipole matrix element values \(\left({M}_{10}{M}_{12}{M}_{23}{M}_{30}\right)\) given in the last columns of Tables 2 and 3 allow us to explain the amplitude changes that occur for both CM and PDM in Fig. 7a, b.

Fig. 7
figure 7

The variations of THG coefficient as a function of incident photon energy for different values of a temperature \(\left(T\right)\) for \(p=0\) and b hydrostatic pressure \(\left(p\right)\) at \(T=300\text{ K}\)

Full size image

4 Conclusion

In this study, we investigated the variations in the total optical absorption coefficients, total relative refractive index changes, nonlinear optical rectification, second-harmonic generation, and third-harmonic generation coefficients within an asymmetric triple δ-doped GaAs quantum well heterostructure, depending on alterations in temperature and hydrostatic pressure. Our analysis reveals the impacts of temperature and pressure on the aforementioned optical properties. Specifically, we consider the situations in which the electron effective mass either remains constant or becomes position-dependent. Under conditions of constant pressure \((p=0)\), we take into account the effect of changes in temperature and under constant temperature \((T=300 \text{K})\) the effect of changes in pressure. Employing both diagonalization and compact density matrix methodologies, we determine subband energy levels alongside their corresponding wave functions, leading to the evaluation of electric dipole moment matrix elements, entering the mathematical expressions for the nonlinear optical coefficients. Our findings reveal that elevating the temperature (or pressure) prompts resonance peaks of these coefficients to shift toward higher (or lower) energy ranges, irrespective of whether the electron’s mass is constant or position-dependent. Furthermore, we observe distinct responses in the peak amplitudes of these optical coefficients at different temperature and pressure values, as elucidated comprehensively in the preceding section. In our opinion, our findings will serve as a valuable resource for theoretical and experimental researchers to understand the optoelectronic properties of GaAs-based δ-doped systems such as δ-doped field effect transistors (δ-FET), δ-multiple independent gate field effect transistors (δ-MIGFET) and δ-doped heterojunction bipolar transistors (δ-HBT).