Influence of external magnetic field on electromagnetically induced grating in a degenerate two-level atomic medium

Abstract

In this work, the external magnetic field is employed as a “knob” to transfer the light energy from the zero-order diffraction to the high-order diffractions of electromagnetically induced grating in a degenerate two-level atomic medium. Under a standing-wave coupling field, the diffraction of the probe beam is created with the diffraction pattern including zero-, first- and second-order diffractions. When the magnetic field is not applied, the absorption grating is formed based on amplitude modulation of the transmission function; most of the probe light energy is focused on the zero-order diffraction (about 70%) and only about 6% of the first-order diffraction. However, when the external magnetic field is applied, the phase grating is formed based on the phase modulation of transmission function; the probe light energy is transferred from zero-order diffraction to first- and second-order diffractions, in which the first-order diffraction efficiency can be obtained about 32% with proper magnetic field strength. Moreover, the probe light energy can also be transferred from zero-order diffraction to first- and second-order diffractions by adjusting the frequency and/or the intensity of the coupling and probe fields in the presence of external magnetic field.

1 Introduction

Diffraction grating is commonly used as dispersive elements in many optical systems for applications such as spectrometers, switching, external cavity lasers, tuning and trimming elements in dense wavelength-division multiplexing, visual display technology, etc., [1]. The diffraction efficiency is an important parameter which can significantly affect the energy divided by the optical diffraction system. For traditional gratings, the high diffraction efficiency can be very challenging to achieve at the necessary spectral region in the desired diffraction mode [2]. Therefore, a number of gratings have been created to improve the diffraction efficiency by relying on either fabrication techniques or optical modulation or optical configuration [1]. However, for a given grating, it is difficult to adjust the high-order diffraction efficiency since the absorption/transmission properties of the grating are usually unchangeable.

Currently, the absorption (transmission) and dispersion properties of an atomic medium can be easily changed via electromagnetically induced transparency (EIT) which is formed at least in a three-level atomic system [3]. In particular, in the presence of the coupling field, a quantum interference of transition probabilities can be established in the atomic system with respect to the probe field. As a result, the total probability can be completely suppressed or enhanced [4]. At the spectral region corresponding to the suppressed probability, the probe field is completely transmitted through the atomic sample, whereas in the spectral region corresponding to the enhanced probability, the probe field is absorbed almost completely (called as electromagnetically induced absorption-EIA). On the other hand, if the coupling beam is a standing wave field, it will cause in space a periodic modulation of the transmitted spectrum of the probe field. That is, the probe field propagates through the atomic sample just as it passes through a diffraction grating [5]. Depending on the amplitude or phase modulation of the transmittance function, the absorption grating or phase grating can be formed. Furthermore, a typical property of the EIT medium is that one can easily change the absorption (transmission) and dispersion by the external magnetic field, so that one can also switch between the absorption grating and the phase grating, and improve the high-order diffraction efficiency.

Experimentally, EIG was first observed with cold sodium atoms in MOT by M. Mitsunaga et al., in 1999 [6]. So far, theoretical and experimental studies on EIG have attracted great attentions [7,8,9,10,11] due to its potential applications in many fields, such as atoms velocimetry [12], realizing optical bistability [13], all-optical switching and routing [14], light storage [15], beam splitting and fanning [16], shaping a biphoton spectrum [17], and modern photonic devices [18], controlling multi-wave mixing processes [19], angular Talbot effect [20], giant Goos-Hänchen shifts [21], and plasmonic metasurfaces effects [22, 23].

The early studies of EIG in EIT-based three-level systems demonstrated that the probe field can be diffracted into the high-order directions and achieved high diffraction efficiencies. Recently, EIG efficiency has been greatly improved in various four-level atomic systems with the support of other external fields such as microwave field [24, 25] and magnetic field [26] as well as coherence effects such as coherent population trapping (CPT) [25], Kerr nonlinearity [27,28,29] and spontaneously generated coherence (SGC) [28,29,30]. Very recently, Lu Zhao has realized electromagnetically induced polarization grating in a degenerate five-level atomic system of ultracold ⁸⁷Rb atoms in a weak magnetic field regime [31]. This five-level system is a combination of two three-level configurations including lambda and ladder schemes for the two right and left circular polarization components of the probe field, therefore, two control laser fields must be used to excite the atom corresponding to the two configurations. The weak magnetic field is used to separate Zeeman magnetic sublevels, however, it is not shown explicitly in the interaction Hamiltonian, so it is difficult to see the influence of the magnetic field on the diffraction pattern. According to the arrangement of this five-level system, all-optical diffraction patterns were performed for both left circular (ladder) and right (lambda) circular polarized components of the probe field, and the first-order diffraction efficiency can be obtained up to 24.6%.

In fact, the atomic optical properties are simply and effectively controlled by the external magnetic field under EIT condition, such as light group velocity [32, 33], optical switching and optical bistability [34,35,36] and so on. Among such ways to improve high-order diffraction efficiency, using a static magnetic field to manipulate optical properties is a simpler and more economical approach compared to using optical fields for the same purpose because the static magnetic field can easily be created by a magnetic coil which is much cheaper than a laser system and it is easy to split the Zeeman atomic levels to form a multi-level atomic configuration. Nevertheless, optical excitation requires the suitable laser frequency to resonate with the selected atomic transition and multiple laser beams are also required to form a multi-level atomic system.

In this work, we use an external magnetic field as a “knob” to transfer the light energy from zero-order diffraction mode to high-order diffraction modes in a simple degenerate two-level atomic system. Under magnetic field, the influence of the intensity and the frequency of the laser fields on the diffraction pattern are also considered which can allow us to select the desired diffraction modes.

2 Theoretical model

Figure 1a depicts a two-level atomic system degenerating in a static magnetic field. Under this magnetic field, the degenerate energy levels of the atom are split into sub-magnetic levels according to the Zeeman effect. The levels $\left| 1 \right\rangle$ and $\left| 3 \right\rangle$ are sub-magnetic levels of the ground state, while the level $\left| 2 \right\rangle$ is an excited hyperfine state. The Zeeman shift of sub-magnetic levels of the ground states $\left| 1 \right\rangle$ and $\left| 3 \right\rangle$ is calculated by [35] $\hbar \Delta_{B} = \mu_{B} m_{F} g_{F} B$ with μ_B is the Bohr magneton, g_F is the Landé factor, and $m_{F} = \pm 1$ is the magnetic quantum number of the corresponding hyperfine level.

Fig. 1

a The degenerate two-level atomic sample placed in a static magnetic field and excited by the left-circularly polarized probe field on the transition $\left| 1 \right\rangle$ (m_F =  + 1) ↔ $\left| 2 \right\rangle$ (m_F = 0) and the right-circularly polarized standing-wave coupling field on the transition $\left| 3 \right\rangle$ (m_F = − 1) ↔ $\left| 2 \right\rangle$ (m_F = 0). b Orientations of probe and coupling laser fields, and external magnetic field propagating through the atomic sample

The atomic system is excited by the probe and coupling laser fields, in which the left-circularly polarized probe field is applied to the transition $\left| 1 \right\rangle$ (m_F =  + 1) ↔$\left| 2 \right\rangle$ (m_F = 0), while the right-circularly polarized standing-wave coupling field is applied to the transition $\left| 3 \right\rangle$ (m_F = − 1) ↔$\left| 2 \right\rangle$ (m_F = 0) to form a three-level lambda atomic configuration with an obtainable EIT window [35]. For this configuration, the magnetic field can move the position of the EIT window toward the short- or long-wavelength region [34,35,36]. In experimental realization [26], the magnetic field B is oriented in the y-direction, whereas the forward and backward components of the standing-wave coupling field are formed along the x-direction, and the probe field enters the medium in the z-direction, as shown in Fig. 1b. We also note that the atomic configuration in Ref. [26] used the π-polarized probe field which only interacts with one transition |F_g = 1, m_F =  $\left. 0 \right\rangle$ ↔|F_e = 0, m_F = $\left. 0 \right\rangle$, while the σ-polarized standing-wave coupling field interacts simultaneously with two transitions |F_g = 1, m_F = − $\left. 1 \right\rangle$  ↔|F_e = 0, m_F = $\left. 0 \right\rangle$ and |F_g = 1, m_F =  + $\left. 1 \right\rangle$  ↔|F_e = 0, m_F = $\left. 0 \right\rangle$to form a four-level lambda atomic configuration; in this case, the magnetic field does not change the position of the EIT window, but separates the transparent spectral region into two symmetric EIT windows through atomic resonance frequency.

We assume that the probe field is a travelling wave with angular frequency ω_p and is given by $\varepsilon_{p} = \tfrac{1}{2}E_{p} e^{{ - i\omega_{p} t + ik_{p} z}} + c.c.$, here E_p is the field amplitude and is unchanged along the x-direction, $k_{p} = \frac{2\pi }{{\lambda_{p} }}$ is the wave vector with $\lambda_{p}$ is the wavelength of the probe laser field. Meanwhile, the standing-wave coupling field with angular frequency ω_c is expressed by $\varepsilon_{c} = \tfrac{1}{2}E_{c} \sin (k_{cx} x)e^{{ - i\omega_{c} t + ik_{cz} z}} + c.c.$, where E_c is the constant amplitude, and the wave vector $\vec{k}_{c} = k_{cx} \hat{x} + k_{cz} \hat{z}$ with $k_{cx}$ can be written as $k_{cx} = \frac{2\pi \sin \phi }{{\lambda_{c} }} \equiv \frac{\pi }{\Lambda }$ and $\Lambda = \frac{{\lambda_{c} }}{2\sin \phi }$, $\lambda_{c}$ is the wavelength of the coupling field, the angle ϕ is made by the direction of the coupling field to the direction of the probe field and Λ is the distance between two consecutive nodes or antinodes. When adjusting the angle ϕ, the value of Λ is also changed.

Semi-classical theory can be used to describe the interaction between atom and laser fields. Total Hamiltonian H of the system is given by:

$$ H = \sum\limits_{n = 1}^{3} {\hbar \omega_{n} \left| n \right\rangle \left\langle n \right|} + \Omega_{p} e^{{ - i\omega_{p} t + ik_{p} z}} \left| 1 \right\rangle \left\langle 2 \right| + \Omega_{c} \sin \left( {\frac{\pi x}{\Lambda }} \right)e^{{ - i\omega_{c} t + ik_{cz} z}} \left| 3 \right\rangle \left\langle 2 \right| + c{\text{.c,}} $$

(1)

where, the Rabi frequencies $\Omega_{p} = d_{21} E_{p} /2\hbar$ and $\Omega_{c} = d_{23} E_{c} /2\hbar$ characterize the intensity of the probe and coupling fields, respectively; d₂₁ and d₂₃ are the dipole matrix elements for the transitions $\left| 1 \right\rangle$ ↔$\left| 2 \right\rangle$ and $\left| 3 \right\rangle$ ↔$\left| 2 \right\rangle$, respectively.

In laser fields, the time evolution of atomic states that are represented by the density matrix ρ is obeyed by the following Liouville equation:

$$ \dot{\rho } = - \frac{i}{\hbar }[H,\rho ] + \Gamma \rho , $$

(2)

where, the term $\Gamma \rho$ presents the relaxation mechanisms of system.

From Eqs. (1), (2) and using electric-dipole and rotating-wave approximations, we found the density matrix equations representing the atomic population and coherence of the system as:

$$ \dot{\rho }_{11}^{{}} = \Gamma_{31} (\rho_{33}^{{}} - \rho_{11}^{{}} ) + \Gamma_{21} \rho_{22}^{{}} - \frac{i}{2}\Omega_{p}^{{}} (\rho_{21} - \rho_{12}^{{}} ), $$

(3)

$$ \dot{\rho }_{33}^{{}} = \Gamma_{31} (\rho_{11}^{{}} - \rho_{33}^{{}} ) + \Gamma_{23} \rho_{22}^{{}} + \frac{i}{2}\Omega_{c}^{{}} \sin \left( {\frac{\pi x}{\Lambda }} \right)(\rho_{32}^{{}} - \rho_{23}^{{}} ), $$

(4)

$$ \dot{\rho }_{22}^{{}} = - (\Gamma_{23} + \Gamma_{21} )\rho_{22}^{{}} + \frac{i}{2}\Omega_{p}^{{}} (\rho_{21}^{{}} - \rho_{12}^{{}} ) - \frac{i}{2}\Omega_{c}^{{}} \sin \left( {\frac{\pi x}{\Lambda }} \right)(\rho_{32}^{{}} - \rho_{23}^{{}} ), $$

(5)

$$ \dot{\rho }_{21}^{{}} = - [\gamma_{21} - i(\Delta_{p} - \Delta_{B} )]\rho_{21}^{{}} + \frac{i}{2}\Omega_{p} (\rho_{22}^{{}} - \rho_{11}^{{}} ) - \frac{i}{2}\Omega_{c}^{{}} \sin \left( {\frac{\pi x}{\Lambda }} \right)\rho_{31}^{{}} , $$

(6)

$$ \dot{\rho }_{23}^{{}} = - {[}\gamma_{23} - i(\Delta_{c} { + }\Delta_{B} {)]}\rho_{23}^{{}} + \frac{i}{2}\Omega_{c} \sin \left( {\frac{\pi x}{\Lambda }} \right)(\rho_{22}^{{}} - \rho_{33}^{{}} ) - \frac{i}{2}\Omega_{p}^{{}} \rho_{13}^{{}} , $$

(7)

$$ \dot{\rho }_{31}^{{}} = - {[}\gamma_{31} - i(\Delta_{p} - \Delta_{c} - 2\Delta_{B} ){]}\rho_{31}^{{}} + \frac{i}{2}\Omega_{p} \rho_{32}^{{}} - \frac{i}{2}\Omega_{c}^{{}} \sin \left( {\frac{\pi x}{\Lambda }} \right)\rho_{21}^{{}} , $$

(8)

where, Γ_nm is the decay rate of the atomic population from the upper state $\left| n \right\rangle$ to the lower state $\left| m \right\rangle$, while γ_nm denotes the damping rate of the atomic coherence ρ_nm which can be represented as $\gamma_{nm} = \frac{1}{2}\left( {\sum\limits_{{E_{j} < E_{n} }} {\Gamma_{nj} } + \sum\limits_{{E_{m} < E_{j} }} {\Gamma_{jm} } } \right)$; $\Delta_{p} = \omega_{p} - \omega_{21}$ and $\Delta_{c} = \omega_{c} - \omega_{23}$ are the frequency detuning of the probe and coupling fields, respectively.

Under the weak field approximation, assuming that the atom is initially in the ground states $\left| 1 \right\rangle$ and $\left| 3 \right\rangle$ with the same populations, $\rho_{11}^{(0)} \approx \rho_{33}^{(0)} \approx 1/2$, and $\rho_{22}^{(0)} \approx 0$. By analytically solving the density matrix Eqs. (3) in the steady-state condition, the off-diagonal density matrix element ρ₂₁ corresponding to the probe response of the medium is obtained as:

$$ \rho_{21}^{{}} = \frac{{\frac{i}{2}\Omega_{p} (\rho_{22}^{(0)} - \rho_{11}^{(0)} )}}{{\gamma_{21} - i(\Delta_{p} - \Delta_{B} ) + \frac{{(\Omega_{c} /2)^{2} \sin^{2} \left( {\frac{\pi x}{\Lambda }} \right)}}{{\gamma_{31} - i(\Delta_{p} - \Delta_{c} - 2\Delta_{B} )}}}} \approx \frac{{ - i\Omega_{p} }}{2A}, $$

(9)

with

$$ A = \gamma_{21} - i(\Delta_{p} - \Delta_{B} ) + \frac{{(\Omega_{c} /2)^{2} \sin^{2} \left( {\frac{\pi x}{\Lambda }} \right)}}{{\gamma_{31} - i(\Delta_{p} - \Delta_{c} - 2\Delta_{B} )}}. $$

(10)

Quantitatively, the probe response of the medium is related to the density matrix by the relation $P = Nd_{21} \rho_{21} \equiv - \tfrac{1}{2}\varepsilon_{0} \chi_{21} E_{p}$. Thus, the probe susceptibility is calculated by:

$$ \chi_{21} = - \frac{{Nd_{21}^{{}} }}{{\varepsilon_{0} E_{p} }}\rho_{21} \equiv \frac{{Nd_{21}^{2} }}{{2\varepsilon_{0} \hbar }}\frac{i}{A}, $$

(11)

with N is the atomic density. We can separate the susceptibility χ₂₁ into real Re(χ₂₁) and imaginary Im(χ₂₁) parts which can be rewritten as:

$$ \chi_{{{21}}} = {\text{ Re}}(\chi_{{{21}}} ) \, + i{\text{Im}}(\chi_{{{21}}} ). $$

(12)

The propagation of the probe field through the atomic medium of length L is described by the Maxwell equation which is written in the slowly varying envelope approximation as follows:

$$ \frac{{\partial \varepsilon_{p} }}{\partial z} = i\frac{\pi }{{\varepsilon_{0} \lambda_{p} }}P. $$

(13)

Using the polarization $P = Nd_{21} \rho_{21} \equiv - \tfrac{1}{2}\varepsilon_{0} \chi_{21} E_{p}$, therefore, Eq. (8) can be rewritten as:

$$ \frac{{\partial \varepsilon_{p} }}{{\partial z^{\prime}}} = i\chi_{21} \varepsilon_{p} , $$

(14)

where $z^{\prime} = (\pi Nd_{21}^{2} /2\varepsilon_{0} \hbar \lambda_{p} )z$ and z’ can be made dimensionless when $(2\varepsilon_{0} \hbar \lambda_{p} /\pi Nd_{21}^{2} )$ has units of z. From Eq. (9) we obtain the normalized transmission function of probe field for the effective length L of the medium as:

$$ T(x) = e^{{ - {\text{Im}} (\chi_{21} )L}} e^{{i{\text{Re}} (\chi_{21} )L}} . $$

(15)

where, the terms $e^{{ - {\text{Im}} (\chi_{21} )L}}$ and $e^{{i{\text{Re}} (\chi_{21} )L}}$ are associated with absorption and phase modulations of the grating, respectively. The Fraunhofer diffraction pattern of the probe field can be obtained by the Fourier transform of the transmission function T(x), as follows:

$$ I_{p} (\theta ) = \left| {F(\theta )} \right|^{2} .\frac{{\sin^{2} (M\pi \sin (\theta )R)}}{{M^{2} \sin^{2} (\pi \sin (\theta )R)}}, $$

(16)

$$ F(\theta ) = \int\limits_{0}^{1} {T(x)\exp ( - 2i\pi x.\sin (\theta )R)dx} , $$

(17)

where θ is the diffraction angle of the probe field associated with the z-direction, R = Λ/λ_p, and M is the parameter that characterizes the spatial width of the probe field. The diffraction order k is defined as k = Rsinθ. The intensity of the k^th-order diffraction pattern is determined by:

$$ I_{p} (\theta_{k} ) = \left| {F(\theta_{k} )} \right|^{2} \equiv \left| {\int\limits_{0}^{1} {T(x)\exp ( - i2k\pi x)dx} } \right|^{2} , $$

(18)

where k = 0, 1, 2, corresponding to the zero-, first-, second- order diffractions.

3 Results and discussion

This model can be realized in the cold ⁸⁷Rb atom confined in the magneto-optical trap (MOT) [38], where the designated states can be selected as: $\left| 1 \right\rangle$  =|5S_1/2, F = 1, m_F = − $\left. 1 \right\rangle$, $\left| 3 \right\rangle$ = |5S_1/2, F = 1, m_F =  + $\left. 1 \right\rangle$ and $\left| 2 \right\rangle$ =|5P_3/2, F = 0, m_F = $\left. 0 \right\rangle$. The atomic parameters are [34, 37]: N = 5 × 10¹⁷ atoms/m³, d₂₁ = 2.5 × 10^–29 C.m, Γ₂₁ = Γ₂₃ = 2π × 5.7 MHz, Γ₃₁ is the relaxation rate of the atomic population between the ground states $\left| 1 \right\rangle$ and $\left| 3 \right\rangle$ due to collisions of atoms which can be taken to be zero for ultracold atoms in MOT. The Landé factor g_F = − 1/2, and the Bohr magneton μ_B = 9.27401 × 10^–24 JT⁻¹. For simplicity of simulation, physical quantities with units of frequency are normalized by γ of the order of MHz. Accordingly, when the Zeeman shift Δ_B is normalized by γ, the magnetic field is also normalized by constant $\gamma_{c} = \gamma \hbar /(\mu_{B}^{{}} g_{F}^{{}} )$. For example, when taking the Zeeman shift Δ_B = 0.3γ, then the magnetic field strength $B = \Delta_{B} \hbar /(\mu_{B} m_{F} g_{F} )$ = 0.3γ_c = 2 × 10^–4 T. By using the analytic expressions (4), (11), (12) and (13), survey figures are easily constructed directly by maple or matlab software.

First, we demonstrate that the absorption (or transmission) spectrum of the atomic medium for the probe field (cw) varies periodically in space with the presence of the coupling field as a standing wave field. Indeed, Fig. 2a depicts the change of the absorption spectrum [Im(ρ₂₁)] according to the position in the atomic sample (x) and probe frequency detuning (Δ_p). It shows that at the node positions of the standing wave (in this case, x = 0, 4, 8, 12, 16) the probe absorption is maximum (and hence no light signal is transmitted through the atomic medium), whereas at antinode positions (x = 2, 6, 10, 14) the probe light field becomes transparent to the medium (i.e., it is completely transmitted). For example, in Fig. 2b the probe absorption spectrum is plotted at the atomic positions x = 0 (complete absorption) and x = 2 (complete transmission). This means that in the standing wave coupling field, the atomic sample acts like a diffraction grating for the probe field which can be observed the diffraction patterns, as shown in the figures below.

Fig. 2

a The variation of probe absorption spectrum Im(ρ₂₁) as a function of the atomic position x and probe detuning Δ_p. Other parameters are Ω_c = 2.5γ, Δ_c = 0, Δ_B = 0 (without magnetic field) and Λ = 4. b The probe absorption at different atomic positions: x = 0 (dashed line) and x = 2 (solid line)

Figure 3 shows the diffraction pattern of the probe field on the atomic sample with standing wave coupling field in the absence of the external magnetic field. From the figure we can observe that the zero-order, first-order and second-order diffractions are localized at sinθ = 0, sinθ =  ± 0.25 and sinθ =  ± 0.5, respectively. In this case, the results in Fig. 3 exhibit the absorption diffraction pattern which is formed based on the amplitude modulation of the transmission function, so that most of the probe light energy is distributed at the central maximum (zero-order diffraction). As the coupling field intensity increases, the zero-order diffraction efficiency also increases, while both the first- and second-order diffraction efficiencies decrease. Specifically, when Ω_c = 1γ, the zero-order diffraction efficiency reaches about 30%, and the first- and second- order diffraction efficiencies share proportions about of approximately 6% and 2%, respectively; by increasing the coupling intensity up to the value Ω_c = 3γ, the zero-order diffraction efficiency increases to about 70%, however, the first- and second-order diffraction efficiencies decrease to about 4% and 1.8%, respectively. This phenomenon is consistent with the transmission behavior of the probe field that as the coupling field intensity increases, the EIT efficiency (or transmission efficiency) also increases [5]. Therefore, the nondiffracted light part is very strong, and the light intensity mainly focuses at the center of the diffraction pattern and transmitted, whereas the available light becomes weaker for first- and second-order diffractions. Thus, the change in coupling intensity does not improve the high-order diffraction efficiencies.

Fig. 3

a The diffraction pattern of the probe field as a function of sinθ and coupling field intensity. b The diffraction pattern at different coupling intensities Ω_c = 1γ (solid line), Ω_c = 2γ (dashed line) and Ω_c = 3γ (dotted line). Other parameters are Δ_p = Δ_c = 0, M = 7, L = 30, R = 4 and B = 0

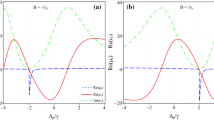
Now, we investigate the diffraction pattern of EIG in the presence of the external magnetic field. Figure 4a displays the probe diffraction pattern as a function of sinθ and magnetic field strength at the coupling intensity Ω_c = 2.5γ. From the figure we can easily observe that when the strength of the external magnetic field is increased, a large amount of energy of the probe field is transferred from zero-order diffraction to first-order diffraction. In particular, based on the sign of the magnetic field, the first-order diffraction intensity can be enhanced at the left diffraction angle when B is negative or the right diffraction angle when B is positive, enabling the diffraction intensity to be concentrated in a preferred mode. More explicitly, in Fig. 4b we plotted the diffraction pattern at a particular value of the magnetic field B =  ± 0.3γ_c (other parameters are the same as in Fig. 4a). It is clearly seen that when B = 0, the zero-order diffraction efficiency is about 65%, while first-order diffraction efficiency is about 3%; when B = 0.3γ_c (dashed line), the zero-order diffraction efficiency is reduced from 65 to 15%, while the first-order diffraction efficiency (at the right angle) is increased up to 32%. Similarly, when B = − 0.3γ_c (dotted line), the first-order diffraction efficiency (at the left angle) is also increased up to 32%. To explain these phenomena, we plotted the absorption and dispersion spectra of the probe field at different values of the magnetic field strength, as shown in Fig. 5. From Fig. 5a, we can see that the center of the EIT window is shifted to the right or left when B = 0.3γ_c or B = − 0.3γ_c, respectively, which increases absorption in the atomic resonance region Δ_p = 0; moving the position of the EIT window also shifts the dispersion curves as we can see in Fig. 5b, this means that at the resonant frequency Δ_p = 0, the dispersion is zero when B = 0 and it is increased when B =  ± 0.3γ_c. In the case of non-zero dispersion (and with small absorption), the phase diffraction pattern is formed based on the phase modulation of the transmission function, which cause the energy transformation from zero-order diffraction to high-order diffractions and enhance the efficiency of the high-order diffractions at the right or left angle (see the dashed or dotted line in Fig. 4b). Besides, in Ref. [26] the magnetic field (both negative and positive signs) increases the probe absorption at the resonant frequency and reduces the absorption on either side of the atomic resonance. This leads to the light energy transformation from zero-order diffraction to first-order diffraction for both left and right angles equally.

Fig. 4

a The diffraction pattern of the probe field as a function of sinθ and magnetic field strength. b The diffraction pattern of the probe field at different magnetic field strength B = 0 (solid line), B = 0.3γ_c (dashed line) and B = -0.3γ_c (dashed line). Other parameters are Δ_p = Δ_c = 0, M = 7, L = 30, R = 4 and Ω_c = 2.5γ

Fig. 5

The absorption (a) and dispersion (b) spectra of the probe field at different magnetic field strength B = 0 (solid line), B = 0.3γ_c (dashed line) and B = -0.3γ_c (dashed line). Other parameters are: Δ_p = Δ_c = 0, M = 7, L = 30, R = 4 and Ω_c = 2.5γ

Next, in Fig. 6 we investigate the dependence of the diffraction pattern on the probe detuning in the presence of magnetic field with B = − 0.3γ_c (a) and B = 0.3γ_c (b). This investigation enables us to select the appropriate probe frequency to achieve the desired diffraction mode. For instance, in the resonant frequency region, the first-order diffraction will prevail, while in regions far from resonance, the zero-order diffraction will prevail.

Fig. 6

The diffraction pattern of the probe field as a function of sinθ and probe detuning for the magnetic field strength B = -0.3γ_c (a) and B = 0.3γ_c (b). Other parameters are Δ_c = 0, M = 7, L = 30, R = 4 and Ω_c = 2.5γ

Similarly, in Fig. 7 we keep the probe detuning at Δ_p = 0 and investigate the dependence of the diffraction pattern on the coupling detuning. Similar to the dependence of the diffraction pattern on the magnetic field strength, the change in the coupling frequency detuning also leads to the transfer of light energy from zero-order diffraction to high-order diffractions. This is related to the fact that the quantities Δ_p, Δ_c and Δ_B are related to each other through two-photon resonance for the formation of the EIT in a three-level lambda system, i.e., Δ_p + Δ_c + Δ_B = 0. Therefore, with the change of Δ_c or Δ_B, the position of the EIT window is also shifted in the same way.

Fig. 7

The diffraction pattern of the probe field as a function of sinθ and coupling detuning for the magnetic field strength B = -0.3γ_c (a) and B = 0.3γ_c (b). Other parameters are Δ_p = 0, M = 7, L = 30, R = 4 and Ω_c = 2.5γ

By adjusting the strength and/or the sign of the external magnetic field, we can significantly improve the high-order diffraction efficiencies. To see more clearly the transformation of light energy from zero to higher order diffractions by the external magnetic field, in Fig. 8, we plotted the zero-, first- and second-order diffraction intensities according to magnetic field strength at the fixed values of Ω_c = 2.5γ and Δ_p = Δ_c = 0. The figure shows the energy transformation from zero-order diffraction to high-order diffraction as follows: when the strength of the external magnetic field increases from B = 0 to B = 0.3γ_c, the zero-order diffraction efficiency decreases rapidly and the first-order diffraction efficiency increases rapidly; when B = 0.3γ_c the first-order diffraction efficiency can reach the maximum value of about 32%, but the second-order diffraction becomes very dim; then the first-order diffraction efficiency increases and finally it decreases as the magnetic field increases from B = 0.3γ_c to B = 1γ_c; when B = 1γ_c, the zero-order diffraction efficiency is about 93% and the higher order diffraction becomes very weak. We also see that the second-order diffraction efficiency can be achieved about 5% at B = 0.1γ_c and B = 0.6γ_c. Thus, we can appropriately use the magnetic field to select the desired diffraction efficiency.

Fig. 8

Variations of the zero- (solid line), first- (dashed line) and second- (dotted line) order diffraction intensities $I_{p} (\theta_{k} )$ as a function of the magnetic field B. Other parameters are Δ_p = Δ_c = 0, M = 7, L = 30, R = 4 and Ω_c = 2.5γ

In Fig. 9, we compare the ability to transfer the light energy from zero-order diffraction to high-order diffractions in two cases: without and with external magnetic field. Specifically, we examine the variation of the diffraction intensity according to the coupling intensity with the absence of the magnetic field (Fig. 9a) and with the presence of the magnetic field (Fig. 9b). As the figures suggest, it is easy to observe that the ability to transfer energy from zero-order to high-order diffractions is very small with the absence of the magnetic field, and the zero-order diffraction intensity increases while the high-order diffraction intensities decreases with the coupling laser intensity increases; the zero-order diffraction efficiency can reach up to 90% when the coupling laser intensity is large enough (about Ω_c = 10γ) and the high-order diffractions are very dim. The situation is completely changed with the presence of the magnetic field, in particular, we can observe that there is the significant energy transmission from zero-order to high-order diffractions. Even in this case at Ω_c = 2.5γ, the first-order diffraction efficiency can achieve 32% greater than the zero-order diffraction efficiency (about 10%), and with Ω_c ≥ 4γ the zero-, first-, second-order diffraction efficiencies can achieve considerable values.

Fig. 9

Variations of the zero- (solid line), first- (dashed line) and second- (dotted line) order diffraction intensity $I_{p} (\theta_{k} )$ as a function of the coupling intensity Ω_c for the magnetic field B = 0 (a) and B = 0.3γ_c (b). Other parameters are Δ_p = Δ_c = 0, M = 7, L = 30 and R = 4

In Fig. 10, we consider the change in diffraction intensity according to the probe frequency detuning with other parameters are fixed at Ω_c = 2.5γ, Δ_c = 0 and B = 0.3γ_c. It is shown that, in the resonant frequency region, the first-order diffraction efficiency is greater than zero-order diffraction efficiency; in the region far from the resonant frequency, the first-order diffraction efficiency decreases while the zero- and second-order diffraction efficiencies are increased.

Fig. 10

Variations of the zero- (solid line), first- (dashed line) and second- (dotted line) order diffraction intensity $I_{p} (\theta_{k} )$ as a function of the probe detuning Δ_p for the magnetic field B = 0.3γ_c. Other parameters are M = 7, L = 30, R = 4, Δ_c = 0 and Ω_c = 2.5γ

Finally, Fig. 11 shows the dependence of diffraction intensity on the coupling frequency detuning with other parameters fixed at Ω_c = 2.5γ, Δ_p = 0 and B = 0.3γ_c. In the presence of external magnetic field, the probe light energy is transferred from zero-order diffraction to first- and second-order diffractions in the vicinity of the resonant frequency of the coupling field. The change in coupling frequency also leads to a shift of the EIT window position around the resonant frequency so that the two-photon resonance condition is satisfied.

Fig. 11

Variations of the zero- (solid line), first- (dashed line) and second- (dotted line) order diffraction intensity $I_{p} (\theta_{k} )$ as a function of the coupling detuning Δ_c for the magnetic field B = 0.3γ_c. Other parameters are M = 7, L = 30, R = 4, Δ_p = 0 and Ω_c = 2.5γ

4 Possible experimental realization

A possible structural diagram of MOT, probe and coupling laser beams, and magnetic field coil to study EIG under an external magnetic field is depicted in Fig. 12a. Meanwhile, Fig. 12b depicts the energy-level diagram for trapping of the ⁸⁷Rb atom and studying EIG. The magnetic field coils M₀ of MOT create a weak inhomogeneous magnetic field B₀ that produces a force $\vec{F} = \nabla (\vec{\mu }.\vec{B}_{0} )$ to confine the atoms, while at the trap center, B₀ = 0. The magnetic coil M creates a homogeneous magnetic field at MOT center that can cause changes in the diffraction pattern of the probe field as investigated above. Note that we can observe the EIG diffraction pattern in the MOT on/off modes as demonstrated in the EIT observation by Hopkins et al. [38]. Furthermore, to suppress the influence of MOT on the EIG diffraction pattern, the probe beam and the magnetic field B should be turned on after the trap is switched off [6, 7].

Fig. 12

a Schematic diagram of the experimental realization. M₀: magnetic field coils of MOT; T: MOT trapping laser beams; C: coupling laser beam acting as a repumping laser beam (R); P: probe laser beam; M: magnetic field coil for EIG investigation. b Energy-level diagram for trapping.⁸⁷Rb atoms, showing also the coupling and probe beams in EIG investigation. The MOT operates with the trapping beams are applied to the transition 5S_1/2 (F = 2) ↔ 5P_3/2 (F′ = 3), the coupling beam acting as the repumping beam is applied to the transition 5S_1/2 (F = 1, m_F = − 1) ↔ 5P_3/2 (F′ = 0, m_F = 0), and the probe beam is scanned through the transition 5S_1/2 (F = 1, m_F =  + 1) ↔ 5P_3/2 (F′ = 0, m_F = 0)

5 Conclusion

We used an external magnetic field to split the submagnetic levels of a degenerate two-level atomic system and form a three-level lambda atom system with only one control laser field for the formation of EIT and EIG. Here, the external magnetic field is explicitly introduced in the interaction Haminton, so it is easy to investigate the influence of the magnetic field on the EIT and EIG spectra. The degenerate two-level atomic model has the following advantages: First, the degenerate two-level atomic configuration does not allow simultaneous observation of the diffraction pattern of the two left and right circular polarization components like in a degenerate multi-level atomic configuration. However, we can still alternate the EIG pattern of the left or right circularly polarized component of the probe beam by changing the polarization of the control beam appropriately (EIG diffraction pattern of the two left and right circular polarization components are identical because of the same lambda configuration). Thus, it can still accomplish the same purpose as the degenerate multi-level atomic configuration; second, the degenerate two-level model is experimentally easier to implement than the multi-level atomic system because it uses fewer laser fields, in particular, trapping fields still have to be used as its implementation in MOT; third, in fact the EIG pattern is also very sensitive to the rate of decoherence between the two ground states (γ₃₁), specifically, the diffraction efficiency decreases as the rate of decoherence increases. In the degenerate two-level atomic model, this decoherence rate can be approximately zero in a cold atomic medium, so the diffraction efficiency is also increased. In our work, first-order diffraction efficiency can be obtained up to 32% with proper magnetic field strength. Furthermore, in the presence of the magnetic field, the probe light energy can also be transferred from zero-order diffraction to first- and second-order diffractions by adjusting the frequency and/or the intensity of the coupling and probe fields, which is difficult to achieve when the magnetic field is absent. Finally, the model can be experimentally implemented based on the proposal as in Sect. 4, in which the strength and the sign of the external magnetic field can be easily changed by adjusting the strength and direction of the current in the magnetic coil.