1 Introduction

Negative index material (NIM), often referred to as left-handed material (LHM) corresponding to simultaneous negative relative permittivity and relative permeability [1], has attracted considerable attention due to abnormal properties, such as reversals of Doppler shift and Cherenkov radiation [1], amplification of evanescent waves [2], subwavelength focusing [2,3,4], negative Goos–Hänchen shift [5], perfect lens [6], quenching spontaneous emission [7, 8], and so on. So far, there have been several methods to generate negative index materials including artificial composite metamaterials [9, 10], photonic crystal structures [11, 12], transmission line simulation [13], and chiral media [14,15,16,17]. However, these negative index materials usually occur in the high frequency range with accompanied strong absorption. Therefore, creating negative index materials in an optical frequency range without absorption is of great interest at present.

Over the last few years, the discovery of the EIT effect [18] has provided a simple method to achieve negative refractive index in the optical range with significantly reduced absorption. Indeed, Oktel et al. [19] and Shen et al. [20] first proposed a scheme for realization of the negative refractive index in a three-level lambda-type atomic medium under the EIT condition. Later, Krowne et al. [21] realized negative refractive index with low absorption using dressed-state mixed parity transitions of atom. Besides the three-level atomic configurations, several other studies on negative index materials have been carried out in four- and five-level atomic systems that can generate multiple frequency ranges of negative refractive index. For example, Thommen et al. [22] and Kastel et al. [23] achieved left-handed electromagnetic properties in four-level atomic systems. Liu et al. [24] shown that left-handed properties can be electromagnetically induced in \(\Lambda \)-type four-level scheme on the \(\hbox {Er}^{\mathrm {3+}}\):\(\hbox {YalO}_{\mathrm {3}}\) crystal. Zhang et al. [25] proposed a scheme for realization of the negative refractive index in a V-type four-level atomic system. Zhao et al. [26,27,28] produced a negative refractive index with vanishing absorption in the four-level system and showed negative refraction can be controlled by an incoherent pump field. Zhang et al [29] showed the negative permittivity and the negative permeability of the medium can be achieved simultaneously in a wider frequency band in a closed V-type four-level dense atomic vapor. Very recently, Othman et al. [30] demonstrated that a negative index of refraction can be achieved over a wide wavelength range with minimal absorption in a five-level atomic system, and Al-Toki et al. [31] studied negative refractive index in a double quantum dot and obtained a high negative refractive index corresponding to neglected absorption under applied electric fields between QD and QD.

Several studies in recent years have focused on switching between positive and negative refractive index. For example, Werner et al. [32] presented that the refractive index of a liquid crystal clad metamaterials can be changed from negative through zero to positive values via the liquid crystal tuning. Zhang et al. [33] proposed that the refractive index of a four-level loop atomic system can be switched from positive to negative by manipulating the relative phase of the applied fields. Ba et al. [34] showed that the position, bandwidth, and magnitude of refractive index of a four-level \(\Lambda \)-type atomic system can be manipulated by modulating the coherent and incoherent driving fields. Dutta et al. [35] and Osman et al. [36] also showed that the position and the band of the frequency region of negative refraction can be controlled by simply changing the incoherent pump rate or the relative phase of the optical fields in the presence of spontaneously generated coherence [37].

In our recent works, we have proposed to use an external magnetic field to control Kerr nonlinearity [38], optical bistability [39], and group velocity [40] in degenerated three-level atomic systems. In this paper, we show that the negative refractive index can be achieved in degenerated three-level atomic system under the EIT condition. The frequency band of the negative refractive index can be controlled by the coupling laser or the external magnetic field.

2 Theoretical model

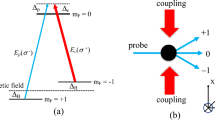
Figure 1 shows the configuration of a degenerated three-level \(\Lambda \)-type atomic system in an external magnetic field interacting with the probe and coupling fields. Here, we assume that the direction of the magnetic field (B) is parallel to the direction of the light beams. When the external magnetic field is applied, the ground-state sublevels \(|1\rangle \) and \(| 3\rangle \) is degenerated via the Zeeman effect. The Zeeman shift of the \(| 1\rangle \) and \(| 3\rangle \) levels is determined by [38] \(\hbar \Delta _{B} =\mu _{B} m_{F} g_{F} B\) with \(\mu _{B} \) is the Bohr Magneton, \(g_{F} \) is the Landé factor and \(m_{F} =\pm 1\) is the magnetic quantum number. We consider that the levels \(| 1\rangle \) and \(| 2\rangle \) have opposite parity, \(d_{21} = \left\langle 2 \right| {\mathbf {\hat{d}}}\left| 1 \right\rangle \ne 0\) where \(\mathbf {{\hat{{d}}}}\) is the electric dipole operator, while the levels \(| 1\rangle \) and \(| 3\rangle \) have the same parity, \(m_{31} =\left\langle 3 \right| {\mathbf {\hat{m}}}\left| 1 \right\rangle \ne 0\) where \(\mathbf {{\hat{{m}}}}\) is the magnetic dipole operator. Hence, the electric and magnetic components of the probe field with the same frequency \(\omega _{p}\) can drive the transitions \(| 1\rangle \leftrightarrow \) \(| 2\rangle \) and \(| 1\rangle \leftrightarrow | 3\rangle \) , simultaneously. The strong coupling field with the frequency \(\omega _{c}\) drives the transition \(| 3\rangle \leftrightarrow | 2\rangle \). Here, we choose the probe and coupling fields to be the left- (\(\sigma ^{\mathrm {-}})\) and right- (\(\sigma ^{\mathrm {+}})\) circularly polarized light, respectively. Therefore, the levels \(| 1\rangle , | 2\rangle \) and \(| 3\rangle \) can be chosen as \(| \hbox {S}_{\mathrm {1/2}} \hbox {F} = 1, \hbox {m}_{\mathrm {F}} = +1\rangle , |\) \(\hbox {P}_{\mathrm {3/2}} \hbox {F}\prime = 2, \hbox {m}_{\mathrm {F}} = 0\rangle \) and \(| \hbox {S}_{\mathrm {1/2}} \hbox {F} = 1, \hbox {m}_{\mathrm {F}} = -1\rangle \), respectively. The decay rates from the \(| 2\rangle \) level to the \(| 1\rangle \) and \(| 3\rangle \) levels are given by \(\gamma _{\mathrm {21}}\) and \(\gamma _{\mathrm {23}}\), respectively. The relaxation rate between the \(| 1\rangle \) and \(| 3\rangle \) ground states is denoted by \(\gamma _{\mathrm {31}}\).

Fig. 1
figure 1

The three-level \(\Lambda \)-type scheme of \(^{\mathrm {87}}\)Rb atom in an external magnetic field interacting with two laser fields. The dashed arrows correspond to excitations when B \(=\) 0

Full size image

The time-evolution equation of the system is obeyed the Liouville equation as follows:

$$\begin{aligned} \dot{{\rho }}=-\frac{i}{\hbar }[H,\,\,\rho ]+\Lambda \rho . \end{aligned}$$
(1)

where \(\Lambda \rho \) represents the relaxation processes.

In the interaction picture, the total Hamiltonian of the system can be written as

$$\begin{aligned} H=-\frac{\hbar }{2}\left[ {{\begin{array}{*{20}c} {2(\Delta _{p} -\Delta _{B} )} &{} {\Omega _{p} } &{} 0 \\ {\Omega _{p} } &{} {2(\Delta _{c} +\Delta _{B} )} &{} {\Omega _{c} } \\ 0 &{} {\Omega _{c} } &{} {2(\Delta _{p} -\Delta _{c} -2\Delta _{B} )} \\ \end{array} }} \right] . \end{aligned}$$
(2)

From equations (1) and (2), the density matrix equations of the system can be derived in the dipole and rotation wave approximations as follows:

$$\begin{aligned}&\dot{{\rho }}_{21} =-[\gamma _{21} +i(\Delta _{p} -\Delta _{B} )]\rho _{21} -\frac{i}{2}\Omega _{p} (\rho _{22} -\rho _{11} )\nonumber \\&\qquad \quad +\frac{i}{2}\Omega _{c} \rho _{31} , \end{aligned}$$
(3a)
$$\begin{aligned}&\dot{{\rho }}_{32} =-[\gamma _{23} -i(\Delta _{c} \text{+ }\Delta _{B} \text{)] }\rho _{32} +\frac{i}{2}\Omega _{c} (\rho _{22} -\rho _{33} )\nonumber \\&\qquad \quad -\frac{i}{2}\Omega _{p} \rho _{31} , \end{aligned}$$
(3b)
$$\begin{aligned}&\dot{{\rho }}_{31} =-[\gamma _{31} +i(\Delta _{p} -\Delta _{c} -2\Delta _{B} )]\rho _{31} -\frac{i}{2}\Omega _{p} \rho _{32} \nonumber \\&\qquad \quad +\frac{i}{2}\Omega _{c} \rho _{21} , \end{aligned}$$
(3c)

where \(\Delta _{p} =\omega _{p} -\omega _{21} \) and \(\Delta _{c} =\omega _{c} -\omega _{23} \) are the frequency detunings of the probe and coupling fields, respectively; \(\Omega _{p} =\frac{d_{21} E_{p} }{\hbar }\) and \(\Omega _{c} =\frac{d_{23} E_{c} }{\hbar }\) are, respectively, the Rabi frequencies of the probe and coupling beams with \(d_{mn}\) is the electric-dipole matrix element for the transition \(| m\rangle -| n\rangle \).

Next, we need to find the solutions for \(\rho _{\mathrm {21}}\) and \(\rho _{\mathrm {31}}\) in the steady state \(\partial \rho /\partial t=0\), which affect the electric and the magnetic responses of the medium for the probe light. Here, we assume that the atom initially populates in state \(|1\rangle \), namely,\(\rho _{11}^{(0)} \approx 1\), and \(\rho _{22}^{(0)} \approx \rho _{33}^{(0)} \approx 0\). From the system of three equations (3a)–(3c), the solutions for \(\rho _{\mathrm {21}}\) and \(\rho _{\mathrm {31}}\) are given by

$$\begin{aligned} \rho _{21}= & {} \frac{id_{21} E_{p} }{2\hbar }\frac{1}{\gamma +i(\Delta _{p} -\Delta _{B} )+\frac{(\Omega _{c} /2)^{2}}{\gamma _{31} +i(\Delta _{p} -\Delta _{c} -2\Delta _{B} )}}, \end{aligned}$$
(4)
$$\begin{aligned} \rho _{31}= & {} \frac{\frac{i}{2}\Omega _{c} }{\gamma _{31} +i(\Delta _{p} -\Delta _{c} -2\Delta _{B} )}\rho _{21} =-\frac{d_{21} E_{p} }{4\hbar }\frac{\Omega _{c} }{[\gamma _{21} +i(\Delta _{p} -\Delta _{B} )][\gamma _{31} +i(\Delta _{p} -\Delta _{c} -2\Delta _{B} )]+\Omega _{c}^{2} /4}. \end{aligned}$$
(5)

For an atomic gaseous medium, the electric susceptibility (\(\chi _{\mathrm {e}})\) and the magnetic susceptibility (\(\chi _{\mathrm {m}})\) are related to the density matrix elements by the following relations [20]:

$$\begin{aligned} \chi _{\mathrm{e}}= & {} \frac{2Nd_{21} }{\varepsilon _{0} E_{\mathrm{p}} }\rho _{21} , \end{aligned}$$
(6)
$$\begin{aligned} \chi _{\mathrm{m}}= & {} \frac{2Nm_{31} }{H_{\mathrm{p}} }\rho _{31} =\frac{2Nm_{31} }{\sqrt{\varepsilon _{\mathrm{r}} \varepsilon _{0} /\mu _{\mathrm{r}} \mu _{0} } E_{\mathrm{p}} }\rho _{31} , \end{aligned}$$
(7)

where N denotes the atomic density, \(d_{21}\) and \(m_{31}\) are, respectively, the electric and magnetic dipole matrix elements, \(E_{\mathrm{p}}\) and \(H_{\mathrm{p}}\) denote the electric and magnetic field envelopes of the probe field with \(H_{\mathrm{p}} =\sqrt{\varepsilon _{\mathrm {r}} \varepsilon _{0} /\mu _{\mathrm {r}} \mu _{0} } E_{\mathrm{p}} \), \(\varepsilon _{\mathrm {0}}\) and \(\mu _{\mathrm {0}}\) are the permeability of vacuum.

The relative permittivity (\(\varepsilon _{\mathrm {r}})\) and relative permeability \((\mu _{\mathrm {r}})\) of the atomic medium are defined in relation to the susceptibilities such that

$$\begin{aligned} \varepsilon _{\mathrm{r}}= & {} 1+\chi _{\mathrm{e}} , \end{aligned}$$
(8)
$$\begin{aligned} \mu _{\mathrm{r}}= & {} 1+\chi _{\mathrm{m}} . \end{aligned}$$
(9)

Substituting (4) into (6) and replacing (5) into (7), we obtain:

$$\begin{aligned} \chi _{\mathrm{e}}= & {} \frac{iNd_{21}^{2} }{\varepsilon _{0} \hbar }\frac{\gamma _{31} +i(\Delta _{p} -\Delta _{c} -2\Delta _{B} )}{[(\gamma _{21} +i(\Delta _{p} -\Delta _{B} )][\gamma _{31} +i(\Delta _{p} -\Delta _{c} -2\Delta _{B} )]+\Omega _{c}^{2} /4}, \end{aligned}$$
(10)
$$\begin{aligned} \chi _{\mathrm{m}}&=\frac{2Nm_{31} }{c\varepsilon _{0} E_{\mathrm{p}} }\sqrt{\frac{(1+\chi _{\mathrm{m}} )}{(1+\chi _{\mathrm{e}} )}} \rho _{31}\nonumber \\&=\frac{im_{31} }{2cd_{21} }\sqrt{\frac{(1+\chi _{\mathrm{m}} )}{(1+\chi _{\mathrm{e}} )}} \left( {\frac{\Omega _{c} }{\gamma _{31} +i(\Delta _{p} -\Delta _{c} -2\Delta _{B} )}} \right) \chi _{\mathrm{e}} , \end{aligned}$$
(11)

In Eq. (11), we used \(\rho _{21} =\frac{\varepsilon _{0} E_{p} \chi _{\mathrm{e}} }{2Nd_{21} }\) and \(c=1/\sqrt{\varepsilon _{0} \mu _{0} } \) is the speed of light in vacuum.

Taking the square of both sides of equation (11), we get:

$$\begin{aligned} \chi ^{2}_{\mathrm{m}} =-\frac{(1+\chi _{\mathrm{m}} )}{(1+\chi _{\mathrm{e}} )}\left( {\frac{m_{31} }{2cd_{12} }\frac{\Omega _{c} }{\gamma _{31} +i(\Delta _{p} -\Delta _{c} )}} \right) ^{2}\chi ^{2}_{\mathrm{e}} , \end{aligned}$$
(12)

And we set:

$$\begin{aligned} F=\frac{\chi _{\mathrm{e}} }{\sqrt{1+\chi _{\mathrm{e}} } }\left( {\frac{m_{31} }{2cd_{12} }\frac{\Omega _{c} }{\gamma _{31} +i(\Delta _{p} -\Delta _{c} )}} \right) . \end{aligned}$$
(13)

Therefore, equation (12) is rewritten as:

$$\begin{aligned} \chi _{\mathrm{m}}^{2} +F^{2}\chi _{\mathrm{m}} +F^{2}=0. \end{aligned}$$
(14)

Equation (14) has the following solutions:

$$\begin{aligned} \chi _{\mathrm{m}}^{\pm } =\frac{-F^{2}\pm \sqrt{F^{4}-4F^{2}} }{2} \end{aligned}$$
(15)

Thus, we can obtain the relative permittivity and the relative permeability as follows:

$$\begin{aligned} \varepsilon _{\mathrm{r}} =1+\frac{iNd_{21}^{2} }{\varepsilon _{0} \hbar }\frac{[\gamma _{31} +i(\Delta _{p} -\Delta _{c} -2\Delta _{B} )]}{[\gamma _{21} +i(\Delta _{p} -\Delta _{B} )][\gamma _{31} +i(\Delta _{p} -\Delta _{c} -2\Delta _{B} )]+\Omega _{c}^{2} /4}, \end{aligned}$$
(16)
$$\begin{aligned} \mu _{\mathrm{r}}^{\pm }= & {} 1+\frac{-F^{2}\pm \sqrt{F^{4}-4F^{2}} }{2}. \end{aligned}$$
(17)

As analyzed in Ref. [20], to be able to obtain a low-loss negative permittivity for the negative index medium, the negative root in (17) is required.

With the help of the expressions for the relative permittivity and the relative permeability, the refractive index of the medium can be determined by:

$$\begin{aligned} n=-\sqrt{\varepsilon _{\mathrm{r}} \mu _{\mathrm{r}} } . \end{aligned}$$
(18)
Fig. 2
figure 2

Real parts of relative permittivity (dotted line) and relative permeability (dashed line) versus probe laser detuning for different values of the coupling intensity \(\Omega _{\mathrm {c}} = 1\gamma \) (a) and \(\Omega _{\mathrm {c}} = 5\gamma \) (b) when \(\Delta _{\mathrm {c}} = 0\) and \(\hbox {B} = 0\). The dash-dotted line is absorption

Full size image
Fig. 3
figure 3

Real parts of relative permittivity (dotted line) and relative permeability (dashed line) versus probe laser detuning for different values of the coupling intensity \(\Omega _{\mathrm {c}} = 1\gamma \) (a) and \(\Omega _{\mathrm {c}} = 5\gamma \) (b) when \(\Delta _{\mathrm {c}} = 0\) and \(\hbox {B} = 0\). The dash-dotted line is absorption

Full size image

3 Results and discussion

Here, we used \(^{\mathrm {87}}\)Rb atoms to study the dependence of the negative refractive index on the external light and magnetic fields. The atomic parameters are [20, 41]: \(N = 10^{\mathrm {23}}\) atoms/\(\hbox {m}^{\mathrm {3}}\), \(d_{21} =2.5377\times 10^{-29}\,\mathrm{C}\,\mathrm{m}\), \(m_{31} =7.26\times 10^{-23}\,\mathrm{A}\,\mathrm{m}^{2}\), \(\gamma _{\mathrm {21}} = \gamma _{\mathrm {23}} = 5.3\,\mathrm{MHz}, g_{F} = -1/2\) and \(\mu _{B} = 9.27401\times 10^{\mathrm {-24}}\hbox {J/T}\). In the following numerical simulations, quantities with units of frequency are normalized by \(\gamma \) which has order of MHz for alkali atoms. In this approach, when the Zeeman shift \(\Delta _{{B}}\) is scaled by \(\gamma \), then the magnetic strength B should be in units of the combined constant \(\gamma _{c} =\gamma \hbar /(\mu _{B} m_{F} g_{F} )\) which also has the units of the Tesla. For example, if the Zeeman shift \(\Delta _{{B}} = 1\gamma \), then the magnetic field strength \(B=\Delta _{B} \hbar /(\mu _{B} m_{F} g_{F} )= 1\gamma _{\mathrm {c}}\).

Fig. 4
figure 4

Real parts of relative permittivity (dotted line) and relative permeability (dashed line) versus probe laser detuning for different values of the magnetic field \(\hbox {B} = -1\gamma _{\mathrm {c}}\) (a) and \(\hbox {B} = 1\gamma _{\mathrm {c}}\) (b) when \(\Omega _{\mathrm {c}} = 5\gamma \) and \(\Delta _{\mathrm {c}} = 0\). The dash-dotted line is absorption

Full size image
Fig. 5
figure 5

Real parts of relative permittivity (dotted line) and relative permeability (dashed line) versus the magnetic field for different values of the probe laser detuning \(\Delta _{\mathrm {p}} = 0\) (a) and \(\Delta _{\mathrm {p}} = 1\gamma \) (b)

Full size image

First, we turn off the external magnetic field (\({B} = 0\) or \(\Delta _{{B}} = 0\)) and investigate the dependence of the negative refractive index on the coupling laser field. The influence of the coupling laser intensity on the real parts of relative permittivity (dotted line) and relative permeability (dashed line) for the probe laser is shown in Fig. 2, where we have fixed the coupling laser frequency to coincide with the resonant frequency of the transition \(| 3\rangle \leftrightarrow | 2\rangle \), whereas the Rabi frequency of the coupling laser is chosen as \(\Omega _{\mathrm {c}} = 1\gamma \) (a) and \(\Omega _{\mathrm {c}} = 5\gamma \) (b). We can see from Fig. 2a that the relative permittivity has a negative real part in the frequency detuning range [0, 0.5\(\gamma \)], while the relative permeability is negative in the range [0, 0.2\(\gamma \)]. Thus, the real parts of permittivity and relative permeability are simultaneously negative in the range [0, 0.2\(\gamma \)] and the medium exhibits left-handed property in the range [0, 0.2\(\gamma \)]. In particular, in this range, the medium has very small absorption due to the EIT effect established. In Fig. 2b with \(\Omega _{\mathrm {c}} = 5\gamma \), we also see that both of permittivity and relative permeability are simultaneously negative in the range [\(0, 0.5\gamma \)]. This means that, as the intensity of the coupling laser is increased, the frequency band of the negative refractive index is also expanded. It is because the width of the EIT window is also increased when the coupling laser intensity increases.

In Fig. 3, we consider the dependence of the negative refractive index on the coupling laser frequency when fixed the coupling laser intensity at \(\Omega _{\mathrm {c}} = 5\gamma \). Here, we plotted the real parts of relative permittivity (dotted line) and relative permeability (dashed line) versus the probe laser for different values of the coupling frequency \(\Delta _{\mathrm {c}} = -1\gamma \) (a) and \(\Delta _{\mathrm {c}}= 1\gamma \) (b). It can be seen from Fig. 3 that the real parts of relative permittivity and relative permeability are simultaneously negative in the range [\(-1\gamma \), \(0.5\gamma \)] when \(\Delta _{\mathrm {c}} = -1\gamma \) and in the range [\(1\gamma \), \(1.5\gamma \)] when \(\Delta _{\mathrm {c}} = 1\) \(\gamma \). That is, the position of negative refractive index is shifted to the low frequency domain when \(\Delta _{\mathrm {c}} = -1\gamma \), and shifted to the high frequency domain when \(\Delta _{\mathrm {c}} = 1\gamma \) compared with the case \(\Delta _{\mathrm {c}} = 0\). This is because when changing the coupling laser frequency, the position of the EIT window is also changed according to the two-photon resonance condition.

In the next investigations, we fix the parameters of the coupling laser at \(\Omega _{\mathrm {c}} = 5\gamma \) and \(\Delta _{\mathrm {c}} = 0\), and study the influence of the external magnetic field on the negative refractive index. In Fig. 4, we plotted the real parts of relative permittivity (dotted line) and relative permeability (dashed line) versus the probe laser detuning when B \(=\) \(-1\gamma _{\mathrm {c}}\) (a) and \(\hbox {B} = 1\gamma _{\mathrm {c}}\) (b). It can find that the real parts of relative permittivity and relative permeability have simultaneously negative value in the range [\(-2\gamma \), \(-1.5\gamma \)] when \(\hbox {B} = 1\gamma _{\mathrm {c}}\) and in the range \([2\gamma \), \(2.5\gamma \)] when \(\hbox {B} = 1\gamma _{\mathrm {c}}\). This means, the frequency band of negative refractive index is also shifted to the low frequency domain when \(\hbox {B} = -1\gamma _{\mathrm {c}}\), and shifted to the high frequency domain when \(\hbox {B} = 1\gamma _{\mathrm {c}}\) compared with the case B \(=\) 0.

In Fig. 5, we consider variation of the real parts of relative permittivity (dotted line) and relative permeability (dashed line) versus the magnetic field when fixed the probe laser detuning at \(\Delta _{\mathrm {p}} = 0\) (a) and \(\Delta _{\mathrm {p}} = 1\gamma \) (b). From Fig. 5, we can find the value domains of the magnetic field such that the medium exhibits negative refractive index, namely \(-0.25\gamma _{\mathrm {c}}\) < B < 0 for \(\Delta _{\mathrm {p}} = 0\) and \(0.25\gamma _{\mathrm {c}}\) < B < \(0.5\gamma _{\mathrm {c}}\) for \(\Delta _{\mathrm {p}} = 1\gamma \). Thus, the external magnetic field can be used as a “knob” to switch positive refractive index into negative refractive index and vice versa. This can give us a convenient way to obtain the desired material with positive or negative index and to control the electromagnetic and optical properties of the material such as Doppler shift and Cerenkov effect, light amplification/absorption and focusing, Goos–Hänchen shift, and so on. This physical phenomenon can be explained that a change in the external magnetic field can lead to a transition between EIT and EIA or between normal and anomalous dispersions [39].

4 Conclusion

The expressions of the relative permittivity and the relative permeability in a degenerated three-level \(\Lambda \)-type atomic system have been derived as a function of the laser parameters and the external magnetic field. Under the EIT condition, the negative refractive index of the system has achieved in an optical frequency band. The position and the band width of the negative refractive index can be controlled by the coupling laser or the external magnetic field. In addition, by adjusting the strength or the sign of the magnetic field the positive refractive index can be converted to the negative refractive index and vice versa. This can give us a convenient way to obtain the desired material with positive or negative index and to control the electromagnetic and optical properties of the material.