1 Introduction

In the last two decades, THz sources have captured the special attention of researchers because of their remarkable influence in many fields like astronomy, spectroscopy, biomedical science, industry [1,2,3,4,5], material characterization, and communication [6, 7]. The various multipurpose properties of THz radiation like penetration through the nonpolar, and nonmetallic materials, nonionizing nature, and reflection by the metallic materials make THz radiations special radiations as compared to others. The cost and size of THz sources create the main hurdle in the development of THz technology [8,9,10,11]. To remove this hurdle, several schemes/techniques were proposed by various researchers. Kumar et al. [12,13,14,15,16,17] have used magnetized carbon nanotubes to enhance the THz generation. Vvedenskii et al. [18]. have studied the THz generation by using two-color lasers both experimentally and theoretically. The amplitude of the emitted THz field can be increased by many folds under the influence of static electric and magnetic fields [8, 19]. Houard et al. [20] have used filamentation to enhance the THz generation under the influence of a static electric field. The cross-focusing and self-focusing of Gaussian laser beams [21,22,23] have been used by researchers to enhance the THz generation. Along with it, a few more models have been developed for the THz generation by considering the interaction of high-intensity laser beams with preformed plasma [24, 25]. In the preformed plasma, both the co-propagating laser beams exert a nonlinear ponderomotive force on the plasma electrons at beat frequency [8, 26]. This nonlinear ponderomotive force is directly proportional to the intensity of the incident laser beams. The non-uniform intensity profile of the incident laser beam provides the nonlinear velocity to the electrons of the magnetized plasma. This nonlinear velocity oscillates at the same frequency as that of the nonlinear ponderomotive force. The coupling between nonlinear velocity and density results in enhanced nonlinear current density. The strong current density is further responsible for the enhancement in the efficiency of the THz generation at the beat frequency. The laser beams with different spatial density profiles have shown different behavior in plasma. Therefore, researchers have used various laser beam profiles like Gaussian, super-Gaussian, cosh-Gaussian, and dark hollow Gaussian [27, 28] for better efficiency of THz generation. Out of these, we prefer the dark hollow Gaussian profile [29,30,31] in the present work because of its special characteristics. The special characteristics of DHLB include various gradients in the distribution of laser intensities, having central dark spots, and as a result different cross-sections in other laser beam profiles. It further results in different ponderomotive forces and therefore different nonlinear currents and hence distinctive and special THz radiation. In the present scheme, a dark hollow Gaussian laser beam can be defined as a ring-shaped laser beam with minimum field intensity at the center of the beam axis. If one considers the ideal conditions then DHLB can be used as an optical laser beam with null intensity at the center. Such laser beams have been attracted by a lot of researchers, because of their utilization in many applications like laser optics, optics-communication, etc. [32,33,34].

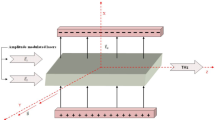
In the present analysis, the dark hollow laser beams are polarized along the x-axis and co-propagating along the z-direction in the underdense magnetized plasma. To magnetize the plasma, the static magnetic field is applied along the y-direction as shown in Fig. 1. The static DC electric field is applied along the x-direction. Both the static magnetic and electric fields are transverse to the direction of propagation of DHLBs. The magnetic field can be externally applied by using a typical magnetic field circuit. For experiment purposes, this circuit may consist of current carrying coil with number of turns 1000, and magnetic core of a mean length of \({ }0.4\;{\text{m}},\) and a cross-sectional area of \({ }0.01\;{\text{m}}^2\) with an air gap of length \(0.01\;{\text{m}}\) and cross-sectional area of \({ }0.0001\;{\text{m}}^2 .\) For iron core with magnetic permeability \( {\upmu }_{{\text{iron}}} = 1000\), a current of \(50{ }\;{\text{A}}\) produces a magnetic field of \(\ 60\;{\text{kG}}\), which is appropriate to the required calculations in our manuscript. The D.C. electric field can be applied with the help of two metallic plates keeping one plate at positive potential and the other at negative potential. We have analyzed the effect of the DC electric field, static magnetic field, and laser parameters on the THz generation. This paper has been arranged into five sections. The nonlinear current density and THz generation have been discussed in Sect. 2. In Sect. 3, we have provided calculations for the efficiency of emitted THz radiation under the influence of mutual interactions of DHLBs and THz radiation with magnetized plasma. In Sect. 4, numerical analysis, graphs, and result discussion are provided. The last section deals with the conclusion.

Fig. 1
figure 1

Schematic depiction of THz generation scheme by beating of DHLBs in magnetized plasma under the influence of D.C. electric field

Full size image

2 Nonlinear current density and THz generation

We consider an underdense and magnetized plasma under the influence of the static electric field. The static magnetic and electric fields are applied along the y and x-direction respectively. The applied static electric field, static magnetic field, and direction of propagation of DHLBs are mutually transverse to each other. The schematic of the present THz generation scheme is shown in Fig. 1. The DHLBs are the specific laser beams having minimum field intensity at the center. Such laser beams are of great importance because of their utilization in many applications like laser optics, optics-communication, etc. Based on the classification of DHLBs, the typical DHLBs can be generated by employing various experimental techniques like multimode fiber technique [35], optical holography technique [36], geometrical optical technique [37, 38], transverse mode converter technique [39], computer-generated hologram [40], hollow-fibers [41], and spatial filtering[42]. The holographic technique with the use of a spatial light modulator is suitable to generate the low-power hollow Gaussian beam of all orders according to the requirement, while geometrical optics and hollow optical fibers can generate the high-power hollow Gaussian beam at low orders. The nonlinear interaction processes known as three-wave mixing in a nonlinear crystal can be used to generate hollow Gaussian beams with high power and high orders. In the present work, DHLBs are polarized along the x-axis and co-propagating along the z-direction in the underdense plasma. According to Taherabadi et al. [43] and Cai et al. [44], the electric field profiles of the DHLBs can be expressed as the finite sum of the Gaussian laser beams represented by the following equation,

$$ {\vec{\text{E}}}_{\text{j}} = {\hat{\text{x}}}\mathop \sum \limits_{{\text{n}}_{\text{j}} = 1}^{{\text{N}}_{\text{j}} } {\text{E}}_{{\text{j}}0} \frac{{\left( { - 1} \right)^{{\text{n}}_{\text{j}} - 1} }}{{\text{N}}}\left[ {\begin{array}{*{20}c} {{\text{N}}_{\text{j}} } \\ {{\text{n}}_{\text{j}} } \\ \end{array} } \right]\left[ {{\text{exp}}\left( {\frac{{ - {\text{n}}_{\text{j}} {\text{x}}^2 }}{{{\text{r}}_0^2 }}} \right) - {\text{exp}}\left( {\frac{{ - {\text{n}}_{\text{j}} {\text{x}}^2 }}{{{\text{pr}}_0^2 }}} \right)} \right]{\text{e}}^{i\left( {{\text{k}}_{\text{j}} {\text{z}} - {\upomega }_{\text{j}} {\text{t}}} \right)} , $$
(1)

where, j = 1, 2 represents the laser index, and p is known as the dark-size adjusting parameter of the laser beam lying in the range \(0 \le {\text{p}} \le 1\). With this parameter, one can easily adjust the central dark size of the DHLBs. The term \(\left[ {\begin{array}{*{20}c} {{\text{N}}_{\text{j}} } \\ {{\text{n}}_{\text{j}} } \\ \end{array} } \right]\) in the electric field profile of DHLBs represents the binomial coefficient with the condition that \({\text{N}}_{\text{j}} > {\text{n}}_{\text{j}} > 0\). The binomial coefficient indicates the number of possible combinations of \({\text{n}}_{\text{j}}\) out of \({\text{N}}_{\text{j}}\). The term \({\text{N}}_{\text{j}}\) is the beam order of the respective laser beam. The area of the dark region across the DHLBs can be increased or decreased by varying the beam order and dark-size parameter. The positive and independent position coefficient \({\text{E}}_{{\text{j}}0}\) is known as the field of the amplitude of laser beams. The term \({\text{r}}_0\) determines the beam waist width of DHLBs. For maximum exposure of laser, beam waist width can be defined as the distance between the two diametrically opposite points in the corresponding cross-section of the beam, where the power per unit area is \(1/e\) times the peak power per unit area of the laser beam. One can adjust the central dark size of DHLBs by varying the value of p. The normalized intensity distribution of considered DHLBs for various values of p has been shown in Fig. 2. The area of the dark region of DHLBs can be increased by increasing the values of \({\text{N}}_{\text{j }} \;{\text{and}}\;{\text{p}}.\) By substituting \({\text{p}} = 0\;{\text{and}}\;{\text{N}}_{\text{j}} = 1\) in Eq. (1), we can get standard Gaussian laser beams. When DHLBs propagate and beat together in the underdense magnetized plasma, these lasers exert ponderomotive force on the electrons of the magnetized plasma at beat frequency \({\upomega } = {\upomega }_1 - {\upomega }_2\) and wavenumber \({\text{k}} = {\text{k}}_1 - {\text{k}}_2 .\) The frequency difference of DHLBs lies in the THz region. The static electric field is applied along the x-direction and it helps the electrons of plasma to experience drift in the opposite direction. This drift velocity is given by the following relation

$$ {\vec{\text{v}}}_{{\text{dc}}} = \frac{{ - {\text{e}}\vec{{\text{E}}}_{{\text{dc}}} }}{{{\text{m}}\upupsilon}}, $$
(2)

where, e, m, and \({\upupsilon }\) represent the electronic charge, electronic mass, and collision frequency of the electrons respectively. The schematic of THz generation by beating DHLBs in magnetized plasma under the influence of a D.C. electric field is shown in Fig. 1. As we have applied both D.C. electric field \({\vec{\text{E}}}_{{\text{dc}}}\) and static magnetic field \({\vec{\text{E}}}_{{\text{dc}}} \) perpendicular to each other and mutually perpendicular to the direction of propagation of DHLBs, the electrons of the plasma do not follow the electric field lines but instead, show drift. Hence, Debye shielding is not possible in this scheme. The DHLBs also impart oscillating velocities to the plasma electrons and are expressed as

$$ {\vec{\text{v}}}_{\text{j}} = \frac{{\text{e}}\vec{{\text{E}}}_{\text{j}} }{{{\text{m}}i{\upomega }_{\text{j}} }} $$
(3)
Fig. 2
figure 2

Normalized intensity distribution of DHLBs with transverse distance for different values of the dark-size parameter (p) keeping beam order of both DHLBs \({\text{N}}_1 = {\text{N}}_2 = 1\)

Full size image

The beating of DHLBs exerts a static ponderomotive force \({\vec{\text{F}}}_{{\text{SPF}}} = {\text{e}}\vec{\nabla }\phi_{{\text{SPF}}}\) and beat frequency ponderomotive force \({\vec{\text{F}}}_{{\text{BPF}}} = {\text{e}}\vec{\nabla }\phi_{{\text{BPF}}}\) on the electrons of plasma. Here \(\phi_{{\text{SPF}}}\) and \(\phi_{{\text{BPF}}}\) are known as the static and beat ponderomotive scalar potential respectively. The static ponderomotive potential can be calculated by using the relation, \( \phi_{{\text{SPF}}} = - \left( {{\text{e}}/4{\text{m}}} \right)\sum_{{\text{j}} = 1,2} {\left( {{\vec{\text{E}}}_{\text{j}} {\vec{\text{E}}}_{\text{j}}^{*} /{\upomega }_{\text{j}} } \right)}\) and it is given as

$$ {{\upphi }}_{{\text{SPF}}} = \frac{{ - {\text{e}}}}{{4{\text{m}}}}\left[ {\frac{{{\text{E}}_{10}^2 }}{{{\upomega }_1^2 }}{\text{f}}_1^2 \left( {{\text{n}}_1 ,{\text{x}}} \right) + \frac{{{\text{E}}_{20}^2 }}{{{\upomega }_2^2 }}{\text{f}}_2^2 \left( {{\text{n}}_2 ,{\text{x}}} \right)} \right], $$
(4)

where, \({\text{f}}\left( {{\text{n}}_1 ,{\text{x}}} \right){\text{ and f}}\left( {{\text{n}}_2 ,{\text{x}}} \right)\) are known as the function terms which are given as

$$ {\text{f}}_1 \left( {{\text{n}}_1 ,{\text{x}}} \right) = \mathop \sum \limits_{n_1 = 1}^N \frac{{\left( { - 1} \right)^{n_1 = 1} }}{{{\text{N}}_1 }}\left[ {\begin{array}{*{20}c} {{\text{N}}_1 } \\ {{\text{n}}_1 } \\ \end{array} } \right]\left[ {{\text{exp}}\left( {\frac{{ - {\text{n}}_1 {\text{x}}^2 }}{{{\text{r}}_0^2 }}} \right) - {\text{exp}}\left( {\frac{{ - {\text{n}}_1 {\text{x}}^2 }}{{{\text{pr}}_0^2 }}} \right)} \right]. $$
(5)
$$ {\text{f}}_2 \left( {{\text{n}}_2 ,{\text{x}}} \right) = \mathop \sum \limits_{n_2 = 1}^N \frac{{\left( { - 1} \right)^{n_2 = 1} }}{{{\text{N}}_2 }}\left[ {\begin{array}{*{20}c} {{\text{N}}_2 } \\ {{\text{n}}_2 } \\ \end{array} } \right]\left[ {{\text{exp}}\left( {\frac{{ - {\text{n}}_2 {\text{x}}^2 }}{{{\text{r}}_0^2 }}} \right) - {\text{exp}}\left( {\frac{{ - {\text{n}}_2 {\text{x}}^2 }}{{{\text{pr}}_0^2 }}} \right)} \right]. $$
(6)

One can easily calculate the beat frequency ponderomotive scalar potential by using the relation, \({{\upphi }}_{{\text{BPF}}} = - {\text{m}}\left( {{\text{v}}_1 .{\text{v}}_2^{*} } \right)/2\) and it is given as

$${{\upphi }}_{{\text{BPF}}} = - \frac{{{\text{eE}}_{10} {\text{E}}_{20} }}{{2{\text{m}}\upomega_1 {\upomega }_2 }}{\text{f}}_1 \left( {{\text{n}}_1 ,{\text{x}}} \right){\text{f}}_2 \left( {{\text{n}}_2 ,{\text{x}}} \right){\text{e}}^{i\left( {{\text{kz}} - {\upomega{\text{ t}}}} \right)} . $$
(7)

The static ponderomotive force causes ambipolar diffusion of plasma along the x-direction. In the steady state, the static ponderomotive force is well balanced by the pressure gradient force. It gives rise to zero frequency transverse density ripple which can be calculated by using the relation \( {\text{n}} = {\text{n}}_0 \left( {{\text{e }}\phi_{{\text{SPF}}} /{\text{T}}_{\text{e}} } \right)\). Here, we have assumed the Maxwellian distribution of electrons, and calculations are performed by using the linear term only. Here, \({\text{T}}_{\text{e}}\) is the equilibrium temperature of plasma electrons.

$$ {\text{n}} = \frac{{{\text{n}}_0 {\text{e}}^2 }}{{4{\text{mT}}_{\text{e}} }}\left[ {\frac{{{\text{E}}_{10}^2 }}{{{\upomega }_1^2 }}{\text{f}}_1^2 \left( {{\text{n}}_1 ,{\text{x}}} \right) + \frac{{{\text{E}}_{20}^2 }}{{{\upomega }_2^2 }}{\text{f}}_2^2 \left( {{\text{n}}_2 ,{\text{x}}} \right)} \right], $$
(8)

The beat frequency ponderomotive force and magnetic field force will control the motion of electrons by using equations of motion. As the static magnetic field is applied along the y-direction, therefore x and z-components of the velocity of plasma electrons are given as

$$ {\text{v}}_{{\omega x}} = \frac{{{\text{e}}^2 {\text{E}}_{10} {\text{E}}_{20} {\upomega }}}{{2{\text{m}}^2 {\upomega }_{\upalpha }^2 {\upomega }_1 {\upomega }_2 }}\left[ {{\text{f}}_3 \left( {\text{x}} \right) + 2i{\text{k}}\left( {\frac{{{\upomega }_{\text{c}} }}{{\upomega }}} \right){\text{f}}_4 \left( {\text{x}} \right)} \right]{\text{e}}^{i\left( {{\text{kz}} - {\upomega{\text{ t}}}} \right)} , $$
(9)
$$ {\text{v}}_{{\omega z}} = \frac{{{\text{e}}^2 {\text{E}}_{10} {\text{E}}_{20} {\upomega }}}{{2{\text{m}}^2 {\upomega }_{\upalpha }^2 {\upomega }_1 {\upomega }_2 }}\left[ {2{\text{kf}}_4 \left( {\text{x}} \right) + i\left( {\frac{{{\upomega }_{\text{c}} }}{{\upomega }}} \right){\text{f}}_3 \left( {\text{x}} \right)} \right]{\text{e}}^{i\left( {{\text{kz}} - {\upomega{\text{ t}}}} \right)} , $$
(10)

where, \({\upomega }_{\upalpha }^2 = \left( {{\upomega }^2 - {\upomega }_{\text{c}}^2 } \right)\) and the substitution terms \({\text{f}}_3 \left( {\text{x}} \right) {\text{and f}}_4 \left( {\text{x}} \right)\) are given as

$$ \begin{aligned} & {\text{f}}_3 \left( {\text{x}} \right) = \mathop \sum \limits_{{\text{n}}_1 = 1}^{{\text{N}}_1 } \mathop \sum \limits_{{\text{n}}_2 = 1}^{{\text{N}}_2 } \frac{{\left( { - 1} \right)^{{\text{n}}_1 + {\text{n}}_2 - 2} }}{{{\text{N}}_1 {\text{N}}_2 }}\left( {\frac{{ - 2{\text{x}}}}{{{\text{Pr}}_0^2 }}} \right)\left[ {\begin{array}{*{20}c} {{\text{N}}_1 } \\ {{\text{n}}_1 } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{N}}_2 } \\ {{\text{n}}_2 } \\ \end{array} } \right] \\ & \quad \left[ {{\text{n}}_1 \left[ {{\text{p}}.{\text{exp}}\left( {\frac{{ - {\text{n}}_1 {\text{x}}^2 }}{{{\text{r}}_0^2 }}} \right) - {\text{exp}}\left( {\frac{{ - {\text{n}}_1 {\text{x}}^2 }}{{{\text{pr}}_0^2 }}} \right)} \right]\left[ {{\text{exp}}\left( {\frac{{ - {\text{n}}_2 {\text{x}}^2 }}{{{\text{r}}_0^2 }}} \right) - {\text{exp}}\left( {\frac{{ - {\text{n}}_2 {\text{x}}^2 }}{{{\text{pr}}_0^2 }}} \right)} \right] + {\text{n}}_2 \left[ {{\text{exp}}\left( {\frac{{ - {\text{n}}_1 {\text{x}}^2 }}{{{\text{r}}_0^2 }}} \right) - {\text{exp}}\left( {\frac{{ - {\text{n}}_1 {\text{x}}^2 }}{{{\text{pr}}_0^2 }}} \right)} \right]\left[ {{\text{p}}.{\text{exp}}\left( {\frac{{ - {\text{n}}_2 {\text{x}}^2 }}{{{\text{r}}_0^2 }}} \right) - {\text{exp}}\left( {\frac{{ - {\text{n}}_2 {\text{x}}^2 }}{{{\text{pr}}_0^2 }}} \right)} \right]} \right]. \\ \end{aligned} $$
(11)
$$ {\text{f}}_4 \left( {\text{x}} \right) = \mathop \sum \limits_{{\text{n}}_1 = 1}^{{\text{N}}_1 } \mathop \sum \limits_{{\text{n}}_2 = 1}^{{\text{N}}_2 } \frac{{\left( { - 1} \right)^{{\text{n}}_1 + {\text{n}}_2 - 2} }}{{{\text{N}}_1 {\text{N}}_2 }}\left[ {\begin{array}{*{20}c} {{\text{N}}_1 } \\ {{\text{n}}_1 } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{N}}_2 } \\ {{\text{n}}_2 } \\ \end{array} } \right]\left[ {{\text{exp}}\left( {\frac{{ - {\text{n}}_1 {\text{x}}^2 }}{{{\text{r}}_0^2 }}} \right) - {\text{exp}}\left( {\frac{{ - {\text{n}}_1 {\text{x}}^2 }}{{{\text{pr}}_0^2 }}} \right)} \right]\left[ {{\text{exp}}\left( {\frac{{ - {\text{n}}_2 {\text{x}}^2 }}{{{\text{r}}_0^2 }}} \right) - {\text{exp}}\left( {\frac{{ - {\text{n}}_2 {\text{x}}^2 }}{{{\text{pr}}_0^2 }}} \right)} \right]. $$
(12)

The nonlinear electron density perturbation can be calculated by using the equation of continuity \(\partial {\text{n}}_{\upomega } /\partial {\text{t}} + \nabla .\left( {{\text{n}}_0 {\vec{\text{v}}}_{\upomega } } \right) = 0.\) This nonlinear density perturbation along the direction of wave propagation is given as

$$ {\text{n}}_{\upomega } = \frac{{{\text{n}}_0 {\text{e}}^2 {\text{E}}_{10} {\text{E}}_{20} }}{{2{\text{m}}^2 i{\upomega }_{\upalpha }^2 {\upomega }_1 {\upomega }_2 }}\left[ {2{\text{k}}^2 {\text{f}}_4 \left( {\text{x}} \right) + i\left( {\frac{{{\upomega }_{\text{c}} }}{{\upomega }}} \right)\frac{\partial }{\partial x}{\text{f}}_3 \left( {\text{x}} \right)} \right]{\text{e}}^{i\left( {{\text{kz}} - {\upomega{\text{ t}}}} \right)} . $$
(13)

One can calculate the nonlinear current density at the frequency \({\upomega }\) and wavenumber k by making nonlinear couplings between various nonlinear terms.

$$ {\text{J}}_{\upomega } = - {\text{en}}_0 {\text{v}}_{\upomega } - {\text{en}}_{\upomega } {\text{v}}_{{\text{dc}}} . $$
(14)
$$ {\text{J}}_{\upomega } = \frac{{{\text{n}}_0 {\text{e}}^3 {\text{E}}_{10} {\text{E}}_{20} {\upomega }}}{{2{\text{m}}^2 {\upomega }_{\upalpha }^2 {\upomega }_1 {\upomega }_2 }}\left[ {\left[ {\left( {\frac{{{\text{eE}}_{{\text{dc}}} }}{{{\text{m}}\upnu \upomega}}} \right)\left\{ {\left( {\frac{{{\upomega }_{\text{c}} }}{{\upomega }}} \right)\frac{\partial }{\partial x}{\text{f}}_3 \left( {\text{x}} \right) - 2{\text{k}}^2 {\text{f}}_4 \left( {\text{x}} \right)} \right\} + \left\{ {1 - \frac{{{\text{e}}^2 }}{{4{\text{mT}}_{\text{e}} }}\left( {\frac{{{\text{E}}_{10}^2 }}{{{\upomega }_1^2 }} + \frac{{{\text{E}}_{20}^2 }}{{{\upomega }_2^2 }}} \right){\text{f}}_4 \left( {\text{x}} \right)} \right\}{\text{f}}_3 \left( {\text{x}} \right)} \right]} \right]{\text{e}}^{{\text{i}}\left( {{\text{kz}} - {\upomega t}} \right)} , $$
(15)

Here \({\upomega }_{\text{c}}\) is known as the cyclotron frequency attained by the plasma electrons under the action of an applied external magnetic field. From Eq. (15), one can observe that nonlinear current density oscillates at frequency \({\omega }\) and wavenumber \({\text{k}}.\) By using Maxwell’s standard equations, the THz wave propagation equation is given as

$$ - \nabla^2 {\vec{\text{E}}}_{{\text{TH}}} + \vec{\nabla }\left( {\vec{\nabla }.{\vec{\text{E}}}_{{\text{TH}}} } \right) - \frac{{{\upomega }^2 }}{{{\text{c}}^2 }}\left( {{{\upepsilon }}{\vec{\text{E}}}_{{\text{TH}}} } \right) = - \frac{{4\uppi{\text{i}}\upomega}}{{{\text{c}}^2 }}{\vec{\text{J}}}_{\upomega } . $$
(16)

where, \({{\upepsilon }}\left( \omega \right)\) is known as plasma permittivity at the THz frequency and given by the relation \({{\upepsilon }}\left( \omega \right) = 1 - {\upomega }_{\text{p}}^2 /{\upomega }^2\). In relation, \({\upomega }_{\text{p}}\) is denoted as the plasma frequency and it is given as \({\upomega }_{\text{p}} = \left( {4{\pi n}_0 {\text{e}}^2 /{\text{m}}} \right)^{1/2}\). The transverse component of the THz electric field (by using Eq. (16)) can be written as

$$ \frac{{\partial^2 {\text{E}}_{{\text{TH}}} }}{{\partial {\text{z}}^2 }} + {\upbeta }^2 {\text{E}}_{{\text{TH}}} = - \frac{{4\uppi{\text{i}}\upomega}}{{{\text{c}}^2 }}{\text{J}}_{\upomega } , $$
(17)

where, \({\upbeta } = \left( {{\upomega }/{\text{c}}} \right)\sqrt {{{\upepsilon }}}\) and \({\text{R}} = - 4\uppi{\text{i}}\upomega {\text{J}}_{\upomega } /{\text{c}}^2 ,\) here c is the speed of electromagnetic waves in a vacuum. By using Eq. (15), one can simplify the R and it can be written as,

$${\text{R}} = - \frac{{i{\text{n}}_0 {\text{eE}}_{10} {\text{E}}_{20} {\upomega }^2 {\upomega }_{\text{p}}^2 }}{{2{\text{m}}{\upomega}_{\upalpha }^2 {\upomega }_1 {\upomega }_2 {\text{c}}^2 }}\left[ {\left[ {\left( {\frac{{{\text{eE}}_{{\text{dc}}} }}{{\text{m}}\upnu \upomega}} \right)\left\{ {\left( {\frac{{{\upomega }_{\text{c}} }}{{\upomega }}} \right)\frac{\partial }{\partial x}{\text{f}}_3 \left( {\text{x}} \right) - 2{\text{k}}^2 {\text{f}}_4 \left( {\text{x}} \right)} \right\} + \left\{ {1 - \frac{{{\text{e}}^2 }}{{4{\text{mT}}_{\text{e}} }}\left( {\frac{{{\text{E}}_{10}^2 }}{{{\upomega }_1^2 }} + \frac{{{\text{E}}_{20}^2 }}{{{\upomega }_2^2 }}} \right){\text{f}}_4 \left( {\text{x}} \right)} \right\}{\text{f}}_3 \left( {\text{x}} \right)} \right]} \right]{\text{e}}^{{\text{i}}\left( {{\text{kz}} - {\upomega{\text{ t}}}} \right)}.$$
(18)

The solution of the above Eq. (17) over the length L of the plasma column can be written as

$$ {\text{E}}_{{\text{TH}}} = \frac{{{\text{Re}}^{i{\beta L}} }}{{2{\upbeta }({\upbeta } - {\text{k}})}}\left[ {{\text{e}}^{ - i\left( {{\upbeta } - {\text{k}}} \right){\text{L}}} - 1} \right]. $$
(19)

By using Eq. (19), one can easily write the normalized THz amplitude as

$$\frac{{{\text{E}}_{{\text{TH}}} }}{{{\text{E}}_{10} }} = \frac{{ - {\text{i}}}}{{\sqrt {{{\upepsilon }}} \left( {\sqrt {{{\upepsilon }}} - 1} \right)}}\left( {\frac{{{\text{eE}}_{20} }}{{{\text{m}}{\upomega}{\text{c}}}}} \right)\left( {\frac{{\upomega }}{{{\upomega }_{\text{p}} }}} \right)^2 \left( {\frac{{{\upomega }_{\text{p}}^2 }}{{{\upomega }_1 {\upomega }_2 }}} \right)\left( {\frac{{{\upomega }_{\text{p}} }}{{{\upomega }_{\upalpha } }}} \right)^2 \left( {\frac{\omega }{\nu }} \right)\left[ {\left[ {\left( {\frac{{{\text{eE}}_{{\text{dc}}} }}{{{\text{m}}{\upnu} {\text{c}}}}} \right)\left\{ {\frac{1}{{{\text{k}}^2 }}\left( {\frac{{{\upomega }_{\text{c}} }}{{\upomega }}} \right)\frac{\partial }{{\partial {\text{x}}}}{\text{f}}_3 \left( {\text{x}} \right) - 2{\text{f}}_4 \left( {\text{x}} \right)} \right\} + \frac{1}{{\text{k}}}\left\{ {1 - \frac{{{\text{e}}^2 }}{{4{\text{m}}^2 {\text{c}}^2 ({\text{v}}_{{\text{th}}} /{\text{c}})^2_{ } }}\left( {\frac{{{\text{E}}_{10}^2 }}{{{\upomega }_1^2 }} + \frac{{{\text{E}}_{20}^2 }}{{{\upomega }_2^2 }}} \right){\text{f}}_4 \left( {\text{x}} \right)} \right\}{\text{f}}_3 \left( {\text{x}} \right)} \right]} \right],$$
(20)

where, \({\text{v}}_{{\text{th}}}\) is known as the thermal velocity of the plasma electrons.

3 THz efficiency under the influence of mutual interactions

In the present beating scheme of dark hollow laser beams in magnetized plasma under the influence of a D.C. electric field, we have achieved the normalized amplitude of emitted THz radiation of the order of \(\ 0.0220\) and this amplitude is higher than some other schemes [43, 45,46,47]. The efficiency of emitted THz radiation is also very important in many practical applications. The efficiency of emitted THz radiation can be calculated as the ratio of the energy of the THz radiation \(\left( {{\text{W}}_{{\text{TH}}} } \right)\) to the energy of propagating dark hollow laser beams \(\left( {{\text{W}}_{\text{L}} } \right)\). The average electromagnetic energy stored per unit volume is given by the relation

$$ {\text{W}}_{{\text{Ej}}} = \frac{ \in }{{8{\uppi }}}\frac{\partial }{{\partial {\upomega }_{\text{j}} }}\left[ {{\upomega }_{\text{i}} \left( {1 - \frac{{{\upomega }_p^2 }}{{{\upomega }_p^2 }}} \right)} \right]\left\langle {\left| {{\text{E}}_{\text{j}} } \right|^2 } \right\rangle . $$
(21)

By using Eq. (20) one can easily calculate the energy associated with emitted THz radiation \( \left( {{\text{W}}_{{\text{TH}}} } \right)\) and by using Eq. (21), efficiency \({\upeta }\) of the THz radiation is given as

$$ {\upeta } = \frac{{{\text{W}}_{{\text{TH}}} }}{{{\text{W}}_{\text{L}} }} = \frac{{{{\upepsilon }}\left| {{\text{E}}_{{\text{TH}}} } \right|^2 }}{{{{\upepsilon }}{\text{E}}_1^2 + {{\upepsilon }}{\text{E}}_2^2 }}. $$
(22)

According to Bakhtiari et al. [48], the numerical calculations performed by the above Eq. (22) to calculate the THz efficiency are said to be correct, when the transfer of energy from the incident dark hollow laser beams to the THz radiation is small or we can say that the above Eq. (22) is valid only if \({\upeta } \ll 1\). If the efficiency \({\upeta }\) is not very small then we have to use a self-consistent method. In this method, we have to consider the mutual interaction effects between the incident dark hollow laser beams, emitted THz radiations, and magnetized plasma. As a result, THz efficiency, by applying corrections can be given as

$$ {\upeta }^{\prime} = \frac{{\upeta }}{{1 + {\upeta }}}. $$
(23)

Now, we can say that \({\upeta }\) is the THz efficiency when no corrections are applied and \({\upeta}^{\prime}\) is the THz efficiency, when corrections have been applied by considering the various mutual interactions. Based on the above discussion, one can say that Eq. (22) is valid when the energy transfer between the incident dark hollow laser beams and THz radiation is very small. Whereas, Eq. (23) is valid for the small, medium, and large amounts of energy transfer between the incident laser beams and THz radiation. In the present scheme, the calculated conversion efficiency is of the order of \(\ 0.00082\) for the optimized values of the above-given parameters. In this scheme, one can obtain the THz radiation of desirable amplitude, power, and efficiency by optimizing the values of externally applied static electric and magnetic fields. By considering the effects of mutual interactions between the DHLBs and emitted THz radiation with magnetized plasma, we are providing more accurate results for the efficiency of THz radiation \(\left( {{\upeta }\ 0.00082} \right)\) and it seems to be quite more than some other schemes [43, 45,46,47]. Above all, THz radiations emitted in this way are provided with an option of varying and balancing the dark region with dark-size parameters, which is not possible in the case of Gaussian laser beams.

4 Results and discussion

To carry out numerical analysis for our proposed scheme, we have used the following DHLBs-plasma parameters along with the applied static electric and magnetic fields. Two carbon dioxide laser beams with angular frequencies \({\upomega }_{1{ }} = 2.40 \times 10^{14} \) rad/s and \({\upomega }_{2{ }} = 2.10 \times 10^{14} \) rad/s have been chosen in such a way that the frequency difference between the \({\upomega }_{1{ }} \;{\text{and}}\;{\upomega }_{2{ }} { }\) lie in the THz region. The corresponding wavelengths of carbon dioxide lasers are \({\uplambda }_1 = 7.90 \;{\mu m}\) and \({\uplambda }_2 = 9.0 \;{\mu m}\). The length of the plasma is of the order of \( 0.0005{ }\;{\text{m}}\). The intensities of both laser beams are of the order \({\text{I}} = 10^{14} \;{\text{W}}/{\text{cm}}^2 .{ }\) The initial beam waist width of DHLBs is \( {\text{r}}_0 = 100\;{\mu m}.\) The plasma frequency is \({\upomega }_{\text{p}} = 1.75 \times 10^{13} \;{\text{rad}}/{\text{s}}\) with electron number density \(1.25 \times 10^{23} \;{\text{m}}^{ - 3} .\) In the present scheme of THz generation, we have applied the static magnetic field in the range of 18 kG to 38 kG which can easily be attained in the laboratory [7, 8]. Also, the D.C. electric field is applied in the range of 25–45 kV/cm The dark-size parameter of DHLBs varies from p = 0.1–0.4. The beam order of both DHLBs varies from Nj = 1–3. The dependence of the normalized amplitude of emitted THz wave on the static magnetic field, electric field, collision frequency, normalized THz frequency, thermal velocity, dark size adjusting parameter, and beam order of DHLBs has been explained from Figs. 3, 4, 5, 6, 7 and 8.

Fig. 3
figure 3

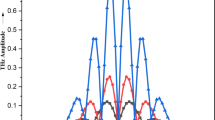
Variation of normalized THz amplitude with normalized THz frequency for different values of the static magnetic field at the optimized value of static electric field \({\text{E}}_{{\text{dc}}} = 45\;{\text{kV}}/{\text{cm}}\), beam order \({\text{N}}_1 = {\text{N}}_2 = 1\) and dark-size parameter \({\text{p}} = 0.1\)

Full size image
Fig. 4
figure 4

Variation of normalized THz amplitude with normalized THz frequency for different values of static electric field keeping other parameters same as that of Fig. 3

Full size image
Fig. 5
figure 5

Variation of normalized THz amplitude with the normalized THz frequency for various values of the normalized velocity of plasma electrons keeping other parameters same as that of Fig. 3

Full size image
Fig. 6
figure 6

Variation of normalized THz amplitude with normalized THz frequency for different values of DHLBs order keeping other parameters same as that of Fig. 3

Full size image
Fig. 7
figure 7

Variation of normalized THz amplitude with the collision frequency for various values of the static electric field keeping other parameters the same as that of Fig. 3

Full size image
Fig. 8
figure 8

Variation of normalized THz amplitude with normalized THz frequency for different values of the dark-size parameter of DHLBs keeping other parameters the same as that of Fig. 3

Full size image

In Fig. 3, we have plotted the graph between normalized THz amplitude and normalized THz frequency for different values of external static magnetic field \({\text{B }} = { }18\;{\text{kG}},\;{ }28\;{\text{kG}},\;{\text{and}}\;{ }38\;{\text{kG}}\) at the optimized value of static electric field \({\text{E}}_{{\text{dc}}} = 45\;{\text{kV}}/{\text{cm}}.\) From Fig. 3, one can easily notice that normalized THz amplitude increases with the increase of the applied static magnetic field. it is also observed that each curve shows an increase in normalized THz amplitude with the increase of normalized THz frequency and attains its maximum value at the resonance point. After attaining this peak value, normalized THz amplitude shows a decrease with the increase of normalized THz frequency. The physics behind this can be explained as: in the presence of the applied static magnetic field, nonlinearities in the system increase which results in the strong nonlinear current and hence, enhancement in the THz generation. It should be noted that we have applied the optimized value of the external magnetic \(38\;{\text{kG}}\) corresponding to the normalized cyclotron frequency \({\upomega }_{\text{c }} /{\upomega }_{\text{p }} = 0.45\) or less because abnormal behavior is observed for the higher values of the magnetic field [49]. Therefore, at the optimized value of the static magnetic field \(38\;{\text{kG}}\), more enhancement of THz generation is observed. Malik and Punia45 in their theoretical work on THz generation by using DHLBs obtained THz radiation of quite a high normalized amplitude on applying a static magnetic field of \(50\;{\text{kG}}\) whereas as in the proposed scheme, we have obtained THz radiation of normalized amplitude of 0.0220 on applying the static magnetic field of \(38\;{\text{kG}}\)\(38{\text{ kG}}.\) Bakhtiari et al. [48] have also explained the importance of the externally applied static magnetic field to enhance the THz generation.

Figure 4 represents the dependence of the normalized THz amplitude on the normalized THz frequency at different values of the applied static electric field \({\text{E}}_{{\text{dc}}} = 25{ }\;{\text{kV}}/{\text{cm}},\;{ }35\;{\text{kV}}/{\text{cm}},\;{\text{and}}\;{ }45\;{\text{kV}}/{\text{cm}},{ }\) when the beam order of DHLBs is N1 = N2 = 1. Other parameters have been kept the same as that of Fig. 3. It is observed that normalized THz amplitude increases with the increase of the applied static electric field. This is because on applying the static electric field, electric force \(\left( - {\text{e}} \vec{{\text{E}}}_{\text{dc}} \right)\) acts on the electrons of the plasma and provides drift to the electrons and makes the nonlinear current strong which leads to enhancing the efficiency of the THz generation. Thus, beat frequency ponderomotive force and D.C. electric force acting on the electrons of magnetized plasma, both are responsible for enhancing the THz amplitude of emitted THz radiation. It is revealed from each graph, that as one shifts to the right or the left from the resonance point, the normalized THz amplitude shows a decrease in its value. Bhasin and Tripathi [50] in their theoretical study of THz generation obtained the THz radiation of normalized amplitude of \(5.9 \times 10^{ - 5}\) by applying an external static electric field of \(50\;{\text{kV}}/{\text{cm }}\) whereas, in the proposed scheme we have achieved the THz radiation of normalized amplitude 0.0220 by applying the electric field of \(45\;{\text{kV}}/{\text{cm}}.\) Hourad et al. [20] have also demonstrated the effect of the external static electric field to enhance the THz generation in their experimental work.

Figure 5 illustrates the dependence of normalized THz amplitude on the normalized THz frequency by varying the normalized velocity \(\left( {{\text{v}}_{{\text{th}}} /{\text{c}}} \right)\) of the plasma electrons. Other parameters have been kept the same as that of Fig. 3. From the graph, one can notice that the normalized amplitude of the emitted THz wave attains its maximum value at \({\text{v}}_{{\text{th}}} /{\text{c}} = 0.18.\) Mehta et al. [51] have also seen that the THz amplitude attains its peak value at thermal velocity 0.19c and this corresponds to the electron temperature \({\text{ T}}_{\text{e}} \ 21\;{\text{keV}}\), which is a very high electron temperature. In our analysis, the thermal velocity of the plasma electrons is valid up to 0.18c. Figure 5 can also explain the dependence of normalized THz amplitude on the electron temperature of the plasma \({ }({\text{T}}_{\text{e}} )\). As the collision frequency \((\nu )\) of the electrons is proportional to the \({\text{T}}_{\text{e}}^{ - 3/2}\), therefore by increasing the temperature, the collision frequency of the electrons and ions decreases, and consequently normalized THz amplitude increases.

Figure 6 shows the variation of normalized THz amplitude with normalized THz frequency at optimized values of static electric and magnetic fields, by varying the order of respective DHLBs. From Fig. 6, one can easily interpret that normalized THz amplitude increases with the decrease in the value of \({\text{N}}_1 \;{\text{and}}\;{\text{N}}_2\). It is clear that THz generation becomes more efficient when \({\text{N}}_1 = {\text{ N}}_2 = 1.\) This is because the decrease in the value of the DHLB order results in a stronger ponderomotive force. This stronger ponderomotive force strengthens the nonlinear current which is responsible for the enhanced THz generation in the system. In special applications, where broad dark region is required one can use higher beam orders. In this way, the beam order of DHLBs also plays a significant role in the enhancement of the THz generation. This feature of DHLBs provides us the advantage over the Gaussian laser beam because, in the Gaussian laser beam, there is no such option available for changing the dark region of the THz field. The carbon dioxide DHLBs proposed in the scheme have an electric field amplitude of the order of \(5.8 \times 10^{10} \) V/m and the corresponding energy/power (P) can be calculated by using the relation \({\text{P}} = {\text{I}}.{\text{ A}} \cong 45\;{\text{ TW}},\) when the beam order of DHLBs is \({\text{N}}_1 = {\text{ N}}_2 = 1.\)

Figure 7 depicts the variation of the normalized THz amplitude with normalized collision frequency at different values of the static electric field \({\text{E}}_{{\text{dc}}} = 25\;{\text{kV}}/{\text{cm}},\;{ }35\;{\text{kV}}/{\text{cm}},\;{\text{and}}\;{ }45\;{\text{kV}}/{\text{cm}}.{ }\) Other parameters have been kept the same as that of Fig. 3. It is observed that the normalized THz amplitude increases with the decrease in the value of the normalized collision frequency. The reduction in the collision frequency leads to increase in the ponderomotive force and hence nonlinear current. It is clear from the fact that the DHLBs impart higher oscillatory velocity to the plasma electrons in the absence of collisions. Similar dependence has been noticed by Singh and Malik [52] in the analysis of THz generation under the effect of the external magnetic field. However, in the present scheme, we have investigated the effect of static electric field for the same.

Figure 8 shows the dependence of normalized THz amplitude on the normalized THz frequency at optimized values of static magnetic and D.C. electric fields (B = 38 kG and \({\text{E}}_{{\text{dc}}} = 45\;{\text{kV}}/{\text{cm}}\)) by varying the dark-size parameter of DHLBs. The other parameters have been kept the same as that of Fig. 3. To have matching conditions for different orders of DHLBs in THz generation, their power is assumed as same. Therefore, for such DHLBs, the maximum value of the electric field for different beam orders is considered constant. The power of incident DHLBs remains constant with respect to the value of the dark-size parameter. From Fig. 8, one can observe that a decrease in the value of the dark-size parameter \(({\text{p}})\) results in the increase of the normalized THz amplitude. This is because decreasing the value of dark-size parameter \({\text{p}}\) results in the decrease of dark region area, which further results in the increase of efficiency of radiation mechanism and hence, significant enhancement of THz generation is observed. Moreover, the dark-size parameter can be varied according to the requirement and nature of the application in the various THz technologies. Thus, the dark-size parameter can be employed for enhancing the normalized THz amplitude. Bakhtiari et al. [53] in their analysis of THz generation by using two DHLBs have shown the dependence of THz efficiency on the dark-size parameter by varying the \({\text{p}}\) from 0.1 to 0.4 whereas, in the proposed scheme, we have shown better results by varying the \({\text{p }}\) from 0.1 to 0.3. The dark-size parameter is very significant in DHLBs because, in the case of Gaussian laser beams, one cannot have any option for changing the dark region of emitted radiations. No doubt that Gaussian laser beams consist of a wide area with high intensity as compared to DHLBs but even then in the present scheme, we preferred the DHLBs because the emitted THz radiations obtained are sensitive to the intensity and dark-size parameter. Hence, one can easily tune the frequency of the emitted THz radiations to use these radiations in modern medical applications like investigating the samples of histopathology, Bessel cell carcinoma tissues, and the treatment of tumors [54]. Moreover, in the proposed scheme, we are also using carbon dioxide DHLBs, which are easily available in modern research laboratories and found to be very suitable and useful in many medical applications especially in surgical procedures because water present in the human body is capable of absorbing the laser beam. It provides an added advantage to our mentioned applications in the manuscript. Hence, the proposed scheme can be implemented practically to use the emitted THz radiations in the above-stated medical applications.

It is also observed that DHLBs have been used as a powerful tool by researchers to study nonlinear particle dynamics both experimentally and theoretically [43, 46, 47]. As a result, it can be used to generate the enhanced normalized THz field amplitude and efficiency by varying various parameters associated with it like a dark-size parameter, beam order, static magnetic field, D.C. electric field, beating frequency, collision frequency, the thermal velocity of plasma electrons, etc. as explained in the above graphical and numerical analysis.

5 Conclusion

In the present scheme of THz generation, we have employed two DHLBs with the same power at different beam orders in the underdense and magnetized plasma under the effect of the D.C. electric field. The effects of various parameters like DHLB beam order, collision frequency, dark-size adjusting parameter, thermal velocity, beating frequency, and D.C. electric and static magnetic fields have been analyzed properly. The significant enhancement in the efficiency of THz generation is observed with the increase of D.C. drift of the electrons due to the applied D.C. electric field. The normalized THz amplitude also shows a strong dependence on the normalized thermal velocity of the plasma electrons. One can easily vary the normalized amplitude, power, and efficiency of emitted THz radiations with the applied D.C. electric and magnetic fields. The emitted THz radiations can also be well tuned by chosing the optimized values of the static electric and magnetic fields applied mutually perpendicular to the direction of THz generation.We have also considered the mutual interactions between the DHLBs and emitted THz radiation with the magnetized plasma to provide more accurate results. In this way, we can develop a proper THz source for the investigation of histopathological samples, Bessel cell carcinoma tissues, and the treatment of tumors.