Introduction

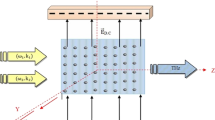
After the rapid development and progress of compact and efficient THz sources, THz technology has proved its advantage in numerous applications in almost every field of life. At present, the THz technology can be used in pharmaceutical industries, security checks [1,2,3,4], remote sensors, communication purposes [5,6,7], and engineering sciences [8,9,10] but still its full potential has not been tapped by the researchers. All over the world, researchers are trying to provide various new schemes of efficient THz generation to tap its full potential. For this, they are using different theoretical and experimental mechanisms. Every mechanism has a common aim to enhance the normalized THz amplitude. Some of the important mechanisms are given as the optical rectification of laser beams [11], carbon nanotubes by using the concept of anharmonicity [12,13,14,15], cross and self-focusing of laser beams [16,17,18], beating of dark hollow laser beams [19], optical mixing of laser beams [20,21,22,23,24,25] filamentation, and amplitude modulated laser beams [26,27,28,29], etc. Different laser profiles like fundamental Gaussian, cosh-Gaussian, etc. have been employed by the researchers to generate THz radiation [25, 30, 31]. The fundamental Gaussian laser has been studied extensively in laser-plasma interactions because of the special focusing properties associated with this laser profile. In the present paper, we have used the amplitude-modulated Gaussian laser beams propagating in the magnetized plasma because of the variation in the intensity in the direction transverse to the laser propagation. The transverse amplitude-modulated laser beams in magnetized plasma exert not only a nonlinear ponderomotive force at beat frequency but a space periodic ponderomotive force, which in association with gradient force produces the transverse density ripples in the magnetized plasma, whereas this is not possible with simple fundamental Gaussian laser beams. Moreover, from the filamentation and amplitude-modulated Gaussian laser beam mechanisms, one can observe a considerable improvement in the amplitude of emitted THz radiation. The THz amplitude can be further enhanced by employing suitable magnetic and electric fields [32,33,34,35]. By getting inspired, we have considered two filamented spatial-Gaussian laser beams propagating in the underdense magnetized plasma. The electric fields \(\vec{E}_1 (\omega_1 ,k_1 )\) and \( \vec{E}_2 (\omega_2 ,k_2 )\) are associated with both filamented spatial-Gaussian laser beams as shown in Fig. 1. These laser beams are propagating along the z-direction, polarizing along the y-direction, and amplitude modulation along the x-direction. The magnetic field is applied over the underdense plasma along the y-direction, parallel to the polarization direction. The applied magnetic field can be generated by employing a circuit consisting of a \((220\mathrm{ A})\) current-carrying coil wrapped over the core with the following dimensions: length\(=50\mathrm{ cm}\), area\(=0.01 {\mathrm{m}}^{2}\), relative magnetic permeability \(=\;1000\) \(\text{and number of turns}=1500.\) A static electric field is applied along the amplitude modulation direction (x-direction) as depicted in Fig. 1. The static electric field can be generated by employing two copper electrodes placed parallel to each other. It is observed that little attention has been paid to the thermal effects in the THz generation processes, whereas it is impossible to ignore the electron temperature in the case of laser-plasma interactions. In the proposed THz generation work, we have investigated the effect of electron temperature on the emitted THz radiations. The present theoretical work is structured as: The second part of the paper consists of mathematical calculations for nonlinear current density under the influence of a static magnetic field and D.C. drift speed of plasma electrons at THz frequency. In the third part, THz generation has been explained with the help of the components of the anisotropic plasma dielectric tensor. The graphs and result discussion have been given in the fourth part of the paper. The conclusion is presented in the last part of the paper.

Fig. 1
figure 1

Schematic of electric field-induced strong THz generation by beating two filamented spatial-Gaussian laser beams in the pre-existing underdense magnetized plasma

Full size image

Nonlinear current density

Two filamented spatial-Gaussian laser beams are propagating in the pre-existing underdense plasma having electron number density\({n}_{0}\). The corresponding plasma frequency is given as \(\omega_P = \left( {n_0 e^2 /m \in_0 } \right)^{1/2} ,\) where m is the rest mass and e is the fundamental charge of the electron. The electric field profiles associated with propagating filamented spatial-Gaussian laser beams can be given as

$$ \vec{E}_j = \widehat{y }\left\{ {1 + \mu_j \cos \left( {qx} \right)} \right\}A_j \exp \left\{ { - i\left( {\omega_j t - k_j z} \right)} \right\},\;j = 1, 2, $$
(1)

where \({\mu }_{j}\) are the modulation indices of the corresponding laser beams and q is the periodicity parameter. The modulation index also plays a very important role in the enhancement of the THz field amplitude as observed in our analysis. These AM Gaussian laser beams provide oscillatory velocities to the electrons of underdense plasma, given by the relation \( \overrightarrow { v}_j = - e \vec{E}_j /mi\omega_j\). The static electric field (\(\vec{E}_d )\) provides drift speed to the plasma electrons which is given by the relation \( \overrightarrow { v}_d = - e\vec{E}_d /m\nu\). The electrons of underdense plasma start drifting in the direction opposite to the external electric field and get collected near the tip of the filament. Such behavior is responsible for the complete screening of static electric field in the underdense plasma. The transient process of redistribution of charges also takes place in this plasma. The temporal nature of the generated electric current depends upon the following factors explained: (i) time period of ionization action in the underdense plasma; (ii) average relaxation time of plasma electrons; and (iii) Time period of plasma oscillations. For exemplary plasma, the average relaxation time and time period of plasma oscillations are longer than the time period of ionization action. Thus, we can elaborate it in such a way that there occurs instantaneous ionization in the plasma, and electric current is generated along the direction of the applied static electric field and this is in accordance with the experimental work of Houard et al. [33]. This electric current helps to make efficient THz generation. The AM Gaussian laser beams beat together in the presence of electric and magnetic fields to exert a ponderomotive force \(\overrightarrow { F}_P^{nl}\), which is equivalent to the vector sum of static ponderomotive force \(\vec{F}_{Pq}^{nl}\) and beat frequency ponderomotive force \( \vec{F}_{P\omega }^{nl}\).The beat frequency ponderomotive force can be calculated by using the beat frequency ponderomotive potential, which is given by the relation \(\phi_{P\omega } = - m\vec{v}_1 \vec{v}_2^* /2e. \) By substituting the value of \(\vec{v}_1\) and \(\vec{v}_2^*\) and using the standard exponential relation for the cosine function, we can calculate the nonlinear beat frequency ponderomotive potential and it is given as \(\phi_{P\omega } = - \left( {0.5eA_1 A_2 /m\omega_1 \omega_2 } \right)\left\{ {1 + 0.5\mu \exp \left( {iqx} \right)} \right\}\exp \left\{ { - i\left( {\omega t - kz} \right)} \right\}\), where \( \mu = \mu_1 + \mu_2 .\) The static ponderomotive force can be calculated by using static ponderomotive potential, which is given by the relation \(\phi_{Pq} = - \left( {0.25e/m} \right)\left\{ {\left( {\mu_1 A_1^2 /\omega_1^2 } \right) + \left( {\mu_2 A_2^2 /\omega_2^2 } \right)} \right\}\exp \left( {iqx} \right).\)

In the present theoretical analysis, the static ponderomotive force is responsible for the repeated ambipolar diffusion of plasma along the direction of the static electric field. This static ponderomotive force is well balanced by the pressure gradient force. This balancing condition results in the formation of zero-frequency transverse density ripples in the underdense plasma. By employing the equation of motion, we can obtain the relation between the density of the transverse ripple and the equilibrium temperature of plasma electrons. This relation is given as \(n_{0q} = en_0 \phi_{Pq} /T\) s [20]. In this relation, \({\text{T}}\) is the equilibrium temperature of electrons in the plasma and \({\text{n}}_{{0}{\text{q}}}\) is the density of the ripple. By using the static ponderomotive potential, \({\text{n}}_{{0}{\text{q}}}\) attains the form. Now, both the forces (i) beat frequency ponderomotive force and (ii) magnetic field force become responsible for providing oscillatory velocity to the plasma electrons. We can easily resolve the velocity of electrons along the x and z-direction to obtain the response of plasma electrons to the nonlinear ponderomotive force along with the cyclotron motion. These velocity components can be written as

$$ v_{Px}^{nl} = - \frac{{ie^2 A_1 A_2 \left\{ {\left( {i\omega q - \omega_c k } \right)\mu \exp \left( {iqx} \right) - 2\omega_c k} \right\}\exp \left\{ { - i\left( {\omega t - kz} \right)} \right\} }}{{\left( {2m\omega_1 \omega_2 \omega_3 } \right)^2 }}, $$
(2)
$$ v_{Pz}^{nl} = - \frac{{ie^2 A_1 A_2 \left\{ {\left( {i\omega k + \omega_c q} \right) \mu \exp \left( {iqx} \right) + 2i\omega k} \right\} i\exp \left\{ { - i\left( {\omega t - kz} \right)} \right\}}}{{\left( {2m\omega_1 \omega_2 \omega_3 } \right)^2 }}, $$
(3)

In the above Eqs. (2) and (3), we have substituted \(\left( {\omega^2 + \omega_c^2 } \right) = \omega_3^2 .\) The term \(\omega_c\) is known as the cyclotron frequency of the plasma electrons and is given by the relation \(\omega_c = eB/m\). Under the influence of the beat frequency nonlinear ponderomotive force, collisional force and externally applied static magnetic field, the electron oscillations of the underdense plasma become nonlinear. This leads to the generation of nonlinear velocities \(v_{Px}^{nl} \;{\text{and}}\; v_{Px}^{nl}\) and thereby nonlinear density perturbations. One can calculate density perturbations \(n_{\omega ,k}^{nl}\), \(n_{\omega ,k + q}^{nl}\) by using the Eqs. (2), (3), and the equation of continuity. The corresponding density perturbations caused by the velocity perturbations are given as

$$ n_{\omega ,k}^{nl} = \frac{{0.5n_0 e^2 A_1 A_2 ik^2 \left( {\omega + i\omega_c } \right)\exp \left\{ { - i\left( {\omega t - kz} \right)} \right\}}}{{\omega \left( {m\omega_1 \omega_2 \omega_3 } \right)^2 }}, $$
(4)
$$ n_{\omega ,k + q}^{nl} = \frac{{n_0 e^2 A_1 A_2 i\mu \left[ {\omega_0^2 \left( {k^2 + q^2 } \right) - \omega_c^2 q^2 + \omega_c k^2 } \right]\exp \left\{ { - i\left( {\omega t - kz - qx} \right)} \right\}}}{{\omega \left( {2m\omega_1 \omega_2 \omega_3 } \right)^2 }} $$
(5)

By considering coupling between various nonlinear terms including D.C. drift speed \(\left( {\vec{v}_d } \right)\) of electrons due to the externally applied static electric field, the nonlinear current density gets modified and one can write this modified nonlinear current density as \( \overrightarrow { J}_{\omega ,k}^{nl} = - \left\{ {\left( {n_0 e \vec{v}_{\omega ,k}^{nl} } \right) + \left( {n_{\omega ,k}^{nl} e \vec{v}_d } \right) + \left( {n_{0,q}^* e \vec{v}_{\omega ,k + q}^{nl} } \right)} \right\}\). On resolving this current density into its components, we get

$$ J_{x \omega ,k}^{nl} = \frac{{ - 0.5n_0 e^4 A_1 A_2 \left( {\omega + i\omega_c } \right)\exp \left\{ { - i\left( {\omega t - kz} \right)} \right\}}}{{m\left( {m\omega_1 \omega_2 \omega_3 } \right)^2 }}\left\{ {\frac{k^2 E_d }{{\omega \nu }} - \frac{0.125eq\mu }{T}\left( {\frac{\mu_1 A_1^2 }{{\omega_1^2 }} + \frac{\mu_2 A_2^2 }{{\omega_2^2 }}} \right)} \right\} $$
(6)
$$ J_{z \omega ,k}^{nl} = \frac{{ - 0.5n_0 e^4 A_1 A_2 \left( {\omega + i\omega_c } \right)\exp \left\{ { - i\left( {\omega t - kz} \right)} \right\}}}{{m\left( {m\omega_1 \omega_2 \omega_3 } \right)^2 }}\left\{ {\frac{mk}{e} + \frac{0.125ek\mu }{T}\left( {\frac{\mu_1 A_1^2 }{{\omega_1^2 }} + \frac{\mu_2 A_2^2 }{{\omega_2^2 }}} \right)} \right\} $$
(7)

The contribution of D.C. drift speed in the nonlinear current density component \(J_{x \omega ,k}^{nl}\) appears more significant as compared to the other nonlinear density component \(J_{z \omega ,k}^{nl} .\) This is because of the large electron collision time period, the electrons of underdense magnetized plasma attain large D.C. drift speed in the presence of externally applied static electric field. As a result, the nonlinear current density component \(J_{x \omega ,k}^{nl} \) is responsible for the strong field THz radiation generation.

Anisotropic plasma dielectric tensor and THz generation

Under the influence of a static magnetic field in the collisionless and underdense plasma, the dielectric constant behaves as an anisotropic plasma dielectric tensor with corresponding components of the given as \( \in_{yz} = \in_{zy} = \in_{yx} = \in_{xy} = 0\), \(\in_{yy} = 1 - \omega_p^2 /\omega^2\) , \(\in_{xx} = 1 + \omega_p^2 /\omega^2 = \in_{zz}\), \(\in_{zx} = - i\omega_c \omega_p^2 /\omega^3 = - \in_{xz}\). The wave equation required for the THz wave propagation can be derived from Maxwell’s standard equations of electromagnetism and can be written as

$$ - \nabla^2 \vec{E} + \nabla \left( {\nabla .\vec{E}} \right) = \frac{4\pi i\omega }{{c^2 }}\vec{J}^{nl} + \frac{\omega^2 }{{c^2 }} \in \vec{E} $$
(8)

With the use of anisotropic plasma dielectric tensor components of dielectric constant and nonlinear current density components from Eq. (6) & (7), one can modify the wave propagation Eq. (8) as.

$$ - 2ik^{\prime} \frac{\partial E_x }{{\partial z}} + \left\{ {k^{^{\prime}2} - \frac{\omega^2 }{{c^2 }}\left( {\smallint_{xx} + \frac{{\smallint_{zx}^2 }}{{\smallint_{zz} }}} \right)} \right\}E_x = \frac{4\pi i\omega }{{c^2 }}\left( {J_x^{nl} + \frac{{ \in_{zx} }}{{ \in_{zz} }}J_z^{nl} } \right) $$
(9)

where \( k^{\prime} = ~k_1 - k_2 + ~q \) represents the wavenumber with which current density oscillates at frequency\(\upomega \). In relation of \( k^{\prime}\), the wavenumber q of transverse density ripple is responsible for phase matching condition by providing it extra momentum. The difference in the frequencies of the propagating laser beams is exactly in the THz range and the phase matching condition is well satisfied therefore strong THz generation is possible in the proposed scheme. By using this phase-matching condition, we can write \( k^{\prime} = \left( {\omega /c} \right)\sqrt {{1 + \left( {\omega_P^2 /i\omega \omega_3^2 } \right)\left\{ {i\omega + \omega_c^2 \omega_P^2 /\left( {i\omega \omega_3^2 + i\omega \omega_P^2 } \right)} \right\}}}\). With the help of this condition and by using \(\mathrm{equations }\left (7\right)\mathrm{and} (8)\), the normalized amplitude of the electric field component of THz radiation along the x-direction is given as

$$ E_{x\omega } = ~ - \frac{{0.25\omega ^{\prime}x^{\prime}abi\left( {\upsilon ^{\prime} - i\omega ^{\prime} - \omega ^{\prime}_c } \right)}}{{k^{\prime\prime}\omega ^2 \left( {i\omega _{P1} - \upsilon ^{\prime}} \right)\left( {i\omega _{P2} + \upsilon ^{\prime}} \right)}}\left\{ {\frac{{k_0^2 E^{\prime}_d }}{{\omega ^{\prime}\upsilon ^{\prime}}} + \frac{{0.125\mu }}{{v^{\prime}_t }}\left( {\frac{{k_0 \omega ^{\prime}_c }}{{i\omega ^{\prime}\omega ^2 - \left( {\upsilon ^{\prime} - i\omega ^{\prime}} \right)}} - q^{\prime}} \right)\left( {\frac{{\mu _1 A_1^{'2} }}{{\left( {i\omega _{P1} - \upsilon ^{\prime}} \right)^2 }} + \frac{{\mu _2 A_2^{'2} }}{{\left( {i\omega _{P2} + \upsilon ^{\prime}} \right)^2 }}} \right) + \frac{{\omega ^{\prime}_c \left( {\upsilon ^{\prime} - i\omega ^{\prime} - \omega ^{\prime}_c } \right)^{ - 1} }}{{i\omega ^{\prime}\omega ^2 - \left( {\upsilon ^{\prime} - i\omega ^{\prime}} \right)}}} \right\} $$
(10)

\(\begin{gathered} where,\;~a = eA_1 /m\omega _p c,\;b = eA_2 /m\omega _p c,~\;\omega ^{\prime} = \omega /\omega _p ,~x^{\prime} = x\omega _p /c,~\; \hfill \\ \omega _{p1} = \omega _1 /\omega _P ,~\;\omega _{p2} = \omega _2 /\omega _p ,~\;\upsilon ^{\prime} = \upsilon /\omega _p ,~\;E^{\prime}_d = eE_d /m\omega _p c.~k_0 = c(k_1 - k_2 )/\omega _p , \hfill \\ \end{gathered} ~\;k^{\prime\prime} = ck^{\prime}/\omega _p ,\;~\omega ^{\prime}_c = \omega _c /\omega _p ,\;~q^{\prime} = cq/\omega _p ,~\;~eE_x /m\omega _P c = E_{x\omega } ~,~~v^{\prime}_t = v_t /c,\) and it is known as the normalized thermal speed of plasma electrons. The emitted THz radiation can easily propagate out of the underdense magnetized plasma because damping for the THz wave is negligible for the chosen parameters of the proposed scheme. The plasma length can also be adjusted in experimental setups according to the skin depth of the magnetized plasma.

Results and discussion

For the numerical simulation, we have chosen a well-specified set of laser plasma parameters based on experimental and theoretical work of THz generation [30,31,32,33]. The role of filamented spatial-Gaussian laser beams is played by the CO2 laser beams having frequencies \( \omega_1 = 2.00 \times 10^{14 } rad s^{ - 1} \left( {\lambda_1 = 9.44 \mu m} \right)\) and \( \omega_2 = 1.85 \times 10^{14} rad s^{ - 1} \left( {\lambda_2 = 10.20 \mu m} \right).\) The peak value of intensity associated with each laser is of the order of \({{I}_{1}\text{=}{I}_{2}\text{=}{10}}^{14} \, {\text{W}}{\text{cm}}^{-2}\) lying in between low to moderate values. This is because the contribution of the D.C. electric field is observed to be much smaller than the beat frequency ponderomotive term at a high value of laser intensities. Moreover, corresponding to low to moderate values of laser intensities relativistic effects are not significant. Figure 2 depicts a graph drawn between the normalized THz field amplitude of emitted THz radiation and normalized THz frequency, for the values of magnetic field lying in the range \({15.0-25.0} \rm{kG}\) at the optimized value of electric field \(\text{15.0 kV}{\text{cm}}^{-1}.\) From the graph, it is clear that the normalized THz field increases with the decrease in the value of normalized THz frequency. The reverse is also true in our case. All three curves show that THz amplitude shows enhancement with the increase of the static magnetic field. One can observe from Fig. 2 that the normalized THz amplitude achieves its maximum value at the optimized value of the magnetic field \(\left(25.0\mathrm{ kG}\right),\) when THz frequency is close to the plasma frequency. The reason behind this is that the static magnetic field modifies the components of the dielectric tensor to generate strong nonlinear current density. It also helps to make maximum momentum transfer between the incident photon and the electron of magnetized plasma. The externally applied magnetic field also increases the cyclotron frequency of the plasma electrons and hence, the nonlinearity of the system. All these factors are collectively responsible for the enhancement of the normalized THz field amplitude. Similar results have been observed by Kumar et al. [12] in their theoretical work on THz generation by applying a suitable static magnetic field. The frequency of the emitted THz radiation (corresponding to \(25.0\mathrm{ kG}\)) is found to lie in the frequency range of molecular rotational and vibrational spectra of deoxyribonucleic acid, which is known as the hereditary material present in human beings [36]. As a result, emitted THz radiation can play an important role in developing a new technique to distinguish between healthier and non-healthier tissues of human beings.

Fig. 2
figure 2

The plot of the normalized amplitude of emitted THz radiation \(\left( {E_{x\omega } } \right)\) with THz frequency \(\left( {\omega /\omega_p } \right)\), at the various values of the externally applied static magnetic field ranging from \(B = 10.0 \;{\text{kG}}\; to\; B = 25.0 \;{\text{kG}}\) for the optimized value of the D.C. electric field \({E}_{d}\text{=15.0 kV}{\text{cm}}^{-1}\) and modulation indices of filamented spatial-Gaussian laser beams\({\mu }_{1}={\mu }_{2}=0.10\)

Full size image

The emitted THz radiation also shows sensitive behavior toward the water and as a result can be absorbed by the water particles [37, 38]. Due to this, emitted THz radiation can be used to detect water at the surface of the earth as well as on other planets. This provides a significant use of THz radiation in astronomical physics.

The graph between normalized THz field amplitude of emitted THz radiation and normalized THz frequency at various values of modulation index \({\mu }_{1}={\mu }_{2}=0.05, 0.08,\mathrm{ and }0.10\) is depicted in Fig. 3. Other parameters are kept the same as that in Fig. 2. From the graph, it is clear that the normalized THz field amplitude rises with the decrease of normalized THz frequency. As one increases the values of modulation indices of the incident filamented spatial-Gaussian laser beams, there occurs enhancement in the normalized THz amplitude. The normalized THz amplitude attains maximum value at the optimized value of static magnetic field \(B=25\mathrm{ KG}, \, \text{static electric field}{ E}_{d}=15.0\mathrm{ kV}{\mathrm{cm}}^{-1}\) and modulation index \({\mu }_{1}={\mu }_{2}=0.10\). This can be justified because an increase in the value of modulation indices of the incident laser beams results in an increase in electron density. Higher electron density further results in a strong nonlinear current, and it leads to strong THz emission. In the graph, each curve has a slight dip in between the normalized THz frequency range of 1.2–1.6. The physics behind this can be explained as: This dip is formed due to the interference of both the filamented spatial-Gaussian laser beams in the underdense magnetized plasma.

Fig. 3
figure 3

The plot of the normalized amplitude of emitted THz radiation \(\left( {E_{x\omega } } \right)\) with the THz frequency \(\left( {\omega /\omega_p } \right)\), at the optimized value of static magnetic field \(\mathrm{B}=25.0\mathrm{ kG}\) and D.C. electric field \(\text{15.0 kV}{\text{cm}}^{-1}\) for various values of modulation indices \({\mu }_{j}=0.05, 0.08,\mathrm{ and }0.10\)

Full size image

In Fig. 4, we have shown the graph between the normalized amplitude of emitted THz radiation \( \left( {E_{x\omega } } \right)\) and the normalized thermal velocity \(\left( {v_t /c} \right)\) at the various values of static magnetic field for the optimized value of D.C. electric field \(\text{15.0 kV}{\text{cm}}^{-1}\) and modulation index \(\mu_1 = \mu_2 = 0.10\). From Fig. 4, it is evident that the normalized thermal velocity of the plasma electrons provides support to the THz generation. This is true in the following two cases: (i) if \(\nu =0 ,\) it means collision-free plasma. (ii) if \(\nu \ll \omega_P ,\) which means collision frequency is negligible as compared to the plasma frequency. However, for the larger collision frequency, the negative impact of electron temperature T is realized and we get diffused THz emission for the higher electron temperature. In the present scheme, the collision frequency is \(\nu = 1.2 \times 10^{13} {\text{rad}}\; {\text{s}}^{ - 1}\) and plasma frequency is \(\omega_P = 7.8 \times 10^{13} {\text{rad}} \;{\text{s}}^{ - 1}\) and it is obvious that \(\nu \ll \omega_P\) therefore, THz amplitude increases with the thermal speed of plasma electrons. The applied static magnetic field also provides support in the enhancement of THz generation.

Fig. 4
figure 4

The plot of the normalized amplitude of emitted THz radiation \( \left( {E_{x\omega } } \right)\) with the normalized thermal velocity \(\left( {v_t /c} \right)\) at the various values of static magnetic field \(B = 15{\text{ kG}},{ }\;20{\text{ kG}},{ }\;{\text{and}}\;{ }25{\text{ kG}}\) for the optimized value of D.C. electric field \(E_d = {15}{\text{.0}}\;{\text{ kVcm}}^{ - 1}\) and modulation indices \(\mu_1 = \mu_2 = 0.10\)

Full size image

To discuss the effect of electron temperature T on the normalized amplitude of the emitted terahertz radiation, we have plotted the graph between normalized THz field amplitude and normalized frequency at the various values of electron plasma temperature T, for the optimized value of static magnetic field\(\text{25.0 kG}\), D.C. electric field \(\text{15.0 kV}{\text{cm}}^{-1}\) and modulation index \(\mu_1 = \mu_2 = 0.10\) as shown in Fig. 5. During the investigation, it is noticed that the electron temperature has a significant effect on the normalized amplitude of emitted THz radiation. One can also observe that the normalized THz amplitude attains its peak value at a particular value of \(\omega /\omega_p\). This is because at this value of \(\omega /\omega_p\), there occurs maximum transfer of laser energy to the emitted THz radiation through nonlinear current in the system.

Fig. 5
figure 5

The plot of the normalized amplitude of emitted THz radiation \(\left( {E_{x\omega } } \right)\) with the THz frequency \(\left( {\omega /\omega_p } \right)\), at the various values of electron plasma temperature for the optimized value of static magnetic field\(B=\text{25.0 kG}\), D.C. electric field \({E}_{d}\text{=15.0 kV}{\text{cm}}^{-1}\) and modulation indices\({\mu }_{1}={\mu }_{2}=0.10\)

Full size image

Figure 6 shows the variation of normalized THz field amplitude of emitted THz radiation with normalized THz frequency at various values of the D.C. electric field \( \left( {5.0 , \;10.0 \;{\text{and}}\; 15.0 {\text{kVcm}}^{ - 1} } \right)\), keeping all other parameters the same as that of Fig. 2. The normalized THz amplitude shows an increasing trend with a decreasing trend of normalized THz frequency. At a particular value of normalized THz frequency, THz amplitude attains a peak value. From the graph, it is also observed that with the increase of applied D.C. electric field, normalized THz amplitude also increases. This is because the nonlinear coupling of electron density with the D.C. drift speed of electrons due to the applied D.C. electric field generates a strong nonlinear current which drives enhanced THz generation. The large collision time period of plasma electrons also helps in attaining large D.C. drift speed under the influence of externally applied D.C. electric field and results in more contribution to the nonlinear current density. Moreover, by applying an external D.C. electric field both the forces beat frequency ponderomotive force and electric force (\(- e\vec{E}_d )\) will act on the electrons of magnetized plasma to contribute directly to the THz amplitude. This is also clear from Eqs. (6) & (9).

Fig. 6
figure 6

The plot of the normalized amplitude of emitted THz radiation \(\left( {E_{x\omega } } \right)\) with the normalized THz frequency \(\left( {\omega /\omega_p } \right)\), at the various values of the D.C. electric field \(E_d = 5.0 \;{\text{kVcm}}^{ - 1} , \;10.0\; {\text{kVcm}}^{ - 1} ,\; {\text{and}} \;15.0\; {\text{kVcm}}^{ - 1}\) for the optimized value of static magnetic field \(\mathrm{B}=\text{25.0 kG}\) and modulation indices \(\mu_1 = \mu_2 = 0.10\)

Full size image

Conclusion

We have demonstrated the electric field-induced strong terahertz (THz) emission by beating two filamented spatial-Gaussian laser beams in the pre-existing underdense magnetized plasma. The externally applied static magnetic field, D.C. electric field, thermal velocity, electron temperature, D.C. drift speed, normalized frequency, and modulation indices of the propagating filamented spatial-laser beams with anisotropic plasma dielectric tensor significantly endorse the enhancement in the normalized amplitude of emitted THz radiation.

So, one can easily tune the emitted THz radiation (according to the need of the situation) by using the above-mentioned parameters. Our scheme is valid only at moderate and low intensities of filamented spatial-Gaussian laser beams of the order of \({10}^{14} \, {\text{W}} \, {\text{cm}}^{-2}\) because at high intensities contribution due to D.C. drift becomes smaller than the ponderomotive force at the beat frequency. Based on the above discussion, our scheme can provide tuned THz radiation in a very cost-effective way to use in medical and astronomical applications like distinguishing between healthier and non-healthier tissues of human beings and detecting water at the surface of the earth as well as on other celestial bodies.