1 Introduction

In the last decade, an increasing number of studies have focused on the realization and development of technologies at micro, nano, and atomic scales, using the quantum phenomena with applications in several areas, especially quantum information processing and quantum thermodynamics [1], and quantum technologies. Among these applications, heat engines are considered a valuable resource for modern society. The development of these engines leads to the production realization of heat engines with high efficiency despite their small size, called quantum heat engines [2,3,4,5,6,7,8,9,10]. In a quantum heat engine, one can produce work from the heat flow of the system between the hot and the cold thermal bath. Quantum mechanics can describe the operating mechanism of the engine and quantum thermodynamics laws using the quantum version of Carnot, Otto, Stirling, and Diesel Cycles [11,12,13,14]. The choice of the thermodynamic cycle and the working substance is very important to increase the efficiency and the work performed by the engine.

In this paper, we propose three InAs quantum dots in the presence of an external electric field as a working substance of a quantum heat engine. Quantum dots (QDs) are nanoscale semiconductor particles that have quantum mechanical properties. In this paper we use the Indium Arsenide (InAs) which is a semiconductor material known for its high electron mobility and direct band-gap. InAs quantum dots are particularly useful in quantum computing due to their ability to confine excitons and facilitate efficient energy transfer. These properties make them ideal for applications in quantum heat engines and other quantum technologies. The motivation for this choice is the possibility of realizing it experimentally, and also its high electron mobility [15, 16], which means that electrons can move quickly and efficiently through the material. This is an important feature in nano-scale devices as it allows for fast and accurate controlling. InAs also have a direct band gap [17], which means that they can efficiently absorb and emit light. In addition InAs double quantum dots exhibit a strong Coulomb blockade effect[18], in which the flow of electrons through the quantum dots is strongly suppressed at low temperatures. This can be used to control the flow of electrons to perform quantum operations. Also, the energy levels of InAs can be precisely controlled using electrical gates, allowing for precise manipulation of the quantum system. Since InAs can be easily integrated with other materials, such as GaAs and Si, which are commonly used in electronics, this makes it possible to incorporate InAs quantum dots into a variety of devices. In this work, we assume that the engine operates following a quantum Otto cycle [19,20,21], this latter is a thermodynamic process that converts heat into useful work, just like a classical Otto cycle used in the internal combustion engine. However, the quantum nature of the system allows for the possibility of more efficient and powerful engines. The quantum Otto engine was selected for this study due to its easy implementation and well-understood thermodynamic processes. Compared to the other engines, the Otto cycle involves simpler isochoric and adiabatic processes, which are easier to control and analyze in quantum systems. Additionally, the Otto engine is known for its robustness in various quantum thermodynamic applications, making it an excellent choice for investigating the effects of the Förster interaction and quantum entanglement in InAs quantum dots. Our objective is to examine the work performed by the heat engine by changing the external electric field in the adiabatic stages, and to study the engine’s behavior against the Förster mechanism effects [22]. The Förster mechanism, also known as Förster resonance energy transfer, is a quantum mechanical process that describes the energy transfer between two chromophores (molecules that absorb light) through non-radiative dipole-dipole coupling [23]. In the context of quantum dots, the Förster mechanism refers to the energy transfer between excitons (electron–hole pairs) in adjacent quantum dots. This interaction allows an exciton in one quantum dot (the donor) to transfer its energy to an exciton in a neighboring quantum dot (the acceptor) without emitting a photon. The Förster mechanism is crucial for the operation and efficiency of quantum heat engines using quantum dots as the working substance. It facilitates efficient energy transfer between quantum dots, enhancing the overall energy exchange processes and affecting both the absorption and release of heat. The efficiency of this energy transfer directly influences the work output of the heat engine. Variations in the Förster interaction parameter \(\lambda\) can lead to significant changes in the work performed by the engine, transitioning it between different operational regimes. Furthermore, the Förster mechanism impacts the entanglement between quantum dots, a key resource in quantum information processing that influences the thermodynamic properties of the system. We also investigate the effect of the temperature of the baths on the efficiency of the quantum heat engine.

2 Model and the quantum Otto engine

2.1 Working substance and thermalization

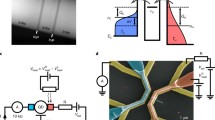
We propose a quantum system composed of three coupled semiconductor InAs quantum dots with a small inter-dot distance, typically on the order of a few nanometers, which allows for significant dipole-dipole interactions between them [24, 25], as a working substance for the quantum Otto engine (see Fig. 1). We use the excitonic electric dipole moments as a qubit in each quantum dot, under an external electric field \(\vec {E}\), and rely on the Förster mechanism between the excitons to explain the energy transfer between the qubits [22].

Fig. 1
figure 1

Schematic of the three quantum dots

Full size image

The Hamiltonian of the system, when an electric field \(\vec {E}\) is applied, is given by,

$$\begin{aligned} H= & {} \sum _{i=1}^{3} \hbar \omega _i \left[ S_z^i +\dfrac{1}{2}\right] + \sum _{i=1}^{3} \hbar {\Omega }_{i} S_{z}^{i} + \sum _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^{3} \hbar J_z \left[ S_z^i +\frac{1}{2}\right] \left[ S_z^j+\frac{1}{2}\right] \nonumber \\{} & {} +\dfrac{1}{2} \sum _{\begin{array}{c} i,j=1\\ i \ne j \end{array}}^{3} \lambda [S_+^i S_-^j + S_-^j S_+^i], \end{aligned}$$
(1)

with, \(S_+^i=(|+\rangle \langle -|)_i\), \(S_-^i=(|-\rangle \langle +|)_i\), and \(S_z^i=\frac{1}{2}(|+\rangle \langle +| - |-\rangle \langle -|)_i\).

In equation (1), \(\omega _i\) is the exciton frequency in each quantum dot i, \(\Omega _i\) is the frequency related to the exciton dipole moment that is a function of the dipole moment and the external electric field (\(\vec {E}\)) at the quantum dot number i, \(\hbar \Omega _i=|\vec {d}.\vec {E}|,\) with \(\vec {d}\) is the electric dipole moment associated to the exciton; it is supposed to be the same for each quantum dot, \(\lambda\) denote the Förster interaction [22] i.e. resonant energy transfer between the excitons, and \(\hbar J_z\) is the static exciton-exciton dipolar interaction energy. In our Hamiltonian, the first term represents the energy associated with the excitons (electron–hole pairs) in each quantum dot. Here, i is the energy of the exciton in the i-th quantum dot, the second term describes the interaction between the excitonic dipole moments and the external electric field, The third term accounts for the static dipole-dipole interaction between excitons in different quantum dots, The last term represents the Förster resonance energy transfer between excitons in different quantum dots. When we introduce into our system thermal fluctuations, the state of the system under thermal equilibrium is given by the reduced density matrix,

$$\begin{aligned} \rho (T)=\frac{1}{Z(T)} e^{-\beta H}= \sum _{i=1}^{4}P_n(T)|\psi _n\rangle \langle \psi _n|, \end{aligned}$$
(2)

Where \(P_n(T)=e^{-\beta E_n}/Z(T)\) are the occupation probabilities of the eigenstates \(|\Psi _n\rangle\), and \(Z(T)=\sum _{i=1}^{n}e^{-\beta E_n}\) is the partition function, with \(\beta =\frac{1}{K_B T}\), \(K_B\) being the Boltzman constant.

2.2 Quantum Otto cycle

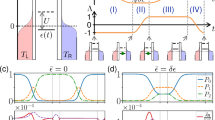
In the following section, we describe the quantum Otto engine cycle, operating in four steps.

Step 1: Quantum isochoric process [26]

The working substance with \(\Omega =\Omega _H\) is in the initial state \(\rho _1\) and is put in contact with a hot bath at temperature \(T=T_H\) until it reaches thermal equilibrium. During this step, the system absorbs an amount of heat from the hot bath (\(Q_H>0\)). At the end of the process, only the occupation probabilities change to \(P_n(T_H)\) while the energy level remains invariant.

Step 2: Quantum adiabatic process [26]

The working substance is isolated from the hot bath and the frequency related to the excitonic dipole moment changes from \(\Omega _H\) to \(\Omega _C\), (with \(\Omega _H > \Omega _C\)), to satisfy the quantum adiabatic theorem [27, 28]. During this step, the system releases an amount of work, without exchanging the heat.

Step 3: Quantum isochoric process

The working substance with \(\Omega =\Omega _C\) now is in contact with a cold bath at temperature \(T=T_C\), and after the thermalization of the system, a quantity of heat is released to the cold bath without a change of work, the occupation probabilities change to \(P_n(T_C)\).

Step 4: Quantum adiabatic process

The working substance is isolated from the cold bath, and the frequency related to the excitonic dipole moment changes from \(\Omega _C\) to \(\Omega _H\). During this step, an amount of work is done, but no heat is exchanged. At the end of this step, the working substance returns to the initial condition and is ready for another cycle (Fig. 2).

Fig. 2
figure 2

Schematic diagram of the quantum Otto cycle

Full size image

At each step of the described Otto cycle, the state and the energy of the system are given by,

$$\begin{aligned} \rho _2=\frac{e^{-\beta _1 H_1}}{Z_1}, \qquad \qquad E_2=Tr \rho _2 H_1,\end{aligned}$$
(3)
$$\begin{aligned} \rho _3=U\rho _2 U^+, \qquad \qquad E_3=Tr \rho _3 H_2,\end{aligned}$$
(4)
$$\begin{aligned} \rho _4=\frac{e^{-\beta _2 H_2}}{Z_2}, \qquad \qquad E_4=Tr \rho _4 H_2,\end{aligned}$$
(5)
$$\begin{aligned} \rho _1=\tilde{U}\rho _4 \tilde{U^+}, \qquad \qquad E_1=Tr \rho _1 H_1, \end{aligned}$$
(6)

where \(H_1=\sum\nolimits _{i=1}^{3} \hbar \omega _i \left[ S_z^i +\dfrac{1}{2}\right] + \sum\nolimits _{i=1}^{3} \hbar \Omega _H S_z^i + \sum\nolimits _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^{3} \hbar J_z \left[ S_z^i +\frac{1}{2}\right] \left[ S_z^j+\frac{1}{2}\right] + \dfrac{1}{2} \sum\nolimits _{\begin{array}{c} i,j=1\\ i \ne j \end{array}}^{3} \lambda [S_+^i S_-^j + S_-^j S_+^i]\), \(H_2=\sum\nolimits _{i=1}^{3} \hbar \omega _i \left[ S_z^i +\dfrac{1}{2}\right] + \sum\nolimits _{i=1}^{3} \hbar \Omega _C S_z^i + \sum\nolimits _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^{3} \hbar J_z \left[ S_z^i +\frac{1}{2}\right] \left[ S_z^j+\frac{1}{2}\right] + \dfrac{1}{2} \sum\nolimits _{\begin{array}{c} i,j=1\\ i \ne j \end{array}}^{3} \lambda [S_+^i S_-^j + S_-^j S_+^i]\), \(Z_1=Tr e^{- \frac{H_1}{K_B T_H}}\), \(Z_2=Tr e^{- \frac{H_2}{K_B T_C}}\), U and \(\tilde{U}\) are unitary operators associated with the second and the fourth steps respectively. In the following, we shall assume a linear time dependence of the chemical potential during the unitary strokes. Then the driving protocol corresponding to the first step \(B \rightarrow C\) can be written as, \(\Omega (t)=\Omega _H-\delta t, \,\) for \(t\in [0,\tau ]\), where \(\delta =\frac{\Omega _H-\Omega _C}{\tau }\) is the sweep rate. The driving protocol during the third step of the cycle \(D \rightarrow A\) is given by, \(\tilde{\Omega }(t)=\Omega (\tau -t)\), for \(t\in [0,\tau ]\). The corresponding unitary evolution then read, \(U=T\, exp[-i\int _0^\tau dt H(\Omega (t)],\) and \(\tilde{U}=T\, exp[-i\int _0^\tau dt H(\tilde{\Omega }(t)].\)

3 Theory

3.1 The work performed

In order to describe the work performed and the heat transfer at the quantum level we use the quantum version of the first law of thermodynamics[26],

$$\begin{aligned} dU=dQ+dW=\sum _n(E_n\,dP_n+P_n \, dE_n) \end{aligned}$$
(7)

In this formula, the heat transfer is related to the change of occupation probabilities, with \(dQ=\sum _n E_n\,dP_n\), and the work done is related to the change in energy levels \(dW=\sum _n P_n \, dE_n\).

For the engine described in section 2, the heat absorbed during the first step \(Q_H\), the heat liberated during the third step \(Q_C\), and \('W'\) the net work performed by the engine are defined by the following expressions:

$$\begin{aligned} Q_{H}=\sum _n E_n^H[P_n(T_H)-P_n(T_L)], \end{aligned}$$
(8)
$$\begin{aligned} Q_{C}=\sum _n E_n^L[P_n(T_L)-P_n(T_H)], \end{aligned}$$
(9)
$$\begin{aligned} W=Q_{H}+Q_{C}=\sum _n[E_n^H-E_n^L][P_n(T_H)-P_n(T_L)], \end{aligned}$$
(10)

The energy levels (\(E_n^H\) and \(E_n^L\)) are obtained by replacing \(\Omega\) by \(\Omega _H\) and \(\Omega _C\) during the first and the third steps respectively. We note that the engine can operate in four modes depending on the signs of W, \(Q_H\), and \(Q_C\)[29, 30]:

[E]: \(Q_H\ge 0\), \(Q_C\le 0\), and \(W\ge 0\), in which the machine operates as a quantum heat engine.

[R]: \(Q_H\le 0\), \(Q_C\ge 0\), and \(W\le 0\), in which the machine operates as a refrigerator.

[A]: \(Q_H\ge 0\), \(Q_C\le 0\), and \(W\le 0\), in which the machine operates as a thermal accelerator.

[H]: \(Q_H\le 0\), \(Q_C\le 0\), and \(W\le 0\), in which the machine operates as a heater.

3.2 Quantum entanglement

Quantum entanglement was introduced as the most striking phenomenon in quantum physics with no counterpart in classical physics [31]. It is considered a precious resource in several areas of quantum information, quantum computation, quantum communication[32], and their effects in quantum heat engines were established [33,34,35,36,37]. It is hard to find an exact expression of this quantity for each quantum system, because the type and the classes of entanglement change with changing the dimension of the quantum systems, and the exact expression is available for a few quantum systems. In this regard, many studies focused on the development of general measures of entanglement.

Concurrence For a general two-qubits system, concurrence [38] is a frequently used measure of entanglement. It is defined by,

$$\begin{aligned} C(\rho )= Max[0,\nu _1-\nu _2-\nu _3-\nu _4], \end{aligned}$$
(11)

where \(\nu _i\)’s are the square roots of the positive eigenvalues of the matrix \(\rho .\tilde{\rho }\) in decreasing order, with \(\tilde{\rho }\) being a spin flipped of \(\rho\), i.e. \(\tilde{\rho }=(\sigma _y \otimes \sigma _y)\rho ^*(\sigma _y \otimes \sigma _y)\), \(\sigma _y\) and \(\rho ^*\) being the Pauli matrix and the complex conjugate of \(\rho\) respectively. Lower bound

For an arbitrary mixed state of three qubits, the lower bound of concurrence [39] is defined as

$$\begin{aligned} {\tau }_{3}=\frac{1}{3}\sum _{\alpha }^{6}[(C_{\alpha }^{12/3})^2+(C_{\alpha }^{13/2})^2+(C_{\alpha }^{23/1})^2], \end{aligned}$$
(12)

with,

$$\begin{aligned} C_{\alpha }^{p} = max \{ 0,\lambda (1)_{\alpha }^{p}-\lambda (2)_{\alpha }^{p} -\lambda (3)_{\alpha }^{p}-\lambda (4)_{\alpha }^{p}\}, \end{aligned}$$
(13)

in which \(\lambda (i)_{\alpha }^{p}\) are the square roots of the four nonzero eigenvalues, in decreasing order, of the non-Hermitian matrix \(\sqrt{\rho \tilde{\rho }_{\alpha }}\), with \(\tilde{\rho }_{\alpha } = (L_{\alpha } \otimes \sigma _y) \rho ^{*} (L_{\alpha } \otimes \sigma _y)\), and \(L_{\alpha }\) being the generators of SO(4).

\({\tau }_{3}\) also characterizes genuine tripartite entanglement that cannot be described by \(C(\rho )\) mentioned in 11, such that, if \({\tau }_{3} =0\), it indicates the absence of any entanglement which means that the state is fully separable. Thus, the lower bound \({\tau }_{3} =0\) can serve as a criterion for detecting and recognizing multipartite entanglement.

4 Results and discussion

In this section, we investigate the behavior of the quantum Otto heat engine, for our system where the energy related to the external electric field \(\vec {E}\) changes between \(\hbar \Omega _C\) and \(\hbar \Omega _H\) (\(\hbar \Omega _H > \hbar \Omega _C\)) in the adiabatic processes. Furthermore, we study the effect of the excitons frequency in each quantum dot \(\hbar \omega\) and the Förster interaction \(\lambda\) on the amount of work performed by the engine. Moreover, we study the relation between the work performed and quantum entanglement between the quantum dot’s qubits

4.1 Work and heat exchange

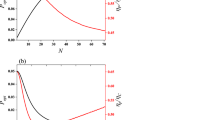
The behaviors of the work performed, the heat liberated \(Q_C\), and the heat absorbed \(Q_H\) by the engine against the Förster interaction energy \(\lambda\) depicted in Fig. 3a. In Fig. 3b we show the effect of the temperature of the hot bath and the energy related to the external electric field \(\hbar \Omega _H\) on the work performed by the engine. We note for this model that the energy parameters \(\hbar \Omega\), \(\hbar \omega\), and \(\hbar J_z\) are assumed to be in the order of meV which is coherent with experimental observations [40, 41].

Fig. 3
figure 3

The work and heat exchange

Full size image

Figure 3a clearly shows distinct regions of the working substance with respect to the Förster interaction energy \(\lambda\). In the first region, characterized by smaller values of \(\lambda\), positive work is observed, indicating that the system functions as a heat engine, this engine absorbs heat from the hot bath \((Q_H>0)\) and transfers it to the cold bath \((Q_C<0)\) while producing useful work. We note that the work is decreased slowly with increasing of the Förster interaction \(\lambda\) until a critical value of this parameter after which, the engine requires a negative work (\(W<0\)) to extract heat from the hot reservoir to the cold reservoir, i.e. the machine works as a heater and the engine cannot produce work. We observe also for a strong Förster interaction, that the heat absorbed \(Q_H\) by the engine becomes again positive, but the work and the heat liberated from the engine are still negative. This means that the engine works as a thermal accelerator where the engine transfers heat from the hot reservoir to the cold one, without producing work. These results show that we can switch from one regime to the other by simply increasing a single parameter, the Förster interaction \(\lambda\).

Figure 3b shows that the temperature of the hot bath \(T_H\) doesn’t affect the general behavior (shape) of the work performed but affects only the amount of this work. This amount increases with increasing temperature of the hot bath because the heat absorbed from the hot bath increases. Moreover, the amount of work increases with the excitonic dipoles moments energy \(\hbar \Omega\). This is due to the larger difference between \(\hbar \Omega _H\) and \(\hbar \Omega _C\) under the quantum adiabatic process, which makes the engine convert a lot of energy to work. We can also observe that for large values of temperature in the hot bath and the excitonic dipole moments \(\hbar \Omega\), the work decreases at the critical point of \(\lambda\). However, the work remains positive, allowing the system to function as a heat engine after this critical point. Nonetheless, it vanishes for large values of \(\lambda\). Now, In order to investigate the effect of the frequency of the excitons in each quantum dot on the work performed by the engine, we present the behaviors of the work performed in Fig. 4a and b.

Fig. 4
figure 4

The behavior of the work as a function of the Förster interaction for different values of the exciton frequency

Full size image

Figure 4a illustrates the behavior of the work done for different values of the exciton frequency \((\hbar \omega _i)\) as a function of the Förster interaction. In this situation, where the \(w_i\)’s are equal, we observe, for lower Förster interaction energies, that the work is positive, indicating that the machine operates as a heat engine. However, for stronger Förster interactions, the work becomes negative, rendering the engine incapable of producing any work. Additionally, the critical value of \(\lambda\) at which the work turns negative varies with the exciton energy (\(\hbar \omega _i\)). This suggests that the work is more resilient against the Förster energy for higher exciton energy values, and its behavior remains consistent. Moreover, the amount of the work decreases as \(\hbar \omega _i\) increases for smaller values of \(\lambda\). Moving on to Fig. 4b, we observe a similar pattern to Fig. 4a. However, in this case, the \(\omega _i\) values differ among the three quantum dots. Either two values are the same while the third one is different, or all three values are distinct. Before reaching the critical values of \(\lambda\), the work exhibits similar behavior as before.

However, as \(\lambda\) increases, the work performed undergoes a death and revival, indicating that the engine fails to produce work at certain critical values of \(\lambda\). After these critical values, the engine can produce work and can be considered as a heat engine. However, the work production of the system becomes negative again for higher \(\lambda\) due to the strong Förster mechanism. Now, the question arises as to why the work done transitions from positive to negative values and why the work exhibits revival when the system lacks symmetry.

4.2 Work and entanglement

To understand the reason behind the decrease and subsequent revival of the work at a critical value of \(\lambda\) observed in Figs. 3 and 4, we analyze its behavior in comparison to the behavior of entanglements in different measures shared between the quantum dots of the system with different values of the exciton frequency in each quantum dot. In particular, we will measure the concurrence between each pair of quantum dots (C12, C23, C13) as well as the lower bound (LB) of the entanglement among the three quantum dots. We can gain insights into the underlying mechanisms driving this phenomenon by examining the relationship between these entanglement measures and the work performed by the engine. The decrease and revival of the work refer to a pattern where the work initially declines, then undergoes a resurgence at a specific value of \(\lambda\). This behavior can be attributed to the interplay between \(\lambda\) and the system’s entanglement. By comparing the behavior of the work with the behavior of entanglement, we can observe a correlation between their patterns. The decrease in work is often accompanied by an increase in entanglement, indicating a connection between these phenomena.

Fig. 5
figure 5

Entanglement and Work versus the Förster interaction \(\lambda\) for different values of the exciton frequencies \(\hbar \omega _{i}\). LB represents the lower bound of entanglement, while \(C_{ij}\) denote the concurrence between pairs of quantum dots

Full size image

It is well known that the entanglement between two quantum systems depends on the strength of the interaction between them. In our case, this interaction can be characterized by a Förster (or dipole-dipole) interaction \(\lambda\), which describes the energy transfer between two quantum dots due to their mutual electric dipole moments. The stronger the Förster interaction is the stronger the entanglement between the two quantum dots will be. Indeed, the Förster interaction can lead to the exchange of energy and information between the dots, which can facilitate the establishment of entanglement. However, it is important to note that the presence of the Förster interaction alone does not guarantee the presence of entanglement. Other factors, such as the initial state of the quantum systems and the presence of external noise or decoherence, can also influence the strength of entanglement. Furthermore, in addition to the influence of the exciton frequency in each quantum dot on the critical value of \(\lambda\) observed in Fig. 4, this frequency plays a significant role in entanglement distribution. The monogamous properties of entanglement dictate that the entanglement between two quantum dots is mutually exclusive. As one quantum dot becomes more entangled with another, its entanglement with other quantum dots diminishes. This monogamous nature of entanglement implies that the frequency of each quantum dot can profoundly impact how entanglement is distributed among the quantum dots in the system.

Figure 5 shows that entanglement is absent for small values of \(\lambda\) and appears at some critical value \(\lambda _c\), which depends on the exciton frequency in each quantum dot; \(\lambda _c\) becoming larger for larger values of \(\hbar \omega\). For example in Figs. 5a and b, we have \(\lambda _c=3meV\) and \(\lambda _c=6meV\) for \(\hbar \omega _i=2meV\) and \(\hbar \omega _i=4meV\) respectively. After \(\lambda _c\) we observe that the entanglement increases and reaches its maximum \(\frac{1}{3}\). This indicates that the entanglement is evenly distributed among the three quantum dots and is achieved by assigning the same frequency value to each of them. However in Figs. 5c and d (when \(\hbar \omega _{1} = \hbar \omega _{2} \ne \hbar \omega _3\)), we observe that only the two quantum dots with identical frequencies exhibit entanglement, reaching its maximum value 1 when lambda is larger. This means that these two quantum dots are maximally entangled, while the other pairs remain separated for all values of \(\lambda\). Another observation can be drawn is that the critical value of \(\lambda\) depends on the frequency of the entangled pairs, and does not depend on the frequency of the other subsystems. Note that at the critical value of \(\lambda\), entanglement appears, and the work performed by the engine disappears. However, work exhibits revival when the system lacks symmetry, and entanglement is shared only between two quantum dots. This implies that the revival of work performed after the decline is due to the third quantum dot. Moreover, we can observe that the entanglement at the end of the cycle is detrimental to the work, and the work cannot be obtained if the entanglement is large enough. Our engine cannot produce work if it becomes entangled at the end of its contact with the cold bath. We can conclude that the influence of entanglement on the work performed by a quantum heat engine can be significant, as entanglement can affect the way that energy is distributed within the system. In a quantum heat engine, entanglement can lead to correlations between the energy levels of the system, which can, in turn, affect the efficiency of the engine. For example, if the system is in a highly entangled state, it may be more difficult to extract work from the system, as the energy levels may be more closely correlated and thus more difficult to manipulate. However, our results indicate that for smaller values of Förster energy, the system demonstrates lower entanglement while still being capable of producing work. This implies that in this specific regime, the energy levels are less correlated and can be more easily manipulated, facilitating work extraction. It is important to note that this observation is specific to our system’s configuration. Physically, the increase of the excitonic dipoles moments energy \(\hbar \Omega\) is due to the increase of the electric field \(\vec {E}\), which makes all dipoles parallel, leading to an increase in the repulsive interaction between dipoles, due to the decrease of entanglement between the double quantum dots at the end of the cycle and the increase of the work performed. Based on the description provided, we can conclude that the system consumes energy in order to create entanglement and then recovers a small quantity after the entanglement is established. This phenomenon can be compared to starting a car, where a relatively significant amount of energy is required to initiate the engine. In this process, various components of the car’s system, including the ignition system and fuel pump, are activated. However, certain non-essential functions are temporarily disabled to conserve and concentrate the available energy specifically for starting the engine. This strategic approach ensures that the system can channel its resources effectively and concentrate its energy on the primary objective of entanglement creation; this can lead to an entanglement cost, approach study, based on these types of heat engines.

5 Conclusion

This paper delved into the intricate world of quantum heat engines, focusing on the quantum Otto cycle with the working substance consisting of three InAs quantum dots. These engines can operate at extremely small scales, offering promising prospects for efficient energy conversion. We have studied their behavior under the influence of external electric field and Förster interaction parameters, shedding light on the fascinating interplay between these parameters and the engine’s performance. We find that the work performed by the quantum heat engine is strongly influenced by the Förster interaction energy (\(\lambda\)) and the temperature of the baths. We have identified distinct regions of operation based on the Förster energy, ranging from a heat engine that absorbs heat and produces work to a thermal accelerator that transfers heat without producing work. Temperature variations in the hot bath directly impact the amount of work extracted, with higher temperatures leading to increased work production. Additionally, the energy of excitonic dipoles (\(\hbar \Omega\)) plays a significant role, with larger differences between \(\hbar \Omega _H\) and \(\hbar \Omega _C\) yielding more work. The study also explored the connection between the work performed by the engine and quantum entanglement among the quantum dots. As the Förster interaction increased, work initially decreased and then revived at critical values of \(\lambda\). This pattern is closely correlated with changes in quantum entanglement. Higher entanglement was associated with decreased work, emphasizing the significance of entanglement in influencing engine performance. Then, the work highlighted that the presence of the Förster interaction contributes to entanglement between quantum dots, which can affect the energy distribution and the efficiency of the engine. The entanglement properties are intricately related to the exciton frequency in each quantum dot, with certain frequency configurations favoring maximal entanglement. Importantly, the presence of entanglement at the end of the cycle can inhibit work production, demonstrating the substantial impact of entanglement on quantum heat engine behavior. Finally, The study suggests that the system incurs an energy cost to establish entanglement. Resources are strategically allocated to initiate the entanglement process, with non-essential functions temporarily disabled. This approach ensures efficient energy utilization, leading to the establishment of entanglement.

In summary, this research unveils the intricate relationship between the Förster interaction, entanglement, and the performance of quantum heat engines. The findings underscore the potential of quantum heat engines as a viable energy conversion technology, while also highlighting the importance of managing entanglement in optimizing their efficiency. Further exploration of these phenomena could pave the way for the development of highly efficient quantum heat engines, contributing to the ever-evolving landscape of energy technology.