Abstract
A three-terminal heat engine based on resonant-tunneling multi-level quantum dots is proposed. With the help of Landauer formula, the general expressions for the charge and heat currents, the power output and efficiency are derived. In the linear response regime an explicit analytic expressions for the charge and heat currents, the maximum power output and the corresponding efficiency is presented. Next, the performance characteristic and optimal performance of the heat engine is investigated in the nonlinear response regime by numerical calculation. Finally, the influence of the main parameters, including the asymmetry factor, the energy-level spacing, the energy difference, the number of discrete energy levels, the bias voltage, and the temperature difference on the optimal performance of the heat engine is analyzed in detail. By choosing appropriate parameters one can obtain the maximum power output and the corresponding efficiency at maximum output power.
Graphical abstract

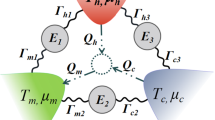
A Schematic diagram of a three-terminal heat engine with resonant-tunneling multi-level quantum dots. A central cavity (red) with chemical potential C is connected μc to the left/right electron reservoir (blue) via multi-level quantum dots. The direction of the arrow indicates the positive direction of the current and heat flow. B The optimized power output Popt in units of \(\frac{{({k_B}T)^2}}{{2\hbar}}\)and the corresponding efficiency ηP in unit of ηC as a function of N for given \(\delta E=0.1k_{B}T\). C The optimized power output Popt and the corresponding efficiency ηP as a function of \(\delta E\) for given N = 11. D The maximum power output Pmax in units of \(\frac{{({k_B}T)^2}}{{2\hbar}}\) and the corresponding efficiency ηP in units of ηC as a function of the temperature difference \(\Delta / T\)
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Thermoelectric devices can be used as power generators to convert heat to electricity based on Seebeck effect or refrigerators to cool a spatial region by external electricity based on Peltier effect, and they could play an important role in the utilization of energy resources. However, present thermoelectric devices still have a very low efficiency in converting heat into electrical work and deliver only moderate powers. To achieve high thermoelectric efficiency, we can use the structure with sharp spectral features, such as quantum dots [1]. Low-dimensional nanostructured materials may also one of the choices to achieve high thermoelectric conversion efficiency. Theoretically, reversible transport can be reached between two electron reservoirs using a delta-function-shaped electronic density of state, but its power is very small [2, 3].
Recently, the thermodynamic performance of three-terminal thermoelectric systems has been researched extensively [4, 5], especially quantum dots. Jordan et al. proposed a three-terminal energy harvester with resonant-tunneling dots and get some important analytic expressions in limit of small level width [6]. Jaliel et al. have experimentally demonstrated that this nanoscale energy harvester can generate a thermal power of 0.13 fW when the temperature difference of each quantum dot is about 67 mK [7]. He et al. propose a model for three-terminal thermionic heat engines based on semiconductor heterostructures and the heat engine performance is discussed in detail in the linear and nonlinear regimes [8]. Prance et al. presented experimentally measurements of a quantum-dot refrigerator designed to cool a 6 μm2 electron gas from 280 mK to below 190 mK [9,10,11]. Jiang et al. studied thermoelectric three-terminal hopping transport through one-dimensional nano-systems and the near-field inelastic heat engine in the linear-response regime [12, 13]. Many scholars have investigated the thermoelectric devices based on resonant-tunneling quantum dots and capacitively coupled quantum dots theoretically [14,15,16,17,18,19,20,21,22,23,24,25,26] and experimentally [27,28,29,30]. Besides resonant-tunneling and coupled quantum dots, other nanostructures, including the quantum point contact and electron cavity [31], quantum wells (or semiconductor superlattices) [32,33,34,35], quantum Hall bar [36, 37], nanowires [38,39,40], energy selective tunnel junctions [41], and superconducting hybrid systems [42, 43] are also the focus of research. Inelastic transport processes assisted by elementary excitations such as photons, phonons and magnons have also been researched extensively in recent years [44,45,46,47,48,49,50,51,52].
On the basis of the previous works, we propose a three-terminal heat engine based on resonant-tunneling multi-level quantum dots. Our work is motivated by a number of advantages that we expect a multi-level quantum dot structure to have over a single-level quantum dot setup. Firstly, multi-level quantum dots should be able to deliver larger currents and therefore, larger power output because of the multi-level resonating channels. Secondly, a multi-level quantum dot structure might be easier to fabricate than a system of self-assembled single-level quantum dots. Finally, due to the small energy-level spacing of large quantum dots or heavily doped semiconductor quantum dots [53], they are ideally suited for low-temperature applications. Of course, we also aim to investigate how the multi-level structure properties of quantum dots deteriorate the efficiency of the heat engine. The main focus in this work is to analyze the thermodynamic performance characteristics and the optimal performance of a three-terminal multi-level quantum dot heat engine. The influence of the main parameters, including the energy-level spacing, the energy difference, the number of discrete energy levels, the asymmetry factor, bias voltage, and temperature difference on the engine’s performance is discussed in detail.
This paper is organized as follows. In Sect. 2, we briefly describe the model and basic physical theory of a three-terminal multi-level quantum dots heat engine. In Sect. 3, we obtain the analytical expressions of the maximum power output and corresponding efficiency in linear regime. In Sect. 4, we analyze the performance characteristic and the optimal performance of the heat engine in nonlinear regime. We summarize the important conclusion of this paper in Sect. 5.
2 Model and theory
The model we consider is schematically illustrated in Fig. 1a. It consists of a central cavity (red) connected via multi-level quantum dots to the left/right electron reservoir (blue) with temperature \(T_{\text{i}}\)(\(i = L\),\(R\)) and chemical potential \(\mu_{\text{i}}\). Each quantum dot has multi-resonant levels relevant for transport. The central cavity is kept at temperature \(T_{\text{C}}\) by a thermal reservoir. This thermal reservoir is treated as a third terminal that provides a heat current \(J\) but no charge to the cavity. The cavity is out of equilibrium, here we assume that fast relaxation processes via electron–electron and electron-phone scattering give rise to a Fermi distribution electrons inside the cavity with temperature \(T_{\text{C}}\) and chemical potential \(\mu_{\text{C}}\). The temperatures of left and right reservoirs are same and lower than that of the central cavity (\(T_{\text{L}} = T_{\text{R}} < T_{\text{C}}\)). When no bias voltage is applied, the chemical potential of left/right electron reservoir are equal (\(\mu_{\text{L}} = \mu_{\text{R}} = \mu_{0}\)). When a bias voltage \(V\) is applied, we take \(\mu_{\text{L}} = \mu_{0} - 1/2eV\) and \(\mu_{\text{R}} = \mu_{0} + 1/2eV\) (e is electronic charge). The positive direction of electrical and energy currents is flowing from the reservoir \(i\) into the cavity. Figure 1b shows a schematic illustration of the proposed energy-band diagram with multi-resonant levels in the right quantum dot. \(E_{\text{i}}\) is the central energy level of the quantum dot \(i\) which is near the Fermi level of the electron reservoir \(i\). The energy difference is \(\Delta E = E_{\text{R}} - E_{\text{L}}\). \(\delta E\) is the energy-level spacing of the quantum dot which we assume to be same for both dots in the following. For simplicity, we assume that each energy level is an independent transport channel and the position of each energy level in quantum dot \(i\) is equidistant [15, 54, 55],
a Schematic diagram of a three-terminal heat engine with resonant-tunneling multi-level quantum dots. A central cavity (red) with chemical potential \(\mu_{\text{C}}\) is connected to the left/right electron reservoir (blue) via multi-level quantum dots. The direction of the arrow indicates the positive direction of the current and heat flow. b Energy band diagram described in a with five discrete energy levels (\(N = 5\)). \(\delta E\) is the energy-level spacing
where \(j\) is an integer with \(0 < j \le N\) when N is the number of discrete energy levels. One of the candidates for this three terminal heat engine which may be suited to experimentally realize is an impurity band in a heavily doped semiconductor quantum dot such as CdS and CdSe. A heavily doped semiconductor is expected to have multiple energy levels originating from impurities, although the process to precisely control the number of impurities in quantum dots should be developed [15].
According to Landauer formula, the charge current and the energy current from the reservoir \(i\) to the central cavity are given by
and
where \(f_{\text{i}} (E - \mu_{\text{i}} ,T_{\text{i}} ) = [\exp [(E - \mu_{\text{i}} )/k_{\text{B}} T_{\text{i}} ] + 1]^{ - 1}\) is the Fermi–Dirac distribution of reservoir \(i\), \(f_{\text{C}} (E - \mu_{\text{C}} ,T_{\text{C}} ) = [\exp [(E - \mu_{\text{C}} )/k_{\text{B}} T_{\text{C}} ] + 1]^{ - 1}\) is the Fermi–Dirac distribution of the central cavity, \(h\) is the Planck’s constant, \(\tau_{i,j^{\prime}} (E)\) is the transmission probability of discrete energy level \(j^{\prime}\) in quantum dot \(i\), which has a resonant energy level \(E_{i,j^{\prime}}\) and a width \(\Gamma _{\text{i}}\),
\(\Gamma _{\text{i}}\) is also called the coupling strength of the quantum dot \(i\) to the cavity and the reservoir \(i\). We assume the asymmetric coupling strength, i.e. \(\Gamma_{\text{L}} = (1 + a)\Gamma\) and \(\Gamma_{\text{R}} = (1 - a)\Gamma\), where \(a\) is the asymmetry factor which satisfies the condition \(- 1 \le a \le 1\), and \(\Gamma \) is the total coupling strength.
According to the conservation of charge and energy in the cavity, there are the relations, \(I_{\text{L}} + I_{\text{R}} = 0\) and \(J_{\text{L}} + J_{\text{R}} + J = 0\). One can use the conservation of charge to determine the chemical potential \(\mu_{\text{C}}\) of the cavity, \(I \equiv I_{\text{L}} = - I_{\text{R}}\) is the net electrical current flowing through the system, while the heat current absorbing from the thermal reservoir is \(J = - J_{\text{L}} - J_{\text{R}}\). In the weak coupling regime \(\Gamma < < k_{\text{B}} T_{\text{C}} ,k_{\text{B}} T_{\text{R}}\), the transmission probability of quantum dot \(i\) is treated as a delta function, i.e. \(\tau_{i,j^{\prime}} (E) \, = \pi \Gamma_{\text{i}} \delta \left( {E \, - \, E_{i,j^{\prime}} } \right)\). Thus, the expressions (2) and (3) for the charge and energy currents can be simplified as
and
\(\hbar\) is reduced Planck constant. Therefore, the electrical power output is
And the efficiency is given by
The working region of the heat engine satisfies
where \(\eta_{\text{C}} = 1 - T_{\text{i}} /T_{\text{C}}\) is the Carnot efficiency and \(\Delta T/T < 2\). We define the average temperature \(T = (T_{\text{C}} + T_{\text{i}} )/2\), and its difference \(\Delta T = T_{\text{C}} - T_{\text{i}}\). In the following numerical calculation, we set \(\Gamma = 0.01k_{\text{B}} T\).
3 Linear response regime
In linear response regime, we need to limit the temperature difference and the voltage bias, i.e. \(eV,k_{\text{B}} \Delta T \ll k_{\text{B}} T\). In terms of the conservation laws of charge and energy, the charge current through the system and the heat current absorbing from the thermal reservoir are derived by [35, 39]
respectively, where \(G\) is electric conductance, \(S\) is Seebeck coefficient, \(\prod\) is the Peltier coefficient, and \(K\) is thermal conductance, i.e.
the auxiliary functions are
The power output is
It can be seen that the power output is a quadratic function of the voltage. When the voltage is zero or at the stopping voltage bias \(V_{stop} = - S\Delta T\), the power output vanishes. Moreover, the maximum power output can be obtained when the voltage is half of the stopping voltage bias i.e. \(V_{\text{m}} = V_{{{\text{stop}}}} /2\). The maximum power output is
For the voltage bias \(V_{\text{m}}\), the corresponding heat current flowing from the thermal reservoir is
The corresponding efficiency at maximum power output is approximately
In linear response regime, \(\eta_{\text{C}} = \Delta T/T_{\text{C}} \approx \Delta T/T\).
Using Eqs. (7)–(19) we can analyze the thermodynamic performance of the heat engine in the linear response regime. In the symmetric coupling strength case, Fig. 2 shows the maximum power output \(P_{\max }\) and the corresponding efficiency at maximum power output \(\eta_{\text{P}} /\eta_{\text{C}}\) varying with the positions of the energy levels \(E_{\text{L}}\) and \(E_{\text{R}}\) at different number of discrete energy levels \(N\). It is seen from Fig. 2 that both the maximum power output and the corresponding efficiency are symmetric with respect to \(E_{\text{L}}\) and \(E_{\text{R}}\). The maximum power output has a saturation value and its saturation value increases as \(N\) increases. However, the corresponding efficiency at maximum power output reaches its maximum value when one of two energy levels is much bigger than \(k_{\text{B}} T\) and the another energy levels is much smaller than \(- k_{\text{B}} T\). And the maximum value of the corresponding efficiency decreases as \(N\) increases. Therefore, we can optimize the power output and corresponding efficiency of the heat engine by adjusting the number of discrete energy levels \(N\). In addition, when \(N = 1\), the corresponding efficiency at maximum power output \(\eta_{\text{P}} \approx \eta_{\text{C}} /2\), because the Peltier coefficient is equal to \(\Pi { = } - ST\) and the thermal conductance \(K \approx 0\).
a The maximum power output \(P_{\max }\) in units of \(\frac{{\left( {k_{\text{B}} \Delta T} \right)^{2} }}{2\hbar }\) and b the efficiency at maximum power output in units of \(\eta_{\text{C}}\) varying with two level positions at \(N = 11\). c and d show the same case as a and b but at \(N = 31\), e and f at \(N = 71\) for given \(\delta E = 0.1k_{\text{B}} T\)
4 Nonlinear response regime
4.1 Performance characteristics
For nonlinear regime, it is not necessary to limit the values of the temperature difference \(\Delta T\) and the bias voltage \(eV\). The temperature difference and the voltage bias are important parameters for studying thermodynamic performance of heat engine. Therefore, Eqs. (7) and (8) can be rewritten as
According to Eqs. (5)–(6) and (20)–(21), we can plot the power output \(P\) varying with the positions of the energy levels \(E_{\text{L}}\) and \(E_{\text{R}}\) at different asymmetry factor \(a\) for given \(\Delta T/T = 1\), as shown in Fig. 3. The bias voltage given at the top left of Fig. 3 is \(eV = 5k_{\text{B}} T\) and one at the bottom right is \(eV = - 5k_{\text{B}} T\). It is found from Fig. 3a that the power output has a maximum value at \(E_{\text{L}} = - E_{\text{R}}\), i.e. \(E_{\text{L}} = -\Delta E/2\), \(E_{\text{R}} =\Delta E/2\). And the maximum value is at \(E_{\text{L}} \approx \pm 5k_{\text{B}} T\) and \(E_{\text{R}} \approx \mp 5k_{\text{B}} T\). In Fig. 3b, the power output also has a maximum value but it is not at \(E_{\text{L}} = - E_{\text{R}}\) when \(a = 0.5\). And the power output in the symmetric case is greater than one in the asymmetric case. Therefore, we may set the asymmetry factor \(a = 0\) and two central energy levels \(E_{\text{L}}\) and \(E_{\text{R}}\) may be donated by the energy difference \(\Delta E\). The power output \(P\) is in units of \(\frac{{\left( {k_{\text{B}} T} \right)^{2} }}{2\hbar }\).
The power output in units of \(\frac{{\left( {k_{\text{B}} T} \right)^{2} }}{2\hbar }\) versus the two central energy levels \(E_{\text{L}}\) and \(E_{\text{R}}\) a at \(a = 0\) and b at \(a = 0.5\). Other parameters are given as \(N = 11\), \(eV = \pm 5k_{\text{B}} T\), \(\delta E = 0.1k_{\text{B}} T\), \(\Delta T/T = 1\)
Figure 4 shows the curves of the power output \(P\) and efficiency \(\eta /\eta_{\text{C}}\) versus the bias voltage \(eV\) at different number of discrete energy levels \(N\) for given \(\Delta E = 10k_{\text{B}} T\), \(\delta E = 0.1k_{\text{B}} T\) and \(\Delta T/T = 1\). It is found from Fig. 4a that the power output \(P\) first increases slowly and then decreases sharply with the increase of \(eV\), and there exist an optimal bias voltage which gives the maximum output power. As \(N\) increases, the maximum power output increases. But it is shown from Fig. 4b that the efficiency first increases slowly and then decreases sharply with the increase of \(eV\) when \(N > 1\). The maximum efficiency gradually decreases with the increase of \(N\). When \(N = 1\) the efficiency increases linearly with the increase of \(eV\). At the stopping voltage the efficiency attains the Carnot value but the power output is zero. The stopping voltage satisfies the relationship \(eV_{{{\text{stop}}}} = \Delta E(1 - T_{\text{i}} /T_{\text{C}} )\) [6]. This means the heat engine can operate in the reversible regime. This result is the same as one in Refs. [2,3,4, 6, 26]. When \(N > 1\), the maximum power output arises while the maximum efficiency reduces. The reason is that as the number of discrete energy levels increases the number of electrons which can pass through the resonant-tunneling channels increases but energy filtering is not efficient. Especially, the performance characteristic curves of the power output versus the efficiency are plotted, as shown in Fig. 4c. It is found that when \(N = 1\) the performance characteristic curve is an open-shaped one. When \(N > 1\), the performance characteristic curves between the power output and the efficiency are the closed loop-shaped ones. This means that the power output does not vanish at maximum efficiency. For actual heat engine, one always wants to get an efficiency as large as possible and at same time obtain one large power output. Thus, the optimal operating regions of the heat engine should be located in those of the performance characteristic curves with a negative slope. Thus the upper and lower bounds for the optimal regions of the power output and the efficiency should be
a The power output in units of \(\frac{{\left( {k_{\text{B}} T} \right)^{2} }}{2\hbar }\) and b the efficiency in units of \(\eta_{\text{C}}\) versus the bias voltage \(eV\) at different number of energy levels. c The performance characteristic curves at different number of energy levels. Here \(\Delta T/T = 1\), \(\Delta E = 10k_{\text{B}} T\), \(\delta E = 0.1k_{\text{B}} T\)
where \(P_{\eta }\), \(P_{\text{m}}\), \(\eta_{mP}\), and \(\eta_{\text{m}}\) four important parameters which determine the lower and upper bounds of the optimized power output and efficiency of a three-terminal heat engine.
4.2 Performance optimization
According to Eqs. (20), (21) and the extremal condition
the optimized power output \(P_{{{\text{opt}}}}\) and the corresponding efficiency \(\eta_{\text{P}}\) varying with the voltage \(eV\) at different number of discrete energy levels \(N\) are plotted in Fig. 5. It is seen from Fig. 5 that the optimized power output \(P_{{{\text{opt}}}}\) first increases sharply and then decreases slowly with the increase of \(eV\). When the bias voltage \(eV \approx 2.4k_{\text{B}} T\), the optimized power output reaches its maximum value. However the corresponding efficiency \(\eta_{\text{P}}\) is a monotonically increasing function of the bias voltage and its slope is gradually reduced. The optimized power output increase as the number of discrete energy levels \(N\) increase, but the corresponding efficiency decreases as the number of discrete energy levels \(N\) increase.
a The optimized power output \(P_{{{\text{opt}}}}\) in units of \(\frac{{\left( {k_{\text{B}} T} \right)^{2} }}{2\hbar }\), b the corresponding efficiency \(\eta_{\text{P}}\) in units of \(\eta_{\text{C}}\) varying with the bias voltage \(eV\) at different number of discrete energy levels \(N\). Here \(\Delta T/T = 1\), \(\delta E = 0.1k_{\text{B}} T\)
Next, using Eqs. (20), (21), (24) and the extremal conditions,
we can further plot the curves of the optimized power output \(P_{opt}\) and the corresponding efficiency \(\eta_{\text{P}}\) versus the number of discrete energy levels \(N\) and energy-level spacing \(\delta E\) for given \(\Delta T/T = 1\), as shown in Fig. 6. It is found from Fig. 6a that the optimized power output is a monotonically increasing function of \(N\) and has a saturation value at \(N \to \infty\), but deviations from that saturation value are exponentially small for large \(N\), for example,\(N = 71\). The reason is that as \(N\) increases the energy levels far from the Fermi level of left/right electron reservoir are not involved in resonant tunneling. The corresponding efficiency \(\eta_{\text{P}}\) is a monotonically decreasing function of \(N\). The results are reasonable when including more levels—the efficiency is decreased, because more back-flow of current is possible, but overall power out is increased because of more parallel channels. Thus, to achieve the maximum power output and at the same time obtain a large efficiency, we should choose a suitable number of discrete energy levels \(N \approx 20\) in a quantum dot.
a The optimized power output \(P_{{{\text{opt}}}}\) in units of \(\frac{{\left( {k_{\text{B}} T} \right)^{2} }}{2\hbar }\) and the corresponding efficiency \(\eta_{\text{P}}\) in units of \(\eta_{\text{C}}\) as a function of \(N\) for given \(\delta E = 0.1k_{\text{B}} T\). b The optimized power output \(P_{{{\text{opt}}}}\) and the corresponding efficiency \(\eta_{\text{P}}\) as a function of \(\delta E\) for given \(N = 11\)
In Fig. 6b, the optimized power output \(P_{opt}\) decreases as the energy-level spacing \(\delta E\) increases and it reaches the minimum value at \(\delta E \approx 3k_{\text{B}} T\) for given \(N = 11\). A lot of the energy levels are far from the Fermi level and the number of effective resonant tunneling channels decreases. The advantage of using multiple energy levels disappears. For \(\delta E\) much smaller than \(k_{\text{B}} T\), optimal (high) efficiency occurs when all 11 levels are close to the energy where the two Fermi functions cross. For \(\delta E\) much larger than \(k_{\text{B}} T\), optimization puts one level at the energy where the two Fermi functions cross, and the others are at very high energies (where the two Fermi functions are both close to 0) or very low energies (where the two Fermi functions are both close to 1). So the corresponding efficiency \(\eta_{\text{P}}\) first decreases and then increases with the increase of \(\delta E\). Thus, to achieve the maximum power output and at the same time obtain a large efficiency, we should choose the dense discrete energy levels in a quantum dot.
Further, we consider the influence of temperature difference on the performance of quantum dot heat engine. We plot the curves of the maximum power output \(P_{\max }\) and the corresponding efficiency \(\eta_{\text{P}}\) versus the temperature difference \(\Delta T/T\) for given the saturation value \(N = 71\) and \(\delta E = 0.1k_{\text{B}} T\), as shown in Fig. 7. It is found from Fig. 7a that the maximum power output is approximately given by \(P_{\max } \approx 0.126\left( {\frac{{\Delta T}}{T}} \right)^{2} \frac{{\left( {k_{\text{B}} T} \right)^{2} }}{2\hbar } = \frac{0.126}{{2\hbar }}\left( {k_{\text{B}} \Delta T} \right)^{2}\), independent of average temperature \(T\). For a small value of \(\Delta T/T\), the maximum power output and the corresponding efficiency \(\eta_{\text{P}}\) are almost the same as those in linear regime when \(N = 71\), as shown in Fig. 2e,f. Due to the quadratic dependence on \(\Delta T\) we obtain the same power output for given value of \(\Delta T\) in the linear and nonlinear regime. However, as the corresponding efficiency \(\eta_{\text{P}}\) at maximum power output grows linearly with the temperature difference \(\Delta T/T\), the heat engine should be operated as much in the nonlinear regime as possible. The optimal position of energy difference \(\Delta E\) and the optimal voltage \(eV\) as a function of the temperature difference \(\Delta T/T\) are plotted, as shown in Fig. 7b. Figure 7b shows that the optimal position of energy difference \(\Delta E\) and the optimal voltage \(eV\) increases monotonically as the \(\Delta T/T\) increases.
a The maximum power output \(P_{\max }\) in units of \(\frac{{\left( {k_{\text{B}} T} \right)^{2} }}{2\hbar }\) and the corresponding efficiency \(\eta_{\text{P}}\) in units of \(\eta_{\text{C}}\) as a function of the temperature difference \(\Delta T/T\); b The optimal energy difference \(\Delta E\) and the optimal voltage \(eV\) as a function of the temperature difference \(\Delta T/T\)
5 Conclusions
WE have investigated the optimal performance of a three-terminal heat engine based on resonant-tunneling multi-level quantum dots. In linear regime, we have derived the explicit analytic expressions for the maximum power output and the corresponding efficiency. In nonlinear regime, we have analyzed the performance characteristics and optimal performance of the heat engine at the maximizing output power. Then, the main results are as following: (1) the performance of the heat engine which works in the symmetry case is better than that in the asymmetry case; (2) the denser the discrete energy levels, the larger the optimal power output and the corresponding efficiency. But we should choose a suitable number of discrete energy levels for given energy-level spacing to achieve the large power output and large efficiency at the same time; (3) the heat engine should be operated as much in the nonlinear regime as possible. The results obtained here are helpful to design and operation of the practical quantum dot heat engines.
Data availability
This manuscript has associated data in a data repository. [Authors’ comment: Authors can confirm that all relevant data are included in the article.]
References
G.D. Mahan, J.O. Sofo, Proc. Natl. Acad. Sci. USA 93, 7436 (1996)
T.E. Humphrey, R. Newbury, R.P. Taylor, H. Linke, Phys. Rev. Lett. 89, 116801 (2002)
M. Esposito, K. Lindenberg, C. Van den Broeck, Europhys. Lett. 85, 60010 (2009)
G. Benenti, G. Casati, K. Saito, R.S. Whitney, Phys. Rep. 694, 1 (2017)
B. Sothmann, R. Sánchez, A.N. Jordan, Nanotechnology 26, 032001 (2015)
A.N. Jordan, B. Sothmann, R. Sánchez, M. Büttiker, Phys. Rev. B 87, 075312 (2013)
G. Jaliel, R.K. Puddy, R. Sánchez, A.N. Jordan, B. Sothmann, I. Farrer, J.P. Griffiths, D.A. Ritchie, C.G. Smith, Phys. Rev. Lett. 123, 117701 (2019)
Y.Y. Yang, S. Xu, J.Z. He, Chin. Phys. Lett. 37, 120502 (2020)
H.L. Edwards, Q. Niu, A.L De Lozanne, Appl. Phys. Lett. 63, 1815 (1993).
H.L. Edwards, Q. Niu, G. A. Georgakis, A.L De Lozanne, Phys. Rev. B 52, 5714 (1995).
J.R. Prance, C.G. Smith, J.P. Griffiths, S.J. Chorley, D. Anderson, G.A.C. Jones, I. Farrer, D.A. Ritchie, Phys. Rev. Lett. 102, 146602 (2009)
J.H. Jiang, O. Entin-Wohlman, Y. Imry, Phys. Rev. B 85, 075412 (2012)
J.H. Jiang, Y. Imry, Phys. Rev. B 97, 125422 (2018)
Y. Zhang, G. Lin, J. Chen, Phys. Rev. E 91, 052118 (2015)
S. Kano, M. Fujii, Nanotechnology 28, 095403 (2017)
R.S. Whitney, R. Sánchez, F. Haupt, J. Splettstoesser, Phys. E 82, 176 (2016)
J.S. Lim, D. Sánchez, R. López, J. Appl. Phys. 20, 023038 (2018)
A.M. Daré, P. Lombardo, Phys. Rev. B 96, 115414 (2017)
H. Su, Z.C. Shi, J.Z. He, Chin. Phys. Lett. 32, 100501 (2015)
Z.C. Shi, W.F. Qin, J.Z. He, Mod. Phys. Lett. B 30, 1650397 (2016)
J.Y. Du, T. Fu, S. Su, J. Chen, Eur. Phys. J. D 75, 232 (2021)
A.-M. Daré, Phys. Rev. B 100, 195427 (2019)
S.S. Qiu, Z.M. Ding, L.G. Chen, Y.L. Ge, Sci. China Technol. Sci. 64, 1641 (2021)
S.K. Manikandan, E. Jussiau, A.N. Jordan, Phys. Rev. B 102, 235427 (2020)
P.A. Erdman, B. Bhandari, R. Fazio, J.P. Pekola, F. Taddei, Phys. Rev. B 98, 045433 (2018)
R.S. Whitney, Phys. Rev. L 112, 130601 (2014)
B. Roche, P. Roulleau, T. Jullien, Y. Jompol, I. Farrer, D.A. Ritchie, D.C. Glattli, Nat. Commun. 6, 6738 (2015)
F. Hartmann, P. Pfeffer, S. Höfling, M. Kamp, L. Worschech, Phys. Rev. Lett. 114, 146805 (2015)
M. Josefsson, A. Svilans, A. Burke, E. Hoffmann, S. Fahlvik, C. Thelander, M. Leijnse, H. Linke, Nat. Nanotechnol. 13, 920 (2018)
A.J. Keller, J.S. Lim, D. Sánchez, R. López, S. Amasha, J.A. Katine, Phys. Rev. Lett. 117, 066602 (2016)
B. Sothmann, R. Sánchez, A.N. Jordan, M. Büttiker, Phys. Rev. B 85, 205301 (2012)
B. Sothmann, R. Sánchez, A.N. Jordan, M. Büttiker, New J. Phys. 15, 095021 (2013)
Y. Choi, A.N. Jordan, Phys. E 74, 465 (2015)
Z.B. Lin, Y.Y. Yang, J.Z. He, Chin. Phys. Lett. 36, 060501 (2019)
Z.B. Lin, W. Li, Y.Y. Yang, J.Z. He, Phys. Rev. E 101, 022117 (2020)
B. Sothmann, R. Sánchez, A.N. Jordan, Europhys. Lett. 107, 47003 (2014)
R. Sánchez, B. Sothmann, A.N. Jordan, Phys. Rev. Lett. 114, 146801 (2015)
A.I. Boukai, Y. Bunimovich, J. Tahir-Kheli, J.K. Yu, I.W.A. Goddard, J.R. Heath, Nature 451, 168 (2008)
Y.Y. Yang, S. Xu, W. Li, J.Z. He, Phys. Scr. 95, 095001 (2020)
S. Xu, Y.Y. Yang, X. Liu, J.Z. He, Acta Phys. Sin. 71, 020501 (2022)
S. Su, Y. Zhang, J. Chen, T.M. Shih, Sci. Rep. 6, 21425 (2016)
S. Pal, C. Benjamin, J. Phys.: Condens. Matter 34, 305601 (2022)
R. Hussein, M. Governale, S. Kohler, W. Belzig, F. Giazotto, A. Braggio, Phys. Rev. B 99, 075429 (2019)
Z.C. Shi, J. Fu, W.F. Qin, J.Z. He, Chin. Phys. Lett. 34, 110501 (2017)
J.H. Jiang, O. Entin-Wohlman, Y. Imry, New J. Phys. 15, 075021 (2013)
C. Li, Y. Zhang, J. He, Chin. Phys. Lett. 30, 100501 (2013)
B. Rutten, M. Esposito, B. Cleuren, Phys. Rev. B 80, 235122 (2009)
B. Cleuren, B. Rutten, C. Van den Broeck, Phys. Rev. Lett. 108, 120603 (2012)
Z.C. Shi, J.Z. He, Y.L. Xiao, Sci. China Phys. Mech. Astronomy 45, 50502 (2015)
C. Li, Y. Zhang, J. Wang, J. He, Phys. Rev. E 88, 062120 (2013)
J.H. Wang, Y.M. Lai, Z.L. Ye, J.Z. He, Y.L. Ma, Q.H. Liang, Phys. Rev. E 91, 050102 (2015)
W. Li, J. Fu, Y.Y. Yang, J.Z. He, Acta Phys. Sin. 22, 220501 (2019)
D. Mocatta, G. Cohen, J. Schattner, O. Millo, E. Rabani, U. Banin, Science 332, 77 (2011)
W. Li, Y.Y. Yang, J. Fu, Z.B. Lin, J.Z. He, ES Energy Environment 7, 40 (2020)
P.A. Erdman, F. Mazza, R. Bosisio, G. Benenti, R. Fazio, F. Taddei, Phys. Rev. B 95, 245432 (2017)
Acknowledgements
This work has been supported by the National Natural Science Foundation (Grant No. 11875034), People’s Republic of China.
Author information
Authors and Affiliations
Contributions
All authors contributed to the design and implementation of the research, to the analysis of the results and to the writing of the manuscript.
Corresponding author
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Liu, X., Gao, J. & He, J. A three-terminal heat engine based on resonant-tunneling multi-level quantum dots. Eur. Phys. J. B 96, 1 (2023). https://doi.org/10.1140/epjb/s10051-022-00470-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjb/s10051-022-00470-2