1 Introduction

Carbon dioxide (CO2), a primary greenhouse gas (GHG), has seen increasing concentrations that significantly impact global climate change [1]. Accurate monitoring of global atmospheric CO2 levels is crucial for understanding and predicting these climate changes [2,3,4,5,6]. Satellites equipped with passive spectrometers, such as the Greenhouse Gases Observing Satellite (GOSAT) and the Orbiting Carbon Observatory-2 (OCO-2) [7, 8], are instrumental for global GHG measurements. However, their dependence on solar radiation for spectral detection imposes limitations, particularly at high latitudes or nighttime, and they are vulnerable to aerosol and cloud scattering interference [9, 10]. Space-borne Integrated Path Differential Absorption (IPDA) lidar technology has emerged to overcome these limitations. It enables active, accurate observations of CO2 both day and night with high accuracy and extensive coverage [11]. IPDA lidar measures the column-averaged dry-air mixing ratio of CO2 (XCO2) [12] by comparing the intensity differences of laser at least at two wavelengths: \({\lambda }_{on}\), which is absorbed by CO2, and \({\lambda }_{off}\), which is almost not absorbed along the same path [13]. Numerous experiments have demonstrated the efficacy of IPDA lidar in CO2 detection. The National Aeronautics and Space Administration (NASA) has developed four primary types of IPDA lidar for its Active Sensing of CO2 Emissions over Nights, Days, and Seasons (ASCENDS) project [14]: (1) NASA’s Goddard Space Flight Center developed fiber pulsed direct detection IPDA lidars that used 30/15 wavelengths at the R16 (1572.335 nm) absorption line [15,16,17,18]. (2) NASA’s Langley Research Center, in collaboration with Harris Corp., developed a three-wavelength fiber intensity-modulated continuous-wave (IM-CW) lidar with \({\lambda }_{on}\) at 1571.112 nm and \({\lambda }_{off}\) at 1571.061/1571.161 nm [19,20,21]. (3) The Jet Propulsion Laboratory (JPL) and Coherent Technologies (later Lockheed Martin Coherent Technologies) jointly developed a dual-wavelength solid-state continuous-wave IPDA lidar employing coherent detection with \({\lambda }_{on}\) at 2050.911 nm and \({\lambda }_{off}\) at 2051.187 nm [22, 23]. (4) NASA’s Langley Research Center (LaRC) also developed a dual-pulse solid-state IPDA lidar employing direct detection with a tunable \({\lambda }_{on}\) and 2051.2500 nm \({\lambda }_{off}\) [13, 24,25,26]. The European Space Agency (ESA) proposed the A-SCOPE mission [27]. The German Aerospace Center (DLR) conducted the CHARM-F airborne experiment, simultaneously measuring CO2 and CH4, using \({\lambda }_{on}\) at 1572.02 nm and \({\lambda }_{off}\) at 1572.12 nm for CO2 [28,29,30]. Additionally, The Methane Remote Sensing LIDAR Mission (MERLIN) is a highly regarded IPDA lidar used for CH4 detection using \({\lambda }_{on}\) at 1645.552 nm and \({\lambda }_{off}\) at 1645.846 nm [31,32,33]. The National Institute of Information and Communications Technology (NICT) in Japan developed a coherent 2 μm IPDA and wind lidar system (Co2DiaWiL) for measuring CO2 and wind speed, with \({\lambda }_{on}\) adjustable between 2051.002 and 2051.058 nm, and \({\lambda }_{off}\) set at 2051.250 nm [34, 35]. The National Centre for Space Studies (CNES) and the French Aerospace Lab (ONERA) introduced the Short-Comb Atmospheric Lidar Experiment (SCALE) for 3 to 13 wavelengths on one absorption line of CO2 [36,37,38]. The Shanghai Institute of Optics and Fine Mechanics of the Chinese Academy of Sciences (SIOM) conducted airborne IPDA lidar experiments with \({\lambda }_{on}\) at 1572.024 nm and \({\lambda }_{off}\) at 1572.085 nm [39, 40]. And the space-borne Aerosol and Carbon Dioxide Detection Lidar (ACDL) payload and the satellite (named DQ-1) were successfully launched in April 2022 with the 1572.024/1572.085 nm wavelengths for CO2 detection [41, 42].

These IPDA lidars operate at two to several dozen wavelengths. The utilization of multiple wavelengths offers additional benefits in mitigating systematic errors, capturing absorption line shapes, obtaining vertical information, and achieving expanded dynamic range [15, 43,44,45,46,47]. However, implementing multiple wavelengths increases the complexity of the laser system, and the precision of wavelength step control presents challenges. More problematically, as different wavelengths are emitted sequentially, the atmospheric and surface conditions along the path change during the flight of space-borne or airborne platforms. Wavelengths essentially traverse different paths, which introduces inherent errors [48]. Dual-comb spectroscopy (DCS) technology is an emerging solution to multi-wavelength challenges [36]. All wavelengths of optical frequency comb (OFC) are sent and detected simultaneously, thus eliminating errors associated with wavelength switching [49]. The concept of frequency comb lidar aims to combine the advantages of lidar and spectrometer instruments. Previous works have demonstrated open-path DCS of atmospheric gases of interest using broad optical frequency combs generated by mode-locked lasers (MML) [50,51,52,53,54,55,56]. However, their fitting to a space mission is beyond the state of the art of today’s short (fs) pulse optical amplifiers. The feature is more modest in the electro-optic frequency comb (EOFC) case. EOFC is a mature multi-wavelength laser source with precise line spacing controllability [57]. The 3–17 wavelengths of EOFC can be limited to one absorption line with a narrow spectral range of 0.2 nm [36,37,38]. It avoids ultra-short pulses’ extremely high peak power while having a higher nonlinearity threshold than single-frequency lasers for fiber amplification. Moreover, Its multiple wavelengths are derived from electro-optic phase modulation, naturally featuring an even and accurately known frequency step.

Electro-optic dual-comb spectroscopy (EO-DCS) is a potential space-borne IPDA lidar technique for XCO2 measurement. Its even line spacing brings a unique wavelength-optimization problem. We simulate the space-borne EO-DCS IPDA lidar to explore the optimal sampling wavelength strategy for XCO2 measurement. Section 2 introduces the principle of EO-DCS measurement, SNR, and geophysical models alongside the inverse method validation. Section 3 analyzes both random and systematic errors, followed by a global evaluation. The results suggest the number of sampling wavelengths, central wavelength, and spacing. The conclusion is provided in Sect. 4.

2 Method

2.1 Measurement method

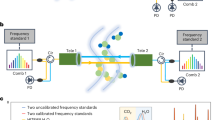
The lidar is based on the dual-comb spectroscopy (DCS) technique, now widely recognized as the most efficient method of acquiring the comb spectrum [49]. The brief instrument setup of the lidar is shown in Fig. 1(a). The lidar system includes a transmitter, receiver, detection, and acquisition module. The frequency of the master laser is \({\upnu }_{0}\), which is on the order of 200 THz. The frequencies \({\upnu }_{01}\) and \({\upnu }_{02}\) are shifted by two acousto-optic modulators (AOMs) and then modulated by two electro-optic phase modulators (PMs), respectively. The frequencies of Comb1 are \({\upnu }_{01}+i{f}_{r1}\), and the frequencies of Comb2 are \({\upnu }_{02}+i{f}_{r2}\), where \(i\) takes integer values. The repetition rate \({f}_{r1}\) and \({f}_{r2}\) are on the order of GHz, with the repetition rate difference \(\Delta f_{r} = f_{r2} {-}f_{r1}\) on the order of MHz. Adjusting the drive signals of AOMs and PMs can result in two optical frequency combs that meet the requirements of DCS detection, a technology that is already very mature [57]. The laser is amplified and then split into two paths. The measurement laser is launched, reflected by the ground, and then passes through the atmosphere again before being received. The reference laser is directly connected to the detector. The conversion of the measurement and reference signals from optical frequency to radio frequency is shown in Fig. 1(b) and (c). Comparing the measurement and the reference can extract the XCO2. Despite the frequency offset between the two frequency combs, the MHz-level repetition rate difference (\(\Delta {f}_{r}\)) is much smaller than the CO2 absorption peak width of a dozen GHz, so we can approximate that the wavelength sampling points of the two combs are coincident. Another key advantage is that DCS adds no instrument lineshape contribution to the measured absorption feature [55].

Fig. 1
figure 1

a Schematic diagram of EO-DCS instruments. b EO-DCS concept for measurement path. c EO-DCS concept for reference path. LPF low-pass filter, ADC analog-to-digital converter, EDFA erbium-doped fiber amplifier

Full size image

The in-orbit operation of the space-borne EO-DCS lidar is shown in Fig. 2.

Fig. 2
figure 2

a The in-orbit operation of the space-borne EO-DCS lidar for XCO2 detection. b R16 transmittance spectrum with 9 sampling wavelengths highlighted

Full size image

The laser pulse is emitted with an efficiency of \({T}_{\text{emit}}\) and then propagates through the atmosphere, which has a transmittance of \({T}_{\text{atm}}\) over the path length \(L\). The pulse is diffusely reflected off the ground surface with a reflectance of \(\rho \), and is subsequently captured by a telescope with a collection area \(A\). In this process, \(\eta \) represents the detector efficiency and \({T}_{\text{instrument}}\) denotes the efficiency of the instrument. The total loss in detection can be expressed using the lidar equation:

$$ T_{{{\text{total}}}} = \rho \eta T_{{{\text{emit}}}} T_{{{\text{instrument}}}} T_{{{\text{atm}}}}^{2} \frac{A}{{L^{2} {\text{ EQ EQ }}}}. $$
(1)

The mean number of photons received in one time-domain sample can be expressed as

$$ \mu = \frac{{T_{{{\text{total}}}} E_{0} t_{{{\text{int}}}} }}{{h\nu t_{{{\text{pulse}}}} }} \cdot \frac{{\sum T_{i} P_{i} }}{{\sum P_{i} }}. $$
(2)

The energy, \({E}_{0}\), contained in a pulse is expressed as the ratio of the average launched power, \({P}_{\text{emit}}\), to the pulse repetition frequency, \({f}_{\text{emit}}\), given by the equation \({E}_{0}=\frac{{P}_{\text{emit}}}{{f}_{\text{emit}}}\); The pulse duration is \({t}_{\text{pulse}}=2\mu s\). Here, \({T}_{i}\) and \({P}_{i}\) represent the transmittance and emitted power at \(i\) th wavelengths along one absorption line.

The noise sources considered in the simulation include quantum noise, solar background noise, detection noise, and speckle noise. The standard deviation of their contribution to the photon count is expressed as

$$ \sigma = \sqrt {var_{{\text{Q}}} + var_{{{\text{BG}}}} + var_{{\text{D}}} + var_{{\text{S}}} } $$
(3)

The time-domain SNR at the central sample of radio frequency (RF) interferogram is \(\frac{\mu }{\sigma }\), and the SNR in the spectrum [36] is

$$ {\text{SNR}}_{f} \left( f \right) = \frac{1}{2} \cdot \frac{{A_{s} \left( f \right)df}}{{\mathop \smallint \nolimits_{0}^{{f_{{{\text{max}}}} }} A_{s} \left( f \right)df}} \cdot \sqrt N \cdot N_{{{\text{shots}}}} \cdot \frac{\mu }{\sigma }, $$
(4)

where \(\frac{1}{2}\) represents the conversion from amplitude to power. \({A}_{s}\left(f\right)\) represents the spectral amplitude, and \(N\) denotes the number of non-zero elements in the Fourier transform’s basis vector. According to the Nyquist theorem, \(N\) equals half the number of sample points in one period, corresponding to the number of emitted wavelengths. By averaging measurements, denoted as \({N}_{\text{shots}}=\sqrt{\frac{{D}_{\text{av}}}{{V}_{\text{sat}}}{f}_{\text{emit}}}\), the SNR can be enhanced by a factor of\(\sqrt{{N}_{\text{shots}}}\). Here, \({D}_{\text{av}}\) represents the spatial resolution in the horizontal direction, \({V}_{\text{sat}}\) represents flight velocity, which can be calculated from the orbital altitude. The \(i\) th wavelength amplitude information,\({A}_{i}\), is ideally extracted. The SNR of \(i\) th RF comb tooth can be expressed as

$$ {\text{SNR}}_{f} \left( i \right) = \frac{1}{2} \cdot \frac{{A_{i} }}{{\mathop \sum \nolimits_{i} A_{i} }} \cdot \sqrt N \cdot N_{{{\text{shots}}}} \cdot \frac{\mu }{\sigma }. $$
(5)

The SNR discussed here is utilized for numerical simulation in Sect. 3.

2.2 Model setup

A comprehensive modeling and retrieval framework was introduced to assess the space-borne EO-DCS’s capability to measure XCO2. Figure 3 illustrates a schematic diagram of the simulation workflow.

Fig. 3
figure 3

Schematic diagram of the simulation framework

Full size image

The fixed profile regularization method couples the XCO2 to the radiative transfer model [58]. The Reference Forward Model (RFM) [59], a GENLN2-based line-by-line radiative transfer model [60], is employed as the forward model. Atmospheric profile data, such as CO2 concentrations, temperature, and pressure, were extracted from the Copernicus Atmosphere Monitoring Service (CAMS) global greenhouse gas reanalysis (EGG4). The XCO2 and the atmospheric profiles are convertible in both directions, subject to specific profile regularization. The land surface reflectance at 1572 nm is derived from Moderate Resolution Imaging Spectroradiometer (MODIS) (Terra + Aqua) through interpolation [61, 62]. The formulas used for these calculations are detailed in Table 1. The water surface’s reflectance was determined based on the water surface wind speed [63, 64]. The global land surface elevation data was obtained from Jonathan de Ferranti [65], while the global aerosol data was sourced from the CAMS Global Reanalysis (EAC4) [66]. In Fig. 3, the spectral transmittance of the sampling wavelength in the DCS system forms the measurement space in the inversion algorithm, and when the number of effective sampling wavelengths is 9, the elements in the measurement space are shown in Fig. 2(b).

Table 1 Data sources used in simulation [61,62,63,64,65]
Full size table

The instrument directs laser beams toward the nadir and measures the laser echo signals reflected from the land and water surface. Two comb lasers operate at fixed frequencies along the R16 absorption line. Table 2 presents the main parameters of the instrument, satellite, and geophysical environment. The technology for producing EO-DCS is very mature [57]. Its amplification at the 1572 nm band is entirely feasible [67,68,69,70]. All parameters can be achieved with the current level of technology.

Table 2 Lidar instrument model specifications
Full size table

XCO2 measurement needs high accuracy, with about 0.3% precision corresponding to approximately 1 ppm, to help reduce uncertainties about carbon sources and sinks [71]. Therefore, we conduct the simulation following this requirement.

2.3 Retrieval algorithm

Determining CO2 concentrations is an ill-posed problem with no unique solution. The optimal estimation method (OEM) is widely adopted for tackling such problems. Rodgers [72] introduced a Bayesian approach to inverse problems, employing the forward model depicted by

$$ y = F\left( {x,b} \right) + \in . $$
(6)

This model is designed to deduce the state vector \(\mathbf{x}\)  based on the measurements \(\mathbf{y}\), where \({y}_{i}\) signifies the \(i\) th spectral element of the observed spectrum, depicted as the orange dots in Fig. 2(b). Here, \(\mathbf{y}\) represents the measured spectrum, while  \(\mathbf{x}\)  delineates the CO2 concentration profile across varying atmospheric layers. The forward model \(\mathbf{F}\left(\mathbf{x},\mathbf{b}\right)\) correlates the state vector \(\mathbf{x}\) with the measurements \(\mathbf{y}\), and \({\varvec{\upepsilon}}\) accounts for measurement noise. The vector of parameters \(\mathbf{b}\) comprises those quantities which influence the measurement, are known to some accuracy, but are not intended as quantities to be retrieved. These parameters are listed in Table 1.

The distributions of \({y}_{i}\) and \({x}_{i}\) are Gaussian, with covariance matrices \({\mathbf{S}}_{\epsilon }\) and \({\mathbf{S}}_{a}\) respectively. By invoking Bayes’ theorem under these assumptions, we can articulate the conditional probability of the state \(\mathbf{x}\) given the measurement \(\mathbf{y}\). Rodgers [35] has formulated

$$ \begin{array}{*{20}c} { - 2\ln P\left( {x|y} \right) = [y - F\left( {x,b} \right)]^{T} S_{\in }^{ - 1} \left[ {y - F\left( {x,b} \right)} \right]} \\ { + \left[ {x - x_{a} } \right]^{T} S_{a}^{ - 1} \left[ {x - x_{a} } \right]} \\ \end{array} $$
(7)

where \(x_{a}\) is the prior vector, and \(- 2{\text{lnP}}\left( {{\text{x}}|{\text{y}}} \right)\) is the cost function (\({\chi }^{2}\)) that measures the goodness of fit of the solution, seeking the state that maximizes the posterior probability density function, which is known as the maximum a posteriori solution (MAP). The Levenberg–Marquardt (LM) methods are suitable numerical methods to solve this. The most probable state \(\mathbf{x}\) can be obtained by performing the following iteration:

$$ \begin{array}{*{20}c} {x_{i + 1} = x_{i} + \left[ {\left( {1 + \gamma } \right)S_{a}^{ - 1} + K_{i}^{T} S_{\in }^{ - 1} K_{i} } \right]^{ - 1} } \\ {\left\{ {K_{i}^{T} S_{\in }^{ - 1} \left[ {y - F\left( {x_{i} } \right)} \right] - S_{a}^{ - 1} \left[ {x_{i} - x_{a} } \right]} \right\}} \\ \end{array} . $$
(8)

The iteration converges to the most probable state \({\varvec{x}}\), where the Jacobian \({\mathbf{K}}_{i}=\partial \mathbf{F}/\partial {\mathbf{x}}_{i}\) and \({\varvec{\gamma}}\) is a scaling constant. The LM iterative process is considered to have converged when \(\Delta {\chi }^{2}/{\chi }^{2}<{10}^{-3}\) within a maximum of 20 iterations. The algorithm used in this study is illustrated in Fig. 4.

Fig. 4
figure 4

Flowchart of the data retrieval

Full size image

A noise-free retrieval is shown in Fig. 5; the state vector components iteratively converge, starting from an initial estimate significantly distant from the true value and approaching it in 5–8 iterations. Inset plots within the main graph that zoom in on the iterations between 15 and 20 to show the infinitesimal error. The algorithm applied in this study is demonstrably unbiased.

Fig. 5
figure 5

Demonstration of the algorithm: Iterative convergence of state space elements \({\mathbf{x}}_{i}\) towards the true state (represented by the red line). Insets provide a magnified view of the 15th to 20th iterations

Full size image

It is important to note that Fig. 5 illustrates the inversion for an ideal, noise-free measurement, which allows for the simultaneous inversion of four parameters without difficulty. In subsequent simulations, the parameters other than XCO2 are attributed to the parameter \(\mathbf{b}\).

3 Results and discussion

3.1 Experiment process

3.1.1 Water–vapor influence

Previous work has demonstrated that water vapor significantly affects the CO2 absorption spectroscopy [73,74,75]. The selection of the R16 absorption line can avoid the influence of H2O [76, 77]. Additionally, it has been found that HDO has a weak absorption peak at R16, which significantly affects the measurements [78]. Figure 6 illustrates the absorption bands for CO2 (R6-R26) and the corresponding H2O/HDO absorption, with the spectroscopic parameters derived from HITRAN [79, 80]. If HDO is not included in the forward model, it will cause 1–3ppm bias; If it does, it will only increase the standard deviation of XCO2 [72, 78]. HDO varies greatly with weather and geographical location, so it is difficult to incorporate it into the basis of wavelength optimization. Therefore, not dealing with HDO is a limitation of our simulation.

Fig. 6
figure 6

Calculated absorption cross section of CO2, H2O and HDO based on HITRAN at 1 atm and 296 K. The selected band is marked by the black dashed rectangle

Full size image

3.1.2 Sampling number and strategy

The number of sampling wavelengths was intentionally chosen to be odd, aligning with the principles of generating optical frequency combs through electro-optic phase modulation. The optimization focused on a narrower range of sampling wavelengths (3–17). This is because, unlike traditional spectroscopic techniques, dual-comb spectroscopy (DCS) technology precisely “dot-samples” the absorption spectroscopy rather than convolving the instrument line shape with the absorption spectroscopy; thus, a smaller number of sampling wavelengths suffices. Moreover, having a large number of sampling wavelengths would result in an even distribution of energy across R16, rendering wavelength optimization meaningless.

To optimize the wavelength sampling strategy, we need to strike the right balance between two conflicting goals: on the one hand, we aim to maximize the SNR by avoiding absorption peaks, and on the other hand, we need to capture the absorption characteristics at the peak, following the principles of IPDA. Figure 7 illustrates these considerations by showing how the wavelength sampling strategy can be optimized by shifting the center wavelength (a) and adjusting the spacing (b).

Fig. 7
figure 7

Schematic diagrams illustrating the sampling wavelength strategy: a Variation of center wavelength; b Variation of the spacing of sampling wavelengths

Full size image

3.2 Random error

The XCO2 error was calculated using two methods. Method 1 generates simulated data based on the space-borne platform parameters and SNR model, then solves XCO2 iteratively. Method 2 involves linearizing the forward model and calculating the error, denoted as \({\mathbf{G}}_{y}\epsilon \), which Rodgers [72] refers to as the retrieval error. The gain matrix \(\mathbf{G}\) is expressed as

$$ G = \left( {K^{T} S_{\in }^{ - 1} K + S_{a}^{ - 1} } \right)^{ - 1} K^{T} S_{\in }^{ - 1} = S_{a} K^{T} \left( {KS_{a} K^{T} + S_{\in } } \right)^{ - 1} . $$
(9)

While these two methods can theoretically yield equivalent outcomes, the practical application reveals distinct limitations for each. The simulation data retrieval method, which relies heavily on the generation of large amounts of data and intense computational work, incurs significant computational costs and high time expenses. This is particularly true when we need to optimize the central wavelength and wavelength interval with high precision, requiring substantial computational resources, making this method unsuitable. On the other hand, the \({\mathbf{G}}_{y}\epsilon \) method requires much less computational effort and easily achieves high precision in calculating the central wavelength and wavelength interval. However, the \({\mathbf{G}}_{y}\epsilon \) method depends on a forward model where the spectral transmittance at sampling wavelengths is not linearly related to XCO2, a phenomenon known as “the nonlinearity of the forward model”. The \({\mathbf{G}}_{y}\epsilon \) method inherently uses the Jacobian matrix, i.e., it linearizes the forward model, which leads to inaccurate results. The degree of inaccuracy depends on the extent of model nonlinearity. For the atmospheric CO2 absorption issue, the stronger the absorption, the more severe the nonlinearity, meaning that sampling wavelengths close to absorption peaks can result in significant errors in the \({\mathbf{G}}_{y}\epsilon \) method’s estimates. For more detailed theory, refer to Rodgers’ book [72].

In Fig. 8, the two methods are demonstrated at 9 sampling wavelengths with an average power of 10 W in (a–d), and their differences and ratios are shown in (e) and (f). A neural network fitting approach is employed to attain the accuracy of Method 1 while also maintaining the continuous stability of Method 2. The corrected results are illustrated in (g) and (h).

Fig. 8
figure 8

a, c the error landscapes using Method 1 and Method 2. The red semi-transparent plane represents the cases where the central sampling wavelength coincides with the R16 absorption peak. The X-axis spans from 6359.907 cm−1 to 6360.027 cm−1 with a resolution of 0.005 cm−1. The Y-axis spans from 0.2 GHz to 3 GHz with a resolution of 0.1 GHz. b, d: 3D surface plots for (a) and (c). e, f Comparative analysis of Method 1 and Method 2. Their ratio varies from 0.9 to 1.6, and their differences span from -0.05 ppm to 0.35 ppm. g, h The two methods are combined. The X-axis spans from 6359.907 cm−1 to 6360.027 cm−1 with a resolution of 0.001 cm−1. The Y-axis spans from 0.1 GHz to 3 GHz with a resolution of 0.02 GHz

Full size image

These results provide insights into the two methods. Although both methods show similar trends, the results from Method 1 are rough despite conducting 300 numerical simulations per point. Method 2’s error image (c) is smooth with a more apparent trend, but the values diverge from the former.

Considering N sampling wavelengths, the strategies can be categorized into N + 1 distinct approaches based on their correlation with the R16 absorption peak. Figure 9 illustrates the regions for 9 sampling wavelengths. The dividing line between Regions 5 and 6 corresponds to the R16 absorption peak.

Fig. 9
figure 9

The sampling wavelength strategies are divided into 10 regions according to the relationship between sampling wavelengths and the R16 absorption peak. The relationship is visualized through a color-coded map

Full size image

Figure 10 shows the wavelength strategy optimization for random error (\({\sigma }_{\text{Ran}}\)) at different powers. The results are compared in (e), where one optimal strategy is shown in (g), and one bad strategy is shown in (f). Figure 11 shows the values of the minimum error in ten regions. The increased scatter on the right side in (e) (Region 7, 8) was caused by a minor peak marked by a blue dotted box in (f) and (g).

Fig. 10
figure 10

Strategy optimization for \({\sigma }_{\text{Ran}}\). The subfigures illustrate the results for different powers: a 2.5 W, b 5 W, c 10 W, and d 20 W. Strategies with minimum error in each region (Fig. 9) are denoted by red dots. Subfigure (e) is a compilation of all red dots. Region 5 is outlined with a red dashed line, with (f) and (g) illustrating two typical strategies. The central wavelength in the schematic diagram is marked with a solid line. The mirror peak is indicated by a blue dashed box, originating from another weak absorption line of CO2

Full size image
Fig. 11
figure 11

Comparative analysis of minimum \({\sigma }_{\text{Ran}}\) values in regions 1 through 10 under different power settings: a 2.5 W, b 5 W, c 10 W, and d 20 W

Full size image

Figure 10 suggests that any sampling wavelength that falls on the absorption peak will cause a surge in \({\sigma }_{\text{Ran}}\) by about 30%. This is due to extremely low transmission at the R16 peak. The criterion for strategy selection can be described as being symmetric around the absorption peak while avoiding it, as illustrated in Fig. 10(g). According to Chen et al. (2014), NASA also employs the method of symmetric sampling wavelengths to reduce retrieval errors and enhance tolerance to laser frequency drift [48].

The comparison in Fig. 10(e) leads us to conclude that a larger spacing should be set under low power, that is, low SNR conditions. The results reflect the balance between obtaining absorption information and reducing transmission losses: when the power is sufficient, the sampling tends to strong absorption, and when the power is insufficient, the part with low loss is preferred.

In Fig. 11, Regions 1 and 10 have the most minor \({\sigma }_{\text{Ran}}\); however, the sampling wavelengths in these two regions are entirely located on one side of the absorption peak, and the spacing is too small. This would result in the simulated scenario being close to a traditional dual-wavelength IPDA lidar, imposing extremely high demands on the system’s wavelength stability. The negative impacts can be seen in the following section.

3.3 Systematic error

This study evaluates three systematic errors related to laser and atmosphere parameters: center wavelength, temperature, and pressure.

3.3.1 Center wavelength

Based on the principle of sampling at the R16 absorption line, the wavelength of the lidar system directly affects the XCO2 retrieval.


The line shape can be fit to determine the center wavelength. However, the accuracy of the fit is subject to various influences, including atmospheric temperature and pressure profiles, as well as the frequency response of optical and electrical devices. These factors inevitably introduce biases into the fitting process, which can interfere with the inversion of XCO2. So, we consider the center wavelength as a parameter in \(\mathbf{b}\). The wavelength-induced error (\({\sigma }_{\uplambda })\) is given by

$$ \sigma_{{\uplambda }} = {\mathbf{G}}_{y} {\mathbf{K}}_{{{\text{wn}}}} \left( {{\mathbf{b}}_{{{\text{wn}}}} - {\hat{\mathbf{b}}}_{{{\text{wn}}}} } \right), $$
(10)

where \({\mathbf{K}}_{\text{wn}}\) is the wavelength Jacobian matrix, and \({\mathbf{G}}_{y}\) is the corresponding Gain matrix. The circumflex indicates an estimated quantity rather than a true state, \({\mathbf{b}}_{\text{wn}}\) is the best estimate of the wavelength, as distinct from the true value \({\widehat{\mathbf{b}}}_{\text{wn}}\) which is the value that the instrument knows about.

A fixed wavelength deviation \({{(\mathbf{b}}_{\text{wn}}-{\widehat{\mathbf{b}}}_{\text{wn}})=\sigma }_{p}= 1\text{ MHz}\) (~ 3.33 × 10–5 cm−1) is tested in Fig. 12(a). Figure 12(b) illustrates the 0.7 GHz cross-section, and \({\sigma }_{\uplambda }\) in (a) are split by two thresholds of 0.2 ppm and 1 ppm, as shown in (c).

Fig. 12
figure 12

Pseudocolor representations of error distributions associated with the retrieval of the center wavenumber and CO2 concentration. a Error due to 1 MHz mismatch of center wavenumber. The black dashed line delineates regions 1 and 10. The red dashed line marks the 0.7 GHz cross-section, as shown in (b). c Thresholding analysis of (a). Mark \({\sigma }_{\uplambda }\) below 0.2 ppm in yellow, and \({\sigma }_{\uplambda }\) between 0.2–1 ppm in black. The red dashed line encircles Region 5, where two kinds of low-error strategies are marked as ① and ②

Full size image

In Fig. 12, the error sharply increases in regions 1 and 10, as the sampling wavelengths for these two regions are all located on one side of the absorption peak. (b) zooms in on a portion of the 0.7 GHz cross-section, where the error approaches zero under specific strategies. From Fig. 12(c), the error remains minimal when the sampling wavelengths are symmetrically distributed with respect to the absorption peak. For example, in Region 5, the low-error region can be divided into two types: ① and ②, where ① is close to the optimal strategy of \({\sigma }_{\text{Ran}}\), as shown in Fig. 10(g). While ② is close to the bad strategy of \({\sigma }_{\text{Ran}}\) as shown in Fig. 10(f). Although they exhibit opposite behaviors regarding \({\sigma }_{\text{Ran}}\), they are both insensitive to wavelength errors. Considering solely \({\sigma }_{\uplambda }\), the optimal sampling is marked in Fig. 12(c): 6359.96 cm−1, 0.51 GHz.

The low error can be qualitatively interpreted from the signs of the terms in the formula. The \({\mathbf{K}}_{\text{wn}}\) exhibits numerical symmetry about the R16 absorption peak but with opposite signs. Conversely, the gain matrix for XCO2 (\({\mathbf{G}}_{{\varvec{y}}}\)) is entirely symmetric about the absorption peak, resulting in the sensitivity (\({{\varvec{A}}}_{\text{wn}}={\mathbf{G}}_{y}{\mathbf{K}}_{\text{wn}}\)) approaching zero.

In summary, the wavelength strategy represented by the yellow pixels in Fig. 12(c) can reduce the errors introduced by wavelength. When spacing is large, it refers to the two cases symmetry of the sampling wavelengths with respect to the absorption peak. When spacing is small, the two cases intersect.

3.3.2 Temperature and pressure

Temperature and pressure are parameters that are included in the parameter \(\mathbf{b}\), and their inaccuracies contribute to systematic errors. The temperature or pressure deviation introduced in this study implies that the overall profiles of these variables are shifted from their true values by a proportional amount. The introduced temperature deviation is approximately 1–2 K, while the pressure deviation is a few millibars.

The effect on XCO2 can be quantified by \({\mathbf{G}}_{\mathbf{y}}{\mathbf{K}}_{\mathbf{b}}\left(\mathbf{b}-\widehat{\mathbf{b}}\right)\), where \({\mathbf{K}}_{\mathbf{b}}\) is the Jacobian matrix associated with temperature or pressure, and \(\left(\mathbf{b}-\widehat{\mathbf{b}}\right)\) denotes the bias in temperature or pressure.

XCO2 errors induced by temperature and pressure bias ( \({\sigma }_{\text{Tem}}\) and \({\sigma }_{\text{Pre}}\)) are depicted in Fig. 13.

Fig. 13
figure 13

XCO2 errors induced by temperature (a) and pressure (b). a XCO2 error due to 0.6% temperature bias at a near-surface temperature of 285.14 K. b XCO2 error due to 0.6% pressure bias at a near-surface pressure of 1013 mb. Region 5 is outlined with a red dashed line

Full size image

The results have shown that a symmetrical and dense distribution of sampling wavelengths contributes to error reduction. Moreover, positioning one of the sampling wavelengths at the absorption peak is also detrimental. The trend remains monotonic within the evaluated range, with no concave minimum found.

\({\sigma }_{\text{Tem}}\) and \({\sigma }_{\text{Pre}}\) are cross-sectional at 0.7 GHz, as shown in Fig. 14, and the changes in transmittance caused by them are shown in Fig. 15.

Fig. 14
figure 14

The error of XCO2 caused by temperature (a) and pressure (b) biases are evaluated at 0.7 GHz spacing cross-sections. The near-surface temperature is 285.14 K, and the near-surface pressure is 1013 mb. Region 5 is outlined with a red dashed line

Full size image
Fig. 15
figure 15

Transmittance variations of 1% temperature (a) and 1% pressure (b). The variations in the R16 line are all on one side of the zero axis (red line). If the transmittance variation are all on one side of the red line (zero line), it indicates that the measurement cannot compensate for the effects of temperature/pressure

Full size image

From Fig. 14, temperature biases ranging from 0.2% to 1% can induce XCO2 errors from 0.2 to 0.8 ppm, whereas pressure biases within the same range can result in errors from 0.3 to 1.4 ppm. It is essential to steer clear of the absorption peak, particularly in scenarios with substantial deviations in temperature or pressure.

In the optimization of wavelength selection for dual-wavelength IPDA lidar, it is possible to identify a “temperature-insensitive frequency” [11] at which the temperature influence can be disregarded.

However, such a strategy does not exist for multi-wavelength approaches because absorption changes caused by temperature or pressure have the same sign on both sides of the R16 absorption peak, preventing the sensitivity (\({\varvec{A}}={\mathbf{G}}_{y}\mathbf{K}\)) from approaching zero. As shown in Fig. 15, biases in temperature/pressure affect the spectral transmittance of R16 on only one side of the red line (same sign), meaning that errors will not be compensated in XCO2 measurements.

3.4 Global Error Evaluation

The above optimization can be expanded to encompass 3 to 17 wavelengths in Fig. 16 under constant total power. The geophysical parameters used in the global assessment are shown in Tables 1 and 2. These parameters are averaged annually, and their median values are used. Land and ocean were assessed separately, with the lidar equation calculations utilizing the median values of global geophysical parameters. The total error, when combined geometrically, is defined by

$$ \sigma_{{{\text{Total}}}} = \sqrt {\sigma_{{{\text{Ran}}}}^{2} + \sigma_{{{\text{Tem}}}}^{2} + \sigma_{{{\text{Pre}}}}^{2} + \sigma_{{\uplambda }}^{2} } . $$
(11)
Fig. 16
figure 16

Errors caused by temperature (1 K), pressure (100 Pa), and wavelength (1 MHz) at 20 W average power accumulated over 50 km for land (a) and 100 km for ocean (b). Errors of 3–17 sampling wavelengths for land/ water are added geometrically and indicated by red dots. Here, “A” represents the wavelength strategy that minimizes \({\sigma }_{\text{Ran}}\), while “B” denotes the strategy that minimizes the total error (Euclidean norm)

Full size image

The \({\sigma }_{\uplambda }\) tends to be very small in “A” bars, as it exhibits the most dramatic fluctuations among the four, as shown in Fig. 12(b). In contrast, it is significant in some “B” bars, indicating that \({\sigma }_{\text{Ran}}\) and \({\sigma }_{\uplambda }\) have not been minimized simultaneously.

The 3-wavelength case has the lowest \({\sigma }_{\text{Ran}}\), enabling it to achieve high-precision XCO2 measurements. It comes with trade-offs of degrees of freedom for signal (DOFs), which means its ability to obtain forward model parameters (such as HDO, doppler shifts and CO2 vertical profile) is weaker [72]. This simulation focuses on XCO2 wavelength optimization and more retrieval requirements are not discussed.

The 11-wavelength case is unique. Its \({\sigma }_{\text{Ran}}\) and \({\sigma }_{\uplambda }\) are minimized simultaneously, which is a good occurrence. Additionally, its \({\sigma }_{\text{Tem}}\) and \({\sigma }_{\text{Pre}}\) remain within acceptable limits.

The 5–17 wavelength case and the 3-wavelength case are two kinds of systems, divided according to the optimal wavelength range in Fig. 17. The 5 to 17 wavelength cases share the same sampling wavelength range of 1.5 FWHM, and their \({\sigma }_{\text{Ran}}\)(green bar) follows formula (12) [81]:

$$ \sigma_{{{\text{Ran}}}} \propto \frac{{\sqrt {\delta v} }}{{{\text{SNR}}}}, $$
(12)

where \(\delta v\) is sampling spacing. It is a known result in signal processing that applies to Gaussian and Voigt profile line shapes [82]. Since the total power is the same, the changes in SNR and \(\sqrt{\delta v}\) cancel each other out, so \({\sigma }_{\text{Ran}}\) of 5 to 17 wavelength cases are very close. The optimal wavelength range of the 3-wavelength case is about 0.7 FWHM, which can achieve a smaller \({\sigma }_{\text{Ran}}\) verified by the simulation calculation.

Fig. 17
figure 17

The optimal spacing and optimal wavelength range are compared to the FWHM of the R16 absorption line

Full size image

Upon evaluation of the global XCO2 errors, optimal sampling strategies were established, encompassing 7, 9, 11, and 13 sampling wavelengths, as demonstrated in Fig. 18. The distribution of global XCO2 errors when employing the optimal strategy with 11 sampling wavelengths is illustrated in Fig. 19, the error in most areas is less than 0.9 ppm.

Fig. 18
figure 18

a Illustration of the optimization process for sampling strategy in global evaluation, using marginal distribution plots for 7, 9, 11, and 13 sampling wavelengths. The intensity of color represents the proportion of the most optimized strategies in the global assessment. Their dual path transmittance is shown in (b–e). The ratio is defined by \(\delta v/\text{FWHM}\)

Full size image
Fig. 19
figure 19

Global XCO2 error distribution for 11 sampling wavelengths

Full size image

4 Conclusion

The performance of a space-borne EO-DCS IPDA lidar for XCO2 measurement has been analyzed. Integrating data simulation with linearization error analysis forms a solid foundation for optimization, which markedly improves the management of random errors. By ensuring a symmetrical distribution of several sampling wavelengths around the R16 absorption line peak, one can halve the random error compared to configurations where a sampling wavelength coincides with the peak. Regarding systematic errors, the strategy optimization effectively mitigates those caused by wavelength biases, reducing potential XCO2 errors from over 2 ppm to nearly zero. However, this approach does not apply to errors induced by atmospheric temperature and pressure; although it can minimize them to some extent, complete theoretical elimination is not possible. Specifically, profile deviations of 0.2–1% may result in XCO2 errors ranging from 0.2 to 0.8 ppm and from 0.3 to 1.4 ppm, respectively.

Considering both random and various systematic errors comprehensively, we have optimized the total error for land and water on a global scale. This optimization has been extended across 3 to 17 sampling wavelengths. The configuration of 11 wavelengths is found to concurrently minimize both random error and error introduced by the wavelengths. Optimization of the global error suggests that the optimal central wavelength for an 11-wavelength sampling scheme is 6359.957 cm−1, with a wavelength spacing of 0.638 GHz. The global error has been analyzed based on these parameters, which could meet the requirement of less than 1ppm XCO2 error.

The space-borne EO-DCS IPDA lidar has excellent potential to supplement the data gaps of XCO2 passive remote sensing with high accuracy and reduce the dependence on environmental parameters. The optimization of the sampling wavelength strategy will contribute to high-precision XCO2 measurement.