Efficient control of three-dimensional atom localization via probe absorption in a phase-coherent atomic medium

Abstract

We propose a new scheme for the study of three-dimensional (3D) atom localization by observing spatially modulated absorption of a weak probe field operating in a multi-wave-mixing induced four-level atomic system. The field-coupled atomic model can be envisaged as a closed-loop double-lambda configuration. By controlling Rabi frequency, detuning, and field-induced collective phase-coherence, different spatial structures of localization patterns are presented with a variety of standing wave field configurations. Our results highlight that 100% detection probability of atom is possible in the present model in many ways with high-precision measurement of spatial absorption. It has been shown that position information of the atom with maximum detection probability can be efficiently controlled by employing a travelling-wave field in association with the standing wave fields in the system. For a specific field configuration, the maximum detection probability of finding the atom can be obtained with a limit of spatial resolution better than $\lambda$/40 in our model. The efficacy of the present model is to find its applications in quantum information processing in the near future.

1 Introduction

In the last few decades, tremendous interest has grown in precise position measurement of atoms both theoretically and experimentally [1,2,3,4], because of its potential application in laser cooling and trapping of neutral atoms [5, 6], Bose-Einstein condensation [7, 8], measurement of the center-of-mass wave function [9], and atom nanolithography [10, 11]. In the earlier study, atomic position information was obtained mainly by measuring the phase shift of off-resonant standing wave. After that coherent control of opto-atomic properties of resonant atom-field coupling in the standing wave regime has been utilized by different authors in a number of works [12,13,14,15,16,17,18,19,20,21] to exhibit the behaviours of one-dimensional (1D) atom localization in subwavelength domain. More specifically, by measuring the upper-level population in a three-level $\Lambda$-type atom, Paspalakis and Knight [12] have proposed the behaviour of atom localization as a consequence of quantum interference. Zubairy and his group [13,14,15] have investigated some schemes of atom localization based on resonance fluorescence, or phase and amplitude control of probe absorption. A scheme has been presented by Liu et. al. [16] to realize atom localization via interacting dark resonances. Subwavelength atom localization via coherent manipulation of Raman gain has been studied by Qamar et. al. [17]. Atom localization owing to coherent population Trapping (CPT) was discussed by Agarwal and Kapale [18]. Similar localization patterns as shown in ref.[18] was experimentally observed by Proite et. al. [19] as a result of electromagnetically induced transparency (EIT). Manipulation of localization peak in the sub-half-wavelength domain via probe absorption has been studied by Wang and Jiang [20] and Dutta et. al. [21] in different atomic configurations. It is to be mentioned here that atomic vapours in nanocell [22, 23] may be ideal for experimental realization of 1D atom localization.

Apart from 1D atom localization, two-dimensional (2D) atom localization has been studied as it is much more useful in atom-nanolithography. 2D atom localization can be achieved for the simultaneous interaction of an atom with two orthogonal standing wave fields [24]. Atom-nanolithography based on 2D atom localization was explained by Gong and his group [25]. Ivanov and Rozhdestvensky [26] discussed 2D atom localization in a four-level tripod-type atomic system via measurement of the atomic population in the case of EIT. 2D atom localization via coherence-controlled absorption spectrum in an N-tripod-type five-level atomic system has been studied by Ding et.al. [27]. To realize 2D atom localization, Gao and coworkers presented three schemes relating to three physical processes: (i) controlled spontaneous emission in a coherently driven tripod-type atomic system [28], (ii) quantum interference in an inverted-Y-type system [29] and (iii) interacting double-dark resonances in a N-type system [30]. Ding et al. [31, 32] reported 2D atom localization by controlling position-dependent spontaneous emission spectrum and probe absorption in different atomic configurations. Li et al. [33] adopted phase phase-sensitive spatially modulated absorption spectrum to exhibit the features of 2D atom localization. Wu and his group [34] reported 2D atom localization in a four-level cycle-configuration atomic model. By controlling the position-dependent spontaneous emission spectrum in an rf-field induced five-level scheme, Wang et al. [35] has described the manipulation of 2D localization peaks in the subwavelength domain. Rahmatullah and S. Qamar [36] have investigated the evolution of 2D atom localization in the presence of superposed standing waves. High precision localization behaviour has been manifested in the work of Wu and Ai [37] in a coherent five-level atomic medium based on EIT. 2D atom localization via spontaneously generated coherence (SGC) has been studied by Shui et al. [38]. 2D atom localization via Autler-Townes microscopy in the sub-half-wavelength domain has also been visualized by Shui et. al. [39]. Field-induced superposition effects on atom localization via position-dependent resonance fluorescence spectrum have been reported by Dutta et. al. [40].

An attempt has been made to visualize 3D atom localization in different atomic systems in the presence of three standing wave fields. By measuring the probe absorption based on EIT in a five-level M-type atomic system, Qi et al. [41] studied 3D subwavelength atom localization. Different 3D localization structures were reported by Ivanov et. al. [42] in a four-level Tripod-type scheme by observing the upper state population. The maximum detection probability of atoms in those two works [41, 42] was not improved. 100% detection probability of atom in 3D localization based on probe absorption in a three-level scheme was proposed by Wang and Yu [43]. This feature was manifested in the subsequent works [44,45,46,47,48,49,50,51,52,53] also. 3D atom localization via EIT was discussed by Wang et al. [44] in a three-level atomic system. Hamedi and Mehmannavaz [45] put forward phase control of 3D atom localization in a four-level atomic system in $\Lambda$ configuration. Three-wave mixing technique in a V-type three-level atom was introduced by Zhu et al. [46] for finding 3D localization. 3D atom localization via spontaneous emission in a four-level atomic system was reported by Wang and Yu [47]. Zhu et al. [48] suggested the process of 3D atom localization from spatial interference in a double two-level atomic system. 3D sub-half-wavelength atom localization via interacting double-dark resonances was described by Yang et al. [49]. Coherent control of 3D atom localization based on different coupled mechanisms was discussed by Wang et al. [50]. High-precision 3D atom localization was reported by Mao and Wu [51] in a microwave-driven atomic system. Chen et al. [52] presented 3D atom localization via spontaneous emission from two different decay channels. High-precision 3D atom localization via phase-sensitive absorption spectra in a microwave-driven four-level atomic system was studied by Zhang et al. [53]. 3D atom localization based on resonance fluorescence microscopy has been reported by Panchadhyayee et al. [54]. 3D atom localization via spontaneous emission in a four-level atomic system has been discussed by Song et al. by mentioning the attainable spatial limit of resolution as 0.04$\lambda$ [55]. Zhang et al. [56] has investigated 3D atom localization using probe absorption in a diamond-configuration atomic system. High-precision 2D and 3D atom localizations via probe absorption in a five-level atomic system have been described by Song et al. [57] by including an incoherent pump field in their model.

Inspired by the works [53, 56], we make an effort to study 3D atom localization based on spatially modulated probe absorption in a four-wave-mixing-induced closed loop configuration in a double-$\Lambda$ atomic system [Fig. 1]. For this purpose, three schemes have been adopted by considering the different combinations of standing and travelling waves in the given model. In one scheme, one strong driving field is taken as a standing wave along the z-direction and another strong driving field is an admixture of two orthogonal standing waves along the x- and y- directions. The second one is associated with a travelling-wave field. In another scheme, orthogonal standing waves along the x- and y- directions in association with a travelling wave and the z-directional standing wave field are reversed for the two driving fields. The localization patterns in the above two schemes are different for choosing different values of Rabi frequencies and detuning parameters. In the last scheme, we have applied the travelling-wave field with the z-directional standing wave for one control field, while the standing waves along x- and y- directions stand for other control field. Such field configuration is different from the first and second schemes. In all the schemes, we have emphasized obtaining a single localization structure in 3D space in the sub-half-wavelength regime. To this aim, the last scheme is shown to have its usefulness in forming a single localization structure with high spatial resolution in the sub-half-wavelength domain. We have qualitatively discussed all the localization behaviours for all the schemes in detail.

Fig. 1

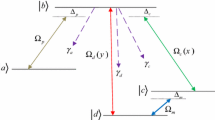
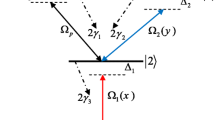
a Field-coupled energy level diagram of a four-level double $\Lambda$-type atomic model which consists of the ground state energy levels ket1 and $\vert {2} \rangle$ and the excited state energy levels $\vert {3} \rangle$ and $\vert {4} \rangle$. $R_c(x,y,z)$, and $R_d(x,y,z)$ represent two space-dependent strong coupling fields. b Scheme I: $R_d(x)$ and $R_d(y)$ represent two standing waves along the x- and y- directions associated with a travelling-wave field of Rabi frequency $R_{d0}$. $R_c(z)$ is a standing-wave field along the z- direction. c Scheme II: $R_c(x)$ and $R_c(y)$ represent two standing waves along the x- and y- directions associated with a travelling-wave field of Rabi frequency $R_{c0}$. $R_d(z)$ is a standing-wave field along the z- direction. d Scheme III: $R_c(x)$ and $R_c(y)$ represent two standing waves along the x- and y- directions. $R_d(z)$ is a standing-wave field along the z- direction associated with a travelling-wave field of Rabi frequency $R_{d0}$. The yellow circle represents the atom

Salient features along with the advantage of the work are described as follows: (i) In the work of Ref. [53], the four-level double-$\Lambda$ system is associated with three-level closed-loop linkage, while our four-level double-$\Lambda$ system incorporates four-level closed-loop linkage. As a consequence, a stronger phase-correlation effect results in modulating the absorptive response of the probe field in the present model. Phase-dependent variation in shaping the localization pattern in 3D space becomes preponderant for the double lambda system using the four-level closed-loop linkage. A similar emergence of the phase-coherence effect occurs in the work of Ref. [56] based on four-level closed-loop linkage in a diamond-type atomic system. But, for the existence of three excited states in this configuration, the model works in a much more dissipative environment when compared to the present model having two excited states; (ii) In the work of Wang and Yu [58], high precision atom localization has been studied by observing the population in the excited states of a four-level double-$\Lambda$ system similar to that used in the present work. In such a localization scheme, trapped population characteristics can be measured by using a similar method of fluorescence shelving technique as noted in Ref. [18]. In comparison to this process, it is a more direct way to observe the localization structures by measuring spatial probe absorption as adopted by us in our model; (iii) In comparison to the results reported in the previous works [53, 56, 58], phase-dependent variation of 3D localization patterns as shown in the present model are distinct, and different owing to a variety of physical conditions; (iv) It is worth noting that 100$\%$ detection probability of atom is shown to be easily achievable by controlling the Rabi frequency of the travelling-wave field in the presence of other system parameters in each of three schemes considered in our model. It reflects the robustness of the given model; (v) By setting properly the value of Rabi frequency of the travelling-wave field along with the other system parameters, obtaining phase-dependent variation of 3D localization patterns with a variety of spatial resolution in the given model is much easier in comparison to other models as investigated earlier; (vi) In contrast to the previous works on 3D atom-localization, the appropriate parameter conditions make the present model suitable to predict the maximum detection probability of atom with a limit of spatial resolution better than ${\Lambda }/40$. This is an advantage for using the present double-$\Lambda$ system; (vii) Last but not the least, by properly setting the values of system parameters like Rabi frequency, detuning, and phase in a different field configuration consisting of one or more travelling waves with the required standing waves, the localization patterns different to those shown in this article will be attainable with more or less enhanced spatial resolution. We have examined this point before furnishing the results in the article. Herein lies the flexibility of the present model.

2 Theoretical formulation

Field-coupled energy-level configuration of our four-level scheme is shown in Fig. 1a, where the dipole allowed transitions $\vert {1} \rangle$-$\vert {3} \rangle$, $\vert {1} \rangle$-$\vert {4} \rangle$, $\vert {2} \rangle$-$\vert {3} \rangle$ and $\vert {2} \rangle$-$\vert {4} \rangle$ are guided by four coherent fields. Transition from $\vert {1} \rangle$ to $\vert {4} \rangle$ is governed by a weak probe field of Rabi frequency $R_p$. Another weak control field of Rabi frequency $R_s$ is used to couple the transition $\vert {1} \rangle$-$\vert {3} \rangle$. The transitions $\vert {2} \rangle$-$\vert {3} \rangle$ and $\vert {2} \rangle$-$\vert {4} \rangle$ are driven by two strong standing wave fields or a combination of travelling wave and standing wave fields with Rabi frequencies $R_c(x,y,z)$ and $R_d(x,y,z)$, respectively. This is to mention here that, for standing wave fields accompanied by travelling-wave fields, we have considered three different schemes (Fig. 1b–d): (I) $R_d(x,y,z)$ is the composition of two standing waves along x- and y- directions, while $R_c(x,y,z)$ represents a standing wave along z- direction, i.e. $R_c(x,y,z)$ = $R_c$ $sin(k_cz)$ and $R_d(x,y,z)$ = $R_{d0}$ + $R_d$ ($sin(k_dx)$ + $sin(k_dy)$), where $R_{d0}$ is the Rabi frequency of an associated travelling wave field; (II) $R_c(x,y,z)$ is the composition of two standing waves along x- and y- directions, while $R_d(x,y,z)$ represents a standing wave along z- direction, i.e. $R_d(x,y,z)$ = $R_d$ $sin(k_dz)$ and $R_c(x,y,z)$ = $R_{c0}$ + $R_c$ ($sin(k_cx)$ + $sin(k_cy)$), where $R_{c0}$ is the Rabi frequency of the travelling-wave field associated with $R_c(x,y,z)$; (III) The Scheme II is modified with the introduction of a travelling wave part ($R_{d0}$) in the field configuration of $R_d(x,y,z)$ and removal of $R_{c0}$ from the field $R_c(x,y,z)$, i.e. $R_d(x,y,z)$ = $R_{d0}$ + $R_d$ $sin(k_dz)$ and $R_c(x,y,z)$ = $R_c$ ($sin(k_cx)$ + $sin(k_cy)$). In Fig. 1b–d, the probe field is considered along an arbitrary direction in 3D space. In experimental realization of 3D localization, as the atomic position, or positions, will be confined at arbitrary locations in 3D space, the direction of application of the probe field in the system will be at arbitrary orientation in 3D space as expected. More specifically, position-sensitive detection of localization pattern requires the application of probe field in the system at arbitrary orientation in 3d space. For the sake of simplicity of numerical calculation, the wave vectors $k_c$ and $k_d$ are taken to be nearly equal. Rabi frequencies of the fields are defined as $R_i$ $=$ $\frac{{{\bar{\mu }}}_{mn}.{\bar{\epsilon }}_i}{2\hbar }$ ($i=p,s,c,d$), where the dipole transitions are specified by $\vert {m} \rangle$-$\vert {n} \rangle$ ($m = 1,2$ and $n =3,4$). $\mu _{mn}$ denotes the dipole moment associated with the corresponding transition. $\bar{\epsilon }_i$ stands for the amplitude of the laser fields. We note that $R_{c0}$ and $R_{d0}$ are the Rabi frequencies of travelling-wave fields applied to the respective transitions as stated above.

We assume that the position of the center-of-mass of the atom is nearly constant during atom-field interaction along the standing wave fields. The transverse kinetic energy of the atom can be neglected as it is small compared to the interaction energy in the standing wave regime. Thus, the kinetic energy part of the atom in the Hamiltonian can be neglected in the Raman-Nath approximation [59]. Under the electric dipole and the rotating-wave approximations, the coherent part of the interaction Hamiltonian of the system can be written as

$$\begin{aligned} {{\mathcal {H}}}= & {} -{\hbar }[-(\Delta _p - \Delta _d) \vert {2} \rangle \langle {2}\vert - (\Delta _p - \Delta _d + \Delta _c) \vert {3} \rangle \langle {3}\vert - \Delta _p \vert {4} \rangle \langle {4}\vert \nonumber \\{} & {} + (R_s \vert {3} \rangle \langle {1}\vert + R_p \vert {4} \rangle \langle {1}\vert + R_c(x,y,z) \vert {3} \rangle \langle {2}\vert + R_d(x,y,z)\vert {4} \rangle \langle {2}\vert \nonumber \\{} & {} + c.c)], \end{aligned}$$

(1)

the detuning parameters $\Delta _p$ $=$ $\omega _{41} - \omega _{p}$, $\Delta _c$ $=$ $\omega _{32} - \omega _{c}$ and $\Delta _d$ $=$ $\omega _{42} - \omega _{d}$. In deriving the Hamiltonian, we have imposed the condition $\omega _s$ $=$ $\omega _p + \omega _c - \omega _d$ i.e. $\Delta _s$ $=$ $\omega _{31} - \omega _{s}$ $=$ $(\omega _{41} + \omega _{32} - \omega _{42}) - (\omega _p + \omega _c - \omega _d)$ $=$ $\Delta _{p} - \Delta _{d} + \Delta _{c}$. Here, $\omega _{j}$ denotes the carrier frequencies of the coherent fields and $\omega _{mn}$ represents the frequencies of the respective atomic transitions.

The system dynamics can be explained by the semiclassical density matrix equation as given by

$$\begin{aligned} \frac{\partial {\rho }}{\partial t} = -\frac{i}{\hbar }[{{\mathcal {H}}},\rho ] + \Lambda \rho \end{aligned}$$

(2)

where the term $\Lambda \rho$ includes the effect of incoherent decay-mechanism inherent to the present model. The required off-diagonal density matrix equations are presented as follows

$$\begin{aligned} {\dot{\rho }}_{21}= & {} -Z_{21} {\rho }_{21} + iR_c^*(x,y,z) \rho _{31} - iR_s \rho _{23} - iR_p \rho _{24} + iR_d^*(x,y,z)\rho _{41} \end{aligned}$$

(3)

$$\begin{aligned} {\dot{\rho }}_{31}= & {} -Z_{31} {\rho }_{31} + iR_s (\rho _{11} - \rho _{33}) + iR_c(x,y,z)\rho _{21} - iR_p \rho _{34} \end{aligned}$$

(4)

$$\begin{aligned} {\dot{\rho }}_{41}= & {} -Z_{41} {\rho }_{41} + iR_p (\rho _{11} - \rho _{44}) + iR_d(x,y,z)\rho _{21} - iR_s \rho _{43} \end{aligned}$$

(5)

where $Z_{21}$ $=$ $\Gamma _{21} + i(\Delta _p - \Delta _d)$, $Z_{31}$ $=$ $\Gamma _{31} + i(\Delta _p - \Delta _d + \Delta _c)$ and $Z_{41}$ $=$ $\Gamma _{41} + i\Delta _p$. $\Gamma _{31}$ $=$ $\frac{\gamma _{31} + \gamma _{32}}{2}$, $\Gamma _{41}$ $=$ $\frac{\gamma _{41} + \gamma _{42}}{2}$ and $\Gamma _{21}$ is stated as small coherence dephasing rate. $\gamma _{mn}$ ($m=4,3$, $n=1,2$) denotes the natural decay rate.

Under weak-field approximation, we treat the Rabi frequencies $R_p$ and $R_s$ to the first order, and, $R_c(x,y,z)$ and $R_d(x,y,z)$ to all orders to solve the given set of density matrix equations to obtain the expression of ${\rho }_{41}$. For $\rho _{11}$ $\approx$ $1$, ${\rho }_{41}$ can be presented as

$$\begin{aligned} {\rho }_{41} = \frac{iR_p(Z_{21}Z_{31} + |R_c(x,y,z)|^2) - iR_c^*(x,y,z)R_d(x,y,z)R_s}{Z_{21}Z_{31}Z_{41} + |R_c(x,y,z)|^2Z_{41} + |R_d(x,y,z)|^2Z_{31}} \end{aligned}$$

(6)

Now, we make the following substitutions: $R_p$ $=$ $|R_p|$ $e^{i\phi _p}$, $R_s$ $=$ $|R_s|$ $e^{i\phi _s}$, $R_c(x,y,z)$ $=$ $|R_c(x,y,z)|$ $e^{i\phi _c}$, $R_d(x,y,z)$ $=$ $|R_d(x,y,z)|$ $e^{i\phi _d}$ and ${\rho }_{41}$ $=$ ${\tilde{\rho }}_{41}$ $e^{i\phi _p}$. Thus, We must mention that the magnitudes of the Rabi frequencies are expressed as $R_p$, $R_s$, $R_c(x,y,z)$ and $R_d(x,y,z)$ in the following discussion of the work. Now, we represent

$$\begin{aligned} {\tilde{\rho }}_{41} = \frac{iR_p(Z_{21}Z_{31} + R_c^2(x,y,z)) - iR_c(x,y,z)R_d(x,y,z)R_s e^{i\phi }}{Z_{21}Z_{31}Z_{41} + R_c^2(x,y,z)Z_{41} + R_d^2(x,y,z)Z_{31}} \end{aligned}$$

(7)

where the collective phase $\phi$ $=$ $\phi _s$ + $\phi _d$ - $\phi _c$ - $\phi _p$.

The polarization induced in the probe transition is given by performing the quantum average over the corresponding transition moment [59] as follows

$$\begin{aligned} {{\mathcal {P}}}_p = \epsilon _0 \chi _p \epsilon _p = 2N{\mu }_{14}{\tilde{\rho }}_{41} \end{aligned}$$

(8)

where $\epsilon _0$ being the free-space permittivity and N the electron density. The susceptibility $\chi _p$ is expressed as

$$\begin{aligned} \chi _p = C \chi \end{aligned}$$

(9)

with $C$ $=$ $\frac{N|{\mu }_{13}|^2}{\epsilon _0{\hbar }{\gamma _{3}}}$ as the dimensionless constant [60] and

$$\begin{aligned} \chi = \frac{\gamma _{41}{\tilde{\rho }}_{41}}{R_p} = \gamma _{41} \frac{iR_p(Z_{21}Z_{31} + R_c^2(x,y,z)) - iR_c(x,y,z)R_d(x,y,z)R_s e^{i\phi }}{R_p(Z_{21}Z_{31}Z_{41} + R_c^2(x,y,z)Z_{41} + R_d^2(x,y,z)Z_{31})} \end{aligned}$$

(10)

C is equivalent to the weight factor of optical density of the medium related to the susceptibility of probe response. For the sake of simplicity of the calculation, C is chosen to be unity. We mention that $Im({\chi })$ and $Re({\chi })$ correspond to probe absorption and dispersion evolved in the system, respectively [56]. This is to note here that the second term in the numerator of the expression (10) indicates the appearance of spatially modulated quantum interference through the product of space-dependent Rabi frequencies.

Position information of the atom in 3D space is obtained by measuring space-dependent absorption, where space dependence of absorption is controlled by spatial Rabi frequencies $R_c(x,y,z)$ and $R_d(x,y,z)$ of Eq. (9). For 3D atom localization, the conditional position probability is nothing but the appearance of localization patterns in the subwavelength region in 3D space. Thus, the behaviors of 3D atom localization can be optimised by measuring the probe absorption under the proper setting of system parameters in different schemes.

3 Results and discussion

In this section, we present the position-dependent three-dimensional information of probe absorption $Im(\chi (x, y, z))$ through isosurface profiles drawn by using MATLAB code for the various values of the parameters involved in the system. These system parameters are field detunings, Rabi frequencies of space-dependent coupling fields, and the collective phase. For three different schemes of spatial field arrangements, the exotic profiles of 3D atom localization in sub-wavelength and sub-half-wavelength domains are obtained via the numerical computation based on Eq. (10). The corresponding isosurface plots of the space-dependent probe absorption $Im(\chi (x, y, z))$ are presented in Figs. 2, 3, 4 for the Scheme I, Figs. 5, 6, 7 for the Scheme II, and Fig. 8 for the Scheme III. To find a realistic analogue of the given model in an atomic system, we have chosen the field-induced transitions for Rubidium ${}^{87}$Rb $D_1$ lines ($5^2S_{1/2}$ $\leftrightarrow$ $5^2P_{1/2}$). The atomic states $\vert {1} \rangle$, $\vert {2} \rangle$, $\vert {3} \rangle$, and $\vert {4} \rangle$ correspond to the ${}^{87}$Rb hyperfine levels, $(S)F = 1$, $(S)F = 2$, $(P)F = 1$, and $(P)F = 2$, respectively. The decay parameters used in the model are $\Gamma _{21} = 0, \gamma _{31} = \gamma _{32} = \gamma _{41} = \gamma _{42} = 6$ MHz. Note that ${}^{87}$Rb is selected as a suitable candidate for versatile applications in the field of quantum optics and laser spectroscopy. The Doppler broadening effect can be eliminated by trapping and cooling atoms in a magneto-optical trap. In experimentation with laser-cooled atoms, Rb has vast applicability due to the presence of several ground states with long lifetimes and easy accessibility of the lowest excited state using diode lasers.

Fig. 2

Probe detuning ($\Delta _p$)-induced variation of atom localization profiles (Scheme - I) with isovalue = 0.6. Parameters: a $\Delta _p$ = 12 MHz; b $\Delta _p$ = 13 MHz; c $\Delta _p$ = 14 MHz; and d $\Delta _p$ = 17 MHz. Other common parameters: $R_c$ = $R_d$ = 10 MHz, $R_{d0}$ = 0, $\Delta _d$ = − 10 MHz, $\Delta _c$ = 10 MHz, $\phi = 0$

Fig. 3

Rabi frequency-induced variation of atom localization profiles (Scheme - I) with isovlaue = 0.6. Parameters: a $R_c$ = 5 MHz, $R_d$ = 10 MHz, $R_{d0}$ = 2 MHz, $\Delta _p$ = 14 MHz; b $R_c$ = 14 MHz, $R_d$ = 7 MHz, $R_{d0}$ = 2 MHz, $\Delta _p$ = 14 MHz; c $R_c$ = 5 MHz, $R_d$ = 10 MHz, $R_{d0}$ = 4 MHz, $\Delta _p$ = 16 MHz; and d $R_c$ = 14 MHz, $R_d$ = 7 MHz, $R_{d0}$ = 4 MHz, $\Delta _p$ = 17 MHz. Other common parameters: $\Delta _d$ = − 10 MHz, $\Delta _c$ = 10 MHz, $\phi = 0$

Fig. 4

Collecetive phase ($\phi$)-induced variation of atom localization profiles (Scheme - I) with isovalue = 0.6. Parameters: a $R_{d0}$ = 2 MHz, $\Delta _p$ = 14 MHz, $\phi$ = $\pi$/2; b $R_{d0}$ = 2 MHz, $\Delta _p$ = 14 MHz, $\phi$ = $\pi$; c $R_{d0}$ = 4 MHz, $\Delta _p$ = 17 MHz, $\phi$ = $\pi$/2; and d $R_{d0}$ = 4 MHz, $\Delta _p$ = 17 MHz, $\phi$ = $\pi$. Other common parameters: $R_c$ = 14 MHz, $R_d$ = 7 MHz, $\Delta _d$ = -10 MHz, $\Delta _c$ = 10 MHz

Fig. 5

Rabi frequency-induced variation of atom localization profiles (Scheme - II) with isovalue = 0.06. Parameters: a $R_c$ = 30 MHz, $R_d$ = 2 MHz; b $R_c$ = 4 MHz, $R_d$ = 25 MHz; and c $R_c$ = 25 MHz, $R_d$ = 20 MHz. Other common parameters: $R_{c0}$ = 0, $\Delta _p$ = 40 MHz, $\Delta _d$ = 0, $\Delta _c$ = 40 MHz, $\phi = 0$

Fig. 6

Collecetive phase ($\phi$)-induced variation of atom localization profiles (Scheme - II) with isovalue = 0.06. Parameters: a $R_c$ = 30 MHz, $R_d$ = 2 MHz, $\phi$ = -$\pi$/2; b $R_c$ = 30 MHz, $R_d$ = 2 MHz, $\phi$ = $\pi$/2; and c $R_c$ = 25 MHz, $R_d$ = 20 MHz, $\phi$ = − $\pi$/12; d $R_c$ = 25 MHz, $R_d$ = 20 MHz, $\phi$ = − $\pi$/6. Other common parameters: $R_{c0}$ = 0, $\Delta _p$ = 40 MHz, $\Delta _d$ = 0, $\Delta _c$ = 40 MHz

Fig. 7

Travelling-wave-field ($R_{c0}$)-induced variation (with/without $\phi$) of atom localization profiles (Scheme - II) with isovalue = 0.06. Parameters: a $R_c$ = 30 MHz, $R_{c0}$ = 5 MHz, $R_d$ = 2 MHz, $\phi$ = 0; b $R_c$ = 30 MHz, $R_{c0}$ = 6 MHz, $R_d$ = 2 MHz, $\phi$ = 0; c $R_c$ = 30 MHz, $R_{c0}$ = 3 MHz, $R_d$ = 2 MHz, $\phi$ = $\pi$/2; d $R_c$ = 25 MHz, $R_{c0}$ = 10 MHz, $R_d$ = 14 MHz, $\phi$ = 0; e $R_c$ = 25 MHz, $R_{c0}$ = 12 MHz, $R_d$ = 14MHz, $\phi$ = 0; f $R_c$ = 25 MHz, $R_{c0}$ = 12 MHz, $R_d$ = 14 MHz, $\phi$ = − $\pi$/6; and g $R_c$ = 25 MHz, $R_{c0}$ = 12 MHz, $R_d$ = 14 MHz, $\phi$ = -$\pi$/4. Other common parameters: $\Delta _p$ = 40 MHz, $\Delta _d$ = 0, $\Delta _c$ = 40 MHz

Fig. 8

Travelling-wave-field ($R_{d0}$)-induced variation of atom localization profiles (Scheme - III) with isovalue = 0.06. Parameters: a $R_c$ = 30 MHz, $R_d$ = 2 MHz, $R_{d0}$ = 0.5 MHz; b $R_c$ = 30 MHz, $R_d$ = 2 MHz, $R_{d0}$ = 1 MHz; c $R_c$ = 26.46 MHz, $R_d$ = 2 MHz, $R_{d0}$ = 1 MHz; d $R_c$ = 20 MHz, $R_d$ = 14 MHz, $R_{d0}$ = 0.5 MHz; e $R_c$ = 18.5 MHz, $R_d$ = 14 MHz, $R_{d0}$ = 1 MHz; and f $R_c$ = 18.42 MHz, $R_d$ = 14 MHz, $R_{d0}$ = 1 MHz. Other common parameters: $\Delta _p$ = 40 MHz, $\Delta _d$ = 0, $\Delta _c$ = 40 MHz, $\phi$ = 0

3.1 3D atom localization for the Scheme I

Firstly, for the Scheme I, we discuss the impact of probe detuning ($\Delta _p$) on the 3D atom localization structures and show how a slight change in the probe detuning parameter introduces an appreciable change in probe absorption. For the investigation of 3D localization features in the Scheme I, the other field detunings are kept fixed ($\Delta _d$ = -10 MHz, and $\Delta _c$ = 10 MHz). In Fig. 2, we plot isosurfaces of probe absorption [$Im(\chi (x, y, z))$] as a function of the positions $(k_x, k_y, k_z)$ for different values of the probe field detuning $\Delta _p$ when the Rabi frequencies are set as $R_c$ = $R_d$ = 10 MHz, $R_{d0}$ = 0, and $\phi = 0$. For $\Delta _p$ = 12 MHz, as shown in Fig. 2a, the isosurfaces of probe absorption show two double-layer lantern-like patterns located at the subspace $(x, y, \pm z)$ and the other subspace $(-x, -y, \pm z)$. The only contrast in the two patterns lies in the positions of occurrence of bulging. This budging effect is seen in opposite portions of the two patterns. When the probe field detuning is increased to $\Delta _p$ = 13 MHz, the isosurface patterns of probe absorption transform into single-layer lantern-like localization structures with smaller volumes (see Fig. 2b). Each of the two lantern-like isosurface profiles contains one ellipsoidal structure inside. The ellipsoidal pattern shown in the $(-x, -y, \pm z)$ subspace is significantly larger than that displayed in the $(x, y, \pm z)$ subspace. The further increase in probe detuning ($\Delta _p$ = 14 MHz) leads to the complete disappearance of the ellipsoidal pattern in the subspace $(-x, -y, \pm z)$ and the reduction of the size of another ellipsoidal pattern in the subspace $(x, y, \pm z)$ (see Fig. 2c). As shown in Fig. 2d, for the detuning $\Delta _p$ = 17 MHz, only two narrow single-layer flower vase-like localization structures evolve, where no internal ellipsoidal pattern is present. The investigation shows prominently that the spatial distribution and precision of 3D atom localization are highly sensitive to the detuning of the probe field ($\Delta _p$).

Now, we explore the variation of the spatial dependence of probe absorption on the Rabi frequencies of control lasers ($R_c$, $R_d$, and $R_{d0}$). We report how the localization structures get modified with the magnitudes of these rabi frequencies and present the plots in Fig. 3. For all the plots shown in Fig. 3, the system is set in the zero-phase condition. First, we set the Rabi frequencies as $R_c$ = 5 MHz, $R_d$ = 10 MHz, $R_{d0}$ = 2 MHz, and the probe detuning as $\Delta _p$ = 14 MHz. The corresponding isosurface is exhibited in Fig. 3a. The isosurface looks like a combination of one broad double-layer lantern-like pattern appearing in the subspace $(x, y, \pm z)$ and one narrow single-layer lantern-like pattern in the other subspace $(-x, -y, \pm z)$. When only $R_c$ and $R_d$ are changed to the values 14 MHz and 7 MHz, respectively, a drastic change occurs in the localization characteristics in Fig. 3b. A ellipsoid-like structure with one side-arm truncated occurs in the $(x, y, \pm z)$ subspace along with its truncated part. A tiny sphere-like pattern emerges in the subspace, $(-x, y, -z)$. For Fig. 3c, the parameter condition of Fig. 3a is modified with an increase in $R_{d0}$ and $\Delta _p$ ($R_{d0}$ = 4 MHz, $\Delta _p$ = 16 MHz). This change leads to the disappearance of the narrow single-layer lantern-like pattern in the subspace $(-x, -y, \pm z)$ when compared to the localization features shown in Fig. 3a. A slight modulation in the parameter condition of Fig. 3b ($R_{d0}$ = 4 MHz, $\Delta _p$ = 17 MHz) shapes the isosurface profile in a rugby ball-like localization pattern in the octant ((x, y, z)) (see Fig. 3d). Thus, we can achieve 100% probability to detect the atom in a sub-half-wavelength regime. Also, according to the field configuration of $R_c(x,y,z)$ and $R_d(x,y,z)$, it is noticeable that the modulation of the extent of localization structures along the z-axis is controlled by the Rabi frequency,$R_c(x,y,z)$. In contrast, their size can be tuned in the $x-y$ plane by changing the Rabi frequency, $R_d(x,y,z)$.

We have explored and shed light on the contribution of the collective phase to the optical properties of the closed-loop atomic system. We have found that the collective phase ($\phi$) acts as a main control knob in shaping coherent structures of 3D localization. To explore the findings in this direction, we have set the magnitudes of the Rabi frequencies ($R_c$ = 14 MHz, and $R_d$ = 7 MHz) the same for all the graphs of Fig. 4. For Fig. 4a, we select $R_{d0}$ and $\Delta _p$ same as those set for Fig. 3b i.e. $R_{d0}$ = 2 MHz, $\Delta _p$ = 14 MHz with the phase, $\phi$ = $\pi$/2. The introduction of $\pi$/2 phase modifies the localization pattern (Fig. 3b for $\phi$ = 0) and shapes it in an inverted calabash-like pattern appearing in the subspace $(x, y, \pm z)$. For the phase $\phi$ = $\pi$ (Fig. 4b), the truncated ellipsoid-like structure evolves in an inverted manner in the subspace $(x, y, \pm z)$ when compared to the localization structures of Fig. 3b. In addition, a clear distinction lies in the change of the position of occurrence of the small sphere-like pattern. In this case, this sphere-like structure appears at the centre. In order to carry on further study, we choose the parameter condition of Fig. 3d with $\phi$ = $\pi$/2 for plotting Fig. 4c. Two rugby ball-like coherent structures of localization with unequal shape emerge in sub-half-wavelength regime (x, y, z). The bigger structure occurs in the coordinate space (x, y, z), whereas the smaller is located in the $(x, y, -z)$ subspace. When the system suffers a change of the collective phase by an amount of $\pi$, the single rugby ball-like localization pattern is observable in the coordinate space $(x, y, -z)$. In this way, we again attain 100% atom localization probability in the sub-half-wavelength domain, as noticed in Fig. 3d. This is to mention here that the collective phase can be easily controlled by using a phase-locked technique [61, 62] for possible experimentation.

We provide a detailed explanation of the localization behaviours in the context of spatially modulated probe absorption involving both one-photon and three-photon excitations. By analysing Eq. (10) we note that the probe absorption is expressed as the sum of two terms. The first term directly corresponds to probe absorption originating as a result of one-photon excitation. This excitation pathway is related to the transition, $\vert {1} \rangle$ $\rightarrow$ $\vert {4} \rangle$ coupled via the probe field ($R_p$). The second term appears due to the indirect contribution of the three-photon excitation mechanism: $\vert {1} \rangle$ $\rightarrow$ $\vert {3} \rangle$, $\vert {3} \rangle$ $\rightarrow$ $\vert {2} \rangle$, then $\vert {2} \rangle$ $\rightarrow$ $\vert {4} \rangle$ coupled by the fields with the Rabi frequencies, $R_s$, $R_c(x, y, z)$, and $R_d(x, y, z)$, respectively. We must mention that the occurrence of the three-photon excitation term, as expressed in Eq. (10), originates from three-field quantum interference. The behaviour of the probe absorption is nothing but the additive contribution of single-photon and multi-photon excitation mechanisms. The phase ($\phi$) resulting from the mentioned interference effect plays a crucial role in modulating the nature of spatial probe absorption. When the phase is $\pi$/2, the contribution of spatially modulated interference effect aids in manifesting two rugby ball-like patterns in two distinct subspaces of the corresponding position-dependent probe absorption patterns. In contrast, when the phase is set to 0 or $\pi$, spatially modulated interference manifests in the reverse manner in comparison to that occurred for $\phi = \pi$/2. As a result, the suppression of probe absorption is found in one of the subspaces. These findings have established the fact that the collective phase-coherence directly influences the probability distribution of finding the atom in different sub-half-wavelength regions. Thus, the collective phase plays a pivotal role in a closed-loop four-level system in controlling high-precision atom localization.

3.2 3D atom localization for the Scheme II

Similar studies on 3D atom localization are extended with the Scheme II. The control parameters are the amplitudes of Rabi frequencies ($R_c$ and $R_d$), collective phase, and the Rabi frequency of the traveling-wave field ($R_{c0}$). To accomplish the whole study on the Scheme II, we set the same values field detuning parameters: $\Delta _p$ = 40 MHz, $\Delta _d$ = 0, and $\Delta _c$ = 40 MHz. First of all, we investigate the impact of the field strengths of the spatial field configurations with Rabi frequencies $R_c(x,y,z)$ and $R_d(x,y,z)$ on the 3D atom localization behaviour and plot the 3D localization profiles in Fig. 5. For drawing the isosurface profiles, we set three different combinations of $R_c$ and $R_d$: (a) $R_c$ = 30 MHz, $R_d$ = 2 MHz; (b) $R_c$ = 4 MHz, $R_d$ = 25 MHz; (c) $R_c$ = 25 MHz, $R_d$ = 20 MHz. The common parameters are: $R_{c0}$ = 0, $\phi = 0$. In Fig. 5a, the parameter conditions ($R_c$ is much larger than $R_d$) tune the system to produce two identical empty barrel-shaped isosurfaces in the (x, y, z) and $(-x, -y, -z)$ subspaces. Then $R_c$ is set to a much lower value than that of $R_d$ to plot Fig. 5b. The coherent localization patterns change drastically to two circular flat discs appearing in the same subspaces as displayed in Fig. 5b. Two identical two sphere-like patterns emerge in the same subspaces for moderate but close values of $R_c$ and $R_d$ (see Fig. 5c). It is clear from the localization structures that the change in the amplitudes of $R_c$ and $R_d$ induces a significant modification of corresponding isosurfaces. However, no prominent change is observed in the probability of finding the atomic position.

Like the Scheme I, we study the effect of the collective phase ($\phi$) on the 3D atom localization in Scheme II and show the 3D localization behaviours in Fig. 6. For Fig. 6a and b, we have introduced the collective phase ($\phi$) with values -$\pi$/2 and $\pi$/2, respectively, keeping the other parameter conditions of Fig. 5a unchanged. Previously, we have presented a detailed analysis to explain $\phi$-induced changes in the localization spectra. Based on the above discussion, we note that the collective phase ($\phi$ = -$\pi$/2) results in the space-dependent interference that leads to the reduction of sizes of two empty barrel-shaped isosurfaces in the (x, y, z) and the $(-x, -y, -z)$ subspaces as observed in Fig. 6a when compared to the localization patterns shown in Fig. 5a. The sign change in $\phi$ only results in the modification of positions of localization structures in Fig. 6b without affecting the isosurface profiles. To extend the study for a separate combination of $R_c$ and $R_d$ ($R_c$ = 25 MHz, $R_d$ = 20 MHz as set for Fig. 5c) we apply $\phi$ = -$\pi$/12 and -$\pi$/6 and present the corresponding localization structures in Fig. 6c and d, respectively. In Fig. 6c, the collective-phase-induced spatial variation of interference leads to the evolution of two sphere-like same isosurfaces with two identical bangle-like isosurfaces. One of the two sphere-like patterns occurs in the (x, y, z) subspace leaving the other in the spatially inverted subspace, i.e., $(-x, -y, -z)$. There is no exception in the case of bangle-like isosurfaces where one is in the $(-x, -y, z)$ subspace with another in the $(x, y, -z)$ subspace. If we compare the localization profile of Fig. 6c with that of Fig. 5c ($\phi$ = 0), the probability of finding the atom becomes reduced. When the phase is set to a more negative value ($\phi$ = -$\pi$/6), only the two bangle-like isosurfaces reshape into two identical doughnut-like localization patterns (see Fig. 6d).

We turn our focus to investigate the impact of the travelling wave ($R_{c0}$) on the spatial distribution of the atom localization in the absence or presence of the collective phase ($\phi$) and plot the 3D localization characteristics in Fig. 7. We initiate the study with the parameter condition of Fig. 5a in the presence of the travelling-wave field ($R_{c0}$ = 5 MHz) and present the isosurface profile in Fig. 7a. The introduction of travelling-wave field results in a significant reduction in the size of the empty barrel-shaped isosurface in the subspace $(-x, -y, -z)$, when compared to that structure given in Fig. 5a and finally shapes in a thin and small rugby ball-like structure. On the contrary, it is shown that the other similar pattern of barrel-shaped isosurface in the subspace (x, y, z) gets amplified. If $R_{c0}$ gets intensified and set at 6 MHz (Fig. 7b), the size of the barrel-shaped isosurface in the subspace (x, y, z) is increased more, and the small rugby ball-like structure disappears. Thus, in this scheme, this parameter condition facilitates the attainment of 100% atom localization in the sub-half-wavelength domain. With the application of the travelling wave of lower strength ($R_{c0}$ = 3 MHz) accompanied by the introduction of phase ($\phi$ = $\pi$/2) we increase the precision of 100% atom localization in the sub-half-wavelength domain of the $(x, y, -z)$ subspace (Fig. 7c). To draw the spatial patterns of atom localization we choose another set with the Rabi frequencies ($R_c$ = 25 MHz, and $R_d$ = 14 MHz) of two space-dependent coupling fields, and plot the localization profiles in Fig. 7d–g. For Fig. 7d, we set the value of $R_{c0}$ = 10 MHz. The localization structures appear as a truncated ellipsoidal isosurface in the coordinate space (x, y, z) and a tiny spherical structure in $(-x, -y, -z)$ subspace. When the strength of $R_{c0}$ is increased to 12 MHz, the 100% sub-half-wavelength atom localization in the (x, y, z) subspace is found attainable again for the Scheme II and exhibited in Fig. 7e. The shape of the truncated ellipsoid is found to increase. The size increase may be noted as a direct consequence of the extinction of the tiny spherical structure in the spatially inverted subspace. The study is further extended to explore how the single localization structure evolves in the presence of the collective phase ($\phi$), and we plot the localization profiles in Fig. 7f and g. If the parameter condition of Fig. 7e includes the phase condition ($\phi$ = -$\pi$/6), two localization structures are generated in Fig. 7f. One truncated ellipsoidal isosurface appears in the (x, y, z) subspace and the bangle-like isosurface is observed in the $(x, y, -z)$ subspace. With the increase in the phase ($\phi$ = -$\pi$/4) the number of localization structures becomes three as observed in Fig. 7g. A new spherical isosurface evolves at the central position with the other isosurfaces mentioned in Fig. 7f. But the contrast lies in the size enhancement of the bangle-like isosurface and size reduction of the truncated ellipsoidal isosurface. The results highlight that the proper tuning of the amplitude of the Rabi frequency of travelling-wave field and the value of the collective phase leads to high-precision 3D atom localization through the effective modulation of space-dependent quantum interference.

3.3 3D atom localization for the Scheme III

In an attempt to explore suitable parameter conditions required for high-precision 3D atom localization, we propose a new scheme (Scheme III). The Scheme III is a modified form of the Scheme II. In the Scheme III, the travelling-wave field ($R_{d0}$) is introduced in the spatial field arrangement of $R_d(x,y,z)$ instead of other field arrangement of $R_c(x,y,z)$. So, $R_{c0}$ is found absent in the present scheme. To report the results, we select the parameter condition of Fig. 5a with $R_{d0}$ = 0.5 MHz and present the corresponding plot in Fig. 8a. In comparison to the localization structures shown in Fig. 5a, the application of $R_{d0}$ affects the localization patterns resulting in the vertical elongation of the empty barrel shaped isosurface present in the (x, y, z) subspace and the vertical contraction of the same residing in the $(-x, -y, -z)$ subspace. Further increase in the traveling wave part of $R_d(x,y,z)$ ($R_{d0}$ = 1 MHz) causes more vertical elongation of the empty barrel-shaped isosurface in the (x, y, z) subspace and the complete disappearance of isosurface in the $(-x, -y, -z)$ subspace (see Fig. 8b). It is to note that single localization structure is achievable in the Scheme III, which confirms the signature of 100% probability of finding the atom in the (x, y, z) subspace i.e. in the sub-half-wavelength region. The value of $R_c$ is then tuned to 26.46 MHz for Fig. 8c. A radical change is noticed in the volume of the localization structure (a very tiny ellipsoid) assuring a significant enhancement in the precision of 3D atom localization in the sub-half-wavelength domain. The spatial limit of resolution of the localization pattern is better than $\lambda$/10 along the z- axis and $\lambda$/50 along the x- and y- axes. To verify the contribution of $R_{d0}$ to the probe absorption profile as well as the spatial patterns of localization, we select the constant amplitude of Rabi frequency ($R_d$ = 14MHz) and plot the localization structures in Fig. 8d–f. To display the localization feature in Fig. 8d, we choose the values of the Rabi frequencies of the coupling field and the traveling-wave field as 20 MHz ($R_c$) and 0.5 MHz ($R_{d0}$), respectively. As a result, two spherical isosurfaces emerge in Fig. 8d. The bigger one is in the (x, y, z) subspace and the smaller one is in the $(-x, -y, -z)$ subspace. Here also, a fine tuning of $R_c$ (18.5 MHz) and the increment in $R_{d0}$ to 1 MHz cause the 100% probability of atom localization in the (x, y, z) subspace as shown in Fig. 8e. This feature guarantees the sub-half-wavelength 3D localization with high precision. When we further tune the $R_c$ value to 18.42 MHz and plot the corresponding figure in Fig. 8f, the 100% probability of ultra-high precision 3D atom localization in the sub-half-wavelength regime (in the (x, y, z) subspace) is assured with a spatial resolution having limit better than $\lambda$/40.

Influence of quantum interference effects in the 3D localization patterns: Now we have investigated how the 3D isosurface profiles are influenced by quantum interference effects. To gain physical insights, we have used the expression (10) and taken the imaginary part of susceptibility ($\chi$). The expression of the spatially modulated probe absorption is recast as

$$\begin{aligned} Im(\chi (x,y,z)) = T_1(x,y,z) + T_2(x,y,z) \end{aligned}$$

(11)

where

$T_1(x,y,z) = \gamma _{41}\frac{(A + R_c^2(x,y,z) -R_sR_c(x,y,z)R_d(x,y,z)cos\phi /R_p)P}{P^2+Q^2}$ and

$T_2(x,y,z) = -\gamma _{41}\frac{(R_sR_c(x,y,z)R_d(x,y,z)sin\phi /R_p - B)Q}{P^2+Q^2}.$

Here, $A = \Gamma _{21}\Gamma _{31} - (\Delta _p - \Delta _d)(\Delta _p - \Delta _d + \Delta _c)$,

$B = \Gamma _{21}(\Delta _p - \Delta _d + \Delta _c) + \Gamma _{31}(\Delta _p - \Delta _d)$,

$P = \Gamma _{41}A - \Delta _pB + \Gamma _{41}R_c^2(x,y,z) + \Gamma _{31}R_d^2(x,y,z)$, and $Q = \Delta _pA + \Gamma _{41}B + \Delta _pR_c^2(x,y,z) + (\Delta _p - \Delta _d + \Delta _c)R_d^2(x,y,z)$.

It is evident from the expression (11) that $Im(\chi (x,y,z))$ is the linear superposition of two terms $T_1(x,y,z)$ and $T_2(x,y,z)$. Both of them exhibit the appearance of explicit quantum interference effects due to the product of space-dependent Rabi frequencies in the numerator of each term. The explicit interference terms are modulated by the collective phase-coherence effect. When the value of the collective phase $\phi$ is equal to 0 ($\pi$/2), the term $T_1$ ($T_2$) can play a major role in forming the localization pattern in the absence of any travelling-wave field. But, for $\phi$ = $\pi$, the explicit interference term of $T_1$ has a negative contribution in comparison to that considered for $\phi$ = 0, whereas the explicit interference term of $T_2$ has a null contribution to the probe absorption. In the presence of Rabi frequencies of the travelling-wave fields in terms $R_c(x,y,z)$ and $R_d(x,y,z)$ i.e., in general, $R_c(x,y,z)$ = $R_{c0}$ + $R_c$ (sin(kx) + sin(ky) + sin(kz)) and $R_d(x,y,z)$ = $R_{d0}$ + $R_d$ (sin(kx) + sin(ky) + sin(kz)), the terms like $|R_c^2(x,y,z)|$ and $|R_d^2(x,y,z)|$ contribute to the interference effect through the terms $R_{c0}$ $R_c$ (sin(kx) + sin(ky) + sin(kz)) and $R_{d0}$ $R_d$ (sin(kx) + sin(ky) + sin(kz)). We call it as implicit interference effect, which plays a vital role in shaping the localization pattern when the travelling-wave field is incorporated into the system.

We have examined the individual contributions of $T_1$ and $T_2$ in shaping the 3D localization structures shown in Figs. 2, 3, 4, 5, 6, 7 and 8. In all the plots of Fig. 2, we have observed the dominant role of $T_1$ over $T_2$ because of the zero value of $\phi$. For Fig. 3, the inclusion of the travelling-wave field ($R_{d0}$) leads to the origination of implicit interference effect. Here also, the contribution of $T_1$ is very significant in comparison to the small perturbative influence of $T_2$. In Fig. 3d, the larger value of $R_{d0}$ intensifies the implicit interference effect in such a way that $T_2$ contributes to the spatial probe absorption with a negative magnitude. The 100$\%$ detection probability of the atom is the direct consequence of this contribution. For all localization features shown in Fig. 4, the main responsible factor is $T_1$ whereas $T_2$ contributes little to shaping the spatial probe absorption profiles. In Fig. 4d, for $\phi$ = $\pi$/2, the magnitude of $T_2$ is ranging from negative to positive values whereas, for $\phi$ = $\pi$, the magnitude of $T_2$ becomes negative. The competitive nature of variations of $T_1$ and $T_2$ with positive magnitudes of $T_1$ and negative magnitudes of $T_2$ results in the appearance of a single localization pattern in the sub-half-wavelength domain. In Fig. 5a, it is noted that the terms $T_1$ and $T_2$ have comparable contributions to the spatial probe absorption even in the absence of any travelling-wave field and for the zero value of the collective phase. In this case, the localization features are the manifestation of the combined effect of $T_1$ and $T_2$ without domination of any of the two terms. However, the $T_1$ term is specifically responsible for the plots shown in Fig. 5b and c. For a non-zero phase value (Fig. 6a and b), comparable contributions of $T_1$ and $T_2$, as mentioned for Fig. 5a, are observed. On the other hand, Fig. 6c and d express a similar kind of dominance of $T_1$ like Fig. 5b and c. In Fig. 7, the comparable magnitudes of $T_1$ and $T_2$ accompanied by a competitive interplay lead to the shaping of localization structures in the presence of the travelling-wave field ($R_{c0}$) and for non-zero values of $\phi$. These isosurface profiles can be envisioned as the resultant effect of explicit quantum interference and implicit interference effects. We now shift our focus to illustrate the role of $T_1$ and $T_2$ in shaping the isosurface profiles presented in Fig. 8. The addition of the travelling-wave field ($R_{d0}$) with other system parameters generates the implicit interference effect in the system. Along with the comparable magnitudes of $T_1$ and $T_2$ with their competitive variation over 3D space, the increase in the magnitude of $R_{d0}$ makes the implicit interference effect predominant and leads to the origination of a single localization pattern in the sub-half-wavelength regime (See Fig. 8b). Finally, the tuning of the $R_c$ value makes the magnitude of $T_1$ purely positive and the magnitude of $T_2$ purely negative. This parameter condition in Fig. 8c enhances the competitive interplay between the $T_1$ and $T_2$ terms and leads to high-precision and high-resolution 3D atom localization. A similar argument concerned with the single localization structure (100$\%$ probability of detecting an atom) is applicable to the localization features shown in Fig. 8e and f.

4 Conclusion

In summary, the proposed schemes focus on achieving three-dimensional (3D) atom localization through the measurement of space-dependent absorption of a weak probe field in a closed four-level double-$\Lambda$-type atomic system. The study employs three spatially varying field configurations based on different combinations of the orthogonal standing waves and travelling-wave fields. It is displayed that 3D atom localization patterns are obtained by varying field detunings, Rabi frequencies of standing-wave and travelling-wave fields, and the collective phase of the driving fields. The proposed schemes lead to the attainment of high-precision and high-resolution 3D atom localization in sub-wavelength and sub-half-wavelength domains by adjusting specific system parameters. Various exotic localization patterns, such as double-layer lantern-like, single-layer lantern-like, single-layer flower vase-like, inverted calabash-like, rugby ball-like, doughnut-like, bangle-like, empty barrel-shaped, sphere-like, ellipsoid-like, and truncated ellipsoid-like structures, can be achieved in our model. On the basis of bare-state analysis of quantum interference effects (explicit and implicit quantum interference effects), we have introduced an expression by using the imaginary part of the spatial probe absorption as a summation of two terms. By investigating the interplay of these two terms containing quantum interference effects, we have qualitatively discussed the appearance of localization patterns obtained in Figs. 2, 3, 4, 5, 6, 7 and 8. Notably, we have shown that the 100% detection probability of finding the atom can be obtained with a limit of spatial resolution better than $\lambda$/40. The proposed 3D atom localization in different schemes finds its potential applications in atom nanolithography and laser cooling. The unique localization patterns, as obtained in the present work, could enhance the capabilities of making precision devices like 3D optical microscopy along with the imaging of atoms.